New Insights into Folding, Misfolding and Nonfolding Dynamics of a WW Domain

Abstract

Intermediate states in protein folding are associated with formation of amyloid fibrils, which are responsible for a number of neurodegenerative diseases. Therefore, prevention of the aggregation of folding intermediates is one of the most important problems to overcome. Recently, we studied the origins and prevention of formation of intermediate states with the example of the Formin binding protein 28 (FBP28) WW domain. We demonstrated that the replacement of Leu26 by Asp26 or Trp26 (in ~15% of the folding trajectories) can alter the folding scenario from three-state folding, a major folding scenario for the FBP28 WW domain (WT) and its mutants, toward two-state or downhill folding at temperatures below the melting point. Here, for a better understanding of the physics of the formation/elimination of intermediates, (i) the dynamics and energetics of formation of β-strands in folding, misfolding and nonfolding trajectories of these mutants (L26D and L26W) is investigated; (ii) the experimental structures of WT, L26D and L26W are analyzed in terms of a kink (heteroclinic standing wave solution) of a generalized discrete nonlinear Schrödinger equation. We show that the formation of each β-strand in folding trajectories is accompanied by the emergence of kinks in internal coordinate space as well as a decrease in local free energy. In particular, the decrease in downhill folding trajectory is ~7 kcal/mol, while it varies between 31–48 kcal/mol for the three-state folding trajectory. The kink analyses of the experimental structures give new insights into formation of intermediates, which may become a useful tool for preventing aggregation.

Graphical Abstract

Introduction

Protein folding is a rapid and complex process that is difficult to characterize because folding does not refer to the progressive pathway of a single conformation. Instead, it pertains to interconversions among ensembles of conformations in a back-and-forth progression from the non-native to the native state. In addition, the non-native and native states themselves may consist of a large ensemble of conformations, interconverting at a rapid rate, and characterized by basins with many minima in each state. The two-state model, deduced from calorimetric experiments,¹ is one of the widely used models for the description of folding of single-domain proteins consisting of the non-native and the native state separated by the energetically unfavorable transition state. In this scenario, at the folding-transition temperature (T_f), the non-native (fully unfolded) and native (fully folded) conformations are equally populated, that is, the equilibrium ensemble contains their 50–50% mixture. This means that, for a folding scenario characterized by single-exponential kinetics, a protein goes directly from the unfolded to the native state without detectable intermediates on the way and, hence, makes it difficult to extract mechanistic information. The origins and heights of the barriers separating the unfolded and native states have been studied both computationally and by experiment. For example, Thirumalai² showed that, at the atomic level, the free-energy barrier height scales as N^1/2, where N is the number of residues; while Akmal and Munoz,³ by investigating six single domain proteins ranging from 56 to 107 residues, found that the barrier height, determined by the relative contribution from local and nonlocal interactions to protein stability, is only a few kcal/mol; and it arises due to the fact that in the folding reaction of two-state proteins the conformational entropy changes at a faster rate than the free energy of stabilization.

Many experimental studies^4–8 have shown that a folding pathway is not always defined in terms of a two-state model. Proteins can fold through intermediate states or undergo one-state (downhill) folding. This scenario of folding was pointed out by Poland and Scheraga 55 years ago.⁹ On the basis of the classical Landau theory for critical transitions, Munoz and Sanchez-Ruiz⁶ showed that the appearance of a peak in heat-capacity curves can very well be explained in terms of a continuous order parameter (enthalpy) at various temperatures and not the competition between the well-defined folded and unfolded state. An analysis of experimental heat-capacity curves showed that the density of states (as a function of enthalpy) has either one maximum or two maxima, indicating either barrierless folding (e.g., for 1BBL) or the existence of a barrier between the folded and unfolded states (e.g., for thioredoxin).⁶ By using simplified atomistic and coarse-grained models, Knott and Chan¹⁰ demonstrated that sharp heat-capacity peaks and steeply increasing sigmoidal curves of the temperature dependence of the radius of gyration generally indicate the presence of a barrier (cooperative folding), while low and broad peaks and less steeply increasing curves of the radius of gyration (such as obtained for 1BBL) indicate barrierless (noncooperative) folding. A marginal cooperativity exhibited in downhill folding causes non-concerted structural disassembly. Characterizing the structural properties of the ensemble of configurations at different temperatures with multidimensional NMR, Munoz¹¹ was able to reconstruct the folding process of the protein, interpreting all the spectroscopic data with statistical mechanical models that included the most relevant partially folded conformations, and determined that downhill folding is characterized by decoupling between structural elements. Moreover, it should be noted that during downhill folding, all the intermediate structures between the denatured and native states are potentially detectable by experiment, which has led to methods that distill mechanistic information from conventional ensemble experiments, such as monitoring how thermal denaturation depends on the structural probe,¹² analyzing heat capacity thermograms in terms of low-dimensional free-energy surfaces,¹³ etc.

Apart from the two-state and downhill models, the observation of two phases in the kinetic progress curves required consideration of a third state, therefore, a three-state model was introduced. The conventional three-state folding model is one in which there is an intermediate state on the pathway from the unfolded to native state, although in some studies¹⁴ a three-state model was defined as a triangular folding mechanism with an energetically trapped intermediate. Kubelka et al.¹⁵ proposed a three-state model in which the interconversion between the intermediate state and native state is much faster than that between the intermediate state and unfolded state. Therefore, the intermediate state lies on the folded side of the major free-energy barrier. Also, the free-energy barrier calculated in this study ranged from 1.6 to 2.0 kcal/mol. It should be noted that, based on recent studies,^16,17 the widely-accepted notion that single- and double-exponential kinetics may emerge during two- and three-state (or multistate) folding, respectively, may not always be the case. We have recently shown that the origins of single- and double-exponential kinetics and their correlations with two- and three-state folding scenarios are related to the relative barrier heights between the various states. In particular, single-exponential kinetics can emerge even in three-state (or multistate) folding when one of the free-energy barriers is much higher than the other.¹⁶ Moreover, it was recently demonstrated that the downhill folding can produce double-exponential kinetics.¹⁷

Protein-folding intermediates on or off the main folding pathway are a common route to the formation of oligomers and amyloid fibrils, which are linked to protein-misfolding diseases^18–22 such as Alzheimer’s²³, Parkinson’s²⁴, Huntington’s²⁵ and Creutzfeldt-Jakob’s²⁶ diseases. Therefore, prevention of the aggregation of folding intermediates is one of the most important problems to surmount. The triple-β-stranded WW domain from the Formin binding protein 28 (FBP28) (PDB ID: 1E0L)²⁷ is a member of the WW domain family. The WW domains, in general, have been the subject of extensive theoretical^{16,21,28−39} and experimental^{5,17,20,27,40−49} studies because of their small size, biological importance, and fast-folding kinetics. From the folding point of view, the FBP28 WW domain (WT) is a very interesting system to study because of its biphasic folding kinetics.^5,28,29

It should be noted that a folding mechanism of the FBP28 was disputable for a long time because of its complexity. There are not only differences between experimental and theoretical results but also, different experiments that reveal different folding scenarios. In particular, closer to its physiological melting temperature and in the absence of a denaturant, experiments by Nguyen et al.⁵ using tryptophan-fluorescence detection revealed slow concentration-independent biphasic kinetics attributed to a folding intermediate. The conclusion regarding three-state folding was challenged by Ferguson et al.,²⁰ who observed that the FBP28 WW domain readily forms fibrils under similar experimental conditions; hence, the biphasic kinetics has been attributed to an off-pathway intermediate that is a gateway for oligomer formation. Later, our theoretical studies^16,31,32,38 confirmed experimental findings⁵ that three-state folding is a main folding scenario for the FBP28 WW domain and strand-crossing hydrophobic cluster of residues Tyr11, Tyr19, and Trp30 is not associated with the formation of intermediates.

Recently, based on the findings^28,29 that biphasic folding kinetics of the FBP28 WW domain can be caused by slower formation of turn 2 (Arg24 and Thr25) contacts relative to the remainder of the protein, and surface-exposed hydrophobic contact (Tyr21 with Leu26) enforcing the correct registry of hairpin 2, we have determined the structures of six new mutants [L26D (PDB ID: 2N4R), L26E (PDB ID: 2N4S), L26W (PDB ID: 2N4T), E27Y (PDB ID: 2N4U), T29D (PDB ID: 2N4V), and T29Y (PDB ID: 2N4W)] by high-resolution NMR spectroscopy, and performed extensive studies of folding dynamics of these systems⁵⁰ with the coarse-grained united-residue (UNRES) force field.^30,33,51,52 It was found that three-state folding is a major folding scenario for all six mutants, however, two-state and downhill folding scenarios were also identified in ~15% of the folding trajectories for L26D and L26W. We also discovered that for formation of intermediates, it is crucial how each hairpin, especially hairpin 1, folds. If both hairpins are formed by the Matheson and Scheraga mechanism⁵³ (also known as a zipper model⁵⁴), then the system may fold through a downhill or two-state folding scenario. If hairpin 1 is formed by the hydrophobic collapse mechanism,⁵⁵ then an intermediate state emerges, and the protein folds through a three-state folding scenario.

Moreover, we tried to elucidate the structural basis for a three-state, downhill and two-state folding by scrutinizing the structures of all mutants and the FBP28 WW domain determined by high-resolution NMR spectroscopy.⁵⁰ For example, for L26D we found that the D26 side chain is consistently oriented toward the Y21 hydroxyl, which suggests the presence of a water-mediated hydrogen bond that stabilizes that specific orientation allowing some “flexibility” during the correct registry of turn 2. In other words, it may either speed up (downhill folding) or slow down (three-state folding) the correct registry of turn 2 in contrast to the FBP28 WW domain. In L26W mutant, the W26 substitution presented contacts more similar to the WT, with the orientation of their side chain in the calculated structures resembling that of L26. We observed contacts between the indole of W26 and the aromatic ring of Y21, but the calculated structures result in several orientations of the W26 ring that are compatible with the experimental restraints and do not affect the turn structure; hence, their correlation with different folding scenarios is not straightforward.

To corroborate these findings (especially for L26W), we performed molecular dynamics (MD) simulations with an all-atom force field along with T-jump experiments for L26D and L26W.⁵⁶ In that study,⁵⁶ our findings from earlier work⁵⁰ were validated both theoretically and experimentally. Therefore, it is important to find out what governs the L26W mutant to alter the folding scenario from three-state folding toward downhill folding.

To answer this question and provide new insights into biphasic kinetics, in this study, we (i) examine three-state and downhill folding, as well as nonfolding of L26D and L26W (Figure 1) in terms of internal coordinates (local motions) and the local free energies along the entire sequence, as well as with principal components (global motions);^{31,32,57–59} and (ii) investigate the experimental structures of the FBP28 WW domain, L26D and L26W from another, complementary point of view. In particular, instead of analyzing individual interactions that contribute to the formation of folded structure, model-independent principles which are based on symmetry are looked for. We suggest that all the physical forces, no matter how strong or weak they are, combine together to give rise to a particular type of protein dynamics, described by a generalized version of the discrete nonlinear Schrödinger (DNLS) equation; and propose that various parametrizations of a kink, or heteroclinic standing wave solution, of a generalized version of the DNLS equation to be utilized as the basic modular building blocks of folded proteins.^60–69 It should be noted that, in most of the Refs. [60–66,68,69] the epithet topological (dark) soliton was used, but here kink is preferred. This choice highlights that the potential in the DNLS equation displays spontaneous breakdown of a discrete symmetry, and the kink describes the ensuing domain wall;^70–74 in the case of a folded protein an individual kink corresponds to a super-secondary structure such as a helix-loop-helix or strand-loop-strand motif. Also, the kink considered here has no direct relationship with the concept of Davydov’s soliton.⁷⁵ The kink in a protein is a purely topological (geometric) structure, and the Davydov’s soliton, in turn, is associated with collective excitations travelling along a chain (perturbations of electron density). The kinks discussed here can be formally related to the spontaneous formation of intrinsic localized modes (ILMs) in proteins.⁷⁶ Indeed, ILMs are large excitations localized on four successive residues and can be viewed as a pair of kink and anti-kink.⁷⁷ However, ILMs occur transiently with a life-time on a picosecond time scale and are characteristic of the unfolded protein state. In the present work, the kinks do not occur in pairs, are stable structures localized on four to five residues, and are characteristic of the native-state.

Figure 1.

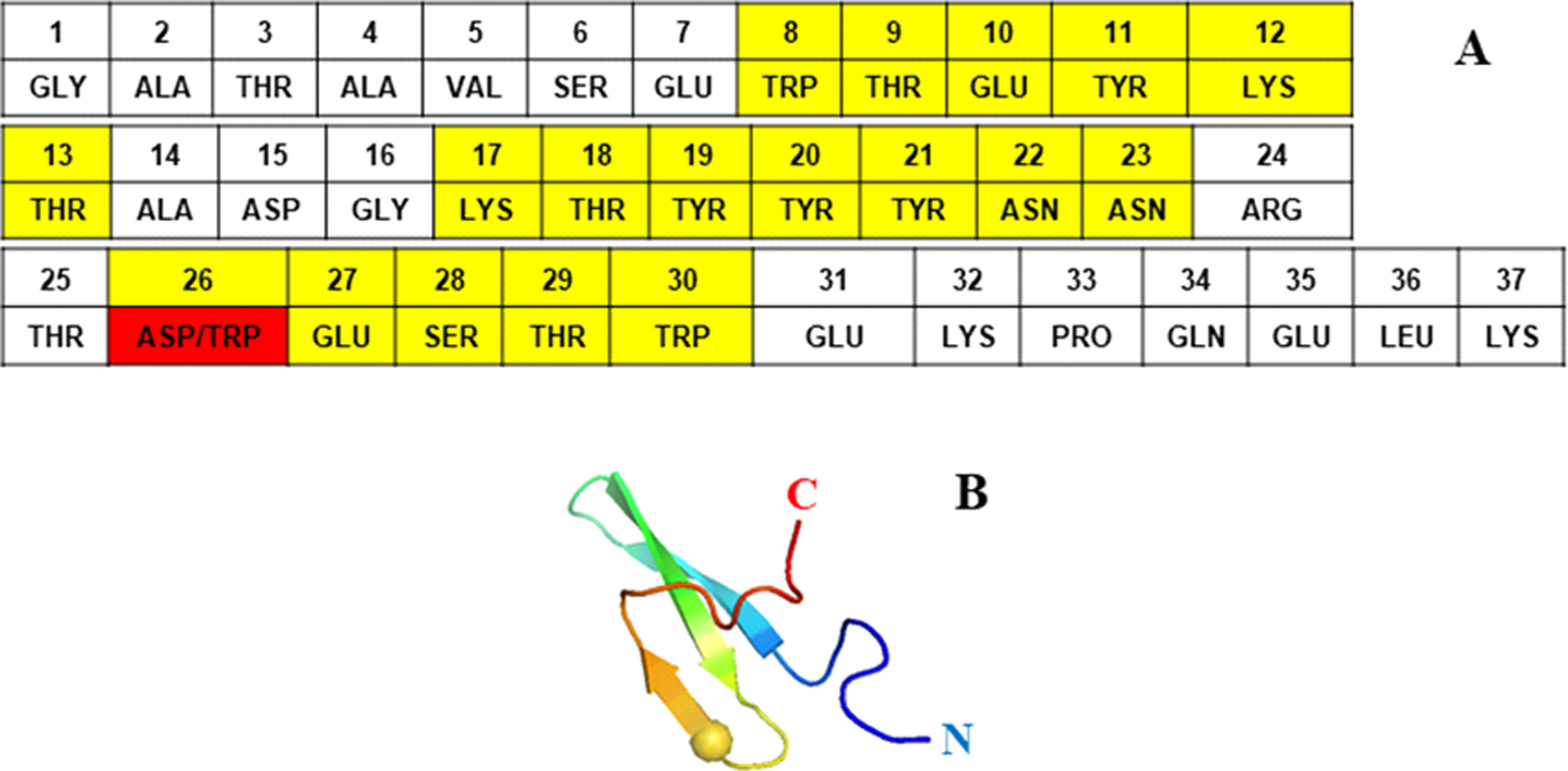
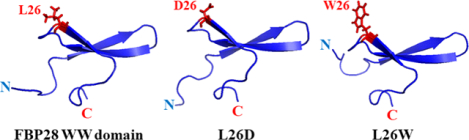
Amino acid sequence of the triple β-strand WW domain from the Formin binding protein 28 (FBP28) (1E0L) (panel A), and experimental NMR-derived structure of 1E0L (panel B). The mutated residue is highlighted in red color (panel A) and represented by sphere (panel B). Residues forming the β-strands are highlighted in yellow color.

One hundred and twenty (for L26D and WT) and ninety-six (for L26W) canonical MD trajectories, generated with the coarse-grained UNRES force field,^30,33,51,52 were run at five and four different temperatures, respectively (24 MD trajectories, with ~ 1.4 μs UNRES time and corresponding effectively to ~ 1.4 ms actual time of each, at each temperature), which were below, very close to, and above the melting temperatures. The timescale of UNRES is extended by about three orders of magnitude because of averaging out the fast motions of the secondary degrees of freedom⁷⁸ and scaling down water friction in MD simulations by a factor of 1,000. Hence, the statistics generated by UNRES is several orders of magnitude larger than those obtained by all-atom MD simulations. The trajectories, in which the mutants fold with three-state and downhill scenarios and do not fold, have been selected and analyzed in terms of the backbone virtual-bond angle θ and the backbone virtual-bond-dihedral angle γ of each residue (see the UNRES model of polypeptide chains in Figure 2), the local free energies,^{30,33,50–52} and principal component analysis.^{31,32,57–59} Experimental structures of FBP28 WW domain, L26D and L26W examined in terms of kinks are determined in Refs. [27,50].

Figure 2.

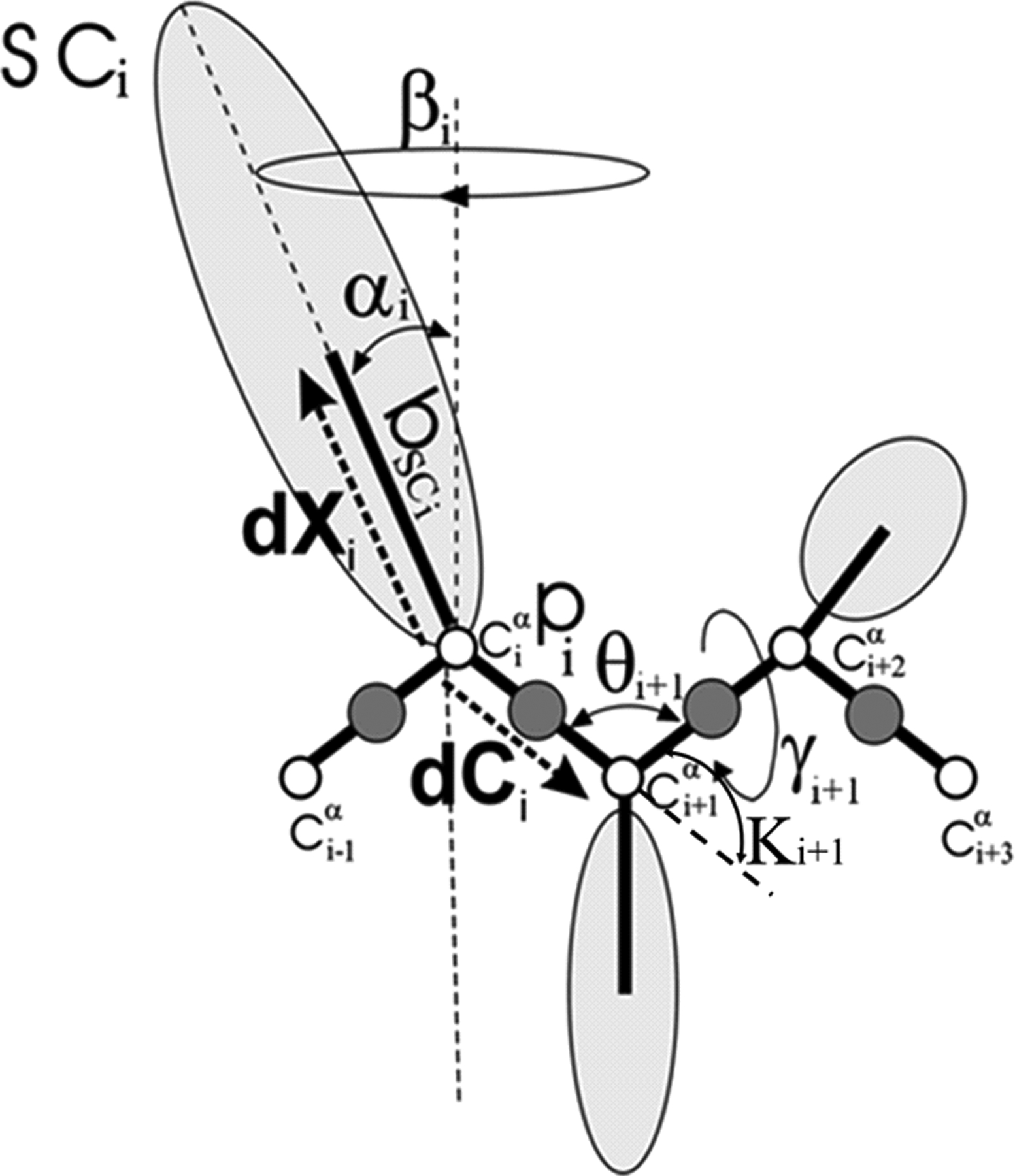
The UNRES model of polypeptide chains. The interaction sites are peptide-bond centers (p), and side-chain ellipsoids of different sizes (SC) attached to the corresponding α-carbons with different “bond lengths”, b_SC. The α-carbon atoms are represented by small open circles. The equilibrium distance of the C^α…C^α virtual bonds is taken as 3.8 Å, which corresponds to planar trans peptide groups. The geometry of the chain can be described either by the virtual-bond vectors dC_i (C^α_i…C^α_i+1), i = 1, 2,…, N - 1 and dX_i (C^α_i…SC_i), i = 2, 3,…, N - 1 (represented by thick dashed arrows), where N is the number of residues, or in terms of virtual-bond lengths, backbone virtual-bond angles θ_i, i = 2, 3,…, N - 1, backbone virtual-bond-dihedral angles γ_i, i = 2, 3,…, N - 2, and the angles α_i and β_i, i = 2, 3,…, N - 1 that describe the location of a side chain with respect to the coordinate frame defined by C^α_i-1, C^α_i and C^α_i+1. The angles κ_i used here are complements of the θ_i angles, i.e., π − θ_i.

Methods

UNRES Force Field.

Detailed descriptions of the UNRES force field and its parametrization are available in references^33,51,52 and at http://www.unres.pl. Therefore, it will be only briefly outlined here. In the UNRES force field,^33,51,52 a polypeptide chain is represented as a sequence of α-carbon (C^α) atoms with united peptide groups (p) located halfway between the consecutive C^α atoms and united side chains (SC) attached to the C^α atoms (Figure 2). The force field has been derived as the potential of mean force (PMF), also termed the restricted free energy function (RFE), of a system of polypeptide chain(s) in solvent, where all degrees of freedom except the coordinates of the C^α atoms and SC centers have been averaged out. The effective energy function contains local and site-site interactions, as well as multibody terms, which have been obtained by decomposing the PMF into factors corresponding to clusters of interactions within and between coarse-grained sites.⁵¹ The SC-SC interaction potentials implicitly include the contribution from solvation.^33,51,52 The force field was calibrated to reproduce the structure and thermodynamics of small model proteins. The force field used in this study was calibrated with the α-helical protein 1ENH and the β-strand protein 1E0L.

Kink and Protein Backbone Geometry.

Since detailed descriptions of kinks of the DNLS equation are available in references,^60–69 the main aspects of it will be only outlined here. Protein geometry is described in terms of the C^α backbone. The C^α atoms coincide with the vertices that are denoted by r_i with i = 1,…, N. At each vertex, there is an orthonormal triplet (n_i, b_i, t_i) with the unit tangent vector,

$${\mathbf{t}}_{\mathit{i}}=\frac{{\mathbf{r}}_{\mathit{i}+1}-{\mathbf{r}}_{\mathit{i}}}{\left|{\mathbf{r}}_{\mathit{i}+1}-{\mathbf{r}}_{\mathit{i}}\right|}$$ (1)

the unit binomial vector,

$${\mathbf{b}}_{\mathit{i}}=\frac{{\mathbf{t}}_{\mathit{i}-1}\times {\mathbf{t}}_{\mathit{i}}}{\left|{\mathbf{t}}_{\mathit{i}-1}\times {\mathbf{t}}_{\mathit{i}}\right|}$$ (2)

and the unit normal vector

$${\mathbf{n}}_{\mathit{i}}={\mathbf{b}}_{\mathit{i}}\times {\mathbf{t}}_{\mathit{i}}$$ (3)

This defines the discrete Frenet frame^63,67 at the vertex r_i. The C^α backbone bond angles κ_i and torsion angles γ_i shown in Figure 2 can be defined in terms of the frame vectors,

$${\kappa }_{i+1,i}\equiv {\kappa }_i=\text{arccos}\left(t_{i+1}\cdot t_i\right),$$ (4)

$${\gamma }_{i+1,i}\equiv {\gamma }_i=\text{sgn}\left[\left(b_{i-1}\times b_i\right)\cdot t_i\right]\cdot \text{arccos}\left(b_{i+1}\cdot b_i\right)$$ (5)

Conversely, when the values of the bond and torsion angles are all known, the discrete Frenet equation

$$\left(\begin{array}{c}{\mathbf{n}}_{i+1}\\ {\mathbf{b}}_{i+1}\\ {\mathbf{t}}_{i+1}\end{array}\right)={\left(\begin{array}{ccc}\text{cos\hspace{0.17em}}\kappa \text{\hspace{0.17em}cos\hspace{0.17em}}\gamma & \text{cos\hspace{0.17em}}\kappa \text{\hspace{0.17em}sin\hspace{0.17em}}\gamma & -\text{sin\hspace{0.17em}}\kappa \\ -\text{sin\hspace{0.17em}}\gamma & \text{cos\hspace{0.17em}}\gamma & 0\\ \text{sin\hspace{0.17em}}\kappa \text{\hspace{0.17em}cos\hspace{0.17em}}\gamma & \text{sin\hspace{0.17em}}\kappa \text{\hspace{0.17em}sin\hspace{0.17em}}\gamma & \text{cos\hspace{0.17em}}\kappa \end{array}\right)}_{i+1,i}\left(\begin{array}{c}{\mathbf{n}}_i\\ {\mathbf{b}}_i\\ {\mathbf{t}}_i\end{array}\right)$$ (6)

Computes the frame at vertex i + 1 from the frame at vertex i. Once all the frames are known, the entire chain is obtained by

$$r_k={\sum }_{i=0}^{k-1}\left|r_{i+1}-r_i\right|\cdot t_i.$$ (7)

Unlike the tangent vector t_i, the normal and binormal vectors (n_i, b_i) do not appear in Eq. (7). Therefore, if these vectors are simultaneously rotated around the vector t, the C^α geometry remains intact and only the way how it is framed changes. In particular, rotation by π constitutes the discrete ℤ₂ gauge transformation,

$${\gamma }_i\to \left\{\begin{array}{c}{\gamma }_i\mathrm{ }-\mathrm{ }\pi ,\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }if\mathrm{ }\mathrm{ }{\gamma }_i\mathrm{ }>\mathrm{ }0\\ {\gamma }_i\mathrm{ }+\mathrm{ }\pi ,\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }if\mathrm{ }\mathrm{ }{\gamma }_i\mathrm{ }<\mathrm{ }0\end{array}\right.$$

$${\kappa }_k\to -{\kappa }_k\text{ for all }k\ge i,$$ (8)

which was proved to be very convenient in analyzing the protein loop structure.^60–69

It should be noted that regular protein secondary structures correspond to definite values of (κ_i, γ_i). For example, for the standard right-handed α-helix

$$\left\{\begin{array}{c}\kappa \approx \frac{\pi }{2}\\ \gamma \approx 1\end{array}\right.$$ (9)

and for the standard β-strand

$$\left\{\begin{array}{c}\kappa \mathrm{ }\approx \mathrm{ }\mathrm{ }1\\ \gamma \approx \pm \pi \end{array}\right.$$ (10)

with the angles in radians.

The variables κ_i and γ_i are mutually connected by the equations of motion, determined by the atomic level interactions along the protein chain. The following is the Landau-Ginzburg-Wilson free energy F of the protein backbone in terms of the discrete virtual bond and torsion angles:^60–69

$$F=-{\sum }_{i=1}^{N-1}{2\kappa }_{i+1}{\kappa }_i+{\sum }_{i=1}^N\left\{{2\kappa }_i^2+\lambda {\left({\kappa }_i^2-m^2\right)}^2+\frac{q}{2}{\kappa }_i^2{\gamma }_i^2-p{\gamma }_i+\frac{r}{2}{\gamma }_i^2\right\}$$ (11)

where λ, q, p, r, and m are parameters. The detailed derivation of Eq. (11) can be found in Refs. [60,61,66,67]; here it suffices to state that this free energy can be shown to relate to the long-distance limit that describes the full microscopic energy of a folded protein in the universal sense of Refs. [79–82]. As such, it does not explain the details of the (sub)atomic level mechanisms that give rise to protein folding.

In order to determine the kink content of the backbones, at first, we should define positions of the inflection points (kink centers). We can find the inflection points by analyzing the three-dimensional structure (protein topology) and the experimental values of the angles (κ_i, γ_i). Inflection points correspond to the centers of kinks. Then, the angular spectrum should be reconstructed using the ℤ₂ transformation at the kink centers (it should be noted that the three-dimensional shape of the protein is invariant under ℤ₂ transformation). After that, for a given kink structure, we look for a minimum of global energy using a combination of simulated annealing and gradient descent methods. For this propose a special toolkit for protein structure visualization and analysis was developed [https://protoin.ru/propro/index.php].⁶⁸

In short, the search for the minimum energy occurs in the following order. The virtual-bond angles κ are first extended to negative values, using the ℤ₂ gauge symmetry (8). The virtual-bond-dihedral angles γ are then expressed as functions of the virtual-bond angles κ

$${\gamma }_i\left[\kappa \right]=\frac{p}{r+q{\kappa }_i^2}\equiv \frac{u}{1+v{k}_i^2}$$ (12)

with u = p/r and v = q/r. By inserting Eq. (12) into Eq. (11), the virtual-bond-dihedral angles γ are eliminated and the following system of equations for the motion of the virtual-bond angles κ is obtained:

$${\kappa }_{i+1}=2{\kappa }_i-{\kappa }_{i-1}+\frac{dV\left[\kappa \right]}{d{\kappa }_i^2}{\kappa }_i\left(i=1,\dots ,N\right),$$ (13)

where κ₀ = κ_{N + 1} = 0 and

$$V\left[\kappa \right]=\frac{p}{r+q{\kappa }^2}+2\left(1-\lambda m^2\right){\kappa }^2+\lambda {\kappa }^4,$$ (14)

where the familiar structure of the generalized DNLS equation is recognized.^60–69 The kink solution to Eq. (13) can be constructed numerically by following the iterative procedure of Ref. [61]. But its explicit form, until now, has not been found in terms of elementary functions. However, an excellent approximation is obtained by naively discretizing the heteroclinic standing wave solution to the continuum nonlinear Schrödinger equation^60–69

$${\kappa }_i=\frac{b\mathrm{ }exp\left[{\sigma }_1\left(i-s\right)\right]+a\mathrm{ }exp\left[-{\sigma }_2\left(i-s\right)\right]}{exp\left[{\sigma }_1\left(i-s\right)\right]+exp\left[-{\sigma }_2\left(i-s\right)\right]}$$ (15)

and with γ_i[κ] evaluated from Eq. (12). Here, s is a parameter that determines the center of the kink. The a, b ∈ [0,π] mod(2π) are parameters which determine the amplitude of the variation of κ and the asymmetry of the inflection regions; they correspond to the minima of the potential energy contribution V [κ] in Eq. (14). The parameters σ₁ and σ₂ are related to the inverse of the range of the kink. It should be noted that, in the case of proteins, the values of a, b are determined entirely by the adjacent helices and strands. Far away from the center of the kink

$${\kappa }_i\to \left\{\begin{array}{c}b\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }mod\left(2\pi \right)\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }i>s\\ a\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }mod\left(2\pi \right)\mathrm{ }\mathrm{ }\mathrm{ }i<s\end{array}\right.$$ (16)

and according to Eqs. (9) and (10), the asymptotic values

$${\kappa }_i\approx \pi /2\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{o}\mathrm{r}\mathrm{ }\mathrm{ }\mathrm{ }-\pi /2\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }{\kappa }_i\approx 1\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{o}\mathrm{r}\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }-1$$ (17)

correspond to the α-helix or β-strand, respectively. In order to satisfy the monotonic character of the profile of Eq. (15), the experimentally measured values of κ_i have to vary monotonically along the amino-acid sequence. Otherwise, a multiple of 2π is added to the experimental values. This does not affect the backbone geometry because κ_i^’s are defined mod (2π). The σ₁ and σ₂ are intrinsically specific parameters for a given loop. But they specify only the length of the loop, not its shape which is defined by the functional form of Eq. (15), and in the case of a and b, they are combinations of the parameters in Eq. (14).

In Eq. (12) for the virtual-torsion angles, γ_i, there are only two independent parameters u and v. As a consequence, the profile of γ_i is determined entirely by the profile of κ_i, and on the structure of the adjacent regular secondary structures.

Finally, we introduce the concept of folding index of a protein backbone. The formation, evolution and structure of a loop along a folding protein can be monitored in terms of topologically determined folding indices. Folding index is defined by following equation:

$${Ind}_f=\frac{\Gamma }{\mathrm{\pi }}$$ (18)

where

$$\mathrm{\Gamma }={\sum }_{i=n_1+2}^{n_2-2}\left\{\begin{array}{c}{\gamma }_{i,i+1}-{\gamma }_{i-1,i}-2\pi \mathrm{ }\mathrm{ }\mathrm{ }if\mathrm{ }{\gamma }_{i,i+1}-{\gamma }_{i-1,i\mathrm{ }}>\pi \\ {\gamma }_{i,i+1}-{\gamma }_{i-1,i}-2\pi \mathrm{ }\mathrm{ }\mathrm{ }if\mathrm{ }{\gamma }_{i,i+1}-{\gamma }_{i-1,i\mathrm{ }}<-\pi \\ {\gamma }_{i,i+1}-{\gamma }_{i-1,i}\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathit{\text{otherwise}}\mathrm{ }\end{array}\right.$$ (19)

Here, Γ is the total rotation angle (in radians) that the projections of the C^α atoms of the consecutive loop residues make around the north pole. The folding index is a positive integer when the rotation is counterclockwise, and a negative integer when the rotation is clockwise. The folding index classifies loop structures and entire folded proteins in terms of its values.⁶⁷

Molecular Dynamics Simulations.

For each mutant, a total of 120 canonical MD simulations were carried out with the UNRES force field. The Berendsen thermostat⁸³ was used to maintain constant temperature. The time step in molecular dynamics simulations was δt = 0.1 mtu (1 mtu = 48.9 fs is the “natural” time unit of molecular dynamics⁸⁴) and the coupling parameter of the Berendsen thermostat was τ = 1 mtu. A total of ~ 3×10⁸ MD steps were run for each trajectory, starting from the fully extended structure.

Results and Discussion

Protein Folding, Misfolding and Nonfolding in Internal Coordinate Space.

Three types of trajectories of the L26D and L26W mutants of the FBP28 WW domain were examined here, in which (i) the protein folds through the intermediate state (i.e., exhibits misfolding during the folding), (ii) the protein exhibits downhill folding (i.e., folds without encountering any significant free energy barrier), and (iii) the protein does not fold. Because the systems fold at the beginning of the trajectories (especially in downhill folding), in order to better illustrate the results, ~ 90% of the trajectories in which the protein remains in the native state were truncated.

One of the main aims of this study was to illustrate how protein folding, misfolding and nonfolding is reflected on internal coordinates and local free energy. As in our previous studies, the protein main chain is described by the positions of the C^α atoms. Assuming constant average virtual bond distances between successive C^α atoms, the protein main chain is entirely described by the backbone virtual-bond angles θ_i between two successive virtual bonds [($C_{i-1}^{\alpha }, C_i^{\alpha }$) and ($C_i^{\alpha }, C_{i+1}^{\alpha }$)], and the backbone virtual-bond-dihedral angles γ_i built from three successive virtual bonds [($C_{i-1}^{\alpha }, C_i^{\alpha }),\mathrm{ }(C_i^{\alpha }, C_{i+1}^{\alpha }$) and ($C_{i+1}^{\alpha }, C_{i+2}^{\alpha }$)]. The contour plots depicted in Figure 3 show how the angles θ_i (panels A, E, I), the angles γ_i (panels B, F, J), and corresponding local free energies of the backbone angles θ_i (panels C, G, K), are changing in the course of time when the protein undergoes three-state folding (panels A – D), downhill folding (panels E – H), and no folding (panels I – L). The root-mean-square deviations (RMSDs) vs time illustrated on panels D, H, L describe how the system folds or does not fold. It should be noted that γ angles explore the neighborhood of 180° in the native state, therefore, in order to avoid confusion, the range of fluctuations of the γ angles, which is between [−180°; 180°], was shifted to [0°; 360°] in panels B, F, J.

Figure 3.

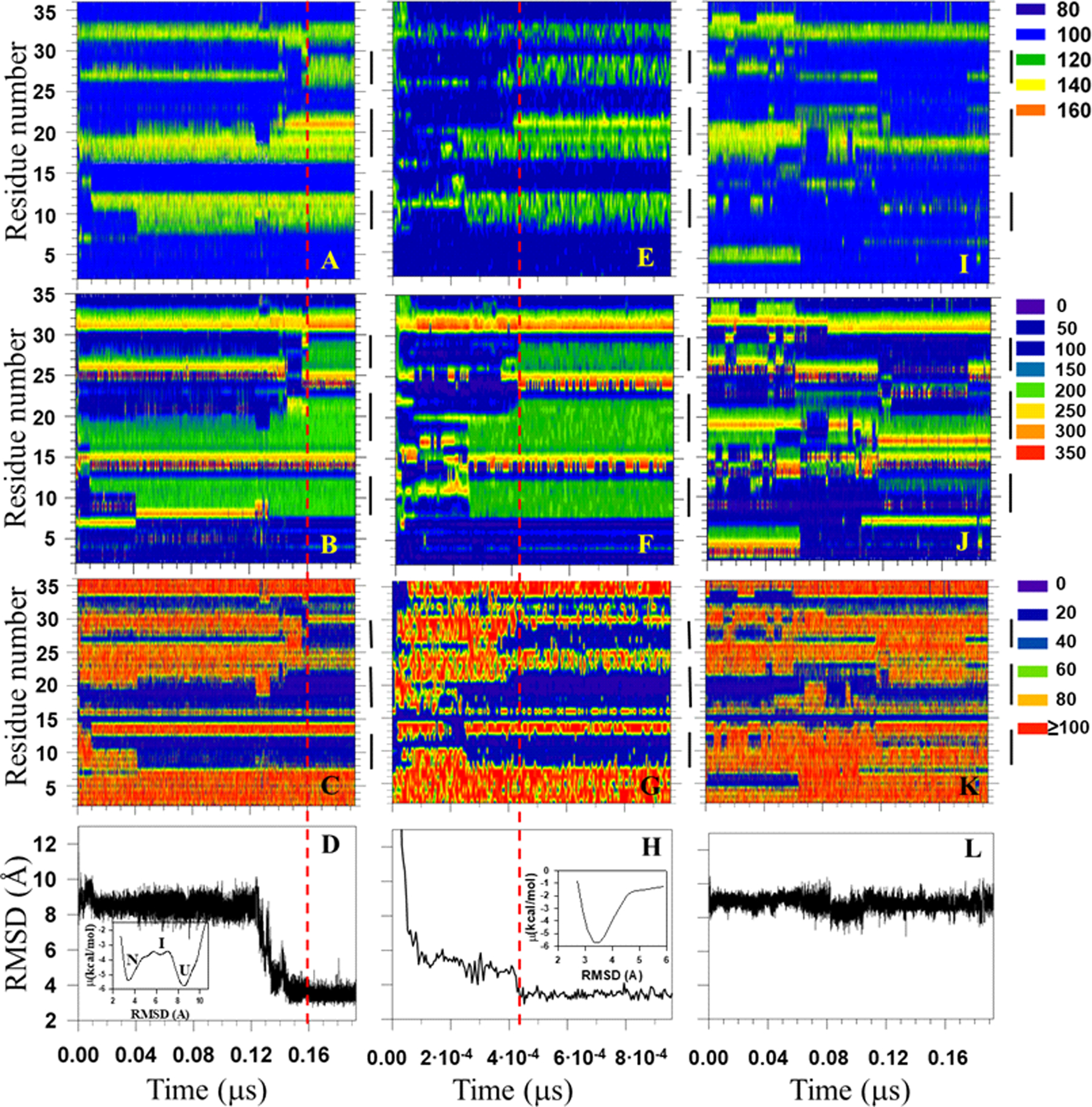
Filled contour plots of the backbone virtual-bond angles θ (in degree) (panels A, E, I), backbone virtual-bond-dihedral angles γ (in degree) (panels B, F, J), and local free energies (in kcal/mol) (panels C, G, K) vs time for three-state folding trajectory of L26D mutant (panels A – C), downhill folding trajectory of L26W mutant (panels E – G), and nonfolding trajectory of L26D mutant (panels I – K). The vertical black lines on each panel correspond to the β-strand regions. The root-mean-square deviations (RMSDs) vs time for three-state folding, downhill folding, and nonfolding trajectory are presented in panels D, H and L, respectively. The insets in panels D and H represent the free-energy profiles (in kcal/mol) as functions of RMSD. Vertical red dashed lines indicate the folding time of L26D and L26W.

The results show a clear correlation between θ, γ angles and local free energies. These variables describe, in detail, how protein folds and why protein does not fold. In particular:

(i). Three-state folding.

Based on the RMSD vs time plot (panel D), the protein remains unfolded during the first 0.12 μs (8Å < RMSD < 10Å), then starts folding (0.12μs < Time < 0.16μs), forming an intermediate state, and reaches native state at 0.16 μs (RMSD ≤ 4Å). The contour plots of θ and γ angles (panels A and B) indicate that the formation of all three β-strands starts much earlier in the beginning of trajectory, while the protein is still in an unfolded state. However, they reach complete formation at different times (values of θ and γ angles in β-strands fluctuate around 120° and 180°, respectively; these regions are represented by green color in the contour plots). In particular, the β-strand 1 forms completely at 0.04 μs; ~ 90% of the β-strand 2 also forms at 0.04 μs, although it reaches complete formation at ~ 0.14 μs; the β-strand 3 forms completely last at 0.16 μs. Corresponding local free energies adequately change with the formation of β-strands (panel C). From these results, we can conclude that one of the reasons for the formation of an intermediate state and misfolding is a slow formation of the third β-strand. These findings are in harmony with results obtained in earlier studies.^{5,16,28,29,31,32,38,50,56} Moreover, for clear demonstration of three-state folding, the free-energy profile as a function of RMSD was calculated (see the inset in panel D). It should be noted that because of averaging out the fast motions of the secondary degrees of freedom, at the course-grained level, the free-energy barriers, illustrated in the inset of panel D, are lower than those at the atomic level.

(ii). Downhill folding.

The RMSD vs time plot, presented in panel H, indicates that the protein only needed ~4.3×10⁻⁴ μs to fold (400 times less time than in the three-state folding case). As in three-state folding, in downhill folding the β-strand 1 forms completely first (~2.5×10⁻⁴ μs), and the β-strands 2 and 3 form completely together at ~4.3×10⁻⁴ μs. Although all three β-strands do not form together, the protein still undergoes downhill folding. The point is that the time difference between the formation of β-strand 1 and β-strands 2 and 3 is very small (~1.8×10⁻⁴ μs) and not enough for the formation of an intermediate state, which can be corroborated by the free-energy profile as a function of RMSD calculated for the 0.19 μs portion of the trajectory (see the inset in panel H). The changes in local free energies in the course of time are in agreement with the changes of θ, γ angles.

(iii). Protein nonfolding.

The RMSD of the MD trajectory, illustrated in panel L, fluctuates between ~ 8 – 10 Å, which indicates that the protein does not fold in the given time. The contour plots of the θ and γ angles, and local free energies, as expected, show very “chaotic behavior”; in particular, β-strand 1 practically does not form at all, instead, transient incomplete α-helical structures can be observed, the formation of β-strand 3 is transient and incomplete, only β-strand 2 forms almost completely. Moreover, β-strand structures appear in the regions of N and C termini.

These results indicate that the formation of β-strand 1 might be crucial for formation of β-strands 2 and 3, and for folding entirely.

It should be noted that local free energies of the backbone dihedral angles γ_i vs time are not shown here, because they behave very similar to ones illustrated in Figure 3.

Apart from studying, in detail, the representative trajectories of the L26D and L26W mutants, it is of interest to know “a general picture” of the folding dynamics of these mutants. Therefore, we joined folding trajectories at different temperatures and calculated the free-energy profiles as functions of RMSD for both mutants. In addition, for comparison, we did the same calculations for the FBP28 WW domain. The results are shown in Figure S1 (Supporting Information). First, it should be noted that, because of both mutants fold with the three-state folding scenario in ~85% of trajectories, none of the free-energy profiles exhibit downhill folding. It is clear that three-state folding in WT is more pronounced than in L26D and L26W, especially at low temperatures. With the increase of temperature intermediate states in all systems gradually disappear, which is in agreement with experiments.^5,56 These results indicate that although mutations did not change the folding scenario in all trajectories, they lowered the barriers, which enable both systems to fold faster and in some trajectories (~15%) without barriers.

Local Free Energies.

As was mentioned in the Introduction, the mechanisms of three-state and downhill folding scenarios were elucidated in our recent study.⁵⁰ In particular, in three-state folding, hairpin 1 forms by a hydrophobic collapse mechanism,⁵⁵ which causes significant delay of formation of both hairpins, especially hairpin 2, and facilitates the emergence of an intermediate state. While in downhill folding both hairpins are formed by the Matheson–Scheraga mechanism⁵³ much faster than in three-state folding. It is of interest to know how local free energies change during the formation of β-strands and hairpins for both mechanisms as the purpose of the present work is to identify why the mutations favor one mechanism relative to another.

Figure 4 illustrates how the free energies of the TRP8-THR13 (panels A, D, G), LYS17-ASN23 (panels B, E, H), ASP26-TRP30 (panels C, I), and TRP26-TRP30 (panel F) segments of L26D and L26W, computed by using the UNRES effective energy function, which has the sense of a free energy,^30,33,51,52 change when the formation of β-strands takes place in three-state folding (panels A-C) and downhill folding (panels D-F), as well as when β-strands do not form fully in nonfolding trajectory (panels G-I). The red horizontal dashed lines in panels D-F correspond to the average UNRES energy averaged over “before” and “after” energy jumps in the downhill folding trajectory, whereas the red dashed curves in panels A-C and G-I correspond to the average UNRES energy averaged over the three-state folding and nonfolding trajectories (it should be noted that the UNRES energy was not averaged over the downhill trajectory due to its shortness).

Figure 4.

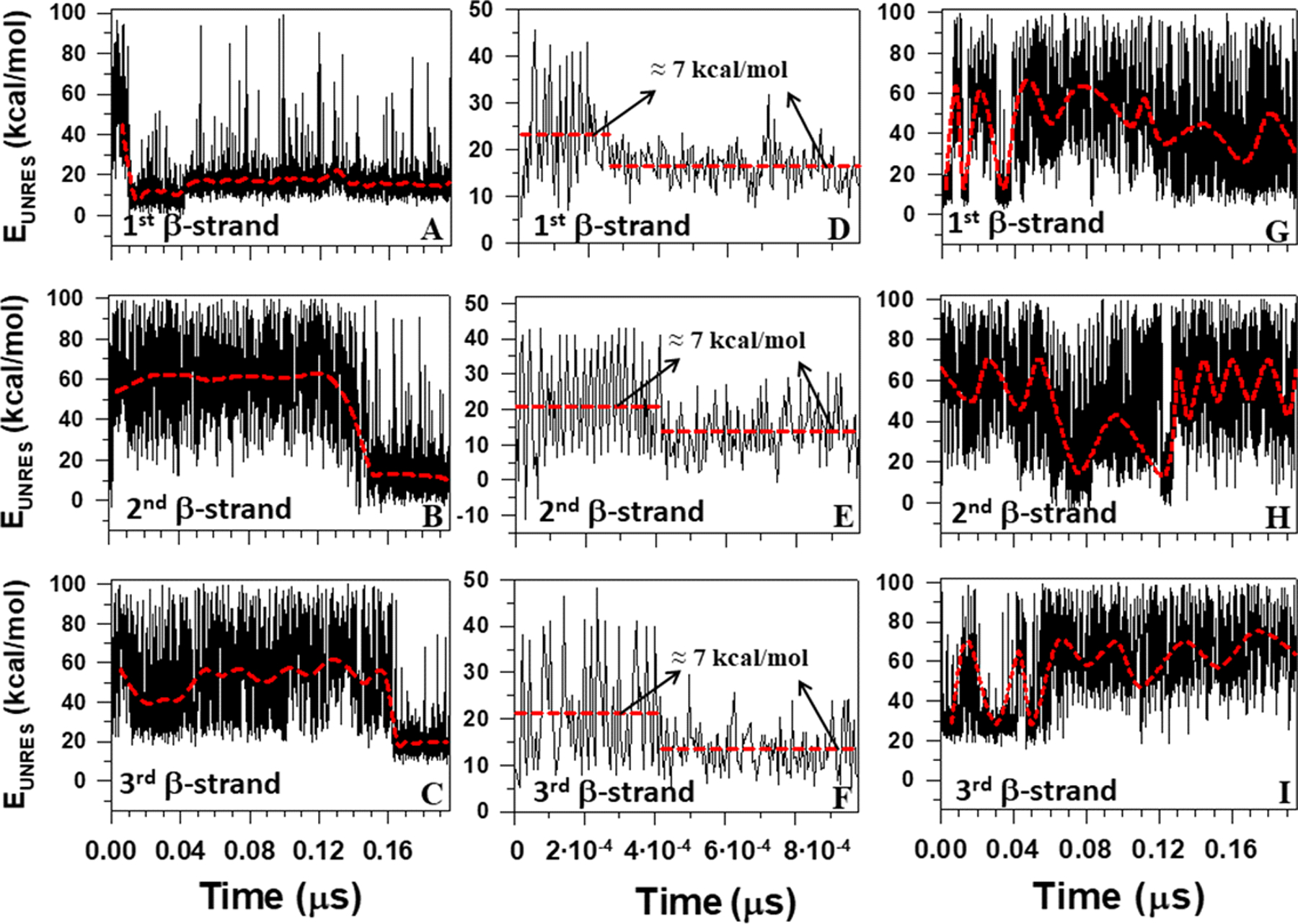
The UNRES energy change during the formation of the first, second and third β-strands for three-state folding trajectory of L26D mutant (panels A-C), downhill folding trajectory of L26W mutant (panels D-F), and nonfolding trajectory of L26D mutant (panels G-I).

It can be seen that in the downhill folding trajectory the local free energy decreases by ~ 7 kcal/mol when β-strands form [Figure 4(D–F)], while the average values of the free-energy decrease during the full formation of β-strands in the three-state folding trajectory are much larger and vary between 31 and 48 kcal/mol [Figure 4(A–C)]. These findings agree with the well-known notion that, for many proteins, only a modest free-energy gain (generally only −3 to −7 kcal/mol) is associated with the correct folding of a protein compared with its innumerable potential misfolded states.⁸⁵ Similar results were reported in a recent study,⁶⁷ in which the dynamics and energetics of the formation of loops in the 46-residue N-terminal fragment of the B-domain of staphylococcal protein A were studied. In particular, it was shown that during the formation of the loops, and consequently the kinks, the free energy over the putative kink region increased by ~ 7 kcal/mol.⁶⁷ Interestingly, 7 kcal/mol is very close to the free energy of dissociation of one phosphate residue from adenosine triphosphate (ATP).⁸⁶ The difference between the previous and presented work is that the UNRES simulations in the previous study⁶⁷ were started from the full right-handed α-helix to obtain a clear picture of the loop (consequently kink) formation, whereas in the presented study the MD simulations are started from the fully extended structure and formation of β-strands are investigated. In the three-state folding trajectory, a hydrophobic collapse is associated with large changes (31–48 kcal/mol) in free energy, which indicates an irreversibility of the process. In other words, if this free energy jump occurs, the protein misfolds as a consequence. It is important to note that the formation of β-strands is accompanied by the emergence of kinks in the internal coarse-grained coordinate space (θ,γ) [as an example, see Figure 5, which is a 3-D representation of Figure 3 (A, E and I)].

Figure 5.

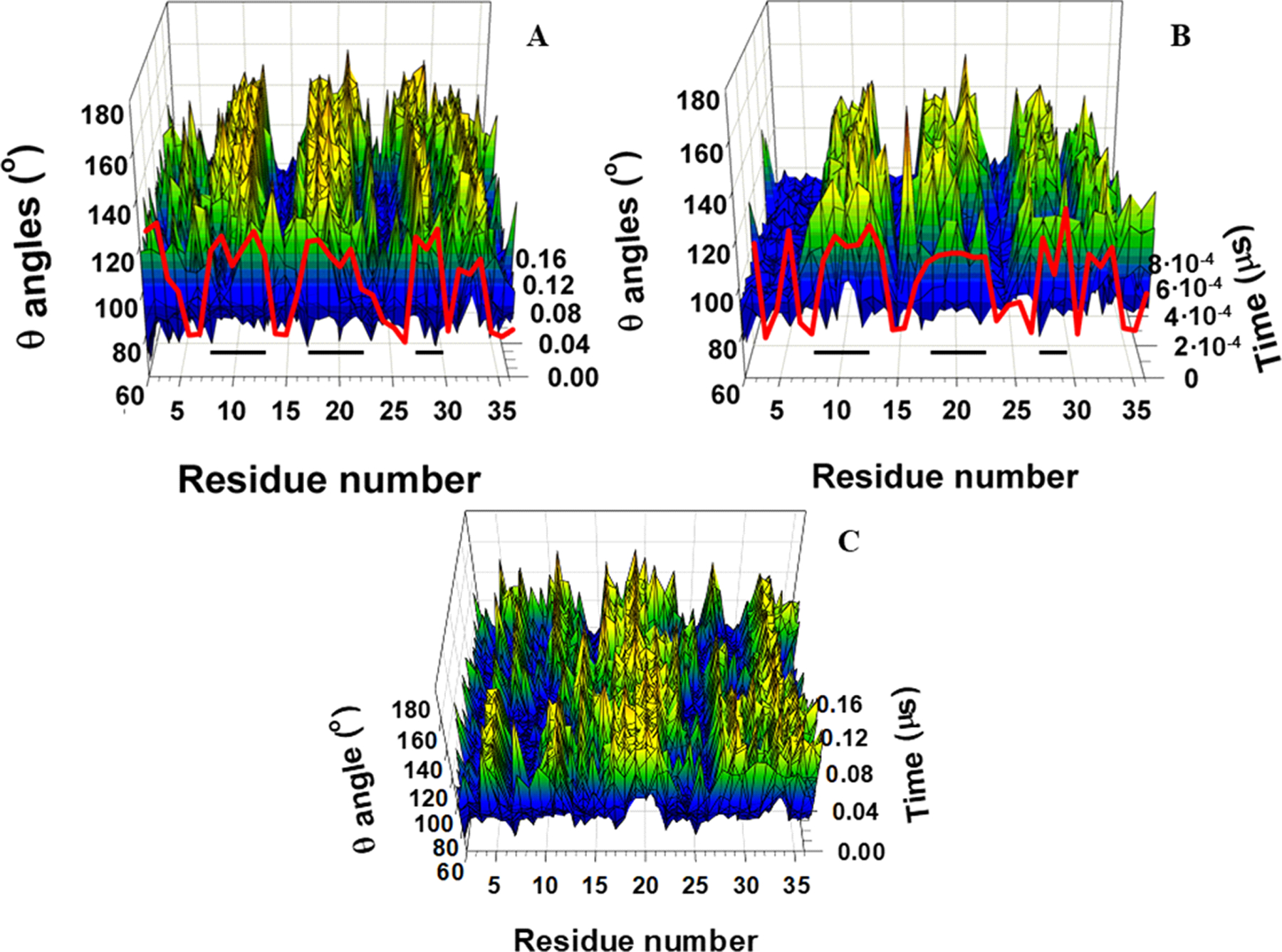
3-D representation of the backbone virtual-bond angles θ vs time for three-state folding trajectory of L26D mutant (panel A), downhill folding trajectory of L26W mutant (panel B), and nonfolding trajectory of L26D mutant (panel C). The NMR-derived structural data (red curves on panels A and B) are computed from the first model of the PDB ID codes 2N4R (L26D) and 2N4T (L26W). The horizontal black lines on panels A and B correspond to the β-strand regions.

Moreover, Figure 4 shows that the free energies of TRP8-THR13, LYS17-ASN23, and ASP26-TRP30 segments in the three-state folding (panels A-C) and nonfolding (panels G-I) trajectories oscillate in the course of time. The amplitude of oscillations in the nonfolding trajectory is much larger than in the three-state folding trajectory, which is not surprising given that the β-strands in the nonfolding trajectory are either formed partially or not formed at all [Figure 3(I, J)]. In addition, the most “oscillating” segment in the three-state folding trajectory of L26D mutant is the third β-strand [Figure 4(C)], which is also logical, given its flexibility and lowest stability. Another explanation for the local energy oscillations was introduced in a recent study.⁶⁷ In particular, it was shown that the local energy change is caused by oscillation in the distance between the two kinks. Here, even very rough monitoring of the formation of β-strands [Figures 3(A, B, I, J) and 5(A, C)] and free-energy oscillations [Figure 4(A–C, G–I)] of β-strands indicates correlations between the free-energy oscillations and kinks’ oscillations. It should be noted that the ability of kinks to oscillate back and forth along the backbone (i.e., appear and disappear in the course of time), when the protein is in an unfolding state, is a very important feature, one that might be used not only for a better understanding of protein folding, but also to open a new door in understanding intrinsically disordered proteins, which have been implicated in a number of human diseases; e.g. cancer, cardiovascular disease, neurodegenerative diseases, diabetes, etc.^{18,19,22–26,87} Therefore, detailed investigation of intrinsically disordered proteins in terms of kinks is planned in the nearest future.

Principal Component Analysis.

Principal component analysis, a covariance-matrix-based mathematical technique, is an effective method for extracting important motions from molecular dynamics trajectories.^{31,32,57–59} PCA rotates the Cartesian or internal coordinate space to a new space with new coordinates, principal components (PCs), a few of which are sufficient to describe a large part of the fluctuations of a protein. Structural fluctuations of θ and γ angles [mean-square fluctuations (MSF)] can be decomposed into collective modes by PCA. The modes have “frequencies” and directions corresponding to the eigenvalues and eigenvectors of the covariance matrix. The modes with the largest eigenvalues correspond to the modes which contribute the most to the structural fluctuations of the protein. It has been shown that the principal modes in folding trajectories are correlated with kink formation.⁶⁷ Therefore, it is of interest to know whether and how the changes of free energies and internal coordinates in the course of time in three-state, downhill and nonfolding trajectories are reflected on PCs, the projections of the trajectories on the eigenvectors.

Figure 6 illustrates the first five PCs of three-state (panels A-E), downhill (panels F-J), and nonfolding (panels K-O) MD trajectories. As was expected, there is a clear correlation between PC1 (Fig. 6A) and the RMSD (Fig. 3D) for the three-state folding trajectory. Although PC2 (Fig. 6B) does not mimic RMSD (Fig. 3D), it identifies the changes in RMSD in the course of time. The free-energy profiles along PC1 and PC2 [see insets in Fig. 6 (A and B)] are highly rugged, i.e., anharmonic, and many local minima appear in a multiple number (two) of coarse-grained minima. Therefore, the free-energy profiles along these two PCs can be characterized as multiply-hierarchical.^31,88 The multiply-hierarchical PCs are main contributors to the total fluctuations and are associated with global collective motions.^31,88 Some correlation between PC3 and PC4 [Fig. 6 (C and D)] and RMSD (Fig. 3D) is noticeable in some parts of the trajectory, these PCs mainly identify the transition from the unfolded state to the native state. The probability distributions along PC3 and PC4 are Gaussian-like with a single peak, and the free-energy profiles are characterized by a number of local minima arranged within a single coarse-grained minimum [see insets in Fig. 6 (C and D)]. These two PCs belong to a singly-hierarchical category.^31,88 The PC5 is not correlated to RMSD. It belongs to a harmonic category (see inset in Fig. 6E).^31,88 Since it involves low-amplitude local minima and corresponds to local motions, PC5 does not contribute significantly to the total fluctuations.^31,88 Similar correlations between PCs and RMSD can be observed for downhill folding trajectory, however, because of very fast folding, free-energy profiles along the PCs do not exhibit multiply-hierarchical, and singly-hierarchical categories. The free-energy profiles along all PCs are harmonic. For this reason, they are not shown in Figure 6.

Figure 6.

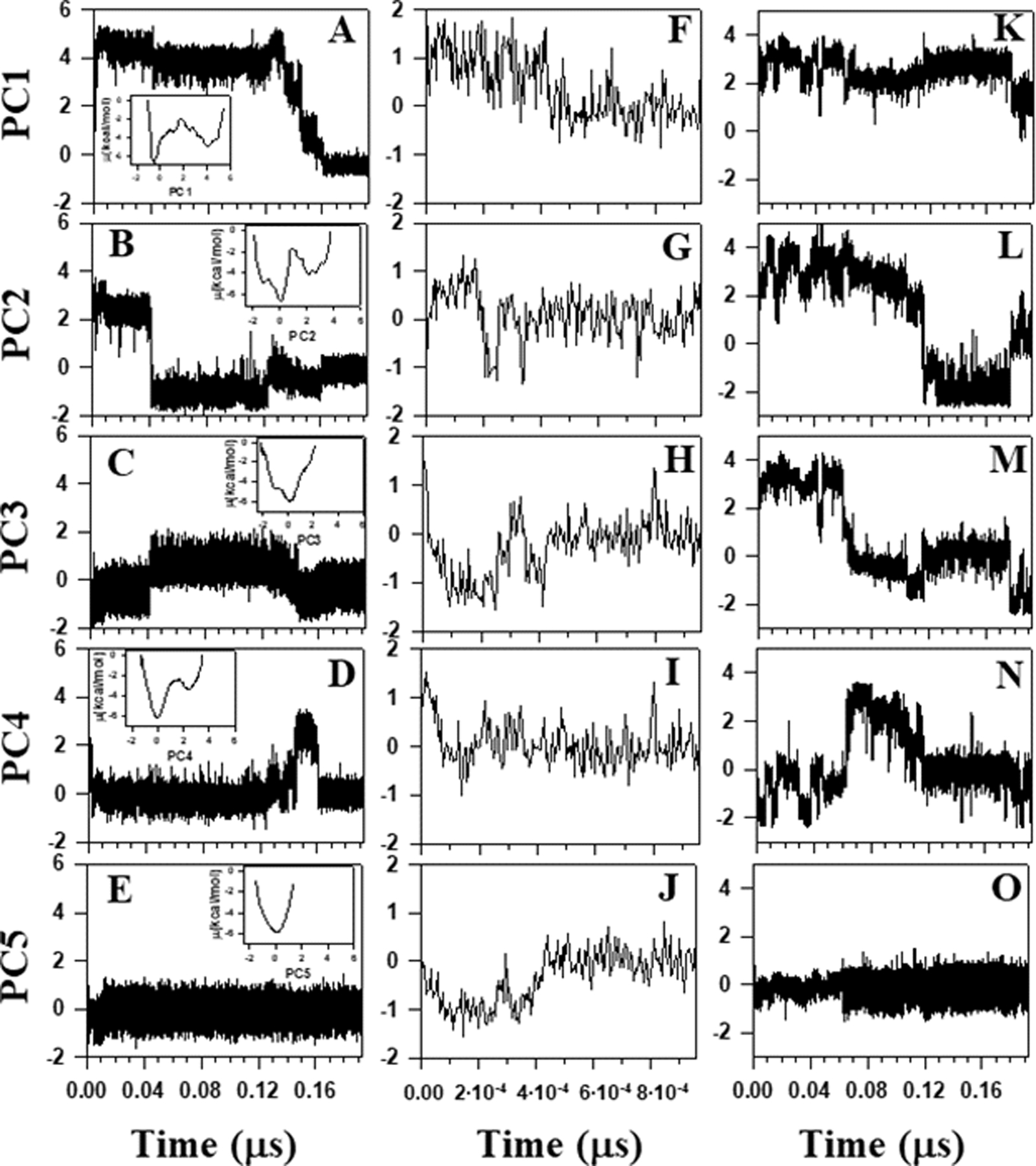
The first five principal components of three-state folding trajectory of L26D mutant (panels A-E), downhill folding trajectory of L26W mutant (panels F-J), and nonfolding trajectory of L26D mutant (panels K-O). The insets in panels A-E represent free-energy profiles of the corresponding principal components for the entire three-state folding trajectory (~ 1.4 μs).

Moreover, comparison of the results depicted in Figs. 3 (A–C, E–G) and 6 (A–C, F–H) illustrate that the first two PCs of three-state and downhill folding trajectories capture the changes in internal coordinates (θ, γ) and local free energies in the course of time. In particular, the formation of all three β-strands is reflected in PCs. This indicates the correlations between local and global motions in folding trajectories. This is not the case for the nonfolding trajectory, in which none of the PCs is correlated to RMSD. Also, because of the “disorderness” and lack of formation of β-strands, it is very difficult (if not impossible) to determine the correlation between the internal coordinates and local free energies and PCs. However, it should be noted that, the first four PCs of the nonfolding trajectory [Fig. 6 (K–N)] oscillate, which indicates that oscillatory behavior of kinks is mirrored on PCs, and that they are correlated.

It is important to note that the percentages of total fluctuations captured by the first PCs in the three-state and downhill folding trajectories are ~40% and 9%, respectively. PCA has proven to be an effective tool for the analysis of protein folding trajectories involving concerted motions of many residues, which can be captured by a few PCs with the largest eigenvalues.³¹ These results indicate that PCA can correctly identify the folding scenario. The point is that, as was mentioned earlier, downhill folding proteins exhibit marginal cooperativity causing non-concerted structural disassembly,¹¹ which consequently may induce non-concerted motions. The percentage of captured fluctuations for downhill folding trajectory is quite low (~9%), which based on the PCA definition is an indication of non-concerted motions. Therefore, the folding scenario can be determined by the percentage of captured fluctuations.

In the end, it should be noted that both local free energy analysis and PCA clearly indicate that the kink analysis can be very effective and useful in uncovering the mechanisms of different folding scenarios. Therefore, kinks and their applications for three different systems are discussed in the following section.

Examination of the Experimental Structures of the FBP28 WW Domain and its Mutants in Terms of Kinks.

The study of kinks is more easily understood from a differential representation of the protein main chain. Indeed, the angle θ_i is directly related to the local curvature κ_i (κ = π − θ) of the protein main chain whereas the angle γ_i is the local torsion of the main chain (see Figure 2 and Methods). Assuming constant virtual bond distances between the C^α atoms, the free-energy of the polymer can be written in terms of (κ,γ) internal coordinates using a Landau-Ginzburg-Wilson free-energy model^60–69 [Eq. (11)]. Minimizing this free-energy relative to κ and γ lead to a nonlinear equation of motion for the curvature similar to a generalized DNLS which admits kinks as particular solutions.

In earlier studies,^60–69 the modular building blocks of folded proteins, i.e. super-secondary structure such as a helix-loop-helix or strand-loop-strand motif, have been described in terms of the kink of a generalized version of the DNLS equation. It was found that the formation of a kink is initiated by an abrupt change in the orientation of a pair of consecutive side chains in the loop region.⁶⁷ It has been shown that in order to obtain a clear picture of kink formation it is necessary to start MD simulations from the full α-helical or β-strand structure and investigate the dynamics of the formation of loops, otherwise it would be blurred by α-helix or β-strand formation.⁶⁷ Moreover, kink analysis enabled us to realize the importance of local interactions, specifically the bimodal character of the potential of mean force in virtual-bond angles κ, as the driving force of folding.⁶⁷ It is notable that the only long-range interaction present in the Landau-Ginzburg-Wilson Hamiltonian^60–69 is a step-wise Pauli exclusion that introduces self-avoidance and prevents chain crossing. The effects of the long-range Coulomb and Van der Waals interactions are accounted for by the global multi-kink profile resulting from the minimization of free energy.⁸⁹ The multi-kink structure describes both local and collective motions. Previously, it has been shown that, using kink parameters that are derived from the experimental folded protein structure, its folding can be simulated.^{65,66,68,69,90,91} Moreover, phase diagram of protein with temperature (T) and acidity (pH) as the thermodynamic variables can be constructed as well.⁶⁹ Therefore, it is of interest to investigate whether a kink analysis of the experimental structures^27,50 can uncover the mechanisms, which govern L26D and especially L26W to fold through downhill folding.

Kink structures of the FBP28 WW domain, L26D and L26W.

In this work, we have carried out a detailed analysis of experimental structures of the FBP28 WW domain (three-state folder) and its mutants, L26D and L26W, which may fold through the three-state, downhill, and two-state folding scenarios, in terms of kinks. Using experimental values of the κ and γ angles (in other words – tertiary structure of protein), we started resolving the kink structures of the FBP28 WW domain, L26D and L26W. The multi-kink is a configuration that minimizes free energy [Eq. (11)], with an acceptable small deviation, RMSD, from the three-dimensional experimental structure. Minimum energy, as well as RMSD fitting, is achieved using a combination of simulated annealing and gradient descent methods. Multi-kink structures that are combinations of 8 individual kinks, differing in the arrangement along the protein chain, were obtained for each system. With RMSD < 0.8 Å, a total of 20 structures were initially obtained for the FBP28 WW domain and L26D, and 60 structures for L26W. For each system, three representative structures were then selected for a detailed analysis. Figure 7 illustrates comparison of the κ and γ angles, experimental and calculated, along the chains of three selected structures of the FBP28 WW domain, L26D and L26W. In addition, for each protein, Figures 8 shows experimental values of the κ and γ angles in the first panels, and most representative kink structures in the three remaining panels. Data on this figure allow us to scrutinize the correlations between the location of kinks and folding paths. [The experimental and three calculated representative structures for the FBP28 WW domain, L26D and L26W are illustrated in Fig. S2 (Supporting Information)].

Figure 7.

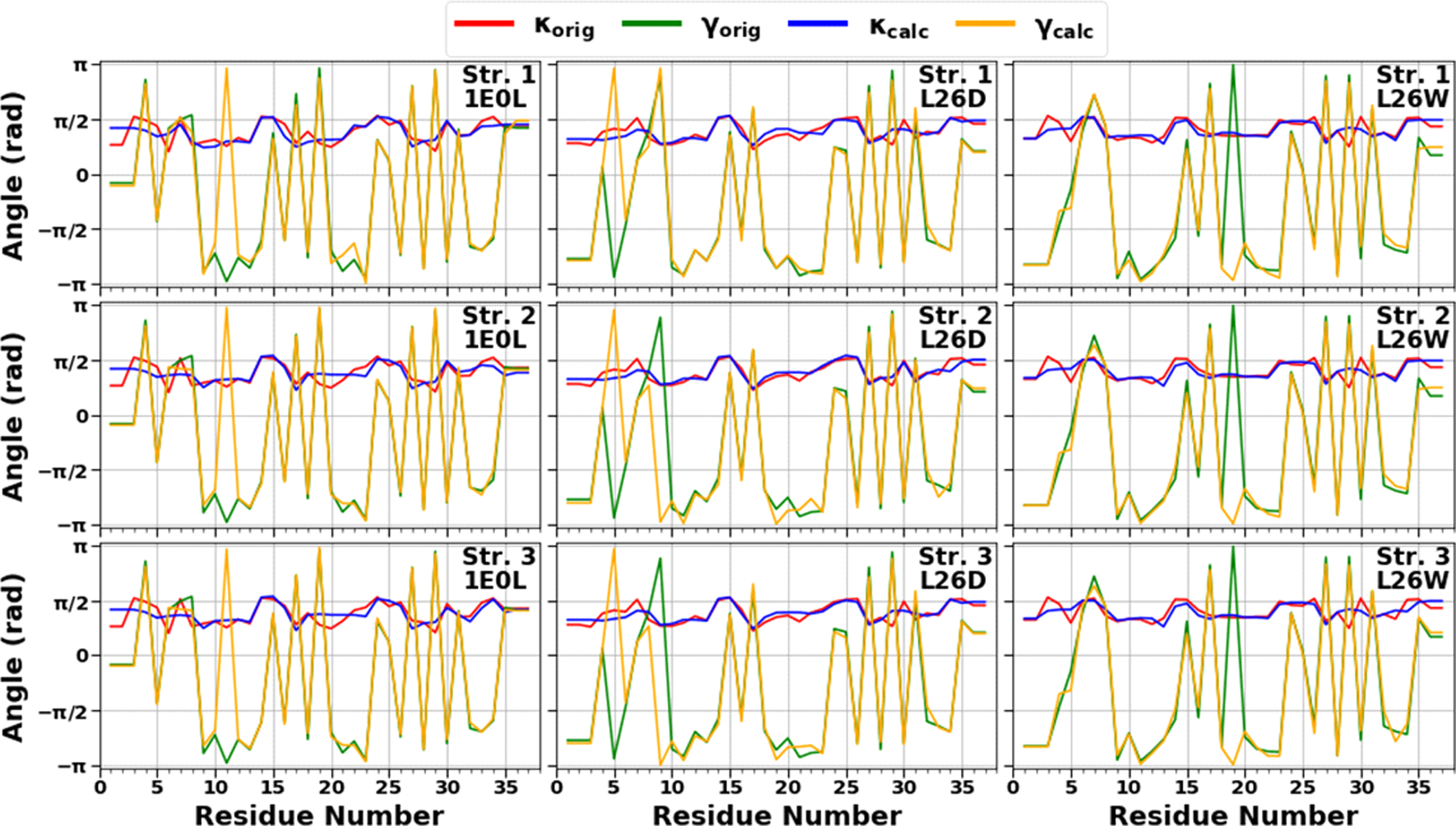
The comparison of experimental and calculated angle spectra of three selected structures for the FBP28 WW domain (left panels), L26D (middle panels) and L26W (right panels) in terms of virtual-bond κ_i (experimental-red, calculated-blue) and torsion γ_i (experimental-green, calculated-yellow) values.

Figure 8.

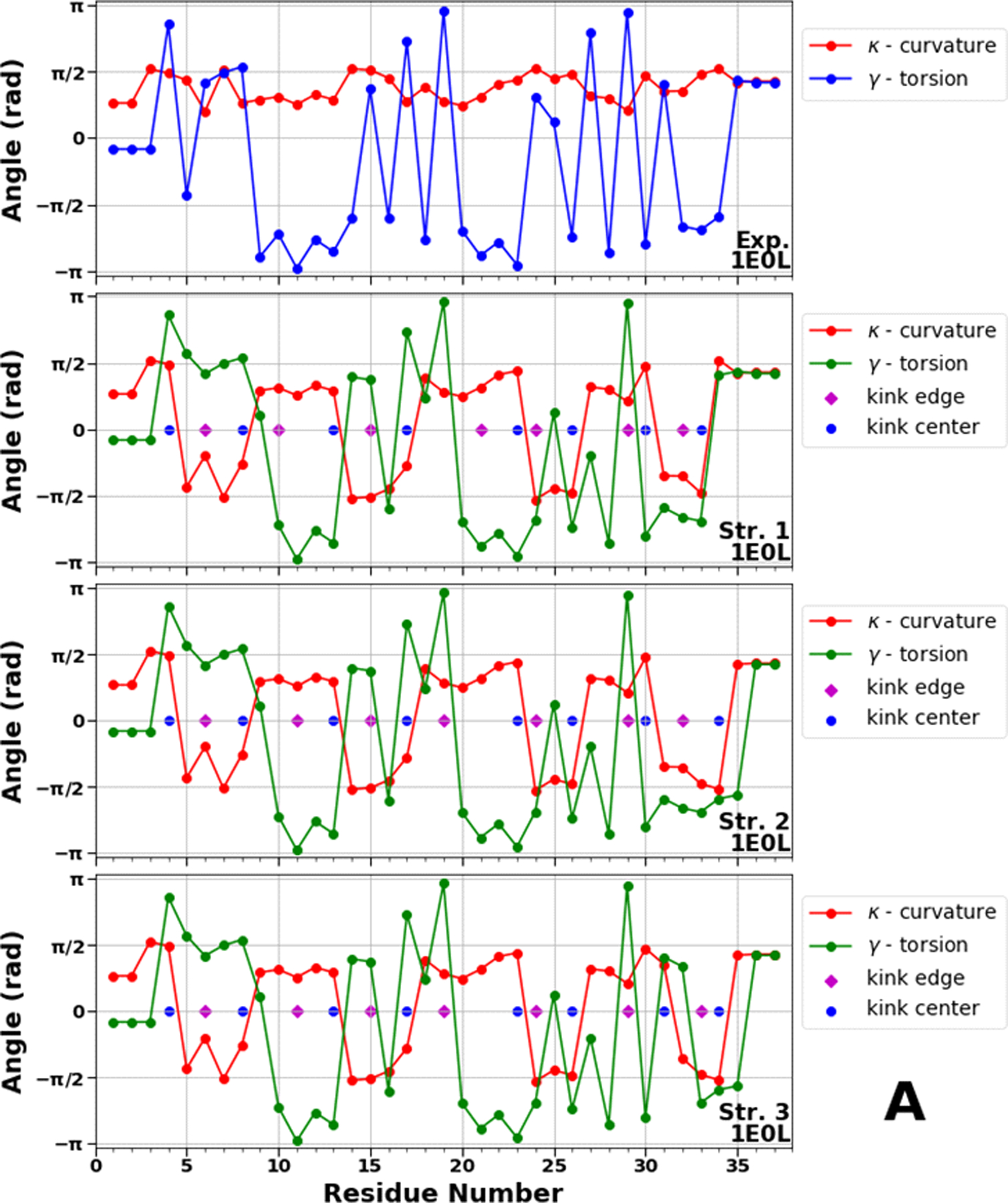
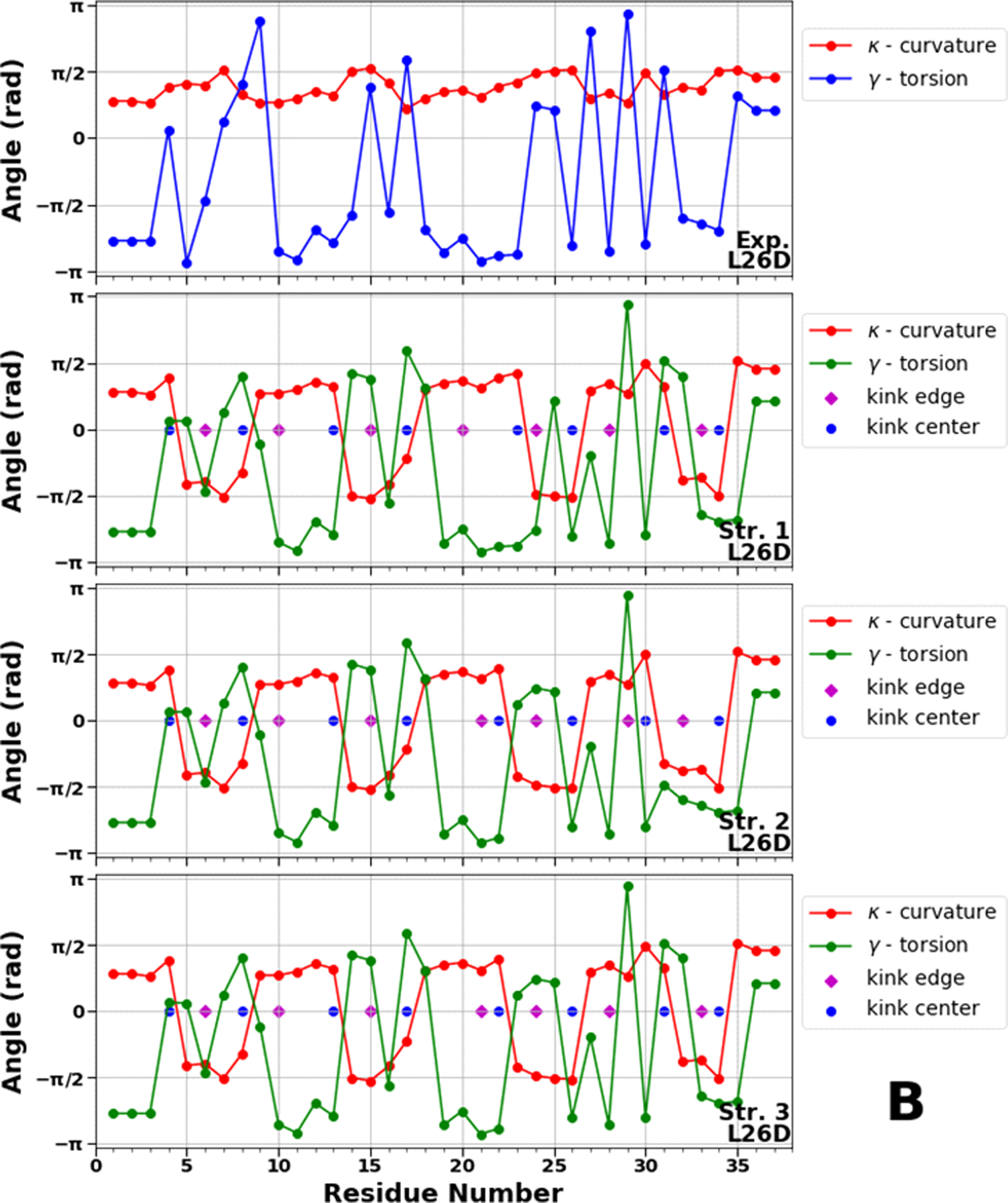
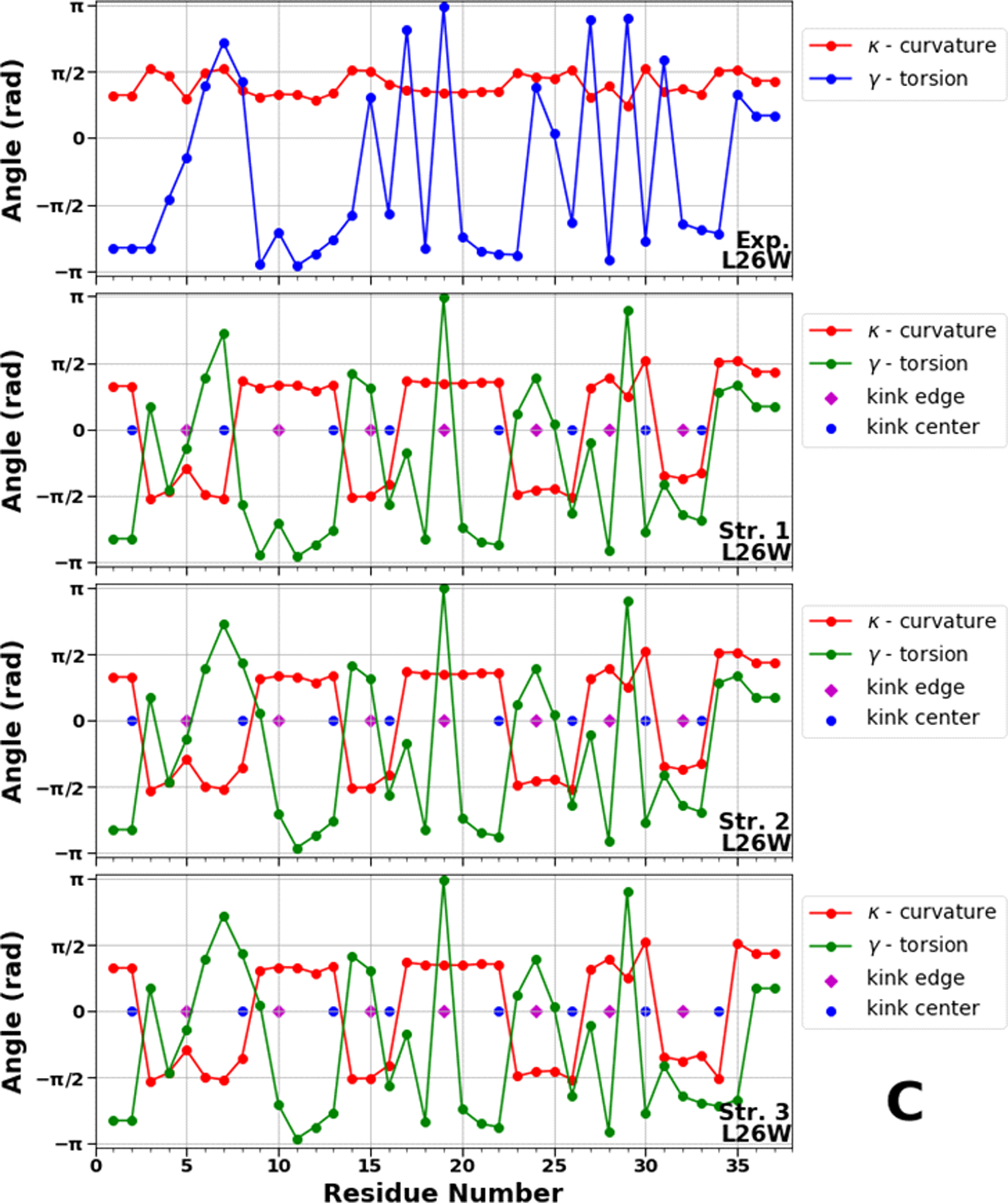
Top panels of A, B and C represent experimental values of the virtual-bond κ_i (red) and torsion γ_i (blue) angle spectra of 1E0L (panel A), 2N4R (panel B) and 2N4T (panel C). Remaining three panels in A, B and C illustrate kink structures, i.e., the virtual-bond κ_i (red) and torsion γ_i (green) angle spectra for three selected structures of 1E0L (panel A), 2N4R (panel B) and 2N4T (panel C), after ℤ₂ gauge transformation (eq. 8) was made. Blue circles represent centers of kinks, purple rhombuses represent the right edges of left kinks.

The kink locations along almost the entire sequence of the FBP28 WW domain in all three structures are the same, only the centers of the 7^th and 8^th kinks are moving between the 30^th and 31^st, and 33^rd and 34^th residues, respectively, which indicates the instability of the C-terminal part of the protein (Figure 8A). These findings are in harmony with earlier results obtained by us and other groups.^{16,21,28,29,31,32,38} Since the FBP28 WW domain is a three-state folder, we consider these kink locations as a reference for three-state folding.

In L26D, the center of the 8^th kink does not change, instead, we observe a movement of the 5^th kink center between the 22^nd and 23^rd residues along with the center of the 7^th kink between the 30^th and 31^st residues (Figure 8B). These results indicate that the C-terminal becomes more stable and turn 2 has more flexibility, which may either speed up (downhill folding) or slow down (three-state folding) the correct registry of turn 2. The resemblance of the locations of kink centers in the 3^rd structure of the FBP28 WW domain (Figure 8A) and the 1^st structure of L26D (Figure 8B) suggests the presence of three-state folding. The differences observed in the 5^th kink (the center is shifted from the 23^rd residue to 22^nd residue) in the 2^nd and 3^rd structures indicate that L26D can fold through two-state or downhill folding. These findings are in agreement with our recent results.⁵⁰

In our recent studies,^50,56 we found that L26W is the fastest folder among all studied mutants, however, examination of the structural basis of L26W did not reveal the reasons for fast folding. The kink structures of L26W (Figure 8C) exhibit different locations of centers in the N-terminal region and turn 1 compare to the FBP28 WW domain and L26D. Firstly, it should be noted that, the center of the 5^th kink in L26W is located at the 22^nd residue, as it was in the fast-folding structures of L26D, which indicates the fast formation of hairpin 2. Secondly, the center of the 2^nd kink in the 1^st structure of L26W is shifted from the 8^th to the 7^th residue, which might be indication of possible destabilization of the delocalized hydrophobic core (Trp8, Tyr20, and Pro33) - “one of the contributors” in the formation of the intermediate state.⁵ Thirdly, the shift of the 4^th kink center from the 17^th to the 16^th residue may speed up the formation of turn 1, which along with the destabilized delocalized hydrophobic core speeds up the folding of the entire system. Finally, the center of the 1^st kink in L26W is shifted by two residues (from the 4^th residue to the 2^nd residue). Since this shift occurs at the N-terminal end, and neither Ala4 nor Ala2 are associated with any hydrophobic core stabilizing the intermediate state, its influence, in our opinion, on the folding scenario is probably not significant. However, it is worth investigating in the future. It is important to mention that these results are correlated with the results obtained in our recent work⁵⁰ for the first two principal modes. In particular, the main contributions of the first two principal modes to the mean-square fluctuations along the θ and γ angles in downhill folding trajectories come from the N terminus, the first β-strand, and the first turn [see Fig. 1(H,I,K,L) of Ref. 50].

Folding index for the FBP28 WW domain, L26D and L26W.

Figure 9 shows the accumulation of the folding index⁴⁸ [Eqs. (18,19)] along the trajectories for the FBP28 WW domain (A), L26D (B), and L26W (C), together with the folding index dependence on length of proteins (D).

Figure 9.

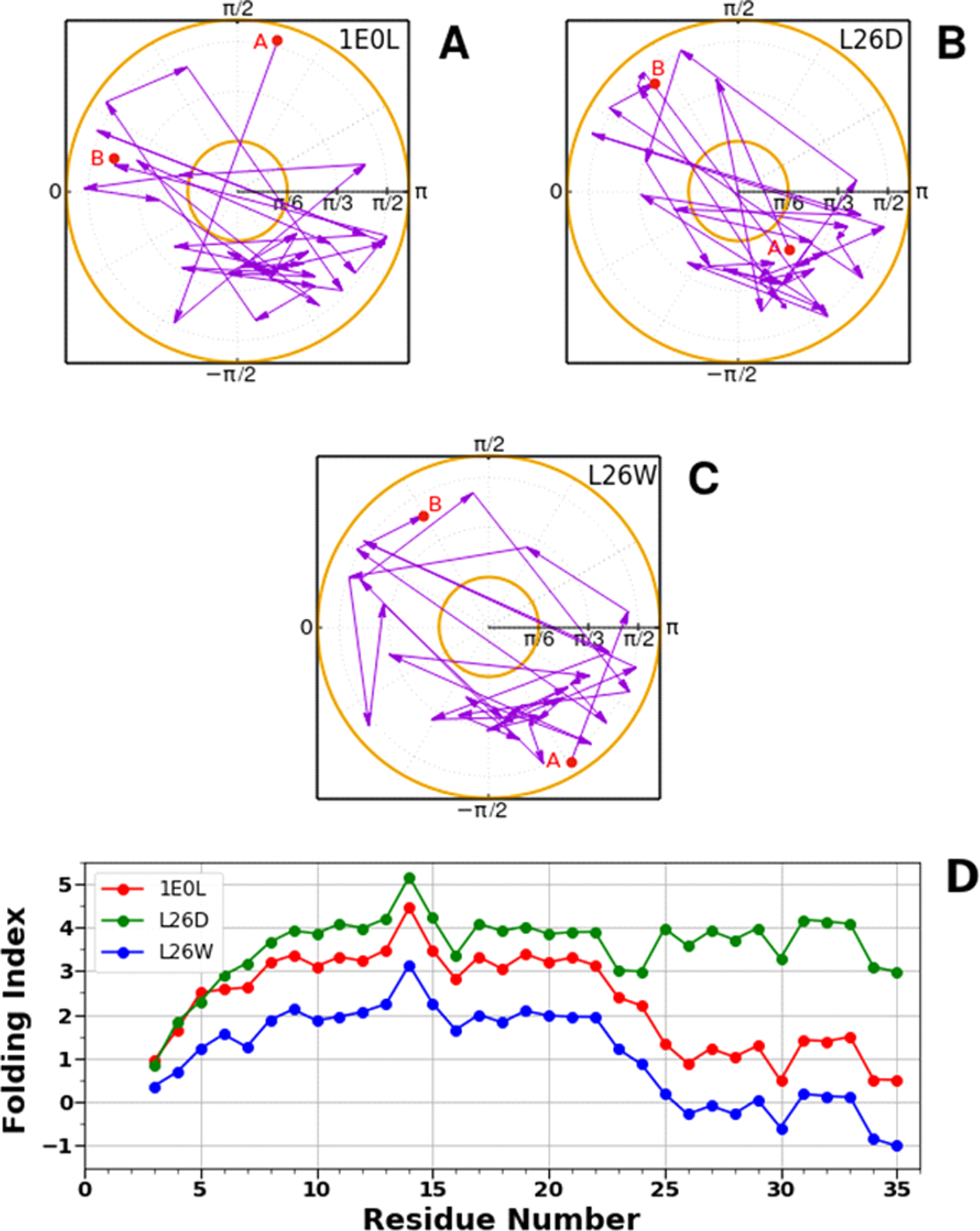
The folding index trajectories for the FBP28 WW domain (A), L26D (B), and L26W (C), and the folding index for the FBP28 WW domain, L26D and L26W (D).

We can see that the folding index does not capture all the differences between the FBP28 WW domain, L26D and L26W, but it indicates the most crucial sites which are involved in alteration of folding scenarios. In particular, (i) the main difference between the folding indices of L26D and the FBP28 WW domain and L26W is observed in the region of the 22^nd and 23^rd residues, which is associated with the speed-up of formation of turn 2; (ii) the folding index of L26W behaves differently in the region of the 6^th and 7^th residues, which is related to possible destabilization of the delocalized hydrophobic core; and also, obtains negative values in the region of the 3^rd β-strand.

Conclusions

The folding, misfolding, nonfolding and energetics of two mutants (L26D and L26W) of the FBP28 WW domain were examined in terms of the backbone virtual-bond angle θ and backbone virtual-bond-dihedral angle γ of each residue, the local free energies, as well as with principal components. It was shown that the “behavior” of θ and γ angles in the course of time provides full information not only about the formation of β-strands but also about folding and reasons for misfolding and nonfolding. Strong correlations between the changes in θ and γ angles and local free energies over the trajectories were observed. The formation of β-strands was accompanied by the emergence of kinks in internal coordinate space and by the decrease of local free energy. In the downhill folding trajectory, the local free-energy decrease was ~ 7 kcal/mol, which falls in the range of free energy that is enough for the correct folding of a protein. In the three-state folding trajectory, the local free-energy decrease was much higher because of the folding mechanism (hydrophobic collapse mechanism), which caused misfolding of the protein first. It was illustrated that the oscillations of the free energies of the β-strand segments observed in the unfolded state of the three-state folding trajectory (third β-strand) and in the entire nonfolding trajectory might be caused by instability of kinks along the backbone prompting a protein to appear “disordered”. It was, also, shown that the local (internal coordinates) and global (principal components) motions in folding trajectories, as well as the kinks and principal components in nonfolding trajectory, are correlated.

Moreover, experimental structures of the FBP28 WW domain, L26D and L26W were analyzed in terms of kinks. It was found that without MD simulations the kinks are able to capture the sites of protein that govern L26D and L26W to change the folding scenario. This feature makes kinks a very effective method not only for better understanding protein folding, but also it would open a new door to the understanding intrinsically disordered proteins, which have been implicated in a number of human diseases.