Abstract
The theoretical charge density study for the gas phase of anti-leprosy drug Dapsone has been carried out in the light of the theory of atoms in molecules using density functional theory employing B3LYP(6-311G++(d, p) hybrid functional completed with dispersion corrections. The Hirshfeld surface analysis as well as fingerprint plots has been utilized to visualize and quantify the intermolecular contacts present in the molecule. The topological properties such as electron density and its Laplacian, delocalization index have been elucidated to throw light into the chemical bonding and atomic and molecular details. The electron localization function has been used to visualize and deduce information on the lone pair and the subshells of the Cl atom. The electrostatic potential visualizes the positive and negative electrostatic potential regions which are susceptible to nucleophilic and electrophilic attack. On the whole, this study provides an exact mechanism, interaction, and topological and electrostatic properties of the drug through theoretical insights which all will be a platform for our further investigation of the interaction between dapsone and dihydropteroate synthase (DHPS).
Keywords: Hirshfeld surface analysis, Quantum chemical calculations, Charge density analysis, Bond topological properties, Electrostatic properties
Introduction
Dapsone, an antibacterial, is primarily and effectively used in the leprosy treatment which is also used in combination with rifampicin and clofazimine for the treatment of Mycobacterium leprae infections (leprosy) [1–4], malaria [5–7], and pneumocystis pneumonia (PCP) [8–10]. Specifically, dapsone stops the bacterial dihydrofolic acid synthesis through the process of binding itself in the active site of the enzyme named 6-hydroxymethyl-7,8-dihydropteroate synthase (DHPS), which takes part in the condensation of para-aminobenzoic acid (pABA) with 6-hydroxymethyl-7,8-dihydropterin-pyrophosphate to form 7,8-dihydropteroate and pyrophosphate [11]. Moreover, dapsone competes with para-aminobenzoate on the active site of DHPS and inhibits the bacterial dihydrofolic acid synthesis [12]. In present literature, Mendes et al. carried out the geometric and electronic study of dapsone and discussed the symmetric and asymmetric conformational isomer of the molecule [13]. Borges et al. carried out the first density functional study of the dapsone derivatives on methemoglobin [14]. Bhattacharya et al. revisited dapsone photophysics in a different solvent [15]. To the best of our knowledge, neither the study of theoretical charge density nor the topological properties for the gas phase of the molecule have been discussed in the literature.
The elaborate study on charge density in the light of AIM theory and electrostatic mapping of a molecule is very important due to their crucial application in determining the interaction of pharmaceutical compounds with a biomolecule. As referred to Bader the pioneer stated in AIM theory: “A Quantum theory [16], while the theory has its origin in quantum mechanics, its vehicle of expression, is the charge density”. The charge density being the most important property is much useful in finding one-electron properties, ground-state properties of the molecules, type and the strength of the chemical bonding between the atoms, information on lattice energies, orbital locating and molecular interactions, etc. Especially hydrogen bonding serves as the principal source for the intermolecular interactions which further helps in tailoring more compounds with desired physical and chemical properties.
In the present work, an attempt has been made to reconstruct the charge density mapping of dapsone (4-[(4-aminobenzene) sulfonyl] aniline) molecule using theoretical models and is thoroughly analyzed with the help of Quantum theory of atoms in molecules for the intuitive information on the molecule itself. In a theoretical model such as DFT (density functional theory) [17], a free dapsone molecule has been treated and analyzed for its electronic properties. The Hirshfeld surface analysis [18, 19] has been carried out for a clear understanding of the intermolecular hydrogen bonding interactions, and the fingerprint plot has been mapped for calculating the percentage of contribution of various bonds present in the molecule. The topology of the charge density has been analyzed, and the critical points in the charge density have been determined. The Lipinski rule of five has been calculated in order to appreciate the potential of the drug. Electrostatic potential (ESP) surfaces have been examined for the identification of not only the electrophilic and nucleophilic regions of the molecule but also understanding the lock and key mechanism. The results obtained from this study will be a manifesto for the further exploration of interpretation of the drug-receptor interactions between the dapsone molecule and the enzyme of dihydropteroate synthase (DHPS).
Computational details
The experimentally determined position values of the atoms of dapsone have been given as input for the theoretical optimization in GAUSSIAN09 software package [20] with DFT method using (B3LYP\6-311G++(d, p)) level of theory [21, 22]. The single-point calculations have been performed once the convergence has been reached. The absence of imaginary frequencies has shown that the minimum energy structure has been achieved. The obtained wave function for the gas phase of the dapsone molecule has been given as an input to the AIM ALL package [23] for calculating the topological properties. The AIM-UC 4.0. [24] and MULTIWFN [25] software packages have been utilized for mapping purposes.
Results and discussion
Description of structure
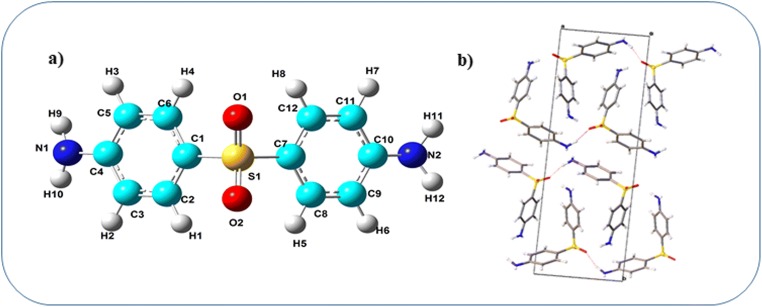
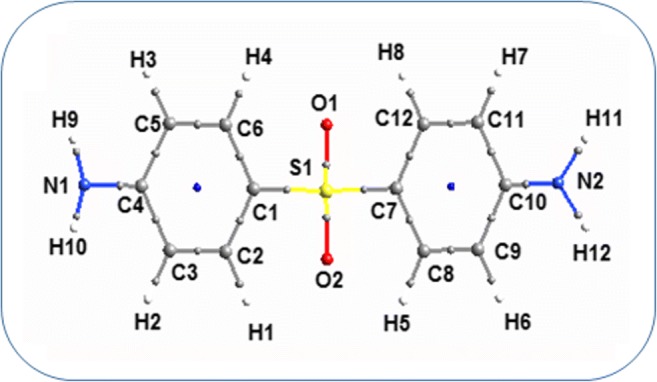
The minimum energy structure of the dapsone molecule has been shown in Fig. 1a. In both the aniline rings, the standard values for C–C and C–H bonds are 1.39 Å and 1.09 Å, and the values from our theoretical calculations lie in the range 1.387–1.406 Å and 1.083–1.085 Å which agrees well with the standard values [26]. The expected bond length for the C–N bond is 1.48 Å, but the optimized bond lengths for the C–N bond are in the range 1.387–1.388 Å where the decrease in bond length might be due to the resonance among C–N bonds. The calculated angle for the plane O1-S1-O2 is found to be 120° which suggests the trigonal planar geometry and sp2 hybridization state for the corresponding central S1 atom.
Fig. 1.
a Optimized structure of dapsone. b View of the crystal packing in dapsone (along the c* axis)
The shapes of the two amine groups are found to be a slight tetrahedral with the expected bond angle 113°. The atoms of N1 and N2 make equal dihedral angles with the respective planes C3-C4-C5 and C9-C10-C11 and are found to be 177°.The torsion angles which are formed by the atoms C1 and C7 with O2-S1-O1 plane individually are found to be 123.4° which clearly suggest the symmetry of the molecule.
Hydrogen bonding interaction
In order to better understand the packing and interactions of the molecule with the neighboring molecules, the information from the experimental cif file has been given as the input for CrystalExplorer software 3.0 [18, 27]. The packing of the molecules in the crystal lattice (Fig. 1b) is viewed along c* axis and the intermolecular interactions are sustained by Van der Waals interactions.
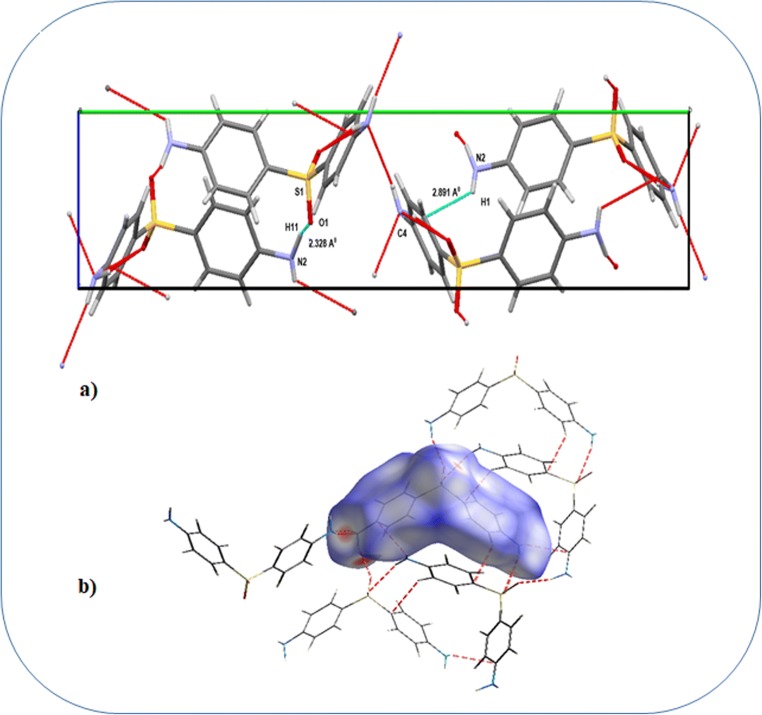
The molecular packing of the crystal is stabilized by N–H…O, N–H…N, and π…π types of intermolecular interactions (Fig. 2) and is classified as strong and weak interactions with respect to their H…A distances. From Fig. 2a, it is obvious that there is no intramolecular N–H…O hydrogen bond formation, but two types of intermolecular N–H…O hydrogen bond formation is possible.
Fig. 2.
a View of the intermolecular hydrogen bonds (along with a axis). b Visualization of the Hirshfeld surface of the strong interactions
The hydrogen bond parameters of the strongest N1–H9…O2 interaction are: H9…O2; 1.990Å and N1–H9, 1.009Å, and the angle is 159.46°, and another weak N2–H11…O1 interaction are: H11…O1; 2.423Å, N2-H11; 1.009Å, and the angle is 145.29°. The hydrogen bonding parameters are given in Table 1. The existence of intermolecular hydrogen bonds between the molecules makes the interactions much stronger which would result in more stable and lower boiling points because the molecules prefer to be close vicinity with respect to each other. The stability of the dapsone molecule is also established by the high chemical hardness value (2.46a.u). Visualization of intermolecular interactions through the Hirshfeld surface analysis and obtaining the quantitative details of the contacts through the fingerprint analysis [28] are necessary to understand qualitatively and quantitatively the intermolecular interactions.
Table 1.
Hydrogen bonding parameters (Åo)
| D---H…A | D--H | H...A | D…A | D---H…A |
|---|---|---|---|---|
| N1–H9…O2 | 1.009 | 1.990 | 2.956 | 159.46 |
| N1–H10…N1 | 1.009 | 2.777 | 3.269 | 163.31 |
| N2–H12…C9 | 1.009 | 2.743 | 3.369 | 120.47 |
| N2–H11…O1 | 1.009 | 2.423 | 3.623 | 145.29 |
| C11–H7…C7 | 1.083 | 2.728 | 3.303 | 139.76 |
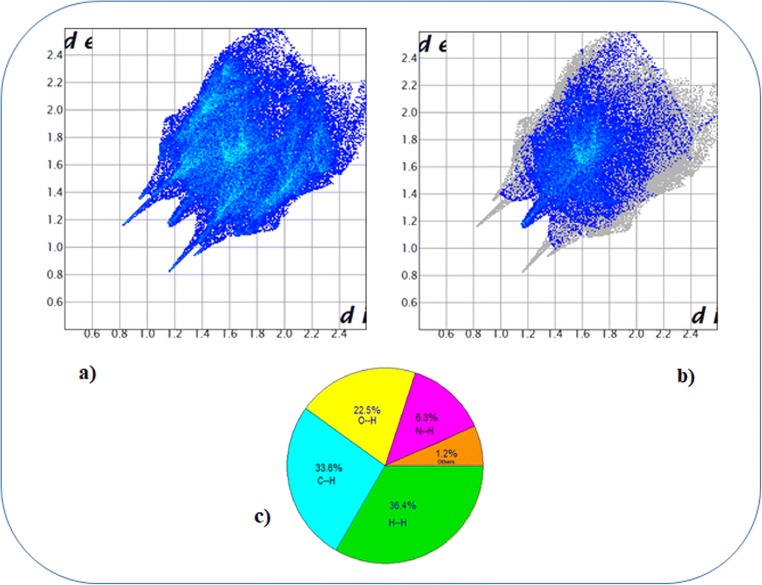
The combination of di and de in the form of a 2D fingerprint plot is used to provide ample information regarding the percentage contribution of various intermolecular contacts present in the molecule. Figure 2b shows thick orange color circular patches which represent the strong N1–H9…O2, N1–H10…N1, and N2–H11…O1 hydrogen-bonding interactions which serve as an attestation for the strong intermolecular interactions. The fingerprint plot of the dapsone molecule (Fig. 3a) shows two sharp spikes at the bottom left and bottom right representing the donor and acceptor of N–H…O interaction. The distinct spike of the H…H type interaction is shown in Fig. 3b. Among the investigated interactions, H…H interaction has a major contribution (36.4%), while the C…H interaction occupies 33.6% of the area of the total Hirshfeld surface. The various intermolecular contacts and their percentage contributions are shown in Fig. 3c.
Fig. 3.
Fingerprint plot a full and b resolved into H…H contacts. c Percentage contribution of various intermolecular contacts in the molecule
Topological properties of electron density
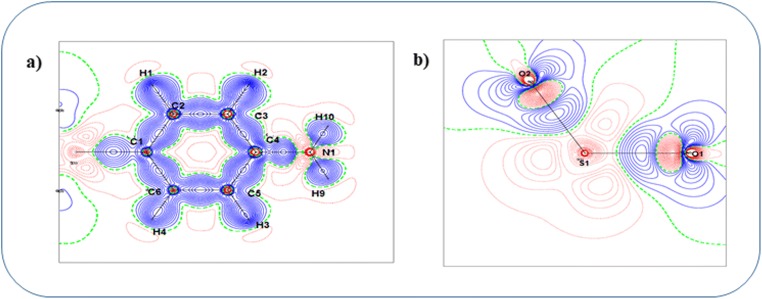
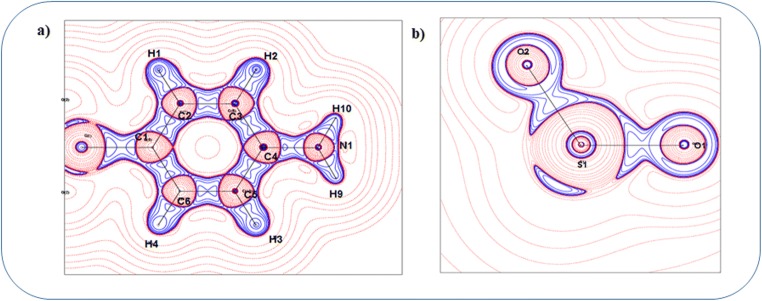
Investigation on topological properties of electron density in the light of AIM theory allows us to look into the details of atomic, molecular, and chemical bonding. Figure 4a shows the static deformation density map of the top aniline ring where all the bonds exhibit covalent nature (Table 2). The closed-shell interactions between S–O atoms are clearly visible in Fig. 4b.
Fig. 4.
Static deformation density map of the a top aniline ring and b SO2 group of the dapsone molecule
Table 2.
Topological properties of the dapsone molecule
| Bonds | ρBCP (e/Å3) | ∇2ρ (e/Å5) | ε | V(r) (a.u.) | G(r) (a.u.) | K(r) (a.u.) | L(r) (a.u.) | DI |
|---|---|---|---|---|---|---|---|---|
| C1–C2 | 2.06 | − 20.2 | 0.20 | − 0.411 | 0.101 | 0.310 | 0.209 | 1.34 |
| C2–C3 | 2.10 | − 20.8 | 0.22 | − 0.425 | 0.104 | 0.320 | 0.216 | 1.42 |
| C3–C4 | 2.05 | − 20.1 | 0.21 | − 0.401 | 0.096 | 0.305 | 0.209 | 1.28 |
| C4–C5 | 2.05 | − 20.1 | 0.21 | − 0.401 | 0.096 | 0.305 | 0.209 | 1.28 |
| C5–C6 | 2.10 | − 20.8 | 0.22 | − 0.425 | 0.104 | 0.320 | 0.216 | 1.34 |
| C1–C6 | 2.06 | − 20.2 | 0.20 | − 0.411 | 0.101 | 0.310 | 0.209 | 1.28 |
| C7–C8 | 2.06 | − 20.2 | 0.20 | − 0.411 | 0.101 | 0.310 | 0.209 | 1.34 |
| C8–C9 | 2.10 | − 20.8 | 0.22 | − 0.425 | 0.104 | 0.320 | 0.216 | 1.42 |
| C9–C10 | 2.05 | − 20.1 | 0.21 | − 0.401 | 0.096 | 0.305 | 0.209 | 0.86 |
| C10–C11 | 2.05 | − 20.1 | 0.21 | − 0.402 | 0.096 | 0.305 | 0.209 | 1.29 |
| C11–C12 | 2.10 | − 20.8 | 0.22 | − 0.425 | 0.104 | 0.320 | 0.216 | 1.34 |
| C7–C12 | 2.06 | − 20.2 | 0.20 | − 0.411 | 0.101 | 0.310 | 0.209 | 1.29 |
| C1–S1 | 1.36 | − 9.14 | 0.09 | − 0.190 | 0.048 | 0.142 | 0.095 | 0.86 |
| C7–S1 | 1.36 | − 9.12 | 0.09 | − 0.189 | 0.048 | 0.142 | 0.094 | 1.42 |
| C4–N1 | 2.04 | − 21.2 | 0.07 | − 0.570 | 0.175 | 0.395 | 0.219 | 1.07 |
| C10–N2 | 2.04 | − 21.2 | 0.07 | − 0.567 | 0.174 | 0.393 | 0.219 | 1.07 |
| C2–H1 | 1.92 | − 23.9 | 0.01 | − 0.319 | 0.035 | 0.283 | 0.248 | 1.42 |
| C3–H2 | 1.88 | − 22.9 | 0.03 | − 0.318 | 0.040 | 0.277 | 0.237 | 0.93 |
| C5–H3 | 1.88 | − 22.9 | 0.03 | − 0.318 | 0.040 | 0.277 | 0.237 | 0.96 |
| C6–H4 | 1.92 | − 23.9 | 0.01 | − 0.319 | 0.035 | 0.283 | 0.248 | 0.84 |
| C8–H5 | 1.92 | − 23.9 | 0.01 | − 0.319 | 0.035 | 0.283 | 0.248 | 0.93 |
| C9–H6 | 1.88 | − 22.9 | 0.03 | −0.318 | 0.040 | 0.277 | 0.237 | 0.96 |
| C11–H7 | 1.88 | − 22.9 | 0.03 | − 0.318 | 0.040 | 0.277 | 0.237 | 0.96 |
| C12–H8 | 1.92 | − 23.9 | 0.01 | − 0.319 | 0.035 | 0.283 | 0.248 | 0.93 |
| S1–O1 | 1.93 | 20.3 | 0.01 | − 0.899 | 0.555 | 0.344 | − 0.210 | 1.19 |
| S1–O2 | 1.93 | 20.3 | 0.01 | − 0.899 | 0.555 | 0.344 | − 0.210 | 1.19 |
| N1–H9 | 2.30 | − 38.5 | 0.06 | − 0.513 | 0.057 | 0.456 | 0.399 | 0.84 |
| N1–H10 | 2.30 | − 38.5 | 0.06 | − 0.513 | 0.057 | 0.456 | 0.399 | 0.96 |
| N2–H11 | 2.30 | − 38.5 | 0.06 | − 0.512 | 0.057 | 0.456 | 0.399 | 0.84 |
| N2–H12 | 2.30 | − 38.5 | 0.06 | − 0.512 | 0.057 | 0.456 | 0.399 | 0.84 |
The range of electron density and Laplacian of C–C bonds in both the phenyl rings is 2.05e/Å3 to 2.105e/Å3 and − 20.1e/Å5 to − 20.8e/Å5. The C–S bonds exhibit very poor electron density as well as Laplacian values which shows that the bonds are weak. Both the C–N bonds show the same charge density and Laplacian values and are found to be 2.045e/Å3 and − 21.25e/Å5, respectively, and this might be stabilized with same charge environment. Similarly, the N–H and C–H bonds show good accumulation of charge density between the bonds (Fig. 5a). In addition to the electron density, the Laplacian and electron localization function also reveal the closed-shell interacting nature of the S–O bonds with the positive Laplacian value (20.35e/Å5) as well as through the plots of Figs. 5b and 6. The lone pairs of O atoms and the K, L, and M shells of S atom are also clearly visible in Fig. 6. The molecular graph with the bond as well as ring critical point has been shown in Fig. 7.
Fig. 5.
Laplacian of the electron density of a top aniline ring and b SO2 group of the dapsone molecule
Fig. 6.
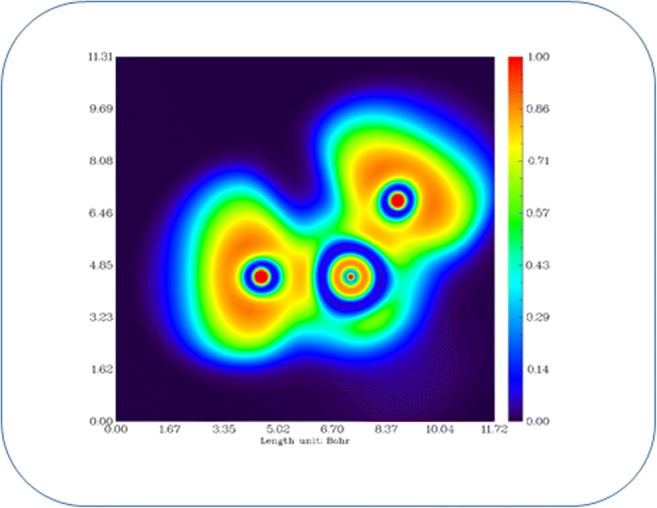
Visualization of electron localization function
Fig. 7.
Molecular graph diagram with a bond (gray small circles) and ring (blue small circles) critical points of dapsone molecule
The very low ellipticity value (ca 0.01) for the bonds S–O and C–H portrays the near cylindrically symmetric nature. The ellipticity values for the C–C bonds are in the range 0.20–0.22, and the increased values show the π character of the C–C bonds.
Among the C–C bonds, the bonds C2–C3 and C8–C9 have the highest delocalization index value which shows not only the strength of the bonds but also denotes the occurrence of resonance/delocalization of the bonds in both the phenyl rings. Among the C–H bonds, the C2–H1 bond has the highest delocalization index value which is supported by the high charge density values (1.92e/Å3) as well as high Laplacian values (− 23.9e/Å5). Similarly, the C7–S1 bond exhibits a high value of the delocalization index (1.42) even though the charge density values of both the C–S bonds are the same. This might be because of the influence of the S1 atom that is higher in C7–S1 bond than the C1–S1 bond.
As the kinetic energy density dominates, the total energy density becomes positive which shows the instability of the bonds. Among all the bonds, the N–H bonds have high total energy density values which show the low stability of the bonds.
Atomic charges and volume
The sulfur atom exhibits a very high positive Bader atomic charge (2.36e) as it is attached with the two most electronegative oxygen atoms (− 1.27e) on both sides. The electronegative N1 and N2 atoms exhibit negative charges (− 1.07e), and they are attached with the two positive H atoms each. The group charge of both the primary amine (−NH2) is negative − 0.23e), and they can donate electrons as donors. Both the C–N bonds are well polarized where the carbon atoms (C4, C10) possess positive charges (0.40e) and the nitrogen atoms (N1, N2) possess negative charges (− 1.07e). The most electronegative atoms O1 and O2 exhibit greater volume, and the values are found to be 111.18 Å3 and 111.19 Å3 respectively (Table 3).
Table 3.
Bader charges and atomic volumes
| Atoms | Q(e) | V(Å3) | Atoms | Q(e) | V(Å3) |
|---|---|---|---|---|---|
| S1 | 2.364 | 54.74 | C11 | − 0.011 | 72.05 |
| O1 | − 1.267 | 111.18 | C12 | 0.014 | 69.36 |
| O2 | − 1.267 | 111.19 | H1 | 0.064 | 35.25 |
| N1 | − 1.074 | 97.69 | H2 | 0.016 | 37.58 |
| N2 | − 1.072 | 97.67 | H3 | 0.016 | 37.59 |
| C1 | − 0.155 | 68.12 | H4 | 0.064 | 35.26 |
| C2 | 0.014 | 69.36 | H5 | 0.064 | 35.23 |
| C3 | − 0.011 | 71.99 | H6 | 0.016 | 37.62 |
| C4 | 0.404 | 54.69 | H7 | 0.016 | 37.62 |
| C5 | − 0.011 | 72.01 | H8 | 0.064 | 35.22 |
| C6 | 0.014 | 69.36 | H9 | 0.374 | 23.84 |
| C7 | − 0.155 | 68.09 | H10 | 0.374 | 23.83 |
| C8 | 0.014 | 69.33 | H11 | 0.373 | 23.86 |
| C9 | − 0.011 | 72.02 | H12 | 0.373 | 23.86 |
| C10 | 0.402 | 54.68 |
Physiochemical properties: PASS analysis
Some of the molecular properties like membrane permeability and bioavailability are straightly connected with some molecular descriptors such as log P (partition coefficient), molecular weight (MW), hydrogen bond acceptors, and donors count in a molecule. Lipinski rule of five [29] which is also used as a filter for drug-like properties says that most molecules with good membrane permeability have log P ≤ 5, molecular weight ≤ 500, number of hydrogen bond donors ≤ 5, and number of hydrogen bond acceptors ≤ 5. Lipinski rule of 5 parameters has been listed in Table 4. The compound satisfies the above conditions and proves itself as a potent drug and physiologically active.
Table 4.
The physiochemical properties of the dapsone molecule
| Lipinski rule of 5 parameters | |
|---|---|
| 1. mi Log P | − 0.70 |
| 2. TPSA | 86.19 |
| 3. MW | 260.4 |
| 4. HBA | 4 |
| 5. HBD | 4 |
| 6. No. of violations | 0 |
| 7. No. of rotatable bonds | 2 |
Electrostatic potential
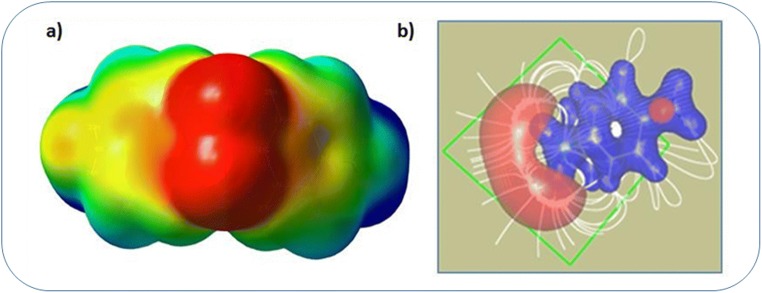
The electrostatic potential is primarily used to trace out the electrostatic positive as well as electrostatic negative regions where the ligand-receptor interactions possibly occur [30]. An asymmetric potential is obtained for the dapsone molecule, and the mapped electrostatic potential surfaces are shown in Fig. 8a where the negative region of the molecule seems to concentrate mainly on O2–S1–O1 (Fig. 8b), and it envelopes mainly on the oxygen atoms O1 and O2 as their respective negative charges are − 1.27e and the average bond length (S1–O1, S1–O2) is 1.47 Å. The color gradient from blue to red shows the positive and negative regions of ESP which pronounces the electrophilic and nucleophilic regions of the molecule. The enveloping of negative nucleophilic to the positive electrophilic seems to enact the lock and key structure as observed in protein-ligand interaction [31]. Figure 8b shows the negative region (red) surrounding O1 and O2, whereas the positive regions (blue) of the molecule show the complete circuits of electric field gridlines, thus distinguishing electrophilic and nucleophilic regions. The grid lines showing the electric field are drawn for the bottom phenyl ring (Fig. 8b) at the isosurface value level 0.24 (blue) to − 0.038 (red) which show the origin of the field grid lines centered at the negative envelope surrounding the atoms O1 and O2 and end up with the positive hydrogen ions.
Fig. 8.
a The isosurface representation of the molecular electrostatic potential of the dapsone molecule. b Lock and key type structure with gridlines of the dapsone molecule
As shown in the lock and key shape of the molecular electrostatic potential of dapsone, the negative potential which is in the vicinity of O1 and O2 atoms is susceptible to severe electrophilic attack. When dapsone is taken as an antibacterial, the nucleophilic/electrophilic region of dapsone interacts with the electrophilic/nucleophilic region of the dihydrofolic acid, and the electrophilicity of the new molecule gets equalized by the electronic charge transfer between the ligand and the receptor [32]. In this manner, dapsone inhibits the growth of a bacterial cell by discontinuing dihydrofolic acid synthesis.
Molecular interaction of dihydropteroate synthase (DHPS) and dapsone
Homology modeling
The crystal structure of DHPS is not available in protein database. Therefore, the proteomic sequence of DHPS (Uniprot ID: P0C0X1) of Mycobacterium leprae was obtained from Uniprot database. The homology modeling of extracted protein sequence was given as an input on the automated SWISS-MODEL server [33]. Based on the integrated deep view method in the server, the complex crystal structure of DHPS of Mycobacterium tuberculosis was selected as a template (PDB ID: 1EYE). Finally, the refined structure was used for further studies.
Ligand preparation
Two-dimensional structure of dapsone (CID: 2955) was obtained from PubChem database. The .sdf file converted into .pdb by using Open Babel tool [34].
Molecular docking
The molecular docking was performed by using Molecular Graphics Laboratory AutoDock (4.2) tools. The preparation of receptor and ligand, grid, and docking calculation was described in the previous studies [35].
Molecular interaction of DHPS and dapsone
Molecular docking calculation of dapsone with target enzyme dihydropteroate synthase (DHPS) generated six clusters of conformers using a root mean square difference (RMSD) tolerance of 2.0°A. The two non-covalent π-cation interactions estimated on the amino acid residues TRP 132 of DHPS with respective oxygen and sulfur atoms of dapsone (Fig. 9). The results suggested that dapsone have played an important role in the dihydrofolic acid synthesis.
Fig. 9.
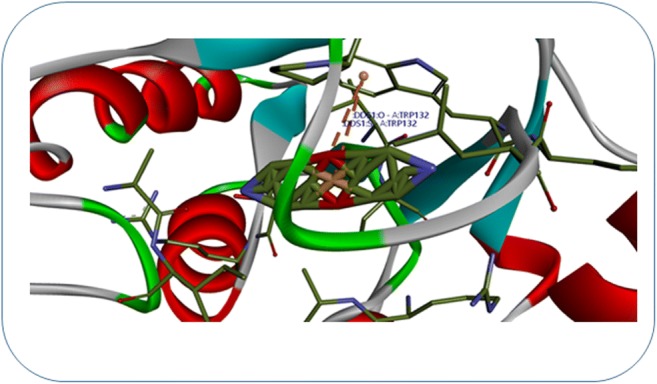
Non-covalent π-cation interactions of dihydropteroate synthase (DHPS) and dapsone. The interacting residues were denoted in blue in color
Conclusions
We have determined the theoretical charge density distribution for the gas phase of dapsone on the basis of the AIM theory. The identification of close contacts and distinguishing them from each other has been accomplished through the Hirshfeld surface analysis and the fingerprint plots. The topological analysis reveals the strength and chemical bonding details of all the covalent bonds in the molecule. The subshells of S atom and lone pairs of O and N atoms are visible in the ELF plots, and the ELF clearly shows the closed-shell interaction of the S–O bonds. In the ESP map, a high electronegative region is found in the vicinity of the O1 and O2 atoms, and this is the active site for electrophilic attack. This theoretical charge density study clearly provides the fine details of structural information, intermolecular interaction, and charge density distribution which are the necessary parameters to interpret the drug-receptor interactions between the dapsone molecule and enzyme of dihydropteroate synthase (DHPS).
Acknowledgments
The authors are grateful to the Principal & Secretary and the Head of PG Department of Physics, The American College, Madurai, India, for their continued encouragement and support during the progress of this work.
Funding information
The authors (S.I, R.N) are grateful for the grant provided by the University Grants Commission, India, in the form of Major Research Project (F.No. 41-848/2012(SR)).
Compliance with ethical standards
Conflict of interest
The authors declare that they have no conflicts of interest.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Natarajan Mookan, Email: natarajanmkudu@mail.zjxu.edu.cn.
Israel Samuel, Email: israel.samuel@gmail.com.
Sarath Babu Mookan, Email: sarathbabum@gargi.du.ac.in.
References
- 1.McEvoy GK. Drug information resources and medication safety. In: Manasse HR Jr, Thompson KK, editors. Medication safety: a guide for health care facilities. Bethesda, MD: American Society of Health-System Pharmacists; 2005. pp. 253–274. [Google Scholar]
- 2.Shepard CC. The experimental disease that follows the injection of human leprosy bacilli into foot-pads of mice. J Exp Med. 1960;112:445–454. doi: 10.1084/jem.112.3.445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Waters MFR. New approaches to chemotherapy for leprosy. Drugs. 1983;26:465–467. doi: 10.2165/00003495-198326060-00001. [DOI] [PubMed] [Google Scholar]
- 4.Wozel G, Blasum C. Dapsone in dermatology and beyond. Arch Dermatol Res. 2014;306:103–124. doi: 10.1007/s00403-013-1409-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Premji Z, et al. Chlorproguanil− dapsone− artesunate versus artemether− lumefantrine: a randomized, double-blind phase III trial in African children and adolescents with uncomplicated plasmodium falciparum malaria. PLoS One. 2009;4:e6682. doi: 10.1371/journal.pone.0006682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Tiono AB, et al. Chlorproguanil–dapsone–artesunate versus chlorproguanil–dapsone: a randomized, double-blind, phase III trial in African children, adolescents, and adults with uncomplicated plasmodium falciparum malaria. Am J Trop Med Hyg. 2009;81:969–978. doi: 10.4269/ajtmh.2009.09-0351. [DOI] [PubMed] [Google Scholar]
- 7.Won YJ, Kim OL, Yu ST, Yoon YW, Choi DY. A case of dapsone syndrome. Korean J Pediatr. 2007;50:493–496. doi: 10.3345/kjp.2007.50.5.493. [DOI] [Google Scholar]
- 8.Castro JG, Morrison-Bryant M. Management of Pneumocystis jirovecii pneumonia in HIV infected patients: current options, challenges and future directions. HIV/AIDS (Auckl) 2010;2:123–134. doi: 10.2147/hiv.s7720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Hughes WT. Use of dapsone in the prevention and treatment of Pneumocystis carinii pneumonia. Clin Infect Dis. 1998;27:191–204. doi: 10.1086/514626. [DOI] [PubMed] [Google Scholar]
- 10.Lee BL, Ileana M, Benowitz NL, Peyton J, Wofsy CB, John MV. Dapsone, trimethoprim, and sulfamethoxazole plasma levels during treatment of Pneumocystis pneumoniain patients with the acquired immunodeficiency syndrome (AIDS): evidence of drug interactions. Ann Intern Med. 1989;110:606–611. doi: 10.7326/0003-4819-110-8-606. [DOI] [PubMed] [Google Scholar]
- 11.Zhu YI, Stiller MJ. Dapsone and sulfones in dermatology: overview and update. J Am Acad Dermatol. 2001;45:420–434. doi: 10.1067/mjd.2001.114733. [DOI] [PubMed] [Google Scholar]
- 12.Chaitanya S, Das M, Bhat P, Ebenezer M. Computational modelling of dapsone interaction with dihydropteroate synthase in Mycobacterium leprae; insights into molecular basis of dapsone resistance in leprosy. J Cell Biochem. 2015;116:2293–2303. doi: 10.1002/jcb.25180. [DOI] [PubMed] [Google Scholar]
- 13.Anna Mendes PS, Schalcher TR, Barros TG, Almeida ED, Maia CSF, Barros CAL, Monteiro MC, Borges RS. J Comput Theor Nanosci. 2011;8(4):1428–1431. doi: 10.1166/jctn.2011.1832. [DOI] [Google Scholar]
- 14.Borges RS, Romero OAS. Structure and reactivity of Imidazolin-Azabutadienes. J Comput Theor Nanosci. 2011;8:1129–1131(3). doi: 10.1166/jctn.2011.1789. [DOI] [Google Scholar]
- 15.Bhattacharya P, Sahoo D, Chakravorti S. Revisit of 4, 4′-diaminodiphenyl sulfone photophysics in different solvents. Ind Eng Chem Res. 2012;51:2505–2514. doi: 10.1021/ie201113b. [DOI] [Google Scholar]
- 16.Salvador P, Ramos-Cordoba E. Communication: an approximation to Bader's topological atom. J Chem Phys. 2013;139(7):071103. doi: 10.1063/1.4818751. [DOI] [PubMed] [Google Scholar]
- 17.Parr RG (1980) Density functional theory of atoms and molecules. In: Horizons of Quantum Chemistry. Springer, pp 5–15. 10.1007/978-94-009-9027-2_2
- 18.McKinnon JJ, Spackman MA, Mitchell AS. Novel tools for visualizing and exploring intermolecular interactions in molecular crystals. Acta Crystallogr Sect B: Struct Sci. 2004;B60:627–668. doi: 10.1107/S0108768104020300. [DOI] [PubMed] [Google Scholar]
- 19.Spackman MA, Byrom PG. A novel definition of a molecule in a crystal. Chem Phys Lett. 1997;267:215–220. doi: 10.1016/S0009-2614(97)00100-0. [DOI] [Google Scholar]
- 20.Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, et al. Gaussian 09, revision A.02. Wallingford: Gaussian Inc; 2009. [Google Scholar]
- 21.Becke AD. Density-functional thermochemistry. I. The effect of the exchange-only gradient correction. J Chem Phys. 1992;96:2155–2160. doi: 10.1063/1.462066. [DOI] [Google Scholar]
- 22.Lee C, Weitao Y, Parr RG. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys Rev B. 1988;37:785–789. doi: 10.1103/PhysRevB.37.785. [DOI] [PubMed] [Google Scholar]
- 23.Keith TA, Gristmill TK (2017) AIMAll (version 17.01.25) software, Overland Park, KS
- 24.Vega AD. AIM-UC: an application for QTAIM analysis. J Comp Methods in Sci Eng. 2014;14:1–3. doi: 10.3233/JCM-140491. [DOI] [Google Scholar]
- 25.Lu T, Chen F. Multiwfn: A multifunctional wavefunction analyzer. J Comput Chem. 2012;33:580–592. doi: 10.1002/jcc.22885. [DOI] [PubMed] [Google Scholar]
- 26.Allen FH, Kennard O, Watson DG, Brammer L, Orpen AG, Taylor R. Tables of bond lengths determined by X-ray and neutron diffraction. Part 1. Bond lengths in organic compounds. J Chem Soc Perkin Trans. 1987;2:S1–S19. doi: 10.1039/P298700000S1. [DOI] [Google Scholar]
- 27.Wolff SK, Grimwood, DJ, McKinnon JJ, Turner MJ, Jayatilaka D, Spackman MA (2012) Crystal Explorer 3.0. University of Western Australia, Perth
- 28.Spackman MA, McKinnon JJ. Fingerprinting intermolecular interactions in molecular crystals. CrystEngComm. 2002;4:378–392. doi: 10.1039/B203191B. [DOI] [Google Scholar]
- 29.Lipinski CA, Lombardo F, Dominy BW, Feeney PJ (2001) Experimental and computational approaches to estimate solubility and permeability in drug discovery and development settings1PII of original article: S0169-409X(96)00423-1. The article was originally published in Adv Drug Deliv Rev 23(1997)3–25. 10.1016/S0169-409X(96)00423-1. Adv Drug Deliv Rev 46:3–26 10.1016/S0169-409X(00)00129-0 [DOI] [PubMed]
- 30.Politzer P, Murray JS. Computational prediction of condensed phase properties from statistical characterization of molecular surface electrostatic potentials. Fluid Phase Equilib. 2001;185:129–137. doi: 10.1016/S0378-3812(01)00463-0. [DOI] [Google Scholar]
- 31.Politzer P, Murray JS. The fundamental nature and role of the electrostatic potential in atoms and molecules. Theor Chem Accounts. 2002;108:134–142. doi: 10.1007/s00214-002-0363-9. [DOI] [Google Scholar]
- 32.Hans-Joachim Böhm, Schneider G (2003) Protein-ligand interactions: from molecular recognition to drug design. 10.1002/3527601813
- 33.Waterhouse A, Bertoni M, Bienert S, Studer G, Tauriello G, Gumienny R, Heer FT, de Beer TAP, Rempfer C, Bordoli L, Lepore R, Schwede T. SWISS-MODEL: homology modeling of protein structures and complexes. Nucleic Acids Res. 2018;46(W1):W296–W303. doi: 10.1093/nar/gky427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.O'Boyle NM, Banck M, James CA, Morley C, Vandermeersch T, Hutchison GR (2011) Open babel: an open chemical toolbox. J Chem 3(1): 33. 10.1186/1758-2946-3-33 [DOI] [PMC free article] [PubMed]
- 35.Selvaraj G, Kaliamurthi S, Thirugnasambandan R. Effect of Glycosin alkaloid from Rhizophora apiculata in non-insulin dependent diabetic rats and its mechanism of action: in vivo and in silico studies. Phytomedicine. 2016;23(6):632–640. doi: 10.1016/j.phymed.2016.03.004. [DOI] [PubMed] [Google Scholar]