Automated Delineation of Cancer Service Areas in Northeast Region of the United States: A Network Optimization Approach

Abstract

Objective

Derivation of service areas is an important methodology for evaluating healthcare variation, which can be refined to more robust, condition-specific, empirically-based automated regions, using cancer service areas as an exemplar.

Data sources/study setting

Medicare claims (2014–2015) for the 9-state Northeast region were used to develop a ZIP-code-level origin-destination matrix for cancer services (surgery, chemotherapy, and radiation).

Study design This population-based study followed a utilization-based approach to delineate cancer service areas (CSAs) to develop and test an improved methodology for small area analyses.

Data collection/extraction methods

Using the cancer service origin-destination matrix, we estimated travel time between all ZIP-code pairs, and applied a community detection method to delineate CSAs, which were tested for localization, modularity, and compactness, and compared to existing service areas.

Principal findings

Delineating 17 CSAs in the Northeast yielded optimal parameters, with a mean localization index (LI) of 0.88 (min.; 0.60, max: 0.98), compared to the 43 Hospital Referral Regions (HRR) in the region (mean LI 0.68; min. 0.18, max. 0.97). Modularity and compactness were similarly improved for CSAs v. HRRs.

Conclusions

Deriving cancer-specific service areas with an automated algorithm that uses empirical and network methods showed improved performance on geographic measures compared to more general, hospital-based service areas.

INTRODUCTION

Medical care epidemiology has occupied a sub-field within epidemiology for many decades^1–6 as a branch examining distributions of disease in relation to specific health care services (exposures) and outcomes. The choice of spatial unit(s) with which to measure disease and related care/outcomes is important for appropriately assessing how well cancer incidence, prevalence, and survival are aligned with the resources needed to address those. A reliable geographic unit is critical for researchers, practitioners, and policy makers to evaluate health care delivery in the United States (US)^6,7. Geopolitical units (e.g. county, state), administrative units (e.g. township, city), or census units (e.g. metropolitan statistical area) are ill suited for health care research because they are not based on local health care markets. The Dartmouth Atlas Project measured health care utilization nationally by deriving health care markets for inpatient care (Hospital Service Areas – HSAs and Hospital Referral Regions - HRRs) and primary care^2,8. Such units are designed to capture local patient care patterns and are defined as units of analysis to examine the geographic variation of the health care system^7,9–12. Furthermore, these units have been instrumental in informing health policy related to workforce issues in Congress^13–17 and other stakeholders^16–19.

An estimated 1.6 million new cancers were diagnosed in 2014, adding to the nearly 13 million Americans living with a history of cancer.²⁰ Now, more than two-thirds of patients enjoy survival beyond 5 years from cancer diagnosis – up from less than half in 1975.²¹ Cancer incidence is expected to rise by 45% from 2010 to 2030, which will increase the need for cancer care along the continuum of services.²² These trends may widen racial disparities in cancer care, which persist despite advances in cancer treatments.²³ Innovations in oncology care, complex treatment paradigms, and specialty settings are likely to create distinct health care markets²⁴ from HSAs and PCSAs for cancer patients. Cancer care has been identified as a distinct patient population with unique sets of services, needs, technologies, and clinical specializations. A new system of Cancer Service Areas (CSAs) is called for to best evaluate cancer care utilization, assess cancer-centered outcomes, identify actionable disparities, and optimize resource allocation.

There have been methodological advancements for delineating HSAs in a Geographic Information Systems (GIS) environment. Previously researchers¹ proposed the most promising approach, namely the community detection method. Built upon a modularity optimization method in the complex network analysis literature, they developed an automated, network-based, and scale-flexible method to delineate HSAs and HRRs that maximize patient flows within each unit and minimize flows between them. In doing so, the expectation is that the resulting units represent service areas that are more tightly tied to the spatial distributions of service utilization among underlying populations.

Innovations in oncology care, complex treatment paradigms, and specialty settings are likely to create unique health care markets for cancer patients²⁴. Well-defined geographical units relevant to distinct patient populations would provide vital information to researchers and policy makers when evaluating specific health care delivery systems^6,7. Despite their popularity, the Dartmouth HSAs and HRRs were based on the 1992–93 Medicare data, with an update in 2006, but require more frequent updating^7,25,26. Thus, they may not be the most appropriate units for analysis pertaining to cancer health care markets. Cancer care, with unique sets of services, needs, technologies, and clinical specializations might be best served with a new system of Cancer Service Areas (CSAs). CSAs would provide an essential tool for evaluating cancer care utilization, assessing cancer-centered outcomes, identifying actionable disparities, and optimizing resource allocation.

This paper describes refinements of the community detection method previously developed¹ as a proficient network optimization method well-suited to the unique challenges and desirable properties of defining condition-specific service areas – namely, CSAs.

STUDY AREA AND DATA

The study area was comprised of the nine-state Northeast Census Region (Maine, New Hampshire, Vermont, Massachusetts, Connecticut, Rode Island, New York, New Jersey, and Pennsylvania) in the US, hereafter, referred to as “Northeast Region” (Figure 1).

Figure 1.

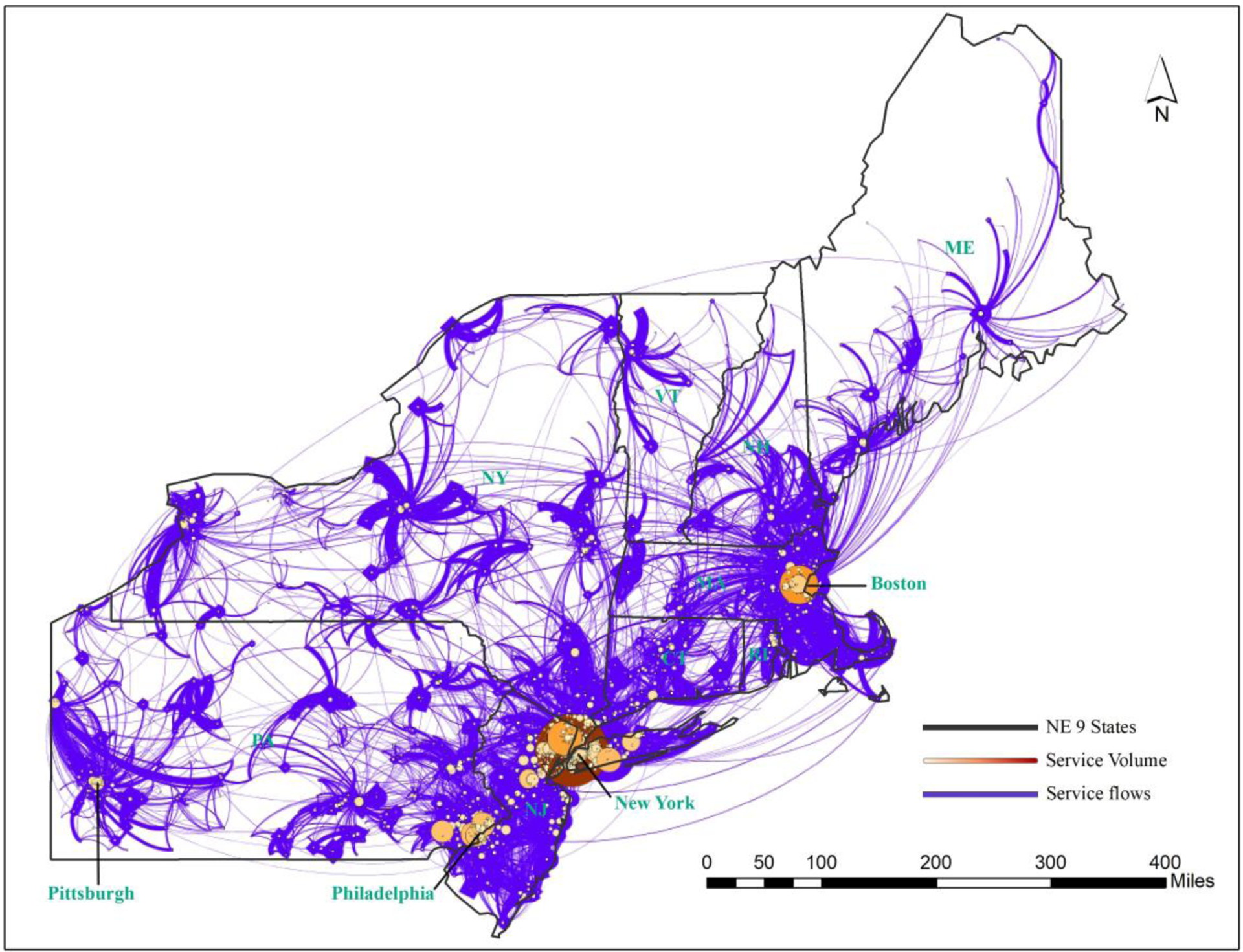
Network of Cancer Service Volumes between ZIP Code Areas in Northeast US (2014–15)

Population

Patients for this study were identified through the Medicare beneficiary denominator file from the Centers for Medicare and Medicaid Services (CMS) from January 1, 2014 to September 30, 2015. Patients who were enrolled in Medicare Parts A and B, aged 65 to 99 years for at least one month per year in the study time frame were included. Patients enrolled in a health maintenance organization plan or had end stage renal disease were removed from the cohort.

Defining a cancer patient denominator

Cancer patients were identified using diagnosis codes (International Classification of Diseases, Ninth Revision, Clinical Modification: ICD-9-CM) listed for 26 cancer types²⁷. Cancer services were ascertained by ICD-9-CM procedure and Current Procedure Terminology (CPT) and Healthcare Common Procedure Coding System (HCPCS) codes found in the Medicare Provider Analysis and Review, Outpatient and Part B claims files. Cancer services were defined as cancer-directed surgical procedures, chemotherapy and radiation treatment codes.

Ascertainment of cancer-related services

We focused on key categories of primary treatment: cancer-directed surgery, chemotherapy, and radiation. A validated set of claims codes for ascertaining chemotherapy and radiation were publicly available through the CMS contracted, Research Data Assistance Center²¹. A validated set of codes for cancer-directed surgery was not publicly available; thus, we created this set with a robust approach (Appendix Table 1).

ZIP Code determination for patient origins and destinations

The patient ZIP code was captured for each service and defined as the ‘origin’ ZIP code. Patient origin ZIP codes (ZIP of residence) for cancer services were linked to Medicare Provider of Services files by provider code in order to obtain a ‘destination’ ZIP code (ZIP of facility location). Service volumes were calculated for each origin-destination (OD) ZIP code pair to create an OD matrix. Volumes of less than 11 were suppressed per CMS data use agreement. Creation of OD matrices was performed in SAS²⁸.

METHOD

Data Initialization

The spatial data included both the polygon and point layers of ZIP code areas. The polygon layer of the ZIP code areas was extracted from the 2015 Cartographic Boundary Shapefiles - ZIP Code Tabulation Areas on the Census web site²⁹. The corresponding point layer was the population-weighted centroids of ZIP code areas, calibrated from the 2010 census population data at the census block level. This enabled aggregation or the population data from the block level to the ZIP code area level, which was used in the CSA delineation algorithm (i.e., controlling for CSA size). Point ZIP codes (typically associated with large business entities) were aggregated to the ZIP code area that enclose those points.

Two important data preparation tasks were implemented.

(1). Estimating the travel time OD matrix between ZIP code areas

Estimating the travel time matrix between a large number of ZIP code areas was computationally challenging. Overall, travel time was first estimated by utilizing road networks with associated speed limits and other parameters in ESRI ArcGIS, and later validated and rectified by invoking Google Maps Distance Matrix API³⁰. This process was implemented in the following steps.

First, for travel time on any OD pair anticipated to be:

1. < 3 hours, a road network of all levels of roads from local/neighborhood streets to interstate highways was used to estimate the network travel time in ArcGIS.

2. 3–6 hours, a road network of all highways (including state and interstate) was used to estimate the network travel time in ArcGIS.

3. > 6 hours, travel time was estimated from its geodetic distance divided by a predefined driving speed of 80km/hour in ArcGIS.

The results from the above three subsets were integrated into a dataset of preliminary travel time estimates.

Secondly, a small randomly sampled subset of zip code pairs (124,350 pairs, about 0.1% of the total pairs) was created, and the corresponding travel times in traffic were estimated by invoking the Google Maps Distance Matrix API.

Finally, regression was run on the 1% samples of travel time between the preliminary ArcGIS estimates and the Google-derived, and the regression result was then used to interpolate travel time for the remaining OD pairs.

(2). Estimating the suppressed service volumes (< 11) between zip code areas

A large number of service volumes between ZIP code areas had values fewer than 11 during the study period and were suppressed. A network without the suppressed service volumes would be highly fragmented and would not yield any meaningful delineation of CSAs. The second major data preparation task was to interpolate the missing service volumes for the 56, 317 OD pairs (subset B) from the 29,875 observed service volumes on corresponding OD pairs (subset A). This was achieved by three steps.

First, a gravity-based regression model estimated the observed data subset A to explain the service volumes between ZIP code areas. Adopting the popular power function for the distance decay effect, the gravity model was written as

$$T_{ij}=a{\left(O_i{D}_j\right)}^{\propto }{d}_{ij}^{-\beta }$$ (1)

where T_ij was the number of service volumes from ZIP code area i to ZIP code area j, O_i and D_j were the total service volumes originated from i and ending at j, respectively, d_ij was the travel time between them obtained from the first data processing task, a was a scalar, α was the elasticity parameter for the product term O_iD_j (assuming an identical elasticity for O_i and D_j) and β was the distance (travel time) decay friction coefficient. Rearranging Equation (1) and taking logarithms on both sides yielded

$${\mathit{\text{lnT}}}_{ij}=\mathit{\text{lna}}+\alpha \text{ln}\left(O_i{D}_j\right)-\beta {\mathit{\text{lnd}}}_{ij}$$ (2)

The model can be estimated by a simple ordinary least squares regression model. In our data acquisition process, we were able to extract the product value of O_iD_j from the OD matrix. In the study area, only a negligible number (15) of records in the study area had the values of O_iD_j less than 11 and suppressed, and none in subset A and all in subset B. The regression based on Equation (2) and data subset A yields:

$${\mathit{\text{lnT}}}_{ij}=2.0361+0.2445\text{ln}\left(O_i{D}_j\right)-0.4309{\mathit{\text{lnd}}}_{ij}$$ (3)

with R²=0.234.

In the second step, the estimated gravity model in Equation (3) was used to interpolate the service volumes based on data subset B. Plugging the values of O_iD_j and d_ij from data subset B into Equation (3) and solving for T_ij yielded the preliminary estimated T_ij, denoted as ${\widehat{T}}_{ij}$. Its values ranged from 3 to 107.

The final step was to further adjust the preliminary estimator ${\widehat{T}}_{ij}$ to ${\widehat{T}}_{ij}^{\prime }$ so that its values fell within its feasible range [1, 10]. A simple monotonic transformation ${\widehat{T}}_{ij}^{\prime }=2\mathit{\text{ln}}{\widehat{T}}_{ij}$ served the purpose, and its values were rounded to integers. For the 15 records of suppressed O_iD_j (i.e., the lowest non-zero value), we can simply assume ${\widehat{T}}_{ij}^{\prime }=1$. The rescaling of the preliminary estimator ${\widehat{T}}_{ij}$ to ${\widehat{T}}_{ij}^{\prime }$ for the lower volume trips recognized that the distance decay effect in cancer service volumes may be captured by different functions in various travel time (and here, flow volume) ranges.

Combining the two subsets with observed T_ij in A and interpolated ${\widehat{T}}_{ij}^{\prime }$ in B yielded a complete set of 86,192 records of service volumes that defined the weight (strength) of edge between two nodes (ZIP code areas) i and j in the network. As shown in Figure 1, the network was composed of nodes and edges linking the nodes, and here the circle size represents the total service volume ending at a node (ZIP code area), and the thickness of a flow line reflects the service volume between two nodes. The network of cancer services in the Northeast region was composed of 5,969 nodes and 86,192 records of service volumes with the total service volume (sum of edge weights) of 2,443,538. New York, Boston and Philadelphia anchored major destinations for cancer services in the region with interwoven complex service flows, and the rest of the region was served by smaller local hospitals drawing patients from their surrounding areas.

Community Detection

This research built upon a previously developed method¹ and made several refinements to address some unique challenges in delineating the CSAs. Similar to an agglomerative hierarchical clustering (i.e., bottom-up) approach, the algorithm began by treating every node as a community, and then successively combined communities together by the best agglomeration to form larger communities, until all nodes in the network were grouped into one single community.

A quality measure in network segmentation was modularity, which compared the total number of (weighted) edges within all communities in a given (weighted) network to that of a null model (i.e., random network)³¹. It was formulated as

$$Q=\frac{1}{2m}{\sum }_{ij}\left(A_{ij}-\frac{k_i{k}_j}{2m}\right)\delta \left(c_i,c_j\right)$$ (4)

where Q was the modularity value, A_ij represented the edge weight between nodes i and j, m = ½Σ_ijA_ij was the sum of weights of all edges in the network, k_i = Σ_jA_ij was the sum of weights of edges linked to node, i (i.e., the degree of node i), c_i was the community to which node i was assigned, and δ(x, y) equals 1 when x = y, and 0 otherwise. Equation (4) had calculated the difference of total within-community edge weights between a real flow network and an expected flow network. The value of Q ranged between −1 and 1, and a higher Q corresponded to a better community segmentation. Therefore, community detection was a modularity optimization process that maximized flows within delineated communities while minimizing inter-community flows.

The mathematical solution to modularity optimization was computationally challenging³². The intrinsic scale of modularity was confirmed to have a resolution limit through several practical examples^33,34. A feasible solution involved tunable resolution parameters to allow community detection at different scales^35,36. Incorporating a resolution parameter, equation (4) was rewritten in terms of the contribution from communities instead of nodes:

$$Q={\sum }_{c\in C}\left(\frac{l_c}{m}-\gamma {\left(\frac{k_c}{2m}\right)}^2\right)$$ (5)

Q was again the modularity value and the sum was over the communities C, l_c was twice the number of edge weights within community c ∈ C, k_c was the sum of the edge weights of the nodes in community c ∈ C, m = ½Σ_ijA_ij was the sum of weights of all edges in the network, and γ was the resolution parameter. When γ =1, the modularity function was equivalent to equation (4). A higher value of γ corresponded to a higher resolution, a larger number of communities or smaller communities. An increase in the number of communities did not necessarily correspond to an increase in modularity, and the global optimal Q indicated the ideal tradeoff between the number of communities and the value of each community and thus the maximum modularity at a particular resolution³⁰.

The Louvain community detection algorithm³⁷ was chosen due to its scale flexibility^1,38. It iterated with two phases. In the first phase, each node i in the network was treated as a unique community. When the node was removed from its original community and grouped into one of its neighboring communities (C_j), a local modularity gain (ΔQ) was calculated³⁷:

$$\Delta Q=\left[\frac{{\Sigma }_{in}+2k_{i,in}}{2m}-{\left(\frac{{\Sigma }_{\mathit{\text{total}}}+k_i}{2m}\right)}^2\right]-\left[\frac{{\Sigma }_{in}}{2m}-{\left(\frac{{\Sigma }_{\mathit{\text{total}}}}{2m}\right)}^2-{\left(\frac{k_i}{2m}\right)}^2\right]$$ (6)

where Σ_in was the sum of weights of all edges inside C_j, Σ_total was the sum of weights of all edges that have one of their ends in C_j, k_i was the sum of weights of edges linked to node i, and k_{i, in} represented the sum of weights of edges from node i to all nodes in C_j. Introducing the resolution parameter γ, equation (6) was rewritten as:

$$\Delta Q=\frac{1}{m}(k_{i,in-}\gamma \frac{k_{i*}{\Sigma }_{\mathit{\text{total}}}}{2m})$$ (7)

Repeat this for all nodes until no modularity gain can be obtained. It returned a local optimum of modularity.

In the second phase, treating the communities identified in the first phase as nodes and using the weights of the edges between the new nodes to define a new network, the first-phase process was applied again to further merge the communities. The two-phase iteration continued until no overall modularity gain could be achieved (global optimum) or ultimately all nodes were merged into one large community. In summary, it was a hierarchal clustering process. Since the number of detected communities and their structures were recorded in each iteration, the method was scale-flexible. It recorded every hierarchy of community structures, and enabled a researcher to derive a given number of communities or conduct a sensitivity analysis at a series of scales³⁹. Our original network for the Northeast region of the US had 5,969 nodes and 86,192 edges, where the cancer service volumes defined the edge weights.

Ensuring Spatial Adjacency and Minimum Region Size

For our task of delineating CSAs, the above algorithm required solutions to several practical issues.

1. The spatial adjacency rule. For any initial community delineated by the algorithm that is not contiguous, it is split into multiple sub-communities, each of which forms a contiguous polygon and a node. The spatial adjacency matrix between the nodes is updated, so are the edges between the nodes. Often a node with small population ends up being merged to its neighbor when the other rules are enforced.

2. The geographic island rule. Some ZIP code areas in the study area are islands off the east coast. To fully incorporate these areas in the CSA delineation, a virtual “bridge” is constructed between an island (composed of one or multiple ZIP code areas) and its nearest ZIP code area on the mainland, and such a bridge is represented as a link in the aforementioned spatial adjacency matrix.

3. The orphan node rule. Some nodes (ZIP code areas or generated communities in the process of clustering) with no edges (zero service volume) linked to their surrounding units are termed “orphan nodes.” An orphan node is merged to its neighboring node with the smallest population size in order to achieve the most balanced overall region size for derived CSAs, an important desirable property in regionalization.

4. The threshold size rule. Similar to HSAs/HRRs, another desirable feature in derived CSAs is a minimum size. The Dartmouth HRRs used a population of 120,000 as the threshold size. Similarly, cancer care is a highly specialized health care, and we use the same threshold of 120,000 persons for CSAs. Any intermediately-derived small community is merged to its neighbor to attain positive modularity gain.

Shown in in Figure 2, the workflow of the CSA delineation method was composed of four steps:

1. Data initialization. First, build a network by defining the nodes as ZIP code centroids (each containing an attribute in population) and the edges as flows between two ZIP code areas (their weights as corresponding service volumes). Secondly, construct a spatial adjacency matrix from the ZIP code polygon layers (use a virtual link to connect a geographic island to its nearest ZIP code area in the mainland). Thirdly, initiate a population threshold (i.e. 120,000) and a resolution.

2. Community detection. Apply the community detection method to delineate preliminary communities whose members (nodes) may not be spatially contiguous. Refine the preliminary communities by enforcing the spatial adjacency rule.

3. Ensuring minimum region size. For any intermediately-derived community (node) with its size below the threshold, group it to its neighbor to attain the maximum gain in modularity. When such a node is an orphan (with no edge linking to any of its neighbors), group it to its smallest neighboring community.

4. Deriving CSAs. Join the result from step 3 to the GIS layer of ZIP code polygon, and derive the contiguous CSAs with related attributes (e.g., total population, localization index, compactness index, etc.) calibrated.

Figure 2.

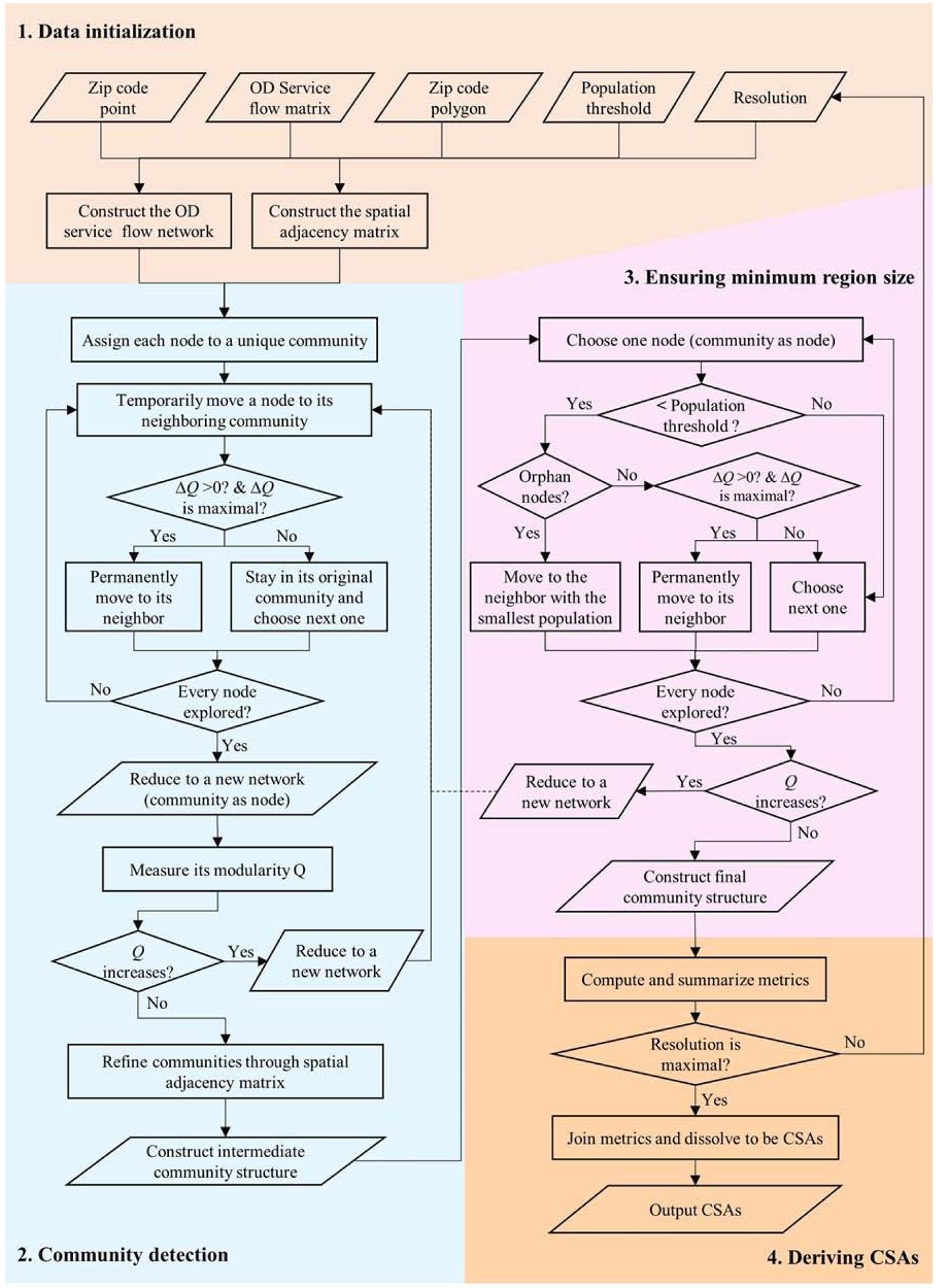
Data Initialization

For our study and using a desktop of Inter(R) Core(TM) i7–4770 CPU@ 3.40GHz with 32GB of memory, Step 1 took 8.75 minutes, and one iteration of Steps 2–4 took less than 1 minute with longer time corresponding to a lower resolution.

GLOBAL OPTIMAL CSAS AND DARTMOUTH-HRRS-COMPARABLE CSAS

One major feature of the network-based modularity optimization method for community detection was its capacity of generating a series of CSAs in response to a user‟s inputs, and thus being scale flexible. To illustrate this, we simulated all 10,000 scenarios for the resolution values ranging 0–10.0 with an increment of 0.001. As the resolution value increased from 0 to 10.0, the number of derived CSAs increased from 1 to 83. As shown in Figure 3, the modularity value peaked at the global optimum of 0.79 with 17 CSAs when resolution was set 1.0, and declined towards both fewer and more CSAs.

Figure 3.

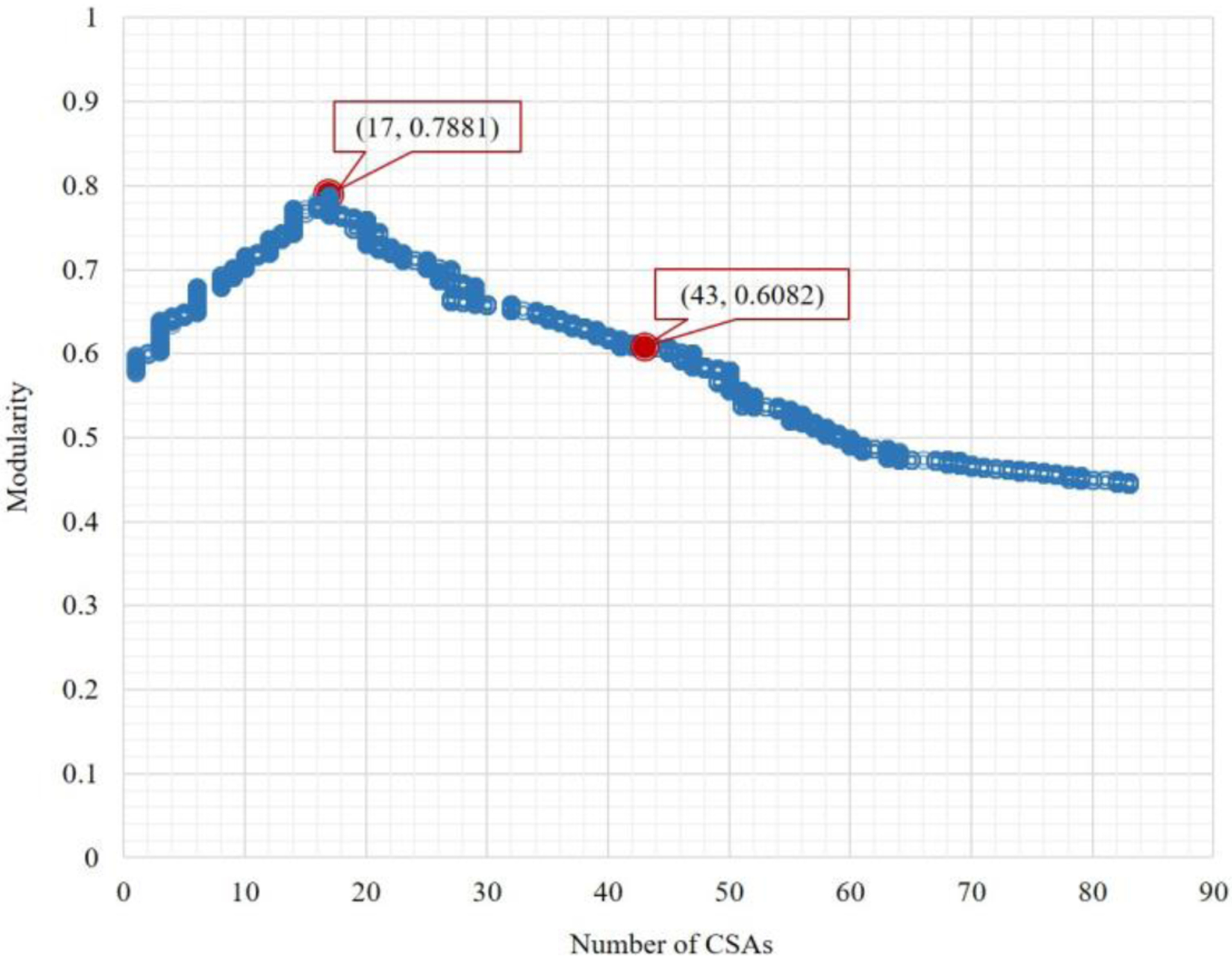
Number of CSAs derived versus modularity

RESULTS

This section examined two cases in depth: (1) 17 CSAs with the global optimal modularity value, and (2) 43 CSAs that are comparable to the Dartmouth HRRs. The former would suggest the optimal configuration of cancer service market in the Northeast Region of the US, and the latter corresponded to the 43 HRRs in the region so a meaningful assessment for the effectiveness of the method could be made by several indicators.

As the most widely-used indicator for local hospitalization patterns, localization index (LI) was the proportion of patients that were treated in the same hospital service area as where they lived. In this study, LI was the ratio of service flows within a CSA (i.e., both trip origins and destinations are in the CSA) divided by the total service flows generated by the CSA (i.e., origins in the CSA and any destinations). In addition to the popular LI, indices such as geometric compactness and region size balance were common measures to evaluate regionalization methods from a geographic perspective (Wang and Robert 2015). Geographic compactness characterized the regularity of a region’s shape based on the perimeter-area corrected ratio or PAC (= P/(3.54*square root (A))), and a lower PAC value indicated a more compact region and was preferred. For example, balanced region sizes, where relatively even population in derived regions, lead to regions that were more comparable.

These measures were reported in Table 1 for the two cases of interest (17 CSAs and 43 CSAs) and the most (83) CSAs. The same indices were also calibrated for the 43 Dartmouth HRRs in the region for comparison. Understandably, the average localization index declined to 0.61 as the number of CSAs increases to 83. Similarly, the averages values of compactness index and population dropped as the number of CSAs increases. Three indices were strongly dependent on scale, and a meaningful comparison needed to be made between cases with similar numbers of units.

Table 1.

Indices for Various CSAs and HRRs in Northeast Region

No. units	Modularity	Localization Index (LI)				Compactness				CSA Population (in 1,000)
		Min	Max	S.D.	Mean	Min	Max	S.D.	Mean	Min	Max	S.D.	Mean
17 CSAs	0.79	0.61	0.98	0.09	0.88	2.10	7.52	1.52	3.73	544	12124	2900	3213
43 CSAs	0.61	0.41	0.98	0.15	0.74	1.56	7.39	1.07	3.03	146	4255	987	1270
43 HRRs	0.70	0.19	0.97	0.18	0.68	1.54	7.83	1.53	3.14	200	4815	1213	1265
83 CSAs	0.44	0.12	0.96	0.20	0.61	1.47	7.78	0.91	2.82	125	2417	451	658

Note: S.D. for standard deviation

As the case of 17 CSAs yielded the highest modularity value, we labelled it as “global-optimal CSAs.” As shown in Figure 3, the delineation of CSAs well captured the interactions between ZIP code areas in service flows. The CSA boundaries did not necessarily align with state borders, but rather enclosed major patient-to-hospital flows with negligible flows between the CSAs. The variation of LI across the CSAs is depicted in Figure 4 The CSA with the lowest LI value (0.61) resided in the center of the study area (Poughkeepsie--Newburgh) and had a population of 1,085,459; and the other 16 CSAs all had LI values above 0.80. One would speculate possible factors influencing the LI values. A simple correlation analysis indicated that CSA population size was positively correlated with LI value, and the correlation was statistically significant. One would suspect that CSAs in high-density large metropolitan areas could have lower LIs because more competition between hospitals was likely to drive down LIs. However, a casual examination of the variability of LI did not suggest necessarily an association with the level of urbanization. For the eight CSAs with LI > 0.90, the CSA with the highest LI = 0.98 was anchored by Pittsburgh, the second highest LI = 0.97 was in the Boston area, the one in the City of New York had the third highest LI= 0.96, and the remaining five were in the Maine, upper state New York, west Pennsylvania, and Philadelphia. No CSAs fell in LI between 0.70 and 0.80, and the rest of CSAs in the middle of the study area had LI between 0.80 and 0.90.

Figure 4.

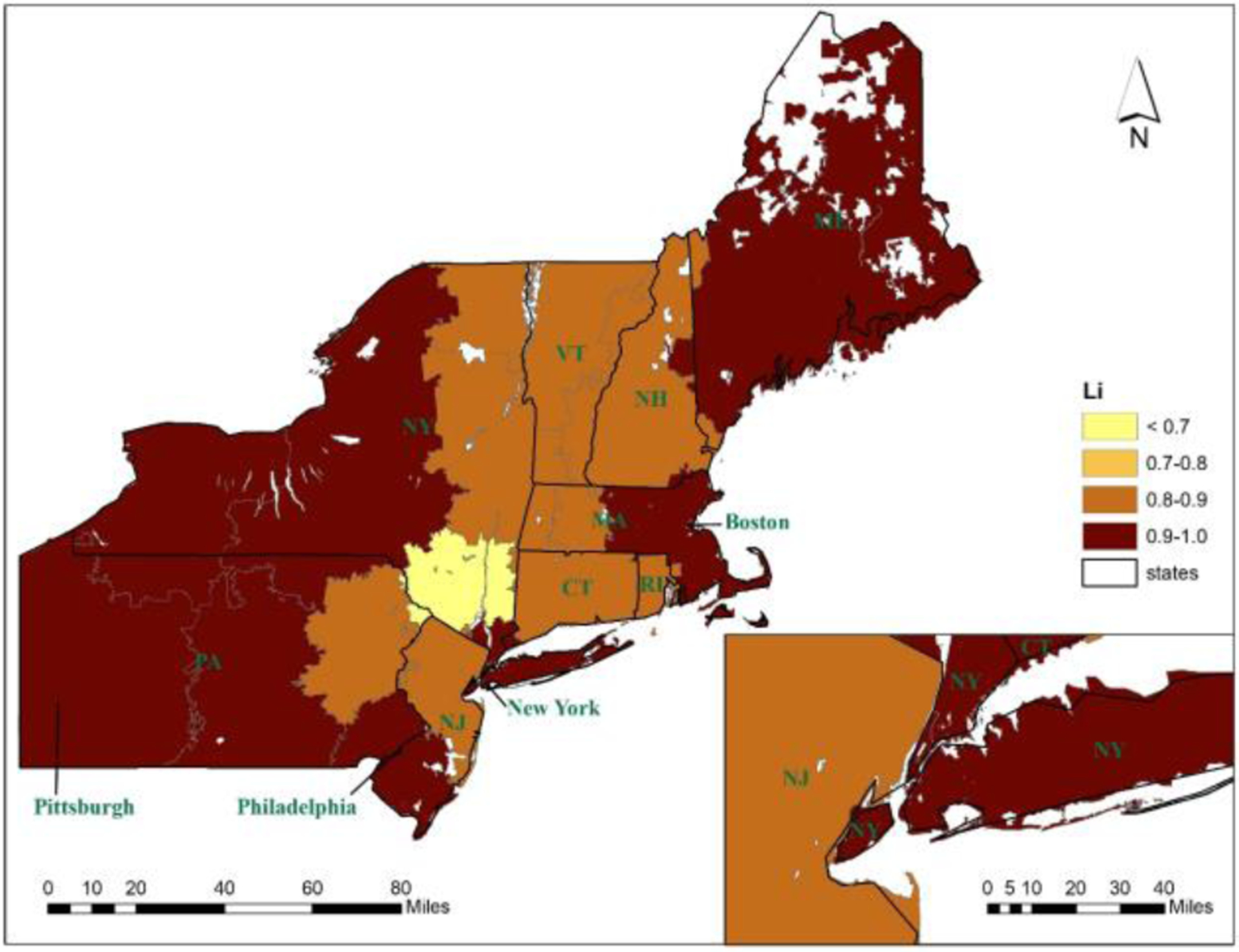
Localization index values in 17 CSAs in the Northeast Region 5

What did we learn from the “global optimal CSAs”? Its derivation was based on a single indicator, modularity, for the quality of network configuration in terms of level of agglomeration in segmented communities or divided submarkets in this study. Perhaps its full value could be only assessed when we have had the chance to examine the change of the study area over time (e.g., CSAs in the same region over years) or the variation of a system across multiple regions of similar size (e.g., CSAs for the study period across census regions in the US). A larger number of global optimal CSAs is likely to reflect a more fragmented market (or more localized submarkets), and a smaller number would correspond to a more tightly-interwoven structure (or more integrated and interdependent system). A similar method¹ yielded 17 global optimal HSAs in Florida, far fewer than the 114 Dartmouth HSAs. That was based on the all-payer inpatient hospital discharge data in one year (i.e., 2011 Healthcare Cost and Utilization Project). While the number of nodes (also ZIP code areas) in Florida was 983, far fewer than 5,969 nodes in this study, its total patient discharges were 2.35 million, very close to our total service volumes of 2.44 million, both of which defined edge weights in the networks.

To demonstrate the advantages of the community detection method, 43 Dartmouth-HRR-comparable CSAs were derived. Some additional CSAs were carved out from the larger 17 CSAs Figure 5 to form the 43 smaller CSAs (multiple sub-markets within each market). Figure 5 overlaid the same number of CSAs and HRRs to highlight the differences between them. Once again, the CSAs were well aligned with service flows that radiated from one or multiple interconnected anchoring nodes, and the flows between the CSAs were minimal Figure 5. In contrast, when the network flows were overlaid with the same number of HRRs defined in the Dartmouth Atlas Figure 5, the discord was evident. Note that only flows with service volume ≥30 were included in Figure 5 (middle and last panel in appendix) to highlight major flows. One CSA at the southwest corner of the region (Pittsburgh: upper-left inset of Figure 5) with closely- interwoven service flows was split into three HRRs. Another example was the east Massachusetts grouped into a massive HRR with a population of 4.79 million (shown in the lower-right inset of Figure 5) but it became four CSAs (shown in the lower-right inset of Figure 5). Decomposition of such a large unit was preferred as it helped balance the CSA size and enabled researchers to examine possible variability within it. As shown in Table 1, overall the average LI was 0.74 in 43 CSAs, significantly higher than 0.68 in 43 HRRs. The range for LI for the CSAs (0.41–0.98) was far more favorable than the HRRs (0.19–0.97).

Figure 5 (Combined Panel).

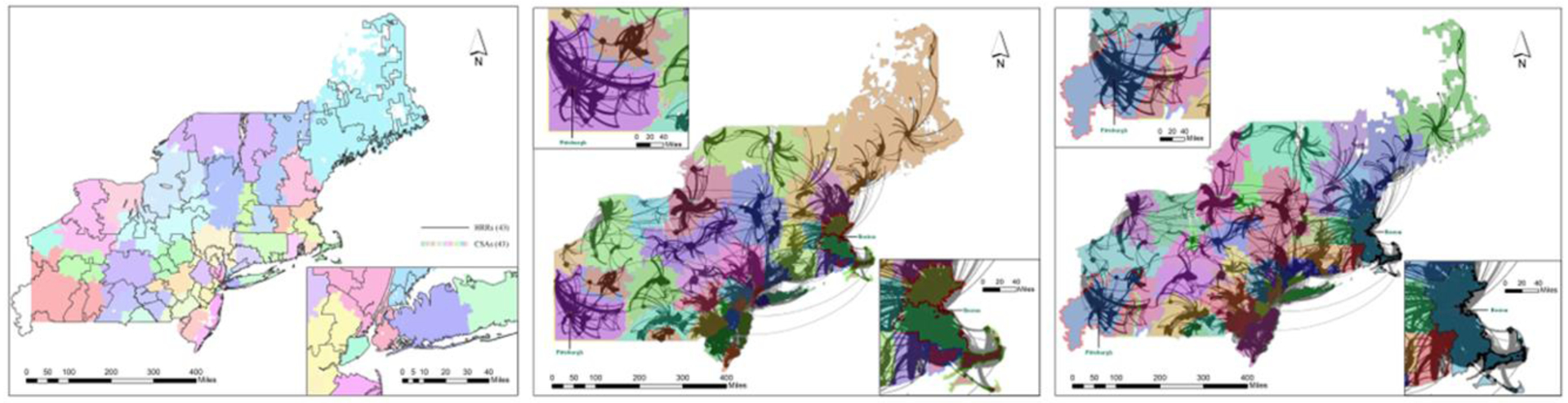
Dartmouth HRRs and Service Flows, then demonstrating the Service Flows overlaid in the Northeast Region (service flows≥30). 6

In terms of shape compactness, the difference in average values between the 43 CSAs and 43 HRRs was insignificant with a slight edge (smaller and thus more compact) for the CSAs, but a much smaller variability in CSAs (standard deviation = 1.07 for CSAs and 1.53 for HRRs). Given the same number of units, the mean for unit population should be the same. Here the average population in 43 HRRs was slightly smaller than that in 43 CSAs as the HRRs crossed the state borders and left out small areas in southwest Pennsylvania, southwest corner of New Jersey and northwest corner of Maine. A lower standard deviation for population (987) in CSAs than that (1,213) in HRRs indicated a better balance region size and thus more favorable.

CONCLUDING REMARKS

Cancer care is distinct from other healthcare services and requires a scientific method to define Cancer Service Areas (CSAs) to capture the structure of its unique market This research reported a pilot study on developing a spatially-constrained community detection method for delineating CSAs that is automated, scale flexible, and computationally efficient. In short, the cancer care market is tangled in a complex patients-to-hospitals network, but mainly evolves around magnets that anchor distinctive local communities. The method could be used in any market or region segmentation with a network-based flow data.

The enhancements of the network-based community detection approach enable the construction of CSAs maximizing cancer patient flows within spatial units and minimizing the flows between units. This is evidenced in more favorable LI values and more balanced region size in the derived CSAs than comparable HRRs. The CSAs were found to be robust, yet versatile as comparative spatial units specific to cancer care. It is also worthwhile to point out that the two major data preparation efforts (i.e., estimating a large OD travel time matrix and interpolating suppressed service flow data) could be beneficial for researchers who encounter similar tasks.

While the method was scale flexible and generated a series of CSAs, it detected the “global-optimal CSAs” in terms of network modularity. The value of such an optimal number of CSAs would need to be examined in more depth in future studies, focused on either temporal changes in a study area or on variation across regions with comparable size. Like other network optimization methods, the Louvain algorithm, the backbone of our method, was a heuristic method and may not be the best one for delineating CSAs or health care markets in general. Other upgrades to our method should consider incorporation of additional constraints for derived regions such as threshold localization index, cap for region size, maximum travel time within a region, or some required property on the geometric shape.