Observation of indentation-induced shear bands in a metal−organic framework glass

Significance

As a newly emerged glass family, the melt-quenched metal−organic framework (MOF) glasses have attracted considerable attention from scientists. Recently, several important breakthroughs have been achieved concerning their structure, glass formation, dynamics, and thermodynamic evolution. However, the fracture behavior of these glasses upon mechanical loading has not yet been reported. Here we obtained a fracture pattern of a MOF glass upon indentation, and revealed anomalous cracking behavior. We detected the occurrence of shear bands with a sliding extent of ∼35 nm. Both the fracture behavior and the deformation mechanism could be associated with the coordinative bonds in ZIFs. This work contributes to obtaining a general picture about the fracture mechanism of brittle glasses.

Abstract

Metal−organic framework (MOF) glasses are a newly emerged family of melt-quenched glasses. Recently, several intriguing features, such as ultrahigh glass-forming ability and low liquid fragility, have been discovered in a number of zeolitic imidazolate frameworks (ZIFs) that are a subset of MOFs. However, the fracture behavior of ZIF glasses has not been explored. Here we report an observation of both cracking pattern and shear bands induced by indentation in a representative melt-quenched ZIF glass, that is, ZIF-62 glass (ZnIm_1.68bIm_0.32). The shear banding in the ZIF glass is in strong contrast to the cracking behavior of other types of fully polymerized glasses, which do not exhibit any shear bands under indentation. We attribute this anomalous cracking behavior to the easy breakage of the coordinative bonds (Zn−N) in ZIF glasses, since these bonds are much weaker than the ionic and covalent bonds in network glasses.

Metal−organic frameworks (MOFs) are composed of metal nodes and organic linkers. An important subset of MOFs is the zeolitic imidazolate frameworks (ZIFs), which exhibit higher thermal and chemical stability than other subsets (1, 2). Like silica or zeolites, ZIFs have a three-dimensional (3D) network structure, which is constituted by interconnected metal−ligand tetrahedra. The tetrahedron consists of one central transition metal and four imidazolate ligands (3–6). Recently, it was discovered that some ZIFs can be melted and subsequently quenched to the glassy state prior to thermal decomposition (7–12). This new family of melt-quenched glasses is structurally and chemically distinct from other traditional glass families such as metallic, organic, and inorganic ones.

Despite progress in understanding the structure and properties of ZIF glasses (12–16), their mechanical properties have been studied to a very limited extent; in particular, their cracking behavior has not been reported so far. However, to understand the nature of ZIF glasses and to find their application fields, it is necessary to study their fracture and deformation behavior. Therefore, in the present work, we investigated the mechanical properties of ZIF glasses by using ZIF-62 glass as a representative object of our study. We chose ZIF-62 glass because it can be made in relatively large, homogeneous bulk samples for mechanical testing, and also because it has already been studied regarding its structure (10) and various material properties (11, 15, 16).

ZIF-62 (Zn(Im)_2-x(bIm)_x) is an excellent glass former, in which the central Zn node is connected by two types of ligands: imidazolate (Im) and benzimidazolate (bIm) (2, 17, 18). ZIF-62 exhibits higher thermal and structural stability in the liquid state compared to other ZIFs; for example, a broader temperature range (about 100 K) exists between melting and decomposition (SI Appendix, Fig. S1) (8, 10). ZIF-62 glasses were found to have ultrahigh glass-forming ability (T_g/T_m = 0.84, where T_g is glass transition temperature and T_m is melting point) and high viscosity (∼10⁵ Pa⋅s) at T_m (10), as well as structural stability upon heating (11). The structural difference between ZIF-62 crystal and glass has recently been revealed by X-ray total scattering and X-ray photoelectron spectroscopy analyses (10). In terms of pair distribution functions, ZIF-62 crystal features a high degree of short- (<about 7 Å), intermediate- (about 7 Å to 20 Å) and long-range (>20 Å) order, whereas ZIF-62 glass is characterized by a high degree of intermediate- and long-range disorder (10). A high degree of intermediate structural disorder in ZIF glasses is also present (14). Indirect evidence for the local structural disorder has been obtained by performing thermal treatment on ZIF-4 glass (14). When heating this glass in a differential scanning calorimeter to the temperature of ZIF-zni formation, an exotherm occurred around a similar temperature, but a Bragg peak was not observed; that is, long-range order did not appear. Thus, the exotherm could be associated with the decrease in the degree of the local structural disorder.

In previous studies, the indentation modulus of ZIF-62 glass was determined to be about 6 GPa, by means of nanoindentation (8), while its Poisson’s ratio was found, by Brillouin scattering, to be 0.45 (10). Usually, glasses with a higher Poisson’s ratio exhibit higher ductility than those with a lower ratio (19). However, the ZIF glass displays an anomalous behavior; that is, it features easy crack nucleation despite its high Poisson’s ratio (see Results). The reason for this anomalous behavior, as well as the detailed fracture mechanism of ZIF glasses, has not been explored so far. To the best of our knowledge, there is only one report on the creep and scratch behaviors of ZIF-62 glass (15). In the present study, we performed microindentation and nanoindentation on ZIF-62 glass to study its deformation and crack initiation behavior and fracture patterns during sharp contact loading. We compare the hardness values of ZIF-62 glass with those of metallic and oxide glasses, explain the origin of their difference, and attempt to clarify its subsurface cracking and deformation mechanism.

Results

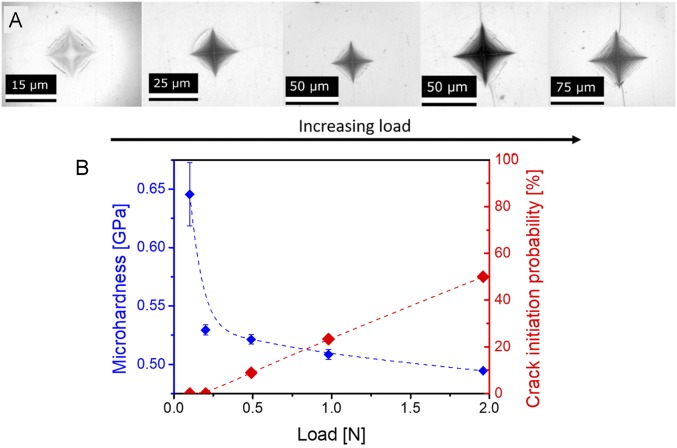
Fig. 1A shows the obtained Vickers indent impressions, suggesting the occurrence of sink-in in the ZIF glass, that is, deformation downward with respect to the sample surface. A change in the cracking pattern with increasing load is observed, that is, the crack probability increases with increasing load, with radial cracks initiating at the highest loads (0.5 N). The crack resistance (CR), as determined from the load at 50% probability of initiation of radial cracks (20), is estimated to be around 2 N (Fig. 1B, red points). The microindentation data are also used to calculate Vickers hardness. As shown in Fig. 1B, the hardness first decreases drastically from 0.65 GPa to 0.53 GPa with increasing load from 0.1 N to 0.2 N, and then gradually decreases from 0.53 GPa to 0.50 GPa for higher indentation loads. This two-step trend is in contrast to the trend for other types of materials, where the indentation size effect typically leads to a continuous nonlinear hardness drop (21). The first stage of the hardness drop for ZIF-62 glass could be ascribed to a drastic decrease in the free volume of the glass network when the load is slightly increased, since the coordinative Zn−N bonds are more easily broken compared to other types of bonds such as metallic, covalent, ionic ones (21). The second stage could be associated with the indentation size effect (22, 23), that is, an increased ratio between indentation surface and deformation volume with decreasing load. This means that the elastic contribution to the total deformation caused by indentation becomes larger at a lower load (24, 25).

Fig. 1.

Indentation behavior and Vickers microhardness for ZIF-62 glass in the load range of 0.1 N to 1.96 N. (A) Indent images (note the different scale) for increasing load as shown by the arrow. (B) Microhardness (blue points) and crack initiation probability (red points) as a function of applied load. The dashed lines are guides for the eyes.

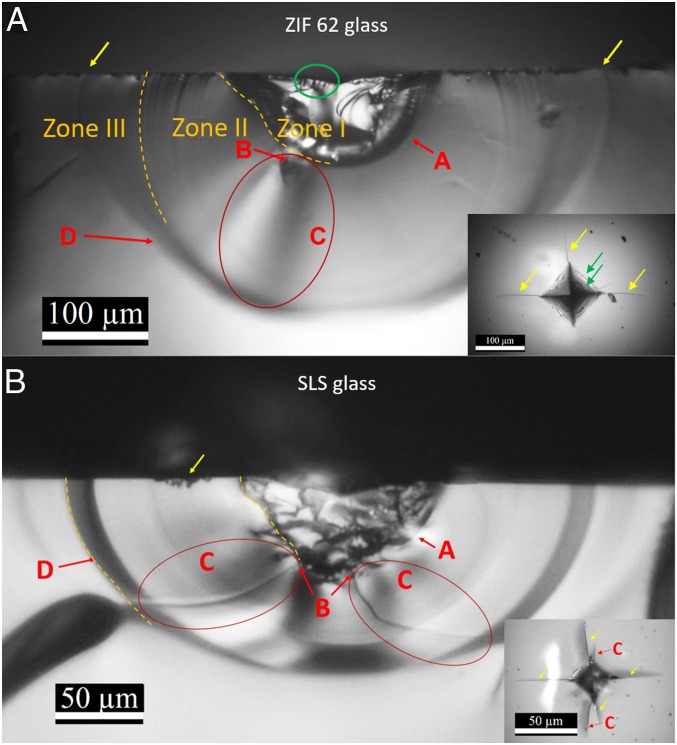
Fig. 2A shows the optical images of the cross-section of an indent along one horizontal crack (Fig. 2A, Inset) generated under the maximum load of 5 N for the ZIF-62 glass. The subsurface area can be divided into three main zones, as marked in Fig. 2A, in order to study the crack initiation and material deformation mechanisms (26). Zone I refers to the process zone (i.e., densified region), which is located below the visible indent and constitutes a strongly deformed contact zone with a clear hemispherical boundary (denoted as A). In zone I, we also observe microcracks originated at the surface (see green ellipse in Fig. 2A). The microcracks will be further illustrated in Fig. 3. Zone II is the nearly spherical elastic zone (27), which lies between zone I and the undeformed glass matrix. In this zone, both median and radial cracks can be observed. The median crack initiates at point B and then propagates further as indicated by C (see the red circles in Fig. 2A). The radial cracks occur as a semicircle (indicated by D in Fig. 2A). Zone III is the semispherical domain, which is situated outside of zone II and is bordered by the glass matrix that is not subjected to deformation during indentation. Here we should note that the extra cracks in this zone might have been created during the bending fracture of the sample for cross-sectional observations. The occurrence of the three zones is a typical feature of most silicate glasses (26, 28), which are topologically similar, despite the difference in bond strength, to the present ZIF-62 glass. This is due to the tetrahedral O−Si−O and Im−Zn−bIm building units in the former and latter, respectively. As shown in Fig. 2B, the standard soda−lime−silica (SLS) window glass, included for comparison, exhibits a fracture pattern similar to the ZIF-62 glass.

Fig. 2.

Cross-section view of an indentation deformed zone on (A) ZIF-62 glass and (B) SLS glass after loading with maximum force of 5 N. Different subsurface features are observed: A, strongly deformed zone; B, initiation point of the median crack; C, propagation zone of the median crack; D, radial crack; yellow arrows, points at which radial cracks reach surface of the sample; green ellipse, examples of the lines visible inside indents, corresponding to shear bands and edge cracks. Insets are top views of indents with radial cracks (yellow arrows) and lines visible inside the indent (examples shown with green arrows) and median cracks for SLS glass (red arrows, C). More detailed top view image of indent on ZIF-62 can be found in SI Appendix, Fig. S2.

Fig. 3.

AFM measurements on the indent walls (1.96 N) of the ZIF-62 glass with visible cracks and shear band: A, radial crack; B, edge crack; C, shear band. (A) Optical microscopy image of 1.96 N indent, with the red square showing the AFM scanned area. (B) A two-dimensional height profile of the AFM scanned area, showing a crack (designated as A) and a shear band (designated as B). Note the change of height in the vicinity of the observed shear band. (C) AFM height profile through a shear band (dashed green line in B), showing an increase in height of around 35 nm at the location of the shear band.

Fig. 3A shows the optical top view image of an indent formed in the ZIF-62 glass under the load of 1.96 N, where we observe a layered indent pattern. In the domain marked by the red square frame, we recorded an atomic force microscopy (AFM) image, showing two distinct cracking features: shear band formation (designated as B) and edge cracking (designated as A), as shown in Fig. 3B. Shear bands or slip lines, which are narrow regions of excessive strain, are typically observed in metallic glasses (29–32), but have also been reported in some modified oxide glasses (33). Remarkably, we are here able to identify the scale of the shear bands. In other words, we discovered a stepwise structural sliding at the nanoscale (here about 35 nm in the vertical direction) within the deformation zone in the ZIF-62 glass upon indentation, as indicated in Fig. 3C. The scale of the shear band varies from one site to another, but is in the range of ∼10 nm to 100 nm. The exact size distribution of the shear band still needs to be determined by collecting more indentation data. Here we focus on the shear band behavior and mechanism. To the best of our knowledge, this behavior has never been observed in other network glasses with fully polymerized structure, that is, completely corner-shared tetrahedral network, for example, in pure silica glass. Small, chipped domains on the sample surface are visible at the end of the radial cracks (yellow arrows on Fig. 2). In Fig. 3A, we also notice that the radial cracks do not originate from the corners of indents, but from the first-formed edge cracks.

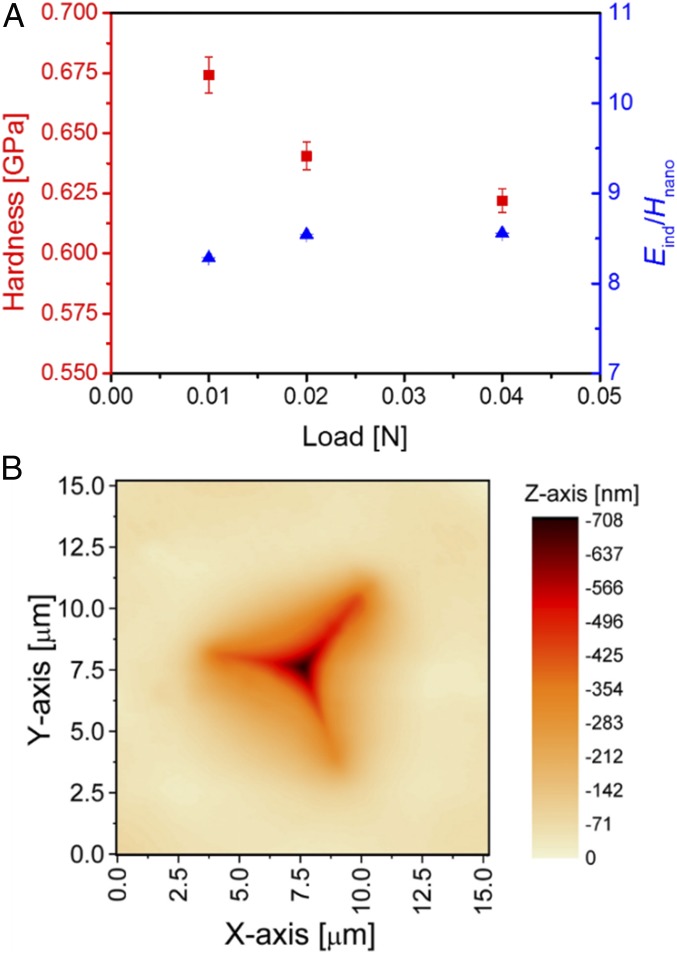
Fig. 4 shows the nanoindentation data, from which we find a decreasing trend in both hardness and indentation modulus with increasing load, similar to that for Vickers microhardness (Fig. 1B). The E_ind/H_nano ratio is about 8.2 at the load of 0.01 N, and then slightly increases to a constant value of 8.5 with increasing load (Fig. 4A). Similarly to the microindentation impressions (Fig. 1A), the nanoindentation impressions after unloading exhibit linearly aligned patterns parallel to the indent edges, being either edge cracks or shear bands (SI Appendix, Fig. S3). The occurrence of cracks at those low loads implies relatively high microbrittleness of ZIF glass. The load–displacement curves (SI Appendix, Fig. S4) have been analyzed to determine the elastic and nonelastic work (see method in SI Appendix, Fig. S5), as well as the relative elastic and nonelastic displacement during indentation (SI Appendix, Table S1). An elastic deformation of about 50% is estimated for all of the applied loads, implying a rather high contribution of elastic deformation to the total deformation induced by indentation loading, compared to most oxide glasses (34). Based on the AFM indent shape analysis (Fig. 4B), only a slight pile-up contribution can be observed in the vicinity of the indents. Observation of pile-up around the indent edges would have been indicative of activated isochoric shear flow during indentation (35). Finally, based on measurements of the longitudinal and transverse sound wave velocities, we calculated the Poisson’s ratio of the ZIF-62 glass to be 0.35. This value is lower than that recently measured by Brillouin scattering (0.45) (10). The origin of this discrepancy still needs to be found in future work.

Fig. 4.

Mechanical properties of ZIF-62 glass as determined by nanoindentation and the nanoindent image obtained by AFM. (A) Hardness (red points) and indentation modulus normalized by nanohardness (E_ind/H_nano, blue points) as a function of applied load. (B) Topographical AFM image of the indent produced under the load of 0.01 N. Note the slight pile-up in the vicinity of the indent.

Discussion

From Fig. 1, the hardness of bulk ZIF-62 glass lies in the range of 0.5 GPa to 0.65 GPa, and it is thus much softer than inorganic network glasses, for example, oxide glasses that possess a range of hardness of 3 GPa to 9 GPa (36). The much lower hardness of ZIF glasses could be attributed to the following four aspects.

First, the 3D ZIF network is constructed through the coordinative bonds between the metal nodes and the N atoms of imidazolate and benzimidazolate ligands. Such bonds are much weaker than, for example, the Si−O bonds in inorganic network glasses. For instance, to break the coordinative bonds of ZIF-4, which is a glass with bond structure similar to ZIF-62, an energy barrier of 81 kJ/mol needs to be overcome (37). In contrast, 443 kJ/mol is required to break the Si−O bonds (38). Consequently, the resistance of the ZIF glasses to densification is significantly lower than that of the oxide glasses.

Second, the density of the topological bond constraints, that is, the number of bond stretching and bond bending constraints per unit of volume, in ZIF glasses is much lower than that in oxide glasses. This is because the volume of the tetrahedral unit Zn(Im/bIm)₄ of ZIF-62 is considerably larger [about 6 Å distance for Zn−Im−Zn (8, 10, 11, 14)] than that of oxide glasses [e.g., 3 Å distance for Si−O−Si (39, 40)] for the same number of linear and angular constraints. It is known that the glass hardness decreases with decreasing volumetric constraint density (41). Thus, the ZIF glasses are softer than the oxide glasses. The detailed calculation of the constraint density will be conducted in a separate work.

Third, ZIF glasses possess a large fraction of organic ligand molecules, which have a higher degree of rotational and translational freedom, for example, compared to the rigid oxide network consisting of [SiO₄] units. Therefore, ZIF glasses are more deformable than oxide glasses upon indentation, as demonstrated in Fig. 2.

Fourth, ZIF materials feature a large amount of free volume, that is, voids. Despite the collapse and disordering of those voids during vitrification, the free volume is still much larger than that of oxide glasses. The larger fraction of voids leads to a lowering of the deformation resistance (42–46).

From the crack pattern of the ZIF glass (Fig. 2A), we can observe both median and radial cracks, as shown in many oxide glasses such as SLS glasses (Fig. 2B). The occurrence of radial cracks correlates well with the relatively high Poisson’s ratio of ZIF glasses (47), yet not with the low elastoplastic E/H ratio which usually corresponds to ring cracking, but not to radial cracking (35, 44, 47). However, the occurrence of the median crack in ZIF glass is an abnormal behavior, since it is a high Poisson’s ratio system (47). This behavior could be related to the coordinative bond in ZIF glasses, which is weaker than the ionic, covalent, and metallic bonds in other families of glasses. The lack of pronounced indent edges in the ZIF-62 glass suggests that sinking-in occurs during loading, while the observed indent shape itself implies a high contribution of elastic deformation to the indentation deformation (48, 49).

In addition, the densification and the stress concentration could play a role in the crack formation during indentation. In oxide glasses, densification does not break the network bonds, but dissipates the energy supplied to the material during indentation. This results in a lower residual stress upon unloading and thus suppresses crack formation to some extent (50). However, given the weak coordinative bond in ZIF-62 glass, it is possible that densification and stress concentration could lead to easier breakage of the network, and thereby promote crack initiation. In our microindentation and nanoindentation experiments, pile-up was hardly detectable, implying that only slight plastic flow occurs. This suggests that densification is predominant in the nonelastic deformation.

As further observed from the indent cross-section (Fig. 2) and AFM measurements on the indent walls (Fig. 3), we have discovered an interesting, anomalous microcracking behavior for the ZIF-62 glass, that is, shear band formation with a discrete jump on the height profile of the indent wall caused by indentation. By “anomalous,” we mean that this phenomenon has not been found in any other fully polymerized 3D network glasses. The nonnetwork metallic glasses and some depolymerized oxide glasses feature shear bands (29–31, 33), but, to our best knowledge, not with a step height of several tens of nanometers, as is the case here. The latter type of shear bands has, however, been observed in some chalcogenide glasses (51). Those typical glasses possess a chain-like network structure, with van der Waals bonding between the chains, effectively lowering the resistance to deformation upon indentation (51). However, the microscopic origin of the shear band formation in the present ZIF glass is distinct from that in the chalcogenide glasses. The occurrence of the shear band also indicates that a localized plastic deformation, rather than macroscopic plastic flow, takes place in ZIF-62 glass.

The shear band formation at the nanoscale is herein verified by the sudden shift of the deformation curve, as measured by AFM (Fig. 3C). The shear bands imply that the stepwise microcrack is accompanied by a stepwise structural sliding upon indentation. More specifically, the formation of shear band must be caused by a translational motion of structural units (52), which, in turn, is due to the Zn−N bond breakage, as these bonds in the ZIF glass are much weaker than other types of bonds, as mentioned above. It should be noted that both the Zn−N bond breakage and reforming process take place dynamically during indentation, and are triggered by the external mechanical energy. The covalent bonds of the ligand molecules in ZIFs are not easily broken; that is, they remain intact during melting, as evidenced by solid-state ¹³C−¹H coupling NMR results (8, 10). Furthermore, due to the weak Zn−N bonds and large linker (imidazole), the Zn−ligand tetrahedra are easily distorted upon melting−quenching; hence, a high degree of short-range disorder is retained in glass state (53), and this also contributes to cracking in ZIF-62 glass.

Here, it should be pointed out that the observed shear band is not a result of melt inhomogeneity, for the following reasons. Usually, one of the major types of inhomogeneous defects in bulk oxide glasses is striae due to an incomplete homogenization process (54). However, the size (length and width in macroscale) of the striae is significantly larger than that of the shear band (in nanoscale) shown in this work. Moreover, the optical transparency of the hot-pressed ZIF-62 glass is similar to that of oxide glasses (16), which is another indication of the high homogeneity of the sample studied in this work. Finally, the spatial fluctuations in the optical transparency of the hot-pressed ZIF-62 glass are rather low (16), again implying the homogeneity of the present sample.

The detection of the shear bands and anomalous fracture behavior in MOF glasses is critical for revealing the impact of bonding features and microstructure of a glass on its mechanical properties. This study is also beneficial for assessing the overall mechanical performances of MOF bulk glasses in order to find their application fields.

Materials and Methods

Sample Preparation and Structural Characterization.

ZIF-62 was synthesized by using the solvothermal method with the Zn:Im:bIm molar ratio of 1:8.5:1.5, which gave the final composition of ZIF-62 crystal Zn(Im)_1.68(bIm)_0.32 based on the relation between the designed and measured Im/bIm ratio reported elsewhere (10). To achieve this ratio, we mixed 17.453 mL of 0.6 M zinc nitrate hexahydrate (Zn(NO₃)₂·6H₂O) (Merck), 33.816 mL of 4 M imidazole (C₃H₄N₂) (Merck), and 21.817 mL of 0.5 M benzimidazole (C₇H₆N₂) (Merck) solutions in N,N-dimethylformamide (DMF) (VWR). This mixture was then magnetically stirred for 1 h. Afterward, the solution was moved to a sealed glass jar (100 mL) and placed in a furnace for 48 h at 403 K. The derived crystals were washed three times in DMF and, finally, once in dichloromethane (Merck). X-ray powder diffraction analysis confirmed that the obtained phase was indeed crystalline ZIF-62 (SI Appendix, Fig. S6A). In order to prepare bulk ZIF-62 glass samples for mechanical testing, we applied the hot-press method (16). The as-prepared crystalline ZIF-62 powder was first put into a metal mold with 10-mm inner diameter. Subsequently, the mold was placed into the hot-press machine (Hefei Kejing Materials Technology Co., Ltd.), in which the sample was compressed under the pressure of 50 MPa and afterward heated under vacuum to 833 K at 5 K/min and held for 30 min. Then, the liquid was cooled down to room temperature, resulting in vitrification. During the hot-press process, the applied pressure and vacuum help, respectively, to remove the bubbles from ZIF-62 melt and prevent the sample from oxidation at high temperature. The glassy nature of the obtained sample was confirmed by X-ray powder diffraction (SI Appendix, Fig. S6A). In order to compare the hot-pressed glass structure to those of both the starting crystalline material and the ambient pressure melt-quenched glass, additional infrared spectroscopy measurements were performed (SI Appendix, Fig. S6C). A difference in infrared spectra between the two samples cannot be identified, indicating that there is no difference in microstructure. Liquid-state NMR measurement was carried out to quantify the ligand ratio in both the crystalline sample and the hot-pressed glass, and the results show that the ligand ratio remains nearly constant after quenching under pressure. This confirms that the ligands do not decompose in a detectable level when the ZIF sample is hot-pressed (SI Appendix, Fig. S6B). Finally, we obtained a 10-mm bulk transparent homogeneous ZIF-62 glass sample without visible bubbles. Samples for indentation measurements were embedded in resin (Struers EpoFix), grinded using SiC paper of grit size 600, 800, 1,200, 2,400, and 4,000, and, finally, polished using a suspension of diamond particles with decreasing size (3, 1, and 0.25 μm).

Mechanical Characterization.

Vickers microindentation was performed using Nanovea CB500 Hardness Tester with loads of 0.1, 0.2, 0.49, 0.98, and 1.96 N to observe the change of microhardness with load and to study the cracking mechanism. The Vickers diamond indenter is a square pyramid with opposite faces at an angle of 136°. For each load, a duration of 6 s was needed to obtain maximum load, while the time of unloading was 60 s. The maximum load was kept for 15 s. In addition to calculating Vickers hardness, we also calculated the probability of crack initiation under loads based on the obtained indent images, which was defined as the ratio between the number of observed cracks and that of indent corners (i.e., four corners per indent). The load corresponding to the crack initiation probability of 50% was considered to be the CR (55).

We examined the crack pattern and shape of the subsurface indent on both ZIF-62 glass and SLS window glass. The composition of SLS is 13Na₂O-6MgO-10CaO-71SiO₂ in mol% and was obtained from Velux A/S. We compare the crack pattern of ZIF-62 glass to that of SLS glass, which is a typical oxide glass that exhibits long radial cracks from the indent corners (56). To view the indent cross-sections of both glass samples, we generated a line of indents with a distance of 1.5 times the indent size between indents, using the maximum load of 5 N. The samples were then broken to obtain fresh fracture surfaces passing through the indents.

To access the deformation patterns, hardness and apparent elastic modulus of ZIF-62 glass were measured under a smaller load (<0.1 N). This was done using nanoindentation (CSM Nanoindentation Tester) with Berkovich tip under maximum loads of 10, 20, and 40 mN. The Berkovich diamond indenter is a three-sided pyramid with the same ratio of project area to depth as the Vickers indenter. The indenter was calibrated using a standard sample of fused silica. The obtained indentation data were analyzed based on the Oliver−Pharr method (57).

AFM measurements were performed using an Ntegra (NT-MDT) instrument and silicon tip cantilevers (NSG10; NT-MDT) in semicontact mode in order to explore the deformation mechanism of ZIF-62 glass under contact loading. Due to the large size of the Vickers microindents, only selected areas (∼3 × 3 µm²) were imaged, while 10-mN nanoindents were imaged in their entirety (∼15 × 15 µm²). The scanning frequency was adjusted according to the size of the topographical image, with the scanning velocity of 3 µm/s for ∼15 × 15 µm² areas and 1 µm/s for the smaller areas. All AFM images have a resolution of 256 × 256 pixels.

Data Availability Statement.

All data discussed in the paper are available in the main text and SI Appendix.