Amyloid assembly is dominated by misregistered kinetic traps on an unbiased energy landscape

Significance

Amyloid fibrils are a type of protein aggregate associated with many neurodegenerative disorders including Alzheimer’s disease. The molecular mechanisms of fibril aggregation have been elusive due to the long time scales involved. Here we present a multiscale simulation algorithm that allows us to “fast forward” through the slow parts of the process and focus all-atom sampling time on faster processes. The results reveal that, in contrast to the folding of native proteins, the kinetics of amyloid aggregation is dominated by nonproductive pathways. This multiscale approach does not involve any free parameters and can be extended to describe other protein binding and assembly processes.

Abstract

Atomistic description of protein fibril formation has been elusive due to the complexity and long time scales of the conformational search. Here, we develop a multiscale approach combining numerous atomistic simulations in explicit solvent to construct Markov State Models (MSMs) of fibril growth. The search for the in-register fully bound fibril state is modeled as a random walk on a rugged two-dimensional energy landscape defined by β-sheet alignment and hydrogen-bonding states, whereas transitions involving states without hydrogen bonds are derived from kinetic clustering. The reversible association/dissociation of an incoming peptide and overall growth kinetics are then computed from MSM simulations. This approach is applied to derive a parameter-free, comprehensive description of fibril elongation of Aβ_16–22 and how it is modulated by phenylalanine-to-cyclohexylalanine (CHA) mutations. The trajectories show an aggregation mechanism in which the peptide spends most of its time trapped in misregistered β-sheet states connected by weakly bound states twith short lifetimes. Our results recapitulate the experimental observation that mutants CHA19 and CHA1920 accelerate fibril elongation but have a relatively minor effect on the critical concentration for fibril growth. Importantly, the kinetic consequences of mutations arise from cumulative effects of perturbing the network of productive and nonproductive pathways of fibril growth. This is consistent with the expectation that nonfunctional states will not have evolved efficient folding pathways and, therefore, will require a random search of configuration space. This study highlights the importance of describing the complete energy landscape when studying the elongation mechanism and kinetics of protein fibrils.

Aggregation of misfolded proteins has been implicated in many devastating and currently incurable medical disorders such as Alzheimer’s and prion diseases (1–3). In these diseases, the misfolded protein forms insoluble fibrils as well as various soluble oligomers. Although the state involved in disease progression is still a matter of dispute (4–8), it is clear that the population of the different aggregated states is a function of the kinetic processes governing their formation. In particular, the fibril state serves as an important sink of protein mass and may be related to distinct clinical outcomes (9). In addition, understanding the mechanism of β-sheet rich assemblies may also be valuable for the design of biomaterials (2, 10).

Experiments have shown that amyloid β (Aβ) fibrils grow one monomer a time, which has been described by a two-step “Dock and Lock” model (11–14). In this model, an Aβ monomer rapidly adheres to a preformed fibril (dock step), followed by a slow lock step where the unstructured incoming peptide adopts an extended β-conformation (8, 11, 15). However, further experimental dissection of the aggregation process is hindered by numerous metastable substates that interconvert rapidly (3). Molecular dynamics (MD) simulation is a powerful tool that can provide a detailed molecular picture to complement experiments (16–18). However, the experimental elongation rate is roughly one layer per second (19, 20), which is not currently feasible with atomistic simulations. While this time scale is accessible to coarse-grained approaches (18, 21–25), the reduced resolution of these models makes it challenging to distinguish sidechains with similar properties and capture mutational effects.

The long time scale of amyloid aggregation contrasts with native protein folding where secondary structure formation occurs on a submicrosecond time scale. To explain this difference, we presented an analytic theory showing that aggregation kinetics were consistent with an ergodic search of β-sheet alignments (26). By identifying the slowest step in the aggregation process, this theory suggests that high-resolution simulations can be realized by accelerating the alignment search. The proof of concept for this new approach was demonstrated in a paper showing how the alignment search could be captured using a Markov State Model (MSM) defined by the two reaction coordinates identified by the theory (27). That work successfully recapitulated nonadditive effects of hydrophobic mutations but was incomplete in several ways. Key steps in the process, including the initial binding, peptide backbone conformational reconfiguration, and transitions between alignments, were either lumped into “black box” states in the MSM or absorbed into free parameters. Secondly, the implicit solvent model, utilized to allow direct comparison between the MSM and brute force simulations, did not allow a direct comparison of the simulation and experiments. As a result, this “minimalist” treatment lacks quantitative predictive power and failed to provide a mechanistic explanation of the curious nonadditive mutation effects.

The present work addresses all of these deficiencies. First, we show how the two-dimensional (2D) MSM can be integrated as the core of a larger MSM describing the full aggregation process. This allows us to compute aggregation rates without free parameters and extensively sample states not included in the original theory. The full MSM shows a detailed mechanism of assembly where weakly bound states serve as a hub connecting the assembly pathway to long-lifetime trapped states. Secondly, due to the highly parallelizable nature of our MSM, we have been able to transition to an explicit solvent model, allowing for direct calculation of aggregation rates. Finally, we explain how the unsatisfying finding that mutation effects are the unpredictable effect of small perturbations is, in fact, the expected outcome within the funnel model of protein folding.

Results

Fibril Elongation Consists of Diffusion, Nonspecific Binding, and β-Alignment Stages.

We have developed a computational framework that can systematically explore the search over β-sheet alignments (26, 27). In this framework, the number of hydrogen bonds (H-bond) and alignment (referred to as the “registry”) between an incoming peptide and the existing fibril are used as reaction coordinates. The process of exploring registries is then converted to a series of H-bond formation and breakage events. Since H-bond formation and breakage occur on the nanosecond time scale, targeted simulations can be deployed to calculate the rates of these events and measure how they are affected by protein sequence and/or environmental factors. The microscopic rates can be then used to construct MSMs for simulating the overall growth process. This is similar to the application of MSMs for protein folding (28–34). The difference is that in our previous work, the state space was obtained from the analytic theory, while traditional applications of MSMs obtain states from kinetic clustering of simulation trajectories. In the present work, we combine the strengths of the two approaches by using the H-bond state space to sample the slow search over registries and atomistic simulations followed by kinetic clustering to resolve states outside of the H-bonding space.

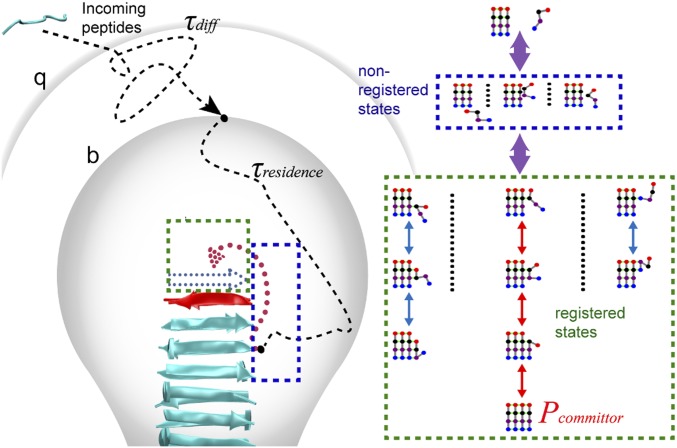
Our model is shown schematically in Fig. 1. The elongation process starts from an unstructured monomer in the bulk solvent, which “docks” to a preformed fibril core and “locks” as a new structured layer (11, 12, 15). The process can be divided into three stages. The first stage is a diffusion-controlled process, in which the incoming peptide migrates from solvent to a separation distance b (35, 36). This stage is similar to Brownian dynamics treatments of diffusion-controlled reactions (35, 36). Simulations were started from a monomer at the b surface, and the rates of monomers reaching the fibril surface or an escape distance q were analyzed. If the monomer reaches the q surface, the monomer is considered to have returned to the bulk solvent. The second stage describes nonspecific interactions between the monomer and fibril, defined as those states without either in-register or misregistered backbone H-bonds (nonregistered states; blue box in Fig. 1). This stage ends when the incoming peptide either forms backbone H-bonds with the core peptide, thereby entering the registered stage (third stage) or dissociates from the fibril surface, returning to the unbound state (the q surface). The third stage represents the peptide’s exploration of β-strand alignments by forming or breaking H-bonds (green box in Fig. 1). The attempt ends when the molecule either forms a full set of H-bonds in the correct registry (red arrow in Fig. 1, Right) or falls off the end of the fibril (returning to nonregistered states). By combining the three stages, our model describes the complete process of fibril growth. The net growth rate can be expressed as

$$k_{\text{growth}}=k_{\text{on}}-k_{\text{off}}=\frac{P_{\text{committor}}}{{\tau }_{\text{diff}}+{\tau }_{\text{residence}}}-\frac{1}{{\tau }_{\text{off}}}\text{,}$$ [1]

in which τ_diff is the average time for a monomer to diffuse from bulk solvent to the b surface, τ_residence is the average time required for a molecule entering the b surface to reach either the fully bound state or return to a separation distance q, τ_off represents the average time required for a fully bound peptide to reach the dissociated state (q surface), and P_committor is the probability that an incoming peptide starting from the b surface becomes incorporated into the fibril in a fully bound in-register state. Although mathematically similar to the Michaelis–Menten equation, the two rate constants appearing in the first term of Eq. 1 refer to a diffusion step and a reconfiguration step, rather than a two-step reaction that occurs after binding (26, 37).

Fig. 1.

Schematic illustration of the random walk model of fibril growth with key kinetic parameters required for calculating the growth rate. The incoming peptide migrates from solvent to a separation distance b with a time τ_diff (first stage). Then within τ_residence, it explores multiple nonregistered (blue box) and registered states (green box) (second and third stage). The peptide is considered to return to the bulk solvent if it reaches the q surface. P_committor is the probability of the peptide arriving at the fully bound in-register state (the red path).

CHA Mutations Induce Many Small Perturbations in H-Bond Transition Rates.

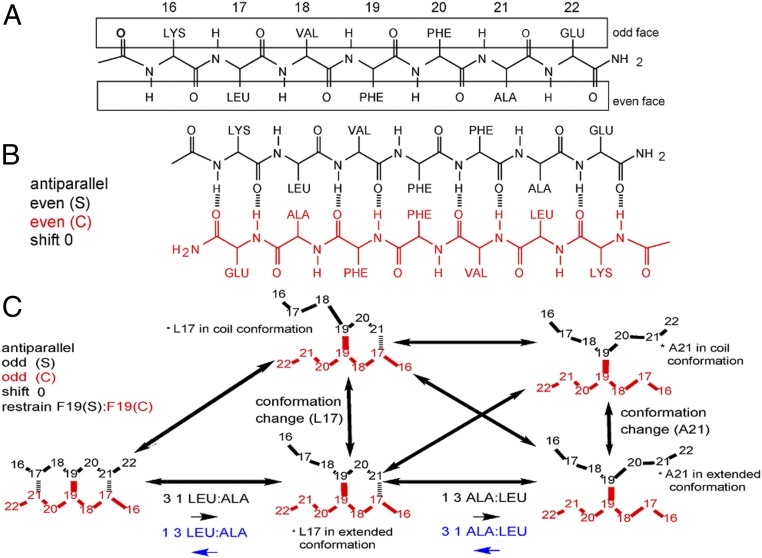
We focus on the fibril growth of the hydrophobic core of Aβ (Aβ_16–22, K₁₆LVFFAE₂₂), which is among the shortest sequences that form fibrils similar to those of full-length Aβ (38–40). All possible register states can be enumerated using a notation similar to our previous work (27) (Fig. 2 and SI Appendix, Fig. S2). A large number of 50-ns explicit solvent simulations were deployed to derive H-bond transition rates (Methods and SI Appendix, Table S1), which enables more realistic rates and allows better description of peptide conformational fluctuations. It turns out that explicit treatment of solvent also necessitates the inclusion of a type of transition between registered states, to account for conformational changes that occur at time scales comparable to those of H-bond formation and breakage (Methods). These transitions will also be necessary when extending the current framework to longer peptides.

Fig. 2.

Backbone H-bonding interactions and states in fibril growth of Aβ_16–22. (A) A preformed Aβ_16–22 fibril has two faces, odd and even, for templating β-sheet formation of an incoming peptide. (B) Illustration of the H-bonding network of the in-register state antiparallel e|e|0. (C) Illustration of all transitions of an incoming peptide with the H-bonding pair 19–19 restrained. Note that internal conformational states of the incoming peptide (extended and coil) are explicitly included. ALA, alanine; GLU, glutamine; LEU, leucine; LYS, lysine; VAL, valine.

As summarized in SI Appendix, Fig. S3, the effects of CHA mutations are not localized to the mutation site; instead, many H-bond transition kinetics are either increased or decreased. This is similar to our observations in the implicit solvent model (27). Thus, the impact of replacing phenylalanine (PHE) by CHA on fibril growth could not be directly inferred by changes in H-bond transition rates, but should be attributed to an accumulation of small effects during fibril growth.

States without β-Sheet Order Serve as a Kinetic Hub.

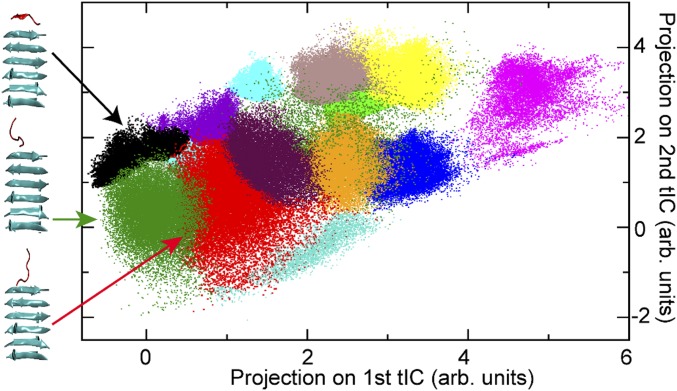
The nonregistered states do not have an identifiable β-sheet alignment and are not included in our original theory (26). However, our implicit solvent simulations showed that they served as a hub connecting β-sheet registries as well as the disassociated state (27). The implicit solvent treatment did not capture the details of nonregistered states and they were agglomerated into a single “nonspecific state.” Explicit solvent simulations revealed that many nonregistered substates exist, and they play distinct roles in mediating fibril growth (Methods). For Aβ_16–22, clustering analysis identified 15 distinct macrostates (Fig. 3), only 3 of which were found close to the docking face of the fibril and connected to registered states. The average transition rates between nonregistered states (∼1 ns) are faster than the average formation rate of the first H-bond pair. The transitions between registered states and the three connected nonregistered states occur in ∼2 to 6 ns. This suggests that the incoming peptide visits many nonregistered states before forming the first pair of hydrogen bonds. In addition, for a specific nonregistered state, all transitions to registered states can be fitted to the same single-exponential function (SI Appendix, Fig. S5), which suggests the transition rate between nonregistered states and the registered states are independent of orientation (antiparallel or parallel) or residue sidechains and only depend on the properties of the nonregistered state (position, peptide conformation, etc.). Thus, a uniform H-bond formation/breakage transition rate was used for each nonregistered state.

Fig. 3.

Nonregistered states identified from kinetic clustering. The simulation trajectories were clustered based on time-lagged independent component analysis (tICA). The states are projected on first two tICAs. The three clusters connected to registered states are colored in black, green, and red. Representative conformations (cluster centers) of the incoming peptide (red) and on the fibril surface (cyan) are shown. Note, as the cluster is based on three-dimensional tICA, some clusters are covered by other clusters and do not show up in the 2D projection.

MSM Captures the Binding Lifetimes of Different Registries.

The final MSM was tested by comparing the calculated lifetimes with results derived directly from unrestrained atomistic simulations for three fully H-bonded antiparallel registries. The results (SI Appendix, Fig. S6) show a good agreement between MSM and direct atomistic simulations. Next, we applied the MSM to analyze the effects of PHE-to-CHA mutations on the registry lifetimes. As summarized in SI Appendix, Fig. S6 the effects of the single and double CHA mutations are similar on each registry, although the magnitudes of lifetime changes are different. For both mutations, the time of one in-register state “antiparallel e|e|0” is increased and the lifetime for the other in-register state “antiparallel o|o|0” is decreased. Also, three antiparallel misregistered states have longer lifetimes for mutated peptides, and three other misregistered states have shorter lifetimes. As such, the net effects of mutations on the overall fibril growth kinetics is not obvious from the registry lifetimes. Instead, it is necessary to examine the ensemble of MSM trajectories to account for the many effects of the mutations.

Expanded MSM Recapitulates Mutational Effects and Solubility Concentrations.

To derive the overall fibril growth kinetics, 10,000 MSM simulations were performed, with 5,000 each on the even and odd faces of the fibril core, to calculate τ_residence and P_committor (Eq. 1). Each simulation was initiated from the separation distance b and terminated when the incoming strand reached the antiparallel fully H-bonded in-register state or the escape distance q. P_committor was calculated as the probability of MSM trajectories reaching the fully H-bonded in-register state, and τ_residence is the average length of all trajectories (Fig. 1B). To calculate τ_off, another set of 10,000 MSM simulations was initiated from the antiparallel in-register fully bound state and performed until the strand reached the escape distance q. P_committor is nearly doubled compared with our previous study with implicit solvent and a single agglomerated nonregistered state (Table 1). This suggests the in-register states are more stable for Aβ_16–22 in the explicit solvent model. In addition, both τ_residence and τ_off are increased by 2 to ∼3 orders of magnitude from the previous study due to the increased residence time of each state (Table 1).

Table 1.

Key kinetic parameters of fiber growth derived from MSM

	Wt	CHA19	CHA1920
Pcommittor	0.87 ± 0.08	0.88 ± 0.09	0.90 ± 0.02
τresidence, ns	1,359.0 ± 56.6	546.2 ± 12.2	588.9 ± 1.25
τoff, ns	40,012 ± 515	41,733 ± 836	23,086 ± 522

Data are means ± SD.

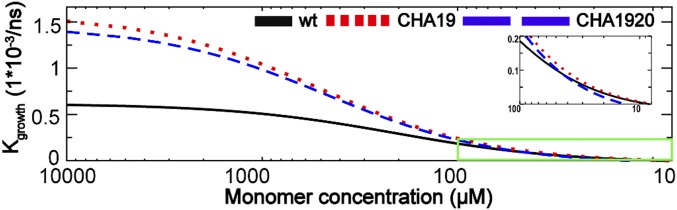
To compare with experimental results, the elongation rate as a function of monomer concentration is estimated. The diffusion time (τ_diff; Eq. 1) is estimated as τ_diff = 1/k_coll C_monomer, in which C_monomer is concentration of peptide monomer and k_coll is collision rate constant. The k_coll is defined as k_coll = 4πσD_monomer, in which σ is the reaction cross section (b surface in our simulation, 28 Å), and D_monomer is the diffusion coefficient (determined from experiments to be 1.7 × 10⁻⁶ cm²/s) (13). The results, plotted in Fig. 4, reveal that the critical concentration (C_c) of peptide monomer from the MSM is ∼8 μM, which is close to the experimental result of ∼33 μM (41). The ability of the current multiscale modeling approach to recapitulate the critical concentration to a factor of ∼4 without any adjustable parameters is noteworthy, particularly considering the comprehensive description of the conformational search process. This also likely reflects significant improvements of explicit solvent force fields made in recent years (42, 43).

Fig. 4.

Predicted net growth rate of Aβ_16–22 fibril as a function of the peptide concentration. Results for the wt, CHA19, and CHA1920 Aβ_16–22 are presented as black solid trace, red dotted trace, and blue dash trace, respectively.

To further investigate the influence of mutations, we examine the origin of the change in elongation rate for the mutated peptides. The increased growth rate of the mutants is due to a decrease of τ_residence, which in turn, arises from destabilizing two main trap states, “parallel o|o|0” and “parallel e|o|−2” (SI Appendix, Table S3). Although the relative free-energy of registered states between the CHA19 and CH1920 double mutation is similar, the double mutation also leads to a decrease in the residence time of in-registered states (SI Appendix, Table S2), which leads to a faster dissociation rate (smaller τ_off) and a decrease in the growth rate.

Experimental studies have suggested that CHA mutations at the 19 and 20 positions have nonadditive effects on overall aggregation kinetics (the growth rate: wild type [wt] << CHA19 < CHA1920 < CHA20 under high monomer concentration [>40 μM]) (41). However, this result could not be directly explained by thermodynamic effects of the mutations, which appear to have an additive effect (the ΔΔG with respect to wt for CHA19, CHA20, and CHA1920 are 0.2, −0.2, and 0.0 kcal mol⁻¹, respectively). To investigate the influence of mutations, MSM simulations of CHA mutants were performed. In the initial high monomer-concentration condition, both CHA19 and CHA1920 exhibited significant kinetic enhancement in fibril elongation (Fig. 4), in agreement with experiments (41). This corresponds to the initial stage (0 to 2 h) characterized by a fast decrease in the monomer concentration. This rapid aggregation reduces the monomer concentration, leading to an increase of τ_diff, which, in turn, leads to a decrease of k_growth. When the monomer is further depleted, the growth rate approaches zero as the monomer approaches the C_c (41).

Fig. 4 shows a saturation in the growth rate at high concentration as the system transitions from diffusion-limited to reaction-limited. This saturation has been observed in the elongation of insulin fibrils (20). In this regime, new molecules tend to arrive at the fibril ends before the previous molecule has completed the search for the in-register state (26). The nonlinearity in the growth rate as a function of concentration indicates that incorrectly bound molecules inhibit further elongation, presumably by offering a poor surface for binding. An alternative to the saturation behavior is that misregistered molecules become incorporated in the fibril as defects (44). These two outcomes could be distinguished in a simulation by attempting to dock a new protein while the previous one is still misregistered and comparing the residence time to the diffusion time. Experimentally, this could be achieved by measuring the elongation rate (absent nucleation effects; ref. 45) in the concentration regime where Fig. 4 shows nonlinearity.

Discussion

The Aggregation Process Is Not Guided by the Free-Energy Landscape.

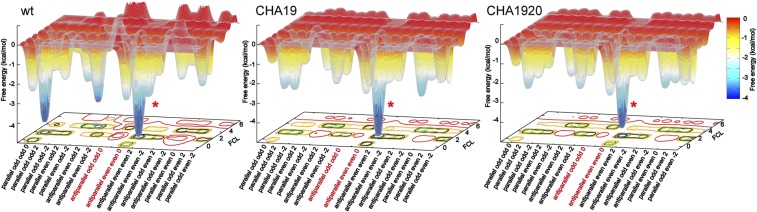
To investigate the association/dissociation pathways, all MSM trajectories were combined and the relevant free energy of each H-bonding state was plotted. This reveals rough free-energy landscapes with numerous local minima (Fig. 5). Importantly, there is no obvious bias to the landscape to guide the system toward the in-register states. Biased landscapes, often described as the funnel model, are necessary for proteins to navigate the overwhelming conformational space as they fold to their native state (46, 47). Without a bias to guide the search, amyloids must exhaustively search the alignment space in order to match the fibril template. This is possible, albeit slow, because of the relative simplicity of the cross-β structure. The free-energy difference between the in-register substates and misregistered substates are <5 kcal/mol. Indeed, the ratio of misregistered states in amyloid is much higher than the misfolded trapped states observed in natural proteins (48, 49). Although the in-register states are more thermodynamically stable (Fig. 5), to reach these states, an incoming Aβ_16–22 peptide needs to visit different misregistered states an average of ∼22 times before it forms the fully bound in-register states.

Fig. 5.

The free-energy landscape of Aβ_16–22 fibril growth. The free energy is derived from all MSM trajectories and measured relative to the substate antiparallel e|e|0 with free chain length [FCL] 6 (i.e., with only one H-bond pair formed at either terminus). The two in-registered states antiparallel e|e|0 and antiparallel o|o|0 are highlighted in red. The fully bound antiparallel e|e|0 state is labeled with a red asterisk. The Inset shows the detail of the region where the growth curve of wt and mutated peptides are diverged.

The lack of a funnel landscape is not surprising. Pathological aggregates do not confer a fitness advantage; thus, there is no reason to expect these molecules to have evolved efficient aggregation pathways. The funnel model helps to understand the result of our previous paper that the mutational effects could not be attributed to a few specific states or pathways (27). The dominance of a small number of states or pathways is the expected outcome from an efficient search through a funnel-like landscape. Conversely, in the absence of an efficient pathway, the system will randomly sample states throughout the conformational ensemble. This means that the net effect of the mutations will necessarily be the accumulation of perturbations throughout the conformational space. A related question is what the free-energy landscape would look like for a functional amyloid (2). An interesting hypothesis for this scenario arises from recent work showing that functional amyloids form weaker steric zippers (50). While this would not bias the landscape toward more aligned registries, the weaker bonds would smooth out the landscape and facilitate the search by minimizing the depth of the free-energy traps.

Misregistered States Compete with In-Register States.

SI Appendix, Table S3 shows the free energies for each registry, as estimated from the fraction of time each state was occupied in the MSM. For each molecule, the free energies are measured relative to the lowest occupancy registry. In the wt Aβ_16–22 peptides, two misregistered states, parallel o|o|0 and parallel e|o|−2, were found to have similar free energy compared with the in-register states (SI Appendix, Table S3). We offer two mechanisms to explain the dominance of the antiparallel in-register states over these low energy states in the fibril. First, electrostatic interactions will disfavor parallel states due to the close proximity of both terminal and sidechain charges. The repulsion due to the amino- and carboxyl-terminal charges will be reduced somewhat for molecules at the fibril ends because fluctuations in the binding states will allow the charges to separate. However, when the next molecule attaches, those termini will get pinned down, resulting in the full electrostatic repulsion. This effect is amplified with each additional parallel molecule that is added. The electrostatic contribution from the termini becomes less important with increasing protein length, which explains the parallel structures of full-length Aβ, IAPP, and others. In addition, mutations which weaken these repulsions may allow these nonproductive pathways to dominate fibril assembly. This assumption is consistent with NMR experiments showing that the E22Q mutation leads to parallel fibrils (51). Interestingly, this mutation is the same as the Dutch mutant of full-length Aβ peptide, which enhances the aggregation propensity (52).

Secondly, while misregistered states, like parallel e|o|−2, bind with high affinity, they may offer a poor template for subsequent fibril growth. An out-of-register shift will result in overhanging amino acids that will bind poorly to subsequent molecules due to the conformational entropy penalty of immobilizing the flexible residues (53). However, under conditions conducive to rapid growth (e.g., when the monomer concentration is high), these registry defects may be trapped within the growing fibril by subsequent monomer addition (44).

MSM Trajectories Show a Molecular Mechanism of Amyloid Formation.

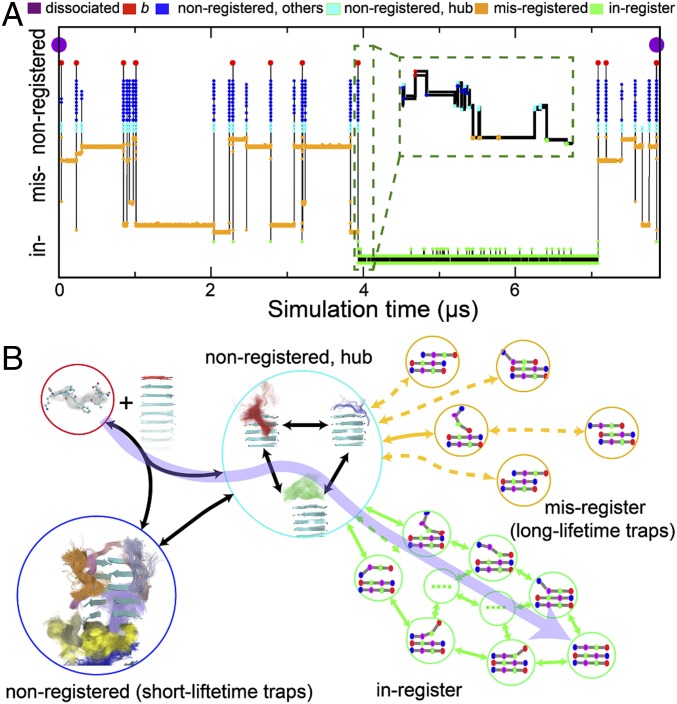
For further insight, we examine a representative trajectory in Fig. 6A, which starts from the dissociated state, reaches the fully bound in-register state, and eventually returns to the dissociated state. In this trajectory, the locking step of the Dock and Lock model occurs in the initial 4 μs. This period is characterized by many rapid transitions between nonregistered states (cyan dots) separated by long periods in misregistered β-sheet states (yellow). The residence time in this stage is dominated by misregistered states (>98%). The end of the locking step (4 μs) begins a long period of stability marked by only small fluctuations from the fully bound state. However, eventually (∼7 μs), there is a fluctuation large enough to remove it from the in-register state, and the molecule finally dissociates. This trajectory shows many events where the molecule briefly detaches from the fibril (red dots) before reattaching. These multiple attempts at finding the in-register state explain the large values of P_committor (Table 1) and show why molecules reaching the docked state are much more likely to proceed to the locked states than fail to incorporate.

Fig. 6.

Overall mechanism of Aβ_16–22 fibril growth. (A) A sample MSM trajectory illustrating the reversible templating transition of an incoming peptide. The trajectory was initiated from a fully dissociated state (marked by the purple dots) and continued until the peptide returned to the dissociated state. The y axis shows the MSM states sampled during the simulation. The MSM states were consolidated based on the registry and total free chain length for clarity (also see Fig. 4). The Inset shows the detail of the transition from nonregistered states (cyan) to the in-register (green) fibril state (near 3.93 μs). (B) Schematic of the fibril elongation mechanism. The aggregation pathway (purple arrow) takes proteins from the soluble state to in-register β-sheet states (green circles), but it accounts for a small fraction of the aggregation time. Instead, molecules spend >98% of the time trapped in misregistered β-sheet states (orange circles). States without β-sheet structure present another off-pathway trap (blue circle), although a few non-β states serve as a hub (cyan circle) connecting the trap states with the aggregation pathway. The assembly pathway is highlighted by the transparent purple arrow.

The overall mechanism is depicted schematically in Fig. 6B. The assembly pathway is highlighted by the purple arrow. This pathway includes the diffusion step, initial contact with the fibril in the non–β-sheet state, and the formation of an in-register β-sheet. However, the molecule spends less than 0.1% of its time on this pathway, instead spending most of the time in off-pathway traps. Of these, the most significant, by far, are the misregistered β-sheets (yellow in Fig. 6). These states are deep free-energy wells (Fig. 5) because of the translational symmetry of the peptide backbone. These traps become deeper for increasing peptide length, leading to exponential increases in the aggregation time (45). These long trap lifetimes have been previously compared with glassy systems (54). While these off-pathway states slow fibril growth, they also inhibit dissolution by binding departing peptides (∼200 times on average in a single dissociation MSM trajectory). The resulting long τ_off is consistent with the experimental result that the locking stage is nearly irreversible (11). The off-pathway states without β-sheet contact, in contrast, are an insignificant contribution to the overall aggregation time (dark blue in Fig. 6). However, they are important in keeping the molecule in close proximity to the fibril. Finally, the hub states (teal in Fig. 6) play a crucial role in facilitating assembly. These states are similar to the non-β traps morphologically, but play a special role because they are close enough to the fibril end to allow direction conversion to and from β-sheet states.

Based on these results, we can speculate on how the assembly mechanism might change for longer peptides such as Aβ_1–42. A major difference with longer molecules is their ability to fold in the solution state. One line of thought is that adoption of the aggregated conformation in the solution state promotes aggregation (55–58). Based on the mechanism observed in our simulations, we believe this hypothesis is unlikely. This is because the formation of tertiary contacts would inhibit the conformational flexibility needed to sample the registry space; trapping segments of the backbone in β-conformation would prevent it from peeling off the template one residue at a time. This means that much larger energy fluctuations would be required to rectify alignment errors. Therefore, formation of ordered fibrils is most likely from peptides that are disordered in the monomer state. However, adoption of the aggregated state will be beneficial for fibril nucleation (53).

Conclusion

Functional proteins have evolved to develop efficient folding pathways where a funnel-shaped free-energy landscape reduces the time spent exploring nonproductive states. This evolutionary pressure does not exist for nonfunctional states like pathological aggregates. In these cases, the free-energy landscape would more closely resemble a golf course (47) or an inverted funnel (44). Without the guidance of a biased landscape, the conformational search will resemble a random search over numerous H-bonded and non–H-bonded binding states. We have developed an analytic theory-motivated, multiscale simulation strategy to derive a comprehensive description of productive and nonproductive pathways in the fibril growth of Aβ_16–22. Without any free parameters, these descriptions quantitatively reproduce the critical fibril growth concentrations and recapitulate the effects and nonadditivity of CHA19 and CHA20 mutations on the growth kinetics. The results reveal that, instead of finding a few dominant pathways or intermediate states, the effects of mutations emerge from the accumulation of small perturbations over the ensemble of partially bound states. This recognition poses challenges for computational methods, which must sample both productive and nonproductive pathways to generate meaningful predictions. We note that majority of modeling treatments of fibril growth to date use pure MD simulations (56–58). They are limited in the conformational search processes that can be explored, even with coarse-grained treatment and/or enhanced sampling techniques. The current work demonstrates how insights from analytic theory can be utilized to meet this challenge by inspiring sampling techniques that can access new time scales and provide a more complete understanding of fibril growth.

Methods

A total of 719 μs of explicit solvent simulations in the CHARMM36m all-atom force field (59, 60) was performed to derive the microscopic kinetic parameters for transition among all H-bonded and nonspecific bound states. See SI Appendix, Supporting Text for detailed simulation and analysis procedures.

Data Availability Statement.

The script for Markov State simulation of fibril growth as well as the transition matrix for the wt Aβ_16–22 peptide are available from GitHub (https://github.com/zhiguangjia/MSM-model-for-amyloid-). The CHARMM scripts for atomistic simulation, analysis, clustering, and kinetic analysis are available upon request.