Abstract
Objective:
This study applied a new external ventricular catheter, which allows intracranial pressure (ICP) monitoring and cerebral spinal fluid (CSF) drainage simultaneously, to study cerebral vascular responses during acute CSF drainage.
Methods:
Six patients with 34 external ventricular drain (EVD) opening sessions were retrospectively analyzed. A published algorithm was used to extract morphological features of ICP recordings and a template-matching algorithm was applied to calculate the likelihood of cerebral vasodilation (VDI) and cerebral vasoconstriction (VCI) based on the changes of ICP waveforms during CSF drainage. Power change (ΔP) of ICP B-waves after EVD opening was also calculated. Cerebral autoregulation (CA) was assessed through phase difference between arterial blood pressure (ABP) and ICP using a previously published wavelet-based algorithm.
Results:
The result showed that acute CSF drainage reduced mean ICP (p=0.016), increased VCI (p=0.02), and reduced ICP B-wave power (p = 0.016) significantly. VCI reacted to ICP changes negatively when ICP was between 10-25 mmHg and VCI remained unchanged when ICP was outside 10-25 mmHg range. VCI negatively (r = −0.44) and VDI positively (r = 0.82) correlated with ΔP of ICP B-waves, indicating that stronger vasoconstriction resulted in bigger power drop in ICP B-waves. Better CA prior to EVD opening triggered bigger drop in the power of ICP B-waves (r = −0.612).
Conclusions:
This study demonstrates that acute CSF drainage reduces mean ICP, and results in vasoconstriction which can be detected through an index, VCI. Cerebral vessels actively respond to ICP changes or CPP changes in a certain range; beyond which, the vessels are insensitive to the changes of ICP and CPP.
Keywords: Cerebral Autoregulation, Cerebrospinal Fluid Drainage, Cerebral Vascular Changes, Intracranial Pressure Waveform, ICP B-waves
Introduction
Measurement of intracranial pressure (ICP) is used to guide targeted therapy of acute brain injury during a patient’s stay in a neurological intensive care unit (NICU) [1-6]. External ventricular drain (EVD) remains the gold standard for both monitoring ICP and diverting cerebrospinal fluid (CSF) from the ventricles in clinical situations requiring management of acute hydrocephalus or temporary CSF drainage [7-9]. Several studies have critically examined the effect of ventriculostomy drainage on elevated ICP[10-13]. It has been proved that CSF drainage significantly reduced ICP and increased cerebral perfusion pressure (CPP) in traumatic brain injury (TBI) patients[10,14,15]. However, how cerebral vessels respond to acute CSF drainage still remains unknown, partly due to the inability of conventional EVD to simultaneously detect ICP waveforms during CSF drainage[7,16], and partly due to the fact that we lack an efficient tool to evaluate cerebral vascular changes continuously. To tackle the first problem, a novel Integra® Camino® FLEX Ventricular Catheter (Integra Lifesciences, County Offaly, Ireland) has been introduced into the market recently [17]. This double-lumen catheter uses one lumen to divert CSF and the other to embed a pressure sensor at the tip to obtain ICP pulse waveforms, thus enabling continuous ICP monitoring even when EVD is open[18-20]. The FLEX catheter could provide a unique opportunity to derive clinically meaningful information even during CSF drainage. Regarding the second issue (i.e. we need an efficient tool to evaluate cerebral vascular changes), a few studies tried to evaluate vascular changes via changes of cerebral arterial blood flow (CBF). The results were inconsistent, with some studies showing significant increase in CBF velocity[21], while others did not find obvious changes in CBF velocity after CSF drainage [10].
Introduced by Hu et al in 2009, a modern signal processing algorithm, Morphological Clustering and Analysis of Intracranial Pulse (MOCAIP) algorithm has been proved an effective tool for ICP waveform detection in brain injury patients [18-20,24]. The MOCAIP algorithm allows a comprehensive quantitative characterization of ICP pulse morphology, including pulse amplitude, time intervals among subpeaks, curvature, slope, and decay time constants through 128 pulse morphological metrics (shown in Supplementary Fig 1). Based on MOCAIP algorithm, the same group applied a template matching algorithm [19] to estimate the likelihood of cerebral vasodilation (VDI) and cerebral vasoconstriction (VCI) based on the changes of ICP waveforms extracted by MOCAIP[18,19]. In the present study, we applied this method to evaluate cerebral vascular changes during acute CSF drainage through ICP recordings detected by the new FLEX catheter.
Moreover, we hypothesize that cerebral autoregulation (CA) is a potential triggering mechanism that causes cerebral vascular responses to acute CSF drainage. With intact CA, a decrease in ICP leads to an increase in CPP which may subsequently cause cerebral vasoconstriction[24-26]. Therefore, an investigation of how the cerebral arterial bed responds to acute CSF diversion is important not only for understanding physiological relevance but also because of its practical implication as a potential status indicator of CA [27]. A robust metric of CA, the wavelet phase difference between ICP and arterial blood pressure (ABP)[28-30] was used to quantify the status of CA. This approach has been validated with a more established metric – pressure reactivity index (PRx) and is proved to be more robust with less variations[28]. Moreover, since the presence of ICP slow waves or B waves (0.33 to 3 cycles per minute) reflects vasogenic activity of CA [31-33], we also studied the power changes of ICP slow waves during acute CSF drainage.
Material and Methods
Patients and Data Collection
The data analyzed in this study were collected from adult patients admitted to University of California, Los Angeles Medical Center (UCLA, Los Angeles, CA, USA) during a period of evaluating Integra® Camino® FLEX Ventricular Catheter (Integra Lifesciences, County Offaly, Ireland) between February and April, 2016. Three patients with severe TBI, two patients with aneurysmal subarachnoid haemorrhage (aSAH), one patient with intraventricular haemorrhage (IVH) were enrolled in the study. Continuous ICP was detected through the FLEX catheter. The continuous ICP, ABP (3 of 6 patients) and electrocardiograph (ECG) signals were obtained from bedside monitor (GE Solaris 8000) through BedMaster™ (Excel Medical, Jupiter, Florida, USA) system at a sampling rate of 240 Hz. The institutional review board (IRB) approved the data analysis and waived the need for consenting patients because of the retrospective nature of the study. The decision to use FLEX catheters was clinically based without considering the needs of this study.
We retrospectively reviewed ICP recordings from each patient and selected the episodes associated with acute CSF drainage that caused ICP reduction (34 episodes in total from the 6 subjects). For each episode, we identified timing of EVD opening (t0) and closure (t1). A during-drainage segment is defined as the segment while EVD is open to drainage, that is from t0 to t1(Fig 1A). A pre-drain segment is a segment of ICP prior to EVD open. A post-drainage segment is defined as the segment after EVD is closed again.
Fig.1.
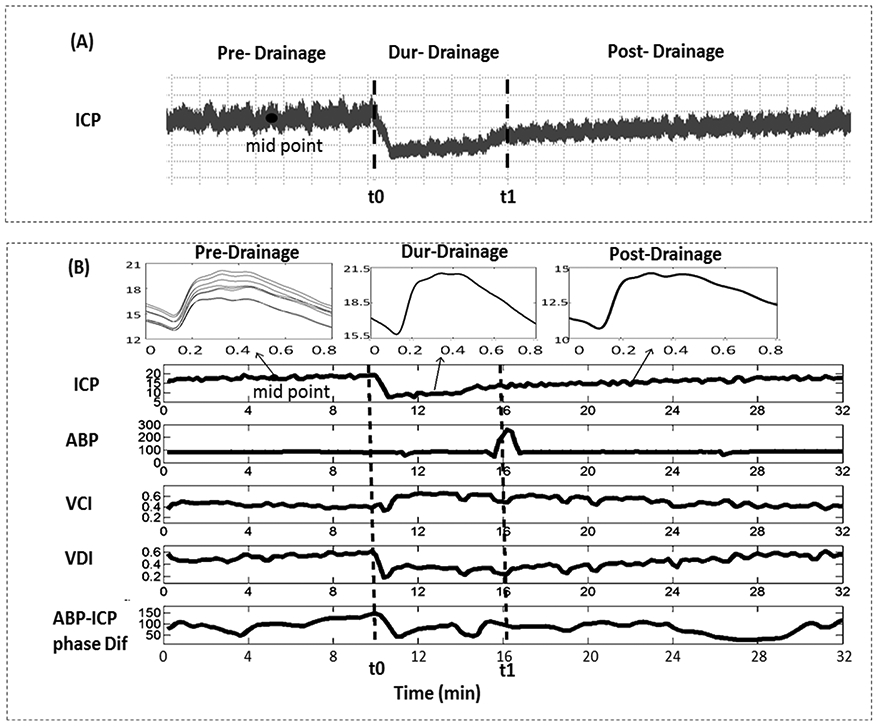
(A) An ICP recording of a traumatic brain injury patient through the Integra® Camino® FLEX Ventricular Catheter. The during-drainage segment refers to segment between [t0, t1] sec, the pre-drainage segment is a segment of ICP prior to EVD open, and the post- drainage segment refers to the section after EVD is closed again. (B) An example of mean ICP, ABP, VCI, VDI, and ABP-ICP phase difference of one recording episode. Vertical lines correspond to EVD opening and closure, respectively. The three small charts in the upper panel represent dominant ICP pulses at pre-drainage (8 dominant pulses that were selected as baseline pulses to be compared to for VCI and VDI calculation), during-drainage, and post-drainage segments. ABP: arterial blood pressure; ICP: intracranial pressure; VCI: vasoconstriction index; VDI: vasodilation index; EVD: external ventricular drains.
Data analysis
Morphological Clustering and Analysis of Intracranial Pulse (MOCAIP)
MOCAIP algorithm was developed and validated in many of our previous publications[18-20,34]. Briefly, this algorithm analyzes a segment of ICP signal to identify each cardiac pulse, clusters them, and forms an average pulse per each cluster. The average pulse of the biggest cluster is termed dominant ICP pulse for the segment. The dominant pulse is further compared to validated ICP pulses in a pre-built ICP pulse library to determine if this pulse is legitimate. The morphology of a legitimate dominant pulse is further quantified using 128 systematically derived metrics based on an optimal designation of three sub-peaks and the corresponding three valley points of a typical triphasic ICP pulse. The details of the algorithm should be referred to our published work [18]. What is relevant in this study is the ability of MOCAIP algorithm to provide a quantitative characterization of ICP pulse waveform in terms of 128 MOCAIP metrics as illustrated in Supplemental Table 1 and Supplemental Fig 1.
Vasodilation and vasoconstriction index
We showed in a previous study that the cerebral vascular changes are reflected in morphological changes of ICP pulses [20]. In a carbon dioxide (CO2) challenge experiment published previously [19], the authors identified 72 consistent MOCAIP metrics related to cerebral vasodilation and constriction, which were saved as a template of expected characteristic ICP pulse morphological changes during cerebral vascular changes. In this study, we compared the changes of MOCAIP metrics of ICP between baseline and CSF drainage, and match them with the template defined above to detect if the cerebral vasculature is in a vasodilatory, a vasoconstrictive, or a neutral state. Specifically, a vasodilation index (VDI) can be calculated as
| (F1) |
In a similar way, a vasoconstriction index (VCI) can be calculated as
| (F2) |
where S+ denotes a set of MOCAIP metrics showing positive change from baseline, S− a set of MOCAIP metrics showing negative change from the baseline, a set of MOCAIP metrics in the template showing positive (negative) changes during a cerebral vasoconstriction phase, and a set of MOCAIP metrics in the template showing positive (negative) changes during a cerebral vasodilation phase. A ∩ B refers to the intersection of two sets. It should be noted that the range of VCI and VDI is between 0 and 1.
To calculate VDI and VCI on a pulse by pulse basis, one only needs to compare the ICP pulse representing the current time to that recorded at a baseline and determine the direction of MOCAIP metric changes. In the present work, we applied MOCAIP algorithm to analyze and derive a dominant pulse from consecutive 12-second ICP signal segments. Instead of using only one baseline ICP pulse, we randomly selected 8 baseline pulses that fell within the pre-drainage segment and reported the average VDI/VCI that was derived by comparing each consecutive dominant ICP pulse to the eight baseline ICP pulses. In this way, we smooth out the variations in VDI/VCI that are likely due to respiration.
Cerebral autoregulation parameter
Wavelet transform based phase difference (WTP) between ABP and ICP, in the low frequency of 0.005 Hz to 0.08 Hz was calculated through complex wavelet transform [29,35-38]. Morlet mother wave was applied to extract the characteristics of ABP/ICP signals. The wavelet phase difference at each scale-frequency point was calculated, and wavelet transform coherence (WTC) was used as an indicator of a reliable phase relationship between input and output. Individual phase difference values with coherence higher than the threshold (decided through Monte Carlo simulations) were kept, while phase difference values with coherence lower than the threshold were deleted. Then the average value along frequency at each time point was calculated. More details about the algorithm can be found in our previous publication[28].
In brief, the continuous wavelet transform Wn (F3) describes the convolution of time series xn with a Morlet mother wavelet(φ) (F4)[39].
| (F3) |
| (F4) |
| (F5) |
where φ* is the complex conjugate of the normalized wavelet function; n is the time-series index, and δt is the sampling time. s is scale, calculated as
| (F6) |
w0 is the reference coefficient (w0 = 2πf0), which shifts the balance between frequency resolution and time resolution.
The cross wavelet transform (XWT) of two time series xn and yn are defined as
| (F7) |
where * denotes complex conjugation. The complex argument pha(Wxy ) can be interpreted as the instantaneous phase difference between xn and yn in time frequency space[35,40,41].
Wavelet transform coherence (WTC) is defined as the squared absolute value of the smoothed cross-wavelet spectrum, normalized by the smoothed wavelet power spectrum of the two signals (F8)
| (F8) |
where and are the wavelet spectral density functions; is the cross-wavelet spectrum ; and the angular brackets indicate the smoothing operator[29,38,42].
The wavelet threshold was decided through Monte Carlo simulations (10000 simulations) and was used to evaluate the distribution of estimated wavelet coherence values corresponding to two uncorrelated signals. In this study, we applied coherence of 0.48 as the threshold (more details can be found in a previous publication[28]). Our previous publications already showed that high wavelet phase shift refers to good CA and low phase shift indicates bad CA[28,43].
Power spectrum analysis to quantify B wave power reduction
Power spectra were calculated using multiple tapper approach [44,45] for ICP B-waves (0.005 - 0.08 Hz) in pre-, during- and post-drainage section, respectively. The relative power change of ICP B-waves (ΔP) from baseline (pre-drainage) to during-drainage section was calculated.
Statistical analysis
Statistical analysis was performed using the IBM SPSS Statistics (version 21) software. The Wilcoxon paired t test (one side) was used to analyze the ability of different parameters (VCI, VDI, ABI-ICP phase difference and power of ICP B-wave) in distinguishing low (pre-drainage) and high (during-drainage) CPP states. Results were considered significant with p < 0.05. The relationships between baseline CA, the mean VCI (VDI) and relative power changes of ICP B waves during CSF drainage were studied using Spearman’s correlation coefficient (r).
Results
The mean age of the six (three males) patients enrolled in the study was 41.2 ± 19.1 (mean ± SD) years old. The mean duration of selected EVD open/close recordings was 47.8 ± 9.4 minutes (25.3 ~ 60.2 minutes, mean ± SD). Table 1 shows mean values of ABP, ICP, VDI, VCI, ABP-ICP phase difference and ICP B-wave power pre-, during- and post- CSF drainage. The Wilcoxon test showed a significant increase in VCI (p = 0.02) and significant decrease in VDI (p = 0.02), mean ICP (p = 0.016), and ICP B-wave power (p = 0.016) after EVD opening. Figure 1B displays one example of the parameters we tested in this study with EVD opened for draining CSF at t0 and then closed at t1.
Table 1.
Mean values of different parameters pre- and during- EVD drainage session
| patient #1 | patient #2 | patient #3 | patient #4 | patient #5 | patient #6 | |
|---|---|---|---|---|---|---|
| Age | 38 | 22 | 25 | 40 | 75 | 47 |
| Diagnosis | TBI | TBI | TBI | aSAH | IVH | IVH |
| Gender | M | F | M | F | M | F |
| N of segments | 5 | 9 | 2 | 5 | 12 | 1 |
| Pre-drainage ICP | 15.81±3.28 | 14.75±1.04 | 20.30±1.54 | 16.03±1.56 | 15.83±4.46 | 14.09 |
| Dur-drainage ICP | 12.21±1.28 | 9.65±1.89 | 18.40±2.77 | 11.10±2.50 | 11.94±3.49 | 9.48 |
| Post-drainage ICP | 13.31±2.82 | 13.35±2.83 | 17.16±0.05 | 14.17±1.82 | 12.36±3.06 | 11.09 |
| Pre-drainage ABP | N/A | 90.47±7.45 | N/A | 149.70±2.50 | N/A | 112.58 |
| Dur-drainage ABP | N/A | 89.84±7.87 | N/A | 150.0±2.69 | N/A | 113.77 |
| Post-drainage ABP | N/A | 92.69±8.71 | N/A | 147.8±2.74 | N/A | 115.39 |
| Pre-drainage VCI | 0.51±0.06 | 0.44±0.08 | 0.18±0.20 | 0.46±0.03 | 0.48±0.05 | 0.54 |
| Dur-drainage VCI | 0.59±0.04 | 0.49±0.12 | 0.23±0.20 | 0.59±0.03 | 0.56±0.08 | 0.68 |
| Post-drainage VCI | 0.57±0.07 | 0.51±0.11 | 0.24±0.24 | 0.48±0.03 | 0.52±0.08 | 0.67 |
| Pre-drainage VDI | 0.44±0.05 | 0.40±0.08 | 0.22±0.18 | 0.49±0.03 | 0.47±0.06 | 0.41 |
| Dur-drainage VDI | 0.36±0.02 | 0.29±0.10 | 0.19±0.21 | 0.37±0.03 | 0.40±0.07 | 0.31 |
| Post-drainage VDI | 0.38±0.05 | 0.33±0.08 | 0.14±0.13 | 0.47±0.03 | 0.43±0.08 | 0.32 |
| Pre-drainage phase | N/A | 93.05±20.99 | N/A | 79.63±21.86 | N/A | 92.85 |
| Dur-drainage phase | N/A | 85.02±24.78 | N/A | 80.45±25.61 | N/A | 93.12 |
| Post-drainage phase | N/A | 98.04±21.57 | N/A | 70.47±24.37 | N/A | 63.34 |
| Pre-drainage power of B wave |
505.86±30.02 | 579.08±89.27 | 460.04±88.08 | 459.16±65.60 | 711.35±316.12 | 667.53 |
| Dur-drainage ICP power of B wave |
405.66±100.54 | 476.92±110.51 | 446.10±77.05 | 439.31±62.80 | 652.08±243.71 | 496.32 |
| Post-drainage ICP power of B wave |
537.4±181.87 | 741.06±205.48 | 461.23±195.27 | 805.60±94.28 | 1197.94±520.22 | 615.37 |
Data format: Average ± SD. EVD: external ventricular drain. TBI: traumatic brain injury; aSAH: aneurysmal subarachnoid haemorrhage (aSAH); IVH: intraventricular haemorrhage; ICP: intracranial pressure; VCI: vasoconstriction index; VDI: vasodilation index; ABP: arterial blood pressure.
Relationship between VCI (or VDI) and ICP (or CPP)
To study the vascular changes in response to acute ICP or CPP changes, we created various bins based on median ICP (or median CPP) with a bin width of 5 mmHg. Mean values and standard errors of VCI and VDI falling in each bin were calculated and plotted against the median ICP value (or median CPP) of each bin. The result showed an inverse ‘S’ curve between ICP and VCI and an ‘S’ curve between ICP and VDI (Fig 2A-2B). Interestingly, when ICP was between 10-25 mmHg, VDI was positively and VCI was negatively correlated with ICP; while outside this ICP range, VDI and VCI were independent from ICP.
Fig. 2.
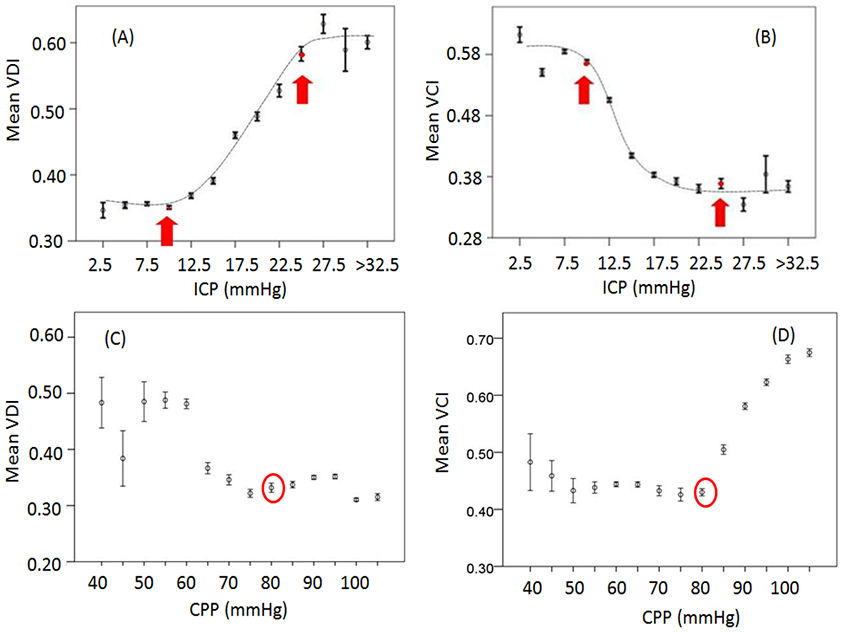
(A) Binned scatter plots of ICP vs. VDI; (B) Binned scatter plots of ICP vs. VCI; (C) Binned scatter plots of CPP vs. VDI; (D) Binned scatter plots of CPP vs. VCI. When ICP is between 10-25 mmHg, VDI is (A) positively and VCI is (B) negatively correlated with ICP. Outside this limit, VDI and VCI are insensitive to changes of ICP. (C) VCI increases while CPP increases above 80 mmHg; (D) VDI increases with the decrease of CPP. ICP: intracranial pressure; VCI: vasoconstriction index; VDI: vasodilation index; CPP: cerebral perfusion pressure; ABP: arterial blood pressure. Error bar: standard error.
VDI started to increase when CPP dropped below 80 mmHg (Fig 2C) and VCI started to increase when CPP increased above 80 mmHg (Fig 2D).
Optimal Cerebral Perfusion Pressure
Previous publications already defined optimal CPP as the CPP level where the best CA is achieved by plotting CA parameters (such as PRx, wavelet phase difference) against CPP[28,46]. In the present study, we created various bins based on median CPP with a bin width of 5 mmHg. Mean values and standard errors of ABP-ICP phase difference falling in each bin were calculated and plotted against the median CPP of each bin. An inverse ‘U’ shape curve was obtained and the best CA (the largest phase difference)[28] was located at CPP ≈ 80 mmHg (Fig.3).
Fig.3.
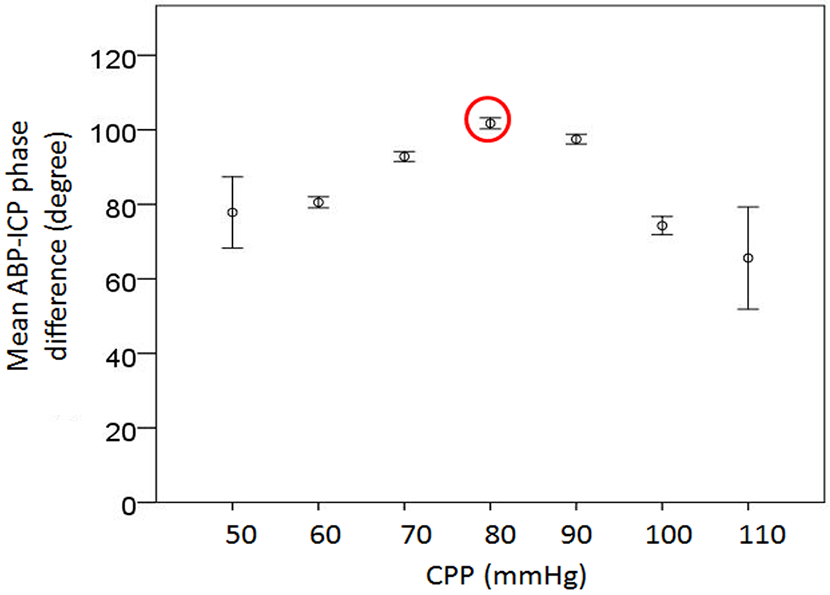
Binned scatter plots of CPP vs. ABP-ICP phase difference; ABP-ICP phase difference reaches the peak (indicating the best cerebral autoregulation) while CPP equals 80 mmHg. ICP: intracranial pressure; VCI: vasoconstriction index; VDI: vasodilation index; EVD: external ventricular drain; ABP: arterial blood pressure.
Baseline CA versus VCI, VDI and ΔP
Figure 4A and 4B show the relationship between VCI, VDI and ΔP (relative change of ICP B-wave power after EVD opening). VCI negatively (r = −0.44, n = 34) and VDI positively (r = 0.82, n = 34) correlated with ΔP, indicating that stronger vasoconstriction resulted in bigger drop in ICP B- wave power during CSF drainage. We further studied how the baseline (prior to EVD opening) CA was related to VCI or ΔP. The result showed a negative relationship between CA (depicted by ABP-ICP phase difference) and ΔP (r = −0.612, n = 16, Fig. 4C). Larger phase difference prior to EVD open, indicating better autoregulation, introduced larger power drop in ICP slow waves during CSF drainage. However, no relationship existed between ABP-ICP phase difference and VCI (r≈0) or VDI (r = 0.05).
Fig.4.
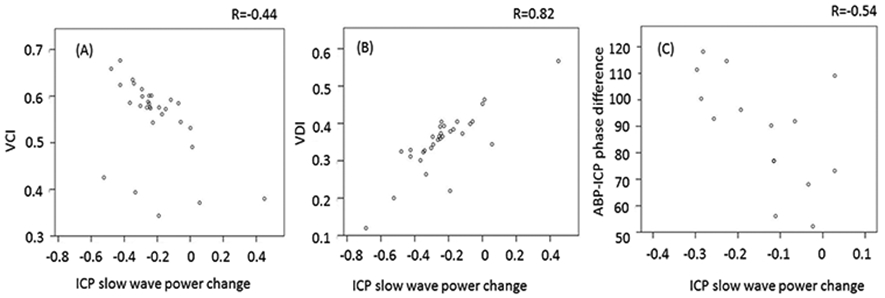
Scatter plots of relative changes(percentage) in power of ICP B-waves vs. VCI (A) or VDI (B) or ABP-ICP phase difference (C). ICP: intracranial pressure; VCI: vasoconstriction index; VDI: vasodilation index; ABP: arterial blood pressure.
Discussion
Continuous ICP monitoring remains a useful tool in the management of patients in NICU[47,48]. In this study, we used a new ventricular catheter which enables continuous ICP monitoring even during CSF drainage to study cerebral vascular changes during acute ICP drop. There are three major findings in this study: (1) an acute decrease of ICP or increase of CPP would result in vasoconstriction which can be detected through an index, VCI; (2) cerebral vessels actively respond to acute ICP changes or CPP changes in a certain range; beyond which, the changes of ICP or CPP cannot cause further vascular responses; (3) the drop of ICP B-wave power during CSF drainage, is positively related to VCI and to CA states at baseline.
First, this study shows a significant increase in VCI during CSF drainage, indicating that an acute decrease in ICP, resulting in increased CPP, leads to cerebral vasoconstriction. CA is a compensatory mechanism which can maintain stable cerebral blood flow despite fluctuating CPP within certain limits [26,49-51]. With intact CA, an increase in CPP leads to vasoconstriction (probably due to a direct ‘myogenic’ effect on the vascular smooth muscle) thereby maintaining flow; on the contrary, a decrease in CPP causes vasodilation[52-54]. This study provides further evidence that the two parameters, VCI and VDI, can be applied to assess acute cerebral vascular changes.
Second, the inverse ‘S’ shape relationship between ICP and VCI is an interesting finding. In this cohort of patients, VCI (VDI) decreases (increased) when ICP increases within the range of 10 to 25 mmHg. The vessels seem to reach their maximum constriction while ICP decreases below 10 mmHg; and inversely, vessels cannot dilate any more while ICP is higher than 25 mmHg. Since CPP is the driven force of cerebral blood flow into the brain and in the present study, the CPP changes are mainly caused by the changes of ICP due to CSF drainage, it is plausible to get this inverse ‘S’ shape relationship between VCI and ICP. The result may suggest within a certain range of ICP, the vessels response to ICP changes quickly to maintain relatively stable cerebral blood flow. The result indicates that the range (ICP: 10~25 mmHg) may correspond to a safe and effective range of ICP, where CPP can be manipulated to achieve optimal perfusion pressure. Further studies are needed to confirm or invalidate this speculation.
Wavelet phase difference measures the delay between input (ABP) and output (ICP) over a range of frequencies and time[55], with high phase difference indicating good CA [56-58] and low phase difference reflecting direct changes in ICP following ABP changes because of impaired CA function[28,59]. A recent study already suggests that wavelet method produces more robust and stable assessment of CA than a well-established metric – PRx [28]. Therefore, we chose wavelet method to assess CA in the current study. With the help of a curve fitting algorithm, the optimal CPP (CPPopt) can be continuously estimated [60-63] by plotting wavelet phase difference against CPP, which produces a reverse U-shape curve and CPP value at the maximum phase difference is associated with the strongest autoregulatory ability[28]. In the current cohort, the optimal CPP value (around 80 mmHg) matches the result of our previous study of 515 TBI patients [28]. Interestingly, the optimal CPP value of 80 mmHg corresponds to the turning point of VCI-CPP curve (Fig 2D). While CPP increases above 80 mmHg, VCI starts to increase; and when CPP is below 80 mmHg, VDI starts to increase. Further study needs to be done to validate the possibility of using VCI to estimate optimal CPP in the future.
Furthermore, the positive relationship between VCI and the decrease of ICP B-wave power further suggests that ICP B-waves reflect vasogenic activity[31-33,64] and the main reason of B-wave reduction during CSF drainage is cerebrovascular constriction.
Finally, in this study, we found a negative relationship between ABP-ICP phase difference at baseline and the decrease of ICP B-wave power during CSF drainage. A possible explanation is that a preserved autoregulation before acute CSF drainage is a prerequisite for observing cerebral vasoconstriction as a response to increased CPP after reducing ICP acutely. The better CA prior to EVD opening (indicated by bigger ABP-ICP phase difference), the bigger cerebral vascular responses and greater decrease in ICP B-wave power it may cause. However, we could not establish a significant correlation between CA of pre-drainage period and VCI (or VDI) during CSF drainage. This phenomenon could potentially be due to the fact that VCI is more of a state indicator than being a metric of degree of cerebrovascular vasoconstriction. Another potential explanation is that a highly nonlinear relationship exists between the actual strength of autoregulation and the extent of cerebral vasoconstriction.
Limitations
We acknowledge the following limitations of the study. The analysis and conclusion of this study heavily replied on our previously proposed VCI and VDI algorithm. The calculation of VCI/VDI was based on the ICP pulse morphological change patterns established using data from CO2 challenge that was performed on patients with chronic hydrocephalus with an indwelling shunt [19].Therefore, our assumption is that CO2-induced cerebral vasodilation is equivalent to cerebral vasodilation that is induced by reduction of CPP and that this equivalence is of a physiologic nature and not disease dependent. Although we were not able to validate these two assumptions, the results we obtained are plausible and future work can be readily performed to establish perhaps more relevant templates of cerebral vasodilation and vasoconstriction for this patient population and the triggering mechanism of cerebral vascular changes. Second, we lack an efficient tool to test cerebral blood flow currently, which is important for brain injury patients. In our study, we noticed that the vessels tried to main stable cerebral blood flow by responding to ICP changes in a certain range. It will be of great potential if we can validate the relationship between VCI or VDI and cerebral blood flow, thus VCI/VDI might be used to detect cerebral blood flow in the future. Finally, the data analyzed in the present study only included 6 patients. The method needs to be tested in more patients. However, the small cohort allows us to be able to study information in details.
Conclusions
This study showed that acute CSF drainage reduced mean ICP, increased CPP, and reduced ICP B-wave power. A plausible explanation of this observation is cerebral vasoconstriction as an autoregulatory response to acute ICP decrease and CPP increase. The study validated VCI as an index to assess cerebral arterial changes for acute brain injury patients. Better CA at baseline and stronger vasoconstriction would result in bigger decrease in power of ICP B-waves during CSF drainage.
Supplementary Material
Funding Acknowledgements
This work was partially supported by the UCSF Middle Career Scientist Award, UCSF Institute for Computational Health Sciences, and National Institutes of Health awards (R01NS076738 and NS106905-01A1).
Footnotes
Conflicts of Interest
The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
References
- 1.Rangel-Castillo L, Robertson CS. Management of Intracranial Hypertension. Crit. Care Clin 2006. p. 713–32. [DOI] [PubMed] [Google Scholar]
- 2.Lane PL, Skoretz TG, Doig G, Girotti MJ. Intracranial pressure monitoring and outcomes after traumatic brain injury. Can J Surg. 2000;43:442–8. [PMC free article] [PubMed] [Google Scholar]
- 3.Czosnyka M, Smielewski P, Timofeev I, Lavinio A, Guazzo E, Hutchinson P, et al. Intracranial pressure: more than a number. Neurosurg Focus. 2007;22:E10. [DOI] [PubMed] [Google Scholar]
- 4.Czosnyka Z, Czosnyka M. Long-term monitoring of intracranial pressure in normal pressure hydrocephalus and other CSF disorders. Acta Neurochir (Wien). 2017;159:1979–80. [DOI] [PubMed] [Google Scholar]
- 5.Chari A, Dasgupta D, Smedley A, Craven C, Dyson E, Matloob S, et al. Intraparenchymal intracranial pressure monitoring for hydrocephalus and cerebrospinal fluid disorders. Acta Neurochir (Wien). 2017;159:1967–78. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Kirkman MA, Smith M. Intracranial pressure monitoring, cerebral perfusion pressure estimation, and ICP/CPP-guided therapy: A standard of care or optional extra after brain injury? Br. J. Anaesth 2014. p. 35–46. [DOI] [PubMed] [Google Scholar]
- 7.Muralidharan R External ventricular drains: Management and complications. Surg Neurol Int. 2015;6:271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Kirmani A, Sarmast A, Bhat A. Role of external ventricular drainage in the management of intraventricular hemorrhage; its complications and management. Surg Neurol Int. 2015;6:188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Staykov D, Kuramatsu JB, Bardutzky J, Volbers B, Gerner ST, Kloska SP, et al. Efficacy and safety of combined intraventricular fibrinolysis with lumbar drainage for prevention of permanent shunt dependency after intracerebral hemorrhage with severe ventricular involvement: A randomized trial and individual patient data meta-analysi. Ann Neurol. 2017;81:93–103. [DOI] [PubMed] [Google Scholar]
- 10.Kerr ME, Weber BB, Sereika SM, Wilberger J, Marion DW. Dose response to cerebrospinal fluid drainage on cerebral perfusion in traumatic brain-injured adults. Neurosurg Focus. 2001;11:E1. [DOI] [PubMed] [Google Scholar]
- 11.Cruz J Combined continuous monitoring of systemic and cerebral oxygenation in acute brain injury: Preliminary observations. Crit Care Med. 1993;21:1225–32. [DOI] [PubMed] [Google Scholar]
- 12.Fortune JB, Feustel PJ, Graca L, Hasselbarth J, Kuehler DH, Wilberger JE, et al. Effect of hyperventilation, mannitol, and ventriculostomy drainage on cerebral blood flow after head injury. J Trauma - Inj Infect Crit Care. 1995;39:1091–9. [DOI] [PubMed] [Google Scholar]
- 13.Papo I, Caruselli G. Long-term intracranial pressure monitoring in comatose patients suffering from head injuries. A critical survey. Acta Neurochir (Wien). 1977;39:187–200. [DOI] [PubMed] [Google Scholar]
- 14.Zweckberger K, Sakowitz OW, Unterberg a W, Kiening KL. Intracranial pressure-volume relationship. Physiology and pathophysiology. Anaesthesist. 2009;58:392–7. [DOI] [PubMed] [Google Scholar]
- 15.Kerr EM, Marion D, Sereika MS, Weber BB, Orndoff a P, Henker R, et al. The effect of cerebrospinal fluid drainage on cerebral perfusion in traumatic brain injured adults. J Neurosurg Anesthesiol. 2000;12:324–33. [DOI] [PubMed] [Google Scholar]
- 16.Slazinkski T, Anderson T, Cattell E, Eigsti J, Heimsoth S. Care of the Patient Undergoing Intracranial Pressure Monitoring / External Ventricular Drainage or Lumbar Drainage. AANN Clin Pract Guidel Ser. 2011;1–38. [Google Scholar]
- 17.Integra Design Verification Report for Camino Flex Ventricular Catheter. p. 49–51. [Google Scholar]
- 18.Hu X, Xu P, Scalzo F, Vespa P, Bergsneider M. Morphological clustering and analysis of continuous intracranial pressure. IEEE Trans Biomed Eng. 2009;56:696–705. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Asgari S, Gonzalez N, Subudhi AW, Hamilton R, Vespa P, Bergsneider M, et al. Continuous Detection of Cerebral Vasodilatation and Vasoconstriction Using Intracranial Pulse Morphological Template Matching. PLoS One. 2012;7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Asgari S, Bergsneider M, Hamilton R, Vespa P, Hu X. Consistent changes in intracranial pressure waveform morphology induced by acute hypercapnic cerebral vasodilatation. Neurocrit Care. 2011;15:55–62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Kempley ST, Gamsu HR. Changes in cerebral artery blood flow velocity after intermittent cerebrospinal fluid drainage. Arch Dis Child. 1993;69:74–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Asgari S, Vespa P, Bergsneider M, Hu X. Lack of consistent intracranial pressure pulse morphological changes during episodes of microdialysis lactate/pyruvate ratio increase. Physiol Meas. 2011;32:1639–51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Connolly M, Vespa P, Hu X. Characterization of cerebral vascular response to EEG bursts using ICP pulse waveform template matching. Acta Neurochir Suppl. 2016;122:291–4. [DOI] [PubMed] [Google Scholar]
- 24.Bouma GJ, Muizelaar JP, Bandoh K, Marmarou A. Blood pressure and intracranial pressure-volume dynamics in severe head injury: relationship with cerebral blood flow. J Neurosurg. 1992;77:15–9. [DOI] [PubMed] [Google Scholar]
- 25.Rangel-Castilla L, Gasco J, Nauta HJW, Okonkwo DO, Robertson CS. Cerebral pressure autoregulation in traumatic brain injury. Neurosurg Focus. 2008;25:E7. [DOI] [PubMed] [Google Scholar]
- 26.Kainerstorfer JM, Sassaroli A, Tgavalekos KT, Fantini S. Cerebral autoregulation in the microvasculature measured with near-infrared spectroscopy. J Cereb Blood Flow Metab. 2015;35:959–66. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Salehi A, Zhang JH, Obenaus A. Response of the cerebral vasculature following traumatic brain injury. J Cereb Blood Flow Metab. 2017;37:2320–39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Liu X, Donnelly J, Czosnyka M, Aries MJH, Brady K, Cardim D, et al. Cerebrovascular pressure reactivity monitoring using wavelet analysis in traumatic brain injury patients: A retrospective study. PLOS Med. 2017;14:7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Tian F, Tarumi T, Liu H, Zhang R, Chalak L. Wavelet coherence analysis of dynamic cerebral autoregulation in neonatal hypoxic-ischemic encephalopathy. NeuroImage Clin. 2016;11:124–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Peng T, Rowley AB, Ainslie PN, Poulin MJ, Payne SJ. Wavelet Phase Synchronization Analysis of Cerebral Blood Flow Autoregulation. IEEE Trans Biomed Eng. 2010;57:960–8. [DOI] [PubMed] [Google Scholar]
- 31.Spiegelberg A, Preuß M, Kurtcuoglu V. B-waves revisited. Interdiscip Neurosurg Adv Tech Case Manag. 2016;6:13–7. [Google Scholar]
- 32.Lemaire JJ, Khalil T, Cervenansky F, Gindre G, Boire JY, Bazin JE, et al. Slow pressure waves in the cranial enclosure. Acta Neurochir (Wien). 2002;144:243–54. [DOI] [PubMed] [Google Scholar]
- 33.Lundberg N Continuous recording and control of ventricular fluid pressure in neurosurgical practice. Acta Psychiatr Scand Suppl. 1960;36:1–193. [PubMed] [Google Scholar]
- 34.Hu X, Xu P, Lee DJ, Vespa P, Baldwin K, Bergsneider M. An algorithm for extracting intracranial pressure latency relative to electrocardiogram R wave. Physiol Meas. 2008;29:459–71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Grinsted a.,Moore JC, Jevrejeva S. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear Process Geophys. 2004;11:561–6. [Google Scholar]
- 36.Keissar K, Davrath LR, Akselrod S. Coherence analysis between respiration and heart rate variability using continuous wavelet transform. Philos Trans A Math Phys Eng Sci. 2009;367:1393–406. [DOI] [PubMed] [Google Scholar]
- 37.Kvandal P, Sheppard L, Landsverk S a, Stefanovska A, Kirkeboen K a. Impaired cerebrovascular reactivity after acute traumatic brain injury can be detected by wavelet phase coherence analysis of the intracranial and arterial blood pressure signals. J Clin Monit Comput. 2013;27:375–83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.A PS. The illustrated wavelet transform handbook, introductory theory and applications in science, engineering, medicine and finance. New York: Talor & Francis; 2002. [Google Scholar]
- 39.Addison PS. The Illustrated Wavelet Transform Handbook: Introductory Theory and Applications in Science, Engineering, Medicine and Finance, Second Edition. Boca Raton: CRC Press, Taylor & Francis Group; 2016. [Google Scholar]
- 40.Brady KM, Easley RB, Kibler K, Kaczka DW, Andropoulos D, Fraser CD, et al. Positive end-expiratory pressure oscillation facilitates brain vascular reactivity monitoring. J Appl Physiol. 2012;113:1362–8. [DOI] [PubMed] [Google Scholar]
- 41.Zhang R, Zuckerman JH, Giller C a, Levine BD. Transfer function analysis of dynamic cerebral autoregulation in humans. Am J Physiol. 1998;274:H233–41. [DOI] [PubMed] [Google Scholar]
- 42.Muizelaar J, Ward J, Marmarou A, Newlon P, Wachi A. Cerebral blood flow and metabolism in severely head-injured children Part 2: Autoregulation. J Neurosurg. 1989;71:72–6. [DOI] [PubMed] [Google Scholar]
- 43.Liu X, Czosnyka M, Donnelly J, Cardim D, Cabeleira M, Hutchinson PJ, et al. Wavelet pressure reactivity index: A validation study. J Physiol. 2018; [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Rao AR, Hamed K. Multi-taper method of analysis of periodicities in hydrologic data. J Hydrol. 2003;279:125–43. [Google Scholar]
- 45.Jeyaseelan AS, Balaji R. Spectral analysis of wave elevation time histories using multi-taper method. Ocean Eng. 2015;105:242–6. [Google Scholar]
- 46.Aries MJH, Czosnyka M, Budohoski KP, Steiner L a., Lavinio A, Kolias AG, et al. Continuous determination of optimal cerebral perfusion pressure in traumatic brain injury. Crit Care Med. 2012;40:2456–63. [DOI] [PubMed] [Google Scholar]
- 47.Trauner DA, Brown F, Ganz E, Huttenlocher PR. Treatment of elevated intracranial pressure in reye syndrome. Ann Neurol. 1978;4:275–8. [DOI] [PubMed] [Google Scholar]
- 48.Hawthorne C, Piper I. Monitoring of intracranial pressure in patients with traumatic brain injury. Front. Neurol. 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Physics C, Hospital SG, Kingdom U. Pressure autoregulation monitoring and cerebral perfusion pressure target recommendation in patients with severe traumatic brain injury based on minute-by-minute monitoring data. 2014;120:1451–7. [DOI] [PubMed] [Google Scholar]
- 50.Panerai RB. Cerebral autoregulation: From models to clinical applications. Cardiovasc. Eng 2008. p. 42–59. [DOI] [PubMed] [Google Scholar]
- 51.Larsen FS, Olsen KS, Hansen B a, Paulson OB, Knudsen GM. Transcranial Doppler is valid for determination of the lower limit of cerebral blood flow autoregulation. Stroke. 1994;25:1985–8. [DOI] [PubMed] [Google Scholar]
- 52.Lang EW, Lagopoulos J, Griffith J, Yip K, Yam A, Mudaliar Y, et al. Cerebral vasomotor reactivity testing in head injury: the link between pressure and flow. J Neurol Neurosurg Psychiatry. 2003;74:1053–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Rosner MJ, Rosner SD, Johnson a H. Cerebral perfusion pressure: management protocol and clinical results. J Neurosurg. 1995;83:949–62. [DOI] [PubMed] [Google Scholar]
- 54.Hemphill JC, Andrews P, De Georgia M. Multimodal monitoring and neurocritical care bioinformatics. Nat. Rev. Neurol. 2011. p. 451–60. [DOI] [PubMed] [Google Scholar]
- 55.Addison PS. Identifying stable phase coupling associated with cerebral autoregulation using the synchrosqueezed cross-wavelet transform and low oscillation morlet wavelets. Conf Proc IEEE Eng Med Biol Soc. 2015;8:5960–3. [DOI] [PubMed] [Google Scholar]
- 56.Lewis PM, Rosenfeld JV., Diehl RR, Mehdorn HM, Lang EW. Phase shift and correlation coefficient measurement of cerebral autoregulation during deep breathing in traumatic brain injury (TBI). Acta Neurochir (Wien). 2008;150:139–46. [DOI] [PubMed] [Google Scholar]
- 57.Donnelly J, Budohoski KP, Smielewski P, Czosnyka M. Regulation of the cerebral circulation: bedside assessment and clinical implications. Crit Care. 2016;20:129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Lee JK, Kibler KK, Benni PB, Easley RB, Czosnyka M, Smielewski P, et al. Cerebrovascular reactivity measured by near-infrared spectroscopy. Stroke. 2009;40:1820–6. [DOI] [PubMed] [Google Scholar]
- 59.Liu X, Czosnyka M, Donnelly J, Budohoski KP, Varsos G V, Nasr N, et al. Comparison of frequency and time domain methods of assessment of cerebral autoregulation in traumatic brain injury. J Cereb Blood Flow Metab. 2014;11:1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Steiner LA, Czosnyka M, Piechnik SK. Continuous monitoring of cerebrovascular pressure reactivity allows determination of optimal cerebral perfusion pressure in patients with traumatic brain injury. Crit Care. 2002;30:733–8. [DOI] [PubMed] [Google Scholar]
- 61.Aries MJ, Czosnyka M, Budohoski KP, Steiner LA, Lavinio A, Kolias AG, et al. Continuous determination of optimal cerebral perfusion pressure in traumatic brain injury. Crit Care Med. 2012;40:2456–63. [DOI] [PubMed] [Google Scholar]
- 62.Depreitere B, Güiza F, Van den Berghe G, Schuhmann MU, Maier G, Piper I, et al. Pressure autoregulation monitoring and cerebral perfusion pressure target recommendation in patients with severe traumatic brain injury based on minute-by-minute monitoring data. J Neurosurg. 2014;120:1451–7. [DOI] [PubMed] [Google Scholar]
- 63.Liu X, Maurits N, Aries M, Czosnyka M, Ercole A, Donnelly J, et al. Monitoring of optimal cerebral perfusion pressure in traumatic brain injured patients using a multi-window weighting algorithm. J Neurotraumà. 2017;34:3081–8. [DOI] [PubMed] [Google Scholar]
- 64.Cardim D, Robba C, Bohdanowicz M, Donnelly J, Cabella B, Liu X, et al. Non-invasive Monitoring of Intracranial Pressure Using Transcranial Doppler Ultrasonography: Is It Possible? Neurocrit Care. 2016;25:473–91. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


