Understanding the computation of time using neural network models

Significance

Perceiving, maintaining, and using time intervals in working memory are crucial for animals to anticipate or act correctly at the right time in the ever-changing world. Here, we systematically study the underlying neural mechanisms by training recurrent neural networks to perform temporal tasks or complex tasks in combination with spatial information processing and decision making. We found that neural networks perceive time through state evolution along stereotypical trajectories and produce time intervals by scaling evolution speed. Temporal and nontemporal information is jointly coded in a way that facilitates decoding generalizability. We also provided potential sources for the temporal signals observed in nontiming tasks. Our study revealed the computational principles of a number of experimental phenomena and provided several predictions.

Abstract

To maximize future rewards in this ever-changing world, animals must be able to discover the temporal structure of stimuli and then anticipate or act correctly at the right time. How do animals perceive, maintain, and use time intervals ranging from hundreds of milliseconds to multiseconds in working memory? How is temporal information processed concurrently with spatial information and decision making? Why are there strong neuronal temporal signals in tasks in which temporal information is not required? A systematic understanding of the underlying neural mechanisms is still lacking. Here, we addressed these problems using supervised training of recurrent neural network models. We revealed that neural networks perceive elapsed time through state evolution along stereotypical trajectory, maintain time intervals in working memory in the monotonic increase or decrease of the firing rates of interval-tuned neurons, and compare or produce time intervals by scaling state evolution speed. Temporal and nontemporal information is coded in subspaces orthogonal with each other, and the state trajectories with time at different nontemporal information are quasiparallel and isomorphic. Such coding geometry facilitates the decoding generalizability of temporal and nontemporal information across each other. The network structure exhibits multiple feedforward sequences that mutually excite or inhibit depending on whether their preferences of nontemporal information are similar or not. We identified four factors that facilitate strong temporal signals in nontiming tasks, including the anticipation of coming events. Our work discloses fundamental computational principles of temporal processing, and it is supported by and gives predictions to a number of experimental phenomena.

Much information that the brain processes and stores is temporal in nature. Therefore, understanding the processing of time in the brain is of fundamental importance in neuroscience (1–4). To predict and maximize future rewards in this ever-changing world, animals must be able to discover the temporal structure of stimuli and then flexibly anticipate or act correctly at the right time. To this end, animals must be able to perceive, maintain, and then use time intervals in working memory, appropriately combining the processing of time with spatial information and decision making (DM). Based on behavioral data and the diversity of neuronal response profiles, it has been proposed (5, 6) that time intervals in the range of hundreds of milliseconds to multiseconds can be decoded through neuronal population states evolving along transient trajectories. The neural mechanisms may be accumulating firing (7, 8), synfire chains (9, 10), the beating of a range of oscillation frequencies (11), etc. However, these mechanisms are challenged by recent finding that animals can flexibly adjust the evolution speed of population activity along an invariant trajectory to produce different intervals (12). Through behavioral experiments, it was found that humans can store time intervals as distinct items in working memory in a resource allocation strategy (13), but an electrophysiological study on the neuronal coding of time intervals maintained in working memory is still lacking. Moreover, increasing evidence indicates that timing does not rely on dedicated circuits in the brain but instead, is an intrinsic computation that emerges from the inherent dynamics of neural circuits (3, 14). Spatial working memory and DM are believed to rely mostly on a prefrontoparietal circuit (15, 16). The dynamics and the network structure that enable this circuit to combine spatial working memory and DM with flexible timing remain unclear. Overall, our understanding of the processing of time intervals in the brain is fragmentary and incomplete. It is, therefore, essential to develop a systematic understanding of the fundamental principle of temporal processing and its combination with spatial information processing and DM.

The formation of temporal signals in the brain is another unexplored question. Strong temporal signals were found in the brain even when monkeys performed working memory tasks where temporal information was not needed (17–21). In a vibrotactile working memory task (17), monkeys were trained to report which of the two vibrotactile stimuli separated by a fixed delay period had higher frequency (Fig. 1D). Surprisingly, although the duration of the delay period was not needed to perform this task, temporal information was still coded in the neuronal population state during the delay period, with the time-dependent variance explaining more than 75% of the total variance (18, 19). A similar scenario was also found in other nontiming working memory tasks (19–21). It is unclear why such strong temporal signals arose in nontiming tasks.

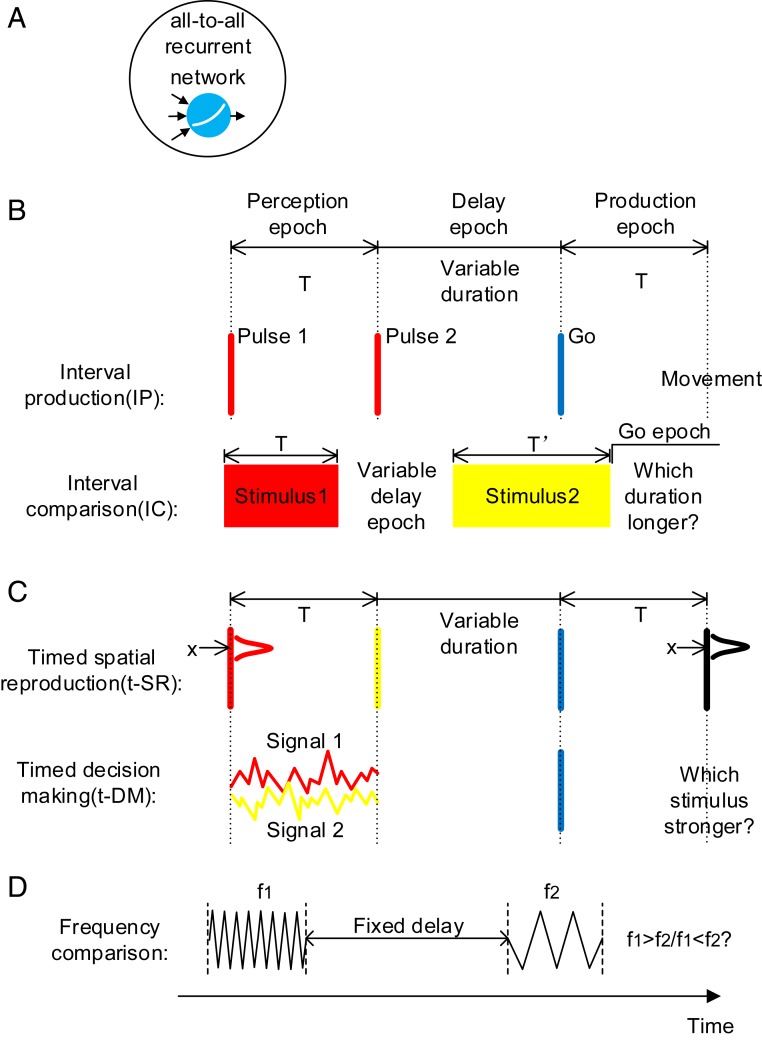
Fig. 1.

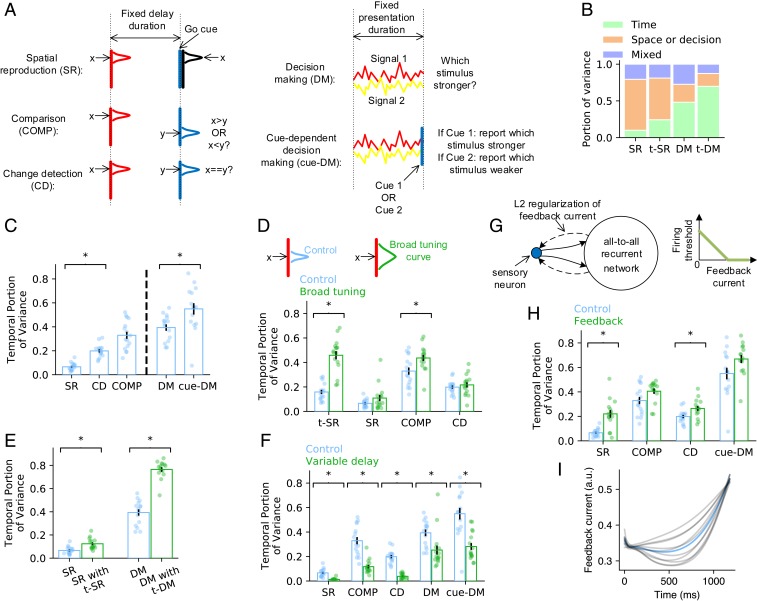
Model setup. (A) All-to-all connected recurrent networks with soft plus units are trained. (B) Basic timing tasks. IP: The duration $T$ of the perception epoch determines the movement time after the go cue. IC: The duration $T$ of the stimulus 1 epoch is compared with the duration $T^{\prime }$ of the stimulus 2 epoch. Stimuli with different colors (red, yellow, or blue) indicate that they are input to the network through different synaptic weights. (C) Combined timing tasks. $T$ determines the movement time after the go cue. Spatial location (t-SR) or decision choice (t-DM) determines the movement behavior. (D) A nontiming task in the experimental study (18). Although the duration of the delay period is not needed to perform the task, there exists strong temporal signals in the delay period.

Previous works showed that, after being trained to perform tasks such as categorization, working memory, DM, and motion generation, artificial neural networks (ANNs) exhibited coding or dynamic properties surprisingly similar to experimental observations (22–25). Compared with animal experiments, ANN can cheaply and easily implement a series of tasks, greatly facilitating the test of various hypotheses and the capture of common underlying computational principles (26, 27). In this paper, we trained recurrent neural networks (RNNs) (Fig. 1A) to study the processing of temporal information. First, by training networks on basic timing tasks, which require only temporal information to perform (Fig. 1B), we studied how time intervals are perceived, maintained, and used in working memory. Second, by training networks on combined timing tasks, which require both temporal and nontemporal information to perform (Fig. 1C), we studied how the processing of time is combined with spatial information processing and DM, the influence of this combination on decoding generalizability, and the network structure that this combination is based on. Third, by training networks on nontiming tasks (Fig. 1D), we studied why such a large time-dependent variance arises in nontiming tasks, thereby understanding the factors that facilitate the formation of temporal signals in the brain. Our work presents a thorough understanding of the neural computation of time.

Results

We trained an RNN of 256 soft plus units supervisedly using back propagation through time (28). Self-connections of the RNN were initialized to one, and off-diagonal connections were initialized as independent Gaussian variables with mean of zero (27), with different training configurations initialized using different random seeds. The strong self-connections supported self-sustained activity after training (SI Appendix, Fig. S1B), and the nonzero initialization of the off-diagonal connections induced sequential activity comparable with experimental observations (27). We stopped training as soon as the performance of the network reached criterion (23, 25) (performance examples are in SI Appendix, Fig. S1).

Basic Timing Tasks: Interval Production and Interval Comparison Tasks.

Interval production task.

In the interval production (IP) task (the first task of Fig. 1B), the network was to perceive the interval $T$ between the first two pulses, maintain the interval during the delay epoch with variable duration, and then produce an action at time $T$ after the go cue. Neuronal activities after training exhibited strong fluctuations (Fig. 2A). In the following, we report on the dynamics of the network in the perception, delay, and production epochs of IP (Fig. 1 has an illustration of these epochs).

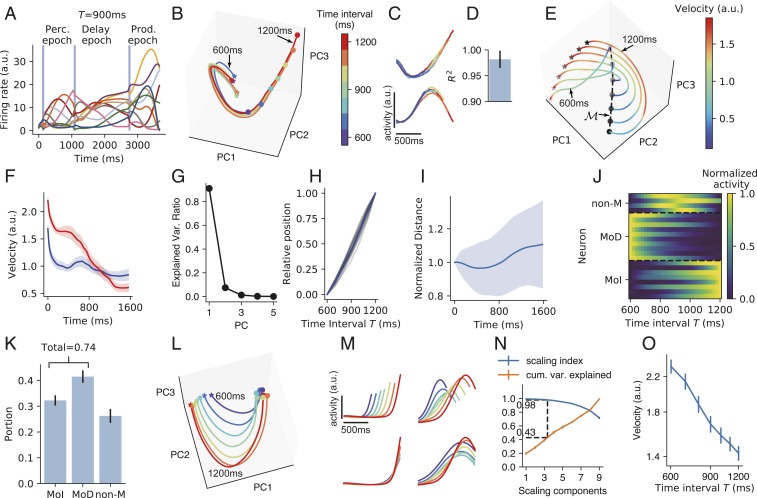
Fig. 2.

IP task. (A) The activities of example neurons (indicated by lines of different colors) when the time interval $T$ between the first two pulses is 900 ms. Vertical blue shadings indicate the pulse input to the network. (B) Population activity in the perception epoch in the subspace of the first three PCs. Colors indicate the time interval $T$. Stars and circles indicate the starting and ending points of the perception epoch, respectively. The trajectories for $T=600$ and 1,200 ms are labeled. (C) Firing profiles of two example neurons in the perception epoch. Line colors have the same meaning as in B. (D) Coefficient of determination ($R^2$) of how much the neuronal firing profile with the largest $T$ can explain the variance of the firing profiles with smaller $T$ in the perception epoch. Error bar indicates SD over different neurons and $T$ values. (E) Population activity in the subspace of the first three PCs in the delay epoch. Colors indicate trajectory speed. The increasing blackness of stars and circles indicates trajectories with $T=600$, 700$\cdots \hspace{0.17em}$1,200 ms. The dashed curve connecting the end points of the delay epoch marks manifold $\mathcal{M}$. (F) Trajectory speed as a function of time in the delay epoch when $T=600$ ms (blue) and 1,200 ms (red). Shaded belts indicate SEM over training configurations. (G) Ratio of explained variance of the first five PCs of manifold $\mathcal{M}$. Error bars that indicate SEM are smaller than plot markers. (H) The position of the state at the end of the delay epoch projected in the first PC of manifold $\mathcal{M}$ as a function of $T$. The position when $T=600$ ms (or 1,200 ms) is normalized to be 0 (or 1). Gray curves: 16 training configurations. Blue curve: mean value. (I) The distance between two adjacent curves in the delay epoch as a function of time, with the distance at the beginning of the delay epoch normalized to be one. Shaded belts indicate SD. (J) Firing rates of example neurons of MoD, MoI, and non-M types as functions of $T$ in manifold $\mathcal{M}$. (K) The portions of the three types of neurons. (L) Population activity in the production epoch in the subspace of the first three PCs. Colors indicate the time intervals to be produced as shown in the color bar of B. Stars and circles indicate the starting and ending points of the production epoch, respectively. (M, Upper) Firing profiles of two example neurons in the production epoch. (M, Lower) Firing profiles of the two neurons after being temporally scaled according to produced intervals. (N) A point at horizontal coordinate $x$ means the SI (blue) or the ratio of explained variance (orange) of the subspace spanned by the first $x$ SCs. Dashed lines indicate that a subspace with SI 0.98 explains, on average, 43% of the total variance. (O) Trajectory speed in the subspace of the first three SCs as the function of the time interval to be produced. In K, N, and O, error bars indicate SEM over training configurations. During training, we added recurrent and input noises (Materials and Methods). Here and in the following, when analyzing the network properties after training, we turned off noises by default. We kept noises for the perception epoch in B–D. Without noise, the trajectories in the perception epoch would fully overlap under different $T$ values.

The first epoch is the perception epoch. In response to the first stimulus pulse, the network started to evolve from almost the same state along an almost identical trajectory in different simulation trials with different $T$ values until another pulse came (Fig. 2B); the activities of individual neurons before the second pulse in different trials highly overlapped (Fig. 2 C and D). Therefore, the network state evolved along a stereotypical trajectory starting from the first pulse, and the time interval $T$ between the first two pulses can be read out using the position in this trajectory when the second pulse came. Behaviorally, a human’s perception of the time interval between two acoustic pulses is impaired if a distractor pulse appears shortly before the first pulse (29). A modeling work (29) explained that this is because successful perception requires the network state to start to evolve from near a state ${\mathbf{s}}_0$ in response to the first pulse, whereas the distractor pulse kicks the network state far away from ${\mathbf{s}}_0$. This explanation is consistent with our results that interval perception requires a stereotypical trajectory.

We then studied how the information of timing interval $T$ between the first two pulses was maintained during the delay epoch. We have the following findings. 1) The speeds of the trajectories decreased with time in the delay epoch (Fig. 2 E and F). 2) The states ${\mathbf{s}}_{\text{EndDelay}}$ at the end of the delay epoch at different $T$ values were aligned in a manifold $\mathcal{M}$ in which the first principal component (PC) explained 90% of its variance (Fig. 2G). 3) For a specific simulation trial, the position of ${\mathbf{s}}_{\text{EndDelay}}$ in manifold $\mathcal{M}$ linearly encoded the $T$ value of the trial (Fig. 2H). 4) The distance between two adjacent trajectories kept almost unchanged with time during the delay neither decayed to zero nor exploded (Fig. 2I): this stable dynamics supported the information of $T$ encoded by the position in the stereotypical trajectory at the end of the perception epoch in being maintained during the delay. Collectively, $\mathcal{M}$ approximated a line attractor (24, 30) with slow dynamics, and $T$ was encoded as the position in $\mathcal{M}$. To better understand the scheme of coding $T$ in $\mathcal{M}$, we classified neuronal activity $f\left(T\right)$ in manifold $\mathcal{M}$ as a function of $T$ into three types (Fig. 2 J and K): monotonically decreasing (MoD), monotonically increasing (MoI), and nonmonotonic (non-M) (Materials and Methods). We found that most neurons were MoD or MoI, whereas only a small portion were non-M neurons (Fig. 2K). This implies that the network mainly used a complementary (i.e., concurrently increasing and decreasing) monotonic scheme to code time intervals in the delay epoch, similar to the scheme revealed in refs. 17 and 31. This dominance of monotonic neurons may be the reason why the first PC of $\mathcal{M}$ explained so much variance (Fig. 2G); SI Appendix, section S2 and Fig. S2 G and H has a simple explanation.

In the production epoch, the trajectories of the different $T$ values tended to be isomorphic (Fig. 2L). The neuronal activity profiles were self-similar when stretched or compressed in accordance with the produced interval (Fig. 2M), suggesting temporal scaling with $T$ (12). To quantify this temporal scaling, we defined the scaling index (SI) of a subspace $\mathcal{S}$ as the portion of variance of the projections of trajectories into $\mathcal{S}$ that can be explained by temporal scaling (12). We found that the distribution of SI of individual neurons aggregated toward one (SI Appendix, Fig. S2B), and the first two PCs that explained most variance have the highest SI (SI Appendix, Fig. S2C). We then used a dimensionality reduction technique that furnished a set of orthogonal directions (called scaling components [SCs]) in the network state space that were ordered according to their SI (Materials and Methods). We found that a subspace (spanned by the first three SCs) that had high SI (=0.98) occupied about 40% of the total variance of trajectories (Fig. 2N), in contrast with the low SI of the perception epoch (SI Appendix, Fig. S2F). The average speed of the trajectory in the subspace of the first three SCs was inversely proportional to $T$ (Fig. 2O). Collectively, the network adjusted its dynamic speed to produce different time intervals in the production epoch, similar to observations of the medial frontal cortex of monkeys (12, 32). Additionally, we found a nonscaling subspace in which mean activity during the production epoch changed linearly with $T$ (SI Appendix, Fig. S2 D and E), also similar to the experimental observations in refs. 12 and 32.

Interval comparison task.

In the interval comparison (IC) task (the second task of Fig. 1B), the network was successively presented two intervals; it was then required to judge which interval was longer. IC required the network to perceive the time interval $T$ of the stimulus 1 epoch, to maintain the interval in the delay epoch, and to use it in the stimulus 2 epoch in which duration is $T^{\prime }$. Similar to IP, the network perceived time interval with a stereotypical trajectory in the stimulus 1 epoch (SI Appendix, Fig. S3 A–C) and maintained time interval using attractor dynamics with a complementary monotonic coding scheme in the delay epoch (SI Appendix, Fig. S3 D–H). The trajectory in the stimulus 2 epoch had a critical point ${\mathbf{s}}_{crit}$ at time $T$ after the start of stimulus 2. The network was to give different comparison (COMP) outputs at the go epoch depending on whether or not the trajectory had passed ${\mathbf{s}}_{crit}$ at the end of stimulus 2. To make a correct COMP choice, only the period from the start of stimulus 2 to ${\mathbf{s}}_{crit}$ (or to the end of stimulus 2 if $T>T^{\prime }$) needs to be timed: as long as the trajectory had passed ${\mathbf{s}}_{crit}$, the network could readily make the decision that $T<T^{\prime }$, with no more timing required. After training, we studied the trajectories from the start of stimulus 2 to ${\mathbf{s}}_{crit}$ in the cases that $T<T^{\prime }$ and found temporal scaling (SI Appendix, Fig. S3 J–N) similar to the production epoch of IP consistently with animal experiments (33, 34). These similarities between IP and IC on how to perceive, maintain, and use time intervals imply universal computational schemes for neural networks to process temporal information.

The average speed of the trajectory after ${\mathbf{s}}_{crit}$ increased with $T$ (SI Appendix, Fig. S3O), whereas the speed before ${\mathbf{s}}_{crit}$ decreased with $T$: this implies that the dynamics after ${\mathbf{s}}_{crit}$ was indeed different from that before.

Combined Timing Tasks: Timed Spatial Reproduction and Timed DM Tasks.

It is a ubiquitous phenomenon that neural networks encode more than one quantity simultaneously (35–37). In this subsection, we will discuss how neural networks encode temporal and spatial information (or decision choice) simultaneously, which enables the brain to take the right action at the right time.

Timed spatial reproduction task.

In the timed spatial reproduction (t-SR) task (the first task in Fig. 1C), the network was to not only take action at the desired time but also, act at the spatial location indicated by the first pulse. Similar to IP and IC, the network used stereotypical trajectories, attractors, and speed scaling to perceive, maintain, and produce time intervals (SI Appendix, Fig. S4). In the following, we will focus on the coding combination of temporal and spatial information.

In the perception epoch, under the two cases when the first pulse was at two locations $x$ and $y$ separately, the activities $r_{i,\text{perc}}\left(t,x\right)$ and $r_{i,\text{perc}}\left(t,y\right)$ of the $i$th neuron exhibited similar profiles with time $t$ (Fig. 3B), especially when $x$ and $y$ had close values. In our simulation, the location of the first pulse was represented by a Gaussian bump with standard deviation (SD) of 2., which is much smaller than the smallest spatial distance 6 between two different colors in Fig. 3 A and B; thus, the similarity of the temporal profiles in Fig. 3B should not result from the overlap of the sensory inputs from the first pulse but rather, should emerge during training.

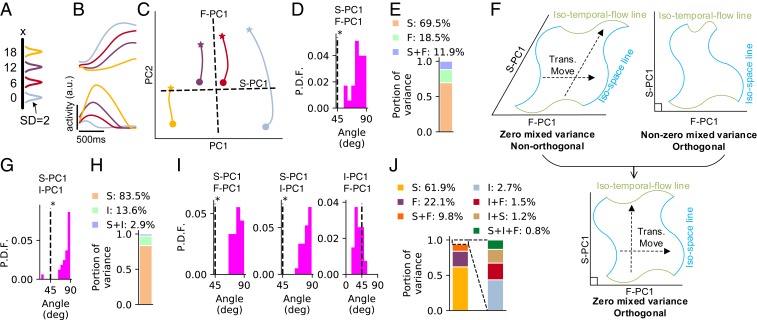
Fig. 3.

The t-SR task. (A) Color scheme that represents the spatial location of the first pulse used in B and C. Location is represented by Gaussian bump with SD of 2. (B) Firing profiles of four example neurons in the perception epoch. (C) Trajectory of the perception epoch in the subspace of the first two PCs. Stars indicate the points after 400 ms of the transient period from the beginning of the perception epoch, and circles indicate the ending points of the perception epoch. Dashed lines represent the projections of F-PC1 and S-PC1 in this subspace. (D) Probability distribution function (P.D.F.) of the angle between F-PC1 and S-PC1 in the perception epoch over 32 training configurations. *Significant ($P<0.05$) larger than $45^{○}$ (t test). (E) Portion of variance explained by spatial information (S), temporal flow (F), and their mixture (S + F) in the perception epoch, averaging over 32 training configurations. (F) Schematic for the meanings of angle and mixed variance. Zero mixed variance implies that different isospace (blue) or isotemporal flow (green) lines are related by translational movement, forming parallelogram-like grids (F, Upper Left); orthogonality (F, Upper Right) implies rectangle-like grids (F, Lower). (G) The distribution of the angle between I-PC1 and S-PC1 in manifold $\mathcal{M}$ (Fig. 2E) at the end of the delay epoch. (H) The portion of variance explained by S, time interval (I), and their mixture (S + I) in manifold $\mathcal{M}$ at the end of the delay epoch. (I) The distributions of the angles between F-PC1, I-PC1, and S-PC1 in the production epoch. (J) The portion of variance explained by S, F, I, and their mixtures in the production epoch. In A–E, $T=\mathrm{1,200}$ ms for the perception epoch; in G–J, $T=600$, 700$\cdots \hspace{0.17em}$1,200 ms for the delay and production epochs.

To quantitatively investigated the coding combination of temporal and spatial information, we studied the first temporal flow PC (F-PC1) of the neuronal population, namely the first PC of ${\left\{{⟨r_{i,\text{perc}}\left(t,x\right)⟩}_x\right\}}_i$, and the first spatial PC (S-PC1), namely the first PC of ${\left\{{⟨r_{i,\text{perc}}\left(t,x\right)⟩}_t\right\}}_i$, with ${⟨\cdot ⟩}_a$ indicating averaging over parameter $a$. By temporal flow, we mean the time elapsed from the beginning of a specific epoch. We found that the angle between F-PC1 and S-PC1 distributed around $90^{○}$, significantly larger than $45^{○}$ (Fig. 3D). This indicates that temporal flow and spatial information were coded in almost orthogonal subspaces (Fig. 3C). We then studied the mixed variance (19). Specifically, the variance explained by temporal (or spatial) information is $v_t={\text{Var}}_{i,t}\left({⟨r_{i,\text{perc}}\left(t,x\right)⟩}_x\right)$ [or $v_x={\text{Var}}_{i,x}\left({⟨r_{i,\text{perc}}\left(t,x\right)⟩}_t\right)$], and the mixed variance is $v_{t+x}=v_{tot}-v_t-v_x$, where $v_{tot}={\text{Var}}_{i,t,x}\left(r_{i,\text{perc}}\left(t,x\right)\right)$ is the total variance. We found that the mixed variance took a small portion of the total variance, smaller than the variance of either temporal or spatial information (Fig. 3E). To understand the implication of this result, we noted that a sufficient condition for $v_{t+x}=0$ is that different isospace (or isotemporal flow) lines are related to each other through translational movement (Fig. 3 F, Upper Left), where an isospace (or isotemporal flow) line is a manifold in the state space with different temporal flow (or space) values but a fixed space (or temporal flow) value. The opposite extreme case $v_{t+x}=v_{tot}$ implies that different isospace (or isotemporal flow) lines are strongly intertwined; SI Appendix, section S3 has details. Together, orthogonality and small mixed variance suggest that isospace and isotime lines interweave into rectangle-like grids (Fig. 3 F, Lower); SI Appendix, Fig. S6 has illustrations of the simulation results.

In the delay epoch, the population states were attracted toward a manifold $\mathcal{M}$ of slow dynamics at the end of the delay epoch (Fig. 2 E–I and SI Appendix, Fig. S4 B–D), maintaining both the duration $T$ of the perception epoch and the spatial information $x$. We studied the coding combination of $T$ and $x$ in $\mathcal{M}$ in a similar way to above. We found that the first time interval PC (I-PC1), namely the first PC to code $T$, was largely orthogonal with S-PC1 (Fig. 3G), and the mixed variance between $T$ and $x$ was small (Fig. 3H).

In the production epoch, the network needed to maintain three pieces of information: temporal flow $t$, time interval $T$, and spatial location $x$. We studied the angle between the first PCs of any two of them (i.e., F-PC1, I-PC1, and S-PC1). We found that S-PC1 was orthogonal with F-PC1 and I-PC1 but that F-PC1 and I-PC1 was not orthogonal (Fig. 3I). For any two parameters, their mixed variance was smaller than the variance of their own (Fig. 3J); Materials and Methods has details.

Collectively, in all of the three epochs, the coding subspaces of temporal and spatial information were largely orthogonal with small mixed variance, suggesting rectangle-like grids of isospace and isotime lines; SI Appendix, Fig. S6 has illustrations.

Timed DM task.

In the timed decision-making (t-DM) task (the second task in Fig. 1C), the network was to make a decision choice at the desired time to indicate which of the two presented stimuli was stronger. Similar to IP, IC, and t-SR, the network used stereotypical trajectories, attractors, and speed scaling to separately perceive, maintain, and produce time intervals (SI Appendix, Fig. S5 A–M). In all of the three epochs of t-DM, the first PC to code decision choice was orthogonal with F-PC1 or I-PC1, and the mixed variance between any two parameters was small (SI Appendix, Fig. S5 N–S); however, F-PC1 and I-PC1 in the production epoch were not orthogonal (SI Appendix, Fig. S5R). These results are all similar to those of the t-SR task.

Decoding Generalizability.

We then studied how the above geometry of coding space influences decoding generalizability: suppose that the population state space is parameterized by $a$ and $b$; we want to know the error of decoding $a$ from a state ${\mathbf{f}}_0$ in an iso-$b$ line $\mathbf{f}\left(a;b_{test}\right)$ after training the decoder using another iso-$b$ line $\mathbf{f}\left(a;b_{train}\right)$ (Fig. 4A). We considered two types of nearest-centroid decoders (20). Decoder 1 projects both ${\mathbf{f}}_0$ and $\mathbf{f}\left(a;b_{train}\right)$ into the first PC of $\mathbf{f}\left(a;b_{train}\right)$ and reads the value of $a$ to be the value that minimized the distance between ${\mathcal{P}}_{dec}\left[\mathbf{f}\left(a;b_{train}\right)\right]$ and ${\mathcal{P}}_{dec}\left[{\mathbf{f}}_0\right]$, where ${\mathcal{P}}_{dec}\left[\cdot \right]$ indicates the projection operation. Decoder 2 first translationally moves the whole iso-$b$ line $\mathbf{f}\left(a;b_{test}\right)$ so that the mass center of ${\mathcal{P}}_{dec}\left[\mathcal{T}\left[\mathbf{f}\left(a;b_{test}\right)\right]\right]$ coincides with that of ${\mathcal{P}}_{dec}\left[\mathbf{f}\left(a;b_{train}\right)\right]$, where $\mathcal{T}$ indicates the translation operation, and then reads $a$ according to ${\mathcal{P}}_{dec}\left[\mathcal{T}\left[{\mathbf{f}}_0\right]\right]$ (Fig. 4A). Apparently, zero error of Decoder 1 requires ${\mathcal{P}}_{dec}\left[\mathbf{f}\left(a;b_{test}\right)\right]$ and ${\mathcal{P}}_{dec}\left[\mathbf{f}\left(a;b_{train}\right)\right]$ to perfectly overlap. If the grids woven by iso-$a$ and iso-$b$ lines are tilted (Fig. 3 F, Upper Left) or nonparallelogram like (Fig. 3 F, Upper Right), which can be quantified by the orthogonality or mixed variance ratio, respectively, introduced in the above section, the projections ${\mathcal{P}}_{dec}\left[\mathbf{f}\left(a;b_{test}\right)\right]$ and ${\mathcal{P}}_{dec}\left[\mathbf{f}\left(a;b_{train}\right)\right]$ may have nonoverlapping mass centers (Fig. 4 B, Upper) or different lengths (Fig. 4 B, Lower), causing decoding error. Decoder 2 translationally moves the mass center of ${\mathcal{P}}_{dec}\left[\mathbf{f}\left(a;b_{test}\right)\right]$ to the position of that of ${\mathcal{P}}_{dec}\left[\mathbf{f}\left(a;b_{train}\right)\right]$, and therefore, its decoding error only depends on the nonparallelogram likeness of grids. Biologically, the projection onto the first PC of $\mathbf{f}\left(a;b_{train}\right)$ can be realized by Hebbian learning of decoding weights (38), the nearest-centroid scheme can be realized by winner-take-all DM (20), and the overlap of the mass centers in Decoder 2 can be realized by homeostatic mechanisms (39) to keep the mean neuronal activity over different iso-$b$ lines unchanged (SI Appendix, Eq. S19).

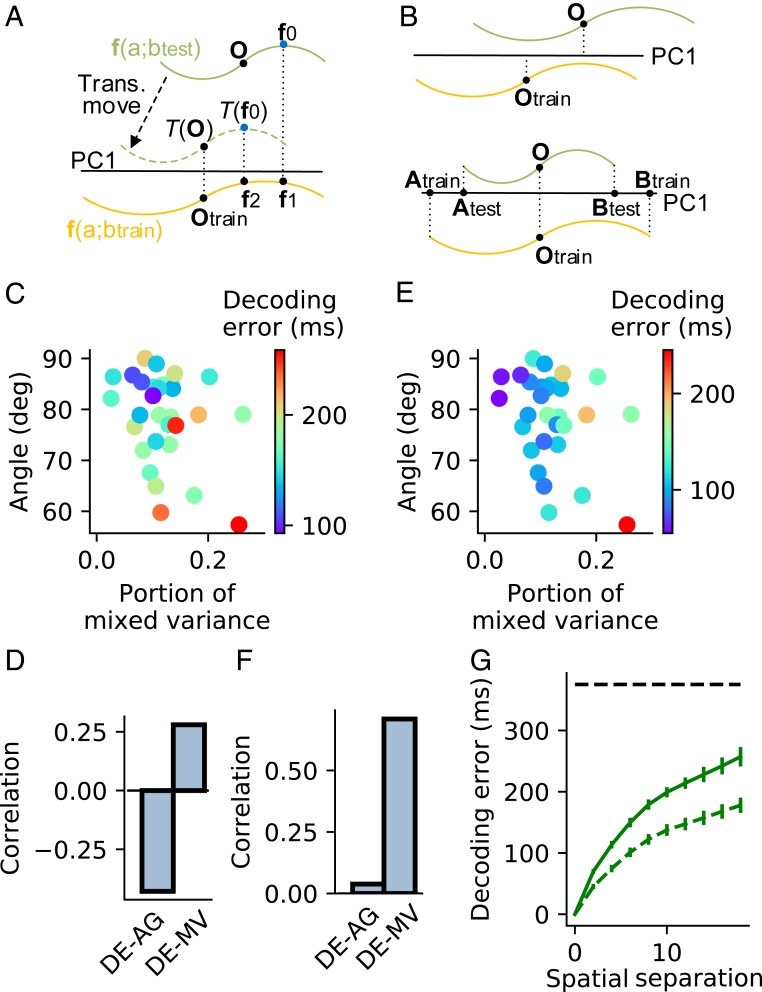
Fig. 4.

Decoding generalizability. (A) A schematic that explains Decoder 1 and Decoder 2. The decoders read the value of $a$ through state ${\mathbf{f}}_0$ in iso-$b$ line $\mathbf{f}\left(a;b_{test}\right)$ (green) after being trained by another iso-$b$ line $\mathbf{f}\left(a;b_{train}\right)$ (orange). Decoder 1 reads $a$ to be the same as that of ${\mathbf{f}}_1$ because ${\mathbf{f}}_0$ and ${\mathbf{f}}_1$ project to the same point on PC1 (black horizontal line) of $\mathbf{f}\left(a;b_{train}\right)$. Decoder 2 first translationally moves $\mathbf{f}\left(a;b_{test}\right)$ so that its mass center $\mathcal{T}\left(O\right)$ after translational movement $\mathcal{T}$ projects to the same point as the mass center $O_{train}$ of $\mathbf{f}\left(a;b_{train}\right)$ on PC1 and then reads $a$ according to $\mathcal{T}\left({\mathbf{f}}_0\right)$, which is the $a$ value of ${\mathbf{f}}_2$. (B) Two error sources of Decoder 1. (B, Upper) The mass centers $O$ and $O_{train}$ do not project to the same point on PC1. (B, Lower) The projections of $\mathbf{f}\left(a;b_{train}\right)$ and $\mathbf{f}\left(a;b_{test}\right)$ on PC1 (lines $A_{train}{B}_{train}$ and $A_{test}{B}_{test}$) do not have the same length. (C) The error of Decoder 1 (indicated by dot color) to read temporal flow across different spatial locations as a function of the angle (AG) and mixed variance (MV) between the temporal flow and spatial subspaces in the production epoch of t-SR task. (D) Correlations between decoding error (DE) and AG and between DE and MV. (E and F) The same as C and D except for Decoder 2. (G) DE as a function of $|x_{train}-x_{test}|$ after Decoder 1 (solid line) or Decoder 2 (dashed line) is trained to read the temporal flow using the isospace line at spatial location $x_{train}$ and then tested at spatial location $x_{test}$. The horizontal dashed line indicates chance level, supposing that the decoder works by random guess. Error bars represent mean $\pm$ SEM across simulation trials. C–F analyze the data averaging over $|x_{train}-x_{test}|$ in individual training configurations. $T=\mathrm{1,200}$ ms. Decoding generalizability in other epochs of the t-SR task and the t-DM task is shown in SI Appendix, Figs. S7 and S8.

Consistent with the decoding scenario above, when decoding temporal flow generalizing across spatial information in the production epoch of t-SR, the error of Decoder 1 negatively correlated with the angle $\theta$ between F-PC1 and S-PC1 and positively correlated with the portion ${\rho }_{mix}$ of mixed variance (Fig. 4 C and D); the error of Decoder 2 depended weakly on $\theta$ and positively correlated with ${\rho }_{mix}$ (Fig. 4 E and F). Materials and Methods has details. Thanks to the angle orthogonality and small mixed variance (Fig. 3), both decoders have above-chance performance (Fig. 4G). Additionally for both t-SR and t-DM tasks, we studied the decoding generalization of temporal (nontemporal) information across nontemporal (temporal) information in all of the perception, delay, and production epochs. In all cases, we found how the decoding error depended on the angle between the first PCs of the decoded and generalized variables, and the mixed variance followed a similar scenario to that above (SI Appendix, Figs. S7 and S8).

Sequential Activity and Network Structure.

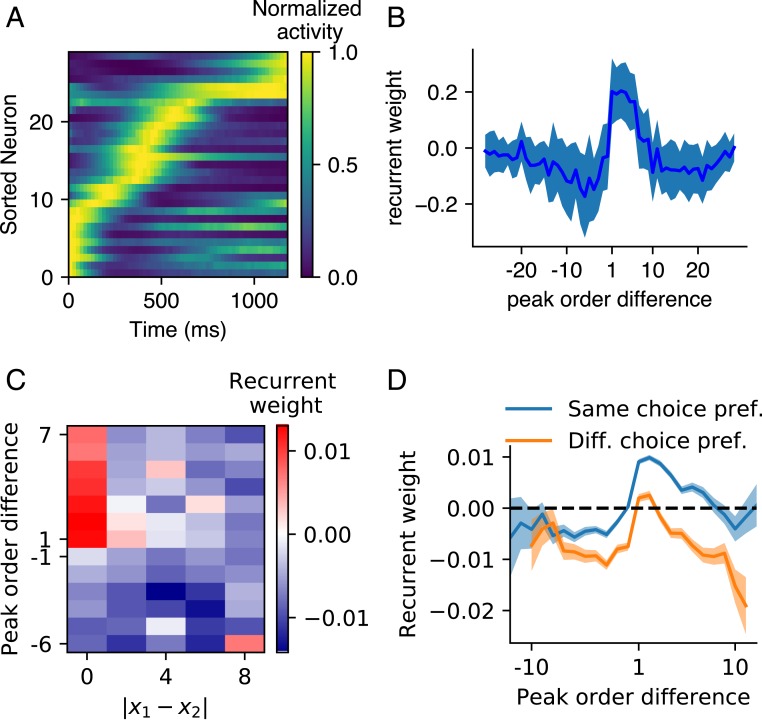
A common feature of the network dynamics in all of the epochs of the four timing tasks above was neuronal sequential firing (Fig. 5A and SI Appendix, Fig. S9 A–C). We ordered the peak firing time of the neurons and then measured the recurrent weight as a function of the order difference between two neurons. We found, on average, stronger connections from earlier- to later-peaking neurons than from later- to earlier-peaking neurons (Fig. 5B and SI Appendix, Fig. S9 D–F) (27, 40, 41). To study the network structure that supported the coding orthogonality of temporal flow and nontemporal information in the perception and production epochs of t-SR (or t-DM), we classified the neurons into groups according to their preferred spatial location (or decision choice). Given a neuron $i$ and a group $\mathcal{G}$ of neurons ($i$ may or may not belong to $\mathcal{G}$), we ordered their peak times and investigated the recurrent weight from $i$ to each neuron of $\mathcal{G}$ (except $i$ itself if $i\in \mathcal{G}$); Materials and Methods has details. In this way, we studied the recurrent weight $w\left(o_{post}-o_{pre},|x_{post}-x_{pre}|\right)$ as a function of the difference $o_{post}-o_{pre}$ between the peak orders of post- and presynaptic neurons and the difference $|x_{post}-x_{pre}|$ of their preferred nontemporal information (Fig. 5 C and D). In t-SR, first, $w\left(o_{post}-o_{pre},0\right)$ exhibited similar asymmetry as that in IP (Fig. 5B) (positive if $o_{post}-o_{pre}>0$ and negative if $o_{post}-o_{pre}<0$), which drove sequential activity. Second, $w\left(1,|x_{post}-x_{pre}|\right)$ decreased with $|x_{post}-x_{pre}|$ and became negative when $|x_{post}-x_{pre}|$ was large enough (Fig. 5C). Together, the network of t-SR can be regarded as of several feedforward sequences, with two sequences exciting or inhibiting each other depending on whether their spatial preferences are similar or far different. The sequential activity coded the flow of time, and the short-range excitation and long-range inhibition maintained the spatial information (42). A similar scenario also existed in the network of t-DM (Fig. 5D), where the sequential activity coded the flow of time, and the inhibition between the sequences of different decision preferences provided the mutual inhibition necessary for making decisions (43).

Fig. 5.

Sequential activity and network structure. (A) An example of neuronal activity (with maximum normalized to one) in the perception epoch of IP task sorted according to peak time. (B) Mean (solid line) and SD (shaded belt) of the recurrent weights as a function of the peak order difference between post- and presynaptic neurons in the perception epoch of IP. (C) Recurrent weight as a function of the difference $|x_1-x_2|$ between the preferred spatial locations of post- and presynaptic neurons and their peak order difference in the perception epoch of t-SR. (D) Recurrent weight as a function of peak order difference in the sequence of neurons with the same (blue) or different (orange) preferred decision choices in the perception epoch of t-DM. The shaded belt indicates SEM. The sequential activity and network structure in other epochs of the four timing tasks of Fig. 1 B and C are shown in SI Appendix, Fig. S9.

The scenario that feedforward structure hidden in recurrent connections drives sequential firing has been observed in a number of modeling works (27, 40, 41). Our work extends this scenario to the interaction of multiple feedforward sequences, which can code temporal flow and nontemporal information simultaneously.

Understanding the Strong Temporal Signals in Nontiming Tasks.

We have shown that in the perception and production epochs of t-SR and t-DM, when the network is required to record the temporal flow and maintain the nontemporal information simultaneously, neuronal temporal profiles exhibit similarity across nontemporal information (Fig. 3B and SI Appendix, Fig. S5A) and that the subspaces coding temporal flow and nontemporal information are orthogonal with small mixed variance (Fig. 3 D, E, I, and J). Interestingly, in tasks that do not require temporal information to perform, such profile similarity, orthogonality, and small mixed variance were also experimentally observed (18, 19). Moreover, the time-dependent variance explained more than 75% of the total variance in some nontiming tasks (18, 19). It would be interesting to ask why nontiming tasks developed such strong temporal signals, thereby understanding the factors that facilitate the formation of time sense of animals.

Before we studied the reasons for the strong temporal signals observed in nontiming tasks, we studied how the requirement of temporal processing influences the temporal signal strength. To this end, we studied the spatial reproduction (SR) task, where the network was to reproduce the spatial location immediately after a fixed delay (Fig. 6 A, Left, first row), and the DM task, where the network was to decide which stimulus was stronger immediately after the presentation of two stimuli (Fig. 6 A, Right, first row). Unlike t-SR (or t-DM) (Fig. 1C), SR (or DM) did not require the network to record time between the two pulses (or during the presentation of the two stimuli). We used $P_t={\text{Var}}_{i,t}\left({⟨r_i\left(t,x\right)⟩}_x\right)/{\text{Var}}_{i,t,x}\left(r_i\left(t,x\right)\right)$ to be the portion of time-dependent variance in the total variance ${\text{Var}}_{i,t,x}\left(r_i\left(t,x\right)\right)$, with $r_i\left(t,x\right)$ being the firing rate of the $i$th neuron at time $t$ and nontemporal information $x$. We compared the portions $P_t\left(\text{t}-\text{SR}\right)$ and $P_t\left(\text{t}-\text{DM}\right)$ in the perception epochs of t-SR and t-DM with the portion $P_t\left(\text{SR}\right)$ in the delay epoch of SR and the $P_t\left(\text{DM}\right)$ during the presentation of stimuli in DM. We found that $P_t\left(\text{SR}\right)<P_t\left(\text{t}-\text{SR}\right)$ and $P_t\left(\text{DM}\right)<P_t\left(\text{t}-\text{DM}\right)$ (Fig. 6B). Therefore, temporal signals are stronger in timing tasks. However, even in the two timing tasks t-SR and t-DM that we studied, the portion of time-dependent variance was smaller than the portion (75%) experimentally observed in nontiming tasks (18, 19) (Fig. 6B). Therefore, there should exist other factors than the timing requirement that are important to the formation of temporal signals.

Fig. 6.

Understanding the strong temporal signals in nontiming tasks. (A) Schematic of the nontiming tasks that we studied. (B) Bar charts show how the total signal variance is split among temporal information, nontemporal information, and the residual variance unexplained by temporal and nontemporal information in SR, t-SR, DM, and t-DM. (C) The portion of total variance explained by temporal signals in nontiming tasks. Error bars represent mean $\pm$ SEM across training configurations. Each dot corresponds to the value in a training configuration. *Significant difference at $P<0.05$ (two-sided Welch’s t test), the same as in D–F and H. (D) The portion of time-dependent variance before (blue) and after (green) broadening the tuning curves of the sensory neurons. (E) The portion of time-dependent variance in SR or DM when the network is trained on SR or DM only (blue) or trained on t-SR or t-DM concurrently (green). (F) The portion of time-dependent variance in fixed delay (blue) or variable delay (green) tasks. (G, Left) Schematic of the feedback connections (dashed arrows) to the sensory neurons (blue dot) to study anticipatory attention. Solid arrows represent feedforward connections. (G, Right) Firing threshold of sensory neuron decreases with feedback current until zero. (H) The portion of time-dependent variance before (blue) and after (green) adding feedback to sensory neurons. (I) Feedback current as a function of time in the delay epoch of SR. Blue line: mean value. Gray lines: individual training configurations.

Specifically, we studied the following four factors: 1) temporal complexity of task, 2) overlap of sensory input, 3) multitasking, and 4) timing anticipation.

Temporal complexity of task.

Temporal complexity measures the complexity of spatiotemporal patterns that the network receives or outputs in a task (27). To test the influence of temporal complexity on the strength of temporal signals, we designed COMP and change detection (CD) tasks that enhanced the temporal complexity of SR and a cue-dependent decision-making (cue-DM) task that enhanced the temporal complexity of DM (Fig. 6A). In COMP, the network was to report whether the spatial coordinate of the stimulus presented before the delay was smaller or larger than that of the stimulus presented after the delay, consistent with its vibrotactile version (18) (Fig. 1D). In CD, the network was to report whether the two stimuli presented before and after the delay were the same (21). In cue-DM, the network was to report the index of the stronger or weaker stimulus depending on the cue flashed at the end of the presented stimuli. COMP and CD have higher temporal complexity than SR because the output not only depends on the stimulus before the delay but also, the stimulus after the delay. Similarly, cue-DM has higher temporal complexity than DM because the output also depends on the cue. We found that $P_t\left(\text{SR}\right)<P_t\left(\text{CD}\right)$, $P_t\left(\text{SR}\right)<P_t\left(\text{COMP}\right)$, and $P_t\left(\text{DM}\right)<P_t\left(\text{cue}-\text{DM}\right)$, suggesting that temporal complexity increases the portion of time-dependent variance (Fig. 6C). It has been empirically found that the task temporal complexity increases the temporal fluctuations in neuronal sequential firing (27). Here, we showed that the temporal fluctuation of the average neuronal activity ${\left\{{⟨r_i\left(t,x\right)⟩}_x\right\}}_i$ over nontiming information also increases with the temporal complexity of the task. The result $P_t\left(\text{SR}\right)<P_t\left(\text{COMP}\right)$ is consistent with the experimental observation that the population state varied more with time in COMP than in SR (20).

Overlap of sensory input.

Suppose that the population states of the sensory neurons in response to two stimuli $x_1$ and $x_2$ are ${\mathbf{s}}_1$ and ${\mathbf{s}}_2$, respectively. If ${\mathbf{s}}_1$ and ${\mathbf{s}}_2$ have high overlap, then the evolution trajectories of the recurrent network in response to $x_1$ and $x_2$ should be close to each other. In this case, the variance of the trajectories induced by the stimulus difference is small, and the time-dependent variance explains a large portion of the total variance. To test this idea, we broadened the Gaussian tuning curves of the sensory neurons in t-SR, SR, COMP, and CD tasks and found an increased portion of time-dependent variance (Fig. 6D).

Multitasking.

The brain has been well trained on various timing tasks in everyday life, and therefore, the animal may also have a sense of time when performing nontiming tasks, which increases the time-dependent variance. To test this hypothesis, we trained networks on t-SR and SR concurrently so that the network could perform either t-SR or SR indicated by an input signal (26). We also trained t-DM and DM concurrently. We only considered these two task pairs because the two tasks in each pair share the same number and type of inputs and outputs (except for a scalar go cue input in t-SR and t-DM); hence, they do not require any changes in the network architecture. We found that both $P_t\left(\text{SR}\right)$ and $P_t\left(\text{DM}\right)$ were larger in networks that were also trained on timing tasks than in networks trained solely on nontiming tasks (Fig. 6E).

Timing anticipation.

In the working memory experiments that observed strong time-dependent variance (18, 19), the delay period had fixed duration. This enabled the animals to learn this duration after long-term training and predict the end of the delay, thereby getting ready to take actions or receive new stimuli toward the end of the delay. If the delay period is variable, then the end of the delay will no longer be predictable. We found that the temporal signals in fixed delay tasks were stronger than those in variable delay tasks (Fig. 6F), which suggests that timing anticipation is a reason for strong temporal signals. A possible functional role of timing anticipation is anticipatory attention: a monkey might pay more attention to its finger or a visual location when a vibrotactile or visual cue was about to come toward the end of the delay to increase its sensitivity to the stimulus. To study the influence of this anticipatory attention to the formation of temporal signals, we supposed feedback connections from the recurrent network to the sensory neurons in our model (Fig. 6G). Feedback currents could reduce the firing thresholds of sensory neurons through disinhibition mechanism (44). We also added L2 regularization on the feedback current (Fig. 6G) to reduce the energy cost of the brain (Materials and Methods). After training, the feedback current stayed at a low level to reduce the energy cost but became high when the cue was about to come to increase the sensitivity of the network (Fig. 6I). We found that adding this feedback mechanism increased the portion of time-dependent variance (Fig. 6H) because the feedback current, which increased with time toward the end of the delay (Fig. 6I), provided a time-dependent component of the population activity.

Collectively, other than the timing requirement in timing tasks, we identified four possible factors that facilitate the formation of strong temporal signals: 1) high temporal complexity of tasks, 2) large sensory overlap under different stimuli, 3) transfer of timing sense due to multitasking, and 4) timing anticipation.

Discussion

In summary, neural networks perceive time intervals through stereotypical dynamic trajectories, maintain time intervals by attractor dynamics in a complementary monotonic coding scheme, and perform IP or IC by scaling evolution speed. Temporal and nontemporal information is coded in orthogonal subspaces with small mixed variance, which facilitates decoding generalization. The network structure after training exhibits multiple feedforward sequences that mutually excite or inhibit depending on whether their preferences of nontemporal information are similar or not. We identified four possible factors that facilitate the formation of strong temporal signals in nontiming tasks: temporal complexity of task, overlap of sensory input, multitasking, and timing anticipation.

Perception and Production of Time Intervals.

In the perception epoch, the network evolved along a stereotypical trajectory after the first pulse (Fig. 2 B and C). Consistently, some neurons in the prefrontal cortex and striatum prefer to peak their activities around specific time points after an event (45). In the brain, such a stereotypical trajectory may be formed by not only neuronal activity state but also, synaptic state, such as slow synaptic current or short-term plasticity. The temporal information coded by the evolution of synaptic state can be read out by the network activity in response to a stimulus (29, 46, 47).

We also studied the trajectory speed with time during the perception epoch. We found that, after a transient period, the speed in the IP task stayed around a constant value (SI Appendix, Fig. S2A), the speed in the IC and t-DM tasks increased with time (SI Appendix, Figs. S3C and S5C), and the speed in the t-SR task decreased with time (SI Appendix, Fig. S4B). Therefore, we did not make any general conclusion on the trajectory speed when the network was perceiving time intervals.

The temporal scaling when producing or comparing intervals has been observed in animal experiments (12, 32, 34). A possible reason why temporal scaling exhibits in both the production epoch of IP and the stimulus 2 epoch of IC (Fig. 2 L–O and SI Appendix, Fig. S3 I–N) is that both epochs require the network to compare the currently elapsed time with the time interval maintained in working memory. In IC, the decision choice is switched as soon as the trajectory has passed the critical point at which the elapsed time $t$ equals the maintained interval $T$; in IP, the network is required to output a movement as soon as $t=T$: both tasks share a DM process around the $t=T$ time point. This temporal scaling enables generalizable decoding of the portion $t/T$ of the elapsed time (SI Appendix, Figs. S7G and S8G), which enables people to identify the same speech or music played at different speeds (48, 49).

When the to be produced interval $T$ gets changed, the trajectory in the perception epoch is truncated or lengthened (Fig. 2 B–D), whereas the trajectory in the production epoch is temporally scaled (Fig. 2 L–O). This difference helps us to infer the psychological activity of the animal. For example, in the fixed delay working memory task when the delay period was changed, the neuronal activity during the delay was temporally scaled (18). This implies that the animals had already learned the duration of the delay and were actively using this knowledge to anticipate the coming stimulus instead of passively perceiving time. However, this anticipation was not feasible before the animal had learned the delay duration. Therefore, we predict that, at the beginning of training, the animal perceived time using stereotypical trajectory, and the scaling phenomenon gradually emerged during training.

Combination of Temporal and Nontemporal Information.

Temporal and nontemporal information is coded orthogonally with small mixed variance (Fig. 3). Physically, time is consistently flowing regardless of the nontemporal information, and much information is also invariant with time. The decoding generalizability that resulted from this coding geometry (Fig. 4) helps the brain to develop a shared representation of time across nontemporal information or a shared representation of nontemporal information across time using a fixed set of readout weights. Decoding generalizability of nontemporal information across time has been studied in working memory tasks (20, 50) and has been considered as an advantage of working memory models in which information is maintained in stable or a stable subspace of neuronal activity (20, 51). Here, we showed that, with this geometry, such advantage also exists for reading out temporal information.

Interestingly, the orthogonality and small mixed variance have been experimentally observed in nontiming tasks (18, 19), and therefore, their formation does not seem to depend on the timing task requirement. Consistently, in the delay epoch of t-SR and t-DM, although the network needed not to record the temporal flow to perform the tasks, temporal flow and nontemporal information were still coded orthogonally with small mixed variance (SI Appendix, Fig. S10 A–D). By comparing the orthogonality and mixed variance in the perception epoch of t-SR and t-DM with those in the nontiming tasks (Fig. 6A), we found that timing task requirement did not influence the orthogonality but generally reduced the mixed variance (SI Appendix, Fig. S10 E and F). The network structure in nontiming tasks also exhibited interacting feedforward sequences (SI Appendix, Fig. S10 G–K).

Strong Temporal Signals in Nontiming Tasks.

Our results concerning the various factors that affect the strength of temporal signals in nontiming tasks lead to testable experimental predictions. The result of sensory overlap (Fig. 6D) implies that sensory neurons with large receptive fields are essential to the strong temporal signals. The result of multitasking (Fig. 6E) implies that animals better trained on timing or music have stronger temporal signals when performing nontiming tasks. The result of temporal complexity (Fig. 6C) implies that animals have stronger temporal signals when performing tasks with higher temporal complexity, which is consistent with some experimental clues (20). The result of timing anticipation (Fig. 6F), consistent with ref. 27, implies that, if the appearance of an event is unpredictable, then the temporal signals should be weakened. Other than anticipatory attention (Fig. 6G), anticipation may influence the temporal signals through other mechanisms. In the fixed delay COMP task (Fig. 1D), suppose that a stimulus $a$ appeared before the delay; then, both the population firing rate and the information about $a$ in the population state increase toward the end of the delay period (52). It is believed that this is because the information about $a$ was stored in short-term potentiated synapses in the middle of the delay to save the energetic cost of neuronal activity, while they got retrieved into the population state near the end of the delay period to facilitate information manipulation (53). This storing and retrieving process may also be a source of temporal signals.

Interval and Beat-Based Timing.

We have discussed the processing of single time intervals using our model. However, recent evidence implies that the brain may use different neural substrates and mechanisms to process regular beats from single time intervals (54, 55). Dynamically, in the medial premotor cortices, different regular tapping tempos are coded by different radii of circular trajectories that travel at a constant speed (55), which is different from the stereotypical trajectory or speed scaling scenario revealed in our model (Fig. 2 B–D and L–O). The distribution of the preferred intervals of the tapping interval-tuned neurons is wide, peaking around 850 ms (56, 57), which is also different from the complementary monotonic tuning scenario in our model (Fig. 2 J and K). Additionally, humans tend to use a counting scheme to estimate single time intervals when the interval duration is longer than 1,200 ms (58), which implies that the beat-based scheme is mentally used to reduce the estimation error of single long intervals even without external regular beats. However, after we trained our network model to produce intervals up to 2,400 ms, it processed intervals between 1,200 and 2,400 ms in similar schemes (SI Appendix, Fig. S11) to that illustrated in Fig. 2 for intervals below 1,200 ms. All of these results suggest the limitation of our model to explain beat-based timing. Modeling work on beat-based timing is the task of future research.

Materials and Methods

Methods are provided in SI Appendix as well as SI Appendix, Figs. S1–S11. In SI Appendix, section S1, we present the details of our computational model, including the network structure, the tasks to be performed, and the methods that we used to train the network model. We also present the details to analyze the interval coding scheme in the delay and production epochs (Fig. 2), the coding combination of temporal and nontemporal information (Figs. 3 and 6B), and decoding generalization (Fig. 4) as well as the firing and structural sequences (Fig. 5). We also explain the relationship between the monotonic coding at the end of the delay epoch and the low dimensionality of the attractor (Fig. 2 G and K) as well as the geometric meaning of mixed variance (Fig. 3) in SI Appendix. Computer code is available from https://github.com/zedongbi/IntervalTiming.