Human POT1 unfolds G-quadruplexes by conformational selection

Abstract

The reaction mechanism by which the shelterin protein POT1 (Protection of Telomeres 1) unfolds human telomeric G-quadruplex structures is not fully understood. We report here kinetic, thermodynamic, hydrodynamic and computational studies that show that a conformational selection mechanism, in which POT1 binding is coupled to an obligatory unfolding reaction, is the most plausible mechanism. Stopped-flow kinetic and spectroscopic titration studies, along with isothermal calorimetry, were used to show that binding of the single-strand oligonucleotide d[TTAGGGTTAG] to POT1 is both fast (80 ms) and strong (−10.1 ± 0.3 kcal mol⁻¹). In sharp contrast, kinetic studies showed the binding of POT1 to an initially folded 24 nt G-quadruplex structure is four orders of magnitude slower. Fluorescence, circular dichroism and analytical ultracentrifugation studies showed that POT1 binding is coupled to quadruplex unfolding, with a final complex with a stoichiometry of 2 POT1 per 24 nt DNA. The binding isotherm for the POT1-quadruplex interaction was sigmoidal, indicative of a complex reaction. A conformational selection model that includes equilibrium constants for both G-quadruplex unfolding and POT1 binding to the resultant single-strand provided an excellent quantitative fit to the experimental binding data. POT1 unfolded and bound to any conformational form of human telomeric G-quadruplex (antiparallel, hybrid, parallel monomers or a 48 nt sequence with two contiguous quadruplexes), but did not avidly interact with duplex DNA or with other G-quadruplex structures. Finally, molecular dynamics simulations provided a detailed structural model of a 2:1 POT1:DNA complex that is fully consistent with experimental biophysical results.

INTRODUCTION

POT1 (Protection Of Telomeres 1) is a telomere single-stranded DNA binding protein found in a variety of organisms (1–4) that is essential for telomere integrity (5,6). POT1 is an integral component of the shelterin complex (7,8) and is the only protein in the complex to bind with high sequence specificity to the G-rich ssDNA 3′-overhang. It does not bind to double stranded telomeric DNA or to the complementary C-rich strand (4). Human POT1 has two functional domains: an N-terminal oligonucleotide-binding (OB) domain that is required for DNA binding and a C-terminal domain that binds the shelterin protein TPP1. In humans, POT1 is involved in regulation of telomere length and telomerase activity (5,6). In vitro, POT1 inhibits telomerase activity at the 3′-end of DNA by controlling accessibility of the single-stranded DNA substrate to telomerase (9). Although the exact role of the DNA binding activity of POT1 is unknown, the crystal structure of human POT1 with the optimal telomeric DNA sequence implies that it physically caps the end of chromosomes by sequestering the last guanine base of DNA into a hydrophobic pocket, making it inaccessible to telomerase (4,10). POT1 capping of the chromosome ends may also prevent the ends from eliciting a DNA damage response (10). However, in vitro binding of shelterin protein TPP1 to POT1 relieves telomerase inhibition and increases the repeat addition processivity of the enzyme (9). POT1 also acts as a positive regulator of telomere length as overexpression of full-length POT1 in telomerase positive cells leads to the lengthening of telomeres (11). POT1 has also been implicated in binding within the hypothetical D-loop part of the proposed T-loop configuration of telomeres (12).

POT1-ssDNA structure

A high resolution crystal structure of human POT1 bound to the optimal human telomeric binding sequence d[TTAGGGTTAG] was reported by the Cech group in 2004 (10). This structure reveals two N-terminal OB domains spanning the length of the bound oligonucleotide. It also can be inferred from the crystal structure that with minimal movement of the terminal bases, longer sequences could be bound by multiple POT1 N-terminal OB domains. There are no high-resolution structures of POT1 bound to long single-stranded telomeric sequences. However, Taylor et al. (13) examined binding of POT1 to 72–144 nt tracts of DNA by electrophoretic mobility shift assays, size-exclusion chromatography and electron microscopy (EM). They found that the ssDNA was fully occupied and coated by POT1 and its variants, with one POT1 bound consecutively to every 12 nt repeat. EM showed that a 144 nt DNA saturated with 12 POT1–TPP1 heterodimers formed ordered, compact assemblies. Similar structures were seen for POT1 alone bound to a 132 nt ssDNA.

Mechanism of POT1 unfolding of telomeric quadruplexes

The mechanism by which POT1 binds to, and unfolds, quadruplex DNA is not fully understood. Early studies of POT1 DNA interactions were limited to short single-stranded oligonucleotides for which binding was uncoupled from any unfolding process (5,14). Several subsequent studies have addressed the unfolding of G4 DNA by POT1. Supplementary Scheme S1 (Supplementary Data) summarizes several proposed models for how POT1 unfolds a telomeric G-quadruplex. First (Supplementary Scheme S1A), the Cech laboratory showed that human POT1 disrupts G4s and speculated that ‘hPOT1 may function simply by trapping the unfolded forms of … telomeric primers in an equilibrium population’, although they could not eliminate unfolding by direct initial binding to the folded G4 (15). They showed that when facilitating telomerase activity, hPOT1 does not act catalytically but formed a stoichiometric complex with the DNA, freeing its 3′ tail. Interestingly, they found that a short antisense oligonucleotide was found to duplicate the effect of POT1 on G4 unfolding and facilitation of telomerase activity.

A second study from the Wang and Opresko laboratories (Supplementary Scheme S1C) used single-molecule atomic force microscopy (AFM) to monitor POT1 binding to longer telomeric G4 structures and proposed a different model (16). In contrast to our subsequent published observations that long telomeric DNA always form structures with the maximal number of quadruplex units (17), they reported that none of the sequences they studied by AFM were fully folded to form the maximal number of G4 units (16). It is possible that their G4 samples were incompletely annealed and equilibrated. In their preparations, POT1 appeared to bind to single-stranded gaps between quadruplex units. The authors proposed a ‘steric driver’ mechanism in which such binding destabilized adjacent quadruplexes (by an unstated mechanism) to cause unfolding, and argued against the simple static trapping mechanism for POT1 unfolding of G4 structures. POT1 molecules were proposed to slide along the exposed single-strand to stabilize the fully unfolded state. Curiously, the antisense oligonucleotide 5′CCTAACCCTAACC was reported to be less effective than POT1 at disrupting G4 structures, in disagreement with the results from the Cech laboratory.

In a third study (Supplementary Scheme S1D) by the Opresko and Myong laboratories, single-molecule FRET results indicated that two POT1 molecules bound sequentially, beginning at the 3′ end, to an initially folded telomeric G4 structure (18). This study seems to be inconsistent with the ‘steric driver’ model. Nor does it fully account for the possible thermodynamic coupling between POT1 binding and G4 unfolding.

A fourth study (Supplementary Scheme S1B) by Ray et al. also used single-molecule FRET (19). These authors reported that POT1 unfolded both the antiparallel telomeric G4 form in Na⁺ and the ‘hybrid’ form in K⁺, albeit with different binding stoichiometries of one and two POT1 molecules per G4, respectively. They reported that POT1 was unable to unfold the parallel telomeric G4 form. They used the phenomenological Hill equation to analyse their binding isotherms, but did note that their estimated binding constant K_eq was a composite term that ‘represents both POT1-mediated GQ unfolding and POT1 binding to the unfolded DNA‘. They were not able to separate these contributions.

Finally, a study from the Taylor laboratory (20) used an electrophoretic mobility shift assay to monitor the interaction of a POT1–TPP1 complex with a variety of telomeric G4 structures. A sequential two-step binding model (Supplementary Scheme S1E) was used to analyse their binding isotherm, and circular dichroism was used to show that the initially folded G4 structure was disrupted by POT1 binding. The authors discussed the complexity of POT1 binding to an initially folded G4 structure, suggesting the possibility that ‘… POT1 binds first to one of the TTA loops, and this interaction weakens the G-quadruplex hydrogen bonding network…’ allowing an additional POT1 to bind. Or, they noted, ‘[a]lternatively, POT1–TPP1 binding may simply trap the unfolded DNA conformation. In this model, the unfolding of the G-quadruplex occurs in a pre-equilibrium step that is followed by POT1–TPP1 binding that prevents refolding’. They were not able to decide definitively which of these mechanisms was most likely, or to quantitatively define the energetic contributions of binding and G4 unfolding

Collectively these studies show that POT1 unfolds G4 DNA to produce a single-strand DNA–POT1 complex, but that there is no consensus for the mechanism or exact pathway by which it does so. The possible thermodynamic linkage between G4 unfolding and POT1 binding has not yet been quantitatively explained. There are inconsistencies between proposed mechanisms, and many unanswered questions about how POT1 unfolds telomeric G4 structures. It is possible that variations among the results of these different studies might be explained by different cations or cation concentrations used in the assays, annealing and storage conditions of reactants, duration of measurements, the time scale and temporal resolution accessible to the particular technique used, and the details of the DNA constructs used, e.g. overhangs length and sequence. Equilibration times vary for each experiment. Whatever their origin, significant gaps remain in our understanding of POT1 binding to its preferred DNA sequence. We report here biophysical studies intended to address these gaps in our understanding of the interaction of POT1 with G4 structures. Our approaches provide new quantitative information about many aspects of POT1 binding to telomeric DNA that help to clarify the situation.

Goals of this study

The primary goal of our study is to understand the mechanism by which POT1 unfolds telomeric G4 structures. In particular, we wish to understand the coupling and thermodynamic linkage between G4 unfolding and POT1 binding. Our study builds on our previous experimental studies of the kinetics and thermodynamics of the folding and unfolding of telomeric G4 structures (21–29). We use a battery of biophysical tools to probe the kinetics and thermodynamics of POT1 binding to both the short single-stranded telomeric DNA recognition sequence and to longer, initially folded, telomeric G4 sequences. First, we provide detailed kinetic and thermodynamic characterizations of POT1 binding to its single-strand recognition sequence. The stopped-flow method we used provides data in the millisecond time range, a time scale inaccessible by all previous studies. Isothermal titration calorimetry data allows us to define the thermodynamic profile of the POT1–ssDNA binding interaction in a more direct way than previous studies. We then used this quantitative information as a foundation for understanding the coupling of POT1 binding to G4 unfolding by additional kinetic and thermodynamic studies. A conformational selection model provides a physically meaningful mechanism to account for our data. That model integrates the information obtained by our studies of the POT1–ssDNA into a coherent mechanistic picture that shows that the energy of POT1 binding to its single-strand recognition sequence is the driving force that overcomes the energetic cost of unfolding G4 DNA. Finally, we use an integrated experimental (FRET and analytical ultracentrifugation) and computational approach to determine a plausible atomistic model of the 2:1 POT1–DNA structure, providing novel insights into the packing and interactions within the stable complex.

MATERIALS AND METHODS

Oligonucleotide preparation

Oligonucleotides and their extinction coefficients are listed in Supplementary Table S1. Unlabeled oligonucleotides were obtained in a desalted, lyophilized state from either IDT (Coralville, IA, USA) or Eurofins Genomics (Louisville, KY, USA). Stock solutions were prepared by adding deionized H₂O to give ∼1 mM concentration and stored at 4°C. Fluorescently tagged oligonucleotides containing a 5′-6FAM FRET donor and a 3′-Tamra acceptor were synthesized and HPLC-purified by Eurofins Genomics. They were reconstituted in deionized H₂O to ∼100 μM and stored in the dark at 4°C. Working solutions of oligonucleotides were prepared diluting the stock solution to the desired final concentration in POT1 buffer, denaturing in a 1 L boiling water bath for ∼10 min followed by annealing by slow cooling to room temperature. Folding of G4 samples was checked by measuring their CD spectrum or, for the FRET-labeled oligonucleotides, by comparing the emission spectra of unfolded and folded samples determined by exciting 6FAM (495 nm) or Tamra (560 nm).

Differential scanning fluorimetry (DSF)

DSF experiments were carried out using an Applied Biosystems StepOne Plus real-time PCR system. Melting curves were determined in 96-well plates using a temperature ramp from 20°C to 99°C. SYPRO Orange dye (30), which preferentially binds to denatured proteins and becomes fluorescent, was used to monitor thermal unfolding of POT1 in the absence and presence of DNA. DNA concentrations were typically at a 10-fold excess to protein (5 μM) in POT1 buffer. Twenty microliters of sample was loaded in each well, which was sealed and centrifuged at 1400 rpm for 2 min. Each unfolding reaction was run in duplicate or triplicate and repeated with at least two different plates. POT1 T_m was determined from the maximum in the first derivative of the melting curve and ΔT_m was estimated from the difference in T_m values with and without DNA.

Equilibrium titrations

O1 DNA. The extent of POT1-ssDNA binding was determined at 25°C by measuring changes in fluorescence accompanying serial additions of ligand to receptor using a FluoroMax-3 fluorometer (Jobin Yvon Inc., Edison, NJ, USA). For experiments in which FRET-labeled O1 was titrated with POT1, the labelled DNA was excited at 495 nm and emission measured at 520 nm. For experiments in which binding was determined by ssDNA-induced quenching of the intrinsic tryptophan fluorescence of POT1, a fixed concentration of protein was titrated with unlabeled O1. Excitation was at 290 nm and emission at 340 nm was recorded. Kinetic experiments (described below) showed that binding of ssDNA to POT1 is fast (relaxation time τ ≈ 80 ms); thus, complex formation between POT1 and ssDNA could be followed by conventional titrations of serial additions of ligand to receptor without complications due to slow processes. Determination of accurate equilibrium dissociation constants from POT1 tryptophan emission experiments required application of an inner filter correction (31) due to the (low) absorbance of the added DNA at the excitation and emission wavelengths. K_d values were estimated for both types of titration by fitting the titration curve to a 1-site ligand depletion model (32) (Equation 1) by the non-linear least squares procedure in OriginPro 2016 (OriginLab, Inc., Northampton, MA, USA).

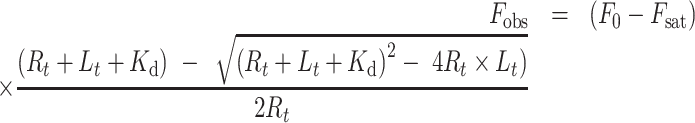(1)

F_obs is the observed fluorescence intensity, F₀ is the fluorescence intensity before ligand addition, F_sat is the fluorescence intensity at saturation, R_t = total receptor concentration, L_t is the total ligand concentration at each addition, and K_d is the dissociation constant. F₀, F_sat and K_d were optimized by non-linear least squares.

FRET-labeled G4s

Binding of POT1 to G4 DNA was slow, requiring >2 h at room temperature to achieve equilibrium. Thus, to determine POT1-G4 K_d values, the slow rate of equilibration required that each point in a titration be determined independently using an individual POT1:G4 mixture rather than by serial additions of POT1 to the same G4 sample. We therefore mixed FRET-labeled G4 with an appropriate concentration of POT1 followed by incubating the samples overnight in the dark at room temperature. Binding isotherms were constructed from these solutions by measuring the increase in 6FAM fluorescence brought about by G4 unfolding and POT1 binding as described above for FRET-O1.

Data analysis

POT1 binding isotherms were fit to the binding models shown in Supplementary Table S3 using user defined functions implemented in GraphPad Prism version 6.07 (GraphPad Software, Inc., San Diego, CA, USA). Monte Carlo simulations used a strategy previously used in our laboratory (33), but were implemented using a tool available in GraphPad Prism.

Kinetic experiments

Stopped-flow kinetics

The kinetics of POT1-FRET-O1 interaction was assessed by stopped-flow mixing using an OLIS RSM-SF instrument (OLIS Instruments, Bogart, GA, USA) in the fluorescence mode. The drive syringes and observation cuvette were maintained at 25°C with a circulating water bath. The 6FAM label of the O1 was excited at 490 nm and the increase in emission subsequent to mixing was measured at right angles to excitation through a 520 nm interference filter. The kinetic data were fit to a single exponential using the non-linear least squares routine in the program OriginPro 2016 to obtain best-fit signal amplitudes and relaxation times.

G4 unfolding kinetics

As previously described (29), unfolding of FRET-G4s is slow and accompanied by an increase in 6FAM emission intensity that accurately tracks the progress of the unfolding reaction. Briefly, a 5-fold excess of either complementary DNA or POT1 was added to pre-folded G4 in POT1 buffer and manually mixed. The kinetics of G4 unfolding was followed at 25°C using the SpectraMax-3 fluorometer with excitation at 490 nm and emission at 520 nm. The kinetic profile of unfolding in the presence of complementary DNA or POT1 required three exponentials with relaxation times of ∼10², ∼10³ and ∼10⁴ s for accurate fitting. The optimized amplitudes and relaxation times were determined by non-linear least squares regression with OriginPro 2016 as previously described (29).

Isothermal titration calorimetry (ITC)

The ITC titrations were obtained using a Microcal VP-ITC microcalorimeter (Microcal, Northampton, MA, USA). The O1 oligonucleotide was dissolved in deionized H₂O and then diluted into POT1 buffer to a final concentration at 56 μM. POT1 was dialyzed overnight in POT1 buffer then diluted to 2.6 μM. ITC titrations were done at 25°C with 5 μl injections, duration 10 s, spaced by 240 s with a filter setting of 5. The reference power was 15 μcal/s, stirring speed 300 rpm and a 60 s initial delay. Data processing and analysis were done using Affinimeter software v. 1 (AFFINImeter, Santiago de Compostela, Spain).

Analytical ultracentrifugation (AUC)

Sedimentation velocity experiments were carried out in a Beckman Coulter ProteomeLab XL-A analytical ultracentrifuge (Beckman Coulter Inc., Brea, CA, USA) at 20°C and 50 000 rpm in standard 2 sector cells. Buffer density was determined on a Mettler/Paar Calculating Density Meter DMA 55A at 20.0°C and viscosity was measured using an Anton Parr AMVn Automated Microviscometer at 20°C. Data were analyzed with the program Sedfit (free software: www.analyticalultracentrifugation.com) using the continuous c(s) distribution model. The partial specific volume of POT1 was calculated from its amino acid composition (0.7453 ml/g) using the Protparam tool in ExPASy (free software: web.expasy.org) and a value of 0.55 ml/g was used for the DNA oligonucleotides (14). The stoichiometry of DNA:POT1 complexes was determined using the two wavelength method described by Brautigam et al. (34). POT1-oligonucleotide mixtures were scanned at both 260 and 280 nm during centrifugation and the absorbance at both wavelengths in the largest species was determined using integration of the peak in the c(s) versus s mode of sedfit. The concentration of each species in the peak could be determined and the stoichiometry obtained using the extinction coefficients of POT1 and oligonucleotide at both wavelengths. The partial specific volumes for protein:DNA complexes were calculated from the weight averages of each component in the complex (35) and used to determine the molecular weight from c(s) versus s analysis. Frictional ratios, f/f₀, were determined using Ultrascan3 (free software: uslims3.uthscsa.edu), since f/f₀ reported by Sedfit analysis is the weight average value for all species present. Calculations were performed on the UltraScan LIMS cluster at the Bioinformatics Core Facility at the University of Texas Health Science Center at San Antonio and multiple High Performance Computing clusters are supported by NSF XSEDE Grant #MCB070038 (to Borries Demeler).

FRET experiments

Fluorescence spectra were recorded at 25°C using a FluoroMax-3 fluorometer (Jobin Yvon Inc., Edison, NJ). Emission spectra were measures for strands labeled only with the donor 6FAM and for the doubly labeled 5′-6FAM-3′-Tamra FRET pair.

Calculation of donor-acceptor FRET efficiency

Calculations of FRET efficiency for 5′-6FAM-3′-Tamra labelled 2GKU in KCl, in its complex with POT1, and in duplex form were carried out by measuring the enhancement of acceptor fluorescence method (36,37) as implemented in the program FRET D&A Fit (www.lfd.uci.edu/∼gohlke). This analysis allows calculation of the FRET efficiency E from the enhancement of acceptor (Tamra) fluorescence resulting from excitation energy transfer from the donor (6FAM). By using the emission spectrum of donor-DNA, the method corrects for overlap of the donor emission with acceptor emission. The apparent distance between donor and acceptor R was estimated from the equation R = R₀·[(1 – E)/E]^1/6 with R₀ = 50 Å (37) assuming a value of 2/3 for the orientation factor κ².

Additional methods

POT1 purification and molecular dynamics simulations are described in Supplementary Data.

RESULTS AND ANALYSIS

Binding of POT1 to a single-stranded DNA oligonucleotide is strong

We studied the equilibrium binding of the single-stranded oligonucleotide d[TTAGGGTTAG] (O1) to POT1 by several spectroscopic methods and by ITC. Figure 1A shows binding isotherms obtained by using either FRET labeled O1 or intrinsic POT1 tryptophan fluorescence. The increase in donor fluorescence suggests that the distance between the donor and acceptor increases upon binding as O1 is immobilized within the POT1 binding site. These data were fit to a 1:1 binding model that yielded estimates for the dissociation constant K_d of 26.4 and 29.6 nM, respectively. Additional titration experiments, done using microscale thermophoresis or by fluorescence with O1 labeled with 2-aminopurine (Supplementary Figure S1), yielded similar K_d estimates as summarized in Supplementary Table S2. Figure 1B shows the results of an ITC binding experiment. A 1:1 binding model fits the data, yielding K_d = 59.4 nM, ΔH_b = −33.3 kcal mol⁻¹ and n = 0.67. The collective binding data (Supplementary Table S2, Figure 1) are in good agreement. The thermodynamic profile determined for the POT1-O1 binding interaction from these data is ΔG = −10.1 ± 0.3 kcal mol⁻¹, ΔH_b = −33.3 ± 0.3 kcal mol⁻¹ and −TΔS = +23.2 ± 0.4 kcal mol⁻¹, as shown in the inset in Figure 1B. The favorable free energy of binding arises from the large favorable enthalpy contribution, and is opposed by entropy.

Figure 1.

Binding of the deoxyoligonucleotide d[TTAGGGTTAG] (‘O1’) to POT1. (A) Isothermal titration experiments monitored by changes in FRET-labeled O1 (5′-6FAM-TTAGGGTTAG-3′-TAMRA) fluorescence (black) or changes in intrinsic POT1 tryptophan fluorescence (red). In the first case, a fixed concentration of O1 was titrated with increasing amounts of POT1. In the second case, a fixed concentration of POT1 was titrated with increasing amounts of unlabeled O1. The lines are the best fits to a 1:1 binding model obtained by nonlinear least-squares fitting of the data, with the results shown in Supplementary Table S2 and discussed in the text. (B) Isothermal titration calorimetry results for the titration of O1 into a POT1 solution. The solid lines shows the best fit to a 1:1 binding model, with the residuals (data – fit) shown at the top of the panel centered around 0. The fitted parameters are reported in the text and in Supplementary Table S2. The inset shows the thermodynamic profile for O1 binding to POT1, showing that the favorable binding free energy (ΔG = −10.1 kcal mol⁻¹) results from the difference between a favorable binding enthalpy (ΔH = −33.3 kcal mol⁻¹) contribution and an unfavorable entropic (−TΔS = +23.2 kcal mol⁻¹) contribution. Reaction conditions: 20 mM potassium phosphate, 180 mM KCl, pH 7.2, 25°C. For FRET experiment, [O1] = 200 nM; for POT1 experiments, [POT1] = 920 nM.

Binding of POT1 to a single-stranded DNA oligonucleotide is fast

Stopped-flow fluorescence experiments to determine the binding rate of FRET-labeled O1 to POT1 are shown in Figure 2A. The key point of these data is that binding is fast, and is complete in about 0.2 s. This observation indicates that the titration experiments described in the previous section were fully equilibrated. The kinetic data in Figure 2A are apparently monophasic over the accessible time range and can be fit to a simple single-exponential reaction model, with a relaxation time (τ₂) near 80.0 ms. Surprisingly, the rate of binding appears to be nearly independent of POT1 concentration

Figure 2.

Kinetics of POT1 binding to FRET-labeled O1 determined by stopped-flow mixing experiments. (A) Changes in O1 donor fluorescence are shown as a function of time (logarithmic scale) for increasing concentrations of added POT1. All data were fit to a single exponential model to obtain a relaxation times near 80 ms. The black, flat, trace at the bottom is a control in which O1 was mixed with buffer in the absence of POT1. Reaction conditions: The concentration of FRET-O1 was 200 nM in 20 mM potassium phosphate, 180 mM KCl, pH 7.2 with 0, 50, 95, 115, 280, 500 and 600 nM POT1 (concentrations after mixing). The temperature was 25°C. (B) Reciprocal relaxation time for the O1-POT1 interaction as a function of the sum of the initial equilibrium reactant concentrations. The concentration term was estimated using the measured K_d value obtained in FRET titration experiments (Supplementary Table S2). The line shows the expected behaviour for the proposed two-step mechanism simulated as described in the text.

The minimal concentration dependence could arise from the existence of a bimolecular interaction step that is faster than can be resolved by our stopped-flow method. If such is the case, one plausible minimal reaction mechanism for O1 binding is

where a fast bimolecular binding step (with rate constants k₁ and k₋₁) forms a transient intermediate that then undergoes a slower unimolecular rearrangement (with rate constants k₂ and k₋₂) to the final complex form. Such a mechanism predicts that the relaxation time of the slow second step becomes constant at high reactant concentrations if the first step is much faster than the second step. Indications of a faster, unresolved, reaction step can been as a sharp vertical jump in fluorescence amplitudes at times within the stooped-flow mixing time. The amplitude of these jumps depends on the added POT1 concentration. Such changes may well signal a faster biomolecular collision between POT1 and O1 faster than we can resolve.

For this two-step mechanism, the reciprocal relaxation time of the slow step is given by the expression

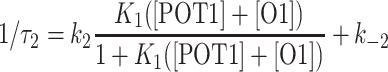where K₁ = k₁/k₋₁ and ([POT1] + [O1]) is the sum of equilibrium concentrations of the reactants (38). Figure 2B shows our kinetic data plotted according to this equation. We calculated the concentration term using the known total O1 and POT1 concentrations and the association constant obtained by FRET titration experiments (Supplementary Table S2). The data are insufficient for a detailed fitting to extract all of the rate and equilibrium constants, but a simulated curve calculated with reasonable approximate values indicates that only a slight concentration dependence observed over the concentration range measured, consistent with the proposed two-step mechanism. The simulated curve used K₁ = 3.6 × 10⁷ M⁻¹, k₂ = 9.3 s⁻¹ and k₋₂ = 4.0 s⁻¹.

The binding of POT1 to an initially folded telomeric G-quadruplex structure is slow because of conformational selection, the mandatory coupling of binding to a rate-limiting G4 unfolding reaction

Figure 3A shows the kinetics of binding of POT1 to a FRET-labeled telomeric G4 (2GKU, Supplementary Table S1) structure that is initially fully folded. The G4 structure is an antiparallel ‘hybrid’ or ‘3+1’ form containing stacked G-quartets, two lateral loops and one side ‘propeller’ loop (39). In this assay, increased fluorescence results as the G4 structure unfolds and the ends of the quadruplex forming sequence separate. In sharp contrast to the fast binding of single-stranded O1, these data show that POT1 binding to G4 is multiphasic and slow, with an apparent average relaxation time (when the overall reaction is 67% complete) of 2000–3000 s. This is about 25 000 times slower than POT1 binding to the single-stranded O1. Three relaxation times of approximately 80, 900 and 16000 s are needed to accurately fit the time course of the POT1-driven unfolding reaction. From our previous kinetic studies of telomeric G4 structures (29), we know that G4 unfolding is multiphasic and slow, and is similar to the observed time range of the POT1 binding reaction. To show this directly, we compared the rate of POT1 binding to the rate of G4 unfolding using the complement trap method, in which DNA (or PNA) with a complementary sequence to the G4 strand (O1c, Supplementary Table S1) is added in excess to drive the rate-limiting G4 unfolding and subsequent fast duplex formation. For the shorter PNA, we assume that two molecules bind to fully unfold the G4. Figure 3A shows that the rate of POT1 binding tracks closely with the rate of G4 unfolding driven by added complementary DNA or by a smaller γ-PNA sequence. Figure 3B shows a transformation of the data in which the extent of G4 unfolding by complementary trap sequences is compared directly to the extent of unfolding by POT1, showing only slight deviations from a linear correlation. These data emphasize that POT1 and complement trap sequences must act by similar mechanisms, with the rate limiting step(s) being G4 unfolding.

Figure 3.

Kinetics of G-quadruplex unfolding by POT1 and DNA or γPNA complementary sequences. (A) The unfolding of the FRET-labeled Tel22 (d[AGGG(TTAGGG)₃]) G-quadruplex determined by hand mixing experiments with changes in donor fluorescence monitored as a function of time. The response has been normalized to show the extent of the reaction with respect to endpoint in order to emphasize kinetic similarities The black line shows unfolding by POT1. The red line shows unfolding using a 22 nt DNA complement to the Tel22 sequence as a trapping reagent (ref). The blue line shows unfolding by the γPNA H-CCCTAA-NH₂. There are negligible differences in the time courses of the unfolding reaction for three unfolding agents. (B) Plot showing the extent of reaction for the DNA (black) or γPNA (blue) complements with respect to POT1. The diagonal line show the expected correlation if the unfolding reactions had exactly the same kinetics. These data emphasize that the kinetic difference of the nucleic acids with respect to POT1 are negligible. Reaction conditions: 20 mM potassium phosphate,180 mM KCl, pH 7.2, 25°C, 200 nM FRET-Tel22, 2 μM γPNA, 2 μM complement or 1.8 μM POT1.

These kinetic results strongly suggest that the interaction of POT1 with an initially folded telomeric G4 structure is governed by a conformational selection mechanism in which binding is coupled to mandatory unfolding of the G4 structure. POT1 binding to single-strand DNA is fast, as shown above, so the slow kinetics seen in Figure 3 must result from the slow, rate-limiting G4 unfolding reaction. The overall coupled reaction is

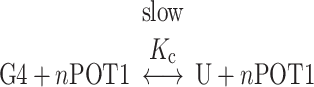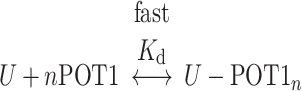where U represents the unfolded G4 and n is the POT1 binding stoichiometry. The two reactions are coupled through U, the unfolded G4 intermediate.

We also studied the rate of POT1 and DNA complement unfolding of telomeric G4 by circular dichroism (CD) monitored at 295 nm, a wavelength selective for G4 formation (Supplementary Figure S2). Interestingly, CD showed a simpler unfolding process with two relaxation times of approximately 20 and 200s, both faster than observed by the FRET measurements shown in Figure 3. The results can be easily reconciled. CD would be highly sensitive to even slight disruption of G-quartet stacking within the G4 structure (for example removal of one strand segment to disrupt the G-quartet structure), whereas FRET is sensitive to the distance between the 5′ and 3′ ends of the quadruplex forming sequence. If binding of multiple POT1 molecules is required to fully unfold the G4 structure (and it is, as will be shown), binding of the first might eliminate the G4-specific CD signal, while additional binding might be needed to fully extend a partially folded strand to yield the maximal FRET change.

Two POT1 molecules bind to the unfolded 24 nt G4 DNA

We studied the product resulting from POT1 unfolding of G4 by analytical ultracentrifugation (AUC), with the results shown in Figure 4. The results show the sedimentation coefficient distributions, c(s), at increasing molar ratios of added POT1. From these data the binding stoichiometry can be inferred. Figure 4A shows the sedimentation positions of the folded G4 alone (1.97S, ≈7600 Da, calculated M_w 7575) or of POT1 alone (2.83S, ≈33 000 Da, calculated M_w 38860). The vertical black and red lines track these positions in the remaining panels. Figure 4E, in which POT1 is at a 3:1 molar excess, shows the ultimate formation of a species with 4.83S and an apparent molecular weight of ≈75 000 Da (dashed horizontal line), as well as some unbound POT1 (red vertical line). The G4 species is completely depleted at this molar ratio (black line). The mass of the complex corresponds to the binding of two POT1 molecules to the unfolded 24 nt G4 DNA, establishing a binding stoichiometry of 2:1. A separate, two-wavelength, analysis of this same data using the known molar extinction coefficients for the G4 DNA and POT1 provided an alternate estimate of 2.2:1 for the binding stoichiometry. The c(s) distributions for other molar ratios (Figure 4B–D) show complex transport behavior that is characteristic of an interacting system (40,41). For such interacting systems, the c(s) peak positions and profile shapes have no simple meaning, and are instead a complex function of reactant concentrations and the equilibrium and rate constants that govern the reaction.

Figure 4.

Determination of POT1 binding stoichiometry by analytical ultracentrifugation. The interaction of POT1 with the 2GKU sequence that forms a hybrid 1 G-quadruplex structures was studied. The distribution of sedimentation coefficients (c(s)) is shown for different molar ratios of added POT1. (A) Sedimentation of the 2GKU quadruplex (black) and free POT1 (red) are shown. (B) Sedimentation of a 0.5:1 molar ration of POT1:2GKU. The black and red lines show the position of free 2GKU and POT1, respectively. The new peak near 4S results from the formation of a 1:1 complex. (C)–(E) Sedimentation distributions for increasing molar ratios of POT1:2GKU, as indicated by the labels in the upper right corner of each panel. As the amount of POT1 increases, the amount of 2GKU (near 2S) is depleted and a complex corresponding to a 2:1 molar ratio (shown by the dashed line) is formed. Reactions were carried out in 20 mM KPO_4, 180 mM KCl, pH 7.2) at room temperature. The 2GKU concentration was 2.5 μM in all experiments while POT1 concentration was varied from 1.25–7.5 μM in B–D. Samples were incubated overnight at room temperature prior to AUC analysis.

Equilibrium studies of POT1 binding to telomeric G4 by conformational selection

Figure 5 shows the binding isotherm for the interaction of POT1 with an initially folded telomeric hybrid G4 structure. Determination and subsequent analysis of this isotherm was both difficult and time consuming. First, because of the slow kinetics described above, each point on the isotherm was determined independently using a separate solution containing a mixture of 200 nM FRET-labeled G4 and varying concentrations of POT1. Each solution was incubated overnight to ensure that equilibrium was attained before FRET measurements. Second, analysis of the binding isotherm by nonlinear least-squares fitting was also challenging. The isotherm is, by eye, slightly sigmoidal in shape, indicative of a complex binding mechanism. For ‘simple’ binding with one class of sites, a smooth hyperbolic shape would be expected. We explored several binding models to fit the data (shown in Supplementary Table S3), including ‘simple’ binding, sequential binding, the phenomenological Hill equation (42) and a conformational selection model that explicitly accounts for the coupling of binding to G4 unfolding.

Figure 5.

Coupled binding of POT1 to an initially folded G-quadruplex. (B) Binding isotherm for the interaction of POT1 to a FRET-labeled G-quadruplex. Each point represents a separate reaction mixture that was allowed to equilibrate for 24 h. The solid line represents the best fit to a conformational selection binding model in which POT1 binding is coupled to a mandatory unfolding of the G-quadruplex, as described in the text. The residuals of the fit are shown in panel (A). (C) Free energy diagram illustrating the thermodynamic linkage between POT1 binding (ΔG_b) and G-quadruplex unfolding (ΔG_c). The large negative coupling free energy (ΔG_coupling) shows that the intrinsic binding affinity of POT1 for single-stranded telomeric DNA drives the unfolding of the G-quadruplex. The binding energy is for the overall interaction of two POT1 molecules per G4. Reaction conditions: 20 mM potassium phosphate,180 mM KCl, pH 7.2, 25°C, 200 nM FRET-G4.

Supplementary Figure S3 shows residual plots from fits to various models, with the best parameter estimates shown in Supplementary Table S3. The ‘simple’ model with one class of binding sites indicates that approximately 2 POT1 molecules are bound with a K_d = 0.95 μM. However, this model shows nonrandom residuals (Supplementary Figure S3A), indicating that it fails to account for the sigmoidal character of the binding isotherm. A fit to a sequential binding model with two POT1 molecules binding with different binding constants (similar to the model of Hwang et al. in Supplementary Scheme S1) gave an improved fit. However, the estimated errors in the fitted binding constants were unacceptably large (>60%) and an unusual, strong, correlation between parameter estimates was observed by Monte Carlo simulations (not shown). A fit of the data to the Hill model (Supplementary Figure S3B) with K_d = 0.32 μM and n = 1.9 shows more random residuals, indicative of a better fit. Comparison of the statistics of fits to the one-site and Hill models (Supplementary Table S3) confirms this, with a clear decrease in the absolute sum of squares of the residuals (ASSR) and the Sy.x parameter that accounts for differences in the number of degrees of freedom resulting from added fitting parameters. This confirms that the sigmoidal character of the binding isotherm in Figure 5A is significant and needs to be accounted for in any model. While the Hill model adequately describes the data in Figure 5A, it is phenomenological and does not fully incorporate important mechanistic details in the underlying reaction mechanism (42–44). ‘K_d’ in the Hill model simply defines the 50% saturation concentration and is not a true dissociation constant. The Hill coefficient ‘n’ lacks physical meaning and at best provides a lower limit for the number of binding sites. For the POT1-G4 interaction, the Hill model neglects any linkage of G4 unfolding to the binding process and fails to account for the energetic contribution of the unfolding step in any way. One modern textbook advises against the use of Hill equation for the analysis of binding data since it lacks mechanistic meaning (45).

We therefore considered a more physically meaningful binding model, the simplest of which is a restricted conformational selection (CS) model as described above. The fitting function for the restricted conformational selection model is

where K_c is the equilibrium constant for G4 unfolding, K_d is the dissociation constant for POT1 binding to the unfolded strand and n is the binding stoichiometry. A detailed discussion of the model and the fitting function was presented in previous work from our laboratory (21).

Figure 5A shows the fit of the unconstrained conformational selection model to the binding data, yielding the parameters K_c = 0.003, K_d = 0.02 μM and n = 2.1 (along with the scaling factor Y_max) (Supplementary Table S3). This model seems to fit the data as well as the Hill model as judged by ASSR and Sy.x measures (Supplementary Table S3), albeit with one additional fitting parameter. However, the error estimates for some parameters are unacceptably large, suggesting that the use of the CS model is perhaps unwarranted. To remedy this, we used a constrained fit in which the binding constant K_d was fixed to the experimental value determined by FRET titrations for POT1 binding to the O1 oligonucleotide (Supplementary Table S2). This strategy reduces the number of adjustable parameters to 3, the same number as for fits to the Hill equation. The resultant fit is statistically as good as fits to the Hill model and to the unconstrained conformational selection model but all fitted parameters now have more reasonable error estimates (Supplementary Table S3). The choice of the constrained CS model provides a physically more meaningful understanding of the underlying reaction mechanism than does the Hill model. The quality of fits to the Hill and constrained CS models were explored by Monte Carlo analysis (Supplementary Figure S4). For 1000 simulations, the results show that the distributions of parameter estimates are reasonable and well behaved for both models.

As an even more ambitious fitting strategy for the data in Figure 5A, we used independently determined experimental values for parameters in the CS model to see if only a single adjustable parameter, K_c, could be determined. K_d was fixed to the O1-POT1 binding constant (Supplementary Table S2), n was fixed to 2.0 as determined by AUC (Figure 4) and Y_max was fixed at 1.0. This approach essentially asks if the binding isotherm in Figure 5A can be quantitatively modeled by the experimentally determined K_d and n values measured independently in the previous sections. The answer is ‘yes’, and the fit yielded the single remaining parameter K_c = 5.57(±0.22) × 10⁻³ (an estimated 4% error in the parameter). The 95% confidence interval for K_c is 5.13 × 10⁻³ to 6.01 × 10⁻³. The overall statistics of the fit (Supplementary Table S3) were only slightly worse than fits with more parameters. Of all of the curve fitting attempts, this approach yields the most well-defined estimate of a single parameter.

As a reality check on the fitted parameters, we compared the results of the constrained CS fits to independently determined values as shown in Table 1. We previously studied in detail the thermodynamics of G4 unfolding by thermal denaturation (22). For the first two steps of a multistep unfolding process, we measured a free energy change of +4.0 ± 0.6 kcal mol⁻¹ at 25°C. This can be compared to ΔG_c = −RTln K_c using best fit K_c values from the constrained CS fits (Supplementary Table S3). The resultant values of +3.3 and +3.1 kcal mol⁻¹ are acceptably close to the independently measured value (Supplementary Table S2). The stoichiometry of POT1 binding was determined to be 2.2 ± 0.1 by fitting our data (Supplementary Table S3), in excellent agreement with the value 0f 2.0 determined independently by AUC. Overall, the physically meaningful conformational selection model provides a reasonable description of the binding isotherm in Figure 5, and yields meaningful quantitative estimates for the underlying equilibrium constants for the steps in the reaction. These quantities can be used to construct the free energy diagram shown in Figure 5B that concisely illustrates how POT1 unfolds a G4 structure. The diagram shows that the energetic cost of unfolding is overcome by the favorable free energy of the binding of two POT1 molecules to the exposed single-strand, and explicitly defines the thermodynamic linkage between POT1 binding and G4 unfolding. The analysis assumes that there is no interaction between the POT1 molecules, a possible additional complexity in the mechanism that would need an additional cooperativity parameter to account for the additional energetic contribution.

Table 1.

Comparison of fitted conformation selection parameters to independently determined values

Parameter	Fit value	Independent estimate	Comment
ΔGc, kcal mol−1	+3.3 ± 0.2, +3.1 ± 0.1	+4.0 ± 0.6	First steps in G4 unfolding determined by thermal denaturation experiments (22)
nPOT1/DNA	2.2 ± 0.1	2.0	Determined by AUC (Figure 4)

POT1 unfolds all G4 forms of telomeric DNA, but not duplex DNA or non-telomeric G4 structures

Human telomeric DNA sequences can adopt several G4 structural forms depending on the exact nucleotides at the 3′ and 5′ ends of the repeat sequence (Supplementary Table S1) and the solution conditions, most critically the identity of the monovalent cation present. These structures include an antiparallel ‘basket’, two different antiparallel ‘hybrid’ structures and a parallel ‘propeller’ structure (Figure 6). We designed experiments to examine how POT1 interacted with these different G4 structural forms, with duplex DNA or with G4 structures formed non-telomeric sequences.

Figure 6.

Specificity of POT1 unfolding of G-quadruplex structures. Four structural forms of human telomere G-quadruplexes are shown at the top of the figure. Formation of each structure depends on solution conditions and the exact oligonucleotide sequence. (A) Kinetics of POT1 unfolding of different G-quadruplex forms. The black and red curves show the unfolding of hybrid 1 (2GKU, Supplementary Table S1; (39)) and hybrid 2 (2JSL, Supplementary Table S1; (54)) structures in K⁺, respectively. The blue curve shows unfolding of the parallel propeller form in polyethylene glycol (Tel22, Supplementary Table S1; (21)). The purple curve shows the unfolding of the antiparallel basket form in Na+ (Tel22, Supplementary Table S1; (55)). (B) Results from a differential scanning fluorometry assay for POT1 binding. The shift in the thermal denaturation temperature of POT1 (ΔT_m) is correlated with the binding affinity for a given nucleic acid structure. ‘CONTROL’ shows the Tm shift observed for POT1 binding to the preferred 10 nt binding sequence O1. ‘CONTROL PEG’ shows this same reaction in the presence of added 40% polyethylene glycol (PEG). (Addition of PEG is needed to form the telomeric parallel G4 structure so this provides a reference for the behaviour of that single structure). Telomeric quadruplex forms are indicated by the red bracket. The data show that all hybrid and basket forms have roughly the same binding affinity for POT1, while the parallel form is slightly less affine. POT1 interactions with several non-telomeric quadruplex structures are indicated by the blue bracket. Notably, POT1 does not unfold and bind to the parallel G-quadruplexes 1XAV and c-kit, or the antiparallel hRAS. Weak interactions with the thrombin binding aptamer (TBA) and a designed quadruplex containing all loop types. Nor does it unfold or bind to a duplex DNA form with the human telomere sequence. (The schematic of telomeric G-quadruplex structures was adapted, with permission, from R. Hansel et al. (2011) Nucl. Acids Res. 39:5766–75). Reaction conditions for unfolding: 20 mM potassium phosphate,180 mM KCl, pH 7.2, 25°C, 200 nM FretG4, 1.8 μM POT1.

Figure 6A shows kinetic FRET unfolding experiments. The data show that the rates of POT1 unfolding of both ‘hybrid’ forms and of the parallel ‘propeller’ form are very similar. In contrast, the rate of unfolding of the antiparallel ‘basket’ form is much faster. For each of these G4 structures, the rate of unfolding by the DNA complementary trap sequence was essentially the same as the rate of unfolding by POT1 (data not shown). POT1 unfolds all of these G4 structural forms under the solution conditions needed to stabilize the structure, but the rate of unfolding depends solely on the intrinsic unfolding rate of the particular structure. The ‘basket’ form in Na⁺ solution is kinetically less stable than the ‘hybrid’ and ‘propeller’ forms and unfolds at a faster rate (23), accounting for the difference seen in Figure 6A.

We also used a differential scanning fluorometry (DSF) thermal shift assay to probe the specificity of POT1 interactions (Figure 6B). The assay uses the fluorophore Sypro Orange to monitor the thermal denaturation of POT1 alone or in the presence of DNA binding sequences. DNA binding stabilizes POT1, increasing the temperature at which it denatures (T_m). POT1 alone, in the DSF assay, has a T_m = 51 ± 0.5°C. The increase in T_m upon DNA binding is proportional to the affinity of the binding interaction (along with binding stoichiometry, enthalpy and other factors). It is important to distinguish here that the DSF assay is a thermodynamic measure of the overall stability of POT1–DNA complexes, since samples were fully equilibrated before the start of the assay. The kinetic data shown in panel A show how rapidly a complex is formed, while this assay monitors the stability of that complex after complete equilibration. As seen in Figure 6B, binding of the control oligonucleotide O1 leads to an increase in T_m of 12–13°C. Binding of telomeric G4 structures initially in the ‘basket’ and ‘hybrid’ forms produces similar increases in T_m, indicating binding similar to the control O1 oligonucleotide sequence. DSF also shows that POT1 interacts with the telomeric parallel ‘propeller’ G4 structure (Figure 6B). In this case, there is a slightly confounding issue arising from the conditions necessary for the formation of the ‘propeller’ structure. The ‘propeller’ structure, while seen in crystals, is not the predominant form in solution (46), so it is necessary to add high concentrations of cosolvents to drive its formation. Polyethylene glycol (PEG) is one such cosolvent. We found in a control experiment that addition of PEG decreases the magnitude of the T_m shift resulting from O1 binding to 8–9°C (Figure 6B, ‘Control PEG’). The thermal shift observed for the parallel ‘propeller’ structure in PEG is similar to that value. While, at first glance, it might appear that the POT1 interaction with the parallel form is weaker than for the basket and hybrid form, that is probably not the case and the apparent difference is instead due to the presence of PEG. These results from DSF indicate that POT1 has little or no preference for any telomeric G4 structural form, and will unfold and bind to all of them equally well.

In contrast, Figure 6B shows that POT1 will not interact with a DNA duplex formed from the telomeric G4-forming sequence and its complementary strand or with duplex AT- and GC-hairpin structures. Nor will POT1 avidly unfold other G4 structures formed by a non-telomeric sequences (Figure 6B, Supplementary Table S1). These include both parallel and antiparallel structures with a variety of loop types and sequences. POT1 does not unfold the 1XAV, c-kit or h-RAS1 G4s at all. It has weak interactions with the TBA, GBA and c-myc G4 structures. Notably, these three have sequence elements in common with the O1 POT1 recognition sequence, namely 5′GGTT, 5′GGGTT and 5′AGGGT, respectively. The slight reactivity of these structures with POT1 emphasizes that the primary force driving G4 unfolding is POT1 affinity for the exposed single strand. These examples suggest that POT1 acts selectively to stabilize unfolded telomeric G4 structures, a consequence of its selective binding to the single-stranded telomeric sequence. The telomeric duplex is not disrupted presumably because the energetic cost of separating the two strands cannot be overcome by the energy from POT1 binding.

POT1 unfolds a telomeric structure containing two G4 units

Supplementary Figure S5 shows that POT1 unfolds a longer 48 nt telomeric G4 structure containing two G4 units. We previously described experimental and computational studies of this structure (47), showing that the G4 units interacted to leave no single-stranded gaps. The kinetics of unfolding are essentially the same as was observed for unfolded monomeric telomeric G4 structures (Figures 3 and 6). Unfolding of the two G4 structure also tracks with the rate of unfolding by addition of complementary strands. Analytical ultracentrifugation studies (not shown) show that the stoichiometry of the final complex is 4:1 POT1:DNA.

The POT1–DNA complex is hydrodynamically compact

In all of the G4-POT1 kinetic studies shown above, we normalized the FRET amplitudes of the time courses to emphasize the similarity of the G4 unfolding rates observed for POT1 and for complement trap sequences. In fact, the overall changes in FRET amplitudes observed at the end of the unfolding reactions are different. Figure 7 shows that the amplitudes of the donor emission spectra of the FAM-TAMRA labeled G4 (A), the POT1–DNA complex (B) and the duplex form (C), along with reference emission spectra obtained with an olionucleotide labeled with only the donor FAM. There are clear differences in the amplitudes of the FAM-TAMRA labeled spectra, which means that the separation of the donor and acceptor are different for the different conformational forms, so their shapes must be different. Comparison of Figure 7B and C indicates that the ends of the G4 sequence are farther apart in the duplex formed by addition of the complementary trap sequence than they are in the POT1 complex. For the complementary trap complex, the G4 unfolds and then forms a rod-like duplex molecule with the ends of the G4 strand maximally separated. In contrast, the POT1 complex must have a less extended shape with the ends of the single-stranded G4 sequence separated to a lesser extent. The spectra in Figure 7 can, in principle, be used to estimate the end-to-end distances of the labeled G4 sequence within the complexes, although with difficulty because of numerous assumptions needed in the calculation and because of the extended linkers used to attach the probes to each end of the DNA. We nonetheless tried by measuring the enhanced fluorescence of acceptor emission, following the analytical method outlined by Clegg (36). Our best estimates show that the donor and acceptor are separated by 74 ± 8 Å in the duplex, but only by 62 ± 5 Å in the POT1 complex. For reference, in the folded G4 structure, the donor–acceptor distance was calculated to be 46 ± 4 Å. We will soon show molecular models that can explain these distances.

Figure 7.

FRET characterization of folded 2GKU (A), the POT1-2GKU complex (B) and the duplex form of the 2GKU sequence produced by addition of its complementary strand (C). In all panels, the red curve is the emission spectra for the single-labeled 5′-6FAM oligonucleotide (donor only). The black curve is the emission spectra of the double-labeled 5′-6FAM-3′-TAMRA oligonucleotide (donor and acceptor). The excitation wavelength was 480 nm for all spectra.

It is interesting to note that addition of the complementary DNA sequence to the POT1–DNA complex results in FRET changes that indicate that POT1 is displaced and a duplex structure is formed (data not shown), This indicates a more favorable free energy for duplex formation than for the POT1–DNA complex formation.

Figure 8 (top) and Table 2 show AUC results that further characterize the hydrodynamic shapes of POT1 and complement trap complexes. The plots show sedimentation coefficient distributions (c(s)), from which frictional ratios (f/f₀) were estimated for each sample. The frictional ratio is defined as the ratio of the frictional coefficient experienced by the sedimenting molecule relative to that of an ideal sphere with the same molecular weight. The value of f/f₀ is a measure of hydrodynamic shape, with spherical molecules having a ratio of 1.0, and more asymmetric molecules having larger ratios. For non-spherical prolate or oblate ellipsoids, the frictional ratio depends on the exact dimensions of the major and minor axes. The value of f/f₀ depends on shape and is independent of molecular weight. We found that the duplex complex has S_20,w = 2.63 ± 0.05 and f/f₀ = 1.58, consistent with a rod-like molecule. The POT1-complex sediments faster, with S_20,w = 4.85 ± 0.05 and f/f₀ = 1.15, indicative of a less extended, more spherical structure. For frictional ratios <1.2, it is difficult to distinguish prolate from oblate ellipsoid shapes. These data are qualitatively consistent with results of the FRET measurements above.

Figure 8.

Top: Analytical ultracentrifugation of 2GKU forms. Sedimentation coefficient distributions (c(s)) are shown. The black curve shows the folded G-quadruplex form. The dashed blue curve shows free POT1. The blue curve shows the 3:1 POT1–2GKU complex. The red curve shows the duplex form of 2GKU. Bottom: Structural model of the POT1–DNA complex. The crescent-shaped MD-derived 2GKU–POT1₂ complex showing two POT1 proteins (ribbons shown in pink and tan) bound to the single-stranded 2GKU oligonucleotide (ribbon shown in blue). For each POT1 protein the ssDNA spans both OB1 and OB2, binding in the continuous basic concave groove, consistent with the crystal structure 1XJV. Binding of the DNA to the POT1 OB1 and OB2 domains leads to an approximate 90° bend in the DNA backbone. There is free rotation about the connecting DNA sequence in between the two POT1 proteins, which leads to an overall ‘w’ shape (although it can twist). Green spheres located at the 3′ and 5′ ends of either structure highlight the oxygen atoms used in distance calculations. Below that is the linear DNA duplex formed by the association 2GKU DNA and its complement.

Table 2.

Hydrodynamic properties of G4 complexes

Molecule	MW kDa	S observed experimental	S calculated	f/f0 experimental	Stokes radius, nmexperimental
POT1	33.7 (31.9 ± 0.8 AUC)	2.83 ± 0.05	2.86	1.25 ± 0.06	2.67
G4 2GKU	7.58 (7.83 AUC)	1.97	1.89	1.28	1.53
2GKU-POT1 2	74.9 (67.4 kD AUC)	4.85	4.63	1.15	3.56
2GKU-duplex	14.7 (15.8 kD AUC)	2.63	2.49	1.58	2.39

Figure 8 (bottom) shows the results of molecular dynamics simulations that provide plausible molecular models for the duplex and POT1 complexes. Addition of the complement trap sequence results in the formation of a canonical duplex complex. Our model predicts a sedimentation coefficient of 2.86S, in excellent agreement with the experimentally determined value (Table 2). The model of POT1-DNA complex is more complicated, with two POT1 molecules bound to the single-stranded DNA that bends to form a crescent-like shape. Supplementary Figure S6 shows the POT1 complex in different orientations. Both POT1 molecules, consisting of OBD 1 and 2, form a continuous basic concave groove where the optimal DNA binding sequence lies, inherently bending the DNA strand. This reduces the distance between the 5′- and 3′-bases where the FRET labels are attached. Our model predicts a sedimentation coefficient of 4.63S, an estimate within 5% of the experimentally determined value (Table 2). The 5′-OH and 3′-OH oxygen atoms were used for end-to-end distances for the DNA in both complexes were measured over the entire 10 ns trajectory of the simulation (Supplementary Figure S7). For the duplex, the end-to-end distance is 78.9 ± 2.9 Å, in good agreement with the 74 ± 8 Å experimental estimate obtained by FRET. In the POT1 complex model, the distance is 55.2 ±3.5 Å, compared to the experimental estimate of 62 ± 5 Å. The values for the models and experiments are within 6–11% of one another, suggesting that the models are reasonable representations of the complexes that form. It should be noted that the molecular dynamics simulations did not contain the actual FRET labels, so it is the trend in the distribution of distances that is important, not the absolute distances.

We examined the model in Figure 8 for possible interactions between the two bound POT1 molecules that might contribute to potential positive cooperativity in their binding. Analysis of the 10 ns molecular dynamics trajectory shows only a transient interaction of two charged residues from the separate POT1 proteins. The overall topology of the POT1 proteins are not perturbed, an indication that there is no structural indication of any cooperative contributions to the binding.

DISCUSSION

These studies suggest that POT1 binds to telomeric G4 structures by a conformational selection mechanism in which binding to the single-stranded repeat sequence is preceded by an obligatory, rate-limiting, unfolding of the quadruplex. We found no evidence to support an alternate mechanism in which POT1 binds directly to a folded G4 structure prior to unfolding. Conformational selection is manifested in both kinetic (Figure 3) and equilibrium (Figure 5, Supplementary Table S3) experiments. Our data and analysis provide quantitative characterization of the underlying reaction. The overall free energy of POT1 unfolding of, and binding to, telomeric G4 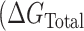) is a sum of two contributions

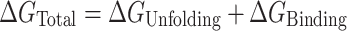where 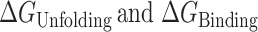are the free energies for G4 unfolding and POT1 binding, respectively. Figure 5B shows how the approximate +3 kcal mol⁻¹ unfavorable free energy cost to unfold G4 is overcome by –20.6 kcal mol⁻¹ binding energy of 2 POT1 molecules to yield a favorable overall reaction of −17.2 kcal mol⁻¹. This conformation selection model is consistent with previous suggestions (15,19,20) that POT1 might ‘trap’ an unfolded G4 intermediate.

The constrained conformational selection and the Hill models provide statistically equivalent fits to the experimental data in Figure 5A, each with three adjustable parameters. Additional constraints allow fits of the binding data to the CS model with a single adjustable parameter, K_c. Why should one model be preferred over the other? We argue that constrained CS models should be preferred because they provide mechanistic insight and quantification that the Hill model does not. Hill himself attested to the lack of physical meaning of the equation that bears his name. In his 1910 article (42), he wrote that in his usage of the equation he derived ‘[m]y object was rather to see whether an equation of this type can satisfy all the observations, than to base any direct physical meaning on n and K’. While the individual fits to the CS and Hill models may be comparable, the lack of any physical context for the Hill parameters lessens their ability to provide functional insights or predictive power to further understanding of the system under study (48). Or, as Bindlev noted, ‘… the real problem with a choice of the modified Hill equation for theory is when it works as a silencer of explorative investigations, thereby preventing possible penetrating analyses’ (49). One recent textbook recommends that ‘[r]esults from fitting data using the Hill equation should not be published except as a prelude to more definitive analysis to define the model and intrinsic equilibrium constants’ (45). That is what we have done. We acknowledge, as one insightful reviewer pointed out, that the actual POT1-G4 binding mechanism may be even more complex than even the CS model describes. In particular, the CS model does not take into account possible cooperative interactions between POT1 molecules in the complex that could either enhance or lessen their binding affinity. Our analysis of the trajectory of the model shown in Figure 8 did not reveal any protein-protein interactions that might contribute to additional binding cooperativity.

We previously characterized the complement unfolding reaction in some detail (23,29) as essential background for understanding POT1 unfolding of G4. The kinetics of telomeric G4 unfolding by POT1 track with the unfolding reaction triggered by the addition complementary DNA or PNA sequences, as shown in Figures 3 and 6. These kinetics are fully consistent with the conformational selection model, and show that the rate limiting step in POT1 binding to initially folded G4 structures is the obligatory unfolding process. We show that binding of POT1 to its single-stranded binding site is fast (Figure 2). Direct binding of POT1 to a folded G4 structure would be expected to be a fast bimolecular interaction on a similar time scale as we observed for the POT1-O1 reaction. We found no evidence for such a direct interaction. Our finding that complementary DNA or PNA sequences can mimic POT1 unfolding of G4 structures is consistent with the early report from the Cech laboratory (15).

We find that POT1 can unfold all telomeric G4 conformational forms, with the rate of unfolding tracking with the intrinsic unfolding rate for each form. This includes a longer telomeric sequence that folds into contiguous G4 units. POT1 does not unfold other G4 structures formed by non-telomeric sequences. It is notable that POT1 cannot unfold a short (22nt) telomeric sequence in duplex form (Figure 6B). The conformational selection model can explain this observation as arising from the much greater free energy cost of unfolding the duplex DNA compared to the folded G4. The free energy cost of melting the 22 nt telomeric duplex is estimated to be 36.4 kcal mol⁻¹ using published nearest neighbor thermodynamic parameters (50). The favorable binding energy of two POT1 molecules is not large enough to overcome that thermodynamic energy barrier. Consistent with this finding is our observation that the complementary DNA strand will displace POT1 from a complex with G4 DNA to form a duplex structure.

FRET measurements and hydrodynamic studies show that the POT1–ssDNA complex is a compact assembly, relative to a DNA duplex structure formed by the same sequence. A stable atomistic model (Figure 8, Supplementary Figure S6) provides details of the assembly, and shows two POT1 molecules bound to the 22 nt telomeric DNA sequence. The POT1 molecules are each bound through their two N-terminal OB domains, as was described in the crystal structure from the Cech laboratory (10). This atomic model accurately predicts measurable experimental hydrodynamic properties, with the sedimentation coefficient prediction within 4–5% of the observed value (Table 2). Our model seems fully consistent with the electron microscopy studies of POT1 bound to long telomeric sequences (13), which showed ordered, compact globular assemblies.

In humans, the 3′ single-strand telomeric overhang is 200 ± 75 nt long (51) and can form multiple G4 units. Our present results provide a firm basis for future studies of POT1 interactions with such longer, perhaps more natural sequences. These studies are underway in our laboratory. We have carefully characterized the structures of long telomeric sequences (17,47,52,53) by molecular dynamics simulations and experimental biophysical studies and have shown that for lengths up to 196 nt they always fold into structures containing the maximal number of possible G4 units, with no single-stranded gaps longer than 3 nt. POT1 would thus encounter an ordered array of G4 structures as a binding substrate in these longer sequences. Our preliminary kinetic and equilibrium binding studies (not shown) indicate that a conformational selection mechanism similar to that described here is also operative for POT1 binding to long telomeric sequences.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

National Institutes of Health (NIH) [GM077422]. Funding for open access charge: NIH funding.

Conflict of interest statement. None declared.