Abstract
A-tracts are A:T rich DNA sequences that exhibit unique structural and mechanical properties associated with several functions in vivo. The crystallographic structure of A-tracts has been well characterized. However, the mechanical properties of these sequences is controversial and their response to force remains unexplored. Here, we rationalize the mechanical properties of in-phase A-tracts present in the Caenorhabditis elegans genome over a wide range of external forces, using single-molecule experiments and theoretical polymer models. Atomic Force Microscopy imaging shows that A-tracts induce long-range (∼200 nm) bending, which originates from an intrinsically bent structure rather than from larger bending flexibility. These data are well described with a theoretical model based on the worm-like chain model that includes intrinsic bending. Magnetic tweezers experiments show that the mechanical response of A-tracts and arbitrary DNA sequences have a similar dependence with monovalent salt supporting that the observed A-tract bend is intrinsic to the sequence. Optical tweezers experiments reveal a high stretch modulus of the A-tract sequences in the enthalpic regime. Our work rationalizes the complex multiscale flexibility of A-tracts, providing a physical basis for the versatile character of these sequences inside the cell.
INTRODUCTION
A-tracts are DNA sequences consisting of four or more consecutive A:T base pairs without a TA step. They are widespread across the genomes of both prokaryotic and eukaryotic organisms, including humans (1–4). Notably, the distribution of A-tracts along eukaryotic genomes has proven to be essential in nucleosome organization with implications in transcription regulation (5–8). In addition, A-tracts have been shown to play an important role in recombination (9,10), replication (11), antiviral response (12,13) and stochastic gene silencing (14).
Many of the functions of A-tracts have been linked to their particular structure and mechanical properties (5,9,10,15). Regarding the structure, A-tracts are known to introduce a directional bend in the DNA helical axis (10). When two or more A-tracts are located in phase with the helical pitch, they induce a significant global curvature of the molecule (16). This curvature contrasts with the anomalously straight conformation reported for a poly (dA:dT) sequence (17,18). The most widely accepted solution to this conflict is the so-called ‘junction model’, where the bending is primarily localized at the edges of the A-tracts (16). Nevertheless, the precise bending mechanism in A-tracts remains a matter of debate (10,19,20).
The reported mechanical properties of A-tracts are to some extent controversial. Early crystallographic studies suggested that A-tracts are conformationally rigid (18,21,22). This rigidity is supported by bulk (23) and single-molecule cyclization experiments (24), the latter showing that insertion of a long (≥10 bp) poly-(dA:dT) fragment inside a random sequence significantly increases its looping time. However, in other single-molecule experiments, DNA molecules containing phased poly-(dA:dT) sequences could be successfully described assuming a standard value of the persistence length, indicative that poly-(dA:dT) sequences might not be particularly rigid to bending deformations (25,26). This assumption is supported by recent molecular dynamics simulations, which reported a similar bending stiffness for poly-(dA:dT) and random DNA sequences (27). Interestingly, other works indicate that poly-(dA:dT) sequences might even be highly flexible to bending (28,29), e.g. in the context of transcription factor mediated DNA looping (29). Finally, with respect to the stretching flexibility, molecular dynamics simulations of short (∼15 bp) duplexes predicted a high stretch modulus for poly-(dA:dT) molecules (30–32), a phenomenon that was attributed to the distinct structure of these sequences. Nevertheless, this theoretical prediction awaits experimental confirmation.
Taken together, these results reveal a complex coexistence of different mechanical properties in A-tracts and call for a unified comprehensive study. Such description should quantitatively distinguish the entropic bendability of these sequences from their intrinsic static bending. This task is non-trivial in either structural or cyclization studies because it requires to precisely know the trajectories of the DNA molecules over distances of hundreds of base pairs. In addition, a full characterization of the mechanical properties of A-tracts should interrogate their response to an external force in order to address their mechanical stiffness to stretching.
In this work, we use atomic force microscopy (AFM), magnetic tweezers (MT) and optical tweezers (OT) to study the mechanical properties of phased A-tracts from the genome of Caenorhabditis elegans at multiple forces and length scales. AFM imaging showed that phased A-tracts induce long-range bending on DNA molecules. The bending could be explained due to the presence of an intrinsically bent structure. MT experiments showed that at low stretching forces (F < 10 pN), the intrinsic bending of phased A-tracts significantly soften the mechanical response of DNA molecules. Finally, OT experiments showed that at higher forces (F > 10 pN), the A-tracts confer DNA an unprecedented stretching rigidity. Altogether, our work unveils the complex interplay between structural and mechanical properties of A-tracts across multiple force scales.
MATERIALS AND METHODS
Selection and cloning of A-tracts DNA from the C. elegans genome
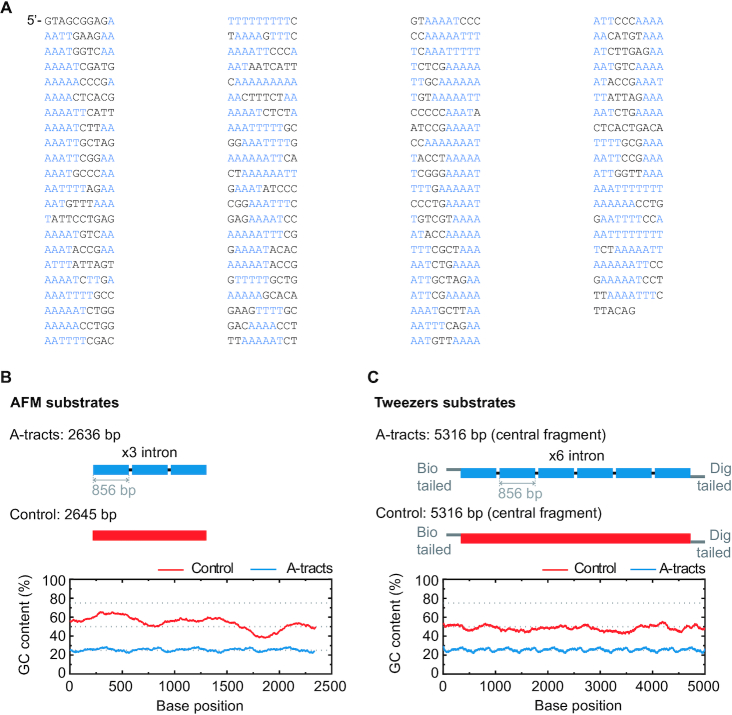
In order to study the mechanical properties of A-tracts at the single-molecule level, we considered a hyperperiodic sequence of 856 bp from the C. elegans genome (4). This segment corresponds to the fourth intron of the gene F54C4.1 that encodes the C. elegans ortholog of human mitochondrial ribosomal protein L40. We will refer to this sequence as the intron (Figure 1A). The intron was PCR amplified from the pPD167.57 plasmid, with the oligonucleotides 58.F Bam-Xho-Psi intron4 and 59.R Apa-Eco-Sal intron4 (Supplementary Table S1). After digestion, the PCR product was electrophoresed on a 1% agarose gel, extracted (QIAGEN Gel Extraction Kit) and cloned into the pNLrep plasmid. This process was performed several times to obtain plasmids with one to six copies of the intron, and constitutes the basis to build the molecules needed for single molecule studies (Figure 1B, C). All plasmids were checked by DNA sequence analysis.
Figure 1.
Sequence and overall organization of DNA molecules under study. (A) Phased A-tract sequence (intron) studied in this work as reported in (34) and Methods section. A-tracts (regions of four or more consecutive A’s and T’s without a TA step) are marked in blue. The sequence was written from the 5′ to the 3′-end in columns of 10 letters to highlight the ∼10 bp periodicity. (B) Top, the A-tract substrate for AFM imaging consisted on three repetitions of the intron, depicted by small blue blocks. A DNA molecule of heterogeneous sequence and similar number of bp was used as a control (red). Bottom, GC-contents of A-tract and control substrates was computed using a homebuilt software and selecting a running window of 300 bp. (C) Top, the DNA substrates for MT and OT contained six repetitions of the intron and were flanked by two oligonucleotides labelled with biotin and digoxigenin. As control, we considered a DNA molecule of heterogeneous sequence and similar number of bp (red). Bottom, GC-content of A-tract and control molecules for tweezers experiments were computed as described in (B).
Synthesis of DNA molecules for AFM experiments
The A-tract substrate for AFM measurements was made of three copies of the intron, resulting in a 2636 bp molecule (A-tract AFM substrate, Supplementary Table S2). This fragment was obtained by digestion of the respective plasmid with XhoI and EcoRV enzymes. As a control, a fragment of DNA of 2645 bp (control AFM substrate, Supplementary Table S2) with a 54% content of GC (Figure 1B) was obtained by digestion of pNLrep-0BspQI site plasmid (previously cloned in the laboratory from pNLrep plasmid) with SalI and ScaI enzymes. Fragments coming from digestion or PCR were electrophoresed on a 1% agarose gel and extracted. DNAs were never exposed to intercalant dyes or UV radiation during their production and were stored at 4°C.
Synthesis of DNA molecules for MT and OT experiments
We fabricated DNA molecules of 5316 bp containing six copies of the intron (A-tract tweezers substrate, Supplementary Table S2). The central fragment of the molecule is flanked by oligonucleotides labelled either with digoxigenin (3′ end) or biotin (5′ end) that specifically bind either to a glass surface covered with Anti-digoxigenin (Roche) or to superparamagnetic beads (MyOne, Dynabeads) covered with streptavidin (Figure 1C). Labeled oligonucleotides were fabricated based on a previously published method (33). Briefly, 27P-XhoI-A and XbaI-A oligonucleotides (Supplementary Table S1) were biotin or digoxigenin tailed using Terminal Transferase (NEB) and either BIO-dUTP or DIG-dUTP, respectively. The modified oligonucleotides were purified using a Qiaquick nucleotide removal kit (Qiagen) and hybridized respectively with 26XhoI-B or 88.XbaI C ApaI (Supplementary Table S1). The central fragment was digested with XhoI and ApaI enzymes and ligated overnight to the two hybridized tailed oligonucleotides using T4 DNA ligase (NEB). Excess of oligonucleotides was removed using Microspin S-400 columns. As a control molecule (Supplementary Table S2), we chose a fragment of DNA with a homogeneous GC content with the same length (Figure 1C). This fragment was PCR amplified with the oligonucleotides 89.F lambda 40002 XhoI and 90.R lambda 45263 ApaI using Lambda DNA (NEB) as a template. This region was selected by running a homemade software that computes the GC content of a given sequence and selecting a running window of 300 bp. The PCR product was digested, electrophoresed on a 1% agarose gel, extracted, and ligated with the same tailed oligonucleotides used to produce the A-tracts molecule.
A-tract molecules presented a low GC-content (∼20%) with periodic patterns that arise from the three and six repetitions of the intron present in the AFM and Tweezers’ substrates, respectively. In contrast, the GC-content of the control molecules are ∼50% (Figure 1B, C). Importantly, all A-tracts constructs showed anomalous gel migration (Supplementary Figure S1), as expected for phased A-tracts (34).
Atomic force microscopy measurements
Air imaging
A 20 μl solution containing 0.3 nM of DNA in 100 mM NaCl, 10 mM Tris–HCl pH 8 and 15 mM MgCl2 was deposited on freshly-cleaved mica (grade V-4 mica from SPI) and incubated for 30 s. Then, the sample was washed with 4 ml of Milli-Q water and dried under nitrogen air-flow. Imaging conditions were similar to the ones described in a previous work (35). Images were taken with an AFM from Nanotec Electronica S.L. with PointProbePlus tips (PPP-NCH Nanosensors, tip stiffness 42 N/m, tip radius ∼10 nm) using amplitude modulation imaging mode in air with a free amplitude of ∼4.2 nm and a set point of ∼3.6 nm. Additional experiments in air at low MgCl2 were performed using 0.3 nM of DNA in 100 mM NaCl, 10 mM Tris–HCl pH 8, 2.5 mM MgAc and 1.5 mM NiCl2 (Table 1).
Table 1.
Mechanical parameters of A-tracts and control molecules obtained in this work. Mechanical parameters from AFM data were calculated from the fits to the 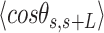 data presented in Figure 2D and Supplementary Figure S5. Errors are the error of the fit. AFM imaging conditions are described in the Materials and Methods section. Mechanical parameters from MT and OT data are the average of the parameters obtained for each molecule and the errors are the standard deviation of the mean. For MT measurements,
data presented in Figure 2D and Supplementary Figure S5. Errors are the error of the fit. AFM imaging conditions are described in the Materials and Methods section. Mechanical parameters from MT and OT data are the average of the parameters obtained for each molecule and the errors are the standard deviation of the mean. For MT measurements, 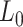 and
and 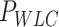 were obtained by fitting the data to Equation (7) in the F < 1 pN regime. For OT measurements,
were obtained by fitting the data to Equation (7) in the F < 1 pN regime. For OT measurements, 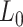 and
and 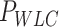 were extracted by fitting the data to Equation (8) in the 1 pN <
were extracted by fitting the data to Equation (8) in the 1 pN < 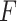 < 10 pN force range.
< 10 pN force range. 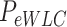 and
and 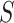 were calculated by fitting the OT data to Equation (9) in the 10–45 pN force range. N denotes the number of molecules
were calculated by fitting the OT data to Equation (9) in the 10–45 pN force range. N denotes the number of molecules
| Atomic force microscopy | ||||||
|---|---|---|---|---|---|---|
| Imaging conditions | Molecule |
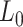 (nm) (nm)
|
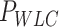 (nm) (nm)
|
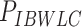 (nm) (nm)
|
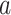 (μm−1) (μm−1)
|
# Traces |
| Air imaging Mg2+ | A-tract | 871 ± 27 (N = 43) | 23 ± 1 | 55 ± 1 | 17 ± 1 | 178 |
| Control | 898 ± 21 (N = 44) | 54 ± 1 | 122 | |||
| Air imaging Mg2+ & Ni2+ | A-tract | 889 ± 28 (N = 41) | 24 ± 1 | 53 ± 1 | 17 ± 1 | 141 |
| Control | 902 ± 24 (N = 38) | 47 ± 1 | 89 | |||
| Liquid imaging Mg2+ & Ni2+ | A-tract | 858 ± 46 (N = 40) | 18 ± 4 | 47 ± 3 | 18 ± 1 | 180 |
| Control | 886 ± 53 (N = 43) | 50 ± 1 | 163 | |||
| Magnetic tweezers | ||||||
| [NaCl] (mM) | Molecule |
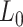 (nm) (nm)
|
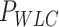 (nm) (nm)
|
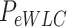 (nm) (nm)
|
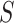 (pN) (pN)
|
N |
| 1 | A-tract | 1921 ± 31 | 22 ± 1 | 14 | ||
| Control | 1945 ± 31 | 49 ± 1 | 15 | |||
| 10 | A-tract | 1910 ± 14 | 19 ± 1 | 25 | ||
| Control | 1940 ± 22 | 45 ± 1 | 18 | |||
| 100 | A-tract | 1946 ± 16 | 15 ± 1 | 28 | ||
| Control | 1866 ± 20 | 44 ± 1 | 20 | |||
| 500 | A-tract | 2039 ± 20 | 12 ± 1 | 29 | ||
| Control | 1923 ± 19 | 41 ± 1 | 19 | |||
| Optical tweezers | ||||||
| [NaCl] (mM) | Molecule |
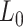 (nm) (nm)
|
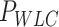 (nm) (nm)
|
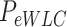 (nm) (nm)
|
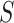 (pN) (pN)
|
N |
| 50 | A-tract | 1890 ± 7 | 20 ±1 | 38 ± 3 | 2560 ± 260 | 9 |
| Control | 1833 ± 7 | 42 ± 2 | 49 ± 5 | 1680 ± 80 | 10 | |
| 100 | A-tract | 1872 ± 16 | 20 ± 2 | 44 ± 3 | 2400 ± 220 | 15 |
| Control | 1836 ± 3 | 42 ± 2 | 47 ± 4 | 1540 ± 90 | 17 | |
| 500 | A-tract | 1839 ± 3 | 21 ± 1 | 37 ± 3 | 2390 ± 190 | 17 |
| Control | 1830 ± 3 | 41 ± 3 | 49 ± 4 | 1560 ± 100 | 13 | |
Liquid imaging
DNA molecules were immobilized for liquid imaging using Ni2+ as previously reported (36,37). A 20 μl solution containing 0.3 nM of DNA in 100 mM NaCl, 10 mM Tris–HCl pH 8 and 7.5 mM MgCl2 was first deposited on freshly-cleaved mica (grade V-4 mica from SPI) and incubated for 60 s to allow molecules to equilibrate. Then, 2 μl of 2.5 mM NiCl2 were added to the solution and incubated for additional 60 s to fix the molecules to the mica surface. The sample was then rinsed four times with 80 μl imaging buffer 10 mM Tris–HCl pH 8 and 10 mM KCl. Images were obtained in a final volume of 80 μl. Images were taken with an AFM from Nanotec Electronica S.L. with Biolever mini tips (AC-40TS Olympus, tip stiffness 0.02–0.1 N/m, tip radius ∼10 nm) using amplitude modulation imaging mode with a free amplitude of 1–2 nm and a set point of ∼0.8 nm.
Images obtained in air and in liquid were taken at a resolution of 1.46 nm/pixel and processed using the ‘Flatten plus’ utility of the WSxM freeware (38,39). Contour lengths were computed by manually tracing the molecules using WSxM. Persistence length of molecules imaged in air were calculated using the tracing routine described in (34,40) by taking 290 nm traces with 2.5 nm point-to-point (l) separation. Persistence length of molecules imaged in liquid were obtained by taking 292 nm traces with l = 4.0 nm.
Magnetic tweezers measurements
We used a magnetic tweezers setup based on an inverted optical microscope illuminated by nearly monochromatic LED light to track micrometer-sized superparamagnetic beads tethered to the surface by the DNA molecule of interest (41,42). The spatial coordinates of the beads are extracted by videomicroscopy analysis of 2D correlation (xy coordinates) and by the analysis of the pattern of diffraction rings (z coordinate). Forces in the range of 0.03–6.5 pN are applied by approximating two vertically-aligned magnets (Supermagnete, W-05-N50-G) separated by a gap of 1 mm. The force applied at a given magnet position was determined from the average extension of the molecule and from the analysis of the Brownian excursions in Fourier space. In addition, motion blur and the ensuing overrating of the force was minimized by tracking at high frequencies (400 Hz). Force-extension curves were obtained by sampling the average extension at a constant force. Molecular extensions were corrected by subtracting the extension at zero force. Double-tethered beads were discarded from our measurement attending to their characteristic rotations-extension response. In addition, we discarded DNA-beads showing large off-center attachment to prevent underrating the persistence length, an artifact previously reported (43,44). Beads with large off-center attachment were identified from the projected circle in the xy plane when magnet turns are applied. All the experiments were performed in a buffer composed of 10 mM Tris–HCl pH 8.0, 1 mM EDTA and supplemented with NaCl at the quoted concentration. The 10 mM Tris–HCl pH 8.0 buffer was prepared from a 1 M Tris–HCl pH 8.0 stock using Trizma® base and adjusting the pH with HCl. The ionic strength (c) was calculated attending to the concentrations of all the ionic species in the solution, assuming ideal conditions. The concentration of ionized Tris was determined from the Henderson-Hasselbalch equation, whereas EDTA was assumed to possess charge –3 at pH 8. In addition to the Tris, HCl and EDTA species, we considered the sodium ions from the EDTA disodium salt employed to prepare the EDTA stock solution as well as the NaOH added to correct its pH. We obtained c0 = 11.67 mM for the EDTA–Tris buffer. Quoted concentrations of supplemented NaCl were added to c0 for each different experiment.
Optical tweezers measurements
Optical tweezers experiments were performed with a highly stable miniaturized counter-propagating dual-beam setup that operates by direct measurement of light momentum (45). Force was determined directly by measuring the deflection of the scattered laser beam with a position sensitive detector using an under-filled microscope objective. Individual DNA constructs labeled with biotin at one end and digoxigenin at the other (see above) were attached between a streptavidin-covered bead (2.1 μm diameter, Kisker Biotech; PC-S-2.0) held by suction on top of a micropipette and an anti-digoxigenin-covered bead located at the optical trap (force sensor). Anti-digoxigenin antibody (Roche; 11 333 089 001) was immobilized by crosslinking on protein G covered beads with nominal size 3.0 μm (Kisker Biotech; PC-PG-3.0). Axial forces were applied to single DNA molecules by displacing the pipette relative to the optical trap. Force–extension curves were obtained at 500 Hz of sampling frequency by moving the optical trap at a pulling rate of 200 nm s−1 with a spatial and force resolution of 1 nm and 1 pN respectively. Our optical tweezers setup controls the distance between the trap center and the pipette (Xtotal), which is different from the end-to-end distance of the DNA molecule (Xend-end). The end-to-end distance was calculated as Xend−end = XTot − (F/k), where F is the force applied to the system, k the stiffness of the trap, and F/k corresponds to the distance (nm) moved by the bead out of the trap center (bead position). The trap stiffness was calibrated by measuring the displacement of the optical trap, while a bead fixed on top of the micropipette is gradually moved in/out of the trap (45). The trap stiffness calibrated for 3.0 μm beads was 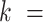 0.135 ± 0.0043 pN nm−1, with a linear spring restoring force up to 80 pN (data not shown). Experiments were done in a buffer of 10 mM Tris–HCl pH 8.0, 1 mM EDTA with the concentration of NaCl specified in the text. Raw data was processed by computing a running average in windows of 100 points. WLC and eWLC fitting parameters were obtained for each molecule and were then averaged. The errors in the parameters are the standard error of this mean.
0.135 ± 0.0043 pN nm−1, with a linear spring restoring force up to 80 pN (data not shown). Experiments were done in a buffer of 10 mM Tris–HCl pH 8.0, 1 mM EDTA with the concentration of NaCl specified in the text. Raw data was processed by computing a running average in windows of 100 points. WLC and eWLC fitting parameters were obtained for each molecule and were then averaged. The errors in the parameters are the standard error of this mean.
RESULTS
In-phase A-tracts bend DNA molecules over long distances
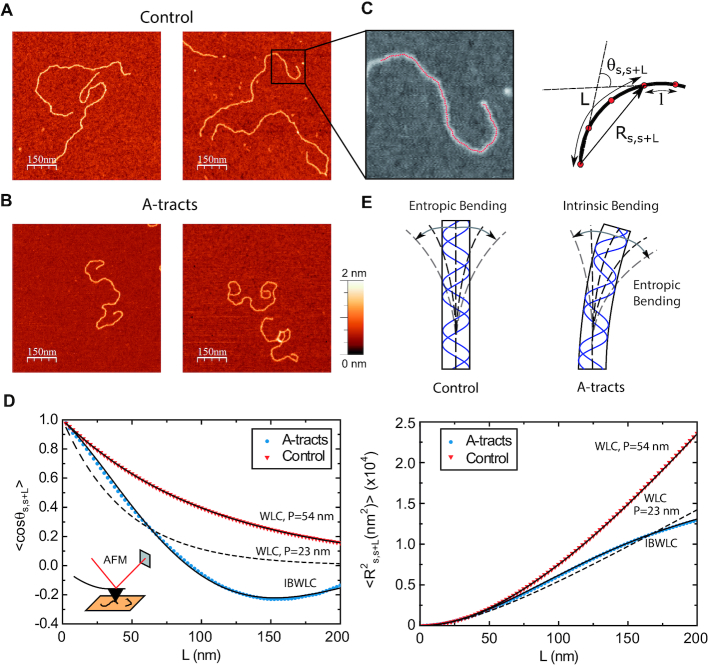
In order to determine the mechanical properties of A-tracts in the absence of force, we used an AFM to image DNA fragments of the genome of C. elegans containing in-phase A-tracts (Figure 1, and Experimental Section). As a control, we imaged DNA molecules with random sequence and similar length. AFM has proven to be an invaluable tool for characterizing DNA mechanical properties, providing a rigorous experimental test of the applicability of polymer models to DNA molecules (25,35,40,46). Using AFM imaging, we captured two-dimensional equilibrium conformations of the control (Figure 2A) and phased A-tracts DNA molecules (Figure 2B). As a first quantitative characterization, we computed the mean contour length of the control and the A-tracts molecules, obtaining values of 898 ± 21 nm (N = 44, error is s.d.) and 871 ± 27 nm (N = 43), respectively (Table 1, Supplementary Figure S2). These values yield a helical rise of ∼0.34 nm bp−1, consistent with the standard value of B-DNA obtained from X-ray crystallography (47) and small-amplitude X-ray scattering interference (48).
Figure 2.
Mechanical properties of A-tracts at zero force. Representative AFM images taken in air of (A) control and (B) A-tract DNA molecules adsorbed on a mica surface using Mg2+ ions. (C) Detailed view of an individual DNA molecule. A series of dots (in red) separated by 2.5 nm were used to define the contour of the DNA molecules. Right, schematic representation of the measured quantities showing the angles between the tangents, 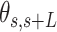 , and the distance,
, and the distance, 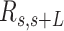 , for two points separated by a contour distance of l = 7.5 nm. (D) The quantities
, for two points separated by a contour distance of l = 7.5 nm. (D) The quantities 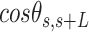 and
and 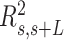 , were averaged over all the traces. The resulting
, were averaged over all the traces. The resulting 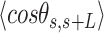 and
and 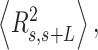 are plotted as a function of the contour distance separation between points,
are plotted as a function of the contour distance separation between points, 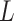 .
. 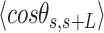 values of control and A-tract molecules were fitted to the WLC and IBWLC using Equations (2) and (5), respectively. This yielded a value of P = 54 ± 1 nm for control DNA and P = 55 ± 1 nm, a = 17 ± 1 μm−1 for the A-tract molecule. Solid lines in the
values of control and A-tract molecules were fitted to the WLC and IBWLC using Equations (2) and (5), respectively. This yielded a value of P = 54 ± 1 nm for control DNA and P = 55 ± 1 nm, a = 17 ± 1 μm−1 for the A-tract molecule. Solid lines in the 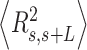 plot are not fits but the representation of Equations 3 and 6 (WLC and IBWLC, respectively) using the fitting parameters obtained from the
plot are not fits but the representation of Equations 3 and 6 (WLC and IBWLC, respectively) using the fitting parameters obtained from the 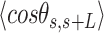 plot. Dashed lines represent best fits of the A-tracts data to the WLC model with P = 23 ± 1 nm. (E) Schematic representation of the WLC and IBWLC models. In the WLC model, the minimum energy corresponds to a straight conformation (zero intrinsic curvature; dashed black line) but the molecule can be entropically bent (dashed grey lines) as a result of its bending flexibility. In the IBWLC model, the molecule has both intrinsic curvature (curved dashed black line) and entropic bending (grey dashed line).
plot. Dashed lines represent best fits of the A-tracts data to the WLC model with P = 23 ± 1 nm. (E) Schematic representation of the WLC and IBWLC models. In the WLC model, the minimum energy corresponds to a straight conformation (zero intrinsic curvature; dashed black line) but the molecule can be entropically bent (dashed grey lines) as a result of its bending flexibility. In the IBWLC model, the molecule has both intrinsic curvature (curved dashed black line) and entropic bending (grey dashed line).
A-tracts molecules appeared more bent than the control ones and were more prone to form loops (see Figure 2 and Supplementary Figure S3), in line with the findings reported in (34). In order to quantify the flexibility of these molecules, we firstly analysed their traces following a previously published protocol (34,35). We calculated pairs of coordinates separated by a distance 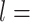 2.5 nm that describe the contour followed by the adsorbed DNA molecules (Figure 2C). From these traces, we obtained the angle,
2.5 nm that describe the contour followed by the adsorbed DNA molecules (Figure 2C). From these traces, we obtained the angle, 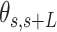 , defined by the tangents at two points separated by a contour distance
, defined by the tangents at two points separated by a contour distance 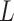 ; and the distance,
; and the distance, 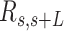 , between these points (Figure 2C). We then averaged
, between these points (Figure 2C). We then averaged 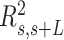 and
and 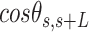 over all the points of the trace and over hundreds of traces. Representing these two quantities,
over all the points of the trace and over hundreds of traces. Representing these two quantities, 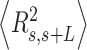 and
and 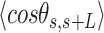 , as a function of
, as a function of 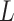 allows direct comparison of AFM data with polymer models, see below (Figure 2D).
allows direct comparison of AFM data with polymer models, see below (Figure 2D).
The mechanical properties of DNA molecules are usually analysed in the context of the worm-like-chain (WLC) model, which describes polymers with harmonic bending energy
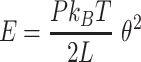 |
(1) |
Where 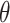 is the bending angle;
is the bending angle; 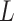 the contour separation as defined for the AFM traces; and
the contour separation as defined for the AFM traces; and 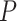 is the persistence length, which is proportional to the bending modulus (
is the persistence length, which is proportional to the bending modulus (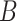 ):
): 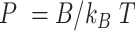 (46,49). Notice that the minimum energy configuration corresponds to
(46,49). Notice that the minimum energy configuration corresponds to 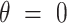 , that is, to straight molecules. Therefore, according to the WLC model, DNA molecules are bent solely by thermal fluctuations, i.e. they are entropically bent. The AFM data can then be fitted to the equations of the WLC in two dimensions (25,46):
, that is, to straight molecules. Therefore, according to the WLC model, DNA molecules are bent solely by thermal fluctuations, i.e. they are entropically bent. The AFM data can then be fitted to the equations of the WLC in two dimensions (25,46):
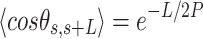 |
(2) |
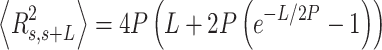 |
(3) |
In agreement with previous works, our control data nicely fit to Equations (2) and (3) with  = 54 ± 1 nm (35,46) (Figure 2D). However, A-tracts data deviated from the WLC behavior, and the best fit to Equation (3) provided an extremely low persistence length of
= 54 ± 1 nm (35,46) (Figure 2D). However, A-tracts data deviated from the WLC behavior, and the best fit to Equation (3) provided an extremely low persistence length of 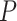 = 23 ± 1 nm (Figure 2D, right panel). This deviation is even more remarkable for the cosine's correlation, for which the WLC predicts an exponential decay (Equation 2). Indeed, the cosine's correlation of the A-tracts molecules reached negative values, with a minimum of
= 23 ± 1 nm (Figure 2D, right panel). This deviation is even more remarkable for the cosine's correlation, for which the WLC predicts an exponential decay (Equation 2). Indeed, the cosine's correlation of the A-tracts molecules reached negative values, with a minimum of 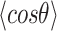 ∼ -0.2 at around
∼ -0.2 at around 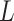 = 150 nm (Figure 2D, left panel). In addition, we performed a deeper analysis of our trajectories and obtained the distribution of bending angles, similarly to previous works (50). This analysis exposed that, contrary to the control molecule and the WLC prediction, the bending angle distribution of A-tracts was not centred at zero for contour lengths of
= 150 nm (Figure 2D, left panel). In addition, we performed a deeper analysis of our trajectories and obtained the distribution of bending angles, similarly to previous works (50). This analysis exposed that, contrary to the control molecule and the WLC prediction, the bending angle distribution of A-tracts was not centred at zero for contour lengths of 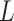 = 100 and 150 nm (see Supplementary Figure S4). These considerations demonstrated that, at zero force, the simple picture of the WLC model that assumes purely entropically bent polymers is not sufficient to describe the flexibility of A-tracts DNA molecules.
= 100 and 150 nm (see Supplementary Figure S4). These considerations demonstrated that, at zero force, the simple picture of the WLC model that assumes purely entropically bent polymers is not sufficient to describe the flexibility of A-tracts DNA molecules.
An intrinsically-bent worm-like-chain model captures the long-range bending induced by in-phase A-tracts
We solved this discrepancy by developing a polymer model that incorporates intrinsic curvature into the WLC, as recently done for collagen fibers (51). This intrinsically-bent WLC (IBWLC) model has a simple, analytical solution that can be used to fit the AFM data, allowing to quantitatively decouple the bending contribution arising from thermal fluctuations (entropic contribution) from that coming from the intrinsic curvature of the A-tracts. This model is based on the assumption that the minimum of bending energy corresponds to a bent trajectory described by the arc of a circle of radius 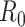 . This assumption has been widely used in the literature (e.g., in cyclization (20,52) and in AFM data (34)) to account for the fact that A-tracts induce a bend in the DNA structure (10). This assumption is sketched in Figure 2E and can be expressed mathematically as
. This assumption has been widely used in the literature (e.g., in cyclization (20,52) and in AFM data (34)) to account for the fact that A-tracts induce a bend in the DNA structure (10). This assumption is sketched in Figure 2E and can be expressed mathematically as
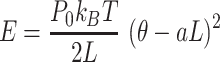 |
(4) |
where 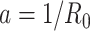 is the intrinsic curvature, and
is the intrinsic curvature, and 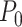 will be termed as natural persistence length of the molecule, which quantifies its resistance to bending similar to the WLC case. Notice that the WLC expression (Equation 1) is recovered in a straightforward manner by making
will be termed as natural persistence length of the molecule, which quantifies its resistance to bending similar to the WLC case. Notice that the WLC expression (Equation 1) is recovered in a straightforward manner by making 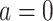 , that is, by deleting the intrinsic curvature; and by substituting
, that is, by deleting the intrinsic curvature; and by substituting 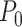 by
by 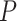 . From Equation (4) we obtained the relevant
. From Equation (4) we obtained the relevant 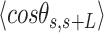 and
and 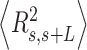 expressions for fitting the experimental data to the IBWLC, in a similar fashion to the WLC case (46):
expressions for fitting the experimental data to the IBWLC, in a similar fashion to the WLC case (46):
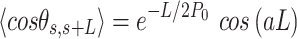 |
(5) |
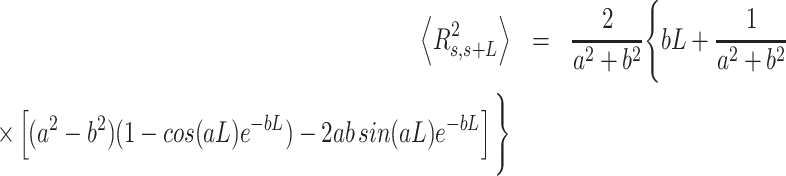 |
(6) |
where we have defined 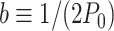 for convenience. A full derivation of the model can be found in (51) and in Supplemental Material.
for convenience. A full derivation of the model can be found in (51) and in Supplemental Material.
A fit of the IBWLC model (Equation 5) to the A-tracts data provided the fitting parameters 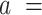 17 ± 1 μm−1 and
17 ± 1 μm−1 and 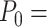 55 ± 1 nm (Figure 2D, left panel). Using these values, we plotted the theoretical expression of
55 ± 1 nm (Figure 2D, left panel). Using these values, we plotted the theoretical expression of 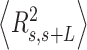 (Equation 6) and found an excellent agreement with the experimental data (Figure 2D, right panel). Remarkably, this agreement held for contour distances that extended up to at least 200 nm. We repeated our AFM measurements in air using an alternative buffer that contains ∼1.5 mM NiCl2 and 2.5 mM MgAc, which has been previously reported to allow proper equilibration of DNA molecules on the mica (35). Furthermore, additional experiments were performed in liquid conditions (Materials and Methods). Mechanical parameters and contour lengths of molecules were very similar under all tested conditions (see Table 1, Supplementary Figures S2, S3 and S5).
(Equation 6) and found an excellent agreement with the experimental data (Figure 2D, right panel). Remarkably, this agreement held for contour distances that extended up to at least 200 nm. We repeated our AFM measurements in air using an alternative buffer that contains ∼1.5 mM NiCl2 and 2.5 mM MgAc, which has been previously reported to allow proper equilibration of DNA molecules on the mica (35). Furthermore, additional experiments were performed in liquid conditions (Materials and Methods). Mechanical parameters and contour lengths of molecules were very similar under all tested conditions (see Table 1, Supplementary Figures S2, S3 and S5).
The IBWLC model enabled us to quantitatively dissociate the intrinsic curvature and the entropic bending contributions to the A-tracts flexibility. The value that we found for the intrinsic curvature (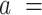 17 ± 1 μm−1) was close to a previous estimation obtained of ∼10 μm−1 from AFM images (34). However, these AFM values of the intrinsic curvature of C. elegans sequences are lower than the curvature inferred (∼90 μm−1) for shorter (∼100 bp-long) artificial sequences with A-tract repetitions in classical gel electrophoresis experiments (see e.g. (52)). Finally, the persistence length essentially coincided with the control and with indirect measurements from cyclization studies on A-tracts (23,53). Altogether, our results indicate that the A-tracts molecule has no enhanced bending flexibility. In other words, deviations from the minimum energy are energetically as costly as for the control molecule, as quantified by a similar persistence length for both molecules. On the contrary, the apparent larger bendability of this molecule stems from a purely structural or static deformation, its intrinsic curvature.
17 ± 1 μm−1) was close to a previous estimation obtained of ∼10 μm−1 from AFM images (34). However, these AFM values of the intrinsic curvature of C. elegans sequences are lower than the curvature inferred (∼90 μm−1) for shorter (∼100 bp-long) artificial sequences with A-tract repetitions in classical gel electrophoresis experiments (see e.g. (52)). Finally, the persistence length essentially coincided with the control and with indirect measurements from cyclization studies on A-tracts (23,53). Altogether, our results indicate that the A-tracts molecule has no enhanced bending flexibility. In other words, deviations from the minimum energy are energetically as costly as for the control molecule, as quantified by a similar persistence length for both molecules. On the contrary, the apparent larger bendability of this molecule stems from a purely structural or static deformation, its intrinsic curvature.
The low-force response of in-phase A-tracts molecules deviates from purely entropic models
AFM experiments showed that the intrinsic A-tracts’ bending is responsible for the anomalous mechanical properties of these molecules at zero force. However, inside the cell the DNA is often subjected to mechanical stress, and to which extent the intrinsic bending of DNA affects its extension under mechanical force is unclear. We employed MT to explore the mechanical response of phased A-tracts sequences at forces F < 6 pN. To this end, we took force-extension curves of DNA molecules containing six repetitions of an A-tract sequence found in C. elegans and compared them with those of a DNA control with heterogeneous sequence and similar number of base pairs (Figure 1C, and Supplementary Table S2). Averaged force-extension curves showed that, at forces F < 5 pN, A-tracts molecules presented significantly lower extensions than those of the control (Figure 3A). Importantly, this decrease in end-to-end distance of the molecule was also found at zero force in the AFM experiments and was rationalized to be an effect of the bends (Equation 3 and Figure 2D, right panel). This effect virtually disappears at a force of ∼5 pN, where both molecules show a similar extension and practically reach their full contour length (∼1.8 μm).
Figure 3.
Mechanical response of A-tracts to forces below 10 pN. (A) Average force-extension curves of A-tracts and control DNA molecules obtained with magnetic tweezers (100 mM NaCl, mean ± s.e.m., N = 20 for the control and N = 28 for the A-tracts). Solid lines are fits to the WLC formula accounting for low force corrections (Equation (7)). (B) Contour length values (mean ± sd) obtained from the fits of the force-extension curves of control (red) and A-tracts (blue) molecules to Equation (7) at different ionic strength conditions. (C) Relation between the persistence length  and the ionic strength (mean ± sd). The lower errors for A-tracts are the result of the larger difference between force-extension curves at low persistence lengths and at low forces. The data was fit to the Barrat and Joanny (BJ) model and to the Odjik–Skolnick–Fixman (OSF). Fitting to the BJ model yielded
and the ionic strength (mean ± sd). The lower errors for A-tracts are the result of the larger difference between force-extension curves at low persistence lengths and at low forces. The data was fit to the Barrat and Joanny (BJ) model and to the Odjik–Skolnick–Fixman (OSF). Fitting to the BJ model yielded  = 40 ± 1 nm,
= 40 ± 1 nm, 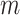 = 30 ± 9 nm·mM1/2 for control molecules and
= 30 ± 9 nm·mM1/2 for control molecules and 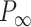 = 11 ± 1 nm,
= 11 ± 1 nm, 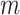 = 38 ± 3 nm·mM1/2 for A-tracts. Fitting to the OSF model yielded
= 38 ± 3 nm·mM1/2 for A-tracts. Fitting to the OSF model yielded 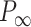 = 42 ± 1 nm,
= 42 ± 1 nm, 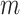 = 89 ± 28 nm·mM for control molecules and
= 89 ± 28 nm·mM for control molecules and 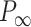 = 13 ± 1 nm,
= 13 ± 1 nm, 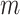 = 126 ± 20 nm·mM for A-tracts. Other models such as the OSF model with fixed
= 126 ± 20 nm·mM for A-tracts. Other models such as the OSF model with fixed 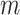 and the Netz–Orland model did not properly describe our data (not shown).
and the Netz–Orland model did not properly describe our data (not shown).
In order to quantify the mechanical properties of A-tracts we naively applied the traditional WLC model that assumes an isotropic rod. In particular, we resorted to the WLC interpolation formula (54):
 |
(7) |
where 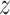 is the extension of the molecule,
is the extension of the molecule, 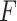 the applied force,
the applied force, 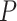 the persistence length and the phenomenological constants
the persistence length and the phenomenological constants 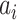 are
are 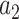 = –0.5164228,
= –0.5164228, 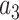 = –2.737418,
= –2.737418, 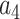 = 16.07497,
= 16.07497, 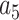 = –38.87607,
= –38.87607, 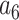 = 39.49944 and
= 39.49944 and 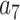 = –14.17718.
= –14.17718.
As expected, force-extension curves of control DNA were well described by the WLC model (Figure 3A, red symbols) and yielded a persistence length of 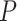 = 44 ± 4 nm, in agreement with previous measurements (35,55) and consistent with our AFM measurements in liquid (
= 44 ± 4 nm, in agreement with previous measurements (35,55) and consistent with our AFM measurements in liquid (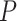 = 50 nm). However, the A-tracts data showed deviations from the expression of the WLC model (Figure 3A, blue symbols). At forces below 1 pN the data were best described by a
= 50 nm). However, the A-tracts data showed deviations from the expression of the WLC model (Figure 3A, blue symbols). At forces below 1 pN the data were best described by a 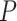 = 15 ± 1 nm, whereas in the 1–4 pN force range, data were better fitted to a higher persistence length of
= 15 ± 1 nm, whereas in the 1–4 pN force range, data were better fitted to a higher persistence length of 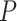 = 21 ± 8 nm. The deviations of the A-tracts data from Equation (7) are hardly surprising, since the purely entropic WLC model does not contemplate the intrinsically bent character of these sequences. Recall that these deviations were also observed in our AFM measurements, where a naive fit of our data to the WLC yielded low values of the persistence length (Figure 2D), similar to the ones obtained from the MT curves (see Table 1).
= 21 ± 8 nm. The deviations of the A-tracts data from Equation (7) are hardly surprising, since the purely entropic WLC model does not contemplate the intrinsically bent character of these sequences. Recall that these deviations were also observed in our AFM measurements, where a naive fit of our data to the WLC yielded low values of the persistence length (Figure 2D), similar to the ones obtained from the MT curves (see Table 1).
We sought for a better model to describe our MT curves. However, to the best of our knowledge, the only attempt to describe the mechanical response of intrinsically-bent DNA molecules has been recently reported by Tompitak et al. (56) (Supplementary Methods). Nevertheless, their model did not properly describe our data and still the force-extension curve was better captured by the WLC (Supplementary Figure S6). Therefore, in absence of a better model, we decided to use the WLC and indirectly quantify the bent character of the A-tracts molecules from the low value of their persistence length.
It has been argued that A-tracts curvature might be a consequence of the interaction of monovalent ions with the minor groove (57–59). Conversely, other works favor an intrinsic ion-independent bending model as a result of the distinct base-pairing and stacking of AT-rich domains (60,61) and even suggest a loss of curvature with the increase of monovalent salt concentration (62). In order to elucidate the role of monovalent ions on A-tracts bending, we obtained additional force-extension curves at NaCl concentrations of 1, 10 and 500 mM (Supplementary Figure S2) and compared them with control sequences. Importantly, the A-tracts deviations from the WLC, and thus the A-tract curvature, persisted over the entire range of NaCl concentrations tested here (Supplementary Figures S7 and S8). The parameters resulting from fitting the control and A-tracts data to the WLC are presented in Figure 3B, C. The contour lengths obtained were similar for both molecules (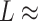 1950 nm) and for all the salt conditions, although slightly larger values were found for A-tracts than for the control at high NaCl concentrations (Figure 3B). In addition, the persistence length of the A-tracts and the control followed a decaying trend with increasing NaCl concentrations, a well-known feature of DNA molecules of arbitrary sequence (35,63) (Figure 3C). In order to further quantify the relation between the persistence length,
1950 nm) and for all the salt conditions, although slightly larger values were found for A-tracts than for the control at high NaCl concentrations (Figure 3B). In addition, the persistence length of the A-tracts and the control followed a decaying trend with increasing NaCl concentrations, a well-known feature of DNA molecules of arbitrary sequence (35,63) (Figure 3C). In order to further quantify the relation between the persistence length, 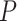 , and the ionic strength,
, and the ionic strength, 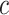 , we analyzed our data using different models based on the Poisson-Boltzmann theory for uniformly charged cylinders (64–66), as recently done in (67). In these models,
, we analyzed our data using different models based on the Poisson-Boltzmann theory for uniformly charged cylinders (64–66), as recently done in (67). In these models, 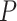 is decomposed into two contributions:
is decomposed into two contributions: 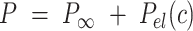 , being
, being 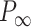 the non-electrostatic contribution to the persistence length, and,
the non-electrostatic contribution to the persistence length, and, 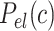 an electrostatic persistence length which originates from the charged nature of the polymer. The best description of our data was provided by the Barrat–Joanny (BJ) model (64), where
an electrostatic persistence length which originates from the charged nature of the polymer. The best description of our data was provided by the Barrat–Joanny (BJ) model (64), where 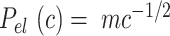 and
and  and
and  are fitting parameters (Figure 3C). When fitting our data to the BJ model, we obtained
are fitting parameters (Figure 3C). When fitting our data to the BJ model, we obtained 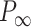 = 40
= 40 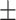 1 nm,
1 nm, 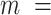 30
30 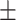 9 nm·mM1/2 for the control molecule; and
9 nm·mM1/2 for the control molecule; and 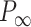 = 11
= 11 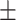 1 nm,
1 nm, 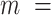 38
38 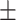 3 nm·mM1/2 for the A-tracts. These values indicate that the difference between the persistence length of the control and A-tracts mostly stems from the non-electrostatic component, which is independent on the ions surrounding the polymer. A similar result was obtained when using the alternative Odjik–Skolnick–Fixman (OSF) model (65,66), where
3 nm·mM1/2 for the A-tracts. These values indicate that the difference between the persistence length of the control and A-tracts mostly stems from the non-electrostatic component, which is independent on the ions surrounding the polymer. A similar result was obtained when using the alternative Odjik–Skolnick–Fixman (OSF) model (65,66), where 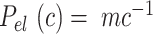 (Figure 3C). Therefore, our results support that the A-tract curvature is intrinsic to the sequence, and that monovalent ions have a similar effect on the mechanical properties of A-tracts and arbitrary DNA molecules.
(Figure 3C). Therefore, our results support that the A-tract curvature is intrinsic to the sequence, and that monovalent ions have a similar effect on the mechanical properties of A-tracts and arbitrary DNA molecules.
A-tracts present a high stretching rigidity
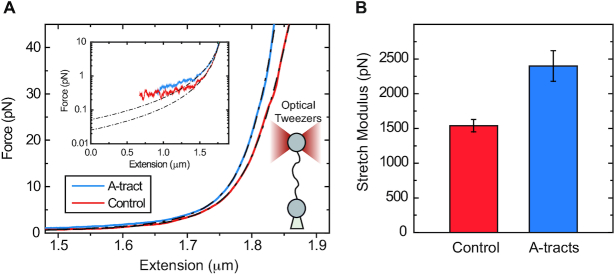
We then ask about the mechanical response of A-tracts in the enthalpic regime. We used optical tweezers (OT) to obtain force-extension curves of the control and the A-tract molecules in a buffer containing 100 mM NaCl (see Materials and Methods section for further details). For the control molecule, we observed a flat overstretching transition at 59 ± 1 pN (N = 5), in agreement with values reported for arbitrary DNA molecules under similar ionic conditions (68–71) (Supplementary Figure S9). However, the overstretching transition of the A-tract molecule started at a lower force of 51.8 ± 0.8 pN (N = 11). In addition, the A-tract overstretching showed a characteristic periodic saw-tooth pattern with six repetitions (Supplementary Figure S9). These repetitions likely correspond to the six copies of the intron, in line with previous OT experiments reporting reproducible sequence-dependent unpeeling of overstretched DNA (72).
To quantify the stretching response of A-tracts molecules, we first fitted force-extension curves in the 1–10 pN range to the inextensible WLC model (Figure 4A, inset) (35):
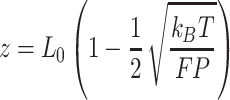 |
(8) |
Figure 4.
Mechanical response of A-tracts to forces above 10 pN. (A) Representative force-extension curves of control and A-tract molecules measured with OT. Dashed lines represent the fits to the eWLC of the control and A-tract molecules in the 10–45 pN range. The values of these particular fits were  1852 nm,
1852 nm,  44 nm,
44 nm, 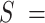 1704 pN and
1704 pN and 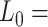 1851 nm,
1851 nm, 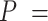 39 nm,
39 nm, 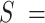 2802 pN for the control and A-tract molecules respectively. Note that the eWLC does not fit well the A-tracts data in the 1–10 pN interval. Inset, the same experimental curves are represented using a logarithmic force scale and showing the fits to the WLC in the 1–10 pN range. The values of these fits were
2802 pN for the control and A-tract molecules respectively. Note that the eWLC does not fit well the A-tracts data in the 1–10 pN interval. Inset, the same experimental curves are represented using a logarithmic force scale and showing the fits to the WLC in the 1–10 pN range. The values of these fits were 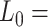 1863 nm,
1863 nm, 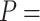 41 nm and
41 nm and 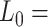 1916 nm,
1916 nm, 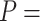 20 nm for the control and A-tracts data respectively. (B) Average stretch modulus (S) of control and A-tracts molecules (see Table 1). Error bars represent the standard error of the mean of the fits. The number of molecules measured were N = 18 and N = 14 for the control and A-tracts, respectively.
20 nm for the control and A-tracts data respectively. (B) Average stretch modulus (S) of control and A-tracts molecules (see Table 1). Error bars represent the standard error of the mean of the fits. The number of molecules measured were N = 18 and N = 14 for the control and A-tracts, respectively.
The values obtained for the control and the A-tracts molecule were 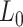 = 1836 ± 3 nm,
= 1836 ± 3 nm, 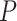 = 42 ± 2 nm and
= 42 ± 2 nm and 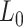 = 1872 ± 16 nm,
= 1872 ± 16 nm, 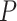 = 20 ± 2 nm, respectively, in agreement with the AFM and MT results (Figure 2D and Table 1).
= 20 ± 2 nm, respectively, in agreement with the AFM and MT results (Figure 2D and Table 1).
With the aim of characterizing the A-tracts mechanical properties in the enthalpic regime (F > 10 pN), we then resorted to the extensible WLC (eWLC) model, which considers that the molecule can be elongated beyond its contour length (63). According to the eWLC, the extension of a DNA molecule depends on the applied force as:
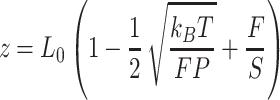 |
(9) |
where 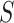 is the stretch modulus and quantifies the enthalpic elongation of the molecule. We used this expression to fit the force–extension curves of the control molecule in the 10–45 pN range. Remarkably, in this range of forces, Equation (9) fits well the experimental data (Figure 4A). We obtained
is the stretch modulus and quantifies the enthalpic elongation of the molecule. We used this expression to fit the force–extension curves of the control molecule in the 10–45 pN range. Remarkably, in this range of forces, Equation (9) fits well the experimental data (Figure 4A). We obtained 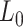 = 1824 ± 3 nm,
= 1824 ± 3 nm, 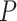 = 47 ± 4 nm and
= 47 ± 4 nm and 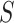 = 1540 ± 90 pN for the control molecule, in agreement with the exhaustive literature on DNA flexibility (35,72,73) (Table 1). The values of the fitting parameters obtained for the A-tracts molecule were
= 1540 ± 90 pN for the control molecule, in agreement with the exhaustive literature on DNA flexibility (35,72,73) (Table 1). The values of the fitting parameters obtained for the A-tracts molecule were 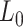 = 1805 ± 8 nm,
= 1805 ± 8 nm, 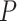 = 44 ± 3 nm, which are similar to those of the control molecule and
= 44 ± 3 nm, which are similar to those of the control molecule and 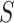 = 2400 ± 220 pN, which is, interestingly, ∼50% higher than the stretch modulus of the control molecule (Figure 4B). Consistently, similar results were obtained at NaCl concentrations of 50 and 500 mM (Supplementary Figures S10, S11 and Table 1) and using different fitting ranges (Supplementary Table S3).
= 2400 ± 220 pN, which is, interestingly, ∼50% higher than the stretch modulus of the control molecule (Figure 4B). Consistently, similar results were obtained at NaCl concentrations of 50 and 500 mM (Supplementary Figures S10, S11 and Table 1) and using different fitting ranges (Supplementary Table S3).
DISCUSSION
A comprehensive picture of the mechanical properties of A-tracts
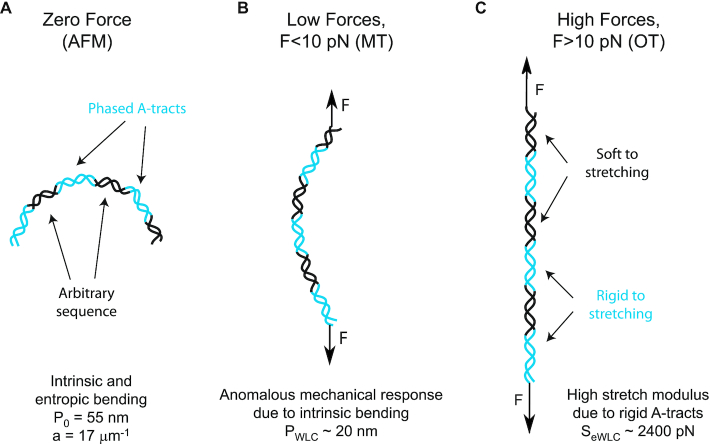
Our results can be brought together to build a comprehensive picture of the multiscale flexibility of A-tracts (Figure 5). At zero force, the in-phase bends of the A-tracts result in a molecule with preferred curvature, as observed in the AFM images (Figure 5A). Such bends are responsible for the measurement of a distinctively small persistence length in these molecules, as found in MT and OT experiments at forces F < 10 pN. We propose that under an external force, these bends are gradually straightened, allowing the molecule to eventually extend to its full contour length. This process of straightening the bends represents an additional source of flexibility that is not captured by the WLC model, which only considers entropic elongation, resulting in a low value of the persistence length (Figure 5B). This would explain the deviations from the WLC model observed in force-extension curves below forces of 10 pN (Figure 3A). According to our data, at forces F > 10 pN, the bends characteristic of A-tracts would have been practically straightened and both the control and the A-tracts molecule show similar values of extension and persistence length (Figures 3A, 4A, 5C and Table 1). Interestingly, a similar idea has been previously proposed in the context of the theoretical kinkable WLC model (74), in which a kinked elastic polymer under force would present a small effective persistence length at low forces and would recover its natural persistence length in the high force limit.
Figure 5.
Schematic representation of the proposed model of the mechanical properties of A-tracts. (A) In the absence of stretching forces, molecules containing phased A-tracts (blue regions) appear largely bent as a consequence of the local structural bends. (B) Forces smaller than 10 pN align and straighten the bends along the pulling coordinate, which results in a significant deviation of the force-extension curves from the WLC model. (C) At forces larger than 10 pN, the bends are fully extended and the local elastic response of A-tracts, is exposed. This force regime unveiled the extraordinary enthalpic rigidity of A-tracts.
At forces F > 10 pN, the A-tracts molecules would be practically straightened allowing us to evaluate the local stretching rigidity of the A-tracts (Figure 5C). We found a remarkably high value for the stretch modulus of A-tracts of ∼2400 pN (Figure 4B), in line with the value (∼2800 pN) reported for a ∼15 bp long poly-(dA:dT) sequence in a recent theoretical work (30) and in agreement with previous simulations that predict a high stretching rigidity for these sequences (27,32). Moreover, this finding supports the high conformational rigidity usually attributed to these sequences in structural studies (18,21,22). A possible explanation for the high A-tract stiffness has been previously proposed in the context of the crookedness model for arbitrary DNA sequences (30). Inside the A-tract the base pair centers are almost perfectly aligned with the helical axis and thus, the molecule can only elongate by unstacking its base pairs, which is energetically expensive. Conversely, the large stretch modulus found here can be regarded as indicative of the particular local structure of the A-tracts that differs from the canonical B-DNA, in the same way as the softer stretching response of dsRNA can be ascribed to its A-form (55,75,76).
Biological Implications
A-tracts appear enriched in the genomes of diverse organisms (1–4) and their particular structure and mechanical properties may play a role on several biological processes including recombination, replication and DNA packaging (9,10). In many of these processes, A-tracts are thought to operate by stabilizing the formation of DNA tertiary structures. For instance, A-tracts have been shown to localize supercoils (77) and might facilitate the formation of loops at regulatory regions (10). In addition, short phased A-tracts might stabilize the highly bent structure adopted by DNA in the nucleosome (7,78) and likely contribute to DNA packaging in the bacterial nucleoid (3). However, somewhat surprising, in other cases A-tracts seem to inhibit bent DNA conformations. Possibly, the most prominent example are poly-(dA:dT) sequences longer than 10 bp, which are thought to resist strong bending and have been shown to significantly destabilize nucleosomes (5,79).
Based on our results, we propose an explanation for this apparent contradiction on A-tracts flexibility, with the aim to achieve a better understanding of the biological function of these sequences. We have shown that phased A-tracts greatly bend the DNA; however, the tracts themselves appear rigid at high forces. This finding suggests that the relative magnitude of these two effects – intrinsic bending and A-tract rigidity – could be modulated by tuning the length and distribution of the A-tracts. In-phase A-tracts shorter than 10 bp would amplify the intrinsic bending, whereas an individual A-tract longer than ∼10 bp would greatly stiffen the DNA. The former should then be involved in bent DNA conformations, such as in supercoils or nucleosomes; whereas the latter would be preferred for rigid sequences that preclude strong distortions in the DNA. This idea is consistent with previous studies showing that short, phased A-tracts are enriched in nucleosome positioning sequences, whereas individual, long A-tracts are associated to nucleosome depleted regions (6,7,77,78,80).
Furthermore, the considerations above raise the question of which of the DNA mechanical properties are interrogated during nucleosome assembly. In particular, if the mechanical properties of poly-(dA:dT) sequences are responsible of their nucleosome-depleting character, one would naively expect a high bending stiffness of these sequences. On the contrary, what we found is that our A-tracts, which are rich in poly-(dA:dT) sequences (Figure 1), are stiff in terms of stretching, but not in terms of bending. This finding is in line with a recent study reporting that a nucleosome-repelling poly-(dA:dT) rich sequence was highly flexible in the context of DNA looping (29). Therefore, we propose that stretching, which reflects a short-scale deformation (30), could play a more relevant role in nucleosome stabilization than the WLC bendability characteristic of long distances of up to several hundreds of nanometers. A similar idea has been proposed in simulation studies (27,30). The high positive charge of the histones could well induce tight bends in the DNA. However, the precise adaptation of the DNA molecule to the shape imposed by the histones relies on very particular local motions of the DNA (27,81,82). A high stretch modulus might preclude these local motions. The hypothesis that bending is not determinant for nucleosome stabilization is supported by the structure of a nucleosome core particle containing a 16 bp-long poly-(dA:dT). This tract is able to bend, but it adopts a distorted configuration that ultimately destabilizes the nucleosome (83). Interestingly, CpG islands, another well-known example of nucleosome destabilizing sequence (84), have also been reported to show a large stretch modulus, in this case of ∼1800 pN (85). Finally, in addition to its role in nucleosome positioning, A-tract rigidity would mechanically stabilize the structural features of these sequences, which constitute a recognition mechanism in DNA–protein interactions (7,15).
In summary, we have investigated the mechanical properties of A-tracts at the single-molecule level using atomic force microscopy (AFM), magnetic tweezers (MT) and optical tweezers (OT). Our AFM measurements reveal the intrinsic curvature of these sequences, as manifested by the deviation of their mechanical properties from the WLC model. We hence used a variation of this model that accounts for polymers with a preferred curvature. This model described our AFM experimental data with exceptional accuracy, and allowed us to quantify the intrinsic and entropic bending of these molecules. In addition, we employed MT and OT to characterize the response of A-tracts under the action of an external force. At low forces the mechanical response of A-tracts is described by a persistence length of ∼20 nm, a hallmark of bent DNA. This reduction of the persistence length of A-tracts was preserved for a wide range of NaCl concentrations, supporting that bending of A-tracts does not rely on the interaction with ions more than bending of the control. Interestingly, OT experiments revealed a ∼1.5-fold increase in the stretching modulus compared to random sequence DNAs. This exceptional stretching stiffness of A-tracts likely reflects the unusual local rigidity of these sequences which has been linked with their efficiency in nucleosome depletion. Our results reconcile contradictory views on A-tracts flexibility and stress the need of appropriate models and techniques to disentangle all the different mechanical deformations that may be involved across wide length scales at different mechanical forces. From a broader perspective, our comprehensive study on the mechanical properties of A-tracts might shed light on the intricate relation between sequence dependent flexibility and function of the double helix.
Supplementary Material
ACKNOWLEDGEMENTS
The authors acknowledge the computer resources, technical expertise and assistance provided by the Red Española de Supercomputacion at the Minotauro Supercomputer (BSC, Barcelona). We thank Andrew Fire (Stanford University, USA) and Ralf Seidel (University of Leipzig, Germany) for providing us biological material required for the fabrication of the DNA molecules.
SUPPLEMENTARY DATA
Supplementary Data are available at NAR Online.
FUNDING
Spanish Ministry of Economy and Competitiveness [CEX2018-000805-M to R.P., MAT2017-83273-R (AEI/FEDER, UE) to R.P., BFU2017-83794-P (AEI/FEDER, UE) to F.M.-H., PGC2018-099341-B-I00 to B.I.]; Comunidad de Madrid [NanoMagCOST P2018 INMT-4321 to B.I., Tec4Bio – S2018/NMT-4443, NanoBioCancer – Y2018/BIO-4747 to F.M.-H.]; F.M.-H. acknowledges support from European Research Council (ERC) under the European Union Horizon 2020 research and innovation [681299]; J.G.V. acknowledges funding from a Marie Sklodowska Curie Fellowship [DLV-795286] within the Horizons 2020 framework; Alberto M.-G. acknowledges support from the International PhD Program of ‘La Caixa-Severo Ochoa’ as a recipient of a PhD fellowship; Alejandro M.-G. acknowledges support from the Competitiveness and Industry Ministry as a recipient of a FPI fellowship [BES-2015-071244]. Funding for open access charge: European Research Council; Spanish Ministry of Economy and Competitiveness.
Conflict of interest statement. None declared.
REFERENCES
- 1. Dechering K.J., Cuelenaere K., Konings R.N., Leunissen J.A.. Distinct frequency-distributions of homopolymeric DNA tracts in different genomes. Nucleic Acids Res. 1998; 26:4056–4062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Behe M.J. An overabundance of long oligopurine tracts occurs in the genome of simple and complex eukaryotes. Nucleic Acids Res. 1995; 23:689–695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Tolstorukov M.Y., Virnik K.M., Adhya S., Zhurkin V.B.. A-tract clusters may facilitate DNA packaging in bacterial nucleoid. Nucleic Acids Res. 2005; 33:3907–3918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Fire A., Alcazar R., Tan F.. Unusual DNA structures associated with germline genetic activity in Caenorhabditis elegans. Genetics. 2006; 173:1259–1273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Segal E., Widom J.. Poly(dA:dT) tracts: major determinants of nucleosome organization. Curr. Opin. Struct. Biol. 2009; 19:65–71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Kaplan N., Moore I.K., Fondufe-Mittendorf Y., Gossett A.J., Tillo D., Field Y., LeProust E.M., Hughes T.R., Lieb J.D., Widom J. et al.. The DNA-encoded nucleosome organization of a eukaryotic genome. Nature. 2009; 458:362–366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Rohs R., West S.M., Sosinsky A., Liu P., Mann R.S., Honig B.. The role of DNA shape in protein-DNA recognition. Nature. 2009; 461:1248–1253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Raveh-Sadka T., Levo M., Shabi U., Shany B., Keren L., Lotan-Pompan M., Zeevi D., Sharon E., Weinberger A., Segal E.. Manipulating nucleosome disfavoring sequences allows fine-tune regulation of gene expression in yeast. Nat. Genet. 2012; 44:743–750. [DOI] [PubMed] [Google Scholar]
- 9. Hagerman P.J. Sequence-directed curvature of DNA. Annu. Rev. Biochem. 1990; 59:755–781. [DOI] [PubMed] [Google Scholar]
- 10. Haran T.E., Mohanty U.. The unique structure of A-tracts and intrinsic DNA bending. Q. Rev. Biophys. 2009; 42:41–81. [DOI] [PubMed] [Google Scholar]
- 11. Tubbs A., Sridharan S., van Wietmarschen N., Maman Y., Callen E., Stanlie A., Wu W., Wu X., Day A., Wong N. et al.. Dual roles of Poly(dA:dT) tracts in replication initiation and fork collapse. Cell. 2018; 174:1127–1142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Chiu Y.H., Macmillan J.B., Chen Z.J.. RNA polymerase III detects cytosolic DNA and induces type I interferons through the RIG-I pathway. Cell. 2009; 138:576–591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Ablasser A., Bauernfeind F., Hartmann G., Latz E., Fitzgerald K.A., Hornung V.. RIG-I-dependent sensing of poly(dA:dT) through the induction of an RNA polymerase III-transcribed RNA intermediate. Nat. Immunol. 2009; 10:1065–1072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Frokjaer-Jensen C., Jain N., Hansen L., Davis M.W., Li Y., Zhao D., Rebora K., Millet J.R.M., Liu X., Kim S.K. et al.. An Abundant Class of Non-coding DNA Can Prevent Stochastic Gene Silencing in the C. elegans Germline. Cell. 2016; 166:343–357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Rohs R., Jin X., West S.M., Joshi R., Honig B., Mann R.S.. Origins of specificity in protein-DNA recognition. Annu. Rev. Biochem. 2010; 79:233–269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Koo H.S., Wu H.M., Crothers D.M.. DNA bending at adenine. thymine tracts. Nature. 1986; 320:501–506. [DOI] [PubMed] [Google Scholar]
- 17. Stellwagen E., Dong Q., Stellwagen N.C.. Flanking A.T basepairs destabilize the B(*) conformation of DNA A-tracts. Biophys. J. 2015; 108:2291–2299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Nelson H.C., Finch J.T., Luisi B.F., Klug A.. The structure of an oligo(dA).oligo(dT) tract and its biological implications. Nature. 1987; 330:221–226. [DOI] [PubMed] [Google Scholar]
- 19. Ulanovsky L.E., Trifonov E.N.. Estimation of wedge components in curved DNA. Nature. 1987; 326:720–722. [DOI] [PubMed] [Google Scholar]
- 20. Bolshoy A., McNamara P., Harrington R.E., Trifonov E.N.. Curved DNA without A-A: experimental estimation of all 16 DNA wedge angles. Proc. Natl. Acad. Sci. USA. 1991; 88:2312–2316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. DiGabriele A.D., Steitz T.A.. A DNA dodecamer containing an adenine tract crystallizes in a unique lattice and exhibits a new bend. J. Mol. Biol. 1993; 231:1024–1039. [DOI] [PubMed] [Google Scholar]
- 22. DiGabriele A.D., Sanderson M.R., Steitz T.A.. Crystal lattice packing is important in determining the bend of a DNA dodecamer containing an adenine tract. Proc. Natl. Acad. Sci. U.S.A. 1989; 86:1816–1820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Zhang Y., Xi Z., Hegde R.S., Shakked Z., Crothers D.M.. Predicting indirect readout effects in protein-DNA interactions. Proc. Natl. Acad. Sci. U.S.A. 2004; 101:8337–8341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Vafabakhsh R., Ha T.. Extreme bendability of DNA less than 100 base pairs long revealed by single-molecule cyclization. Science. 2012; 337:1097–1101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Rivetti C., Walker C., Bustamante C.. Polymer chain statistics and conformational analysis of DNA molecules with bends or sections of different flexibility. J. Mol. Biol. 1998; 280:41–59. [DOI] [PubMed] [Google Scholar]
- 26. Brunet A., Chevalier S., Destainville N., Manghi M., Rousseau P., Salhi M., Salome L., Tardin C.. Probing a label-free local bend in DNA by single molecule tethered particle motion. Nucleic Acids Res. 2015; 43:e72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Drsata T., Spackova N., Jurecka P., Zgarbova M., Sponer J., Lankas F.. Mechanical properties of symmetric and asymmetric DNA A-tracts: implications for looping and nucleosome positioning. Nucleic Acids Res. 2014; 42:7383–7394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Hogan M., LeGrange J., Austin B.. Dependence of DNA helix flexibility on base composition. Nature. 1983; 304:752–754. [DOI] [PubMed] [Google Scholar]
- 29. Johnson S., Chen Y.J., Phillips R.. Poly(dA:dT)-rich DNAs are highly flexible in the context of DNA looping. PLoS One. 2013; 8:e75799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Marin-Gonzalez A., Vilhena J.G., Moreno-Herrero F., Perez R.. DNA Crookedness Regulates DNA Mechanical Properties at Short Length Scales. Phys. Rev. Lett. 2019; 122:048102. [DOI] [PubMed] [Google Scholar]
- 31. Lankas F., Cheatham T.E. 3rd, Spackova N., Hobza P., Langowski J., Sponer J.. Critical effect of the N2 amino group on structure, dynamics, and elasticity of DNA polypurine tracts. Biophys. J. 2002; 82:2592–2609. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Lankas F., Sponer J., Hobza P., Langowski J.. Sequence-dependent elastic properties of DNA. J. Mol. Biol. 2000; 299:695–709. [DOI] [PubMed] [Google Scholar]
- 33. Camunas-Soler J., Frutos S., Bizarro C.V., de Lorenzo S., Fuentes-Perez M.E., Ramsch R., Vilchez S., Solans C., Moreno-Herrero F., Albericio F. et al.. Electrostatic binding and hydrophobic collapse of peptide-nucleic acid aggregates quantified using force spectroscopy. ACS Nano. 2013; 7:5102–5113. [DOI] [PubMed] [Google Scholar]
- 34. Moreno-Herrero F., Seidel R., Johnson S.M., Fire A., Dekker N.H.. Structural analysis of hyperperiodic DNA from Caenorhabditis elegans. Nucleic Acids Res. 2006; 34:3057–3066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Herrero-Galan E., Fuentes-Perez M.E., Carrasco C., Valpuesta J.M., Carrascosa J.L., Moreno-Herrero F., Arias-Gonzalez J.R.. Mechanical identities of RNA and DNA double helices unveiled at the single-molecule level. J. Am. Chem. Soc. 2013; 135:122–131. [DOI] [PubMed] [Google Scholar]
- 36. Heenan P.R., Perkins T.T.. Imaging DNA equilibrated onto Mica in liquid using biochemically relevant deposition conditions. ACS Nano. 2019; 13:4220–4229. [DOI] [PubMed] [Google Scholar]
- 37. Ares P., Fuentes-Perez M.E., Herrero-Galan E., Valpuesta J.M., Gil A., Gomez-Herrero J., Moreno-Herrero F.. High resolution atomic force microscopy of double-stranded RNA. Nanoscale. 2016; 8:11818–11826. [DOI] [PubMed] [Google Scholar]
- 38. Horcas I., Fernandez R., Gomez-Rodriguez J.M., Colchero J., Gomez-Herrero J., Baro A.M.. WSXM: a software for scanning probe microscopy and a tool for nanotechnology. Rev. Sci. Instrum. 2007; 78:013705. [DOI] [PubMed] [Google Scholar]
- 39. Gimeno A., Ares P., Horcas I., Gil A., Gomez-Rodriguez J.M., Colchero J., Gomez-Herrero J.. ‘Flatten plus’: a recent implementation in WSxM for biological research. Bioinformatics. 2015; 31:2918–2920. [DOI] [PubMed] [Google Scholar]
- 40. Wiggins P.A., van der Heijden T., Moreno-Herrero F., Spakowitz A., Phillips R., Widom J., Dekker C., Nelson P.C.. High flexibility of DNA on short length scales probed by atomic force microscopy. Nat. Nanotechnol. 2006; 1:137–141. [DOI] [PubMed] [Google Scholar]
- 41. Carrasco C., Gilhooly N.S., Dillingham M.S., Moreno-Herrero F.. On the mechanism of recombination hotspot scanning during double-stranded DNA break resection. Proc. Natl. Acad. Sci. U.S.A. 2013; 110:E2562–E2571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Pastrana C.L., Carrasco C., Akhtar P., Leuba S.H., Khan S.A., Moreno-Herrero F.. Force and twist dependence of RepC nicking activity on torsionally-constrained DNA molecules. Nucleic Acids Res. 2016; 44:8885–8896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Madariaga-Marcos J., Hormeno S., Pastrana C.L., Fisher G.L.M., Dillingham M.S., Moreno-Herrero F.. Force determination in lateral magnetic tweezers combined with TIRF microscopy. Nanoscale. 2018; 10:4579–4590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Klaue D., Seidel R.. Torsional stiffness of single superparamagnetic microspheres in an external magnetic field. Phys. Rev. Lett. 2009; 102:028302. [DOI] [PubMed] [Google Scholar]
- 45. Smith S.B., Cui Y., Bustamante C.. Optical-trap force transducer that operates by direct measurement of light momentum. Methods Enzymol. 2003; 361:134–162. [DOI] [PubMed] [Google Scholar]
- 46. Rivetti C., Guthold M., Bustamante C.. Scanning force microscopy of DNA deposited onto mica: equilibration versus kinetic trapping studied by statistical polymer chain analysis. J. Mol. Biol. 1996; 264:919–932. [DOI] [PubMed] [Google Scholar]
- 47. Bloomfield V.A., Crothers D.M., Tinoco I.. Nucleic Acids: Structures, Properties and functions. 2000; Sausalito, California: University Science Books. [Google Scholar]
- 48. Mathew-Fenn R.S., Das R., Harbury P.A.. Remeasuring the double helix. Science. 2008; 322:446–449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Lifshitz E.M., Kosevich A.M., Pitaevskii L.P. Butterworth-Heinemann . Theory of Elasticity (Third Edition). 1986; Oxford: 38–86. [Google Scholar]
- 50. Pataskar A., Vanderlinden W., Emmerig J., Singh A., Lipfert J., Tiwari V.K.. Deciphering the gene regulatory landscape encoded in DNA biophysical features. iScience. 2019; 21:638–649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Rezaei N., Lyons A., Forde N.R.. Environmentally controlled curvature of single collagen proteins. Biophys. J. 2018; 115:1457–1469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52. Koo H.S., Crothers D.M.. Calibration of DNA curvature and a unified description of sequence-directed bending. Proc. Natl. Acad. Sci. USA. 1988; 85:1763–1767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Podtelezhnikov A.A., Mao C., Seeman N.C., Vologodskii A.. Multimerization-cyclization of DNA fragments as a method of conformational analysis. Biophys. J. 2000; 79:2692–2704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54. Bouchiat C., Wang M.D., Allemand J., Strick T., Block S.M., Croquette V.. Estimating the persistence length of a worm-like chain molecule from force-extension measurements. Biophys. J. 1999; 76:409–413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Lipfert J., Skinner G.M., Keegstra J.M., Hensgens T., Jager T., Dulin D., Kober M., Yu Z., Donkers S.P., Chou F.C. et al.. Double-stranded RNA under force and torque: similarities to and striking differences from double-stranded DNA. Proc. Natl. Acad. Sci. U.S.A. 2014; 111:15408–15413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56. Tompitak M., Schiessel H., Barkema G.T.. Force responses of strongly intrinsically curved DNA helices deviate from worm-like chain predictions. EPL (Europhys. Lett.). 2016; 116:68005. [Google Scholar]
- 57. Shui X., McFail-Isom L., Hu G.G., Williams L.D.. The B-DNA dodecamer at high resolution reveals a spine of water on sodium. Biochemistry. 1998; 37:8341–8355. [DOI] [PubMed] [Google Scholar]
- 58. Shui X., Sines C.C., McFail-Isom L., VanDerveer D., Williams L.D.. Structure of the potassium form of CGCGAATTCGCG: DNA deformation by electrostatic collapse around inorganic cations. Biochemistry. 1998; 37:16877–16887. [DOI] [PubMed] [Google Scholar]
- 59. Hud N.V., Plavec J.. A unified model for the origin of DNA sequence-directed curvature. Biopolymers. 2003; 69:144–158. [DOI] [PubMed] [Google Scholar]
- 60. Toth K., Sauermann V., Langowski J.. DNA curvature in solution measured by fluorescence resonance energy transfer. Biochemistry. 1998; 37:8173–8179. [DOI] [PubMed] [Google Scholar]
- 61. Levene S.D., Wu H.M., Crothers D.M.. Bending and flexibility of kinetoplast DNA. Biochemistry. 1986; 25:3988–3995. [DOI] [PubMed] [Google Scholar]
- 62. Stellwagen E., Peters J.P., Maher L.J. 3rd, Stellwagen N.C.. DNA A-tracts are not curved in solutions containing high concentrations of monovalent cations. Biochemistry. 2013; 52:4138–4148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63. Baumann C.G., Smith S.B., Bloomfield V.A., Bustamante C.. Ionic effects on the elasticity of single DNA molecules. Proc. Natl. Acad. Sci. U.S.A. 1997; 94:6185–6190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64. Barrat J.L., Joanny J.F.. Persistence length of polyelectrolyte chains. Europhys. Lett. (EPL). 1993; 24:333–338. [Google Scholar]
- 65. Odijk T. Polyelectrolytes near the rod limit. J. Polym. Sci.: Polym. Phys. Ed. 1977; 15:477–483. [Google Scholar]
- 66. Skolnick J., Fixman M.. Electrostatic persistence length of a wormlike polyelectrolyte. Macromolecules. 1977; 10:944–948. [Google Scholar]
- 67. Guilbaud S., Salome L., Destainville N., Manghi M., Tardin C.. Dependence of DNA Persistence length on ionic strength and ion type. Phys. Rev. Lett. 2019; 122:028102. [DOI] [PubMed] [Google Scholar]
- 68. Bustamante C., Bryant Z., Smith S.B.. Ten years of tension: single-molecule DNA mechanics. Nature. 2003; 421:423–427. [DOI] [PubMed] [Google Scholar]
- 69. Smith S.B., Cui Y., Bustamante C.. Overstretching B-DNA: the elastic response of individual double-stranded and single-stranded DNA molecules. Science. 1996; 271:795–799. [DOI] [PubMed] [Google Scholar]
- 70. Cluzel P., Lebrun A., Heller C., Lavery R., Viovy J.L., Chatenay D., Caron F.. DNA: an extensible molecule. Science. 1996; 271:792–794. [DOI] [PubMed] [Google Scholar]
- 71. Wenner J.R., Williams M.C., Rouzina I., Bloomfield V.A.. Salt dependence of the elasticity and overstretching transition of single DNA molecules. Biophys. J. 2002; 82:3160–3169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72. Gross P., Laurens N., Oddershede L.B., Bockelmann U., Peterman E.J.G., Wuite G.J.L.. Quantifying how DNA stretches, melts and changes twist under tension. Nat. Phys. 2011; 7:731. [Google Scholar]
- 73. Broekmans O.D., King G.A., Stephens G.J., Wuite G.J.. DNA twist stability changes with Magnesium(2+) concentration. Phys. Rev. Lett. 2016; 116:258102. [DOI] [PubMed] [Google Scholar]
- 74. Wiggins P.A., Phillips R., Nelson P.C.. Exact theory of kinkable elastic polymers. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2005; 71:021909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75. Chou F.C., Lipfert J., Das R.. Blind predictions of DNA and RNA tweezers experiments with force and torque. PLoS Comput. Biol. 2014; 10:e1003756. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76. Marin-Gonzalez A., Vilhena J.G., Perez R., Moreno-Herrero F.. Understanding the mechanical response of double-stranded DNA and RNA under constant stretching forces using all-atom molecular dynamics. Proc. Natl. Acad. Sci. U.S.A. 2017; 114:7049–7054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77. Kim S.H., Ganji M., Kim E., van der Torre J., Abbondanzieri E., Dekker C.. DNA sequence encodes the position of DNA supercoils. eLife. 2018; 7:e36557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78. Satchwell S.C., Drew H.R., Travers A.A.. Sequence periodicities in chicken nucleosome core DNA. J. Mol. Biol. 1986; 191:659–675. [DOI] [PubMed] [Google Scholar]
- 79. Field Y., Kaplan N., Fondufe-Mittendorf Y., Moore I.K., Sharon E., Lubling Y., Widom J., Segal E.. Distinct modes of regulation by chromatin encoded through nucleosome positioning signals. PLoS Comput. Biol. 2008; 4:e1000216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80. Segal E., Fondufe-Mittendorf Y., Chen L., Thastrom A., Field Y., Moore I.K., Wang J.P., Widom J.. A genomic code for nucleosome positioning. Nature. 2006; 442:772–778. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81. Richmond T.J., Davey C.A.. The structure of DNA in the nucleosome core. Nature. 2003; 423:145–150. [DOI] [PubMed] [Google Scholar]
- 82. Tolstorukov M.Y., Colasanti A.V., McCandlish D.M., Olson W.K., Zhurkin V.B.. A novel roll-and-slide mechanism of DNA folding in chromatin: implications for nucleosome positioning. J. Mol. Biol. 2007; 371:725–738. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83. Bao Y., White C.L., Luger K.. Nucleosome core particles containing a poly(dA.dT) sequence element exhibit a locally distorted DNA structure. J. Mol. Biol. 2006; 361:617–624. [DOI] [PubMed] [Google Scholar]
- 84. Deaton A.M., Bird A.. CpG islands and the regulation of transcription. Genes Dev. 2011; 25:1010–1022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85. Pongor C.I., Bianco P., Ferenczy G., Kellermayer R., Kellermayer M.. Optical Trapping nanometry of hypermethylated CPG-Island DNA. Biophys. J. 2017; 112:512–522. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.