Optimal policies for control of the novel coronavirus disease (COVID-19) outbreak

Highlights

• •Investigation of a mathematical model of the novel coronavirus
• •Pioneer research on policies regarding COVID-19
• •A multi-objective genetic algorithm which proposes strategies to achieve high-quality schedules by adjusting various factors
• •The first research that proposes policies for COVID-19 by considering its economic consequences

Abstract

Understanding the early transmission dynamics of diseases and estimating the effectiveness of control policies play inevitable roles in the prevention of epidemic diseases. To this end, this paper is concerned with the design of optimal control strategies for the novel coronavirus disease (COVID-19). A mathematical model of severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) transmission based on Wuhan's data is considered. To solve the problem effectively and efficiently, a multi-objective genetic algorithm is proposed to achieve high-quality schedules for various factors including contact rate and transition rate of symptomatic infected individuals to the quarantined infected class. By changing these factors, two optimal policies are successfully designed. This study has two main scientific contributions that are: (1) This is pioneer research that proposes policies regarding COVID-19, (2) This is also the first research that addresses COVID-19 and considers its economic consequences through a multi-objective evolutionary algorithm. Numerical simulations conspicuously demonstrate that by applying the proposed optimal policies, governments could find useful and practical ways for control of the disease.

1. Introduction

Coronaviruses are a family of enveloped viruses with a single-stranded RNA, positive-sense, and viral particles resembling a crown. In December 2019, an outbreak of novel coronavirus disease emerged in Wuhan, China, and has rapidly spread to other countries [1]. By April 18th, the new virus has infected more than 2,200,000 people and killed at least 156,000. Now, there exist no anti-viral treatments or vaccines officially approved for the management or prevention of COVID-19. This way, unfortunately, the outbreaks are still spreading at an alarming rate [2].

Over the past several years, numerous studies were carried out to model various disease dynamics, including human immunodeficiency virus (HIV), Tuberculosis, Malaria, and influenza [3], [4], [5], [6]. Mathematical modeling of diseases enables long and short-term prediction of disease incidence. Thus, it provides a profound understanding of the system for disease control and prevention [7,8]. So far, theoretical epidemiology has provided remarkable technical and conceptual developments. Not only does this field of study aim to anticipate and analyze the spread of various diseases, but also it aims to control diseases as effectively as possible [9].

Identification of various factors that affect the spreading rate of the novel coronavirus dramatically helps to control the outbreak. This way, from the advent of this disease, several studies have been done to provide accurate information for implementing disease outbreak responses. Tang et al. [10] used ordinary differential equations and Markov Chain Monte Carlo methods (MCMC) to estimate the transmission risk and implication for public health interventions. Li et al. [11] analyzed data in Wuhan and determined the epidemiologic, and they found out that the mean incubation period was 5.2 days. By taking to account the impact of the variations in the disease, Zhao et al. [12] modeled the epidemic curve of COVID-19 cases, in mainland China from January 10 to January 24, 2020, reporting. A Bats-Hosts-Reservoir-People transmission network model has been developed by Chen et al. [13,14] to simulate the potential transmission from the infectious sources to human. Wang et al. [15] formulated a complex network model, and then based on their model, they analyzed the possible time node and the risk impact of resumption on the secondary outbreak in Wuhan and surrounding areas. Roosa et al. [16] have used various models to predict the number of confirmed cases in the coming days in Hubei province.

It is undeniable that after a while, due to the pressure of economic operation and the needs of people's normal life, some countries will leave primary responses of epidemic prevention and take new control strategies [14]. In this condition, some crucial questions need to be answered meticulously and promptly. When can citizens return back to their normal life? Does changing the emergency response mean that people can relieve themselves from self-production? What policies should governments pursue to prevent outbreaks as well as economic collapse?

The current study aims to solve the abovementioned questions. To the best of the authors' knowledge, no studies have been done to design an optimal controller for the novel coronavirus. To this end, a dynamical model of the novel coronavirus is used to predict the growth of the disease in different conditions. Then, using a multi-objective genetic algorithm, we try to address these questions. The effects of different policies are evaluated. Actually, through a multi-objective genetic algorithm, we find optimal solutions that governments can use as their strategies regarding the novel COVID-19.

2. Mathematical modeling and methods

In this study, a deterministic “Susceptible-Exposed-Infectious-Recovered” compartmental model is investigated. Also, the model considers appropriate compartments relevant to interventions such as isolation, quarantine, and treatment. This model is based on the epidemiological status of the individuals, clinical progression of the disease, and intervention measures, which has been proposed by Tang et al. [10]. They have parametrized the model by considering data obtained for the confirmed cases of COVID-19 in China and estimated the disease transmission using the Markov Chain Monte Carlo (MCMC) method.

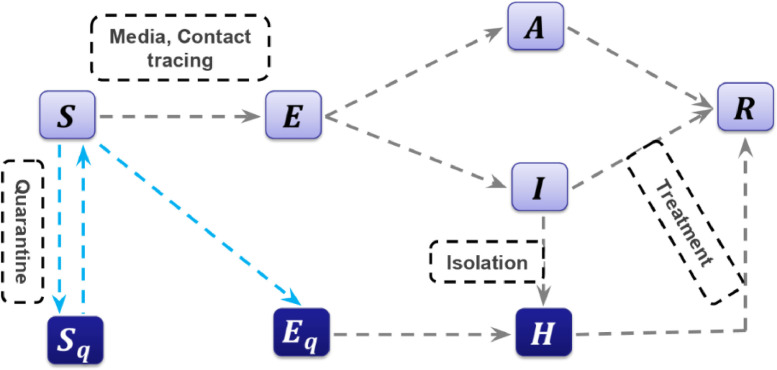
The structure of the investigated model with quarantine and isolation is illustrated in Fig. 1 . The populations are classified into eight compartments; Susceptible people (S), exposed people (E), asymptomatic infected people (pre-symptomatic) (A), infected people with symptoms (I), hospitalized (H), and recovered (R) people. Also, in this model, quarantined susceptible people and isolated, exposed people are represented by S_q and E_q, respectively [10].

$$\begin{array}{c}{\displaystyle \frac{d}{\mathit{dt}}S=-(\beta c+\mathit{cq}(1-\beta ))S(I+\theta A)+\lambda s_q}\hfill \\ {\displaystyle \frac{d}{\mathit{dt}}E=-\beta c(1-q)S(I+\theta A)+\sigma E}\hfill \\ {\displaystyle \frac{d}{\mathit{dt}}I=\sigma \varrho E-({\delta }_I+\alpha +{\gamma }_I)I}\hfill \\ {\displaystyle \frac{d}{\mathit{dt}}A=\sigma (1-\varrho )E-{\gamma }_{A}A}\hfill \\ {\displaystyle \frac{d}{\mathit{dt}}{S}_q=(1-\beta )\mathit{cqS}(I+\theta A)-\lambda S_q}\hfill \\ {\displaystyle \frac{d}{\mathit{dt}}{E}_q=\beta \mathit{cqS}(I+\theta A)-{\delta }_q{E}_q}\hfill \\ {\displaystyle \frac{d}{\mathit{dt}}H={\delta }_{I}I+{\delta }_q{E}_q-(\alpha +{\gamma }_H)H}\hfill \\ {\displaystyle \frac{d}{\mathit{dt}}R={\gamma }_{I}I+{\gamma }_{A}A+{\gamma }_{H}H}\hfill \end{array}$$ (1)

where c is contact rate, β is the probability of transmission per contact, and q is quarantined rate of exposed individuals. Moreover, σ denotes the transition rate of exposed individuals to the infected class. λ indicates the rate at which the quarantined uninfected contacts were released into the wider community. ϱ stands for the probability of having symptoms among infected individuals. α is the disease-induced death rate. δ_I is the transition rate of symptomatic infected individuals to the quarantined infected class. δ_q represents the transition rate of quarantined exposed individuals to the quarantined infected class. Also, γ_I, γ_A, and γ_H denote the recovery rate of infected individuals, asymptomatic infected individuals, and quarantined infected individuals.

Fig. 1.

Diagram of novel coronavirus [10].

With contact tracing, the proportion q of individuals exposed to the virus is quarantined. The quarantined individuals depending on whether they are effectively infected or not, can either move to E_q or S_q . Also, the other proportion ($1-q$), consists of individuals that exposed to the virus and are missed from the contact tracing. Hence, they either move to the exposed people (E) or stay in the susceptible component (S). People who are not quarantined if they are infected, at a rate of $\beta c\left(1-q\right),$ will move to compartment E. The quarantined individuals, if they are infected, move to the compartment E_q at a rate of βcq. In addition, the quarantined individuals who are not infected move to compartment S_q with rate of ($1-\beta )cq$. The contact rate (c) is given by [17]:

$$c=\left(c_0-c_b\right)e^{-r_{1}t}+c_b$$ (2)

where c ₀ denotes the contact rate at the initial time. The final contact rate is represented by c _b. Also, r ₁ indicates the exponential decreasing or increasing rate of the contact rate. Actually, $c\left(0\right)=c_0$ and$\underset{t\to \infty }{lim}c\left(t\right)=c_b,$ . By changing the constant rate, we can measure the effects of self-isolation of all individuals, including susceptible individuals on public health intervention improvement. Although in this study it is assumed that the contacts are decreasing with respect to time, the proposed model could be considered with other policies such as starting with minimum contact rate, and then the contact rate can be considered as increasing function with respect to time.

δ_I(t) is considered to be an increasing function with respect to time; hence, it is considered as follows:

$$\frac{1}{{\delta }_I\left(t\right)}=(\frac{1}{{\delta }_{I0}}-\frac{1}{{\delta }_f})e^{-r_{2}t}+\frac{1}{{\delta }_f}$$ (3)

where δ _I0 is the initial diagnose rate, r ₂ is the exponential decreasing rate, and  δ_If is the fastest diagnose. δ_I(t) is highly dependent on available resources and government efforts. Tables 1 and 2 list the value of parameters and initial condition of the novel coronavirus.

Table 1.

Estimated parameters for COVID-19 in Wuhan, China [10].

Parameter	Estimated mean value	Parameter	Estimated mean value
β	2.1011 × 10−8	δq	0.1259
q	1.8887 × 10−7	γI	0.33029
σ	1/7	γA	0.13978
λ	1/14	γH	0.11624
ϱ	0.86834	α	1.7826 × 10−5

Table 2.

Initial values estimation for COVID-19 in Wuhan, China [17].

Initial values	Value	Initial values	Value
S(0)	10893000	Sq(0)	167000
E(0)	16000	Eq(0)	0
I(0)	2000	H(0)	1000
A(0)	1000	R(0)	2000

2.2. Genetic algorithm

In 1970s John Holland [18] has invented the genetic algorithm. The genetic algorithm employs iterative and stochastic search strategy to find an optimum route. Basically, the genetic algorithm imitates the process of evolution based on Darwin's survival-of-the-fittest strategy. A population of candidate solutions called individuals to an optimization problem is evolved into superior solutions. This way, the population is evaluated, and the best solutions are selected to reproduce and mate to create the next generation. After a number of generations, good traits dominate the population and augment the quality of solutions. Due to genetic algorithm's fascinating features and its strong convergence, up to now, researchers have developed this algorithm and used that to address a wide variety of problems in different fields of study [19,20].

3. Numerical results

A multi-objective approach is used to find optimal decision rules as the Pareto frontier. Since there is a trade-off among all the objectives, the multi-objective approach is the best way to solve such problems. The optimality of Pareto is a suitable sense to specify which policy is prior to other possible solutions. Table 3 represents the configuration of the genetic algorithm.

Table 3.

Genetic algorithm configuration parameters.

Parameter	Value
Crossover fraction	0.8
Population size	70
Selection function	Tournament
Mutation function	Constraint-dependent
Crossover function	Intermediate
Migration direction	Forward
Migration fraction	0.2
Migration interval	20
Stopping criteria	50000

In the simulation results based on reference [17] in the case that there are no optimal policies $c_0=14.781,c_f=$2.9253, $q=1.8887\times 10-7,$ ${\delta }_{I0}=0.13266$ and${\delta }_{If}=2.7367$.

3.1. Strategy A

We can combine cost functions J ₁ and J ₂ with different weights and then use single cost functions to obtain the best solution for our problem. However, such a method would result in a single solution. We aim to consider both epidemy prevention and economic concerns simultaneously, and in this condition, it is injudicious to compose these two different factors. Hence, a multi-objective method is utilized, and the results are presented with a range of Pareto optimal solutions to easily judge the trade-offs and choose one policy for implementation.

In this strategy, three decision variables including c ₀, c_f, and q are considered. The cost functions are selected as follow:

$$\begin{array}{c}{J}_1=\sum E\left(t\right)+A\left(t\right)\hfill \\ J_2=-{\eta }_1\left(c_0+c_f\right)+{\eta }_{2}q\hfill \end{array}$$ (4)

Cost function J ₁ is considered to reduce the accumulated infected people. Also regarding the fact that the economic affairs are highly dependent on the contact rate and the quarantined rate of exposed individuals we have considered cost function J ₂.

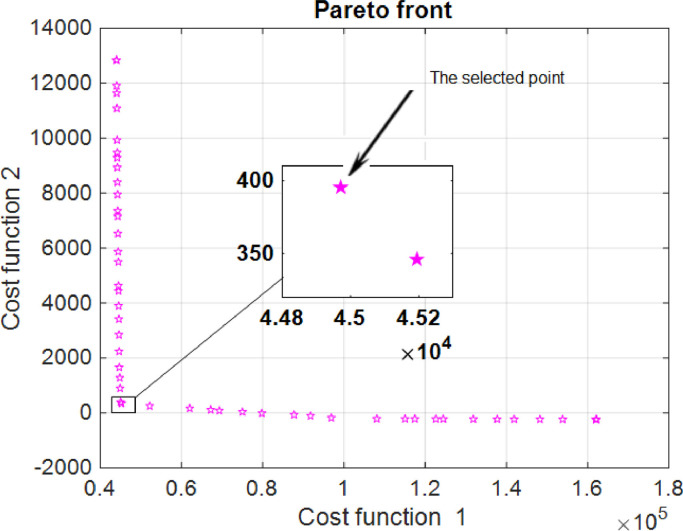
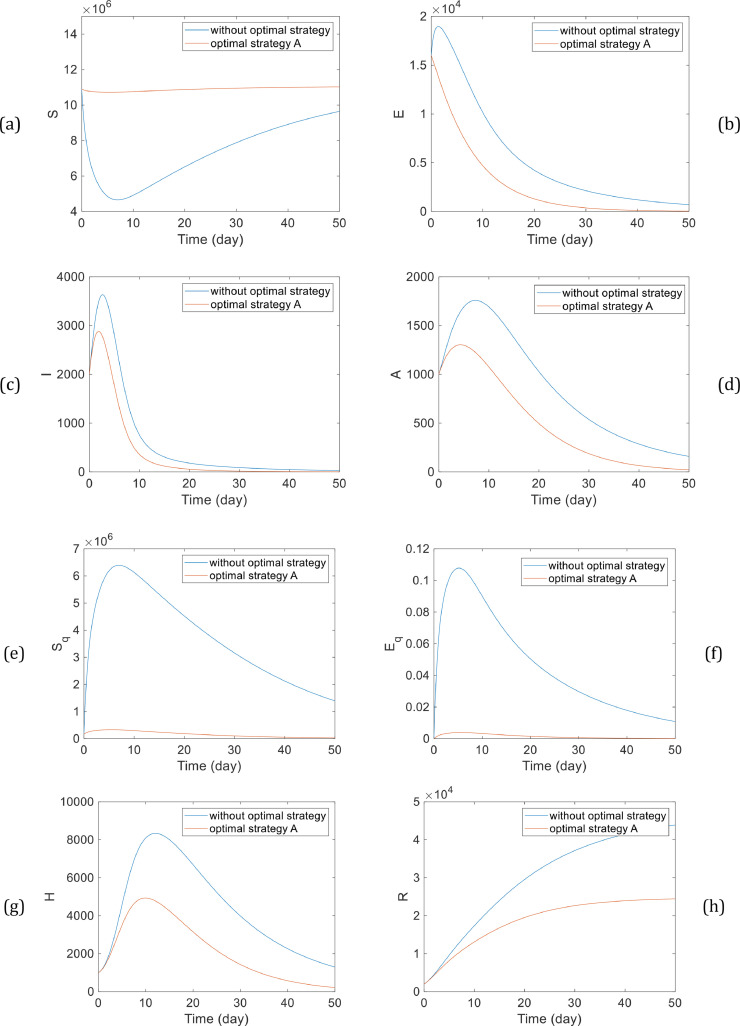
Fig. 2 illustrates the Pareto front obtained from the multi-objective genetic algorithm optimization. Based on Fig. 2, we could choose the optimal controllers, which effectively reduce both cost functions. The number of individuals with strategy A is illustrated in Fig. 3 . As is shown, the maximum number of infected people has decreased compared to the case with no optimal control effort, and the rate of decreasing the population of infectious people is significantly faster. As it is shown in Fig. 3, this strategy dramatically improves the situation and prevent the epidemy.

Fig. 2.

Pareto fronts of cost functions with strategy A.

Fig. 3.

The number of individuals with strategy A, (a) susceptible population (b) exposed population (c) symptomatic infected population (d) asymptomatic infected population (e) quarantined susceptible population (f) quarantined exposed population (g) quarantined infected population (h) recovered population.

In addition, Fig. 3 shows that the number of quarantined infected population has decreased faster than the case when there is no optimal strategy. Also, based on Fig. 3, the maximum number of infected people has declined significantly, and the population has decreased sharper than the time when no optimal strategy is applying to the system. It can be concluded that the contact rate of susceptible people and individuals in the infectious class must decrease by an optimal strategy, and we need to apply contact and travel restrictions.

3.2. Strategy B

In this case, two decision variables including δ _I0 and δ_If are considered in order to minimize the following cost function

$$\begin{array}{c}{J}_1=\sum E\left(t\right)+A\left(t\right)\hfill \\ J_2=\left({\delta }_{I0}+{\delta }_{If}\right)\hfill \end{array}$$ (5)

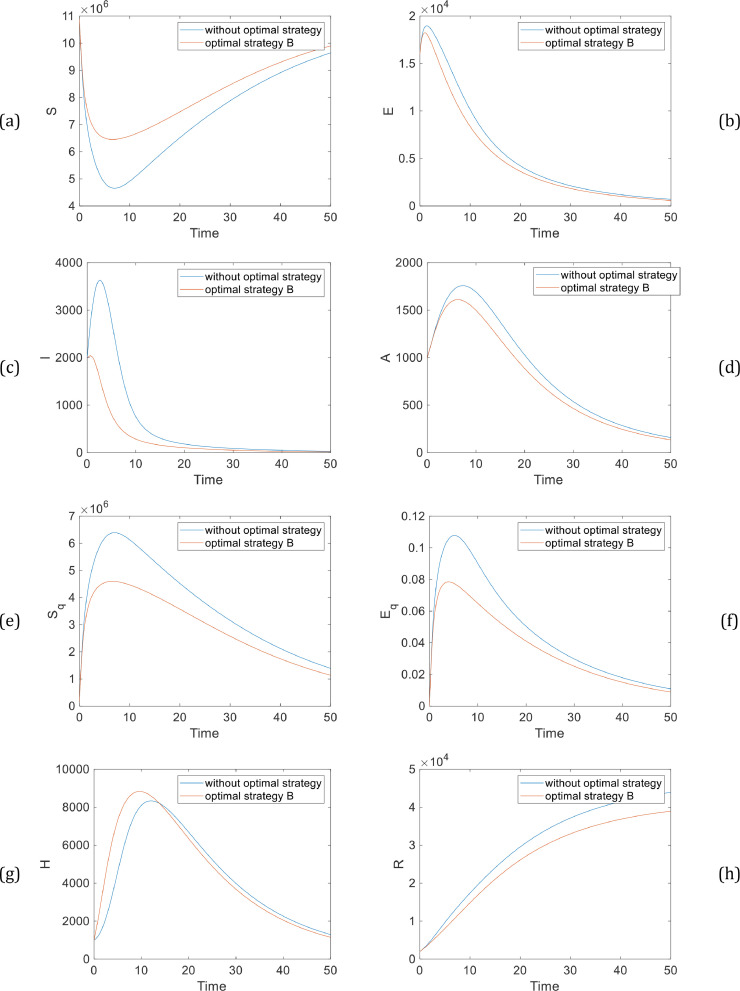
The Pareto front of cost functions in strategy B is illustrated in Fig. 4 . Also, Fig. 5 shows the number of components in strategy B. According to Fig. 5, this optimal strategy can dramatically help to reduce the growth rate of the disease. However, in strategy A, when we set contact restrictions, the population of both symptomatic and asymptomatic will decrease, the results of simulation clearly demonstrate that the population of the symptomatic infected population with strategy B has been plunged more than strategy A. The simulation results show that governments must choose optimal strategies to prevent the disease until the end of the epidemy.

Fig. 4.

Pareto fronts of cost functions with strategy B.

Fig. 5.

The number of individuals with strategy B, (a) susceptible population (b) exposed population (c) symptomatic infected population (d) asymptomatic infected population (e) quarantined susceptible population (f) quarantined exposed population (g) quarantined infected population (h) recovered population.

To recapitulate briefly, we propose two optimal policies to control the disease outbreak. Utilizing the model that has been investigated in this study and parameter estimation methods such as MCMC, at first, governments can estimate the model of the epidemy in their countries. Then, using a multi-objective genetic algorithm, they can set their optimal policies to prevent the epidemy efficiently. Through this method, governments could consider factors such as contact rate and transition rate of symptomatic infected individuals to the quarantined infected class and then they could wisely set their policy to prevent economic collapse and spread of the outbreak, simultaneously.

4. Conclusion

In this study, the model and control policies of the novel coronavirus were investigated. Firstly, the state-space model of the disease has been investigated, and the impact of critical parameters on the epidemy have been described. Then, in order to efficiently design strategies, a multi-objective genetic algorithm was proposed, and through the multi-objective genetic algorithm, optimal policies were designed. Numerical simulations clearly show that considering the control of the spreading of the diseases as an optimization problem can help governments to choose strategies that prevent the disease outbreak as well as economic collapse. This way, this study can provide a reference for the prevention and optimal control strategies in various countries. As a future suggestion, other factors such as the rate at which the quarantined uninfected contacts are released in the societies can be considered as control actions for the prevention of the outbreak.

Declaration of Competing Interest

This statement is to certify that no conflict of interest exits in the submission of this manuscript. Also, the manuscript is approved for publication by all authors. I would like to declare that the work described was an original research that has not been published previously, and not under consideration for publication elsewhere. All the authors listed have approved the manuscript that is enclosed.