Abstract
In the repeatability analysis, when the measurement is the mean value of a parametric map within a region of interest (ROI), the ROI size becomes important as by increasing the size, the measurement will have a smaller variance. This is important in decision-making in prospective clinical studies of brain when the ROI size is variable, e.g., in monitoring the effect of treatment on lesions by quantitative MRI, and in particular when the ROI is small, e.g., in the case of brain lesions in multiple sclerosis. Thus, methods to estimate repeatability measures for arbitrary sizes of ROI are desired. We propose a statistical model of the values of parametric map within the ROI and a method to approximate the model parameters, based on which we estimate a number of repeatability measures including repeatability coefficient, coefficient of variation, and intra-class correlation coefficient for an ROI with an arbitrary size. We also show how this gives an insight into related problems such as spatial smoothing in voxel-wise analysis. Experiments are conducted on simulated data as well as on scan-rescan brain MRI of healthy subjects. The main application of this study is the adjustment of the decision threshold based on the lesion size in treatment monitoring.
Keywords: repeatability coefficient, coefficient of variation, intra-class correlation coefficient, quantitative imaging biomarkers, region of interest
I. Introduction
Knowledge about the accuracy of quantitative brain imaging biomarkers is important in studying the brain tissue function in healthy subjects as well as diagnosis and treatment planning in patients. Repeatability (test-retest reliability) analysis may help us interpret a level of change in a tissue biological parameter as a real biological change or as a measurement error. Conventionally, repeated scans are acquired on a group of subjects and the desired parametric maps are generated. The mean value of the parametric map is then calculated within the desired ROIs. Repeatability may then be evaluated by measures such as repeatability coefficient (RC), coefficient of variation (COV), and intra-class correlation coefficient (ICC). RC provides an estimate for the between-measurement variance so that the difference between two measurements is expected to be between −RC and RC for 95% of subjects. COV represents the extent of variability in relation to the mean of measurements where smaller COV implies higher repeatability. ICC ranges from 0 to 1 and describes how strongly two within-subject measurements resemble each other relative to the variation between subjects.
The repeatability measures will depend on the ROI size as with increasing the ROI size, the mean value within the ROI tends to have a smaller variance. Thus, it is important to compute and report the repeatability measures for the desired ROI sizes. For example, to determine if a real change has occurred in a tissue after therapy, the level of change is compared with a threshold, conventionally the RC value calculated from a repeatability study [1]. As the RC value depends on the ROI size, the threshold needs to be adjusted based on the ROI size.
Evaluation of the effect of ROI size on repeatability becomes particularly important when there is variability in ROI, e.g. in studying tumors [2] [3] [4] [5], and when the ROI is small, e.g., in studying brain lesions in multiple sclerosis [6] [7] [8] [9] [10]. Although it is not the focus of this study, the effect of ROI size also relates to several other problems such as spatial smoothing in voxel-wise analysis as well as applications of arterial input function in dynamic MRI. In voxel-wise analysis, the corresponding voxels of coregistered images are compared [11] [12]. This means the size of ROI under study is essentially one voxel. Spatial smoothing is applied to reduce the effects of mis-coregistration, noise, signal variations, etc. [13]. This also has the effect of increasing the effective ROI size. However, spatial smoothing also results in the loss of spatial information. Therefore, the filter size becomes important [14], which may be optimized experimentally [15] [16] [17] and may be set to the smallest that gives the desired repeatability measures. This will be later discussed for the particular case of voxel-wise analysis for functional diffusion maps when applying average filtering.
Previous studies have experimentally reported improved repeatability for larger ROIs of brain apparent diffusion coefficient (ADC) [18] and brain volume measurements [19]. In this paper, we propose a statistical model of the voxel intensities to approximate three frequently used measures of repeatability, namely RC, COV, and ICC, for a desired ROI size. While the previous works experimentally studied the effect of ROI size on the repeatability measures, here we provide an analytical model to study the same. We conduct experiments on simulated data as well as on parametric maps generated from repeated brain MRI scans of 21 healthy subjects [20]. The main application of this work is treatment monitoring in prospective studies. Although we show how this problem is related to a number of other problems including smoothing in voxel-wise analysis, we do not provide a direct guideline for problems such as optimizing the filter size, as those are out of the scope of this work and require other comprehensive studies. This model, however, could potentially help future efforts of filter design in voxel-wise analysis.
II. MATERIALS AND METHODS
A. Statistical model
Assume the image of the brain is acquired K times for N subjects, the same ROIs are generated, and the mean value of a parametric map across all voxels within the ROI is calculated as a measurement. We propose the following model to represent the measurement for subject i, within voxel j in repetition k.
| (1) |
where μ is the overall voxels mean for the population; τi is the effect of subject i on the measurement; λk is the deviation from the overall mean due to the kth scan; γik the interaction effect between subject i and scan k; βij is the effect of voxel j within the ROI of subject i; and εijk is a random error. Let us assume that the all main and interaction effects except for the voxel effect are random, and normally independently distributed. That is, τi~N(0, ), λk~N(0, ), and γik~N(0, ). Also let us assume that voxel effects βij and random errors εijk are normally distributed with mean of zero and spatially correlated. We also assume that random errors are independent of the effects. As we will explain later, the assumption of normality is not necessary but under its assumption we will be able to obtain more accurate estimation of the repeatability measures.
To take into account the spatial dependence between intensities of the voxels within an ROI, knowing that the spatial dependence decreases with increasing the distance between voxels, we propose to use exponential covariogram model [21]:
| (2) |
where , ρβ, and ηβ are model parameters, and r is the distance between voxels j1 and j2. The choice of exponential model was based on experiments we conducted on the MRI data used in this paper (experiments not presented but described in the Supplementary Material, Section I). Other models may also be used depending on the data, in which case our derived formulas will be still valid (the formulas are independent of the covariogram model, but the parameter estimation method may need minor update depending on the model). Similarly, we use exponential covariogram model with parameters , ρε, and ηε for cov(εij1k, εij2k). The spatial dependence between εijk variables within an ROI is partially caused by coregistration errors.
Suppose that all subjects have the ROI of size M. Then the measurement within an ROI is obtained by
| (3) |
B. Repeatability coefficient
Provided that ROI measurements follow model (3), RC is estimated by , where WMS is the within-subject mean square [1] and is calculated as follows.
| (4) |
We can show that (see Supplementary Material, Section II):
| (5) |
where E{⋅} is the expected value and
| (6) |
Thus,
| (7) |
As the exact equation for the expected value of RC cannot be derived, we may use the first order Taylor series to approximate it by:
| (8) |
As will be discussed later, the main applications of this study are related to the usage of RC in monitoring of treatment.
C. Coefficient of variation
Under model (3), the coefficient of variation is estimated by
| (9) |
where . Using equation (5) and the Taylor expansion, the expected value of COV is written as
| (10) |
D. Intra-class correlation coefficient
Under model (3), ICC is calculated by [22]:
| (11) |
where BMS, EMS, RMS are between target mean squares, residual mean squares, and between rater mean squares, respectively. It can be shown that (see Supplementary Material, Section II):
| (12) |
| (13) |
| (14) |
Where
| (15) |
Consequently, the expected values of numerator and denominator in equation (11) respectively are
| (16) |
| (17) |
and using the first order Taylor series,
| (18) |
and thus,
| (19) |
Note that the approximations in equations (8), (10), and (19) do not use the normality assumption of equation (1). Under normality assumption, we have provided second-order Taylor series approximations (thus more accurate) to RC, COV, and ICC in the Supplementary Material.
Note that and are functions of ROI size M and will also depend on the shape of ROI as the spatial covariance is a function of distance between voxels. Thus, RC, COV, and ICC are functions of M as well as the ROI shape. This also means that given the model parameters, we are able to estimate RC, COV, and ICC for arbitrary ROI size and shape.
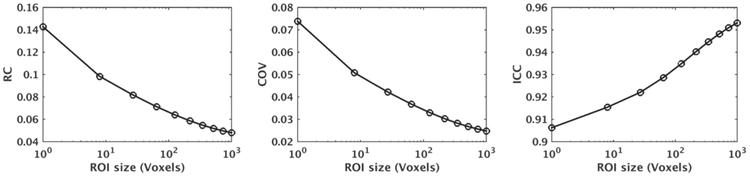
Fig. 1 plots expected values of repeatability measures versus ROI size for RC, COV, and ICC using the model parameters μ = 0.7, στ = 0.08, σλ = 10−4, σγ = 0.015, σβ = 0.15, ρβ = 0.02, ηβ = 1.2, σε = 0.05, ρε = 0.002, & ηε = 1.5. These parameters were selected to be close to the parameters that we estimated for fractional anisotropy (FA) of corpus callosum (CC) in the MRI dataset used in the experiments of Section III-B (we rounded the parameters for simple reporting). For simplicity, the ROIs were selected to be cubes with size L3 voxels, for L = 1,2, … ,10, but ROIs with an arbitrary shape (e.g., spherical) could also be evaluated using the derived equations. We have plotted the approximate measures from the second-order Taylor expansion as given in Supplementary Material, Section IV. As shown, for the given model parameters and ROI shape, with increasing the ROI size, RC and COV decrease whereas ICC increases.
Fig. 1.
RC, COV, and ICC curves versus ROI size for the model parameters μ = 0.7, στ = 0.08, σλ = 10−4, σγ = 0.015, σβ = 0.15, ρβ = 0.02, ηβ = 1.2, σε 0.05, ρε = 0.002, and ηε = 1.5 for cubic ROIs calculated using second-order Taylor expansion.
E. Repeatability measures for a desired ROI
In order to estimate the repeatability measures for a desired ROI, we first need to estimate the parameters of the measurement model in (1) (i.e., μ, , , , , ρβ, ηβ, , ρε, and ηε). For this purpose, we propose a hybrid least-square (LS) and method-of-moment (MOM) approach based on the measurements of N available subjects. We begin with finding the population moments. We note that
| (20) |
| (21) |
and
| (22) |
Following MOM, we need to substitute the population moments with their point estimates calculated from the available sample, and then, solve the above system of equations to estimate the parameters. However, since the number of parameters is larger than the number of equations, using MOM, we cannot distinctly estimate any of variance components but . To overcome this issue, we suggest an ROI subsampling approach as follows. For each subject, a sample of M ≤ MT. connected voxels is randomly chosen from the ROI with the size of MT. Then these subsamples are used to calculate BMS, EMS, and WMS using equations (S-1), (S-6) (provided in Supplementary Material, Section II), and (4). This procedure is repeated Nrepeat times for a fixed M, and the average of the calculated BMS, EMS, and WMS across the repetitions is found. Next, the whole procedure is repeated for a new M. Following this approach will lead to a number of estimations for E{EMS}, E{BMS}, and E{WMS} for different values of M, the ROI size.
Finally, using this information, the LS method can be utilized to estimate , , ρβ, ηβ, , , ρε, and ηε based on equations (20) and (21). Here, we have two non-linear LS problems. The LS problem related to equation (20) is convex with respect to , , and Ρβ, given ηβ. The LS problem related to equation (21) is convex with respect to , , and ρε, given ηε. Thus, given ηε and ηβ, the rest of parameters can be explicitly obtained by setting the corresponding derivatives to zero. Thus, the problem boils down to finding tuning parameters ηβ and ηε that minimize the estimation error. This is done by a linear search approach over a grid parameter in pre-specified interval. As the equations (20) and (21) have four parameters each to estimate, we will need average values of BMS-EMS, EMS, and WMS-EMS for at least four ROI sizes. The parameter μ may be estimated by finding the grand average of all measurements across the subjects. These parameter estimates along with equations (8), (10), and (19) can further be used to predict RC, COV, and ICC for ROIs with arbitrary sizes and shapes.
It is also interesting to compare the variance of RC, COV, and ICC estimates obtained by the proposed procedure described above with the variance of these measured when they are directly calculated from M‣ available voxels. For the latter, we have derived the variances of RC, COV, and ICC in the Supplementary Material under normality assumption in model (1). For the estimated RC, COV, and ICC using our proposed method, the equations for finding their variances would be more involved. Therefore, we evaluate their variances by simulation and calculate the average of variances.
If the ROI contains multiple tissue types, as long as the intensities of parametric maps obey model (1), the proposed method is valid. As shown later, the main changes in the repeatability measures occur for small ROIs, which have smaller chance of containing multiple tissue types.
We test the proposed model using simulation and brain MRI data as follows.
F. Simulation
Fig. 2 shows the block diagram of our simulation. We use the model introduced in (1) to simulate data points with the model parameters provided in Section II-D for a cube ROI of size 10×10×10 (i.e., MT = 1000) and for N = 21 and K = 2. The choice of cube ROI is just for simplicity. ROIs with any shape other than cube can also be considered. Also, the choice of voxel volume does not affect our analysis. The above ROI is assumed to be the available ROI for the estimation of model parameters. We then estimate the parameters using the proposed hybrid method. We generate connected voxels by considering all possible cubic sub-ROIs of size L×L×L, for L = 1, 2, 5, and 10. We use fixed-shaped ROIs to eliminate the effect of ROI shape in the simulation. To test the performance of the proposed method on ROIs with arbitrary size, we generate repeatability curves versus ROI size for cubic ROIs of size L×L×L voxels for L = 1,2, … ,10, using the estimated parameters and compare them with the ground truth calculated from true model parameters and generate the mean square error (MSE) between them. We generate the ground truth repeatability measures using the second-order Taylor expansion equations given in Supplementary Material, Section IV. We repeat the simulations Nrepeat =5000 times and calculate the mean, variance, and MSE of the generated curves. Furthermore, to compare with numeric estimation we separately simulate data points using the same model parameters for cube ROIs of size L×L×L voxels for L = 1,2, … ,10 and directly calculate the repeatability measures (numerical calculation) using equations (4), (9), and (11). We repeat this Nrepeat =5000 times and calculate the mean, variance, and MSE of the generated curves. The number of repetitions Nrepeat =5000 was chosen to be sufficiently large to generate accurate (smooth) variance curves.
Fig. 2.
Block diagram of the simulation. We repeat the whole process 5000 times with the same model parameters and generate average curves of RC, COV, and ICC versus ROI size.
G. Brain MRI dataset
We use a dataset of 21 healthy subjects with repeated brain MRI scans [20] to evaluate the effect of the ROI size. The subjects had no history of neurological conditions (11 M/10 F, 22-61 years old). Each subject had two MRI scans with a short break between them. A number of structural and functional images were acquired in each scan. We use MPRAGE (1.2 mm × 1.0 mm × 1.0 mm resolution), T2-weighted (1.0 mm × 0.94 mm × 0.94 mm resolution), DTI (32 directions, b-value = 700 s/mm2, 0.83 mm × 0.83 mm × 2.2 mm), and ASL images (1.87 mm × 1.87 mm × 7.95 mm resolution) of this dataset. The image acquisition parameters are given in [20]. DTI is a promising method for in vivo characterization of the microstructural properties of WM [23]. ASL is used for measuring tissue perfusion using a freely diffusible intrinsic tracer [24]. We process the images of each subject as follows.
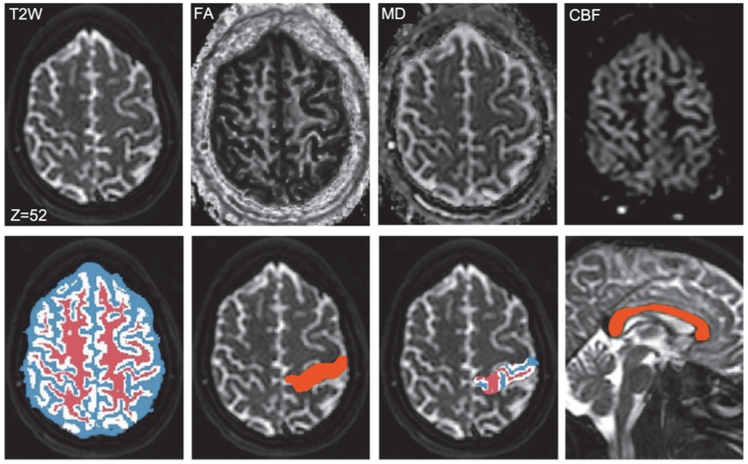
We automatically segment the whole brain of scan 1 into several regions by non-rigid registration of the Harvard-Oxford atlas [25], distributed with FMRIB Software Library (FSL, http://www.fmrib.ox.ac.uk/fsl/), to the MPRAGE image using ANTS [26]. Since this atlas does not have a label for the CC, we manually outlined the CC and added it to the atlas. We also use a segmentation algorithm [27] in FSL to segment the MPRAGE image into WM, GM, and CSF. We then map both generated label volumes to the T2W image of scan 1 (see Fig. 3) using rigid coregistration between MPRAGE and T2W images in SPM (http://www.fil.ion.ucl.ac.uk/spm/). We generate FA and mean diffusivity (MD) maps from DTI data of both scans using FSL and coregister them to the T2W image of scan 1 using rigid coregistration between B0 and T2W images. We also generate cerebral blood flow (CBF) maps from ASL images of both scans using the method described in [20] and map them to the T2W image of scan 1 by rigid coregistration between ASL and T2W images in SPM. Therefore, FA, MD, and CBF maps of both scans as well as two label maps will be available in the space of T2W image of scan 1 (Fig. 3). In this way, although the original resolutions of the parametric maps were different, we analyze them all in the same space, i.e., space of T2W image. We normalize CBF maps to the CBF mean value within the WM mask generated by FSL in order to obtain relative CBF values. The accuracy of atlas-based segmentation is not a concern here since the same segmentation outcome is used for both scans. We conduct three studies:
Fig. 3.
Sample parametric maps and label volumes in the space of T2W image of scan 1. Row one: Sample T2W image along with FA, MD, and CBF maps. Row two: Label maps of WM (red), GM (white), and CSF (blue); cross-section of a selected region in the parietal lobe; segmentation of the selected region into WM, GM, and CSF; and label map of the CC.
Study 1
Here we are interested in studying the effect of ROI size on region-based analyses of FA, MD, and CBF, as well as in verifying our statistical model and the estimation technique. We select three anatomical regions as follows. We select a segmented region in the parietal lobe and use tissue segmentation labels to divide the region into WM and GM sub-regions (see Fig. 3). FA, MD, and CBF are analyzed within these two regions as well as within the CC. All three anatomical regions are analyzed as follows. We randomly generate ROIs with ST voxels from each region and then apply the proposed algorithm to generate curves of RC, COV, and ICC versus ROI size and average over 100 repetitions. We then calculate the MSE between the estimated values and their ground truth. Implementation details including the method to generate near-spherical shaped ROIs and the ground truth are presented in the Supplementary Material, Section V.
Study 2
The aim of this study is just to show how the problem of smoothing in voxel-wise analysis is related to the effect of ROI size. In the analysis of functional maps, such as functional diffusion maps [28], smoothing can change RC and the required threshold for determining the changed regions as it increases the effective ROI size by combining the voxels through weighted averaging the original voxels. We apply a Gaussian filter with full-width half maximum (FWHM) of 3.5 mm and repeat study 2 to show the effect of smoothing on the repeatability of voxel-wise analysis.
III. Results
A. Simulation
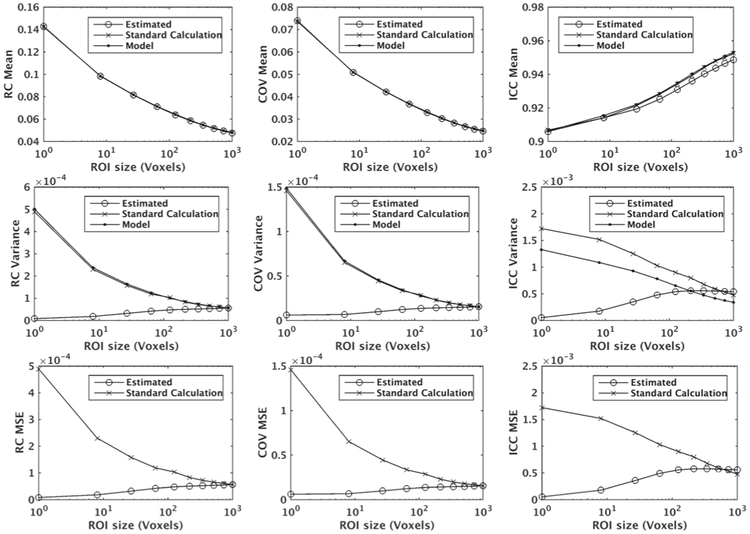
The results are presented in Fig. 4. In all figures, the volumes of ROIs are given in terms of the number of voxels in the space of T2W image (i.e., voxel sizes of 1.0 mm × 0.94 mm × 0.94 mm). As shown, the mean of estimated values obtained from our proposed hybrid estimation method are close to the approximated true mean. The MSE values are also small compared to the repeatability measures. The variances of the estimated values are smaller or comparable to the corresponding variances when estimated conventionally using the sample variance function. This is a desirable property of the proposed method. Variance and MSE values of the estimations using the proposed method are smaller for smaller ROIs since all voxels within the 10×10×10 ROI are used for the estimation of the repeatability measures (and more samples means lower variance). For ICC, the estimated value is slightly lower than its ground truth when the sub-sample ROI size is large. This is because the randomness between subsamples decreases as the ROI size increases and consequently the information obtained from sub-samples become quite similar. For the variance of ICC, there is a difference between the values generated by the model (ground truth calculated by formulas provided in the Supplementary Material) and those calculated conventionally, which is caused by the limitation of the approximation of var(ICC) provided in equation (S-15) in the Supplementary Material.
Fig. 4.
Mean values (row 1), variances (row 2), and MSE values (row 3) of the repeatability measures (RC, COV, and ICC) estimated using our proposed hybrid method from simulated data points denoted by “Estimated”, standard method using their definition denoted by “Standard Calculation”, and using the true model parameters denoted by “Model”. MSE curves (row 3) were generated by comparison with the true model. The data points were generated by 5000 simulations using the model proposed in equation (1) with normal distribution.
B. Brain MRI dataset
Study 1
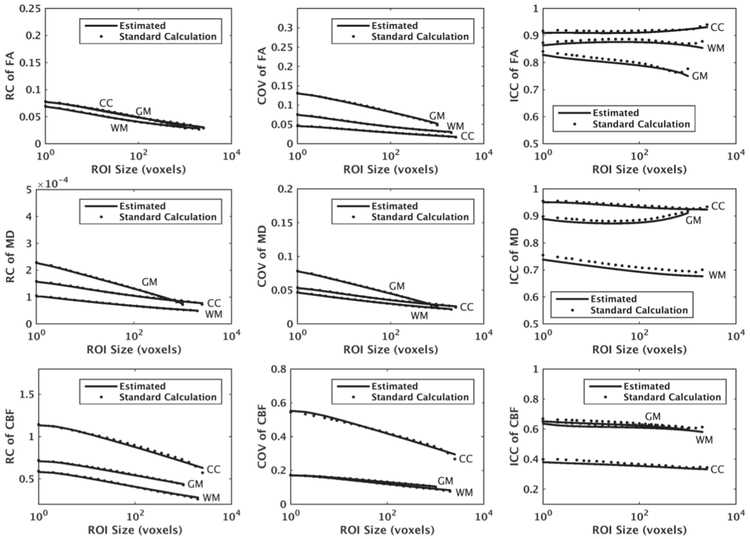
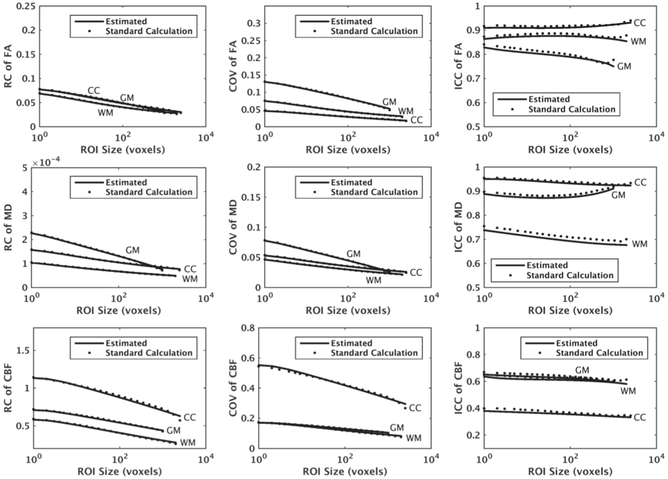
Fig. 5 shows the estimated values of repeatability measures for FA, MD, and CBF maps with ST = 2000, ST = 1000, and ST = 2500, for WM, GM, and CC, respectively. To choose four ROI sizes for curve fitting, we divided the interval [1, ST] into four equi-distant intervals in the logarithmic scale. Specifically, we chose indices 1, 6, 12, and 22. We picked point 22 instead of 23 (i.e., ST voxels) to avoid uncertainly of a single sample point. As shown, there is a good agreement between the mean curves of the estimated measurements and their ground truth. The MSE averaged over different ROI sizes had maximum values of 7.1e-4, 1.6e-4, and 8.7e-4 for RC, COV, and ICC, respectively.
Fig. 5.
Average RC, COV, and ICC of mean FA, mean MD, and mean CBF within WM and GM of a segmented region in the parietal lobe as well as CC versus ROI size, estimated using our proposed method, denoted by “Estimated”, along with their ground truth values denoted by “Standard Calculation”. We assumed ST = 2000, ST = 1000, and ST = 2500 voxels were available for WM, GM, and CC, respectively, and obtained the averages over 100 repetitions.
We observe that the rate of change in the repeatability measures is higher for smaller ROI sizes. In a voxel-wise analysis where the effective ROI size is one voxel, RC is at its maximum and changes dramatically by increasing the ROI size. When the image is smoothed or interpolated into a different resolution or space, the effective ROI size may change as the voxels are combined. This affects the repeatability coefficients and is studied next.
Study 2
The results of studying the effect of smoothing on the repeatability of voxel-wise analysis are presented in Fig. 6. By comparing Figs. 5 and 6, we observe that smoothing substantially changes the repeatability measures of FA and MD, in particular in the case of ROI with size of one voxel or equivalently voxel-wise analysis. The effect of smoothing on the repeatability measures of CBF was smaller compared to FA and MD due to the large voxel size of the original CBF maps and thus smoother voxels in the space of T2W images making them less affected by smoothing.
Fig. 6.
Average RC, COV, and ICC of mean FA, mean MD, and mean CBF within WM and GM of a segmented region as well as CC versus ROI size, after smoothing the images and estimated using our proposed method, denoted by “Estimated”, along with their ground truth values denoted by “Standard Calculation”. Comparing with Fig. 5, we can observe the effect of smoothing on the repeatability measures.
IV. DISCUSSION
We presented a statistical model along with a parameter estimation method to estimate repeatability measures for brain ROIs with arbitrary sizes. This is important in treatment planning when the knowledge about whether a change has occurred in a tissue is desirable, e.g., in monitoring changes in MRI-based parametric maps within brain tumors following treatment [2] [3] [4] [5]. The threshold based on which a decision is made (e.g., RC of measurement) can be adjusted according to each individual tumor size using our proposed method. However, note that the threshold also depends on the imaging protocol and vendor. Thus, a relation between threshold and ROI size needs to be derived for each imaging protocol and vendor.
We observed that the major changes in repeatability measures occur for small ROIs. Thus, adjusting the threshold becomes more important for small lesions, such as brain lesions in multiple sclerosis with reported average size of 36 mm2 in 2D MRI scans [29]. Our proposed method may be used for monitoring treatment of multiple sclerosis using various imaging biomarkers [7] [8] [9] [10] and in particular myelin water fraction using FAST-T2 [6]. Other applications that may involve small lesions include monitoring brain metastases by diffusion-weighted MRI [30] [31] and MRI perfusion [32], and brain focal lesions by MRI in mild traumatic brain injury [33]. Obviously, if a particular structure (e.g., hippocampus) is studied by ROI-based method, then the ROI size has smaller range of variations and our method may not be applicable.
Model parameters depend on factors such as tissue type, the extent of partial volume effect, and the signal-to-noise ratio (SNR) of the image within the ROI. For example, regions closer to the brain center usually have lower SNR due to the lower coil sensitivity in those regions. In our method, we had assumed that the ROIs under study had similar model parameters, with the ROI size or shape the only difference between them. We tested the proposed method for ROIs containing one tissue type. To test whether the proposed method practically works for ROIs containing multiple tissue types, we repeated Study 1 in Section II for WM+GM. The method accurately estimated the repeatability measures (results presented in Fig. S1 of the Supplementary Material).
Although we assumed all the random effects in model (1) followed a normal distribution, this assumption was not used in the derivation of first-order Taylor series approximation of the mean of the repeatability measures. It was only used to approximate means and variances using the second-order Taylor approximation (see the Supplementary Material). This assumption may not be valid in practice especially when the measurements have some intrinsic limited range of variations, for example in the case of FA values that range from 0 to 1. Despite this, the curves of the repeatability measures generated for FA, MD, and CBF using the second-order Taylor approximation for the dataset of repeated MRI scans had good agreement with their defined ground truth. This indicates that the proposed method is robust to the violation of the normality assumption.
Since the repeatability measures depend on the number of voxels and that in turn depends on the resolution, the question arises as to what resolution we should select given a fixed acquisition time. In MRI, the tradeoff between SNR and resolution is nonrecoverable [34] [35] and thus we need to find the best compromise. We note that the random error εijk of the parametric map in model (1) depends on both SNR and the resolution of MRI. This is because εijk models the overall effect of sources of variation such as segmentation and registration errors, partial volume effect, and noise. Thus, the best repeatability measures are not obtained by maximizing SNR. Unfortunately, deriving an analytical solution is not trivial and experiments need to be conducted to get the best compromise.
The problem of ROI size is also related to some other problems that involve ROIs with small size. Here we review several of such cases in the neuroimaging studies. Functional diffusion maps have recently become popular as an early and quantitative biomarker of clinical brain tumor treatment outcome [28]. In this technique, longitudinal maps of MD are generated from DTI data and mapped to a common space, typically a T2W image of the same subject. Voxel-wise differences of MD maps, before and after therapy, are then generated. Using a predetermined thresholded Δ, the tumor is classified into three regions of increased MD, decreased MD, and no change if the difference is above Δ, below Δ, and between −Δ and Δ, respectively. These regions are then studied to evaluate response to therapy. A threshold of 4×10−4 mm2/sec has been suggested in the literature [28] although more specific thresholds ranging from 2.5×10−4 mm2/sec to 7.5×l0−4 mm2/sec have been later proposed for WM, GM, their combination, and combination of WM, GM, and CSF [36]. These reported thresholds correspond to RC values and agree with our RC values for ROI size of one voxel (Fig. 5).
Spatial smoothing may be carried out (typically Gaussian filtering with FWHM of 4 mm to 12 mm) before running standard voxel-wise statistics and thresholding [12]. We applied a Gaussian filter with FWHM of 3.5 mm and showed that it decreased the RC values of FA and MD approximately by half (compare Figs. 5 and 6). Since smoothing can be regarded as a weighted averaging, it has the effect of increasing the effective ROI size if it is done within one tissue type to avoid partial volume effect. As βij and εijk in model (1) are the only terms that have spatial information (i.e., change from voxel to voxel), smoothing will affect both, whereas the goal is to reduce the effect of error term εijk while keeping βij intact. The right amount of smoothing may be decided based on a compromise between improving the repeatability and preserving the spatial information. Knowing the desired repeatability measures depending on the application, the smallest filter size can be estimated using the curves of the repeatability measures versus filter size. In the case of average filtering, our proposed method can generate the repeatability curves. Determining the desired repeatability measure will be based on the particular application and the data, and is out of scope of this paper.
In some image acquisitions, parametric maps are generated and standardized (normalized) using a reference region, which may be small. Examples include dynamic contrast enhanced (DCE) MRI, dynamic susceptibility contract (DSC) MRI, ASL, and positron emission tomography (PET). In DCE- and DSC-MRI, the parametric maps are generated by deconvolution of the dynamic image with a reference signal called arterial input function (AIF). AIF is the MRI signal of a feeding artery and may be determined from a few automatically or manually detected voxels. Reliable estimation of AIF is essential for a reliable generation of perfusion maps. AIF voxels need to be small enough in order to avoid the problem of partial volume effect. But as repeatability of measurements is relatively poor for smaller ROIs, measurements based on AIF determined from a small number of voxels may not be reliable. The size of AIF ROI could be set to the smallest one that gives the desired repeatability measures. In ASL, CBF is dependent on the equilibrium signal intensity within the CSF calculated from the inversion recovery sequence by segmentation of the CSF region [37]. As ASL images have relatively large voxels, the CSF may contain small number of voxels, in particular when the CSF is small. This may affect the repeatability of CBF measurements. Similar issues exist in other imaging techniques that use reference tissue, such as PET imaging [38] [39].
Supplementary Material
Acknowledgments
This work was supported in part by the National Institutes of Health (NIH) grant 5P41EB015896-18, George Family Foundation, MIT-MGH Grand Challenge 3 for Neuroscience (P.I.: Ovidiu Andronesi, MGH), NIH grants 1R01CA211238-01, 4U24CA180918-04, 5U24CA180927-03, And 5R01EY019474-05, and National Science Foundation grant 1622542.
Contributor Information
Kourosh Jafari-Khouzani, Email: kjafari@icadmed.com, Athinoula A. Martinos Center for Biomedical Imaging, Department of Radiology, Massachusetts General Hospital and Harvard Medical School, Boston, MA, USA. He is now with iCAD Inc., Nashua, NH..
Kamran Paynabar, H. Milton Stewart School of Industrial and Systems Engineering, Georgia Institute of Technology, Atlanta, GA, USA..
Fatemeh Hajighasemi, Department of Medical Sciences, Najafabad Azad University, Isfahan, Iran..
Bruce Rosen, Athinoula A. Martinos Center for Biomedical Imaging, Department of Radiology, Massachusetts General Hospital and Harvard Medical School, Boston, MA, USA..
References
- [1].Barnhart HX and Barboriak DP, "Applications of the repeatability of quantitative imaging biomarkers: a review of statistical analysis of repeat data sets," Translational oncology, vol. 2, pp. 231–5, December 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Schmainda KM, Zhang Z, Prah M, Snyder BS, Gilbert MR, Sorensen AG, et al. , "Dynamic susceptibility contrast MRI measures of relative cerebral blood volume as a prognostic marker for overall survival in recurrent glioblastoma: results from the ACRIN 6677/RTOG 0625 multicenter trial," Neuro Oncol, vol. 17, pp. 1148–56, August 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Voglein J, Tuttenberg J, Weimer M, Gerigk L, Kauczor HU, Essig M, et al. , "Treatment monitoring in gliomas: comparison of dynamic susceptibility-weighted contrast-enhanced and spectroscopic MRI techniques for identifying treatment failure," Invest Radiol, vol. 46, pp. 390–400, June 2011. [DOI] [PubMed] [Google Scholar]
- [4].Padhani AR and Khan AA, "Diffusion-weighted (DW) and dynamic contrast-enhanced (DCE) magnetic resonance imaging (MRI) for monitoring anticancer therapy," Target Oncol, vol. 5, pp. 39–52, March 2010. [DOI] [PubMed] [Google Scholar]
- [5].Padhani AR, "Dynamic contrast-enhanced MRI in clinical oncology: current status and future directions," J Magn Reson Imaging, vol. 16, pp. 407–22, October 2002. [DOI] [PubMed] [Google Scholar]
- [6].Vargas WS, Monohan E, Pandya S, Raj A, Vartanian T, Nguyen TD, et al. , "Measuring longitudinal myelin water fraction in new multiple sclerosis lesions," Neuroimage Clin, vol. 9, pp. 369–75, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Barillot C, Edan G, and Commowick O, "Imaging biomarkers in multiple Sclerosis: From image analysis to population imaging," Med Image Anal, vol. 33, pp. 134–139, October 2016. [DOI] [PubMed] [Google Scholar]
- [8].Londono AC and Mora CA, "Nonconventional MRI biomarkers for in vivo monitoring of pathogenesis in multiple sclerosis," Neurol Neuroimmunol Neuroinflamm, vol. 1, p. e45, December 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Tourdias T and Dousset V, "Neuroinflammatory imaging biomarkers: relevance to multiple sclerosis and its therapy," Neurotherapeutics, vol. 10, pp. 111–23, January 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Filippi M and Agosta F, "Imaging biomarkers in multiple sclerosis," J Magn Reson Imaging, vol. 31, pp. 770–88, April 2010. [DOI] [PubMed] [Google Scholar]
- [11].Ashburner J and Friston KJ, "Voxel-based morphometry--the methods," Neuroimage, vol. 11, pp. 805–21, June 2000. [DOI] [PubMed] [Google Scholar]
- [12].Smith SM, Jenkinson M, Johansen-Berg H, Rueckert D, Nichols TE, Mackay CE, et al. , "Tract-based spatial statistics: voxelwise analysis of multi-subject diffusion data," Neuroimage, vol. 31, pp. 1487–505, July 15 2006. [DOI] [PubMed] [Google Scholar]
- [13].Lee JE, Chung MK, Lazar M, DuBray MB, Kim J, Bigler ED, et al. , "A study of diffusion tensor imaging by tissue-specific, smoothing-compensated voxel-based analysis," Neuroimage, vol. 44, pp. 870–83, February 01 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Jones DK, Symms MR, Cercignani M, and Howard RJ, "The effect of filter size on VBM analyses of DT-MRI data," Neuroimage, vol. 26, pp. 546–54, June 2005. [DOI] [PubMed] [Google Scholar]
- [15].White T, O'Leary D, Magnotta V, Arndt S, Flaum M, and Andreasen NC, "Anatomic and functional variability: the effects of filter size in group fMRI data analysis," Neuroimage, vol. 13, pp. 577–88, April 2001. [DOI] [PubMed] [Google Scholar]
- [16].Mikl M, Marecek R, Hlustik P, Pavlicova M, Drastich A, Chlebus P, et al. , "Effects of spatial smoothing on fMRI group inferences," Magn Reson Imaging, vol. 26, pp. 490–503, May 2008. [DOI] [PubMed] [Google Scholar]
- [17].Zhang H, Avants BB, Yushkevich PA, Woo JH, Wang S, McCluskey LF, et al. , "High-dimensional spatial normalization of diffusion tensor images improves the detection of white matter differences: an example study using amyotrophic lateral sclerosis," IEEE Trans Med Imaging, vol. 26, pp. 1585–97, November 2007. [DOI] [PubMed] [Google Scholar]
- [18].Bonekamp D, Nagae LM, Degaonkar M, Matson M, Abdalla WM, Barker PB, et al. , "Diffusion tensor imaging in children and adolescents: reproducibility, hemispheric, and age-related differences," Neuroimage, vol. 34, pp. 733–42, January 15 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Reig S, Sanchez-Gonzalez J, Arango C, Castro J, Gonzalez-Pinto A, Ortuno F, et al. , "Assessment of the increase in variability when combining volumetric data from different scanners," Human brain mapping, vol. 30, pp. 355–68, February 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Landman BA, Huang AJ, Gifford A, Vikram DS, Lim IA, Farrell JA, et al. , "Multi-parametric neuroimaging reproducibility: a 3-T resource study," NeuroImage, vol. 54, pp. 2854–66, February 14 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Hu J, "Covariogram, Examples of," in Encyclopedia of Environmetrics, ed: John Wiley & Sons, Ltd, 2006. [Google Scholar]
- [22].Shrout PE and Fleiss JL, "Intraclass correlations: uses in assessing rater reliability," Psychological bulletin, vol. 86, pp. 420–8, March 1979. [DOI] [PubMed] [Google Scholar]
- [23].Alexander AL, Lee JE, Lazar M, and Field AS, "Diffusion tensor imaging of the brain," Neurotherapeutics, vol. 4, pp. 316–29, July 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Petcharunpaisan S, Ramalho J, and Castillo M, "Arterial spin labeling in neuroimaging," World J Radiol, vol. 2, pp. 384–98, October 28 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Makris N, Goldstein JM, Kennedy D, Hodge SM, Caviness VS, Faraone SV, et al. , "Decreased volume of left and total anterior insular lobule in schizophrenia," Schizophr Res, vol. 83, pp. 155–71, April 2006. [DOI] [PubMed] [Google Scholar]
- [26].Avants BB, Epstein CL, Grossman M, and Gee JC, "Symmetric diffeomorphic image registration with cross-correlation: evaluating automated labeling of elderly and neurodegenerative brain," Medical image analysis, vol. 12, pp. 26–41, February 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Zhang Y, Brady M, and Smith S, "Segmentation of brain MR images through a hidden Markov random field model and the expectation-maximization algorithm," IEEE Trans Med Imaging, vol. 20, pp. 45–57, January 2001. [DOI] [PubMed] [Google Scholar]
- [28].Moffat BA, Chenevert TL, Lawrence TS, Meyer CR, Johnson TD, Dong Q, et al. , "Functional diffusion map: a noninvasive MRI biomarker for early stratification of clinical brain tumor response," Proc Natl Acad Sci U S A, vol. 102, pp. 5524–9, April 12 2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Wang L, Lai HM, Thompson AJ, and Miller DH, "Survey of the distribution of lesion size in multiple sclerosis: implication for the measurement of total lesion load," J Neurol Neurosurg Psychiatry, vol. 63, pp. 452–5, October 1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Thoeny HC and Ross BD, "Predicting and monitoring cancer treatment response with diffusion-weighted MRI," J Magn Reson Imaging, vol. 32, pp. 2–16, July 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Turkbey B, Aras O, Karabulut N, Turgut AT, Akpinar E, Alibek S, et al. , "Diffusion-weighted MRI for detecting and monitoring cancer: a review of current applications in body imaging," Diagn Interv Radiol, vol. 18, pp. 46–59, Jan-Feb 2012. [DOI] [PubMed] [Google Scholar]
- [32].Taunk NK, Oh JH, Dave A, Beal K, Vachha B, Holodny A, et al. , "Early Posttreatment Assessment of MRI Perfusion Biomarkers Can Predict Long-Term Response of NSCLC Brain Metastases to SRS: A Longitudinal Analysis," International Journal of Radiation Oncology*Biology*Physics, vol. 99, p. S84, 2017/October/01/ 2017. [Google Scholar]
- [33].Huang YL, Kuo YS, Tseng YC, Chen DY, Chiu WT, and Chen CJ, "Susceptibility-weighted MRI in mild traumatic brain injury," Neurology, vol. 84, pp. 580–5, February 10 2015. [DOI] [PubMed] [Google Scholar]
- [34].Edelstein WA, Glover GH, Hardy CJ, and Redington RW, "The intrinsic signal-to-noise ratio in NMR imaging," Magn Reson Med, vol. 3, pp. 604–18, August 1986. [DOI] [PubMed] [Google Scholar]
- [35].Parker DL and Gullberg GT, "Signal-to-noise efficiency in magnetic resonance imaging," Med Phys, vol. 17, pp. 250–7, Mar-Apr 1990. [DOI] [PubMed] [Google Scholar]
- [36].Ellingson BM, Malkin MG, Rand SD, Connelly JM, Quinsey C, LaViolette PS, et al. , "Validation of functional diffusion maps (fDMs) as a biomarker for human glioma cellularity," J Magn Reson Imaging, vol. 31, pp. 538–48, March 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].van Osch MJ, Teeuwisse WM, van Walderveen MA, Hendrikse J, Kies DA, and van Buchem MA, "Can arterial spin labeling detect white matter perfusion signal?," Magn Reson Med, vol. 62, pp. 165–73, July 2009. [DOI] [PubMed] [Google Scholar]
- [38].Wong KP, Wardak M, Shao W, Dahlbom M, Kepe V, Liu J, et al. , "Quantitative analysis of [18F]FDDNP PET using subcortical white matter as reference region," Eur J Nucl Med Mol Imaging, vol. 37, pp. 575–88, March 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Rissanen E, Tuisku J, Luoto P, Arponen E, Johansson J, Oikonen V, et al. , "Automated reference region extraction and population-based input function for brain [(11)C]TMSX PET image analyses," J Cereb Blood Flow Metab, vol. 35, pp. 157–65, January 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.