Molecular structure and electron distribution of 4-nitropyridine N-oxide: Experimental and theoretical study of substituent effects

Abstract

The molecular structure of 4-nitropyridine N-oxide, 4-NO₂-PyO, has been determined by gas-phase electron diffraction monitored by mass spectrometry (GED/MS) and by quantum chemical calculations (DFT and MP2). Comparison of these results with those for non-substituted pyridine N-oxide and 4-methylpyridine N-oxide CH₃-PyO, demonstrate strong substitution effects on structural parameters and electron density distribution. The presence of the electron-withdrawing –NO₂ group in para-position of 4-NO₂-PyO results in an increase of the ipso-angle and a decrease of the semipolar bond length r(N→O) in comparison to the non-substituted PyO. The presence of the electron-donating –CH₃ group in 4-CH₃-PyO leads to opposite structural changes. Electron density distribution in pyridine-N-oxide and its two substituted compounds are discussed in terms of natural bond orbitals (NBO) and quantum theory atoms in molecule (QTAIM).

Graphical abstract

1. Introduction

Pyridine-N-oxide derivatives have attracted (a) great interest in chemistry and biotechnology because of their accentuated oxidizing properties, high polarity, and their ability to be both charge donors and acceptors. Heterocyclic compounds with N-oxide groups have achieved widespread utility foremost because of their pronounced biological activity [1]. In the literature we can find the evidence of bactericidal, analgesic, anticonvulsant, apoptotic, and antimicrobial activity of N-oxides [2,3]. These properties allow to use N-oxides as inhibitor of HIV-1 reverse transcriptase [4,5], as antiviral agent against various SARS corona virus strains [6], and as antiadhesive and quorum-sensitive inhibitor [7]. Some complexes with pyridine-N-oxides are used in agriculture to regulate plant growth rates [8]. According to numerous studies, the biochemical activity of N-oxides is due to the complexation with the metalloporphyrins in living organisms [[9], [10], [11]]. Obviously, the reactivity of N-oxides may vary due to different substituents in the ring [12]. The variation of the substituents gives wide possibilities to chemical modifications of N-oxides and allows to change their complexing properties, and, as the result, to influence the biological activity. Apparently, the substitution of pyridine-N-oxide with a strong electron-withdrawing -NO₂ group would lead to an electron density redistribution, and thus would widen the scope of its reactivity. It is often assumed that the presence of the nitro group in substituted pyridine-N-oxides is responsible for a substantial increase in the antifungal activity [13]. Nitro-pyridine-N-oxides are also known to be used in photonics for design and development of new organic nonlinear optical (NLO) materials [[14], [15], [16], [17], [18]]. In order to elucidate the factors underlying these and other properties of pyridine-N-oxides a detailed information about the structural properties as well as about the electron density distribution in the molecules is needed.

The available literature data about molecular structure of gaseous N-oxides is not sufficient. Only four pyridine-N-oxides have been studied by gas-electron diffraction (GED). Chiang J.F. et al. [19,20] carried out GED studies of pyridine-N-oxide and three of its para-substituted compounds. However, the structural data reported in Refs. [20] should be criticized. Thus, e.g. N–C bond lengths in 4-NO₂-PyO, 4-Cl-PyO, 4-Me-PyO obtained by Chiang J.F. et al. [20] are even longer than r(C–C) in the benzene ring, and are strongly overestimated compared to the calculated values [21] and X-ray crystallographic data [22,23]. Furthermore, the CNC bond angle values in the pyridine ring of 4-NO₂-PyO and 4-Cl-PyO given in Ref. [20] are not consistent with sp² hybridization of the nitrogen atom and do not agree with calculated [21] and X-ray data [22,23]. The discrepancies in molecular structure of substituted N-oxides according to GED by Chiang J.F. et al. [19,20] and other methods motivated us to perform a new gas-electron diffraction study of 4-substituted-N-oxide. The first GED reinvestigation was performed for 4-methylpyridine-N-oxide [24] because of the largest structural contradictions for this molecule. Now more sophisticated methods for the analysis of GED data are available, including the possibility of quantum chemical results to be used in the interpretation of the experimental data. This allows us to determine the structural parameters more precisely compared to the studies performed in 1982. The experimental structural data for 4-methylpyridine-N-oxide obtained in our study [24] are in a good agreement with the theoretical parameters as well as the experimental X-ray data.

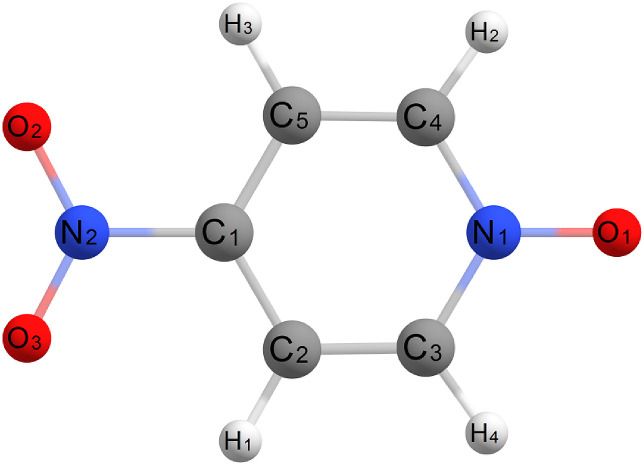
The present work continues our research of substituted-N-oxide structures. We performed new gas-electron diffraction study of 4-nitropiridine-N-oxide (Fig. 1 ). This molecule was chosen because of the substituent nature. The nitro-group is known to be strong electron-withdrawing, whereas the methyl group is a good electron donor. Thus, the comparison of 4-NO₂-PyO structure with that of 4-Me-PyO allows to reveal the substituent effects. This work presents also a theoretical study (DFT and MP2) of the molecular structure of 4-NO₂-PyO along with the related molecules. Electron charge distribution was studied in the framework of NBO scheme. As an alternative to conventional Lewis model which was realized in NBO the topological analysis of ρ(r) in the framework of Bader’s quantum theory of atoms in molecule (QTAIM) [25] was performed for 4-NO₂-PyO in the present work.

Fig. 1.

Molecular structure of 4-nitropyridine-N-oxide and atom notations.

2. Experimental section

The electron diffraction patterns and the mass spectra were recorded simultaneously using the techniques described previously [26,27]. Two series of GED/MS experiments at two different nozzle-to-plate distances have been performed. The conditions of GED/MS experiments and the relative abundance of the ions in mass spectra of 4-NO₂-PyO are shown in Table 1 and Table S1, respectively. The temperature of molybdenum effusion cell was measured by a W/Re-5/20 thermocouple calibrated by melting points of Sn and Al. The wavelength of the fast electrons was determined from the diffraction patterns of polycrystalline ZnO. Optical densities were measured by a computer-controlled MD-100 (Carls Zeiss, Jena) microdensitometer [28]. The molecular intensities were obtained in the ranges 2.5 ÷ 23.9 Å⁻¹ (short camera) and 1.3 ÷ 16.1 Å⁻¹ (long camera). The molecular intensities and the radial distributing curves are shown in Fig. 2, Fig. 3 respectively. Fig. 4 and Table S1 present the mass spectrum recorded simultaneously with GED data.

Table 1.

The conditions of GED/MS experiment.

nozzle-to-plate distance, mm	338	598
fast electron beam, μA	1.47	0.64
temperature of effusion cell, K	431(5)	401(5)
accelerating voltage, kV	79.2	79.5
(electron wavelength), Ǻ	0.04200(3)	0.04192(4)
ionization voltage, V	50(1)	50(1)
exposure time, s	130–140	50–60
residual gas pressure, Torr	1.0⋅10−6	2.5·10−6
s-values range, Å−1a	2.5–23.9	1.3–16.1

^as = (4π/λ)sinθ/2, λ is electron wavelength and θ is scattering angle.

Fig. 2.

Experimental (dots) and theoretical (solid) molecular intensity curves for 4-NO₂-PyO and the difference (experimental – theoretical) at two nozzle-to-plate distances, L₁ = 598 mm and L₂ = 338 mm.

Fig. 3.

Experimental (dots) and theoretical (solid) radial distribution curves for 4-NO₂-PyO and the difference curve (experimental – theoretical).

Fig. 4.

The mass spectra of 4-nitropyridine N-oxide recorded simultaneously with GED patterns.

3. Quantum chemical calculations

All quantum chemical calculations were performed using the GAUSSIAN 09 program set [29]. The hybrid DFT computational methods, namely Becke’s three-parameter hybrid functional B3LYP [[30], [31], [32], [33], [34]] and Perdew–Burke-Ernzerh of hybrid functional PBE0 [35], as well as second order Møller–Plesset perturbation theory, MP2, were used. The correlation-consistent basis sets augmented with diffuse functions (aug-cc-pVTZ) have been taken to describe the electronic shells of O, C, N and H atoms. Structure optimizations were followed by calculations of the vibrational frequencies in order to ensure that a minimum on the potential energy hyper-surface had been reached. All calculations have been performed for the closed-shell electronic state.

The geometrical parameters of the calculated equilibrium structure derived with different theory methods are given in Table 2 together with the experimental results.Vibrational amplitudes and corrections, Δr = r_h1−r_a, were derived from theoretical force fields (B3LYP/aug-cc-pVTZ) by Sipachev’s method (approximation with taking into account the nonlinear kinematic effects at the level of the first order perturbation theory for the transformation of Cartesian coordinates into internal coordinates), using the program SHRINK [[36], [37], [38]]. Selected values are listed in Table 3 (excluding non-bonded distances involving hydrogen).

Table 2.

Experimental and calculated geometric parameters of 4-nitropyridine-N-oxide.^a.

	(rh1, ∠h1)b	(re, ∠e) B3LYP/aug-cc-pVTZ	(re, ∠e) PBE0/aug-cc-pVTZ	re, ∠e) MP2/aug-cc-pVTZ
r(N1–O1)	1.267(3) p1c	1.264	1.252	1.259
r(N2–O2)	1.227(3) (p1)	1.224	1.214	1.232
r(N1–C3)	1.373(4) p2	1.373	1.367	1.380
r(N2–C1)	1.460(4) (p2)	1.460	1.452	1.453
r(C2–C3)	1.378(4) p3	1.372	1.369	1.374
r(C1–C2)	1.395(4) (p3)	1.389	1.385	1.391
r(C2–H1)	1.094(8) p4	1.079	1.081	1.080
r(C3–H4)	1.092(8) (p4)	1.077	1.079	1.079
∠ C3N1C4	118.6(9) p5	118.9	118.8	118.5
∠ N1C3C2	121.8(6) p6	121.3	121.5	121.5
∠ C3C2C1	118.8(9)	119.3	119.2	119.1
∠ C2C1C5	120.1(9)	119.9	119.9	120.1
∠ C1N2O2	117.8(6)p7	117.5	117.4	117.4

^aDistances in Å and angles in degrees. For atom numbering see Fig. 1.

^bUncertainties in r_h1 σ=(σ_sc²+(2.5σ_LS)²)^1/2 (σ_sc = 0,002r, σ_LS–standard deviation in least-squares refinement), for angles σ = 3σ_LS.

^cp_i – parameter refined independently. (p_i) – parameters calculated from the independent parameter p_i by a difference Δ = p_i-(p_i) from the quantum chemical calculations (B3LYP/aug-cc-pVTZ).

Table 3.

Root–mean–square vibrational amplitudes and vibrational corrections for 4-nitropyridine-N-oxide calculated from the molecular force field. Interatomic distances and vibrational amplitudes obtained from the GED refinements.^a).

	rh1b	l(GED)c	lcalc(B3LYP)	rh1-ra (B3LYP)
C3–H4	1.092(8)	0.078(3) l1d)	0.075	0.0017
C2–H1	1.094(8)	0.078(3) l1	0.075	0.0016
N2–O2	1.227(3)	0.043(3) l1	0.040	0.0004
N1–O1	1.267(3)	0.045(3) l1	0.042	0.0005
C2–C3	1.378(4)	0.048(3) l1	0.045	0.0003
N1–C3	1.373(4)	0.050(3) l1	0.047	0.0005
C1–C2	1.395(4)	0.049(3) l1	0.046	0.0006
N2–C1	1.460(4)	0.055(3) l1	0.052	0.0008
O2⋯O3	2.171(6)	0.048(4) l2	0.049	0.0034
C3⋯O1	2.295(6)	0.057(4) l2	0.058	0.0020
C1⋯O2	2.304(5)	0.059(4) l2	0.060	0.0022
C3⋯C4	2.362(9)	0.055(4) l2	0.057	0.0046
C1⋯C3	2.386(6)	0.054(4) l2	0.055	0.0029
N1⋯C2	2.404(6)	0.054(4) l2	0.055	0.0035
C2⋯C5	2.417(9)	0.055(4) l2	0.056	0.0049
N2⋯C2	2.472(6)	0.064(4) l2	0.065	0.0040
C2⋯O3	2.731(7)	0.095(3) l3	0.096	−0.0111
C2⋯C4	2.758(7)	0.062(3) l3	0.063	0.0060
N1⋯C1	2.775(8)	0.061(3) l3	0.062	0.0042
C2⋯O1	3.557(8)	0.059(7) l4	0.061	0.0081
C2⋯O2	3.565(7)	0.065(7) l4	0.066	0.0196
C3⋯N2	3.726(9)	0.065(7) l4	0.066	0.0091
C1⋯O1	4.042(10)	0.064(11) l5	0.064	0.0102
C3⋯O3	4.107(9)	0.098(11) l5	0.098	0.0004
N1⋯N2	4.235(11)	0.068(11) l5	0.068	0.0119
C3⋯O2	4.690(10)	0.070(9) l6	0.072	0.0231
N1⋯O2	4.928(11)	0.085(9) l6	0.087	0.0157
N2⋯O1	5.502(13)	0.068(21) l7	0.071	0.0202
O1⋯O2	6.170(13)	0.106(13) l8	0.093	0.0250

^aValues in Å, atom notifications are shown on Fig. 1.

^bUncertainties in r_h1 – distances are σ=(σ_sc²+(2.5σ_LS)²)^1/2 (σ_sc = 0,002r, σ_LS–standard deviation in least–squares refinement).

^cUncertainties for amplitudes are σ = 3σ_LS.

^dGroup number of amplitude.

The potential energy function of the internal rotation of the nitro group about the C1–N2 bond was investigated. For this purpose, we carried out relaxed potential energy surface scans by the variation of the dihedral angle τ(C2C1N2O3) in steps of 10° between 0° and 180° with B3LYP/aug-cc-pVTZ method. Analysis of this potential function (Fig. 5 ) shows that there is only one stable geometric configuration with τ about 0° (see Fig. 1 for atom numbering). It should be noted that the internal rotation barrier is a sufficiently large, 7.70 kcal/mol (B3LYP/aug-cc-pVTZ), 8.00 kcal/mol (PBE0/aug-cc-pVTZ) or 7.16 kcal/mol (MP2/aug-cc-pVTZ).

Fig. 5.

Potential function (B3LYP/aug-cc-pVTZ) of –NO₂ group internal rotation in 4-NO₂-PyO molecule.

The NBO 5G program [39], implemented for natural orbital analysis in PC GAMESS [40], was used to obtain the net atomic charges and Wiberg bond indexes. B3LYP/aug-cc-pVTZ wave functions were used in the NBO analyses.

The topological analysis of electron density distribution function ρ(r) for 4-NO₂-PyO and PyO was carried out using AIMAll Professional software [41]. The visualization of molecular models are realized by ChemCraft [42] program.

4. Structure analysis

The heaviest ion in mass spectrum observed during the combined GED/MS experiment was [NO₂-PyO]⁺ (Fig. 4, Table S1). No ions were detected, which could arise from impurities.This proves that only NO₂-PyO monomers are present in the vapour under the conditions of the GED experiment. Furthermore, view of the mass spectrum (Fig. 4) recorded simultaneously with the electron diffraction patterns corresponds to the mass spectrum of 4-NO₂-PyO given in NIST database [43]. The theoretical sM(s) functions calculated with the following assumptions. According to quantum chemical calculations, a planar structure with C _2v overall symmetry of the molecule was assumed. Independent r_h1 parameters were used to describe the molecular structure. Starting parameters from B3LYP/aug-cc-pVTZ calculations were refined by a least-squares procedure of the molecular intensities. The differences between all C–C bond distances, N–O bond distances, and C–N bond distances as well as between all C–H bond distances were constrained to calculated values (B3LYP/aug-cc-pVTZ). Vibrational amplitudes were refined in groups with fixed differences. With the abovementioned assumptions, four bond distances and three bond angles (Table 2) were refined simultaneously with eight groups of vibrational amplitudes (Table 3). Only two correlation coefficients had absolute values larger than 0.7: (r(N1–C3))/(r(C2–C3)) = -0.90, and (∠N1C3C2)/(∠C3N1C4) = −0.75. The best agreement factor is R_f = 3.6%. Results of the least squares analysis are given in Table 2 (geometric parameters) and Table 3 (vibrational amplitudes).

The model with nitro group plane turned relative to the pyridine ring plane was also tested in the GED analysis. This refinement leads to Rf = 3.71% for τ(C2C1N2O3) fixed at 10° and Rf = 4.00% for τ(C2C1N2O3) fixed at 15°. The statistical Hamilton criterion [44] at the 0.01 significance level distinctly reveals that the nitro group rotation angle relative to the plane of the pyridine ring is not more exceed than 12° because the critical value Rf = 3.78%.

5. Results and discussion

5.1. Structure of 4-nitro-pyridine-N-oxide. Substituent effect on the structure of pyridine-N-oxides

Table 2 summarizes the structural parameters of 4-nitro-pyridine-N-oxide. We can note a perfect agreement between calculated and experimental molecular structure parameters. Thus, changing the calculation method has no significant influence on the values of structural parameters. The differences in theoretical values for bond distances do not exceed 0.020 Å, whereas the calculated values of the bond angles are almost equal, independent of the theoretical level. Both, quantum chemistry and GED analysis result in C _2v overall symmetry of the molecule with a planar pyridine ring. The nitro-group is coplanar with the heterocycle plane. Obviously, this position provides a conjugation between the π-system of the pyridine ring and the NO₂ group. Furthermore, Fig. 2 presenting the calculated (B3LYP/aug-cc-pVTZ) –NO₂-group rotation potential curve clearly shows that changing of the torsional angle τ(C2C1N2O3) by more than for 12° leads to a significant increase in energy. M. Dakkouri and V. Typke performed theoretical investigation of the structure of 2-nitropyridine-N-oxide [45]. It is astonishing to note that the endocyclic bond lengths of the pyridine N-oxide ring is almost equal, independent of the position of the nitro group.

Table 4 compares the structure of pyridine-N-oxide and its two substituted obtained by GED, X-ray and DFT. Taking into account that the structural parameters obtained by different methods have different physical meaning, we can note a good agreement of the values obtained in our research (therein and [24]) with the theoretical results (therein and [21]) and, also, with the parameters for the crystals [46,47] in contrast to the values recommended by Chiang J. F. et al. [20]. Apparently, some increase of the semipolar N→O bond lengths in a crystal phase compared to the free molecules is due to intermolecular hydrogen bonding. All parameters presented in Table 4 confirm the hyperconjugation in the pyridine ring and the sp² hybridization concept of the nitrogen and carbon atoms in the ring. The exceptions are only the data by Chiang J. F. et al. [20], which are rather strange as we mentioned above. Unfortunately, large uncertainties in GED parameters for PyO [19] do not allow a comparison of the experimental structures. Thus, we can compare only the values obtained in our GED study (therein and [24]) and the calculated values. The structural data for free molecules in Table 4 show that the insertion of the methyl or nitro group in para – position to the PyO has no significant effect on the structural parameters of the pyridine ring, excluding only the ipso-angle ∠ C2C1C5, which is changes from 117.7° in PyO to 115.9° in 4-Me-PyO and 119.9° in 4-NO₂-PyO (B3LYP/aug-cc-pVTZ). It is interesting to note, that the substituent effects on the geometry of heterocyclic ring are rather similar to the tendencies for the benzene ring [48,49]. Thus, the presence of the electron-withdrawing –NO₂ group leads to the increase of the ipso-angle, whereas electron-donating –CH₃ substituent produces the opposite effect.

Table 4.

Molecular parameters of several N-oxides (Ǻ, deg.).

	4-NO2-PyO				PyO			4-Me-PyO
	GED [55]	GED [this work]	X-ray [23] 300 K	B3LYP/aug-cc-pVTZ	GED [19]	X-ray [47] 295 K	B3LYP/aug-cc-pVTZ	GED [55]	GED [24]	X-ray [46]	B3LYP/aug-cc-pVTZ
r(N1–O1)	1.281(22)	1.267(3)	1.304	1.264	1.290(15)	1.305	1.276	1.405	1.275(3)	1.309	1.279
r(N2–O2)	1.262	1.227(3)	1.235∗	1.224
r(N1–C3)	1.469(66)	1.373(4)	1.373∗	1.373	1.384(11)	1.357	1.367	1.430(33)	1.364(3)	1.342	1.365
r(C2–C3)	1.386(25)	1.378(4)	1.364∗	1.372	1.382(9)	1.357	1.378	1.354(48)	1.379(3)	1.391	1.377
r(C1–C2)	1.447(19)	1.395(4)	1.392∗	1.389	1.393(8)	1.375	1.390	1.321(63)	1.397(3)	1.371	1.395
r(C1-R)	1.628(13)	1.460(4)	1.460	1.460				1.577(27)	1.505(3)	1.497	1.503
r(C-Hring)	1.050	1.093(8)a	0.93∗	1.078∗	1.070	0.940	1.079	1.040	1.086(3)	1.049	1.080
r(C-Hmethyl)								1.095	1.097(3)	1.033	1.091
∠ C3N1O1	124.3	120.7(9)	119.9∗	120.5	119.5	120.6	120.7	117.2(16)	121.2(8)	120.2	121.0
∠ N1C3C2	125.4(24)	121.8(6)	120.9∗	121.3	118.1	120.9	121.3	115.9(11)	122.1(8)	120.6	121.5
∠ C3C2C1	120.3(10)	118.8(9)	118.3∗	119.3	124.4	120.7	120.5	121.0(29)	120.8(6)	121.0	121.5
∠ N1C4H2	108.0	119.1(7)	115.6∗	114.0	120.5	109.3	113.9	104.8	119.0(5)	118.7	114.0
∠ C3C2H1	113.1	120.6(7)	119.6∗	120.3	110.0	117.4	118.3	115.9	119.6(5)	117.7	117.9
∠ C1N2O2	114.5	117.8(6)	118.3∗	117.5
∠ C2C1C5	117.2b	120.1(7)	120.5	119.9	114.1(25)	117.9	117.7	120.6b	116.6(6)	117.2	115.9

^a- average value.

^b– calculated from data of Ref. [55].

Furthermore, the r(N1→O1) semipolar bond lengths appear to be also sensitive to a substituent nature. Thus, the presence of electron withdrawing-NO₂ group in 4-NO₂-PyO results in a shortening of r(N→O) in comparison with PyO, while in 4-Me-PyO with the donor substituent the bond length N→O increases.

5.2. Substituent effect on the electron density distribution in the pyridine-N-oxides

5.2.1. NBO analysis

The calculated net atomic charges along with the Wiberg bond indexes for PyO and two its derivatives are summarized in Table 5 . In all three cases the C–C and C–N bond orders in the ring, as well as the values of the distances from Table 2, Table 4 show that these bonds do not correspond to either single nor double bonds. This confirms the existence of π-conjugation in the pyridine rings. The C1–N2 bond distance as well as Q(C1–N2) for 4-NO₂-PyO corresponds to the single C–N bond in contrast to the assumption about conjugation of –NO₂ group with the pyridine ring. One can note that Wiberg bond index Q(N1–O1) in all three molecules cannot be interpreted as exact single or double bond. Furthermore, the introduction of various substituents in the pyridine ring may either facilitate the transfer of electron density from oxygen to the heterocycle and reduce the negative charge on the oxygen atom or, contrariwise, increase the negative charge on the oxygen. Thus, the introduction of electron-donating –CH₃ substituent increases the bond length N→O, reduces the correspondent Wiberg bond index and significantly increases the electron density on oxygen. In contrast, the introduction of electron-withdrawing -NO₂ group in the pyridine ring reduces the bond distance r(N→O), increases the Wiberg bond index Q(N→O) and, consequently, makes this bond more rigid and reduces the negative charge on oxygen. Obviously, in this case the presence of strong acceptor -NO₂ group results in a withdrawal of charges from the ring atoms and the N-oxide oxygen. Surprisingly, the total natural charge of the pyridine ring decreases with the insertion both -NO₂ or methyl group to para-position.

Table 5.

Net atomic charges (q, ē) and Wiberg bond indexes according to NBO scheme (B3LYP/aug-cc-pVTZ).

	4-NO2-PyO	PyO	4-Me-PyO
q(O1)	−0.469	−0.527	−0.539
q(N1)	0.107	0.088	0.082
q(O2)	−0.375
q(N2)	0.498
q(C3)	−0.010	−0.013	−0.004
q(C2)	−0.184	−0.208	−0.211
q(C1)	0.028	−0.216	−0.026
q(ring)∗	−0.253	−0.570	−0.374
q(R)∗	−0.252	0.214	0.042
Q(N1–O1)	1.328	1.283	1.271
Q(N2–O2)	1.486
Q(N2–C1)	0.945
Q(N1–C3)	1.182	1.202	1.203
Q(C3–C2)	1.505	1.484	1.485
Q(C2–C1)	1.353	1.413	1.382

^∗q(ring) – total natural charge of the heterocyclic ring (C1–C2–C4–N1–C5–C3). q(R) - total natural charge of the substituent.

5.2.2. Aromatiсity of PyO and its derivatives

Analyzing the average values of bond length in the pyridine ring Chiang J.F. et al. [20] have concluded that the aromaticity increases in the series: 4-nitropyridine-N-oxide (4-NO₂-PyO), 4-chloropyridine-N-oxide (4-Cl-PyO), pyridine-N-oxide (PyO), 4-methylpyridine-N-oxide(4-Me-PyO). However, as noted above, the average values of the bond lengths in the pyridine ring of the molecules studied (Table 4) do not change with the insertion of the substituent in para-position. To study the substituent effect on the aromaticity the nuclear independent chemical shifts NICS(1) have been calculated. NICS(1) values correspond to the negative isotropic shielding (in ppm) at 1 Å above the ring plane [[50], [51], [52]]. It is of important to note that in a vast number of papers it has been elaborately shown that (depending on the size of the ring) the in-plane aromaticity which is indicated by the isotropic NICS(0) value contains considerable contribution of in-plane σ-aromaticity resulting from the diamagnetic shielding of the σ electronic framework. Thus the NICS(1) value regards to be a better descriptor of the π contribution to aromaticity due to the apparent decrease of the local contributions of the σ framework at larger distances from the ring center. All NICS values were computed by employing the standard GIAO method implemented in the Gaussian software package by using B3LYP/aug-cc-pVTZ approximation. The calculated values of NICS(1): −7.29 (PyO), −6.95 (4-NO₂-PyO) and −7.18 (4-Me-PyO) are quite close to each other. Some decrease of NICS(1) for 4-NO₂-PyO can hardly be considered as noticeable effect of the substituent to the aromaticity.

5.2.3. QTAIM analysis

To be more accurate in interpretation of changes of structural features from PyO to 4-NO₂-PyO we have analyzed the topological properties of the electron density for these molecules employing the quantum theory of atoms in molecules (QTAIM) developed by R. Bader [25]. The set of topological properties of ρ(r) has been obtained for the molecular wave function of PyO and 4-NO₂-PyO at B3LYP/aug-cc-pVTZ approach. The molecular graphs and net atomic charges for C _2v structures of PyO and 4-NO₂-PyO are illustrated in Fig. 6 . The Laplacian map in the plane of pyridine ring is presented on Fig. 7 and shows the regions of local charge depletion (∇² ρ _b > 0) and concentration (∇² ρ _b < 0) in PyO and 4-NO₂-PyO molecules. The most important topological properties of electron density at the bond critical points (BCP) are summarized in Table 6 . It is clear that the charge densities at BCP (ρ _b) are correlated with the correspondent bond distance. The negative values of the Laplacian (∇² ρ _b) and total electronic energy density (H _b) indicate the occurrence of shared interaction which implies a covalent nature of the chemical bonds for both molecules studied. The values of the electronic delocalization index δ can be considered as the bond order characteristics. These values (see Table 6) are in satisfactory agreement with the Wiberg bond indexes (Table 5) and confirm that the bonds in the pyridine ring are neither single nor double. As additional criteria of π-bonding contribution the bond ellipticity ε is used in QTAIM. Among the endocyclic bonds of 4-NO₂-PyO molecule the highest value of ε = 0.233 is for C2–C3 bond. Accordingly, this bond possesses highest π-character in the ring (in comparison ε = 0.200 for benzene [53]). Surprisingly, the ellipticity value ε = 0.172 for C1–N2 bond is rather large, that could be a sign of the partial π-character of this bond in spite of the delocalization index value (δ = 0.887) corresponds to single (sigma) bond, as well as a bond r(C1–N2) length.

Fig. 6.

The molecular graphs for PyO (left) and 4-NO₂-PyO (right)molecules and net atomic charges (e). The bond critical points are green, ring critical point is yellow.

Fig. 7.

The Laplacian map in the ring plane of PyO (left) and 4-NO₂-PyO (right) molecules. The solid lines (blue) correspond to local charge accumulation (∇²ρ_b < 0), dashed lines (red) represent a local charge depletion (∇²ρ_b > 0).

Table 6.

Bond lengths and topological parameters of ρ(r)^∗ in some bond critical points of 4- nitropyridine-N-oxide and pyridine-N-oxide (B3LYP/aug-cc-pVTZ).

	re, Å	ρb	∇2ρ	λ1	λ3	λ3	Hb	ε	δ
4- nitropyridine-N-oxide
N1–O1	1.264	0.453	−0.767	−1.183	−1.100	1.516	−0.517	0.076	1.557
N2–O2	1.224	0.508	−1.142	−1.141	−1.272	1.542	−0.671	0.109	1.646
N1–C3	1.373	0.316	−0.784	−0.697	−0.582	0.495	−0.460	0.198	1.094
C1–N2	1.460	0.272	−0.758	−0.592	−0.505	0.378	−0.321	0.172	0.887
C2–C3	1.372	0.335	−1.141	−0.762	−0.618	0.238	−0.402	0.233	1.414
C2–C1	1.389	0.325	−1.087	−0.733	−0.613	0.260	−0.378	0.195	1.300
pyridine-N-oxide
N1–O1	1.275	0.439	−0.680	−1.134	−1.057	1.510	−0.483	0.073	1.523
N1–C3	1.367	0.319	−0.790	−0.711	−0.589	0.510	−0.468	0.206	1.110
C2–C3	1.378	0.331	−1.121	−0.753	−0.612	0.244	−0.394	0.230	1.395
C2–C1	1.390	0.323	−1.073	−0.723	−0.609	0.260	−0.374	0.186	1.368

∇²ρ-the Laplacian(a.u.).

λ₁, λ₂, λ₃- electron density Hessian matrix eigenvalues (a.u.).

H_b - the total electronic energy density (a.u.).

ε- the bond ellipticity.

δ- the electronic delocalization index.

^∗- ρ- the electron density(a.u.).

The net atomic charges obtained by QTAM approach are presented in Fig. 6 and in Table 7 . Some differences of the net atomic charges obtained by NPA, Natural Population Analysis, (Table 5) and by QTAIM approach (Table 7) should be noted, although the general trends in the values remain from PyO to 4-NO₂-PyO. According to QTAIM results, the atomic charge on the ipso carbon atom C1 in 4-NO₂-PyO significantly changes in comparison with PyO because of a neighbor to acceptor –NO₂ group. The electron density on C2, C5 and N1 atoms in 4-NO₂-PyO is decreased also due to negative mesomeric effect which takes place inside the pyridine ring. The total charge q(ring) of the heterocyclic ring in PyO has a positive value + 0.274e which is increased up to +0.626e when –NO₂ group has been introduced. Indeed, the electron-withdrawing –NO₂ group is a part of π-conjugated system of the molecule, and as result electron density is shifted from O1 atom and pyridine ring towards the substituent. The negative total charge of –NO₂ group q(R) has a value −0.529e, that additionally supports the suggestion mentioned above. We would like to point out the magnitude of electron density into pyridine ring is changed quantitatively but topologically electron density distribution does not changed dramatically between non- and substituted pyridine-N-oxides (see Fig. 7 and Table 6). At the same time a decrease of the charge on O1 atom can lead to a decrease in the complex formation ability of the substance.

Table 7.

Net atomic charges (q, ē) as obtained by QTAIM analysis.

	PyO	4-NO2-PyO
q(O1)	−0.568	−0.521
q(N1)	−0.555	−0.521
q(O2)	–	−0.465
q(N2)	–	0.402
q(C3)	0.391	0.395
q(C2)	0.020	0.058
q(C1)	0.007	0.241
q(ring)∗	0.274	0.626
q(R)∗	0.034	−0.529

^∗q(ring) – total charge of the heterocyclic ring (C1–C2–C4–N1–C5–C3). q(R) - total charge of the substituent.

The redistribution of electron density in 4-NO₂-PyO affects to geometrical structure of the pyridine ring. The introduction of–NO₂ is accompanied by an increase of ρ _b from 0.323 a.u. in PyO to 0.325 a.u. in 4-NO₂-PyO and of ellipticity value ε from 0.186 to 0.195 for C1–C2 bond, respectively (see Table 6). That leads to magnification of electrostatic repulsion between these bonds and as result the ipso-angle C2C1C5 is changed from 117.7° in PyO to 119.9° in 4-NO₂-PyO (B3LYP/aug-cc-pVTZ).It is interesting to note the same tendency is observed for crystal data where the ipso-angle C2C1C5 increased from 117.9° to 120.5° (see Table 4).

We can suspect the similar changes in electron density for crystal phase as for free molecules observed. Indeed, the PyO molecules are aggregated into crystal pack mostly due to hydrogen bonds between oxygen atom of semipolar bond N→O and hydrogen atoms in 2- and 6- ring positions of neighboring molecules PyO [23]. According to Wang Y. et al. [23] the crystal pack of 4-nitropyridine-N-oxide is formed by parallel layers. Furthermore, the oxygen atom of N→O semipolar bond of one molecule is situated approximately above the center of N–C distance between nitro group and pyridine ring of another molecule, wherein the N⋯O distance is shorter than the C⋯O distance (2.99 Å and 3.06 Å correspondingly). The reason of layered structure could be an appearance of additional hydrogen bonds due to negatively charged oxygen atoms of –NO₂ group and increased positive charges of the hydrogen atoms in 4-NO₂-PyO molecule in comparison to pyridine-N-oxide. Such assumption fully corresponds to net atomic charges distribution obtained by QTAM for free PyO and 4-NO₂-PyO molecules (see Fig. 6). The mutual molecules position in crystal can be explained by electrostatic attraction between negatively charged oxygen and positively charged nitrogen and carbon atoms. Moreover according to result of calculations the charge of nitrogen atom in –NO₂ is larger than that for carbon (+0.402e and +0.241e correspondingly), it is the possible explanation for shorter N⋯O contact in comparison to C⋯O distance. As we can see the simple electrostatic model which employing the Bader’s atomic charges of free 4-NO₂-PyO molecule allows describing correctly the arrangement of these molecules inside the crystal. Galmés B. et al. [54] had attempted to characterize the geometric features of the nitropyridine-1-Oxides complexes employing the molecular electrostatic potential and results of QTAIM. The position of 4-NO₂-PyO molecules in the crystal pack has been described as interaction between р-hole donor nitro group of one molecule and oxygen atom of N→O semipolar bond of another. Both conceptions work well however the simple electrostatic model of atomic charges seems to be easier for understanding.

The most interesting features of the topological analysis of 4-NO₂-PyO are related to the N1→O1 semipolar bond. Along with the substantially high electron density concentration and rather large value of the electronic delocalization index, the bond ellipticity value is noticeably low. These features confirm that N1→ O1 bond is predominantly covalent and possess the cylindrical symmetry. On the other hand, NBO analysis shows the presence of lone pare LP(O1) interaction with the antibonding π∗(N1–C3) NBO [21] in the pyridine-N-oxide molecules. Apparently, the question about the semipolar N→O bond nature requires further research.

6. Conclusion

In our research we are trying to understand the influence of the nature of substituents on the properties of N-oxides. In this work the molecular structure of 4-nitropyridine N-oxide has been studied by GED/MS and quantum chemical calculations (DFT and MP2). Both, quantum chemistry and GED analyses resulted in the C _2v molecular symmetry with the planar pyridine ring and –NO₂ group which is coplanar to the six-membered heterocycle. Furthermore, the rotation of –NO₂-groupmore than for 12° leads to the significant increase in energy.

The electron density distribution and molecular structure of 4-NO₂-PyO are compared with non-substituted PyO and with 4-Me-PyO. The total charge of the heterocyclic ring in PyO increases when –NO₂ group has been introduced. Indeed, the electron-withdrawing –NO₂ group is a part of π-conjugated system of 4-NO₂-PyO molecule, and as result electron density is shifted towards the substituent. The electron density redistribution with the substituent introduction results foremost in the values of heterocycle ipso-angle. Thus, the presence of the electron-withdrawing –NO₂ group leads to an increase of the ipso-angle, whereas electron-donating –CH₃ substituent in 4-Me-PyO produces the opposite effect.

Surprisingly, the r(N1→O1) semipolar bond appears to be also sensitive to a substituent in para-positon nature. The presence of electron withdrawing –NO₂ group in 4-NO₂-PyO results in a shortening of r(N→O) in comparison with PyO, the corresponding bond order increases, and the negative net charge on the oxygen atom decreases, while in 4-Me-PyO with the donor substituent all changes are opposite. Furthermore, the semipolar N1→O1 bond reveals very interesting properties. According to QTAIM N1→O1 semipolar bond is predominantly covalent and possess the cylindrical symmetry. At the same time the electron density concentration is substantially high in comparison with the values for all bonds in heterocycle and the value of the electronic delocalization index for N1→O1 bond is rather large, that is usually appropriate to the bonds with π-contribution. The value of δ(N1→O1) is even close to δ(N2→O2).

The presence of different substituents in the heterocycle may vary the properties and, as the result, the reactivity of N-oxides. Apparently, the variation of the substituents gives wide possibilities to chemical modifications of N-oxides and allows to change their biological activity.

CRediT authorship contribution statement

Natalya V. Belova: Conceptualization, Methodology, Data curation, Investigation, Writing - original draft. Oleg A. Pimenov: Investigation, Formal analysis, Data curation, Visualization, Writing - original draft. Vitaliya E. Kotova: Data curation, Formal analysis. Georgiy V. Girichev: Methodology, Writing - review & editing.

Declaration of Competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following is the Supplementary data to this article: