Statistical tests for latent class in censored data due to detection limit

Abstract

Measures of substance concentration in urine, serum or other biological matrices often have an assay limit of detection. When concentration levels fall below the limit, the exact measures cannot be obtained. Instead, the measures are censored as only partial information that the levels are under the limit is known. Assuming the concentration levels are from a single population with a normal distribution or follow a normal distribution after some transformation, Tobit regression models, or censored normal regression models, are the standard approach for analyzing such data. However, in practice, it is often the case that the data can exhibit more censored observations than what would be expected under the Tobit regression models. One common cause is the heterogeneity of the study population, caused by the existence of a latent group of subjects who lack the substance measured. For such subjects, the measurements will always be under the limit. If a censored normal regression model is appropriate for modeling the subjects with the substance, the whole population follows a mixture of a censored normal regression model and a degenerate distribution of the latent class. While there are some studies on such mixture models, a fundamental question about testing whether such mixture modeling is necessary, i.e. whether such a latent class exists, has not been studied yet. In this paper, three tests including Wald test, likelihood ratio test and score test are developed for testing the existence of such latent class. Simulation studies are conducted to evaluate the performance of the tests, and two real data examples are employed to illustrate the tests.

1. Introduction

Measures of substance concentration in urine, serum or other biological matrices that fall below the assay limit of detection are pretty common in environmental science and medical research.^1–10 When the concentrations are under the limit of detection, accurate measures cannot be obtained. Instead, their values are only partially known and left censored. For example, triclosan is a broad-spectrum antimicrobial chemical and widely used in household and health care related products. Currently the detection limit for urine triclosan concentration is 2.3ng/ml. Only triclosan concentrations greater than or equal to 2.3ng/ml can be detected. For triclosan concentrations lower than 2.3ng/ml, the value is censored. Instead of a precise measure of the triclosan concentration, the value is only partially known, namely that is somewhere between 0 and 2.3. Methods for handling censored data due to detection limit include deletion or substitution with 0, the detection limit, or half or one-third of the detection limit. These methods are commonly used in practice despite their inappropriateness.^1,11–15

When data are collected from a single normal distribution with some observations under the detection limit, a Tobit regression model should be applied.^4,16–22 The Tobit regression model is widely applied in economics,^23–27 and other fields such as medical research^10,28–32 and environmental research.^6,7,33–35 In cases where the data are not from a normal distribution, data transformation such as log-transformation can be employed first, and the Tobit regression model can then be applied on the transformed data.

A Tobit regression model assumes that the underlying latent continuous measure follows a single normal distribution, but the observed outcome is subject to censoring due to the detection limit. Given a distribution and detection limit, the proportion of under detection can be approximately determined. However, when there is a subgroup of subjects who don’t have the substance at all, their measures are of course under the detection limit and thus are censored. In such case, the subgroup of subjects make up a latent class as their measures are always censored, and the data can exhibit more censored observations than what would be expected according to the Tobit regression model, and makes the Tobit regression model assumption violated. This latent class issue was acknowledged in Halsey et al.³⁶ Some methods such as a mixture model were proposed to address this issue.^37–39 However, a fundamental question about whether there is a latent class is not studied in the literature.

In this paper, three tests including the Wald test, likelihood ratio (LR) test and score test⁴⁰ are developed for testing if a latent class exists. A brief review of the Tobit regression models and mixture Tobit regression models are given first in Section 2, and the three tests are developed in Section 3. Simulation studies to investigate and compare the performance of tests are given in Section 4, and two real data examples to illustrate the methods are given in Section 5. The paper is concluded with a discussion in Section 6.

2. Tobit model and mixture Tobit model

Consider an independent sample (x_i, y_i), i = 1, …, n, where x_i = (x_i1, x_i2, …, x_ip) is a p-dimensional covariate, and y_i is the observed censored measurement. The observed y_i is obtained based on a latent variable $y_i^{*}$, which is assumed to have a linear relationship with x_i through a parameter vector β, i.e.

$$y_i^{*}={\mathbf{x}}_i^{\top }\beta +{\epsilon }_i,{\epsilon }_i\sim \mathrm{N}\left(0,{\sigma }^2\right)$$ (1)

Let L be the lower detection limit, and a Tobit model censored at L is defined as

$$y_i=\{\begin{array}{ll}{y}_i^{*}\hfill & \text{if}{y}_i^{*}\ge L\hfill \\ L\hfill & \text{if}{y}_i^{*}<L\hfill \end{array}$$

Due to censoring, the variable $y_i^{*}$ cannot be measured (or detected) if its value is below L. In such cases, its value is substituted by the threshold L. Under the assumption that the underlying variable $y_i^{*}$ follows a normal distribution with mean ${\mu }_i={\mathbf{x}}_i^T\beta$, where the design matrix includes a constant for the intercept, then the observed y_i follows a Tobit model, denoted as y_i ~ Tobit (μ_i, σ², L), and has the following distribution

$$\mathrm{Pr}\left(Y_i=y_i\right)=\{\begin{array}{ll}\frac{1}{\sqrt{2\pi }\sigma }\exp \left(-\frac{{\left(y_i-{\mu }_i\right)}^2}{2{\sigma }^2}\right)\hfill & \text{if}{y}_i>L,\hfill \\ \mathrm{\Phi }\left(\frac{L-{\mu }_i}{\sigma }\right)\hfill & \text{if}{y}_i=L\hfill \end{array}$$

The Tobit regression model can be expressed as

$$y_i|{\mathbf{x}}_i\sim \text{i.d.}\text{Tobit}\left({\mu }_{\mathrm{i}},{\sigma }^2,\text{L}\right),{\mu }_{\mathrm{i}}={\mathbf{x}}_{\mathrm{i}}^{\text{T}}\beta$$ (2)

Let r_i be an indicator indicating whether y_i is censored or not, with r_i =1 for y_i = L and r_i = 0 for y_i > L. The likelihood function for the ith subject is given by

$$L_i={\left[\mathrm{\Phi }\left(\frac{L-{\mu }_i}{\sigma }\right)\right]}^{r_i}{\left[\frac{1}{\sqrt{2\pi }\sigma }\exp \left(-\frac{{\left(y_i-{\mu }_i\right)}^2}{2{\sigma }^2}\right)\right]}^{\left(1-r_i\right)}$$ (3)

where Φ(·) is the cumulative distribution function of the standard normal. Given the likelihood in equations (3) and model (2), maximum likelihood method can be applied to estimate β and σ.

For the Tobit regression model, the proportion of under the detection limit is $E\left[\mathrm{\Phi }\left(\frac{L-{\mu }_i}{\sigma }\right)\right]$, and can be estimated by $\frac{{\sum }_{i=1}^n{r}_i}{n}$. But when there is a latent class of subjects who don’t have the substance at all, their measures are of course under the detection limit and thus are censored. In such case, the data can exhibit more censored observations than what would be expected according to the Tobit regression model, i.e. the proportion of under-detection is much higher than $E\left[\mathrm{\Phi }\left(\frac{L-{\mu }_i}{\sigma }\right)\right]$.

When there is a latent class such as non-exposure, the Tobit regression model for a single population such as exposure is not appropriate to model such censored data anymore, and some methods such as a mixture model were proposed to address this issue.^37–39 Let ω be the probability of the latent class. Data from a mixture of the latent class with probability ω and Tobit model with probability (1 − ω), named mixture Tobit model and denoted as mTobit (ω, μ_i, σ², L), has likelihood function for the ith subject expressed as

$$L_i={\left[\omega +(1-\omega )\mathrm{\Phi }\left(\frac{L-{\mu }_i}{\sigma }\right)\right]}^{r_i}{\left[(1-\omega )\frac{1}{\sqrt{2\pi }\sigma }\exp \left(-\frac{{\left(y_i-{\mu }_i\right)}^2}{2{\sigma }^2}\right)\right]}^{\left(1-r_i\right)}$$ (4)

The mTobit (ω, μ_i, σ², L) is a mixture of a latent class with probability ω and a Tobit model with probability (1 − ω). Thus, the proportion of under detection now becomes $\omega +(1-\omega )E\left[\mathrm{\Phi }\left(\frac{L-{\mu }_i}{\sigma }\right)\right]$, which is always greater than $E\left[\mathrm{\Phi }\left(\frac{L-{\mu }_i}{\sigma }\right)\right]$ for ω > 0. Therefore, ω is a parameter indicating the excessive observations under the detection limit.

If the probability of the latent class depends on some covariates, say u_i, a generalized linear model such as a logistic regression model can usually be applied to model the latent class and a linear model is used to model the Tobit component. A mixture Tobit regression model can have the following form

$$y_i|{\mathbf{x}}_i\sim \text{i.d.}\text{mTobit}\left({\omega }_i,{\mu }_i,{\sigma }^2,\mathrm{L}\right),\mathrm{logit}\left({\omega }_i\right)={\mathbf{u}}_i^{\top }{\beta }_{\omega },{\mu }_i={\mathbf{x}}_i^T{\beta }_{\mu }$$ (5)

The covariates u_i and x_i in the two components can be the same or different. If the probability ω does not depend on any covariates, i.e. ω is a constant, then there is no need for a link function, and thus the mTobit model in equation (5) can actually be represented as a linear regression model with

$$y_i|{\mathbf{x}}_i\sim \text{i.d.}\text{mTobit}\left({\omega }_{\text{i}},{\mu }_{\text{i}},{\sigma }^2,\text{L}\right),{\omega }_{\text{i}}=\omega ,{\mu }_{\text{i}}={\mathbf{x}}_{\text{i}}^{\text{T}}\beta$$ (6)

Given the likelihood in equations (4) and model (5) or (6), we can apply the maximum likelihood method to obtain the MLE of β_ω, β_μ or β, as well as ω and σ.

Under equation (5), the probability ω_i is always positive, and thus the models (2) and (5) are not nested, and commonly used tests such as the Wald and LR tests cannot be directly applied to test the latent class. However, if we simply assume the probability ω_i is a constant as in equation (6), the Tobit regression model (2) is now nested in the mTobit regression model (6) as it corresponds to the cases with ω=0 under equation (6). Therefore, the Wald, LR and score tests for testing whether ω=0 can be applied. When ω is a constant and no link function is necessary as in equation (6), ω can have a negative value to imply that not only there is no latent class, but also the probability of data censored is lower than what would be expected under equation (2), i.e. the data exhibits less amount of observations under detection than what would be expected under the Tobit model. Thus, ω=0 is actually an interior point and we don’t have the non-standard condition issue when ω can only take non-negative values.

3. Tests for the latent class

In this section, we will develop three tests, the Wald, LR, and score tests, for testing whether there is a latent class in a Tobit model.

3.1. Wald test

The Wald test for testing H₀ : ω=0 vs. H_A : ω ≠ 0 is developed based on the MLE estimate of ω under the mTobit model (6). Let ${\mu }_i={\mathbf{x}}_i^T\beta$ be the mean of the Tobit component, and the log-likelihood for the ith subject is

$$l_i=r_i\log \left[\omega +(1-\omega )\mathrm{\Phi }\left(\frac{L-{\mu }_i}{\sigma }\right)\right]+\left(1-r_i\right)\left[\log (1-\omega )-\log (\sqrt{2\pi }\sigma )-\frac{{\left(y_{i-}{\mu }_i\right)}^2}{2{\sigma }^2}\right]$$

So, the log-likelihood for the whole sample is

$$l(\omega ,\beta ,\sigma )={\sum }_{i=1}^n{r}_i\log \left[\omega +(1-\omega )\mathrm{\Phi }\left(\frac{L-{\mu }_i}{\sigma }\right)\right]+\left(1-r_i\right)\left[\log (1-\omega )-\log (\sqrt{2\pi }\sigma )-\frac{{\left(y_i-{\mu }_i\right)}^2}{2{\sigma }^2}\right]$$ (7)

Taking the first derivative of l(ω, β, σ) □ corresponding to ω, β, σ, we have

$$S_{{\beta }_s}=\frac{\partial l}{\partial {\beta }_s}=\sum _{i=1}^n\left\{-\frac{r_i}{{\phi }_i}(1-\omega )A_i\frac{x_{is}}{\sigma }+\left(1-r_i\right)\frac{y_{i-}{\mu }_i}{{\sigma }^2}{x}_{is}\right\},s=1,2,\dots ,p$$ (8)

$$S_{\sigma }=\frac{\partial l}{\partial \sigma }=\sum _{i=1}^n\left\{-\frac{r_i}{{\phi }_i}{A}_i(1-\omega )\frac{L-{\mu }_i}{{\sigma }^2}+\left(1-r_i\right)\left[-\frac{1}{\sigma }+\frac{{\left(y_i-{\mu }_i\right)}^2}{{\sigma }^3}\right]\right\}$$ (9)

$$S_{\omega }=\frac{\partial l}{\partial \omega }=\sum _{i=1}^n\left\{\frac{r_i-{\phi }_i}{(1-\omega ){\phi }_i}\right\}$$ (10)

where $A_i=\frac{1}{\sqrt{2\pi }}\exp \left(-\frac{{\left(L-{\mu }_i\right)}^2}{2{\sigma }^2}\right)$ and ${\phi }_i=\omega +(1-\omega )\mathrm{\Phi }\left(\frac{L-{\mu }_i}{\sigma }\right)$. The MLE of ω, β and σ can be obtained by simultaneously solving $S_{{\beta }_s}=0$, s = 1, 2, …, p, S_σ = 0 and S_ω = 0. The asymptotic variance of the MLE of ω can further be estimated by the Fisher information matrix. Let $\widehat{\omega }$ be the MLE of ω under equation (6) and ${\widehat{\sigma }}_{\omega }$ the estimated variance of $\widehat{\omega }$. Then, the Wald statistic is defined as $S_{Wald}={\widehat{\omega }}^2/{\widehat{\sigma }}_{\omega }^2$. Under H₀ : ω = 0, the Wald statistic asymptotically follows a chi-square distribution, i.e. $S_{Wald}={\widehat{\omega }}^2/{\widehat{\sigma }}_{\omega }^2\sim {\chi }_1^2$. Since the parameter ω is only one-dimensional, it is equivalent to the Z-statistic

$$Z_{Wald}=\widehat{\omega }/{\widehat{\sigma }}_{\omega }\sim N(0,1)$$ (11)

For a two-sided test against the alternative H_A : ω ≠ 0, i.e. the amount of observations under detection is different from what would be expected by the Tobit model in either direction, with a type I error α, we reject H₀ if $\left|Z_{Wald}\right|>Z_{\alpha /2}$, where Z_a/2 is the 100(1 – α/2) percentile of the standard normal. For a one-sided test with alternative H_A : ω > 0, i.e. the amount of observations under detection is more than what would be expected under a Tobit regression model, we reject H₀ if Z_Wald > Z_α.

It is worth to note that the Hessian matrix of mTobit models can be singular, and thus the MLEs may not exist. For example, if the mean ${\mu }_i^{\prime }s$ are small while the detection limit L is large, in which most of the outcomes are undetectable, or the ${\mu }_i^{\prime }s$ are large while L is small, in which there are too few observations under detection, the optimization of the log-likelihood of the mTobit models (6) is likely to fail, and thus the MLEs do not exist. In such cases, the Wald test cannot be applied.

3.2. Likelihood ratio test

The LR test is based on the likelihoods of the data under both models (6) and (2). Let $\widehat{\omega }$, $\widehat{\beta }$ and $\widehat{\sigma }$ be the MLE of ω, β, and σ under equation (6), and ${\widehat{\beta }}^{\prime }$ and ${\widehat{\sigma }}^{\prime }$ be the MLE of β and σ under equation (2). Then, the corresponding log-likelihood at the MLEs for the two models are $l(\widehat{\omega },\widehat{\beta },\widehat{\sigma })$ and $l(0,{\widehat{\beta }}^{\prime },{\widehat{\sigma }}^{\prime })$. The LR statistic would then be

$$S_{LR}=2(l(\widehat{\omega },\widehat{\beta },\widehat{\sigma })-l(0,{\widehat{\beta }}^{\prime },{\widehat{\sigma }}^{\prime }))\sim {\chi }_1^2$$ (12)

The LR statistic S_LR asymptotically follows a ${\chi }_1^2$ distribution as there is only one more parameter in the mTobit model than the Tobit model. For a two-sided test with type I error α, we reject H₀ if $S_{LR}>{\chi }_{1,1-\alpha }^2$, where ${\chi }_{1,1-\alpha }^2$ is the 100(1 − α) percentile of a χ² distribution. For a one-sided test with alternative H_A : ω > 0, we may combine the test statistic with the estimate $\widehat{\omega }$ by restricting on the cases where $\widehat{\omega }>0$. The H₀ is rejected when $\widehat{\omega }>0$ and $S_{LR}>{\chi }_{1,1-2\alpha }^2$. Note that the 100(1 − 2α) percentile of a χ² distribution is used for type I error α because, under H₀, there is about a 50% chance for $\widehat{\omega }$ to be negative or positive.

The LR test requires the fit of both the Tobit and mTobit models, as well as the existence of MLEs, and thus suffers the same issue as the Wald test.

3.3. Score test

Without actually fitting a mTobit model, the score statistic can be computed under H₀ : ω = 0. The score functions are the first derivative of (7) corresponding to β, σ and ω, which is given by equations (8), (9) and (10). Under the null hypothesis H₀ : ω=0, and given the MLE $\widehat{\beta }$ and $\widehat{\sigma }$ of β and σ, based on equations (8), (9) and (10), we have $S_{{\beta }_s}|\widehat{\beta }=0$, s = 1, 2, …, p, $S_{\sigma }|\widehat{\sigma }=0$, and ${S_{\omega }|}_{\widehat{\beta },\widehat{\sigma },\omega =0}={\sum }_{i=1}^n\frac{r_i-{\widehat{B}}_i}{{\widehat{B}}_i}$, where ${\widehat{B}}_i=\mathrm{\Phi }\left(\frac{L-{\widehat{\mu }}_i}{\widehat{\sigma }}\right)$. Therefore the score function under H₀ and MLE of β and σ becomes

$$U^T(\widehat{\beta },\widehat{\sigma },0)=\left(0,0,\dots ,0,0,\sum _{i=1}^n\frac{r_i-{\widehat{B}}_i}{{\widehat{B}}_i}\right)$$ (13)

where $U^T(\widehat{\beta },\widehat{\sigma },0)$ is a vector with (p + 2) elements with the first p zeros are for the score values of ${\widehat{\beta }}_1,{\widehat{\beta }}_2,\dots ,{\widehat{\beta }}_p$, and the (p + 1)^th zero is for the score value of $\widehat{\sigma }$.

Let J(β, σ, ω) be the expected information matrix, and $\mathbf{J}(\widehat{\beta },\widehat{\sigma },0)$ be the estimate of J(β, σ, ω) under H₀ : ω = 0 and $\widehat{\beta }$, $\widehat{\sigma }$, then $\mathbf{J}(\widehat{\beta },\widehat{\sigma },0)$ can be expressed as

$$\begin{gathered} \mathbf{J}(\widehat{\beta },\widehat{\sigma },0)={\mathbf{J}(\beta ,\sigma ,\omega )|}_{\widehat{\beta },\widehat{\sigma },\omega =0}=\left[\begin{array}{ccc}{\widehat{\mathbf{J}}}_{\beta \beta }& {\widehat{\mathbf{J}}}_{\beta \sigma }& {\widehat{\mathbf{J}}}_{\beta \omega }\\ {\widehat{\mathbf{J}}}_{\sigma \beta }& {\widehat{\mathbf{J}}}_{\sigma \sigma }& {\widehat{\mathbf{J}}}_{\sigma \omega }\\ {\widehat{\mathbf{J}}}_{\omega \beta }& {\widehat{\mathbf{J}}}_{\omega \sigma }& {\widehat{\mathbf{J}}}_{\omega \omega }\end{array}\right] \\ =\left[\begin{array}{lll}{\mathbf{E}\left(-\frac{d^{2}l(\cdot )}{d\beta d\beta }\right)|}_{\widehat{\beta },\widehat{\sigma },\omega =0}& {\mathbf{E}\left(-\frac{d^{2}l(\cdot )}{d\beta d\sigma }\right)|}_{\widehat{\beta },\widehat{\sigma },\omega =0}& {\mathbf{E}\left(-\frac{d^{2}l(\cdot )}{d\beta d\omega }\right)|}_{\widehat{\beta },\widehat{\sigma },\omega =0}\\ {\mathbf{E}{\left(-\frac{d^{2}l(\cdot )}{d\beta d\sigma }\right)}^T|}_{\widehat{\beta },\widehat{\sigma },\omega =0}& {\mathbf{E}\left(-\frac{d^{2}l(\cdot )}{d\sigma d\sigma }\right)|}_{\widehat{\beta },\widehat{\sigma },\omega =0}& {\mathbf{E}\left(-\frac{d^{2}l(\cdot )}{d\sigma d\omega }\right)|}_{\widehat{\beta },\widehat{\sigma },\omega =0}\\ {\mathbf{E}{\left(-\frac{d^{2}l(\cdot )}{d\beta d\omega }\right)}^T|}_{\widehat{\beta },\widehat{\sigma },\omega =0}& {\mathbf{E}\left(-\frac{d^{2}l(\cdot )}{d\sigma d\omega }\right)|}_{\widehat{\beta },\widehat{\sigma },\omega =0}& {\mathbf{E}\left(-\frac{d^{2}l}{d\omega d\omega }\right)|}_{\widehat{\beta },\widehat{\sigma },\omega =0}\end{array}\right] \end{gathered}$$ (14)

where ${\widehat{\mathbf{J}}}_{\beta \beta }$ is a p×p matrix, ${\widehat{\mathbf{J}}}_{\beta \sigma }$ and ${\widehat{\mathbf{J}}}_{\beta \omega }$ are p × 1 matrix, ${\widehat{\mathbf{J}}}_{\sigma \sigma }$, ${\widehat{\mathbf{J}}}_{\sigma \omega }$ and ${\widehat{\mathbf{J}}}_{\omega \omega }$ are scalar. Other elements ${\widehat{\mathbf{J}}}_{\sigma \beta }={\widehat{\mathbf{J}}}_{\beta \sigma }^T$, ${\widehat{\mathbf{J}}}_{\omega \beta }={\widehat{\mathbf{J}}}_{\beta \omega }^T$ and ${\widehat{\mathbf{J}}}_{\omega \sigma }={\widehat{\mathbf{J}}}_{\sigma \omega }^T$.

Given the estimate of the expected information matrix $\mathbf{J}(\widehat{\beta },\widehat{\sigma },0)$, the score statistic for testing ω=0 can be written as

$$\begin{gathered} S_{Score}=U^T(\widehat{\beta },\widehat{\sigma },0){[\mathbf{J}(\widehat{\beta },\widehat{\sigma },0)]}^{-1}U(\widehat{\beta },\widehat{\sigma },0) \\ =\frac{{\left({\sum }_{i=1}^n\frac{r_i-{\widehat{B}}_i}{{\widehat{B}}_i}\right)}^2}{{\widehat{\mathbf{J}}}_{\omega \omega }-{\widehat{\mathbf{J}}}_{\omega \beta }{\widehat{\mathbf{J}}}_{\beta \beta }^{-1}{\widehat{\mathbf{J}}}_{\beta \omega }-{\widehat{\mathbf{J}}}_{\omega \beta }VW{V}^T{\widehat{\mathbf{J}}}_{\beta \omega }+{\widehat{\mathbf{J}}}_{\omega \sigma }W{V}^T{\widehat{\mathbf{J}}}_{\beta \omega }+{\widehat{\mathbf{J}}}_{\omega \beta }VW{\widehat{\mathbf{J}}}_{\sigma \omega }-{\widehat{\mathbf{J}}}_{\omega \sigma }W{\widehat{\mathbf{J}}}_{\sigma \omega }} \end{gathered}$$ (15)

where $V={\widehat{\mathbf{J}}}_{\beta \beta }^{-1}{\widehat{\mathbf{J}}}_{\beta \sigma }$ and $W={({\widehat{\mathbf{J}}}_{\sigma \sigma }-{\widehat{\mathbf{J}}}_{\sigma \beta }{\widehat{\mathbf{J}}}_{\beta \beta }^{-1}{\widehat{\mathbf{J}}}_{\beta \sigma })}^{-1}$. Under H₀ : ω=0, the statistic $S_{Score}\sim {\chi }_1^2$. The technical details for developing the score test are given in the Web Appendix.

For a two-sided test with type I error α, we reject H₀ : ω = 0 vs. H_A : ω ≠ 0 when $S_{Score}>{\chi }_{1,1-\alpha }^2$. For a one-sided test H₀ : ω = 0 vs. H_A : ω > 0, we can consider the statistic $Z_{\mathit{Score}}=\frac{{\sum }_{i=1}^n\frac{r_i-{\widehat{B}}_i}{{\widehat{B}}_i}}{s_I}$, where s_I is the square-root of the (p + 2, p + 2)^th term of the inverse of the Fisher information matrix evaluated at ω=0, $\widehat{\beta }$ and $\widehat{\sigma }$, i.e. $s_I^2={[\mathbf{J}(\widehat{\beta },\widehat{\sigma },0)]}_{(p+2,p+2)}^{-1}$. Under H₀ : ω = 0, the statistic Z_Score ~ N(0, 1). We reject the null hypothesis if Z_Score > Z_α for the one-sided test with type I error α.

Compared to the Wald and LR tests, the score test only requires fitting a Tobit model (2), the Wald test requires fitting an mTobit model, and the LR test requires fitting both models. When the MLE for the mTobit model doesn’t exist, the Wald test and LR test cannot be applied, but the score test can be still performed. Hence, the score test is preferred to the other two tests in such situations.

4. Simulation studies

4.1. Simulation setup

We use simulation studies to examine and compare the performance of the three tests. In all the simulation studies, we consider a one-sided test to test whether there is a latent class in the data, i.e. we tested H₀ : ω = 0 vs H_A : ω > 0. Two sets of simulation studies are considered, one with data generated from a Tobit model, in which type I error of rejecting the null hypothesis is assessed when H₀ : ω = 0 is true, and the other with data generated from a mTobit model. In this case, the power of rejecting the null hypothesis is assessed when it is not true. In all the simulation studies, the detection limit L is fixed to be −1, and the variance for the Tobit model is fixed to be 4, but with varying means, i.e. y ~ Tobit (μ, 4, −1). The varying mean yields different proportions of data under the detection limit and allows us to investigate how the performance changes with different proportions of data undetected. For the Tobit model, we consider three scenarios, a constant mean and mean changing with covariates from either a bounded uniform distribution or an unbounded normal distribution. For the mTobit model, we consider five scenarios: no covariates for both the latent class and the Tobit component, no covariates for the latent class only, and covariates for both the latent class and the Tobit component. For all the scenarios, small (50 and 100), moderate (200 and 500) and large (1000) sample sizes are considered, and a Monte Carlo (MC) sample size of 1000 is used. The simulations are carried out using R.⁴¹ For the Wald and LR tests, we used the R function “optim” to find the MLE $\widehat{\omega }$ of ω, and the standard error of $\widehat{\omega }$ is based on estimated Hessian matrix.

4.2. Tobit response

Under the Tobit model, the null hypothesis H₀ : ω = 0 (vs. H₁ : w > 0) is true, and the type I error of rejecting H₀ is used to evaluate the performance of the tests. In addition to providing rejection rates across the 1000 MC replications, we also used QQ plots, a plot of p values based on the asymptotic distribution of test statistic versus the corresponding empirical type I errors, which can serve as the true nominal level, based on 1000 MC replications, for a comprehensive evaluation of the performances. For a test to have a good performance, the p-value calculated based on the asymptotic distribution of the test statistics should be close to its corresponding empirical type I error. Thus, a QQ plot close to the diagonal line indicates a good performance, while deviation of the QQ plot from the diagonal line indicates how poor the performance is. Since the nominal level is usually very small, such as 0.05, we focused on the (0, 0) end of the QQ plot. If a QQ plot lies above (under) the diagonal lines, then the tests are less (more) likely to reject the null hypothesis than it should be.

4.2.1. No covariate

Data y_i is generated from N (μ, 4), with mean μ = −1.5, −0.5, 0.5 and 1.5. y_i is replaced by −1 if its value is less than −1. The corresponding proportion of data under the detection limit is about 60%, 40%, 22% and 10%, respectively. The p values of rejecting the null hypothesis are summarized in the QQ plots presented in Figure 1. Overall, the LR test outperforms other two tests and performs very well in general, even when sample size is small. As expected, all the tests perform better as the sample size increases. When the sample size is 1000, the tests perform quite well except the Wald test when μ = −1.5 and –0.5, which corresponds to 60% or 40% of under detection.

Figure 1.

QQ plots of theoretical p-values and the corresponding empirical type I errors for the Tobit model without covariates and sample sizes 50, 100, 200, 500, and 1000.

The performances of the Wald test and score test are clearly affected by the proportion of data under detection. When the proportion of under detection is large, such as μ = –1.5 or –0.5, the score test and Wald test do not perform well, especially when the sample size is small. In these cases, the QQ plots for the Wald and score tests lie below the diagonal lines, which indicate that the two tests are more likely to falsely reject the null hypothesis. This is further confirmed by the rejection rates summarized in Table S1 as a supplementary material. The rejection rates for the Wald test and score test are uniformly higher than the nominal level 0.05. The rates for the Wald test goes as high as 33% at its worst situation when μ is small. As μ increases, i.e. less data falls below the detection limit, the p values are closer to the nominal level. When μ = 1.5, i.e. about 10% of the data are under detection, the QQ lines for the score and Wald tests are very close to the diagonal line as the rejection rates are close to 0.05. It seems that the proportion of under detection does not have notable impact on the LR test, its performance is pretty stable with varying proportion of data under detection, and the rejection rates vibrate around 0.05.

As we noted in Section 3, the LR and Wald tests depend on the existence of an MLE for the mTobit model. Our simulation studies show that this can be problematic. In our study, out of the 1000 samples, when μ = −1.5, MLEs cannot be obtained, and hence the Wald and LR statistics cannot be applied for 52, 19 and 4 samples for sample sizes 50, 100, and 200, respectively. For μ = −0.5, there are eight samples for which the MLE cannot be obtained for sample size 50. For most of cases, there are no under-limit observations at all, thus the MLEs do not exist as the likelihood function (4) is monotone in ω. Note, however, that as a mixture of Tobit and degenerate components, equation (6) is a special case of the mixture model. Since the components of origin are known for observations over the limits, the model (6) is in general identifiable and the methods apply for large samples.

4.2.2. Covariate x ~ Uniform (0, 1)

In this study, the covariate x is generated from a uniform distribution on [0, 1], and y is simulated from Tobit(μ_i, 4, −1) with μ_i = α − x_i, where α is set to be −1, 0, 1 and 2, corresponding to about 60%, 40%, 22% and 10% of the data being under the detection level. Shown in Figure 2 are the QQ plots of the theoretical p value versus the corresponding empirical type I error of the three tests for different sample sizes and α values. The patterns and trends of QQ plots for the three tests are very similar to those in Figure 1 when there are no covariates for the Tobit model. Again, in general, the LR test still outperforms the other tests. Large deviations from the diagonal lines are observed for the Wald test, especially for data with a large proportion of under detection level and small sample sizes. The score test performs pretty well when the proportion of under detection level is around 20% or less. In most of cases, the QQ plots for the score test and Wald tests lie below the diagonal line, and the two tests are also more likely to falsely reject the null hypothesis. The rejection rates across the 1000 replications are summarized in Table S2 in the supplementary material. The Wald test and score test have rejection rates higher than the nominal level 0.05. While for the LR test, the rejection rates are pretty close to the nominal level.

Figure 2.

QQ plots of theoretical p-values and the corresponding empirical type I errors for the Tobit model with uniformly distributed predictors and sample sizes 50, 100, 200, 500, and 1000.

There are still some samples for which the Wald and LR tests cannot be applied as the MLEs do not exist. Out of 1000 samples, when α = −1, the Wald and LR statistics cannot be applied for 36, 13 and 3 samples for sample sizes 50, 100 and 200, respectively. For α = 0, 1 and 2, there are 5, 13 and 112 samples which don’t have MLEs. Those samples are most prevalent for a sample size of 50.

4.2.3. Covariate x ~ N(0, 1)

The covariate x is generated from N(0, 1), and y is generated from Tobit (μ_i, 4, −1) with μ_i = α − x_i, where α is set to be −1.5, −0.5, 0.5 and 1.5, which corresponds to a proportion of about 59%, 41%, 25% and 13% under detection, respectively. The QQ plots are presented in Figure 3. The patterns and trends for the Wald test and score test are pretty similar to that in Figures 1 and 2. However, the LR test performs a little worse than the previous cases based on the plots. The score test performs slightly better than the LR test with the Wald test the worst, especially when the large proportion of data under detection. The rejection rates are summarized in Table S3 as supplementary.

Figure 3.

QQ plots of theoretical p-values and the corresponding empirical type I errors for the Tobit model with normally distributed predictors and sample sizes 50, 100, 200, 500, and 1000.

The number of samples that MLE does not exist are 63, 38, 96 and 265 for α = −1.5, −0.5, 0.5 and 1.5, respectively, and most of them are for sample size 50. When sample size increases to 1000, the issue can be very minor.

4.3. mTobit Model

Next we simulate data from a mixture Tobit model to assess the performance of the tests in terms of power of detecting the latent class when the latent class does exist. We generate data with and without covariates for both the Tobit component and the latent class. We consider the covariate from either uniform or normal distribution. For the Tobit component, the data are generated similarly to the above cases, while for the latent class, we consider two scenarios, no covariates and with covariates.

4.3.1. No covariate for the mTobit model

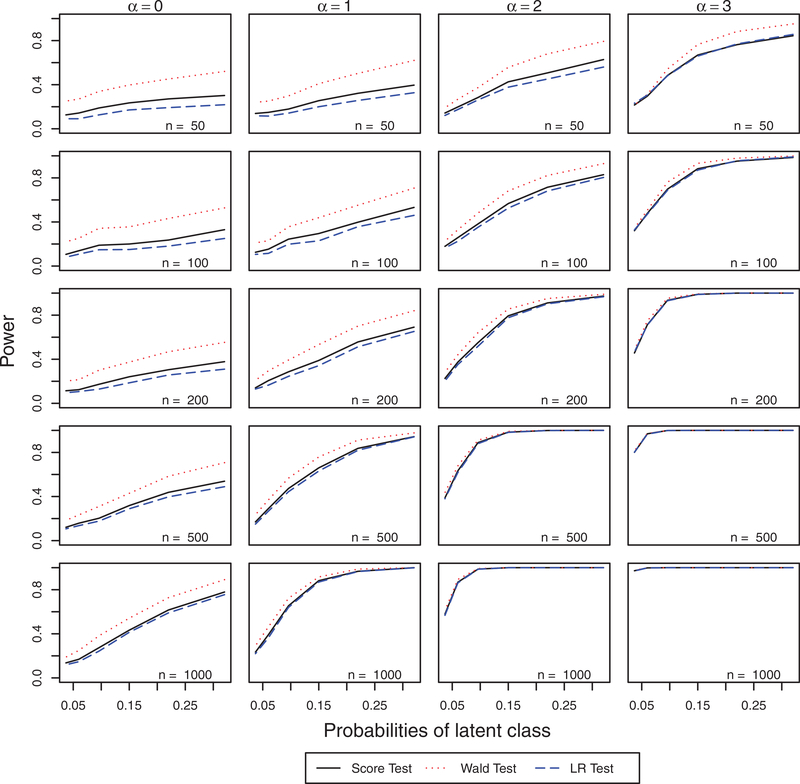
In this case, we generated data from a mixture Tobit model y ~ mTobit (ω, μ, σ², L) with μ = −0.5, 0.5, 1.5 and 2.5, which corresponds to about 40%, 23%, 11% and 4% of data under detection for Tobit component. We let ω = 0.05k, k = 1, 2, …, 6 to investigate how the power changes with ω varying from very small (5%) to moderate (30%). Figures 4 shows the empirical powers of being able to detect the latent class, i.e. the proportion of rejecting the null hypothesis, with a type I error of 5%. The figures show that the power of the LR test in general is less than the Wald and score tests, with the Wald test giving the highest power. This coincides with the fact that the Wald test tends to be more likely to reject the null hypothesis. When μ is fixed, as expected, the power increases as the proportion of the latent class and sample size increases. However, the power is also significantly affected by μ. Since the detection limit is fixed, μ reflects how likely the data is censored, with higher values of μ meaning the data is less likely to be censored. The plots indicate that with fixed ω and sample size, as more data from the Tobit components are censored, the tests are less powerful in detecting the latent class.

Figure 4.

Power of detecting the latent class in mTobit model when there are no covariates for both Tobit model and the latent class.

4.3.2. Covariate x ~ Unif[0, 1]

The data is simulated similarly as in Section 4.3.1 but with the Tobit component depending on a covariate x from Unif[0,1]. For the Tobit component, we use the same setting as in Section 4.2.2, i.e. μ = α − x for the mean of the Tobit regression component with α = 0, 1, 2 and 3. These α’s correspond with about 40%, 23%, 11% and 4% data under detection for Tobit component. While for the latent class, two scenarios are considered below, one with covariate and the other without covariate for ω.

No covariate for ω: As in Section 4.3.1, we still let ω = 0.05k, k = 1, 2, …, 6. The mTobit model is generated as below

$$y\sim \mathrm{mTobit}(\omega ,\mu ,4,1),\mu =\alpha -x,\alpha =0,1,2,3\text{and}\omega =0.05\text{k},\text{k}=0,1,\dots ,6$$

Summarized in Figure 5 are the empirical powers for detecting the latent class when x follows a uniform distribution. The patterns are very similar to those in Section 4.3.1. Again the LR test has the lowest power and the Wald test has the highest power in most cases. As sample size and ω increase, the power increases as well. However, for fixed sample size and ω, more censored data in the Tobit component results in lower power as the tests are less likely to distinguish the data of the latent class from those of the Tobit component if they both are under detection.

Figure 5.

Power of detecting the latent class in mTobit model with uniform distributed covariate for Tobit component only.

Covariate for ω: Assume the probability of the latent class follows a generalized linear model with logit link and covariate x. The outcome y is generated according to the following model

$$y\sim \text{mTobit}(\omega ,\mu ,4,-1),\mu =\alpha -x,\mathrm{logit}(\omega )=-b+x$$ (16)

where α is the same as the above, b is set to be 0.5, 1.0, 1.5, 2.0, 2.5 and 3.0, which in average corresponds to a probability of 0.32, 0.22, 0.15, 0.10, 0.06 and 0.04, respectively, for the latent class.

Shown in Figure 6 are the empirical powers for detecting the latent class when the covariate x is uniformly distributed. The patterns are very similar to those when the latent class does not depend on any covariates.

Figure 6.

Power of detecting the latent class in mTobit model with uniform distributed covariate for both the Tobit component and the latent class component.

4.3.3. Covariate x ~ N(0, 1)

The data is simulated similarly as in Section 4.3.2 but with the Tobit component depending on a covariate x from N(0,1), i.e. the mean of the Tobit component is defined by μ = α − x with x ~ N(0,1). The α is set to be −0.5, 0.5, 1.5 and 2.5 which corresponds to about 41%, 25%, 13% and 6% of data under detection for Tobit component. We also consider two scenarios, one with covariate and the other without covariate for ω.

No covariate for ω

As in section 4.3.2, we set ω = 0.05k, k = 1, 2, …, 6 for the latent class. The powers are summarized in Figure 7. The patterns are very similar to those in Figure 5. As expected, as ω and sample size increase, the powers increase too. The power also increases as the data are less censored for fixed sample size and ω.

Figure 7.

Power of detecting the latent class in mTobit model with normal distributed covariate for Tobit component only.

Covariate for ω

Assume the probability of latent class depend on the covariate x through logit(ω) = −b + x, the data are generated according to the following model

$$y\sim \text{mTobit}(\omega ,\mu ,4,-1),\mu =\alpha -x,\mathrm{logit}(\omega )=-b+x$$ (17)

where α is the same as the above, b is set to be 0.5, 1.0, 1.5, 2.0, 2.5 and 3.0 corresponding a probability of 0.38, 0.28, 0.19, 0.13, 0.08 and 0.05, respectively, for the latent class.

Figure 8 shows the empirical power of detecting the latent class. The results are similar to other cases. The LR test continues to have a little lower power than the other two tests, while the Wald test has the highest power as it tends to be more likely to reject the null hypothesis.

Figure 8.

Power of detecting the latent class in mTobit model with normal distributed covariate for Tobit component only.

For all the above simulations, the means of the estimated ω are summarized in Table S4 as supplementary material.

To assess the performance of the tests for more covariates and possible correlated covariates, we also have conducted simulation studies using covariates in equation (19) with outcome generated as

$$y_i\sim \mathrm{mTobit}\left(\omega ,{\mu }_i,{\sigma }^2,L\right),{\mu }_i={\beta }_0+{\beta }_{1}Ag{e}_i+{\beta }_{2}Gende{r}_i+{\beta }_{3}Rac{e}_i+{\beta }_{4}BM{I}_i$$

where β₀ = −1, β₁ = 1, β₂ = 0.5, β₃ = 1 and β₄ = 2. We consider ω = 0.0, 0.1, 0.2 and 0.3 to examine the rejection rate for ω = 0.0 and power for ω = 0.1, 0.2 and 0.3. The rejection rates and powers are summarized in Table S5 in the Web Appendix.

5. Case studies

In this section, we use two real data examples to illustrate the tests. The first one is the NHANES 2003–2010 Study to examine if there is a latent class in the urinary triclosan concentrations, the second one is the Bogalusa Heart Study to examine if the serum metabolites have a mixture Tobit distribution.

5.1. NHANES 2003–2010 study

NHANES is a continuous program that examines a nationally representative sample of about 5000 persons each year to assess the health and nutritional status of adults and children in the general population of the USA (http://www.cdc.gov/nchs/nhanes.htm). Demographic, socioeconomic, dietary, and health-related data were collected via interviews. Blood and urine samples were also collected for laboratory testing. In four surveys conducted between 2003 and 2010, urinary triclosan concentration was measured in a random sample of survey participants aged 6years or older. Literature shows that triclosan has potential to alter both gut microbiota and endocrine function and has a negative impact on human health.^42,43 In the 2003–2010 NHANES database, urinary triclosan concentration was measured in 3659 children (6–19years old) and 6566 adults (20years or older). Of these, 2898 children and 5066 adults had detectable levels of urinary triclosan, which means that there are about 22% participates with their triclosan concentration undetected for a detection limit 2.3ng/ml. Li et al.⁴³ treated the censored data as missing and used the complete dataset to examine the relationship between triclosan and body mass index, while Lankester et al.⁴² treated the triclosan as a categorical variable and the censored data was classified as a single category. Here we apply the three tests to test if there is a latent class in the urinary triclosan concentration.

Due to the skewed distribution, a logarithm transformation is first conducted before testing the null hypothesis H₀ : ω=0 vs. H_A : ω > 0. We assume a mTobit regression model with covariates age, gender, race, education, BMI, urine cotinine and creatinine for the transformed data, that is

$$\begin{gathered} y_i\sim \text{mTobit}\left(\omega ,{\mu }_i,{\sigma }^2,L=\log (2.3)\right), \\ {\mu }_i={\beta }_0+{\beta }_{1}Ag{e}_i+{\beta }_{2}Gende{r}_i+{\beta }_{3}Rac{e}_i+{\beta }_{4}Ed{u}_i+{\beta }_{5}BM{I}_i \\ +{\beta }_{6}Cotinin{e}_i+{\beta }_{7}Creatinin{e}_i \end{gathered}$$ (18)

The estimated probability of the latent class is −0.000012 and the associated p-values of testing H₀ : ω = 0 vs H_A : ω > 0 are 0.5000, 0.5037 and 0.768 for the Wald test, LR test and score test, respectively. All the tests yield the same conclusion that there is no evidence to reject H₀, i.e. there is no latent class in the urinary triclosan concentration. The results are not surprising, because the study participants are 6year or older, and it is very likely that everyone has been exposed to triclosan to some degree. Some of measures are not detected because of their low concentration, instead of not being exposed to triclosan at all.

5.2. Bogalusa Heart Study

The Bogalusa Heart Study, a series of long-term studies in a semirural biracial (65% white and 35% black) community in Bogalusa, Louisiana, was founded in 1973. This study focuses on the early natural history of cardiovascular disease since childhood. More details about the BHS can be found here (https://www.clersite.org/bogalusaheartstudy/). In the current BHS study, a total of 1466 metabolites were quantified from 1360 BHS blood samples. The BHS blood samples include 1261 unique BHS participants with blood samples collected during the 2013–2016 visit cycle, 64 random blind duplicate samples from a random sample of the same participants of the 2013–2016 visit cycle, and 35 replicate samples collected during the 2017–2019 visit cycle. Quality control procedures were conducted and data were cleaned. The cleaned analysis dataset includes 1202 metabolites for 1261 unique BHS participants from the 2013 to 2016 visit cycle. Among the 1202 metabolites, 167 have a missing rate or below detection rate >50% and 1035 have a missing rate or below detection rate ≤50%. Among the 1035 metabolites, 398, 401, 77, 56, 52 and 51 metabolites had 0%, <10%, 10–20%, 20–30%, 30–40% and 40–50% missing values or values below detection limit, respectively. The metabolites with more than 50% missing values were categorized as 1 for missing or below detection limit, the ones with greater than below detection limit but less than median were categorized as 2, and the ones with equal or greater than the median were categorized as 3.

To illustrate the tests, we consider metabolites with missing values less than 50% and apply the three tests to test whether there is a latent class in these serum metabolites. To account for individual differences, the Tobit regression component is adjusted for age, gender, race and BMI, i.e. the mTobit model is given by

$$y_i\sim \mathrm{mTobit}\left(\omega ,{\mu }_i,{\sigma }^2,L\right),{\mu }_i={\beta }_0+{\beta }_{1}Ag{e}_i+{\beta }_{2}Gende{r}_i+{\beta }_{3}Rac{e}_i+{\beta }_{4}BM{I}_i$$ (19)

There are a total 31 metabolites identified to have a latent class with p value less than 0.001 for at least one of the three tests. The metabolites, the estimated probability of the latent class, as well as the associated p-values for the three tests are provided in Table 1. Several of the identified metabolites belong to the xenobiotic super-pathway. This pathway includes many drug metabolites which we would expect to have a latent class.

Table 1.

Metabolits identified with a latent class based on p value less than 0.001 for at least one of the Wald test, LR test and Score test.

Metabolites	Super-pathway	Est. of Prob. (latent class)	P value
			Wald	LR	Score
Y_100003260	Amino Acid	0.105	5.77 × 10−12	1.65 × 10−8	2.17 × 10−6
Y_35	Amino Acid	0.021	1.75 × 10−3	3.09 × 10−4	6.69 × 10−3
Y_241	Amino Acid	0.058	8.64 × 10−10	5.85 × 10−10	1.48 × 10−7
Y_100002185	Amino Acid	0.227	0.00 × 100	4.06 × 10−11	5.56 × 10−9
Y_1094	Amino Acid	0.024	1.22 × 10−2	5.77 × 10−7	7.10 × 10−2
Y_100015735	Lipid	0.189	0.00 × 100	0.00 × 100	0.00 × 100
Y_273	Lipid	0.020	5.02 × 10−7	0.00 × 100	1.15 × 10−7
Y_100019957	Lipid	0.162	6.68 × 10−11	7.13 × 10−7	3.83 × 10−5
Y_100015833	Lipid	0.074	6.88 × 10−5	4.60 × 10−4	3.24 × 10−3
Y_100019958	Lipid	0.136	1.54 × 10−8	3.96 × 10−6	1.16 × 10−4
Y_100008934	Lipid	0.074	0.00 × 100	0.00 × 100	0.00 × 100
Y_100005716	Lipid	0.172	2.56 × 10−10	1.11 × 10−5	1.07 × 10−4
Y_100008921	Lipid	0.042	1.30 × 10−2	2.10 × 10−4	1.28 × 10−2
Y_100009154	Lipid	0.254	0.00 × 100	0.00 × 100	1.00 × 10−15
Y_100009345	Lipid	0.035	2.47 × 10−5	2.06 × 10−5	8.51 × 10−5
Y_100015666	Lipid	0.033	1.74 × 10−4	2.05 × 10−4	9.28 × 10−4
Y_100015609	Lipid	0.104	0.00 × 100	0.00 × 100	0.00 × 100
Y_100015731	Lipid	0.271	0.00 × 100	1.34 × 10−9	2.55 × 10−8
Y_100015792	Lipid	0.022	1.06 × 10−3	6.95 × 10−4	2.14 × 10−3
Y_207	Nucleotide	0.282	0.00 × 100	5.27 × 10−8	4.71 × 10−7
X_17335	Unknown	0.424	0.00 × 100	0.00 × 100	0.00 × 100
X_21788	Unknown	0.140	1.54 × 10−7	2.64 × 10−5	6.28 × 10−5
X_21796	Unknown	0.064	6.14 × 10−11	3.86 × 10−12	2.51 × 10−6
X_22776	Unknown	0.215	1.18 × 10−6	1.30 × 10−3	9.30 × 10−3
X_23294	Unknown	0.417	0.00 × 100	1.10 × 10−14	0.00 × 100
X_23637	Unknown	0.010	3.76 × 10−3	5.41 × 10−4	5.95 × 10−3
X_24832	Unknown	0.022	5.63 × 10−5	3.50 × 10−7	1.51 × 10−3
Y_100004601	Xenobiotics	0.398	0.00 × 100	0.00 × 100	0.00 × 100
Y_100001623	Xenobiotics	0.056	0.00 × 100	0.00 × 100	0.00 × 100
Y_100003696	Xenobiotics	0.167	6.43 × 10−11	2.45 × 10−7	1.04 × 10−4
Y_100002324	Xenobiotics	0.117	1.40 × 10−14	1.51 × 10−9	1.42 × 10−8

6. Discussion

In this paper, we have developed three tests for testing if there is a latent class in a Tobit regression model. The simulation studies show that the Wald test gives inflated type I errors, especially when sample size is small and the proportion of data under detection is large. The Wald test tends to be more likely to reject the null hypothesis, and therefore it yields elevated powers compared to the other tests. The LR test controls for the type I error very well when there are no covariates or covariates from uniform distribution. The trend of score test in controlling for type I error is pretty stable regardless of covariates. When there are covariates, the score test performs slightly better than the LR test, especially when the covariates are from unbounded normal distribution.

The proportion of data under detection has impact on the type I error of the tests, especially on the Wald test. When the proportion of the data under the detection level is large, the Wald test doesn’t provide valid type I error, especially for small to moderate sample sizes. The impact of the proportion seems small for the LR test. The impact of the proportion of censored data on the score test is somewhere between the LR test and the Wald test.

The proportion of under detection also has impact on the power. Even with large sample size 1000 and large probability of the latent class, the power is not high if the proportion of under detection is large. In such cases, the tests are not powerful to distinguish data from the latent class and data from Tobit model but under detection. In general, the Wald test has the highest power because it tends to be more likely rejecting the null hypothesis. In the paper, we focused on cross-sectional data where one measure is obtained from each subject. One may improve the power by obtaining repeated measurements. However, since repeated measurements from the same subjects are unavoidably correlated, it may be necessary to study the correlation structure. While in principle approaches in other latent class situations such as those studied in literature^44,45 should be adapted to the current situation, future research is needed to generalize the tests to such cases.

Since the simulated data sets with nonexistence of MLE for mTobit model were discarded in our simulation studies, the type I error and power can be affected for Wald and likelihood ratio test, but the performance of score test is not affected. Based on the performances of the tests in terms of both power and controlling type I error, the Wald test is the least favorable. The choice of LR test versus score test depends on covariates. If no covariates, the LR test would be preferred, while if the covariates are unbounded, the score test would be preferred. However, both the LR test and the Wald test require the MLE of the mTobit model which can be problematic, especially when the sample size is small and the proportion of data under detection is large, and therefore the LR test and Wald test may not be applied. The score test only needs the MLE for Tobit model, and in general it can be applied. Thus, only the score test can be used if the MLE does not exist for the mTobit model.

The tests proposed in the paper for latent class assume constant probability for the latent class, and it may depend on some covariates. The extension of the tests to this case is the next natural step.