Spatiotemporal Dynamics of Dilute Red Blood Cell Suspensions in Low-Inertia Microchannel Flow

Abstract

Microfluidic technologies are commonly used for the manipulation of red blood cell (RBC) suspensions and analyses of flow-mediated biomechanics. To enhance the performance of microfluidic devices, understanding the dynamics of the suspensions processed within is crucial. We report novel, to our knowledge, aspects of the spatiotemporal dynamics of RBC suspensions flowing through a typical microchannel at low Reynolds number. Through experiments with dilute RBC suspensions, we find an off-center two-peak (OCTP) profile of cells contrary to the centralized distribution commonly reported for low-inertia flows. This is reminiscent of the well-known “tubular pinch effect,” which arises from inertial effects. However, given the conditions of negligible inertia in our experiments, an alternative explanation is needed for this OCTP profile. Our massively parallel simulations of RBC flow in real-size microfluidic dimensions using the immersed-boundary-lattice-Boltzmann method confirm the experimental findings and elucidate the underlying mechanism for the counterintuitive RBC pattern. By analyzing the RBC migration and cell-free layer development within a high-aspect-ratio channel, we show that such a distribution is co-determined by the spatial decay of hydrodynamic lift and the global deficiency of cell dispersion in dilute suspensions. We find a cell-free layer development length greater than 46 and 28 hydraulic diameters in the experiment and simulation, respectively, exceeding typical lengths of microfluidic designs. Our work highlights the key role of transient cell distribution in dilute suspensions, which may negatively affect the reliability of experimental results if not taken into account.

Significance

Handling red blood cells in vitro using microfluidics is a crucial aspect of biophysical research for mechanistic understanding of blood flow in health and disease. We report, analyze, and discuss effects in dilute red blood cell suspensions under low inertia that can lead to erroneous interpretations of microfluidic experiments if not taken into account properly. In particular, the decay of lift forces in high-aspect-ratio channels, the lack of cell dispersion at low concentrations, and the axial acceleration of red blood cells can bias the long-range cell distribution and slow down the recovery of cell-free layers. It cannot therefore be presumed that, under these conditions, the cells are regularly distributed and present the common concentration peak at the channel center.

Introduction

Red blood cells (RBCs) occupy around 45% of the blood volume and play a crucial role in maintaining the normal function of tissues and organs in humans and animals. They transport oxygen and carbon dioxide, regulate blood viscosity, and affect the circulation of nutrients and immune cells. Pioneered by Chien and Skalak in the 1960s–1980s (1, 2, 3), there has been extensive research carried out theoretically, experimentally, and numerically to elucidate the behavior of single RBCs and characterize the dynamics of RBC suspensions (see recent reviews (4, 5, 6, 7, 8)). However, despite major progress, a rigorous and quantitative connection between microscale RBC dynamics and macroscale hemorheology is still lacking (9).

Up to this date, various factors affecting blood microrheology have been determined by theoretical or numerical models of RBCs or biomimetic vesicles, including (but not limited to) 1) viscosity contrast (between inner and outer fluids) (10), deformability (11), orientation (12), and initial position (13) of the cell; 2) shear component (distinct in linear and quadratic flows) (14), suspending viscosity (15), flowline curvature (16), and wall confinement (17) of the flow; and 3) two-body or multibody hydrodynamic interactions between cells (18). Most studies focus on the individual dynamics or pairwise interaction of cells or the characteristic signatures of the overall suspension system, e.g., effective viscosity and normal stress differences.

Much less attention has been paid to the collective behavior of cells, e.g., their spatiotemporal organization or local microstructures, at a realistic length scale in three-dimensional space. Common reasons for avoiding such studies include their complexity of analytical modeling or the prohibitiveness of computational cost. In fact, the RBC behavior at subsuspension level plays a key role in bridging the RBC dynamics and hemorheology. From an experimental perspective, the maturing of microfluidic technologies over the last two decades has provided a powerful tool to explore the otherwise inaccessible behavior of complex biofluids at the microscale. It is now widely employed for blood flow experiments aimed at various applications (19, 20, 21). For practical reasons in microfluidics, dilute (concentration ϕ < 10%) or semidilute RBC suspensions are commonly used, in which the clogging of samples is minimal and the measurements of individual cells are quantitatively accurate (22, 23, 24). Through observation of dilute or semidilute RBCs in polydimethylsiloxane (PDMS) microfluidic channels, many intriguing properties of RBC flow at the microscale have been demonstrated, such as uneven cell-plasma partitioning (25), long-range hydrodynamic interaction (26), wall-induced lift of cells in tumbling motion (27), cytoplasmic viscosity-promoted polylobes on cell membrane (28), and diffusion-governed collective spreading of cell suspensions (29).

From experiments with a semidilute RBC suspension (ϕ = 16%), Sherwood et al. (30) revealed a strongly heterogeneous distribution of cells, which presented locally skewed rather than axisymmetric hematocrit (Ht) profiles. With much lower RBC concentration (ϕ ≤ 5%), Shen et al. (31) found an even more heterogeneous RBC distribution eventually leading to inversion of the classic Zweifach-Fung effect (governing cell partitioning) downstream of bifurcations. More recently, Iss et al. (32) and Abay et al. (33) discovered emergent self-organization or focusing behavior of cells in dilute RBC suspensions arising from geometric features of the microfluidic channel, such as confinement and constriction. These studies imply that the spatial arrangement of RBCs in microchannels can be highly dynamical and varies from one location to another. Such local characteristics, if ignored, may give rise to inaccurate estimation of the hemodynamics in the microfluidic channels and affect the physiological relevance of the in vitro experiments designed to imitate in vivo systems.

This work aims to elucidate the spatiotemporal distribution of RBCs in a dilute suspension flowing through a typical microfluidic channel of rectangular cross section. For a dilute suspension (Ht ≤ 1%) of horse RBCs in the microchannel, cell density profiles are obtained by a direct cell-counting routine developed in house. As a result, we observe a counterintuitive cell distribution with off-center two-peak ordering rather than a single peak near the centerline, even in the negligible inertia regime. Immersed-boundary-lattice-Boltzmann simulations performed for an equivalent system confirm the experimental finding and provide insight into the underlying mechanisms. The study is organized as follows: the experimental and numerical methods are introduced in Materials and Methods. In Counterintuitive RBC Distribution, cell density profiles from experiments and simulations are presented. Flow Properties and RBC Dynamics provides analysis of the observed cross-streamline migration and explores the mechanism behind the density profiles. Discussion compares this study with existing works and states the key implications of our findings. Conclusions concludes the work.

Materials and Methods

The materials and methods used for the experiments and the simulations involved in this study are outlined in Microfluidic Experiments and Computational Modeling, respectively. Further information is provided in the Supporting Materials and Methods.

Microfluidic experiments

RBC suspensions in Dextran40 were prepared using horse blood (see Fig. S1 for photomicrography of the RBC suspension) provided by TCS Biosciences (Botolph Claydon, UK), in anticoagulant EDTA (1.5 mg/mL). The procedures for sample processing are described in Fig. S2. The steady shear rheology of Dextran 40 was determined by a rotational rheometer (DHR2; TA Instruments (Elstree, UK), with minimal resolvable torque 0.1 nNm) using a cone-plate geometry of 60 mm diameter and angle θ = 1° (CP60/1), 30 μm truncation gap. The density and shear viscosity values used to calculate dimensionless numbers (e.g., Reynolds number Re and capillary number Ca) for experiments are 1.07 g/mL and 5.0 mPa s, respectively.

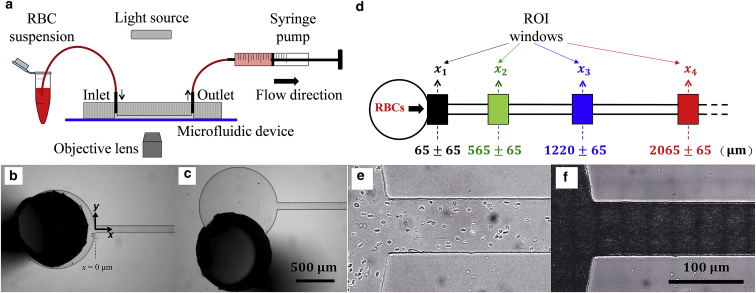
The microfluidic device was manufactured by soft-lithography using an SU8 mold produced by photolithography (microLIQUID, Arrasate-Mondragón, Spain). The microfluidic channel was made in PDMS (Sylgard 184, Dow Corning; Ellsworth Adhesives Ltd, Southend, UK) and bonded to a glass slide substrate with oxygen plasma (Zepto, Diener; Henniker Scientific Ltd, Warrington, UK). The channel has a rectangular cross section, with the width and depth dimensions (W = 87 μm, H = 31 μm) determined by optical microscopy. Fig. 1 a shows a schematic of the experimental setup, in which the sample is infused into the inlet of the microdevice using the withdraw function of the syringe pump located at the outlet. With this proposed system, the sample-containing Eppendorf can be gently stirred at regular time intervals to minimize cell sedimentation, which typically limits the duration of experiments. To test the effect of inlet conditions, inlet ports are manually punched onto the PDMS so that the tubing connection can be either aligned (Fig. 1 b) or misaligned (Fig. 1 c) with the centerline of the microdevice. The results presented in this study are for the aligned case, unless otherwise stated.

Figure 1.

Experimental setup. (a) A schematic of the experimental setup is given. (b and c) Inlet configuration of the microfluidic device is given, showing optical images of the flow entry region where the inlet port is (b) aligned and (c) misaligned relative to the channel centerline. In (b), the coordinate axes are shown. (b) and (c) share the same scale bars, representing 500 μm. (d) A schematic showing designated ROIs for the measurement of probability density distribution (PDD) of RBCs in the suspension is given. (e) An individual frame of RBCs flowing in the microchannel and (f) a composite image combining 300 frames of the same region are shown, obtained using the Z-projection method based on minimal intensity. In (e) and (f), Q = 0.2 μL/min, and they share the same scale bars, representing 100 μm. To see this figure in color, go online.

The experimental setup used an inverted microscope (IX71, Olympus; Olympus Medical, Essex, UK) for flow visualization and a syringe pump (Nemesys; Cetoni, Korbussen, Germany) for fluid control. The microfluidic device was illuminated using a halogen lamp. Videos were acquired by a sensitive monochrome CCD camera (XM10, Olympus) using a 10× magnification objective with a numerical aperture of 0.25 to guarantee that the depth of field and image depth are large enough to observe cell trajectories across the entire channel height (Fig. 1 e). An algorithm was developed in house based on ImageJ software to detect and count the cells automatically (Figs. S3 and S4). The RBC probability density distribution (PDD) along the width direction of a given region of interest (ROI; see Fig. 1 d) is then calculated using a minimum of 300 frames, containing more than 8000 cells (Figs. S5–S7). The cell-free layer (CFL) is determined as half the difference between the overall channel width and the RBC core width, using composite images (see Fig. 1 f) generated via the Z-projection method. The detailed procedure is described in Figs. S8 and S9.

Computational modeling

The immersed-boundary-lattice-Boltzmann method (34) is employed to model blood flow as a suspension of deformable RBCs. The fluid flow governed by the Navier-Stokes equations is solved by the lattice-Boltzmann method with a standard D3Q19 lattice (35), Bhatnagar-Gross-Krook (BGK) collision operator (36), Guo’s forcing scheme (37) and the Bouzidi-Firdaouss-Lallemand implementation of no-slip boundary condition at the walls (38). To precisely control the volume flow rate within the channel, inflow and outflow open boundaries are implemented with the Ladd velocity boundary condition (39). The RBCs are modeled as Lagrangian membranes using a finite-element approach. The fluid flow and RBC membrane are coupled through the immersed-boundary method (40), which tackles the interpolation of velocities and the spreading of forces. The model is implemented in the parallel lattice-Boltzmann flow simulator HemeLB (41) (open source at http://ccs.chem.ucl.ac.uk/hemelb) by incorporating a new, to our knowledge module for discrete deformable cells. Details about the model configuration (Fig. S10), simulation setup (Fig. S11), and numerical analysis (Figs. S12–S14) can be found in the Supporting Materials and Methods. See Table 1 for the key simulation parameters.

Table 1.

Key Simulation Parameters

Parameter	Symbol	Value	Parameter	Symbol	Value
Channel Geometry			RBC Model
Width	W	96 μm	Cell radius	rrbc	4 μm
Depth	H	30 μm	Viscosity contrast	λ	1.0
Length	L	1320 μm	Feeding hematocrit	HF	1%
Hydraulic diameter	Dh	45.7 μm	Local hematocrit	Ht	variable
Simulation Setup
Particle Reynolds number	Rep	0.03	Shear modulus	${\tilde{\kappa }}_s$	5.00 × 10−4
Capillary number	Ca	0.6	Bending modulus	${\tilde{\kappa }}_b$	4.50 × 10−5
LB relaxation parameter	${\tilde{\tau }}_{\text{BGK}}$	1.0	Reduced bending modulus	${\tilde{\kappa }}_b\Delta x^2/\left({\tilde{\kappa }}_s{r}_{\text{rbc}}^2\right)$	1/400
Voxel size	Δx	0.6667 μm	Cell-cell interaction	${\tilde{\kappa }}_{cc}$	${\tilde{\kappa }}_b$
Time step	Δt	7.41 × 10−8 s	Cell-wall interaction	${\tilde{\kappa }}_{cw}$	10 ${\tilde{\kappa }}_b$

The symbol “∼” represents simulation units (dimensionless).

Each RBC is modeled as a closed finite-element membrane with 720 triangular facets (meshing resolution matching the lattice size Δx for numerical stability and accuracy (42)), with its unstressed shape assumed as a biconcave discoid. The RBC membrane is elastic, with its mechanical properties controlled by five moduli which govern different energy contributions. They are strain modulus κ_s, bending modulus κ_b, dilation modulus κ_α, surface modulus κ_S, and volume modulus κ_V. For more details of the RBC model, please refer to (34). To tackle close contact among cells or between the cell and the wall (albeit rare in the dilute suspensions we consider), a repulsion potential decaying with inverse distance between neighboring RBC surfaces is numerically implemented with interaction intensities (see κ_cc and κ_cw in Table 1) comparable to the bending elasticity of the RBC membrane. The behavior of RBCs in flow is determined by two nondimensional numbers: the particle Reynolds number Re_p and the capillary number Ca. Re_p represents the ratio of particle inertia/fluid viscous force and is defined based on the channel Reynolds number Re_c:

$$R{e}_{\text{p}}=R{e}_{\text{c}}{\left(2r_{\text{rbc}}/D_{\text{h}}\right)}^2,R{e}_{\text{c}}={\rho }_{\text{ex}}\overline{u}{D}_{\text{h}}/{\eta }_{\text{ex}},$$ (1)

where r_rbc is the RBC radius and D_h is the hydraulic diameter of the rectangular channel, $\overline{u}$ is the cross-sectional mean velocity of the unperturbed flow, and ρ_ex and η_ex are the density and dynamic viscosity of the suspending fluid, respectively. Ca represents shear-induced deformation of the RBC membrane and is defined using its shear elasticity (governed by the strain modulus κ_s):

$$Ca={\tau }_{\text{rbc}}{\dot{\gamma }}_{\text{c}},{\tau }_{\text{rbc}}={\eta }_{\text{ex}}{r}_{\text{rbc}}/{\kappa }_s,{\dot{\gamma }}_{\text{c}}=8\overline{u}/D_{\text{h}},$$ (2)

where τ_rbc is a characteristic timescale for the RBC membrane to relax to its equilibrium shape from a transient state and ${\dot{\gamma }}_{\text{c}}$ is the characteristic wall shear rate in equivalent Poiseuille flow. Both Ca and the viscosity contrast λ (between RBC cytosol and the suspending fluid) are kept the same for experiments and simulations to ensure comparability (see values in Table 1).

Results

The experimental and simulation results on the RBC distribution in the channel are shown in Counterintuitive RBC Distribution. Additional data of RBC dynamics and the mechanisms leading to the observed RBC distribution are provided in Flow Properties and RBC Dynamics.

Counterintuitive RBC distribution

The main results of the study are reported here, focusing on the dynamical distribution of RBCs in a dilute suspension. Experimentally, by continuously feeding RBCs at fixed hematocrit (H_F ≤ 1%) into the microfluidic device, the transverse motion of cells can be evaluated by monitoring the PDD (see the Probability density distribution (PDD) of RBCs section in the Supporting Materials and Methods) of RBCs at sequential locations along the axial direction. This process is also replicated numerically to corroborate the experimental observations and provide further insights into the 3D motion of cells in a microchannel of rectangular cross section.

Off-center two-peak profile

In experiments with negligible inertia (Re_p < 2 × 10⁻⁴), we observe an evident increase of cell concentration close to each wall, manifested by the augmentation of two off-center peaks in the PDD profile depicting RBC fractions across the channel width (Fig. 2 a, Q = 0.2 μL/min). The locations of the two peaks are approximately symmetric about the channel centerline and keep moving inwards until a certain distance ∼0.2–0.3W/2 from the wall is reached (i.e., y/0.5W = 0.7–0.8). Beyond this distance, the inward migration of cells ceases (compare x = 1220, 2065 μm in Fig. 2 a); this eventually causes an off-center two-peak (OCTP) ordering in the density profile. In contrast, in the central region, the cell concentration remains nearly unchanged. By comparing the PDD profiles along the channel length, a cell population originally close to each wall is found to cross streamlines and progressively shift inwards (see x = 65,565, 1220 μm). For an initial cell distribution with significant left-right asymmetry induced by misaligned flow inlet (see Fig. 1 d), the same inward motion of cells near the wall occurs (Fig. S6). The observed quasisteady OCTP distribution of RBCs clearly deviates from the commonly reported cell distribution (or hematocrit profile) in microscale channels, which typically exhibit a core of cells near the channel center, accompanied by a cell-depleted layer near the channel wall (43,44). To rule out the possibility that such an OCTP distribution is exclusive to the volume flow rate Q = 0.2 μL/min, Q is also varied up to 4.0 μL/min for the aligned configuration (Fig. S7). Qualitatively similar evolution of the PDD profile is identified for all cases, featuring the development or enhancement of density peaks at two symmetric locations near the lateral channel walls.

Figure 2.

RBC distribution across the channel obtained by projecting cells either horizontally or vertically. (a) Experimental PDD profiles (lines, with error bars indicating the standard deviation of two experiments) at x = 65, 565, 1220, and 2065 μm vs. simulation hematocrit Ht histograms (bars) at x = 150, 450, 750, and 1050 μm are given, showing the widthwise distribution of RBCs at H_F = 1%. Note that the experimental PDDs have been scaled by a constant to be superimposed onto the simulation Ht histograms. (b) (Simulation) Widthwise Ht profiles at H_F = 2% are shown. (c) (Simulation) Widthwise Ht profiles at H_F = 5% are shown. (d–f) (Simulation) Corresponding depthwise Ht profiles at H_F = 1, 2, and 5%, respectively, are shown. To see this figure in color, go online.

To understand the peculiar cell distribution observed in experiments, numerical simulations for a H_F = 1% RBC suspension flowing at low Reynolds number (Re_p = 0.03) are performed in a long straight microchannel of identical hydraulic diameter (D_h = 45.7 μm) and similar aspect ratio (AR = W/H = 3.2). In simulations, we have access to the three-dimensional organization of RBCs within the channel and can observe the RBC distribution from not only the width direction W but also the depth direction H, contrary to common experimental set-ups in which only one dimension is observable. To quantify the RBC distribution, we analyze the time-averaged hematocrit (Ht) distribution across respective directions of the channel (Fig. 3 a). In the W direction, the RBC distribution agrees well with the experimental findings of the OCTP pattern, and equivalent “pseudoequilibrium” position of the peaks are found, i.e., y_eq/(0.5W) = 0.7 (Fig. 2 a).

Figure 3.

For a Figure360 author presentation of this figure, see https://doi.org/10.1016/j.bpj.2020.03.019.

Figure360 (Simulation) Cross-sectional visualization of RBC patterns. (a) An example of the hematocrit (Ht) analysis is given, showing superimposed RBCs from multiple simulation snapshots (at designated time intervals) in sequential sampling boxes (blue) measuring 50 μm long each at target locations (ROIs) downstream of the channel entrance. Cells within each sampling box are projected and allocated into 10 bins across the width (W) and depth (H) directions for counting, respectively, with their position determined by center of mass. (b) Cross-sectional slices show the accumulative transverse pattern of RBCs at x = 0D_h, 10D_h, and 23D_h away from the entrance, combining snapshots from 50 consecutive time steps. The first, second, and third rows represent snapshots of the H_F = 1% RBC suspension in a straight rectangular channel with aspect ratios AR = 3.2, 1.7, and 1.0 (varying W = 96, 50.3, and 30 μm while keeping H = 30 μm fixed), respectively. To see this figure in color, go online.

A distinct initial state of the suspension is found in the H direction upon the entry of cells into the rectangular channel (at x = 150 μm ≈ 3.3D_h). Whereas the widthwise distribution presents a more or less centralized pattern (Fig. 2 a), the depthwise distribution features two primary density peaks (Fig. 2 d). Furthermore, a substantial inward march of cells toward the channel centerline can be observed, with marked shifts of both density peaks. Downstream of the channel, a pronounced five-layered ordering develops, featuring a cell-depletion band next to each wall, two cell-enrichment bands neighboring the center, and one cell-suppression band right at the center (see x = 1050 μm ≈ 23D_h in Fig. 2 d). An arguable equilibrium position for the primary density peaks exists at ∼0.7 times the half channel depth away from the wall, i.e., z_eq/(0.5H) = 0.3.

Effect of feeding hematocrit

The OCTP pattern can still be observed in simulated RBC suspensions of moderately higher concentration, in which the feeding hematocrit H_F is increased to 2% (Fig. 2, b and e) and 5% (Fig. 2, c and f), respectively. However, the magnitude of the near-wall density peaks relative to the central region are in general weakened. Notably, in the depthwise distribution of H_F = 5% (Fig. 2 f), the two peaks (for which the local hematocrits can reach as high as 8–9% and presumably violate the dilute limit) are progressively smoothed out downstream of the channel, and the OCTP pattern vanishes at x = 1050 μm. Meanwhile, the central band is growing enriched with cells, and the overall Ht profile becomes flattened, suggesting considerable RBC dispersion taking place to even out regional density heterogeneities.

Effect of channel aspect ratio

The occurrence of OCTP patterns across both dimensions of the channel suggests the phenomenon of RBC focusing. Indeed, by investigating the transverse organization of RBCs in sequential cross sections (x = 0D_h, 10D_h, 23D_h), we observe the gradual formation of a RBC loop reminiscent of the classic “tubular pinch effect” arising from inertia (Fig. 3 b), yet our experiments and simulations are all under negligible inertia, as indicated by the low Reynolds number. Reducing the channel aspect ratio from the original AR = 3.2 to AR = 1.7 and AR = 1.0 does not remove the focusing behavior but brings the RBC loop closer to channel center. Examination of the Ht profiles in the AR = 1.7, 1.0 channels against the original AR = 3.2 channel reveals an inward shift of the OCTP equilibrium position in the width direction from y_eq/(0.5W) = 0.7 to y_eq/(0.5W) = 0.5, 0.3 (Fig. S12, a and c). In the case of AR = 1.0, at which the two dimensions are identical, the equilibria from the W and H directions become equivalent, i.e., y_eq/(0.5W) = z_eq/(0.5H) = 0.3 (Fig. S12, c and d).

Flow properties and RBC dynamics

To reveal the underlying physics behind the intriguing OCTP distribution of RBCs presented in Counterintuitive RBC Distribution, we investigate several key aspects of the problem, including the origin of transverse cell migration, the effect of channel geometry, the distribution of cell velocity, the formation of the cell-depletion layer, and the variation of tube hematocrit. The two main questions we aim to address are 1) how do the two density peaks in the PDD profile come into being? 2) Why do the peaks keep building up instead of being dispersed?

Mechanism for cell migration

Given its small Reynolds number, our RBC flow practically falls into the low-inertia regime, in which viscous effects dominate. For deformable objects in viscous flow, the phenomenon of their lateral drift away from the wall is well documented, dating back to the 1830s when Poiseuille first observed a plasma layer (or CFL) in frog arterioles and venules (45). The origin of such motion of RBCs was later determined to be the noninertial hydrodynamic lift arising from unbalanced pressure forces on the cell. This lift can drive cells in microscale vessels and channels to cross streamlines and migrate toward the central area, ultimately leading to the formation of a two-phase flow featuring a cell core and a fluid periphery (43,44). After the discovery by Goldsmith and Mason (46), the lateral migration of deformed particles in noninertial flows has been confirmed by other experimental studies (47, 48, 49, 50) and numerous modeling reports (51, 52, 53, 54, 55, 56, 57, 58, 59). In principle, there are three mechanisms for the cross-streamline motion of RBCs in low-Reynolds-number shear flows: 1) wall-repulsion-induced lift force on RBCs, 2) shear-gradient-induced asymmetric deformation of RBCs, and 3) hydrodynamic diffusion (or shear-induced diffusion) between RBCs due to cell-cell interactions. Depending on the flow properties (e.g., velocity profile, shear distribution, and wall confinement) and cell conditions (e.g., position, shape, and rigidity), the direction and strength of RBC motion under the combined effect of the above mechanisms can be difficult to determine.

Decay of lift velocity

The presence of RBCs at H_F = 1% (or below) does not significantly disturb the apparent velocity profiles from their unperturbed states (compare Figs. S15, c and d and S16); we can therefore analyze the transverse motion of RBCs with respect to the unperturbed flow. Subject to the complex flow pattern in the channel as elaborated by Fig. S15, the motion of RBCs within are likely to be affected by both the solid wall and the fluid shear gradients. At low Reynolds number, this motion can be conveniently decomposed into two orthogonal directions, hereby the W and H directions, on assuming negligible inertia and invoking the Stokes equations. Fig. 4, a and b show the statistical RBC lift velocities V₁ (relative to the unperturbed flow mean velocity $\overline{u}$) in 10 subdivisions of a cross section, divided either widthwise (W) or depthwise (H). Compared with the depthwise lift, the widthwise lift is found to decay much faster as the cell-wall distance increases. Whereas V_1,z vanishes at 0.75 times H/2 away from the wall (i.e., z/(0.5H) = 0.25), V_1,y already becomes negligible at 0.35 times W/2 away from the wall (i.e., y/(0.5W) = 0.65). The contrast of lift decay between the two directions can be explained by the shear-rate and shear-rate-gradient profiles in the cross section (Fig. S15, e and f). As the cells migrate toward the channel centerline, the local shear rate diminishes to zero, with a much faster drop in W than in H. Meanwhile, the local shear gradient also quickly vanishes in the W direction, whereas that in the H direction decreases in a relatively mild way. Consequently, the contributions of both the wall-induced lift and shear-gradient-induced lift in the W direction are weakened more quickly.

Figure 4.

(Simulation) Statistical lift velocities of RBCs within x = (50 ± 8) μm. (a) and (b) characterize the RBC migration along the y direction (widthwise) and z direction (depthwise), respectively. For statistical analysis in both (a) and (b), the channel is fictitiously folded along the channel centerline and then divided into 10 bins, followed by the assignment of cells according to the position of their center of mass. A positive lift velocity here indicates an inward motion of RBCs toward the channel centerline, vice versa. The short line and triangle in the boxplots represent the median and mean lift velocity for each bin, respectively. The horizontal caps show the statistics from Welch's t-tests between neighboring groups, where ^∗p < 0.05 is considered as statistical significance; ^∗∗p < 0.01, ^∗∗∗∗p < 0.0001. To see this figure in color, go online.

The distribution of lift velocities in both the width and depth directions coincides with the overall evolution of the Ht profiles presented in Fig. 2, a and d: whereas a “pseudoequilibrium” position close to the wall exists for the widthwise migration (beyond which the lateral motion of cells ceases), the depthwise cell migration is more substantial and results in a “pseudoequilibrium” position much closer to the channel center. Therefore, a correlation between the decaying lift of cells and their spatial distribution in the cross-sectional direction can be inferred.

Growth of CFL

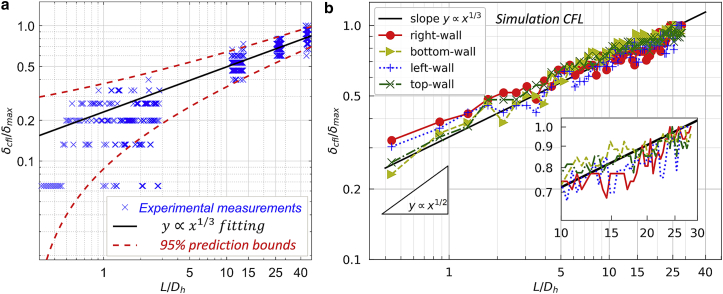
We now move on to investigate how the transverse motion of RBCs contributes to the spatial development of CFL along the channel axis. In the lower-flow-rate experiment Q = 0.2 μL/min (H_F ≤ 1%), the growth of CFL thickness (recording the averaged CFL from the two lateral walls) over 46D_h manifests an evident power-law behavior with a best-fit exponent of 0.39 (R² = 0.93; Fig. 5). For the other experiment with higher flow rate Q = 0.8 μL/min (hence larger Re), nearly identical power-law behavior is found for the CFL development. Similarly, the numerical CFLs over 28D_h (recording separate CFLs for individual lateral or vertical walls in simulation) also present power-law trends, but with a certain discrepancy in the fitting exponents when compared to the experimental value of 0.39: for the widthwise CFLs at the right and left walls, the values are 0.26 (R² = 0.91) and 0.29 (R² = 0.94), respectively; for the depthwise CFLs at the bottom and top walls, they are 0.29 (R² = 0.91) and 0.25 (R² = 0.95), respectively (Fig. 5). Part of the discrepancy in CFL growth rates between the experiment and simulation is attributed to the usage of different RBC types, namely horse RBCs and human RBCs (Ca = 0.6 here), the latter of which has higher deformability in nature when exposed to shear. By tuning down the shear elasticity of the modeled cells in simulation (Ca = 0.1), which imitates aging human RBCs of increased stiffness, the discrepancy between the experimental and numerical data is significantly reduced, with numerical exponents of 0.29–0.34 achieved (inset of Fig. 5).

Figure 5.

Comparison of experimental CFL (empty circles) measured in the width direction of the channel (averaged between opposite walls) under Q = 0.2, 0.8 μL/min vs. numerical CFLs (solid symbols) calculated along each wall of the channel (right/bottom/left/top walls). Both the experimental and numerical CFL values δ_cfl have been normalized by the maximal CFL thickness δ_max detected within the whole investigated range, and the development lengths L are normalized by the channel hydraulic diameter D_h. The main frame and the inset of the figure contain the same experimental data but different numerical data from two simulations: the former with normal human RBCs in which Ca = 0.6 and the latter with aging human RBCs in which Ca = 0.1. To see this figure in color, go online.

Despite the difference between the growth rates of experimental and simulation CFL, a neutral finding is that no critical saturation of the CFL increase can be identified throughout the investigated range (see raw data of the CFLs in Figs. S9 b and S13 a). This means that the development of CFL in a typical microfluidic channel (rectangular cross section) for a dilute suspension can take much longer than earlier estimates provided for microvessels or cylindrical tubes (60, 61, 62, 63). In particular, Katanov et al. (61) reported a universal length L_c ≤ 25D (independent of flow rate and hematocrit) for full CFL development in vessels between D = 10 and 100 μm, whereas we find L_c > 28D_h in simulation (only serving as a lower-bound estimate because we have limited our flow domain to such a length for tractable computational cost) and L_c > 46D_h in experiment (hydraulic diameter of the channel D_h ≈ 45.7 μm). Based on our numerical findings of the “pseudoequilibrium” positions for the widthwise cell migration (up to 0.3 times half channel width from wall) and depthwise cell migration (up to 0.7 times half channel depth from wall), the CFL thickness in the simulation may continue to grow until reaching 10–14 μm, which is considerably larger than the values of 6–8 μm we have monitored within L_c ≤ 28D_h (Document S1. Supporting Materials and Methods and Figs. S1–S18, Figure360. An Author Presentation of Fig. 3, Document S2. Article plus Supporting Material a).

Reduction of tube hematocrit

The long-range development of CFL will inevitably affect the local rheological properties of the suspension. As shown in Table 2, the tube hematocrit Ht measured from either of our simulated geometries (CTRAC-L: large-contraction inlet; all simulation data and plots presented elsewhere in the study are from this geometry. CTRAC-S: small-contraction inlet. See more details of CTRAC-L and CTRAC-S in the Supporting Materials and Methods) drops continuously along the channel axis compared to the feeding hematocrit H_F, even after 1050 μm (∼23D_h) away from the entrance. This reduced volume fraction of blood flow in microchannels versus the discharge hematocrit (H_D ≈ H_F) is known as the Fåhræus effect, in which Ht/H_D = ${\overline{U}}_{\text{B}}/{\overline{V}}_{\text{x}}$ < 1 (${\overline{U}}_{\text{B}}$ and ${\overline{V}}_{\text{x}}$ are average velocities of the overall blood flow and the cells, respectively) (64,65). It stems from the cross-streamline motion of RBCs toward the high-velocity region around the channel centerline, which empowers the cells within the channel to travel faster on average than the ambient fluid in the streamwise direction. Owing to the fairly long CFL development length (>28D_h in simulation), the cross-sectional distribution of RBC fluxes, and consequently the average ratio of cell/fluid velocities, (Figs. S17 and S18) continues to change till the very end of the channel, leaving consistent measurement of tube hematocrits within the microchannel difficult.

Table 2.

Variation of Tube Hematocrit along the Channel Axis in Simulation

Inlet type	HF	Ht (150 μm)	Ht (450 μm)	Ht (750 μm)	Ht (1050 μm)	Ht (1150 μm)
CTRAC-L	1%	0.810%	0.749%	0.703%	0.696%	0.685%
CTRAC-S	1%	0.705%	0.661%	0.659%	0.622%	0.619%

Discussion

In the following, we will discuss and compare our findings in Results with existing studies and interpretations and elaborate on their implications for experimental studies of dilute blood flow.

Comparison with existing studies

Hydrodynamic lift

The mechanism of hydrodynamic lift for tank-treading particles in shear flows has been analyzed theoretically by Olla and Seifert in the 1990s (66,67). A simplified scaling law V₁ ∼ $\dot{\gamma }$/h² was derived for the lift velocity V₁ under constant shear, as a function of the shear rate $\dot{\gamma }$ and cell-wall distance h (68). This quadratic scaling has been widely employed in the literature as an approximation to estimate the lateral migration of particles in various flow conditions. However, recent studies show that in pressure-driven channel flows where nonconstant shear (or nonzero shear gradient) exists, e.g., Poiseuille flow, the curvature of the velocity profile modifies the scaling law in a nontrivial way and would significantly slow down the spatial decay of the lift velocity (54,59,69,70). Indeed, through systematic measurement of the lateral migration of various vesicles in bounded planar Poiseuille flow under different confinement degrees, Coupier et al. revealed that the scaling V₁ ∼ $\dot{\gamma }$/h² would fail to predict the trajectory of the vesicle, whereas a markedly different empirical law V₁ ∼ $\dot{\gamma }$/h held (50). Losserand et al. confirmed the scaling V₁ ∼ $\dot{\gamma }$/h using RBC experiments and further refined the empirical law (71).

To examine whether the lateral migration of RBCs in our simulation obeys the lift scaling that Coupier et al. (50) and Losserand et al. (71) proposed for Poiseuille flow, we adopt theoretical shear rates from the asymptotic solution of pressure-driven flow in a rectangular channel (72) and calculate the lift velocities, applying V₁ ∼ $\dot{\gamma }$/h (abandoning all prefactors for generality). Furthermore, with weighted normalization, we obtain the dimensionless theoretical lifts (${\hat{V}}_{\text{l},y}$ and ${\hat{V}}_{\text{l},z}$) for both the W and H directions (Fig. 6, a and b). For comparison with the theoretical prediction, numerical medians of our numerical lift velocities are extracted from Fig. 4, a and b. After rescaling and overlapping them onto the theoretical curves, we observe satisfactory data agreement across the H direction but only partial agreement in the W direction for the near-wall region only. Approaching the central region in the W direction, the theoretical prediction breaks down. This is actually expected because the velocity profile there is abruptly blunted and significantly deviates from a parabolic shape. We have also examined against our simulation data the theoretical prediction given by V₁ ∼ $\dot{\gamma }$/h², which would overestimate the spatial decay of the lift in general and failed to yield an agreement with the simulation data (data not shown here).

Figure 6.

The theoretical prediction of RBC lift velocities (line curves and contour plots) given by V₁ ∼ $\dot{\gamma }$/h. (a) and (b) represent the width and the depth directions of the channel, respectively. z- and y-values in the legends represent positions relative to the midplane in each direction (see the sketch in Fig. S15, c and d), with z = 0 and y = 0 denoting the widthwise and depthwise midplanes, respectively. The black dots represent rescaled values of the numerical lift velocities extracted from Fig. 4, a and b. The black vertical lines in (a) and (b) indicate the center of the outmost layer of cells at x = 50 μm detected in the RBC simulation. To see this figure in color, go online.

CFL

CFL characterization is an active research field owing to its prominent role in regulating blood viscosity and local hemodynamics. Limited by the complexity of in vivo imaging and measurement (73), glass capillaries and PDMS microchannels have been widely used to mimic a simplified microcirculatory environment for in vitro observation of CFLs under different rheological conditions (74). Meanwhile, versatile computational tools have been developed, and plenty of in silico studies on CFL have emerged (44). However, most in vitro or in silico studies assume a steady CFL for a given channel segment and hence fail to capture the highly dynamical nature of realistic CFLs as in the microcirculation (75,76), albeit that some authors have made improvements by proposing a nominal CFL development length by multiplying the mean flow velocity and characteristic flow time (15,61). It is only recently that exact analyses of the spatiotemporal heterogeneity of CFL were presented (62,77,78), detailing the spatial development and recovery of the CFL alongside microchannels in the presence of upstream disturbances.

In this study, having confirmed the spatial variation of lift velocity V₁ ∼ $\dot{\gamma }$/h (rather than V₁ ∼ $\dot{\gamma }$/h²) against the cell-wall distance h for individual RBCs, estimation can be made for the longitudinal development of δ_cfl in a dilute suspension using an analytical approach (see the Supporting Materials and Methods). Our derivation shows that considering a = 1 (corresponding to V₁ ∼ $\dot{\gamma }$/h) in Eq. S1 yields a power-law scaling for the CFL as expressed in Eq. S11: δ_cfl ∼ ${\ell }^{\beta }$, β = 1/3, where $\ell$ is the axial distance along the channel. The exponent of 1/3 here is surprising because it coincides with the power-law scaling for vesicle/RBC motion in simple shear flow with constant shear rate (see Eq. 3 in (49)). Note that because δ_cfl ∼ ${\ell }^{1/3}$ is derived on the basis of a parabolic velocity profile under the assumption of planar Poiseuille flow (constant shear-rate gradient), whereas the flow patterns in a real microchannel are far more complex (see Fig. S15), its accuracy for the prediction of spatial CFL development remains to be verified by our experimental measurements and numerical results.

The power-law growth δ_cfl ∼ ${\ell }^{1/3}$ predicted by the scaling analysis assuming ideal Poiseuille flow turns out to agree well with both our experimental and numerical CFLs at H_F = 1%, for which the best-fitted power-law exponents were earlier shown to be 0.39 and 0.25–0.29, respectively (Fig. 5). In further regression analyses of the experimental and numerical CFLs, both data sets are found to collapse on δ_cfl ∼ ${\ell }^{1/3}$ (Fig. 7, a and b). Furthermore, the instantaneous slopes for the numerical data are nearly independent of $\ell$ at the early stage of CFL development, presenting a roughly steady increase of 1/3 (see Fig. 7 b). This implies the predominant role of a single mechanism for the transverse motion of cells, which is sensibly the hydrodynamic lift as our scaling analysis suggests. Moving downstream of the channel, a continual increase of the CFL is observed upon approaching $\ell$ = 28D_h but with slower growth, indicated by decreasing slopes noticeably smaller than the original 1/3 (see inset of Fig. 7 b). This deceleration in CFL growth is expected, down to the fact that the lift forces are weakened as the cells migrate further away from the wall and enter the low-shear region with blunted velocity profiles, where the lateral motion of cells slows down. In simulations of higher feeding hematocrit H_F = 2% and H_F = 5%, the scaling of δ_cfl ∼ ${\ell }^{1/3}$ still holds for early-stage development of the CFL until reaching far downstream of the channel (see Fig. S14, e and f). Notably, for H_F 5%, the slope approximates zero between $\ell$ = 20–25D_h and suggests a saturated CFL. This is in line with what was found in the evolution of Ht profiles (Fig. 2, c and f), in which exceedingly amplified local hematocrits (∼8–9%) break the dilute regime and lead to considerable RBC dispersion that resists further drift of cells away from the wall.

Figure 7.

Regression analysis of the CFL development. (a) Experimental and (b) numerical CFLs as in Fig. 5 are shown, expressed here in log-log scale. The CFL values δ_cfl are normalized by the maximal CFL thickness δ_max detected within the whole investigated range, and the development lengths L are normalized by the channel hydraulic diameter D_h. The inset of (b) shows a zoom-in view of the numerical CFL trends within L = 10 ∼ 28D_h. To see this figure in color, go online.

From previous simulations of much denser RBC suspensions (Ht = 15–45%) in cylindrical tubes (61), a similar power-law behavior was reported for the steep increase of CFL thickness at an initial development stage before a second timescale induced by relaxation of the RBC core came into play. However, the power-law exponents under several shear rates were considerably smaller than 1/3 even at the very beginning. The deviation from 1/3 was caused by the cell-cell interactions existing in their dense suspensions, which obstructed the initial migration of RBCs and led to slower CFL growth than in a dilute suspension like ours. Arguably, the authors reasoned for the ideal growth factor of 1/3 by invoking the lift force scaling F₁ ∼ V₁ ∼ 1/h² (where $\dot{\gamma }$ is a constant and does not affect the scaling) derived from simple shear flows (52,56). Although such reasoning does explain the qualitative trend of their CFL growth, the simple shear flow approximation itself for quadratic flows in a microchannel (where $\dot{\gamma }$ varies) is questionable, which may fail to capture important features of the RBC distribution in the presence of shear-rate gradients, as recent theories of particle migration at low Reynolds number demonstrate (79,80).

Implications and limitations

What we have covered so far not only elucidates the “aberrant” RBC distribution observed in our experiment and simulation contradicting earlier findings, but also has wider implications for experimentalists working on dilute suspensions, especially in high-aspect-ratio microfluidic devices. In brief, microfluidic designs need to be longer if their purpose is to investigate the microscopic behavior of a dilute suspension after completed lateral migration. Experimentally, it is notoriously difficult to accurately control the inlet distribution of a cell or particle suspension under various entrance effects. Therefore, local observations are frequently reported based on the assumption that the suspension organization is free of transient effects at the chosen ROI as long as the ROI is adequately far away from the entrance. However, the required length as revealed by our study turns out more demanding than commonly believed (60, 61, 62, 63). Some key messages are as follows:

• 1)For experiments of dilute RBC suspensions in high-aspect-ratio channels, e.g., AR = W/H > 3, the hydrodynamic lift of RBCs is substantially suppressed because of the existence of low-shear-rate and low-shear-gradient zones in the center. Consequently, the full development of a CFL in these channels may require a much longer length (L_c > 28D_h in simulations and L_c > 46D_h in experiments) than what is normally expected for cylindrical tubes (L_c ≤ 25D, according to (61)). To achieve full CFL development within L_c = 20–25D_h in rectangular channels, RBC suspensions with H_F ≥ 5% should be adopted. Furthermore, the relevance of in vitro measurements of cellular behavior using such high-aspect-ratio microchannels to the realistic microcirculatory blood flow needs reappraisal. After all, the vessels in the microcirculation are more likely to have circular cross sections and considerably different velocity profiles, which the radial distribution of RBCs relies on.
• 2)When determining the organization of a dilute suspension (e.g., hematocrit profile) in a typical microchannel of rectangular cross section, local measurements may be misleading if the channel is short or only moderately long. This is because heterogeneities emerging in the suspension (e.g., density peaks) will persist and hinder the formation of an equilibrium cell distribution owing to the lack of RBC dispersion under weak cell-cell interactions. In particular, if certain upstream disturbances exist (e.g., geometric constriction or expansion), history effects need to be considered when recording local suspension properties such as the tube hematocrit. Comparing the cases CTRAC-S and CTRAC-L in Table 2, with channel geometry, unperturbed flow rate, and feeding hematocrit all being the same, yet the tube hematocrits measured at sequential locations constantly differ by more than 6% (relative change). The reason is simply their differently configured flow inlets, causing unequal degrees of disturbance to the initial distribution of cells.
• 3)Phenomena violating empirical laws may occur downstream of bifurcations if the upstream RBC suspension is at an intermediate stage of development and has special cell distribution, e.g., the OCTP profile observed in our study. Recently, a counterintuitive inversion of hematocrit partition against the classic Zweifach-Fung effect in a bifurcating channel was reported by Shen et al. (31), arising from the formation of consecutive layers of high and low RBC hematocrits in the parent branch. The juxtaposed configuration of RBCs discovered by that study is in line with the five-layered ordering of cells we find in the depth direction of our RBC flow (Fig. 2, d–f). Therefore, the phenomenon Shen et al. captured might also have been a consequence of inadequate channel length for the suspension to be fully developed in the parent branch.

Some limitations of this study are as follows: 1) although the numerical model simulates human RBCs, horse RBCs were used in experiments because of laboratory restrictions. This causes a certain degree of discrepancy between the simulation and experiment, but its influence on the suspension behavior we studied, such as cell focusing and CFL development, is shown to be quantitative instead of qualitative. 2) The effect of inlet configuration on suspension organization has not been characterized in a quantitative manner, which can potentially provide more specific guidance for experimentalists to improve their microfluidic designs by reducing transient effects. We aim to address this issue in future studies, involving geometric factors such as constrictions, expansions, and bifurcations. 3) The experimental data are insufficient for analysis of instantaneous growth rates of the CFL thickness as has been performed for the simulation. More measurements using a denser arrangement of ROIs, though quite challenging, should be made in future experiments to enable precise comparison with simulations. 4) To make the real-scale (channel length >1 mm) simulations tractable, we have largely reduced the parameter space and refrained from an exhaustive investigation combining a range of flow scenarios and cell conditions. A parametric study integrating all these effects will lead to enhanced understanding of the intricate behavior of dilute suspensions processed in microfluidic devices.

Conclusions

We performed both microfluidic experiments and numerical simulations of dilute blood suspensions in a low-Reynolds-number channel flow (Re_p $\ll$ 1). Surprisingly, an OCTP ordering of RBCs was found, which is reminiscent of the “tubular pinch effect” typical of the radial distribution of particles in inertial microfluidics (81,82). However, the transverse motion of cells in our case has an entirely different origin: the non-inertial hydrodynamic lift of deformable particles (46).

Back to the two primary questions we set out to address (see the opening paragraph of Flow Properties and RBC Dynamics), how do the two density peaks in the PDD profile come into being, and why do the peaks keep building up instead of being dispersed? The reason behind the persistence of significant density peaks is the deficiency of hydrodynamic interactions among cells in the dilute limit, at which shear-induced diffusion remains weak and falls short to smooth out density heterogeneities brought by the lateral migration of cells. Consequently, the evolution of the density profiles is predominantly determined by the decay of hydrodynamic lift within the suspension, which exhibits distinct patterns in the width and depth directions of a high-aspect-ratio microchannel and contributes to a counterintuitive (OCTP) profile of cells in the larger dimension. Additionally, depending on the inflow configuration, the initial distribution of cells upon their entry into the channel varies substantially, which brings extra complexity to the restoration of a converged density profile and the development of an equilibrium CFL.

Our findings highlight the importance of local and transient characteristics at the dilute limit for an RBC-laden flow in microchannels. Experimentalists should therefore be cautious when working with dilute suspensions in microfluidics and make judicious assumptions about suspension properties with the presence of upstream disturbance to the flow, especially when the microscopic behavior of the suspension is the focus of research.

Author Contributions

Q.Z. and J.F. designed the research, analyzed the data, and wrote the article. Q.Z. performed the simulations. J.F. performed the experiments. L.C. assisted in validation of the computational model. M.O.B. and P.R.H. discussed the results and revised the manuscript. M.O.B. supervised the study. M.S.N.O. and T.K. conceived the research idea, supervised the study, and edited the manuscript.

Editor: Mark Alber.