Abstract
We expand the standard fluorescence recovery after photobleaching (FRAP) model introduced by Axelrod et al. in 1976. Our goal is to capture some of the following common artifacts observed in the fluorescence measurements obtained with a confocal laser scanning microscope in biofilms: 1) linear drift, 2) exponential decrease (due to bleaching during the measurements), 3) stochastic Gaussian noise, and 4) uncertainty in the exact time point of the onset of fluorescence recovery. To fit the resulting stochastic model to data from FRAP measurements and to estimate all unknown model parameters, we apply a suitably adapted Metropolis-Hastings algorithm. In this way, a more accurate estimation of the diffusion coefficient of the fluorophore is achieved. The method was tested on data obtained from FRAP measurements on a cultivated biofilm.
Significance
Diffusion and mass transport in biofilms is presumed to play an important role in the resistance against antimicrobial agents and the secretion thereof. Fluorescence recovery after photobleaching (FRAP) measurements give insight into these transport processes. In this article, the authors expand the standard FRAP model by a black box part that addresses some artifacts commonly observed in the measurements. This is done to improve the estimations of diffusion coefficients considerably, aiming at a more comprehensive description of diffusion processes inside the biofilm. We expect that the methods are transferable to FRAP measurements on materials other than biofilms.
Introduction
Diffusion and mass transport in biofilms have been studied for decades yet have still not been understood completely. They are presumed to play an important role in the resistance against antimicrobial agents and the secretion thereof (1). However, there are different ways of mass transport into and inside a biofilm. First, the studies of mass transport inside the biofilm from the bulk medium are more numerous than the studies investigating transport inside the biofilm (2, 3, 4, 5, 6, 7). Second, there is a huge emphasis on oxygen transport in the biofilm (8, 9, 10, 11). But how does diffusion inside of the biofilm work? How are nutrients transported from one part of the biofilm to another, if any? How are products excreted? One way to look inside a biofilm is by usage of the confocal laser scanning microscope (CLSM) and the fluorescence recovery after photobleaching (FRAP) technique. An important challenge here is the visualization of the transported compounds. Because most of the substrates and products from microbial biofilms (e.g., glucose and lactic acid) do not have any viably detectable fluorescence, other substances have to be used to be able to perform the FRAP experiments. In 1974, Peters et al. (12) started using fluorescein isothiocyanate as a marker for diffusion measurements. Since then, it has been widely used in many different studies (13, 14, 15, 16, 17). The first model for describing mobility of compounds by FRAP was developed by Axelrod et al. (18). Since then, several improvements were created for this basic model, such as simplified computations or using the ratio between bulk fluid diffusion/biofilm diffusion (19, 20, 21), as well as the technique itself (22,23). In this study, the authors build upon these models and expand them to improve the estimations of diffusion coefficients, aiming at a more comprehensive description of diffusion processes inside the biofilm.
The principle behind FRAP is based on the idea that after the induction of an irreversible bleaching of a fluorophore with a strong laser pulse, the subsequent observation of the recovery of the fluorescence in the bleached region reveals insight into the processes governing transport and diffusion of this fluorophore. Because fluorescence recovery can only originate from fluorescing material that diffuses into the bleached region from its surroundings, the development of the recovery and the corresponding increase in fluorescence intensity allow the model-based estimation of, e.g., the diffusion coefficient of the fluorophore. Finally, this in turn gives insight into the transport processes inside the system under observation (23,24).
An important step in the analysis of each FRAP experiment is the evaluation of the measurement data, which has to be based on a mathematical model. In the past, these models were kept very simple to guarantee that their solutions could be provided by simple explicit formulas (16, 17, 18,21,25). Nevertheless, the restrictive model assumptions necessary for the explicit solvability of these models made by Axelrod or others building on this model (19,22) are often problematic or even not valid for the real systems under consideration. This is especially true in the case of biofilms. The simplifying assumptions usually made are, e.g., that the bleaching during the measurement (in the postbleaching phase) is neglected, that the probe is homogenous at the region of interest (ROI), that the processes in the third dimension are neglected, and that the laser profile has a very simple geometry (Gauss profile or circle) (26). Apart from these properties, which are inherent in the real system and well understood, there may be additional artifacts in the measurements like gradients in the fluorescence intensity or steady changes of it even if no bleaching is done. So that the mathematical analysis achieves better results, it is therefore necessary to deal with more complex models. The downside is that these models do not yield solutions given by simple explicit formulas.
In this article, we expand the standard FRAP model by a black box part that addresses some artifacts commonly observed in the measurements but that violate the assumptions made for the standard FRAP model. In detail, the model will capture the following disturbances of the fluorescence measurements: 1) a linear drift, 2) an exponential decrease (due to bleaching during the measurements), 3) stochastic Gaussian noise, and 4) uncertainty in the exact time point of the onset of fluorescence recovery. We adopt a Bayesian approach and apply a Markov chain Monte Carlo (MCMC) algorithm to fit the expanded model to the data obtained from FRAP measurements and to estimate all unknown model parameters, including the diffusion coefficient. The MCMC algorithm practically computes approximations to the (joint) posterior distribution of all model parameters. The advantage is that the posterior distribution better reflects the whole range of equally probable parameter sets compared with other parameter estimation methods that typically return only one single parameter set (such as, e.g., maximal likelihood or minimal cost optimization).
We expect that the methods are transferable to FRAP measurements on materials other than biofilms. Adaptations of the model and algorithm might be necessary in each individual case, depending on what effects occur in the FRAP measurements (e.g., nonstandard diffusion or different types of disturbances), but the overall procedure will remain as presented here.
Many variations on the standard FRAP model can be found in the literature, concerning, e.g., different spatial bleaching profiles (rectangular, strip, three-dimensional) or nonstandard diffusion or other modifications of the model that should prevent under- or overestimation (see, e.g., the introduction in (27) or (28)). Also, MCMC has been applied to FRAP estimation previously (see, e.g., (29,30)). Nevertheless, we focus on an aspect that is still mostly either completely neglected or not addressed in an adequate way: the explicit modeling of those parts in the signal (i.e., the FRAP images) that are not directly related to the FRAP procedure itself, but rather are induced by uncontrolled processes occurring in the surroundings, i.e., processes in the biofilm not related to FRAP, artifacts caused by the measurement equipment, environmental influences, etc.; in short, all the parts of the signal that are considered to be “nuisance” in the measurements. The main contribution of our article is the focus on this nuisance part, thus balancing it with and giving to it the same importance as to the true FRAP signal part.
Materials and Methods
Biofilm cultivation and microscopy
Reactor construction
Biofilms were cultivated in a flow cell (FC). The FC used in this study was a modified version of a custom-made flow cell described by (31). For application of fluorescent dyes, an inlet pointing at the sample well was added (Fig. 1) to ensure homogenous distribution of the applied dye. The height of the flow channel was decreased to 1.6 mm to a total reactor volume of 1.5 mL, allowing full coverage of the biofilm volume with the given objective. Computational fluid dynamics simulation (data not shown) proved the flow to be laminar.
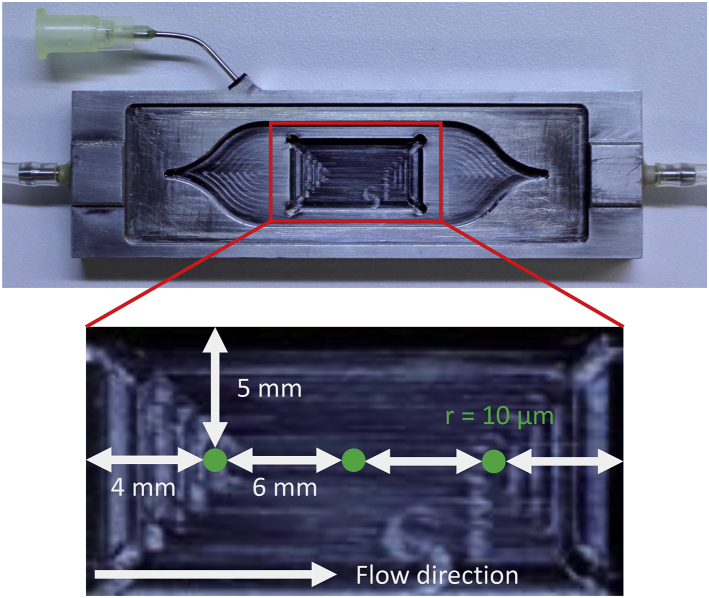
Figure 1.
Top: FTC with dye inlet and sample well. The bottom shows the measurement positions on a 10 × 20-mm metallic surface fitted into the well of the same size in the FC. The positions are evenly spaced 5 mm from the long edge and 4 mm (upstream/downstream) or 10 mm (center) from the short edge, respectively. The ROI is 20 μm in diameter. To see this figure in color, go online.
Bacterial cultivation
For this study, biofilms of the lactic acid producing the organism Lactococcus lactis subsp. lactis (DSMZ 20729) were generated. All cultivations were carried out at 30°C in de Man, Rogosa, and Sharpe (MRS) medium (32) and were split into three phases. 1) The preculture was made with 100 mL of MRS (pH 7) and 20 g/L glucose in a bottle shaken at 130 rpm to an OD600 (optical density at 600 nm) of 4, which was then used to inoculate the batch culture. 2) The batch culture was made with the medium being recycled through the FC to allow for bacterial attachment and initial biofilm formation; the 100 mL bottle of preculture (pH 7) was connected to the FC and 20 g/L glucose and pumped at 5 mL/min for 15 min, with a 60-min break between each interval (Ismatec IPC peristaltic pump; IDEX Health & Science, Wertheim, Germany) for 16 h. 3) The continuous culture was made with 250 mL of MRS (pH 5.5) and 10 g/L glucose, 0.25 mL/min flow for up to 12 h, during which all measurements were carried out.
FRAP measurements
FRAP measurements were carried out on a Leica SP5 II confocal laser scanning microscope (Leica Microsystems, Wetzlar, Germany) with an active beam expander module. In the first 8 h of biofilm growth in continuous mode, pictures of the surface were taken at 0 and 3 h. Starting with the 5-h time point, 100 μL of fluorescent dye was added. Starting at the 7-h time point, dye was applied every hour until 12 h. The dyes used were uranin (VWR International, Darmstadt, Germany) at a concentration of 0.75 mg/mL to an end concentration in the reactor of 0.05 mg/mL and fluorescein isothiocyanate dextran 4kDa (FD4) (TdB Consultancy, Uppsala, Sweden) at a concentration of 225 mg/mL to an end concentration in the reactor of 15 mg/mL. Neither dye is known to have any biological effect on or reaction with prokaryotes (uranin, see (33); FD4, widely used, no reports of adverse effects). Pumping was continued for 2 min after application to allow for the dye to spread across the whole reactor volume and was then shut off to not disturb the measurement. FRAP time series were taken with a 63 × 0.9 water immersion objective in the biofilm at a set distance from the substrate as well as in the bulk fluid above the biofilm. The measurement parameters were as follows: 256-pixel image size, 1400-Hz scanning speed (bidirectional), 6× zoom, 20-μm circular bleach radius, 75% laser power (argon laser), 5% acousto-optical filter (scan)/100% acousto-optical filter (bleach), and pinhole of 2 Airy units. Each measurement was separated into a prebleach, bleach, and postbleach phase. The prebleach phase had 15 frames, the bleach phase had five frames, and the postbleach phase had 60 frames. The frame time was 0.195 s. Eight-bit tagged image file format was used as a data format. Three positions for measurement were chosen on the 10 × 20 mm sample, as shown in Fig. 1.
Mathematical modeling of FRAP: review
The FRAP model was introduced and solved for circular and Gaussian laser profiles by Axelrod and his co-workers (18). Soumpasis (19) corrected a typo in that article (in the main formula (14), the Bessel function I2 should be I1) and developed a simplified and numerically more stable formula for circular profiles. Before presenting our modifications, we restate the model developed in (18,19).
The fundamental model describes the time development of the spatially distributed fluorophore concentration in reaction to a certain laser intensity profile. A twofold reaction takes place: fluorescence and bleaching. The laser-induced fluorescence can be detected by a photo-optic sensor or a camera. Bleaching is the irreversible destruction of part of the fluorophore. It is assumed that most of the fluorophore is mobile. In our case, we will limit this mobility to standard diffusion. Nevertheless, it is often convenient to assume that a fraction of the fluorophore remains immobile.
In what follows, for each time t and each spatial coordinate r, we denote the concentration of the unbleached fluorophore by C(r, t) for the mobile fraction and Cim(r, t) for the immobile fraction, respectively. Furthermore, let I(r, t) be the laser intensity and let F(r, t) be the corresponding laser-induced fluorescence of the fluorophore.
Underlying process model
Let a laser intensity profile I(r, t) be given. The mobile part of the unbleached fluorophore develops over time according to a reaction-diffusion equation of the form
| (1) |
starting with a uniformly constant concentration C0 at some initial time T0, i.e., C(r, T0) = C0 for all r. The term C(r, t) on the right-hand side of the differential equation describes a standard diffusion process, with being the Laplace operator and D being the constant diffusion coefficient of the fluorophore. The term –αI(r, t)C(r, t) models a first-order bleaching reaction of the fluorophore depending on the rate constant α and the laser intensity I(r, t). The minus sign signifies that bleaching destroys the fluorophore irreversibly.
Similarly, but without the diffusion part, the concentration Cim of the immobile fraction of the unbleached fluorophore follows the differential equation
| (2) |
with the constant initial condition Cim(r, T0) = Cim,0 for all r.
The fluorescence induced by the laser is then given by
| (3) |
with some constant q (which depends on the type of laser and fluorophore).
FRAP measurements
The aim of FRAP experiments is to infer knowledge about the diffusion coefficient D by inducing a bleaching reaction in a certain region (ROI) and the subsequent observation of the time development of the fluorescence inside the ROI. Therefore, three phases of a FRAP experiment can be distinguished: the prebleaching phase (T0 ≤ t < –T) before bleaching starts at time t = –T, the bleaching phase (–T ≤ t < 0) of time duration T, and the postbleaching phase (0 ≤ t < ∞) starting at time t = 0. Because the bleaching destroys the fluorophore irreversibly inside the ROI, a subsequent observed recovery of the fluorescence can only be due to a transport of unbleached fluorophore from the surroundings of the bleached region via diffusion. The velocity of the recovery allows the computation of estimates of the diffusion coefficient D. Here, a model assumption is that the surroundings of the ROI are virtually unbounded. Practically, this means that the probe carrier is large enough and that the ROI is located far from its edges. This guarantees that the amount of fluorophore at the outside of the bleaching region is virtually infinite in each direction such that the bleached region can fully recover to its initial fluorescence.
Laser beam modes
The laser beam operates in two different modes during a FRAP measurement: the bleaching mode and the measurement mode. In both modes, the laser intensity will be based on the same time-independent intensity profile I(r). In detail,
| (4) |
where A > 1 is an attenuation factor applied during fluorescence measurement. Practically, the CLSM will be operated in its so-called Flymode, that is, each line is scanned twice: during a forward scan, and only in the bleaching phase, the laser intensity is increased when the laser is located over the ROI and attenuated when outside of the ROI, whereas during the backward scan, the laser beam is constantly attenuated to perform the fluorescence measurement. With this technique, bleaching and measurement are intertwined during the scanning cycle of each frame, and measurements are obtained in all three phases at equidistant time steps Δt (frame length).
Circular intensity profile
We assume that the bleaching region (ROI) has a circular two-dimensional shape with radius w. Originally, a fixed laser beam was used, and the intensity profile was meant to coincide with the laser beam profile itself. In our case, the CLSM offers the possibility to scan a larger ROI with a user-chosen intensity profile. Even though the ROI will be scanned by the CLSM line by line, it will be assumed that the complete region is scanned instantaneously and that each point on that region is scanned with a uniform beam intensity. The circular intensity profile I(r) and thus the bleaching reaction are symmetric around the origin, such that the coordinates r can be given as a (one-dimensional) radial distance from the center of the ROI. The intensity profile is therefore given by
| (5) |
where P0 is the total laser power over the bleaching region.
Bleaching
To simplify the computations, further model assumptions have been introduced by (18). The two main assumptions are as follows:
A1. The attenuation factor A is high enough such that virtually no bleaching occurs during fluorescence measurement.
A2. The duration time T of the bleaching phase is short enough such that virtually no diffusion occurs during that phase.
As a result, always only one part of the diffusion-reaction equation governing the mobile fluorophore concentration is significantly driving the concentration dynamics in each of the FRAP phases. During the bleaching phase,
| (6) |
is assumed, leading to the following closed-form solution of the concentration at the end of bleaching (t = 0):
| (7) |
Similarly, the concentration of the immobile fluorophore at time t = 0 is given by
| (8) |
On the other hand, during the pre- and postbleaching phases, despite the measurements, it is assumed that only diffusion is present for the mobile fluorophore,
| (9) |
whereas the immobile fluorophore remains constant at its level Cim(r, 0) reached at time t = 0.
Determination of diffusion coefficient
The total fluorescence F(t) inside the ROI over time, observed with the attenuated measurement profile I(r, t) = I(r), is given by
| (10) |
Considering the constant fluorescence values F− = F(t) for T0 ≤ t < T (prebleaching), F0 = F(0) (end of bleaching), and F∞ = limt → ∞ F(t) (asymptotic limit at postbleaching), F(t) will be represented as
| (11) |
where the fractional fluorescence recovery f(t), defined as
| (12) |
is a function of time with values in the interval [0, 1]. In (18,19), it has been shown that f(t) can be explicitly computed under the given assumptions and with a circular laser profile as
| (13) |
with I0 and I1 being the modified Bessel functions and τD being the characteristic diffusion time, related to the diffusion constant by
| (14) |
Note that the fluorescence F∞ after full recovery differs from the fluorescence F− before bleaching in the case that part of the fluorophore is immobile. The fraction of total fluorophore in the ROI that is mobile is given by (F∞ − F0)/(F− − F0).
Measurement data
For each frame i of a FRAP measurement cycle, let be a matrix representing the intensity values detected during the corresponding laser scan at time ti. Let JROI be a set of indices (j1, j2) representing the pixel coordinates of the ROI and denoted by #JROI its cardinality (number of pixels in the ROI). Then, the measurement data yi are given by the mean of the measured intensity values inside the ROI:
| (15) |
An example of a sequence of fluorescence scans of frames during the prebleaching and postbleaching phase on a biofilm probe is shown in Fig. 2.
Figure 2.
Scanned images during prebleaching and postbleaching phase. The circular ROI is adjacent to the right-hand edge of the images and has a radius of 10 μm.
Estimation of the diffusion coefficient
Let i0 be the number of the last frame in the bleaching phase (assumed to be measured at time t = 0). Following the model assumptions, it is expected that
| (16) |
holds for all i = i0, …, n. An estimate of the diffusion coefficient D can thus be obtained with the following procedure:
-
1
Normalize the data yi for all i = i0,…, n using (estimates of) F0 and F∞ according to
| (17) |
-
2
Find the parameter τD by fitting the curve f(t) to the normalized data .
-
3
Set .
The parameter search concerning τD can be performed in several ways, e.g., by applying a (nonlinear) least-squares approach (e.g., steepest descent). Alternatively, the parameters F0 and F∞ may be included into the search, in which case one will directly try to fit F(t) to the unnormalized data yi.
FRAP with black box error model
Difficulties with the standard approach
Several difficulties with the standard approach may occur. To keep the model equations simple and solvable in closed form, many simplifying model assumptions had to be introduced that do not always apply to the real system. The two main assumptions A1 and A2 are often violated. Problems with A1 may occur if, to excite a measurable fluorescence signal, the laser intensity has to be relatively high. This can be the case if, for example, the overall fluorescence concentration is quite low for some reason. As a result, bleaching during measurements is unavoidable. Problems with A2 may occur in particular when the diffusion coefficient is high. In fact, the higher the diffusion coefficient, the faster the fluorescence recovery. To compensate for fast recoveries, the time interval Δt between two measurement frames should be decreased together with an eventual increase in the resolution of the ROI. Both actions may be inhibited by limits in the scanning frequencies of the microscope. At the same time, it might be necessary to increase the depth of bleaching, which would require an increase in the time duration of the bleaching phase. As a result, fluorescence recovery already occurs during bleaching.
Additionally, unmodeled random processes independent from the recovery process may disturb the fluorophore concentration and thus severely interfere with the parameter estimations. In our experiments, we observed that the fluorescence recovery did not asymptotically reach a constant value F∞ as expected, but rather showed a constant drift, either increasing or decreasing, obviously independent from the recovery process. This effect presumably stems from the technical and biological system employed. A biofilm is never completely homogenous, and a microscope can never be fully shielded against environmental influences. A possible cause for the drift could be the very structure of the biofilm: it can have pores and canals, thus causing some kind of mixed diffusion between the dense biofilm and less-dense liquid medium. Furthermore, the flow cell is much bigger than the bleaching spot, and thus, it could be possible that—despite blocking in- and outlet during measurement—there is still some movement in the liquid. It is unlikely that the dye accumulates in the biofilm, which could lead to self-quenching and, consequently, to a constant increase in fluorescence after bleaching (because there would be less active dye and thus less quenching). Autofluorescence can also be ruled out because L. lactis is not known to have any autofluorescence. To fully elucidate the reason for this phenomenon, further studies are to be carried out.
Furthermore, it is not obvious how to get good estimates of the values F0 and F∞. It might be tempting to build means over the measurements of the prebleaching value F− as an estimate for F∞, but if part of the fluorophore is immobile and cannot recover from bleaching, then F∞ < F−, and measurements of F− cannot be used to predict F∞. On the other hand, F0 is the fluorescence at the exact time t = 0 at the very beginning of the recovery. Shortly after this time point, the recovery curve f(t) is very steep; rapid changes in fluorophore concentration occur because the diffusion rate is very high because of the high concentration differences of unbleached fluorophore between the ROI and its surroundings. So, small deviations from the exact point in time of the intensity measurement scheduled for time t = 0 may lead to large deviations from the true value of F0. Additionally, because of the physical process of scanning, there is always some uncertainty concerning the exact times of bleaching and measurements.
To cope with these difficulties, we propose to change the traditional approach in two ways: first, we extend the original model by adding an explicit error model to the measurement equation with some new unknown parameters, and second, we apply a Metropolis-Hastings (MH) algorithm to estimate the complete parameter vector.
Our extended model
We supplement the FRAP model by adding a simple black box model, which captures several random disturbances in the measurements. Based on our observations, we capture the following phenomena:
-
1
To capture effects related to the bleaching of the fluorophore during the fluorescence measurements with an attenuated laser intensity, we add an exponential decay term b0exp(–b1t), where b0 is the value of the exponential at time t = 0 and b1 is the rate of exponential decay. This kind of bleaching is most prominently visible at the very beginning of the measurements (i.e., shortly after time t = –T in the prebleaching phase).
-
2
To capture the observed drifting of the fluorescence signal, we add a linear drift term a1t, with a1 being the slope.
-
3
We also explicitly add a Gaussian noise term σηi for each measurement frame i, where each ηi is independently and standard normally distributed and where σ is the spread (i.e., standard deviation) of the stochastic measurement noise.
Accordingly, the mathematical model for the measurement yi at time ti is given by
| (18) |
for i = 1, …, n, (where, in general, (μ, σ2) denotes the univariate normal distribution with mean μ and variance σ2) with new unknown parameters b0, b1, a1, and σ, and with F(t) as defined in Eqs. 11 and 13. It should be noted that we did not include an additional constant offset term in the equation because such a constant can be subsumed under the parameters F−, F0, and F∞, which renders it redundant.
Furthermore, to capture the uncertainty concerning the true onset of the postbleaching phase, the times ti will be modeled as
| (19) |
where i = 1,…, n is the frame number, i0 is the frame number of the last bleaching frame, Δt is the time length of one frame, and s0 ∈ [0, 1] is a relative time shift that captures the uncertainty in the beginning of the onset of fluorescence recovery.
A prototypical sketch of FRAP measurement values predicted by the original FRAP model, the new error model, and the combined model is shown in Fig. 3.
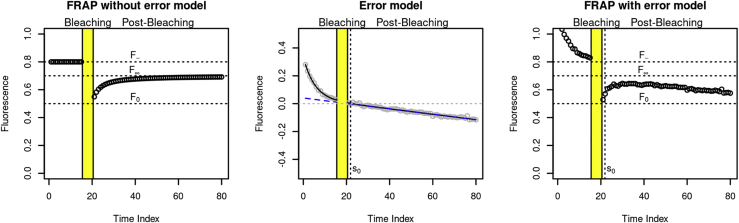
Figure 3.
FRAP model (left), error model (middle), and FRAP model with error model combined (right). The error model in the middle panel consists of four parts: 1) a linear drift (parameter a1, here negative, designated by a dashed line with negative slope), 2) an exponentially decreasing curve that asymptotically approaches the drift (parameters b0 and b1, designated by the solid black curve), 3) additive Gaussian noise (parameter σ2, gray circles), and 4) a time shift (parameter s0, dotted vertical line). The combined model (right panel) is this error model added to the original FRAP model (left panel). The resulting simulated data look very much like a real FRAP measurement (compare to Figs. 6 and 7). To see this figure in color, go online.
In the following, we will gather all measurements yi and all unknown model parameters into vectors y and θ, respectively, i.e.,
| (20) |
and
| (21) |
If convenient, we will denote the single components of θ by θ1, θ2, ...,θΝ (where in the extended model).
Estimation of diffusion coefficient D
To estimate the diffusion coefficient D, it is necessary to estimate all unknown parameters:
-
1)
Estimate the complete parameter vector θ based on the measurements y.
-
2)
Set .
We adopt a Bayesian approach and apply a Metropolis-Hastings algorithm to perform the estimation of the unknown parameter vector θ. Details of this approach will be given in the following sections.
Bayesian approach
The Bayesian model is given by a joint probability density of observations and parameters, p(y, θ), which factorizes into a product of likelihood p(y|θ) (measurements y conditioned on parameters θ) and prior density p(θ):
| (22) |
The likelihood is directly given by the model equation Eq. 18 as
| (23) |
where denotes the univariate Gaussian density with mean μi and variance σ2. Here,
| (24) |
Note that here, in the extended model, the ti-values are unknown values, too, because they depend on the value of the unknown parameter s0, according to
| (25) |
For i = i0, we get t0 = –s0Δt, which is practically always strictly less than 0 because the random variable s0 is practically always strictly greater than 0. For this reason, the measurements corresponding to the last bleaching frame i0 will not be included into the computation of the likelihood (the same is generally true for all other frames of the bleaching phase; the corresponding measurements will never influence the likelihood).
On the other hand, the prior p(θ) still needs to be chosen. We decided for an independent uninformative prior, i.e.,
| (26) |
with
| (27) |
where 1[0, 1] is the indicator function of the interval [0, 1].
The target of the estimation procedure is the posterior density p(θ|y), given by Bayes’ theorem as
| (28) |
where the marginal data likelihood p(y) is given by
| (29) |
Because the posterior cannot be expressed in a closed form expression, its evaluation must be based on the algorithmic computation of approximations. We applied the MH algorithm, which, given some quite arbitrary proposal distributions (given through probability densities qj for each parameter θj, j = 1 ,…,N), produces a sequence of random samples θ (1), θ (2), θ (3), … of parameter vectors whose distribution approaches the target distribution given by the posterior density p(θ|y).
MH algorithm
The Metropolis-Hastings algorithm (34), adapted to our needs, is written in pseudocode as follows:
-
1
Initialization: Set to an arbitrary value.
-
2
for all k = 1, 2, 3, …
-
3
for all j = 1, 2, …, N
-
4
Proposal: Generate a random sample from the proposal distribution with density :
-
5
Acceptance: Accept the proposed sample with probability given by the following acceptance ratio:
i.e., set
-
6
end for
-
7
end for
We have implemented the Metropolis-Hastings algorithm from the scratch in the language R (35).
Initial values and proposal distributions
The initial parameter vector θ(1) has been constructed from crude estimates of the single parameters, i.e., observation means for F0, F∞, and F−, and fixed values for the remaining variables. One loop of our MH algorithm consists of the sequential updating of each of the variables in turn. We used geometric random walk proposals for the positive variables τD, b1, and σ2 and (linear) random walk for the remaining variables. The relative time shift s0 follows a random walk restricted to the interval [0, 1] with reflections at the boundaries. The variances of all these distributions had been fixed after a series of preliminary test runs of the MH algorithm. The exact initial parameter values and proposal distributions can be found in Table 1.
Table 1.
Initial Values and Proposal Distributions of Parameters θj
| Parameter θj | Initial Value | Distribution of Proposal |
|---|---|---|
| τD | Δt | |
| F0 | ||
| F∞ | ||
| F− | F∞ | |
| a1 | 0 | |
| b0 | 0 | |
| b1 | 1 | |
| σ2 | 0.0052 | |
| s0 | 0.5 |
Note that initial τD = Δt has been chosen to be the frame length Δt = 0.195 [s]. The proposal distribution of is a normal distribution restricted to [0, 1] with reflection at the boundaries, denoted here by . Further, initial is the median of the total observed fluorescence in the ROI, taken over all bleaching frames.
Note that with these choices of proposal distributions, their corresponding ratio terms in the acceptance ratio formula are simply given by
| (30) |
and together with our previous choice of improper prior densities, both ratios will cancel out each other in the computation of the acceptance ratio a during each step of the MH algorithm. Thus, the acceptance ratio simplifies to a likelihood ratio:
| (31) |
We generally discard the first half of the produced samples (burn-in phase).
Results and Discussion
Single FRAP measurements were performed for the following:
-
1
two fluorophores: uranin and FD4;
-
2
three positions: pos001, pos002, pos003 (see Fig. 1, positions are numbered from left to right following the flow direction);
-
3
seven times (age of biofilm) at 5, 7, 8, 9, 10, 11, 12 h; and
-
4
two depths: inside the biofilm and above it in the medium.
Each of these 84 measurements results in a set of 80 frames (15 prebleach, five bleach, 60 postbleach) in the format of Tagged Image File Format images, which have been directly used to compute the total fluorescence in the ROI. With these data, Metropolis-Hastings analyses have been performed on two different models, i.e., on a FRAP model 1) with error model and 2) without error model; i.e., in this case, we fixed the parameters a1, b0, b1, σ2, and s0 to their initial values given in Table 1 (this specifically means a1 = b0 = 0 such that linear drift and exponential decrease are neglected). In this way, the benefits of the error model can be seen by comparison of the two models.
For each single FRAP measurement, we run the Metropolis-Hastings algorithm until 100,000 samples of parameter vectors have been produced. We discarded the first half of the samples (i.e., 50,000) as burn in, despite the fact that convergence was usually reached already much earlier after a few thousand steps. Accordingly, in each case, all statistical analyses were based solely on the last 50,000 samples. Additionally, for each single-MCMC run, convergence of the Markov chains and accuracy of all parameter estimates have been tested with standard hypothesis tests. A further description and the results of these tests can be found in the Supporting Materials and Methods.
Because the radius of the ROI is w = 10 μm, the diffusion coefficient D can be computed from the sampled characteristic times τD by
| (32) |
Estimation results: overview
In Figs. 4 and 5, the results of all 184 MH runs are shown. Each result is represented by a single box-and-whisker diagram. A comparison of the estimation results obtained with error model (left-hand sides in both figures) and without error model (corresponding right-hand sides) reveals that the additional flexibility present in the error model has an overall positive effect on the results. This is most obvious when the measurements inside the biofilm (dark gray boxes) are considered. On the one hand, the estimations with error model are relatively stable for both uranin and FD4 in the sense that 1) the variation inside each measurement is moderate and nearly equal over all times (5–12 h), indicated by the nearly equal sizes of the boxes, and 2) the variation of the medians (bars inside the boxes) between different measurements is moderate. On the other hand, the estimations without error model show different aberrations for uranin and for FD4. In the uranin case, the variance within one measurement is lower (i.e., smaller boxes), whereas the variance between different times is much higher. On the contrary, in the FD4 case, the variance within one measurement is often extremely high (very large boxes), whereas the median of many measurements (made inside the biofilm) is often higher than the median of the corresponding measurement in the medium. This is against what one would expect because the diffusion coefficient inside the biofilm should be lower than in the medium.
Figure 4.
Analysis of FRAP data of uranin diffusion in a biofilm: with error model (left) and without error model (right). For each FRAP measurement, corresponding MH samples (after burn-in phase) of the diffusion coefficient D are represented by box-and-whisker diagrams. In each single box-and-whisker diagram, the box itself displays the samples between the first and third quartiles (interquartile range), whereas the inner band depicts the median. The whiskers extend to the most extreme data point that is no more than 1.5 times the interquartile range from the box. The remaining data points (outliers) are plotted as dots.
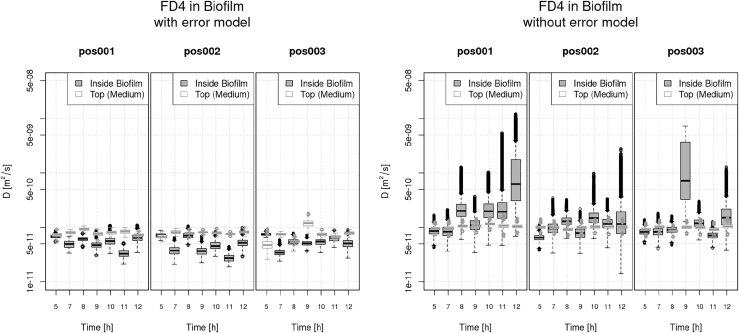
Figure 5.
Analysis of FRAP data of FD4 diffusion in a biofilm: with error model (left) and without error model (right). For a description of the box-and-whisker diagrams, see Fig. 4.
Two typical examples
We pick out two single-FRAP measurements as typical examples.
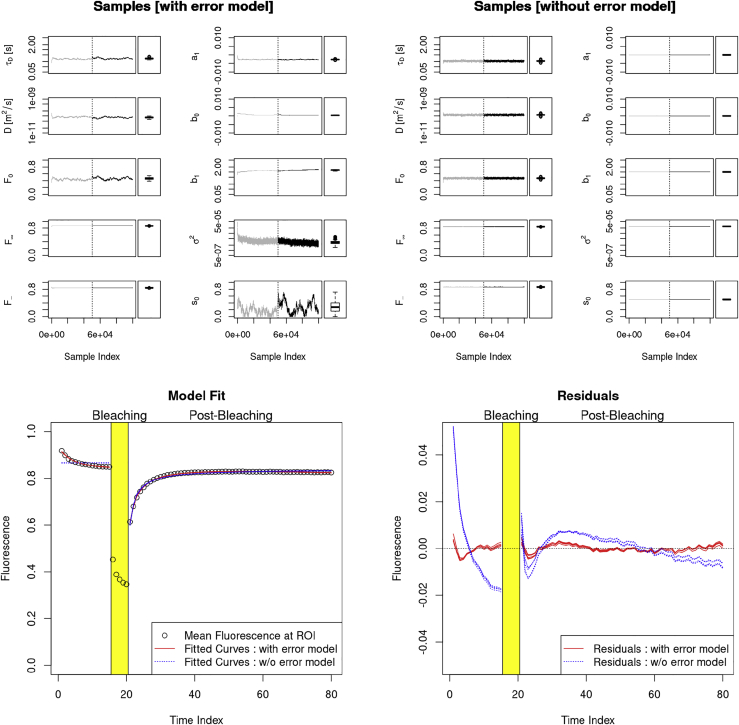
Our first example is the FD4 measurement at 10 h, position 001, measured in the medium (Fig. 6). The data show a rapid exponential decrease in the prebleaching phase and a slight but significant negative drift in the postbleaching phase. Because negative drifts cannot be compensated by adjusting the parameters of the FRAP model, the predictions obtained without the error model do not fit well to the measured data. Nevertheless, despite the bad fit, the estimates of the diffusion coefficients are comparable to the ones estimated with the extended model. On the other hand, the estimates obtained with the extended model provide a much better fit to the data, which shows that the extended model can much better represent the measurements. This, in turn, heightens the confidence in the validity of the estimated parameters.
Figure 6.
Example 1: FD4 at 10 h, position 001, measured in the medium. The upper row shows samples produced during the MH runs with error model (left) and without error model (right). Shown here is the development of the samples over the MH run time, separately for each parameter, and a box-and-whisker diagram (see Fig. 4) representing the samples after the burn-in phase. For τD, D, b1, and σ2, a log scale has been used on the y axis. The end of the burn-in phase has been marked with a vertical line. The samples of burn-in phase are in gray. Note that in the case without error model, the parameters a1, b0, b1, σ2, and s0 are kept fixed to their respective initial values (as given in Table 1) throughout the complete MH run (left-most plot column). The lower row shows several model fits (left) and residuals (right). Shown here are the data (black circles) and five model prediction curves with parameters randomly selected from the MH estimations after burn-in, fitted with and without error model, respectively. To see this figure in color, go online.
The second example is taken from the uranin measurement at 8 h, position 002, measured inside the biofilm (Fig. 7). Here, the Gaussian noise is higher than in the FD4 measurement of the previous example. The drift in the postbleaching phase is now positive. Positive drifts can be compensated even in the case in which no error model is used, but in this case, the estimated parameters are forced to deviate from their appropriate values to obtain this compensation. This leads to an overall good fit of the predicted curve, whereas the estimated diffusion coefficient is heavily underestimated. An equally good fit is obtained as well in the case with error model, but here, the additional parameters of the extended model capture the compensation. As a result, the estimation of the diffusion coefficient is quite in line with what one would expect. Thus, in this example, too, the confidence in the results obtained with the extended model is much higher.
Figure 7.
Example 2: uranin at 8 h, position 002, measured inside the biofilm. For further description, see Fig. 6. To see this figure in color, go online.
Conclusions
We have extended the standard FRAP model by a black box part covering some commonly experienced artifacts in the FRAP measurement data, and we have estimated all unknown model parameters (inclusively, the diffusion coefficient) through application of a suitably adapted Metropolis-Hastings algorithm. The estimations based on this extended model showed to be much more stable in comparison to estimations obtained without the additional error model. This has been shown on experiments with two different fluorophores in a biofilm. The methodology is not restricted to the application on biofilms and might be easily adapted to other FRAP measurements on other materials. Nevertheless, the proposed model does not capture all disturbances or violations of model assumptions. If one wants to weaken these assumptions, one finally has to abandon the simplified model leading to the basic equation Eq. 13 and has to work with the reaction-diffusion equation Eq. 1 directly. Accordingly, the application of sequential parameter estimation methods might be advantageous or even necessary.
Author Contributions
A.W. and R.U. designed the research. J.C. carried out the experiments and measurements. J.H. analyzed the data. J.H. and J.C. wrote the article.
Acknowledgments
We gratefully adopted references (27, 28, 29, 30) from a comment made by one of the anonymous reviewers.
This work was funded by the Deutsche Forschungsgemeinschaft (German Research Foundation) under grants LA 1454/6-1 and UL 170/14-1.
Editor: Ruth Baker.
Footnotes
Supporting Material can be found online at https://doi.org/10.1016/j.bpj.2020.03.017.
Supporting Material
References
- 1.Stewart P.S. Theoretical aspects of antibiotic diffusion into microbial biofilms. Antimicrob. Agents Chemother. 1996;40:2517–2522. doi: 10.1128/aac.40.11.2517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Stevens D.K., Berthouex P.M., Chapman T.W. The effect of tracer diffusion in biofilm on residence time distributions. Water Res. 1986;20:369–375. [Google Scholar]
- 3.Libicki S.B., Salmon P.M., Robertson C.R. The effective diffusive permeability of a nonreacting solute in microbial cell aggregates. Biotechnol. Bioeng. 1988;32:68–85. doi: 10.1002/bit.260320111. [DOI] [PubMed] [Google Scholar]
- 4.Stoodley P., de Beer D., Lewandowski Z. Liquid flow in biofilm systems. Appl. Environ. Microbiol. 1994;60:2711–2716. doi: 10.1128/aem.60.8.2711-2716.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Yang S., Lewandowski Z. Measurement of local mass transfer coefficient in biofilms. Biotechnol. Bioeng. 1995;48:737–744. doi: 10.1002/bit.260480623. [DOI] [PubMed] [Google Scholar]
- 6.Picioreanu C., van Loosdrecht M.C., Heijnen J.J. A theoretical study on the effect of surface roughness on mass transport and transformation in biofilms. Biotechnol. Bioeng. 2000;68:355–369. doi: 10.1002/(sici)1097-0290(20000520)68:4<355::aid-bit1>3.0.co;2-a. [DOI] [PubMed] [Google Scholar]
- 7.Rani S.A., Pitts B., Stewart P.S. Rapid diffusion of fluorescent tracers into Staphylococcus epidermidis biofilms visualized by time lapse microscopy. Antimicrob. Agents Chemother. 2005;49:728–732. doi: 10.1128/AAC.49.2.728-732.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.De Beer D., Stoodley P., Lewandowski Z. Liquid flow and mass transport in heterogeneous biofilms. Water Res. 1996;30:2761–2765. [Google Scholar]
- 9.Horn H., Hempel D.C. Mass transfer coefficients for an autotrophic and a heterotrophic biofilm system. Water Sci. Technol. 1995;32:199–204. [Google Scholar]
- 10.Kumar A., Hille-Reichel A., Van Langehove H. Oxygen transport within the biofilm matrix of a membrane biofilm reactor treating gaseous toluene. J. Chem. Technol. Biotechnol. 2012;87:751–757. [Google Scholar]
- 11.Gade P.A.V., Olsen T.B., Sams T. Modelling of ciprofloxacin killing enhanced by hyperbaric oxygen treatment in Pseudomonas aeruginosa PAO1 biofilms. PLoS One. 2018;13:e0198909. doi: 10.1371/journal.pone.0198909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Peters R., Peters J., Bähr W. A microfluorimetric study of translational diffusion in erythrocyte membranes. Biochim. Biophys. Acta. 1974;367:282–294. doi: 10.1016/0005-2736(74)90085-6. [DOI] [PubMed] [Google Scholar]
- 13.Lawrence J.R., Wolfaardt G.M., Korber D.R. Determination of diffusion coefficients in biofilms by confocal laser microscopy. Appl. Environ. Microbiol. 1994;60:1166–1173. doi: 10.1128/aem.60.4.1166-1173.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.de Beer D., Stoodley P., Lewandowski Z. Liquid flow in heterogeneous biofilms. Biotechnol. Bioeng. 1994;44:636–641. doi: 10.1002/bit.260440510. [DOI] [PubMed] [Google Scholar]
- 15.Pluen A., Netti P.A., Berk D.A. Diffusion of macromolecules in agarose gels: comparison of linear and globular configurations. Biophys. J. 1999;77:542–552. doi: 10.1016/S0006-3495(99)76911-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Braga J., Desterro J.M.P., Carmo-Fonseca M. Intracellular macromolecular mobility measured by fluorescence recovery after photobleaching with confocal laser scanning microscopes. Mol. Biol. Cell. 2004;15:4749–4760. doi: 10.1091/mbc.E04-06-0496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Waharte F., Steenkeste K., Fontaine-Aupart M.-P. Diffusion measurements inside biofilms by image-based fluorescence recovery after photobleaching (FRAP) analysis with a commercial confocal laser scanning microscope. Appl. Environ. Microbiol. 2010;76:5860–5869. doi: 10.1128/AEM.00754-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Axelrod D., Koppel D.E., Webb W.W. Mobility measurement by analysis of fluorescence photobleaching recovery kinetics. Biophys. J. 1976;16:1055–1069. doi: 10.1016/S0006-3495(76)85755-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Soumpasis D.M. Theoretical analysis of fluorescence photobleaching recovery experiments. Biophys. J. 1983;41:95–97. doi: 10.1016/S0006-3495(83)84410-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.de Beer D., Stoodley P., Lewandowski Z. Measurement of local diffusion coefficients in biofilms by microinjection and confocal microscopy. Biotechnol. Bioeng. 1997;53:151–158. doi: 10.1002/(SICI)1097-0290(19970120)53:2<151::AID-BIT4>3.0.CO;2-N. [DOI] [PubMed] [Google Scholar]
- 21.Braeckmans K., Peeters L., Demeester J. Three-dimensional fluorescence recovery after photobleaching with the confocal scanning laser microscope. Biophys. J. 2003;85:2240–2252. doi: 10.1016/s0006-3495(03)74649-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Gordon G.W., Chazotte B., Herman B. Analysis of simulated and experimental fluorescence recovery after photobleaching. Data for two diffusing components. Biophys. J. 1995;68:766–778. doi: 10.1016/S0006-3495(95)80251-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Bryers J.D., Drummond F. Local macromolecule diffusion coefficients in structurally non-uniform bacterial biofilms using fluorescence recovery after photobleaching (FRAP) Biotechnol. Bioeng. 1998;60:462–473. [PubMed] [Google Scholar]
- 24.Meyvis T.K., De Smedt S.C., Demeester J. Fluorescence recovery after photobleaching: a versatile tool for mobility and interaction measurements in pharmaceutical research. Pharm. Res. 1999;16:1153–1162. doi: 10.1023/a:1011924909138. [DOI] [PubMed] [Google Scholar]
- 25.Klonis N., Rug M., Tilley L. Fluorescence photobleaching analysis for the study of cellular dynamics. Eur. Biophys. J. 2002;31:36–51. doi: 10.1007/s00249-001-0202-2. [DOI] [PubMed] [Google Scholar]
- 26.Seiffert S., Oppermann W. Systematic evaluation of FRAP experiments performed in a confocal laser scanning microscope. J. Microsc. 2005;220:20–30. doi: 10.1111/j.1365-2818.2005.01512.x. [DOI] [PubMed] [Google Scholar]
- 27.Yang J., Köhler K., Burroughs N.J. An improved strip FRAP method for estimating diffusion coefficients: correcting for the degree of photobleaching. J. Microsc. 2010;238:240–253. doi: 10.1111/j.1365-2818.2009.03347.x. [DOI] [PubMed] [Google Scholar]
- 28.Sprague B.L., McNally J.G. FRAP analysis of binding: proper and fitting. Trends Cell Biol. 2005;15:84–91. doi: 10.1016/j.tcb.2004.12.001. [DOI] [PubMed] [Google Scholar]
- 29.Gousseva V., Simaan M., Swain P.S. Inferring the lifetime of endosomal protein complexes by fluorescence recovery after photobleaching. Biophys. J. 2008;94:679–687. doi: 10.1529/biophysj.107.115188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Feilke M., Schneider K., Schmid V.J. Bayesian mixed-effects model for the analysis of a series of FRAP images. Stat. Appl. Genet. Mol. Biol. 2015;14:35–51. doi: 10.1515/sagmb-2014-0013. [DOI] [PubMed] [Google Scholar]
- 31.Schlegel C. Technical University Kaiserslautern, Cuvillier-Verlag; Göttingen, Germany: 2016. Produktive Biofilme auf mikrostrukturierten Metalloberflächen: Dissertation. [Google Scholar]
- 32.De Man J.C., Rogosa M., Sharpe M.E. A medium for the cultivation of lactobacilli. J. Appl. Bacteriol. 1960;23:130–135. [Google Scholar]
- 33.Arbeitskreis “Human- und ökotoxikologische Bewertung von Markierungsmitteln in Gewässern” Human- und ökotoxikologische Bewertung von Markierungsmitteln in Gewässern. Grundwasser. 1997;2:61–64. [Google Scholar]
- 34.Hastings W.K. Monte Carlo sampling methods using Markov chains and their applications. Biometrika. 1970;57:97–109. [Google Scholar]
- 35.R Core Team . R Foundation for Statistical Computing; Vienna, Austria: 2019. R: a language and environment for statistical computing. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.