Abstract
Diffusion obstacles in membranes have not been directly visualized because of fast membrane dynamics and the occurrence of subresolution molecular complexes. To understand the obstacle characteristics, mobility-based methods are often used as an indirect way of assessing the membrane structure. Molecular movement in biological plasma membranes is often characterized by anomalous diffusion, but the exact underlying mechanisms are still elusive. Imaging total internal reflection fluorescence correlation spectroscopy (ITIR-FCS) is a well-established mobility-based method that provides spatially resolved diffusion coefficient maps and is combined with FCS diffusion law analysis to examine subresolution membrane organization. In recent years, although FCS diffusion law analysis has been instrumental in providing new insights into the membrane structure below the optical diffraction limit, there are certain exceptions and anomalies that require further clarification. To this end, we correlate the membrane structural features imaged by atomic force microscopy (AFM) with the dynamics measured using ITIR-FCS. We perform ITIR-FCS measurements on supported lipid bilayers (SLBs) of various lipid compositions to characterize the anomalous diffusion of lipid molecules in distinct obstacle configurations, along with the high-resolution imaging of the membrane structures with AFM. Furthermore, we validate our experimental results by performing simulations on image grids with experimentally determined obstacle configurations. This study demonstrates that FCS diffusion law analysis is a powerful tool to determine membrane heterogeneities implied from dynamics measurements. Our results corroborate the commonly accepted interpretations of imaging FCS diffusion law analysis, and we show that exceptions happen when domains reach the percolation threshold in a biphasic membrane and a network of domains behaves rather like a meshwork, resulting in hop diffusion.
Significance
In this work, for the first time, we directly correlate the nanoscale organization of SLBs exhibiting diverse domain configurations, as revealed by AFM, with membrane organization as inferred by fluorescence correlation spectroscopy (FCS) diffusion law analysis performed by ITIR-FCS. Our results show that more than one type of nanoscale membrane configurations can manifest the same apparent diffusive mode on the micron scale, and thus, interpretation of FCS diffusion law analysis results require validation by additional experiments. This direct comparison of structure with dynamics will facilitate a better interpretation of FCS diffusion law analysis results in membrane studies.
Introduction
The cellular plasma membrane is a heterogeneous bilayer structure composed of thousands of diverse lipids and proteins. Investigated for over a century, it still is at the forefront of research because it has been slow to yield the secrets of its structure and dynamics. Typically, a plasma membrane contains nanoscale transient lipid-protein, protein-protein, and lipid-lipid assemblies along with the dynamic cytoskeleton fences underneath the membrane and the extracellular matrix (1). Often, the sizes of these nanoscale compartments and assemblies lie in the range of 10–300 nm (1), and depending on the molecular interactions between the components, these transient assemblies exhibit specific lifetimes. The main reason for our lack of understanding of the plasma membrane is that it does not possess a static structure but rather is highly dynamic, with structures below the optical resolution limit forming and disassembling at timescales that are too short to obtain measurements with a sufficient signal/noise ratio to elucidate details of this complex, constantly changing assembly. The plasma membrane is also not isolated but exists in a dynamic equilibrium with constant exchange with the cell interior and exterior by endo- and exocytosis and by interactions with other cell or tissue structures, in particular the cytoskeleton and extracellular matrices. Finally, the details of the plasma membrane also depend on the cell type, and one can find very different physicochemical characteristics depending on what cell type and cell stage one is investigating (2).
Researchers have tried to replicate plasma membrane characteristics and use various mimics, from planar SLBs to small and large unilamellar vesicles, with varying composition and symmetric or asymmetric lipid distribution across the two leaflets, and even cell-derived giant plasma membrane vesicles (3, 4, 5, 6, 7, 8). However, none of the mimics have been able to fully replicate the dynamic equilibrium and complex dynamics of cellular plasma membranes, and researchers need to find means to study these structures in live cells. In addition to the membrane dynamics, the size of transient assemblies lies in the range of 5–200 nm, which is below the diffraction limit. Because the membrane structure cannot be directly measured, dynamics is used as a surrogate, and structure is inferred from dynamical features. A commonly used method that uses this strategy is the FCS diffusion law analysis.
FCS is a widely used tool to study the diffusion of various plasma membrane components. FCS achieves this by illuminating a diffraction limited spot (∼4–500 nm in diameter) and monitoring the fluorescence fluctuations from this single spot as single fluorescently labeled probe molecules enter and exit its perimeter. Because of the mathematical evaluation by correlation functions, FCS inherently averages over many such single-molecule passages and thus provides an average diffusion coefficient. The mode of diffusion, whether it is Brownian free diffusion or whether the probe molecules undergo a more complex movement of interactions with barriers and traps, cannot be easily extracted from a single FCS measurement. A solution to this problem came with the investigation of the dependence of the correlation function and the recovered diffusion coefficient on the length scales over which it is measured. Krichevsky et al. (9) suggested the extraction of the mean-square displacement from each point of the correlation function. The other, arguably more widely used technique is subsumed under the title of the FCS diffusion law analysis (10). In this case, FCS is measured for different spot radii, and the average time that probe molecules need to traverse the spots is plotted against the spot area. The diffusion law then states that if the y-intercept is 0 within the margins of error, then the probes undergo free diffusion. It has been shown that hop diffusion introduced by meshwork-like barriers, which probe molecules need to overcome, leads to a negative intercept (11). Transient trapping or confinement in domains is assumed to lead to positive intercepts. This has been shown to coincide with expectations for several standard probes (2,12,13) and was successfully applied to various systems (2,12, 13, 14, 15, 16). However, there were also several exceptions and corrections to the simple interpretation of the diffusion law analysis. First, for a meshwork or transient trapping to be resolvable, i.e., to lead to nonzero y-intercepts, the meshwork needs to be sufficiently dense and hinder the diffusion in a significant way, and the size, density, and trapping time of domains need to be above a certain threshold (17). Second, if domains are mobile, they might not be detected, and a zero intercept might be seen (18). Third, if both meshwork and domain trapping are present, their common result will be a weighted average, and thus, the absolute value of the intercept might not be indicative of the diffusive mode (19). In this case, additional tests that disrupt the meshwork or domains need to be performed, and the subsequent positive (for meshwork) or negative (for domains) change in the intercept indicates hop diffusion or transient trapping. Lastly, in some experiments on SLBs composed of lipid mixtures, negative intercepts were observed despite the fact that no meshwork, but rather domain trapping, was expected (16,20). Therefore, in this work, we combine AFM with ITIR-FCS to address these issues. AFM provides nanometer resolution on SLBs, whereas ITIR-FCS is a camera-based FCS modality, which provides dynamics information on the diffusion coefficient and, because multiple pixels can be binned, also provides the FCS diffusion law plots from a single measurement. Instead of using cell membranes, we conducted this study on SLBs because the composition and, therefore, the size and density of domains can be controlled, and the membrane structure is accessible by AFM. The experiments are done on those bilayers, which exhibit characteristic zero, positive, and negative intercepts and thus serve as model bilayer systems harboring distinct domain features. The choice of lipid bilayer compositions is based on previously published articles (16,20). Beyond what has already been shown, we demonstrate that membranes with small domains near the percolation threshold with low to intermediate confinement strength exhibit a negative FCS diffusion law intercept indicative of hop diffusion. Our complementary results on the structure and dynamics of membranes containing domains set guidelines that aid in a better interpretation of diffusion data obtained from ITIR-FCS and FCS diffusion law analysis.
Materials and Methods
Sample preparation
Lipids and dyes
1,2-dioleoyl-sn-glycero-3-phophocholine (DOPC), 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC), 1,2-dimyristoyl-sn-glycero-3-phosphocholine (DMPC), 1,2-distearoyl-sn-glycero-3-phosphocholine (DSPC), 1,2-dilauroyl-sn-glycero-3-phosphocholine (DLPC), and cholesterol (Chol) are used in this study. The head-labeled rhodamine dye 1,2-dimyristoyl-sn-glycero-3-phosphoethanolamine-N- (lissamine rhodamine B sulfonyl) (ammonium salt) (RhoPE) are used as the fluorescent probe for SLBs. All the lipids and dyes were purchased from Avanti Polar Lipids (Alabaster, AL).
Substrate preparation for supported lipid bilayers
Glass cover slides were cleaned before they were used for the SLB preparation. The glass slides were rinsed with Hellamax detergent solution. Then, glass slides were sonicated for 30 min each with detergent solution, 2 M sulphuric acid, and deionized water. In between the sonication cycles, glass slides were rinsed ∼50 times with deionized water.
Mica substrates were freshly prepared before each experiment. Glass slides were cleaned according to the above-mentioned protocol. Freshly cleaved mica sheets of thickness 10–15 μm were glued to the glass slide with ∼1 μL of optical quality glue (NOA 88; Norland Products, Cranbury, NJ). The refractive index of both cured glue and mica is 1.56. The mica sheet was gently pressed, and a uniform ∼2-μm thick layer of glue was formed, which was then cured by placing the layered substrate under an ultraviolet lamp for at least 30 min.
Preparation of supported lipid bilayers of various lipid compositions
The calculated concentrations of the lipids and dye (the working concentration of total lipid and dye was 650 μM and 100 nM, respectively) were assembled in a cleaned round-bottom flask. The components were vortexed for thorough mixing and then evaporated in a rotary evaporator (Rotavap R-210; Buchi, Flawil, Switzerland) for 3–4 h to produce a thin, uniform lipid film. The dried lipid film was resuspended in buffer (10 mM HEPES and 150 mM NaCl (pH 7.4)), resulting in a turbid solution of multilamellar vesicles. This vesicle suspension was sonicated using a bath sonicator (FB15051 Model; Thermo Fisher Scientific, Singapore) until clarity to form large unilamellar vesicles was achieved.
The buffer was mixed with vesicles obtained by the above-described procedure in a 1:1 ratio and were deposited on a freshly cleaned glass cover slide (24 × 50-1, Fisher Brand Microscope cover glass; Thermo Fisher Scientific). It was incubated at 65°C for 60–80 min, followed by cooling at room temperature for 20 min. Then, the unfused vesicles were removed by washing with buffer with the desired pH 20 times. SLBs equilibrated at room temperature were used for ITIR-FCS measurements.
ITIR-FCS
Imaging FCS is a camera-based FCS method that employs uniform plane illumination (Total internal reflection (TIR) and selective plane illumination microscopy (SPIM)) and fast array detectors (electron-multiplying charge-coupled device (EMCCD), scientific Complementary metal–oxide–semiconductor (sCMOS), and single-photon avalanche diode) to record the signal from a whole region of interest (ROI) (21). In this work, imaging FCS is performed with the total internal reflection fluorescence illumination and EMCCD detection. Unlike confocal FCS, imaging FCS implemented in the TIR mode does not require repeated calibration of the observation area because the camera chip provides the xy sectioning and the TIR mode of illumination provides z-sectioning. ITIR-FCS is ideal for samples closely located to the cover slide, such as SLBs and cell membranes. ITIR-FCS provides a spatially resolved diffusion coefficient and a number of particle maps, which are important ways of assessing the sample heterogeneity.
For the ITIR-FCS, measurements done in this study are performed using an objective type total internal reflection fluorescence microscope (IX-71; Olympus; Singapore) with a high-numerical-aperture oil immersion objective (PlanApo, 100×, numerical aperture 1.45; Olympus). The excitation light from the lasers (488 nm (Spectra-Physics Lasers, Mountain View, CA) and 532 nm (Samba; Cobolt, Solna, Sweden)) was introduced into the microscope by adjusting two tilting mirrors. After being reflected by a dichroic mirror (Z488/532RPC; Semrock, Rochester, NY), the beam was focused on the back focal plane of the objective. It was total internally reflected at the glass-water interface by adjusting the incident angle of the excitation beam again by the orientation of the same set of tilting mirrors. The laser power used was in the range of 0.8–1 mW. The immersion medium of the objective was mineral oil (refractive index 1.516; Olympus). The fluorescence from the sample was reflected through the same objective, followed by transmission through the same dichroic mirror. After being filtered by an emission filter, finally, it was imaged on the CCD chip of a water-cooled (−80°C), back-illuminated EMCCD camera (Andor iXON 860, 128 × 128 pixels; Andor Technology, South Winds, CT).
A region of interest typically of the size of 21 × 21 pixels is selected. The signal was simultaneously recorded from the whole region of interest (ROI) in the form of a stack of 30,000–50,000 frames with the required time resolution. The software Andor Solis for imaging (version 4.18.30004.0 and 4.24.30004.0) was used for data acquisition. The pixel side length of the CCD chip in the device is 24 μm, corresponding to a pixel side length of 240 nm in the sample plane. The camera was operated in the kinetic mode, and baseline clamp was used to minimize baseline fluctuations. The readout speed was 10 MHz with 4.7× maximal analog/digital gain and 25-μs vertical shift speed. If not stated otherwise, an EM gain of 300 was used. The data were saved as 16-bit Tiff files. The temporal intensity trace from each pixel was autocorrelated using the multitau correlation scheme using a FIJI plug-in ImFCS 1.49, a home-written software (available at http://www.dbs.nus.edu.sg/lab/BFL/imfcs_image_j_plugin.html), to generate autocorrelation functions (ACF) (22). The data were bleach corrected using a fourth-order polynomial function. Imaging FCS illuminates a large area, resulting in a depletion of fluorophores with time due to photobleaching. Unlike in confocal FCS, in which the observation volume is small compared to the surrounding area, the bleached fluorophores cannot be replenished from the immediate vicinity. Consequently, there is a long-term decay on the timescales of seconds that offsets the correlation curve. This is corrected by fitting a model function f(t) to the decaying intensity trace and then applying a transformation that restores the flat intensity trace, conserving the variance of the intensity fluctuations (21). The ACF for each pixel was individually fitted with the following one-particle model for a diffusion using the same software. The fit model in a TIR-camera setup deviates from the one used for confocal systems because in this case, the intensity is constant in the xy plane and the z direction is not considered because we work with a two-dimensional (2D) system. It is a good approximation because the bilayer roughness is not more than 10 nm in an evanescent field that is ∼100 nm, and the pixels on the detection array are square. The fitting function is written as below (22):
Here, G(τ) represents the ACF as a function of correlation time (τ) and N, a, D, and σ are the number of particles per pixel, pixel side length, diffusion coefficient, and standard deviation (SD) of the Gaussian approximation of the microscope point spread function (PSF), respectively. G∞ represents the convergence value of the ACF at long correlation times.
The fitting of ACFs with theoretical models provides the diffusion coefficient (D) and the number of particles (N). Because it is an imaging-based FCS modality, D and N maps are obtained for the whole ROI (22). In ITIR-FCS, the data are represented as the mean ± SD. The SD is obtained from the measurements over 441 pixels per experiment. The SD of an ITIR-FCS measurement not only contains contributions from the measurement variability but also from the heterogeneity of the system.
Overall, ITIR-FCS measurements provide spatially resolved 2D number-of-particle and diffusion-coefficient maps. The data can also be represented in the form of histograms. ITIR-FCS data can be used to perform FCS diffusion law analysis.
To determine EArr, we measured the diffusion coefficient of DOPC bilayers at a temperature range of 298–310 K, and Arrhenius plots were generated. Mathematically, these plots are described by the Arrhenius equation mentioned as below:
where D is the diffusion coefficient (m2/s), Do is a pre-exponential factor (m2/s), T is the absolute temperature (K), R is the molar gas constant (8.314 J K−1 mol−1), and EArr is the Arrhenius activation energy (J/mol). Plotting ln(D) against 1/T produces the Arrhenius plot, and EArr is obtained from the slope of a line fitted to the data.
Implementation of FCS diffusion law analysis in ITIR-FCS
To perform FCS diffusion law analysis in ITIR-FCS data, the same set of data that is obtained in an ITIR-FCS experiment is used. Variable observation areas (Aeff) are obtained by postacquisition pixel binning (1 × 1 to 5 × 5), followed by convolution with the PSF of the microscope system. The image of an individual point-like particle is described by the PSF, and therefore, the signal originating from a single particle is detected over an extended area. If any part of the particle image overlaps with the pixel, the particle will be detected by that pixel. Therefore, the observation area for a pixel is the convolution of the PSF with the pixel area. The PSF for the system can be determined based on the fact that the diffusion coefficient for free diffusion is a constant, independent of the area observed. We thus measure the diffusion coefficient of a DOPC bilayer at different binned areas. The PSF-value at which the diffusion coefficient is independent of the binned area is the PSF of the system. The Aeff/D is plotted against Aeff, and the plot is fitted to a line with the standard error of the mean-weighted diffusion law equation to obtain the y-intercept τ0. The typical margin of error on SLBs is ±0.1, and thus, intercepts in that range are indistinguishable from free diffusion. Only intercepts larger than 0.1 can be attributed to domain trapping in our setup (23).
Simulations of domain-obstructed diffusion in imaging fluorescence correlation spectroscopy
For domain simulations, image grids with an array of randomly located circular, static, and nonoverlapping domains were created. A stack of 100,000 images of 20 × 20 pixels were created using the FIJI plug-in mentioned above for ITIR-FCS data analysis. The particles were randomly distributed on the image grid. The pixel size was set to 240 nm, and the time resolution was 1 ms. Simulations were then run with a time step (Δt) of 100 on each frame such that each step is much smaller than the domain size and the interdomain distances. For diffusion of the particles in the consecutive frames, the particle movement was determined using Din within a domain and Dout outside domains. The density of domains was modulated by adjusting the interdomain distances. Upon encountering the domain boundary, a particle is either reflected at the domain boundary or it enters or exits the domain with the probabilities Pin or Pout, respectively. All simulation parameters are given in Table 2. The distance traversed by each particle at each time step and in each dimension (x and y) is determined by a Gaussian distribution with a mean of 0 and a variance of 2DsimΔt, where Dsim is the diffusion coefficient of the simulated particles, and it varies within and outside the domains. The photon emission process is simulated by Poisson statistics, in which a Poisson-distributed random number is assigned to each particle. The mean of this Poisson distribution is given by the counts per particle and second times the time step = 1 ms. The counts per particle and second value was 10,000 for all simulations presented here. Initially, particles were placed randomly on the simulated area, and the simulations were optimized for the equilibration and convergence. The convergence was tested by calculating the τ0 for stacks of overlapping 30,000 frames each within the 100,000 frames that were used for the analysis. We observed that for the initial 30,000 frames, the calculated FCS diffusion law intercepts (τ0) were generally higher than that was calculated from the remaining 70,000 frames that provided a constant τ0. Thus, these frames were discarded to ensure the equilibration of the system, and the rest of the 70,000 frames were used for the analysis. This is because in phase-separated bilayers, it takes ∼30,000 frames for the proper randomization of particles within and outside the domains.
Table 2.
Description of Simulation Parameters Used
| Parameter | Description | Values Used in Simulations |
|---|---|---|
| Pixel size | size of an individual pixel on camera chip | 0.24 μm |
| Aeff | convolution of pixel area with PSF | 0.42 μm |
| No. of pixels | number of pixels on the image grid | 400 |
| Din | diffusion coefficient inside the domain | 0.1 |
| Dout | diffusion coefficient outside the domain | 0.3 |
| Dout/Din | ratio of the diffusion coefficients outside and inside the domain | 3 |
| Pin | probability of entering the domain | 0.5 |
| Pout | probability of exiting the domain | 0.15 |
| r | domain radius | 20 nm |
| Δt | time difference between two successive frames | 1 ms |
| Steps per frame | number of times a particle moves in one frame | 100 |
Atomic force microscopy data acquisition and analysis
AFM measurements were performed using a JPK Nanowizard3 Bioscience AFM equipped with JPK Vortis SPMControl controller with XYZ closed-loop feedback (JPK Instrument, Berlin, Germany) attached to an inverted microscope. The imaging was done in quantitative imaging mode. Silicon nitride cantilevers from Bruker, Singapore (model: DNP-10) are used for the imaging. The cantilevers spring constants were calibrated using the thermal noise method. The spring constants were estimated in the range of 0.1 N/m. We used setpoint <1 nN, and pixel time was kept around 15 ms for measurement. Data processing was done using the JPK Data Processing software. The calculation of lipid phase fractions from histogram data corresponding to AFM images is performed on R. For spatial autocorrelation analysis, we used an ImageJ plug-in developed by Walter (24).
Results
We correlate the arrangement of diffusion obstacles, i.e., domains on lipid bilayers imaged by AFM, with the information on dynamics obtained using ITIR-FCS and FCS diffusion law analysis. AFM measures the lateral organization of the lipid bilayers by imaging topographic details of the membranes in the form of domain lateral size and domain height with respect to the surrounding fluid lipids. This method offers lateral and vertical resolution in the range of nanometers (in this study, lateral resolution is down to ∼10 nm; vertical resolution is down to 0.1 nm). The best lateral resolution that can be achieved in AFM is a function of the convolution of the tip shape with the object to be probed. Thus, the best resolution is on the order of the tip size, which is 10 nm in our case. However, the size of lipid domains in most of the lipid bilayers analyzed in our study are larger than the tip diameter, and tip convolution does not significantly influence our AFM results. ITIR-FCS allows multiplexed FCS measurements on a region of interest quantifying membrane dynamics yielding two parameters, namely the diffusion coefficient (D), and the diffusion law intercept (τ0). The diffusion coefficient is a measure of molecular mobility, which is sensitive to the percentage of gel phase lipids and overall domain confinements in the membranes, whereas the diffusion law intercept investigates the mode of diffusion exhibited by the probe molecules.
Because AFM is a label-free scanning-based method, whereas ITIR-FCS uses fluorescence probes, the two methods have very different preferences for the sample substrates. Owing to the optical transparency, glass is the most commonly used substrate for samples studied using fluorescence-based methods. On the other hand, the atomic flatness of the substrate is more favorable for AFM, and thus, mica is the most commonly used substrate (25). Because membrane properties are influenced by the substrate (26) and to compare our AFM and ITIR-FCS results with the existing literature, the experiments have been performed on both glass and mica. First, we compared the roughness profile of glass and mica (Fig. S1, A and B). In our substrates, the roughness of glass ranges from 1 to 4 nm, and mica ranges from 0.2 to 0.4 nm. Similar differences in the roughness profiles of glass and mica were reported previously (27).
Validation of ITIR-FCS diffusion law analysis for a sample exhibiting free diffusion
DOPC is fluid at room temperature, so pure DOPC SLBs have been used as a sample that shows free diffusion of probe molecules. DOPC SLBs prepared on both glass and mica were analyzed using AFM and ITIR-FCS.
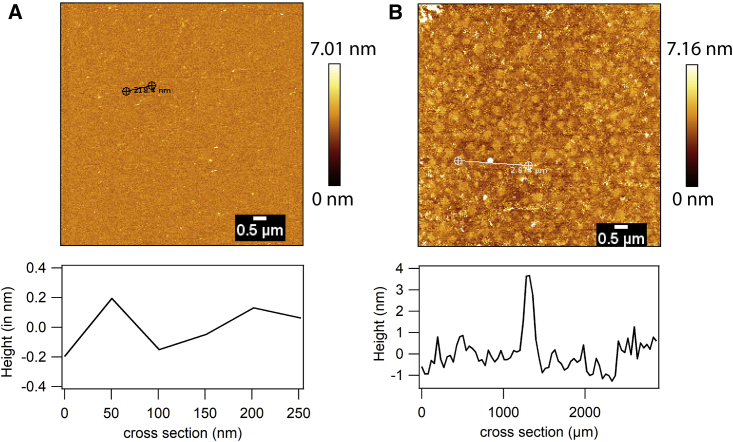
DOPC SLBs imaged on glass were rougher (0–3 nm) compared to the ones on mica (0–0.4 nm), as expected from the substrate roughness (Fig. 1, A and B). ITIR-FCS experiments performed on DOPC SLB prepared on glass and mica yielded similar D (1.6–2.3 μm2/s) and τ0 (−0.05 to 0.06 s) (t-test, p-value > 0.05), consistent with free diffusion (Fig. 3 A; Table 1).
Figure 1.
An analysis of membrane topology of DOPC-supported lipid bilayers prepared on (A) glass and (B) mica using atomic force microscopy. Membrane topology is assessed in terms of height profile over various cross sections. Representative cross sections are shown. To see this figure in color, go online.
Figure 3.
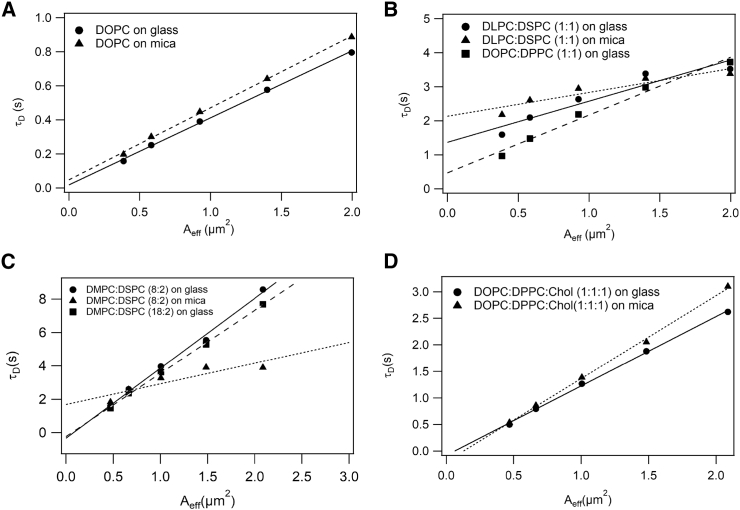
Representative ITIR-FCS diffusion law plots obtained for (A) DOPC bilayers show zero intercept on both glass and mica. (B) DLPC/DSPC (1:1) bilayers show positive intercept on both glass and mica; DOPC/DPPC (1:1) bilayers show positive intercept on glass. (C) DMPC/DSPC (8:2) bilayers show negative intercept on glass and a positive intercept on mica; DMPC/DSPC (18:2) bilayers shows a negative intercept on glass. (D) DOPC/DPPC/Chol (1:1:1) bilayers show negative intercept on both glass and mica. The coefficient of variation associated with diffusion coefficients calculated at variable spatial scales ranges between 20 and 30% for the bilayers measured on glass and 20–45% for the bilayers measured on mica is shown.
Table 1.
Diffusion Coefficients and Diffusion Law Intercepts of Lipid Bilayers Prepared on Glass and Mica
| Lipid Composition | Substrate | D (μm2/s) | τ0 (s) |
|---|---|---|---|
| DOPC | glass | 2.18 ± 0.09 | 0.00 ± 0.02 |
| DOPC | mica | 1.86 ± 0.44 | 0.01 ± 0.03 |
| DLPC/DSPC (1:1) | glass | gel phase: 0.09 ± 0.04, fluid phase: 0.36 ± 0.18 | 2.67 ± 0.52 |
| DLPC/DSPC (1:1) | mica | gel phase: 0.07 ± 0.03, fluid phase: 0.19 ± 0.06 | 2.90 ± 1.07 |
| DOPC/DPPC (1:1) | glass | 0.57 ± 0.07 | 0.43 ± 0.08 |
| DMPC/DSPC (8:2) | glass | 0.36 ± 0.02 | −0.43 ± 0.11 |
| DMPC/DSPC (8:2) | mica | 0.28 ± 0.07 | 1.27 ± 0.04 |
| DMPC/DSPC (18:2) | glass | 0.49 ± 0.17 | −0.14 ± 0.20 |
| DOPC/DPPC/Chol (1:1:1) | glass | 1.08 ± 0.27 | −0.21 ± 0.04 |
| DOPC/DPPC/Chol (1:1:1) | mica | 1.09 ± 0.24 | −0.21 ± 0.11 |
The data are the average of at least four independent trials, and errors represent the standard deviation.
In previous publications from our group (2,20), the Arrhenius activation energy (EArr) was calculated for the lipid diffusion in SLBs and cell membranes as an indicator of membrane packing and membrane phase behavior. EArr is the amount of energy that a molecule requires to diffuse laterally from one site in the membrane to another. It is estimated by measuring the diffusion coefficient of lipid bilayers at a temperature range of 298–310 K. To determine any influence of the two substrates on EArr, DOPC SLBs prepared on glass and mica were measured at a temperature range of 298–310 K, and EArr was calculated to be 16.29 ± 3.21 and 21.8 ± 3.16 kJ/mol on glass and mica, respectively. These values are consistent with those obtained for liquid-disordered membranes (17.66 ± 3.10 kJ/mol) and differ strongly from the liquid-ordered or gel (57.75 ± 11.71 kJ/mol) phase (20). Thus, the influence of these substrates on bilayer packing is not significantly different (t-test, p-value > 0.05). However, previous studies have reported that a difference in the roughness of different substrates can influence the bilayer properties, e.g., the phase transition temperature (26,28).
Validation of ITIR-FCS diffusion law analysis for lipid bilayers with positive intercept
Next, we analyzed phase-separated bilayers that exhibit positive τ0 in our ITIR-FCS setup. FCS diffusion law plots are obtained by an analysis of the dependence of diffusion over spatial scales. It uses average diffusion coefficients from variable observation areas, and thus, it includes contributions from both gel and fluid phases. However, the diffusion coefficients that we have reported in Table 1 are averages from the individual phases wherever possible.
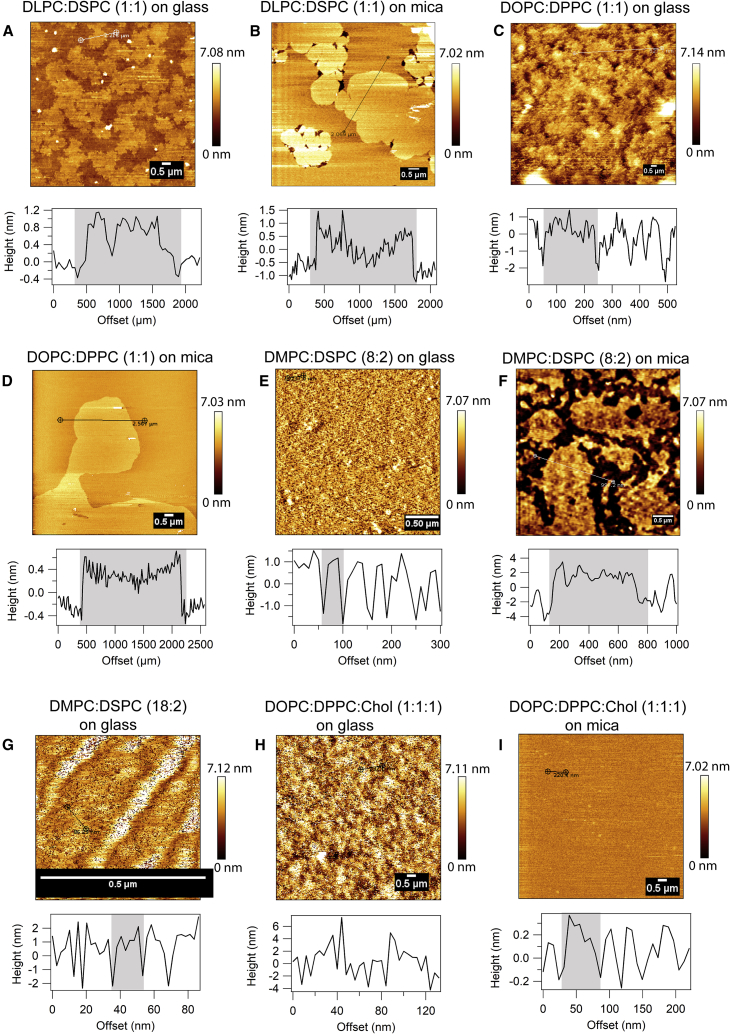
First, DLPC/DSPC (1:1) bilayers were examined on glass and mica. At room temperature, DLPC manifests a fluid phase, whereas DSPC is a gel phase lipid, and because of the immiscibility of the two lipids, this composition forms phase-separated bilayers. As reported previously, RhoPE partitions equally into both phases (20). In previous AFM studies, this combination of lipids has been shown to form domains (29,30). In this bilayer, the domains are optically visible, and ITIR-FCS studies from our group have reported a positive intercept (31). On glass, the AFM image of DLPC/DSPC (1:1) bilayers showed partially connected, high-density domains of the size of 1–2 μm with a height difference of ∼1 nm (Fig. 2 A). The ITIR-FCS measurements provide an average D of 0.17 ± 0.04 μm2/s and a τ0 of 2.67 ± 0.52 s (Fig. 3 B; Table 1). Because this bilayer is phase separated, it has two characteristic D-values for the gel and the fluid phase (gel phase: 0.09 ± 0.04 μm2/s, fluid phase: 0.36 ± 0.18 μm2/s). On mica, the same composition shows domain sizes ranging from 2 to 5 μm, and the height difference was similar to that on glass (Fig. 2 B). ITIR-FCS measurements provide a D of 0.07 ± 0.03 μm2/s for gel phase and 0.19 ± 0.06 μm2/s for fluid phase accompanied by a τ0 of 2.90 ± 1.07 s (Fig. 3 B; Table 1), which suggests similar diffusion properties of this bilayer on both substrates. However, there were geometrical differences in the domains obtained on glass and mica. The domains imaged on glass were irregularly shaped, presumably because of the glass roughness, whereas domains imaged on mica show more rounded boundaries.
Figure 2.
AFM images of various supported lipid bilayers with distinct domain configurations and their respective cross sections. Membrane configuration of DLPC/DSPC (1:1) bilayers on (A) glass and (B) mica is shown. Membrane configuration of DOPC/DPPC (1:1) bilayer on (C) glass and (D) mica is shown. Membrane configuration of DMPC/DSPC (8:2) bilayer on (E) glass and (F) mica is shown, and (G) DMPC/DSPC (18:2) bilayer is shown on glass. Membrane configuration of DOPC/DPPC/Chol (1:1:1) bilayer on (H) glass and (I) mica is shown. Each AFM image is accompanied by its corresponding height profile. The gray-shaded area in the height profile indicates the lateral size of domains. Scale bars, 0.5 μm. To see this figure in color, go online.
Next, we investigated DOPC/DPPC (1:1) SLBs. At room temperature, DOPC exists in the fluid phase, whereas DPPC exists in the gel phase. This is an interesting case because on glass, this bilayer is optically homogeneous but has been reported to show a positive diffusion law intercept (20). Previous AFM-based studies have demonstrated that this composition forms micrometer-sized domains on mica (4). However, the structure of this bilayer on glass is not known. DOPC/DPPC (1:1) bilayers on glass were imaged by AFM, and we found that there were irregularly shaped domains with sizes ranging from 100 to 200 nm (Fig. 2 C). The height differences of domains with respect to the surrounding fluid lipids was ∼1.5 nm. For this lipid composition, bilayers on mica exhibited micrometer-sized domains with circular geometry (Fig. 2 D) consistent with previous work (4). ITIR-FCS experiments performed on bilayers prepared on glass showed a D of 0.57 ± 0.07 μm2/s and a τ0 of 0.43 ± 0.08 s (Fig. 3 B; Table 1). DOPC/DPPC (1:1) bilayers prepared on mica undergo constant reorganizations because the quality of FCS data obtained in this case was unreliable. Thus, we did not include it for any further analysis.
Validation of ITIR-FCS diffusion law analysis for lipid bilayers with negative intercept
In this section, we studied phase-separated bilayers that exhibit a negative τ0. First, RhoPE-labeled DMPC/DSPC (8:2) bilayers were studied on both glass and mica. At room temperature, DMPC exhibits both a fluid and gel phase (4) because its phase transition temperature is 23°C, whereas the phase transition temperature of DSPC is 55.6°C, and it thus exists in the gel phase. Because of the nonideal mixing of the two lipids, this composition forms phase-separated bilayers. DMPC/DSPC is one of the most thoroughly studied lipid bilayers characterized by several methods, including differential scanning calorimetry, neutron scattering, NMR, electron spin resonance, Raman spectroscopy, Fourier transform infrared spectroscopy, computer simulations, and AFM (8,32, 33, 34, 35, 36). The existence of nanoscale domains was reported for this bilayer composition (37). Because of the extensive information about this bilayer system, it was utilized by Favard et al. (16) to test the quantitative accuracy of confocal-based FCS diffusion laws, and they reported a negative τ0. However, this study did not directly visualize the membrane structure, but compared its results with AFM images reported by others on different substrates, experimental setups, and conditions. Here, we directly compare DMPC/DSPC (8:2) and DMPC/DSPC (18:2) bilayers on glass and mica using AFM and ITIR-FCS.
On glass, DMPC/DSPC (8:2) bilayers showed a high density of domains, exhibiting an interdomain distance of 32–58.3 nm with a typical diameter of 30–50 nm and a height difference of ∼2.5 nm (Fig. 2 E). The interdomain distance that we report is the center-to-center distance between the domains. The ITIR-FCS measurements provide a D of 0.36 ± 0.02 μm2/s and a τ0 of −0.43 ± 0.11 s (Fig. 3 C; Table 1). On mica, the same composition showed domain sizes ranging from 200 to 500 nm with interdomain distances of 300–700 nm, and the height difference was similar to that on glass (Fig. 2 F). Interestingly, for this lipid composition, the shape of domains was irregular on both glass and mica. The ITIR-FCS measurements provide a D of 0.28 ± 0.07 μm2/s and a τ0 of 1.27 ± 0.04 s on mica (Fig. 3 C; Table 1). This result, and especially the opposite sign of the diffusion law intercept on the two substrates, indicates that domain size and density are an important determinant of τ0.
Subsequently, we investigated DMPC/DSPC (18:2) SLBs to determine the influence of domain size and density on the FCS diffusion law analysis. AFM images of DMPC/DSPC (18:2) bilayers on glass showed the existence of irregularly shaped domains with sizes ranging from 10 to 30 nm (Fig. 2 G) with interdomain distances in the range of 12–39 nm. The height differences were similar to what was obtained for DMPC/DSPC (8:2), i.e., 2.5 nm. ITIR-FCS experiments performed on this bilayer on glass showed a D of 0.49 ± 0.17 μm2/s and a τ0 of −0.14 ± 0.20 s (Fig. 3 C; Table 1). D of this bilayer was somewhat higher than that for DMPC/DSPC (8:2), and τ0 fluctuates from zero to slightly negative values.
Another lipid bilayer composition that exhibits negative τ0 in ITIR-FCS is DOPC/DPPC/Chol (1:1:1) (20). Chol influences the phase behavior of the membrane by associating with other lipids. Chol prefers to associate with gel-phase lipids over fluid-phase lipids (38). So, in the case of DOPC/DPPC/Chol (1:1:1) bilayers, chol associates with DPPC and imparts an overall fluidizing effect to the membrane as compared to DOPC/DPPC (1:1). This composition is a better mimic of cell membranes (39). AFM images of DOPC/DPPC/Chol (1:1:1) bilayers on glass did not show any distinct domains (Fig. 2 H). This could be because of highly dynamic domains in this bilayer, unresolvable height differences because of leveling by chol, the roughness of the glass, and the very small size of lipid domains on the glass for this composition (Fig. 2 H), which were not resolvable by the current lateral resolution of AFM. The height profile for these bilayers was very similar to DOPC bilayers on glass (Fig. 1 A). However, ITIR-FCS experiments performed on these bilayers provided a D of 1.08 ± 0.27 μm2/s and a τ0 of −0.21 ± 0.04 s (Fig. 3 D; Table 1). On mica, AFM images showed a high density of domains ranging from 20 to 50 nm in size (Fig. 2 I). The height differences of domains from the surroundings were ∼0.3 nm. D of this bilayer on mica was 1.09 ± 0.24 μm2/s with a τ0 of −0.21 ± 0.11 s (Fig. 3 D; Table 1), very similar to values on glass. AFM images of lipid bilayers that exhibit negative intercepts show very small (10-50 nm) and a dense network of domains as implied by the regular spikes (peaks) of a defined length and height in the cross sections. In case of DOPC bilayers (Fig. 1), the cross sections do not show the presence of any lipid domains because there are no regular peaks of similar lengths and heights, whereas in the case of DMPC/DSPC bilayers on glass and DOPC/DPPC/Chol bilayer on mica, regular spikes are observed in the cross-sectional profiles, indicating the presence of lipid domains. However, it could be difficult to visualize the domains in these samples directly.
Thus, for a better visualization of the AFM data in case of bilayers exhibiting hop diffusion, we have shown 1) magnified images of all the relevant bilayer samples with color scales adjusted such that different lipid phases are clearly observed (Fig. S2) and 2) spatial autocorrelations calculated from AFM images of various lipid bilayer samples (Fig. S3). Glass, mica, and DOPC on glass or mica did not show spatial correlations beyond the substrate surface roughness, indicating that DOPC bilayers are smooth and have no own structure. In the case of DMPC/DSPC (8:2) bilayers prepared on glass and DOPC/DPPC/Chol (1:1:1) bilayers prepared on mica, we observed positive autocorrelations with a width following the domain sizes seen on these bilayers, confirming the analysis of the AFM images. Bilayers with larger domains exhibited wider spatial correlations compared to the bilayers that show hop diffusion.
Demonstration of domain-obstructed diffusion exhibiting negative intercepts by simulations
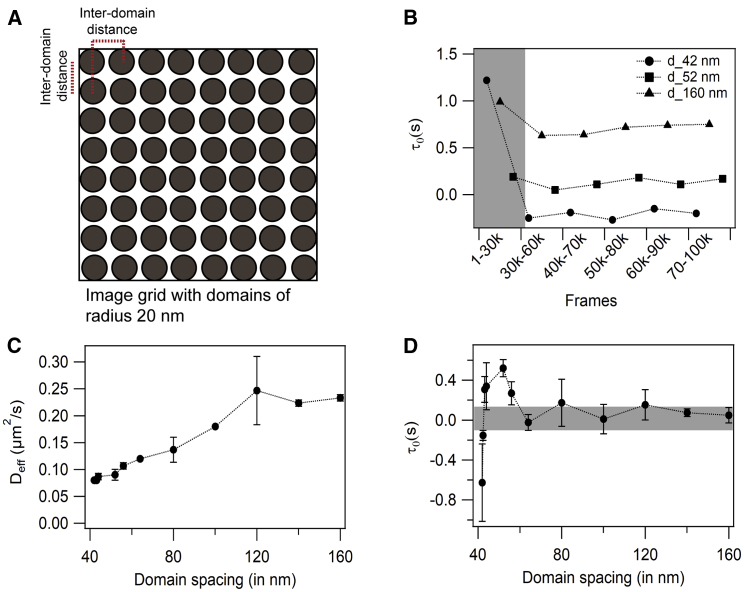
In AFM images of samples with negative intercepts, we find a high density of very small domains with sizes in the range of 10–50 nm. We therefore performed 2D simulations on diffusing particles with similar dynamic parameters encountering similar structures. A 2D plane with an array of static, circular, and nonoverlapping domains was created (Fig. 4 A). The diffusion coefficient inside the domains (Din) was kept at 0.1 μm2/s, and the diffusion coefficient outside the domains (Dout) was 0.3 μm2/s. The domain radii were set to 20 nm ± 10%. However, the shape of domains was kept circular, unlike the irregularly shaped domains observed in AFM images. When a particle encounters a domain boundary, it can either be reflected or it can enter or exit the domain with certain probabilities, denoted as Pin and Pout, respectively. Generally, the value of Pin used is higher than that of Pout (10,17). Here, the simulations have been performed at two Pin/Pout ratios of 3.3 (Pin = 0.5 and Pout = 0.15) and 20 (Pin = 0.1 and Pout = 0.005), mimicking different confinement strength (ratio of the probability of a molecule entering to the probability of a molecule exiting the domain) (10,17). The density of domains was altered by varying the interdomain center-to-center distances. The simulation parameters for the data shown in Fig. 4 are listed in Table 2.
Figure 4.
Systematic analysis of diffusion regime characterized by negative intercept using simulation experiments. (A) An image grid with an array of domains of radius 20 nm is shown. (B) Proof of simulation convergence for interdomain distance of 42 nm (solid circle), 52 nm (solid square), and 160 nm (solid triangle) is shown. (C) The dependence of effective diffusion coefficient on interdomain distance is shown. (D) The dependence of diffusion law intercept on interdomain distance is shown. The gray-shaded region (±0.1 s) is the range in which we assume free diffusion in our setup due to experimental errors. Error bars represent the standard deviations. The data shown are simulated for a Pin = 0.5 and Pout = 0.15 and interdomain distances varying from 42 to 160 nm. To see this figure in color, go online.
To test whether a high density of domains is crucial for obtaining a negative τ0, diffusion law analysis was performed for square image grids of a 1-μm2 area with varying interdomain distances (Fig. 4 A). Initially, particles were distributed randomly on the image grid. Because the different properties of the domains and the nondomain area will lead to different partitioning, we first determined how long the systems needed to converge to equilibrium. We simulated image stacks of 100,000 frames at a time resolution of 1 ms. Analysis of the diffusion law demonstrated that systems need a minimum of 30,000 frames to converge to equilibrium because we generally obtained a higher diffusion law intercept upon analyzing the first 30,000 frames and a constant value from the remaining 70,000 frames, each calculated by analyzing overlapping 30,000 frames in a sliding window fashion. Thus, we discarded the first 30,000 frames from the simulations and used only the remaining 70,000 for the analysis (Fig. 4 B). The simulations were performed with interdomain distances varying from 42 to 160 nm. The number of steps was optimized so that the size of each step is much smaller than the size of domains and the interdomain distances. In this study, a step size of 0.3 nm was used. With increasing interdomain distance and concomitant increase in the fraction of liquid-disordered phase area, there was an increase in the effective diffusion coefficient (Fig. 4 C). At the same time, τ0 undergoes a transition from negative to positive values of the diffusion law intercept with the increase in interdomain distances, and eventually, τ0 becomes zero at an interdomain distance of 60 nm (Fig. 4 D). When the distance between adjacent domains was 42 nm, i.e., with a solid-ordered fraction ∼72%, the value of τ0 was −0.62 s (Fig. 4 D). As the interdomain distance increased to 43.4 nm, i.e., when solid-ordered fraction dropped to 67%, τ0 increased to positive values and reached 0 at an interdomain distance of 50–60 nm, i.e., when only 38% area was covered by domains. The error associated with D is significantly less than that with τ0. To test the effect of higher confinement strength, simulations were performed on the same system with a Pin/Pout ratio of 20 (Table S1). Under these conditions, when the interdomain distance was 42 nm, the diffusion of molecules was extremely slow (D = 0.008 μm2/s) with a τ0 of 39 s. This is presumably because ∼70% of the total area is covered with domains, and the confinement strength of the domains is too high to allow significant molecular diffusion. As a result, molecules spend most of the time inside the domains, resulting in a low D. At this confinement strength, as the interdomain distances increase, there is a drop in τ0, but the value remains positive even at 180 nm separation. This indicates that the τ0-values are strongly dependent on confinement strength of the domains. For the confinement strength as high as 20, we observed no negative intercepts. It indicates that the interplay between domain size, spacing, and confinement strength is responsible for the intercept value. From a particular confinement strength onwards, trapping always wins over meshwork-like behavior, at least at the domain fractions determined here.
Discussion
The FCS diffusion law analysis has been effectively used to determine the diffusive modes of lipid and proteins in lipid bilayers and cell membranes (2,12,16,20,40, 41, 42). However, there are cases in which the known or expected diffusion mode is not recovered from the simple interpretation of positive, zero, and negative values corresponding to transient trapping, free, and hop diffusion. This was, in particular, the case for some samples with expected or known domain structure that nevertheless gave negative intercepts. We therefore combined AFM and ITIR-FCS measurements to gain a better understanding of the dependence of the FCS diffusion law intercept on the nanometer bilayer structure.
Experiments on pure DOPC bilayers established that despite the difference in surface properties, the diffusion properties on glass and mica are comparable, as demonstrated by similar D-, τ0-, and EArr-values obtained for samples on both substrates. AFM images for DOPC bilayers on glass showed height differences between 1 and 4 nm, which was about 10 times more than what was observed on mica because of substrate roughness (Fig. 1).
In the case of phase-separated lipid bilayers, AFM images show that the substrate influences the domain organization. The geometry of domains in DLPC/DSPC (1:1) and DOPC/DPPC (1:1) bilayers exhibited more rounded boundaries on mica but more irregular boundaries on glass (Fig. 2). The size of domains was generally severalfold larger on mica than on glass. For instance, in the case of DLPC/DSPC (1:1) bilayers, the size of domains is ∼2-fold larger on mica than on glass, and in the case of DMPC/DSPC (8:2) bilayer, this increases to even an ∼6-fold difference, consistent with literature (37). A possible explanation is the interaction of the bilayer with the substrate and the transmission of this effect from the inner to the outer leaflet (43,44). The roughness of the glass surface can act as pinning sites, which restrict the large-scale domain formation in the membrane, thereby inducing formation of smaller domains on glass than on mica. The effect of the substrate is less prominent on membrane fluidity, and we obtain similar D, independent of the substrate, consistent with reports by Benda et al. (45). However, the diffusion law intercept τ0, an indicator of the diffusion mode, is strongly dependent on the membrane organization. Because membrane organization is different on glass and mica even for the same lipid composition, τ0 varies and, therefore, can be used to probe the lateral membrane organization.
Our results show that DLPC/DSPC (1:1) bilayers exhibit micrometer-sized, partially connecting domains on both substrates (Fig. 2). For these bilayers, τ0 is positive, with a higher value for the one on mica, which exhibits larger domain sizes. According to the existing description of microdomain partitioning, domain size is proportional to the confinement strength (10), and therefore, larger domains result in higher τ0-values. On DOPC/DPPC (1:1) bilayer on glass, we found a lower τ0 than for DLPC/DSPC (1:1), consistent with the smaller domain size in this bilayer. DLPC/DSPC (1:1) bilayers on both substrates, DMPC/DSPC (8:2) bilayers on mica, and DOPC/DPPC (1:1) on glass show nonlinear, concave diffusion law plots. These are also the bilayers that show more or less visible domains. The diffusion law plots in these cases are not linear because the domains are not beyond the diffraction limit. So, we observe an influence of domain size on the diffusion law plot. Besides domain sizes and confinement strength, other factors such as domain density and line tension also influence τ0 (46,47).
The AFM images show that the height differences in DOPC/DPPC (1:1) bilayer were 1.5 nm, whereas in DOPC/DPPC/Chol (1:1:1), it was ∼0.3 nm. These observations support the results published by Bag et al. (20) that a variation in height differences results in distinct membrane organization. These distinct membrane organizations are reliably predicted by imaging FCS diffusion law analysis. The AFM images for the bilayers that exhibit a negative FCS diffusion law intercept show a high density of gel domains with a size of 10–50 nm as observed in the case of DMPC/DSPC (8:2) and DMPC/DSPC (18:2) bilayers. Muresan et al. (37) imaged equimolar DMPC/DSPC bilayers by AFM and also reported gel domains of 10–50 nm with rather irregular shape.
Neutron diffraction measurements revealed that the average center-to-center distance between the small DSPC domains was smaller than 10 nm (32). The lower magnitude of τ0 in DMPC/DSPC (18:2) as compared to DMPC/DSPC (8:2) indicates the sensitivity of this parameter toward domain size and density. In case of DOPC/DPPC/Chol (1:1:1) on mica, the membrane structure was similar to DMPC/DSPC mixture except for the height difference. DMPC exhibits a 14-carbon acyl chain, and DSPC exhibits an 18-carbon acyl chain. On the other hand, DOPC and DPPC are both asymmetric lipids, with one chain consisting of 16 carbons and the other with 18 carbons with an additional double bond in DOPC. The variation in height differences in the two lipid mixtures can be attributed to the relative variation in the acyl chain lengths of the bilayer components (48).
The structural features observed by AFM images for bilayers with negative intercept were used for simulations to investigate the dependence of τ0 on domain density more in detail. Simulation results show that a negative intercept was observed when the interdomain distance was ∼42–43 nm for a Pin/Pout ratio of 3.3. With the increase in the distance between the domains, there was a progression in the intercept from negative to positive values. It is evident from the results that the interdomain distance and confinement strength are crucial determinants of FCS diffusion law intercepts.
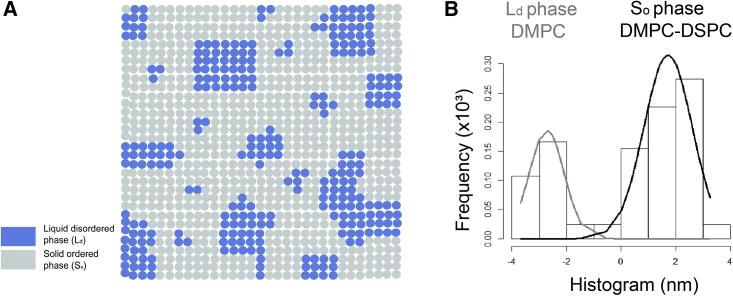
According to the FCS diffusion law analysis, a negative τ0 is due to the membrane compartmentalization by a meshwork, and a probe molecule has to hop over the mesh boundaries to continue diffusion (10). This explanation is more relevant in the context of cell membranes where the actin cytoskeleton is present. However, in this study, we show that small lipid domains can also show a negative intercept. To explain how lipid domains arranged in this manner can create mesh-like boundaries, it was proposed that a two-component bilayer can form coexisting phases (gel and fluid) at a specific temperature. Upon cooling the lipid bilayer below the transition temperature, a point is reached when the solid phase can form, connecting domains in the bilayer, thereby disconnecting the fluid phase into isolated domains (Fig. 5 A). This point is known as the percolation threshold of the bilayer (49). In a fluorescence recovery after photobleaching-based study, percolation thresholds at varying temperatures were determined for DMPC/DSPC mixtures (50,51). AFM images and simulation results indicate that at an intermediate confinement strength, lipid bilayers show negative intercepts when the bilayer is near the percolation threshold, which is reached when the area of the solid fraction is ∼70% (50). For further validation, we calculated the fraction of solid-ordered and liquid-disordered phases in the AFM images of DMPC/DSPC (8:2) bilayers and found a fraction of the solid-ordered phase of ∼78% (Fig. 5 B). Thus, model membranes near the percolation threshold can have a similar effect as cytoskeleton fences on protein diffusion (52). Also, we cannot exclude that the substrate also influences this meshwork-like behavior of percolating domains by influencing the phases and their organization as observed in case of DMPC/DSPC (8:2) bilayers. So, it is quite possible that on free-standing bilayers, the effects are somewhat different. However, our simple simulations, which do not take any substrate into account, also show negative intercepts, and thus we think this is a universal phenomenon even if it might have different thresholds at which negative τ0 intercepts are reached. For a better understanding, we performed a quantitative analysis of our AFM data, and we estimated the minimal domain size (r) and the maximal interdomain distance (d) observed in each of the phase-separated bilayer samples. Then, we calculated the minimal r/d ratio for each of the samples (Table S2). Our results show that the phase-separated bilayers that are characterized by negative intercepts show an r/d ≥ 0.25.
Figure 5.
(A) Schematic of a membrane matrix close to the percolation threshold at which the solid-ordered phase forms a continuous phase, whereas the liquid-disordered phase forms a discontinuous phase. (B) Histograms of peak heights in relation to the average surface level (0 point on x axis) in DMPC/DSPC (8:2) bilayer prepared on glass (bar graph) are shown. The peak at negative x axis values represents the fraction of the liquid-disordered phase, and the peak at positive x axis values represents the fraction of the solid-ordered phase. The grey and black curves represent Gaussian fits to the liquid disordered and solid ordered phases, respectively. To see this figure in color, go online.
However, samples that exhibit a positive intercept show an r/d ratio of around 0.1. It is important to note that in an experimental setup, there are a range of domain sizes and interdomain distances that exist, and we do not have direct information about the confinement strengths. However, we calculate only the minimal possible r/d-values in each sample because it provides us a threshold around or above which a sample can be considered close to the percolation threshold. Consistent with our experimental results, simulation results also show a similar trend that at higher r/d-values, negative intercepts are observed, whereas at smaller r/d-values for the same domain sizes and confinement strengths, positive intercepts are obtained. The r/d-values obtained from the AFM image analysis and simulation experiments cannot be directly compared because in experiments, confinement strengths vary for each sample, and we have a range of domain sizes and interdomain spacings. Overall, these results show that a high density of domains, close to percolation threshold is essential to obtain the negative intercepts.
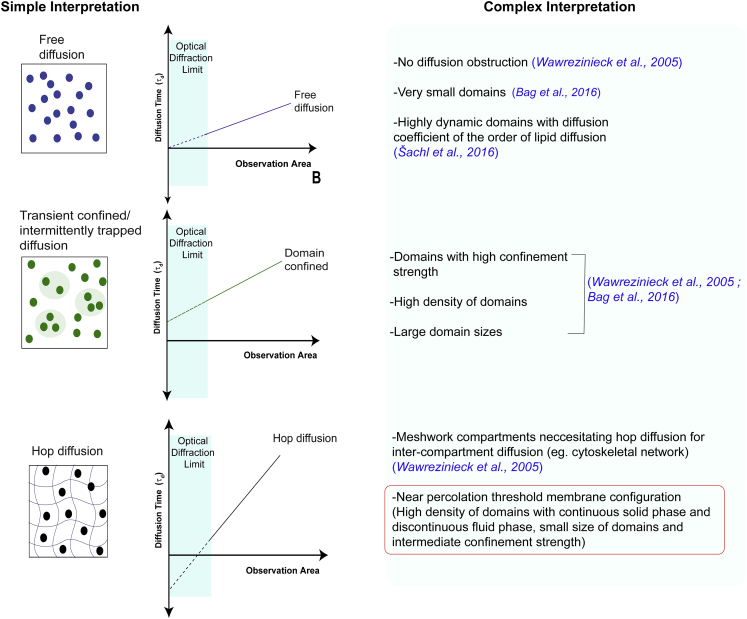
According to the hop diffusion model, proteins that attempt to cross the boundaries of one compartment to diffuse into another compartment can be resisted by the fixed fence posts. However, in a recent study, it was shown that cytoskeleton fences are not fixed fences but can change dynamically (53). Similarly, a particle diffusing through percolating domains is constantly hindered by the surrounding obstacles that are arranged in the form of a maze over many length scales (54). The particle traverses a fractal structure with numerous dead ends. In such a structure, often a particle encounters a compartment boundary more than once before crossing it, leading to obstructed diffusion. These results demonstrate how different membrane configurations with varying domain density and size lead to FCS diffusion law intercepts that do not follow a simple model of interpretation (Fig. 6). In particular, this work shows how small domains at high density with intermediate confinement strength lead to diffusion that is better described by hop diffusion than by transient trapping on the length scales observed. Because membranes with domains near the percolation threshold exhibiting hop diffusion are observed on both glass and mica, our observation of hop diffusion in such membrane configurations is valid irrespective of substrate properties.
Figure 6.
Schematic illustration of FCS diffusion law analysis describing complex interpretations associated with each of the diffusion mode. As marked in the figure, previous literature has described possible interpretations for free diffusion and domain-confined diffusion. In this work, we show that in addition to meshwork organization, biphasic membranes near the percolation threshold can also exhibit hop diffusion. To see this figure in color, go online.
Conclusions
FCS diffusion law analysis or similar plots have been widely used to infer structures that cannot be imaged because they are beyond the measurement systems achievable spatial resolution. However, the FCS diffusion law and its intercept is an indicator of the diffusion mode and not necessarily of the underlying structure in which diffusion takes place. There are already several publications outlining various limits of the FCS diffusion law analysis. Here in this article, we add one more exception, namely the case of biphasic lipid bilayers near the percolation threshold, exhibiting small domains at high density and intermediate confinement strength. These bilayers can show negative intercepts contrary to the simple interpretation that domain confinement or transient entrapment should lead to positive intercepts. Thus, the attribution of structures to particular FCS diffusion law intercepts might be permissible in simple cases, but complex cases require extra information. This can be in the form of extra spatiotemporal information (e.g., AFM, Near-field scanning optical microscopy, Stimulated emission depletion-FCS) or additional biological information (disruption of domains or meshwork by chemical agents). In the presence of this extra information, the FCS diffusion law analysis remains an important tool to infer structural and organizational features below the resolution limit from dynamic information.
Author Contributions
A.G. performed all the ITIR-FCS experiments. A.G. and I.Y.P. performed AFM experiments. A.G. analyzed data. A.G. and T.W. wrote the manuscript. T.W. conceived and supervised the project.
Acknowledgments
A.G. is the recipient of the research scholarship from the National University of Singapore. T.W. gratefully acknowledges funding by the Singapore Ministry of Education (MOE2016-T2-2-121).
Editor: Roland Winter.
Footnotes
Supporting Material can be found online at https://doi.org/10.1016/j.bpj.2020.04.004.
Supporting Material
References
- 1.Kusumi A., Suzuki K.G.N., Fujiwara T.K. Hierarchical mesoscale domain organization of the plasma membrane. Trends Biochem. Sci. 2011;36:604–615. doi: 10.1016/j.tibs.2011.08.001. [DOI] [PubMed] [Google Scholar]
- 2.Huang S., Lim S.Y., Wohland T. Plasma membrane organization and dynamics is probe and cell line dependent. Biochim. Biophys. Acta Biomembr. 2017;1859:1483–1492. doi: 10.1016/j.bbamem.2016.12.009. [DOI] [PubMed] [Google Scholar]
- 3.Lee I.H., Saha S., Groves J.T. Live cell plasma membranes do not exhibit a miscibility phase transition over a wide range of temperatures. J. Phys. Chem. B. 2015;119:4450–4459. doi: 10.1021/jp512839q. [DOI] [PubMed] [Google Scholar]
- 4.Mingeot-Leclercq M.-P., Deleu M., Dufrêne Y.F. Atomic force microscopy of supported lipid bilayers. Nat. Protoc. 2008;3:1654–1659. doi: 10.1038/nprot.2008.149. [DOI] [PubMed] [Google Scholar]
- 5.Heberle F.A., Feigenson G.W. Phase separation in lipid membranes. Cold Spring Harb. Perspect. Biol. 2011;3:1–13. doi: 10.1101/cshperspect.a004630. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Schneider F., Waithe D., Sezgin E. Diffusion of lipids and GPI-anchored proteins in actin-free plasma membrane vesicles measured by STED-FCS. Mol. Biol. Cell. 2017;28:1507–1518. doi: 10.1091/mbc.E16-07-0536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Veatch S.L., Polozov I.V., Keller S.L. Liquid domains in vesicles investigated by NMR and fluorescence microscopy. Biophys. J. 2004;86:2910–2922. doi: 10.1016/S0006-3495(04)74342-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Shahedi V., Orädd G., Lindblom G. Domain-formation in DOPC/SM bilayers studied by pfg-NMR: effect of sterol structure. Biophys. J. 2006;91:2501–2507. doi: 10.1529/biophysj.106.085480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Bernheim-Groswasser A., Shusterman R., Krichevsky O. Fluorescence correlation spectroscopy analysis of segmental dynamics in actin filaments. J. Chem. Phys. 2006;125:084903. doi: 10.1063/1.2244550. [DOI] [PubMed] [Google Scholar]
- 10.Wawrezinieck L., Rigneault H., Lenne P.F. Fluorescence correlation spectroscopy diffusion laws to probe the submicron cell membrane organization. Biophys. J. 2005;89:4029–4042. doi: 10.1529/biophysj.105.067959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Destainville N., Dumas F., Salomé L. What do diffusion measurements tell us about membrane compartmentalisation? Emergence of the role of interprotein interactions. J. Chem. Biol. 2008;1:37–48. doi: 10.1007/s12154-008-0005-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Lenne P.F., Wawrezinieck L., Marguet D. Dynamic molecular confinement in the plasma membrane by microdomains and the cytoskeleton meshwork. EMBO J. 2006;25:3245–3256. doi: 10.1038/sj.emboj.7601214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ng X.W., Teh C., Wohland T. The secreted signaling protein Wnt3 is associated with membrane domains in vivo: a SPIM-FCS study. Biophys. J. 2016;111:418–429. doi: 10.1016/j.bpj.2016.06.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Gupta A., Muralidharan S., Wohland T. Long acyl chain ceramides govern cholesterol and cytoskeleton dependence of membrane outer leaflet dynamics. Biochim. Biophys. Acta Biomembr. 2020;1862:183153. doi: 10.1016/j.bbamem.2019.183153. [DOI] [PubMed] [Google Scholar]
- 15.Eggeling C., Ringemann C., Hell S.W. Direct observation of the nanoscale dynamics of membrane lipids in a living cell. Nature. 2009;457:1159–1162. doi: 10.1038/nature07596. [DOI] [PubMed] [Google Scholar]
- 16.Favard C., Wenger J., Rigneault H. FCS diffusion laws in two-phase lipid membranes: determination of domain mean size by experiments and Monte Carlo simulations. Biophys. J. 2011;100:1242–1251. doi: 10.1016/j.bpj.2010.12.3738. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Bag N., Ng X.W., Wohland T. Spatiotemporal mapping of diffusion dynamics and organization in plasma membranes. Methods Appl. Fluoresc. 2016;4:034003. doi: 10.1088/2050-6120/4/3/034003. [DOI] [PubMed] [Google Scholar]
- 18.Šachl R., Bergstrand J., Hof M. Fluorescence correlation spectroscopy diffusion laws in the presence of moving nanodomains. J. Phys. D Appl. Phys. 2016;49:114002. [Google Scholar]
- 19.Veerapathiran S., Wohland T. The imaging FCS diffusion law in the presence of multiple diffusive modes. Methods. 2018;140–141:140–150. doi: 10.1016/j.ymeth.2017.11.016. [DOI] [PubMed] [Google Scholar]
- 20.Bag N., Yap D.H.X., Wohland T. Temperature dependence of diffusion in model and live cell membranes characterized by imaging fluorescence correlation spectroscopy. Biochim. Biophys. Acta. 2014;1838:802–813. [PubMed] [Google Scholar]
- 21.Krieger J.W., Singh A.P., Wohland T. Imaging fluorescence (cross-) correlation spectroscopy in live cells and organisms. Nat. Protoc. 2015;10:1948–1974. doi: 10.1038/nprot.2015.100. [DOI] [PubMed] [Google Scholar]
- 22.Sankaran J., Shi X., Wohland T. ImFCS: a software for imaging FCS data analysis and visualization. Opt. Express. 2010;18:25468–25481. doi: 10.1364/OE.18.025468. [DOI] [PubMed] [Google Scholar]
- 23.Sankaran J., Bag N., Wohland T. Accuracy and precision in camera-based fluorescence correlation spectroscopy measurements. Anal. Chem. 2013;85:3948–3954. doi: 10.1021/ac303485t. [DOI] [PubMed] [Google Scholar]
- 24.Walter V. Institut Charles Sadron; 2017. Lipid membrane interactions with self-assembling cell-penetrating peptides. PhD thesis. [Google Scholar]
- 25.Mu D.J., Engel A., Mu M.E. Adsorption of biological molecules to a solid support for scanning probe microscopy. J. Struct. Biol. 1997;188:172–188. doi: 10.1006/jsbi.1997.3875. [DOI] [PubMed] [Google Scholar]
- 26.Seeger H.M., Di Cerbo A., Facci P. Supported lipid bilayers on mica and silicon oxide: comparison of the main phase transition behavior. J. Phys. Chem. B. 2010;114:8926–8933. doi: 10.1021/jp1026477. [DOI] [PubMed] [Google Scholar]
- 27.Váró G., Szegletes Z. Artificial and natural membranes. In: Frewin C., editor. Atomic Force Microscopy Investigations into Biology: From Cell to Protein. IntechOpen; 2012. pp. 219–234. [Google Scholar]
- 28.Tero R. Substrate effects on the formation process, structure and physicochemical properties of supported lipid bilayers. Materials (Basel) 2012;5:2658–2680. [Google Scholar]
- 29.Lin W., Blanchette C.D., Longo M.L. Lipid asymmetry in DLPC/DSPC-supported lipid bilayers: a combined AFM and fluorescence microscopy study. Biophys. J. 2006;90:228–237. doi: 10.1529/biophysj.105.067066. Published online October 7, 2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Ratto T.V., Longo M.L. Obstructed diffusion in phase-separated supported lipid bilayers: a combined atomic force microscopy and fluorescence recovery after photobleaching approach. Biophys. J. 2002;83:3380–3392. doi: 10.1016/S0006-3495(02)75338-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Bag N., Sankaran J., Wohland T. Calibration and limits of camera-based fluorescence correlation spectroscopy: a supported lipid bilayer study. ChemPhysChem. 2012;13:2784–2794. doi: 10.1002/cphc.201200032. [DOI] [PubMed] [Google Scholar]
- 32.Gliss C., Clausen-Schaumann H., Bayerl T.M. Direct detection of domains in phospholipid bilayers by grazing incidence diffraction of neutrons and atomic force microscopy. Biophys. J. 1998;74:2443–2450. doi: 10.1016/S0006-3495(98)77952-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Sugár I.P., Michonova-Alexova E., Chong P.L. Geometrical properties of gel and fluid clusters in DMPC/DSPC bilayers: Monte Carlo simulation approach using a two-state model. Biophys. J. 2001;81:2425–2441. doi: 10.1016/s0006-3495(01)75890-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Michonova-Alexova E.I., Sugár I.P. Component and state separation in DMPC/DSPC lipid bilayers: a Monte Carlo simulation study. Biophys. J. 2002;83:1820–1833. doi: 10.1016/S0006-3495(02)73947-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Ngo A.T., Jakubek Z.J., Johnston L.J. Membrane order parameters for interdigitated lipid bilayers measured via polarized total-internal-reflection fluorescence microscopy. Biochim. Biophys. Acta. 2014;1838:2861–2869. doi: 10.1016/j.bbamem.2014.07.020. [DOI] [PubMed] [Google Scholar]
- 36.Tamm L.K., Lai A.L., Li Y. Combined NMR and EPR spectroscopy to determine structures of viral fusion domains in membranes. Biochim. Biophys. Acta. 2007;1768:3052–3060. doi: 10.1016/j.bbamem.2007.09.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Muresan A.S., Diamant H., Lee K.Y. Effect of temperature and composition on the formation of nanoscale compartments in phospholipid membranes. J. Am. Chem. Soc. 2001;123:6951–6952. doi: 10.1021/ja015792r. [DOI] [PubMed] [Google Scholar]
- 38.Hakobyan D., Heuer A. Phase separation in a lipid/cholesterol system: comparison of coarse-grained and united-atom simulations. J. Phys. Chem. B. 2013;117:3841–3851. doi: 10.1021/jp312245y. [DOI] [PubMed] [Google Scholar]
- 39.Kaiser H.-J., Lingwood D., Simons K. Order of lipid phases in model and plasma membranes. Proc. Natl. Acad. Sci. USA. 2009;106:16645–16650. doi: 10.1073/pnas.0908987106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Eggeling C., Ringemann C., Hell S.W. Direct observation of the nanoscale dynamics of membrane lipids in a living cell. Nature. 2009;457:1159–1162. doi: 10.1038/nature07596. Published online December 21, 2008. [DOI] [PubMed] [Google Scholar]
- 41.Stanly T.A., Fritzsche M., Jackson D.G. The cortical actin network regulates avidity-dependent binding of hyaluronan by the lymphatic vessel endothelial receptor LYVE-1. J. Biol. Chem. 2020;295:5036–5050. doi: 10.1074/jbc.RA119.011992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Andrade D.M., Clausen M.P., Eggeling C. Cortical actin networks induce spatio-temporal confinement of phospholipids in the plasma membrane--a minimally invasive investigation by STED-FCS. Sci. Rep. 2015;5:11454. doi: 10.1038/srep11454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Honigmann A., Mueller V., Eggeling C. STED microscopy detects and quantifies liquid phase separation in lipid membranes using a new far-red emitting fluorescent phosphoglycerolipid analogue. Faraday Discuss. 2013;161:77–89. doi: 10.1039/c2fd20107k. discussion 113–150. [DOI] [PubMed] [Google Scholar]
- 44.Ngamsaad W., May S., Triampo W. Pinning of domains for fluid – fluid phase separation in lipid bilayers with asymmetric dynamics. Soft Matter. 2011;7:2848–2857. [Google Scholar]
- 45.Benda A., Benes M., Heyrovsky J. How to determine diffusion coefficients in planar phospholipid systems by confocal fluorescence correlation spectroscopy. Langmuir. 2003;9:4120–4126. [Google Scholar]
- 46.Ingólfsson H.I., Arnarez C., Marrink S.J. Computational ‘microscopy’ of cellular membranes. J. Cell Sci. 2016;129:257–268. doi: 10.1242/jcs.176040. [DOI] [PubMed] [Google Scholar]
- 47.Usery R.D., Enoki T.A., Feigenson G.W. Line tension controls liquid-disordered + liquid-ordered domain size transition in lipid bilayers. Biophys. J. 2017;112:1431–1443. doi: 10.1016/j.bpj.2017.02.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.García-Sáez A.J., Chiantia S., Schwille P. Effect of line tension on the lateral organization of lipid membranes. J. Biol. Chem. 2007;282:33537–33544. doi: 10.1074/jbc.M706162200. [DOI] [PubMed] [Google Scholar]
- 49.Saxton M.J. Lateral diffusion in an archipelago. The effect of mobile obstacles. Biophys. J. 1987;52:989–997. doi: 10.1016/S0006-3495(87)83291-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Almeida P.F., Vaz W.L., Thompson T.E. Lateral diffusion and percolation in two-phase, two-component lipid bilayers. Topology of the solid-phase domains in-plane and across the lipid bilayer. Biochemistry. 1992;31:7198–7210. doi: 10.1021/bi00146a024. [DOI] [PubMed] [Google Scholar]
- 51.Vaz W.L., Melo E.C., Thompson T.E. Translational diffusion and fluid domain connectivity in a two-component, two-phase phospholipid bilayer. Biophys. J. 1989;56:869–876. doi: 10.1016/S0006-3495(89)82733-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Fujiwara T., Ritchie K., Kusumi A. Phospholipids undergo hop diffusion in compartmentalized cell membrane. J. Cell Biol. 2002;157:1071–1081. doi: 10.1083/jcb.200202050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Freeman S.A., Vega A., Grinstein S. Transmembrane pickets connect cyto- and pericellular skeletons forming barriers to receptor engagement. Cell. 2018;172:305–317.e10. doi: 10.1016/j.cell.2017.12.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Krapf D. Mechanisms underlying anomalous diffusion in the plasma membrane. Curr. Top. Membr. 2015;75:167–207. doi: 10.1016/bs.ctm.2015.03.002. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.