Abstract
Proline-rich motifs (PRMs) are widely used for mediating protein-protein interactions with weak binding affinities. Because they are intrinsically disordered when unbound, conformational entropy plays a significant role for the binding. However, residue-level differences of the entropic contribution in the binding of different ligands remain not well understood. We use all-atom molecular dynamics simulation and the maximal information spanning tree formalism to analyze conformational entropy associated with the binding of two PRMs, one from the Abl kinase and the other from the nonstructural protein 1 of the 1918 Spanish influenza A virus, to the N-terminal SH3 (nSH3) domain of the CrkII protein. Side chains of the stably folded nSH3 experience more entropy change upon ligand binding than the backbone, whereas PRMs involve comparable but heterogeneous entropy changes among the backbone and side chains. In nSH3, two conserved nonpolar residues forming contacts with the PRM experience the largest side-chain entropy loss. In contrast, the C-terminal charged residues of PRMs that form polar contacts with nSH3 experience the greatest side-chain entropy loss, although their “fuzzy” nature is attributable to the backbone that remains relatively flexible. Thus, residues that form high-occupancy contacts between nSH3 and PRM do not reciprocally contribute to entropy loss. Furthermore, certain surface residues of nSH3 distal to the interface with PRMs gain entropy, indicating a nonlocal effect of ligand binding. Comparing between the PRMs from cAbl and nonstructural protein 1, the latter involves a larger side-chain entropy loss and forms more contacts with nSH3. Consistent with experiments, this indicates stronger binding of the viral ligand at the expense of losing the flexibility of side chains, whereas the backbone experiences less entropy loss. The entropy “hotspots” as identified in this study will be important for tuning the binding affinity of various ligands to a receptor.
Significance
Receptor-ligand binding relies not only on specific interactions between amino acids, but changes in the degrees of molecular flexibility upon binding, i.e., conformational entropy, are also critical. Our computational analysis identifies “entropy hotspot” residues that incur large entropy changes upon the binding of intrinsically disordered cellular and viral ligands to a protein receptor domain. These residues are located at the binding interface as well as away from the interface. Our results elucidate how the viral peptide binds to the receptor with a higher affinity, and our approach is applicable to the analysis and design of ligands binding to other target receptors.
Introduction
Intrinsically disordered proteins (IDP) or proteins containing intrinsically disordered regions (IDR) are abundant in cells (1), and they are widely involved in recognition between proteins (2, 3, 4, 5, 6, 7). Many IDPs/IDRs undergo disorder-to-order transitions upon binding to their partner proteins. The high entropic penalty for disorder-to-order transition leads to a relatively low binding affinity (5,7,8), which may help with reversible signaling when quick turnover is desired (2,5,9). In systems with a higher binding affinity, the entropic penalty is offset by favorable enthalpy and/or it is reduced by retaining the “fuzziness” in the complexed state (3,7,8). Such fully or partially unstructured yet functional protein complexes have challenged the traditional notion of a lock-and-key binding mechanism involving well-defined structural states (1).
The proline-rich motif (PRM) is one of the most abundant linear motifs found in IDPs/IDRs (10,11). The cyclic structure of proline limits conformational degrees of freedom (DOFs) (12), and PRMs tend to form left-handed polyproline type II (PPII) helices upon binding to its receptor (13). In a PPII helix, backbone carbonyl and side-chain groups are exposed and can form intermolecular contacts (12). This makes PRMs as common recognition motifs for many signaling proteins such as Src homology 3 (SH3) and WW domains (10,11,14,15). The binding generally involves negative (favorable) enthalpy and negative (unfavorable) entropy changes (6,8,16); the latter is due to the PPII helix formation upon binding (8,17, 18, 19).
Despite the importance of conformational entropy for binding, residue-level contribution has been difficult to quantify. Previous analysis considered mainly changes in the backbone conformation, whereas less is known about specific contributions of side chains (8). Experimentally, the “entropy meter” approach that empirically relates NMR-derived order parameters of side-chain methyl groups to entropy has been effective (20, 21, 22, 23, 24), but it is difficult to apply to proteins with a low content of methyl-bearing amino acids such as SH3 and its ligands. On the other hand, various computational methods have been developed for calculating conformational entropy. Early efforts included normal mode analysis (NMA) (25, 26, 27) and direct enumeration of side-chain rotamers (28,29). However, NMA cannot account for transitions between energy minima because it relies on an harmonic approximation of the potential energy surface about a single energy minimum. The direct enumeration approach becomes prohibitive for large proteins. NMA has also been applied to different snapshots of a molecular dynamics (MD) simulation trajectory. This mitigates the problem of working only around a single energy minimum, and it has been used for the study of ligand binding to SH3 domains (30,31). However, the computational cost of NMA limited the number of coordinate frames used, which likely resulted in only a small contribution of entropy to the binding specificity of different ligands (31). These limitations were partly addressed by a Monte Carlo simulation of side chains while the protein backbone was held fixed (32). It yielded total side-chain entropies among various systems correlating well with experimental values. Despite much insight this study provided, because of the simplified interaction potential that was introduced to allow Monte Carlo moves and because of the backbone being fixed to the crystallographic conformation, the accuracy and applicability of the method were limited when comparing entropy changes in the binding of different ligands or for finding residue-level contributions to entropy.
The above suggests that detailed residue-level analysis of the entropy of ligand binding based on unbiased atomistic MD simulation has been difficult. To this end, we employ the maximal information spanning tree (MIST) approach (33,34). MIST is an approximation method that overcomes the difficulty of direct enumeration arising from the large number of DOFs in typical biomolecular systems. It first calculates entropies of individual DOFs and then it adds corrections arising from higher order correlated motions among DOFs in such a way that the estimated entropy monotonically approaches the exact value as higher order correlations are accounted for. MIST yielded results that agree well with experimental estimates based on the entropy meter approach for several different systems (20). We apply MIST to study the binding between two PRMs and an SH3 domain. We use the N-terminal SH3 (nSH3) domain of a signaling adaptor protein CrkII (35,36). Among its various ligands (37,38), we used PRMcAbl and PRMNS1 (Fig. 1). PRMcAbl is from the C-terminal disordered region of the cAbl protein (35,39,40). PRMNS1 is from the C-terminal tail of the nonstructural protein 1 (NS1) of the 1918 Spanish influenza A virus (41,42). Upon binding to CrkII with high affinity, NS1 inhibits CrkII’s interaction with other proteins including cAbl, thereby suppressing the host cell’s immune response (41, 42, 43). Our earlier study has shown that PRMNS1 retains conformational flexibility even after binding to the nSH3 domain (44). This prompts the potential difference of entropy associated with the binding of the viral PRMNS1 and the cellular PRMcAbl ligands.
Figure 1.
Structural overview of nSH3:PRMcAbl and nSH3:PRMNS1. (a) Sequences of the two ligands are shown. Relative positions are marked below, where the central Leu is at position 0. The position index increases N-terminally (40,43). (b) Two structures superimposed relative to the nSH3 domain are shown. PRMcAbl and PRMNS1 are colored differently, and the central PxxP motif is white. Major subdomains of nSH3 (n-Src and RT loops, and 310 helix) that interact with the PRM are shown in solid colors. The rest of nSH3 is semitransparent. To see this figure in color, go online.
We carry out MD simulations of different nSH3:PRM systems either in a complex or in isolation. A 500-ns simulation for each system yielded convergence of the backbone amide bond order parameter and conformational entropy. By using the MIST method, we found that side chains are mainly responsible for entropy changes in the stably folded nSH3, whereas for PRM that form a PPII helix upon binding, both backbone and side chains contribute comparably to entropy changes. Analysis of per-residue entropy and intermolecular contacts yielded residues that incur large side-chain entropy changes upon binding (i.e., entropy hotspots). We found nonreciprocal contributions of the entropy hotspot residues forming contacts at the nSH3:PRM interface as well as the long-range effect of ligand binding, which increases entropies of residues distal to the interface. Comparing between PRMNS1 and PRMcAbl, the former involves greater overall entropy loss and also forms a larger number of high-occupancy contacts with nSH3, which suggests a stronger and more rigid binding of the influenza peptide, consistent with its stronger binding affinity (40,43). Given that NS1 is a high-priority target for developing anti-influenza compounds (45) and with the diversity of the SH3 domain and its ligands (14,37,38,46), this approach elucidating the residue-specific entropy contributions will be of practical utility as well as being applicable to studies of other protein-protein interactions in general.
Methods
Structures used
We used six simulation systems as follows:
-
1)
nSH3:PRMcAbl: Protein Data Bank (PDB) code 5IH2 (1.8-Å resolution) (40);
- 2)
- 3)
-
4)
nSH3: Isolated from nSH3:PRMcAbl;
-
5)
PRMcAbl: Isolated from nSH3:PRMcAbl; and
-
6)
PRMNS1: Isolated from nSH3:PRMNS1B.
Among the above, nSH3:PRMNS1A and nSH3:PRMNS1B are two different crystal structures of the nSH3:PRMNS1 complex, labeled in the same way as in our previous study (44).
Simulation
For simulation, we used CHARMM (47,48) with the param36 all-atom force field (49). Before solvation, a four-stage energy minimization was carried out. In each stage, backbone heavy atoms were harmonically restrained, and 100 steps of steepest descent followed by 300 steps of the adopted basis Newton-Raphson minimization were performed. The stiffness of the harmonic restraint was, in kcal/molÅ2 units, 5 (stage 1), 1 (stage 2), 0.1 (stage 3), and 0 (stage 4; no restraint). The system was solvated in a cubic TIP3P water box (50) of a side length of ∼60 Å (nSH3:PRM), 56 Å (nSH3 only), and 54 Å (PRM only). Ions (Cl− and Na+) were added to neutralize the system at ∼150-mM concentration. Simulation systems had ∼21,000 (nSH3:PRM), 16,000 (nSH3 only), and 15,000 (PRM only) atoms.
After solvation, the four-stage energy minimization explained above was applied again for the protein. The system was heated from 0 to 300 K over 100 ps followed by equilibration for 160 ps at 300 K. These were performed under a constant temperature and pressure (NPT) condition at 1 atm without any restraints. Each production run was under the constant volume and temperature (NVT) condition at 300 K for 500 ns. The integration step size was 2 fs. Lengths of covalent bonds involving hydrogen atoms were fixed by applying the SHAKE algorithm (51). The nonbonded interaction had a 12-Å cutoff. The particle-mesh Ewald summation method (52) was used to account for long-range electrostatic interactions under a periodic boundary condition. The Domain Decomposition (DOMDEC) module (53) of CHARMM was used to enhance parallel performance. Coordinates were saved every 5 ps. Visualization of structures were done using VMD (54) or UCSF Chimera (55). Calculations of root mean-square fluctuation (RMSF), order parameter, entropy, and contact occupancy were all based on the 100–500 ns interval to avoid the effect of the initial state. The 100-ns cutoff was determined by the relaxation times calculated for the angular reorientational correlation functions of the backbone amide N-H bonds, as explained below.
Order parameter
After aligning coordinate frames to the initial frame using backbone heavy atoms, we calculated the Lipari-Szabo squared generalized order parameter S2 (56). Let be the unit vector for the amide N-H bond with Cartesian components μi (i = 1, 2, 3). Then,
| (1) |
where indicates the average over coordinate frames (57,58). To calculate S2 for nSH3 or PRM within an nSH3:PRM complex, we aligned the backbone heavy atoms of the respective part to be consistent with the uncomplexed case. Statistical uncertainty was estimated by subsampling the trajectory every eighth frame and calculating the SD in S2 from the eight subsamples. This method was more effective than using eight consecutive 50-ns intervals because relaxation times differ across the protein.
To assess the convergence of our trajectory, we calculated the angular reorientational correlation function CI(t) (57):
| (2) |
where is the second Legendre polynomial. For each t, the average was taken over τ, ranging from 100 to (500 − t) ns.
Order parameters were also estimated from NMR relaxation experiments, as described previously (44). Using Modelfree version 4.20 (59,60) and FAST-Modelfree softwares, R1, R2, and heteronuclear nuclear Overhauser effect were analyzed according to the Lipari-Szabo model-free formalism (56,61). An isotropic diffusion model was used for the analysis of the free nSH3 domain, and an axially symmetric model was used for nSH3:PRM complexes (8).
Entropy
We used backbone and side-chain rotation angles as DOFs: for backbone, ϕ and ψ angles (62), and for the side chain, the dihedral χ angles (63). Compared to bond lengths and bond angles, χ angles are the main contributors to the side-chain entropy (20,26,29). Angles were measured using the CORREL facility of CHARMM. For a coordinate trajectory, histograms of angles were constructed with a bin size Δ = 10°. It is the smallest among bin sizes used previously, ranging from 10° (21) to 120° (20). Other choices, Δ = 8° and 15°, were also used as a test, but our main results did not depend on the precise choice of Δ. For a statistical uncertainty estimate, we subsampled the 100–500-ns interval every four frames and used the four sets, each containing the number of frames equal to 100 ns.
MIST
To calculate the conformational entropy using MIST (33,34), we started with the first order in which DOFs are treated independently. From the histogram of a given DOF, we built the normalized probability distribution function (PDF) (m: DOF index, i: bin index). The first-order MIST (MIST1) entropy is as follows:
| (3) |
where kB is the Boltzmann constant.
We used the joint PDF to calculate the second-order mutual information between DOF m and n:
| (4) |
The second-order MIST (MIST2) entropy is calculated by including I2 for one DOF at a time, in which only the maximal I2 between the current DOF and all previously added DOFs is included:
| (5) |
The third-order MIST (MIST3) is calculated similarly, by evaluating the third-order mutual information between DOF p and a pair of DOFs {q, r}:
| (6) |
so that,
| (7) |
For a given p, only the maximal I3 from all pairs of DOFs with indices less than p is included in the sum. If a certain DOF r is statistically independent of p and q, Eq. 6 becomes identical to Eq. 4. So Eq. 7 includes pairwise correlations for MIST2. In principle, higher order MIST can yield a more accurate (and smaller) estimation of entropy. But without a strong multivariate correlation, the improvement is marginal, whereas the computational cost steeply rises, and the high-dimensional joint PDF becomes less accurate because of the limited sample size. Thus, calculations up to the second or third order are practical (20,22).
For nSH3, we excluded the first A134 and the last R191 from entropy calculation, as done previously (40). We also excluded the terminal residues of PRMs (8). The number of DOFs were 235 for nSH3, 59 for PRMNS1, and 45 for PRMcAbl. Entropies were calculated using custom-written R language scripts and also using FORTRAN 95 codes parallelized with OpenMP.
Entropy per residue
The backbone entropy of each residue was calculated using the joint PDF,
| (8) |
which is identical to the two-DOF version of Eq. 5. For side chains, the number of DOFs (χ angles) varies between 1 and 5, where we used up to MIST3.
Results and Discussion
Order parameter
To test whether the 500-ns simulation time was adequate for analyzing conformational motion, we calculated the backbone amide bond order parameters (see Supporting Materials and Methods for details). Based on the relaxation time of the angular reorientational correlation function CI(t) (Eq. 2; Figs. S1 and S2), we decided to use the 100–500-ns interval for all analysis. Our computational and experimental order parameters agreed reasonably well for nSH3 (Fig. S3). Upon complex formation, PRMs undergo larger changes in order parameter and RMSF of the backbone Cα atoms (Figs. S3–S6). This reflects that nSH3 remains stably folded, whereas PRMs undergo disorder-order transition as they bind. Similar behaviors were observed in conformational entropy changes, as discussed below.
Entropy change upon ligand binding
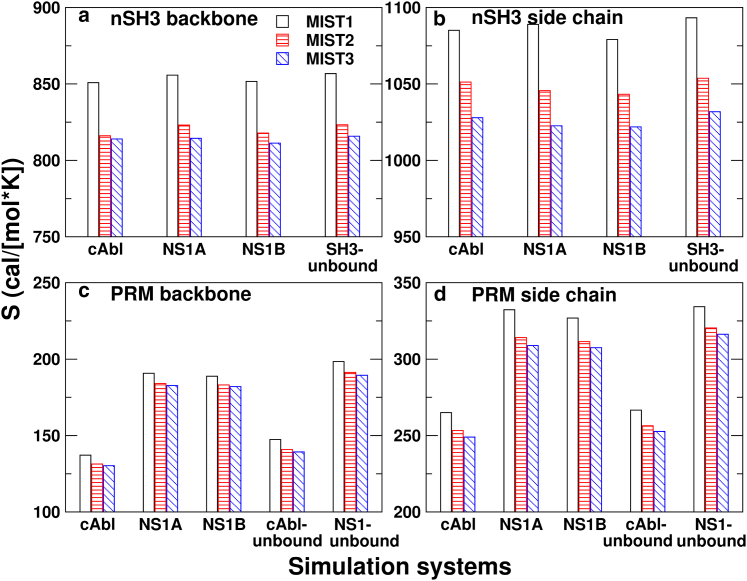
We calculated the backbone and side-chain conformational entropies separately or together. For higher accuracy, we used up to MIST3 approximation. The MIST1 entropy (Eq. 3) is the sum of entropies calculated for individual DOFs. Correlations among DOFs make the actual entropy less than the MIST1 entropy ((5), (7)). In systems studied here, the MIST1 entropy takes up the dominant portion, whereas MIST2 or MIST3 entropies are slightly reduced (Fig. 2). This indicates that correlations among DOFs are not strong. To examine whether using the 100–500 ns interval was adequate for entropy calculation, we calculated the MIST2 entropy for time intervals starting from 100 ns in 20-ns increments. Plateauing of calculated entropies suggests that the 400-ns duration was reasonable (Fig. S7).
Figure 2.
Comparison of MIST entropies. (a and b) nSH3 and (c and d) PRM are shown. Respective MIST calculations were performed separately for (a and c) the backbone and (b and d) side chains. Vertical axes in all panels are in the same range, 150 cal/(molK), to highlight relative differences. SDs in calculated entropies are at most 0.15 cal/(molK). To see this figure in color, go online.
Backbone entropy change of nSH3
Previous NMR-based estimates of backbone entropy changes associated with the PRM:SH3 complex formation were −7.0 ± 4.3 cal/(molK) (8) and −5 ± 2 cal/(molK) (17). Although direct comparison is difficult because these values are for different SH3:PRM systems, our calculated values (top row of Table 1) are similar in magnitude. Comparing between the two complexes in this study, the backbone entropy change of nSH3 is smaller for the PRMcAbl-bound form than the PRMNS1-bound form.
TABLE 1.
Entropy Changes upon Complex Formation
| nSH3:PRMcAbl | nSH3:PRMNS1A | nSH3:PRMNS1B | ||
|---|---|---|---|---|
| Backbone | nSH3 | −1.80 ± 0.215 | −2.38 ± 0.204 | −4.47 ± 0.184 |
| PRM | −8.99 ± 0.041 | −6.74 ± 0.057 | −7.43 ± 0.088 | |
| Side chain | nSH3 | −3.83 ± 0.187 | −9.13 ± 0.171 | −9.82 ± 0.202 |
| PRM | −3.75 ± 0.114 | −7.44 ± 0.161 | −8.83 ± 0.154 | |
| Net Change | −28.64 ± 0.336 | −36.56 ± 0.310 | −38.99 ± 0.317 | |
Numbers are in units of cal/(molK). MIST3 was used. Because correlations among DOFs are more extensive in the complex, the net change in entropy (bottom row) is greater in magnitude than the sum of backbone and side-chain entropy changes. Dependence of the calculated entropy on the bin size Δ is in Fig. S8, which has little impact on relative magnitudes of different entropy terms.
As previously reported, ligand binding decreases the backbone entropy of the SH3 domain (8,17). However, it is the smallest among the entropy changes listed in Table 1. This reflects that the stable nSH3 fold is little affected by the binding of a PRM, which was also seen in the analysis of the order parameter and the backbone Cα RMSF (Supporting Materials and Methods).
Backbone entropy change of PRMs
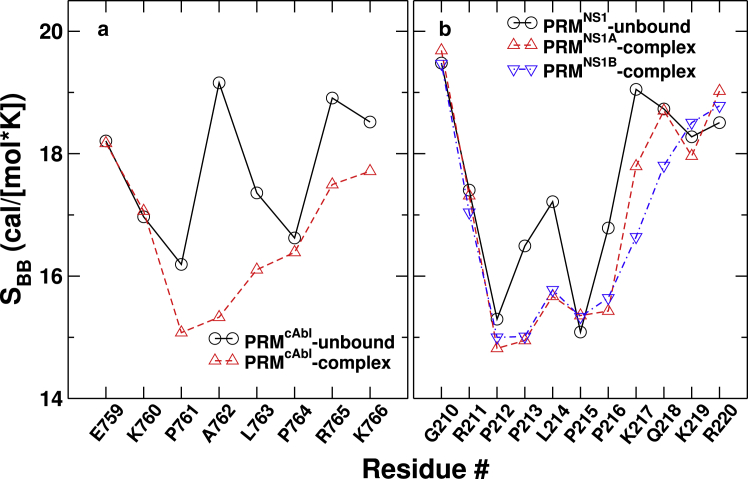
PRMs undergo disorder-order transition upon binding to nSH3 so that their backbone conformational entropy changes are larger compared to nSH3 (Table 1, first versus second rows). Between the two ligands, although PRMcAbl is shorter than PRMNS1, it involves a greater backbone entropy loss (Table 1, second row). At the level of individual residues, PRMcAbl shows large backbone entropy loss in the PxxP motif, especially A762, and also in the last two residues at the C-terminus (Fig. 3 a). The corresponding residue in PRMNS1 is P213 (Fig. 1), whose backbone is less flexible. The PxxP motif of PRMNS1 is surrounded by additional prolines, which impose a stronger conformational restraint on the backbone. This contributes to the small backbone entropy change upon binding. Furthermore, the two C-terminal residues of PRMNS1 show little changes in the backbone entropy upon binding (Fig. 3 b), suggesting that they remain mobile. The first two N-terminal residues in both PRMs also remain mobile.
Figure 3.
Per-residue backbone entropy of PRM in the complex and unbound states. (a) Shown is PRMcAbl. (b) Shown is PRMNS1. To see this figure in color, go online.
Side-chain entropy change in nSH3
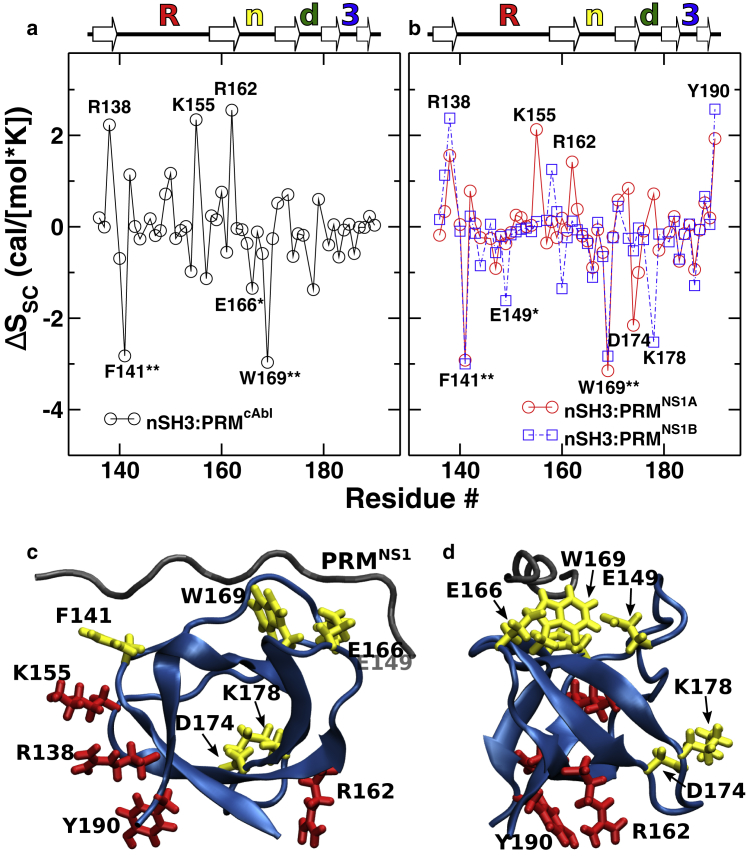
For nSH3, side-chain entropy changes are 2.1–3.8 times greater than backbone entropy changes (first versus third rows in Table 1). This is due to the restriction of the side-chain motion upon the binding of a PRM. However, residue-level analysis revealed that certain side chains gain entropy upon binding (Fig. 4). Side-chain entropies of R138, K155, and R162 in nSH3 increased substantially when complexed with PRMcAbl and to a lesser extent with PRMNS1 (Fig. 4, a and b). Y190 at the C-terminus of nSH3 is located next to R138, and its side-chain entropy increased in both of the two SH3:PRMNS1 systems (Fig. 4, b and c). These residues are bulky and surface exposed, and none of them interacts directly with PRMs. Only K155 formed contact with the N-terminal tyrosine of the two PRMs (Fig. 1 a) but with less than 1% occupancy. Increase in the side-chain entropy of these residues should thus be an indirect effect of PRM binding. Supporting this idea is a previous study reporting strain propagation across the entire c-Src SH3 domain as a compensatory response to ligand binding (64). A detailed analysis of the intra-nSH3 contacts revealed that the side-chain entropy increase in remote residues is mostly a result of the propagation of changes in lateral contacts of surface residues upon ligand binding (see Fig. S9 and Tables S1–S3 for details). The breakage of hydrogen bonds plays a significant role in increasing the side-chain entropy, although rearrangements of lateral nonpolar contacts are also involved. This explains why side-chain entropy increase occurs for large charged or polar residues on the surface of the protein. An additional possibility is the perturbation of the surface hydration structure upon ligand binding that in turn can affect the mobility of surface-exposed side chains of nSH3 (65). Further studies are needed to elucidate the allosteric effect of ligand binding on the side-chain motion.
Figure 4.
Per-residue side-chain entropy change of nSH3 upon ligand binding. Positive value means higher entropy in the complexed state. (a) nSH3:PRMcAbl and (b) nSH3:PRMNS1 are shown. Major subdomains (Fig. 1) are marked above each panel: RT loop (“R”), n-Src loop (“n”), distal loop (“d”), and 310 helix (“3”). (c and d) Locations of residues in nSH3 are marked in (a) and (b). Red/yellow: per-residue side-chain entropy increased/decreased is shown. (c) Side view: image shown viewed from below in Fig. 1b. (d) View from the right of (c) is shown. To see this figure in color, go online.
Residues that showed a substantial decrease in side-chain entropy are mainly in the ligand binding pocket. The largest side-chain entropy loss in nSH3 among all three systems was in two nonpolar residues, F141 and W169 (Fig. 4). Both are highly conserved across SH3 domains (46,66). They form high-occupancy nonpolar contacts with the PRM (Table 2), which restricts their side-chain motion. E149 in the RT loop and E166 in the n-Src loop that form hydrogen bonds with the C-terminal positively charged residues of PRM (Fig. 4 d) also lose side-chain entropy substantially (for simplicity, we call a salt bridge involving hydrogen atom also a hydrogen bond; Table 2). Other residues that form high-occupancy contacts with the PRM (Table 2) also contribute to the side-chain entropy loss but to a lesser extent.
Table 2.
List of High-Occupancy Contacts and Side-Chain Entropy Changes
| H-Bond |
Nonpolar Contact |
|||||
|---|---|---|---|---|---|---|
| nSH3 | PRM | Occupancy | nSH3 | PRM | Occupancy | |
| nSH3:PRMcAbl | E166n (−1.35) | R767 (−3.48) | 0.987 | F141R (−2.82) | K760 (−0.45) | 0.930 |
| Y1863 (−0.59) | P761 (+0.02) | 0.939 | F141R (−2.82) | P761 (+0.02) | 0.769 | |
| – | – | – | F143R (+0.00) | L763 (−0.63) | 0.928 | |
| – | – | – | Q168n (−0.58) | P764 (+0.24) | 0.949 | |
| – | – | – | W169n (−2.97) | L763 (−0.63) | 0.840 | |
| – | – | – | P1833 (−0.66) | L763 (−0.63) | 0.876 | |
| – | – | – | P1853 (+0.05) | P764 (+0.24) | 0.772 | |
| – | – | – | Y1863 (−0.59) | P761 (+0.02) | 0.876 | |
| nSH3:PRMNS1A | D142R (+0.78) | R211 (−1.26) | 0.839 | F141R (−2.92) | R211 (−1.26) | 0.900 |
| D147R (−0.91) | K217 (−1.41) | 0.839 | F141R (−2.92) | P212 (−0.03) | 0.785 | |
| D150R (−0.12) | K217 (−1.41) | 0.943 | F143R (+0.06) | L214 (−0.84) | 0.955 | |
| E166n (−0.89) | R220 (−4.50) | 0.968 | Q168n (−0.56) | P215 (+0.93) | 0.970 | |
| Y1863 (−0.94) | P212 (−0.03) | 0.978 | W169n (−3.15) | L214 (−0.84) | 0.897 | |
| – | – | – | W169n (−3.15) | K217 (−1.41) | 0.951 | |
| – | – | – | P1833 (−0.75) | L214 (−0.84) | 0.886 | |
| – | – | – | P1853 (+0.04) | P215 (+0.93) | 0.870 | |
| – | – | – | Y1863 (−0.94) | R211 (−1.26) | 0.831 | |
| – | – | – | Y1863 (−0.94) | P212 (−0.03) | 0.926 | |
| – | – | – | Y1863 (−0.94) | L214 (−0.84) | 0.754 | |
| nSH3:PRMNS1B | D142R (+0.23) | R211 (−2.11) | 0.721 | F141R (−3.00) | R211 (−2.11) | 0.928 |
| D147R (−1.57) | K217 (−4.47) | 0.933 | F141R (−3.00) | P212 (+0.08) | 0.746 | |
| E149R (−0.37) | K217 (−4.47) | 0.825 | F143R (−0.14) | L214 (−1.00) | 0.949 | |
| E149R (−0.37) | R220 (−1.71) | 0.799 | Q168n (−0.65) | P215 (+0.94) | 0.939 | |
| D150R (−0.18) | K217 (−4.47) | 0.985 | W169n (−2.83) | L214 (−1.00) | 0.872 | |
| E166n (−1.10) | R220 (−1.71) | 0.783 | W169n (−2.83) | K217 (−4.47) | 0.920 | |
| Y1863 (−1.29) | P212 (+0.08) | 0.979 | P1833 (−0.71) | L214 (−1.00) | 0.914 | |
| – | – | – | P1853 (+0.06) | P215 (+0.94) | 0.826 | |
| – | – | – | Y1863 (−1.29) | R211 (−2.11) | 0.858 | |
| – | – | – | Y1863 (−1.29) | P212 (+0.08) | 0.926 | |
| – | – | – | Y1863 (−1.29) | L214 (−1.00) | 0.741 | |
Hydrogen bond (H-Bond) includes salt bridges. Residues of nSH3 are marked with superscripts with the corresponding subdomains (3: 310 helix; R: RT loop; and n: n-Src loop). Side-chain entropy change of each residue upon complex formation (in cal/(molK)) is in parentheses.
Away from the binding interface, D174 in nSH3:PRMNS1A and K178 in nSH3:PRMNS1B in the distal loop also showed notable side-chain entropy loss (Fig. 4, b–d). This may be a long-range effect, similar to the entropy increase in distal residues upon ligand binding. A previous NMR study of ligand binding to c-Src SH3 domain showed that changes in motion occur both near and away from the ligand binding interface (17). Both D174 and K178 form hydrogen bonds with the nearby E176 in the distal loop with different contact occupancies. In isolated nSH3, their contact occupancies are 50.7% (D174-E176) and 78.7% (K178-E176). In nSH3:PRMcAbl, these occupancies increase by less than 4.6% upon complex formation, which is consistent with their moderate side-chain entropy changes (Fig. 4 a). For nSH3:PRMNS1A, the occupancy of D174-E176 increases to 90%, whereas for K178-E176, it decreases to 8.7% (cf., Table S2), which contributes to the relatively large decrease in side-chain entropy of D174 (Fig. 4 b). However, E176 did not experience any corresponding side-chain entropy loss. For nSH3:PRMNS1B, the D174-E176 bond had nearly the same occupancy in the complex, 55.5%, and the occupancy of K178-E176 increased to 88.1%, again in line with the side-chain entropy loss of K178. Thus, the contact occupancy and side-chain entropy changes upon complex formation are somewhat correlated when the occupancy increases to a high value, which may be due to a restriction in side-chain motion. However, two residues forming a high-occupancy contact do not experience comparable side-chain entropy loss, as seen for E176.
Side-chain entropy change in PRMs
Similar to nSH3, residues in PRMs that showed large side-chain entropy loss (marked by stars in Fig. 5) formed high-occupancy contacts with nSH3 (Table 2), although the converse does not necessarily hold. Contact analysis suggests a different mechanism underlying the entropy changes between nSH3 and PRMs. For nSH3, the largest side-chain entropy losses were by residues that form nonpolar contacts (i.e., F141 and W169). But their binding partners in PRM do not experience correspondingly large entropy loss. For example, L763 in PRMcAbl and L214 in PRMNS1 contact W169, but their side-chain entropy changes are not significant (Table 2). When a PRM binds, F141 and W169 of nSH3 become buried in the interface (Fig. 4 c), whereas their nonpolar contact residues in PRM are still partially exposed, which allows more room for motion. For PRM, on the other hand, all residues that had more than 2 cal/(molK) side-chain entropy loss formed high-occupancy hydrogen bonds with nSH3 (R767 in PRMcAbl, R220 in PRMNS1A, and K217 in PRMNS1B; single star in Fig. 5 and Table 2). Compared to nonpolar contacts, hydrogen bonds are more directional, where the acceptor-hydrogen-donor angle is greater than 120° (67,68). The directional constraint can suppress side-chain motion more effectively than nonpolar contacts do.
Figure 5.
Per-residue side-chain entropy change of PRMs upon binding to nSH3. (a) nSH3:PRMcAbl and (b) nSH3:PRMNS1 are shown. Residues that form high-occupancy contacts with nSH3 (Table 2) are marked by stars. Hydrogen bond: one star. Nonpolar: two stars. To see this figure in color, go online.
Net entropy change
When entropy change upon ligand binding is calculated for the whole system, the correlation effect between nSH3 and PRM additionally lower the entropy of the complex relative to the unbound states. This causes the net entropy change of the whole system to be greater than the sum of individual entropy changes (Table 1, last versus other rows). Between nSH3:PRMcAbl and nSH3:PRMNS1, the latter involves a greater change in side-chain entropy. Although this is partly due to PRMNS1 being longer than PRMcAbl, the former also involves a larger per-residue entropy loss (Fig. 5).
The net entropy change in ligand binding in nSH3:PRMNS1 is 7.9–10.4 cal/(molK) greater than that of nSH3:PRMcAbl (Table 1, last row). At 300 K, this corresponds to 2.4–3.1 kcal/mol, which is comparable to the free energy of a hydrogen bond (69). With nSH3:PRMNS1 also forming more contacts (Table 2), the emerging picture is that PRMNS1 achieves a higher binding affinity to nSH3, in which the favorable enthalpy change afforded by the extensive contact formation is greater than the entropy loss, which is consistent with its role as a viral peptide (43). The weaker binding and relatively smaller changes of entropy in PRMcAbl is also consistent with the experiment (40), and it enables easier regulation of the interaction with nSH3 of CrkII.
It is notable that the side-chain dynamics is different from the backbone dynamics. The backbone entropy loss of PRMcAbl is larger than that of PRMNS1, whereas the converse holds for the side-chain entropy loss. If only the backbone order parameter or backbone entropy were considered, which has been easier to measure experimentally, one might conclude that PRMNS1 is more flexible than PRMcAbl in the bound state. It is thus essential to also consider the side-chain dynamics to establish a more complete understanding of the entropy contribution.
Conclusions
Dissecting the relative contributions of backbone and side-chain entropies, for individual residues or together, provides important details about the binding of PRMs to nSH3. Present results suggest that side chains play a critical role for determining entropy changes associated with the binding. For the stably folded nSH3, side-chain entropy change is larger than that of the backbone. For PRMs, as they belong to IDRs, both the backbone and side chains contribute comparably to the entropy change. As a result, considerable fraction of the net entropy change is due to PRMs, even though they are much smaller than nSH3 in size. We also note that, because entropy is a state function, only separate simulations of the uncomplexed PRMs and nSH3 and nSH3:PRM complexes were needed for calculation. Although analysis of the binding and unbinding processes of the PRM will provide additional kinetic information, it is beyond the scope of this study.
We found that ligand binding induces per-residue side-chain entropy changes both at the nSH3:PRM interface and across nSH3. For residues of nSH3 that form high-occupancy contacts with PRM, side-chain entropy decreases to varying extents, the largest of which were the highly conserved and nonpolar F141 and W169. Analogously, for an SH2 domain, ligand binding did not incur any significant changes in the backbone motion, whereas a few “hotspot” residues at the interface made a large contribution to the binding free energy (70). Unlike nSH3, the side-chain entropy loss of PRMs is large for residues that form high-occupancy hydrogen bonds. Consistent with the nonreciprocal changes in side-chain entropy at the interface, a previous NMR study of a calmodulin domain and its target domains noted a “surprisingly noncomplementary” distribution of motion at the interface (71). Side-chain entropy changes in remote surface-exposed residues likely arises from propagation of the rearrangements in the contacts across surface residues upon ligand binding. A long-range effect of ligand binding has also been observed in other systems including SH3 domains (17,64) and an MDM2 domain with p53-derived peptides (72). Entropy changes in charged or polar residues in distal regions may play an allosteric role for electrostatic interactions with other domains (73,74).
Between nSH3:PRMcAbl and nSH3:PRMNS1, the higher binding affinity of the latter (40,43) appears to be driven by the favorable enthalpy change that compensates for the unfavorable entropy loss. The smaller backbone entropy change in PRMNS1 is due to its central region that remains relatively rigid in the unbound state and also due to its C-terminal region that form “fuzzy” contacts so that the region stays flexible in the bound state, whereas its side chains lose entropy substantially. Taken together, these results elucidate the role of entropy hotspots in influencing the conformational flexibility of the complex.
Decomposition of the free energy contributions of hotspot residues (75) into enthalpic and entropic contributions may provide new insight into how specificity is tuned for proteins with multiple binding partners (71). Moreover, the sites that are distant from the binding interface but undergo considerable changes in conformational entropy may conversely regulate protein-protein interactions, called dynamic allostery (76,77). In this regard, the allosteric hotspots may serve as viable targets for the rational development of protein-protein interaction modulators.
This work combining entropy and contact analysis, together with experimental studies using various NMR relaxation methods (78,79), will facilitate the understanding of the side-chain dynamics and its role in molecular recognition. Furthermore, interfacial water molecules likely play a significant role as well (16,65,80,81), which is a subject of future studies.
acknowledgments
Simulations were performed on machines at the Texas A&M High-Performance Research Computing Facility.
Research reported in this publication was supported by the National Institute of General Medical Sciences of the U.S. National Institutes of Health under award number R01GM127723.
Editor: Amedeo Caflisch.
Footnotes
Supporting Material can be found online at https://doi.org/10.1016/j.bpj.2020.03.026.
Contributor Information
Jae-Hyun Cho, Email: jaehyuncho@tamu.edu.
Wonmuk Hwang, Email: hwm@tamu.edu.
Supporting Citations
References (82,83) appear in the Supporting Material.
Author Contributions
J.S. designed research, performed and analyzed simulation, and wrote the manuscript. Q.S. processed experimental data. J.-H.C. designed research, performed and analyzed experiment, and wrote the manuscript. W.H. designed research, analyzed simulation, and wrote the manuscript.
Supporting Material
References
- 1.Uversky V.N., Dunker A.K. Biochemistry. Controlled chaos. Science. 2008;322:1340–1341. doi: 10.1126/science.1167453. [DOI] [PubMed] [Google Scholar]
- 2.Dunker A.K., Brown C.J., Obradović Z. Intrinsic disorder and protein function. Biochemistry. 2002;41:6573–6582. doi: 10.1021/bi012159+. [DOI] [PubMed] [Google Scholar]
- 3.Tompa P., Fuxreiter M. Fuzzy complexes: polymorphism and structural disorder in protein-protein interactions. Trends Biochem. Sci. 2008;33:2–8. doi: 10.1016/j.tibs.2007.10.003. [DOI] [PubMed] [Google Scholar]
- 4.Mittag T., Kay L.E., Forman-Kay J.D. Protein dynamics and conformational disorder in molecular recognition. J. Mol. Recognit. 2010;23:105–116. doi: 10.1002/jmr.961. [DOI] [PubMed] [Google Scholar]
- 5.Uversky V.N. A decade and a half of protein intrinsic disorder: biology still waits for physics. Protein Sci. 2013;22:693–724. doi: 10.1002/pro.2261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Wright P.E., Dyson H.J. Intrinsically disordered proteins in cellular signalling and regulation. Nat. Rev. Mol. Cell Biol. 2015;16:18–29. doi: 10.1038/nrm3920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Shammas S.L., Crabtree M.D., Clarke J. Insights into coupled folding and binding mechanisms from kinetic studies. J. Biol. Chem. 2016;291:6689–6695. doi: 10.1074/jbc.R115.692715. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Zeng D., Shen Q., Cho J.H. Thermodynamic contribution of backbone conformational entropy in the binding between SH3 domain and proline-rich motif. Biochem. Biophys. Res. Commun. 2017;484:21–26. doi: 10.1016/j.bbrc.2017.01.089. [DOI] [PubMed] [Google Scholar]
- 9.Dyson H.J., Wright P.E. Intrinsically unstructured proteins and their functions. Nat. Rev. Mol. Cell Biol. 2005;6:197–208. doi: 10.1038/nrm1589. [DOI] [PubMed] [Google Scholar]
- 10.Kay B.K., Williamson M.P., Sudol M. The importance of being proline: the interaction of proline-rich motifs in signaling proteins with their cognate domains. FASEB J. 2000;14:231–241. [PubMed] [Google Scholar]
- 11.Macias M.J., Wiesner S., Sudol M. WW and SH3 domains, two different scaffolds to recognize proline-rich ligands. FEBS Lett. 2002;513:30–37. doi: 10.1016/s0014-5793(01)03290-2. [DOI] [PubMed] [Google Scholar]
- 12.Theillet F.X., Kalmar L., Uversky V.N. The alphabet of intrinsic disorder: I. Act like a Pro: on the abundance and roles of proline residues in intrinsically disordered proteins. Intrinsically Disord. Proteins. 2013;1:e24360. doi: 10.4161/idp.24360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Rath A., Davidson A.R., Deber C.M. The structure of “unstructured” regions in peptides and proteins: role of the polyproline II helix in protein folding and recognition. Biopolymers. 2005;80:179–185. doi: 10.1002/bip.20227. [DOI] [PubMed] [Google Scholar]
- 14.Mayer B.J. SH3 domains: complexity in moderation. J. Cell Sci. 2001;114:1253–1263. doi: 10.1242/jcs.114.7.1253. [DOI] [PubMed] [Google Scholar]
- 15.Li S.S. Specificity and versatility of SH3 and other proline-recognition domains: structural basis and implications for cellular signal transduction. Biochem. J. 2005;390:641–653. doi: 10.1042/BJ20050411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Palencia A., Cobos E.S., Luque I. Thermodynamic dissection of the binding energetics of proline-rich peptides to the Abl-SH3 domain: implications for rational ligand design. J. Mol. Biol. 2004;336:527–537. doi: 10.1016/j.jmb.2003.12.030. [DOI] [PubMed] [Google Scholar]
- 17.Wang C., Pawley N.H., Nicholson L.K. The role of backbone motions in ligand binding to the c-Src SH3 domain. J. Mol. Biol. 2001;313:873–887. doi: 10.1006/jmbi.2001.5083. [DOI] [PubMed] [Google Scholar]
- 18.Creamer T.P. Left-handed polyproline II helix formation is (very) locally driven. Proteins. 1998;33:218–226. [PubMed] [Google Scholar]
- 19.Ferreon J.C., Hilser V.J. Thermodynamics of binding to SH3 domains: the energetic impact of polyproline II (PII) helix formation. Biochemistry. 2004;43:7787–7797. doi: 10.1021/bi049752m. [DOI] [PubMed] [Google Scholar]
- 20.Kasinath V., Sharp K.A., Wand A.J. Microscopic insights into the NMR relaxation-based protein conformational entropy meter. J. Am. Chem. Soc. 2013;135:15092–15100. doi: 10.1021/ja405200u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Baxa M.C., Haddadian E.J., Sosnick T.R. Loss of conformational entropy in protein folding calculated using realistic ensembles and its implications for NMR-based calculations. Proc. Natl. Acad. Sci. USA. 2014;111:15396–15401. doi: 10.1073/pnas.1407768111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Sharp K.A., O’Brien E., Wand A.J. On the relationship between NMR-derived amide order parameters and protein backbone entropy changes. Proteins. 2015;83:922–930. doi: 10.1002/prot.24789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Caro J.A., Harpole K.W., Wand A.J. Entropy in molecular recognition by proteins. Proc. Natl. Acad. Sci. USA. 2017;114:6563–6568. doi: 10.1073/pnas.1621154114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Wand A.J., Sharp K.A. Measuring entropy in molecular recognition by proteins. Annu. Rev. Biophys. 2018;47:41–61. doi: 10.1146/annurev-biophys-060414-034042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Karplus M., Kushick J.N. Method for estimating the configurational entropy of macromolecules. Macromolecules. 1981;14:325–332. [Google Scholar]
- 26.Karplus M., Ichiye T., Pettitt B.M. Configurational entropy of native proteins. Biophys. J. 1987;52:1083–1085. doi: 10.1016/S0006-3495(87)83303-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Grünberg R., Nilges M., Leckner J. Flexibility and conformational entropy in protein-protein binding. Structure. 2006;14:683–693. doi: 10.1016/j.str.2006.01.014. [DOI] [PubMed] [Google Scholar]
- 28.Lee K.H., Xie D., Amzel L.M. Estimation of changes in side chain configurational entropy in binding and folding: general methods and application to helix formation. Proteins. 1994;20:68–84. doi: 10.1002/prot.340200108. [DOI] [PubMed] [Google Scholar]
- 29.Doig A.J., Sternberg M.J. Side-chain conformational entropy in protein folding. Protein Sci. 1995;4:2247–2251. doi: 10.1002/pro.5560041101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Wang W., Lim W.A., Kollman P.A. An analysis of the interactions between the Sem-5 SH3 domain and its ligands using molecular dynamics, free energy calculations, and sequence analysis. J. Am. Chem. Soc. 2001;123:3986–3994. doi: 10.1021/ja003164o. [DOI] [PubMed] [Google Scholar]
- 31.Hou T., Chen K., Wang W. Computational analysis and prediction of the binding motif and protein interacting partners of the Abl SH3 domain. PLoS Comput. Biol. 2006;2:e1. doi: 10.1371/journal.pcbi.0020001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.DuBay K.H., Geissler P.L. Calculation of proteins’ total side-chain torsional entropy and its influence on protein-ligand interactions. J. Mol. Biol. 2009;391:484–497. doi: 10.1016/j.jmb.2009.05.068. [DOI] [PubMed] [Google Scholar]
- 33.King B.M., Tidor B. MIST: maximum information spanning trees for dimension reduction of biological data sets. Bioinformatics. 2009;25:1165–1172. doi: 10.1093/bioinformatics/btp109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.King B.M., Silver N.W., Tidor B. Efficient calculation of molecular configurational entropies using an information theoretic approximation. J. Phys. Chem. B. 2012;116:2891–2904. doi: 10.1021/jp2068123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Feller S.M. Crk family adaptors-signalling complex formation and biological roles. Oncogene. 2001;20:6348–6371. doi: 10.1038/sj.onc.1204779. [DOI] [PubMed] [Google Scholar]
- 36.Rodrigues S.P., Fathers K.E., Park M. CrkI and CrkII function as key signaling integrators for migration and invasion of cancer cells. Mol. Cancer Res. 2005;3:183–194. doi: 10.1158/1541-7786.MCR-04-0211. [DOI] [PubMed] [Google Scholar]
- 37.Wu X., Knudsen B., Kuriyan J. Structural basis for the specific interaction of lysine-containing proline-rich peptides with the N-terminal SH3 domain of c-Crk. Structure. 1995;3:215–226. doi: 10.1016/s0969-2126(01)00151-4. [DOI] [PubMed] [Google Scholar]
- 38.Matsuda M., Ota S., Kurata T. Interaction between the amino-terminal SH3 domain of CRK and its natural target proteins. J. Biol. Chem. 1996;271:14468–14472. doi: 10.1074/jbc.271.24.14468. [DOI] [PubMed] [Google Scholar]
- 39.Takino T., Tamura M., Yamada K.M. Tyrosine phosphorylation of the CrkII adaptor protein modulates cell migration. J. Cell Sci. 2003;116:3145–3155. doi: 10.1242/jcs.00632. [DOI] [PubMed] [Google Scholar]
- 40.Bhatt V.S., Zeng D., Cho J.H. Binding mechanism of the N-terminal SH3 domain of CrkII and proline-rich motifs in cAbl. Biophys. J. 2016;110:2630–2641. doi: 10.1016/j.bpj.2016.05.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Horimoto T., Kawaoka Y. Influenza: lessons from past pandemics, warnings from current incidents. Nat. Rev. Microbiol. 2005;3:591–600. doi: 10.1038/nrmicro1208. [DOI] [PubMed] [Google Scholar]
- 42.Melén K., Kinnunen L., Julkunen I. Nuclear and nucleolar targeting of influenza A virus NS1 protein: striking differences between different virus subtypes. J. Virol. 2007;81:5995–6006. doi: 10.1128/JVI.01714-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Shen Q., Zeng D., Cho J.H. The molecular mechanisms underlying the hijack of host proteins by the 1918 Spanish influenza virus. ACS Chem. Biol. 2017;12:1199–1203. doi: 10.1021/acschembio.7b00168. [DOI] [PubMed] [Google Scholar]
- 44.Shen Q., Shi J., Cho J.H. Molecular mechanisms of tight binding through fuzzy interactions. Biophys. J. 2018;114:1313–1320. doi: 10.1016/j.bpj.2018.01.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Kleinpeter A.B., Jureka A.S., Petit C.M. Structural analyses reveal the mechanism of inhibition of influenza virus NS1 by two antiviral compounds. J. Biol. Chem. 2018;293:14659–14668. doi: 10.1074/jbc.RA118.004012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Larson S.M., Di Nardo A.A., Davidson A.R. Analysis of covariation in an SH3 domain sequence alignment: applications in tertiary contact prediction and the design of compensating hydrophobic core substitutions. J. Mol. Biol. 2000;303:433–446. doi: 10.1006/jmbi.2000.4146. [DOI] [PubMed] [Google Scholar]
- 47.Brooks B.R., Bruccoleri R.E., Karplus M. CHARMM: a program for macromolecular energy, minimization, and dynamics calculations. J. Comput. Chem. 1983;4:187–217. [Google Scholar]
- 48.Brooks B.R., Brooks C.L., III, Karplus M. CHARMM: the biomolecular simulation program. J. Comput. Chem. 2009;30:1545–1614. doi: 10.1002/jcc.21287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Hart K., Foloppe N., Mackerell A.D., Jr. Optimization of the CHARMM additive force field for DNA: improved treatment of the BI/BII conformational equilibrium. J. Chem. Theory Comput. 2012;8:348–362. doi: 10.1021/ct200723y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Jorgensen W., Chandrasekhar J., Klein M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983;79:926–935. [Google Scholar]
- 51.Ryckaert J.-P., Ciccotti G., Berendsen H.J. Numerical integration of the cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. J. Comput. Phys. 1977;23:327–341. [Google Scholar]
- 52.Feller S.E., Pastor R.W., Brooks B.R. Effect of electrostatic force truncation on interfacial and transport properties of water. J. Phys. Chem. 1996;100:17011–17020. [Google Scholar]
- 53.Hynninen A.P., Crowley M.F. New faster CHARMM molecular dynamics engine. J. Comput. Chem. 2014;35:406–413. doi: 10.1002/jcc.23501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Humphrey W., Dalke A., Schulten K. VMD: visual molecular dynamics. J. Mol. Graph. 1996;14:33–38, 27–28.. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- 55.Pettersen E.F., Goddard T.D., Ferrin T.E. UCSF Chimera--a visualization system for exploratory research and analysis. J. Comput. Chem. 2004;25:1605–1612. doi: 10.1002/jcc.20084. [DOI] [PubMed] [Google Scholar]
- 56.Lipari G., Szabo A. Model-free approach to the interpretation of nuclear magnetic resonance relaxation in macromolecules. 1. Theory and range of validity. J. Am. Chem. Soc. 1982;104:4546–4559. [Google Scholar]
- 57.Chandrasekhar I., Clore G.M., Brooks B.R. A 500 ps molecular dynamics simulation study of interleukin-1 beta in water. Correlation with nuclear magnetic resonance spectroscopy and crystallography. J. Mol. Biol. 1992;226:239–250. doi: 10.1016/0022-2836(92)90136-8. [DOI] [PubMed] [Google Scholar]
- 58.Trbovic N., Cho J.H., Palmer A.G., III Protein side-chain dynamics and residual conformational entropy. J. Am. Chem. Soc. 2009;131:615–622. doi: 10.1021/ja806475k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Mandel A.M., Akke M., Palmer A.G., III Backbone dynamics of Escherichia coli ribonuclease HI: correlations with structure and function in an active enzyme. J. Mol. Biol. 1995;246:144–163. doi: 10.1006/jmbi.1994.0073. [DOI] [PubMed] [Google Scholar]
- 60.Cole R., Loria J.P. FAST-Modelfree: a program for rapid automated analysis of solution NMR spin-relaxation data. J. Biomol. NMR. 2003;26:203–213. doi: 10.1023/a:1023808801134. [DOI] [PubMed] [Google Scholar]
- 61.Lipari G., Szabo A. Model-free approach to the interpretation of nuclear magnetic resonance relaxation in macromolecules. 2. Analysis of experimental results. J. Am. Chem. Soc. 1982;104:4559–4570. [Google Scholar]
- 62.Stites W.E., Pranata J. Empirical evaluation of the influence of side chains on the conformational entropy of the polypeptide backbone. Proteins. 1995;22:132–140. doi: 10.1002/prot.340220206. [DOI] [PubMed] [Google Scholar]
- 63.IUPAC-IUB Commission on Biochemical Nomenclature (CBN) Abbreviations and symbols for the description of the conformation of polypeptide chains. J. Biol. Chem. 1970;245:6489–6497. [PubMed] [Google Scholar]
- 64.Cordier F., Wang C., Nicholson L.K. Ligand-induced strain in hydrogen bonds of the c-Src SH3 domain detected by NMR. J. Mol. Biol. 2000;304:497–505. doi: 10.1006/jmbi.2000.4274. [DOI] [PubMed] [Google Scholar]
- 65.Zafra-Ruano A., Luque I. Interfacial water molecules in SH3 interactions: getting the full picture on polyproline recognition by protein-protein interaction domains. FEBS Lett. 2012;586:2619–2630. doi: 10.1016/j.febslet.2012.04.057. [DOI] [PubMed] [Google Scholar]
- 66.Harkiolaki M., Lewitzky M., Feller S.M. Structural basis for SH3 domain-mediated high-affinity binding between Mona/Gads and SLP-76. EMBO J. 2003;22:2571–2582. doi: 10.1093/emboj/cdg258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.De Loof H., Nilsson L., Rigler R. Molecular dynamics simulation of galanin in aqueous and nonaqueous solution. J. Am. Chem. Soc. 1992;114:4028–4035. [Google Scholar]
- 68.Wood P.A., Allen F.H., Pidcock E. Hydrogen-bond directionality at the donor H atom – analysis of interaction energies and database statistics. CrystEngComm. 2009;11:1563–1571. [Google Scholar]
- 69.Fersht A.R. The hydrogen bond in molecular recognition. Trends Biochem. Sci. 1987;12:301–304. [Google Scholar]
- 70.Ward J.M., Gorenstein N.M., Post C.B. Constraining binding hot spots: NMR and molecular dynamics simulations provide a structural explanation for enthalpy-entropy compensation in SH2-ligand binding. J. Am. Chem. Soc. 2010;132:11058–11070. doi: 10.1021/ja910535j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Marlow M.S., Dogan J., Wand A.J. The role of conformational entropy in molecular recognition by calmodulin. Nat. Chem. Biol. 2010;6:352–358. doi: 10.1038/nchembio.347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Schon O., Friedler A., Fersht A.R. Binding of p53-derived ligands to MDM2 induces a variety of long range conformational changes. J. Mol. Biol. 2004;336:197–202. doi: 10.1016/j.jmb.2003.11.051. [DOI] [PubMed] [Google Scholar]
- 73.Ozkirimli E., Yadav S.S., Post C.B. An electrostatic network and long-range regulation of Src kinases. Protein Sci. 2008;17:1871–1880. doi: 10.1110/ps.037457.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.DuBay K.H., Bowman G.R., Geissler P.L. Fluctuations within folded proteins: implications for thermodynamic and allosteric regulation. Acc. Chem. Res. 2015;48:1098–1105. doi: 10.1021/ar500351b. [DOI] [PubMed] [Google Scholar]
- 75.Clackson T., Wells J.A. A hot spot of binding energy in a hormone-receptor interface. Science. 1995;267:383–386. doi: 10.1126/science.7529940. [DOI] [PubMed] [Google Scholar]
- 76.Tzeng S.R., Kalodimos C.G. Protein activity regulation by conformational entropy. Nature. 2012;488:236–240. doi: 10.1038/nature11271. [DOI] [PubMed] [Google Scholar]
- 77.Motlagh H.N., Wrabl J.O., Hilser V.J. The ensemble nature of allostery. Nature. 2014;508:331–339. doi: 10.1038/nature13001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Stafford K.A., Ferrage F., Palmer A.G., III Side chain dynamics of carboxyl and carbonyl groups in the catalytic function of Escherichia coli ribonuclease H. J. Am. Chem. Soc. 2013;135:18024–18027. doi: 10.1021/ja409479y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Weininger U. Optimal isotope labeling of aromatic amino acid side chains for NMR studies of protein dynamics. Methods Enzymol. 2019;614:67–86. doi: 10.1016/bs.mie.2018.08.028. [DOI] [PubMed] [Google Scholar]
- 80.Palencia A., Camara-Artigas A., Luque I. Role of interfacial water molecules in proline-rich ligand recognition by the Src homology 3 domain of Abl. J. Biol. Chem. 2010;285:2823–2833. doi: 10.1074/jbc.M109.048033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Martin-Garcia J.M., Ruiz-Sanz J., Luque I. Interfacial water molecules in SH3 interactions: a revised paradigm for polyproline recognition. Biochem. J. 2012;442:443–451. doi: 10.1042/BJ20111089. [DOI] [PubMed] [Google Scholar]
- 82.Jarymowycz V.A., Stone M.J. Fast time scale dynamics of protein backbones: NMR relaxation methods, applications, and functional consequences. Chem. Rev. 2006;106:1624–1671. doi: 10.1021/cr040421p. [DOI] [PubMed] [Google Scholar]
- 83.Maragakis P., Lindorff-Larsen K., Shaw D.E. Microsecond molecular dynamics simulation shows effect of slow loop dynamics on backbone amide order parameters of proteins. J. Phys. Chem. B. 2008;112:6155–6158. doi: 10.1021/jp077018h. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.