Beta and Gamma Oscillations Index Cognitive Interference Effects Across a Distributed Motor Network

Abstract

The planning and execution of an efficient motor plan is essential to everyday cognitive function, and relies on oscillatory neural responses in both the beta (14 – 30 Hz) and gamma (> 30 Hz) bands. Such motor control requires not only the integration of salient information from the environment, but also the inhibition of irrelevant or distracting inputs that often manifest as forms of cognitive interference. While the effects of cognitive interference on motor neural dynamics has been an area of increasing interest recently, it remains unclear whether different subtypes of interference differentially impact these dynamics. We address this issue using magnetoencephalography and a novel adaptation of the Multi-Source Interference Task, wherein two common subtypes of cognitive interference are each presented in isolation, as well as simultaneously. We find evidence for the subtype-invariant indexing of cognitive interference across a widely distributed set of motor regions oscillating in the beta range, including the bilateral primary motor and posterior parietal cortices. Further, we find that superadditive effects of cognitive interference subtypes on behavior are paralleled by gamma oscillations in the contralateral premotor cortex, and determine that these gamma oscillations also predict the superadditive effects on behavior.

1. Introduction

The ability to effectively prepare and execute an efficient motor plan is essential to normative function. However, this seemingly simple concept belies an extremely complex set of cognitive processes, known to involve a network of cortical regions distributed across the frontal and parietal lobes. For example, the so-called “motor-strip” of the precentral gyrus has been established as the source of population-level vector-codes for directed motor plans, with a clearly defined homuncular organization. Directly anterior to this primary motor (M1) region is the premotor cortex, which has been found to be essential to the planning and execution of complex motor directives, as well as the observation and interpretation of motor actions in others (Hanakawa et al., 2008; Rizzolatti et al., 2002). The posterior parietal cortices have also been implicated in goal-directed movements, and are thought to be extremely important in the integration of motor plans with information from stimuli in the visual environment (Desmurget et al., 1999; Hanakawa et al., 2008; Mountcastle et al., 1975).

In addition to these well-studied spatial/anatomical characteristics, the spectral and temporal properties of the neural responses serving movement are becoming increasingly understood. Among the most important spectral features are neural oscillatory responses in the beta (~14 – 30 Hz) and gamma (> 30 Hz) frequency-bands. Decreases in spontaneous beta synchrony from baseline levels typically begin several hundred milliseconds prior to the onset of a movement, and quickly dissipate shortly after the movement is terminated. Thus, this response has been termed the peri-movement beta event-related desynchronization, or beta ERD (Cheyne et al., 2006; Engel and Fries, 2010; Gaetz et al., 2010; Heinrichs-Graham et al., 2018b; Heinrichs-Graham and Wilson, 2015, 2016; Jurkiewicz et al., 2006; Pfurtscheller and Lopes da Silva, 1999; Wilson et al., 2014; Wilson et al., 2013). The beta ERD is most commonly localized to the M1 region contralateral to movement, however robust beta ERDs have also been observed in the ipsilateral M1, parietal areas, premotor cortices, supplementary motor area, and cerebellum (Brovelli et al., 2004; Cheyne et al., 2006; Heinrichs-Graham et al., 2016; Heinrichs-Graham and Wilson, 2015, 2016; Kurz et al., 2014; Wilson et al., 2014; Wilson et al., 2010; Wilson et al., 2011). The function of this response has been a topic of intense study for decades, and relevant research generally supports the notion that the beta ERD is essential for movement planning. For instance, the amplitude of the beta ERD has been found to be altered by cue-related factors (Heinrichs-Graham et al., 2016), movement certainty (Doyle et al., 2005; Kaiser et al., 2001; Tzagarakis et al., 2010) and complexity (Heinrichs-Graham and Wilson, 2015), and the similarity between potential movement options (Grent-’t-Jong et al., 2014; Praamstra et al., 2009). In contrast, oscillatory movement-related gamma synchronizations (MRGS) are commonly reported in the 60 – 90 Hz range, are much more temporally-constrained than their beta-band counterparts, and are almost exclusively located in the contralateral M1 region (Gaetz et al., 2011; Gaetz et al., 2013; Heinrichs-Graham et al., 2018a; Muthukumaraswamy, 2010, 2011; Trevarrow et al., 2019; Wilson et al., 2010). As the name suggests, MRGS responses are also increases in synchrony from baseline levels. Due to its relative spatial and temporal discreteness, the MRGS has long been interpreted as a neural signature of movement execution, however very few studies to date have investigated the potential for this signal to be modulated by “higher-order” task demands, such as cognitive interference.

Cognitive interference occurs when there is a conflict between cognitive representations and task demands, such that behavior is impaired in some measurable way. The two most thoroughly studied subtypes of cognitive interference are conflicts at the stimulus perception (i.e., stimulus-stimulus) and response selection (i.e., stimulus-response) stages. To study these different forms of interference, a number of cognitive tasks have been developed. Among the most established are the Eriksen “flanker” task, where the presence of irrelevant distractor stimuli flanking the target stimulus have been found to impair performance (stimulus-stimulus interference), and the Simon task, where the spatial location of the target stimulus conflicts with the mapping of pre-potent motor responses (stimulus-response interference). In a recent study, we used a novel adaptation of the Multi-Source Interference Task (MSIT; Bush and Shin, 2006; Bush et al., 2003) to investigate the non-motor, “cognitive-perceptual” neural responses that index the divergent effects (i.e., subtype-specific) of cognitive interference (Wiesman and Wilson, 2019b), and found that alpha and gamma-frequency oscillations in posterior visual and parietal cortices dissociably code for Flanker and Simon interference subtypes. Surprisingly, we also found that gamma oscillations in the left superior parietal cortex covaried robustly with the superadditive effects of cognitive interference on behavior, indicating that both subtypes of interference taxed this region considerably.

Despite a substantial literature exploring the effects of cognitive interference on non-motor neural dynamics (Bush and Shin, 2006; Frühholz et al., 2011; González-Villar and Carrillo-de-la-Penñ, 2017; Hanslmayr et al., 2008; Liu et al., 2004; McDermott et al., 2017; Peterson et al., 2002; van Veen and Carter, 2002; Wiesman and Wilson, 2019a, b; Zhu et al., 2010), very little research has examined the impact of such interference on the neural dynamics of movement. Further, only three studies to date have examined the effects of cognitive interference on the oscillatory neural responses that are known to serve motor function. Two of these studies (Grent-’t-Jong et al., 2013; Heinrichs-Graham et al., 2018a) examined the effects of stimulus-stimulus interference on the beta ERD and MRGS using a flanker task, and both found that the amplitude of the beta ERD was greater on trials with greater cognitive interference. Interestingly, regarding the MRGS, one found a modulation of only the amplitude of this response (Grent-’t-Jong et al., 2013), while the other found only a modulation of the peak frequency (Heinrichs-Graham et al., 2018a). However, this discrepancy is likely accounted for by the fact that the first study did not examine peak frequency, nor fully account for the potential influence of differences in reaction time (RT) between task conditions on the MRGS amplitude. A third study (Gaetz et al., 2013) used the classical version of the established MSIT to investigate the influence of subtype-nonspecific cognitive interference on the MRGS. Although this study found a modulation of the MRGS amplitude by cognitive interference load, like (Grent-’t-Jong et al., 2013) they did not account for the potential confounding influence of reaction time differences by condition. While all three of these studies provided essential information regarding the effects of cognitive interference on motor-related oscillatory dynamics, it remains uncertain how different subtypes of interference might play a role. It may be the case that differing subtypes of cognitive interference influence motor oscillations differentially, which would provide important and novel information regarding the functional significance of these neural responses. Alternatively, it seems equally likely that the interference subtypes will not differentially affect these motor oscillations, signifying that these neural responses are affected by cognitive interference in general, but are subtype invariant. Finally, since the previous studies examined either only one subtype of interference in isolation (Grent-’t-Jong et al., 2013; Heinrichs-Graham et al., 2018a), or two subtypes presented simultaneously (Gaetz et al., 2013), the potential for divergent and superadditive effects of cognitive interference subtypes on these neural dynamics remains uncertain, as such effects could not be examined given the task design in these previous investigations.

In the current study, we use magnetoencephalography (MEG) to investigate the potential for divergent and superadditive effects of cognitive interference on the neural dynamics supporting movement; namely the beta ERD and MRGS responses. Towards this goal, we have developed a novel adaptation of the MSIT (Figure 1; see also Bush and Shin, 2006; Bush et al., 2003) that consists of four trial conditions including Flanker (stimulus-stimulus), Simon (stimulus-response), and Multi-Source (combined stimulus-stimulus and stimulus-response) interference, as well as a control (no interference) condition. We hypothesized that increased interference would lead to enhanced beta ERD responses in key motor regions, aligning with previous studies on this topic. Although the stimulus-response subtype might be expected to preferentially interfere with motor oscillations, previous reports have found that stimulus-stimulus interference also affects these neural responses robustly. Thus, we did not have specific hypotheses regarding whether differing subtypes of interference would differentially impact this response. However, given our previous findings (Wiesman and Wilson, 2019b), we did expect that superadditive effects of Multi-Source interference would manifest in the form of an increased MRGS.

Figure 1. Experimental paradigm.

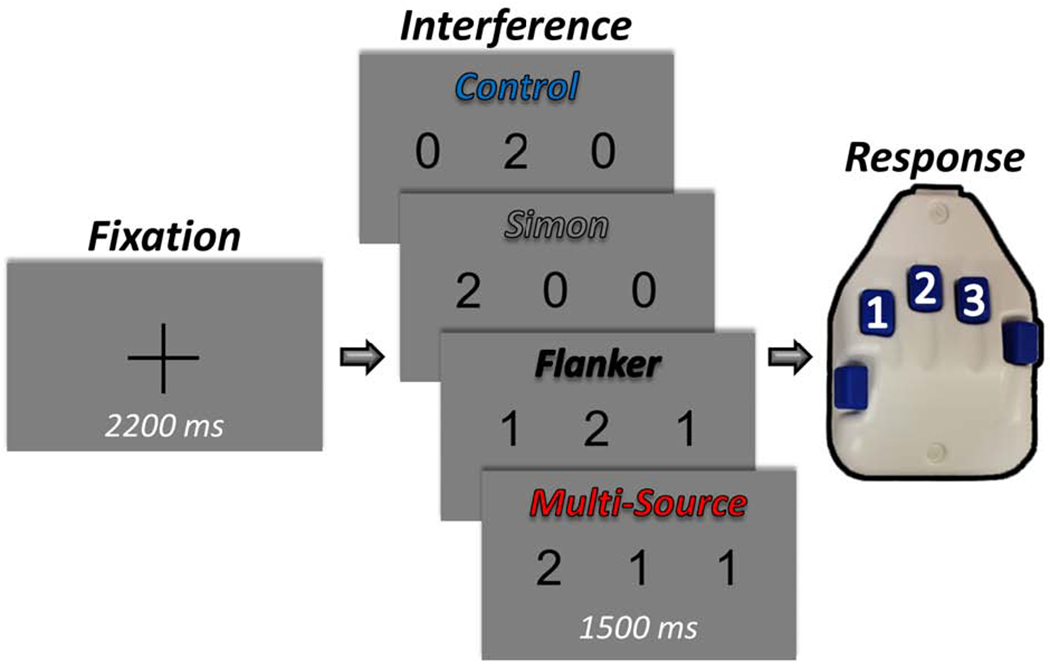
Each trial started with a central fixation cross presented for an interstimulus interval of 2000-2400 ms. A row of three equally-spaced integers between 0 and 3 then replaced the fixation, and these stimuli were presented for 1500 ms. Two of the number stimuli were always identical (task-irrelevant), and the third unique to that trial (task-relevant). Participants were given a five-finger button pad and instructed that the index, middle, and ring finger locations represented the integers 1, 2, and 3, respectively. Participants were instructed that on each trial they would be presented with a row of three integers, and that the objective was to indicate the “odd-number-out” by pressing the button corresponding to its numerical identity (and not its spatial location). Using these stimuli, four interference conditions were possible: (1) Control (no interference), (2) Simon (stimulus-response interference), (3) Flanker (stimulus-stimulus interference), and (4) Multi-Source.

2. Materials and Methods

It should be noted that this study is a comprehensive re-analysis of data reported in a previous manuscript (Wiesman and Wilson, 2019b). Importantly, the nature of the behavioral and MEG data analyses differs substantially, and none of the neural responses reported here were included in the previous report. In the current study, we investigated the effects of cognitive interference on the brain responses which were time-locked to the motor response, rather than those locked to the visual stimulus that were the focus of the previous study.

2.1. Participants

Twenty-three healthy young adults were recruited (M_age = 26.09; age range: 20–33 years; 16 males; 21 right-handed). Exclusion criteria included any medical illness affecting CNS function, any neurological or psychiatric disorder, history of head trauma, current substance abuse, and any non-removable metal implants that would adversely affect MEG data acquisition. All participants had normal or corrected-to-normal vision. The Institutional Review Board at the University of Nebraska Medical Center reviewed and approved this investigation. Written informed consent was obtained from each participant following detailed description of the study. All participants completed the same experimental protocol.

2.2. MEG Experimental Paradigm and Behavioral Data Analysis

We used a modified version of the MSIT (Wiesman and Wilson, 2019b) to engage cognitive interference networks (Figure 1). Briefly, each trial started with a central fixation cross presented for an interstimulus interval of 2000-2400 ms that was randomly-varied across trials. A vertically-centered row of three equally-spaced integers from 0 to 3 then replaced the fixation, and these stimuli were presented for 1500 ms. Two of the number stimuli were always identical (task-irrelevant), and the third unique to that trial (task-relevant). Prior to beginning the experiment, participants were given a five-finger button pad and instructed that the index, middle, and ring finger locations represented the integers 1, 2, and 3, respectively. Participants were then instructed that on each trial they would be presented with a horizontal row of three integers, and that the objective was to indicate the “odd-number-out” by pressing the button corresponding to its numerical identity (and not its spatial location). Speed and accuracy were also stressed to the participant at this point. Using these stimuli, four interference conditions were possible: (1) Control (no interference; e.g., 0 2 0), (2) Simon (stimulus-response interference; e.g., 2 0 0), (3) Flanker (stimulus-stimulus interference; e.g., 1 2 1), and (4) Multi-Source (e.g., 2 1 1). Trial types and responses were pseudo-randomized over the course of the experiment, such that no interference condition nor any response was repeated more than twice in a row. Participants completed 100 trials of each interference condition, for a grand total of 400 trials, and a total recording time of ~24 minutes. Custom visual stimuli were programmed in Matlab (Mathworks, Inc., Massachusetts, USA) using Psychophysics Toolbox Version 3 (Brainard, 1997) and back-projected onto a nonmagnetic screen. For each participant, accuracy data were computed as a percentage (correct/total trials). Reaction time (RT) data were also extracted for each individual trial and incorrect and noresponse trials were removed. As noted above, our analysis of the RT data differed from the previous report (Wiesman and Wilson, 2019b) in important ways. First, outliers were excluded based on a standard threshold of ± 2.5 standard deviations from the mean, and subsequently mean RT values were computed for each participant. No such outlier exclusion was performed in the previous manuscript and harmonic means were used for the main RT analyses in this previous report. These metrics (i.e., accuracy and RT) were analyzed for main effects of interference condition using two four-way repeated measures ANOVAs, implemented in JASP (2018). We next tested for superadditive effects of Multi-Source cognitive interference on behavior. To this end, we first computed the interference effect of each interference condition within each participant (i.e., the Flanker, Simon, and Multi-Source conditions) by subtracting each behavioral metric in the Control condition from the same metric in each condition (e.g., Simon RT - Control RT). From this, we were left with participant-level accuracy and RT values reflecting the difference in task performance caused by each type of interference. To test for superadditivity, we computed paired-samples t-tests separately for accuracy and RT between the Multi-Source interference condition and the summed effects of interference from the Simon and Flanker conditions, added within each participant. Using these tests, a rejection of the null hypothesis would indicate that the simultaneous presentation of two interference types (Multi-Source) affects task performance at a different magnitude than what would be expected by an additive model (Simon + Flanker).

2.3. MEG Data Acquisition

All recordings were conducted in a one-layer magnetically-shielded room with active shielding engaged for environmental noise compensation. Neuromagnetic responses were sampled continuously at 1 kHz with an acquisition bandwidth of 0.1– 330 Hz using a 306-sensor Elekta MEG system (Helsinki, Finland) equipped with 204 planar gradiometers and 102 magnetometers. Participants were monitored during data acquisition via real-time audio-video feeds from inside the shielded room. Each MEG dataset was individually corrected for head motion and subjected to noise reduction using the signal space separation method with a temporal extension (i.e., tSSS; Taulu and Simola, 2006).

2.4. Structural MRI Processing and MEG Coregistration

Preceding MEG measurement, four coils were attached to the participant’s head and localized, together with the three fiducial points and scalp surface, using a 3-D digitizer (Fastrak 3SF0002, Polhemus Navigator Sciences, Colchester, VT, USA). Once the participant was positioned for MEG recording, an electric current with a unique frequency label (e.g., 322 Hz) was fed to each of the coils. This induced a measurable magnetic field and allowed each coil to be localized in reference to the sensors throughout the recording session. Since coil locations were also known in head coordinates, all MEG measurements could be transformed into a common coordinate system. With this coordinate system, each participant’s MEG data were co-registered with individual structural T1-weighted MRI data (N = 13), where available, or alternatively were fitted to a template MRI (N = 10) using the scalp surface points, in BESA MRI (Version 2.0) prior to source-space analysis. Importantly, these two approaches have been shown to yield very similar results (Holliday et al., 2003). Further, none of our key neural metrics (i.e., the beta ERD responses from the repeated measures ANOVAs and the left premotor MRGS response from the superadditivity analysis) significantly differed according to whether a template or individual MRI was used (beta L-M1: p = .164; beta R-M1: p = .253; beta L-PPC: p = .970; beta R-PPC: p = .561; gamma L-premotor: p = .936). Moreover, all of our relevant statistical contrasts were within-subjects, which further mitigates concerns about any of our results being driven by a systematic bias between coregistration methods.

Individual structural T1-weighted data was acquired using either a Siemens Skyra 3T MRI scanner with a 32 channel head coil and a MP-RAGE sequence (TR = 2400 ms; TE = 1.94 ms; flip angle = 8°; FOV = 256 mm; slice thickness = 1mm (no gap); voxel size = 1 x 1 x 1 mm) or a Philips Achieva 3T X-series scanner using an eight-channel head coil and a 3D fast-field echo sequence (TR = 8.09 ms; TE = 3.70 ms; FOV = 240 mm; slice thickness = 1mm (no gap); in-plane resolution: 1 x 1 mm). Again, the use of different MR-scanners was of little consequence in this study since (1) these structural images were only used to co-register and warp the functional data (i.e., source-imaged MEG) into a standardized space, and (2) all relevant statistical contrasts were performed within-subjects, mitigating any concern that our results could be driven by co-registration differences between subjects. Structural MRI data were aligned parallel to the anterior and posterior commissures and transformed into standardized space. Following source analysis (i.e., beamforming), each participant’s 4.0 x 4.0 x 4.0 mm source-level MEG images were also transformed into standardized space and spatially resampled.

2.5. MEG Preprocessing, Time-Frequency Transformation, and Sensor-Level Statistics

Cardiac and ocular artifacts were removed from the data using signal-space projection (SSP), and the projection operator was subsequently accounted for during source reconstruction (Uusitalo and Ilmoniemi, 1997). The continuous magnetic time series was then divided into 3500 ms epochs, with the baseline extending from −1600 to −1100 ms prior to movement onset (i.e., button press). Importantly, this time window always fell within the visual fixation period, and thus our results were not biased by visual differences in the baseline period. Epochs containing artifacts were rejected using a fixed threshold method, supplemented with visual inspection. An average of 345.52 (SD = 12.71) trials per participant were used for further analysis. The number of accepted trials did not differ across the four conditions (p > .90).

The artifact-free epochs were next transformed into the time-frequency domain using complex demodulation (Kovach and Gander, 2016), with a frequency range of 4 to 100 Hz, and a time-frequency resolution of 2 Hz/25 ms. The resulting spectral power estimations per sensor were then averaged over trials to generate time-frequency plots of mean spectral density. These sensor-level data were normalized by each respective bin’s baseline power, which was calculated as the mean power during the −1600 to −1100 ms time period. The specific time-frequency windows used for subsequent source imaging were determined by statistical analysis of the sensor-level spectrograms across all conditions and the entire array of gradiometers. Each data point in the spectrogram was initially evaluated using a mass univariate approach based on the general linear model. To reduce the risk of false positive results while maintaining reasonable sensitivity, a two stage procedure was followed to control for Type 1 error. In the first stage, paired-sample t-tests against baseline were conducted on each data point and the output spectrogram of t-values was thresholded at p < 0.05 to define time-frequency bins containing potentially significant oscillatory deviations across all participants. In stage two, the time-frequency bins that survived the threshold were clustered with temporally and/or spectrally neighboring bins that were also above the threshold (p < 0.05), and a cluster value was derived by summing all of the t-values of all data points in the cluster. Nonparametric permutation testing was then used to derive a distribution of cluster-values and the significance level of the observed clusters (from stage one) were tested directly using this distribution (Ernst, 2004; Maris and Oostenveld, 2007). For each comparison, at least 1,000 permutations were computed to build a distribution of cluster values. Based on these analyses, the time-frequency windows that contained significant oscillatory events across all participants were subjected to a beamforming analysis.

2.6. MEG Source Imaging and Statistics

Cortical oscillatory activity was imaged using dynamic imaging of coherence sources (DICS; Gross et al., 2001), which applies spatial filters to time-frequency sensor data in order to calculate voxel-wise source power for the entire brain volume. The single images are derived from the cross spectral densities of all combinations of MEG gradiometers averaged over the time-frequency range of interest, and the solution of the forward problem for each location on a 4.0 x 4.0 x 4.0 mm grid specified by input voxel space. Following convention, we computed noise-normalized, source power per voxel in each participant using active (i.e., task) and passive (i.e., baseline) periods of equal duration and bandwidth. Such images are typically referred to as pseudo-t maps, with units (pseudo-t) that reflect noise-normalized power differences (i.e., active vs. passive) per voxel. This generated participant-level pseudo-t maps for each time-frequency-specific response identified in the sensor-level cluster-based permutation analysis. MEG pre-processing (including artifact rejection, SSP of cardiac and ocular artifacts, and data epoching), time frequency analysis, and imaging used the Brain Electrical Source Analysis (BESA version 6.1) software.

To initially investigate the spatial location of each time-frequency-specific neural response to the task, we computed grand-average maps for each, collapsing across all interference conditions. These grand-average maps were used to discern the nature of each response, and thus ensure that all responses used for further analysis were of a motor origin. Again, this differed substantially from the previous analysis of these data (Wiesman and Wilson, 2019b), wherein only neural responses to the visual stimulus were considered. Importantly, we focus our interpretation here on those statistical effects that occurred in motor-related cortical regions, as this was where our neural responses of interest (i.e., the beta ERD and MRGS) were most robust. However, for the sake of transparency, we also report the location and statistical parameters for all effects outside of motor regions in the supplementary material (Table S1). To examine interference-related differences in frequency-specific neural activity, we then computed whole-brain repeated-measures ANOVAs for each time-frequency response of interest (beta and gamma). From the resulting significant clusters, pseudo-t values per participant were extracted from the peak voxel of each cluster, and these were used in post-hoc testing. Post-hoc testing consisted of two levels. First, we performed paired-samples t-tests between conditions on data from regions exhibiting a significant ANOVA effect, in order to better interpret the directionality and statistical significance of these effects. Next, to better understand the relative evidence for our effects, including those that did not meet the traditional criteria for rejecting the null hypothesis (i.e., p < .05), we computed Bayesian t-tests between these conditions to examine whether they presented evidence for or against the null hypothesis. Briefly, as opposed to a frequentist statistical approach, where one simply rejects or fails to reject the null hypothesis using arbitrary cutoffs (i.e., p–values), Bayes Factors (BF₁₀) represent the likelihood of the alternative hypothesis producing the same observed pattern in the data as compared to the null hypothesis, and thereby facilitates the interpretation of effects that seem to support the null hypothesis (rather than simply fail to reject it).

Finally, we computed whole-brain statistical maps investigating the potential for superadditivity of Multi-Source interference on the neural dynamics, similar to the comparisons made to test for superadditivity in the behavioral metrics (see above). For this analysis, we first performed a voxel-wise subtraction of the control condition map from each of the three interference condition maps for each participant per time-frequency component (i.e., beta and gamma). This produced participant-level whole-brain interference effect maps for each of the Simon, Flanker, and Multi-Source conditions. We then summed the voxel-wise values of the Simon and Flanker interference effect maps to produce a whole-brain map (per participant, per neural response), which represented the null hypothesis of an additive model. To then test the potential for superadditivity statistically, whole-brain paired-samples t-tests were computed between the Multi-Source interference model maps and these additive-model maps. It is important to note that these tests were performed one-tailed, since a two-tailed test would also investigate significant sub-additive effects, and such an analysis was not justified by the behavioral data. The end result of this analysis was two spectrally-defined (i.e., one beta and one gamma) whole-brain statistical maps showing the cortical regions that exhibited a significantly larger interference effect in the Multi-Source condition than what would be expected from the additive model (H₁: Multi-Source > Simon+Flanker). Once again, pseudo-t values per participant were extracted from the peak voxel of each cluster in these maps for further testing. To account for multiple comparisons, a significance threshold of p < .01 was used for the identification of significant clusters in all whole-brain statistical maps, accompanied with a cluster (k) threshold of at least 200 contiguous voxels. Additionally, to increase rigor, second-level multiple comparison corrections were also performed on the whole-brain images using a much more stringent cluster-based permutation procedure, similar to the one described in Section 2.5 (initial threshold: p = .01, 10,000 permutations). Importantly, as this second-level correction was relatively stringent, we opt to still report those effects that only survived the first-level correction, albeit with diminished confidence in their robustness.

3. Results

3.1. Spectral, Temporal, and Spatial Definitions of Neural Responses to the Task

Prior to testing for main effects of cognitive interference, we first needed to determine the temporal, spectral, and spatial locations of motor-related neural responses to the task, regardless of condition. We first transformed the data into time-frequency space, and observed robust neural activity in the beta and gamma bands (Figure 2) in sensors near the sensorimotor cortices. Specifically, a significant desynchronization was observed in the beta band (18 – 26 Hz) from 400 ms before movement to 100 ms after movement onset. In addition, we observed a significant synchronization from baseline in the gamma band (64 – 84 Hz) beginning 200 ms before movement and persisting until 100 ms after movement. Note that we did not image the post-movement beta rebound response (red area in top spectrogram) for two reasons. First, this task was ill-designed to investigate interference effects on this response, as the temporal offset of the visual stimuli occurred during the response and varied trial-to-trial due to variation in RT. Second, this response occurred well after movement and we were primarily interested in interference effects on the planning and execution of movement.

Figure 2. Spectral, temporal, and spatial definitions of oscillatory motor responses.

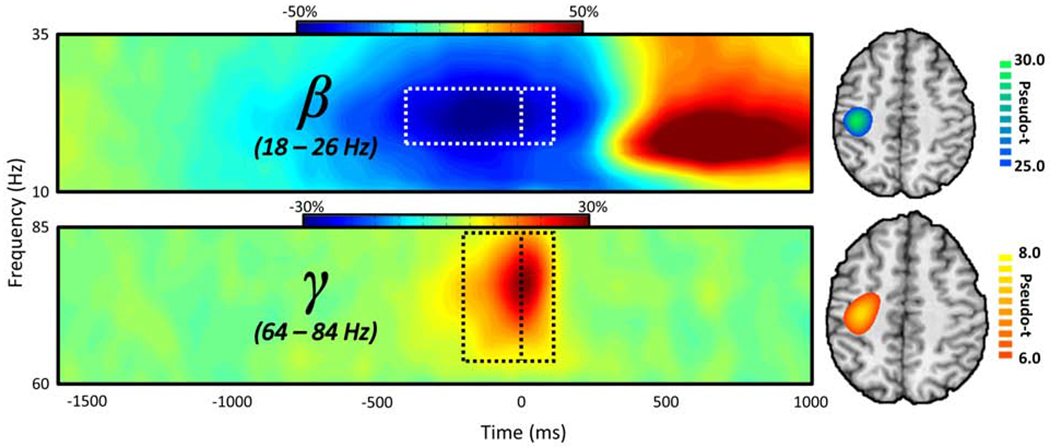
The representative MEG sensor-level spectrograms (left; beta – M0442; gamma – M0432) display the time-frequency representations of neural responses identified by cluster-based permutation analysis (see Methods). Time (in ms) is denoted on the x-axis, frequency (in Hz) is denoted on the y-axis, and the dashed line at 0 ms indicates the motor response. The dashed rectangle surrounding this line indicates the time-frequency definitions identified for source imaging by the cluster-based permutation test. The color scale bar for percent change from baseline is displayed above each plot. Each spectrogram represents group-averaged data from one gradiometer sensor that was representative of the neural responses in sensors over somato-motor regions. On the far right is the source-imaged representation of each response (beta ERD and MRGS), with the color scale bar to the right denoting response amplitude in pseudo-t units.

3.2. Effects of Cognitive Interference on Task Performance

Behavioral results from this study have been reported in a previous publication (Wiesman and Wilson, 2019b), but note that we fully reanalyzed these data using a substantially different approach that is described in the methods section. Briefly, participants performed well on the task, with a mean accuracy of 96.49% (SD = 2.29%) and a mean reaction time (RT) of 739.32 ms (SD = 116.80 ms). Repeated-measures ANOVAs revealed a significant effect of interference condition on both accuracy (F(3,66) = 22.37, p < .001) and RT (F(3,66) = 195.10, p < .001; Figure 3). Post-hoc comparisons for accuracy revealed that participants were significantly less accurate in the Simon (t(22) = −4.56, p < .001) and Multi-Source (t(22) = −5.43, p < .001) conditions than in the Control condition. Further, participants were significantly less accurate in the Multi-Source condition than both the Simon (t(22) = −2.60, p = .016) and Flanker (t(22) = −6.49, p < .001) conditions. Finally, participants were significantly less accurate in the Simon condition compared to the Flanker condition (t(22) = −4.53, p < .001). The results of the post-hoc comparisons for RT were generally similar to the accuracy results. Participants were significantly slower to respond on the Simon (t(22) = 10.32, p < .001), Flanker (t(22) = 15.53, p < .001), and Multi-Source (t(22) = 19.52, p < .001) trials relative to the Control trials. Further, participants were significantly slower in the Multi-Source condition than both the Simon (t(22) = 15.61, p < .001) and Flanker (t(22) = 10.50, p < .001) conditions. Interestingly, and in contrast to the accuracy results, participants performed significantly worse on Flanker than Simon trials (t(22) = 4.34, p < .001).

Figure 3. Effects of cognitive interference on behavior.

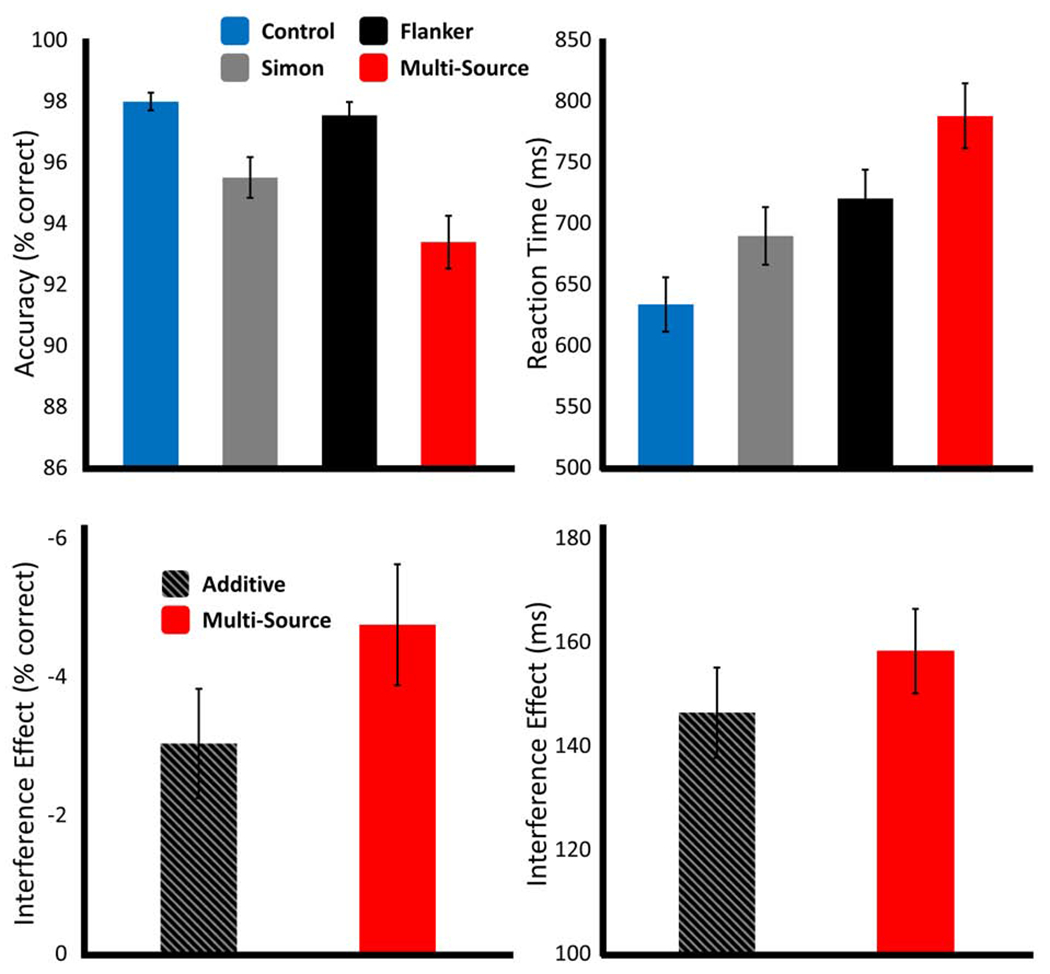
Results from the behavioral analyses, with data for the main effect of interference condition (top), and for the superadditivity analyses (bottom). Bar graphs represent the mean per condition for accuracy (left; % correct) and reaction time (right; ms), with error bars representing the standard error of the mean (SEM).

Upon visual inspection of these data, it became apparent that a superadditive effect of Multi Source interference on task performance was likely. Indeed, paired-samples t-tests between the effect of Multi-Source interference and the additive model (Simon interference + Flanker interference) were significant for both accuracy (t(22) = −2.25, p = .035) and RT (t(22) = 2.13, p = .044), such that the concurrent presentation of the two interference sources significantly worsened behavior, as compared to their additive effects in isolation (Figure 3). Note that despite the significant differences in analytical approaches, a similar superadditive effect was also observed for the RT data (but not the accuracy data) in Wiesman and Wilson (2019b).

3.3. Motor-related Neural Oscillations are Modulated by Cognitive Interference Irrespective of Subtype

To investigate potentially-divergent effects of cognitive interference subtypes on motor-related oscillatory neural dynamics, we computed whole-brain repeated measures ANOVAs for the beta ERD and MRGS participant-level response maps separately. For the beta ERD, a robust main effect of condition was observed across four well-established motor-network regions, including peaks in bilateral M1 and bilateral posterior parietal cortex (PPC; Figure 4). This distributed effect was robust, surviving stringent multiple comparisons correction at the right PPC and M1 (p < .001) and left PPC (p = .003), but not the left M1. Post-hoc testing revealed that beta activity in all four of these regions generally exhibited the same direction of effect. With the exception of the Simon condition in the left M1 peak, where the effect was trending, beta suppression in response to the interference conditions was significantly higher than in the control condition (all p’s < .05), but did not significantly differ between interference conditions (all p’s > .05). For the MRGS, no significant ANOVA effects were found within the canonical motor network. We next computed Bayesian post-hoc analysis on the beta ERD interference data to examine whether there was greater evidence for or against the null hypothesis of no significant difference by interference condition (i.e., H₀: Simon = Flanker = Multi-Source). In every case, this analysis suggested greater evidence for the null hypothesis than the alternative hypothesis (i.e., a difference in beta ERD amplitude between interference conditions), although the strength of this evidence only reached what would typically be considered as mild to moderate (see Table S2 for full results of the Bayesian post-hoc analysis). It should be noted that beta ERD ANOVA effects were also observed in the right cerebellum, right dorsolateral prefrontal, and left supramarginal cortices, and in the right superior parietal cortex for the MRGS analysis. However, the overall response amplitude in these regions was negligible, and thus we do not focus our interpretation on these effects. Further, out of all of these regions, only the right dorsolateral prefrontal beta ERD peak survived multiple comparisons correction (p = .003). Regardless, for the sake of transparency, comprehensive post-hoc results for all significant regions are reported in Table S1.

Figure 4. Effects of cognitive interference on the beta ERD.

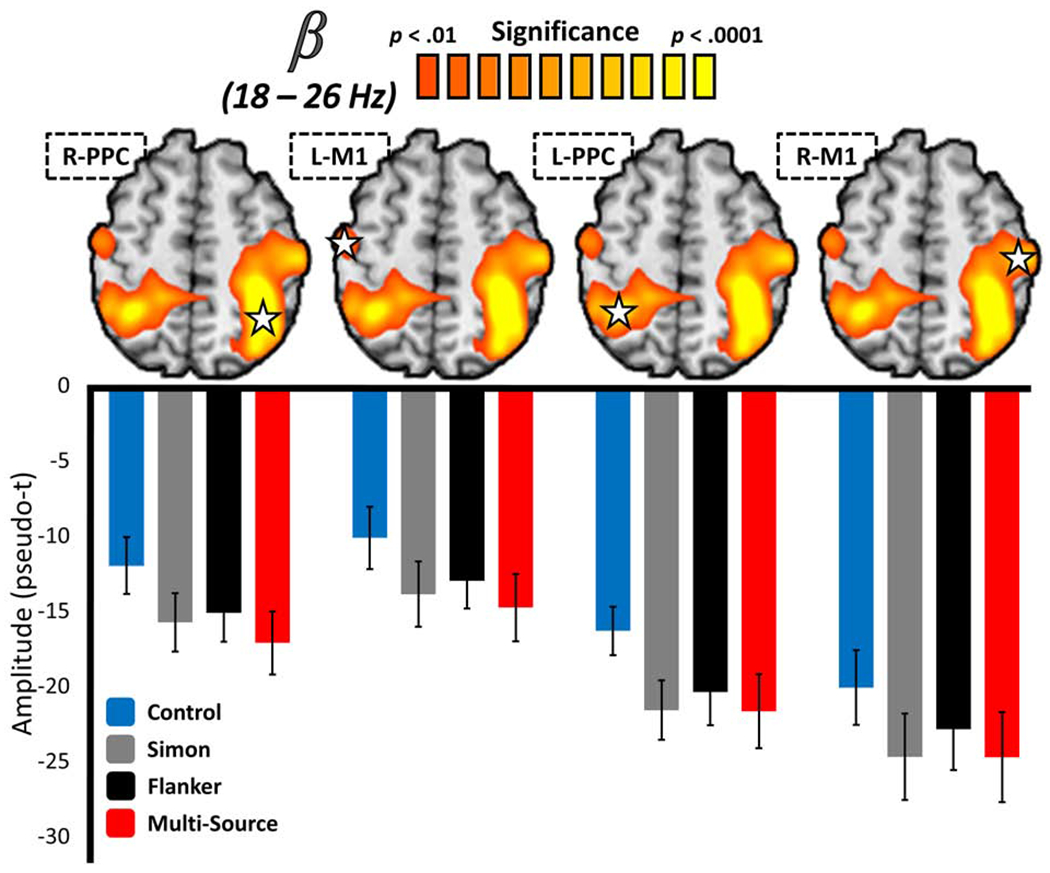
Functional images (above) reflect the significant results of a whole-brain repeated-measures ANOVA testing for a main effect of interference condition on the beta ERD response, with the color scale bar at the top denoting voxel-wise significance. Below each image are the average response amplitude values (in pseudo-t) for the peak voxel (star) in the cluster per interference condition, with error bars denoting SEM. In virtually all cases, beta ERD responses were significantly stronger in interference conditions than the control condition, but did not differ amongst interference conditions. The functional image in (D) displays the significant results of a whole-brain statistical test for superadditivity in the motor-related gamma synchronization, with the color scale bar at the top again representing voxel-wise significance. The bar graph below represents the average response amplitude values (in pseudo-t) for the peak superadditive voxel per interference condition, with error bars denoting SEM. The scatterplot to the right represents the relationship between response amplitude values extracted from the peak voxel of the whole-brain statistical superadditivity image to the left (x-axis; pseudo-t), and the superadditive effect of cognitive interference on task accuracy (y-axis; Multi-Source/Additive). A line of best-fit has been overlaid on the plot, along with the correlation coefficient for the relationship.

3.4. The MRGS Indexes Interference Superadditivity in Premotor Cortex

Next, we examined the source of the superadditive effects of Multi-Source interference previously observed on behavior by computing whole-brain superadditivity statistical comparisons for the beta ERD and MRGS responses. Briefly, superadditivity suggests that the interference effects of the Simon and Flanker subtypes are greater when they are presented concurrently, as compared to when they are presented individually, and indicates shared neural resources between cognitive processes. To test where these shared neural resources reside, we computed whole-brain maps of the additive model (i.e., whole-brain Simon interference + whole-brain Flanker interference) and tested these against whole-brain maps of the Multi-Source interference effect. Only the MRGS response exhibited a superadditive effect of cognitive interference, and this effect was spatially constrained to the premotor cortex contralateral to movement (Figure 5), although it did not survive our stringent cluster-based permutation testing approach to multiple comparisons correction. Supporting the association between movement-related gamma oscillations in this region and the superadditive effect on behavior, MRGS amplitude values extracted from the peak voxel of this cluster significantly covaried with the superadditive effect on accuracy (r = .40; p = .036, one-tailed). In other words, participants with greater MRGS responses in the premotor cortex tended to exhibit a greater superadditive effect on accuracy. No significant superadditive effects were observed on the beta ERD.

Figure 5. Superadditive effects of interference subtypes on the MRGS.

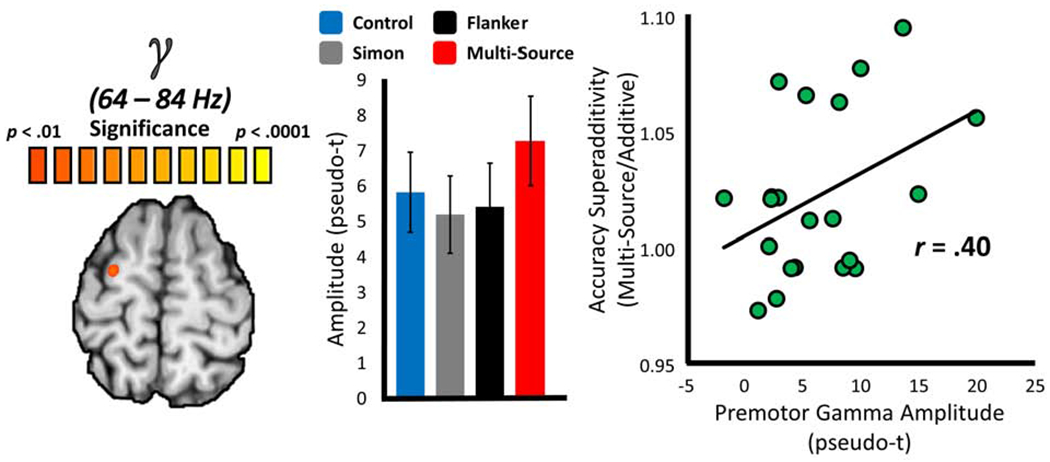
The functional image to the far left displays the results of a whole-brain statistical test for superadditivity in the motor-related gamma synchronization (MRGS), with the color scale bar at the top representing voxel-wise significance. The bar graph (middle) represents the average response amplitude values (in pseudo-t) for the peak superadditive voxel per interference condition, with error bars denoting SEM. The scatterplot to the right represents the relationship between response amplitude values extracted from the peak voxel of the whole-brain statistical superadditivity image to the left (x-axis; pseudo-t), and the superadditive effect of cognitive interference on task accuracy (y-axis; Multi-Source/Additive). A line of best-fit has been overlaid on the plot, along with the correlation coefficient for the relationship.

4. Discussion

This study is a comprehensive re-analysis of the data previously reported in (Wiesman and Wilson, 2019b). Importantly, although the underlying neural recordings and behavioral data remain the same, the nature of the data analysis is completely different, including both behavioral and MEG components, and none of the neural responses reported here were included in the previous report. Essentially, the brain responses investigated in the current study are time-locked to the motor response rather than the visual stimulus, as was the case in the previous study, and thus reflect motor-related versus stimulus/cognitive related processing. Our approach to the behavioral analysis also differed from Wiesman and Wilson (2019b). More explicitly, we take a different, arguably more intuitive, approach to analysis of the accuracy and reaction time data in this manuscript, leading to complementary new findings in the current report. Finally, the a priori hypotheses and conceptual basis for this study also differ substantially from those of our previous work.

Using MEG and a novel adaptation of an established cognitive interference task, we probed the potential for divergent and superadditive effects of two subtypes of cognitive interference on the oscillatory neural dynamics supporting a simple movement (i.e., a button press). Our primary findings were twofold: (1) a robust, but not subtype-specific nor compounding effect of cognitive interference on the beta ERD and (2) a more subtle superadditive effect of simultaneously-presented cognitive interference subtypes on the MRGS in premotor cortex. Below we discuss the significance and implications of these findings, as they relate to the established literature regarding oscillatory neural dynamics in the human motor system.

Our finding of a main effect of interference conditions on the beta ERD in M1 is not particularly surprising, as this has been the focus of, and consensus among, two previous studies on the topic (Grent-’t-Jong et al., 2013; Heinrichs-Graham et al., 2018a). What is perhaps surprising though, is both the spatial profile and nature of this effect. Firstly, our finding of an increased beta ERD with increased interference was located not only within bilateral M1 cortices (as has been found previously), but also across bilateral PPC. In fact, of these beta ERD responses, both of the bilateral PPC effects survived stringent cluster-based permutation correction, while only the right-lateralized peak in the bilateral M1 effect survived such a correction. No previous studies investigating the effects of cognitive interference on motor oscillations have reported such an effect in the PPC, however, this is likely attributable to the fact that neither of the previous studies in this area performed whole-brain statistical measures at the level of the cortex (Grent-’t-Jong et al., 2013; Heinrichs-Graham et al., 2018a). This finding is especially pertinent, as the PPC has been implicated in the integration of motor plans and visual information from the environment (Desmurget et al., 1999; Hanakawa et al., 2008; Mountcastle et al., 1975), and the beta ERD in this region has specifically been found to be modulated by the complexity of the to-be-executed motor plan in a task utilizing visual sequence stimuli (Heinrichs-Graham and Wilson, 2015). Tentatively, this finding and others indicate that beta oscillations in the PPC may serve a role in integrating “bottom-up” and “top-down” signals, in the sense that these responses appear to be important for integrating top-down motor control with goal-directed processing of bottom-up visual information. A previous study by Feurra et al. (2011) also supports the concept of a functional distinction between primary motor and posterior parietal cortices. In this study, the authors used non-invasive beta-frequency electrical stimulation over the primary motor and posterior parietal cortices, and show that only stimulation of M1, but not of PPC, altered the amplitude of TMS-induced motor evoked potentials. Secondly, the post-hoc Bayesian analysis of these data indicated that, although the beta ERD did generally increase (i.e., exhibit a greater decrease from baseline) as a function of cognitive interference, there was no difference in the amplitude of the beta ERD as a function of interference subtype. Further, the amplitude of this response also did not significantly vary as to whether these subtypes were presented in isolation or in tandem. This suggests that the beta ERD in these distributed motor regions does not index the additive effects of cognitive interference, but rather a more general conflict between incoming bottom-up visual information and the eventual execution of the appropriate top-down motor response.

As reported previously (Wiesman and Wilson, 2019b), these data exhibited an interesting, albeit surprising, pattern of behavioral results that indicated a superadditive effect of cognitive interference on task performance. To investigate the potential for a spectrally-specific oscillatory neural index of this phenomenon in the motor system, we computed whole-brain superadditivity statistical maps for both the beta ERD and MRGS. Intriguingly, we found that the MRGS, but not the beta ERD, exhibited a superadditivity effect in premotor cortex contralateral to movement, although this effect did not survive stringent cluster-based permutation testing. However, the amplitude of the gamma ERS response at this location was also significantly related to the superadditive effect on accuracy, providing further support for the relevance of this response to motor interference resolution. The premotor cortices have been robustly linked to the planning and execution of complex motor actions (Hanakawa et al., 2008; Rizzolatti et al., 2002); a conceptualization which aligns well with our findings of a compounding effect of cognitive interference in this region. Interestingly, we also found a similar pattern of gamma superadditivity in superior parietal cortices in our previous report (Wiesman and Wilson, 2019b). This suggests that superadditive effects of cognitive interference might be spectrally limited to the gamma range, however this view certainly requires further support. In addition, gamma-frequency activity in frontal cortices are well-supported as being essential for “top-down” control of goal-directed actions (Benchenane et al., 2011; Doesburg et al., 2008; Jensen et al., 2007). Thus, this finding expands upon this literature by showing that frontal gamma signals are also essential for similar top-down control in the context of the resolution of cognitive conflict in the motor system.

A number of previous tasks have found significant relationships between beta-frequency motor oscillations and behavior (Heinrichs-Graham et al., 2018b; Heinrichs-Graham and Wilson, 2016; kühn et al., 2004; Pogosyan et al., 2009), however, we found no such relationship here. Despite this null finding, we can reasonably infer from the direction of our behavioral and beta ERD findings that the well-known pattern of greater beta desynchronizations being related to reduced performance is preserved in this study. In contrast, and as mentioned previously, the amplitude of the premotor gamma frequency response was significantly correlated with accuracy on the task. This relationship was such that, as the gamma amplitude increased, the superadditive effect on accuracy also increased. The direction of this relationship further supports our conceptualization of the gamma premotor oscillations as a top-down control signal, and lends credence to the link between this response and the superadditive effect on behavior.

Although our findings are novel and of major interest, the limitations of this work should also be considered. First, although we modulated the degree of cognitive interference at numerous levels, the motor action being integrated with these interference effects was exceedingly simple (i.e., a button press). Because of this, we were unable to examine the potential for interactive and dissociative effects of varying difficulties of motor complexity with stimulus-stimulus versus stimulus-response interference, which might be particularly interesting in light of our findings of a non-subtype-specific effect of interference on the beta ERD in PPC. Secondly, while our initial frequentist statistical approach showed robust evidence for rejection of the null hypothesis in many cases, our post-hoc Bayesian approach only indicated mild-to-moderate evidence for its acceptance in others. Interestingly, this evidence qualitatively appeared stronger in PPC than in M1 areas, but studies with larger sample sizes might further clarify this finding. Thirdly, as described in the methods, our task design did not allow careful investigation of the impact of cognitive interference on the post movement beta rebound (PMBR) response, and future studies should explore this avenue. Finally, the interactions between the brain regions identified in this study were not investigated, and thus more in-depth functional connectivity studies of this topic would be enlightening.

Despite these limitations, these findings provide compelling new evidence for a nuanced coding of cognitive interference across a distributed and spectrally-specific series of motor regions. This is important for a number of reasons. For example, we establish that, although beta dynamics in the human motor system are affected by cognitive conflict, this influence does not differ as a function of interference subtype. This indicates that, while some portion of previously reported interference effects on behavior are likely due to conflict in the motor system, this cannot account for these effects entirely. More generally, these findings provide further evidence that neural activity at the level of the motor system is a key component in the processing of cognitive conflict in the human brain. In addition, and aligning with our previous investigation (Wiesman and Wilson, 2019b), we find that gamma-frequency activity is specifically impacted by the superposition of distinct subtypes of cognitive interference. This provides a potential target to examine the impacts of competing stimulus inputs in cognitively-taxing environments. By delineating the spectral specificity of these interference effects on motor function (i.e., general interference on beta oscillations and superadditive effects on gamma oscillations), we also provide more precise targets for future studies that might use non-invasive stimulation of motor cortices, with the goal of modulating goal-directed performance in health and disease.

Table 1.

Behavioral means and standard deviations per condition.

	Condition	Mean (SD)
Reaction Time (ms)	All Conditions	739.32 (116.80)
	Control	639.46 (109.52)
	Simon	697.18 (116.13)
	Flanker	728.80 (116.80)
	Multi-Source	798.37 (131.35)
Accuracy (% correct)	All Conditions	96.49 (2.29)
	Control	98.42 (1.42)
	Simon	95.86 (3.28)
	Flanker	97.96 (2.13)
	Multi-Source	93.68 (4.28)

SD: standard deviation.