Abstract
Catalysis in confined spaces, such as those provided by supramolecular cages, is quickly gaining momentum. It allows for second coordination sphere strategies to control the selectivity and activity of transition metal catalysts, beyond the classical methods like fine-tuning the steric and electronic properties of the coordinating ligands. Only a few electrocatalytic reactions within cages have been reported, and there is no information regarding the electron transfer kinetics and thermodynamics of redox-active species encapsulated into supramolecular assemblies. This contribution revolves around the preparation of M6L12 and larger M12L24 (M = Pd or Pt) nanospheres functionalized with different numbers of redox-active probes encapsulated within their cavity, either in a covalent fashion via different types of linkers (flexible, rigid and conjugated or rigid and nonconjugated) or by supramolecular hydrogen bonding interactions. The redox probes can be addressed by electrochemical electron transfer across the rim of nanospheres, and the thermodynamics and kinetics of this process are described. Our study identifies that the linker type and the number of redox probes within the cage are useful handles to fine-tune the electron transfer rates, paving the way for the encapsulation of electroactive catalysts and electrocatalytic applications of such supramolecular assemblies.
Introduction
Catalytic transformations are essential for the preparation of chemicals and materials in a sustainable manner.1−3 Although homogeneous catalysis is a well-developed field, many challenges still remain.4 In general, control over the selectivity, stability, and activity of the catalyst are key parameters to consider.5 The selectivity and activity of molecular catalysts can be optimized by fine-tuning the electronic and steric properties of the ligands coordinated to the metal center. As a result, catalyst development to date has been dominated by the design and synthesis of sophisticated novel and increasingly complex ligands. More recently, the field of cage catalysis has proven its potential to control crucial catalyst parameters.5−12 Indeed, it has been demonstrated that molecular catalysts encapsulated in supramolecular cages display novel selectivity in several reactions, affording products that are inaccessible by conventional methods. Other potential positive cage effects include (i) higher stability of encapsulated catalysts vs. species in bulk solvent and (ii) enhanced reaction rates due to local environment effects and substrate preorganization.13−21
Cage catalysis is now rapidly developing and many examples spanning a wide variety of catalytic transformations can be found in literature.6−8 Chief among these are palladium catalyzed reactions, hydrolysis reactions, SN2 reactions, rearrangement reactions, and photochemical reactions.14,21−24 Interestingly, so far, there are only a few reports of catalytic redox reactions in supramolecular cages.25,26 Furthermore, little is known about the feasibility of heterogeneous electron transfer from an electrode to a redox-active species encapsulated by a supramolecular cage. The few reported examples concern small supramolecular assemblies where the redox probe is readily accessible or in close proximity to the electrode surface so that direct electron transfer is possible.27−29 Similarly, the reported redox-active cages are supramolecular assemblies where the outer shell of the cage is functionalized with redox probes or the building blocks themselves are redox-active.27,30,31 In this contribution, we explore the redox-chemistry of supramolecular M6L12 and M12L24 cages with different redox-active moieties in their interior. Detailed electrochemical studies allow the evaluation of the thermodynamics and kinetics of electron transfer from the electrode to the electrochemical probes inside the spheres. We evaluate the effect of the linker between the probe and the rims of the cage by using (i) a ferrocene (Fc) moiety covalently attached to a ditopic bis(pyridine) building block through a flexible linker (Figure 2, FcBB A); (ii) a tetrathiafulvalene (TTF) moiety covalently attached to a planar and fully conjugated bis(pyridine) building block, resembling the structure of a molecular wire (Figure 2, TTFBB B); (iii) a TTF-containing bis(pyridine) building block featuring a biphenyl moiety with a built-in 90° twist between two adjacent aromatic rings to break the conjugation of the structure (Figure 2, twistedTTFBB C), and (iv) using supramolecularly encapsulated ferrocenyl sulfonate redox probes that are encapsulated via hydrogen bonding interactions to guanidinium functionalities20 present in the interior of a supramolecular cage (Figure 2, D). Furthermore, as shown in Figure 3, the redox probe concentration in the cage interior is modulated by using a mixture of unfunctionalized building block BBH E and redox-probe-functionalized derivatives, i.e., FcBB A or TTFBB B. We show that the rates of electron transfer are highly dependent on the type of linker used. Flexible and nonconjugated linkers significantly decrease the rates of heterogeneous electron transfer to quasi-reversible Nernstian regimes, while the fully conjugated linker negligibly affects the electron transfer. Furthermore, the rates of electron transfer are also dependent on the number of redox probes encapsulated within the nanosphere; the rates exponentially decrease when the number of redox species present in the nanosphere increases. On the other hand, thermodynamics of electron transfer are not affected by redox probe encapsulation. This study is relevant to the development of catalyst-functionalized cages for electrocatalytic transformations so that the heterogeneous electron transfer rates can be matched with the rate at which the catalyst operates in order to avoid (i) accumulation of reducing/oxidizing equivalents that could potentially be harmful to the catalyst and (ii) a lack of reducing/oxidizing equivalents that can compromise the stability of reactive intermediates.
Figure 2.
Overview of the building blocks prepared. A–C and supramolecular encapsulation of redox probes via hydrogen bonding between sulfonate groups and guanidinium functionalized cage.
Figure 3.
Overview of cage self-assembly stoichiometry and Spartan model of the resulting cage (Pt6E10B2)12+ optimized at molecular mechanics level (MMFF). The cage frame is shown in wire style, platinum corner as gray spheres, and TTF moieties in yellow and white style.
Results and Discussion
Strategy
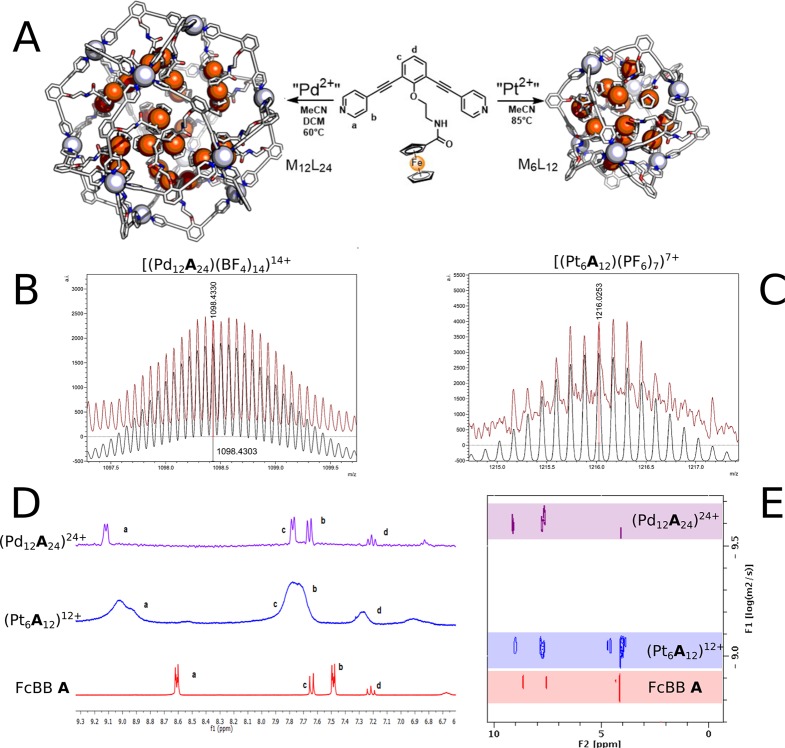
With electrocatalysis as future application in mind, we set out to investigate the electrochemical behavior of redox-active centers encapsulated inside M6L12 and M12L24 Fujita-type nanospheres,32−34 as depicted in Figure 1. These supramolecular assemblies, based on ditopic bis(pyridine) building blocks held together by tetracoordinated square planar palladium or platinum corners, are interesting because their relatively large size (about 3 nm diameter for M6L12 and 5 nm diameter for M12L24) can be exploited to simultaneously accommodate several redox probes. This allows for the independent study of different variables: (i) the number of “guests” can be easily tuned by changing the ratio of functionalized vs unfunctionalized building blocks prior to cage self-assembly; (ii) the ease of functionalization of the standard ditopic bis(pyridine) building block enables synthetic strategies to introduce a diverse range of linkers between the redox probe and the rim of the cage, which may affect the electron transfer process; (iii) different redox probes can be encapsulated within the nanospheres to study electron transfer processes that are key for electrocatalysts. Furthermore, the nanosphere size can be precisely controlled by the choice of metal corners; palladium ions preferentially afford larger M12L24 nanospheres, while platinum precursors result in the formation of M6L12 cages.35
Figure 1.
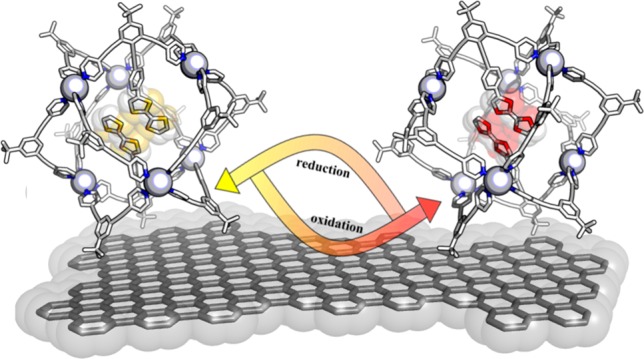
Representation of modified M6L12 nanospheres (specifically [Pt6E10B2]12+) with two encapsulated TTF redox probes undergoing heterogeneous electron transfer at a glassy carbon electrode. TTF (left) in its reduced form and (right) in its oxidized form. The cage frame is optimized at the molecular mechanics level (MMFF) and shown in wire style; carbon in white, nitrogen in blue, and metallic corners as gray spheres.
As the environment in the cage cavity differs from that of the bulk solution, kinetics and thermodynamics of electron transfer of encapsulated redox probes are expected to differ relative to their respective free diffusing species. In particular, the type of linker employed to connect the redox probe to the cage framework can have significant impact on the kinetics of electron transfer. Thus, linear and conjugated linkers resembling molecular wires with large frontier orbital overlap are expected to have less influence on the electron transfer rates compared to flexible or nonconjugated ones. The number of encapsulated redox probes is also expected to be a key parameter, as the proximity of different probes might induce electrostatic interactions, which can affect both the redox potentials of the individual units but also the electron transfer rates.
Synthesis and Characterization of the Supramolecular Cages Functionalized with Redox Probes
Detailed information regarding the synthesis of the respective building blocks and their analytical characterization (1H, 13C, and DOSY NMR spectroscopy as well as high resolution mass spectrometry) can be found in the Supporting Information (SI). Single crystals of building blocks A–C, suitable for X-ray diffraction, were grown either by layering a CH2Cl2 solution of the building blocks with hexanes or by slow evaporation of solvents. The molecular structure for FcBB A confirms the presence of the flexible nonconjugated amide-derived linker that covalently connects the ferrocene unit to the bis(pyridine) backbone. The TTF-containing building blocks B and C display more rigidity along the entire molecular structure. For TTFBB B, the torsion between the central phenyl ring of the backbone and the TTF moiety is only 2.9°, with TTF in the usual boat conformation with 158° torsion between its two 5-membered rings. The twisted building block TTFBB C shows similar angles but the most important feature is the 89.5° torsion between the two adjacent phenyl rings along the linker structure.
The supramolecular M12L24 assemblies were prepared according to literature procedures,20 by mixing a PdII metal precursor (with weakly coordinating anions, typically tetrafluoroborate or hexafluorophosphate-salts) with two equivalents of bis-pyridine building block. After addition of a suitable solvent (in general MeCN-d3 or mixtures of MeCN-d3 and DCM-d2, for solubility reasons) the solutions were stirred overnight in a closed Schlenk flask at 60 °C. The characterization methods available to confirm the formation of the assemblies are showcased for the palladium nanocage containing 24 FcBBs A, [Pd12A24]24+ (Figure 4). Data for all assemblies are compiled in the SI.
Figure 4.
(A) Representation of [Pt6A12]12+ nanosphere (right) and [Pd12A24]24+ nanosphere (left). The cage structures are optimized at molecular mechanics level (MMFF) and shown in wire style; carbon in white, nitrogen in blue, oxygen in red, metallic corners as gray spheres (right is Pt, left is Pd,) and Fe ions as orange spheres. (B) Obtained (red) and calculated (black) CSI-MS for the 14+ species [(Pd12A24)(BF4)14]14+. (C) Obtained (red) and calculated (black) CSI-MS for the 7+ species [(Pt6A12)(PF6)7]7+. (D) 1H-NMR of FcBB A (red), [Pt6A12]12+ (blue) and [Pd12A24]24+ (violet). (E) 1H-DOSY-NMR overlay for FcBB A (red), [Pt6A12]12+ nanosphere (blue) and [Pd12A24]24+ nanosphere (violet) in a 1:1 mixture of CD2Cl2 and CD3CN at 25 °C.
The formation of the desired assembly is first supported by 1H NMR spectroscopy. Upon pyridine coordination to the metal corners, the ortho-pyridine protons undergo deshielding, which results in a low-field shift of such protons of approximately 0.4 ppm (Figure 4). The symmetry and broadening of the 1H NMR spectrum is also an indication for the formation of highly symmetric, large assemblies.36 Second, a DOSY NMR spectrum of the reaction solution features a single species with a log D value of −9.6 m2 s–1, in agreement with previously reported data on similar nanospheres.20,32,37 In contrast, under the same experimental conditions, the free building block, being considerably smaller than the supramolecular cage assembly, shows a log D value of −8.9 m2s–1. Cryospray-ionization mass spectrometry (CSI-MS) confirms the formation of a species with overall [Pd12A24]24+ composition. The spectrum shows several signals belonging to the desired species, in particular species of the type [(Pd12A24)](24–n)+(BF4)n with different numbers of anions. The measured signals and their isotopic patterns are in agreement with the simulated spectra that are compiled in the SI (Figures 4 and S12–S21).
Similarly, performing the same self-assembly process using a PtII precursor affords smaller Pt6A12 cages after stirring the reaction mixture at 85 °C for 2 days (Figures 4 and S34–S40). Because the length of the TTF functionalized building blocks is about 1.5 nm for TTFBB B and about 2.0 nm for twistedTTFBB C, and given their rigid nature, it is unlikely that 12 of those building blocks self-assemble into M6L12 spheres as a result of the significant steric hindrance induced in the cage interior. This is supported by rudimentary molecular mechanics calculations (Spartan). Therefore, nanospheres containing the redox-active TTF building blocks were prepared by using mixtures of TTF building blocks and unfunctionalized building block BBH E to generate cage assemblies of the type M6ExL12–x (L = TTFBB B or twistedTTFBB C). When cage self-assembly is performed with two different building blocks LI and LII, the resulting solution contains a mixture of cages of the type MyLIxLII2y–x (y = 6, 12), containing different amounts of building block LII, specifically the amount of LII follows a Gaussian distribution centered around the value 2y–x. Thus, when mixed building block cages are mentioned, those are always to be intended as mixtures of different species as opposed to specific single composite species. For small Pt6L12 cages with sterical demanding building blocks such as TTFBB B or twistedTTFBB C, rudimentary molecular modeling shows that the cavity of such cages is congested when more than three TTF containing building blocks are present (Figure S162). CSI MS data confirms that for (Pt6EnB12–n)12+ these cages formed predominantly with n = 0, 1, and 2 with the ratio of different composites changing according to the stoichiometry chosen and in negligible amounts n = 3 (Figures S51–S61 and S64–S71); species with four or higher TTF containing building blocks were not observed by CSI-MS measurements. Exact quantification of single composites is unfortunately not possible due to differences in ionizability of the different species under MS conditions. Formation of larger M12L24 Pd-cages containing TTF redox moieties was unsuccessful as mixing the TTF building blocks with the palladium precursor in an attempt to form large Pd12L24 cages resulted in palladium black formation within minutes.
The formation and characterization of a guanidinium functionalized supramolecular cage, [(Pd12D24)](OTf)24, was carried out as described previously.20 Encapsulation of ferrocenyl sulfonate guests via hydrogen bonding was confirmed by 1H NMR titration studies. The shifts of all relevant peaks are consistent with the ferrocene unit being encapsulated (Figure S81). About 24 equiv of ferrocenyl sulfonate can be added to the cage solution, while the addition of an excess leads to formation of a precipitate. The latter is assumed to be a guanidinium cage with 24 ferrocenyl sulfonate moieties in the interior and ferrocenyl counterions at the outside. If more solvent is added to the NMR sample, the precipitate remains, but addition of more guanidinium cages leads to dissolution of the precipitate and the resulting 1H NMR spectrum is identical to the one of a guanidinium cage with encapsulated ferrocenyl sulfonates. The encapsulation of the ferrocene derivative is also confirmed by DOSY NMR spectroscopy (Figure S82). A diffusing species containing all the signals belonging to the cage and those of the ferrocene moiety is present at a log D value of −9.35. A second diffusing species with a lower diffusion coefficient is present and identified as the tetrabutylammonium counterions that are released after binding the ferrocenyl sulfonates to the guanidinium. CSI-MS data were recorded for solutions of [(Pd12D24)](OTf)24 with different amounts (3, 8, and 16 equiv) of [FcSO3]− guest, showing in all cases the expected signals for host–guest complexes, in agreement with the isotopic patterns (Figures S83–S107). Several attempts to grow single crystals of cage samples suitable for X-ray diffraction were undertaken specifically by vapor diffusion and solvents layering (several solvents combinations) at room temperature, at +5 °C and at −20 °C. Unfortunately, all the attempts were unsuccessful.
Electrochemistry of Covalently Encapsulated Redox Probes
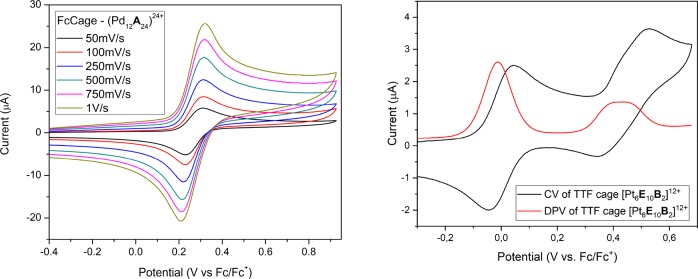
Cyclic voltammograms of nanospheres containing redox moieties clearly show a single reversible wave, corresponding to the oxidation of the redox probes, as illustrated for the [Pd12A24]24+ cage in Figure 5 (left). For the TTF-containing cages, a second quasi-reversible wave is present at more anodic potential, corresponding to the second oxidation of the TTF moiety. Figure 5 (right) shows a typical example of such a voltammetric plot.
Figure 5.
Left: Cyclic voltammograms at different scan rates for [Pd12A24]24+ in a 1:1 mixture of MeCN and DCM. Right: Cyclic voltammogram and differential pulse voltammetric (DPV) measurement for [Pt6E10B2]12+ in MeCN, showing both the first and second oxidation waves of the TTF probe.
Comparison of the data set obtained for the cage samples with the data set obtained for their respective free diffusing redox active building blocks reveals a small shift of the half-wave potential (typically in the order of ±10–50 mV) upon encapsulation of the redox-active probes, which suggests that oxidation of the redox probes is only slightly different (±0.2–1.2 kcal mol–1). Table 1 summarizes the values of the half-wave potentials measured for the different cages and building blocks.
Table 1. Summary of the E1/2 Redox Potentials and Calculated k° of Heterogeneous Electron Transfer for the Redox-Active Building Blocks A–C and Their Respective Cages (with Different Amounts of Redox Probe Present)a.
| sample | no. of redox probes | E1/21 first oxidation (V vs Fc/Fc+) | k1° (cm s–1) | E1/22 secnd oxidation (V vs Fc/Fc+) | k2° (cm s–1) |
|---|---|---|---|---|---|
| FcBB, A | 0.262 | 4.569 × 10–2 | |||
| [Pt6A12]12+ | 12 | 0.215 | 9.94 × 10–3 | ||
| [Pt6E11A1]12+ | 1 | 0.211 | 2.90 × 10–3 | ||
| [Pd12E23A]24+ | 1 | 0.281 | 6.98 × 10–3 | ||
| [Pd12A24]24+ | 24 | 0.314 | 6.1 × 10–4 | ||
| TTFBB, B | 0.029 | 5.382 × 10–2 | 0.489 | 1.237 × 10–2 | |
| [Pt6E11B]12+ | 1 | 0.022 | 3.780 × 10–2 | 0.448 | 6.51 × 10–4 |
| [Pt6E10B2]12+ | 2 | 0.036 | 1.442 × 10–2 | 0.448 | 3.09 × 10–4 |
| twistedTTFBB, C | –0.037 | 7.046 × 10–2 | 0.340 | 2.147 × 10–2 | |
| [Pt6E11C]12+ | 1 | –0.021 | 4.64 × 10–3 | 0.343 | 1.09 × 10–3 |
Data for FcBB A and FcBB A containing cages were recorded in a 1:1 mixture of MeCN and DCM, while data for TTF containing building blocks and their cages were collected in MeCN.
Analysis of peak current vs square root of the scan rate plots provides further details on the electrochemical process. In all cases, both for the assembled cages containing redox-probes and for the stand-alone redox-active building blocks, the plots show a linear trend over a broad scan speed range, indicating Nernstian behavior (Figure S112). The linear trend is also an indication that the analytes under investigation are in solution and do not adsorb to the electrode surface during the electrochemical measurement nor do they react with the working electrode.38,39 As shown in Figures S119 and S132, stability of cages upon electrochemical events is also supported by the overlap of consecutive voltammetric traces. For the cage samples, the slopes of the lines are smaller than for their respective building blocks, in agreement with their difference in size. From these slopes, using the Randles–Sevcik equation,39 diffusion coefficients can be calculated, which agree, within experimental error, with diffusion coefficients obtained from DOSY NMR spectroscopy.
Heterogeneous electron transfer rate constants k° were calculated by the method originally proposed by Nicholson in 1965 and revised by Paul and Leddy in 1995.40,41 This method is based on peak potential separation; it relates k° to the parameter ψ, which can be calculated from the parametric equation proposed by Paul and Leddy.40−42 Because this method relies on the peak potential separation, for it to be reliable, it is important that any residual solution resistance is properly compensated for. The calculated k° values for the cages under investigation and for the free diffusing building blocks are compiled in Table 1.
The calculated rates of heterogeneous electron transfer k° for the free building blocks are well within the Nernstian reversible regime displaying fast electron transfer kinetics. Oxidation of the twisted TTF building block C proceeds with a k° of 7.04 × 10–2 cm s–1 that is close to the one reported for free TTF.43 The TTF moiety of building block B displays a slower rate of heterogeneous electron transfer (5.382 × 10–2 cm s–1), suggesting that the TTF moiety is part of a larger π-system (vide infra). For both TTF containing building blocks B and C, the second electron transfer rate constant k2° is lower than the first one, consistent with the fact that the doubly oxidized TTF units possess an aromatic configuration with 6π electrons in each TTF system; formation or breaking of this aromatic stable configuration leads to molecular reorganization, and this required movement of the atoms upon this redox event translates into a slower heterogeneous electron transfer rate.
Linker Influence
To compare the different type of linkers employed, this section will focus on assemblies with two different building blocks containing on average only one redox probe per cage: specifically [Pt6E11A]12+, containing the flexible ferrocene functionalized building block A, [Pt6E11B]12+ containing the linear TTF building block B; and [Pt6E11C]12+ containing the twisted version of the TTF building block where conjugation is broken. When the redox probe is encapsulated with a flexible and nonconjugated linker such as for cage [Pt6E11A]12+, approximately a 16-fold decrease in electron transfer rate constant is observed. The electron transfer is slowed by more than 1 order of magnitude compared to the electron transfer rate of the free building block. Electron transfer is however attributed to the intrinsic linker flexibility, which allows the redox probe to bend toward the large cage windows so that direct electron transfer from the electrode surface can still occur. For cages containing one TTF moiety, the rigidity of the linkers prevents bending of the unit toward the cage windows and therefore electron transfer is unlikely to happen by close contact of the electrode surface and the probe. For the cage containing TTFBB B, the rate of electron transfer for the free building block compared to the encapsulated analogue differs only slightly, staying within the Nerstian reversible regime. The reason for the overall fast electron transfer is attributed to the fully conjugated linker, resembling the structure of a molecular wire, facilitating the electron transfer step. Importantly, this indicates that the cage framework itself not only has negligible influence on thermodynamics but also on the electron transfer kinetics.
For the cage containing building block C, the rate of electron transfer is slowed about 15 times compared to its free building block. The TTF moiety is encapsulated within the interior of the cage, but it also has a 90° twist along the rigid linker structure, which effectively breaks conjugation, as indicated by DFT orbital computations (Figures S163–S167). The absence of frontier orbital overlap prohibits fast electronic communication between the TTF moiety and the rest of the structure, leading to overall slower kinetics.
Influence of the Number of Redox Probes
The heterogeneous electron transfer rates are different when more than one redox probe is encapsulated within the cavity of the nanosphere. In fact, for [Pt6A12]12+ containing 12 Fc redox probes, the electron transfer rate is about 4 times slower than that for its free diffusing building block. The presence of 12 redox probes within the interior of the nanosphere was expected to more drastically affect the rates of electron transfer; however, as the cavity of this particular nanosphere is sterically crowded (see modeling structures Figure 4 right) and the linker flexibility allows the ferrocene units to bend toward the cage rim, fast direct electron transfer from the electrode is facilitated by such conformations. The larger nanospheres of the type M12L24 provide a large cavity with less steric repulsion and as such the redox probes reside on average more in the center of the structure, away from the cage windows (Figure 4 left). When only one Fc redox moiety is encapsulated within the cavity of the larger nanosphere (i.e., [Pd12E23A]24+), the rate of electron transfer is about 6.5 times slower compared to that of the free diffusing building block and about 1.5 times slower compared to that of the crowded [Pt6A12]12+. This indeed suggests that for the small [Pt6A12]12+ nanosphere the ferrocene units are on average in closer proximity to the electrode. Interestingly, the cage [Pd12A24]24+ containing 24 ferrocene units shows a rate of heterogeneous electron transfer k° of 6.10 × 10–4 cm·s–1 that is about 75-fold slower than that for the free diffusing building block and 1 order of magnitude slower than that of the previously discussed [Pd12E23A]24+ containing only one redox probe. As such, this trend indicates that the number of redox active moieties within the cage framework also has a strong impact on the overall electron transfer rate. Interestingly, as shown in Figure 5, voltammograms of cages containing more than one redox-active fragment feature a single oxidation wave. Although these oxidation waves are broader than those of the freely diffusing building block, the single oxidation wave indicates that the thermodynamics of electron transfer do not change significantly even when the interior of the cage contains 24 redox probes.
The redox-active moieties are encapsulated within the volume defined by the 5 nm diameter sized M12L24 cage and thus are in proximity to one another. This could in principle lead to electronic and electrostatic communication between individual redox sites. However, as suggested by the single oxidative event observed by cyclic voltammetry, the redox probes are sufficiently isolated from each other to be electrochemically manipulated. This behavior is often seen in literature for ferrocenyl or TTF dendrimers and polymers, both in solution or immobilized on electrode surfaces.44−46 Important for this behavior is the fast molecular tumbling rate of the cage in solution. The tumbling rate can be roughly estimated through Newtonian motion laws of spherical objects. For a spherical object of about 5 nm in diameter, the tumbling rate in acetonitrile is roughly 2 × 108 s–1 at room temperature.47 As the tumbling rate of the cage in solution is considerably faster than the time scale of the voltammetric experiment, all redox-active probes within the molecular cage are identical, even at very fast scan rates, and on average equally distant from the electrode surface.48 Still, this phenomenon alone is not sufficient to explain the single-wave behavior for a given electrochemical event. Electrostatic repulsion of the newly generated charges in the interior of the cage also does not seem to influence the redox potential of other nearby units. The solution for the electrochemical experiment always contains large amounts of a salt such as TBAPF6 (tetrabutyl ammonium hexafluorophosphate) as the supporting electrolyte. Charges generated in the interior of the cage upon oxidation of the redox probes are balanced by diffusion of electrolyte, thereby keeping the net charge inside the cavity of the cage constant.49 Without accumulation of charges in the interior of the cage, electrostatic repulsion is minimized and the thermodynamics of electron transfer do not change drastically while the kinetics can be slowed to the limit of reversibility due to slow ion rearrangement.
This set of experiments shows that the nature of the linker connecting the redox probe to the backbone of the building block plays a crucial role for the feasibility of the electron transfer and it determines its kinetics. As a result, it is possible to vary the kinetics of electron transfer from the electrode surface to a redox moiety encapsulated within the interior of a supramolecular cage while keeping the thermodynamics unaltered. The three building blocks discussed show fast electrode kinetics when studied as free species in solution. The electrode kinetics of cages containing building block A or C are slowed to the limit of reversibility. This is not a general cage effect, as shown by the supramolecular assembly containing building block B, where the electron transfer kinetics are marginally affected and the redox events stay within the Nernstian reversible regime.
Radical–Radical Interactions in the Cage Interior
The formation of radical species after electrochemical events was further monitored by electron paramagnetic resonance (EPR) spectroscopy. Cage solutions containing on average 1 and 2 equiv of redox moiety of the type (Pt6E12–nBn)12+ (n = 1, 2), were subjected to bulk electrolysis at constant potential at 0.35 V vs Fc/Fc+. As mentioned earlier, such cages are a mixture of different species rather than single composite solutions. CSI-MS data shows that species present in solution are (Pt6E12)12+, (Pt6E11B)12+, (Pt6E10B2)12+, and to a lesser extent (Pt6E9B3)12+ with their ratio changing according to the stoichiometry chosen. Importantly the ratio of the different composites changes not only according to Gaussian distribution but also according to steric congestions. Simultaneous presence of more than three TTF units in one cage is unlikely due to steric constrains within the cavity of the small Pt6L12 cages (Figure S162). Although it is not possible to exclude the formation of species with larger TTF numbers based on CSI-MS data, we can at least conclude that if these species exist, they are present in low concentrations only. Importantly, the different composites present in solution have different ionizability under CSI-MS conditions; thus, accurate quantification of mixture compositions is difficult to obtain. The plot of the current measured in time is shown in Figure 6 together with its integration plot, which provides information about the average number of electrons transferred per cage. The analysis confirms that each TTF unit in the sample is oxidized by one electron, generating encapsulated TTF cation radicals (TTF+•) that can be detected by EPR spectroscopy. Figure 7 shows the typical room temperature EPR spectrum of the radical cation of the free TTFBB B, i.e., the expected quartet pattern of a monosubstituted TTF with coupling to three hydrogen atoms. By contrast, the room temperature EPR spectrum for the caged TTF radical cations shows a broad signal at the same g value. Broadening of EPR signals is common and typically ascribed to zero-field splitting, which may in this case result from radical–radical interactions in the cage interior.50,51 EPR simulations for both the free as well as the encapsulated TTF cation were simulated using an AB2-pattern with three S = 1/2 nuclei, in agreement with a monosubstituted TTF moiety. Comparing the line width of the two TTF cations, a significant increase of 52% is observed for the encapsulated system (Figures S168 and S169). Furthermore, within the cage cavity, the TTF cation has a decreased contribution of the “A”-nucleus to the hyperfine pattern (AAiso = 2.2455 MHz) compared to the free TTFBB cation (AAiso = 3.598 MHz).
Figure 6.
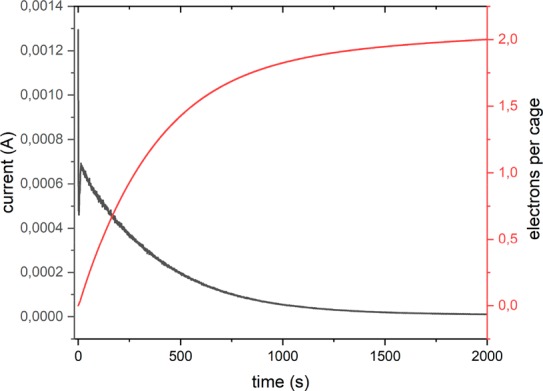
Plot of current measured during electrolysis at constant potential (0.35 V vs Fc/Fc+) of cage solution (Pt6E10B2)12+ in MeCN (black) and its integral (red), informative on the number of electrons transferred during the electrolysis.
Figure 7.
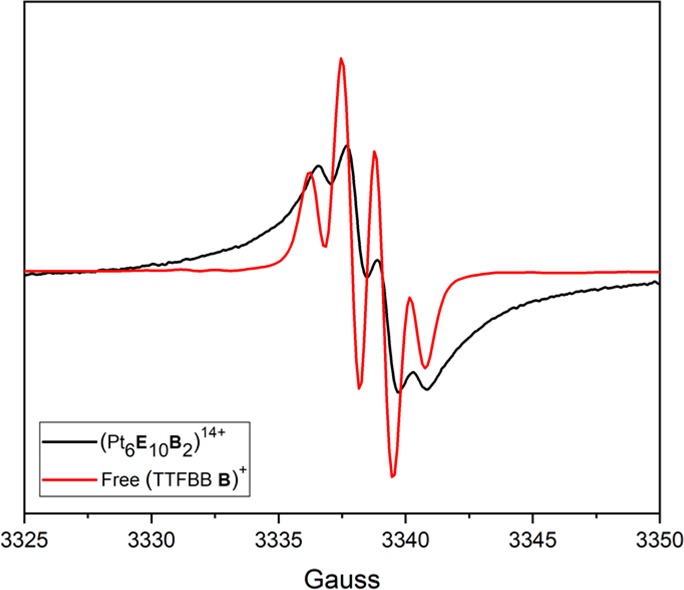
Room temperature EPR signal of mono-oxidized TTFBB B (red) and its cage (Pt6E10B2)14+ (black), after bulk electrolysis at 0.35 V vs Fc/Fc+ in MeCN.
To gain insights into the nature of such interactions, the TTF/TTF•+ redox-couple was monitored by UV–vis for free TTFBB B and for cages containing on average 1 or 2 equiv of TTFBB B, respectively (Figure 8). From literature, it is known that one-electron oxidation of TTF generates very stable and deeply colored radical cationic species that can form (TTF+•)2 dimers or, depending on the conditions (e.g., inducing proximity effects), mixed valence dimeric (TTF)(TTF)+• species.52−61 The latter have an absorption maximum around 900 nm in the UV–vis-NIR spectrum as well as a broad absorption at approximately 2000 nm, whereas the radical dimer, (TTF+•)2, displays absorption around 800 nm.52−61 For the free TTF building block B, only a band at 650 nm was observed, indicating that neither radical dimerization nor mixed valence species are formed. For the cage solution containing on average 2 equiv of TTFBB B, a 5-fold increase in absorption at 800 nm is observed compared with free (TTFBB B)+ or cage (Pt6E11B)13+ containing only 1 equiv of TTFBB B. This is consistent with radical dimer absorption (TTF+•)2. Typically, the extinction coefficient for the charge transfer band around 800 nm is higher than the one for the absorption around 650 nm of TTF+•. Assuming that this is true also for the system under investigation, it implies that the extent of radical dimerization is a minor effect; most radicals within the cage probably exist as isolated TTF•+. Data for the cage solution (Pt6E11B)12+ containing on average 1 equiv of TTFBB B show a similar behavior as the free building block as seen in Figure 8.
Figure 8.
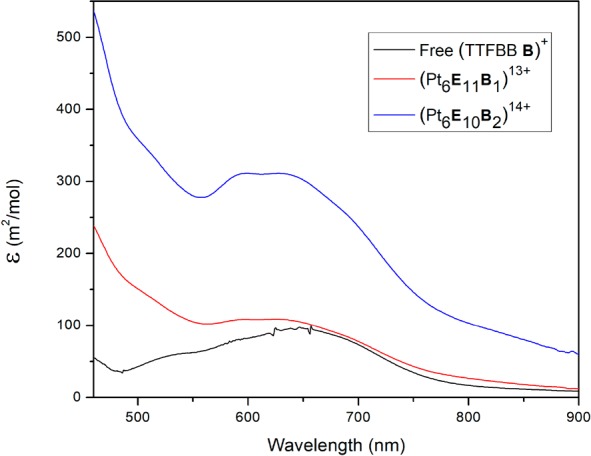
UV–vis spectra of free (TTFBB B)+, cage (Pt6E11B)13+, and (Pt6E10B2)14+ after bulk electrolysis at 0.35 V vs Fc/Fc+ in MeCN.
Overall, the combined data support retention of the supramolecular cage assemblies upon electrochemical reactions involving redox-probes in their interior. Despite that most radicals within the cage probably exist as isolated TTF•+, the combination of EPR and spectroelectrochemistry measurements reveals the presence of some interactions between the radicals within the nanosphere to form to a lesser extent (TTF•+)2 radical dimer species.
Electrochemistry of Supramolecularly Encapsulated Redox Probes
Next the electrochemistry of redox probes that were supramolecularly encapsulated within nanospheres via hydrogen bonding was evaluated. To probe the encapsulation of ferrocenyl sulfonate by guanidinium cages, a titration of ferrocenyl sulfonate into a solution of guanidinium cages was carried out while monitoring the voltammetric response after every addition of redox probe. The guanidinium cage itself does not show any electrochemical anodic response in the potential window of interest. When ferrocenyl sulfonate is added to this solution, a reversible wave appears (E1/2 = 0.20 V vs Fc/Fc+, ΔEp = 70 mV). Figure 9 shows that increasing amounts of ferrocenyl sulfonate result in higher peak currents but no significant potential shift is observed. When about 22 equiv of ferrocenyl sulfonate is added, some precipitate forms, in line with the NMR titration described earlier. From this point, the peak current measured decreases with increasing amounts of ferrocenyl sulfonate, indicating that the ferrocenyl sulfonate induces precipitation of the cage from solution. After about 50 equiv of ferrocenyl sulfonate, a new reversible wave appears that is shifted cathodically by about 150 mV (E1/2 = 0.05 V vs Fc/Fc+). This last wave is identical to an authentic sample of free ferrocenyl sulfonate.
Figure 9.
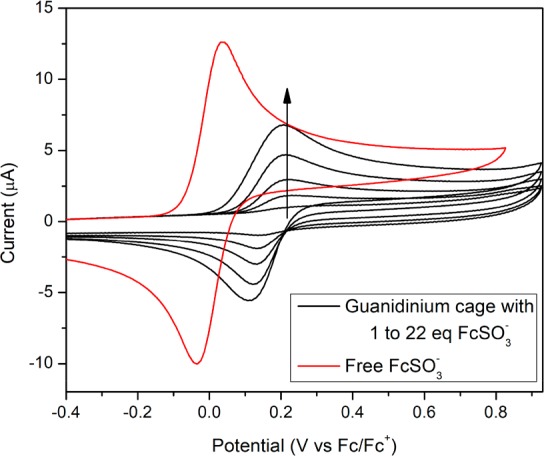
Cyclic voltammogram of free tetrabutylammonium ferrocenyl sulfonate (red) and titration of different equivalents of this compound into a guanidinium functionalized cage (Pd12D24)48+ in MeCN showing increasing peak current while E1/2 remains constant.
At first glance, the electron transfer process appears to be more energetically demanding, as suggested by the large potential shift of approximately 150 mV (∼3.5 kcal mol–1) measured between free and encapsulated ferrocenyl sulfonate. However, this shift in potential is ascribed to the multifold interaction between the sulfonate and guanidinium groups. The hydrogen bonding between the two complementary functional groups (guanidinium and sulfonate) is expected to effectively reduce the electron density at the ferrocene moiety, therefore rendering its oxidation more difficult. To support this, a new titration was carried out, monitoring peak potential shifts of ferrocenyl sulfonate upon addition of increasing amounts of n-butylguanidinium hexafluorophosphate. Indeed, progressive anodic shifting of the redox-event is observed with an increasing concentration of guanidinium species (Figures S156 and S157). Interestingly, about 25–30 equiv of guanidinium salt is necessary to reproduce a similar potential shift as observed when the ferrocenyl sulfonate is encapsulated by the guanidinium cage, reflecting the stronger binding within the sphere due to the ditopic binding mode. Importantly, the shift can be entirely attributed to hydrogen bonding.
The data are consistent with the ferrocene derivative remaining encapsulated throughout the electrochemical experiment. First, the ferrocenyl peak potential is constant during the entire titration experiment, which is in line with strong binding of sulfonates inside the cage, as previously reported (cage binding affinity to sulfonates, ∼2.1 × 105 M–1).20 Second, the shape of the voltammogram remains symmetric, which indicates that the ferrocene undergoes both electrochemical events (oxidation and back-reduction) at the inside of the nanosphere. In fact, if the ferrocenyl sulfonate would leave the cage after the oxidation event and be back-reduced outside the cage, the shape of the voltammogram would be asymmetric with a peak potential separation ΔEp of approximately 300 mV instead of the 70 mV experimentally observed.
The ferrocenyl sulfonate displays fast kinetics of electron transfer (k° 4.25 × 10–2 cm s–1), similar to the cases of the reported ferrocene derivatives and the ferrocene containing building block A.62−65 However, when this redox probe is encapsulated within the cavity of the guanidinium functionalized nanosphere (1 equiv), the rate of electron transfer is about 20 times lower compared to the freely diffusing species. Furthermore, increasing numbers of redox-active guests result in an exponential decrease of the heterogeneous electron transfer rate, similar to that observed for the covalently encapsulated redox probes (Figure 10). For the supramolecularly anchored system, the rate of electron transfer becomes about 250 times slower when 22 ferrocenyl sulfonates reside in the nanosphere. The thermodynamics of electron transfer are again only slightly affected, as indicated by the constant E1/2 of the encapsulated ferrocenyl species.
Figure 10.
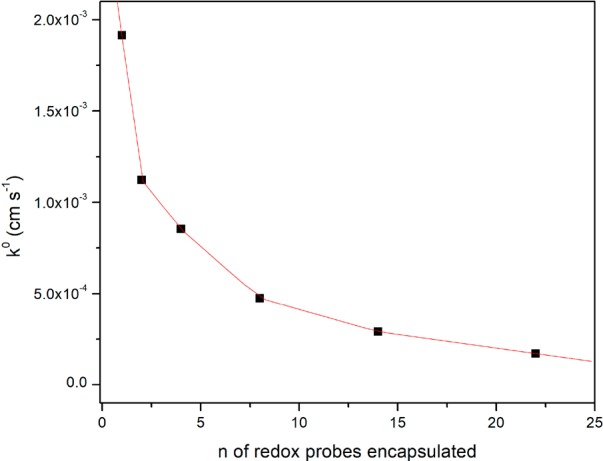
Trend of heterogeneous electron transfer rate k° for increasing amounts of tetrabutylammonium ferrocenyl sulfonate encapsulated within the cavity of a guanidinium functionalized cage (Pd12D24)48+.
The drastic drop in electron transfer rate also confirms that the ferrocenyl probes stay encapsulated during the entire course of the voltammetric measurement; the guanidinium groups hold the redox probes in place by strong cooperative binding, ensuring effective encapsulation and insulation from the bulk solution and from the electrode, resulting in kinetics of electron transfer that are in the quasi-reversible Nernstian regime.
Conclusions
In this work, we have demonstrated the feasibility of the electron transfer of redox-active species encapsulated in M6L12 and M12L24 supramolecular assemblies. The linker connecting the redox probe to the cage building block is a useful handle to tune the rate of electron transfer. Envisioning that an (electroactive) catalyst can be encapsulated into a supramolecular assembly, the nature of the linker employed as well as the number of redox species present within the nanosphere could potentially be exploited to fine-tune and match the electron transfer rate to the rate at which the catalyst operates. This strategy could be advantageous in order to avoid accumulation of reducing/oxidizing equivalents which could potentially be harmful to the catalyst.
Acknowledgments
Maximilian Dürr, Nicole Orth, and Ivana Ivanović-Burmazović, currently at Friedrich-Alexander-Universität Erlangen, are acknowledged for collection of preliminary CSI-MS data on cages of the type (Pd12A24)(24–n)+(BF4)n. Dr. Wojciech Dzik is thanked for work on one of the X-ray structure determinations. Ed Zuidinga is acknowledged for assistance with HR-MS analysis.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacs.0c01869.
Experimental details on synthesis and characterization (1H/31P/13C NMR, MS, XRD), all raw data pertaining to electrochemistry (PDF)
Author Contributions
† R.Z. and E.O.B. contributed equally to this work.
This work is part of the research program of the Foundation for Fundamental Research on Matter (FOM), which is part of The Netherlands Organisation for Scientific Research (NWO).
The authors declare no competing financial interest.
Supplementary Material
References
- Johansson-Seechurn C. C. C.; Kitching M. O.; Colacot T. J.; Snieckus V. Palladium-Catalyzed Cross-Coupling: A Historical Contextual Perspective to the 2010 Nobel Prize. Angew. Chem., Int. Ed. 2012, 51 (21), 5062–5085. 10.1002/anie.201107017. [DOI] [PubMed] [Google Scholar]
- Noyori R. Synthesizing our future. Nat. Chem. 2009, 1 (1), 5–6. 10.1038/nchem.143. [DOI] [PubMed] [Google Scholar]
- Franke R.; Selent D.; Börner A. Applied Hydroformylation. Chem. Rev. 2012, 112 (11), 5675–5732. 10.1021/cr3001803. [DOI] [PubMed] [Google Scholar]
- Cornils B.; Herrmann W. A. Concepts in homogeneous catalysis: the industrial view. J. Catal. 2003, 216 (1–2), 23–31. 10.1016/S0021-9517(02)00128-8. [DOI] [Google Scholar]
- Brown C. J.; Toste F. D.; Bergman R. G.; Raymond K. N. Supramolecular Catalysis in Metal–Ligand Cluster Hosts. Chem. Rev. 2015, 115 (9), 3012–3035. 10.1021/cr4001226. [DOI] [PubMed] [Google Scholar]
- Vriezema D. M.; Comellas Aragonès M.; Elemans J. A. A. W.; Cornelissen J. J. L. M.; Rowan A. E.; Nolte R. J. M. Self-Assembled Nanoreactors. Chem. Rev. 2005, 105 (4), 1445–1490. 10.1021/cr0300688. [DOI] [PubMed] [Google Scholar]
- Leenders S. H. A. M.; Gramage-Doria R.; de Bruin B.; Reek J. N. H. Transition metal catalysis in confined spaces. Chem. Soc. Rev. 2015, 44 (2), 433–448. 10.1039/C4CS00192C. [DOI] [PubMed] [Google Scholar]
- Mouarrawis V.; Plessius R.; van der Vlugt J. I.; Reek J. N. H. Confinement Effects in Catalysis Using Well-Defined Materials and Cages. Front. Chem. 2018, 6, 623. 10.3389/fchem.2018.00623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ballester P. Effects of Nanoconfinement on Catalysis. Edited by Rinaldo Poli. Angew. Chem., Int. Ed. 2017, 56 (27), 7713–7714. 10.1002/anie.201704055. [DOI] [Google Scholar]
- Yoshizawa M.; Klosterman J. K.; Fujita M. Functional Molecular Flasks: New Properties and Reactions within Discrete, Self-Assembled Hosts. Angew. Chem., Int. Ed. 2009, 48 (19), 3418–3438. 10.1002/anie.200805340. [DOI] [PubMed] [Google Scholar]
- Wiester M. J.; Ulmann P. A.; Mirkin C. A. Enzyme Mimics Based Upon Supramolecular Coordination Chemistry. Angew. Chem., Int. Ed. 2011, 50 (1), 114–137. 10.1002/anie.201000380. [DOI] [PubMed] [Google Scholar]
- Raynal M.; Ballester P.; Vidal-Ferran A.; van Leeuwen P. W. N. M. Supramolecular catalysis. Part 1: non-covalent interactions as a tool for building and modifying homogeneous catalysts. Chem. Soc. Rev. 2014, 43 (5), 1660–1733. 10.1039/C3CS60027K. [DOI] [PubMed] [Google Scholar]
- Pluth M. D.; Bergman R. G.; Raymond K. N. Acid Catalysis in Basic Solution: A Supramolecular Host Promotes Orthoformate Hydrolysis. Science 2007, 316 (5821), 85–88. 10.1126/science.1138748. [DOI] [PubMed] [Google Scholar]
- Pluth M. D.; Bergman R. G.; Raymond K. N. Supramolecular Catalysis of Orthoformate Hydrolysis in Basic Solution: An Enzyme-Like Mechanism. J. Am. Chem. Soc. 2008, 130 (34), 11423–11429. 10.1021/ja802839v. [DOI] [PubMed] [Google Scholar]
- Horiuchi S.; Murase T.; Fujita M. Diels–Alder Reactions of Inert Aromatic Compounds within a Self-Assembled Coordination Cage. Chem. - Asian J. 2011, 6 (7), 1839–1847. 10.1002/asia.201000842. [DOI] [PubMed] [Google Scholar]
- Murase T.; Horiuchi S.; Fujita M. Naphthalene Diels–Alder in a Self-Assembled Molecular Flask. J. Am. Chem. Soc. 2010, 132 (9), 2866–2867. 10.1021/ja9107275. [DOI] [PubMed] [Google Scholar]
- Yoshizawa M.; Tamura M.; Fujita M. Diels-Alder in Aqueous Molecular Hosts: Unusual Regioselectivity and Efficient Catalysis. Science 2006, 312 (5771), 251–254. 10.1126/science.1124985. [DOI] [PubMed] [Google Scholar]
- Koblenz T. S.; Wassenaar J.; Reek J. N. H. Reactivity within a confined self-assembled nanospace. Chem. Soc. Rev. 2008, 37 (2), 247–262. 10.1039/B614961H. [DOI] [PubMed] [Google Scholar]
- Dong Z.; Luo Q.; Liu J. Artificial enzymes based on supramolecular scaffolds. Chem. Soc. Rev. 2012, 41 (23), 7890–7908. 10.1039/c2cs35207a. [DOI] [PubMed] [Google Scholar]
- Wang Q.-Q.; Gonell S.; Leenders S. H. A. M.; Dürr M.; Ivanović-Burmazović I.; Reek J. N. H. Self-assembled nanospheres with multiple endohedral binding sites pre-organize catalysts and substrates for highly efficient reactions. Nat. Chem. 2016, 8 (3), 225–230. 10.1038/nchem.2425. [DOI] [PubMed] [Google Scholar]
- Gramage-Doria R.; Hessels J.; Leenders S. H. A. M.; Tröppner O.; Dürr M.; Ivanović-Burmazović I.; Reek J. N. H. Gold(I) Catalysis at Extreme Concentrations Inside Self-Assembled Nanospheres. Angew. Chem., Int. Ed. 2014, 53 (49), 13380–13384. 10.1002/anie.201406415. [DOI] [PubMed] [Google Scholar]
- Cullen W.; Misuraca M. C.; Hunter C. A.; Williams N. H.; Ward M. D. Highly efficient catalysis of the Kemp elimination in the cavity of a cubic coordination cage. Nat. Chem. 2016, 8 (3), 231–236. 10.1038/nchem.2452. [DOI] [PubMed] [Google Scholar]
- Chen S.; Li K.; Zhao F.; Zhang L.; Pan M.; Fan Y.-Z.; Guo J.; Shi J.; Su C.-Y. A metal-organic cage incorporating multiple light harvesting and catalytic centres for photochemical hydrogen production. Nat. Commun. 2016, 7, 13169. 10.1038/ncomms13169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jing X.; He C.; Yang Y.; Duan C. A Metal–Organic Tetrahedron as a Redox Vehicle to Encapsulate Organic Dyes for Photocatalytic Proton Reduction. J. Am. Chem. Soc. 2015, 137 (11), 3967–3974. 10.1021/jacs.5b00832. [DOI] [PubMed] [Google Scholar]
- Nurttila S. S.; Zaffaroni R.; Mathew S.; Reek J. N. H. Control of the overpotential of a [FeFe] hydrogenase mimic by a synthetic second coordination sphere. Chem. Commun. 2019, 55 (21), 3081–3084. 10.1039/C9CC00901A. [DOI] [PubMed] [Google Scholar]
- Yu F.; Poole D. III; Mathew S.; Yan N.; Hessels J.; Orth N.; Ivanović-Burmazović I.; Reek J. N. H. Control over Electrochemical Water Oxidation Catalysis by Preorganization of Molecular Ruthenium Catalysts in Self-Assembled Nanospheres. Angew. Chem., Int. Ed. 2018, 57 (35), 11247–11251. 10.1002/anie.201805244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang F.; Wang N.; Du Z.; Wang J.; Lan Z.; Yang R. Thiophene-Coated Functionalized M12L24 Spheres: Synthesis, Characterization, and Electrochemical Properties. Chem. - Asian J. 2012, 7 (10), 2230–2234. 10.1002/asia.201200413. [DOI] [PubMed] [Google Scholar]
- Bivaud S.; Balandier J.-Y.; Chas M.; Allain M.; Goeb S.; Sallé M. A Metal-Directed Self-Assembled Electroactive Cage with Bis(pyrrolo)tetrathiafulvalene (BPTTF) Side Walls. J. Am. Chem. Soc. 2012, 134 (29), 11968–11970. 10.1021/ja305451v. [DOI] [PubMed] [Google Scholar]
- Sun W.-Y.; Kusukawa T.; Fujita M. Electrochemically Driven Clathration/Declathration of Ferrocene and Its Derivatives by a Nanometer-Sized Coordination Cage. J. Am. Chem. Soc. 2002, 124 (39), 11570–11571. 10.1021/ja0206285. [DOI] [PubMed] [Google Scholar]
- Croue V.; Goeb S.; Salle M. Metal-driven self-assembly: the case of redox-active discrete architectures. Chem. Commun. 2015, 51 (34), 7275–7289. 10.1039/C5CC00597C. [DOI] [PubMed] [Google Scholar]
- Plessius R.; Orth N.; Ivanović-Burmazović I.; Siegler M. A.; Reek J. N. H.; van der Vlugt J. I. Reversible multi-electron storage in dual-site redox-active supramolecular cages. Chem. Commun. 2019, 55 (84), 12619–12622. 10.1039/C9CC07138E. [DOI] [PubMed] [Google Scholar]
- Tominaga M.; Suzuki K.; Kawano M.; Kusukawa T.; Ozeki T.; Sakamoto S.; Yamaguchi K.; Fujita M. Finite, Spherical Coordination Networks that Self-Organize from 36 Small Components. Angew. Chem., Int. Ed. 2004, 43 (42), 5621–5625. 10.1002/anie.200461422. [DOI] [PubMed] [Google Scholar]
- Harris K.; Sun Q.-F.; Sato S.; Fujita M. M12L24 Spheres with Endo and Exo Coordination Sites: Scaffolds for Non-Covalent Functionalization. J. Am. Chem. Soc. 2013, 135 (34), 12497–12499. 10.1021/ja4043609. [DOI] [PubMed] [Google Scholar]
- Tominaga M.; Suzuki K.; Murase T.; Fujita M. 24-Fold Endohedral Functionalization of a Self-Assembled M12L24 Coordination Nanoball. J. Am. Chem. Soc. 2005, 127 (34), 11950–11951. 10.1021/ja054069o. [DOI] [PubMed] [Google Scholar]
- Fujita D.; Takahashi A.; Sato S.; Fujita M. Self-Assembly of Pt(II) Spherical Complexes via Temporary Labilization of the Metal–Ligand Association in 2,2,2-Trifluoroethanol. J. Am. Chem. Soc. 2011, 133 (34), 13317–13319. 10.1021/ja2059236. [DOI] [PubMed] [Google Scholar]
- Yan X.; Wei P.; Liu Y.; Wang M.; Chen C.; Zhao J.; Li G.; Saha M. L.; Zhou Z.; An Z.; Li X.; Stang P. J. Endo- and Exo-Functionalized Tetraphenylethylene M12L24 Nanospheres: Fluorescence Emission inside a Confined Space. J. Am. Chem. Soc. 2019, 141 (24), 9673–9679. 10.1021/jacs.9b03885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kikuchi T.; Murase T.; Sato S.; Fujita M. Polymerisation of an Anionic Monomer in a Self-Assembled M12L24 Coordination Sphere with Cationic Interior. Supramol. Chem. 2008, 20 (1–2), 81–94. 10.1080/10610270701742579. [DOI] [Google Scholar]
- Bentley C. L.; Bond A. M.; Hollenkamp A. F.; Mahon P. J.; Zhang J. Applications of convolution voltammetry in electroanalytical chemistry. Anal. Chem. 2014, 86 (4), 2073–81. 10.1021/ac4036422. [DOI] [PubMed] [Google Scholar]
- Lee K. J.; Elgrishi N.; Kandemir B.; Dempsey J. L. Electrochemical and spectroscopic methods for evaluating molecular electrocatalysts. Nat. Rev. Chem. 2017, 1, 0039 10.1038/s41570-017-0039. [DOI] [Google Scholar]
- Nicholson R. S. Theory and Application of Cyclic Voltammetry for Measurement of Electrode Reaction Kinetics. Anal. Chem. 1965, 37 (11), 1351–1355. 10.1021/ac60230a016. [DOI] [Google Scholar]
- Paul H. J.; Leddy J. Direct Determination of the Transfer-Coefficient from Cyclic Voltammetry - Isopoints as Diagnostics. Anal. Chem. 1995, 67 (10), 1661–1668. 10.1021/ac00106a003. [DOI] [Google Scholar]
- Guidelli R.; Compton R. G.; Feliu J. M.; Gileadi E.; Lipkowski J.; Schmickler W.; Trasatti S. Defining the transfer coefficient in electrochemistry: An assessment (IUPAC Technical Report). Pure Appl. Chem. 2014, 86 (2), 245. 10.1515/pac-2014-5026. [DOI] [Google Scholar]
- Grampp G.; Kapturkiewicz A.; Jaenicke W. Homogeneous and Heterogeneous Electron Transfer Rates of the Tetrathiafulvalene-System. Ber. Bunsenges. Phys. Chem. 1990, 94 (4), 439–447. 10.1002/bbpc.19900940403. [DOI] [Google Scholar]
- Nlate S.; Ruiz J.; Blais J.-C.; Astruc D. Ferrocenylsilylation of dendrons: a fast convergent route to redox-stable ferrocene dendrimers. Chem. Commun. 2000, (5), 417–418. 10.1039/a908791e. [DOI] [PubMed] [Google Scholar]
- Astruc D. Ferrocenyl dendrimers: multi-electron redox reagents and their applications. New J. Chem. 2011, 35 (4), 764–772. 10.1039/c0nj00875c. [DOI] [Google Scholar]
- Cuadrado I.; Morán M.; Casado C. M.; Alonso B.; Lobete F.; García B.; Ibisate M.; Losada J. Ferrocenyl-Functionalized Poly(propylenimine) Dendrimers. Organometallics 1996, 15 (25), 5278–5280. 10.1021/om9605948. [DOI] [Google Scholar]
- Green S. J.; Pietron J. J.; Stokes J. J.; Hostetler M. J.; Vu H.; Wuelfing W. P.; Murray R. W. Three-Dimensional Monolayers: Voltammetry of Alkanethiolate-Stabilized Gold Cluster Molecules. Langmuir 1998, 14 (19), 5612–5619. 10.1021/la9803629. [DOI] [Google Scholar]
- Molina A.; Gonzalez J.; Laborda E.; Compton R. G. On the meaning of the diffusion layer thickness for slow electrode reactions. Phys. Chem. Chem. Phys. 2013, 15 (7), 2381–2388. 10.1039/c2cp43650g. [DOI] [PubMed] [Google Scholar]
- Szalóki G.; Croué V.; Carré V.; Aubriet F.; Alévêque O.; Levillain E.; Allain M.; Aragó J.; Ortí E.; Goeb S.; Sallé M. Controlling the Host–Guest Interaction Mode through a Redox Stimulus. Angew. Chem., Int. Ed. 2017, 56 (51), 16272–16276. 10.1002/anie.201709483. [DOI] [PubMed] [Google Scholar]
- Sudy B.; Rasmussen K.; Grampp G. ESR studies on the pressure and temperature dependence of electron self-exchange kinetics between tetrathiafulvalene (TTF) and its radical cation in ionic liquids and organic solvents. Mol. Phys. 2015, 113 (11), 1378–1385. 10.1080/00268976.2014.995144. [DOI] [Google Scholar]
- Riplinger C.; Kao J. P. Y.; Rosen G. M.; Kathirvelu V.; Eaton G. R.; Eaton S. S.; Kutateladze A.; Neese F. Interaction of Radical Pairs Through-Bond and Through-Space: Scope and Limitations of the Point–Dipole Approximation in Electron Paramagnetic Resonance Spectroscopy. J. Am. Chem. Soc. 2009, 131 (29), 10092–10106. 10.1021/ja901150j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coskun A.; Spruell J. M.; Barin G.; Fahrenbach A. C.; Forgan R. S.; Colvin M. T.; Carmieli R.; Benítez D.; Tkatchouk E.; Friedman D. C.; Sarjeant A. A.; Wasielewski M. R.; Goddard W. A.; Stoddart J. F. Mechanically Stabilized Tetrathiafulvalene Radical Dimers. J. Am. Chem. Soc. 2011, 133 (12), 4538–4547. 10.1021/ja110584c. [DOI] [PubMed] [Google Scholar]
- Yoshizawa M.; Kumazawa K.; Fujita M. Room-Temperature and Solution-State Observation of the Mixed-Valence Cation Radical Dimer of Tetrathiafulvalene, [(TTF)2]+•, within a Self-Assembled Cage. J. Am. Chem. Soc. 2005, 127 (39), 13456–13457. 10.1021/ja053508g. [DOI] [PubMed] [Google Scholar]
- Spruell J. M.; Coskun A.; Friedman D. C.; Forgan R. S.; Sarjeant A. A.; Trabolsi A.; Fahrenbach A. C.; Barin G.; Paxton W. F.; Dey S. K.; Olson M. A.; Benítez D.; Tkatchouk E.; Colvin M. T.; Carmielli R.; Caldwell S. T.; Rosair G. M.; Hewage S. G.; Duclairoir F.; Seymour J. L.; Slawin A. M. Z.; Goddard W. A.; Wasielewski M. R.; Cooke G.; Stoddart J. F. Highly stable tetrathiafulvalene radical dimers in [3]catenanes. Nat. Chem. 2010, 2 (10), 870–879. 10.1038/nchem.749. [DOI] [PubMed] [Google Scholar]
- Bejger C.; Davis C. M.; Park J. S.; M. Lynch V.; Love J. B.; Sessler J. L. Palladium Induced Macrocyclic Preorganization for Stabilization of a Tetrathiafulvalene Mixed-Valence Dimer. Org. Lett. 2011, 13 (18), 4902–4905. 10.1021/ol201992x. [DOI] [PubMed] [Google Scholar]
- Torrance J. B.; Scott B. A.; Welber B.; Kaufman F. B.; Seiden P. E. Optical properties of the radical cation tetrathiafulvalenium (TTF)+ in its mixed-valence and monovalence halide salts. Phys. Rev. B: Condens. Matter Mater. Phys. 1979, 19 (2), 730–741. 10.1103/PhysRevB.19.730. [DOI] [Google Scholar]
- Faour L.; Adam C.; Gautier C.; Goeb S.; Allain M.; Levillain E.; Canevet D.; Sallé M. Redox-controlled hybridization of helical foldamers. Chem. Commun. 2019, 55 (40), 5743–5746. 10.1039/C9CC02498K. [DOI] [PubMed] [Google Scholar]
- Wang W.-K.; Chen Y.-Y.; Wang H.; Zhang D.-W.; Liu Y.; Li Z.-T. Tetrathiafulvalene-Based Macrocycles Formed by Radical Cation Dimerization: The Role of Intramolecular Hydrogen Bonding and Solvent. Chem. - Asian J. 2014, 9 (4), 1039–1044. 10.1002/asia.201301729. [DOI] [PubMed] [Google Scholar]
- Zhang D.-W.; Tian J.; Chen L.; Zhang L.; Li Z.-T. Dimerization of Conjugated Radical Cations: An Emerging Non-Covalent Interaction for Self-Assembly. Chem. - Asian J. 2015, 10 (1), 56–68. 10.1002/asia.201402805. [DOI] [PubMed] [Google Scholar]
- Fumanal M.; Capdevila-Cortada M.; Miller J. S.; Novoa J. J. Keys for the Existence of Stable Dimers of Bis-tetrathiafulvalene (bis-TTF)-Functionalized Molecular Clips Presenting [TTF]•+···[TTF]•+ Long, Multicenter Bonds at Room Temperature. J. Am. Chem. Soc. 2013, 135 (37), 13814–13826. 10.1021/ja405352p. [DOI] [PubMed] [Google Scholar]
- Rosokha S. V.; Kochi J. K. Molecular and Electronic Structures of the Long-Bonded π-Dimers of Tetrathiafulvalene Cation-Radical in Intermolecular Electron Transfer and in (Solid-State) Conductivity. J. Am. Chem. Soc. 2007, 129 (4), 828–838. 10.1021/ja064166x. [DOI] [PubMed] [Google Scholar]
- Diggle J. W.; Parker A. J. Solvation of ions—XX. The ferrocene—ferricinium couple and its role in the estimation of free energies of transfer of single ions. Electrochim. Acta 1973, 18 (12), 975–979. 10.1016/0013-4686(73)87030-6. [DOI] [Google Scholar]
- Kadish K. M.; Ding J. Q.; Malinski T. Resistance of nonaqueous solvent systems containing tetraalkylammonium salts. Evaluation of heterogeneous electron transfer rate constants for the ferrocene/ferrocenium couple. Anal. Chem. 1984, 56 (9), 1741–1744. 10.1021/ac00273a051. [DOI] [PubMed] [Google Scholar]
- Abbott A. P.; Miaw C. L.; Rusling J. F. Correlations between solvent polarity scales and electron transfer kinetics and an application to micellar media. J. Electroanal. Chem. 1992, 327 (1), 31–46. 10.1016/0022-0728(92)80134-P. [DOI] [Google Scholar]
- Jarošová R.; De Sousa Bezerra P. M.; Munson C.; Swain G. M. Assessment of heterogeneous electron-transfer rate constants for soluble redox analytes at tetrahedral amorphous carbon, boron-doped diamond, and glassy carbon electrodes. Phys. Status Solidi A 2016, 213 (8), 2087–2098. 10.1002/pssa.201600339. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.