A deep learning-based approach for automatic segmentation and quantification of the left ventricle from cardiac cine MR images

Abstract

Cardiac MRI has been widely used for noninvasive assessment of cardiac anatomy and function as well as heart diagnosis. The estimation of physiological heart parameters for heart diagnosis essentially require accurate segmentation of the Left ventricle (LV) from cardiac MRI. Therefore, we propose a novel deep learning approach for the automated segmentation and quantification of the LV from cardiac cine MR images. We aim to achieve lower errors for the estimated heart parameters compared to the previous studies by proposing a novel deep learning segmentation method. Our framework starts by an accurate localization of the LV blood pool center-point using a fully convolutional neural network (FCN) architecture called FCN1. Then, a region of interest (ROI) that contains the LV is extracted from all heart sections. The extracted ROIs are used for the segmentation of LV cavity and myocardium via a novel FCN architecture called FCN2. The FCN2 network has several bottleneck layers and uses less memory footprint than conventional architectures such as U-net. Furthermore, a new loss function called radial loss that minimizes the distance between the predicted and true contours of the LV is introduced into our model. Following myocardial segmentation, functional and mass parameters of the LV are estimated. Automated Cardiac Diagnosis Challenge (ACDC-2017) dataset was used to validate our framework, which gave better segmentation, accurate estimation of cardiac parameters, and produced less error compared to other methods applied on the same dataset. Furthermore, we showed that our segmentation approach generalizes well across different datasets by testing its performance on a locally acquired dataset. To sum up, we propose a deep learning approach that can be translated into a clinical tool for heart diagnosis.

1. Introduction

Cardiovascular diseases (CVDs) are serious health problems as they account for the highest rate of mortality worldwide (WHO, 2017). In the US, approximately 836,546 die each year suffering from CVDs (Association, 2018). Cardiac magnetic resonance (CMR) is a valuable imaging technique that provides the cardiologist with a non-invasive quantitative assessment for the heart function. Through segmentation of the LV from short-axis view CMR cine images, the cardiologist can obtain functional heart parameters such as end-systolic volume (ESV), end-diastolic volume (EDV), ejection fraction (EF), wall mass, and regional indexes (e.g., wall thickening) (Frangi et al., 2001). Tissue motion estimation is an established field in medical imaging (Gao et al., 2017b,a). Myocardial tissue tracking is a valuable method for the assessment of myocardial strain (Amzulescu et al., 2019). The mentioned parameters are important for heart diagnosis and treatment. However, they require accurate determination of the myocardial walls. Manual segmentation of LV consumes significant effort and time and is prone to inter- and intra-subject variability (Souto et al., 2013). Therefore, there is a need for developing accurate techniques for automatic extraction of LV cavity and myocardium in an effort to provide more accurate estimation of ventricular metrics.

Recently, deep learning has achieved outstanding success over traditional image processing techniques in many medical image analysis fields (Litjens et al., 2017; Abdeltawab et al., 2019). Deep learning is a branch of machine learning that has the power of learning the right representation from the data itself, avoiding the burden of performing feature engineering on the underlying data. The learned representation resembles a hierarchy of progressively abstract concepts, where each concept is described by less abstract, simpler concepts (Goodfellow et al., 2016). Convolutional neural network (CNN) is a deep learning model that is efficient in processing 2D or 3D image data and has performed well in computer vision tasks (Krizhevsky et al., 2012; Herath et al., 2017). CNN was initially used for image classification, where the whole image is assigned to a certain class. However, CNN is now remodeled for image segmentation tasks via building a fully convolutional neural network (FCN) that replaces the full connected layers in CNN by convolution layers. In a FCN architecture, dense classification is applied in the image domain and each pixel is assigned to the class with the highest predicted probability.

The success of CNN in image analysis and the need for accurate estimation of LV parameters motivated us to build a framework for heart function quantification with a reasonable accuracy compared with the human operator. In this paper, we propose a novel fully automated method for the segmentation of LV cavity and myocardium and the estimation of physiological heart parameters from cine CMR images. Our main contribution is the accurate quantification of the LV functional parameters and the achievement of a lower error compared to previous methods applied on the same cardiac dataset. We reached our goal by proposing a novel framework that is based on FCNs and has the following contributions:

• The extraction of a region-of-interest (ROI) that encompasses the LV from CMR images using an efficient method that is based on FCN. ROI extraction before final cardiac segmentation alleviates the class-imbalance problem and reduces the computational and memory requirement.

• A novel FCN architecture for cardiac segmentation following ROI extraction. The network follows the same idea of the U-net of passing the input to a contracting path followed by an expanding path. However, it has several bottleneck layers that refer to different representation to the input. The up-sampling of these layers are combined to obtain the final segmentation. The proposed architecture has less number of parameters than the established models such as U-net (Ronneberger et al., 2015), yet it demonstrated a better performance.

• A novel loss function called radial loss that minimizes the difference between the predicted LV contours and the ground truth contours was incorporated with the cross-entropy loss.

• The generalization strength of our proposed segmentation approach was evaluated by measuring the segmentation performance of our approach when trained on the whole ACDC training dataset and tested on another dataset (local dataset). We achieved good segmentation accuracy which was comparable to another model that used only our local dataset.

2. Related work

Segmentation of the LV from cardiac cine MR images has received considerable attention over the past years. Researchers started by proposing semi-automatic segmentation approaches as reviewed by Petitjean and Dacher (2011). These methods such as presented in Auger et al. (2014), Grosgeorge et al. (2013), Peng et al. (2016), Ayed et al. (2012) used active contours, graph cut, dynamic programming, or atlas-based techniques. However, semi-automatic methods require significant user intervention which makes it unsuitable for applications where segmentation’s speed is crucial. As a remedy of that limitation, fully-automatic methods have been introduced in heart segmentation literature. Among automatic methods are the Level-set approaches proposed in Liu et al. (2016) and Queirós et al. (2014). Although their methods result in accurate segmentation, level-set needs initialization and it is modeled to segment one anatomical structure only. Traditional image processing operations such as thresholding, edge detection and morphology procession, have been proposed in Wang et al. (2015), Ringenberg et al. (2014). However these methods do not perform well when their prior assumptions are not satisfied. Furthermore, shape priors have been integrated in cardiac segmentation approaches, such as the work in Woo et al. (2013), Wu et al. (2013), Bai et al. (2015). However, imperfect prior information does not achieve optimal segmentation. The shape prior might be based on specific assumptions that may not be valid for a given testing image. On the other hand, deep learning has the power of representation learning given enough training dataset. Therefore, in deep learning there is no need for shape prior information because the FCN will learn how to segment the LV automatically from a test image.

Deep learning achieved good results in many medical imaging domains. For example, the U-net architecture of Ronneberger et al. (2015) was used for the segmentation of the coronary artery border from the coronary CT angiography images (Gao et al., 2020). The authors firstly applied Hough Transform for aorta detection and coronary artery localization. Also, a CNN was used for vessel border detection in intracoronary images (Gao et al., 2019a). Gao et al. (2019b) implemented a deep neural network in a framework aimed to implicit strain reconstruction from radio frequency images. They added privileged-information into network’s training to help it achieve the actual process of ultrasound elastography. The first application of FCN in CMR image segmentation was proposed by Tran (2016) where a region of interest (ROI) centered at the heart cavity was extracted from the image before segmentation. The cavity center was assumed to be at the image center which might not be true in all circumstances. Poudel et al. (2016) proposed a recurrent FCN by modifying the U-net. They used the spatial dependencies between slices during the segmentation of the endocardium of LV. Tan et al. (2017) segmented the LV by applying linear regression using CNN. Their approach consists of two primary stages: finding the LV center followed by the estimation of the radiuses of the endo-cardial contour (EnC), and epicardial contour (EpC) in polar space. Oktay et al. (2018) presented a regularized CNN by the addition of anatomical prior. Their model is suited for cardiac image analysis tasks such as segmentation and enhancement. Zheng et al. (2018) proposed an iterative cardiac segmentation method that starts from the base to the apex of the LV. In each iteration, a new form of the U-net segments the heart and the output is used to predict the segmentation of the next slice to maintain 3D consistency. Furthermore, Bai et al. (2018) used a FCN that is inspired from VGG-16 network (Simonyan and Zisserman, 2014) to segment the LV and right ventricle (RV) from the short axis CMR and the right atrium and left atrium from long-axis CMR. Khened et al. (2019) presented a new computationally efficient DenseNet that is based on FCN for cardiac segmentation. They estimated clinical indices from the segmentation maps to develop a system for heart disease classification. Tao et al. (2019) used U-net to implement a framework for automated estimation of left ventricular parameters from CMR. They assessed the performance of their method by a multi-vendor and multi-center datasets.

3. Materials and methods

Fig. 1 shows our framework of automated cardiac segmentation, and estimation of LV functional parameters and mass. The steps of our framework are (i) extraction of an ROI centered at the center of LV cavity using a deep learning network called FCN1, (ii) ROI cropping for all CMR images, (iii) segmentation of the LV cavity and myocardium using a deep learning network called FCN2, and (iv) estimation of LV functional parameters and mass. The following sections illustrate the pipeline in detail.

Fig. 1.

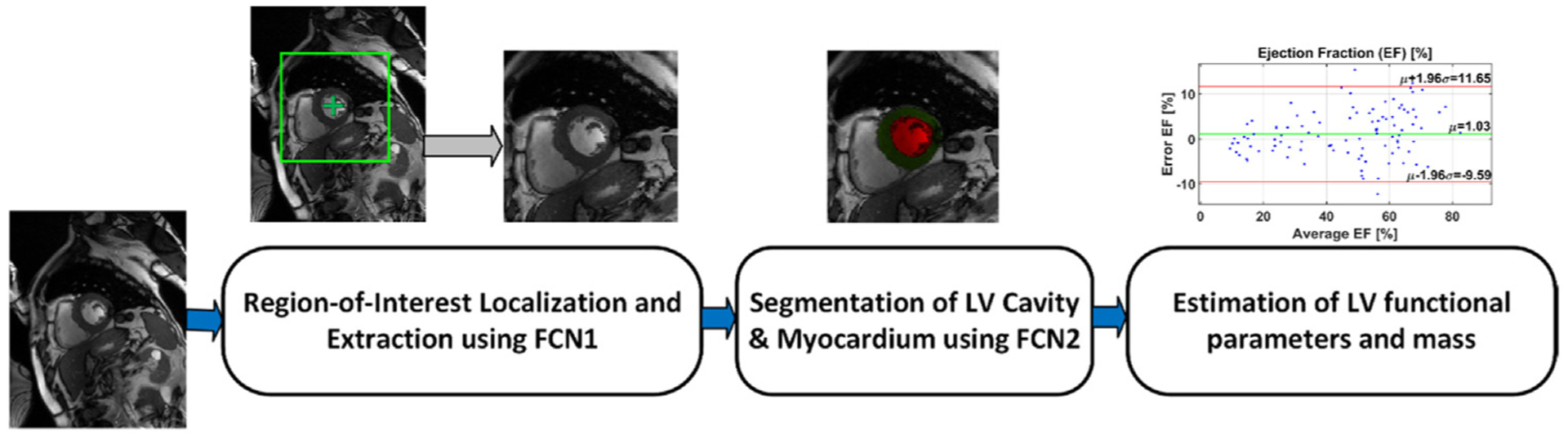
The proposed framework for automated cardiac segmentation, and estimation of LV functional parameters and mass.

3.1. Region-of-interest (ROI) extraction

The short-axis CMR images contain the heart and other surrounding tissues that dominate most of the image. In such cases, deep learning models that perform dense classification in the image spatial domain tend to be biased towards the majority class (the surrounding tissues). Therefore, extracting an ROI that localizes the heart tissues is a necessary pre-processing step before the final segmentation of the heart. Furthermore, ROI extraction reduces the computational cost and boosts speed. In our pipeline, the ROI was extracted using a bounding box of size 128 × 128 pixels that was centered at the LV cavity center point. We estimated the LV center point by a deep learning approach that uses a FCN, called FCN1, which is similar to the U-net. The ROI extraction process is depicted in Fig. 2.

Fig. 2.

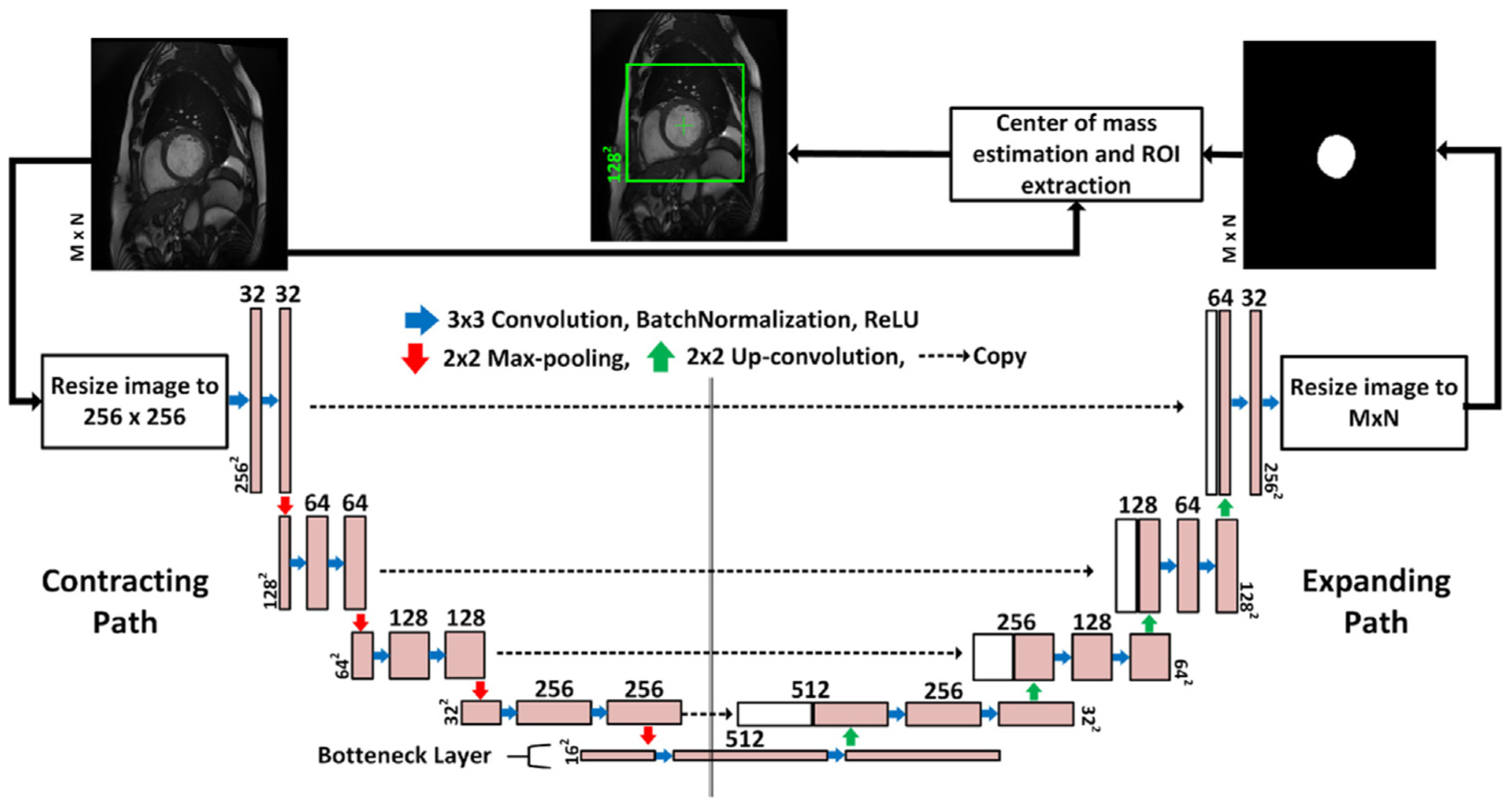
The LV-ROI extraction process using a fully convolutional network named FCN1. The input to the network is the original 2D CMR images which are re-sized to 256 × 256 pixels and the output is segmentation maps for the LV cavity, which are re-sized again to the same spatial dimension as the input. The blue arrow indicates convolution operation with a kernel size 3 × 3, and the number of kernels increases from 32 to 512 in the contracting path, and decreases from 512 to 1 in the expanding path. Zero-padding was used to maintain the same spatial resolution after convolution. The red (green) arrow refers to max-pooling (up-convolution) operation that decreases (increases) the spatial dimension by a factor of 2. Finally, the dashed arrow copies contextual information from the contracting path and concatenates it to the expanding path.

The network was trained to segment the LV cavity from the original CMR images. Then, the ROI center was set to the center of mass of the segmented region. We expected that the output of the network would suffer from the class-imbalance problem that results in a high number of false negative (FN) pixels. However, the primary purpose of this network is to provide an estimate for the LV center point. The LV cavity in apical slices comprises a very small proportion of the whole image. Therefore, the network might fail to segment the cavity due to the high degree of class imbalance. To overcome this problem, the center of LV of the previous slice was used as a center for the slice that results in a black segmentation map from FCN1. By doing so, we maintain the 3D consistency of the LV without harming the overall performance because extracted ROIs that truly do not contain LV tissues will again result in black segmentation maps from FCN2.

Although training a FCN takes time and effort to tune its hyper-parameters, after training our method can extract the LV-ROI in terms of milliseconds which is faster than other methods that use Hough Transform (Khened et al., 2019).

3.2. Cardiac segmentation

The proposed network for the segmentation of the LV cavity and myocardium is shown in Fig. 3. It is based on the FCN that was adapted for segmentation tasks (Long et al., 2015). By convention, the FCN passes the input through a contracting path followed by an expanding path. In the contracting path the spatial dimensions are progressively reduced till a bottleneck layer with an abstract and dense representation of the input. While in the expanding path, the spatial dimensions of the bottleneck are restored to the original input dimensions by applying transposed convolutions. By definition, a bottleneck layer lies between a contracting and an expanding path and has reduced dimensions compared to the previous layer. It contains a representation of the input with a reduced dimensionality (Ronneberger et al., 2015). Our proposed network has several expanding paths that regenerate the input dimensions from several bottlenecks with different representations to the input. Then, the output of each expanding path was concatenated into a single layer which was introduced to an inception module inspired from Google research (Szegedy et al., 2016). The inception module is depicted in Fig. 4. The addition of the inception module which has kernels with different sizes allows the learning of various-scales features. Kernels with small sizes detect small cardiac regions while kernels with larger sizes detect larger cardiac areas and remove the false positive areas that share similar spatial properties as the targeted cardiac area. Finally, the output of the inception module was processed by a convolution layer. To obtain a segmentation map, a sigmoid layer was applied on the output of the network. Network FCN2 contains multiple versions from FCN1 with different depths. In other words, FCN2 has four versions of FCN1’s architecture and they all share the same contracting path. The output of each network is concatenated in one layer to form the final segmentation Fig. 5 shows the relationship between the FCN1 and FCN2.

Fig. 3.

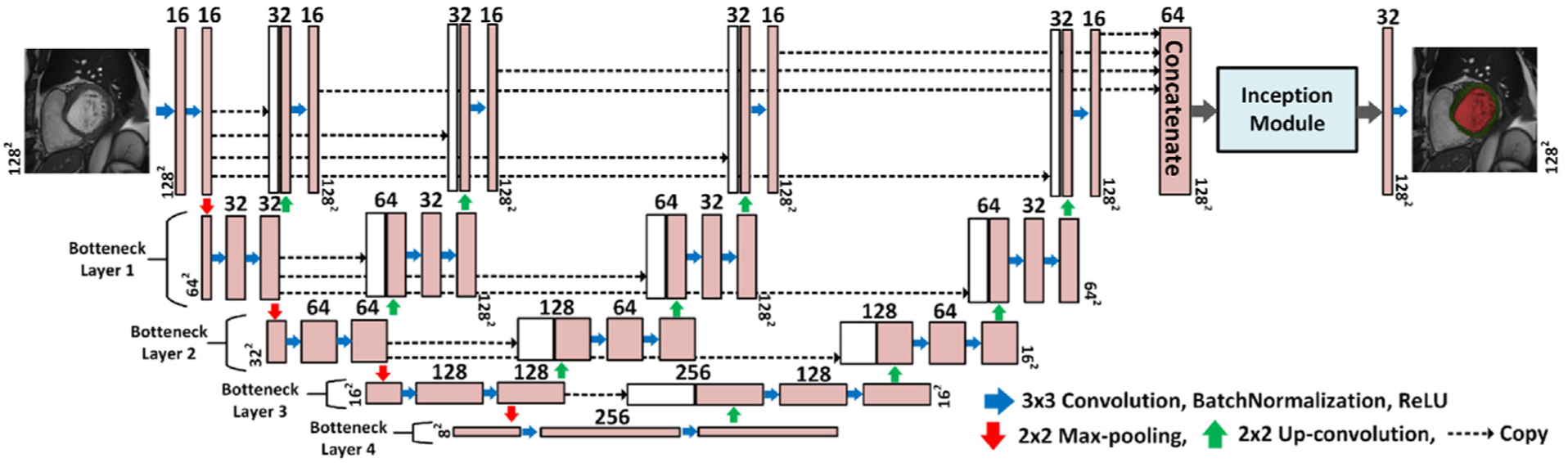
The proposed network architecture for cardiac segmentation. The input to the network is the extracted LV-ROI of size 128 × 128 pixels and the output is the segmentation maps for the LV cavity (red) and mayocardium (green). The blue arrow indicates convolution operation with a kernel size 3 × 3, and the number of kernels increases from 16 to 256 in the contracting path, and decreases from 256 to 1 in the expanding path. Zero-padding was used to maintain the same spatial resolution after convolution. The red (green) arrow refers to max-pooling (up-convolution) operation that decreases (increases) the spatial dimension by a factor of 2. Finally, the dashed arrow copies feature maps from layer to another.

Fig. 4.

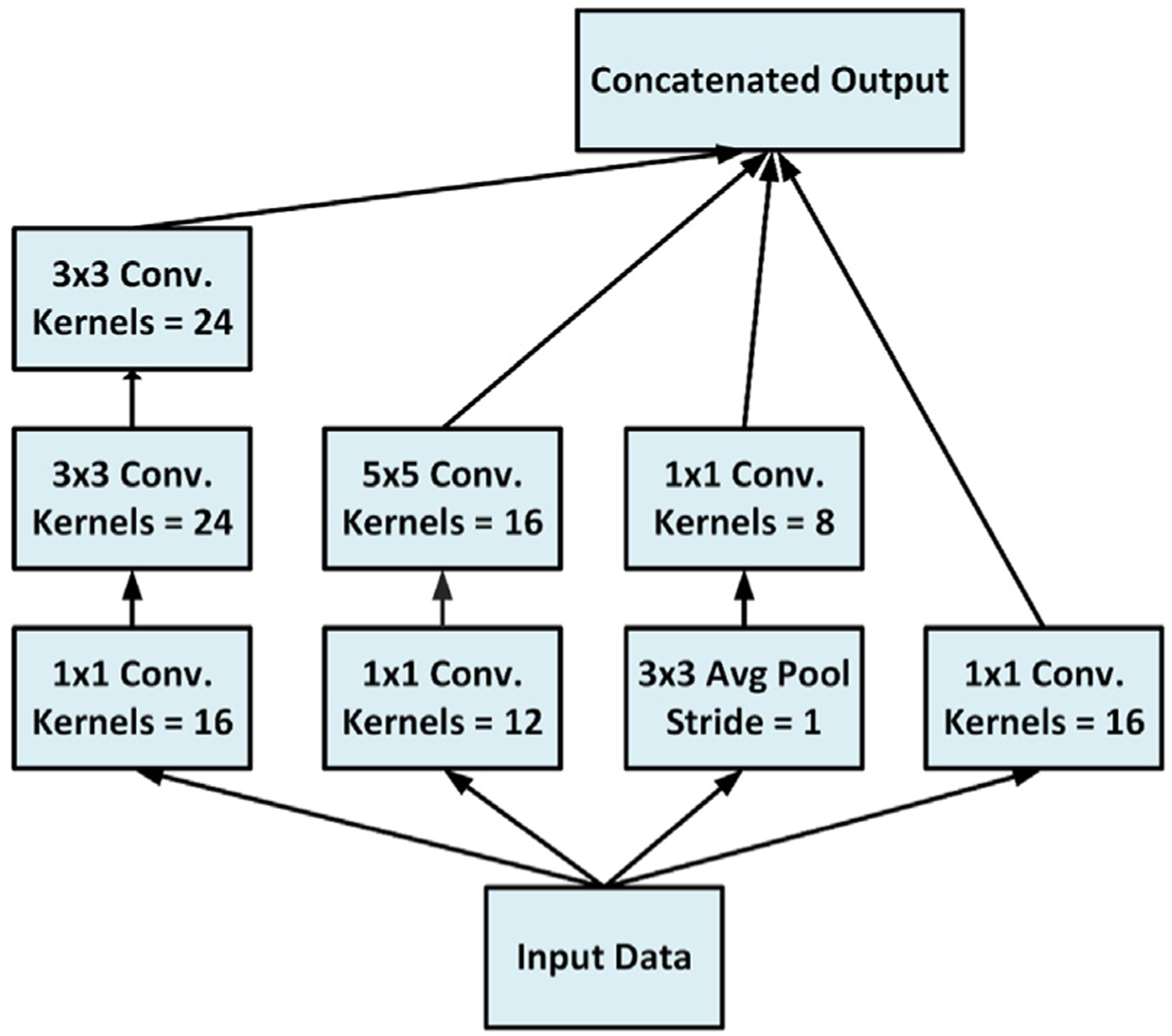
The architecture of the used inception module in FCN2. The module has parallel processing paths with filters of different sizes, i.e.: 1 × 1, 3 × 3, and 5 × 5 convolutions, and 3 × 3 average pooling layers. The resulted feature maps are then concatenated in the final layer.

Fig. 5.

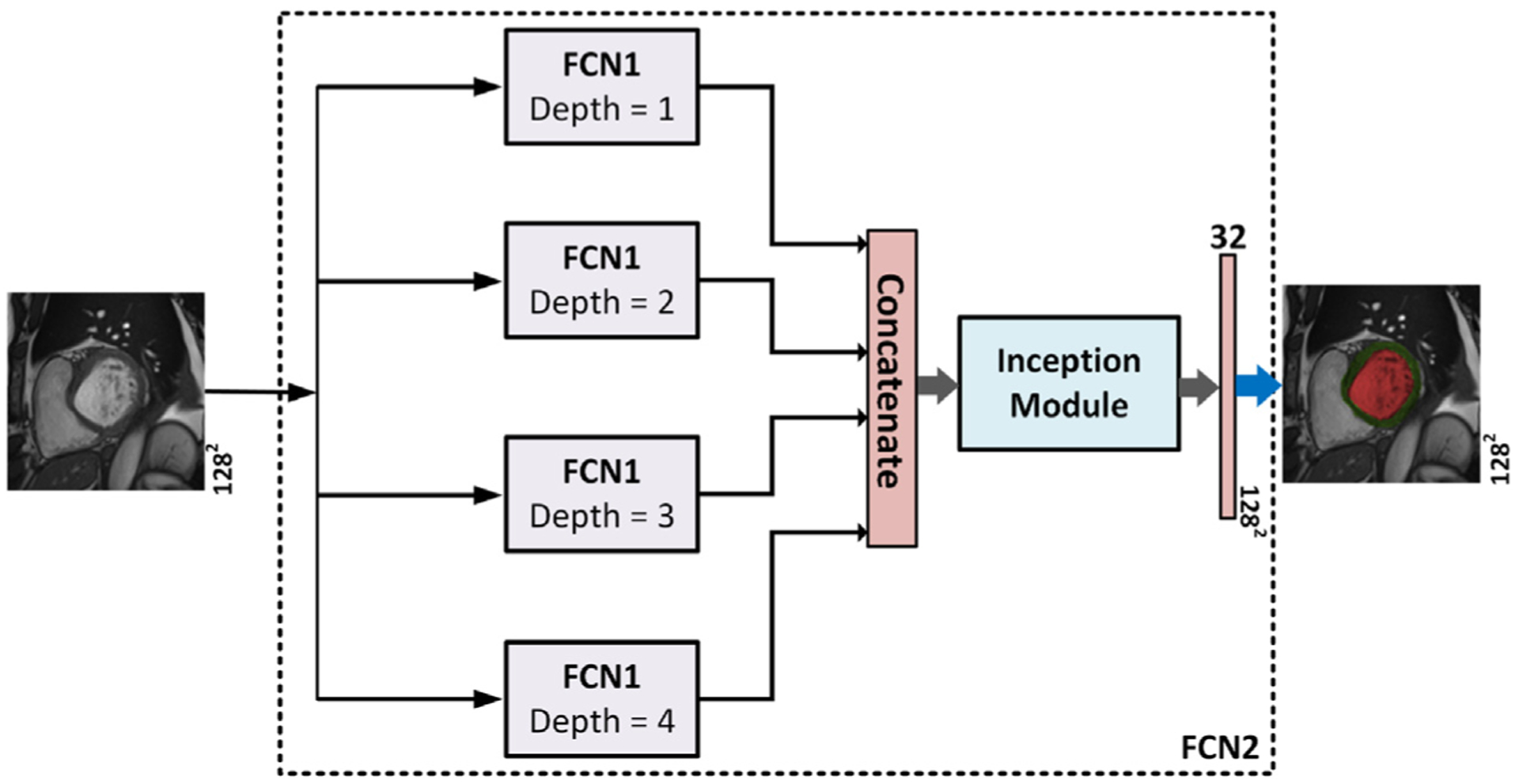
The relationship between network FCN1 and network FCN2. Network FCN2 has four FCN1s with various depths and the output of each network is concatenated to form the final segmentation.

3.3. Loss function

The extraction of an LV ROI from CMR images alleviates the class imbalance problem and boosts the performance of cross entropy (CE) loss. Therefore, we will use CE to keep its advantages, such as smooth training. Furthermore, we propose the radial loss to obtain a good segmentation for the LV contours. There are other loss functions that were proposed in DL segmentation literature and used segmentation metrics as loss functions such as Dice loss (Kamnitsas et al., 2018). However, these approaches produce under-segmented regions with many false positive pixels (Kamnitsas et al., 2018). Consequently, they were excluded from our analysis. Let W refers to the parameters of the trained network, X = {X₁, X₂, …, X_N}refers to the set of training images of size N, and Y = {Y₁, Y₂, …, Y_N} refers to the set of manual segmentation label maps. The CE loss is given by:

$$L_{CE}=-\text{log}p\left(Y_i|X_i,W\right)=-\sum _{c=1}^C\sum _{p_j\in X_i}{Y}_{i,c,p_j}\text{log}{\widehat{Y}}_{i,c,p_j}$$ (1)

Where p(Y_i|X_i, W) represents the predicted probabilistic map resulted form the network after the sigmoid layer when the network’s input is X_i an its parameters W, c refers to class index, p_j refers to a pixel in image X_i, $Y_{i,c,p_j}$ refers to the true probability that pixel p_j belongs to class c, and ${\widehat{Y}}_{i,c,p_j}$ refers to the predicted probability that pixel p_j belongs to class c.

Exploiting the fact that LV has a radial shape, we propose a novel radial loss. The distance between the center of mass point of a segmented region to its surface at a certain radial direction is defined as the radial distance (RD) at that angel. Hence, if we have a segmented region surface S and ground truth surface G, the local radial distance error d at a polar angle θ is defined in (2) and is shown in Fig. 6:

$$d=s_{\theta }-g_{\theta }$$ (2)

where s_θ and g_θ are the RDs from the center of mass point to the surfaces S and G, respectively. Now, by constructing equi-spaced radial lines, we can estimate the RDs for the surfaces S and G and store them in the same radial order in vectors s and g, respectively. The RD loss is defined as L2 penalty:

$$L_{RD}=\frac{1}{M}{\Vert s-g\Vert }_2$$ (3)

where M is the number of constructed radial lines. The surfaces S and G for an image X_i can be obtained by applying a Sobel filter on the predicted probabilistic map Ŷ_i and the ground truth Y_i, respectively. At the beginning of the training, the segmented myocardium from Ŷ_i might be noisy and discontinuous. Therefore, estimating the RDs for a vector s by calculating the distance between the previously estimated LV center point from FCN1 and the border of a region S that encloses this center point, excludes the scattered regions in Ŷ_i that do not belong to the LV. The loss is an Euclidean norm which can be differentiated by a deep learning library. The L_RD can be adapted for both the endo-cardial contour (EnC) and the epicardial contour (EpC) of the LV as follows:

$$L_{RD}=\frac{1}{M}{\Vert s_{EnC}-g_{EnC}\Vert }_2+\frac{1}{M}{\Vert s_{EpC}-g_{EpC}\Vert }_2$$ (4)

Our final loss function is defined as:

$${L=L}_{CE}{+L}_{RD}$$ (5)

Fig. 6.

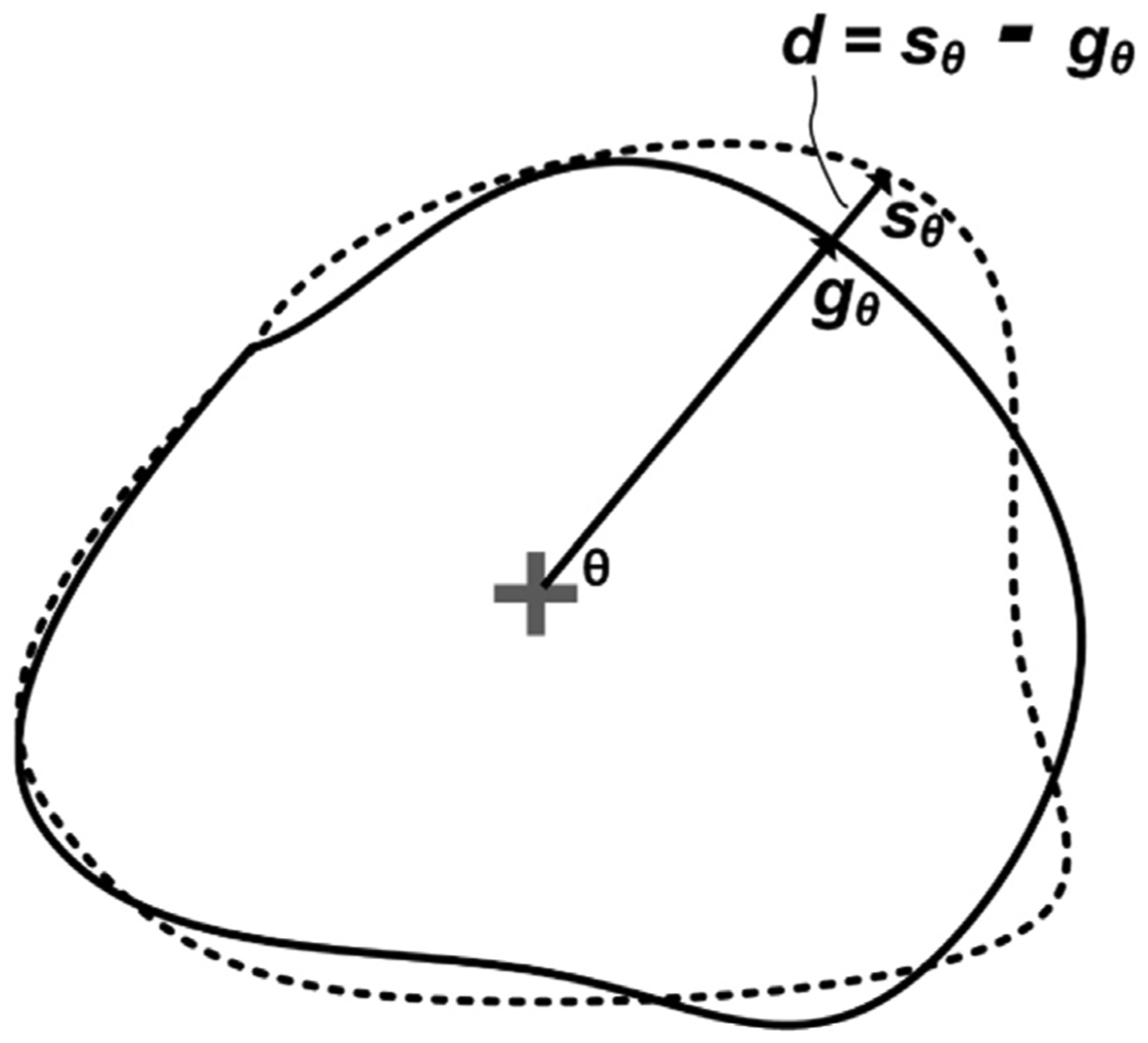
The true contour (solid line) and the predicted contour (dashed line) in polar space where d represents the local radial distance error at a polar angle θ.

3.4. Network training settings

Both FCN1 and FCN2 were built using Pytorch deep learning framework (Paszke et al., 2017). The weights of the convolutional layers were initialized using Kaiming initialization (He et al., 2015). Network’s hyper-parameters are the variables that should be set before network training. These variables determine network architecture such as the number of kernels and network’s training such as the learning rate. We adopted a grid search approach to find the optimal values of the hyper-parameters that achieve the best results in terms of segmentation metrics. The search space for the initial number of kernels was {8, 16, 32}, the learning rate of the Adam (Kingma and Ba, 2014) optimizer was {0.01, 0.001, 0.0001}, the learning momentum was {0.9}, the batch size was {8, 16, 32}, the number of epochs was 100:50:300. Data augmentation is a way to increase the size of the training set and to overcome the problem of over-fitting during the training of deep networks. Therefore, we employed a data augmentation strategy with random translations, scaling, and rotation.

3.5. Physiological heart assessment

Our methodology aims to provide an automatic and accurate way to evaluate the heart function. In this paper, we estimate parameters related to the LV function and mass (Frangi et al., 2001), which are defined as follows:

1. Left ventricular volume (LVV): is the preliminary measure that is required for the derivation of other important parameters such as EF. We used Simpson’s method, which computes LVV as the sum of several smaller volumes with the same configuration.

2. Left ventricular mass (LVM): is used to characterize LV hypertrophy. To estimate the LVM, two assumptions are made: (i) the interventricular septum is part of the LV and (ii) the volume of the myocardium, V_m, is the total volume delineated by EpCs of the LV, V_EpC, minus the LV cavity volume, V_EnC at the phase of end diastole (ED). The LVM can be estimated by multiplying V_m by the density of the myocardial tissue ρ = 1.05 g/cm³:

   $$V_m=V_{EpC}\left(t_{ED}\right)-V_{EnC}\left(t_{ED}\right)$$ (6)

   $$LVM=\rho \times V_m$$ (7)

   For inter-patient comparisons, the LVM is normalized by body weight or total surface area.

3. Stroke volume (SV): is the blood volume ejected between the phase of end diastole (ED) and the phase of end systole (ES).

   $$SV=V_{EnC}\left(t_{ED}\right)-V_{EnC}\left(t_{ES}\right)$$ (8)

   SV can be normalized by the total body surface area to obtain the SV index (SVI).

4. Ejection fraction (EF): is one of the most important parameters for the evaluation of LV function. It is defined as:

   $$EF=\frac{SV}{V_{EnC}\left(t_{ED}\right)}\times 100\%$$ (9)

   Normal values of EF range from 57% to 78% for the LV (Lorenz et al., 1999).

4. Experimental results

4.1. Cardiac datasets

We performed our LV segmentation and function quantification experiments on two different datasets. Namely, a locally-acquired dataset and the publicly available dataset from the ACDC MICCAI challenge 2017 (Bernard et al., 2018).

4.1.1. ACDC-2017 dataset

consists of 150 exams for different patients. According to the physiological heart parameters, the patients are categorized into five classes with equal number of patient. The classes are (i) normal subjects, (ii) patients with previous myocardial infarction, (iii) patients with dilated cardiomyopathy, (iv) patients with hypertrophic cardiomyopathy, and (v) patients with abnormal right ventricle. The dataset was then divided into two sets: (i) a training set consisting of 100 subjects along with their manual annotation at the end diastolic (ED) and the end systolic (ES) phases in all captured heart slices; (ii) a testing set consisting of 50 patients without annotation. The two sets have even distributions of patients classes. The cine CMR images were captured in breath hold with a retrospective or prospective gating and with a SSFP sequence in short-axis orientation. The short-axis slices covered the whole LV. The parameters were: slice thickness = 5 or 8 mm, inter-slice gap = 5 or 8 mm, and spatial resolution = 1.37–1.68 mm²/pixel.

4.1.2. Locally-acquired dataset

was used to assess the generalizability of our segmentation approach across different data distributions. In this dataset, cross-sectional CMR images were collected from eleven patients with a history of myocardial infarction and who were involved in a study approved by the institutional review board (IRB). The dataset consists of 26 CMR scans that cover multiple heart sections and at each section, 25 frames were captured to cover the cardiac cycle. The total number of 2D CMR images is about 6K images. The dataset’s acquisition device was a 1.5 T Espree system, Siemens Medical Solutions Inc., USA with parameters: TR = 4.16 ms, TE = 1.5 ms, angle of flip = 80° and 1 average, slice thickness = 8 mm, and in-plane resolution = 1.4 × 3.1 mm².

4.2. Framework training and validation

We analyzed the performance of our proposed pipeline for the automated segmentation of LV cavity and myocardium, and the estimation of physiological heart parameters using the ACDC dataset, which consists of 100 patients with their manual annotations. We adopted a ten-fold cross-validation to train and validate FCN1, and FCN2. Each fold had an equal number of cases from the five mentioned cardiac diagnoses by stratified sampling. In other words, the networks were trained and tested ten times with a training set of 90 patient data (average of 1800 2D images) and a testing set of 10 patients (average of 200 2D images). Additionally, we tested the generalization of our segmentation method using the locally collected dataset.

The output of the segmentation network is a probabilistic map where each pixel is assigned a probability of belonging to the object. To obtain the final segmented binary image, Otsu thresholding (Otsu, 1979) was applied on the probabilistic map. Furthermore, connected components were determined to remove the false positive pixels. Finally, we applied morphological operations, such as gap filling, to fill the gaps in the resulted binary segmentation. Segmentation accuracy was assessed in terms of the Dice score and Hausdorff distance (HD) metrics.

4.3. Evaluation of LV-ROI extraction

In order to evaluate the performance of our proposed method of LV-ROI extraction, FCN1 was trained and validated by the ACDC dataset in a ten-fold cross-validation scheme, and in each fold the center of mass of the segmented LV cavity P_s was estimated for each image. Then, two metrics were used to assess the network performance; namely (1) the Euclidean distance between the predicted center point P_s and the manually-annotated center of mass of LV cavity P_m, and (2) the percentage of images with predicted ROI that includes all pixels related to LV cavity and myocardium. Table 1 shows the statistics of the Euclidean distance between P_s and P_m for the 1902 images of the ACDC dataset. Our approach achieved an acceptable accuracy and outperformed the approach in Khened et al. (2019). The average time to extract the desired ROIs of one subject at ED and ES phases is about 700 ms. Also, the extracted ROIs contained all the LV cavity and myocardium tissues.

Table 1.

Statistics of the difference in pixels between the LV center of mass point from the manual segmentation (P_m) and the predicted LV center of mass point (P_s) for our approach and the method in Khened et al. (2019). STD stands for standard deviation.

	Mean	STD	Max.
Hough transform (Khened et al., 2019)	4.00	3.83	36.24
Proposed (FCN1)	1.41	1.65	5.00

4.4. Evaluation of the proposed loss function

After ROI extraction, we performed segmentation using FCN2 with L_CE loss only and with the proposed loss L_CE + L_RD. Table 2 shows a comparison between the segmentation performance of the two loss functions for LV cavity and myocardium (MYO). We can see that L_CE alone gave a good performance because the class-imbalance problem was alleviated by the ROI extraction step. On the other hand, the proposed loss showed a superior performance in terms of both Dice score and HD metrics. Furthermore, the proposed loss had a better segmentation quality, as shown in Fig. 7. Thanks to the ability of RD loss to minimize the distance between the true LV contours and the predicted contours.

Table 2.

Comparison between two different loss functions in terms of the average values of segmentation accuracy obtained from a ten-fold cross-validation on the data set.

Loss function	Dice coeff.		HD (mm)
	LV Cavity	MYO	LV Cavity	MYO
LCE	0.93	0.86	9.52	11.41
LCE + LRD	0.94	0.89	6.71	7.13

Fig. 7.

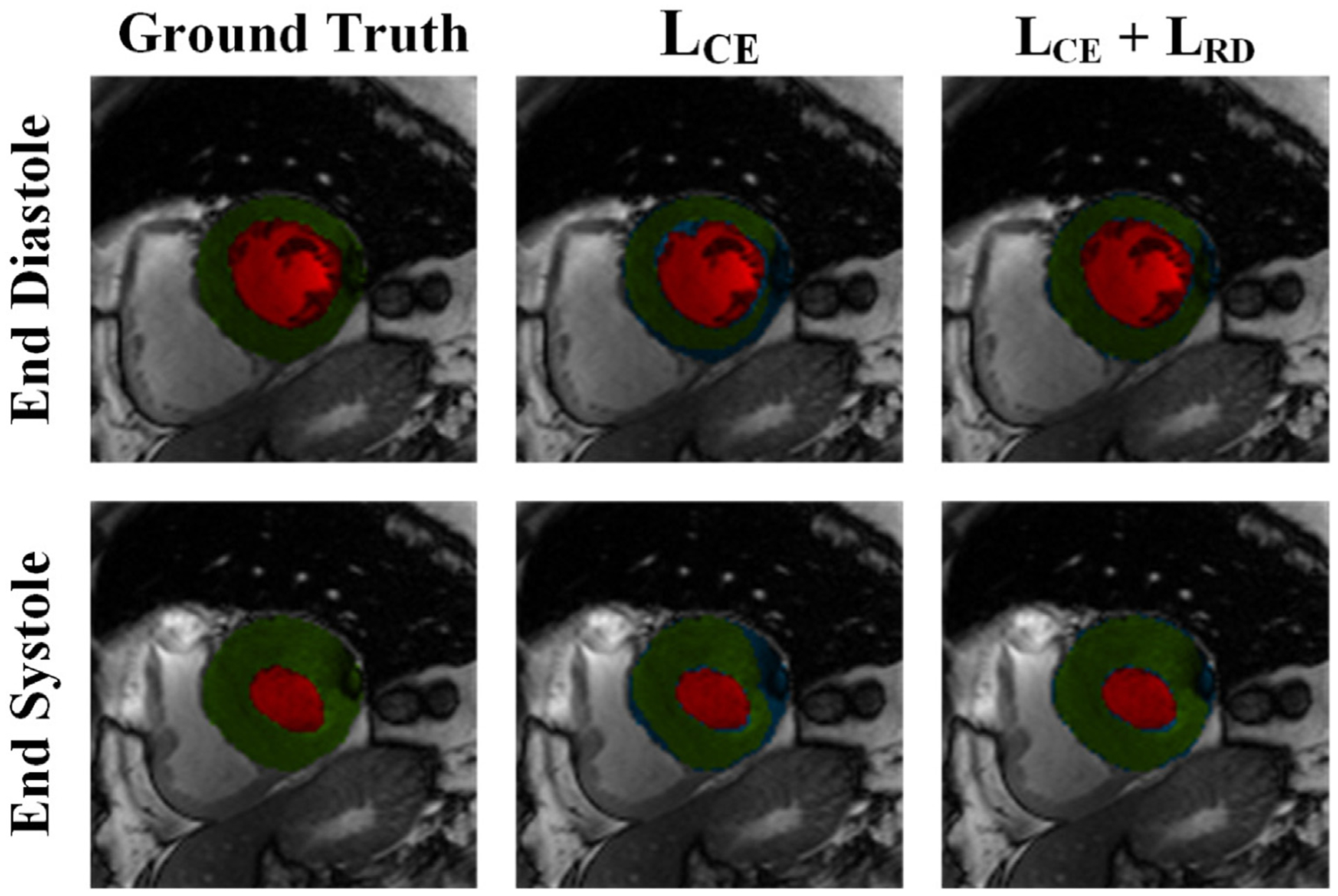
Comparison between the manual segmentation of a LV slice in ED and ES phases, the predicted segmentation from FCN2 with L_CE loss, and the predicted segmentation from FCN2 with proposed loss (L_CE + L_RD). Red, and green regions refer to the LV cavity, and myocardium, respectively, while blue color refers to segmentation error. Visual qualitative improvements in the segmentation can be noticed with the proposed loss function.

4.5. Evaluation of the proposed network model FCN2

To assess the performance of the proposed model FCN2, we compared it with two other models, namely: (1) the original U-net (Ronneberger et al., 2015) with four layers and an initial convolution layer that had 64 kernels, (2) the ConvDeconv net introduced in Noh et al. (2015). All of the three models were trained with the same settings as described in Section 3.4 in a ten-fold cross-validation scheme. Table 3 compares the proposed model FCN2 against the other models in terms of the resulted segmentation accuracy and the required computational cost reflected by the number of learnable parameters. As shown, FCN2 showed the best segmentation quality for all segmented regions. On the other hand, ConvDeconv net had the lowest performance, which might be due to the absence of concatenation connections that add high-resolution features to the expanding path. FCN2 performs better than the original U-net that starts with 64 kernels. Therefore we did not include a U-net with fewer kernels into comparison. Another advantage for FCN2 is that it has fewer parameters, consequently, it needs less GPU memory usage and training time.

Table 3.

Evaluation results for three different segmentation techniques. The values of the segmentation metrics (Dice and HD) are presented as the average values during a ten-fold cross-validation strategy. The table also shows the number of learnable parameters for each model.

Method	Dice coefficient				HD (mm)				# of Param.
	LV Cavity		MYO		LV cavity		MYO
	ED	ES	ED	ES	ED	ES	ED	ES
U-net (Ronneberger et al., 2015)	0.94	0.90	0.83	0.85	8.22	10.53	9.81	11.51	31M
ConvDeconv net (Noh et al., 2015)	0.92	0.88	0.80	0.83	9.14	11.34	10.81	11.95	252M
FCN2 (proposed)	0.96	0.92	0.88	0.89	6.31	7.42	7.11	7.25	2.5M

Fig. 8 shows FCN2’s segmentation results for three different slices of the same heart along with their manual segmentation at ED and ES phases of the cardiac cycle. Overall, the proposed approach gave accurate segmentation with some erroneous results at apical slices. For all of the mentioned analysis, we chose FCN2 segmentation results for the estimation of physiological heart parameters.

Fig. 8.

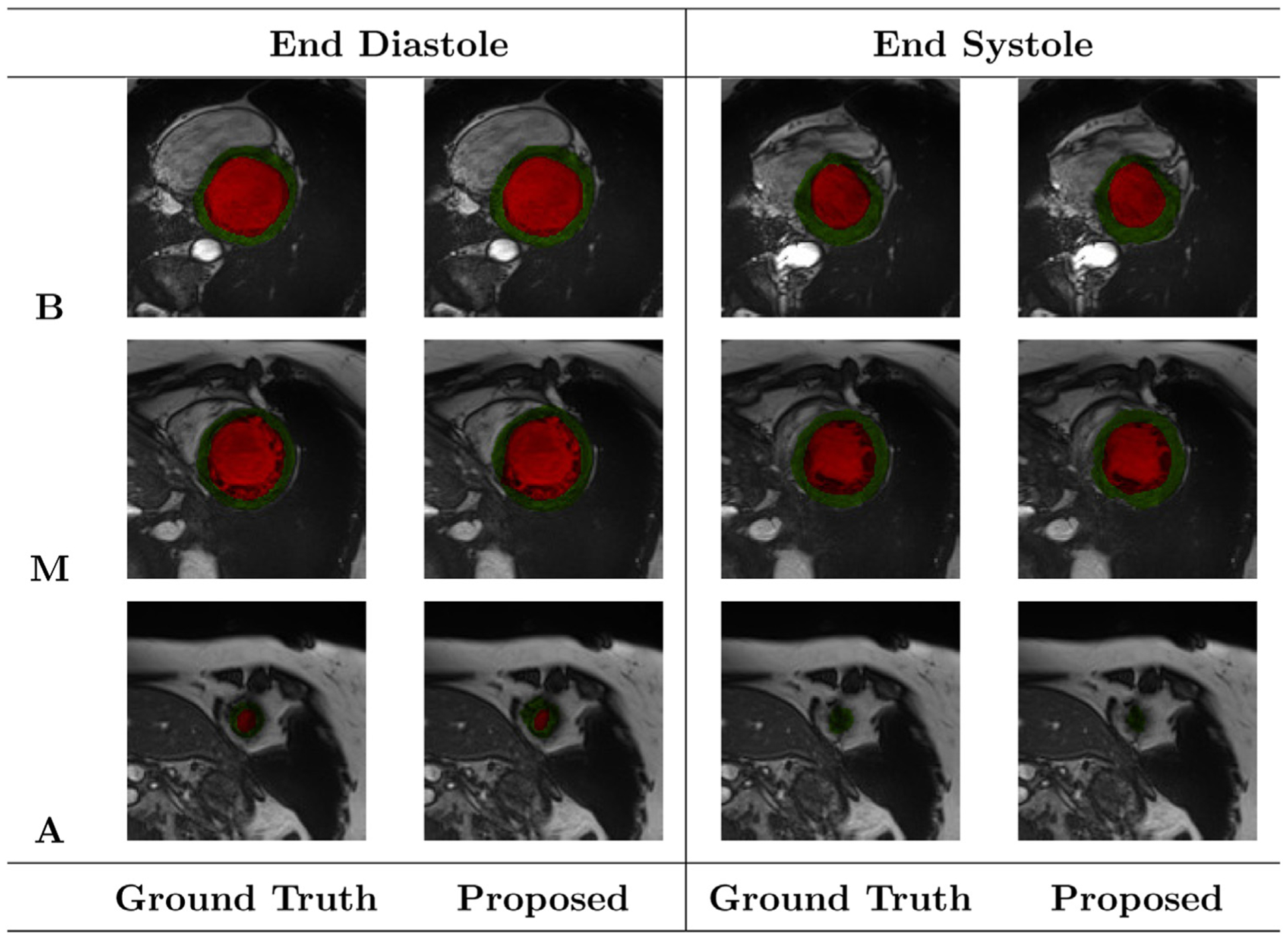
Segmentation results of the FCN2 network at ED and ES phases of one patient during a ten-fold cross-validation. Red, and green regions refer to the LV cavity, and myocardium, respectively. The letters B, M, and A refer to Basal, Mid-cavity, and Apical slices, respectively. The colors red and green indicate LV cavity and LV myocardium, respectively.

4.6. Generalization evaluation

In this section, we evaluate the generalization capability of our proposed segmentation approach. Table 4 compares the segmentation performance of two models:

1. Our approach when the local dataset was used both for training and testing.

2. Our approach when trained on ACDC training dataset and tested on the local dataset.

For the second model, although ACDC dataset is composed of about 1.4K images captured at the ED and ES phases only, our approach achieved good segmentation accuracy for LV segmentation at all cardiac phases of the local dataset. The results of the second model are slightly inferior than the first that use the same dataset distribution. However, the results indicate that our approach generalizes well to different datasets, and it was successful in segmenting the full cardiac cycle image frames when trained only on a dataset that has annotations only in ED and ES phases.

Table 4.

Comparison between two models for our segmentation performance. Model A: Training and testing on the local dataset. Model B: Training on ACDC dataset and testing on the local dataset. The estimates are average values.

Model	Dice coef.		HD (mm)
	LV cavity	MYO	LV cavity	MYO
Model A	0.95	0.87	9.31	8.52
Model B	0.94	0.85	11.12	9.74

4.7. Physiological parameters estimation

Following LV cavity and myocardium segmentations from the CMR images, five functional parameters were estimated; namely the EDV, ESV, LVM, SV, and EF, which were described in Section 3.5. To assess the degree of agreement between the manual segmentation values and the estimated values from the predicted segmentation, Bland-Altman plots (Bland and Altman, 1986) were constructed, as shown in Fig. 9. These plots show the bias μ (average difference) and the 95% agreement limits (σ± 1.96 SD). In Bland-Altman plot, normality of the differences must be verified. Therefore, we applied Shapiro-Wilk test for normality with 5% significance level and the P-values for EDV, ESV, LVM, SV, and EF were 0.082, 0.052, 0.061, 0.154, 0.787, respectively. The P-values are larger than 0.05 and the test accepted normality. Our estimated parameters have an average of only three outlying points which comprise about only 3% of the studied cases.

Fig. 9.

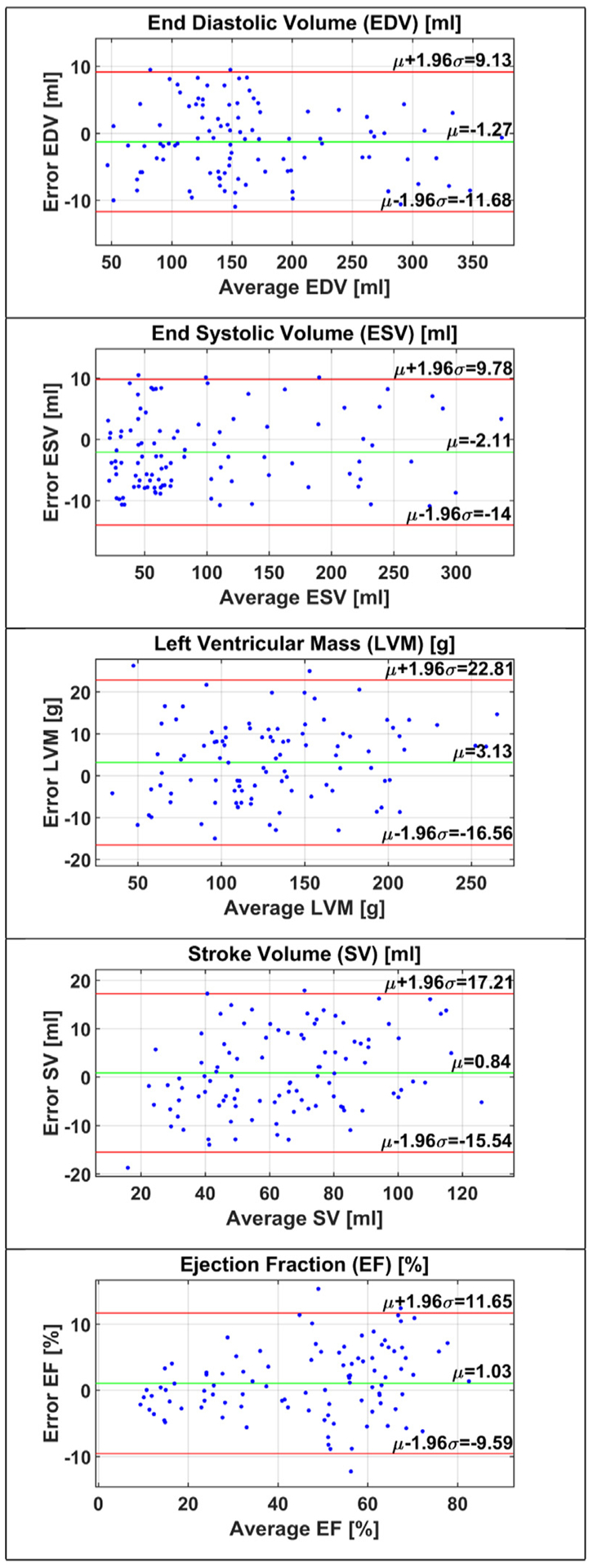
Bland-Altman plots for functional parameters. Top-to-down: EDV, ESV, LVM, SV, and EF, where μ is the bias of the estimated values from the ground truth and μ ± 1.96σ represents the 95% confidence interval. To achieve a good agreement, bias should approach the zero value and the error points should lie within the confidence interval.

Table 5 summarizes the error statistics in EDV, ESV, and EF estimations for our method and other methods applied on the ACDC dataset. The errors of EDV and ESV measures have the lowest bias and standard deviation. Furthermore, error of EF measure has a lower standard deviation than the method in Wolterink et al. (2017). In general, our approach showed acceptable differences that are comparable to intra- and inter-operator variability in the manual estimation of functional parameters from CMR images as reported in Sardanelli et al. (2008), Suinesiaputra et al. (2018).

Table 5.

The differences between the manual and automated estimation of the functional parameters presented as average (std.) for the proposed approach and other approaches applied on the ACDC dataset.

Reference	EDV (ml)	ESV (ml)	EF (%)
Wolterink et al. (2017)	−1.57 (6.31)	−2.51 (7.66)	1.23 (4.99)
Grinias and Tziritas (2017)	1.43 (9.95)	2.61 (17.60)	−0.05 (8.61)
Proposed	−1.27 (5.31)	−2.11 (6.06)	1.03 (5.42)

5. Discussion

In this work we seek a method based on deep learning to develop an efficient segmentation framework that has the capability of providing accurate and automated segmentation to the LV cavity and myocardium in addition to providing accurate quantification of the LV functional parameters that are essential for heart functional assessment. The framework has a novel network architecture and essential contributions are described below.

First, The idea of having an initial network (FCN1) that performs ROI extraction task from original CMR images, established its success by providing accurate estimation of LV center point and faster performance during detection. We compared our method with a method that has the same objective of LV localization and ROI extraction but uses the Hough transform. Table 1 shows how our method outperformed a method that relies on Hough transform for LV localization. Furthermore, our method extracts the ROIs of one subject at ED and ES in only 700 ms and was able to generate ROIs that encompass the desired LV cavity and myocardium tissues. Therefore, our LV-ROI extraction is accurate, fast, and reliable.

The selection of the appropriate ROI size was based on choosing the lowest possible size that produces myocardial segmentation without any clipping for accurate further estimation of physiological heart parameters. In our experiments, we chose an ROI of size 128 × 128 because this was the minimum size that encompasses the LV cavity and myocardium in our cardiac datasets. This ROI size has two advantages: (i) reducing the time and computations requirements during network training and inference. (ii) alleviating the class imbalance problem by removing the unnecessary surrounding tissues. At the end, our implementation can handle arbitrary sizes.

Secondly, our network FCN2 constructs the final segmentation from multiple bottleneck layers, which are considered different representations to the input with different dimensionalities. The network produced accurate segmentation for the LV cavity and myocardium as shown in Fig. 8. It also outperformed popular segmentation models, such as U-net and the ConvDeconv networks in terms of the Dice Score and HD distance as shown in 3. Another advantage of FCN2 is the efficient use of memory and time by requiring a lower number of learnable parameters.

Moreover, the careful choice of the deep learning model components is important for the overall success of the model. Therefore, we implemented a novel loss function called radial loss, which is suitable for the LV segmentation problem due to the underlying radial shape of EnC and EpC. Our final loss is a combination from both the radial loss and the baseline cross-entropy. The latter is widely used in the domain of deep learning segmentation due to its nice differentiable properties and ability to produce smooth training. It is considered the standard loss function in many applications, particularly image segmentation. As shown in Table 2 and Fig. 6, our loss function resulted in a better performance when compared to a loss function composed of cross-entropy alone. The superiority of our method is attributed to the fact that the radial loss works on minimizing the distances between the predicted contours and the actual contours of the LV. On the other hand, cross-entropy alone works on measuring the pixel-wise error between the predicted probability of the predicted mask from the network and the ground truth. Then, it sums these errors for all pixels. Data augmentation is a smart way to avoid over-fitting and to increase the training samples, which is beneficial in the case of limited annotated data. By performing data augmentation, we achieved good average Dice and HD values for the segmentation of LV cavity and myocardium.

In Bland-Altman plots of Fig. 9, the small negative biases of EDV and ESV measurements indicate that they both were slightly underestimated. However, the measurements of ESV had a higher bias than of EDV and, consequently, the estimated EF, defined in (9), had a positive bias. The errors in measurements that are outside the confidence interval of the Bland-Altman plots lead to misdiagnosis for patients with CVD. Therefore, a good heart segmentation method should not produce outlying points by minimizing the segmentation errors that propagate to the next stage of functional parameters estimation.

Additionally, we compared our framework with other frameworks that tried to estimate cardiac parameters from the ACDC dataset to show the advantages of our methods based on the reported errors of each method. In general, our approach gave acceptable errors for the estimated parameters and outperformed the previous methods, as shown in Table 5. Furthermore, it is important to mention that our methodology is not limited to a certain dataset; we showed that good results can be obtained from utilizing a different dataset, even with a model trained by a sparse dataset (ACDC-2017) and tested on a dataset that covers the whole cardiac cycle.

6. Conclusions

In this paper, we proposed a novel deep learning framework, with the ultimate goal of automated quantification of LV function and mass from short-axis CMR images. Our designed FCNs for LV-ROI extraction and LV segmentation demonstrated superior results when applied on the publicly available ACDC 2017 dataset. Furthermore, we reached our goal and our method gives lower error for the estimated parameters when compared to previous methods. The estimated LV function and mass global parameters are frequently used in the clinical practice of cardiac functional analysis. In fact, recent approaches suggested the integration of these parameters with each other for accurate cardiac diagnosis and prediction of cardiovascular events (Mewton et al., 2013). It is noteworthy that the errors of the estimated parameters are comparable to the errors reported when manual delineation of the cardiac structures is the pursued approach. Therefore, our proposed deep learning framework has an established potential for easing and automating the cardiac functional analysis process. Our future work incorporates a complete computer aided diagnostic system for cardiac disease classification and detection.