Assembly and Stability of Simian Virus 40 Polymorphs

Abstract

Understanding viral assembly pathways is of critical importance to biology, medicine and nano-techology. Here, we study the assembly path of a system with various structures, the simian vacuolating virus 40 (SV40) polymorphs. We simulate the templated assembly process of VP1 pentamers, which are the constituents of SV40, into icosahedal shells made of N=12 pentamers (T = 1). The simulations include connections formed between pentamers by C-terminal flexible lateral units, termed here “C-terminal ligands”, which are shown to control assembly behavior and shell dynamics. The model also incorporates electrostatic attractions between the N-terminal peptide strands (ligands) and the negatively charged cargo, allowing for agreement with experiments of RNA templated assembly at various pH and ionic conditions. During viral assembly, pentamers bound to any template increase its effective size due to the length and flexibility of the C-terminal ligands, which can connect to other VP1 pentamers and recruit them to a partially completed capsid. All closed shells formed other than the T = 1 feature the ability to dynamically rearrange and are thus termed “pseudo-closed”. The N=13 shell can even spontaneously “self-correct” by losing a pentamer and become a T = 1 capsid when the template size fluctuates. Bound pentamers recruiting additional pentamers to dynamically rearranging capsids allows closed shells to continue growing via the pseudo-closed growth mechanism for which experimental evidence already exists. Overall, we show that the C-terminal ligands control the dynamic assembly paths of SV40 polymorphs.

Graphical Abstract

Understanding viral assembly pathways is critical to biology¹ and biotechnology.^2–7 In particular, virus-like particles (VLPs) have become attractive candidates for many applications in nano- and bio-technology, such as catalysis,⁸ gene therapy⁹ and vaccination.¹⁰ One extensively studied virus for biological applications is the simian vacuolating virus 40 (SV40), a member of the polyomavirus family. Discovered in 1960,¹¹ SV40 is an enveloped virus that, in vivo, is made of up of 3 unique proteins, VP1, VP2, and VP3. VP2 and VP3 are located on the inner part of the viral capsid, while the outer part is made up of 72 VP1 pentamers.¹² Together these proteins form a 48 nm, T = 7¹³ icosahedral capsid around a double stranded DNA (dsDNA) genome that is wrapped around ~ 20 histone octamers. In this conformation, as in many viruses, the dsDNA is strongly compacted by oppositely charged proteins including polyamines.¹⁴ In vitro, it has been shown that a full capsid shell made of only 72 VP1 pentamers will assemble around the bare dsDNA to form the 48 nm T = 7 capsid.^15,16 Other structures will also form around a variety of other templates including RNA,^17–19 nanoparticles,^20–23 and even micron sized particles.²⁴ The simplest structure is a T = 1 icosahedral capsid which is made up of only 12 VP1 pentamers.²⁵ The ability to form multiple structures is part of what makes SV40 VP1 an attractive candidate for technological applications.¹⁰ In particular, it is possible for VP1 to achieve T=1, T=7, and intermediate capsid sizes by being 5 or 6 coordinated (a pentamer or a hexamer respectively). This offers an opportunity to study viral assembly pathways and explore templates to modify assembly mechanisms.

The VP1 pentamer is made up of 5 identical polypeptide chains, each around 360 amino acids in length. The binding between these chains is very strong,²⁶ and thus the VP1 pentamer can be considered a single unit that has five-fold symmetry. Each chain can be functionally divided into 3 parts: the C-terminal ligands, the N-terminal ligands, which function as the template binding domain, and the globular body. The middle sections of the chains form the globular section of the protein and their structure has been described in great crystallographic detail.¹² The final 12 residues on the N-terminal ligands are unstructured but contain positively charged residues. These residues bind negatively charged templates through a charged interaction and have been included in previous models of capsid assembly^27,28 where the cargo is assumed to be a flexible polyelectrolyte that is essential for driving the assembly. This interaction has been shown to be independent of the C-terminal ligands.²⁹ In previous models of viral assembly,^27,28 the N-terminal peptides are termed arms while here they are termed N-terminal ligands, and in those models the C-terminal ligands are not included. The C-terminal ligands interdigitate with the body to form the connections between VP1 pentamers. These connections are essential to the formation of the capsid as their removal makes capsid assembly impossible.³⁰ The exact connection mechanism and topology vary based on the symmetry of the capsid,¹⁵ the presence of multivalent ions,¹⁶ and local coordination.¹² Cryo-EM reconstructions of the T = 1 and T = 7 capsids have shown that the C-terminal ligands have a very specific topology,¹² while attempts to reconstruct the C-terminal ligand topology of intermediate-sized particles were unsuccessful¹⁵ suggesting these intermediates may have no well defined topology or arrangement of 5 and 6-coordinated VP1 pentamers.

The actual assembly process of viruses is not fully understood.^31,32 Many models have been used to understand equilibrium phase behavior³³ and equilibrium capsid shapes.³⁴ However, they can lack dynamic assembly information. Modeling these dynamic pathways is difficult as due to the large size of the completed capsids, atomistic detail becomes intractable and as such more coarse-grained approaches have been taken. There are multiple coarse-grained models, some of which observe polymorphism,³⁵ based on the assembly of regular polygons,^27,35–38 so-called shape-based models. These shapes tile together to form static capsids. However, there is experimental evidence that the VP1 pentamer assembly is a highly dynamic process and models are required to explain the growth mechanism. As Donald Caspar stated “they [VP1 pentamers] will behave like an animate creature … erratically flexing its donor organ near the end of each tentacle and grasping with its acceptor organ near the base of each face of its five-sided head.”³⁹ Thus, we propose a model for the assembly of SV40 polymorphs, not based on the assembly of rigid shapes, but one that allows the C-terminal ligands to bind to a specific point on the body of the VP1 pentamer, which is now a globular cylinder that preserves the 5-fold symmetry of the VP1 protein (see Figure 1). The proposed model also implicitly mimics the interactions between the N-terminal ligands and a negatively charged template in various pH and ionic conditions (see Figure 2), in agreement with our experimental results on the assembly of the VP1 pentamers on 524 nucleotide RNA.

Figure 1:

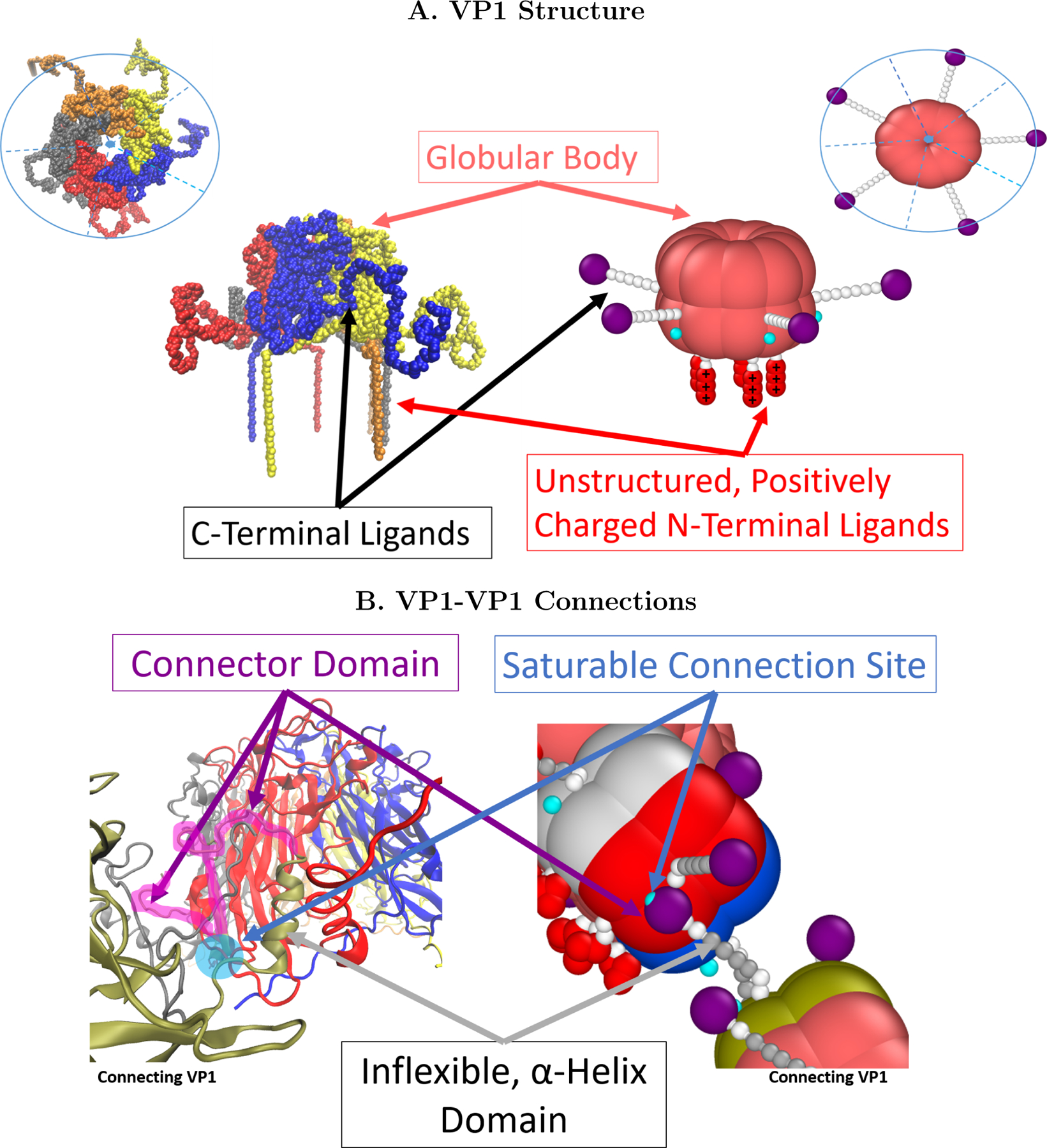
(A) Images of VP1 based on protein data bank (PDB) entry 1SVA¹² and its coarse-grained equivalent. The pink beads are rigid and represent the globular portion of the protein. The modeled VP1 pentamer can be split into 5 identical units, just as the real VP1 pentamer contains 5 chains with the same primary structure. Each unit has a rigidly attached C-terminal ligand comprised of nine beads which are only rigid in the middle (but are freely rotating) and terminate by a purple connector bead.(B) The connector beads hybridize with the cyan connection site with an energy given by the parameter ∈. Each unit also contains an N-terminal ligand made of 5 flexibly connected beads. The first two are uncharged while the last 3 represent the positively charged residues found on this part of the VP1 protein.

Figure 2:

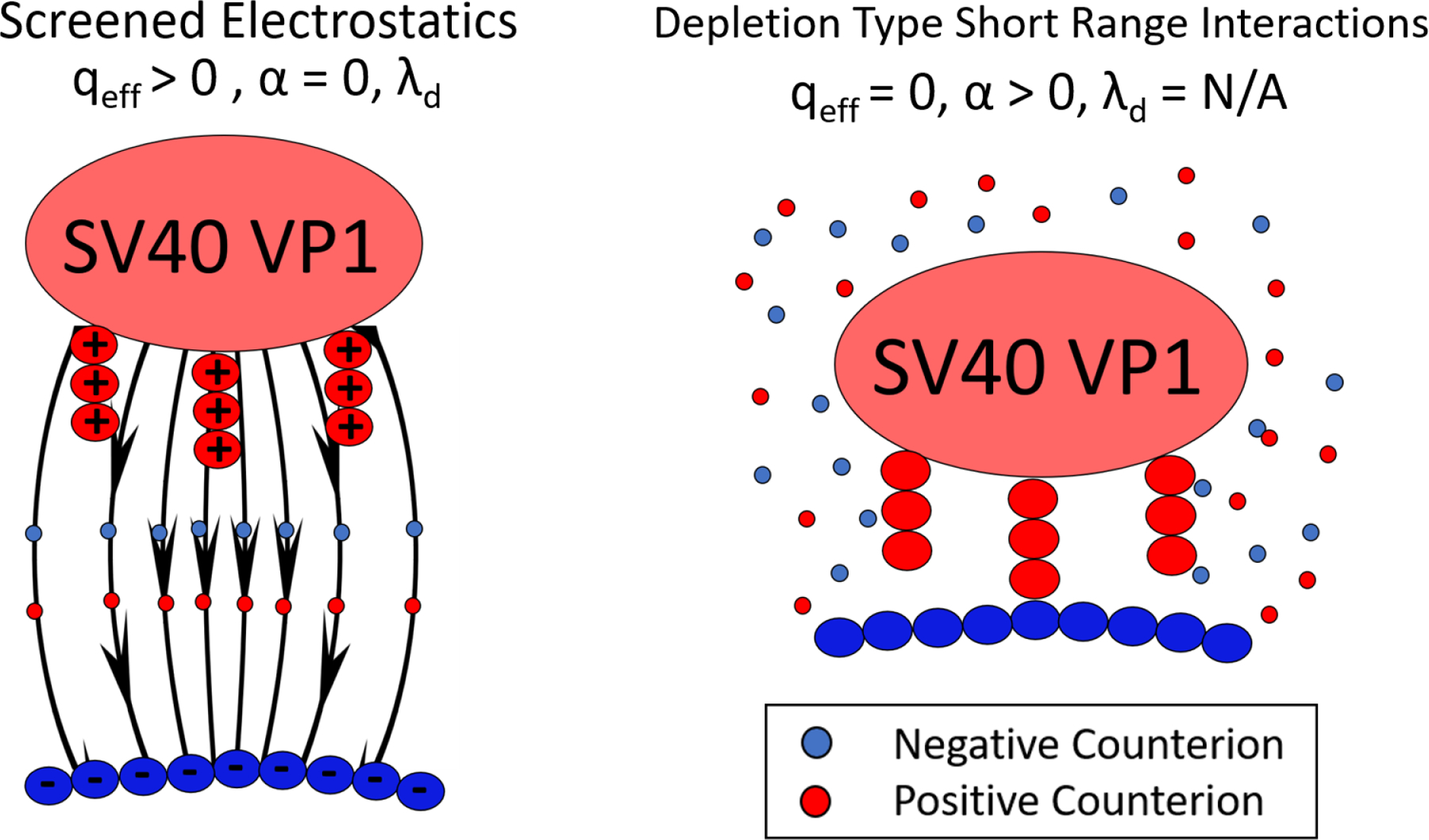
The two general cases of the implicit ion model. (Left) The case of screened electrostatics where the salt provides uniform screening of the electrostatic interactions present in the system. The strength of this screening is given by the Debye screening length,λ_d, as shown in Equation 1. (Right) The case of template binding at high salt. We model this by putting the q_eff=0 and adding a short range attraction, α, that comes from depletion since Debye-Huckel is not valid (Equation 2).

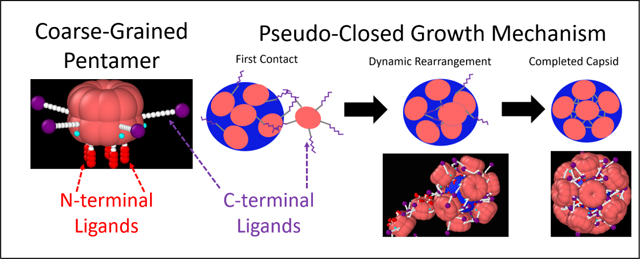
The inclusion of the C-terminal ligands in the simulations allows us to show the following “animate behavior”,³⁹ (1) the T = 1 capsid is a static structure while other incomplete and pseudo-closed structures (i.e., 13 VP1 pentamers and slightly smaller structures which may or may not be closed) are dynamic. (2) Fluctuations in template size can cause this 13 VP1 pentamer structure to spontaneously release a VP1 pentamer and reform the T = 1 capsid in what appears to be a self-correcting mechanism. (3) During assembly, C-terminal ligands are able to first connect to a partially completed capsid and then the N-terminal ligands bind to the spherical template.(4) This increases the effective size and flexibility of any partial capsid regardless of the template, making it more effective in recruiting additional VP1 pentamers. (5) This mechanism leads to pseudo-closed structures that continue to grow by forming connections with additional VP1 pentamers via the free C-terminal ligands and connection sites on the structure. The structure can then dynamically rearrange, allowing the N-terminal ligands of the additional VP1 pentamer to bind the template.

Results/Discussion

Capsid Structures

Simulations of the behavior of a single capsid are first performed in order to understand the products which may be present during assembly. Here, all simulations are performed with ∈ = 8k_BT because it gives the necessary strength to assemble the VP1 pentamers into icosahedral shells (lower values do not lead to this assembly and larger values lead to aggregation of the VP1 pentamers in the bulk as shown in Figure S1 in the SI).

Icosahedral Capsid (T=1, N=12)

Simulations of the T = 1 capsid (i.e., a rigid template with N=12 bound VP1 pentamers) are performed at different curvatures using ∈ = 8 k_BT, λ_d = 1.0 nm, and q_eff = 1. Icosahedral symmetry is observed in agreement with experiments and the definition of a T=1 icosahedral lattice. This is measured by the distribution of pairwise distances between the centers of VP1 pentamers. Figure 3 shows that at the lowest free energy, obtained for a radius of 9 nm, three pair correlation peaks are observed. The first peak is the nearest neighbor peak, followed by the second and third characteristic distances peaks. Using these peaks, $8.2\left(\frac{16.4}{2}\right)$ is the center to vertex distance and 8.6 is the edge length. For a regular icosahedron the ratio of these distances, $\frac{d_{\text{center},\text{vertex}}}{\text{edge length}}$ is 0.95 which is equal to $\frac{8.2}{8.6}$. The last peak can also be used to estimate the total capsid diameter by adding twice the height of a pentamer above the center of mass (6.6 nm) to the third peak giving a total equilibrium capsid size of ≈23 nm. This is in good agreement with the reported values of 24.5 nm from solution X-ray scattering experiments.¹⁸ Also in good agreement with experiments, is the existence of 3 helix triangles (see top right of Figure 3), which have been observed in cryo-electron microscopy (EM).¹⁵ This suggests the 3 helix structure is somewhat determined by capsid geometry since the orientational dependence of the hydrophobic interactions, credited for stabilizing the 3 helix structure, does not exist in this model. In addition to the 3 peaks, the pair distribution of the VP1 pentamers shows large regions of zero probability indicating that VP1 penatmers are vibrating only about the T = 1 icosahedral lattice points, but not sliding past each other. This is true of the T = 1 capsid over many template sizes and implies that it could withstand changes in solution conditions that may swell^16,40 or shrink the template. In the experimental section, we will show evidence this may be occurring as pH is increased.

Figure 3:

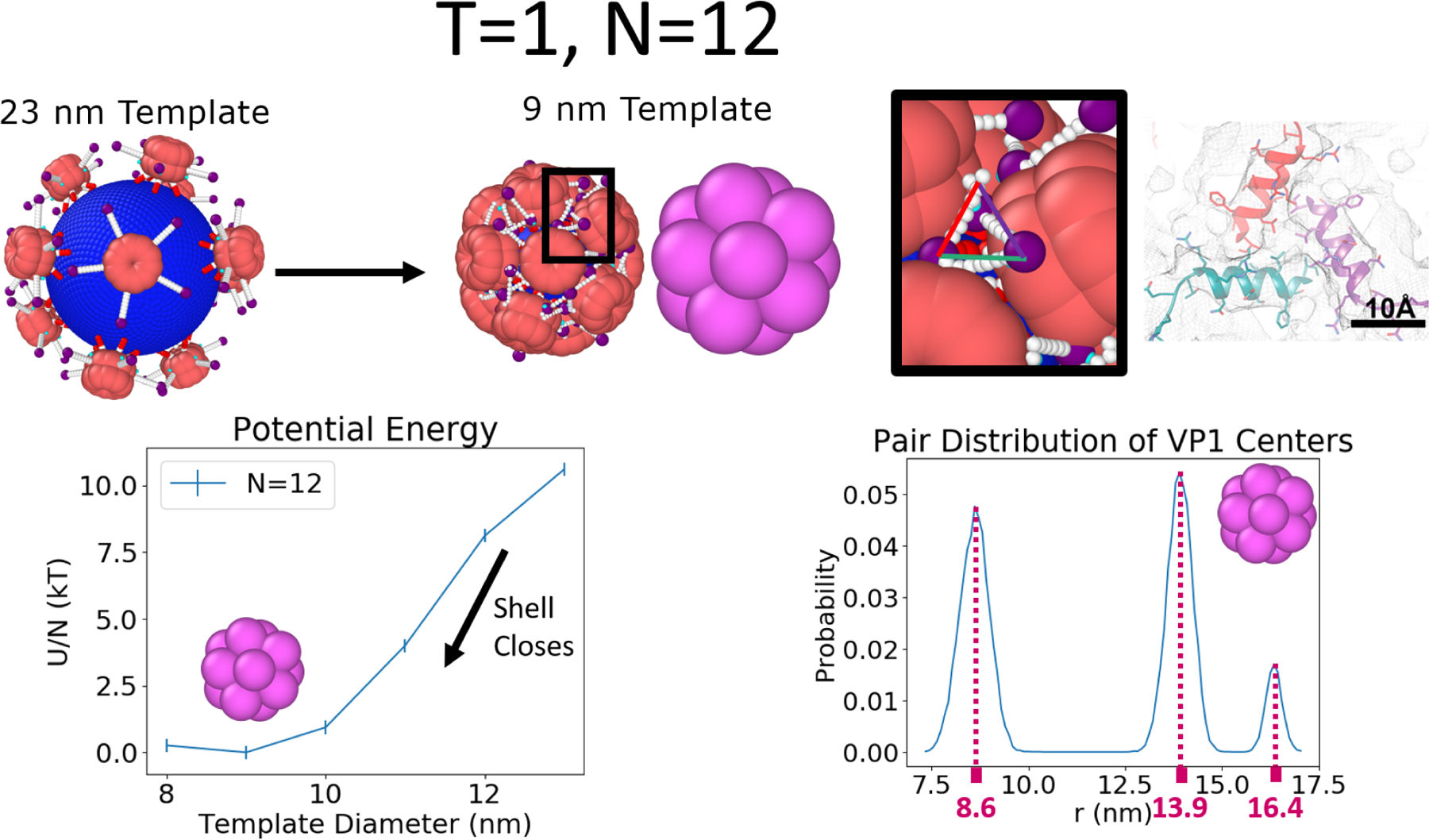
The T = 1 capsid is made of N=12 VP1 pentamers. The relative potential energy per VP1 and pairwise distance distribution of the capsid as a function of the template diameter is measured by first allowing 12 VP1 pentamers to bind to a large template and then slowly reducing the size of the capsid such that no VP1 pentamers are released during this process illustrated at the top left of the figure. Results on the bottom left show that the minimum of the potential energy occurs at a template diameter of 9 nm. On the bottom right, we see 3 peaks matching the icosahedral symmetry (see main text) and large regions of zero probability, indicating the static nature of the VP1 pentamers in this configuration. Since this static T = 1 configuration is stable over many template sizes we believe that it would also be robust against changes in template size based on changes in salt, pH, etc., provided that these changes do not impact the VP1-VP1 or VP1-template interactions too much. This minimum energy structure also recovers the presence of a three helix triangle located at the three fold symmetry points of the icosahedron,¹⁵ shown at the top right. The image of the three-helix triangle with the scale bar was adapted with permission from Kler et al., ACS Chemical Biology 2013, 8, 2753–2761. Copyright 2013 American Chemical Society.

Non-Icosahedral Shell: N=13

The stability of closed shells geometries that can not contain icosahedral symmetry, but may be an “off-path” intermediate are also important in understanding viral assembly. This section focuses on one example of this class of shells, the N=13 capsid. As shown in Figure 4, icosahedral symmetry is disrupted by the 13th VP1 pentamer, which occupies a 6 coordinated position. A mix of 6 and 5 coordinated VP1 pentamers are also observed in the T = 7 capsid,¹² which is made up of 72 VP1 pentamers (12 five-coordinated pentamers and 60 six-coordinated pentamers). Both of these structures follow the Euler formula for closed shells of regular polygons, V-E+F=2, which predicts that the number of six-folds is smaller by 12 than the number of total units under the constraint that only hexagons and pentagons are allowed (see Supporting Information for derivation). It is important to note that the location of the six-fold is dynamic relative to the template, implying the VP1 pentamers neighboring the six-coordinated VP1 pentamer are constantly reorganizing relative to each other. This is shown by non-zero probability at all distances at the bottom left of Figure 4. Since it is a closed, non-icosahedral shell that has dynamic behavior it will be referred to as pseudo-closed. This is in contrast to the T = 1 capsid which displayed regions of zero-probability and thus no reorganization. The underlying reason for the dynamics of the shell seems to be topological frustration of trying to insert a six-coordinated VP1 pentamer with only five C-terminal ligands into the shell. Shrinking the template to be smaller than 12 nm in diameter causes one of the VP1 pentamers to spontaneously detach and the T = 1 forms again. This may function as a self-correcting mechanism for assembly with flexible, dynamic templates. The released VP1 pentamer is always a nearest neighbor to a six-coordinated pentamer and its release seems to alleviate the internal stress caused by the six-coordination of the VP1 pentamer. In the T = 7 capsid, there is no α− helix in the γ subunit of the six-coordinated VP1 pentamer and this may help to relieve this stress.

Figure 4:

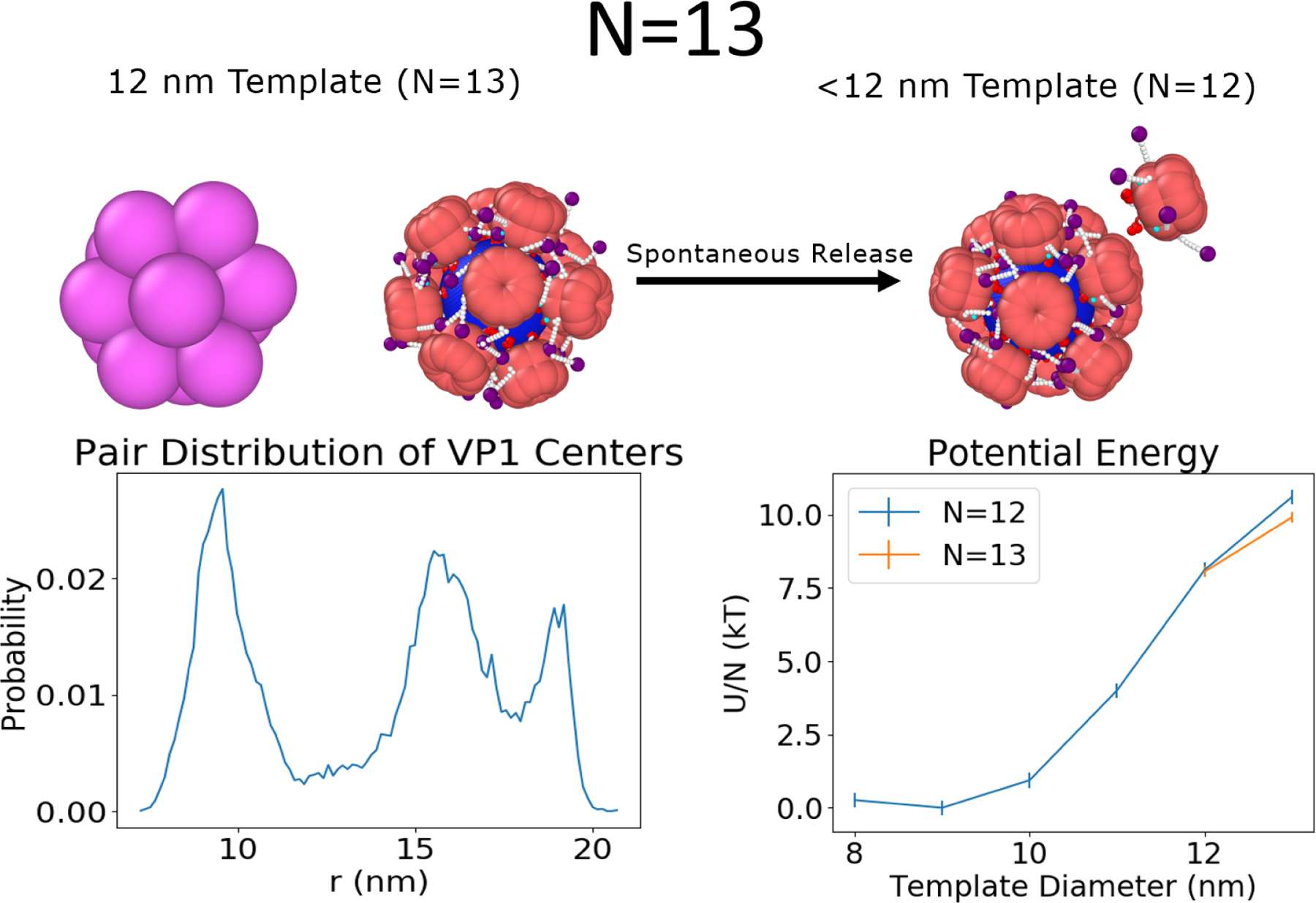
(Left) The N=13 shows deviation from the icosahedral symmetry observed in the case of the N=12, T = 1 capsid. Instead, a six-coordinated VP1 pentamer is observed (top left), consistent with the Euler formula for closed shells made of regular polygons. The six-coordinated VP1 pentamer is also mobile as shown by the absence of zero-probability regions in the pairwise distribution function (which were observed for N=12 in Figure 3). (Right) This structure is only favored over the T = 1 for 12 nm and above templates where it has a lower energy per VP1 pentamer (^U/N) than the T = 1 capsid. At smaller template diameters, one VP1 pentamer will be spontaneously released and the T = 1 capsid reforms.

Assembly Paths: N=10 and N=11

The investigation of structures smaller than the T = 1 (i.e., N=10 and N=11) provides the opportunity to understand possible intermediate states that may occur during assembly. The N=10 on a 10 nm is a dynamic, pseudo-closed shell like the N=13 and shows VP1 pentamers that have no exact position or specific coordination number (see Figure 5). While one half of the capsid seems to have five coordinated VP1 pentamers the other contains four VP1 pentamers that assume relatively larger fluctuations, which on average cover the template. When the template diameter is 11 nm, the pentamers spontaneously regain icosahedral symmetry with two mobile holes that are second nearest neighbors. The N=11 capsid (see Figure S2 in the SI) has only one hole, which does not close when the template size is varied. As mentioned earlier, these structures are intermediate states in the assembly of T = 1 capsids. The N = 11 and 11 nm N = 10 capsids show clear binding sites surrounded by free arms for the 11th and 12th VP1 to be added to the elongating capsid and this growth mechanism will be explored in the section: Elongation Mechanism on the Spherical Template. However, it is unclear how the 11th VP1 would be added to the pseudo-closed capsid. The pseudo-closed growth mechanism by which this is accomplished is also discussed in its own section Closed Shell Growth.

Figure 5:

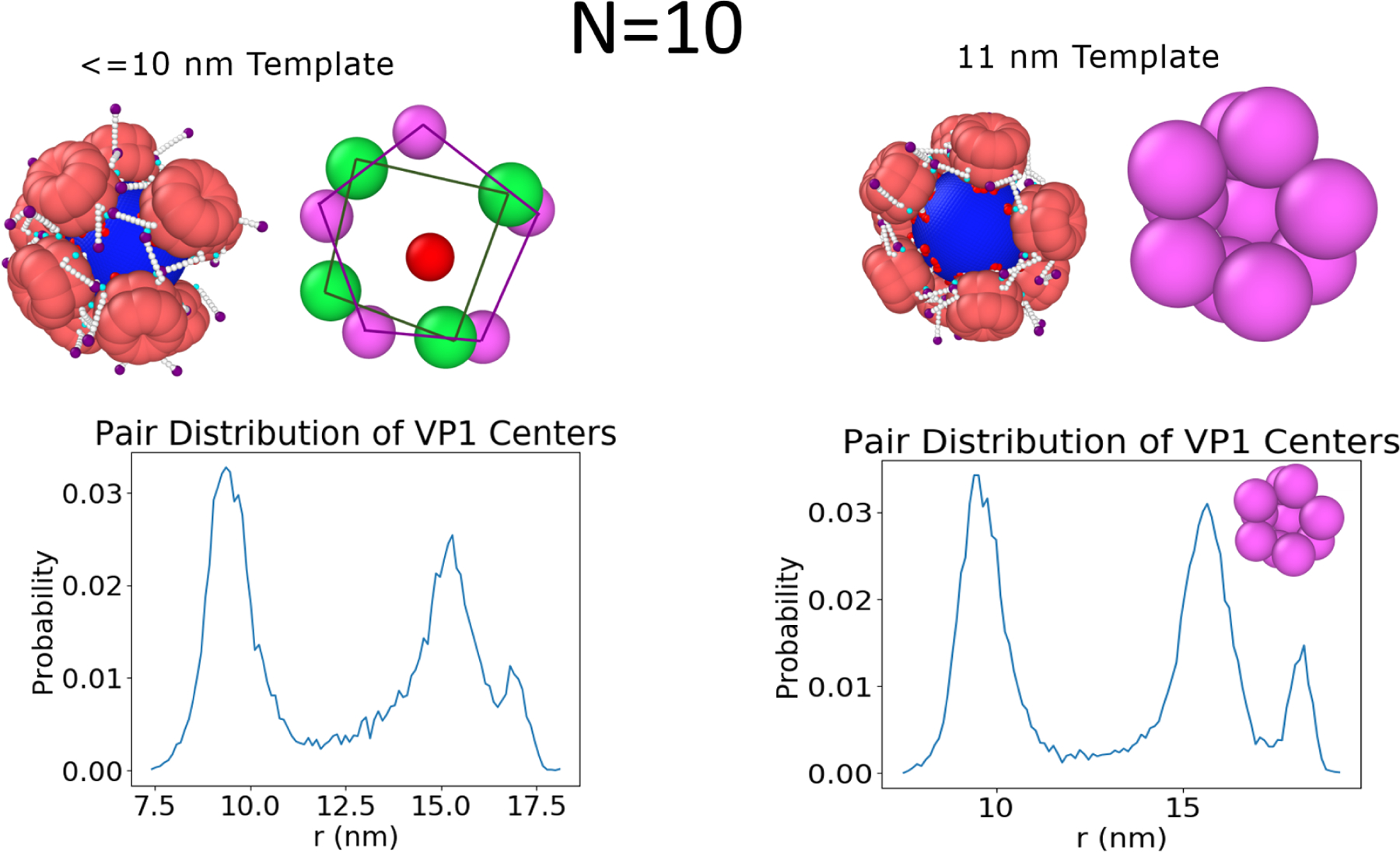
The N = 10 capsid can adopt different configurations based on the curvature of the template.(Right) The 11 nm template shows icosahedral symmetry like the N = 11 and T = 1 case, just with two holes that are second nearest neighbors. (Left) For templates less than 11 nm, the capsid shows half of the template with a 5 fold symmetry, while the other 4 VP1 pentamers are found in an unstructured state.

Assembly Factors

The assembly simulations (see details in the SI) can be performed using any value of the following parameters: q_eff, λ_d, α, and template diameter. Using these parameters, we show the effect of salt concentration, pH, and the importance of finely tuned C-terminal ligand interactions. The model is then updated to better represent the full length of the C-terminal ligands and the implications of this parameter are discussed. These results are compared with experiments and the underlying mechanisms of assembly are examined in the simulations. Finally, by changing the template diameter from 11 to 10 nm, the growth of closed shells is evaluated.

Salt Concentration

The effect of salt is explored through three parameters,λ_d, q_eff, and, which are functions of the ionic strength of the solution. Biological salt simulations were run using λ_d = 1.0 nm (or 92 mM added salt) and q_eff = 1. The effect of salt is explored through a lower salt concentration, where λ_d is increased to 1.4 nm (or 47 mM added salt), and a higher salt concentration, where the charge is completely screened and depletion interactions in the form of Equation 2 are taken into account. The results of these studies are shown in Figure 6. The graphs at the bottom of Figure 6 show how the fraction of templates with N-bound VP1 pentamers, F(N), progresses as a function of the fractional simulation time, t. F(N) was sampled 20 times throughout the simulation with the average of the first four being reported as $t=\raisebox{1ex}{$4$}\!\left/ \!\raisebox{-1ex}{$20$}\right.=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$5$}\right.$, the next four as $t=\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$5$}\right.$, etc. The results show that VP1 pentamers bind very quickly at first and then the rate slows as available surface area is used while the amount of free VP1 pentamers decreases. Increasing the Debye screening length weakly increases the speed of assembly. At high salt concentrations, reliance only on short range interactions slightly decreases the formation of T = 1 capsids even when α is large enough to nucleate capsids. This is in part due to issues that arise when attempting to add the final VP1 pentamers as discussed in the next section. When the short range attraction is too weak (α = 1 k_BT), no nucleation is observed at all.

Figure 6:

Fraction of Templates with N bound pentamers at different time points along the simulations. Assembly of T = 1 capsids is sensitive to added salt concentration as shown by the fraction of templates having N=12 capsids at t=5/5. (Left) Assembly occurs only slightly faster when the Debye length is increased relative to biological salt conditions (Center).(Right) Having only short ranged attraction decreases the observed fraction of T = 1 capsids assembled even when the attraction is strong.

Elongation Mechanism on the Spherical Template

The assembly simulations made it clear that the most difficult aspect of T = 1 assembly was adding the final VP1 pentamers to the incomplete capsid. This is somewhat different from the case of a flexible cargo like ssRNA which may act as an antenna, attract pentamers, and facilitate the assembly and the final closure of the capsid.¹⁸ However, as was shown in our recent paper,⁴¹ few percent of particles with 11 (instead of 12) pentamers cannot be excluded at the signal-to-noise level of the experimental data.

In Figure S1 in the SI, even when ∈ = 7 k_BT there were a large fraction of N = 10 capsids, thus arriving at the N = 10 state was not the main issue. The inability to complete the capsid is due to the fact that these are the states where it is very hard to find free surface area on the spherical template to bind to. To understand how the binding of the final VP1 pentamers occurs, we observe successful binding of a 12th VP1 pentamer to an N = 11 capsid, which has icosahedral symmetry with one hole where binding can occur (see Figure S2 in the SI). The snapshots for this process are shown in Figure 7. At first, the VP1 pentamer made a single connection with the N = 11 capsid. The pentamer is then able to make more connections and stabilize itself on the capsid. This stabilization does not mean that the pentamer will bind, in fact the opposite occurs as the new connections form in such a way that it is orientationally impossible for the VP1 pentamer to bind the spherical template. To get out of this state, some of these connections have to dissociate and make the VP1 pentamer weakly attached, before creating new connections that orient the pentamer so that binding is possible. It is important to note that this process could not occur without the C-terminal ligands.

Figure 7:

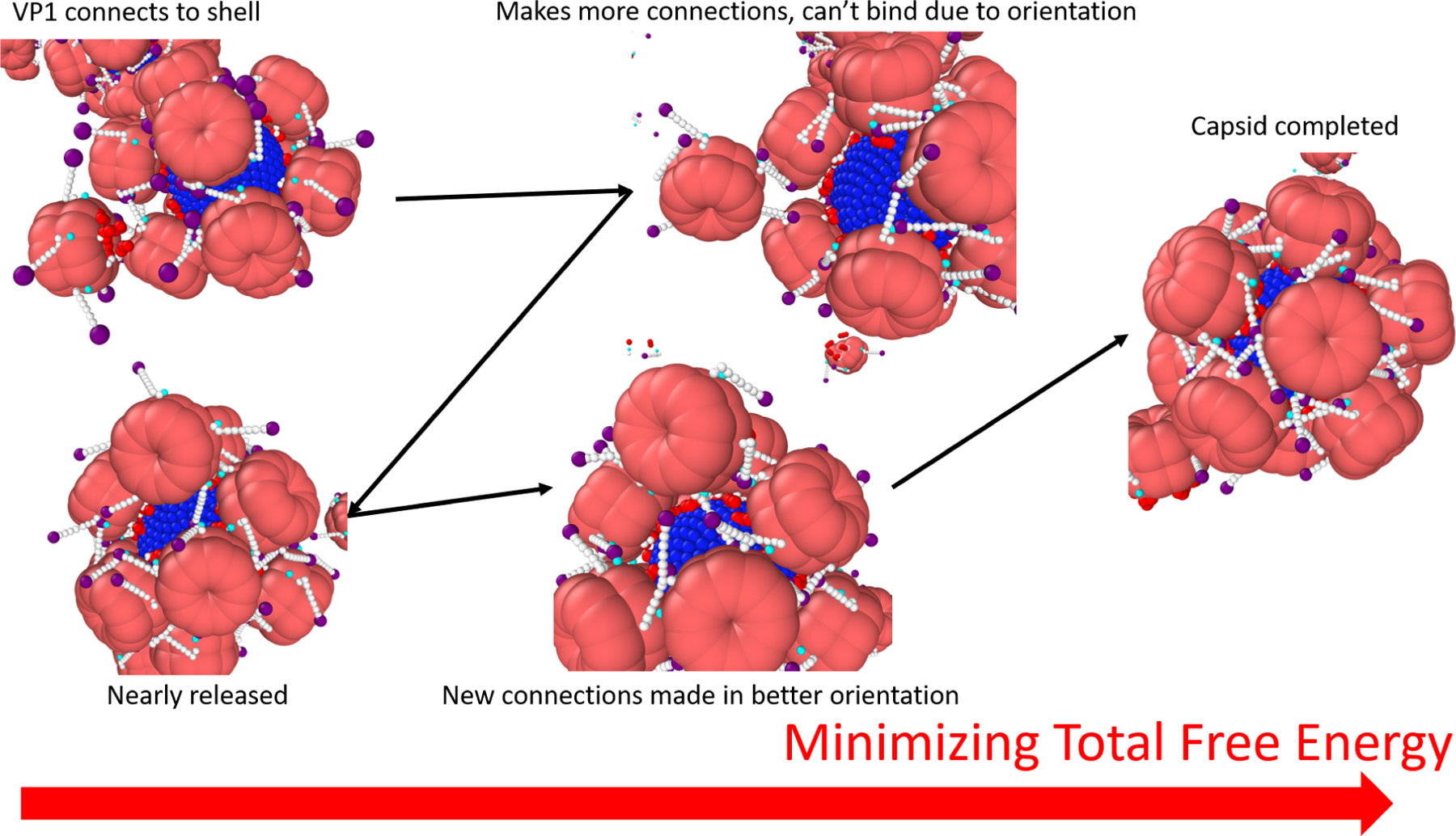
An example of binding of the final VP1 pentamer to an N=11 capsid during a simulation using ∈ = 8 k_BT,λ_d = 1.0 nm, q_eff = 0, and a 10 nm template. The black arrows point forward in time, while the red arrow points to a decrease in the total free energy. The process requires cooperative interactions between the final VP1 pentamer, the bound VP1 pentamers, and the template. This process shows that the C-terminal ligands stabilize the 12th VP1 pentamer on the partially assembled capsid until it finds an orientation where it can bind to the surface of the template. To find this orientation, the VP1 pentamer searches a rough free energy landscape and thus it is important that the interactions are weak enough to be reversible.

The character of this path makes it easy to understand why it was so difficult to attach the final VP1 to an N = 11 capsid. It also illustrates why the binding process is so sensitive to both the connection strength and electrostatics. If ∈ is too low the connections will not be able to stabilize the VP1 on the partial capsid whereas if ∈ is too high the connections may be too stable in the wrong orientation and the VP1 may eventually bind another template, leading to aggregation^41,42 as in Figure S1 in the SI. In this picture, the salt concentration controls how well oriented the capsid needs to be in order to bind the template. At higher λ_d (low salt) the final pentamer will be more strongly attracted even if it is farther away, whereas it will need to almost be in contact to bind via purely short range interactions. Some of these orientational effects could be mitigated by a flexible template that would grab the N-terminal ligands and held to orient the final VP1.

C-terminal Ligand Length

The full length of the connector domain is not included in the simplistic model depicted in Figure 1. This means the variety of possible attractive interactions involving connector regimes and distance from the globular body at which they would occur are not present. This could be especially important in making first contact when attempting to add the final VP1 pentamer to an N=11 capsid, see Figure 8. To more accurately represent the 60 amino acid C-terminal ligand, 2 more beads were added to the end of the C-terminal ligand with equilibrium bond lengths of 2 nm, doubling the contour length (see Figure 9 in the SI). The potential between these beads is such that at a cost of 2 k_BT the contour length of the new section can be 2 or 6 nm giving the C-terminal ligand a spring-like extensibility. This model accounts for the many possible configurations of the C-terminal ligand after the α−helix, which were “not well ordered”¹⁵ in cryo-EM reconstructions of the T = 1 particle. The interactions of the simplistic model are kept completely identical whereas the additional two beads will have an interaction strength of 1 k_BT with all other types of beads in the system.

Figure 8:

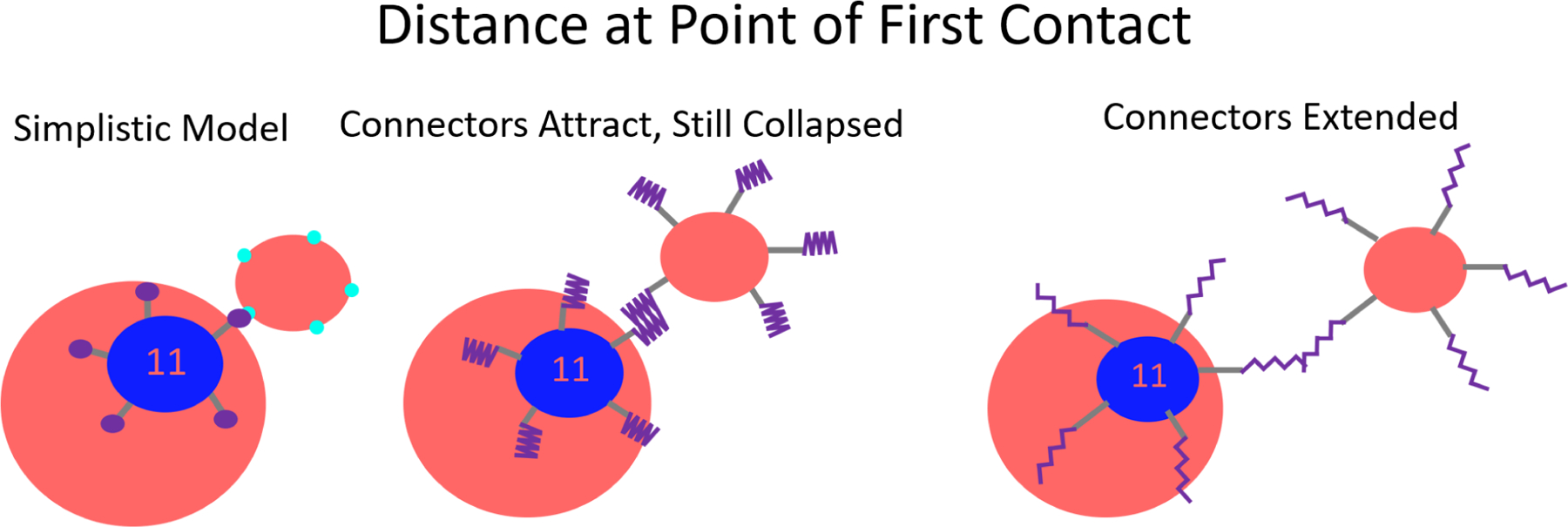
An illustration of the shortcomings of the simplistic model to represent the ease of making the first contact. Considering the full extensibility of the connector domain, the first contact between a partial capsid and a VP1 pentamer can occur at a much longer interaction distance.

The C-terminal ligand is composed of positively and negatively charged, hydrophobic, and hydrophilic residues so in some conformations it can have a small, but attractive interaction with any portion of a template or other VP1 pentamer. These sections of the C-terminal ligands will essentially behave as random copolymers, which have been shown to orient themselves to energetically favorable conformations.⁴³

As shown in Figure 9, the inclusion of the full C-terminal ligand increased the rate of assembly and yield of T = 1 capsids. This shows that the entire C-terminal ligand plays a role in assembly by increasing the range at which VP1 pentamers interact and helping to overcome the diffusion limit. This is often considered to be the role of a flexible polyelectrolyte template, but here we show the same effect can be obtained by including the extended C-terminal ligands of VP1 pentamers on a rigid template.^20–24 It follows that the effect does not actually require a template at all,⁴¹ although it would also serve to amplify the flexibility of a polyelectrolyte especially as it approaches full encapsidation.

Figure 9:

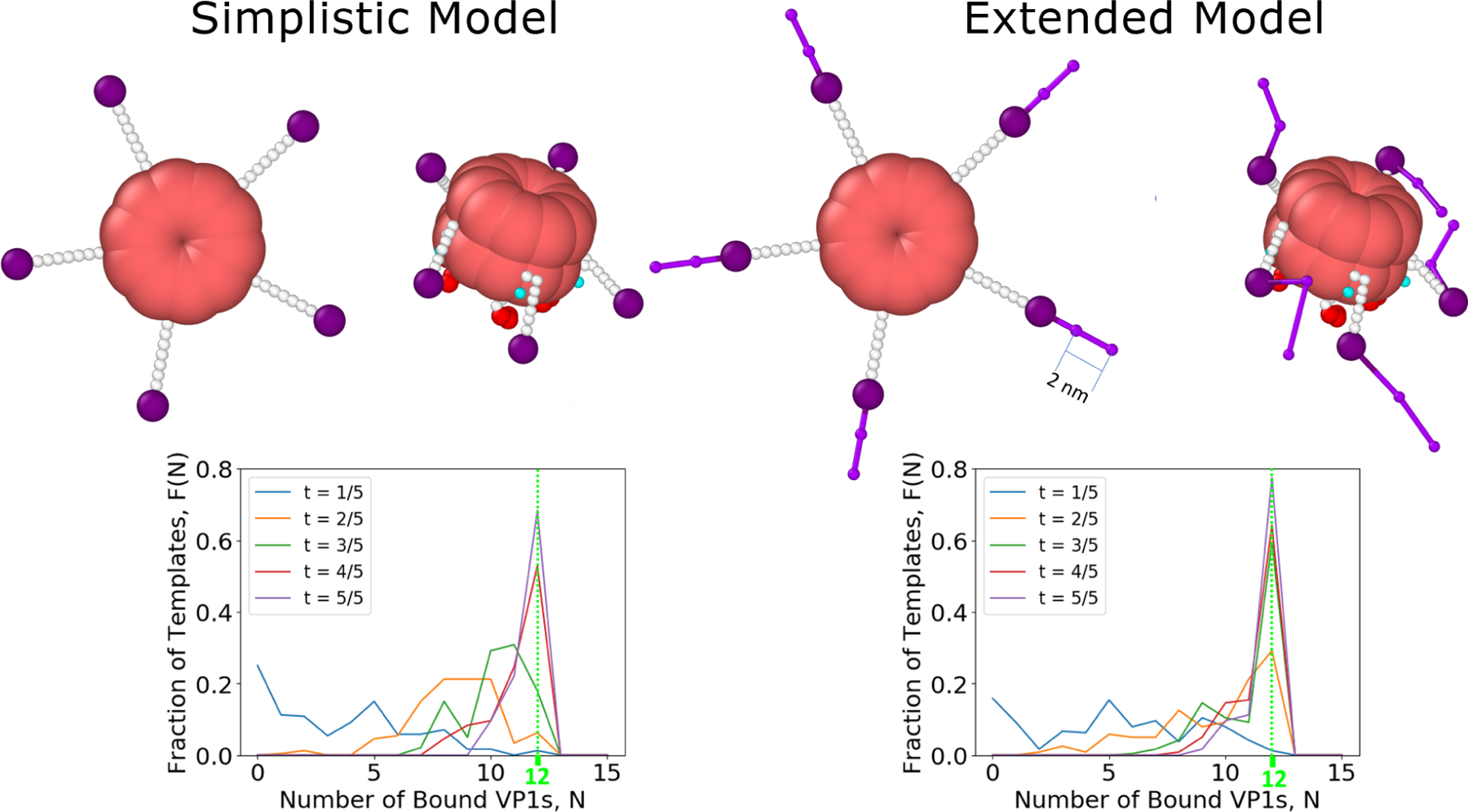
(Top) The difference between the simplistic and extended model is displayed both in an initial conformation and in a typical conformation of a free VP1 pentamer. (Bottom) Inclusion of the full length connector in the model increases the rate of assembly. More T = 1 capsids are present at every step of the simulations.

Experiments of VP1 Pentamer Assembly on ssRNA

The interaction of SV40 VP1 with short RNA was examined by synchrotron solution small-angle X-ray scattering⁴⁴ (SAXS). Figure 10 shows the scattering intensity of equilibrated assembly reactions, done at increasing concentrations of NaCl. The Debye screening lengths in these experiments vary between ≈ 0.4 and 1.2 nm (when taking into account the buffer and added salt concentrations, see Materials and Methods). The resultant oscillatory curves are very similar to those reported in our earlier paper, at which T = 1 VLPs with an outer diameter of 24.5 nm were analyzed.¹⁸ The scattering intensity is plotted as a function of q, the magnitude of the scattering vector. The locations of the minima along the curves correspond to the dimensions of the particles and to the typical correlation distances between subunits in the capsid.

Figure 10:

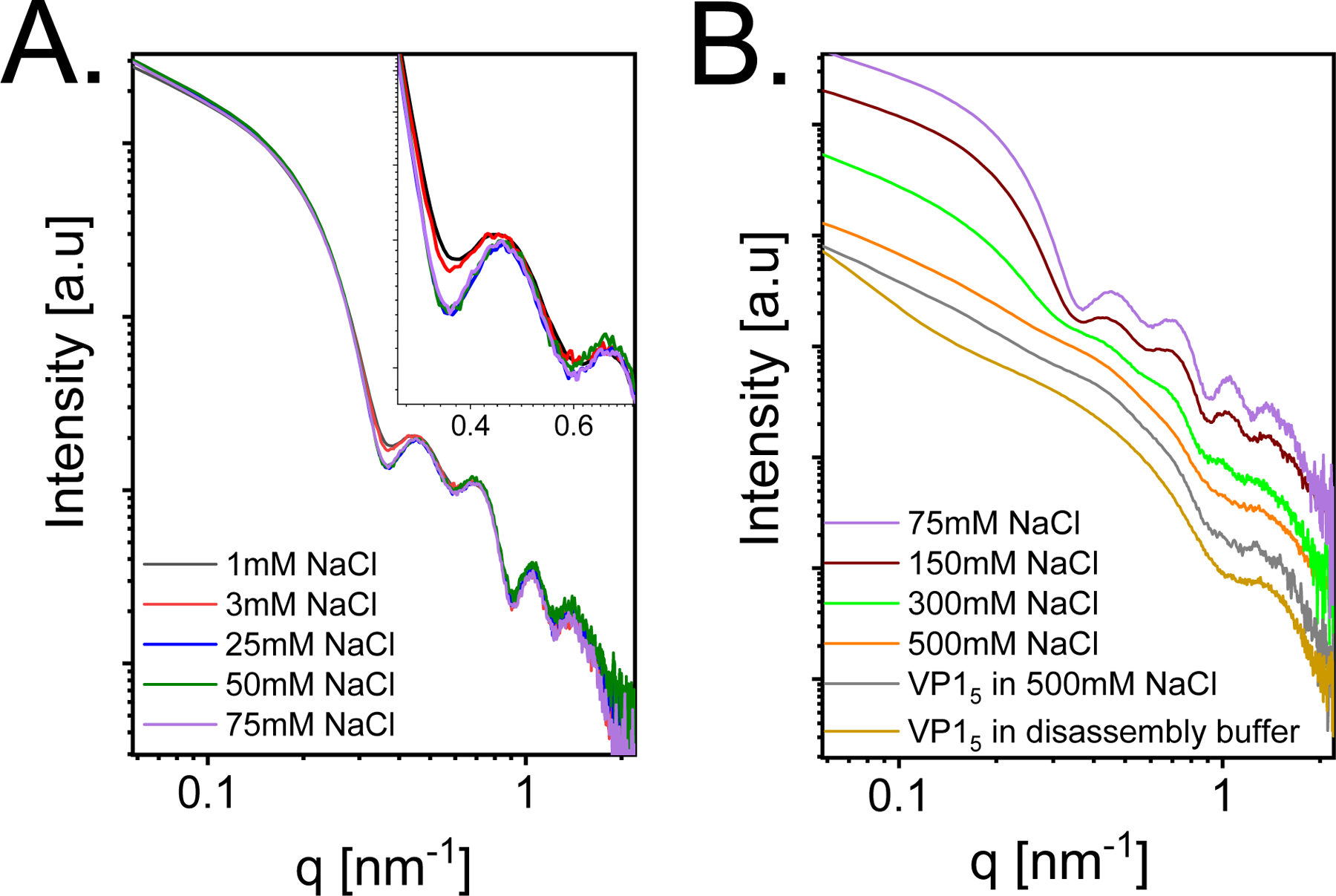
Azimuthally integrated background-subtracted synchrotron small-angle X-ray scattering (SAXS) intensity curves as a function of the magnitude of the scattering vector, q. 13 μM SV40 VP1 pentamers were mixed with 0.87 μM 524nt RNA at 1:1 volume ratio, at pH 7.2 and different final NaCl concentrations, as indicated in the figure. (A) Assembly reactions at low salt concentrations (1–75 mM). The inset shows the first two minima on an expanded scale. (B) Assembly reactions at high salt concentrations (75–500 mM). At 500 mM the orange curve resembles the scattering curve of 6.5 μM SV40 VP1 pentamers in the assembly buffer and 500 mM (gray curve) or 13 μM SV40 VP1 pentamers before mixing with the RNA (in the disassembly buffer, see Methods). The curves were vertically shifted for clarity of representation.

Figure 10A shows that the oscillations became sharper as the salt concentration was increased from 1 to 75 mM, indicating a rise in the fraction of T = 1 particles. Further increase of the NaCl concentration (Figure 10B), however, led to lower yield of assembled T = 1 particles. A similar trend was observed in the simulations (Figure 6). At 500 mM (orange curve in Figure 10B) the scattering curve resembles the scattering curve of VP1 pentamers in the absence of RNA at the same solution conditions (gray curve). The dominant contribution to the scattering intensity at 500 mM (with and without RNA) came from free VP1 pentamers and small amount of irregular assemblies as seen from the similarity to the SAXS curve of VP1 pentamers in the disassembly buffer (see Methods), before mixing with the RNA (dark yellow curve).¹⁸

Figure 11 shows the effect of increasing the pH from 7.2 to 8.9. Higher pH values led to deprotonation and reduced the total positive charge on the N-terminal ligands of the pentamer that interact with the RNA. As a result, the affinity of the pentamers to the RNA decreased. Figure 11 shows that as long as the pH was 8.7 or less, the intensity at q → 0, which is proportional to the average molecular mass of the particles,¹⁶ did not change. The sharpness of the minima, however, decreased with increasing pH, suggesting that the degree of polydispersity of the assembled particles increased with pH. This might be attributed to weaker binding between the VP1 pentamers as well as between the RNA and the pentamers. As a result, the fluctuations in the VLP structure increased. At pH 8.9, the intensity at q → 0 was lower, hence the average mass decreased, suggesting that the mass fraction of complete VLPs decreased.

Figure 11:

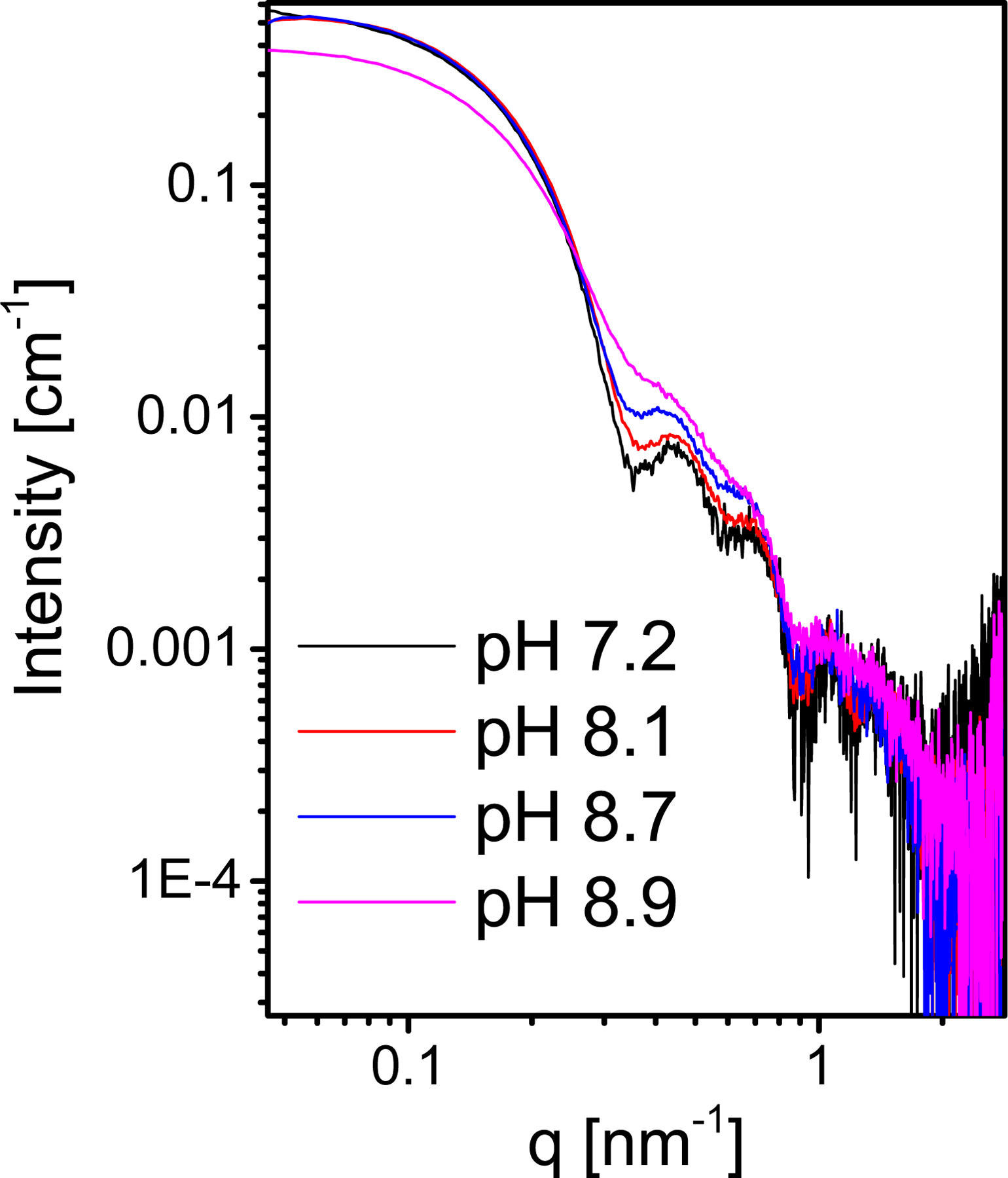
Background-subtracted SAXS absolute intensity curves from 6.3 μM SV40 VP1, mixed with 0.42 μM 524nt RNA, in 150 mM NaCl at different pH values, as indicated in the figure (see Materials and Methods).

The experiments and simulations show a similar trend for salt concentrations above 75 mM, which occur in the regime where screening approximations are fairly accurate. In the experiments shown in Figure 10, the best assembly occurred at the Debye length between 0.8 and 1 nm in agreement with the simulations (Figures 6 and 10). In both cases, as the salt concentration was increased, and the Debye length shortened, the fraction of large particles decreased. The simulations in Figure 6 also show a complete stop to assembly like in the experiments at 500 mM when α = 1 k_BT (see Equation 2), suggesting that this binding energy (between the VP1 pentamers and the RNA) was relatively weak. This conclusion is consistent with the work of Li et al.⁴⁵, which showed no depletion effects from the salt in 300 – 500 mM NaCl.

By increasing the pH, positive charges on the N-terminal ligands deprotonate and the charge fraction of the N-terminal ligands decreases. Experiments showed that as the pH was increased from 7.2 to 8.7 there was an increase in the polydispersity of the capsids, but the average mass of the assembled particles remained unchanged 11. The decrease in positive charge on the N-terminal ligands would have to be compensated by more positive ions within the RNA, swelling the RNA, and thus increasing the template size.⁴⁶ Simulations were able to mimic the pH effects elucidated in more accurate representations,⁴⁷ by changing q²_eff (Equation 1) without adding in the depletion term (Equation 2). Figure S2 in the SI shows that as the charge interaction is weakened it becomes harder to add the 11th and 12th VP1 pentamers, leading to a greater polydispersity. If N ≤ 11 capsids exist then N ≥ 13 capsids should also exist to keep the average mass unchanged. Simulation results from Figure 4 showed that in order for N ≥ 13 structures to be stable the template must expand in size. Alternatively, T = 1 capsids may assume larger fluctuations owing to pentamer-pentamer and pentamer-template interactions and lead to higher polydispersity. In Figure 3, the T = 1 was shown to be stable over a range of template diameters.

At pH 8.9 simulations and experiments were in agreement. The simulations showed that there was not enough charge on the VP1 pentamers to easily bind the RNA with the correct curvature and form a capsid, hence less completed particles were observed (see Figure S2 in the SI).

Closed Shell Growth

Until now only the growth of incomplete capsids by elongation has been discussed, however, the growth of pseudo-closed shells (dynamic shells with no holes) can also occur. Figure 12 compares the assembly around spherical templates with diameters of 10 nm and 11 nm. As shown in Figure 5, the N=10 states on these templates were pseudo-closed and icoshedral with 2 holes respectively. Although in the end of the simulations both templates had some T = 1 capsids (i.e., N=12 at t=5/5, where t is the fractional simulation time) there was a clear difference in the dynamics. The N = 10 state had a much longer lifetime on the 10 nm template than on the 11 nm template, as the 10 nm template has its largest peak at N = 10 at $\text{t}=\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$5$}\right.$. The higher stability can be attributed to the configurations assumed by the N = 10 particles at different curvatures, shown in Figure 5. Figure 12 shows the pairwise distance distributions of VP1 pentamers as a function of time. The presence of the two different N = 10 configurations is most clear for $t=\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$5$}\right.$ at which N = 10 is the dominant structure on both templates. The 11 nm template displays the icosahedral pair distribution while the 10 nm template has a pseudo-closed shape similar to the N = 10 capsid on a 10 nm template in Figure 5. Thus the pseudo-closed state grows at a much slower rate, although it is surprising that it continues to grow at all.

Figure 12:

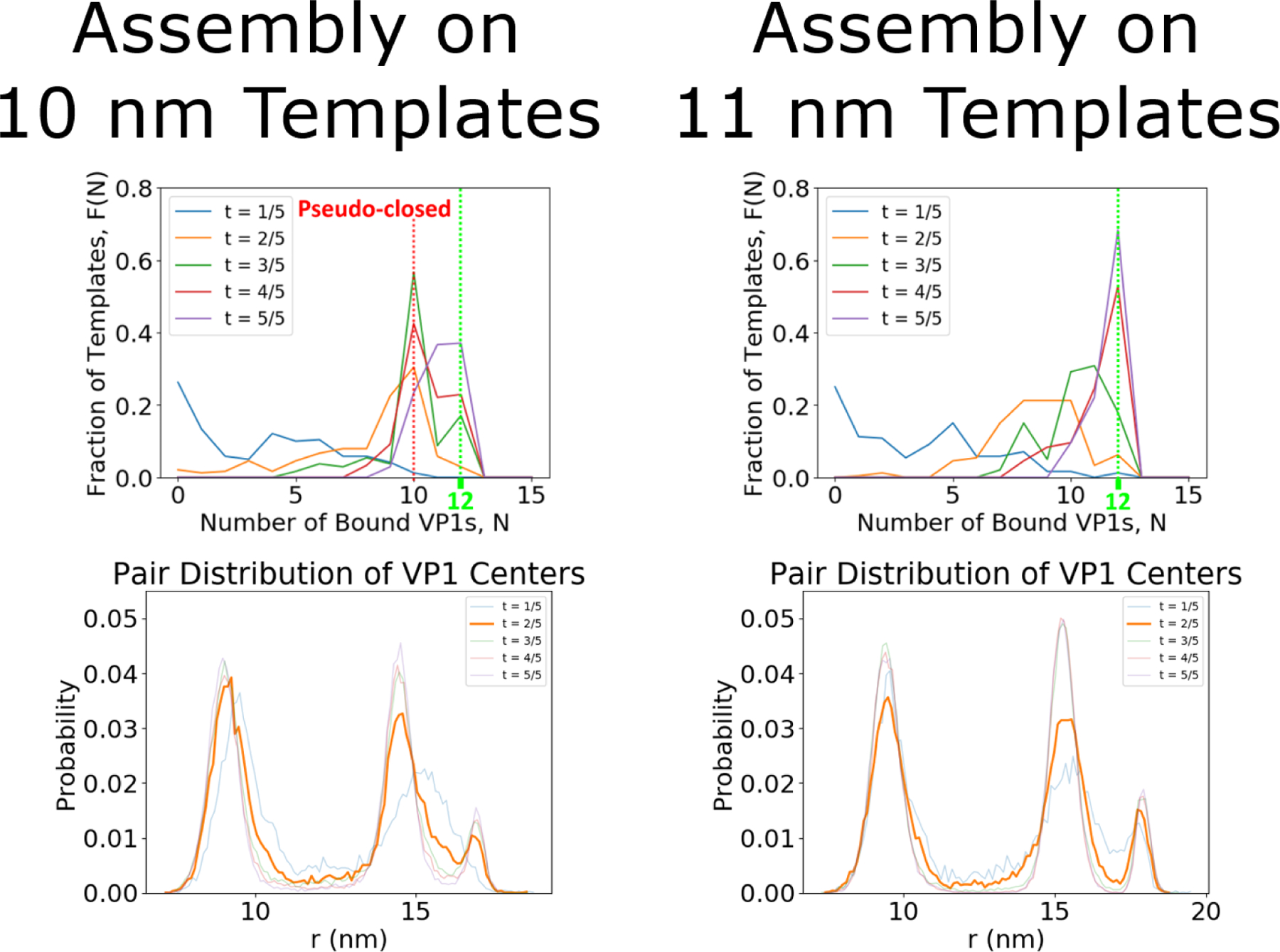
Assembly simulations around spherical templates with a diameter of 10 and 11 nm. The top figures show the fraction of templates with N bound VP1 pentamers as a function of the fractional simulation time, t. The bottom shows the pairwise distance distributions of VP1 pentamers in each case. A peak is observed at N = 10 pentamers on the 10 nm template owing to lack of available binding sites, as compared to the 11 nm case. The lack of available template binding sites is shown by the lack of icosahedral symmetry seen in the pair distribution (especially at $t=\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$5$}\right.$).

The further growth of the N = 10 state on the 10 nm capsid is due to its dynamic character. Free VP1 pentamers first connect to a pseudo-closed shell and then dynamically rearrange to allow the connected VP1 pentamer to join the shell (Figure 13). The N = 10 state on a 10 nm capsid has nearly the same local packing density as the T = 1, N = 12 capsid. Yet, the results show that a T = 1 capsid does not continue to add VP1 pentamers, because the capsid can not rearrange. The growth mechanism of pseudo-closed capsids was slower than the elongation stage, most likely, owing to the difficulty in connecting to a pseudo-closed shell and the longer rearrangement time scales. Previous experimental work¹⁸ suggests that either these pseudo-closed N=10 particles are not forming or that the time scale of the rearrangement is still untraceably fast. However, there is experimental evidence of this growth mechanism for closed shells of sizes between the T = 1 and T = 7 capsid. Attempts to solve the structure of these particles have failed.¹⁵ We are suggesting here that they are dynamic/pseudo-closed shells and therefore they are able to grow via the pseudo-closed growth mechanism we describe in this paper. Our pseudo-closed growth mechanism explains this and other important experimental observations. Slow, stochastic growth via the pseudo-closed mechanism explains why particles often exist in heterogeneous size distributions.^15,19 It also explains how Van Rosmalen, et al. observed ≈ 33 nm particles that become ≈ 45 nm particles after long incubation times.⁴⁸ Furthermore, it explains the EM images produced by Kanesashi¹⁹ of VP1 pentamers bound to 30 ± 5 nm particles without templates, shown in Figure 13.

Figure 13:

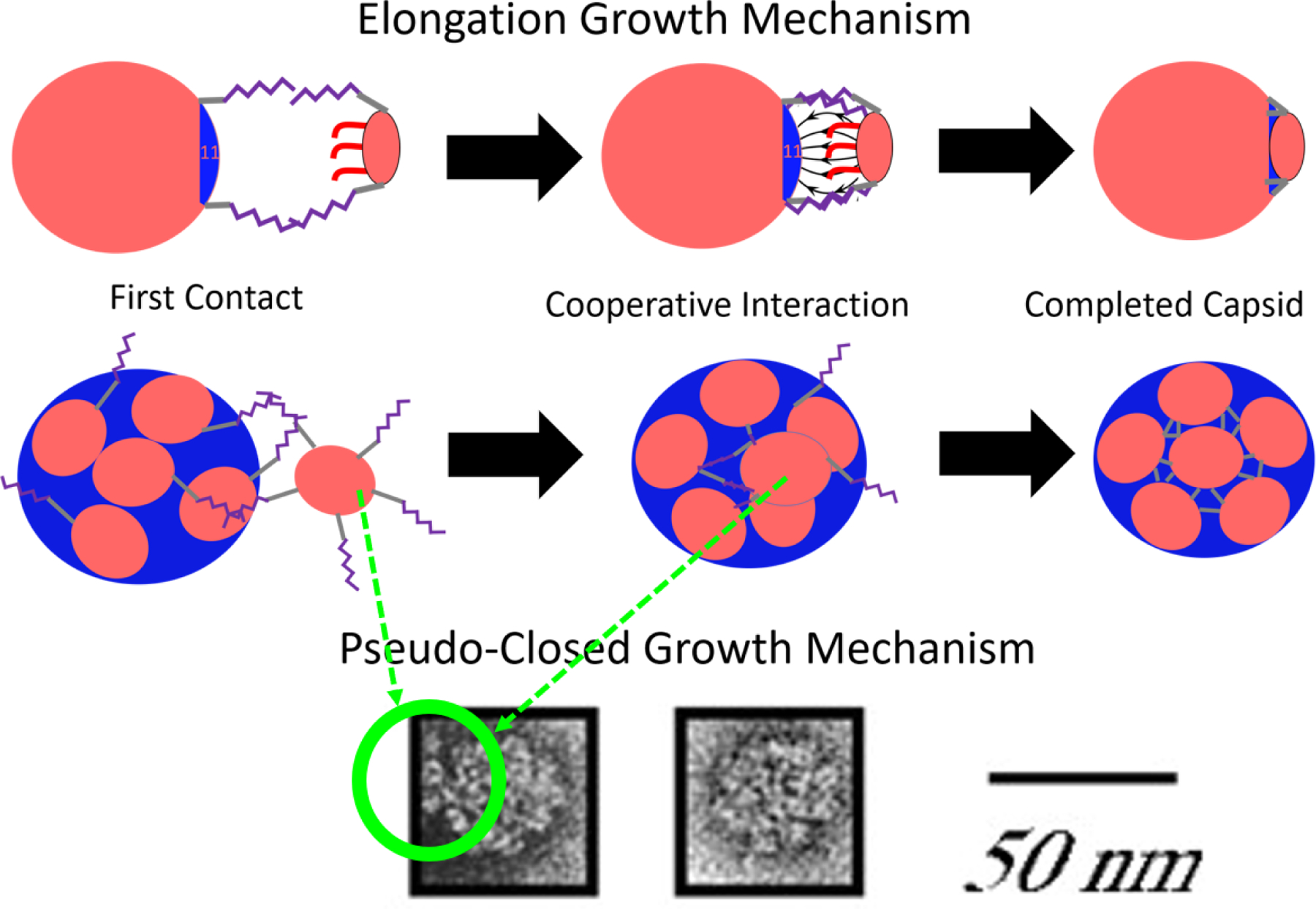
The full proposed growth mechanism of VP1 pentamers to an incomplete or pseudo-closed template. The VP1 pentamer first contacts a stray C-terminal ligand of a VP1 pentamer already bound to the template. This binding can happen at large distances due to the length of the connector domains. If the capsid is incomplete, cooperative interactions can then bring the VP1 pentamer and the incomplete capsid together, and align them such that the final VP1 pentamer perfectly fits into the icosahedral hole on the template. This process is referred to as the elongation growth mechanism. If the capsid is pseudo-closed, the connected VP1 will have to allow the capsid to dynamically rearrange in order to add a VP1 pentamer to the capsid in a much slower process. The images at the bottom show what appears to be C-terminal ligand connections being made by free VP1 pentamers on pseudo-closed particles larger than T = 1 and smaller than T = 7 using electron microscopy,¹⁹ republished with permission of the Microibology Society, from Simian Virus 40 VP1 Capsid Protein Forms Polymorphic Assemblies In Vitro, Kanesashi et al., Journal of General Virology 2003, 84, 7, 2003; permission conveyed through Copyright Clearance Center, Inc. It should be noted that there is no template in this image and thus the VP1 pentamers are connected to the pseudo-closed capsid and to each other only by C-terminal ligand interactions.

Conclusions

We developed a model to study the assembly behavior of explicit VP1 pentamers with C-terminal ligands on rigid templates to form T = 1 capsids. The results of the simulations are consistent with assembly experiments of VP1 pentamers on 524 nt RNA, when the pH and salt concentration were varied. Therefore, the length and flexibility of C-terminal ligands can recruit additional pentamers to the growing capsid regardless of template flexibility. Simulations of single capsids show that the T = 1 capsid is static whereas all other structures are dynamic and VP1 pentamers are mobile relative to each other. Dynamic rearrangement of VP1 pentamers facilitates both the shrinking of the N = 13 back to a T = 1 capsid and the growth mechanism of pseudo-closed shells, where dynamic shells can continue to add VP1 pentamers despite being already closed. This mechanism has been previously suggested based on experimental data. Our model shows that the C-terminal ligands are critical for the understanding of the kinetic growth of VP1 polymorphs, especially via the pseduo-closed growth mechanism.

Methods/Experimental

Samples preparation for SAXS measurements

We have used 524 nucleotide RNA as a template for SV40 VP1 assembly. The RNA was in vitro transcribed from linearized pETc11-Cp149 using a MegaScript T7 kit (Ambion). It is likely that the actual sequence does not make a significant contribution to the assembly. Previous work has suggested that the branching of RNA has an effect on its ability to be encapsidated⁴⁹ and structural predictions of RNA can be made based on its sequence.⁵⁰ However, it is difficult to correlate sequence and branching for RNAs made of hundreds nucleotides like the 524 nucleotide RNA used in our experimental studies. For example, the structures of long noncoding RNAs, which are at least 200 nucleotides, are more conserved than the nucleotide sequences that construct them.⁵¹ In any case, our work shows that the length of the C-terminal ligands dominate the RNA to control the assembly dynamics.

Empty SV40 VP1 VLPs were produced in Spodoptera frugiperda 9 (Sf9) insect cells by a disassembly-reassembly protocol, as described.¹⁸ Purified empty VP1 capsids were dialyzed twice against two disassembly buffers. The first buffer contained 20 mM 2-Amino-2-hydroxymethyl-propane-1,3-diol (Tris) at pH 8.9, 5 mM EDTA and 2 mM DTT. In the second dialysis, the disassembly buffer contained 20 mM Tris at pH 8.9, 2 mM EDTA and 2 mM DTT. The disassembled VP1 pentamers were mixed with equal volumes of RNA in the assembly buffer, containing 100 mM of buffer and various concentrations of NaCl. The type of buffer varied according to the desired final pH value for the assembly. For pH 7.2 3-morpholinopropane-1-sulfonic acid (MOPS) was used. For pH 8.1, 2-[4-(2-hydroxyethyl)piperazin-1-yl]ethanesulfonic acid (HEPES) was used. For pH 8.7 or 8.9, Tris buffer was used. The buffers were prepared by dissolving the buffer and adjusting the pH using either 37% HCl or 10 M NaOH solutions.

SAXS measurement setup and data reduction

SAXS measurements were measured in the flow-cell setup at ID02 beamline in ESRF (Grenoble).⁵² All measurements were taken at room temperature and buffer background measurements were taken before and after each VLP sample. Data reduction was perform as explained earlier.⁵³ The averaged background signals were then subtracted from the averaged sample signals.

Coarse-Grained Model

This section explains the logic behind the coarse-grained model. The explicit parameters and potentials used in our simulations can be found in the Supporting Information (SI).

VP1 Model

The coarse-grained VP1 model can be divided into 3 parts as shown in Figure 1. The first is the globular body made of 20 beads forming a rigid cylinder 8 nm in diameter and 6 nm in height. These dimensions correspond to the actual VP1 pentamer. 10 beads form a lower base ring whereas the other 10 are located 2 nm above the base ring. The body also contains 5 saturable connection sites, which allow interactions between VP1 pentamers. The second part of the structure comprises the C-terminal ligand of each VP1. Each VP1 pentamer contains 5 semiflexible C-terminal ligands, attached to the globular body. Each C-terminal ligand is made of 9 beads with a final connector bead, attracted to the connection sites via a Lennard-Jones potential whose strength is determined by a parameter ∈. All of the interactions between the long connector domain, which has collapsed to fill the space between globular bodies, and the VP1 body in the final capsid state can be reduced to a single parameter using this approach. The connector beads also repel each other in order to avoid multiple C-terminal ligands connecting to a single connection site, thus making the connection sites saturable. Angle potentials along the C-terminal ligand create an inflexible domain, which represents an α − helix in the C-terminal ligand of the real VP1. The C-terminal ligand, though rigid, rotates freely. The VP1 pentamer also contains 5 N-terminal ligands, made of a flexible chain containing 5 beads. The final 3 beads are positively charged to represent the charged residues in the unstructured N-terminals near neutral pH.

Template Model

The VP1 pentamers assemble around rigid, impenetrable spheres which have a uniform surface charge density (see the top of Figure 3). The total charge is −524e, which is the same as the total charge on the RNA used in the experiments. This choice of a rigid, spherical template is informed by the knowledge that the final conformation of polymers encapsidated by spherical viruses also tend to be spherically symmetrical^54,55 or close to it⁵⁶ and thus will be accurate for completed capsids.

The rigid sphere excludes an en masse assembly path where a flexible polyelectrolyte first binds all viral capsomers in an unorganized fashion and then the capsid anneals in a slower step, which requires the template to change conformation as shown in other theoretical⁴² and experimental work.⁵⁷ However, previous work with SV40 on short RNA’s, the same RNA used in the experimental section of this paper, did not show an annealing step⁵⁸ in the assembly and instead proposed that it follows the nucleation - elongation mechanism, where incomplete capsids form before all VP1 pentamers are added. This same mechanism has also been shown in monte carlo simulations on cargo made of monomers, which are not covalently bonded to one another.⁵⁹ Although this work with SV40⁵⁸ suggested the importance of the flexible template in binding VP1 pentamers to the incomplete capsid, here we show that the C-terminal ligands of the VP1 pentamers increase the effective size and flexibility of the incomplete capsid no matter the template. To summarize, even though the rigid sphere does not capture the flexibility of the RNA, it is accurate to describe the conformation of the RNA inside of closed capsids. Moreover, once the partial capsid forms the C-terminal ligands determine the effective size of the aggregate. We expect this partial capsid will form via nulceation-elongation as previous experiments have ruled out en masse assembly on 524 nucleotide RNA.

Solution Salt Conditions

Electrostatics in these simulations are handled using an implicit ion model with two types of interactions. First, we extend the two state model of Alexander et al. for spherical symmetry⁶⁰ to the case of compacted flexible polymers^61,62 to construct an electrostatic potential for the template. This model introduces nonlinear effects in a Yukawa potential due to ion condensation via an effective reduced charge, q_eff, which can be computed using the nonlinear Poisson-Boltzmann equation for ion penetrable spheres⁶³ as opposed to the dense colloids used by Alexander et al.⁶⁰ We note that polymer entropic effects are negligible as well as the ionic correlations inside the collapsed polymer in monovalent salts⁶¹ (only in the presence of multivalent ions are these correlations significant⁶⁴). Therefore, we do not include short-range interactions explicitly but assume the template is spherical, as mentioned in the Template Model section.

With these assumptions, the electrostatic energy is represented by a Yukawa potential given by,

$$F_{ele}=\frac{-q_{eff}^2{l}_b{e}^{-\frac{r}{{\lambda }_d}}}{r}$$ (1)

where q_eff is in units of the elementary charge e, l_b = e²/(4π∈₀∈_rk_BT) is the Bjerrum length (∈₀ and ∈_r are the permittivity of vacuum and the relative dielectric constant of the medium, respectively)), ${\lambda }_d=\frac{1}{\sqrt{4\pi l_B{c}_s}}$ is the Debye length, which in NaCl can be approximated by ${\lambda }_d\left(nm\right)=\frac{0.304}{\sqrt{I\left(M\right)}}$, where I is the ionic strength of the solution. This form of the Debye length breaks down at salt concentrations above about 300 mM.^65,66 Since the effective charge, q_eff quantifies the portion of the charge not compensated by counterion condensation, at low salt concentrations (low ionic strength), q_eff approaches 1 while at very high salt concentration q_eff approaches 0. This form of the potential also provides an opportunity to mimic the deprotonation of the N-terminal ligands when the pH is increased. The deprotonation of specific amino acids at different solution pH is a highly complex function on the local environment.⁴⁷ Instead of modeling this complexity, we simply decrease the N-terminal charge as this gives the correct general trend. Since only the N-terminal ligand charges are affected and not the template charges, the N-terminal ligand charge fraction can simply be considered as $q_{eff}^2$. The second type of interaction takes place at high salt concentration (above 300 mM), where in the case of not strongly charged surfaces, as in our system, the interaction is given by a short range attraction driven by the electrolyte correlations that generate a depletion type attraction at short distances, as shown by Li et al.,⁴⁵ who showed that at high NaCl concentrations, the collective interactions between the salt ions produce depletion interactions between nanoparticles, similar to those generated by oligomers (see Appendix in ⁴⁵). Therefore, we added a short range attraction between the charged N-terminal ligand beads and the template of strength, α

$$F_{\mathit{\text{short}}}\left(r\right)=\{\begin{array}{cc}0& r\ge R+1\\ -\alpha & r<R+1\end{array}$$ (2)

where R is the radius of the template. In molecular dynamics simulations, this attraction is implemented as an interaction between N-terminal ligand beads and a particle, located at the center of mass of the rigid template. α is positive at high salts where depletion interactions dominate.

The total free energy contribution of the implicit salt is then given by

$$F_{\mathit{\text{total}}}\left(I\right))=F_{\mathit{\text{short}}}\left(\alpha \left(I\right)\right)+F_{ele}\left(q_{eff}\left(I\right),{\lambda }_d\left(I\right)\right).$$ (3)

Simulation Methods

Two types of simulations were run. In the first, one large rigid template was initialized and surrounded with a given number of VP1 pentamers which bind immediately to the surface. The diameter of the template is then reduced slowly such that no VP1 pentamers are released during this process until the template becomes too small for all of the VP1 pentamers to bind. Individual states are then run for longer times in order to study the capsid at different curvatures.

The second type is the assembly simulations. VP1 pentamers and templates were initialized in ordered arrays evenly spaced throughout the simulation box. The absolute concentration of VP1 pentamers and templates is much higher than what is typical of experiments in order to complete the assembly process in reachable time scales.

All simulations are run in HOOMD⁶⁷ using Langevin integration.