Super-Resolution Reconstruction for Two- and Three-Dimensional LA-ICP-MS Bioimaging

Abstract

The resolution of laser ablation-inductively coupled plasma-mass spectrometry (LA-ICP-MS) elemental bioimaging is usually constrained by the diameter of the laser spot size and is often not adequate to explore in situ subcellular distributions of elements and proteins in biological tissue sections. Super-resolution reconstruction is a method typically used for many imaging modalities and combines multiple lower resolution images to create a higher resolution image. Here, we present a super-resolution reconstruction method for LA-ICP-MS imaging by ablating consecutive layers of a biological specimen with offset orthogonal scans, resulting in a 10× improvement in resolution for quantitative measurement of dystrophin in murine muscle fibers. Layer-by-layer image reconstruction was also extended to the third dimension without the requirement of image registration across multiple thin section specimens. Quantitative super-resolution reconstruction, combined with Gaussian filtering and application of the Richardson-Lucy total variation algorithm, provided superior image clarity and fidelity in two- and three-dimensions.

Graphical Abstract

The resolution of an image for most practical applications of laser ablation-inductively coupled plasma-mass spectrometry (LA-ICP-MS) using single quadrupole instruments is governed by the laser spot size, the ICP-MS total integration time, and the laser scan speed. In this context, the resolution may be defined by each sampling event of the specimen represented by each pixel of the image.

The size of a pixel in the direction of the line scan is given by v_lt_sc, where v_l is the scan speed of the laser and t_sc is the total integration time.¹ Manipulation of t_sc or v_l varies the resolution of the image in the direction of the line scan. For example, halving the total integration time will halve the lateral pixel size. This scenario has been frequently used to construct images with anisotropic (rectangular) pixels of improved resolution in the scan direction only, while the spacing between consecutive scans is defined by the diameter of the laser spot at the sample.^2–5 The anisotropic ratio (AR) of a pixel is given by eq 1,

$$\text{AR}=\frac{d_1}{v_l{t}_{\text{sc}}}$$ (1)

where d_l is the diameter of the laser spot.

Conventional LA-ICP-MS imaging has made major contributions to our understanding of the role of transition metals and other elements in health and disease at lateral resolutions of 25 μm² to 2500 μm² using laser spot sizes of 5 to 50 μm.^6,7 However, there remains a pressing need to improve the resolution to adequately image subcellular localization of biometals, and more recently, biomolecules via immunohistochemically assisted imaging mass spectrometry.⁸ Here, proteins and other biomolecular targets may be interrogated in tissues by tagging antibodies with lanthanide doped polymers⁹ or metal nanoparticles.¹⁰ A major difficulty for both of these imaging approaches is the square relationship between signal intensity and spot size, which limits the practical spot size for quadrupole-based instruments to approximately 4 to 10 μm.^5,11 Below this, there is not enough material in each sampling event for detection.

Efforts to go beyond this resolution limit have involved laser oversampling and application of various deconvolution algorithms. For example, Van Malderen et al.¹² imaged the 3D distribution of ⁵⁵Mn in corrosion growth rings of glass at sub-micrometer resolution via overlapping spot sampling, and deconvolution with an iterative Richardson-Lucy total variation (RLTV) algorithm. An alternative approach is super resolution reconstruction (SRR) to produce high resolution images from noisy or low-resolution images. SRR is a mature technique used in many image-based fields including astronomy,^13,14 magnetic resonance imaging,^15,16 and light microscopy.¹⁷ SRR reconstructs a higher resolution image by combining multiple images, which are acquired at subpixel distance offsets. SRR requires a nonuniform interpolation algorithm to populate pixels not filled by the lower resolution images,^18,19 which typically involve linear, cubic, and nearest-neighbor interpolation strategies.²⁰ The SRR algorithm may also be applied in three dimensions in a similar manner to MRI.^21–23

3D image reconstructions by laser ablation-inductively coupled plasma-mass spectrometry (LA-ICP-MS) are conventionally performed by sampling of consecutive slices of a specimen and image registration of each of these slices for integration into a final 3D image of voxels that is a representation of the original sample.^9,24–27

This work demonstrates a novel method of super resolution reconstruction (SRR) to improve the fidelity and resolution of immunohistochemically assisted quantitative LA-ICP-MS imaging with consecutive offset orthogonal raster scans in two and three dimensions. In the case of three-dimensional imaging, continuous orthogonal sampling of the specimen was undertaken until the specimen was completely ablated, eliminating image registration required by conventional approaches.

METHOD

Instrumentation.

All LA-ICP-MS analyses were conducted on an Agilent 7700x series ICP-MS (Agilent Technologies, Mulgrave, Vic, Australia) coupled to a New Wave Research NWR193 (Kennelec Scientific, Mitcham, Vic, Australia) ArF excimer laser emitting at a wavelength of 193 nm. Laser ablation and ICP-MS parameters were optimized with a gelatin standard containing Gd with a laser spot size of 15 μm, scan speed of 30 μm·s⁻¹, and laser frequency of 20 Hz with the Ar carrier gas at 1.15 L·min⁻¹. Calibration curves and construction of images were performed in MassImager, an in-house imaging data processing software package developed by Robin Schmid from the University of Münster, and FIJI used for image visualization.²⁸ The resulting calibration equations were used to convert the signal intensities of every voxel in each image to concentrations expressed as ng·g⁻¹.

For solution analyses, an Agilent Technologies 7700x ICP-MS (Agilent Technologies, Mulgrave, Vic, Australia) was used with sample introduction via a micromist concentric nebulizer (Glass Expansion, West Melbourne, Vic, Australia) and a Scott type double pass spray chamber cooled to 2 °C. ICP-MS extraction lens parameters were selected to maximize the sensitivity of a 1% HNO₃:HCl solution containing 1 ng/mL of Li, Co, Y, Ce, and Tl. Helium was added into the octopole reaction cell to reduce interferences. Calibration curves were constructed and processed using Agilent Technologies Mass-hunter software.

Reagents.

Gadolinium(III) nitrate hexahydrate, Tris-HCl (pH 7.4), ethylenediaminetetraacetic acid (EDTA; 10 mM), polyethylene glycol (M_n 400), and gelatin from bovine skin (100 mg; Type B) were purchased from Sigma-Aldrich (Castle Hill, NSW, Australia).

Grace Bio-Laboratories (Bend, OR, U.S.A.) supplied 6 Hybriwell gasket (20 × 9.8 mm) and clear polycarbonate cover with two ports (item number 612107, depth 0.25 mm, volume 50 μL). Ultrapure HNO₃ and a certified Gd standard were supplied by Choice Analytical (Thornleigh, New South Wales, Australia). Antidystrophin monoclonal antibody (MANDYS8, sc-58754) was supplied by Santa Cruz Biosciences (Dallas, Texas, U.S.A.). MaxPar Labeling kit was purchased from Fluidigm (South San Francisco, CA, U.S.A.). Mouse on Mouse (M.O.M.) Blocking Reagent (MKB-2213) was purchased from Vector Laboratories (Burlingame, CA, U.S.A.). Superblock (TBS; 37535) and TBS containing 0.1% Tween-20 (28360, TBS-T) were supplied by Thermofisher, (Waltham, Ma, U.S.A.).

Standard Preparation.

Matrix matched gelatin standards were prepared from a modification of a previously described method.²⁹ Briefly, a stock solution of 25 mg·L⁻¹ Gd was prepared by dissolving 323.89 mg of gadolinium(III) nitrate hexahydrate in 100 mL of pH 7.4 aqueous buffer comprising 100 mM Tris-HCl, 10-mM EDTA, and 1% w/w polyethylene glycol. A series of gelatin standards were prepared by dilutions of this stock solution in the buffer to levels shown in Supporting Information, Table S1 and addition of 100 mg of gelatin to 900 μL of the dilutions at 53 °C with periodic vortexing.

Flat homogeneous standard sections suitable for laser ablation were prepared by adhesion of six Hybriwell gaskets and clear polycarbonate covers with two ports to a glass slide. The slide was heated to 53 °C for 1 min on a dry heat block before pipetting 50 μL of the metal−gelatin standard mixture via the port.

The standard slide was cooled to room temperature for 30 min and then to −20 °C in a freezer for 30 min or until the gel was frozen. The adhesive gasket and polycarbonate covers were then removed, and the standards were stored at room temperature until required for use.

To determine the concentration of the standards, 100 μg of each standard was dissolved in 1 mL of 20% HNO₃ (v:v), diluted to 5 mL, and analyzed by solution ICP-MS. A 7-point calibration curve for quantification of the digest gelatin was constructed by diluting a 10 mg·L⁻¹ standard of Gd as per Supporting Information, Table S2. ¹⁰³Rh was used as an inline internal standard.

Sample Preparation.

Wild-type C57BL/6 mice were purchased from Jackson Laboratories (Bar Harbor, ME, U.S.A.) and quadricep muscle was dissected under guidelines of the Institutional Animal Care and Use Committee at the University of California, Los Angeles (#2000−029−61D). All mice used in the study were male.

The MANDYS8 antidystrophin antibody (Santa Cruz Biotechnology) was labeled with ¹⁵⁸Gd using a MaxPar polymer label by the manufacturer (Fluidigm).

The 10 μm thick (for 2D) and 50 μm thick (3D) cryosections of mouse quadriceps were prepared for immunolabeling as follows. Air-dried samples were washed in duplicate for 2 min with TBS at pH 7.4. Sections were then blocked with mouse on mouse blocking reagent for 60 min as per manufacturer’s instructions. Sections were washed 2 × 2 min with TBS containing 0.1% Tween-20 (TBS-T). A 1:100 dilution of the tagged antidystrophin antibody to give a final concentration of 2 μg.mL⁻¹ was made with Superblock diluent. The sections were incubated with this solution for 30 min at room temperature. The sections were washed in triplicate for 3 min with TBS-T followed by an ultrahigh purity water wash. Sections were air-dried and stored in a dry dust free environment until required for analysis by LA-ICP-MS.

Optimization of Image Acquisition Parameters.

The laser repetition frequency was maintained at 20 Hz (time between laser pulses = 50 ms) and the integrated analysis time of each plume in the ICP-MS was equal to or an integer multiple of 50 ms to minimize aliasing. Lateral resolution improvements below the spot size of the laser was based on anisotropic oversampling by the ICP-MS in the direction of the line scan. The lateral sampling interval (Δx) is a function of the total integration time, that is,

$$\Delta x=v_1{t}_{\text{sc}}$$ (2)

Seven ablation conditions were considered (Table 1), spanning various scan speeds and total integration times representing ARs from 1 to 10. The laser spot size was kept constant at 15 μm for all experiments.

Table 1.

Super Resolution Reconstruction Acquisition Parameters

	1	2	3	4	5	6	7
spot size (μm)	15	15	15	15	15	15	15
scan speed (μm·s−1)	15	60	30	15	15	15	15
total integration time (s)	1	0.125	0.25	0.5	0.25	0.125	0.1
acquisition time for 300 μm × 300 μm area (mins)	13.4	3.4	6.7	13.4	13.4	13.4	13.4
sampling interval (μm)	15	7.5	7.5	7.5	3.8	1.9	1.5
anisotropic ratio (AR)	1	2	2	2	4	8	10

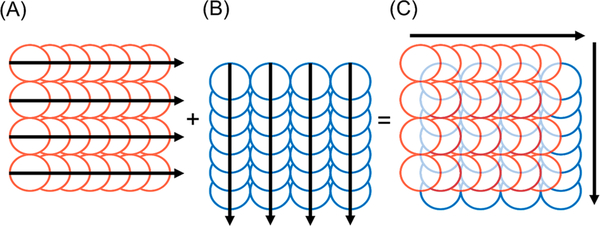
Two raster pattern scans were performed for each condition in Table 1. The first data matrix was acquired from consecutive line scans from left to right for a given distance across the specimen, each line scan offset by the magnitude of the spot size of the laser (Figure 1A). This was followed by the collection of the second data matrix from a pattern scan in an orthogonal direction to the first (Figure 1B), with the origin of ablation offset by half the magnitude of the spot size in the scanning directions of both layers (Figure 1C). The area of ablation for each pattern was a square of 300 μm by 300 μm. The acquisition time for each raster pattern ranged from 3.4 to 13.4 min for the two layers. Standards were ablated in the same manner before and after each acquisition scheme using the same spot size, scan speed and integration time.

Figure 1.

Orthogonal acquisition: (A) first line scans, (B) second line scans offset by half the magnitude of the laser spot size in both directions, (C) combined pattern for SRR processing. Arrows denote direction of scan.

For 3D images, the sample acquisition parameters consisted of a 15 μm spot size moving at 30 μm·s⁻¹ scan speed with a total integration time of 0.125 s, equivalent to an AR of 4. All samples were 50 μm thick and were ablated in 10-layer acquisitions. Standards were ablated at the beginning, middle, and end of each 10-layer batch in the same manner as the 2D samples. The optical focus was used to test the depth of field for ablation. Refocusing of layers by 5 μm of depth per layer pair was compared to unfocused ablation.

Super Resolution Reconstruction.

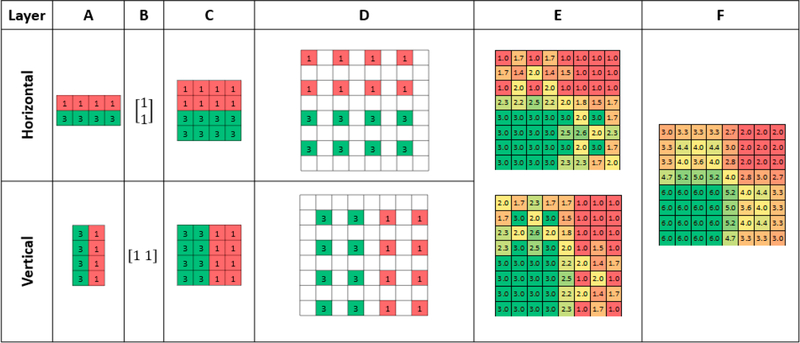
The two matrices described above were made conformable for addition using the Kronecker Product³⁰ of the raw data (Figure 2A), and the row, or column matrix as applicable (Figure 2 B), resulting in matrices with equal dimensions (Figure 2C). These matrices were then up-sampled with null values into a checkerboard pattern (Figure 2D) and shifted by the appropriate initial offset, stacked into a 3D array and trilinearly interpolated³¹ (Figure 2E). Finally, the two populated matrices were summed to create a 2D image (Figure 2F).

Figure 2.

SRR processing of two sequentially simulated ablated layers. (A) The two layers acquired with an AR of 2 in the horizontal and vertical directions. (B, C) Representation of the two layers brought to congruence using the Kronecker Product. (D) Up-sampling with null values into a checkerboard pattern. (E) Layers offset and stacked into a 3D array and null values and trilinearly interpolated. (F) Populated layers summed together to produce final 2D image.

Due to the depth difference between layers, step E was performed with the layers stacked on top of each other in order of ablation. For 2D images, the two layers were summed together in the z-axis to create the image. Conversely, 3D images were maintained as stacks of 2D images for further processing with trilinear interpolation between the layers.

Processing Algorithms.

Two algorithms of data processing were applied to mitigate data convolution. The first consisted of smoothing with a Gaussian kernel with dimensions equivalent to the spot size of the laser to correct the square pixel from circular laser beam artefacts, as described previously.³²

The second consisted of minimizing beam related spreading of the signal using Richardson−Lucy Total Variance Regularization (RLTV)¹² applied via the DeconvolutionLab 2 in Fiji.³³ A synthetic point spread function (PSF) comprising two Gaussians diagonally offset by the radius of the laser beam was applied, as per the original scanning pattern offset. For 3D maps, the two Gaussian PSFs were applied individually to each layer.

Quantification was performed by applying the same processing workflow to the gelatin standards in order to account for any changes to the raw data.

Image Processing Software.

Image processing was performed using MATLAB for SRR then FIJI for image filtering. The MATLAB code for SRR was written in-house and is available from (https://github.com/Elemental-Bio-Imaging-Facility). The default FIJI Gaussian filter and the DeconovolutionLab2³³ plugin for Richardson-Lucy total variance deconvolution (RLTV) were used in this experiment. Processing was performed on both samples and calibration standards. 3D images were constructed using vtk files and imported into Paraview³⁴ for visualization.

Statistical Analysis.

Statistical analyses on the raw and processed data was performed with the Real Statistics plugin for Excel.³⁵ The LODs and LOQs were estimated from the calibration curves according to the following equations:

$\text{LOD}=\frac{3\sigma }{S}\text{and}\text{LOQ}=\frac{10\sigma }{S},$ where σ was estimated by the standard error in the y-intercept and S was the slope of the calibration curve.

RESULTS AND DISCUSSION

Optimization of Image Acquisition Parameters.

We chose to use the expression of dystrophin in murine tissue as an exemplar target. Dystrophin is a protein found in muscle fibers and is part of the dystrophin-glycoprotein complex (DGC), a transmembrane multimeric complex that links the intracellular cytoskeleton and the extracellular matrix,³⁶ and provides structural stability to the sarcolemma during muscle use.³⁷ It is a low abundant protein with a clearly defined location in the muscle membrane (Figure 3), making it a suitable target for examining the improvements of SRR imaging, and the subsequent processing algorithms.

Figure 3.

Representative photomicrograph of dystrophin in murine quadriceps. The expression of the protein is clearly seen as a honeycomb structure in the membranes of the muscle fibers. The protein was stained with Gd-labeled MANDYS8 primary antibody and detected using a goat antimouse secondary antibody (Sigma) conjugated to alkaline phosphatase with NBT/BCIP substrate (Sigma).

Seven scenarios were considered for investigation and optimization of image acquisition parameters (Table 1) of various laser scan speeds ranging from 15 to 60 μm s⁻¹, and total integration times between 0.100 and 1.00 s, representing ARs from 1 to 10, which may be thought of as a magnification factor to improve image fidelity and clarity. The spot size was maintained at 15 μm for all experiments as preliminary scans (data not shown) indicated excellent signals of Gd for the sample under investigation, while spot sizes below 15 μm did not provide sufficient intensities for subsequent SRR. Spot sizes above 15 μm performed equally well in terms of AR magnification, however the criteria of optimization were resolution improvement and acquisition speed.

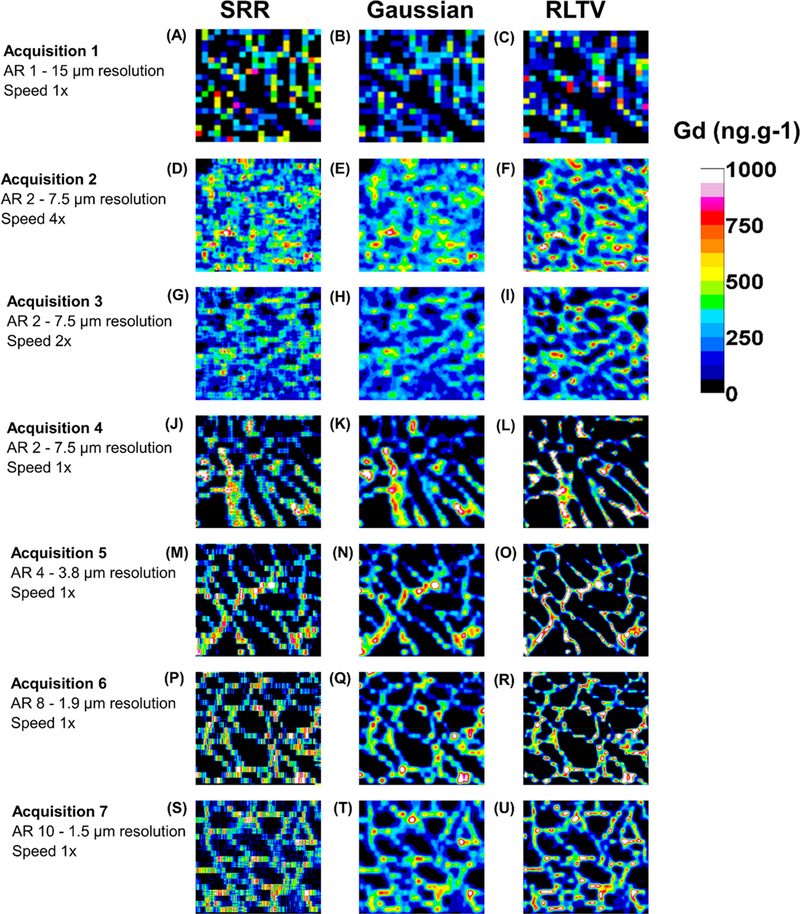
Figure 4 depicts the resulting images from each of the seven acquisitions. Each figure was quantified against calibration curves consisting of five gelatin standards (Supporting Information, Table S1). Figure 4A–C was constructed using conventional acquisition parameters (without SRR) in which the scan speed was 1× the magnitude of the spot size, and the total integration time was 1 s, equivalent to a resolution of 15 μm per voxel and consisted of two passes without offset in the horizontal direction to maintain equivalence of ablated mass for direct comparisons of later acquisitions. Figure 4A depicts the distribution of dystrophin as measured by the proxy Gd and is difficult to discern with patchy coverage and of limited utility. Figure 4B shows the result of application of the Gaussian filter, and Figure 4C shows the result of RLTV processing. As expected, each of these processes did not improve the clarity of the image when compared against the raw image.

Figure 4.

Image panel of acquisition parameter optimization. Seven acquisitions were considered representing ARs ranging from 1 to 10. The SRR images are in column 1, except for (A), which was constructed in the conventional manner. Column 2 contains the images after application of the Gaussian filter, while column 3 represents images after RLTV.

Consider acquisitions 2, 3, and 4, where the AR was constant at 2 (equivalent to a lateral and axial resolution of 7.5 μm per voxel) and the scan speed was decreased from 60, 30, and 15 μm·s⁻¹, representing increments of 4×, 2×, and 1× the magnitude of the spot size. In each experiment, the total integration time of the mass spectrometer was increased by a factor of the same increment in order to maintain an AR of 2.

Visual inspection of Figure 4D (acquisition 2, speed 4×) shows improved Gd coverage and emergence of the characteristic “honeycomb” structure of dystrophin within the muscle fiber membranes. Figure 4E shows smoothing of the image after application of the Gaussian filter, while Figure 4F demonstrates that the RLTV algorithm was effective for improving image clarity.

Similarly, Figure 4G–I depicts the raw and processed images (acquisition 3, speed 2×) with half the scan speed of the former acquisition. Although the AR was maintained at 2 as before, the image clarity was superior in all three images. This improvement in clarity was a direct consequence of the washout time of the cell on this instrument (~1 s) becoming decreasingly significant as a proportion of acquisition time per laser pulse. The image clarity following application of the processing algorithms was again superior to the raw SRR image.

This effect is even more prominent in acquisition 4, in which the total scan speed was at the same magnitude of the spot size (Figure 4J–L). Here, the distribution of dystrophin is clearly visible in the raw image and further improved by application of the Gaussian filter and the RLTV algorithm.

In general, image blur effects were acceptable at scan speeds below two times the magnitude of the spot size, that is, 30 μm·s⁻¹. Although faster scan speeds increased the Gd signal, the image blur was generally not suitable for SRR acquisition.

Acquisition 5 demonstrates that the AR can be further increased to 4, representing a lateral and axial resolution per voxel of 3.8 μm (Figure 4M–O). The dystrophin distribution is clearly visible in the raw image and is further clarified by application of the processing algorithms. Acquisitions 6 (Figure 4P–R) and 7 (Figure 4S–U) show that the AR can be further increased to 8 and 10, representing lateral and axial resolutions of 1.9 and 1.5 μm per pixel, respectively, resulting in processed images of excellent clarity and fidelity.

In consideration of these factors, the best compromise between resolution, acquisition time, and cell washout effects was when the scan speed was less than two times the magnitude of the spot size. This compromise is only applicable to the instrument in our laboratory as new cell designs available from various vendors have significantly reduced washout times to approximately 1 to 5 ms,³⁸ which are coupled to time of flight mass spectrometers.³⁹

Calibration.

The effects of the workflow and the various processing algorithms on calibration curves are shown in Supporting Information, Figure S1. Figure S1A shows a representative calibration curve, and an image panel of each of the six gelatin standards (Figure S1B) obtained from ablation of a 300 μm by 300 μm square of the first layer in the horizontal direction with a 15 μm spot size, scanning speed of 30 μm·s⁻¹, and a total integration time of 0.25 s.

In this case, the lateral resolution was 7.5 μm, and the axial resolution was 15 μm, representing an AR of 2. Similarly, Figure S1C shows the calibration curve and the image panel of the six gelatin standards (Figure S1D) at 300 μm × 300 μm ablated from the second layer diagonally offset at 7.5 μm (half the magnitude of the spot size) from the first. A representative post-ablation raster pattern of a standard is shown in Supporting Information, Figure S2.

The analytical figures of merit for these acquisitions and the subsequent processing algorithms are shown in Supporting Information, Table S3.

The calibration curve of the horizontal layer had excellent linearity and a y-intercept close to the origin at 2.4 CPS, and a slope of 0.1433 CPS/ng·g⁻¹. The calibration curve of the second vertical layer also had excellent linearity and a y-intercept close to the origin at 2.0 CPS, and a slope of 0.1237 CPS/ng·g⁻¹. Summation of the slopes of these two curves yields a value of 0.2670 CPS/ng·g⁻¹ and a y-intercept of 4.4 CPS. The LODs and LOQs were similar for both acquisitions.

The effects of the first processing step combining two offset layers of orthogonal acquisition using SRR representing an AR of 2 is shown inFigure S1E. The calibration curve remained linear and again was close to the origin at 12.1 CPS. The slope of the calibration curve was 0.2659 CPS/ng·g⁻¹ and was not significantly different (p-value 0.870) from the summation of the slopes of the two previous cases. This was consistent with an expected doubling of the slope due to summation of two layers into a single layer, that is, two passes of the laser would be expected to double the signal intensity per voxel as twice the amount of material was ablated when compared against a single pass.

The calibration image panel (Figure S1F) now consists of square voxels made conformable by application of the Kronecker product and bilinear interpolation of null values in the product matrix. Inspection of this standard image panel clearly shows the homogeneous distribution of Gd throughout each level of standard. The LOD of 89 ng·g⁻¹ and the LOQ of 270 ng·g⁻¹ increased by approximately 15% when compared against average values from acquisitions of the single layers.

After application of the Gaussian function (Figure S1G), the slope was not significantly different from the SRR (p-value 0.326), while the intercept, linearity, LOD, and LOQ were similar to the SRR processing step, indicating that for homogeneous distributions of Gd, this smoothing function would have negligible impact on quantification. Final application of the RLTV algorithm (Figure S1I), again had no significant difference in the slope compared against the Gaussian (p-value 0.117), and negligible impact on the linearity, y-intercept, LOD and LOQ. The image panel (Figure S1J) appears almost identical to the Gaussian smoothed image.

The average response (CPS) and% RSDs for standards near the LOQ or above (standards 4–6) is shown in Supporting Information, Table S4 for each of the described scenarios. A one-way ANOVA showed a significant difference for averages of the response in all standards when the summed responses were compared against the processed averages (p-value < 0.05). In contrast, no significant difference was observed after application of one-way ANOVA for SRR, Gaussian, and RLTV (p-value 0.24, std 4; p-value 0.09, std 5; and p-value 0.07, std 6). The initial processing with SRR, which included trilinear interpolation, decreased the %RSD in all levels of standards when compared against simple summation. Subsequent application of the Gaussian function decreased the %RSD further still, while application of the RLTV increased the % RSD to levels like that of the SRR processing. In all three processing cases, the %RSD was lower than the raw acquisition data. These data demonstrate that the processing algorithms were quantitively invariant for homogeneous standards, while the Gaussian filter provided the lowest %RSDs.

Quantification.

In order to determine the effect of the calibration processing algorithms on quantification of heterogeneous distributions within tissue sections, a single layer was ablated in the horizontal direction with a 15 μm spot at 30 μm· s⁻¹ and 0.25 s integration time, equivalent to an AR of 2 (acquisition 3). This same horizontal data matrix was transposed vertically (layer 2) to simulate the ablation of a second layer, offset diagonally at 7.5 μm and subjected to each of the processing steps described above. The average concentrations and% RSD of this double layer test is shown in Supporting Information, Table S5. This test was designed to ensure that that the workflow was also quantitatively invariant for heterogeneous specimens as no significant difference would be expected for average concentrations of Gd within the processing algorithms, and a similar trend for %RSDs, as was observed for the calibration data. For each processing step, the simulated two-layer sample was quantified by application of the corresponding processing step to the calibration data.

As expected, application of one-way ANOVA showed there was no significant difference in average concentration of Gd between layer 1, layer 2, and the summed layers (p-value 1). However, there was a significant difference between the average concentrations when all scenarios were compared (p-value < 0.05). There was no significant difference in average concentration of Gd within processing algorithms (p-value 0.15). As before, the %RSD was reduced after SRR processing when compared against the raw data quantification. The % RSD was further reduced after application of the Gaussian filter and increased after application of the RLTV processing step.

Supporting Information, Figure S3, shows the effect of each of the processing steps on image construction for the simulated scenario described above. Figure S3A and B depict the horizontal anisotropic acquisition and the transposed image, respectively. The image is of low clarity and characteristic “honeycomb” structure is difficult to discern. Application of SRR (Figure S3C) shows the SRR composite image, demonstrating increasing clarity, while the Gaussian filter smoothed the image further (Figure S3D). Finally, the importance of the RLTV algorithm is shown in Figure S3E, where the distribution of dystrophin is clearly seen.

Three-Dimensional Reconstruction.

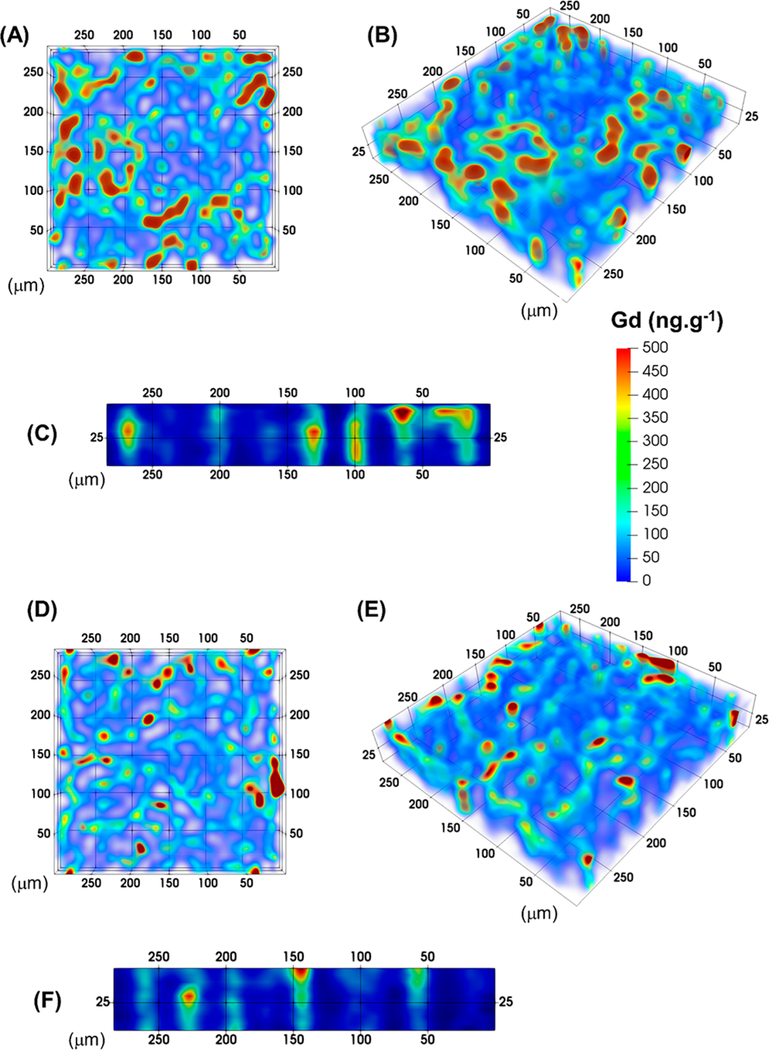
Two scenarios were considered for three-dimensional reconstructions, single focus ablation, and refocusing the laser after each laser pass. These two scenarios were considered to examine the possibility that the collimated top hat beam shape of the laser and the depth of field for ablation may generate artifacts in areas where the sample may have different densities or thicknesses. Two regions of 300 μm × 300 μm were ablated at an AR of 4 with a spot size of 15 μm and at 30 μm s⁻¹ and a total integration time of 0.125 s, with a single focus continuous acquisition and refocusing at each pass in increments of 5 on 50 μm sections. In both cases, the specimen was removed completely after 10 passes. The total acquisition time was approximately 70 min for each region. Each acquisition was processed with SRR, Gaussian filtering and RLTV and is shown in Figure 5. Figure 5A,B shows the planar and oblique views, while Figure 5C shows the isometric view of the refocused laser acquisition. The distribution of dystrophin is seen throughout the 10 sections of acquisition. The continuity of the dystrophin along the muscle fibers in the third dimension was maintained, indicating that refocusing of the laser beam was a viable method for three-dimensional acquisitions.

Figure 5.

Three-dimensional reconstructions of continuously ablated 50 μm section. (A) Planar view of single focus acquisition. (B, C) Oblique and isometric views of refocused laser acquisition at 5 μm for each pass. (D, E, and F) Planar, oblique, and isometric views of single focus laser acquisition. The structural integrity of the dystrophin is clearly seen throughout the 10 layers.

Similarly, Figure 5D,E shows the planar and oblique views, and Figure 5F shows the isometric view of the single focused laser acquisition. The distribution of dystrophin is clearly seen from the planar view. The isometric view displays a generally lower signal of Gd when compared to the refocusing method possibly due to reduced ablation efficiency when not refocusing. However, the oblique view shows equivalent signal down the full 10 layers of ablated muscle fiber, and the signal difference was most likely due to sample heterogeneity. Therefore, the single focus method was comparable to the refocusing method for up to a sample thickness of 50 μm. The advantage of no focus is that no prior testing of ablation depth per laser pass is required saving both sample tissue and time.

CONCLUSIONS

In summary, these data demonstrate that the SRR, Gaussian, and RLTV processing algorithms provide superior image fidelity, with no significant differences in concentration quantification within the post-acquisition processing procedures. The average concentrations of Gd across the heterogeneous sample increased by approximately 10%, when compared against the raw data. Although this change was significantly different at α = 0.05 when compared against the raw data, the processing steps would not affect the final interpretation of the distributions of dystrophin as relative quantification is required for this application. The lowest % RSD were obtained with the Gaussian filter. On the other hand, the best image clarity was obtained after RLTV, so visual interpretation of structures within tissue sections should be performed after the final RLTV processing step.

Continuous ablation of 50 μm thick tissue sections and methods of a single focus and refocusing of the laser at 5 μm increments with each pass were equivalent for three-dimensional images. When compared against conventional approaches, the single focus and refocusing methods were improved in both terms of image clarity, resolution, and simplicity. The single focus method is recommended up to a sample thickness of 50 μm due to the simplicity of setup. The conventional approach usually requires ablation of individual sections followed by image registration and reconstruction of the final image by stacking the slices into a contiguous representation of the specimen. The SRR approach removes the requirement for serial sectioning and image registration and eliminates anomalies associated with cutting artifacts. Furthermore, the three-dimensional volume of the SRR approach is only limited by the focusing range of the laser and could potentially be applied to whole organ imaging such as murine brain, kidney, pancreas, and so on.

The ablation cell wash-out was the most significant limitation for the total acquisition time of the specimen for any given experiment and was limited to laser scan speeds of approximately 2d_l μm·s⁻¹. Beyond this speed, image blur effects negated the benefits of SRR processing. It is anticipated that this image blur problem would not be significant at speeds greater than 2d_l μm·s⁻¹ with new cell designs with significantly reduced washout times. Limitations of the “speed limit” of acquisitions and the maximum ARs would then migrate primarily to factors such as laser pulse frequency and speed of the mass spectrometer duty cycle, requiring the use of higher frequency laser systems and sensitive time-of-flight instruments.

Ethical Statement.

Animal procedures were performed in accordance with the Institutional Animal Care and Use Committee at the University of California (Los Angeles, U.S.A.; ARC #2000−029−61D).