New kind of interference in the case of X-ray Laue diffraction in a single crystal with uneven exit surface under the conditions of the Borrmann effect. Analytical solution

The analytical solution of the problem of X-ray spherical-wave Laue diffraction in a single crystal with a linear change of thickness on the exit surface is derived. General equations are applied to a specific case of plane-wave Laue diffraction in a thick crystal under the conditions of the Borrmann effect.

Abstract

The analytical solution of the problem of X-ray spherical-wave Laue diffraction in a single crystal with a linear change of thickness on the exit surface is derived. General equations are applied to a specific case of plane-wave Laue diffraction in a thick crystal under the conditions of the Borrmann effect. It is shown that if a thickness increase takes place at the side of the reflected beam, the related reflected wave amplitude is calculated as a sum of three terms, two of which are complex. If all three terms have a comparable modulus, it can lead to an increase in the reflected beam intensity by up to nine times due to interference compared with the value for a plane parallel shape of the crystal. The equation for the related transmitted wave amplitude contains only two terms. Therefore, the possibility to increase intensity is smaller compared with the reflected beam. The analytical solution is obtained after a solution of the integral equations by means of the Laplace transformation. A general integral form of the Takagi equations derived earlier is used. The results of relative intensity calculations by means of analytical equations coincide with the results of direct computer simulations.

1. Introduction  

We analyze the effect of X-ray wave diffraction in a single crystal in the Laue case when the transmitted and reflected waves go out of a sample through the exit surface of the crystal plate. This case was first investigated experimentally by Kato & Lang (1959 ▸). The authors used a narrow slit for obtaining coherent images. The narrow slit played the role of a secondary source with a small transverse section. Such a type of experimental setup has been widely used for many years for investigating the degree of perfection of a crystal lattice. This method is called section topography.

The theory for describing this experimental setup was developed by Kato (1961 ▸, 1968 ▸) for the case of zero distance between a source and a crystal. Kato used the method of Fourier transformation for a representation of an incident spherical wave as a superposition of plane waves because the angular dependence of the amplitudes of transmission and reflection in the case of an incident plane wave was known in the analytical form. It turned out that the diffraction picture on the exit surface of a crystal exists only in the Borrmann fan between the directions of transmitted and reflected beams. Then this picture is translated to the detector without transformations.

At the same time Takagi (1962 ▸) proposed another variant of the theory based on a set of differential equations. These equations are named after him. A direct numerical solution of the Takagi equations allows analysis of an arbitrary kind of incident wave while taking into account crystal lattice distortions and an arbitrary shape of the sample. For the perfect crystal lattice the set of differential equations can sometimes be solved as a convolution of the wavefunction on the crystal boundary with a crystal propagator (Green function) which has an analytical expression through the Bessel functions. Such solutions for various crystal boundaries and various kinds of reflection were presented by Slobodetskii et al. (1968 ▸), Uragami (1969 ▸, 1970 ▸, 1971 ▸), Afanas’ev & Kohn (1971 ▸) and Saka et al. (1972 ▸).

Later a generalized theory of the spherical-wave diffraction in the Laue case was developed by Afanas’ev & Kohn (1977a ▸,b ▸), Kohn (1979 ▸) and Kohn et al. (2000 ▸). This theory took into account the distance between a source and a detector. One of the main results was a prediction of the diffraction focusing effect for divergent radiation and a crystal in the form of a plate. This effect is similar to the Pendry (2000 ▸) focusing effect for visible light. Experimental study of this effect was performed by Aristov et al. (1978 ▸, 1980 ▸, 1982 ▸, 1986a ▸,b ▸), Aristov, Snigirev et al. (1986 ▸) and Koz’mik & Mihailiuk (1978 ▸).

A direct numerical solution of the Takagi equations was used for investigating section topography for various crystal lattice defects. The method is described by Epelboin (1977 ▸). One can read a review of the results in the book by Authier (2005 ▸). The inhomogeneous distribution of the radiation field in the case of X-ray diffraction inside the crystal of a special form (parallelepiped or cylinder) was investigated by Olekhnovich & Olekhnovich (1978 ▸, 1980 ▸), Saldin (1982 ▸), Uragami (1983 ▸), Shulakov et al. (1996 ▸), Punegov et al. (2016 ▸) and Shabalin et al. (2017 ▸). Both analytical and numerical approaches were used.

Recently, in the work by Kohn & Smirnova (2020 ▸), the effect of strong interference inside the narrow transition layer was discovered in a thick, perfect crystal with a triangular cutout at the exit surface. This effect was investigated by means of two techniques: the direct numerical solution of the Takagi equations and approximate analytical solution on the basis of the convolution of the field on some crystal boundary and Green function which was derived, for example, by Afanas’ev & Kohn (1971 ▸). However, the analytical solution was presented without a derivation. The authors used the result of an old paper by Afanas’ev & Kohn (1972 ▸) which is not correct for the case of a triangular cutout.

In addition, the triangular cutout is not easy to perform due to the narrow angle at the top of the triangle. Such an object was analyzed in the old paper by Afanas’ev & Kohn (1972 ▸) as a model object for the etch pit at the exit of dislocation on the surface. In this work we analyze another object, namely a linear change of thickness on the exit surface. We discover the same effect of strong interference if the boundary of the thickness change makes an angle with the direction normal to the entrance surface slightly less than the Bragg angle. We consider the case of the reflected beam side of the Borrmann fan. Our results show narrow peaks of reflected beam intensity with a maximum value that is more than seven times larger compared with the intensity in the case of the Borrmann effect without interference.

In this work we present the total analytical solution of the task which was used for numerical calculations in the particular case of an incident plane wave. A specific feature of this task is that the standard convolution does not give a direct solution but only an integral equation because some fields on the boundary are not known. Therefore we need to obtain an analytical solution of the integral equation. In the next section we present a formulation of the task and a method for analytical solution. Then we describe the results of calculations and discuss our findings.

2. Experimental setup and analytical solution of the Takagi equations  

An assumed experimental setup is shown in Fig. 1 ▸. A monochromatic spherical wave from a point source of X-rays located at a distance L from the sample is incident at the Bragg angle and has finite angular divergence. The sample is a single crystal in the form of a plate but with a local linear change of thickness on the exit surface. The thickness is changed from the value to the value .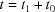

Figure 1.

The experimental setup assumed in this work.

We take into account the fact that any source of X-rays (synchrotron or laboratory) consists of many independent point sources because electrons inside the storage ring of a synchrotron source or atoms inside the anode of an X-ray tube radiate spontaneously without correlation between them. Monochromatization of radiation is realized by a standard technique and does not influence the phase front of the incident wave. The monochromator is assumed in Fig. 1 ▸ but not shown. The effective transverse size of the source is taken into account by summing intensity from all points of the source transverse section.

A local linear change of the crystal thickness on the exit surface is a source of sharp spatial inhomogeneity of intensity of the transmitted and reflected beams in the direction along the surface. It is measured by position-sensitive detectors separately for each beam. The beams are measured at some distance from the sample where the beams do not intersect each other in space. For the sake of simplicity we will calculate the beam intensity in the thick part of the exit surface of the sample with thickness t.

The most effective way to solve the problem is to divide it into two steps. At the first step one calculates the intensity distribution for the thickness . At this step the exit surface is even and the sample is homogeneous along the x axis of the crystal coordinate system. Inhomogeneity can arise only from the incident wave and the diffraction effect. The task can be solved by the method of Fourier transformation with the use of an analytical solution for the case of an incident plane wave.

We assume that the angular divergence of the incident wave is large and there is no necessity to use a modified Fresnel propagator (Kohn, 2018 ▸). The incident wave function in the paraxial approximation can be written as

where the v coordinate is counted along the direction from the source to the crystal (the left set of axes in Fig. 1 ▸), λ is the wavelength of X-rays, and the Fresnel propagator has the form

Note that the intensity is independent of the coordinate normal to the plane of the figure.

We represent (1) as the Fourier integral over q variable and take into account that describes small angular divergence of the incident wave near the Bragg angle . Now the incident wave has the form of superposition over the plane waves with the wavevectors . Let us consider the case of symmetrical Laue diffraction with the wavevector h. It is known that the wavevector of the transmitted wave stays the same due to plane-wave diffraction in the crystal plate (Authier, 2005 ▸; Pinsker, 1978 ▸). Using the analytical solution for the plane wave we can write the solution for the transmitted wave at the first step as follows:

Here and below we omit the factor because it does not influence the intensity. The Fourier image of the Fresnel propagator has the analytical expression

On the other hand, a solution of the task for a plane incident wave is well known (Authier, 2005 ▸; Pinsker, 1978 ▸; Kohn, 2002 ▸).

We write it in the form convenient for calculations,

where

It is assumed that the parameter g has a positive imaginary part, , , are the Fourier components of the crystal susceptibility on the reciprocal-lattice vectors 0, h, −h, respectively, and the parameter = describes a possible deviation in the angular position of the crystal from the Bragg angle.

The expression for the reflected wave is similarly

where

Here . In this case the wavevector of the plane wave is equal to and the reflected wave direction makes the Bragg angle with the direction of an incident wave.

Thus we know the radiation wave functions and for the transmitted and reflected beams as a result of diffraction in the crystal of thickness . The next problem is to search for an analytical solution on the exit surface of the crystal with the thickness t. First of all we need to change the coordinate system from (u, v) to (x, z) as shown in Fig. 1 ▸. The angle between the axes u and x is and we obtain values on the axis x and on the new set of points by means of interpolation after a projection from u to x axes along the v axis. At the second step we need to solve the Takagi equations (Takagi, 1962 ▸)

Here as above = , and are the coordinates along the directions of the transmitted and reflected waves, u is the displacement vector due to possible distortion of the crystal lattice, and the parameter = . The angle describes an angular position of the crystal relative to the central ray in the incident spherical wave.

We are interested in the case when and the crystal lattice is perfect (). Under the latter condition a solution of Takagi equations (11), (12) can be obtained as the integrals over some boundary inside the Borrmann fan which has a top in the observation point and side lines along the directions of transmitted and reflected waves (Slobodetskii et al., 1968 ▸; Uragami, 1969 ▸, 1970 ▸, 1971 ▸; Afanas’ev & Kohn, 1971 ▸; Saka et al., 1972 ▸).

We consider the case of an incident plane wave when the Bragg conditions are met exactly. In this case the condition should be fulfilled where

We note that a perfect collimation of the incident beam can be realized with a compound refractive lens (Snigirev et al., 1996 ▸).

Fig. 2 ▸ shows the region of linear change of thickness on the exit surface together with the Borrmann fan where at least one of two wavefunctions depends on the x coordinate. We will use an approach that was used for the first time by Afanas’ev & Kohn (1972 ▸). Instead of the real wavefields , , we consider the differences between these fields and the solutions 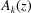for a sample with a plane plate shape. The latter solutions are known in an analytical form. The integral equations are the same for the differences, but the boundary conditions are different because the differences are equal to zero in the areas where inhomogeneity does not influence the fields.

Figure 2.

The boundary of a linear change of thickness on the exit surface of a crystal and the Borrmann fan where the fields depend on the x coordinate. See text for details.

In reality we consider the functions

where

Here and the coefficients depend on the normalization. For the incident plane wave they are equal to for , respectively. Note that the functions are equal to zero outside the triangle acd in Fig. 2 ▸.

According to the integral form of the theory (Afanas’ev & Kohn, 1971 ▸), the function at the point p on the line ab is determined by  the functions on the lines ad and db. However, on the line ad. Therefore, we have a formal solution as follows:

Here

where , , are the coordinates of the point p. Here and below is the Bessel function of the nth order. On the other hand, the function on the line db is a solution of the integral equation

if the function is known on this line.

In our case the line db is straight. Let us introduce the coordinates ξ and for the points on the line and at the point . Relations between the coordinates are as follows:

Let A be an argument of function (17). Taking into account (19) we easily obtain that on the line db

where

Here is the length of the segment and is the length of the segment pb. We are interested in the intensity dependence on η for the transmitted and reflected waves.

The integral in equation (18) is counted from 0 to . We make a replacement with the same limits. Then the derivative is defined by

and equation (18) takes the form

Note that the integrals are the convolution of two functions.

Equation (24) can be solved by applying the Laplace transformation

and the property that convolution of two functions corresponds to the product of their Laplace transforms. Therefore, we have

Here we use the second notation in equation (25) for the Laplace transform. We found the table integral (Gradshteyn & Ryzhik, 1963 ▸, equation 6.646.1) which can be transformed to the following form:

Here

We substitute equation (27) for into equation (26) and perform computation. As a result, using the notation we obtain

On the other hand,

As a result, we obtain a solution of equation (24) which can be written as follows after a reverse replacement :

Let us consider equation (16). Here the argument of the Bessel function depends on the coordinates of the point p on the line ab. These coordinates are equal to , while the coordinates of the point on the line are defined in equation (19). Direct calculations give the following result:

Now we can write equation (16) in the following form:

The integral is a convolution of two functions once again and it is useful to apply the Laplace transformation. However, this time the functions have more complicated arguments. We apply the Laplace transformation (27) to the third term in equation (36) and substitute equation (29). According to equation (27) we obtain this term in the form

After a transition from the q space to the ξ space we obtain the following expression for the sum of the second and third terms:

Having made the necessary calculations one can obtain a more suitable equation for the wavefunction of the reflected wave from equation (36):

This equation allows us to calculate the unknown function on the line ab through the known function on the line bd. The latter function is known because the function on this line is the same as that on the line de due to the fact that between these lines the space is empty. That is why its value at the point is equal to that at the point (see Fig. 2 ▸). The difference is easy to calculate.

The equation for the function on the line ab can be written similarly to equation (36) with some evident changes:

We apply the Laplace transformation to the first term in the right-hand part of this equation taking into account equation (27) and substitute from equation (29). As a result we obtain the expression equal to the second term after replace­ment of by . For the sum of two terms we have

Now we can write the final equation as follows:

where

It is much easier to calculate the functions on the line bc. The field can be obtained from the line de by simple transition along the direction of the reflected beam. For the plane incident wave this is independent of x. The field can be obtained from the line bd by simple transition along the direction of the transmitted beam. Therefore, the field at the point is equal to that at the point . The field on the line bd is calculated by means of equation (31).

3. Results and discussion  

We consider the case of 440 diffraction of X-rays with the photon energy = 12 keV in the silicon single crystal for = 2 mm, = 0.2 mm. The Bragg angle = 32.55°. Here we assume the incident plane wave with L much larger than . Experiments with the use of synchrotron radiation for such a distance can be realized by means of a compound refractive lens (Snigirev et al., 1996 ▸).

Taking equation (15) into account we obtain for the function on the line bd the following equation:

It is convenient to analyze the ratio of the beam intensities for the total thickness t for the case of a crystal with a linear change of thickness to the case of a crystal without a change. We consider the function on the line ab. Equations (39) and (15) allow us to write the expression for as follows:

where

It is convenient to make a replacement in integral (46) with the same limits. Finally we have

Note that when = = (where m denotes the maximum value of η), the second and third terms in equation (45) are equal to zero, i.e. the solution is not changed at the boundary of the Borrmann fan. At the other limit η = 0 we have = . Therefore, the relative intensity depends weakly on the height of a linear change of thickness. However, the real intensity is independent of . It is equal to the value for the thickness .

We obtained that the equation for relative intensity contains three terms, and two of them are complex values. The interference of three terms with a comparable (equal) modulus can increase the intensity by up to nine times. It was demonstrated that the direct computer simulations show an increase in the maximum intensity by more than seven times. Equation (45) allows us to analyze how this occurs.

Equations (42) and (15) allow us to write the expression for on the line ab as follows:

where

Now the expression contains two terms. If the second term has the modulus close to unity, the interference can increase the intensity by up to four times. However, computer simulations do not show such an increase.

Let us consider the ratio on the line bd. In this case the coordinate η is counted from the point b to the point d, and = . The point corresponds to the point in Fig. 2 ▸. With the same calculations as before we can obtain

where

Here we took into account that the fields at the point η on the line bc and on the line bd are the same, and = . At the point η = 0 equation (51) gives the same value as equation (38). If η = η_m = , we have = . This value is slightly greater than unity because the real field is not absorbed in the empty space but the denominator corresponds to the field which is absorbed.

We performed the computer program in the language ACL (Kohn, 2017 ▸) for a calculation of the relative intensity = |, k = 0, h on the basis of equations (45), (49), (51). The argument η can be recalculated to the argument where is half of the Borrmann fan width. In the case considered in this work = 0.1276 mm. We consider three various cases of a linear change of thickness with the parameter equal to 0.5, 0 and −0.5. The boundary of the exit surface for these cases is demonstrated in Fig. 3 ▸ where the R values are shown.

Figure 3.

Various kinds of crystal boundary on the exit surface. The numbers specify the values of the parameter R.

The results of calculation are presented in Figs. 4 ▸–6 ▸ ▸. Fig. 4 ▸ shows the curves for the case with . In this case we obtain an increase in the relative intensity of the reflected beam by up to eight times. The curve contains many well pronounced peaks of a small width. The relative intensity of the transmitted beam in the same region has the same number of peaks, but some of them are weakly pronounced. The highest peaks occur at the same x coordinate, but the transmitted beam intensity is only two times higher than unity.

Figure 4.

Relative intensity on the exit surface within the Borrmann fan, namely on the line ab in Fig. 2 ▸. The top panel is for the transmitted beam (T), the bottom panel is for the reflected beam (R). x ₀ = 0.1276 mm, R = 0.5.

Figure 5.

Relative intensity on the exit surface within the Borrmann fan, namely on the line ab in Fig. 2 ▸. The top panel is for the transmitted beam (T), the bottom panel is for the reflected beam (R). x ₀ = 0.1276 mm, R = 0.

Figure 6.

Relative intensity on the exit surface within the Borrmann fan, namely on the line ab in Fig. 2 ▸. The top panel is for the transmitted beam (T), the bottom panel is for the reflected beam (R). x ₀ = 0.1276 mm, R = −0.5.

Figs. 5 ▸ and 6 ▸ demonstrate the curves for the cases with and −0.5. In these cases the length of the left region increases, but the number of peaks stays the same. Only peak width increases. The structure of the peaks is changed as well. The height of the highest peak for the transmitted beam stays the same, but for the reflected beam it becomes two times smaller.

4. Conclusion  

The analytical solution of each problem allows better understanding of the reason for effects under consideration. We have found the effect of a strong increase in the reflected beam intensity in a narrow region of a thick single crystal with a linear change of thickness on the exit surface. An increase in the reflected beam intensity by more than seven times was calculated by means of direct computer simulations. However, a numerical solution of the Takagi equations cannot give an understanding of how it works.

In this paper we present an analytical solution of the Takagi equations on the basis of the integral form of these equations derived earlier. In the particular case of a linear change of thickness the integral form of equations has the form of an integral equation as a convolution of two complex functions. Such integral equations have been solved by means of the Laplace transformations. We have found that the final expression for the relative wave amplitude of the reflected beam contains three terms, two of which are complex. The interference of these terms can increase the intensity by up to nine times if all the terms have a comparable modulus.

For the relative wave amplitude of the transmitted beam there are only two terms. Therefore, the possibility to increase the intensity is modest. The analytical solutions have a rather complex structure. However, they can be useful in the analysis of how the effect depends on various parameters. The numerical results obtained with the use of the analytical expression coincide completely with the results of direct computer simulations.