Predicting Clinical Outcomes with Patient Stratification via Deep Mixture Neural Networks

Abstract

The increasing availability of electronic health record data offers unprecedented opportunities for predictive modeling in healthcare informatics including outcomes such as mortality and disease diagnosis as well as risk factor identification. Recently, deep neural networks (DNNs) have been successfully applied in healthcare informatics and achieved state-of-art predictive performance. However, existing DNN models either rely on the pre-defined patient subgroups or take the “one-size-fits-all” approach and are built without considering patient stratification. Consequently, those models are not able to discover patient subgroups and the risk factors are thereafter identified for the entire patient population, failing to account for potential group differences. To address this challenge, we propose the use of deep mixture neural networks (DMNN), a unified DNN model for simultaneous patient stratification and predictive modeling. Experimental results on a clinic dataset show that our proposed DMNN can achieve good performance on predicting diagnosis of acute heart failure. With DMNN’s ability to incorporate patient stratification, we are able to systematically identify group-specific risk factors for different patient subgroups which could potentially shed light on revealing factors that contribute to outcome differences.

1. Introduction

With the surge in volume and availability of electronic health record (EHR) in recent years, predictive modeling in healthcare informatics offers enormous opportunities for accurate prediction of adverse clinical outcomes¹. Unlike the conventional structured data, EHR usually consists of heterogeneous data elements such as continuous features (labs, vital signs et.al), categorical features (sex, ethnicity, diagnosis et.al) and missing values. Hence, predictive models should be able to handle such complex data. Due to the intrinsic complex biological mechanism of clinical outcomes, predictive models should be capable of capturing the high-level information among those different data elements. Moreover, as patient subgroups exhibit differential health outcomes that are potentially associated with different risk factors, a successful model would ideally take these aspects into consideration for patient stratification. The net effect of this could provide finer risk factor identification for patient subgroups (in contrast to the entire patient population) and promote the understanding of health disparities. With the aforementioned considerations, building effective predictive models is a challenging problem in healthcare informatics.

Recently, deep neural networks (DNNs) have achieved remarkable success in computer vision and natural language processing2, ³. Compared with traditional machine learning models, DNNs can learn high-level feature representations via layer-by-layer nonlinear transformations from structured or unstructured data without feature engineering. With the merit of automatic high-level feature learning, DNNs have been widely applied in healthcare informatics and achieved state-of-art predictive performance in various tasks such as ICU outcome predictions, diagnosis, phenotype discovery and disease progression monitoring^4–8.

Although DNNs are successful in healthcare informatics, previous works do not specifically take into considerations the discovery of patient stratification. Whereas multi-task learning approaches⁹ are effective, they often rely on the pre-defined patient subgroups. As shown in the motivating example (see below), there may exist patient subgroups and each subgroup is associated with some specific risk factors. Existing “one-size-fits-all” approach in this case is not desirable even though DNNs can still be able to achieve good performances with a large amount of training data. When interpreting the trained models, the identified risk factors are associated with the entire patient population rather than each individual subgroup. With the lack of granularity in patient subgroups, the associated risk factors are identified for the entire population and do not account for the patient heterogeneity.

While patient stratification relies heavily on the medical domain knowledge, some traditional machine learning models are capable of discovering patient subgroups. For example, unsupervised learning (e.g clustering)^10,11 can group similar patients into clusters; in the study of treatment effect, tree methods^12–15 also group patients that are homogeneous in tree splitting criterion. However, those two methods do not aim at predictive modeling and hence are not applicable in our problem. For supervised learning, linear model based method (such as mixture of Gaussian regression¹⁶ and supervised biclustering¹⁷) can inherently group patients that follow the same input-outcome relations. However as basing on linear models, they are not capable of capturing high-level information from EHR data.

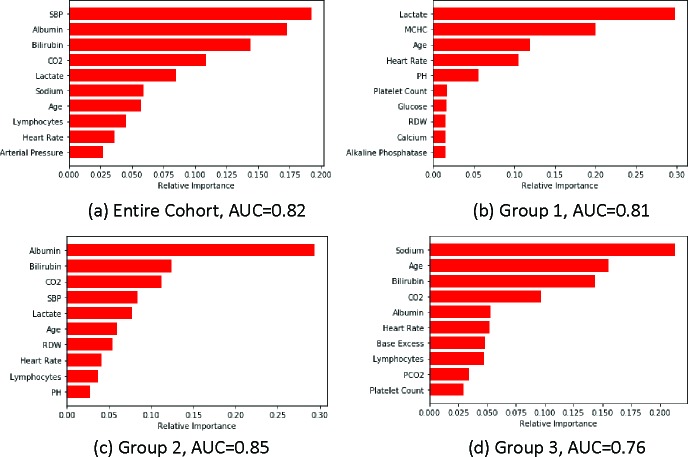
Motivation example of patient subgroups For a motivating example on the possible patient subgroups with their associated risk factors, we performed a preliminary experiment for predicting in-hospital mortality using the MIMIC III dataset¹⁸. As blood pressure level is a risk indicator for many diseases¹⁹, we stratify patients into 3 subgroups based on the systolic blood pressure (SBP) measured in the first hour after ICU admission (Group 1: SBP≤90, Group 2: 90<SBP<120, Group 3: SBP≥120). We use labs from the lab chart in MIMIC III and demographics as the input features. We deployed gradient boosting machine (GBM)²⁰ as the predictive model and evaluated GBM performance with 75%/25% train-test split. After model training where model parameters are selected by cross-validation on training data), we identified the most important risk factors using feature importance given by GBM. Figure 1 reports the results with predictive AUC on testing data. We see from the figure that for the entire patient population (Figure 1(a)), the important risk factors have an “averaging” effect from other three patient subgroups, and patient subgroups exhibit rather different risk factor patterns. For example, lactate is the most important feature in low SBP group (Figure 1(b)) while not important for high SBP group (Figure 1(d)). On the contrary, sodium is the most important risk factors for high SBP group yet not important for normal (Figure 1(c)) and low SBP groups. Those observations imply disparities in patient health conditions and identification of the associated risk factors could potentially enable more effective interventions and treatments.

Figure 1:

Top 10 risk factors for different patient groups. AUC is reported on testing data. Different patient subgroups exhibit rather different sets of risk factors.

In this paper, in response to the aforementioned challenges, we introduce a unified DNN model, termed as deep mixture of neural networks (DMNN), that simultaneously predicts clinical outcomes and discover patient subgroups. DMNN consists of an embedding network with gating (ENG) and several local predictive networks (LPNs). ENG embeds raw input features into high-level feature representation which is further used as input for LPNs. Unlike the existing DNN models without subgroup identification, patients will be grouped that share similar functional relations between inputs and clinical outcomes via the gating mechanism in ENG, and each functional relation is modeled by one LPN. The subgroup discoveries enable us to apply existing interpretation techniques to identify subgroup-specific risk factors. By explaining the local input-outcome relations captured by LPN within each patient subgroup, the subgroup-specific sets of risk factors can provide information to account for health disparities. To demonstrate the effectiveness of DMNN, we conduct extensive experiments on a clinic dataset for predicting the diagnosis of acute heart failure. DMNN can achieve state-of-art predictive performance when comparing with other baseline machine learning models. We apply mimic learning technique⁸ for interpretation on DMNN and show that DMNN can provide informative risk factors for clinical decision making.

2. Related Work

Deep Predictive Model Applications of deep learning models have been flourishing due to the increasing availability of EHR data. Tang et.al²¹ and Purushotham et.al⁴ benchmark the performance of DNNs with comparison to other machine learning models on MIMIC III data. Che et.al⁸ proposed DNN model that incorporates prior knowledge of medical ontologies as regularization for predicting ICU outcomes. Choi et.al⁶ proposed a recurrent neural network with GRU for predictions of heart failure onset. Li et.al⁵ and Suo et.al⁷ develop multi-task DNN models for predicting disease progression and diagnosis where multiple targets are used as an approach of regularization. Another line of predictive modeling with deep learning is to utilize the power of deep unsupervised learning to learn high-level feature representations in the latent vector space. DNN feature learning significantly reduces the workload of feature engineering especially for complex data like EHR and can be used in the downstream predictive tasks. For example, Miotto et.al²² and Lasko et.al²³ learn patient representations from EHR, and Choi et.al²⁴ embeds diagnosis codes and procedure codes into vector space. The learned representations are then used to predict patient health outcomes. However, those methods don’t specifically consider the heterogeneity in patients and consequently, model interpretations are for the entire patient population, lacking granularity to account for subgroup differences.

Patient Subgroup Discovery Subgroup identification is one of the most important tasks in medical science and has been studied in various settings. For example, Seymour et.al¹⁰ and Lu et.al²⁵ use unsupervised clustering techniques to group patients by sepsis and cancer subtypes respectively. In the study of treatment efficacy, subgroups are identified as the patients that have similar treatment responses. In this context, tree methods^12–15 are developed that patients are grouped in the leaf node that are homogeneous treatment effect. For predictive modeling that is studied in this paper, finite mixture of (Gaussian and logistic) regression (FMR)^16,26,27 and mixture of experts (ME)^28,29 were used to identify patient subgroups. However, FMR and ME models are based on the conventional machine models which is less capable of extracting high-level information compared with DNNs. Also, they usually require clean and structured data to train and are not capable of handling complex EHR data (e.g multi-modal and sequential data). To address those challenges in FMR and ME, our proposed DMNN builds a unified DNN architecture that not only exploits the predictive power of DNNs but also be able to discover patient subgroups.

3. Method

In this section, we present the proposed method. We start with the introduction of feed-forward neural network as a general-purpose DNN for predictive modeling. From the perspective of feature learning, FNN can be viewed as the embedding network that learns high-level feature representations (e.g the penultimate layer). We then describe in detail the structure of our DMNN model.

Notations: We use (x, y) to represent a sample in the data, where x is the input feature vector and y be the label.

3.1. Deep neural network models

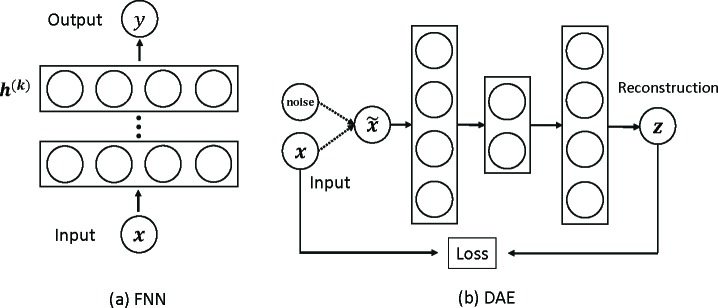
Feed-forward neural network (FNN) FNNs are fully connected neural networks with multiple layers (input, hidden and output layers) equipped with nonlinear activations. Through hidden layers, FNNs transform the input features and capture high-level information among them; the hidden vector in the penultimate layer is then viewed the learned feature representations based on which the output layer makes predictions, as shown in Figure 2(a). Mathematically, the learning procedure of a FNN of k hidden layers is given as follows (x⁽⁰⁾ = x):

$$\begin{array}{l}{h}^{(i+1)}=\sigma (W^{(i)}{x}^{(i)}+b^{(i)}),i=0,\cdot \cdot \cdot ,k-1\\ \widehat{y}=f(W^{(k)}{h}^{(k)}+b^{(k)})\end{array}$$

Figure 2:

Deep neural network models FNN and denoise autoencoder based on FNN.

where W ⁽ⁱ⁾ and b⁽ⁱ⁾ are the weight matrix and bias term respectively of compatible dimensions, h⁽ⁱ⁾ is the hidden state vector and σ is the non-linear activation function such as sigmoid, tanh or ReLU, ŷ is the prediction and f (·) is the prediction function according to the tasks (e.g softmax or sigmoid for classification, identity function for regression).

An special application of FNN is the denoise autoencoder (DAE) for unsupervised feature learning, where the output of FNN is the reconstruction of the input. In DAE, the input is corrupted by a noise and then fed into the autoencoder. Figure 2(b) shows an example of 5-layer DAE. The learned feature representation is the bottleneck hidden layer. The idea behind DAE is that high-level feature representations that effectively capture the information in raw input features should be able to well reconstruct the raw features with robustness to noise. In the proposed DMNN model (see below), we use DAE to initialize our DMNN embedding network with gating to help training process.

3.2. Deep mixture of neural networks (DMNN)

DMNN Structure Although existing DNN models achieve state-of-art predictive performance, they don’t explicitly take into considerations the heterogeneity in patient health conditions (e.g subgroup structure), which could potentially hamper the model interpretation. However, determining patient subgroups usually require domain knowledge in the medical science which may not always be available for complex data. Hence, the goal of DMNN is not only to achieve comparable or better predictive performance but also enable the discovery of patient subgroups. In DMNN, the patient subgroups are defined that share the same functional input-output relations.

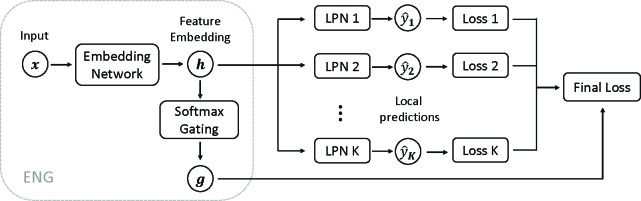
One challenge remaining in the partition of patient subgroups is determining which subgroup each patient belongs to. As such membership indicators can be viewed as latent variables in the modeling process, inspired by the classic mixture of experts and the recent deep unsupervised model, we use a DNN to learn feature representations from the input and then predict the membership indicator using softmax (e.g gating) based on the feature representations (termed as embedding network with gating, ENG). The learned features are then fed into multiple FNNs for prediction. However, the importance of those FNNs is gated by the membership indicator in the final loss function (termed as local predictive network, LPN). As such, patients with similar gating patterns are grouped and the FNN can capture the “local” input-outcome functional relation. Figure 3 displays an overview of DMNN structure.

Figure 3:

Overview of DMNN with ENG and and K LPNs.

Mathematically, for each training example (x, y), ENG in DMNN outputs the feature representation h and a vector of gating values g:

h, g = ENG(x).

The each local predictive network LPN_i makes prediction ŷ _i and we obtain its respect loss function L _i:

ŷ _i = LPN_i(h)

L _i(x) = f(ŷ _i, y), i = 1,..., K

where f is the loss function: squared error f (ŷ, y) = (ŷ – y)² for regression and cross-entropy f (ŷ, y) = –(y log ŷ + (1 –y) log ŷ)) for classification.

The final loss function for training example x is the sum of loss functions of all K LPNs, weighted by the gating value g = (g ₁, …, g_k):

$$L_{final}(x)={\displaystyle \sum _{i=1}^K{g}_i{L}_i(x).}$$ (1)

By minimizing the final loss, model parameters are learned when the loss function converges to a (local) minimum. Note that K is treated as hyperparameter and the optimal K is selected via cross-validation or validation data.

Subgroup identification in DMNN In DMNN framework, subgroups will be identified as the set of patients that share the similar functional input-output relation. In other words, clinical outcomes for patients within the same subgroup should be predicted well by some LPN. Intuitively, this implies that we can group patient according to the gating values g: patient x belongs to subgroup k where k = arg max_k{g_i : i = 1, …, gK }, as a better LPN should have a larger gating value. Indeed, we can perform analysis similar to mixture of experts on the final loss function to see the rationale behind DMNN’s subgroup identification.

From the final loss function Eq. (1), we see that each LPN is encouraged to fit each training sample well, e.g., low error value (though weighted differently). If one LPN captures the input-outcome relation well and gives less error than other LPNs, ENG in DMNN is encouraged to produce larger gating value for that specific LPN (simultaneously reduce other gating values due to the softmax function). Moreover, this will make the ENG embed similar patients closer to each other in the late feature space. Consequently, those patients will exhibit similar gating values. With the clustering effect of ENG, DMNN is capable of discovering patient subgroups.

3.3. Model interpretation by knowledge distillation

Model interpretability is as important as accuracy in clinical research. While deep learning models are generally difficult to interpret, recent progress in knowledge distillation^30,31 for DNNs enables us to understand what DNNs learn from the data. The main idea is that after an accurate but complex DNN (teacher model) is trained, the knowledge can be transferred to train another simpler model (student model) by predicting the soft labels predicted by the teacher. Training with soft labels is an implicit regularization for the student model with which it can achieve as good performance as the teacher model^31,32. If the student model that learns knowledge from the teacher DNN model is interpretable, we can then interpret the DNN through the student model. For our DMNN model, we take the approach developed in Che et.al³² for interpretation. We first train DMNN as the teacher model and then train the interpretable gradient boosting machine for regression (GBR) as the student model to mimic DMNN’s predictive behavior. GBR uses the probability generated by DMNN as target. For each subgroup identified by DMNN, we train GBR and use the feature importance in GBR to identify important risk factors for that subgroup.

4. Results and Discussions

In this section, we apply DMNN on a clinical dataset collected from patients presenting signs and symptoms of acute heart failure (AHF) in the emergency department (ED) of three urban academic medical centers in Detroit. The task is to predict whether a patient ultimately will be assigned a diagnosis of AHF. Our goal is two-fold: (1) accurately predict the risk of AHF, so that further actions can be effectively taken to avoid adverse outcomes; (2) identify the associated risk factors within the patient subgroups to promote the understanding of health disparities.

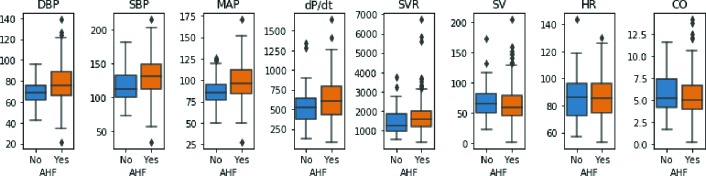
Data information and preprocessing The data contain health records for 335 patients with suspected AHF, among which 78% (261/335) of patients actually have AHF onset. There are 26 features in the data, including 5 demographics (age, race, gender, weight and height), 6 vital signs (initial SBP, initial DBP, initial heart rate (HR), respiratory rate (RR), oxygen saturation (OS) and temperature) when presenting in ED, 7 initial lab results (troponin, natriuretic peptide (NP), sodium, BUN, creatinine, eGFR and Hemaglobin), and 8 hemodynamic features measured using a noninvasive device (SBP, DBP, MAP, dP/dt, SVR, SV, HR and CO). Table 1 shows the details of feature characteristics. Figure 4 is the boxplot of hemodynamic features for comparing AHF against non-AHF patients. From the figure, we can see that while non-AHF and AHF patients share some similar statistics (such as median value, 25th and 75th quantiles), AHF patients show larger variance in hemodynamic features compared with non-AHF patients . This observation implies the existence of large heterogeneity in health conditions among patients in the ED who present with suspected AHF.

Table 1:

Feature statistics (mean and standard deviations for continuous features, percentage for categorical features.). In the table, AA represents African Americans, F female and P positive.

Demo	Stats	Vitals	Stats	Labs	Stats	Hemodynamics	Stats
Age	59.15 (12.51)	Initial SBP	153.27 (33.06)	Troponin (P)	162 (48.4%)	DBP	75.87 (17.51)
Race (AA)	297 (88.7%)	Initial DBP	91.23 (20.73)	NP	3663.42 (6388.41)	SBP	127.86 (29.572)
Gender (F)	174 (51.8%)	Initial HR	91.56 (18.71)	Sodium	138.81 (4.15)	MAP	94.98 (21.01)
Weight	99 (30.92)	RR	20.66 (4.75)	BUN	27.00 (20.46)	dP/dt	602 .90 (258.89)
Height	172.85 (28.37)	OS	96.30 (4.55)	Creatinine	2.04 (2.47)	SVR	1615.43 (752.03)
		Temperature	97.95 (0.67)	eGFR	60.48 (31.20)	SV	66.05 (26.78)
				Hemaglobin	11.78 (2.35)	HR	85.74 (15.01)
						CO	5.55 (2.16)

Figure 4:

Box plot for AHF v.s non-AHF. It can be observed that AHF and non-AHF patients share some similar feature characteristics in hemodynamic features, yet AHF group exhibits larger variance. This implies large heterogeneity in patient health conditions for AHF onset.

For missing values in the dataset (missingness is about 0.6%), we impute them with mean values for continuous features and the majority value for categorical features. Note that the imputation in our experiments is based on training data to prevent possible information leak to testing data (after train/test split). As features have different scales, we also perform data normalization for features to have zero mean and unit variance.

Implementation and evaluation details We implement DMNN using Pytorch. In the experiment, DMNN is of depth 4, consisting of the input layer, two hidden layers of size 40 and 20 respectively which act as the ENG part in DMNN and multiple output layers; the embedding of the 2nd hidden layer will be fed into the softmax layer to obtain gating values and LPNs for predictions which are linear models. Sigmoid function is used in hidden layers for non-linear activation. By initial experiments on the number K of LPNs, we found K = 2 work well with this relatively small dataset. Since deep neural network can be easily overfitted and the gating mechanism may degenerate (i.e model may only use one LPN), we apply unsupervised learning techniques to initialize the ENG in DMNN. We first train a 5-layer (dimension 26-40-20-40-26) denoise autoencoder (DAE) and use the encoder to initialize embedding part of ENG; after DAE is trained, we extract the bottleneck feature representations and use K-means for clustering; we then train the ENG to predict the cluster labels. With ENG initialized, DMNN is trained via stochastic gradient descent in conjunction with L2 regularization.

We test different machine learning models for performance evaluation. Those baseline models include logistic regression (LR), decision trees (DT), K-nearest neighbor (KNN), gradient boosting machine (GBM), feedforward neural network(FNN) of the same hidden dimensions, random forest (RF). We use Python scikit-learn package for model implementation. In the experiment, training data are divided into training/testing by a split 85%/15%. Within the training data, we further split out 10% as validation data for selecting model parameters. The evaluation metrics are the area under receiver operating characteristic curve (AUROC) and area under precision-recall curve (AUPRC). We repeat the train/test procedure 5 times and the average predictive performance on the testing data is reported.

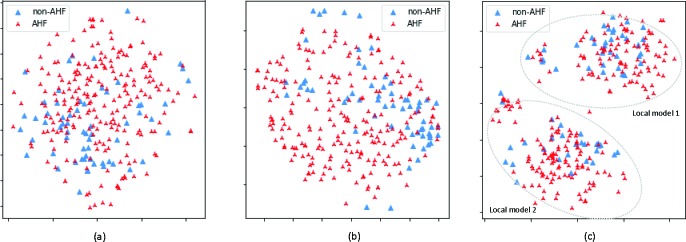
Predictive performance Table 2 shows the predictive performance on the testing data. We see from the table that DMNN performs better than other baseline models. As shown in Figure 5, patients can be clustered into two subgroups. In contrast with baselines that only build a global predictive model for all patients, DMNN builds a local predictive model for each patient subgroup that is able to capture the local functional input-output relations, resulting in performance gain. We also observe that all models achieve good performance in terms of AUPRC and relatively worse performance for AUC. This is due to that the majority of the patients (78%) have AHF onset, and all models can predict AHF well at the cost of misclassifying non-AHF patients as AHF. From Figure 5, we see that there is a large overlap between AHF and non-AHF patients; from Figure 4, non-AHF and AHF patients have similar characteristics for hemodynamic features. Those two observations imply that patients in ED with possible AHF are similar, yet those with the highest likelihood of diagnosis are rather different. This heterogeneity makes it difficult for models to differentiate AHF and non-AHF patients effectively, leading to a lower AUC score compared with AUPRC score.

Table 2:

Average AUC and AUPRC on testing data along with standard deviations.

	LR	GBM	DT	KNN	FNN	RF	DMNN
AUC	0.69 (0.09)	0.70 0.07)	0.58 (0.08)	0.66 (0.04)	0.69 (0.05)	0.71 (0.06)	0.74 (0.07)
AUPRC	0.88	0.90	0.81	0.85	0.89	0.90	0.92
	(0.05)	(0.03)	(0.03)	(0.04)	(0.02)	(0.01)	(0.03)

Figure 5:

2D t-SNE plot. (a) Raw input features; (b) feature embedding from FNN; (c) feature embedding from DMNN; DMNN feature embedding exhibits two patient subgroups; a local model is fitted for each subgroup.

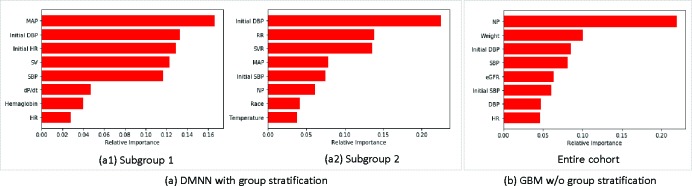
Feature analysis We interpret the DMNN model via knowledge distillation as introduced in Section 3.3. To do so, the interpretable gradient boosting machine for each patient subgroup is trained to learn the input-output relation captured by DMNN. As GBM mimics the predictive behavior of DMNN, we can then identify risk factors and their dependence relations to the onset of AHF. Figure 6 shows the top8 features that are important for predicting AHF. We see that both DMNN and GBM share some features such as blood pressure (initial SBP, initial DBP, SBP and DBP), indicating BP is a universal risk factor for AHF. As shown in Table 1, blood pressure level (initial SBP 153.27mm Hg, initial DBP 91.23mm Hg, SBP 127.86mm Hg and DBP 75.87mm Hg) indicates that patients with elevated values are more likely to be diagnosed with AHF. Comparing DMNN with GBM, important risk factors for DMNN are rather different from those of GBM. For example, natriuretic peptide (NP) identified in GBM is the single most important risk factor for the diagnosis of AHF. However in DMNN, NP is only important in Subgroup 2 and not very important in terms of predictive power in Subgroup 1. While NP level is informative in the diagnosis of heart failure, the difference in NP importance in those models possibly implies large disparity in the development of AHF. Within DMNN, both subgroups also share MAP as an important feature yet have subgroup specific features. In Subgroup 1, SV, dP/dt and HR are important hemodynamic features whereas in Subgroup 2, SVR and RR are identified important.

Figure 6:

Top 8 important features.

Discussions To further understand the dependence relation between features and AHF in patient subgroups, the partial dependence plots (PDP) for five important features (initial DBP, MAP, RR, SV, SVR) in either Subgroup 1 or 2 are shown in Figure 7. Both subgroups follows a similar dependence relation for initial DBP and MAP: as their level increases, the risk of AHF also increases. But for RR, SV and SVR, the dependence relation differs. In Subgroup 2, RR and SVR have a positive dependence relation on AHF onset while no such relation in Subgroup 1. In Subgroup 1, patients are at high risk of AHF if SV level is too low or too high; whereas in Subgroup 2, SV is not very predictive for AHF. As DMNN performs well in AHF prediction as shown in Table 2, the difference between two subgroups provides useful information for clinicians in disease diagnosis.

Figure 7:

Partial dependence plot for important features for Subgroup 1 or 2.

5. Conclusion

In this paper, we propose DMNN, a deep mixture model for predictive modeling as well as patient stratification. DMNN identifies patient subgroup via gating mechanism that aims at capturing similar functional input-output relations among patient population. With subgroup discovery, DMNN can identify subgroup-specific risk factors (in terms of AHF prediction) and such granularity can potentially help clinicians understand subgroup differences, which is an advantage of DMNN compared with traditional “one-size-fits-all” approaches. Experiments on an AHF prediction task show that our proposed method can achieve state-of-art performance and discover risk factors that might be missed by traditional methods. One limitation of this work is that DMNN is not able to characterize patient subgroup (i.e. phenotyping). Hence, for future works, we will expand our work to incorporate information from multimodal data such as medical images, clinical notes and time series data to further improve DMNN for better characterization of patient subgroups.