Predicting Polypharmacy Side-effects Using Knowledge Graph Embeddings

Abstract

Polypharmacy is the use of drug combinations and is commonly used for treating complex and terminal diseases. Despite its effectiveness in many cases, it poses high risks of adverse side effects. Polypharmacy side-effects occur due to unwanted interactions of combined drugs, and they can cause severe complications to patients which results in increasing the risks of morbidity and leading to new mortalities. The use of drug polypharmacy is currently in its early stages; thus, the knowledge of their probable side-effects is limited. This encouraged multiple works to investigate machine learning techniques to efficiently and reliably predict adverse effects of drug combinations. In this context, the Decagon model is known to provide state-of-the-art results. It models polypharmacy side-effect data as a knowledge graph and formulates finding possible adverse effects as a link prediction task over the knowledge graph. The link prediction is solved using an embedding model based on graph convolutions. Despite its effectiveness, the Decagon approach still suffers from a high rate of false positives. In this work, we propose a new knowledge graph embedding technique that uses multi-part embedding vectors to predict polypharmacy side-effects. Like in the Decagon model, we model polypharmacy side effects as a knowledge graph. However, we perform the link prediction task using an approach based on tensor decomposition. Our experimental evaluation shows that our approach outperforms the Decagon model with 12% and 16% margins in terms of the area under the ROC and precision recall curves, respectively.

Introduction

Polypharmacy side-effects are a specific case of adverse drug reactions that can cause significant clinical problems and represent a major challenge for public health and pharmaceutical industries ⁽¹⁾. Pharmacology profiling leads to identification of both intended (target) and unintended (off-target) drug-induced effects, i.e. biological system perturbations. While most of these effects are discovered during pre-clinical and clinical trials before a drug release on the market, some potentially serious adverse effects only become known when the drug already is in use. Indeed, a recent review of epidemiological studies in Europe, states that 3.5% of hospitalisation admissions are due to adverse drug reactions and 10% of patients experience an adverse drug reaction during their hospitalisation ⁽²⁾. An adverse drug reaction is a major cause of morbidity (resulting in reduction of patients’ quality of life) and mortality ^{(3, 4)}. Recent estimates set the number of yearly drug-induced fatalities to 100,000 in the USA and almost 200,000 in Europe, making it the fourth cause of death before pulmonary disease or diabetes ^{(5, 2)}.

When more drugs are used jointly (i.e. polypharmacy), the risk of adverse effects rises rather rapidly ^{(6, 7)}. Therefore, reliable automated prediction of such risks are highly desirable to mitigate their impact on patients. Among the recent approaches is the Decagon model ⁽⁸⁾ which has achieved state-of-the-art performance by modelling the data related to polypharmacy side-effects as a knowledge graph and formulating finding possible adverse effects as a link prediction task over the knowledge graph.

The link prediction is solved using an embedding model based on graph convolutions in the Decagon model ⁽⁸⁾. Despite its effectiveness, this approach still suffers from a high rate of false positives. Here, we propose a related knowledge graph embedding technique that, instead, uses multi-part embedding vectors to predict polypharmacy side-effects. Contrary to the Decagon model ⁽⁸⁾, the link prediction problem is solved using an approach based on tensor decomposition. This is known to lead to superior performance in the general link prediction problem ^{(9, 10)}.

Our approach models drug pairs and their side-effects as a knowledge graph, where interacting drugs modelled as nodes and their corresponding side-effects are modelled as edges. We then use a tensor factorisation based knowledge graph embedding model to learn vector representations of both the drugs and side-effects. Finally, the learnt embeddings are used to predict unknown drug–drug interactions polypharmacy side-effects. Our experimental evaluation shows that this approach outperforms the Decagon model with 12% and 16% margins in terms of the area under the ROC and precision-recall curves, respectively.

The rest of the paper is organised as follows: Background and related work section provides reviews on the basic notions related works to the addressed problem. Data section comments on the data used. The proposed method is detailed in the methods section. Experiments and Results and discussion sections describe the experiments we performed and discuss the outcome results. The paper is concluded in in the conclusions section where we also discuss the future directions of our research.

Background and related work

In this section, we present a set of preliminary topics and concepts that are used across this study. We present the knowledge graph as a technique to model linked data, and we also present knowledge graph embedding models in the context of learning link prediction on knowledge graphs.

Knowledge graph embedding. Knowledge graphs are structured knowledge bases which are used to model linked data. They model knowledge entity as graph nodes and relations between them are modelled with graph edges. In recent years, knowledge graphs have become a popular means for data representation in the semantic web community to create the “web of data”, which is a network of interconnected entities that can be easily interpreted by both humans and machines ⁽¹¹⁾. They have also been used as a convenient means for modelling information in many different domains, including general human knowledge ⁽¹²⁾, biomedical information ⁽¹³⁾ and language lexical information ⁽¹⁴⁾. Knowledge graphs are now used in different applications such as enhancing semantics of search engine results ^{(15, 16)}, biomedical discoveries ⁽¹⁷⁾, or powering question answering and decision support systems ⁽¹⁸⁾.

Knowledge graphs model facts that are formatted as (subject, predicate, object) triples such as (drugi, interacts-with, proteinj ), where the subject and object are entities and the predicate is a relation between them.

Knowledge graph embedding models are representation learning models that embed components of the knowledge graph including entities and relations into a low-dimensional continuous vector space. In the context of link prediction, these embeddings are then used to rank triples according to their factuality. In recent years, knowledge graph embedding models have witnessed multiple developments that allowed them to excel in the task of link prediction over knowledge graphs ⁽¹⁹⁾, where they are known to provide state-of-the-art predictive accuracy ⁽⁹⁾.

Knowledge graph embedding models operate in a multi-phase procedure. Initially, they consume input triples and initial embeddings of entities and relations. They then use an iterative optimisation routine to update these embeddings until they reach a local optima state (according to training iterations and parameters). In practice, training data is divided into batches and the optimisation routine is applied on each batch independently. First, the knowledge graph embedding model generates negative training samples, where this procedure typically uses uniform random corruptions of the subjects and objects of the training triples. The model then looks up the corresponding embeddings of the components (subject, predicate and object) of both the true and corrupted triples. The embeddings are then used to compute a score for each triple using a model-dependant scoring function. The model then computes a training loss that models the difference between the scores of true and corrupted triples. Finally, the loss function is used to compute gradient updates to the knowledge component embeddings in order to maximise the scores of true triples and minimise the scores of negative samples.

Different knowledge graph embeddings models vary in terms of the scoring functions and loss objectives i.e. the loss function they utilise. For example, the Translating Embedding (TransE) model ⁽²⁰⁾ model the interactions of triple embeddings in its scoring function as a translation from the subject vector to the object vector using the relation vector in the embedding space. On the other hand, other models such as the RESCAL ⁽²¹⁾, DistMult ⁽²²⁾ and ComplEx ⁽²³⁾ models learn scores using the product of the embeddings of the investigated triples components. Other models such as the Graph Convolution Network model (GCN) ⁽²⁴⁾ —which is the base work of the Decagon model ⁽⁸⁾— models embedding interactions using a graph convolutional filter on the embeddings of the triples components and their neighbouring entities.

In the rest of this paper, we use E and R to denote the set of all entities and relations in a knowledge graph respectively, where N_e and N_r represent the number of instances in E and R respectively. We also use Θ_E and Θ_R which denote the embeddings of entities and relations respectively, where Θ_E (i) is the embedding of entity i, Θ_R(j) is the embedding of relation j, and f_m(s, r, o, Θ) denotes the score of the fact that a subject entity s is connected to an object entity o with a relation r based on the embedding values Θ of the model m.

Link prediction on knowledge graphs. In recent years, various predictive frameworks were developed to predict new links in knowledge graphs, where these frameworks serve in various applications such as semantic search engines ^{(15, 16)}, biomedical discoveries ⁽¹⁷⁾, and question answering systems ⁽¹⁸⁾. Link prediction models can be categorised into two categories: graph-feature based models and latent-feature based models.

Graph-feature based models utilise graph features like paths and graph patterns to predict possible connecting links between graph entities. For example, the path ranking algorithm (PRA) ⁽²⁵⁾ uses connecting paths between entities generated by random walks to infer possible links between them. Where as other models like the subgraph feature extraction model (SFE) ⁽²⁶⁾ and the distinct subgraph path (DSP) ⁽²⁷⁾ employ a combination of connecting path and subgraph paths of two entities to predict their possible associations.

On the other hand, latent-feature based models i.e. knowledge graph embedding models, use a generative approach to learn low-rank embeddings for knowledge entities and relations in order to score their possible associations. These approaches use multiple techniques like tensor factorisation (as in the DistMult model ⁽²⁰⁾) and latent distance similarity (as in the TransE model ⁽²²⁾) to model possible interactions between graph embeddings and provide scores for possible graph links. For further information on both approaches, Nickel et. al. ⁽²⁸⁾ provides an extended review for both graph-feature based and latent-feature based models in the task of link prediction in knowledge graphs.

Modelling polypharmacy data. Computation methods have been widely used to model drugs’ associations to target proteins ^{(29, 30, 31)} in order to identify potential new drug therapeutic uses and new possible side-effects. In addition, other types of models were developed to directly learn the associated adverse side-effects of drugs ^{(32, 33)}. Despite the success of such models, their objective of these methods was, however, limited to the side-effects that occur due to the use of individual drugs.

The use of drug combinations i.e. polypharmacy is known to be an important solution for complex and terminal diseases ^{(34, 35)}. However, the risk of adverse effects in polypharmacy rises rather rapidly ^{(6, 7)} compared to the use of individual drugs due to unwanted drug-drug interactions. This encouraged research in developing computational methods to predict the possibility of interactions between combinations of drugs ^{(36, 37, 38)}. Although these works were able to provide predictions for unknown drug-drug interactions, they were limited to predicting the existence of such interactions and not their associated side-effects. Recently, Zitnik et. al. ⁽⁸⁾ introduced the first method for predicting polypharmacy side-effects, the Decagon model, where they modelled the polypharmacy side-effects data as a knowledge graph. They then transformed the problem of predicting polypharmacy side-effects to a link prediction task on a knowledge graph, where they applied graph convolution network embedding models to predict new drug combination side-effects. In a recent work, Malone et. al. ⁽³⁹⁾ suggested using other knowledge graph embedding models such as the DistMult ⁽²⁶⁾ and KB_LRN ⁽⁴⁰⁾ models, where they have shown that these models are capable of outperforming the Decagon model in predicting polypharmacy side-effects.

Data

In this study, we use the dataset compiled by Zitnik et al. ⁽⁸⁾ which includes information about multiple polypharmacy drug side-effects ¹. The dataset also contains facts about single drug side-effects, protein-protein interactions and protein-drug targets. In the following, we discuss and summarise the content of this dataset.

Side-effects data. The drug side-effects represented in the dataset are collected from the SIDER (Side Effect Resource) database ⁽⁴¹⁾ and the OFFSIDES and TWOSIDES databases ⁽⁷⁾. These side-effects are then categorised into two groups: mono-drug and polypharmacy drug-drug interaction side-effects. The mono drug side-effects are the side effects observed from the use of a single drug from the OFFSIDES and SIDER database, while the polypharmacy side-effects are the ones that are associated with the interaction of drug pairs from the TWOSIDES and SIDER databases.

We have also use the same data splitting procedure introduced by Zitnik et. al. ⁽⁸⁾ where we have separated the side-effects in dataset into two groups according to their coverage, The group of highly represented polypharmacy side-effects (more than 500 associated drug combinations) is considered in for evaluation and testing, while other low represented side-effects are considered only for the training of the models.

Protein and drug interactions data. The investigated dataset contains both protein-protein interactions and drug-protein interactions. The protein-protein interactions represent a collection of physical interactions experimentally assessed in humans and compiled from different public sources ^{(42, 43, 44, 45)}. On the other hand, the drug-protein interactions are obtained from the STITCH database ⁽⁴⁴⁾. These interactions denote the associations between drugs and their target proteins in the human body that allow the drugs to activate their expected therapeutic effects and their other unwanted effects (side-effects).

Methods

In the following, we discuss the different components of our predictive method and how it works.

Embeddings representation. The knowledge graph embedding model that we use follow a generative approach to learn low-rank embedding vectors for knowledge entities and relations. For learning the embeddings, multiple techniques can be used, such as tensor factorisation (c.f. the DistMult model ⁽²⁰⁾) or latent distance similarity (c.f. the TransE model ⁽²²⁾). The goal of all these techniques is to model possible interactions between graph embeddings and to provide scores for possible graph links. In the following, we provide details on the knowledge graph embedding procedure and the design of our model, the TriVec model.

The TriVec model is a tensor factorisation based knowledge graph embedding model that extends the works of the DistMult ⁽²²⁾ and ComplEx ⁽²³⁾ models. It represents each entity and relation using three embedding vectors such that the embedding of entity i is ${\Theta }_E(i)=\left\{e_i^1,e_i^2,e_i^3\right\}$ where all embedding vectors have the same size K (a user-defined embeddings size). Similarly, the embedding of relation j is ${\Theta }_R(j)=\left\{w_j^1,w_j^2,w_j^3\right\}$. e^m and w^m denote the m part of the embeddings of the entity or the relation, and m ∈ {1, 2, 3} represents the three embeddings parts. The embeddings in the TriVec model are initially with random values generated by the Glorot uniform random generator⁽⁴⁶⁾. The embedding vectors are then updated during the training procedure to provide optimised scores for the knowledge graph facts.

Training procedure. The TriVec is a knowledge graph embedding model that follows the multi-phase procedure discussed in (Section ) to effectively learn a vector representation for entities and relations of a knowledge graph. First, the model initialises its embeddings with random noise. It then updates them by iterative learning on the training data. In each training iteration i.e. epoch, the model splits the training data into mini-batches and executes its learning pipeline over each batch. The learning pipeline of the model learns the embeddings of entities and relations by minimising a negative softmax log-loss that maximises the scores of true facts and minimises the scores of unknown facts (assumed false during training). This loss is defined as follows:

$$\begin{array}{l}{L}_{spo}^{\text{TriModel}}=-{\varphi }_{spo}+\log \left({\displaystyle {\sum }_{o\text{'}}\exp ({\varphi }_{spo\text{'}})}\right)\\ -{\varphi }_{spo}+\log \left({\displaystyle {\sum }_{s\text{'}}\exp ({\varphi }_{s\text{'}po})}\right)\\ +\frac{\lambda }{3}{\displaystyle {\sum }_{k=1}^K{\displaystyle {\sum }_{m=1}^3(|e_s^m{|}^3+|w_p^m{|}^3+|e_o^m{|}^3)}}\end{array}$$ (1)

where K denotes the embedding size, φ_spo denotes the score of the (s, p, o) triple, x^’ represents an entity $e:e\ne x,e\in \epsilon ,e_i^m$ is the embedding part m of the entity embedding ${\Theta }_E(i),w_i^m$ is the embedding part m of the relation embedding ΘR(i), φ_spo denotes the score of the triple (s, p, o), m denotes the embedding part index, λ denotes a configurable regularisation weight parameter and |x| is the absolute of x. The term $+\frac{\lambda }{3}{\displaystyle {\sum }_{k=1}^K{\displaystyle {\sum }_{m=1}^3(|e_s^m{|}^3+|w_p^m{|}^3+|e_o^m{|}^3)}}$ is the 3 k=1 m=1 s p o nuclear 3-norm, which is a regularisation term ⁽⁹⁾ that enhances model generalisation over datasets with large entity vocabularies.

The scores of the TriVec model are computed using an embeddings interaction function (scoring function) that is defined as follows:

(display-formula) 2

It uses a set of three interactions: one symmetric interaction: $(e_s^2{e}_p^2{e}_o^2)$ and two asymmetric interactions: $(e_s^1{e}_p^1{e}_o^3)$ and $(e_s^3{e}_p^3{e}_o^1)$. This approach models both symmetry and asymmetry in simple form similar to the DistMult ⁽²²⁾ model s p o where the DistMult model can be seen as a special case of the TriVec model if the first and third embeddings parts are equivalent (e1 = e3).

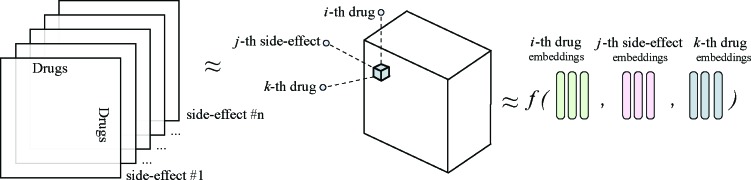
Modelling polypharmacy side-effects. The TriVec model is a tensor factorisation based embedding model that solves the problem of link prediction as a 3D tensor completion, where the tensor dimensions represent entities and relations. In the task of predicting polypharmacy side-effects, the drug combinations are modelled as the subjects and objects of triples while the corresponding polypharmacy side-effects are modelled as relations. In the training process, the model processes the different types of assertions such as protein-protein interactions, drug-protein interactions, drug-drug interactions, single drug side effects and polypharmacy side-effects. This allows the model to learn efficient embeddings for the components corresponding to the different entities and relations in the knowledge graph. In the prediction phase, the TriVec model then learns the probability of polypharmacy side-effects associations to drug combinations by completing a 3D tensor of drugs and polypharmacy side-effects as shown in (Figure 1).

Figure 1:

Flow diagram of the scoring function of TriModel applied to polypharmacy side-effects drug combinations. The subject (s), and the object (o) represent the drug combination while their corresponding polypharmacy side-effect is represented as the relation (r). All these components are represented using three embedding vectors of size k. The score of a triple (s, p, o) is defined as f (s, p, o) = �k ck , where c = i1 + i2 + i3, i1 = s1 · r1 · o3, i2 = s2 · r2 · o2, and i3 = s3 · r3 · o1.

Experiments

In this section, we discuss the setup of our experiments, the evaluation protocol and the detail of the frameworks and technologies used to implement our experiments.

Benchmarking dataset. In this study, we build a benchmarking dataset to evaluate our model following the evaluation protocol proposed by Zitnik et. al. ⁽⁸⁾. We first divide polypharmacy side-effects assertions into groups according to the side-effect type. We then divide the assertions of each group into three groups: training, validation and testing with 80%, 10% and 10% percentages of the data respectively. This process is applied to the polypharmacy side-effect groups with 500 or more assertions to assure a minimum of 50 validation and testing instances for each side-effect. We then add other types of assertions such as drug-protein interactions, protein-protein interactions and single drug side-effects into the training data.

For each validation and testing splits, we generate negative samples by using random unobserved drug combinations as negatives. This process is executed independently for each polypharmacy side-effect, where the positive to negative ratio is 1:1. (Table 1) shows a summary of the statistics of different components in the data generated for the set of all polypharmacy side-effects.

Table 1:

Summary of statistics of entities, relations and triples in the different splits of the benchmarking dataset.

Dataset	Entities	Relations	Triples	P. Side-effects
Training data	32K	967	4.7M	3.7M
Validation data	643	963	459K	459K
Testing data	643	963	459K	459K
All	32K	967	5.6M	4.6M

Experimental setup. We use the supporting knowledge graph to perform a grid search to learn the model’s best hyperpa- rameters. In all of our experiments we initialise our model’s embeddings using the Glorot uniform random generator ⁽⁴⁶⁾ and we optimise the training loss using the Adagrad optimiser, where the learning rate (lr) ∈ {0.1, 0.01, 0.001}, embeddings size (K) ∈ {50, 100, 150, 200} and batch size (b) ∈ {512, 1024, 4000, 6000}. The rest of the grid search hyperparameters are defined as follows: the regularisation weight (λ) ∈ {0.1, 0.3, 0.35, 0.01, 0.03, 0.035} and dropout (d) ∈ {0.0, 0.1, 0.2, 0.01, 0.02}. The number of training epochs is fixed to 1000. We found that the best hyperparameters for our models are {lr = 0.1, k = 100, b = 6000, λ = 0.03, d = 0.2}.

Evaluation protocol. In our experiments, we follow the evaluation protocol introduced by Zitnik et. al ⁽⁸⁾, and we evaluate the TriVec model on the testing data split using three evaluation metrics: area under the ROC curve, area under the precision recall curve and average precision at 50 positives. The testing data contains both positive and negative data samples with a ratio of 1:1. We also use the same negative sampling procedure in the study of Zitnik et. al. ⁽⁸⁾ where we only consider combination that never appear as positive to be used as negatives the results. All the reported evaluation scores in our study represent the average of its corresponding scores for all the investigated polypharmacy side-effects.

Implementation. We use Tensorflow framework (GPU) along with Python 3.5 to perform our experiments. All experiments were executed on a Linux machine with processor Intel(R) Core(TM) i70.4790K CPU @ 4.00GHz, 32 GB RAM, and an nVidia Titan Xp GPU. The source code and the dataset splits used in our experiments are published at: https://github.com/samehkamaleldin/pse-kge.

Results and Discussion

In this section we discuss the outcomes of our experiments and we compare the predictive accuracy of our proposed approach with other state-of-the-art approaches.

Comparison with other approaches. (Table 2) shows the results of our experiments, where the models are compared in terms of the area under the ROC and precision recall curves and the average precision at 50. The results show that our model, the TriVec model, significantly outperforms other models with 12%, 16% and 22% margins (relative to other models’ scores) in terms of the area under the ROC, precision recall curves and with an average precision at 50 compared to the Decagon model. The results also show that our methods outperforms other knowledge graph embedding models such as the RESCAL, TransE, DistMult, ComplEx and KBLRN models on all metrics.

Table 2:

Summary of the results of our experiments. † represents the results of the state-of-the-art models that are obtained from the study of Zitnik et. al. (8). * represents the results of the state-of-the-art models that are obtained from the study of Malone et. al. (39).

Model	AUC-ROC	AUC-PR	AP@50
RESCAL † (21)	0.693	0.613	0.476
DEDICOM † (47)	0.705	0.637	0.567
Deep Walk † (48)	0.761	0.737	0.658
Concatnated Features † (8)	0.793	0.764	0.712
Decagon † (8)	0.872	0.832	0.803
TransE (20)	0.949	0.934	0.962
DistMult * (22)	0.923	0.898	0.899
KBLRN * (39)	0.899	0.878	0.857
ComplEx (23)	0.965	0.944	0.952

Additionally, the results show that models such as the TransE, TriVec and ComplEx models achieve significantly high scores (above 90%) in terms of the area under both the ROC and precision recall curves. We suggest that this is due to the easy nature of the evaluation protocol that uses a 1:1 negative to positive ratio in the testing set. Therefore, we suggest that future works should adapt high negative to positive ratios such as 1:10 or 1:50.

Other potential applications. Knowledge graph embedding models can operate on any data in a graph form, therefore, they can be easily adopted to model different biological networks. For example, our TriVec method can be used can used for modelling drug protein target networks ^{(49, 10)} where the method is used to predict new drug protein target which can be used for drug repurposing. Our method can also be used to perform tensor factorization task on complex biological systems to model functions such as protein functions. For example, the study of Mohamed et. al. ⁽⁵⁰⁾ shows the capabilities of the method in predicting tissue-specific protein functions where it models proteins, their biological functions and their tissues as a tensor. They then tensor factorization to predict protein function in a specific human body tissues.

Limitations. Our approach depends on known polypharmacy side-effects to learn efficient representations of both the drugs and the side-effects. This requires rich information about the investigated drugs e.g. drug interactions with other drugs and proteins. However, this type of information about the drug combinations and their associated side-effects is limited due to the recency of polypharmacy approaches and the limited clinical test applied on them ⁽⁷⁾. This problem affects the predictive accuracy of our proposed model and other graph embedding based models when they are applied on drugs with limited known assertions.

Conclusions and Future Work

In this study, we have explored the problem of predicting polypharmacy side-effect using computer simulations. We have modelled the polypharmacy side-effects data as a knowledge graph and we have applied a knowledge graph embedding model, the TriVec model, on this knowledge to predict new polypharmacy side-effects as link prediction on knowledge graphs. We have executed experimental evaluation to compare our approach to state-of-the-art models using a standard benchmarking pipeline. The results of our experiments have shown that our approach outperforms all the state-of-the-art approaches with 10%, 13% and 22% margins in terms of the area under the ROC, precision recall curves and average precision at 50.

In our future works, we intend to investigate learning embeddings of drugs according to their chemical structure to allow learning polypharmacy side-effects of drug combinations of drugs with limited known polypharmacy assertions.

Funding and acknowledgements

The work presented in this paper was supported by the CLARIFY project funded by European Commission under the grant number 875160, and by the Insight Centre for Data Analytics at the National University of Ireland Galway, Ireland (supported by the Science Foundation Ireland grant (12/RC/2289_P2). The GPU card used in our experiments is granted to us by the Nvidia GPU Grant Program.