Abstract
It has been confirmed that the coronavirus disease 2019 (COVID-19) can transmit through droplets created when an infected human coughs or sneezes. Accordingly, 1.83-m (6-feet) social distancing is advised to reduce the spread of the disease among humans. This is based on the assumption that no air circulation exists around people. However, it is not well investigated whether the ambient wind and relative humidity (RH) will cause SARS-CoV-2 laden droplets to transport farther in the air, and make the current social distancing policy insufficient. To provide evidence and insight into the “social distancing” guidelines, a validated computational fluid-particle dynamics (CFPD) model was employed to simulate the transient transport, condensation/evaporation, and deposition of SARS-CoV-2 laden droplets emitted by coughs, with different environmental wind velocities and RHs. Initial droplet diameters range from 2 to 2000 μm, and the wind velocities range from 0 to 16 km/h, representing different wind forces from calm air to moderate breeze. The comparison between a steady-state wind and a gust with a constant frequency has also been performed. Ambient RHs are 40% and 99.5%. The distances between the two virtual humans are 1.83 m and 3.05 m (6 feet and 10 feet). The facial covering effect on reducing the airborne transmission of the cough droplets has also been evaluated. Numerical results indicate that the ambient wind will enhance the complexity of the secondary flows with recirculation between the two virtual humans. Microdroplets follow the airflow streamlines well and deposit on both human bodies and head regions, even with the 3.05-m (10-feet) separation distance. The rest of the microdroplets can transport in the air farther than 3.05 m (10 feet) due to wind convection, causing a potential health risk to nearby people. High RH will increase the droplet sizes due to the hygroscopic growth effect, which increases the deposition fractions on both humans and the ground. With the complex environmental wind and RH conditions, the 6-feet social distancing policy may not be sufficient to protect the inter-person aerosol transmission, since the suspending micro-droplets were influenced by convection effects and can transport from the human coughs/sneezes to the other human in less than 5 seconds. Due to the complex real-world environmental ventilation conditions, a social distance longer than 1.83 m (6 feet) needs to be considered. Wearing masks should also be recommended for both infected and healthy humans to reduce the airborne cough droplet numbers.
Keywords: SARS-CoV-2-laden cough droplets, Social distancing, Computational fluid-particle dynamics (CFPD), Wind and gust, Relative humidity, Mask
Highlights
-
•
Air transmission of cough droplets with condensation and evaporation effects are modeled between two virtual humans.
-
•
Relative humidity (RH) has a noticeable influence on droplet size change dynamics.
-
•
High RH (99.5%) lead to higher deposition fractions of cough droplets on both virtual humans than low RH (40%).
-
•
Six-feet social distancing policy for COVID-19 may not be sufficient with ambient wind.
1. Introduction
As the world faces a large outbreak of coronavirus disease 2019 (COVID-19) epidemic, the airborne transmission risk of the novel severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) was first confirmed by the National Health Commission of the People's Republic of China (Wang & Du, 2020), and then by the Center for Disease Control and Prevention (CDC). Although the virus diameter of SARS-CoV-2 is from 50 to 200 nm (Guzman, 2020), it has been confirmed that SARS-CoV-2 spreads through inhalation or ingestions of droplets they contaminate. As a result, coughing, sneezing, and touching infected surfaces are primary sources of infection. As a cellular entry receptor for SARS-CoV-2 (Zhang, Penninger, Li, Zhong, & Slutsky, 2020), Angiotensin Converting Enzyme 2 (ACE-2) are abundantly present in humans in the epithelia of the lung and small intestine, as well as present in mucosae (mouth and nose) or conjunctiva (eyes). Therefore, it is critical to prevent the SARS-CoV-2 laden droplets from reaching the respiratory systems or the eyes. To slow the spread of COVID-19 via airborne transmission, a “social distancing” policy of approximately 1.83 m (6 feet) is recommended as of May 2020. However, this social distance is defined with static ambient air which is not realistic. The current social distancing policy also neglects the effect of relative humidity (RH) (Drossinos & Stilianakis, 2020). In addition, it is often assumed that most of the respiratory droplets fall and reach the floor within such a distance from the emission source. However, emitted micro-droplets have low Stokes numbers (Finlay, 2001), which can be significantly influenced by the convection of ambient airflow and transport much farther than 1.83 m. Such an unknown effect can increase the complexity of social distancing policy making and may pose potential risks to people in contact with the airborne SARS-CoV-2. Therefore, it is necessary to systematically investigate how the ambient wind and RH can influence the air transmission of SARS-CoV-2-laden droplets generated by coughs from a COVID-19 positive patient to a healthy human subject standing farther than 1.83 m (6 feet) away. Such research is also crucial because visualizing the airborne transmission of the SARS-CoV-2-laden droplets between humans can inform people to be aware of the importance to personal protection equipment (PPE), and to be responsible for helping reduce the spread of the virus to protect vulnerable population groups, i.e., seniors with underlying conditions such as influenza, cystic fibrosis, and diabetes.
Supported by benchmark experimental data from cough aerosol characterizations (Bourouiba, Dehandschoewercker, & Bush, 2014; Johnson & Morawska, 2009; Xie, Li, Sun, & Liu, 2009; Yang, Lee, Chen, Wu, & Yu, 2007), numerical studies (Chen & Zhao, 2010; Gupta, Lin, & Chen, 2011; He, Niu, Gao, Zhu, & Wu, 2011; Li, Shang, Yan, Yang, & Tu, 2018; Y. K. Yang, Kang, Hwang, & Park, 2017; Zhang & Li, 2012; Zhu, Kato, & Yang, 2006) have been done to either characterize cough aerosol clouds or simulate aerosol transport phenomena in both indoor and outdoor environments. However, most of the numerical studies, either using Euler-Euler or Euler-Lagrange based models, neglected the condensation and evaporation of the cough droplets, which may limit the validity of droplet trajectory predictions. Based on our literature review, there are three papers investigated the condensation and evaporation effects of cough droplets (Chen & Zhao, 2010; Li et al., 2018; Yan, Li, & Tu, 2019). Specifically, using a Euler-Lagrange based method with a single virtual human, Chen and Zhao (2010) claimed that the indoor temperature and RH have a negligible effect on the dispersion of saliva droplets with initial diameters from 0.1 to 200 μm in an indoor environment with specific ventilation conditions. Li et al. (2018) investigated the cough droplet transport and size change dynamics of a virtual human in a static ambient air condition. Yan et al. (2019) investigated the thermal effect of the human body on the evaporation of the cough droplets for a virtual human in a sitting position. All three papers employed a single virtual human, and did not investigate potential exposure health risks to the cough droplets for a second virtual human nearby.
This study employed a well-validated computational fluid-particle dynamics (CFPD) model (Chen, Feng, Zhong, & Kleinstreuer, 2017; Feng, Kleinstreuer, Castro, & Rostami, 2016; Y Feng, Kleinstreuer, & Rostami, 2015; Yu Feng et al., 2018; Haghnegahdar, Zhao, & Feng, 2019; Zhao, Feng, Bezerra, Wang, & Sperry, 2019) with the modeling capability of predicting droplet size changes due to condensation and evaporation to simulate SARS-CoV-2-laden droplets transmission between two virtual humans, to quantify the wind and RH effects on the droplet deposition on the human body and head region, and provide guidance on fine-tuning the social distancing policy based on environmental parameters. Specifically, using benchmark data of cough aerosol characterizations (Duguid, 1946; Yang, Li, Yan, & Tu, 2018), this study simulated the transient transport, condensation/evaporation, and deposition of SARS-CoV-2 laden droplets emitted by a cough between two virtual humans with different environmental wind velocities. Initial droplet diameters range from 2 to 2000 μm, and the wind velocities range from 0 to 16 km/h, representing different Beaufort wind scales from calm air to moderate breeze. The two ambient RHs employed in this study are 40% and 99.5%. The distance between the two virtual humans are selected as 1.83 m, and 3.05 m (6 feet, and 10 feet). Trajectories and size changes of SARC-CoV-2-laden droplets and transient laminar-to-turbulent airflow fields are visualized. Furthermore, local deposition patterns of the virus-laden droplets are calculated and compared with environmental weather conditions.
This study provides particulate transport dynamics on understanding the basic aerosol science of SARS-CoV-2-laden droplets spread through the air. The research is significant since it will benefit the research community and regulatory agencies, with the potential to enhance the fundamental understanding of how environmental and human factors can influence the airborne viral transmission from person to person. The insight and quantitative exposure data of the head region and the human body will provide direct evidence for prevention guidance to reduce exposure and infection risks. This study can also be extended to provide high-resolution virus-laden droplet transport and deposition predictions in human respiratory systems with different social distancing paradigms, and to estimate the SARS-CoV-2 RNA load in the airways for further understanding of the viral infection, replication, and pathogenesis noninvasively in the near future, and for better preparations against the post-pandemic period with a high possibility of the resurgence (Kissler, Tedijanto, Goldstein, Grad, & Lipsitch, 2020).
2. Methodology
2.1. Geometry and computational mesh
A confined environment, i.e., a cuboid space with two virtual humans separated at different distances, i.e., 1.83 m and 3.05 m (6 feet and 10 feet), are reconstructed (see Fig. 1 ). The two virtual humans are identical to the model used in the previous study (Zhao et al., 2019). The mouth opening is created for the virtual human on the left with a hydraulic diameter equal to 10 mm. The center coordinate of the opening is (0, 0, 0.034) m.
Fig. 1.
Schematic of the computational domain with two virtual humans and the hybrid mesh details.
Unstructured hybrid polyhedron plus prism meshes were generated using ANSYS Fluent Meshing 19.2 (ANSYS Inc., Canonsburg, PA). Six prism layers were created near the wall surface to contain the viscous sub-layers to calculate near-wall gradients accurately. Mesh details are shown in Fig. 1. The thickness of the first prism layer guarantees y+<1 to capture the laminar-to-turbulence transition sites using the Transition Shear Stress Transport (SST) Model (Menter, Kuntz, & Langtry, 2003). Specifically, y+ is the dimensionless wall distance, or local near-wall Reynolds number (Yu Feng et al., 2018). The mesh topology was determined by refining the mesh until grid independence of the flow field solutions was achieved. As an example, the final mesh of the computational domain with the 6-feet separation distance between the two virtual humans contains 2,638,753 elements and 9,572,670 nodes.
2.2. Governing equations
To predict the transport, size change, and deposition of the emitted virus-laden droplets generated from a cough, the well-validated Euler-Lagrange based multiphase flow model has been employed (Haghnegahdar et al., 2019; Zhao et al., 2019). The governing equations are listed as follows:
2.2.1. Continuous phase (airflow)
With the Eulerian descriptions, the ambient airflow field can be predicted by solving the conservation laws. The governing equations are given in tensor form as:
| (1) |
| (2) |
where represents the fluid velocity, p is the pressure, and [m/s2] is gravity aligned with the positive x-direction. In Eq. (2), the viscous stress tensor is defined by:
| (3) |
The cough jet and the environmental wind will generate a complex laminar-to-turbulent airflow field. Thus, the well-validated shear stress transport (SST) transition model (Menter et al., 2003) was adopted in this study, based on its overall good performance, predicting “laminar-to-turbulent” transition onset, computational efficiency and reasonable accuracy when compared to large eddy simulation (LES).
For turbulence simulation predicted by the Reynolds-averaged Navier–Stokes equations (RANS) model, the fluctuating velocity component will be recovered by (Wang & James, 1999):
| (4) |
| (5) |
| (6) |
| (7) |
where are the random numbers from the standard normal distribution. In Eqs. (5), (6), (7), f i are the damping factors to reflect the anisotropic magnitudes of in the near-wall region based on the Direct Numerical Simulation (DNS) results (Kim, Moin, & Moser, 1987; Matida, DeHaan, Finlay, & Lange, 2003). In Eq. (5), y + is the dimensionless wall distance defined as:
| (8) |
where y is the distance to the nearest wall, is the kinematic viscosity, and is the wall shear stress.
2.2.2. Discrete phase (cough droplets transport and size change dynamics)
In light of the large droplet-to-air density ratio, negligible droplet rotation, and limited thermophoresis, droplet trajectories was calculated by solving the translation equation of the discrete phase, i.e.,
| (9) |
where , , , and F i G are the drag force, lift force, Brownian motion-induced force, and gravity, respectively. Specifically, can be given by:
| (10) |
where d d is the droplet diameter, is the Cunningham correction factor (Allen & Raabe, 1985), and the drag force coefficient is defined as
| (12) |
where the constants , and are determined by the droplet Reynolds number. It is worth mentioning that is only considered significant when droplets evaporate into small sizes.
The condensation and evaporation between ambient water vapors and the water liquid in cough droplets are considered by solving the mass and energy balance for each droplet (Chen et al., 2017; Feng et al., 2016; Y Feng et al., 2015; Haghnegahdar et al., 2019), i.e.,
| (13) |
(k=1 for water) where is the average mass flux of evaporable component e on the surface, which can be expressed as (Chen et al., 2017)
| (14) |
where is the density of the ambient air, and Sh is the Sherwood number (Clift, Grace, & Weber, 2005), which is defined as
| (15) |
where is the Schmidt number, and is the mass diffusivity of component e.
In Eq. (14), and are the mass fractions of evaporable component e on the droplet surface and in the gas phase far from the droplet, respectively. C m is known as the Fuchs-Knudsen number correction (Ferron, Kreyling, & Haider, 1988), which is defined as
| (16) |
where Kn is the Knudsen number . Specifically, is the ratio between the diffusion coefficient of water vapor and the mean thermal velocity of the condensing water vapor, and is the mass thermal accommodation coefficient. Furthermore, can be obtained using the modified Raoult's law (Chen et al., 2017) which is given by
| (17) |
where is the activity coefficient of component e, is the mole fraction of e in the droplet, is gas constant, is the droplet temperature, is the saturation pressure of component e at temperature , and is the correction factor for the Kelvin effect, which characterize the effects of surface curvatures (Finlay, 2001). Specifically, can be given by
| (18) |
where is the surface tension of the droplet, is the molar mass of component e, R is the universal gas constant, and is the droplet density.
The energy balance equation of the droplet is give by
| (19) |
where Nu is the Nusselt number can be calculated using
| (20) |
in which is the Reynolds number of the droplet, and Pr is the Prandtl number.
2.3. Boundary and initial conditions
2.3.1. Transient cough-jet airflow waveform
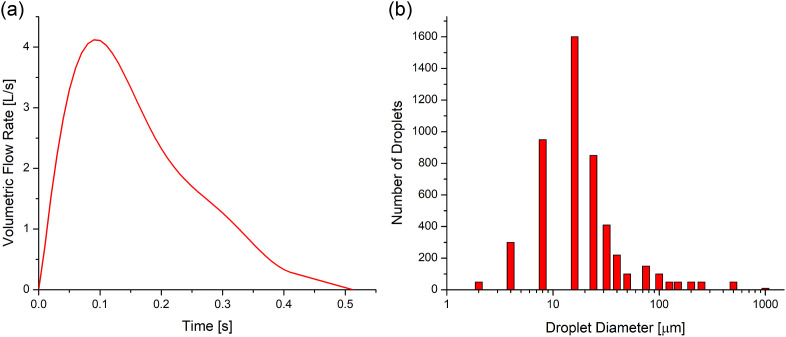
The transient cough-jet airflow waveform is based on the experimental measurements of the transient flow of a cough for 25 subjects (Kuga, Ito, Chen, Wang, & Kumagai, 2020; Yang et al., 2018) (see Fig. 2 (a) ). Fourier series is used to generate the correlations of the transient airflow waveform applied as the boundary condition at the mouth opening of the coughing virtual human (left in Fig. 1). The temperatures of the body shells and exhaled cough jet are assumed to be 37 °C.
Fig. 2.
Cough-jet boundary conditions at the mouth opening of the infected virtual human: (a) Transient cough-jet waveform based on experimental measurements of 25 subjects (Yang et al., 2018), and (b) cough droplet size distribution (Duguid, 1946).
2.3.2. Initial size distribution of cough droplets
A cough can turn human mouths into atomizers (Settles, 2006). In this study, the widest span of the cough droplet size distribution measurements was used (Duguid, 1946) (see Fig. 2 (b)). Specifically, those droplets consist of saliva and mucus and range in diameters from 2 to 2000 μm. Although there are other size distributions documented in the open literature (Bourouiba et al., 2014; Johnson & Morawska, 2009; Xie et al., 2009; Yang et al., 2017), it is more insightful to choose the widest size distribution span to investigate how droplet sizes can influence their airborne transmission trajectories and deposition. Other size distributions will be employed in future numerical studies to evaluate the size distribution variability on the virus-laden droplet aerosol dynamics. Cough droplets consist of 10.4% NaCl, and 89.6% water (Haghnegahdar et al., 2019).
2.3.3. Wall boundary conditions
Deposition occurs once the droplet contacts the body shells of the virtual humans and ground. Droplet size and spatial location were recorded when the droplet deposited on the boundary or escaped from the computational domain.
2.3.4. Ambient wind scale, temperature, and relative humidities (RHs)
The ambient wind velocities range from 0 to 16 km/h, representing Beaufort wind scales from calm air to moderate breeze (Beer, 2013). The potentially most risky wind direction, from the infected virtual human (left in Fig. 1) to the other virtual human (right in Fig. 1), has been employed. The wind inlet temperature is assumed to be 27 °C. Two RHs are used in this study, i.e., (1) RH = 40%, which is the lower bound of the ideal humidity for health and comfort, and (2) RH = 99.5%, which is the highly humid environment close to saturation.
2.3.5. Initial airflow fields
It is assumed that the wind velocity and direction are steady-state. Accordingly, the steady-state airflow fields with different ambient wind conditions were employed to initialize the numerical simulations before introducing the transient cough-jet waveform and the emitted virus-laden droplets. An example can be found in Fig. 1 at the midplane Y = 0.
2.4. Numerical setup
ANSYS Fluent 2019 R1 (ANSYS Inc., Canonsburg, PA) was used to simulate the transient airborne transmission of the cough droplets carried by the ambient airflows, with condensation and/or evaporation. The flow time step is t f = 1.0e-3 s, and the maximum droplet time step is t d = 1.0e-5 s. Both time steps are determined based on in-house time-step independence tests. All simulations stopped at 15 s, or stopped earlier when the suspending droplets in the domain are less than 1% of the total number of droplets injected. Numerical simulations were performed on a local Dell Precision T7910 workstation (Intel®Xeon® Processor E5-2683 v4 with dual processors, 64 cores, and 256 GB RAM). Using 32 cores, it took approximately 8 hours to complete one simulation with an 15-s flow time duration. In-house user-defined functions (UDFs) and Matlab codes were employed for:
-
(1)
Generating the polydispersed droplet injection files;
-
(2)
Specifying transient cough-jet waveform at the mouth of the infected virtual human;
-
(3)
Recovering the anisotropic corrections on turbulence fluctuation velocities;
-
(4)
Modeling the Brownian motion for droplets that can potentially shrink to less than 1 μm due to evaporation;
-
(5)
Calculating droplet-size change dynamics considering the interactions with the ambient water vapor.
3. Results and discussion
3.1. Model validations
It is worth mentioning that the CFPD model and the in-house codes have been well validated in previous publications (Chen et al., 2017; Yu Feng et al., 2018; Haghnegahdar et al., 2019; Zhao et al., 2019). The validations with benchmark experimental data in previous publications include:
-
(1)
Laminar-to-turbulence airflow field predictions using the SST k-ω transition model (Feng et al., 2016). Specifically, comparisons of airflow velocity magnitude and iso-surfaces show good matches between the employed SST k-ω transition model and the experimental measurements (Banko, Coletti, Schiavazzi, Elkins, & Eaton, 2015) have been done in the same subject-specific human airway model.
-
(2)
Droplet-size change dynamics with different droplet compositions (Chen et al., 2017; Feng et al., 2015; Haghnegahdar et al., 2019). Specifically, the size change dynamics model was validated by the comparisons of the evaporation and condensation dynamics of multi-component NaCl-water droplets and cigarette aerosol particles with benchmark experiments and computational studies (Li, Montassier, & Hopke, 1992; Zhang, Kleinstreuer, & Hyun, 2012).
-
(3)
Discrete phase transport and regional deposition predictions (see Fig. S2 in the supplemental material in a previous publication (Haghnegahdar, Feng, Chen, & Lin, 2018)). Specifically, regional deposition efficiencies (RDEs) predicted by the CFPD model employed in this study were compared with benchmark experimental data in physical models of lung airways, with the inhalation flow rate from 15 to 60 L/min. Comparisons show good agreements between the numerical and experimental studies.
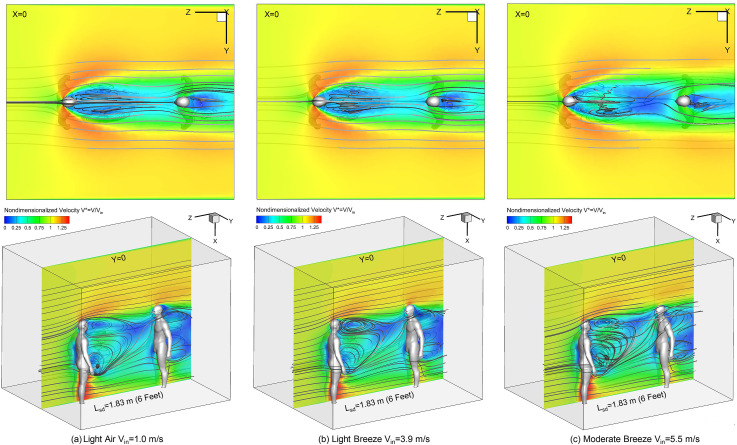
3.2. Airflow field vs. wind velocity Vin
Figures. 3 (a)–(c) visualize airflow fields and localized recirculations of the wake flow using the nondimensionalized air velocity contours V* = V/Vin at planes X = 0 and Y = 0 with streamlines. The distributions of V* have no significant changes with the increase in wind velocity Vin. However, when Vin increases, the strength and complexity of the recirculating flows are enhanced, which can be observed form the topology variations of the streamlines at Y = 0. The intensified recirculating flows have impacts on the cough droplet transport with higher Vin (see Section 3.3). Furthermore, high-velocity flows exist outside of the wake flow formed downstream to the human who coughs (left in Fig. 1), which can be both observed from the velocity contours at planes X = 0 and Y = 0. Specifically, as the V* contours shown at plane X = 0 in Figs. 3 (a)–(c), the higher velocity outside of the wake flow generates secondary flows and vortices rotating towards the centerline between the two virtual humans. These horizontal secondary flow patterns also restrict the dispersion of the cough droplets in Y direction during their transport, and most of the droplets were not able to escape from the wake flow region (see Section 3.3). The airflow streamlines also indicate that the wind flow near the ground is able to pass between the legs of the left virtual human and rise towards the head region of the right virtual human, which indicates the possibility to lift settling droplets toward the face of the healthy virtual human to the right. In addition, the recirculation zone downstream to the healthy virtual human (right in Fig. 1) lead to droplet deposition on the backside.
Fig. 3.
Initial contours of nondimensionalized air velocity (V* = V/Vin) at Plane X = 0 (top) and Plane Y = 0 (bottom) with different ambient wind velocities (Lsd = 1.83 m (6 feet)): (a) light air Vin = 1.0 m/s, (b) gentle breeze Vin = 3.9 m/s, and (c) moderate breeze Vin = 5.5 m/s.
3.3. Wind and RH effects on droplet transport and deposition
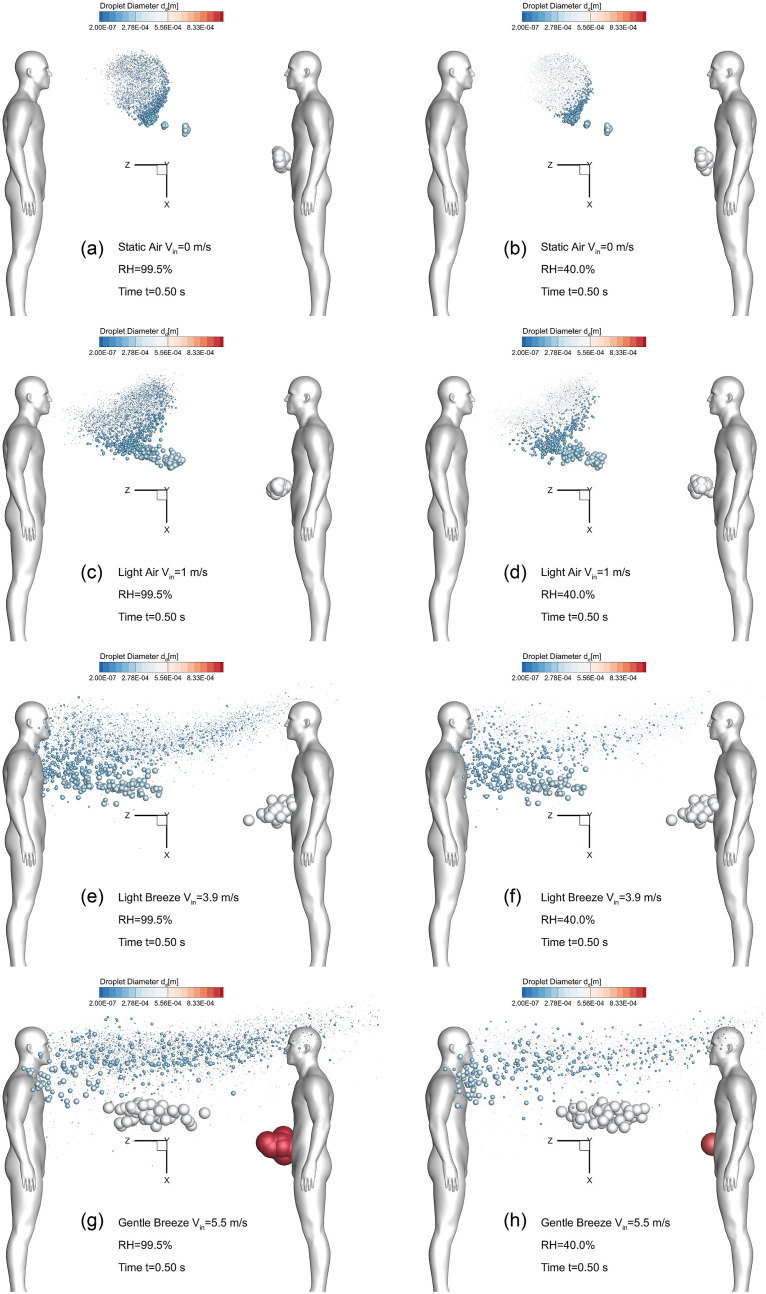
To manifest the wind and RH effect on the airborne droplet transmission, Fig. 4, Fig. 5, Fig. 6, Fig. 7 show the droplet trajectories and their size changes at different time stations with different wind velocities Vin and RHs. Selecting t = 0.5 s as the representative time when the cough jet ends, the droplet sizes and positions in different cases are visualized in Figs. 4 (a)–(h). With Vin increases from 0 to 5.5 m/s, the convection due to the ambient wind becomes more dominant to small droplets. This can be proved by the smaller distance between the frontier of the droplet cloud and the healthy human to the right in the figures with Vin increases. It is interesting to see that larger droplets are not affected by the enhanced wind velocity when Vin<5.5 m/s. Specifically, the large droplets in gray color, all traveled approximately 1.81 m at t = 0.5 s in Figs. 4 (a)–(f). Such an observation indicates that those the inertia and gravitational sedimentation are dominant for those large droplets. The exceptions are shown in Figs. 4 (g) and (h). The enhanced localized turbulence intensity and airflow momentum in the recirculation zones between the two virtual humans, larger droplets are influenced and moved back towards the left human who coughs. Indeed, with high wind velocity entering the computational domain, the local airflow velocities in the recirculation zone have higher velocity magnitude and turbulence intensity. Therefore, the convection effect is more dominant so that it can influence the larger droplets and conquer their inertia, forcing them to follow the backward recirculation flow. Such trajectories led to the deposition patterns of the droplets in gray color shown in Figs. 8 (c) and (d). Moreover, the RH effect on the droplet size change dynamics is noticeable. Droplet sizes in cases with RH = 99.5% (see Figs. 4 (a), (c), (e) and (g)) are larger than the cases with RH = 40% (see Figs. 4 (b), (d), (f), and (h)) This is because the high RH (99.5%) enhances the hygroscopic growths of the droplets, while the low RH (40%) leads to droplet shrinkage due to the evaporation.
Fig. 4.
Wind velocity and RH effects on the droplet transmission patterns at t = 0.5 s: (a) Vin = 0 m/s and RH = 99.5%, (b) Vin = 0 m/s and RH = 40.0%, (c) Vin = 1 m/s and RH = 99.5%, (d) Vin = 1 m/s and RH = 40.0%, (e) Vin = 3.9 m/s and RH = 99.5%, (f) Vin = 3.9 m/s and RH = 40.0%, (g) Vin = 5.5 m/s and RH = 99.5%, and (h) Vin = 5.5 m/s and RH = 40.0%.
Fig. 5.
Droplet sizes and positions at different time stations (Lsd = 1.83 m (6 feet), RH = 40.0%, Vin = 0 m/s): (a) t = 0.10 s, (b) t = 0.25 s, (c) t = 0.5 s, (d) t = 1.0 s, (e) t = 5.0 s, (f) t = 15.0 s.
Fig. 6.
Droplet sizes and positions at different time stations (Lsd = 1.83 m (6 feet), RH = 40%, Vin = 5.5 m/s): (a) t = 0.10 s, (b) t = 0.25 s, (c) t = 0.5 s, and (d) t = 1.0 s.
Fig. 7.
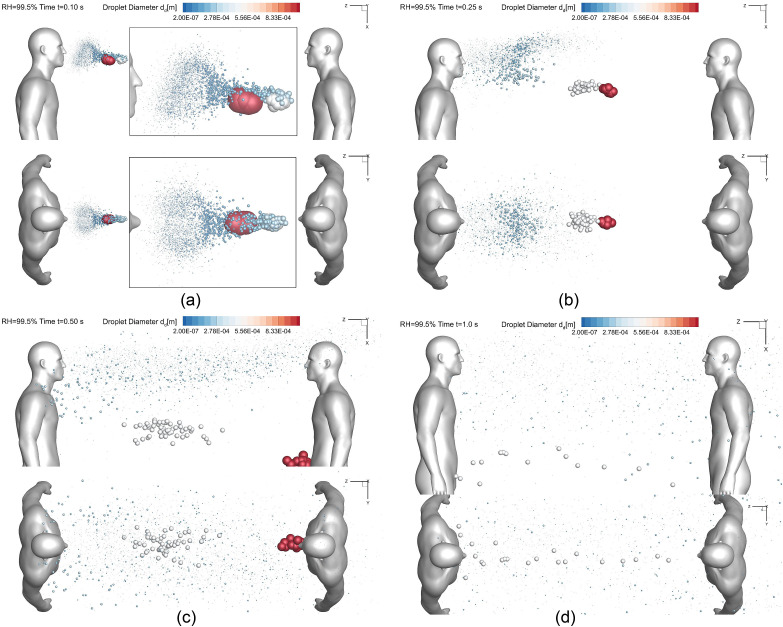
Droplet sizes and positions at different time stations (Lsd = 1.83 m (6 feet), RH = 99.5%, Vin = 5.5 m/s): (a) t = 0.10 s, (b) t = 0.25 s, (c) t = 0.5 s, and (d) t = 1.0 s.
Fig. 8.
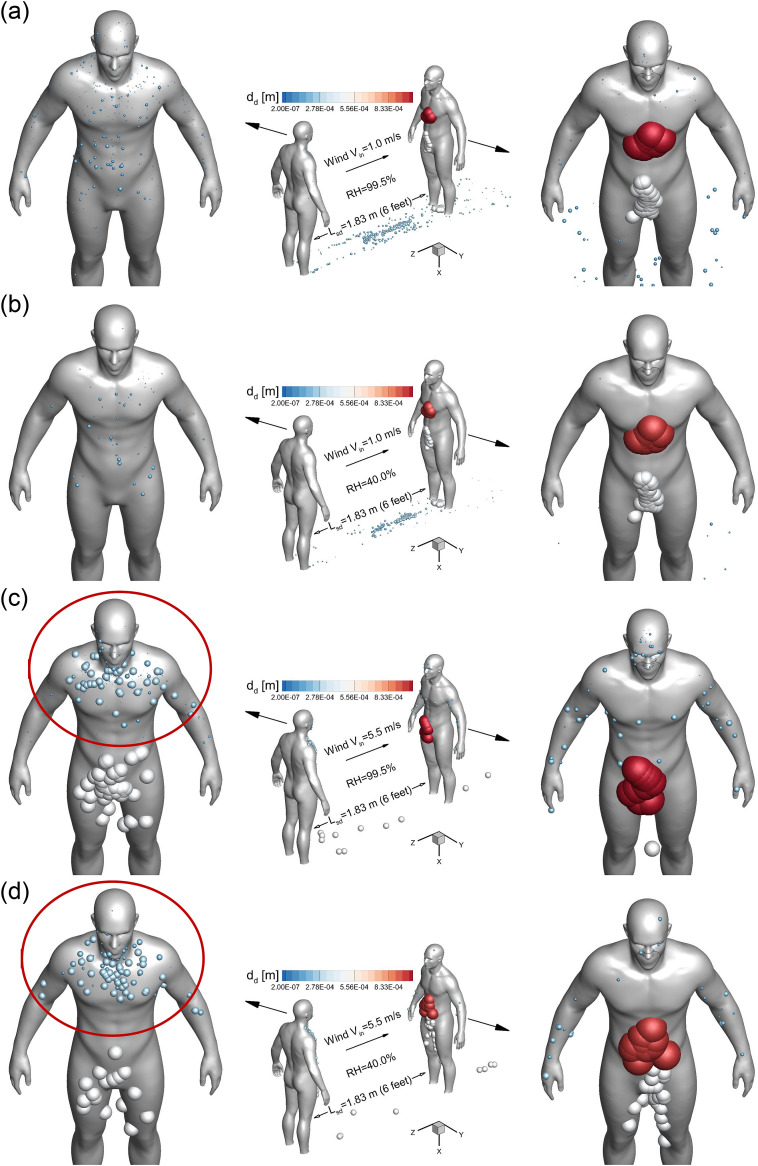
Wind velocity and RH effects on the droplet deposition patterns at t = 0.5 s: (a) Vin = 1.0 m/s and RH = 99.5%, (b) Vin = 1.0 m/s and RH = 40.0%, (c) Vin = 5.5 m/s and RH = 99.5%, and (d) Vin = 5.5 m/s and RH = 40.0%.
Comparisons of the droplet transport dynamics shown in Fig. 5, Fig. 6, Fig. 7 from two different angles can provide the insight of wind and RH influence on the airborne transmission of SARS-CoV-2 laden droplets. Figures. 5 (a)–(f) visualize the cough droplets positions and sizes at different times in static air from t = 1.0 s to t = 15.0 s. Droplets can only obtain momentum and energy from the cough jet when the ambient wind velocity is zero (see Fig. 2 (a)). It can be observed that large droplets move faster and stay more concentrated than small droplets. This is because large droplets have relatively high Stokes number, indicating the less dominant effect of viscous dissipation forces acting on them. Therefore, they are more “capable” of keeping their initial momentums. In contrast, with the larger ratio between surface area and volume, small droplets lose their initial momentum and kinetic energy more quickly due to the viscous dissipation effect from the drag force mainly. Thus, they are dispersed very fast in static air. Figs. 5 (e) and (f) demonstrate that with the current 1.83 m (6-feet) social distancing policy, microdroplets can still transport to the head region of the healthy virtual human standing on the right. Therefore, the current social distancing policy may not be 100% safe even for the ideal static air condition.
The comparisons between Fig. 5, Fig. 6 manifest the wind effect on the droplet transport. With Vin = 5.5 m/s, the wind convection is dominant on small droplet trajectories. Specifically, the droplets are restricted in the region with a width approximately equal to the with of the shoulders. This is because the horizontal recirculation flows towards the centerline between the two humans (see Figs. 3(a)–(c)). In addition, the dominant wind convection conveys extra momentum and kinetic energy to the droplets and accelerates them to move faster towards the head region of the healthy human to the right following the airflow streamlines (see Fig. 5, Fig. 6). With the recirculation effect in the vertical direction compared with the static air, some droplets traveled backward and stayed around the left human who coughs. Therefore, the ambient wind will make the small droplets transport dynamics become more complex, and can potentially provide higher kinetic energy to them and make them travel farther in the air.
Fig. 6, Fig. 7 show the influence of RH on droplet transmission, both with Vin = 5.5 m/s and 1.83-m (6-feet) social distance. The same observations can be found, i.e., RH = 99.5% lead to droplet hygroscopic growths while RH = 40% lead to water evaporation from droplets. Despite of the differences of droplet size change dynamics due to the RH, droplet trajectory differences shown in Fig. 6, Fig. 7 are not obvious. To further reveal the difference, investigations have been done to identify the RH effect on droplet depositions on human bodies and the ground.
Accordingly, Fig. 8, Fig. 9 show the local deposition patterns and regional deposition fractions (DFs) of the cough droplets with different Vin and RH conditions. With Vin = 1.0 m/s, high RH leads to higher depositions of small droplets on both humans and the ground (see Figs. 8 (a) and (b)), while the deposition patterns of large droplets colored in gray and red are similar and not influenced significantly by the RH. With Vin = 5.5 m/s, high RH still lead to higher depositions of small droplets on the healthy human standing on the right, as shown in Figs. 8 (c) and (d). However, small droplet deposition patterns are similar on the human who coughs, which are located around the head region and the upper body above the chest (see the deposition patterns in the red circles in Figs. 8 (c) and (d)). For larger droplets in gray, higher RH increases their depositions on the human who coughs, but reduces the deposition on the healthy human. Such phenomena are possibly due to the different droplet size change dynamics, which altered the transient droplet-air interactions, the resultant droplet trajectories, and their deposition sites. Comparing the deposition patterns between Vin = 1.0 m/s and 5.5 m/s at the same RHs, stronger wind leads to more depositions of larger droplets on both humans. It is because that the stronger secondary flows induced by the high wind velocity and momentum can alter the droplet trajectories with larger diameters. Those droplets follow the streamlines and recirculate before the the deposition led by gravitational sedimentation and inertial impaction could happen. Besides, it is obvious that both humans have SARS-CoV-2 laden droplets on their body and head region during a single cough event. Therefore, it is necessary to avoid body contact with others before changing clothes and washing hands after possible exposure to the airborne virus.
Fig. 9.
Wind velocity and RH effect on droplet deposition and suspension with Lsd = 1.83 m (6 Feet): (a) DF on the coughing human, (b) DF on the ground, (c) DF on the healthy human, and (d) suspending droplet number fractions at the end of simulations.
Because of the discrepancies of RH and wind influences on the depositions between large and small droplets, regional deposition fractions (DFs) are calculated and shown in Figs. 9 (a)–(d). It can be concluded from Figs. 9 (a)–(c) that, high RH increases the deposition fractions (DFs) on both humans and the ground. However, the higher deposition does not necessarily mean higher exposure risk or infection risks, since research indicates that higher RH above 40% may be detrimental to reduce the survival of many viruses including different types of coronavirus (Casanova, Jeon, Rutala, Weber, & Sobsey, 2010; Chan et al., 2011; Dietz et al., 2020; Kim, Ramakrishnan, Raynor, & Goyal, 2007). It is interesting that increasing the wind velocity from 3.9 m/s to 5.5 m/s decreases the DFs on both human bodies (see Figs. 9 (a) and (c)). Therefore, the wind effect on the droplet deposition is obscure and needs further investigation with different wind velocities and directions. Figure 9 (d) visualized the fraction of droplets suspending in the computational domain at t = 15 s. For static air condition (Vin = 0), there are more droplets suspending in the air with RH = 40% than RH = 99.5%. Such an observation indicates that high RH may lead to faster gravitational sedimentation of airborne droplets due to the hygroscopic growth effect. For the cases with ambient winds, the fractions of suspending droplets are not significantly influenced by the RH. Figure 9 (d) also shows that increasing wind velocity will result in stronger convection, which provides faster airborne transmission of the droplets and less suspending droplets in the computational domain.
To further investigate the influence of Vin and RH, the suspending and deposited droplet diameters at different times are shown in Figs. 10 (a) and (b). Figure 10 (a) visualizes the average diameter changes of suspending droplets with different RHs before any droplet deposit in or escape from the computational domain. It can be clearly seen that RH = 99.5% induces hygroscopic growths of the droplets, while RH = 40% induces water evaporation and droplet size reduction. It worth mentioning that the wind effect is negligible on the droplet size changes of suspending droplets, since the wind volumetric flow rate is much higher than the cough jet, so that the RH in the computational domain is determined by the RH carried by the wind velocity. Figure 10 (b) shows the diameters of deposited droplets at different times. With the same RH, droplets deposit faster with high wind velocity due to the strengthened convection than the cases with low wind velocity. For the two cases with RH = 40%, the deposited droplets with the same initial diameters become smaller if they deposit at later times. For the case with RH = 99.5%, the deposited droplets with the same initial diameters become larger if they deposited at later times.
Fig. 10.
Wind velocity and RH effects on the droplet diameter change dynamics: (a) suspending droplet size changes at different times, and (b) deposited droplet size changes at different times.
3.4. Social distance Lsd and transient wind effects on droplet transport and deposition
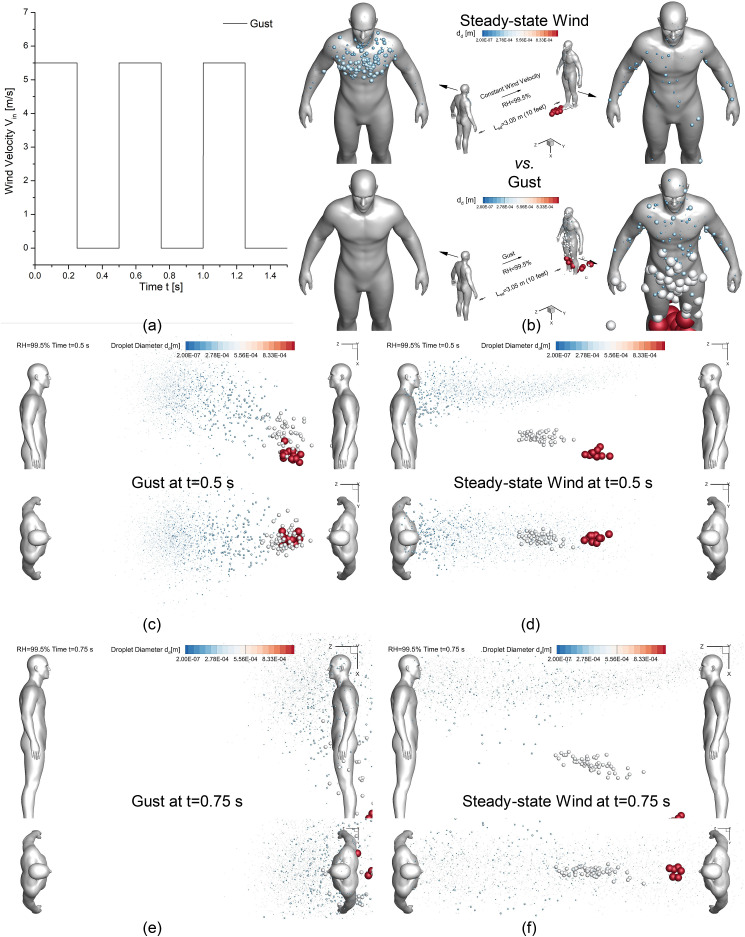
Since Fig. 8, Fig. 9 have demonstrated that Lsd = 1.83 m (6 feet) is not able to sufficiently protect the healthy virtual human from being in contact with the cough droplets when Vin is not zero, it is beneficial to investigate whether a longer Lsd will be a better standard to be used for the social distancing policy. Therefore, two additional simulations for Lsd = 3.05 m (10 feet) and RH = 99.5% were done with two different wind conditions, i.e., steady-state moderate breeze Vin = 5.5 m/s, and a transient gust with a specific periodic waveform shown in Fig. 11 (a) . Droplet deposition patterns and transport dynamics of the two 10-feet cases are visualized in Figs. 11 (b)–(f), in comparison with the 6-feet case with the same RH and wind velocity (see Figs. 7(a)–(d) and Fig. 8 (c)).
Fig. 11.
Droplet transmission and deposition difference between gust and steady-state wind: (a) Gust velocity profile vs. time, (b) deposition pattern comparison, (c) gust at t = 0.5 s (d) steady-state wind at t = 0.5 s (c) gust at t = 0.75 s (d) steady-state wind at t = 0.75 s.
With the steady-state Vin = 5.5 m/s, the comparison between Figs. 8 (c) and Fig. 11 (b) demonstrates that enlarging Lsd from 1.83 m (6 feet) to 3.05 m (10 feet) can effectively reduce large droplet deposition on both virtual humans. Specifically, the reduction of the large droplet deposition on the human who coughs (left in the figures) is due to the altered wake flow patterns between the two humans with the Lsd extension. Compared with Lsd = 1.83 m (see Fig. 7 (c)), large droplets in gray in Lsd = 3.05 m case avoided entering the recirculation region and traveled faster forward (see Fig. 11 (d)). Another evidenceis the deposition pattern differences shown in between Figs. 8 (c) and Fig. 11 (b). No large droplets deposit on the human who coughs in Fig. 11 (b) than Fig. 8 (c), indicating that no large droplets moved backward in Lsd = 3.05 m cases. The other groups of large droplets in red are dominated by the gravitational sedimentation and deposit on the ground due to the larger Lsd = 3.05 m (see Fig. 8 (c) and Fig. 11 (b)). In contrast, microdroplets in blue are still able to follow the mainstream and transport to the head region of the healthy human (right in Fig. 7 (d) and Figs. 11 (d) and (f)). Thus, although Lsd = 3.05 m is able to reduce the exposure risks to airborne SARS-CoV-2 laden droplets with the slightly reduced DF from 2.4% to 1.9% compared with Lsd = 1.83 m with Vin = 5.5 m/s and RH = 99.5%, there are still depositions on the healthy human who stands 3.05 m (10 feet) away from the human who coughs.
Additional comparisons have been made to compare the cough droplet transport and deposition with between the steady-state wind and transient gust conditions (see Figs. 11 (a)–(f)). It is worth mentioning that the gust employed in this study is with a fixed frequency, i.e., 2.0 Hz. Different gust frequencies will be investigated in the future to draw more generalized conclusions. Based on the comparison between the droplet positions at two different time stations (see Figs. 11(c)–(f)), it is interesting to find that the gust condition was able to convect the cough droplets faster towards the healthy human direction than the steady-state wind condition. The gust also leads to higher deposition on the healthy human and no deposition on the human who coughs (see Fig. 11 (b)). The difference in droplet transport and deposition between the steady-state wind and the gust is due to the difference in the recirculating flow patterns between the two virtual humans. Specifically, the interval gust condition will not generate the quasi-steady-state recirculations. As a result, it leads to faster transport of the droplets towards the downstream direction. Without moving upstream, no droplets deposited on the human who coughs, and more droplets transported downstream and deposited on the healthy human. Thus, with the same peak wind velocities, the gust enhances the exposure risk of the healthy human compared with the steady-state wind condition.
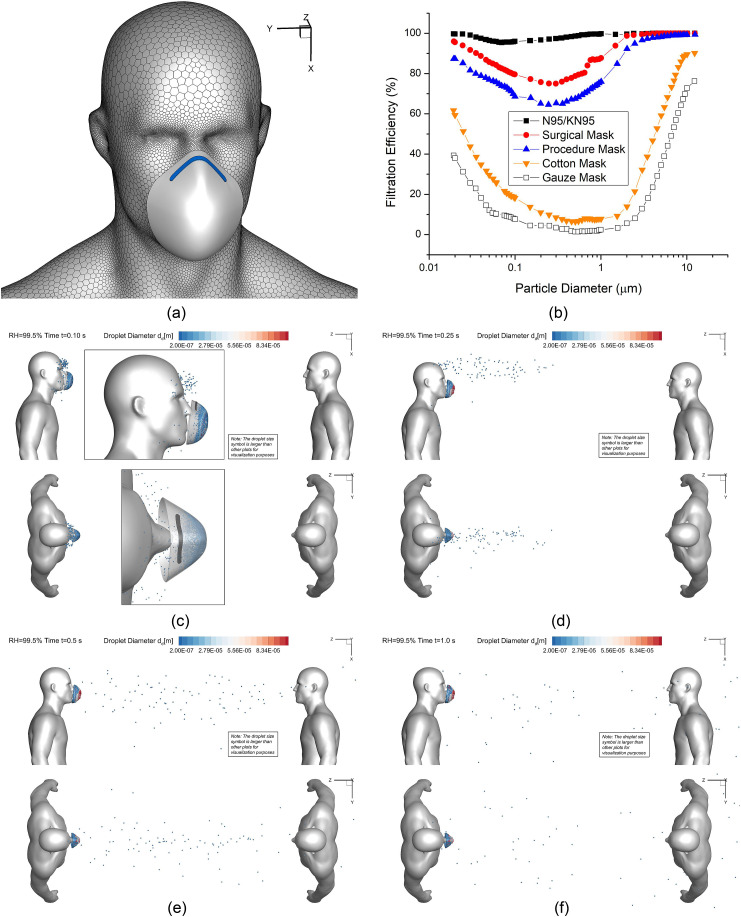
3.5. N95 mask effect on the potential exposure risks
To further investigate the effectiveness of facial covering, a virtual N95 filtering facepiece respirator (FFR) was reconstructed and positioned close to the virtual human who coughs (see Fig. 12 (a) ). The average gap between the face contour and the edge of the N95 mask was intentionally exaggerated to approximately 1.8 cm, mimicking the worst scenario with the inappropriate mask seal. Employing the realistic filtration efficiencies as a function of particle diameter (see Fig. 12 (b)), a customized C code was programmed to reflect the probabilities of capturing droplets with different diameters, when the cough droplets enter the N95 mask which is assumed to be a porous media region. For example, when entering the N95 mask region, the C code will generate a random number between 0 and 1 for each droplet. If the random number is lower than the filtration efficiency for the specific droplet diameter, the particle will be assigned a velocity equal to zero, which indicates it has been captured by the mask. For the computational domain of the N95 mask, the porosity is 0.88, and the viscous resistance coefficient is 1.12e10 m-2. The values are obtained from existing studies (Zhang, Li, Shen, & Cai, 2016).
Fig. 12.
Droplet sizes and positions at different time stations for the scenario with the facial mask intentionally located at approximately 1.8 cm from the face (Lsd = 1.83 m (6 feet), RH = 99.5%, Vin = 5.5 m/s): (a) face mask geometry, (b) mask filtration efficiencies vs. particle diameter, (c) t = 0.10 s, (d) t = 0.25 s, (e) t = 0.5 s, and (f) t = 1.0.
To investigate the riskiest case for Lsd = 1.83 m (6 feet), Vin = 5.5 m/s and RH = 99.5% were selected for the simulation with the N95 mask. The droplet transport dynamics at different time stations are visualized in Figs. 12 (c)–(f) for the comparisons with the case without N95 mask (see Fig. 7 (a)–(d)). As shown in Figs. 12 (c)–(f), although there are still cough droplets that cannot be captured by the mask, the total number of the cough droplets transport in the air is significantly lower than the case without the mask (see Fig. 7). With the mask, airborne droplets are all relatively small. Their initial time entering the freestream airflow is slightly delayed. Those small droplets can still follow the mainstream airflow (see Fig. 3 (c)) and reach the healthy virtual human standing on the right. Thus, it can be concluded that wearing facial masks can significantly reduce the airborne transmission of cough droplets, even if it is without proper seal with the face. It is recommended that people should wear facial coverings with minimized gaps with their faces, in order to maximize the effectiveness.
3.6. Recommendations on viral load estimations
Viral load is not considered in this numerical study, based on the fact that viral loading in a cough droplet is still unknown. However, for the future work, it can be assumed that the viral RNA load copies/ml in the cough droplet is identical to the specimen collected from COVID-19 patients exhibiting coughing symptoms (Kim et al., 2019), or the saliva data from infected ferrets, which is 101.73±0.54 copies per ml (Kim et al., 2020).
3.7. Recommendations on social distancing policy: Beyond aerosol dynamics
The minimum infectious dose of SARS-CoV-2 is unknown so far, but researchers suspect that it is low. More viruses may lead to more severe COVID-19 symptoms. Therefore, it is certain that lowering the exposure risks to airborne SARS-CoV-2 will reduce the infection risks. Indeed, it is not 100% likelihood of infection when SARS-CoV-2 laden droplets deposit on human bodies or head regions. However, increasing social distance and avoiding standing at the downwind position when talking to other people will effectively reduce the exposure risks. If the wind direction is constant, it is ideal that the two humans should make sure that “the discussion should be orthogonal to the wind,” meaning the wind should be in a direction perpendicular to the centerlines connecting the two humans. However, wind velocity and direction varies from time to time in reality.
Furthermore, recent studies (van Doremalen et al., 2020, Van Doremalen et al., 2020) demonstrate that aerosols containing SARS-CoV-2 remained infectious in air, on surfaces, and in tissue-culture assays with only a slight reduction in infectivity for hours of observation. Based on the observation from this study, microdroplets can either suspend and transport in the air farther than 1.83 m (6 feet) or deposit on human bodies. Thus, only keeping the social distancing guidelines as of May 2020 is not sufficient, and the guidelines should be scrutinized further. Wearing PPEs, avoiding handshakes, and washing hands frequently are necessary.
During the current period without COVID-19 vaccines, the current social distancing policy needs to be refined with larger separation distances to slow down the spread of the virus. However, it does not necessarily mean that a more strict social distancing policy will be 100% beneficial for the long term. More effective social distancing policies have the possibility to slow down the development of herd immunity to COVID-19 and may enhance the chance for the resurgence (Kissler et al., 2020). Therefore, more factors beyond the aerosol dynamics need to be integrated for decision making.
4. Conclusions
To slow the spread of the COVID-19 virus via airborne transmission, although a “social distancing” policy of approximately 1.83 m (6 feet) is recommended, it needs to be scrutinized. By visualizing the trajectories and fates of SARS-CoV-2-laden droplets with various ambient conditions using the CFPD method with modeling the condensation/evaporation effects between the ambient water vapor and the droplets, this study finds that the 1.83 m (6 feet) social distancing policy is the “minimum requirement” and is not sufficient to avoid the contact of SARS-CoV-2 due to the complexity of environmental wind conditions. These conclusions do not consider the sneeze droplet cloud that can span approximately up to 8 m (27 feet) (Bourouiba, 2020). Therefore, a safe social distance is highly dependent on different factors, so it is highly recommended that people wear masks and other face coverings when in public. Major conclusions are listed as follows:
-
(1)
A carrier of COVID-19 who coughs can produce virus-laden droplets in micron size that remain viable in the air exposing healthy people near (6 feet) and far (10 feet) from the source in a static air environment.
-
(2)
Wind effect on the droplet transport and deposition is complex and highly dependent on the wake flow patterns and localized secondary flow intensities between the two virtual humans, as well as the steadiness of the wind. It is certain that the current 6-feet social policy is not sufficient to protect people from SARS-CoV-2 exposure generated by coughs with the ambient wind.
-
(3)
High RH=99.5% leads to higher deposition fractions on both human bodies and the ground, which is not necessarily related to higher exposure risks. High RH=99.5% can enhance the condensation effect, and the cough droplet sizes keep growing during their transport in the air until the partial pressure at the droplet surface is equal to the saturation pressure of water vapor. In contrast, RH=40% triggers the evaporation of the water in cough droplets, thereby leading to droplet size reduction, which may lead to a longer time suspended in the air.
-
(4)
Although longer social distance can reduce the cough droplet depositions on the human body, there are still SARS-CoV-2 laden droplets that may suspend near the head region or deposit on the healthy human.
-
(5)
Even wearing facial masks in an unrealistically loose condition when coughing can significantly reduce the suspension of small droplets in the air.
5. Limitations of the study and future work
The present numerical study is subjected to the following simplifications and assumptions:
-
(1)
The virtual humans are assumed to be static without any motion;
-
(2)
The atomization and coagulation between cough liquid ligand and droplets were not modeled, and the experimental data of the droplet size distribution is assumed to be the immediate size distribution emitted from the mouth opening;
-
(3)
The study does not consider the effect of other critical factors on the airborne transmission of the SARS-CoV-2-laden droplets; and
-
(4)
The resultant inhalation, transport, and deposition of SARS-CoV-2-laden droplets, and the triggered immune system responses were not modeled and studied. Indeed,
Inspired by the limitations of this study, future work will:
-
(1)
Use large eddy simulation (LES) instead of RANS model combined with overset mesh method to model the turbulence ambient airflow fields waked by the walking motion of human (Edge, Paterson, & Settles, 2005; Settles, 2006);
-
(2)
Consider the atomization and coagulation between liquid bulk and droplets using the hybrid volume of fluid (VOF)-discrete phase model (DPM) method (Balasubramanian, Kumar, Nakod, Schütze, & Rajan, 2020; Xiao, Liu, & Liu, 2019);
-
(3)
Perform extensive parametric analysis to seek for other vital factors that can influence the airborne transmission of the SARS-CoV-2 laden droplets, e.g., droplet size distributions generated by different emission activities (e.g., sneeze (Hassani & Khorramymehr, 2019), vigorous breath, and loud speech (Asadi et al., 2019)), human heights, and emitted jet waveforms, jet spread angle variability (Gupta, Lin, & Chen, 2009), mouth opening variabilities during the emission, and environmental temperature; and
-
(4)
Integrate the human respiratory system with the virtual human body shell to simulate the resultant transport and deposition of COVID-19 virus-laden droplets in airways and the stimulated immune system responses using established multiscale models (Haghnegahdar et al., 2019; Kuga et al., 2020; Zhao et al., 2019)
The future work will be done continuously to enhance the fundamental understanding of the airborne transmission of SARS-CoV-2 for better preparations against the post-pandemic period with the high possibility of resurgence (Kissler et al., 2020).
Acknowledgment
The research was partially funded through the award for project number HR19-106, from the Oklahoma Center for the Advancement of Science and Technology (OCAST). The use of ANSYS software (ANSYS Inc., Canonsburg, PA) as part of the ANSYS-CBBL academic partnership is gratefully acknowledged. The authors are grateful for the guidance of CFD mesh generation by Mr. Dr. Shailesh Ozarkar (Lead Application Engineer, ANSYS Inc.).
References
- Allen M.D., Raabe O.G. Slip correction measurements of spherical solid aerosol particles in an improved Millikan apparatus. Aerosol Science and Technology. 1985;4(3):269–286. doi: 10.1080/02786828508959055. [DOI] [Google Scholar]
- Asadi S., Wexler A.S., Cappa C.D., Barreda S., Bouvier N.M., Ristenpart W.D. Aerosol emission and superemission during human speech increase with voice loudness. Scientific Reports. 2019;9(1):1–10. doi: 10.1038/s41598-019-38808-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balasubramanian A.K., Kumar V., Nakod P., Schütze J., Rajan A. Paper presented at the AIAA scitech 2020 forum. 2020. Multiscale modelling of a doublet injector using hybrid VOF-DPM method. [Google Scholar]
- Banko A., Coletti F., Schiavazzi D., Elkins C., Eaton J. Three-dimensional inspiratory flow in the upper and central human airways. Experiments in Fluids. 2015;56(6):117. doi: 10.1007/s00348-015-1966-y. [DOI] [Google Scholar]
- Beer T. Beaufort wind scale. Encyclopedia of Natural Hazards. 2013:42–45. [Google Scholar]
- Bourouiba L. Turbulent gas clouds and respiratory pathogen emissions: Potential implications for reducing transmission of COVID-19. JAMA. 2020;323(18):1837–1838. doi: 10.1001/jama.2020.4756. [DOI] [PubMed] [Google Scholar]
- Bourouiba L., Dehandschoewercker E., Bush J.W. Violent expiratory events: On coughing and sneezing. Journal of Fluid Mechanics. 2014;745:537–563. doi: 10.1017/jfm.2014.88. [DOI] [Google Scholar]
- Casanova L.M., Jeon S., Rutala W.A., Weber D.J., Sobsey M.D. Effects of air temperature and relative humidity on coronavirus survival on surfaces. Applied and Environmental Microbiology. 2010;76(9):2712–2717. doi: 10.1128/AEM.02291-09. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chan K., Peiris J., Lam S., Poon L., Yuen K., Seto W. The effects of temperature and relative humidity on the viability of the SARS coronavirus. Advances in virology. 2011;2011:1–7. doi: 10.1155/2011/734690. 734690, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen C., Zhao B. Some questions on dispersion of human exhaled droplets in ventilation room: Answers from numerical investigation. Indoor Air. 2010;20(2):95–111. doi: 10.1111/j.1600-0668.2009.00626.x. [DOI] [PubMed] [Google Scholar]
- Chen X., Feng Y., Zhong W., Kleinstreuer C. Numerical investigation of the interaction, transport and deposition of multicomponent droplets in a simple mouth-throat model. Journal of Aerosol Science. 2017;105:108–127. doi: 10.1016/j.jaerosci.2016.12.001. [DOI] [Google Scholar]
- Clift R., Grace J.R., Weber M.E. Courier Corporation; 2005. Bubbles, drops, and particles. [Google Scholar]
- Dietz L., Horve P.F., Coil D.A., Fretz M., Eisen J.A., Van Den Wymelenberg K. 2019 novel coronavirus (COVID-19) pandemic: Built environment considerations to reduce transmission. mSystems. 2020;5(2) doi: 10.1128/mSystems.00245-20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Doremalen N., Bushmaker T., Morris D.H., Holbrook M.G., Gamble A., Williamson B.N. Aerosol and surface stability of SARS-CoV-2 as compared with SARS-CoV-1. New England Journal of Medicine. 2020;382:1564–1567. doi: 10.1056/NEJMc2004973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drossinos Y., Stilianakis N.I. What aerosol physics tells us about airborne pathogen transmission. Aerosol Science and Technology. 2020:1–5. doi: 10.1080/02786826.2020.1751055. [DOI] [Google Scholar]
- Duguid J. The size and the duration of air-carriage of respiratory droplets and droplet-nuclei. Epidemiology and Infection. 1946;44(6):471–479. doi: 10.1017/S0022172400019288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edge B.A., Paterson E.G., Settles G.S. 2005. Computational study of the wake and contaminant transport of a walking human. [Google Scholar]
- Feng Y., Kleinstreuer C., Castro N., Rostami A. Computational transport, phase change and deposition analysis of inhaled multicomponent droplet--vapor mixtures in an idealized human upper lung model. Journal of Aerosol Science. 2016;96:96–123. doi: 10.1016/j.jaerosci.2016.03.001. [DOI] [Google Scholar]
- Feng Y., Kleinstreuer C., Rostami A. Evaporation and condensation of multicomponent electronic cigarette droplets and conventional cigarette smoke particles in an idealized G3–G6 triple bifurcating unit. Journal of Aerosol Science. 2015;80:58–74. [Google Scholar]
- Feng Y., Zhao J., Kleinstreuer C., Wang Q., Wang J., Wu D.H. An in silico inter-subject variability study of extra-thoracic morphology effects on inhaled particle transport and deposition. Journal of Aerosol Science. 2018;123:185–207. doi: 10.1016/j.jaerosci.2018.05.010. [DOI] [Google Scholar]
- Ferron G., Kreyling W., Haider B. Inhalation of salt aerosol particles—II. Growth and deposition in the human respiratory tract. Journal of Aerosol Science. 1988;19(5):611–631. doi: 10.1016/0021-8502(88)90213-3. [DOI] [Google Scholar]
- Finlay W.H. Academic press; 2001. The mechanics of inhaled pharmaceutical aerosols: An introduction. [Google Scholar]
- Gupta J., Lin C.H., Chen Q. Flow dynamics and characterization of a cough. Indoor Air. 2009;19(6):517–525. doi: 10.1111/j.1600-0668.2009.00619.x. [DOI] [PubMed] [Google Scholar]
- Gupta J.K., Lin C.H., Chen Q. Transport of expiratory droplets in an aircraft cabin. Indoor Air. 2011;21(1):3–11. doi: 10.1111/j.1600-0668.2010.00676.x. [DOI] [PubMed] [Google Scholar]
- Guzman M. 2020. Bioaerosol size effect in COVID-19 transmission. [Google Scholar]
- Haghnegahdar A., Feng Y., Chen X., Lin J. Computational analysis of deposition and translocation of inhaled nicotine and acrolein in the human body with e-cigarette puffing topographies. Aerosol Science and Technology. 2018;52(5):483–493. doi: 10.1080/02786826.2018.1447644. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haghnegahdar A., Zhao J., Feng Y. Lung aerosol dynamics of airborne influenza A virus-laden droplets and the resultant immune system responses: An in silico study. Journal of Aerosol Science. 2019;134:34–55. doi: 10.1016/j.jaerosci.2019.04.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hassani K., Khorramymehr S. In silico investigation of sneezing in a full real human upper airway using computational fluid dynamics method. Computer Methods and Programs in Biomedicine. 2019;177:203–209. doi: 10.1016/j.cmpb.2019.05.031. [DOI] [PubMed] [Google Scholar]
- He Q., Niu J., Gao N., Zhu T., Wu J. CFD study of exhaled droplet transmission between occupants under different ventilation strategies in a typical office room. Building and Environment. 2011;46(2):397–408. doi: 10.1016/j.buildenv.2010.08.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim S.W., Ramakrishnan M., Raynor P.C., Goyal S.M. Effects of humidity and other factors on the generation and sampling of a coronavirus aerosol. Aerobiologia. 2007;23(4):239–248. doi: 10.1007/s10453-007-9068-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim Y.-I., Kim S.-G., Kim S.-M., Kim E.-H., Park S.-J., Yu K.-M., Casel M.A.B. Infection and rapid transmission of SARS-CoV-2 in ferrets. Cell Host & Microbe. 2020;27(5):704–709. doi: 10.1016/j.chom.2020.03.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim J., Moin P., Moser R. Turbulence statistics in fully developed channel flow at low Reynolds number. Journal of Fluid Mechanics. 1987;177:133–166. doi: 10.1017/S0022112087000892. [DOI] [Google Scholar]
- Kim J.Y., Ko J.-H., Kim Y., Kim Y.-J., Kim J.-M., Chung Y.-S., Chin B.S. Viral load kinetics of SARS-CoV-2 infection in first two patients in Korea. Journal of Korean Medical Science. 2019;35(7) doi: 10.3346/jkms.2020.35.e86. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson G.R., Morawska L. The mechanism of breath aerosol formation. Journal of Aerosol Medicine and Pulmonary Drug Delivery. 2009;22(3):229–237. doi: 10.1089/jamp.2008.0720. [DOI] [PubMed] [Google Scholar]
- Kissler S., Tedijanto C., Goldstein E., Grad Y., Lipsitch M. 2020. Projecting the transmission dynamics of SARS-CoV-2 through the post-pandemic period. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuga K., Ito K., Chen W., Wang P., Kumagai K. A numerical investigation of the potential effects of e‐cigarette smoking on local tissue dosimetry and the deterioration of indoor air quality. Indoor Air. 2020;0:1–21. doi: 10.1111/ina.12666. [DOI] [PubMed] [Google Scholar]
- Li W., Montassier N., Hopke P. A system to measure the hygroscopicity of aerosol particles. Aerosol Science and Technology. 1992;17(1):25–35. doi: 10.1080/02786829208959557. [DOI] [Google Scholar]
- Li X., Shang Y., Yan Y., Yang L., Tu J. Modelling of evaporation of cough droplets in inhomogeneous humidity fields using the multi-component Eulerian-Lagrangian approach. Building and Environment. 2018;128:68–76. doi: 10.1016/j.buildenv.2017.11.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matida E., DeHaan W., Finlay W., Lange C. Simulation of particle deposition in an idealized mouth with different small diameter inlets. Aerosol Science & Technology. 2003;37(11):924–932. doi: 10.1080/02786820300932. [DOI] [Google Scholar]
- Menter F.R., Kuntz M., Langtry R. Ten years of industrial experience with the SST turbulence model. Turbulence, heat and mass transfer. 2003;4(1):625–632. [Google Scholar]
- Settles G.S. Fluid mechanics and homeland security. Annual Review of Fluid Mechanics. 2006;38:87–110. doi: 10.1146/annurev.fluid.38.050304.092111. [DOI] [Google Scholar]
- Van Doremalen N., Bushmaker T., Morris D., Holbrook M., Gamble A., Williamson B. Aerosol and surface stability of SARS-CoV-2 as compared with SARS-CoV-1. New England Journal of Medicine. 2020;382:1564–1567. doi: 10.1056/NEJMc2004973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J., Du G. COVID-19 may transmit through aerosol. Irish Journal of Medical Science. 2020:1–2. doi: 10.1007/s11845-020-02218-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y., James P. Assessment of an eddy-interaction model and its refinements using predictions of droplet deposition in a wave-plate demister. Chemical Engineering Research and Design. 1999;77(8):692–698. doi: 10.1205/026387699526827. [DOI] [Google Scholar]
- Xiao Y., Liu W., Liu D. Paper presented at the 2019 2nd world conference on mechanical engineering and intelligent manufacturing (WCMEIM) 2019. Simulation of liquid atomization in cyclone atomizer based on VOF-DPM coupling model. [Google Scholar]
- Yang S., Lee G.W., Chen C.-M., Wu C.-C., Yu K.-P. The size and concentration of droplets generated by coughing in human subjects. Journal of Aerosol Medicine. 2007;20(4):484–494. doi: 10.1089/jam.2007.0610. [DOI] [PubMed] [Google Scholar]
- Yang Y.K., Kang I.S., Hwang J.H., Park J.C. CFD simulation for air-borne infection analysis in AII-room. International Journal of Mechanical & Mechatronics Engineering. 2017;11(5):1047–1052. [Google Scholar]
- Yan Y., Li X., Tu J. Thermal effect of human body on cough droplets evaporation and dispersion in an enclosed space. Building and Environment. 2019;148:96–106. doi: 10.1016/j.buildenv.2018.10.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang L., Li X., Yan Y., Tu J. Effects of cough-jet on airflow and contaminant transport in an airliner cabin section. The Journal of Computational Multiphase Flows. 2018;10(2):72–82. doi: 10.1177/1757482X17746920. [DOI] [Google Scholar]
- Xie X., Li Y., Sun H., Liu L. Exhaled droplets due to talking and coughing. Journal of The Royal Society Interface. 2009;6(suppl_6):S703–S714. doi: 10.1098/rsif.2009.0388.focus. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang H., Penninger J.M., Li Y., Zhong N., Slutsky A.S. Angiotensin-converting enzyme 2 (ACE2) as a SARS-CoV-2 receptor: Molecular mechanisms and potential therapeutic target. Intensive Care Medicine. 2020:1–5. doi: 10.1007/s00134-020-05985-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang L., Li Y. Dispersion of coughed droplets in a fully-occupied high-speed rail cabin. Building and Environment. 2012;47:58–66. doi: 10.1016/j.buildenv.2011.03.015. [DOI] [Google Scholar]
- Zhang X., Li H., Shen S., Cai M. Investigation of the flow-field in the upper respiratory system when wearing N95 filtering facepiece respirator. Journal of Occupational and Environmental Hygiene. 2016;13(5):372–382. doi: 10.1080/15459624.2015.1116697. [DOI] [PubMed] [Google Scholar]
- Zhang Z., Kleinstreuer C., Hyun S. Size-change and deposition of conventional and composite cigarette smoke particles during inhalation in a subject-specific airway model. Journal of Aerosol Science. 2012;46:34–52. doi: 10.1016/j.jaerosci.2011.12.002. [DOI] [Google Scholar]
- Zhao J., Feng Y., Bezerra M., Wang J., Sperry T. Numerical simulation of welding fume lung dosimetry. Journal of Aerosol Science. 2019;135:113–119. doi: 10.1016/j.jaerosci.2019.05.006. [DOI] [Google Scholar]
- Zhu S., Kato S., Yang J.-H. Study on transport characteristics of saliva droplets produced by coughing in a calm indoor environment. Building and Environment. 2006;41(12):1691–1702. doi: 10.1016/j.buildenv.2005.06.024. [DOI] [Google Scholar]