Abstract
We investigated the global structure of intrinsic cross-frequency dynamics by systematically examining power-based temporal associations among a broad range of oscillation frequencies both within and across EEG-based current sources (sites). We focused on power-based associations that could reveal unique timescale dependence independently of interacting frequencies. Large spectral-power fluctuations across all sites occurred at two characteristic timescales, sub-second and seconds, yielding distinct patterns of cross-frequency associations. On the fast sub-second timescale, within-site (local) associations were consistently between pairs of β—γ frequencies differing by a constant Δf (particularly Δf ~ 10 Hz at posterior sites and Δf ~ 16 Hz at lateral sites) suggesting that higher-frequency oscillations are organized into Δf amplitude-modulated packets, whereas cross-site (long-distance) associations were all within-frequency (particularly in the >30 Hz and 6–12 Hz ranges, suggestive of feedforward and feedback interactions). On the slower seconds timescale, within-site (local) associations were characterized by a broad range of frequencies selectively associated with ~10 Hz at posterior sites and associations among higher (>20 Hz) frequencies at lateral sites, whereas cross-site (long-distance) associations were characterized by a broad range of frequencies at posterior sites selectively associated with ~10 Hz at other sites, associations among higher (>20 Hz) frequencies among lateral and anterior sites, and prevalent associations at ~10 Hz. Regardless of timescale, within-site (local) cross-frequency associations were weak at anterior sites indicative of frequency-specific operations. Overall, these results suggest that the fast sub-second-timescale coordination of spectral power is limited to local amplitude modulation and insulated within-frequency long-distance interactions (likely feedforward and feedback interactions), while characteristic patterns of cross-frequency interactions emerge on the slower seconds timescale. The results also suggest that the occipital α oscillations play a role in organizing higher-frequency oscillations into ~10 Hz amplitude-modulated packets to communicate with other regions. Functional implications of these timescale-dependent cross-frequency associations await future investigations.
Introduction
Because oscillatory dynamics are prevalent in the brain (e.g., [1]), many EEG, MEG, and Electrocorticography (ECoG) studies have examined the roles of oscillatory neural activity in perception (e.g., [2–5]), attention (e.g., [6–9]), memory (e.g., [10]), cognition (e.g., [11–14]), and the general control of neural communications (e.g., [15]). Some studies examined the dynamics of oscillatory activity while people rested with their eyes closed to identify intrinsic spatial networks of oscillatory activity (e.g., [16–19]) that may correlate with individual differences (e.g., [20]) or neural dysfunctions (e.g., [21–23]). The strategies used by most prior studies were to examine phase-phase, power-power, and/or phase-amplitude associations within specific frequency bands or specific combinations of frequency bands to identify spatial networks mediated by those bands.
The goal of the current study was complementary in that instead of identifying spatial networks based on associations within specific frequency bands, we examined the global distribution of cross-frequency associations, focusing on both local characteristics reflected in cross-frequency associations within individual EEG-derived current sources (which we call sites here) and long-distance characteristics reflected in cross-frequency associations between sites. Importantly, we observed that spectral power universally (across oscillation frequencies and sites) fluctuated on two distinct timescales, sub-second and seconds. Because these fast and slow fluctuations are mathematically orthogonal (see below), distinct cross-frequency mechanisms may operate on these timescales, potentially yielding timescale-dependent patterns of cross-frequency associations at local and long-distance levels. We thus examined power-power associations that can independently transpire on different timescales; that is, slow cross-frequency co-variations in spectral power may occur irrespective of the presence of fast co-variations, and vice versa. In contrast, the timescale of a phase-phase or phase-amplitude coupling is constrained by the interacting oscillation frequencies. Analyses of spectral-power associations (though less temporally precise than analyses of phase coupling) provide additional advantages for characterizing the overarching structure of cross-frequency interactions.
First, spatial patterns of spectral-power associations may reveal the distribution of particularly consequential cross-frequency interactions because adjusting phase coupling would likely have more impact for coordinating interactions between oscillatory activities that are concurrently elevated in power, thereby influencing larger neural populations (because larger spectral power implies larger synchronously oscillating populations). Power-based associations may also reveal interactions that are phase insensitive; for example, synchronized oscillatory output from one population may excite another population into generating oscillatory activity at a different frequency. Second, analyses of spectral-power associations may reveal the global distribution of phase-amplitude couplings. Specifically, consistent covariations of power between pairs of oscillation frequencies differing by a constant Δf at a given current source imply the presence of beating at Δf, that is, the presence of oscillation at the pair-average frequency, Hz, being amplitude-modulated at ΔfHz. This in turn implies phase-amplitude coupling because the periodic ΔfHz modulation of the amplitude (power) of a Hz oscillation is likely mediated by its interaction with the phase of a ΔfHz oscillation.
To facilitate straightforward interpretations of our results, we applied only minimal and necessary data transformations: (1) taking the temporal derivative of EEG to reduce the non-oscillatory background spectra, (2) applying the surface-Laplacian transform to localize neural sources in a purely data-driven manner and to reduce volume conduction and electrode-referencing effects, and (3) applying Morlet-wavelet convolution to extract spectral power as a function of time.
Overall, the results have revealed surprisingly simple local and long-distance patterns of intrinsic spectral-power associations characterized by oblique (parallel to diagonal), diagonal, and columnar patterns depending on timescale (sub-second or seconds), region (posterior, central, lateral, vs. anterior) and spatial scale (within vs. across EEG-derived current sources). These patterns of spectral-power associations provide a reference for understanding how intrinsic cross-frequency dynamics adjust to behavioral demands and sensory dynamics. Further, while recent studies have demonstrated the relevance of α rhythm in visual perception and its association with occipital α oscillations, the current results suggest that the occipital α oscillations play a role in organizing higher-frequency oscillations into ~10 Hz amplitude-modulated packets to communicate with other areas.
Materials and methods
Participants
Twenty-four Northwestern University students (15 women, 1 non-binary; ages 18 to 24 years, M = 21.25, SD = 1.57) gave informed written consent to participate for monetary compensation ($10/hr). All were right-handed, had normal hearing and normal or corrected-to-normal vision, and no history of concussion. They were tested individually in a dimly lit room. The study protocol (including the consent procedure) was approved by the Northwestern University Institutional Review Board.
EEG recording and pre-processing
While participants engaged in spontaneous thought with their eyes closed for approximately 5 minutes, EEG signals were recorded from 60 scalp electrodes (although we used a 64-electrode montage, we excluded EEG signals from noise-prone electrodes, Fpz, Iz, T9, and T10 from analyses) at a sampling rate of 512 Hz using a BioSemi ActiveTwo system (see www.biosemi.com for details). Two additional electrodes were placed on the left and right mastoid area. The EEG data were preprocessed using EEGLAB and ERPLAB toolboxes for MATLAB [24,25]. The data were re-referenced offline to the average of the two mastoid electrodes, bandpass-filtered at 0.01 Hz-80 Hz, and notch-filtered at 60 Hz (to remove power-line noise that affected the EEG data from some participants). To reduce any effects of volume conduction and reference electrode choices, as well as to facilitate data-driven EEG current source discrimination, we applied the surface-Laplacian transform to all EEG data (e.g., [26–28]) using the Perrin and colleagues’ method (e.g., [29–31]) with a typical set of parameter values (e.g., [32]).
EEG analysis
The use of EEG temporal derivative
We refer to the surface-Laplacian transformed EEG signals simply as EEG signals. In all figures, whenever units are not shown, they are arbitrary (a.u.), and the shaded regions indicate ±1 standard error of the mean. An example 1 s EEG waveform at a central site FCz from one participant is shown in Fig 1A (black curve). The waveform reflects the synchronized electrical activity from a large neural population that generates a distinct current source at FCz. The mean spectral-amplitude profile (i.e., fast Fourier transform, FFT) computed on 59 consecutive 5 s waveforms for the same participant is shown in Fig 1B (black curve; the shaded region represents ±1 standard error of the mean). The general linear decrease in the spectral amplitude for higher frequencies with a slope of approximately 1 (in log-log scale) reflects the 1/Δf background profile largely explained by the neuronal Ornstein-Uhlenbeck process that exhibits a random-walk type behavior (e.g., [33,34]; see [35] for a review of the various factors that contribute to the 1/fβ background). The spectral “bumps” seen around 10 Hz, 20 Hz, and 30 Hz indicate the characteristic bands of oscillation frequencies that the neural population reflected at this site for this person may utilize for neural communication and/or information processing. Taking the temporal derivative of EEG (, where Δt is the temporal resolution, i.e., 1/512 s; see black curve in Fig 1C) largely removes the 1/Δf background (due to trigonometric properties) to highlight the oscillation bumps (see black curve in Fig 1D). While Fig 1D shows an example at one site from one participant, we confirmed that the background spectral-amplitude profiles were generally flattened after taking the temporal derivative. Because we wished to investigate the dynamics of oscillatory activity (over and above the general 1/fβ background), we used the EEG temporal derivative, which we call EEGd.
Fig 1. The use of the temporal derivative of EEG, EEGd, and DCT-phase-scrambled controls for examining intrinsic cross-frequency spectral-power associations.
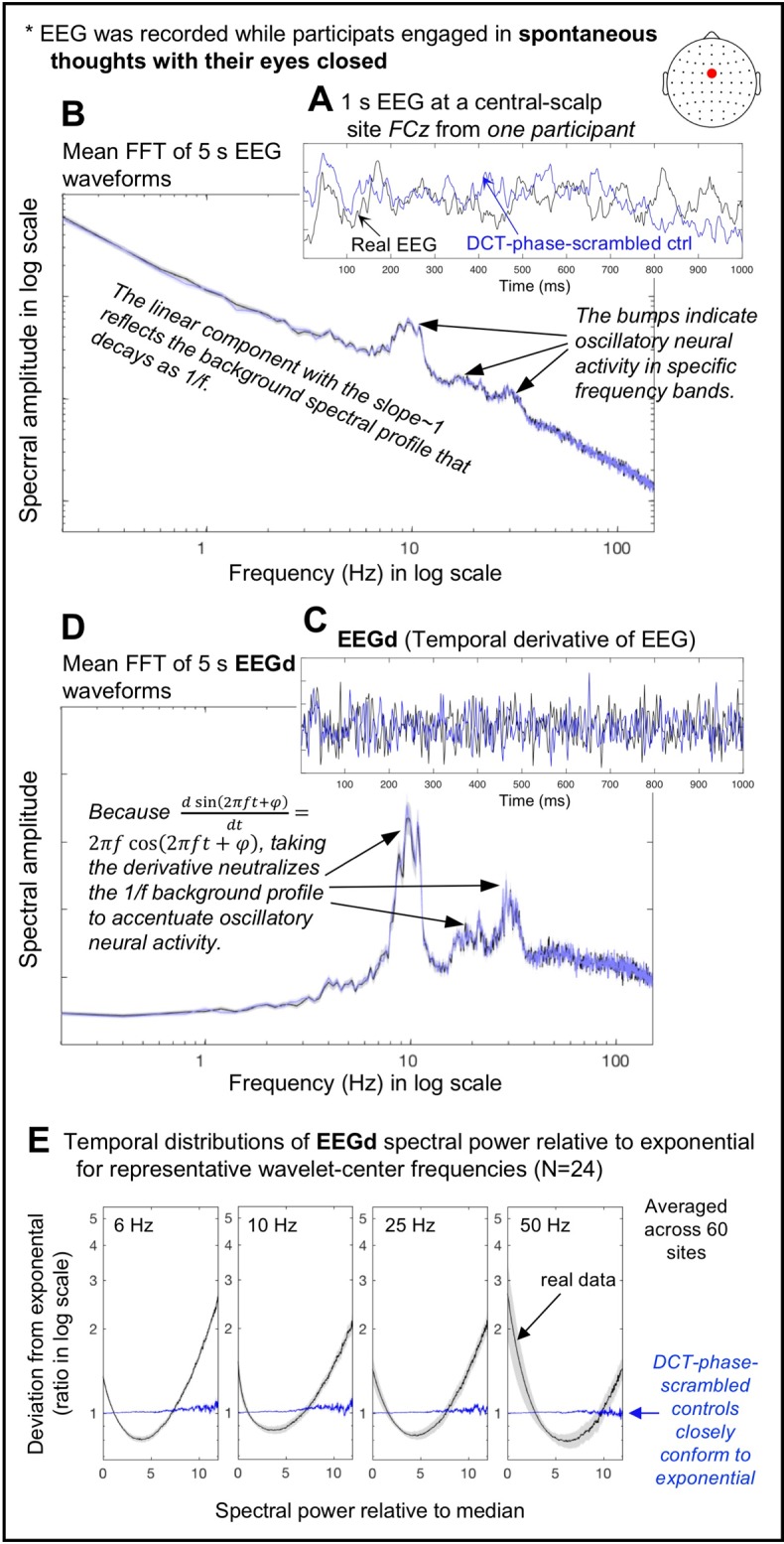
A. An example of a 1 s EEG waveform (black) and its DCT-phase-scrambled control (blue) at FCz from one participant. B. Mean fast Fourier transforms (FFTs) computed on the fifty-nine 5 s waveforms (same site and participant) for the real EEG (black) and its DCT-phase-scrambled control (blue) plotted in a log-log format. C. The temporal derivatives, which we call EEGd, of the example EEG waveform (black) and its DCT-phase-scrambled control (blue) shown in A. D. Mean FFTs computed on the fifty-nine 5 s waveforms (same site and participant) for the real EEGd (black) and its DCT-phase-scrambled control (blue) plotted in a semi-log format. For B and D, the shaded regions represent ±1 standard error of the mean based on the FFTs computed on multiple 5 s waveforms. E. Temporal distributions of EEGd spectral power for representative wavelet-center frequencies (6, 10, 25, and 50 Hz) for the real data (black) and their DCT-phase-scrambled controls (blue), plotted as deviations from exponential fits to the DCT-phase-scrambled controls (averaged across all sites). The deviations are shown as ratios in log scale, and spectral power (x-axis) has been normalized to the median (per frequency per site per participant). The shaded regions represent ±1 standard error of the mean with participants as the random effect. Note that the DCT-phase-scrambled data provide suitable stochastic controls because their exponential spectral-power distributions imply a Poisson point process.
Computing spectral power as a function of time
The spectral-amplitude profiles shown in Fig 1B and 1D are time-averaged (standard fast Fourier transforms). As we wished to understand how the brain dynamically coordinates oscillatory activity, we used a Morlet wavelet-convolution method (e.g., [32]) to extract spectral amplitudes as a function of time to investigate how spectral power (amplitude squared) fluctuated over time. Specifically, each EEGd waveform was decomposed into a time series of spectral power using 200 Morlet wavelets with their center frequencies, fc’s, and factor n’s (roughly the number of cycles per wavelet, which is related to the temporal standard deviation of the wavelet by, ), both logarithmically spaced (because neural temporal-frequency tunings tend to be approximately logarithmically scaled; e.g., [36,37]). The fc’s spanned the range of 3 Hz to 60 Hz and the n’s spanned the range of 3 to 16, resulting in the temporal resolutions of SD = 159 ms (at 3 Hz) to SD = 42 ms (at 60 Hz) and spectral resolutions of FWHM (full width at half maximum) = 2.36 Hz (at 3 Hz) to FWHM = 8.83 Hz (at 60 Hz). These values struck a good balance for the temporal/spectral-resolution trade-off, and are typically used in the literature (e.g., [32]).
Generating phase-scrambled controls
To remove spurious cross-frequency associations between proximate fc’s due to partial spectral overlaps of Morlet wavelets, we generated phase-scrambled controls whose spectral power fluctuated stochastically (i.e., unpredictably in a memory free manner) while their time-averaged spectral-amplitude profiles matched those of the real data. While phase-scrambling can be performed using several different methods, we chose discrete cosine transform, DCT (e.g., [38]). In short, we transformed each 5 min EEG waveform with type-2 DCT, randomly shuffled the signs of the coefficients, and then inverse-transformed it with type-3 DCT, which yielded a phase-scrambled version. DCT phase-scrambling is similar to DFT (discrete Fourier transform) phase scrambling except that it is less susceptible to edge effects. We verified that DCT phase-scrambling yielded a desired outcome, generating waveforms whose spectral-power fluctuations conformed to exponential distributions (Fig 1E) indicative of a Poisson point process (i.e., a stochastic process), with virtually no distortions to the time-averaged spectral-amplitude profiles of EEG or EEGd (e.g., the blue and black curves overlap in Fig 1B and 1D). In passing, it is noteworthy that the distributions of spectral-power fluctuations of the real data deviated from exponential in a U-shaped manner with disproportionately frequent occurrences of near-zero and high values (Fig 1E), indicative of intermittent bursts (relative to stochastic variations).
We used EEGd from 60 sites in conjunction with their DCT-phase-scrambled controls to extract intrinsic spectral-power associations over and above any artifact due to partial wavelet overlaps. Because of the 5 min length of the data (containing 153,600 time points at the 512 Hz sampling rate), 200 wavelet-center frequencies, and 60 sites per participant, even one set of phase-scrambled data would be unlikely to generate accidental patterns of spectral-power associations. We verified that the control patterns of spectral-power associations generated with different versions of phase-scrambled data (using different random seeds) were virtually indistinguishable, especially when two or more control patterns were averaged. To be conservative, we generated four versions of phase-scrambled data to compute four sets of control spectral-power associations (per site per participant), and used their averages as the controls (see below). We are thus reasonably certain that the control patterns accurately captured the spurious associations due to partial wavelet overlap.
Computing spectral-power associations
For assessing power-based cross-frequency coupling, we chose not to use a conventional correlation measure. One reason is that the stochastic distribution of EEGd spectral power is not normal but exponential (Fig 1E). The other reason is that it is difficult to remove artifacts due to wavelet overlap in the frequency domain using a conventional correlation measure (see below). Instead, we computed top-bottom-percentile based temporal associations. This method has advantages including (1) not being susceptible to outliers and (2) the straightforwardness of the computed association values that directly indicate the log power modulation in frequency Y that is temporally associated with statistically large power variations in frequency X. We computed spectral-power associations at individual scalp-based current sources—within-site associations—as well as between pairs of current sources—cross-site associations.
Within-site (local) spectral-power associations
To evaluate a within-site spectral-power association from a probe frequency, fprobe, to a test frequency, ftest, we first identified the time points corresponding to the top and bottom 15% in the fprobe power time-series. This criterion was reasonable for an approximate exponential distribution (Fig 1E), capturing a good proportion (accounting for approximately 70% of the total variability in the sum of squares) of statistically large variations. The ftest power was averaged separately over the time points corresponding to the top-15% and bottom-15% for the fprobe power time-series, and the strength of fprobe-to-ftest spectral-power association was computed as the natural-log (Ln) ratio of these averages (thus normalizing for absolute power). Thus, a larger positive association value indicates that the top/bottom-15% variation in the probe-frequency power was associated with greater same-signed co-variation in the test-frequency power in Ln-ratio (analogous to positive correlation, indicating that the test-frequency power was higher when the probe-frequency power was in the top 15% than when it was in the bottom 15%). A larger negative association value indicates that the top/bottom-15% variation in the probe-frequency power was associated with greater opposite-signed co-variation in the test-frequency power in Ln-ratio (analogous to negative correlation, indicating that the test frequency power was lower when the probe-frequency power was in the top 15% than when it was in the bottom 15%). Association values near zero indicate the lack of consistent association (i.e., the top/bottom-15% power in the probe frequency tended to be equivalently coincident with higher or lower test-frequency power). In this way, we computed the strengths of probe-frequency-to-test-frequency spectral-power associations for all combinations of wavelet-center frequencies to generate a 2-dimensional, 200-probe-frequency-(y-axis)-by-200-test-frequency-(x-axis), association matrix per site per participant and averaged across participants. A cross-frequency association matrix computed in this way need not be symmetric about the diagonal. That is, X-Hz power modulation coincident with the top/bottom-15% Y-Hz power variation may be stronger or weaker than the Y-Hz power modulation coincident with the top/bottom-15% X-Hz power variation.
As mentioned above, because the wavelets used to extract spectral-power values had non-negligible spectral widths, proximate frequencies would appear to be associated due to partial wavelet overlap. This artifact would generate spurious positive associations near the diagonal (with the diagonal representing the Ln-ratio of the top-15% to bottom-15% power for each frequency). To remove this artifact, spectral-power associations were computed in the same way with the corresponding DCT-phase-scrambled data. To reliably estimate the artifact, we generated control associations by averaging four association matrices computed using four different versions of phase-scrambled data (see above). We removed spurious associations due to partial wavelet overlap by taking the difference (in Ln-ratio) between the real and control associations (note that removing this artifact would not be as straightforward using a conventional correlation measure). This procedure also made the diagonal meaningful because values along the diagonal indicate the magnitudes of the top/bottom-15% variations in the real data relative to those expected by stochastic variation.
Cross-site (long-distance) spectral-power associations
Cross-site spectral-power associations were similarly computed. For example, to evaluate the spectral-power association from a probe frequency at site S1, S1-fprobe, to a test frequency at site S2, S2-ftest, we identified the time points corresponding to the top and bottom 15% in the S1-fprobe power time-series. Then, the S2-ftest power was averaged separately over the time points corresponding to the top-15% and bottom-15% for the S1-fprobe power, and the strength of S1-fprobe-to-S2-ftest spectral-power association was computed as the Ln-ratio of these averages. A larger positive association value indicates that the top/bottom-15% variation in the probe frequency power at S1 was associated with greater same-signed co-variation in the test-frequency power at S2 in Ln-ratio (analogous to positive correlation, indicating that the test-frequency power at S2 was higher when the probe-frequency power at S1 was in the top 15% than when it was in the bottom 15%). A larger negative association value indicates that the top/bottom-15% variation in the probe-frequency power at S1 was associated with greater opposite-signed co-variation in the test-frequency power at S2 in Ln-ratio (analogous to negative correlation, indicating that the test frequency power at S2 was lower when the probe-frequency power at S1 was in the top 15% than when it was in the bottom 15%). Association values near zero indicate the lack of consistent association (i.e., the top/bottom-15% power in the probe frequency at S1 tended to be equivalently coincident with higher or lower test-frequency power at S2). In this way, we computed the strengths of S1-probe-frequency-to-S2-test-frequency spectral-power associations for all combinations of S1 and S2 wavelet-center frequencies to generate a 2-dimensional, 200-S1-probe-frequency-(y-axis)-by-200-S2-test-frequency (x-axis), association matrix per site-pair per participant and averaged across participants. Note that the diagonal indicates cross-site within-frequency spectral-power associations. The use of DCT-phase-scrambled controls was unnecessary in this case because partial wavelet overlap would not generate any spurious associations between data from separate sites.
The within-site and cross-site spectral-power associations were computed for the sub-second timescale (within a 500 ms interval) and the seconds timescale (across 500 ms intervals). The justification for examining spectral-power associations on these specific timescales is provided in the results section (see 1. Spectral power intrinsically fluctuates on two distinct timescales). Each 5 min EEG recording was divided into six-hundred 500 ms intervals. The sub-second timescale spectral-power associations were computed at a 512 Hz temporal resolution within each 500 ms interval and averaged across all intervals (per site or site-pair per participant). The seconds timescale associations were computed at a 500 ms resolution (with the data temporally averaged within each 500 ms interval) across the entire 5 min period (using each 500 ms interval as time unit). Thus, the sub-second-timescale and seconds-timescale spectral-power associations were mathematically independent.
Results and discussion
Spectral power intrinsically fluctuates on two distinct timescales
Half a second is a landmark timescale in that consciously accessible perceptual representations are thought to form through feedforward and feedback interactions within this timescale (e.g., [5,39,40]), and typical motor behavior such as spontaneous tapping, walking, and natural saccades have periodicities in this timescale (e.g., [41–43]). It is thus feasible that distinct neural interactions may transpire on (1) the within-500-ms timescale—potentially contributing to generating the basic building blocks of perceptual and motor processing—and (2) the across-500-ms timescale—potentially contributing to chaining these building blocks into cognition and action. Consistent with this reasoning, our data suggest that spectral power intrinsically fluctuates on these timescales.
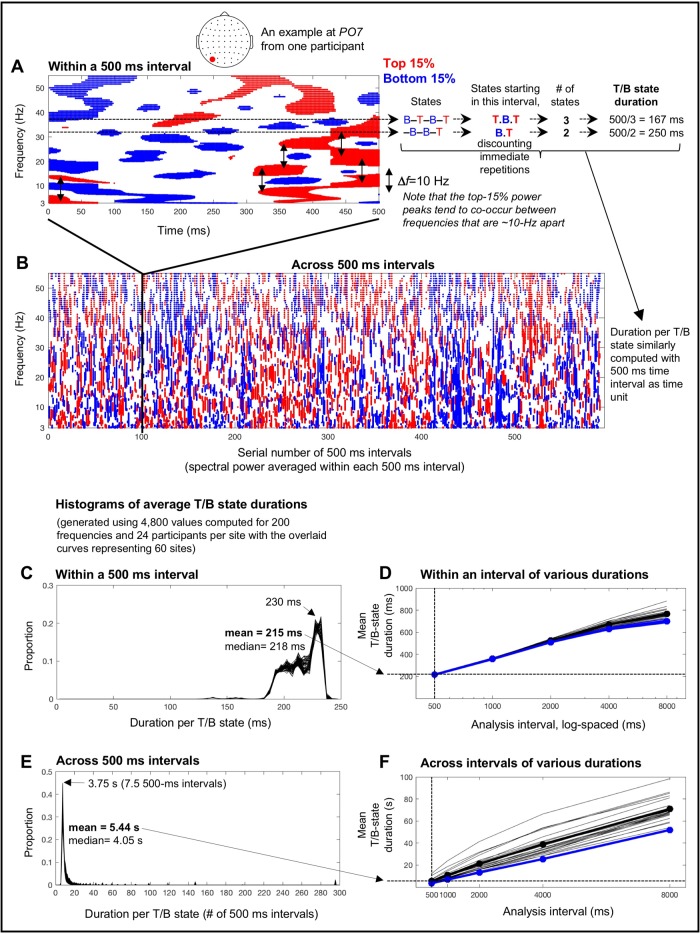
Spectral-power fluctuations during a 500 ms interval from a posterior site, PO7, from one participant is shown in Fig 2A. As we focused on large (±15th percentile) variations (see the Methods section), the top-15% power is indicated in red, the bottom-15% power is indicated in blue, and intermediate power is shown as blank. This example clearly shows that spectral power goes through about 1–2 (red-blue) cycles per frequency within 500 ms. To confirm this observation across all 500 ms intervals for all sites and participants, we quantified the average duration of a top/bottom state (per 500 ms interval) as follows. For each frequency (i.e., for each wavelet-center frequency, fc), we identified the state sequence; in the upper example shown in Fig 2A, the sequence is, bottom-15% → in-between → top-15% → in-between → bottom-15% → in-between → top-15%, or [B–T–B–T] where “–” indicates “in-between.” We binarized the T/B states by ignoring the in-between states, and only counted states that began within the 500 ms interval of interest (to avoid redundant counting of states across 500 ms intervals). Thus, this example included 3 states, T, B and T, so that the estimated average duration of a T/B state for this frequency would be 500 ms/3 = 167 ms (Fig 2A). When the same (T or B) state recurred across an in-between state, we considered them to be a single state. In the lower example shown in Fig 2A, the identified sequence is, [–B–B–T], but the number of states would be 2, that is, a B followed by a T (combining the two B’s across the in-between state), so that the estimated average duration of a T/B state for this frequency would be 500 ms/2 = 250 ms (Fig 2A). We computed the average T/B-state duration in this way for each of the six-hundred 500 ms intervals (over the 5 min EEG recording period) and averaged them across the 600 intervals per frequency per participant per site. We then generated a histogram of the average within-500-ms-interval T/B-state durations per site using the 4,800 values computed for the 200 frequencies and 24 participants; the histograms for the 60 sites are overlaid in Fig 2C. It is clear that the distributions of the average T/B-state durations were globally similar (i.e., similar across all 60 sites) and tightly peaked at ~230 ms with a negative tail that pulled the mean down to ~215 ms. This indicates that a 500 ms interval consistently contained a little over one cycle of substantial power fluctuation, confirming that 500 ms may provide an appropriate sub-second timescale to examine fast power fluctuations whose low/high states last ~230 ms.
Fig 2. Intrinsic spectral-power variations on the characteristic sub-second (~230 ms) and seconds (~3.75 s) timescales.
A. An example of the top-15% (red) and bottom-15% (blue) spectral-power variations within a 500 ms interval (taken from a 5 min EEG recording; see B) at a posterior site, PO7, from one participant. Note that spectral power tends to peak in pairs of frequencies that are ~10 Hz apart (the vertical arrows indicating Δf~ 10 Hz). The average duration of the top and bottom states was estimated per frequency by identifying the state sequence (“B” for bottom, “T” for top, and “–” for in-between states in the illustration), counting the top and bottom states that started within the interval while discounting immediate repetitions, and dividing the interval duration (500 ms in this case) by the number of T/B states. Two examples are shown for two different frequencies (see text for details). The average T/B-state duration computed for each of the six-hundred 500 ms intervals over the 5 min EEG recording period were averaged per frequency per participant per site. B. An example of the top-15% (red) and bottom-15% (blue) power variations occurring across 500 ms intervals (spectral power averaged within each 500 ms interval) over the 5 min period. The average duration of the top and bottom states was estimated in the same way as for the 500 ms interval (see A) but using 500 ms intervals as time unit. C. Histograms of average within-500-ms-interval T/B-state durations (averaged across 600 intervals) based on the 4,800 values computed for 200 wavelet-center frequencies and 24 participants per site; histograms from the 60 sites are overlaid. The mode of ~230 ms with the mean of ~215 ms indicate that each brief high/low-power state typically lasted about a quarter of a second. D. Mean within-interval T/B-state durations similarly computed using different analysis intervals, 1000, 2000, 4000, and 8000 ms in addition to 500 ms, for both the real (black) and phase-scrambled (blue) data (the thin lines showing individual participants’ data). The mean within-interval T/B-state duration approximately logarithmically increased with the length of analysis intervals. Note that the real and phase-scrambled curves virtually overlap, indicating that within-interval T/B-state durations depend primarily on spectral-amplitude compositions regardless of phase relations. Also note that individual differences are negligible for within-interval T/B-state durations computed with short (< 1000 ms) analysis intervals. E. Histograms of average across-500-ms-interval T/B-state durations based on the 4,800 values computed for 200 wavelet-center frequencies and 24 participants per site; histograms from the 60 sites are overlaid. The mode of ~3.75 s and the mean of 5.44 s indicate that each longer high/low-power state typically lasted several seconds. F. Mean across-interval T/B-state durations similarly computed using different analysis intervals (1000, 2000, 4000, and 8000 ms in addition to 500 ms) for both the real (black) and phase-scrambled (blue) data (the thin lines showing individual participants’ data). The mean across-interval T/B-state duration approximately linearly increased with the length of analysis intervals. Note that the real and phase-scrambled curves nearly overlap for the 500 ms interval, indicating that T/B-state durations measured across 500 ms intervals primarily depend on spectral-amplitude compositions regardless of phase relations. Also note that individual differences are small for across-interval T/B-state durations computed with short (< 1000 ms) analysis intervals. We chose 500 ms as the analysis interval because it revealed the sub-second (within-interval) and seconds (across-interval) timescales of spectral-power fluctuations (1) that were relatively stable, depending on spectral-amplitude compositions regardless of phase relations, (2) that were highly consistent across participants, and (3) that appeared to support maximally distinct patterns of fast and slow spectral-power associations (see text for details).
An equivalent analysis was conducted for spectral-power fluctuations across 500 ms intervals over the 5 min period with the spectral power averaged within each 500 ms interval. The spectral-power-fluctuation data at PO7 from the same participant is shown in Fig 2B with the time axis indicating the serial number of 500 ms intervals. This example clearly shows that the spectral power fluctuated between the top-15% (red) and bottom-15% (blue) states at a relatively stable rate. We computed the average T/B-state duration by dividing the entire duration (six-hundred 500-ms intervals) by the number of T/B states (counted in the same way as above) per frequency per participant per site. We generated a histogram of the average T/B-state durations per site using the 4,800 values computed for the 200 frequencies and 24 participants, and overlaid the histograms for the 60 sites (Fig 2D). It is clear that the distributions of the average T/B-state durations across 500 ms intervals were globally similar (i.e., similar across all 60 sites) and tightly peaked at about seven-and-a-half 500-ms intervals or ~3.75 s with a positive tail that pushed the mean up to ~5.44 s. Thus, slower spectral-power fluctuations occurred on the timescale of several seconds.
Note that temporal estimates of the fast and slow fluctuations depend on the choice of the analysis interval. We chose 500 ms partly because it is a “landmark” timescale for human perception, cognition, and action (see above). The use of 500 ms analysis intervals also facilitated the goal of identifying distinctly timescale-dependent spectral-power associations.
Spectral-power fluctuations include both fast and slow components as shown in Fig 2A and 2B. Thus, estimates of within-interval T/B-state durations would necessarily increase with the use of longer analysis intervals because slower fluctuations would be included in the estimates. Indeed, the mean within-interval T/B-state duration approximately logarithmically increased with the length of analysis intervals (Fig 2D). The mean across-interval T/B state duration increased approximately linearly with the length of analysis intervals (Fig 2F). This is not surprising because we used non-overlapping intervals so that the within- and across-interval analyses of spectral-power dynamics were mathematically independent. The use of non-overlapping intervals made the temporal resolution for measuring across-interval power fluctuations inversely related to the length of the analysis interval.
Interestingly, both the within- and across-interval T/B-state durations were similar for the real (black curves) and phase-scrambled (blue curves) data for short (< 1000 ms) analysis intervals (Fig 2D and 2F), suggesting that the fast and slow spectral-power fluctuations revealed with short (< 1000 ms) analysis intervals primarily depend on spectral-amplitude compositions regardless of phase relations. It is also noteworthy that inter-participant variability was low (thin lines in Fig 2D and 2F) for both the fast (within-interval) and slow (across-interval) T/B-state durations obtained with short (< 1000 ms) analysis intervals, especially for those obtained with 500 ms intervals.
As shown below, the use of 500 ms analysis intervals revealed robust patterns of fast (within-interval) spectral-power associations. For the purpose of characterizing the timescale dependence of spectral-power associations, the use of the shortest analysis interval that generates distinct patterns of spectral-power associations would be advantageous for characterizing spectral-power associations on the fastest timescale because the use of longer intervals would intermix slower associations. For characterizing distinct spectral-power associations operating on the slower (across-interval) timescale that are mathematically independent of the fast (within-interval) associations, the use of 500 ms analysis intervals (relative to the use of longer analysis intervals) would also be most effective by providing the highest temporal resolution for characterizing the slow across-interval dynamics. We verified this line of reasoning as follows.
We computed both within-interval and across-interval spectral-power associations for representative sites (for examining within-site spectral-power associations) and for representative site-pairs (for examining cross-site spectral-power associations), using 500, 1000, 2000, 4000, and 8000 ms analysis intervals. As shown below, the use of 500 ms analysis intervals revealed distinct patterns of fast (within-interval) and slow (across-interval) spectral power associations. Within-interval spectral-power associations computed with longer analysis intervals became progressively similar to the across-interval associations computed with a 500 ms analysis interval, confirming that the use of longer analysis intervals results in intermixing fast and slow associations. Across-interval spectral-power associations computed with longer analysis intervals largely maintained the patterns obtained with 500 ms analysis intervals except that the association magnitudes became weaker, confirming that the characteristic slow (across-interval) spectral-power associations are most effectively revealed with 500 ms analysis intervals (relative to longer analysis intervals).
In summary, the analyses presented in Fig 2 and the above observations suggest that the use of 500 ms analysis intervals reveals mathematically independent spectral-power dynamics on the sub-second (with high/low-power states typically lasting ~230 ms) and seconds (with high/low-power states typically lasting ~3.75 s) timescales with the following advantages: (1) these sub-second and seconds timescales are relatively stable, depending primarily on spectral-amplitude compositions regardless of phase relations, (2) they are highly consistent across participants, and most significantly (3) they appear to support maximally distinct patterns of spectral-power associations.
Within-site (local) spectral-power associations on the (fast) sub-second timescale
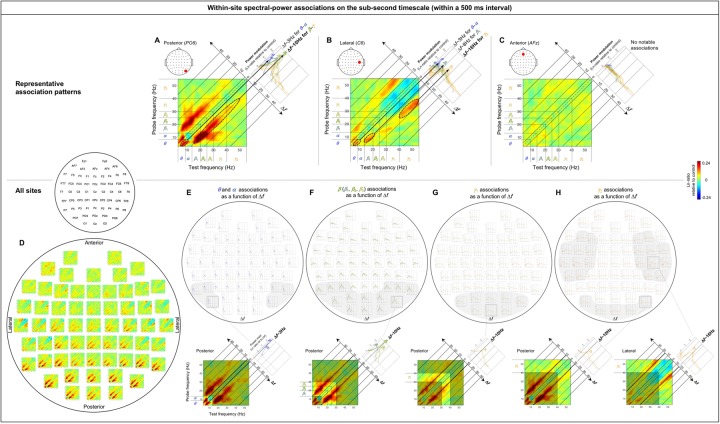
The within-site spectral-power associations (in Ln-ratio relative to the phase-scrambled controls; see Materials and Methods/EEG analysis/Computing spectral-power associations) on the sub-second timescale (within a 500 ms interval) are marked by strong associations along the 45° lines parallel to the diagonal (see the 2D cross-frequency association plots in Fig 3A, 3B and 3D). This indicates that the associations are characterized by specific frequency differences, particularly, Δf~ 3 Hz, Δf~ 10 Hz, and Δf~ 16 Hz. The representative association patterns are shown in Fig 3A–3C. Posterior, lateral, and anterior sites yielded distinct patterns.
Fig 3. Within-site spectral-power associations on the sub-second timescale (within a 500 ms interval).
The sub-second-timescale spectral-power associations were computed at 512 Hz temporal resolution within each 500 ms interval and averaged across all intervals (per site per participant) and averaged across participants. Each 2D-association plot shows the strengths of the same-signed (positive values, warmer colors) or opposite-signed (negative values, cooler colors) power modulation at all test frequencies (x-axis) that temporally coincided with the top/bottom-15% power variation at each probe frequency (y-axis), computed as Ln-ratio relative to the DCT-phase-scrambled control (to remove artifacts due to partial wavelet overlap; see text for details). Any asymmetry across the diagonal indicates directional differences; X-Hz power modulation coincident with the top/bottom-15% Y-Hz power variation may be stronger/weaker than the Y-Hz power modulation coincident with the top/bottom-15% X-Hz power variation. A-C. Representative association patterns. The strong positive associations along the 45° lines (A and B) indicate that spectral-power associations occurred at constant frequency differences, f’s. The accompanying line plots show the association strengths for major frequency bands as a function of Δf(warmer-colored curves representing higher-frequency bands), averaged across the y-side and x-side of the diagonal as the associations were approximately symmetric about the diagonal. The plots clearly show that the association strengths peaked at specific Δfvalues. A. An example from a representative posterior site (PO8) characterized by the Δf~ 3 Hz associations for the θ-α frequencies (small dashed ellipse) and particularly by the Δf~ 10 Hz associations for the β-γ frequencies (large dashed ellipse), suggesting that the θ-α and β-γ frequencies are amplitude-modulated at ~3 Hz and ~10 Hz, respectively, at posterior sites (see text for details). B. An example from a representative lateral site (C6) primarily characterized by the Δf~ 16 Hz associations for the higher γ frequencies (large dashed ellipse), suggesting that the higher γ frequencies are amplitude-modulated at ~16 Hz at lateral sites. C. An example from a representative anterior site (AFz) characterized by the lack of notable associations, suggesting that different frequency bands operate relatively independently at anterior sites. D-H. Association patterns at all sites. D. 2D-association plots. E-H. Corresponding line plots showing the association strengths for major frequency bands as a function of f. The line plots are shown separately for the θ-α (E), β (β1, β2, β3) (F), γ1 (G), and γ2 (H) bands to reduce clutter. The lower panels show representative 2D-association plots to highlight the specific bands included in the line plots. E. Line plots of association strengths for the θ and α frequencies, peaking at Δf~ 3 Hz at posterior sites (especially in the regions shaded in gray). F. Line plots of association strengths for the β (β1, β2, β3) frequencies, peaking at Δf~ 10 Hz at posterior sites (especially in the region shaded in gray). G. Line plots of association strengths for the γ1 frequencies, peaking at Δf~ 10 Hz at posterior sites (especially in the region shaded in gray). H. Line plots of association strengths for the γ2 frequencies, peaking at Δf~ 10 Hz at posterior sites and Δf~ 16 Hz at lateral sites (especially in the regions shaded in gray). In all parts the shading on the line plots represents ±1 standard error of the mean with participants as the random effect.
A representative posterior site shows systematic associations for the θ-α frequencies along the Δf~ 3 Hz lines and particularly for the β-γ frequencies along the Δf~ 10 Hz lines (e.g., Fig 3A, dashed ellipses). Note that the Δf~ 10 Hz associations can be seen within a single 500 ms interval as frequent co-occurrences of top-15% states in pairs of frequencies separated by ~10 Hz (e.g., vertical arrows in Fig 2A). We evaluated the inter-participant consistency of these patterns in three ways. One way was by plotting the association strength as a function of Δffor each major frequency band (labeled θ, α, β1, β 2, β 3, γ1 and γ2 in the figures). In this way, the associations for the θ-α frequencies along the Δf~ 3 Hz lines (e.g., the main panel in Fig 3A) correspond to the θ and α curves both peaking at Δf~ 3 Hz (e.g., the upper-right panel in Fig 3A), while the associations for the β-γ frequencies along the Δf~ 10 Hz lines (e.g., the main panel in Fig 3A) correspond to the β1, β2, β 3, γ1 and γ2 curves all peaking at Δf~ 10 Hz (e.g., the upper-right panel in Fig 3A). The tall peaks compared with the relatively small error regions (±1 standard error of the mean with participants as the random effect) indicate that the peaked associations along the Δf~ 3 Hz and Δf~ 10 Hz lines at posterior sites are consistent across participants (the conventional t-value would be the ratio of the height of each peak to the width of the corresponding error region).
A representative lateral site shows associations for the θ-α frequencies along the Δf~ 3 Hz lines, for the β1 frequencies along the Δf~ 8 Hz lines, and particularly for the γ2 frequencies along the Δf~ 16 Hz lines (combined with negative associations along the Δf~ 8 Hz lines) (e.g., the main panel in Fig 3B). The inter-participant consistency of these associations is reflected in the θ and α curves peaking at Δf~ 3 Hz, the β1 curve peaking at Δf~ 8 Hz, and the γ2 curve substantially peaking at Δf~ 16 Hz and dipping at Δf~ 8 Hz (e.g., the upper-right panel in Fig 3B) relative to the corresponding error regions.
A representative anterior site shows the lack of any notable spectral-power associations (e.g., the main panel in Fig 3C) reflected in the relatively flat curves hovering around zero for all frequency bands (the upper-right panel in Fig 3C).
A second way in which we evaluated the consistency of cross-frequency association patterns was to confirm within-region similarity. In particular, the associations characterized by the θ-α frequencies peaking at Δf~ 3 Hz (see the posterior region of Fig 3D and 3E) and the β-γ frequencies peaking at Δf~ 10 Hz (see the posterior region of Fig 3D and 3F–3H) are shared among posterior sites, those characterized by the γ2 frequencies peaking at Δf~ 16 Hz (see the lateral region of Fig 3D and 3H) are shared among lateral sites, and the relative lack of spectral-power associations (see the anterior region of Fig 3D–3H) are shared among anterior sites. A third way in which we evaluated data consistency was to confirm that the same conclusions about the spectral-power association patterns could be drawn based on the data from the odd or even numbered participants (see S1A–S1C Fig). We did not compute conventional p-values adjusted in various ways to more or less “control for” multiple comparisons because those would not add substantively to the above methods of evaluating reliability for the purpose of identifying characteristic patterns of spectral-power associations.
Within-site (local) spectral-power associations on the (slower) seconds timescale
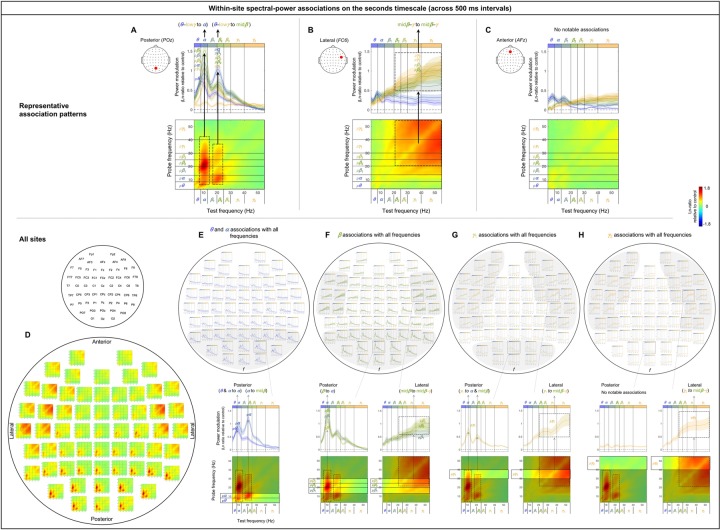
The within-site spectral-power associations on the seconds timescale (across 500 ms intervals) are characterized by vertical and horizontal directions. The representative association patterns (all involving positive associations) are shown in Fig 4A–4C. At a representative posterior site, large (top/bottom-15%) power variations in the θ-lowγ frequencies (the y-axis indicating probe frequencies) were selectively associated with the power modulation in the α band and also midβ band to a lesser degree (the x-axis indicating test frequencies), forming a vertical column at the α band and to a lesser degree at the midβ band (e.g., the dashed rectangles in the lower panel in Fig 4A). The inter-participant consistency of these associations is reflected in the accompanying line plots in which the association strengths are averaged within each probe-frequency band (labeled with “p”) and plotted as a function of test frequency. The α-band column (α-column) and the lesser midβ-band column are reflected in the pθ, pα, pβ1, pβ 2, pβ 3, and pγ1 curves consistently peaking at the α band and also at midβ band to a lesser degree (e.g., the upper panel in Fig 4A).
Fig 4. Within-site spectral-power associations on the seconds timescale (across 500 ms intervals).
The seconds-timescale spectral-power associations were computed at 500 ms temporal resolution across the entire 5 min period (per site per participant) and averaged across participants. Each 2D-association plot shows the strengths of the same-signed (positive values, warmer colors) or opposite-signed (negative values, cooler colors) power modulation at all test frequencies (x-axis) that temporally coincided with the top/bottom-15% power variation at each probe frequency (y-axis), computed as Ln-ratio relative to the DCT-phase-scrambled control (to remove artifacts due to partial wavelet overlap; see text for details). Any asymmetry across the diagonal indicates directional differences; X-Hz power modulation coincident with the top/bottom-15% Y-Hz power variation may be stronger/weaker than the Y-Hz power modulation coincident with the top/bottom-15% X-Hz power variation. A-C. Representative association patterns. The strong positive associations along the vertical and horizontal directions indicate that spectral-power associations are characterized by multiple frequencies being associated with a specific frequency band or with one another. The accompanying line plots show the association strengths of each probe-frequency band (labeled with “p”; warmer-colored curves representing higher-probe-frequency bands) with all test frequencies (x-axis). The plots clearly show that the association strengths peaked at specific test frequencies. A. An example from a representative posterior site (POz) characterized by the associations of the θ-lowγ frequencies with the α band and to a lesser degree with the midβ band (dashed rectangles), suggesting that the α band and to a lesser degree the midβ band play a role in coordinating cross-frequency interactions at posterior sites. B. An example from a representative lateral site (FC6) characterized by the broad associations among the midβ-γ frequencies (dashed square). C. An example from a representative anterior site (AFz) characterized by the lack of notable associations, suggesting that different frequency bands operate relatively independently at anterior sites. D-H. Association patterns at all sites. D. 2D-association plots. E-H. Corresponding line plots showing the association strengths of each probe-frequency band with all test frequencies (x-axis). The line plots are shown separately for the θ-α (E), β (β1, β2, β3) (F), γ1 (G), and γ2 (H) bands to reduce clutter. The lower panels show representative 2D-association plots to highlight the specific probe-frequency bands included in the line plots. E. Line plots showing the association strengths of the θ and α probe-frequency bands (labeled “pθ” and “pα”) with all test frequencies. The θ and α bands are both associated with the α band while the α band is additionally associated with the midβ band at posterior sites (especially in the region shaded in gray). F. Line plots showing the association strengths of the β (β1, β2, β3) probe-frequency bands (labeled “pβ1,” “pβ3,” and “pβ3”) with all test frequencies. The β (β1, β2, β3) bands are primarily associated with the α band at posterior sites, while the β2 and β3 bands are broadly associated with the midβ-γ bands at lateral sites (especially in the regions shaded in gray). G. Line plots showing the association strengths of the γ1 probe-frequency band (labeled “pγ1”) with all test frequencies. The γ1 band is associated with the α and midβ bands at posterior sites, while it is broadly associated with the midβ-γ bands at lateral sites (especially in the regions shaded in gray). H. Line plots showing the association strengths of the γ2 probe-band (labeled “pγ2”) with all test-frequency bands. The γ2 band is broadly associated with the midβ-γ bands at lateral sites (especially in the regions shaded in gray). In all parts the shading on the line plots represents ±1 standard error of the mean with participants as the random effect.
At a representative lateral site, power variations in the midβ-γ frequencies were broadly associated with one another (e.g., the dashed square in the lower panel in Fig 4B), with the inter-participant consistency of these associations reflected in the pβ2, pβ 3, pγ1, and pγ2 curves consistently elevated across the midβ-γ range (e.g., the upper panel in Fig 4B).
At a representative anterior site, there were no notable spectral-power associations (e.g., the lower panel in Fig 4C), reflected in the curves representing all probe-frequency bands being relatively flat and hovering around zero (e.g., the upper panel in Fig 4C).
Fig 4D–4H shows that these characteristic patterns of spectral-power associations are consistent within each region. Specifically, the associations marked by the α-column (and the midβ-column to a lesser degree) characterized by the pθ, pα, pβ1, pβ 2, pβ 3, and pγ1 curves consistently peaking at the α band (and at the midβ band to a lesser degree) are shared among posterior sites (see the posterior region of Fig 4D, 4E–4G). The associations marked by the broad square-shaped relationship across the midβ-γ frequencies characterized by the pβ2, pβ 3, pγ1, and pγ2 curves consistently elevated across the midβ-γ range are shared among lateral sites (see the lateral regions of Fig 4D, 4F–4H). The lack of notable spectral-power associations characterized by the curves for the entire range of probe frequencies being relatively flat and hovering around zero is shared among anterior sites (see the anterior region of Fig 4D, 4E–4H). Further, these characteristic patterns of spectral-power associations are evident in the data from both the odd and even numbered participants (S1D–S1F Fig).
In summary, the patterns of within-site (local) spectral-power associations (nearly exclusively positive) were distinct for the sub-second (within a 500 ms interval) and seconds (across 500 ms intervals) timescales. The (fast) sub-second-timescale associations were characterized by 45° lines parallel to the diagonal, indicative of associations at constant f’s, whereas the (slower) seconds-timescale associations were characterized by columns, indicative of multiple frequencies being selectively associated with a specific band or with one another. In particular, the (fast) sub-second-timescale oblique associations were primarily characterized by the θ-α frequencies associated at Δf~ 3 Hz and the β-γ frequencies associated at Δf~ 10 Hz at posterior sites (e.g., Fig 3A; also see the posterior region of Fig 3D, 3E–3H), and the β-γ frequencies associated at Δf~ 16 Hz at lateral sites (e.g., Fig 3B; also see Fig the lateral regions of 3D, 3H). The (slower) seconds-timescale columnar associations were primarily characterized by the θ-lowγ frequencies associated with the α band (also midβ band to a lesser degree) at posterior sites (e.g., Fig 4A; also see the posterior region of Fig 4D, 4E–4G), and the midβ-γ frequencies broadly associated with one another at lateral sites (e.g., Fig 4B; also see the lateral regions of Fig 4D, 4F–4H). No notable spectral-power associations were found on either timescale at anterior sites (e.g., Figs 3C and 4C; also see the anterior region of Figs 3D, 3E–3H, 4D and 4E–4H).
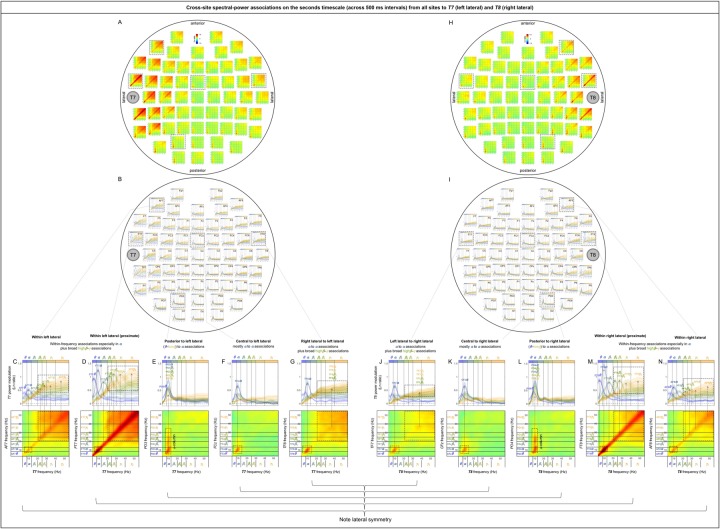
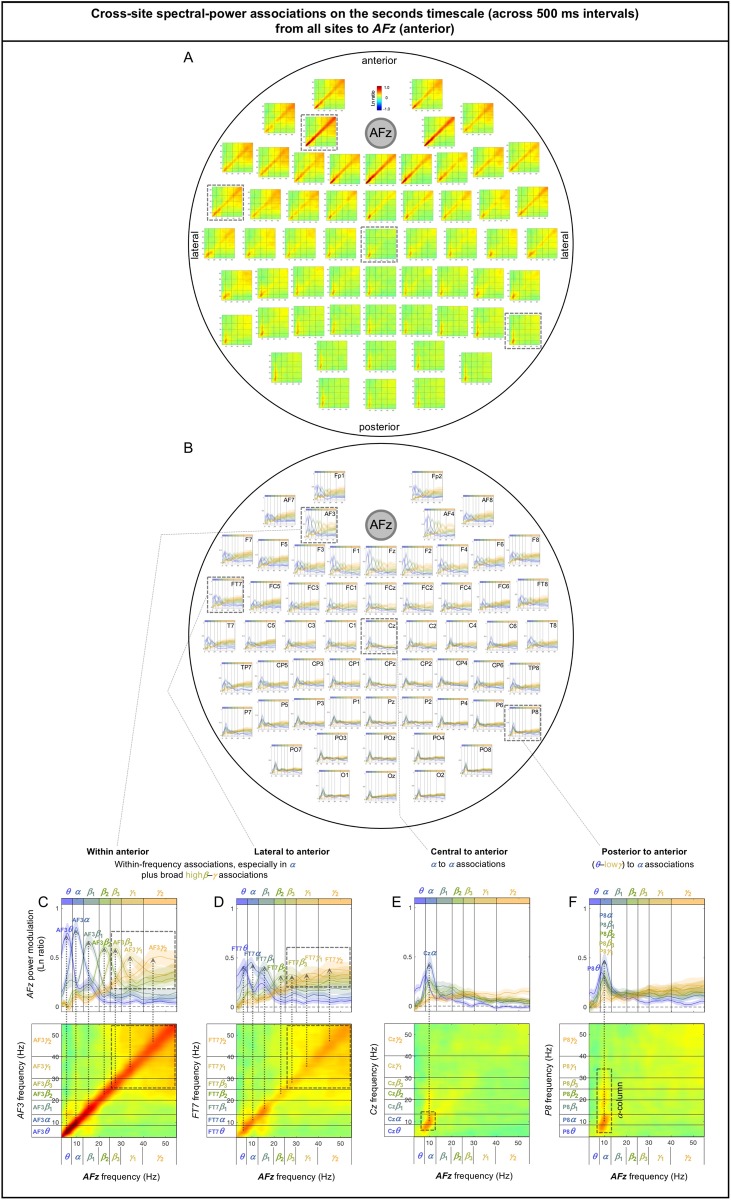
Cross-site (long-distance) spectral-power associations on the (fast) sub-second timescale
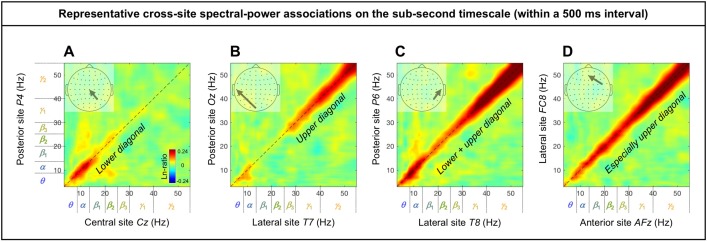
The cross-site spectral-power associations (in Ln ratio) on the sub-second-timescale (within a 500 ms interval) are characterized by the diagonal, indicative of within-frequency interactions, while the ranges of associated frequencies varied from site-pair to site-pair (representative examples shown in Fig 5). While there are 60 x 59 (3,540) site combinations, characteristic patterns of cross-site associations can be identified by examining the associations from all sites to representative sites: Oz for the posterior region, Cz for the central region, AFz for the anterior region, and T7 and T8 for the left-lateral and right-lateral regions, respectively. Examining cross-site associations in this way (i.e., from all sites to a target site) allowed us to directly compare the impact of each site on a target site by evaluating the spectral-power modulation (in Ln-ratio) at the target site coincident with large (top/bottom-15%) spectral-power variations at each of the other sites.
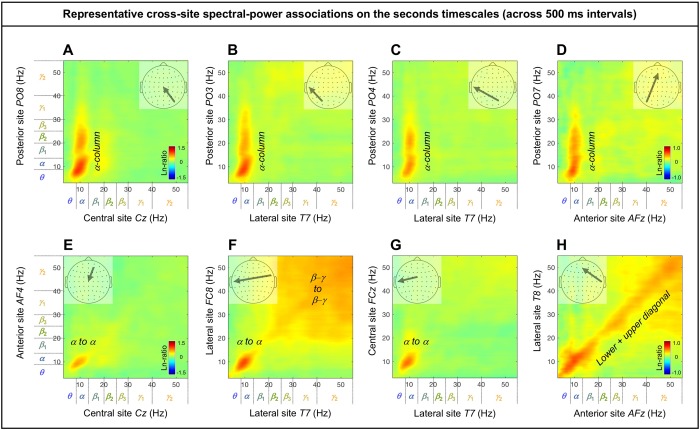
Fig 5. Representative examples of cross-site spectral-power associations on the sub-second timescale (within a 500 ms interval).
Each 2D spectral-power-association plot shows the strengths of the same-signed (positive values, warmer colors) or opposite-signed (negative values, cooler colors) power modulation (in Ln-ratio) for all test-site frequencies (x-axis) that temporally coincided with the top/bottom-15% power variation at each probe-site frequency (y-axis). The sub-second-timescale spectral-power associations were computed at 512 Hz temporal resolution within each 500 ms interval, averaged across all intervals and then across participants. The associations (all positive) were characteristically diagonal, indicative of within-frequency associations, while the ranges of associated frequencies varied from site-pair to site-pair. A. Within-frequency associations in the lower diagonal involving the θ-lowβ frequencies from a posterior site P4 to a central site Cz. B. Within-frequency associations in the upper diagonal involving the γ frequencies from a posterior site Oz to a lateral site T7. C. Within-frequency associations in the lower and upper diagonal involving the θ-α and γ frequencies from a posterior site P6 to a lateral site T8. D. Stronger within-frequency associations in the higher frequencies from a lateral site FC8 to an anterior site AFz.
The spectral-power associations to Oz (a representative posterior site) from all other sites are shown in Fig 6A. The inter-participant consistency of the association patterns was evaluated in three ways. Because all associations were characteristically diagonal (Fig 6A), we computed the diagonal magnitudes (Fig 6B) with the gray regions indicating ±1 standard error of the mean (with participants as the random effects). Large frequency-dependent variations relative to the widths of the error regions indicate statistical reliability (the conventional t-values being their ratio). A second way in which we evaluated data consistency was to note bilateral symmetry. While large-scale neural interactions are expected to show general bilateral symmetry, spurious patterns would not. A third way was to confirm that the same conclusions about the association patterns could be drawn based on the data from the odd or even numbered participants (see S2 and S3 Figs).
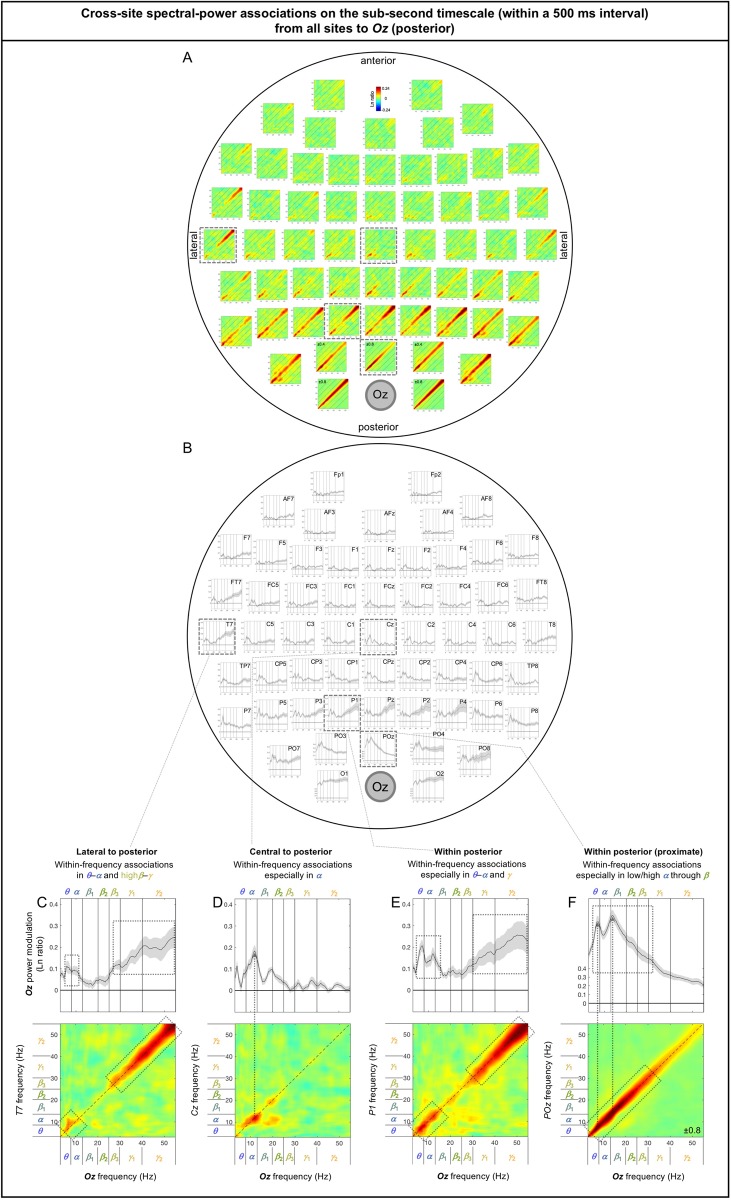
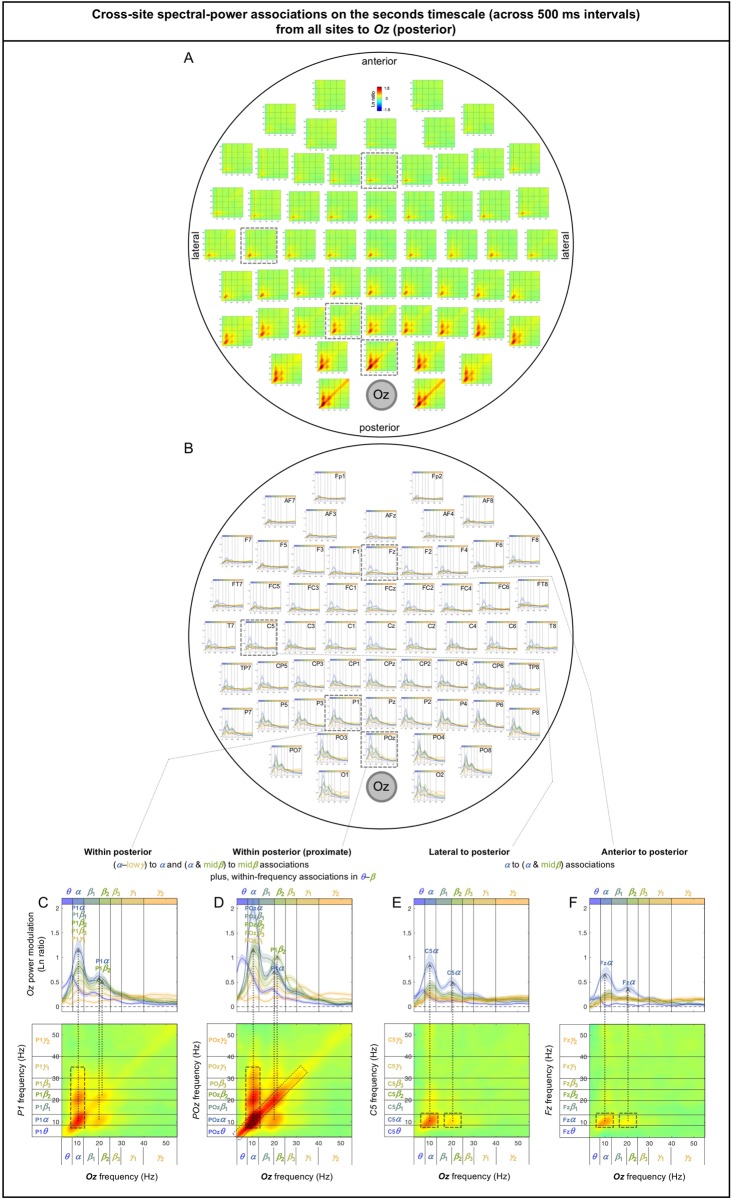
Fig 6. Cross-site spectral-power associations on the sub-second timescale (within a 500 ms interval) from all sites to Oz (a representative posterior site).
A. 2D spectral-power association plots. All associations were characteristically diagonal, indicative of within-frequency associations, while the ranges of associated frequencies varied across site-pairs. B. The values along the diagonal with the shaded regions indicating ±1 standard error of the mean (with participants as the random effect). C-F. Representative associations. C. T7 (a left-lateral site) to Oz spectral-power associations, characterized by within-frequency associations in the θ-α and highβ-γ bands, skipping the middle (β band). D. Cz (a central site) to Oz spectral-power associations, characterized by within-frequency associations primarily in the α band. E. P1 (a posterior site) to Oz spectral-power associations, characterized by within-frequency associations particularly in the θ-α and γ bands, skipping the middle (β band). F. POz (an adjacent site) to Oz spectral-power associations, characterized by within-frequency associations particularly in the θ through lowβ bands. The color scale is shown at the top of part A (also indicated within association plots when different; for example, “±0.4” indicates that the color scale for the corresponding association plot ranges from –0.4 to +0.4).
Although we applied the surface-Laplacian transform to all EEG data to reduce the influences of volume conduction, diagonal associations could reflect volume conduction especially between adjacent sites (e.g., [32]). Nevertheless, any spurious contributions from volume conduction would be largely frequency independent because spectral-power profiles tended to be similar between adjacent sites. For example, although the overall strong diagonal associations to Oz from its lateral neighbors, O1 and O2, may primarily reflect volume conduction (Fig 6A and 6B), the fact that the associations were relatively weak in the α band (Fig 6B) may reveal a characteristic of cross-site neural interactions.
Overall, the sub-second-timescale cross-site spectral-power associations to Oz (a representative posterior site) from other sites were all diagonal (within-frequency) and generally diminished with distance (Fig 6A and 6B), except that the γ-band associations from lateral sites (especially from T7 [Fig 6C] and T8) remained strong. In general, the within-frequency associations to Oz were dominated by the α or θ-α bands (e.g., Fig 6D and 6F) or by combinations of the θ-α and γ bands (e.g., Fig 6C and 6E), but were never dominated by the β band (also see Fig 6A and 6B).
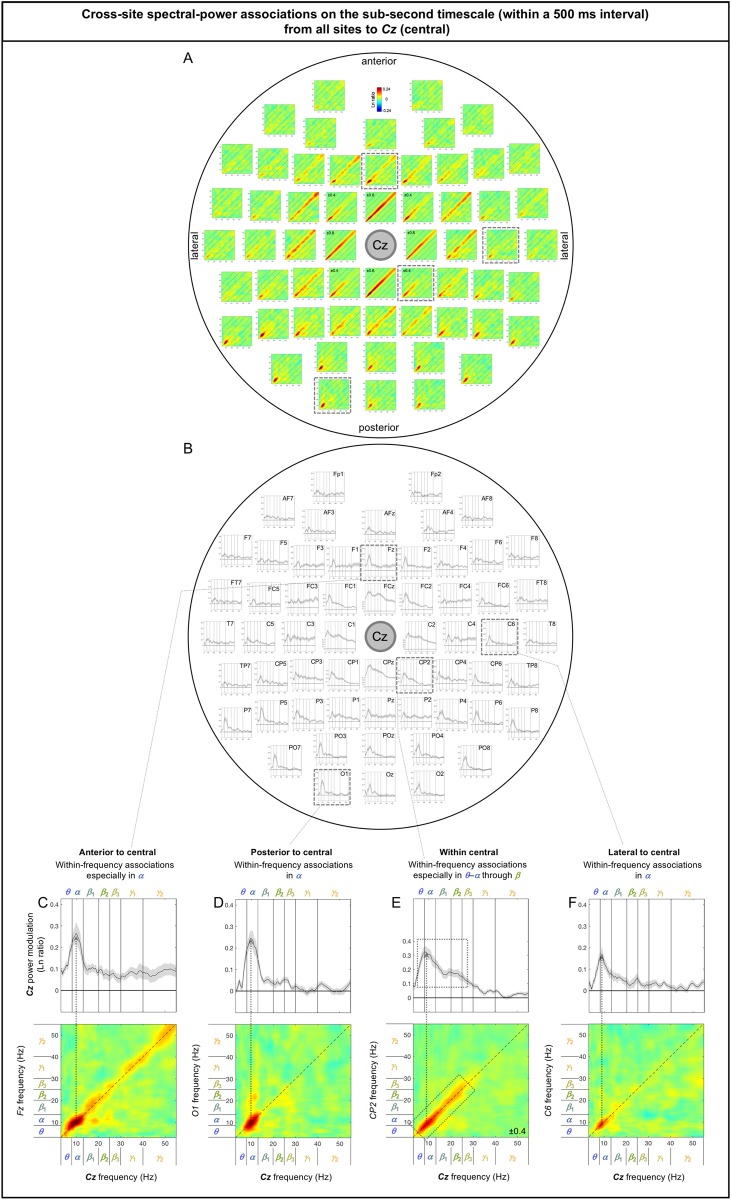
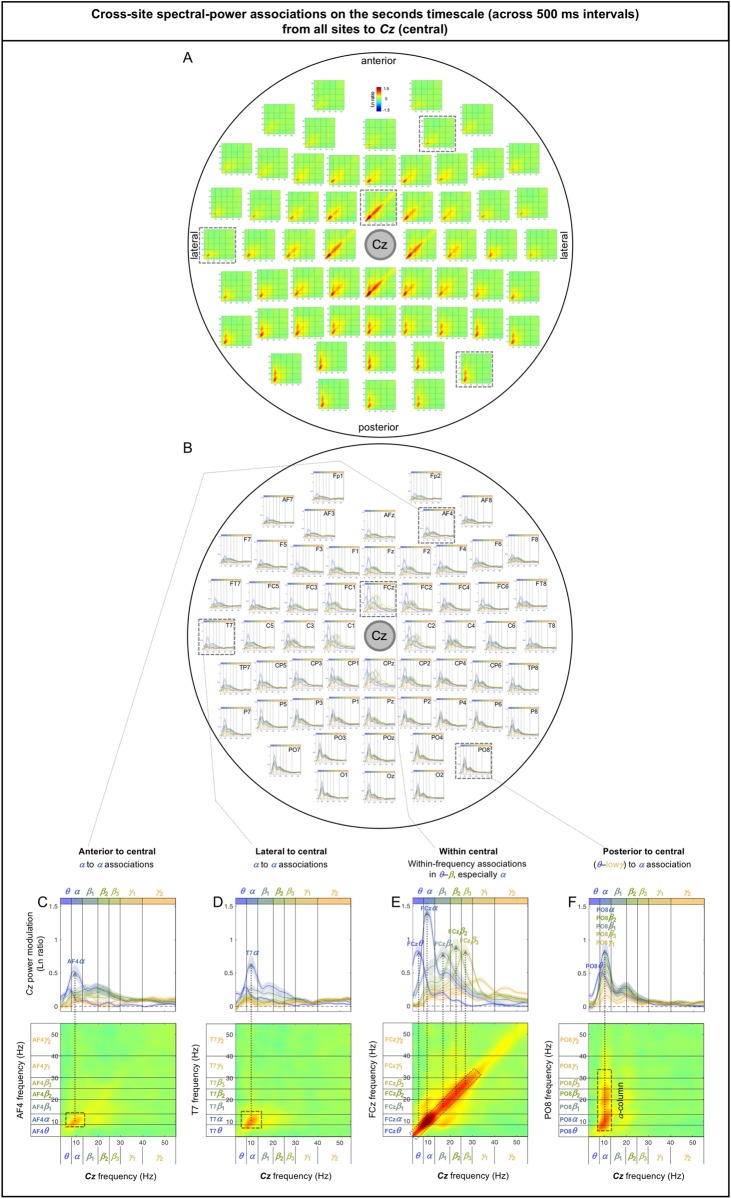
The sub-second-timescale cross-site spectral-power associations to Cz (a representative central site) from other sites were also all diagonal (within-frequency) and generally diminished with distance (Fig 7A and 7B), except that the α-band associations from posterior sites remained strong (e.g., Fig 7D; also see the posterior region of Fig 7A and 7B). The within-frequency associations to Cz were generally dominated by the α band (e.g., Fig 7C–7F), while some associations from within the central region were relatively frequency independent (e.g., from FC3, FC4, C3, C4; also see Fig 7A and 7B).
Fig 7. Cross-site spectral-power associations on the sub-second timescale (within a 500 ms interval) from all sites to Cz (a representative central site).
A. 2D spectral-power association plots. All associations were characteristically diagonal, indicative of within-frequency associations, while the ranges of associated frequencies varied across site-pairs. B. The values along the diagonal with the shaded regions indicating ±1 standard error of the mean (with participants as the random effect). C-F. Representative associations. C. Fz (an anterior site) to Cz spectral-power associations, characterized by within-frequency associations particularly in the α band. D. O1 (a posterior site) to Cz spectral-power associations, characterized by within-frequency associations in the α band. E. CP2 (a central site) to Cz spectral-power associations, characterized by within-frequency associations particularly in the θ-α through β bands. F. C6 (a lateral site) to Cz spectral-power associations, characterized by within-frequency associations in the α band. The color scale is shown at the top of part A (also indicated within association plots when different; for example, “±0.4” indicates that the color scale for the corresponding association plot ranges from –0.4 to +0.4).
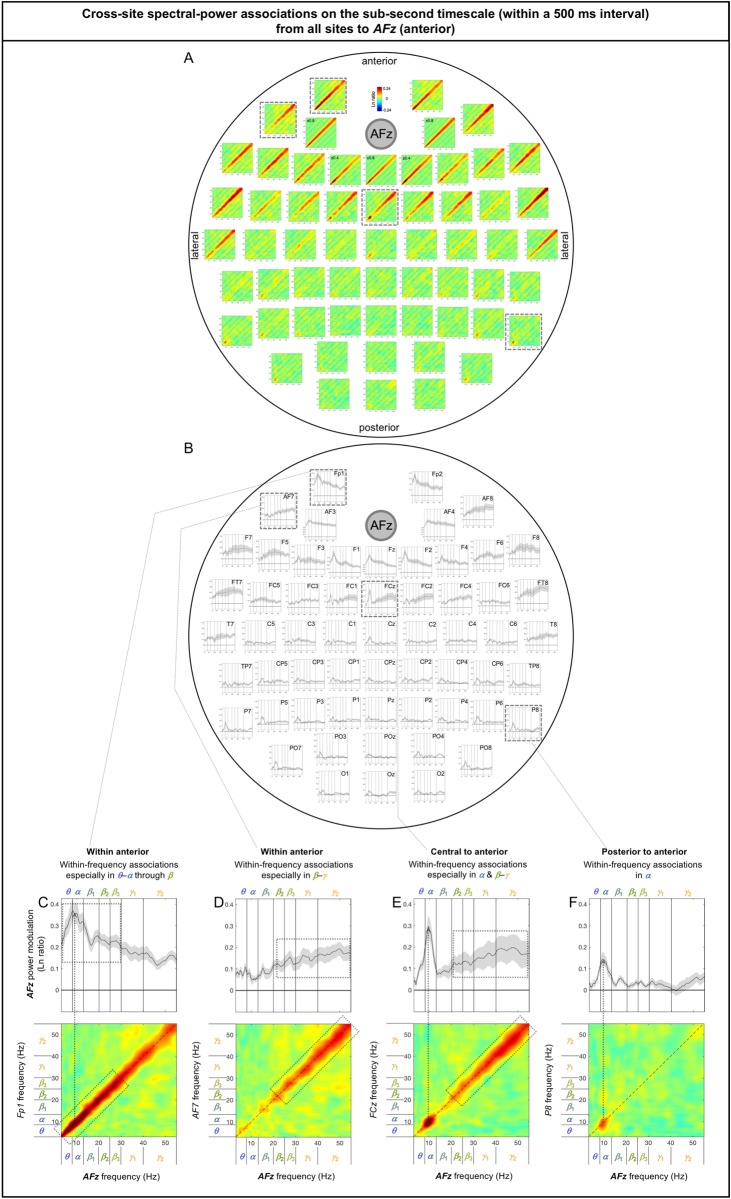
The sub-second-timescale cross-site spectral-power associations to AFz (a representative anterior site) from other sites were also all diagonal (within-frequency) and generally diminished with distance (Fig 8A and 8B), except that the α-band associations from some posterior sites remained strong (e.g., from P7, PO7, P8 [Fig 8F], PO8). The within-frequency associations to AFz were generally dominated by the α band (e.g., Fig 8C and 8F), the β-γ bands (e.g., Fig 8D), or combinations of the α and β-γ bands (e.g., Fig 8E), but were never dominated by the β band (also see Fig 8A and 8B). It is noteworthy that the associations to AFz from a pair of neighboring sites, Fp1 (Fig 8C) and AF7 (Fig 8D) were opposite, that is, the associations from Fp1 were dominated by the α band whereas those from AF7 were dominated by the β-γ bands; this spectrally opposite relationship was replicated on the right side for the associations from Fp2 and AF8 (Fig 8A and 8B) and obtained from both the odd and even numbered participants (S2G–S2I Fig). These spectrally opposite association patterns from neighboring sites indirectly confirm that the surface-Laplacian transform was reasonably effective at revealing distinct neural sources.
Fig 8. Cross-site spectral-power associations on the sub-second timescale (within a 500 ms interval) from all sites to AFz (a representative anterior site).
A. 2D spectral-power association plots. All associations were characteristically diagonal, indicative of within-frequency associations, while the ranges of associated frequencies varied across site-pairs. B. The values along the diagonal with the shaded regions indicating ±1 standard error of the mean (with participants as the random effect). C-F. Representative associations. C. Fp1 (an anterior site) to AFz spectral-power associations, characterized by within-frequency associations particularly in the θ-α through β bands. D. AF7 (an anterior site) to AFz spectral-power associations, characterized by within-frequency associations particularly in the β-γ bands. Note that although Fp1 and AF7 are adjacent anterior sites the frequency characteristics of their associations with AFz were opposite (the low-to-middle bands for Fp1 and the middle-to-high bands for AF7); this pattern was replicated on the right side at Fp2 and AF8 (see A and B). E. FCz (a central site) to AFz spectral-power associations, characterized by within-frequency associations particularly in the α and midβ-γ bands. F. P6 (a posterior site) to AFz spectral-power associations, characterized by within-frequency associations in the α band. The color scale is shown at the top of part A (also indicated within association plots when different; for example, “±0.4” indicates that the color scale for the corresponding association plot ranges from –0.4 to +0.4).
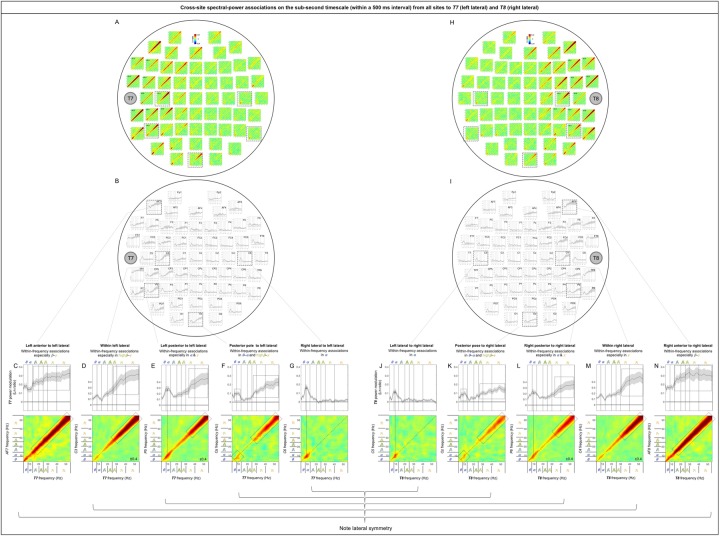
The sub-second-timescale cross-site spectral-power associations to T7 and T8 (representative left and right lateral sites) from other sites were also all diagonal (within-frequency) and generally diminished with distance (Fig 9A and 9B, 9H and 9I), except that the α-band associations from some contralateral sites (e.g., C6 [Fig 9G] and P8 for T7 and C5 [Fig 9J] and P7 for T8) and the highβ-γ associations from Oz (Fig 9F and 9K) remained strong. The within-frequency associations to T7 and T8 were generally dominated by the β-γ, highβ-γ, or γ band (primarily from the ipsilateral central and anterior regions; e.g., Fig 9C and 9D, 9M and 9N), the α band (primarily from the contralateral regions; e.g., Fig 9G and 9J), or combinations of the θ-α or α band and the highβ-γ or γ band (primarily from ipsilateral posterior and central regions; Fig 9E and 9F, 9K and 9L), but were never dominated by the β band (also see Fig 14A and 14B, 14H and 14I).
Fig 9. Cross-site spectral-power associations on the sub-second time scale (within a 500 ms interval) from all sites to T7 (a representative left lateral site) and T8 (a representative right lateral site).
A, H. 2D spectral-power association plots for T7 and T8. All associations were characteristically diagonal, indicative of within-frequency associations, while the ranges of associated frequencies varied across site-pairs. B, I. The power-modulation values along the diagonal with the shaded regions indicating ±1 standard error of the mean (with participants as the random effect). C-G, J-N. Representative associations for T7 or T8. Note the bilateral symmetry. C, N. AF7/AF8 (ipsilateral anterior sites) to T7/T8 spectral-power associations, characterized by within-frequency associations particularly in the β-γ bands. D, M. C3/C4 (ipsilateral sites) to T7/T8 spectral-power associations, characterized by within-frequency associations in the highβ-γ bands (D) or the γ band (M). E, L. P5/P6 (ipsilateral posterior sites) to T7/T8 spectral-power associations, characterized by within-frequency associations particularly in the α and γ bands. F, K. Oz (a posterior site) to T7/T8 spectral-power associations, characterized by within-frequency associations in the θ-α and highβ-γ bands. G, J. C6/C5 (contralateral sites) to T7/T8 spectral-power associations, characterized by within-frequency associations in the α band. The color scale is shown at the top of part A (also indicated within association plots when different; for example, “±0.4” indicates that the color scale for the corresponding association plot ranges from –0.4 to +0.4).
Fig 14. Cross-site spectral-power associations on the seconds timescale (across 500 ms intervals) from all sites to T7 (a representative left lateral site) and T8 (a representative right lateral site).
A, H. 2D spectral-power association plots for T7 and T8. Some associations are columnar, indicating multiple frequencies associated with a specific (primarily α) band, some are square, indicating broad associations among multiple frequencies, and some are diagonal, indicating within-frequency associations. B, I. Replotting of A. Each curve shows the spectral-power modulation at T7 or T8 associated with the probe-site power variation in each major frequency band (lower-to-higher frequency bands labeled with cooler-to-warmer colors), with the shaded regions indicating ±1 standard error of the mean (with participants as the random effect). In other words, each curve shows a horizontal slice of a 2D-association plot for a specific probe-site frequency band (see the rectangular boxes in the bottom panels). C-G, J-N. Representative associations for T7 and T8. Note the bilateral symmetry. C, N. AF7/AF8 (ipsilateral anterior sites) to T7/T8 spectral-power associations, characterized by the diagonal (within-frequency) associations (especially in the α band) as well as the broad associations among the highβ-γ bands. D, M. FT7/FT8 (adjacent sites) to T7/T8 spectral-power associations, characterized by the diagonal (within-frequency) associations (especially in the α band) as well as the broad associations among the highβ-γ bands (similar to C, N, but stronger). E, L. PO3/PO4 (posterior sites) to T7/T8 spectral-power associations, characterized by the θ-lowγ band at PO3/PO4 associated with the α band at T7/T8—α-column. F, K. FCz (a central site) to T7/T8 spectral-power associations, characterized by the α band at FCz associated with the α-band at T7/T8. G, J. TF8/TF7 (contralateral sites) to T7/T8 associations, characterized by the α band at TF8/TF7 associated with the α band at T7/T8 as well as the broad associations among the highβ-γ bands. Note that spectral-power associations from most posterior sites to T7/T8 are characterized by α-columns, that is, the θ-lowγ bands at most posterior sites were associated with the α band at T7/T8 (see the posterior region of A, B and H, I). The color scale is shown at the top of part A and H.
Note that the sub-second-timescale cross-site association patterns to Oz (posterior), Cz (central), AFz (anterior), T7 (left lateral), and T8 (right lateral) were generally bilaterally symmetric (Fig 6A and 6B [posterior], 7A-B [central], 8A-B [anterior], 9A vs. 9H, 9B vs. 9I, 9C-G vs. 9J-N [lateral]). Further, the above conclusions hold for data from either the odd or even numbered participants (see S2A–S2C Fig [posterior], S2D–S2F Fig [central], S2G–S2I Fig [anterior], S2J–S2L Fig, S2M–S2O Fig [lateral]).
In summary, the (fast) sub-second-timescale (within a 500 ms interval) cross-site (long-distance) spectral-power associations (all positive) are characterized by diagonal, within-frequency associations dominated by different frequency ranges. Although the frequency dependence varied from site-pair to site-pair, some characteristic patterns emerged. Not surprisingly, the association strengths generally diminished with distance, though some associations remained strong. Those “super” long-distance associations tended to be dominated by the α band, such as the associations from inferior posterior sites (PO7, PO3, POz, PO4, PO8, O1, Oz, and O2) to a representative central site, Cz (Fig 7A and 7B), from lateral posterior sites (P7, P5, PO7, P6, P8, and PO8) to a representative anterior site, AFz (Fig 8A and 8B), and from contralateral sites (FT8, C6, TP8, P8, and PO8; FT7, C5, TP7, P8, and PO7) to representative left and right lateral sites T7 and T8 (Fig 9A and 9B, 9H and 9I). A few super long-distance associations were dominated by the β-γ bands, such as those from a posterior site, Oz, to representative left and right lateral sites, T7 and T8 (Fig 9A–9B, 9H–9I). Overall, the associations to Oz (a representative posterior site), AFz (a representative anterior site), and T7/T8 (representative left and right lateral sites) were dominated by the θ-α bands, β-γ bands, or combinations of the θ-α and β-γ bands, whereas the associations to Cz (a representative central site) were dominated by the α band. Notably, no associations were dominated by the β band.
Cross-site (long-distance) spectral-power associations on the (slower) seconds timescale
The cross-site spectral-power associations (in Ln-ratio) on the seconds timescale (across 500 ms intervals) are characterized by columnar, square, and diagonal patterns. Notably, the associations from posterior sites to other sites are characterized by “α-columns,” that is, the posterior spectral-power variations in the θ-lowγ bands were selectively associated with the α-band power modulation at other sites (e.g., Fig 10A–10D). Other associations are characterized by the α-band to α-band associations (e.g., Fig 10E–10H), broad associations among the β-γ bands (Fig 10F and 10H to some degree), and within-frequency (diagonal) associations (e.g., Fig 10H).
Fig 10. Representative examples of cross-site spectral-power associations on the seconds timescale (across 500 ms intervals).
Each 2D spectral-power-association plot shows the strengths of the same-signed (positive values, warmer colors) or opposite-signed (negative values, cooler colors) power modulation (in Ln-ratio) for all test-site frequencies (x-axis) that temporally coincided with the top/bottom-15% power variation at each probe-site frequency (y-axis). The seconds-timescale spectral-power associations were computed at 500 ms temporal resolution across the entire 5 min period, and averaged across participants. We obtained several characteristic patterns of associations. A-D. The “α-column” associations from posterior sites to other sites characterized by the posterior θ-lowγ bands selectively associated with the α band at other sites. E-H. Other patterns of associations (not involving posterior sites) characterized by the α to α associations (E-H), broad associations among the β-γ bands (F and H to some degree), and within-frequency (diagonal) associations (H).
As we did above for the sub-second-timescale associations, we examined the associations from all sites to representative sites in the posterior (Oz), central (Cz), anterior (AFz), left-lateral (T7), and right-lateral (T8) regions. To assess the inter-participant consistency of the association patterns, we generated line plots corresponding to each 2D-association plot, where each curve shows the test-site spectral-power modulation coincident with the probe-site top/bottom-15% power variation in each major frequency band (lower-to-higher frequency bands labeled with cooler-to-warmer colors), with the shaded regions indicating ±1 standard error of the mean (with participants as the random effect). In other words, each curve shows a horizontal slice of the corresponding 2D-association plot for a specific probe-site frequency band (see the rectangular boxes in the bottom panels in Figs 11–14). Overall, spectral-power associations to all five target sites diminished with distance (Figs 11–14) as they did on the sub-second timescale.
Fig 11. Cross-site spectral-power associations on the seconds timescale (across 500 ms intervals) from all sites to Oz (a representative posterior site).
A. 2D spectral-power association plots. Some associations are columnar, indicating multiple frequencies associated with a specific (primarily α) band, and some are diagonal, indicating within-frequency associations. B. Replotting of A. Each curve shows the spectral-power modulation at Oz associated with probe-site power variation in each major frequency band (lower-to-higher frequency bands labeled with cooler-to-warmer colors), with the shaded regions indicating ±1 standard error of the mean (with participants as the random effect). In other words, each curve shows a horizontal slice of a 2D-association plot for a specific probe-site frequency band (see the rectangular boxes in the bottom panels). C-F. Representative associations. C. P1 (a posterior site) to Oz spectral-power associations, characterized by the α-lowγ bands at P1 associated with the α-band at Oz (α-column), and the α-&-midβ bands at P1 somewhat associated the midβ band at Oz. D. POz (an adjacent site) to Oz spectral-power associations, characterized by the α-lowγ bands at POz associated with the α band at Oz (α-column), the α-β bands at POz somewhat associated with the midβ band at Oz (as in C, but stronger), and the diagonal (within-frequency) associations in the θ-β bands. E. C5 (a lateral site) to Oz spectral-power associations, characterized by the α band at C5 associated with the α band (and the midβ-band to some degree) at Oz. F. Fz (an anterior site) to Oz spectral-power associations, characterized by the α band at Fz associated with the α band (and the midβ band to some degree) at Oz (as in E). The color scale is shown at the top of part A. Note that spectral-power associations from most posterior sites to Oz contain α-columns. The color scale is shown at the top of part A.
The seconds-timescale cross-site spectral-power associations to Oz (a representative posterior site) from other sites were characterized by two general patterns depending on the region. The associations from within the posterior region to Oz were characterized by (1) the α-lowγ-band (posterior) to α-band (Oz) associations, α-columns, and (2) the α-&-midβ-band (posterior) to midβ-band (Oz) associations to a lesser degree (e.g., Fig 11C–11D; also see the posterior region of Fig 11A–11B). The associations from outside the posterior region to Oz were characterized by the α-band (non-posterior) to α-band (and to midβ-band to a lesser degree) (Oz) associations (e.g., Fig 11E–11F; also see the inferior-anterior, central, and lateral regions of Fig 11A–11B). In addition, the associations from proximate sites to Oz included within-frequency (diagonal) associations such as the θ-β-band associations from POz (Fig 11D) and broadband associations from O1 and O2 (see the bottom of Fig 11A), though the latter may primarily reflect volume conduction.
The seconds-timescale cross-site spectral-power associations to Cz (a representative central site) from posterior sites were characterized by the θ-lowγ-band (posterior) to α-band (Cz) associations, α-columns (e.g., Fig 12F; also see the posterior region of Fig 12A–12B). The associations from non-posterior sites to Cz generally included the α-band (non-posterior) to α-band (Cz) associations (e.g., Fig 12C–12E; also see the anterior, central, and lateral regions of Fig 12A–12B). In addition, the associations from proximate sites to Cz included within-frequency (diagonal) associations in the θ-β bands (e.g., Fig 12E; also see the sites surrounding Cz in Fig 12A–12B).
Fig 12. Cross-site spectral-power associations on the seconds timescale (across 500 ms intervals) from all sites to Cz (a representative central site).
A. 2D spectral-power association plots. Some associations are columnar, indicating multiple frequencies associated with a specific (primarily α) band, and some are diagonal, indicating within-frequency associations. B. Replotting of A. Each curve shows the spectral-power modulation at Cz associated with the probe-site power variation in each major frequency band (lower-to-higher frequency bands labeled with cooler-to-warmer colors), with the shaded regions indicating ±1 standard error of the mean (with participants as the random effect). In other words, each curve shows a horizontal slice of a 2D-association plot for a specific probe-site frequency band (see the rectangular boxes in the bottom panels). C-F. Representative associations. C. AF4 (an anterior site) to Cz spectral-power associations, characterized by the α band at AF4 associated with the α band at Cz. D. T7 (lateral) to Cz spectral-power associations, characterized by the α band at T7 associated with the α band at Cz (as in C). E. FCz (an adjacent site) to Cz spectral-power associations, characterized by the diagonal (within-frequency) associations in the θ-β (especially α) bands. F. PO8 (a posterior site) to Cz spectral-power associations, characterized by the θ-lowγ bands at PO8 associated with the α band at Cz—α-column. Note that spectral-power associations from most posterior sites to Cz are characterized by α-columns, that is, the θ-lowγ bands at most posterior sites were associated with the α band at Cz (see the posterior region of A and B). The color scale is shown at the top of part A.
The seconds-timescale cross-site spectral-power associations to AFz (a representative anterior site) from posterior sites were characterized by the θ-lowγ-band (posterior) to α-band (AFz) associations, α-columns (e.g., Fig 13F; also see the posterior region of Fig 13A–13B). The associations from non-posterior sites generally included the α-band (non-posterior) to α-band (AFz) associations (e.g., Fig 13E; also see the anterior, central, and lateral regions of Fig 13A–13B). In addition, the associations from anterior and lateral sites to AFz included broad associations in the highβ-γ band as well as within-frequency (diagonal) associations (e.g., Fig 13C–13D; also see the anterior and dorsal-lateral regions of Fig 13A–13B).
Fig 13. Cross-site spectral-power associations on the seconds timescale (across 500 ms intervals) from all sites to AFz (a representative central site).
A. 2D spectral-power association plots. Some associations are columnar, indicating multiple frequencies associated with a specific (primarily α) band, some are square, indicating broad associations among multiple frequencies, and some are diagonal, indicating within-frequency associations. B. Replotting of A. Each curve shows the spectral-power modulation at AFz associated with the probe-site power variation in each major frequency band (lower-to-higher frequency bands labeled with cooler-to-warmer colors), with the shaded regions indicating ±1 standard error of the mean (with participants as the random effect). In other words, each curve shows a horizontal slice of a 2D-association plot for a specific probe-site frequency band (see the rectangular boxes in the bottom panels). C-F. Representative associations. C. AF3 (an adjacent anterior site) to AFz spectral-power associations, characterized by the diagonal (within-frequency) associations (especially in the α band) as well as the broad associations among the highβ-γ bands. D. T7 (lateral) to AFz spectral-power associations, characterized by the diagonal (within-frequency) associations (especially in the α band) as well as the broad associations among the highβ-γ bands (as in C, but weaker). E. Cz (a central site) to AFz spectral-power associations, characterized by the α band at Cz associated with the α band at AFz. F. P8 (a posterior site) to AFz spectral-power associations, characterized by the θ-lowγ bands at P8 associated with the α band at AFz—α-column. Note that spectral-power associations from most posterior sites to AFz are characterized by α-columns, that is, the θ-lowγ bands at most posterior sites were associated with the α band at AFz (see the posterior region of A and B). The color scale is shown at the top of part A.
The seconds-timescale cross-site spectral-power associations to T7 and T8 (representative left and right lateral sites) from posterior sites were characterized by the θ-lowγ-band (posterior) to α-band (T7/T8) associations, α-columns (e.g., Fig 14E, 14L; also see the posterior region of Fig 14A–14B, 14H–14I). The associations from non-posterior sites to T7 and T8 generally included the α-band (non-posterior) to α-band (T7/T8) associations (e.g., Fig 14C–14D, 14F–14G, 14J–14K, 14M–14N; also see the anterior, central, and lateral regions of Fig 14A–14B, 14H–14I). In addition, the associations from the ipsilateral and contralateral sites to T7 and T8 included broad associations in the highβ-γ bands (e.g., Fig 14C–14D, 14G, 14J, 14M–14N; also see the lateral regions of Fig 14A–14B, 14H–14I) as well as within-frequency (diagonal) associations from the ipsilateral sites (e.g., Fig 14C–14D, 14M–14N).
Note that the seconds-timescale cross-site association patterns to Oz (posterior), Cz (central), AFz (anterior), T7 (left lateral), and T8 (right lateral) were generally bilaterally symmetric (Fig 11A–11B [posterior], Fig 12A–12B [central], Fig 13A–13B [anterior], Fig 14A vs. 14H, Fig 14B vs. 14I, Fig 14C–14G vs. 14J–14N [lateral]). Further, the above conclusions hold for data from either the odd or even numbered participants (see S3A–S3C Fig [posterior], S3D–S3F Fig [central], S3G–S3I Fig [anterior], S3J–S3L Fig, S3M–S3O Fig [lateral]).
In summary, the (slower) seconds-timescale (across 500 ms intervals) cross-site (long-distance) spectral-power associations (all positive) are characterized by the α-band to α-band associations prevalent across most site pairs (Figs 11–14), within-frequency (diagonal) associations from proximate sites (Figs 11–14), broad highβ-γ-band associations involving lateral and anterior targets (Figs 13 and 14), and notably by the θ-lowγ-band to α-band associations, α-columns, from posterior sites to other sites (Figs 12–14).
General discussion
The observed EEG spectral power intrinsically fluctuated on at least two distinct timescales, the sub-second timescale (within a 500 ms interval) with the low and high states typically lasting ~230 ms, and the seconds timescale (across 500 ms intervals) with the low and high states typically lasting ~3.75 s (Fig 2). Distinct patterns of intrinsic spectral-power associations were observed on these sub-second and seconds timescales, characterized by region—anterior, lateral, central, versus posterior—and spatial scale—within versus between EEG-derived current sources. While future research is necessary to understand the functional implications of these intrinsic spectral-power association patterns on perceptual, attentional and cognitive processes, we consider some straightforward interpretations.
The overall results suggest that the fast sub-second-timescale coordination of spectral power is limited to local amplitude modulation and insulated within-frequency long-distance interactions, while the characteristic columnar patterns of cross-frequency interactions emerge on the slower seconds timescale.
In particular, the sub-second associations for the β-γ frequencies at Δf~ 10 Hz at posterior sites (e.g., Fig 3A) suggest that the β-γ oscillations, implicated in a variety of attentional and cognitive processes (e.g., [7,10,11–13,15,44]), are amplitude-modulated at ~10 Hz in the occipital region. In general, the detection of consistent co-occurrences of f1 Hz and f2 Hz oscillations at a single source implies the presence of a (f1+f2)/2 Hz oscillation being amplitude-modulated at |f2–f1| Hz. Thus, the consistent co-occurrences of the β-γ oscillations at Δf~ 10 Hz at posterior sites suggest that the β-γ oscillations are amplitude-modulated at ~10 Hz in the occipital region. Amplitude-modulation at ~10 Hz may in turn imply that the amplitude dynamics of the β-γ oscillations may be phase-coupled to α-band (8–12 Hz) oscillations in the occipital region. Indeed, a human MEG study reported that γ bnad (30–70 Hz) amplitude variations were coupled to the phase of α (8-13Hz) oscillations primarily in the occipital area during rest with the eyes closed [17]. A monkey unit-recording study also reported that γ band (30-200Hz) amplitude variations were coupled to the phase of α (7-14Hz) oscillations in V1 during rest [45]. These results taken together suggest that occipital α oscillations play a role in organizing β-γ oscillations into α-band amplitude-modulated (AM) packets. If so, α power may covary with β-γ power in the posterior region because extensively synchronized (high power) α oscillations may be required to organize extensively synchronized (high power) β-γ oscillations into α-band AM packets.
We did not find consistent posterior associations between the α and β-γ frequencies on the sub-second timescale. This may not be surprising. The fact that the β-γ associations were primarily confined along the 45° lines at Δf~ 10 Hz (e.g., Fig 3A) suggests that the β-γ frequency oscillations were amplitude-modulated at Δf~ 10 Hz relatively independently of one another; otherwise, the spectral power across the β-γ frequencies would have been broadly associated. This means that the α-band AM packets for different frequency pairs would have been temporally dispersed within a 500 ms interval. Therefore, even if the α oscillations played a role in organizing the β-γ oscillations into α-band AM packets, the α power would not necessarily fluctuate with the β-γ power on the sub-second timescale. For example, within any given sub-second interval, the α power would have likely been consistently high when the various β-γ oscillations (to be organized into α-band AM packets) were elevated and consistently low when the various β-γ oscillations were reduced. This reasoning predicts that the associations between the α power and the β-γ power should be observed on a longer timescale. Indeed, on the seconds timescale, posterior sites yielded vertical columns at the α band—α-columns, indicating that the α power co-varied with the β-lowγ power over the slower timescale. Thus, the Δf~ 10 Hz characteristic of the sub-second-timescale associations and the α-column characteristic of the seconds-timescale associations at posterior sites jointly suggest that occipital α oscillations play a role in organizing β-γ oscillations into α-band AM packets.
This interpretation raises the possibility that the posterior processes mediated by β-γ oscillations may be transmitted to other regions as α-band AM packets. If so, the posterior β-γ oscillations may generate α oscillations at the receiving neural populations through non-linear interactions involving rectification. Examples of such rectifying interactions have been seen as binocular beats (e.g., [46]), heard as binaural beats (e.g., [47]), and observed in visual and auditory evoked EEG potentials (e.g., [48,49]). Thus, the β-γ power variations organized into α-band AM packets at posterior sites may be associated with α power variations at other sites. Our results support this prediction. The cross-site spectral-power associations from posterior sites to other sites were consistently characterized by α-columns (e.g., Fig 10A–10D; also see the posterior region of Figs 11–14), indicating that the θ-lowγ power (including the β-γ power) variations at posterior sites selectively coincided with the α power modulation at other sites on the seconds timescale. The fact that these associations were columnar rather than square-shaped (which would have indicated broad associations across the β-γ frequencies) is consistent with the above interpretation that different β-γ frequencies in the posterior region are relatively independently organized into α-band AM packets. Thus, the occipital operations involving β-γ oscillations may be frequency-wise organized into α-band AM packets to coordinate their interactions with other regions.
This interpretation is consistent with prior results suggesting that visual perception, awareness, and/or attention oscillate in the α rhythm (e.g., [3,50]). For example, stimulus visibility has been shown to correlate with the specific phase of the posterior EEG α oscillations (e.g., [2], but see [6]). Our results suggest that this correlation between visibility and the posterior α oscillations may be partly mediated by the α-band modulation of the information carried by β-γ band oscillations. This possibility is consistent with the proposal that the occipital α rhythms may contribute to periodically organizing early spatially-parallel visual signals, carried by the γ-band oscillations, into strength-based temporal code; that is, the gradual lifting of the inhibitory phase within each α-oscillation cycle may allow stronger signals to overcome the inhibition earlier, resulting in the strength-based temporal sequencing of the spatially-parallel visual sensory signals within each α-oscillation cycle (e.g., [9]). This process, which may be detected as α-band amplitude-modulation of γ-band power (as in the current results), may facilitate the serial attending and recognition of objects in downstream visual processing.
So far, we have inferred occipital α-phase-to-β-γ-amplitude coupling based on the characteristic Δf~ 10 Hz spectral-power associations for the β-γ frequencies on the sub-second timescale (e.g., Fig 3A). Additionally, we observed the Δf~ 3 Hz spectral-power associations for the θ-α-frequencies at posterior sites (e.g., Fig 3A). Does this imply δ-phase-to-θ-α-amplitude coupling in the posterior region? We also observed the Δf~ 16 Hz associations for the γ frequencies at lateral sites (e.g., Fig 3B). Does this imply lowβ-phase-to-γ-amplitude coupling in the lateral region?
We sought corroborating evidence for the relationship between the Δfassociations and phase-amplitude coupling. Our strategy was to determine whether the types of phase-power coupling implied by the Δfspectral-power associations matched the phase-amplitude coupling assessed with a standard method of computing the Modulation Index, MI (e.g., [51,52]). In short, the mean amplitude of the faster frequency band—amplitude frequency or Af—that coincides with each phase bin of the slower frequency band—phase frequency or Pf—is computed (over some temporal interval) to determine the degree to which the distribution of the Af amplitude over the Pf phase is peaky (i.e., the degree to which large Af amplitudes are concentrated at specific phase(s) of the Pf oscillation), using an entropy measure [51]. The specific equation of MI yields a value of 0 if the distribution is flat and 1 if the distribution is maximally peaky (i.e., if the Af amplitudes are non-zero only at a single Pf phase bin). We used the full data length (~300 s) to compute MI’s, and also subtracted the control MI’s computed with the corresponding phase-scrambled data (per site per participant).
The sub-second Δf~ 3 Hz associations for the θ-α-frequencies at posterior sites (e.g., Fig 3A) potentially imply a selective coupling of the θ-α amplitudes to the phase of the δ-band oscillations. However, we did not observe that the MI’s for the Pf of 3–4 Hz was selectively elevated for the Af of θ-α bands at the corresponding sites (data not shown). Thus, it is inconclusive as to whether the Δf~ 3 Hz associations at posterior sites imply phase-amplitude coupling.
The results were more encouraging for the Δf~ 10 Hz and Δf~ 16 Hz associations. The Δf~ 10 Hz associations for the β-γ-frequencies at posterior sites potentially imply a coupling of β-γ amplitudes to the phase of the α-band oscillations (a representative example from PO8 shown in Fig 15B). This would selectively elevate MI for the combinations of Pf = 8–12 Hz (α band) with Af = 15–30 Hz (β band) and Af = 30–55 Hz (γ band). This prediction was confirmed (representative results from PO8 shown in Fig 15C; see the data points highlighted in the dashed rectangle). To confirm selectivity, MI for the combination of Pf = 13–17 Hz (lowβ band) with neither Af = 15–30 Hz (β band) nor Af = 30–55 Hz (γ band) was elevated (see non-highlighted data points in Fig 15C). Similarly, the Δf~ 16 Hz associations for the γ-frequencies at lateral sites (e.g., Fig 3B) potentially imply a coupling of the γ amplitudes to the phase of the lowβ-band oscillations (a representative example from C6 shown in Fig 15E). This would selectively elevate MI for the combination of Pf = 13–17 Hz (lowβ band) with Af = 30–55 Hz (γ band). This prediction was confirmed (representative results from C6 shown in Fig 15F; see the data point highlighted in the dashed rectangle). To confirm selectivity, MI for the combination of Pf = 13–17 Hz (lowβ band) with Af = 15–30 Hz (β band) was not elevated; neither was MI elevated for the combination of Pf = 8–12 Hz (α band) with Af = 15–30 Hz (β band) or Af = 30–55 Hz (γ band) (see non-highlighted data points in Fig 15F).
Fig 15. Relationship between the posterior Δf~ 10 Hz and lateral Δf~ 16 Hz spectral-power associations on the sub-second timescale and phase-amplitude coupling assessed as the Modulation Index (MI).
A. The spatial distribution of the spectral-power associations on the sub-second timescale (same as Fig 3D). B. A representative example of the posterior Δf~ 10 Hz (8–12 Hz, α band) associations for the β-γ frequencies at PO8. This pattern of spectral-power associations may imply a phase-amplitude coupling of the phase-frequency band (Pf) corresponding to Δf(8–12 Hz, α band) with the amplitude-frequency band (Af) in both the β (green bars) and γ (gold bars) ranges (see dashed rectangles and arrows). C. The phase-amplitude coupling assessed as MI (MI for real data minus MI for phase-scrambled data) at PO8. As implied by the spectral-power associations shown in B, MI was elevated selectively for the combination of Pf = 8–12 Hz (α band) with both Af = 15–30 Hz (β band) and Af = 30–55 Hz (γ band) (highlighted with the dashed rectangle). To confirm selectivity, MI was not elevated for the combination of Pf = 13–17 (lowβ band) with Af = 15–30 Hz (β band) or Af = 30–55 Hz (γ band). The error bars represent ±1 standard error of the mean with participants as the random effect. D. Left. Spatial distribution of MIz (z-normalized across sites per participant to focus on the spatial patterns of MI) averaged for the combinations of Pf = 8–12 Hz (α band) with Af = 15–30 Hz (β band) and Af = 30–55 Hz (γ band) (e.g., the dashed rectangle in C) predicted to be elevated by the posterior spectral-power associations shown in B. The posterior distribution of MIz largely parallels the posterior distribution of the Δf~ 8–12 Hz associations (see A). Right. The MIz distributions plotted separately for the odd and even numbered participants showing the degree of inter-participant variability. E. A representative example of the lateral Δf~ 16 Hz (13–17 Hz, lowβ band) associations for the γ frequencies at C6. This pattern of spectral-power associations may imply a phase-amplitude coupling of the phase-frequency band (Pf) corresponding to Δf(13–17 Hz, lowβ band) with the amplitude-frequency band (Af) in the γ (gold bars) range (see the dashed rectangles and arrows). F. The phase-amplitude coupling assessed as MI (MI for real data minus MI for phase-scrambled data) at C6. As implied by the spectral-power associations shown in E, MI was elevated selectively for the combination of Pf = 13–17 Hz (lowβ band) with Af = 30–55 Hz (γ band) (highlighted with dashed rectangle). To confirm selectivity, MI was not elevated for the combination of Pf = 13–17 (lowβ band) with Af = 15–30 Hz (β band); neither was it elevated for the combination of Pf = 8–12 Hz (α band) with Af = 15–30 Hz (β band) or Af = 30–55 Hz (γ band). The error bars represent ±1 standard error of the mean with participants as the random effect. G. Left. Spatial distribution of MIz (z-normalized across sites per participant to focus on the spatial patterns of MI) for the combination of Pf = 13–17 Hz (lowβ band) with Af = 30–55 Hz (γ band) (e.g., the dashed rectangle in F) predicted to be elevated by the lateral spectral-power associations shown in E. The lateral distribution of MIz largely parallels the lateral distribution of the Δf~ 13–17 Hz associations (see A). Right. The MIz distributions plotted separately for the odd and even numbered participants showing the degree of inter-participant variability.
We compared the spatial distributions of the Δf~ 10 Hz and Δf~ 16 Hz spectral-power associations (Fig 15A) with the spatial distributions of MI values for the expected phase-power coupling. To this end, we plotted the spatial distribution of the average of the MI values for the combinations of Pf = 8–12 Hz (α band) with Af = 15–30 Hz (β band) and Af = 30–55 Hz (γ band), predicted to be elevated in relation to the Δf~ 10 Hz spectral-power associations (e.g., Fig 15B–15C). These MI values were first z-normalized across sites per participant (MIz) so that the analysis focused on the spatial patterns of MI. The distribution of MIz covered the posterior region (Fig 15D, left) largely paralleling the posterior distribution of the Δf~ 10 Hz association (Fig 15A). The posterior MIz distribution appears to be reasonably reliable as the patterns obtained from the odd and even numbered participants were similar (Fig 15D, right). Similarly, we plotted the spatial distribution of MIz for the combination of Pf = 13–17 Hz (lowβ band) with Af = 30–55 Hz (γ band), predicted to be elevated in relation to the Δf~ 16 Hz spectral-power associations (e.g., Fig 15E–15F). The distribution covered the lateral region (Fig 15G, left) largely paralleling the lateral distribution of the Δf~ 16 Hz association (Fig 15A). Again, the lateral MIz distribution appears to be reasonably reliable as the patterns obtained from the odd and even numbered participants were similar (Fig 15G, right).
These results provide indirect evidence suggesting that at least the spectral-power associations at Δf~ 10 Hz and Δf~ 16 Hz on the sub-second timescale are related to amplitude-modulation of higher-frequency oscillations by the phase of Δfoscillations. For the posterior Δf~ 10 Hz associations on the sub-second timescale that imply α-phase-to-β-γ-amplitude coupling, our results suggest a coherent interpretation relating them to the α-column associations on the seconds timescale observed at posterior sites and between posterior and non-posterior sites (see above). However, the current results do not provide a coherent interpretation for the lateral Δf~ 16 Hz associations that imply lowβ-phase-to-γ-amplitude coupling.
Explanations are also required as to why the (fast) sub-second-timescale cross-site (long-distance) diagonal associations were dominated by α (8-15hz), β-γ (>30Hz), or a combination of α and β-γ frequencies, but never dominated by β (15-30Hz) frequencies (e.g., Fig 5; also see Figs 6–9). Given that diagonal associations indicate insulated within-frequency interactions (i.e., independent interactions for different frequencies), the fast, long-distance diagonal associations may reflect feedforward (dominated by frequencies above ~40 Hz; [44]) and feedback (dominated by 5–20 Hz while peaking at ~10Hz; [44]) interactions. Note that, although our participants rested with their eyes closed, they continuously received and processed environmental sensory stimuli. The fact that the fast diagonal long-distance associations to Cz (a representative central site) were never dominated by the β-γ frequencies (Fig 7) may potentially suggest that central sites do not strongly engage in feedforward interactions while people rest with their eyes closed.
The cross-site associations generally diminished with distance. However, there were cases where strong associations persisted between distant sites (with weaker associations at intermediate distances). Those “super” long-distance associations were typically α-band to α-band on both the sub-second and seconds timescales, but there were some exceptions, including the fast within-frequency β-γ associations from lateral sites, T7/T8, to the inferior posterior site, Oz, and vice versa, on the sub-second timescale (e.g., Figs 6C, Fig 9F and 9K), and the slower broad β-γ associations from distant contralateral sites such as TF8/TF7 to lateral sites, T7/T8, on the seconds timescale (e.g., Fig 14G and 4J; also see Fig 14A–14B and 14H–14I). The former may be relevant to hierarchical visual processing occurring on the (fast) sub-second timescale whereas the latter may be relevant to cross-hemisphere coordination occurring on the (slower) seconds timescale.
When analyzing cross-frequency associations using frequency decomposition methods, one needs to be mindful of the artifactual harmonics generated by non-sinusoidal waveforms. In particular, recent computational studies have demonstrated that non-sinusoidal waveforms of α oscillations could generate harmonics that mimic the coupled β-γ oscillations (e.g., [53,54]). This waveform artifact could contribute broad spectral-power associations among the α through β-γ frequencies as the power of artifactual β-γ harmonics would synchronously covary with the power of the non-sinusoidal α oscillations. Nevertheless, because the signals at each EEG current-source (site) reflect extensive spatial summation of neuronal signals at variable delays, any observable effects of artifactual spectral-power associations due to the harmonics generated by non-sinusoidal waveforms would have been attenuated [55]. Further, most of the characteristic spectral-power associations we obtained on the sub-second and seconds timescales are not characterized by broad associations among the α through β-γ frequencies.
Finally, the distinct patterns of intrinsic spectral-power associations characterized by the parallel-to-diagonal, diagonal, columnar, and square associations may provide a useful reference for understanding how intrinsic global dynamics adjust to sensory dynamics and behavioral demands. For example, we have obtained some preliminary results suggesting that, while people watched a silent nature video, the intrinsic posterior Δf~ 10Hz associations for the β-γ power on the sub-second timescale (obtained while participants rested with their eyes closed) strengthened but Δfshifted to the lowerα/upperθ frequencies (leaving the lateral Δf~ 16Hz associations for the γ frequencies unchanged), while the α-column associations from posterior sites to other sites on the seconds timescale disappeared (Menceloglu, Grabowecky, & Suzuki, unpublished data). While these preliminary results suggest that intrinsic spectral-power associations undergo characteristic adjustments from resting with the eyes closed to free viewing, they need to be confirmed and the sources of the adjustments investigated, for example, by determining whether they are due to the eyes being open per se, the presence of visual stimulation, and/or the act of free viewing. Investigating such adjustments in relation to various sensory dynamics and behavioral demands may contribute to an understanding of how internal neural dynamics are optimized for interacting with environmental dynamics.
In summary, we examined the global distribution of spectral-power associations, focusing on both the local characteristics reflected in the cross-frequency associations within individual EEG-derived current sources (sites) and the long-distance characteristics reflected in the cross-frequency associations between sites. Distinct association patterns emerged on the (fast) sub-second and (slower) seconds timescales, suggesting that the fast coordination of spectral power appears to be limited to local amplitude modulation (suggestive of phase-power coupling) and insulated within-frequency long-distance interactions (dominated by the α and γ bands, likely reflecting feedforward and feedback processes), while the characteristic columnar patterns of cross-frequency interactions emerge on the slower timescale. While the functional significance of these intrinsic spectral-power associations awaits future research, the patterns of associations within the posterior region and between the posterior and other regions suggest that the intrinsic occipital dynamics are structured in such a way that the β-γ oscillations are organized into α-band (~10 Hz) amplitude-modulated packets to interact with other regions.
Supporting information
(JPEG)
(JPEG)
(JPEG)
Data Availability
Relevant data are in the paper and its Supporting Information files. Additionally, the EEG data are deposited at Dryad under doi: 10.5061/dryad.hdr7sqvf9.
Funding Statement
Yes. NIH T32 grant to MM.
References
- 1.Buzsaki G. (2006). Rhythms of the Brain, Oxford University Press. [Google Scholar]
- 2.Mathewson K. E., Gratton G., Fabiani M., Beck D. M., & Ro T. (2010). To see or not to see: prestimulus alpha phase predicts visual awareness. Journal of Neuroscience, 29, 2725–2732. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Mathewson K. E., Lleras A., Beck D. M., Fabiani M., Ro T., Gratton G. (2011). Pulsed out of awareness. EEG alpha oscillations represent a pulsed-inhibition of ongoing cortical processing. Frontiers in Psychology, 2, A99, 1–15. 10.3389/fpsyg.2011.00001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Voytek B., Canolty R. T., Shestyuk A., Crone N. E., Parvizi J., & Knight R. T. (2010). Shifts in gamma phase-amplitude coupling frequency theta to alpha over posterior cortex during visual tasks. Frontiers in Human Neuroscience, 4, A191, 1–9. 10.3389/neuro.09.001.2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Dehaene S., & Changeux J.-P. (2011). Experimental and theoretical approaches to conscious processing. Neuron, 70, 200–227. 10.1016/j.neuron.2011.03.018 [DOI] [PubMed] [Google Scholar]
- 6.Busch N. A., & VanRullen R. (2010). Spontaneous EEG oscillations reveal periodic sampling of visual attention. Proceedings of the National Academy of Sciences, 107(37), 16048–16053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Klimesch W. (2012). Alpha-band oscillations, attention, and controlled access to stored information. Trends in Cognitive Sciences, 16(12), 606–617. 10.1016/j.tics.2012.10.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Bonnefond M, & Jensen O. (2015). Gamma activity coupled to alpha phase as a mechanism for top-down controlled gating. PLoS ONE, 10(6): e0128667, 1–11. 10.1371/journal.pone.0128667 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Jensen O., Gips B., Bergmann T. O., & Bonnefond M. (2014). Temporal coding organized by coupled alpha and gamma oscillations prioritize visual processing. Trends in Neurosciences, 37(7), 357–369. 10.1016/j.tins.2014.04.001 [DOI] [PubMed] [Google Scholar]
- 10.Duzel E., Penny W. D., & Burgess N. (2010). Brain oscillations and memory. Current Opinion in Neurobiology, 20, 143–149. 10.1016/j.conb.2010.01.004 [DOI] [PubMed] [Google Scholar]
- 11.Donner T. H., & Siegel M. (2011). A framework for local cortical oscillation patterns. Trends in Cognitive Sciences, 15(5), 191–199. 10.1016/j.tics.2011.03.007 [DOI] [PubMed] [Google Scholar]
- 12.Engel A. K., & Fries P. (2010). Beta-band oscillations—signaling the status quo? Current Opinion in Neurobiology, 20, 156–165. 10.1016/j.conb.2010.02.015 [DOI] [PubMed] [Google Scholar]
- 13.Palva S., & Palva M. (2007). New vistas for a-frequency band oscillations. Trends in Neurosciences, 30(4), 150–158. 10.1016/j.tins.2007.02.001 [DOI] [PubMed] [Google Scholar]
- 14.Palva J. M., Palva S., & Kaila K. (2005). Phase synchrony among neuronal oscillations in the human cortex. Journal of Neuroscience, 25(15), 3962–3972. 10.1523/JNEUROSCI.4250-04.2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Fries P. (2005). A mechanism for cognitive dynamics: neural communication through neural coherence. Trends in Cognitive Sciences, 9(10), 474–480. 10.1016/j.tics.2005.08.011 [DOI] [PubMed] [Google Scholar]
- 16.Müller V., Perdikis D., Oertzen T., Sleimen-Malkoun R, Jirsa V., & Lindenberger U. (2016). Structure and topology dynamics of hyper-frequency networks during rest and auditory oddball performance. Frontiers in Computational Neuroscience, 10, Article 108, 1–25. 10.3389/fncom.2016.00001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Osipova D., Hermes D., & Jensen O. (2008). Gamma-power is phase-locked to posterior alpha activity. PLoS ONE, 3(12), e3990, 1–7. 10.1371/journal.pone.0003990 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Palva S., & Palva J. M. (2012). Discovering oscillatory interaction networks with M/EEG: challenges and breakthroughs. Trends in Cognitive Sciences, 16(4), 219–230. 10.1016/j.tics.2012.02.004 [DOI] [PubMed] [Google Scholar]
- 19.Hipp J. F., Hawellek D. J., Corbetta M., Siegel M., & Engel A. K. (2012). Large-scale cortical correlation structure of spontaneous oscillatory activity. Nature Neuroscience, 15(6), 884–890. 10.1038/nn.3101 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Scally B., Burke M. R., Bunce D., & Delvenne J.-F. (2018). Resting-state EEG power and connectivity are associated with alpha peak frequency slowing in healthy aging. Neurology of Aging, 71, 149–155. [DOI] [PubMed] [Google Scholar]
- 21.Adebimpe A., Arabi A., Bourel-Ponchel E., Mahmoudzadeh M., & Wallois F. (2016). EEG resting state functional connectivity analysis in children with benign epilepsy with centrotemporal spikes. Frontiers in Neuroscience, 10, Article 143, 1–9. 10.3389/fnins.2016.00001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Antonakakis M., Dimitriadis S. I., Zervakis M., Micheloyannis S., Resaie R., Babajani-Feremi A., et al. (2016). Altered cross-frequency coupling in resting-state MEG after mild traumatic brain injury. International Journal of Psychophysiology, 102, 1–11. 10.1016/j.ijpsycho.2016.02.002 [DOI] [PubMed] [Google Scholar]
- 23.Gonzalez G. F., Simt D. J. A., van der Molen M. J. W., Tijms J., Stam C. J., de Geus E. J. C., et al. (2018). EEG resting state functional connectivity in adult dyslexics using phase lag index and graph analysis. Frontiers in Human Neuroscience, 12, Article 341, 1–12. 10.3389/fnhum.2018.00001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Delorme A., & Makeig S. (2004). EEGLAB: an open source toolbox for analysis of single-trial EEG dynamics including independent component analysis. Journal of Neuroscience Methods, 134(1), 9–21. 10.1016/j.jneumeth.2003.10.009 [DOI] [PubMed] [Google Scholar]
- 25.Lopez-Calderon J., & Luck S. J. (2014). ERPLAB: an open-source toolbox for the analysis of event-related potentials. Frontiers in Human Neuroscience, 8, 213 10.3389/fnhum.2014.00213 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Hjorth B. (1980). Source derivation simplifies topographical EEG interpretation. American Journal of EEG Technology 20, 121–132. [Google Scholar]
- 27.Kayser J., Tenke C. E. (2006). Principal components analysis of Laplacian waveforms as a generic method for identifying ERP generator patterns: I. Evaluation with auditory oddball tasks. Clinical Neurophysiology, 117, 348–368. 10.1016/j.clinph.2005.08.034 [DOI] [PubMed] [Google Scholar]
- 28.Tenke C. E., & Kayser J. (2012). Generator localization by current source density (CSD): Implications of volume conduction and field closure at intracranial and scalp resolutions. Clinical Neurophysiology, 123, 2328–2345. 10.1016/j.clinph.2012.06.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Perrin F., Pernier J., Bertrand O., Giard M. H., & Echallier J. F. (1987). Mapping of Scalp Potentials by Surface Spline Interpolation. Electroencephalography and Clinical Neurophysiology, 66 (1), 75–81. 10.1016/0013-4694(87)90141-6 [DOI] [PubMed] [Google Scholar]
- 30.Perrin F., Pernier J., Bertrand O., & Echallier J. F. (1989). Corrigenda EEG 02274. Electroencephalography and Clinical Neurophysiology 76, 565. [DOI] [PubMed] [Google Scholar]
- 31.Perrin F., Pernier J., Bertrand O., & Echallier J. F. (1989). Spherical Splines for Scalp Potential and Current Density Mapping. Electroencephalography and Clinical Neurophysiology 72(2): 184–187. 10.1016/0013-4694(89)90180-6 [DOI] [PubMed] [Google Scholar]
- 32.Cohen M. X. (2014). Analyzing Neural Time Series Data: Theory and Practice, MIT Press. [Google Scholar]
- 33.Koch C. (1999). Biophysics of Computation: Information Processing in Single Neurons. Oxford. [Google Scholar]
- 34.Mazzoni A., Panzeri S., Logothetis N. K., & Brunel N. (2008). Encoding of naturalistic stimuli by local field potential spectra in networks of excitatory and inhibitory neurons. PLoS Computational Biology, 4(12): e1000239 10.1371/journal.pcbi.1000239 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.He B. J. (2014). Scale-free brain activity: past, present, and future. Trends in Cognitive Sciences, 18(9), 480–487. 10.1016/j.tics.2014.04.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Hess R. F. & Snowden R. J., (1992) Temporal properties of human visual filters: Number, shapes and spatial covariance, Vision Research, 32, 47–60. 10.1016/0042-6989(92)90112-v [DOI] [PubMed] [Google Scholar]
- 37.Lui L. L., Bourne J. A., Rosa M. G. P. (2007). Spatial and temporal frequency selectivity of neurons in the middle temporal visual area of new world monkeys (Callithrix jacchus). European Journal of Neuroscience, 25, 1780–1792. 10.1111/j.1460-9568.2007.05453.x [DOI] [PubMed] [Google Scholar]
- 38.Kiya H., Ito I., & Miron S. (2010). "Phase scrambling for image matching in the scrambled domain" in Signal Processing, InTech, 97–414. [Google Scholar]
- 39.Lamme V. A., Zipser K., & Spekreijse H. (2002). Masking interrupts figure-ground signals in V1. Journal of Cognitive Neuroscience, 14(7), 1044–1053. 10.1162/089892902320474490 [DOI] [PubMed] [Google Scholar]
- 40.Fahrenfort J. J., Scholte H. S., & Lamme V. A. (2007). Masking disrupts reentrant processing in human visual cortex. Journal of Cognitive Neuroscience, 19(9), 1488–1497. 10.1162/jocn.2007.19.9.1488 [DOI] [PubMed] [Google Scholar]
- 41.Collyer C. E., Broadbent H. E., & Church R. M. (1994). Preferred rates of repetitive tapping and categorical time production. Perception & Psychophysics, 55(4), 443–453. [DOI] [PubMed] [Google Scholar]
- 42.Pachi A., & Ji T. (2005). Frequency and velocity of people walking. Structural Engineering, 83(3), 36–40. [Google Scholar]
- 43.Pelz J. B., & Rothkopf C. (2007). Oculomotor behavior in natural and man-made environments In van Gompel R., Fischer M., Murray W., & Hill R. (Eds.), Eye Movements: a window on Mind and Brain (first., pp. 661–676). Amsterdam: Elsevier. [Google Scholar]
- 44.Michalareas G., Vezoli J., van Pelt S., Schoffelen J.-M., Kennedy H., & Fries P. (2016). Alpha-beta and gamma rhythms subserve feedback and feedforward influences among human visual cortical areas. Neuron, 89, 384–397. 10.1016/j.neuron.2015.12.018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Spaak E., Bonnefond M., Maier A., Leopold D. A., & Jensen O. (2012). Layer-specific entrainment of gamma-band neural activity by the alpha rhythm in monkey visual cortex. Current Biology, 22(24), 2313–2318. 10.1016/j.cub.2012.10.020 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Baitch L. W. & Levi D. (1989). Binocular beats: psychophysical studies of binocular interaction in normal and stereoblind humans. Vision Research, 29(1), 27–35. 10.1016/0042-6989(89)90171-5 [DOI] [PubMed] [Google Scholar]
- 47.Licklider J. C., Webster J. C., & Hedlun J. M. (1950). On the frequency limits of binaural beats. Journal of the Acoustical Society of America, 22, 468–473. [Google Scholar]
- 48.Baitch L. W. & Levi D. (1988). Evidence for nonlinear binocular interactions in human visual cortex. Vision Research, 28(10), 1139–1143. 10.1016/0042-6989(88)90140-x [DOI] [PubMed] [Google Scholar]
- 49.Pratt H., Starr A., Michalewski H. J., Dimitrijevic A., Bleich N., & Mittleman N. (2009). Cortical evoked potentials to an auditory illusion: binaural beats. Clinical Neurophysiology, 120(8), 1514–1524. 10.1016/j.clinph.2009.06.014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.VanRullen R., Reddy L., & Koch C. (2005). Attention-driven discrete sampling of motion perception. Proceedings of the National Academy of Sciences, 102(14), 5291–5296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Tort A. B. L., Komorowski R., Eichenbaum H., and Kopell N. (2010). Measuring phase-amplitude coupling between neuronal oscillations of different frequencies. Journal of Neurophysiology, 104, 1195–1210. 10.1152/jn.00106.2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Hülsemann M. J., Naumann E., and Rasch B. (2019). Quantification of phase-amplitude coupling in neuronal oscillations: comparison of phase-locking value, mean vector length, modulation index, and generalized-linear-modeling-cross-frequency-coupling. Frontiers in Neuroscience. 13:573 10.3389/fnins.2019.00573 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Lozano-Soldevilla D., ter Huurne N., Oostenveld R. (2016). Neuronal Oscillations with Non-sinusoidal Morphology Produce Spurious Phase-to-Amplitude Coupling and Directionality. Frontiers in Computational Neuroscience, 10, 87 10.3389/fncom.2016.00087 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Velarde O.M., Urdapilleta E., Mato G., Dellavale D. (2019). Bifurcation structure determines different phase-amplitude coupling patterns in the activity of biologically plausible neural networks. NeuroImage, 202, 116031 10.1016/j.neuroimage.2019.116031 [DOI] [PubMed] [Google Scholar]
- 55.Schaworonkow N., & Nikulin V. V. (2019). Spatial neuronal synchronization and the waveform of oscillations: Implications for EEG and MEG. PLoS Computational Biology 15(5): e1007055 10.1371/journal.pcbi.1007055 [DOI] [PMC free article] [PubMed] [Google Scholar]