Abstract
Electrocardiogram (ECG) data compression has numerous applications. The time for generating compressed samples is a vital factor when we consider ambulatory devices, with the fact that data should be sent to the physician as soon as possible. In addition, there are some wearable ECG recorders that have limited power, and may only be capable of doing simple algorithms. With the aim of increasing the speed and simplicity of the compressors, we propose a system architecture that can generate compressed ECG samples, in a linear method and with CR 75%. We used sparsity of the ECG signal and proposed a system based on compressed sensing (CS) that can compress ECG samples, almost in real-time. We applied CS in a very small size in order to accelerate the compression phase and accordingly reducing the power consumption. Also, in the recovery phase, we used the recently developed Kronecker technique to improve the quality of the recovered signal. The system designed based on full-adder/subtractor (FAS) and shift registers, without using any external processor or any training algorithm.
Keywords: Compressed sensing (CS), Electrocardiogram (ECG), Compressor
Introduction
The speed of generating information and data outruns the speed of technology for designing capacious memory card. For example, a clinical examination that involved recording the ECG signals has to record the data, day and night. Since for certain patients, they use wearable ECG recorders that monitor their heart behavior intermittently. Moreover, this data will be stored for future assessment and checking the patients treatment behavior in the long run. Besides, there are conditions in which we have to send the ECG data on communication channels or telephone lines, i.e. remote health monitoring. Compression can be used for efficient use of communication channel in bandwidth limited networks, or efficient use of storage capacity [1, 2]. Then in most works, they used compression methods for transmission links and data storage. As the ADC is more willing to consume more power, the focus of researchers have been centered on this module to reduce the power consumption with keeping the accuracy and resolution high [3]. Since the ECG signal is a good compressible signal and has redundant information, numerous ECG compression algorithms have been proposed [4–10]. There are a few factors that can help us to compare the compressors and their applied algorithms. The first factor is the compression ratio (CR) that is an important factor for evaluating different methods. we used the CR as follow
| 1 |
where m and n are the number of compressed and original samples, respectively. The second factor is the compression algorithm’s complexity that can be more considerable when we talk about limited and weak ECG-recorders. The power consumption usually has a linear relation with the complexity of systems. Supplying the power for 24-h ambulatory or remote ECG recorders is very important, that encourage us to focus on systems that have low power consumption. The third factor is the processing speed that in emergency situations will be much more important. Considering the ambulatory ECG recorders, whatever the data sooner to be presented to a physician, the next orders from a physician can be given sooner as well. The fourth factor is the accuracy of the reconstructed signal that assesses the performance of the compression algorithm. Percentage root means square difference (PRD) and signal-to-noise ratio (SNR) are two common measures that can assess the quality of reconstruction. PRD measure can be calculated as follows,
| 2 |
| 3 |
where x(n) is the original ECG signal, is the reconstructed ECG signal, is the mean of original signal, and N denotes the length of signal. In [11], Zigel et al. established a link between the diagnostic distortion and the PRD. they proposed the different values of PRD for the reconstructed ECG signals and a qualitative assessment as perceived by the specialist was given. Table 1 shows the classified quality and corresponding SNR and PRD.
Table 1.
Assessment of quality of reconstruction [11]
| Quality | PRD | SNR |
|---|---|---|
| “Very good” | ||
| “Good” | ||
| “Undetermined” |
Table 1 shows that for PRD smaller than 2% the quality of reconstructed signal can be categorized as very good, for PRD among 2–9%, it is good, and above 9%, it is not possible to precisely determine the quality of the reconstructed signal.
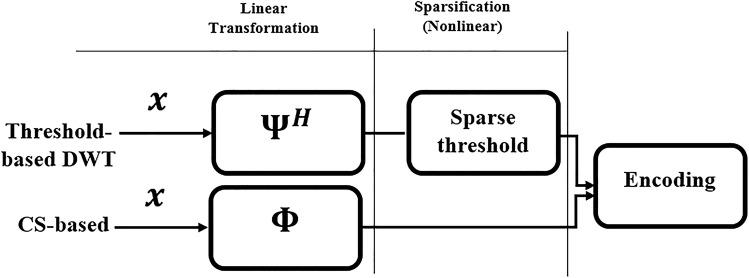
Compressed Sensing utilizes a novel approach to compression of signals. In the last decade this method was used for compression of images [12, 13], radar acquisitions [14, 15], sensor data [16, 17], traffic cloud data [18], etc. Recently, compressed sensing has been used as a reliable ECG data compression method. There are some inherent factors in CS-based compression that outperform conventional ECG compression methods. CS-based methods can be divided into two phases, compression, and recovery. The compression phase is linear since it is the multiplication of a matrix and a vector. In CS-based compression, there is no decision making process and feed-back. In addition, to generate compressed samples we have not any threshold in the sparse domain (for example in wavelet domain). On the other hand, there are ECG compression algorithms that require some nonlinear processing. One of the most common ECG compression algorithms is a digital wavelet transform (DWT) based algorithms, which is the basis of almost well-known compression algorithms for ECG signals [10]. In such transform-based compression algorithms, after mapping signal in the wavelet domain, a threshold level is used to preserving some large coefficients and throwing away small coefficients. Checking the coefficients by the threshold level requires time, power and computational resources. But in CS-based compression, compressed data is generated, at once. Figure 1 shows the schematics of both linear and nonlinear methods of compression. It is obvious that in CS-based compression after linear transformation, samples are sent to the encoding section without doing any process. However, in threshold DWT-based, a sparsification stage is followed by the first step.
Fig. 1.
Schematic of the two compression methods
In [4], Mamaghanian et al. showed that CS can be used as a reliable method of compression for ECG signals, and also, how this method can be more energy-efficient, and more importantly to be a real-time compression method. Also. in this work, we focused on the speed, and simplicity of the compressor and applied CS in a size that has not been reported. In addition, to enhance the quality of the reconstructed signal, we used adaptive dictionary learning which presents better sparse representation in the sparse domain. Considering the compression phase of CS, the length of the sparse signal plays a significant role. In CS, the length of the sparse signal has a direct relation with the size of the projection matrix, the CR, the computation complexity, and the order of sparsity. Given , length of x is equal with the number of columns in ; as the former increases, the latter increases accordingly. Then, has more elements and requires much storage space. In addition, the product of by x requires multiplications, and additions. Table 1 contains the relation of the size of the measurement matrix and the number of required multiplications and additions for certain sizes. It shows that if the size of the measurement matrix increases, the required operation will be dramatically increased. Hence it can be more efficient if we sense signals in a smaller length. In our work, we concentrated on a very small size sensing process, to have a shorter delay, computation complexity, and power consumption. This fact will be much more important when CS is applied in devices that have limited power supply and computational capability.
It can be inferred from Table 2 that selecting a measurement matrix with a smaller size can lead to less computational resources, power consumption and time of processing. Therefore, we utilized CS in a very small dimension to propose a CS-based compressor. For , we present a system that works based on linear compression, and the mathematics of CS is used to prove the veracity of this design. This compressor is composed of a few fast, low-powered, and inexpensive Integrated Circuits (IC) such as full-adder/subtractor (FAS) and a shift register. After sampling an ECG signal, some FASs randomly add or subtract the new sample with the previous value of FASs. After a few add/sub-cycles, the last output value of FASs is transferred as compressed samples. Shift registers are used to define the state of FAS, whether to add or subtract the current output with the next sample. After sending compressed data in a stationary medical center, reconstruction can be done.
Table 2.
Required number of multiplication/addition operations in CS for sensing 1024 ECG samples
| Size of measurement (m, n) matrix | Multiplication operation | Addition operation |
|---|---|---|
| (4, 16) | 4096 | 3840 |
| (8, 32) | 8192 | 7936 |
| (16, 64) | 16,384 | 16,128 |
| (32, 128) | 32,768 | 32,512 |
| (64, 256) | 65,536 | 65,280 |
Decreasing the projection matrixs size will affect the order of sparsity. There are two different classes of sparsifying bases: first class is fixed dictionaries such as wavelet transform dictionary or discrete cosine transform (DCT). The second class is adaptive dictionaries that usually present better sparse representation. There are various adaptive dictionary learning algorithms, such as the method of optimal direction (MOD) [19], and K singular value decomposition (K-SVD) [20] which can present efficient sparsifying dictionary if the training set has been selected accurately. For the case of wearable ECG recorders that are used by a patient, after training a dictionary, the probability of major change in ECG data of patients is low; hence adaptive sparsifying dictionary methods can be applied to produce a more efficient sparsifying dictionary. Since the sparsity has a direct relation with the quality of the reconstructed signal, it leads to compensate for the effect of decreasing the length of the projection matrix. In this work, adaptive dictionary learning is used for the ECG signal, and the result shows that it can be a well alternative to the fixed dictionaries used by previous researches.
Compressed sensing
Compressed sensing (CS) is a new sampling model for acquiring and reconstructing a potentially sparse signal, by solving an underdetermined linear system [21]. Aside from compression, CS can also be used for denoising and enhancement of signals [13]. Sparsity is one of the most important perquisites of CS where almost communication and medical signals have a sparse representation. For example, through dictionaries such as Karhunen–Love (KL), discrete cosine transform (DCT), or Wavelet transform, one can map a speech, voice, image, video, or specifically an ECG signal to a sparse domain. In addition, adaptive dictionary learning can be used to generate an efficient dictionary, and in comparison with those fixed dictionaries, adaptive methods usually present a better sparse representation. Signal s can be called k-sparse when it has only k nonzero coefficients and other coefficients to be zero. This definition of sparsity is not in line with the nature of real signals. Because almost practical signals after projection in the sparse domain have k nonzero coefficients and small coefficients. By an orthonormal projection matrix , x maps to sparse domain, i.e. . Given a k-sparse signal , to obtain the compressed measurements, it is enough to multiplying measurement matrix , , by x, i.e. , where y is measurement vector that has lower dimension than x. For simplicity and decreasing the extra notations, we set . For reconstructing the original signal in noiseless case, if s is sparse enough , it can be reconstructed from lesser m measurements by solving the minimization problem, in (4),
| 4 |
and also for noisy case, (5) can be solved.
| 5 |
where is the estimated sparse signal and is upper bound on the Euclidean norm of the contributed noise. Some hypothesizes have been proposed to guarantee the stable recovery of the initial signal. It is proved that Restricted Isometry Property (RIP) [22] is sufficient condition for exact reconstruction of sparse signal,
| 6 |
where is isometry constant of a matrix A, and its value is between zero to one. Checking RIP of a matrix is infeasible, but random measurement matrices with overwhelming probability preserve the RIP condition. For example, Binomial distribution is a sub-Gaussian distribution (probability distribution with strong tail decay property) that can preserve the RIP condition. In contrast to the compression phase in CS, in the recovery phase, we have to solve a rather complex problem, because, we face an underdetermined system of equations. To do recovery, there are numerous algorithms, such as Basis Pursuit [23], Greedy algorithms [24, 25] which are faster than Basis Pursuit but dont provide as good estimation of original signal as Basis Pursuit can, and also Smooth-L0 (SL0) [26], that is about two to three times faster than current linear programming algorithms. In this study, since we compress the signal in very small size, ordinary recovery technique may not bring high quality. However, In [27], Zanddizari et al. proposed a preprocessing approach based on kronecker technique to improve the quality of the reconstructed signal. The Kronecker-based CS recovery also has been employed for the recovery of many different signals. Khoshnevis et al. used similar method for compression of visual event related potentials (ERP) that were extracted from background EEG signals [28]. They were able to achieve a high recovery rate by adding the kronecker step to the CS algorithm. There are other areas of biomedical signal processing that have benefited from CS method, and using Kronecker technique for improving the quality of reconstructed signal such as Magnetic resonance imaging (MRI) [29], ECG [30] and speech [31].
CS-based compressor
In this CS-based ECG compressor, we convert every 16 consecutive samples to 4 compressed samples, or measurements. For generating compressed samples, we take advantage of CS and we apply this theory to practice. To achieve , the dimensions of input ECG signal is , and measurement matrix is . Through multiplication of by x, , each block of 16 consecutive ECG samples are mapped to 4 compressed samples of y. For selecting an appropriate measurement matrix, there are many random distributions that with high probability preserve the RIP condition. We chose a random measurement matrix from binomial distribution. The elements of each row are loaded into one shift register, in such a way that as on or and as off or . The number of shift-registers is equal with the number of rows; in the measurement matrix we have 4 rows, so we should have 4 shift registers as well. Every row of measurement matrix has 16 elements, so the shift registers should have 16-bit, too. We choose a measurement matrix and this matrix will be fixed as a permanent specification of this CS-based ECG compressor. Figure 2 shows this matrix, and how its rows should be loaded into shift registers. All rows of this matrix have been loaded to four 16-bit shift registers. Now, suppose that the , which has been shown in Fig. 2, to be multiplied by a 16-sample block of an ECG signal. It will add or subtract 16 samples by each other, and generate four compressed samples. For instance, regarding the first row of this measurement matrix, components in this row define which sample should be added and which one should be subtracted. If we have one FAS, we just need to set the state of FAS, when to be in addition mode or when to be in subtraction mode. The lowest bit of the shift registers is used to select the mode of FASs. In words, for determining the state of FAS, either addition or subtraction, the state-select pin of this IC can be connected to the lowest bit of the shift registers.
Fig. 2.
Initial loading of measurement matrix to shift registers (SF), shift registers contain the information of measurement matrix
Figure 3 describes the proposed design. The raw ECG samples are connected to four FASs. The output of each FAS is fed back to itself, to do the whole process of multiplication. After 16 clocks, 16 consecutive ECG samples will be randomly mixed, in parallel via 4 FASs. After every 16 clocks, shift registers restart and the output of FASs are sent to the medical centre. Later on, FASs are reset and compression for new block can be started again. The number of shift registers and FASs depends on the required CR, the order of sparsity of input sparse signal, and the desired SNR. In current paradigm, every 16 samples are projected to 4 compressed samples; the CR is 75% or 4:16. Achieving more compression rate is feasible, but the reconstructed signal might have some discrepancy. As mentioned before, the number of bits in the shift registers determines the number of consecutive samples that must be randomly mixed. The rate of coming raw ECG samples does not play an important role in compression phase. It just determines the speed of shift registers and FASs. Whatever the samples generate faster, the shift registers and FASs must work faster as well. This compressor does not require any pre-synchronization to reconstruct signal, or sending side information to data centre for reconstruction. It just requires sending measurement matrix to medical centre for once. This compressor can be classified as a linear compressor, because it does multiplication of a matrix by a vector. To generate compressed samples, we do not use any processor, or any decision making process. For example, in many compression algorithms we have to set threshold for mapped data, and it is obvious that doing the task of keeping great coefficients and throwing away the coefficients below the threshold level need rather complex decision making algorithms.
Fig. 3.

Schematic diagram of CS-based compressor in which each 16-sample block of ECG samples converts to 4 compressed samples. The lowest bit of every shift register defines the mode of each FAS. Coming sample is added or subtracted by the current output-value of FAS. After 16 cycles, shift registers are restarted and the outputs of FASs are sent
In this model the simplicity of compressor has been regarded as the first goal, and with respect to this fact that the simplicity has direct relation with power consumption, this compressor is economic. For examples, there are ambulatory ECG recorders that intermittently generate samples, and they send captured data to a remote medical center. Here, consumption power of the compressor plays an important role because the ambulatory recorders have limited power supply. There is another feature that bold this compressor, and it is the speed of generating compressed samples. This sampler, in a way, can be considered as real-time compressor. Because, we compress consecutively, and just there is a delay of 16 cycles, that in practice this can be ignored. In contrast, almost previous works try to capture a block of raw ECG samples, then, applying their compression algorithm. The main reason behind our decision for mapping every 16 samples to 4 compressed samples is the quickness, and simplicity of the system. Although in this way, we might have lost the higher compression ratio, but the used costs and the achieved performance of this model should not be overlooked. In next section, we show the experimental results, to evaluate the performance of this ECG compressor.
Experimental results
In most recent CS-based compression methods, researchers did not concentrate on the dimension of the ECG vector and projection matrix. They usually used block of 256, 512, or 1024 samples for compressing data. As the size of projection matrix increases, the delay of system in compression phase will be increased as well. To show the elapsed time in sensing phase versus the size of measurement matrix, we simulated CS sensing phase in LPC 1769 ARM Cortex-M3, operating at CPU frequency of 100 MHz. In this simulation random Bernoulli distribution was used to generate a set of projection matrices with different sizes,
| 7 |
In this simulation, CR was considered constant, 75%, and 1024 samples of an ECG signal were chosen for compression. The result in Fig. 4 shows that if we sense signal in smaller dimensions, the elapsed time of sensing will be significantly lesser.
Fig. 4.

Effect of projection matrixs size on the compression time
In Fig. 4 red line is the elapsed time of compression phase where ; it is evident that for this size of projection matrix, the elapsed time is much lesser than that of the larger size. This is the main reason that we applied CS in such small dimension. In this work, the records from MIT–BIH Arrhythmia Database are used to show the performance of the proposed design [32]. Also, to verify the performance of the proposed compressor, we at first compressed the ECG samples, and then in reconstruction different sparsifying dictionaries were used to compare the effect of sparsifying dictionary on reconstructed signal. In contrast to previous research, we chose adaptive dictionary learning to generate efficient sparsifying dictionary. We compared the quality of reconstructed signal with fixed dictionaries, namely, wavelet dictionary that has been used in previous CS-based compression method [1]. The result shows that adaptive dictionary per patients ECG data can improve the quality of reconstructed signal. In next step, we increase the CR of this model, and show how it has relation with reconstructed SNR. Since in remote health monitoring, always noise affects the compression performance, we added noise and check the stability and robustness of this compressor against noise effect. There are numerous reconstruction algorithms in CS, we use smothe-L0 method, since it is very fast and simple. For recovery, there are different sparsifying dictionaries; whatever a dictionary to be chosen precisely, the quality of recovered signal will be improved as well. We tested this factor for ECG signals, and the simulation results showed us that adaptive dictionary learning will generate the best sparsifying. Figure 5 shows the reconstructed SNR for different sparsifying dictionaries: DCT, KL, Wavelet, and adaptive dictionaries. In [4], orthogonal Daubechies wavelets (dB 10) have been used, since it is one of the best wavelet families for ECG compression. However, through dictionary learning we could increase the reconstructed signal quality. These dictionaries have been used for different ECG signals; at least each signal has been sampled for 10 s. For generating the adaptive dictionary, we used method of optimal direction (MOD), as learning algorithm.
Fig. 5.

The effect of sparsifying dictionary on the quality of reconstructed signal
Adaptive dictionary learning usually presents better sparse representation; sparsity has direct relation with the quality of reconstructed signal. When the wearable ECG recorders are used for a patient, training set will be more accurate. Because the correlation between training set of learning process and captured data will be high. In adaptive dictionary learning whatever training set contains more information of whole signal, the produced dictionary will be more precise. ECG data, inherently is a periodic signal and can be applied for adaptive dictionary learning. Our simulations show improvement in signal recovery quality in comparison with [4], where fixed dictionary was used. In addition, as introduced in Sect. 2, to improve the quality of ECG signal, very recently developed Kronecker technique in the recovery has been used that could improve the quality of the signal up to 7 dB [27, 33].
Since in medical signal processing, the last and most important factor is the viewpoint of the physician toward the model, we compared the quality of reconstruction based on Table 1. The output SNR shows that the recovered ECG signal contains all diagnostic information of the original signal. For example, in Fig. 6 we tested three different ECG Data- code: 100, 101 and 104 from MIT–BIH Arrhythmia Database. We learned dictionary for every patient separately, and applied fast compression method for . The reconstructed signal quality was measured by SNR. The result shows that for wearable ECG recorders that use per patient, dictionary leaning can present very good sparsifying dictionary. To evaluate the difference between the original ECG signal and the recovered ECG signal, we zoomed in some part of the reconstructed ECG signal no. 104. Figure 7 shows that the difference between the original signal and the recovered signal is very small. Because, with respect to the scale of the amplitude of the original signal and the reconstructed signal, the difference is negligible.
Fig. 6.

The performance of compressor for three different patients ECG data. Solid line (in red) shows original ECG signal, and dashed line (in blue) shows the reconstructed signal for the . The original signal is the raw ECG samples that have been recorded for 10 s from MIT–BIH Arrhythmia-sample number: 100, 101 and 104 from top to down. The PRD of record number 100 is 57.9 dB, 101 is 56.9 dB, and 104 is 58.4 dB
Fig. 7.

Close up of the difference between the original and the reconstructed signal
In addition, noise as ubiquitous signal always has unwanted effects in communication and medical systems. A good compressor should robust enough to tolerate up to a certain level of noise. To challenge our design, we inputted an Additive White Gaussian Noise (AWGN) to the compressed samples, later on, we applied the reconstruction algorithm. We increased the power of noise from 0 to 40 dB. Figure 8 illustrates how the reconstructed SNR can be decreased, when compressed samples exposed to AWG noise signal.
Fig. 8.
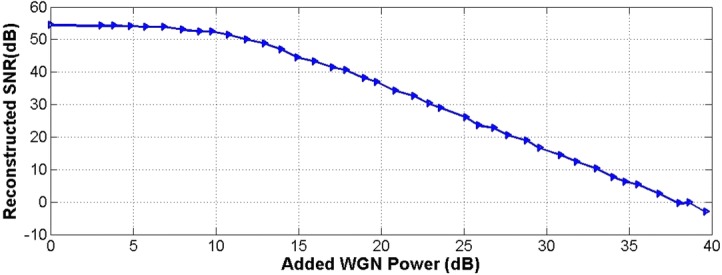
Robustness of proposed compressor: Comparing the reconstructed SNR against additive white Gaussian noise (AWG)
Up to 12 dB noise, the performance is approximately fixed, and it reflects the robustness of this method against noise. The reason behind this robustness is RIP condition. RIP guarantees that we can recover signal even in noisy condition. Figure 8 shows us that the proposed compressor can be used, in situation that we suffer from noise. remote health monitoring always accompanied with an unwanted noise. CS-based compressor can be used to do stable compression and decompression, even in spite of the existence of limited power noise.
Conclusion
Electrocardiogram (ECG) data compression has numerous applications, including mobile health and internet of cyber medical microsystems. In this paper a compressed sensing base compressor design was proposed. This design is fast and simple, and can be used to achieve , with typical elementary ICs. CS, as one of the fast method of compression is employed to compress the ECG samples, and in recovery phase, we chose adaptive dictionary learning to enhance the quality of reconstructed signal. Applying CS in very small dimension was focused in this research; simulations showed that this method can be used to generate compressed ECG samples in a fast and energy-efficient way. Through an adaptive dictionary learning, we reached better quality than those fixed dictionary such as DCT and wavelet. This compressor does not send any side information, and without using any processor, or storing raw data, or adding any delay to the functionality of the compressor, the compressed version of ECG signal can be generated. Since the data of an ECG signal, usually is taken from a few sensors, and not from one sensor, we can apply distributed CS, to increase CR and quality of reconstruction signal.
Compliance with ethical standards
Conflict of interest
Vahid Izadi declares that he has no conflict of interest. Pouria Karimi Shahri declares that he has no conflict of interest. Hamed Ahani declares that he has no conflict of interest.
Ethical approval
This article does not contain any studies with human participants performed by any of the authors.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Vahi Izadi, Email: vizadi@uncc.edu.
Pouria Karimi Shahri, Email: pkarimis@uncc.edu.
Hamed Ahani, Email: hahani@uncc.edu.
References
- 1.MalekpourShahraki M, Barghi H, Azhari SV, Asaiyan S. Distributed and energy efficient scheduling for IEEE802. 11s wireless EDCA networks. Wirel Pers Commun. 2016;90(1):301–323. [Google Scholar]
- 2.Malekpourshahraki M, Stephens B, Vamanan B. Ether: providing both interactive service and fairness in multi-tenant datacenters. In: Proceedings of the 3rd Asia-Pacific workshop on networking 2019. ACM; 2019. p. 50–6.
- 3.Izadi V, Abedi M, Bolandi H. Supervisory algorithm based on reaction wheel modelling and spectrum analysis for detection and classification of electromechanical faults. IET Sci Meas Technol. 2017;11(8):1085–1093. [Google Scholar]
- 4.Mamaghanian H, Khaled N, Atienza D, Vandergheynst P. Compressed sensing for real-time energy-efficient ECG compression on wireless body sensor nodes. IEEE Trans Biomed Eng. 2011;58(9):2456–2466. doi: 10.1109/TBME.2011.2156795. [DOI] [PubMed] [Google Scholar]
- 5.Ravelomanantsoa A, Rabah H, Rouane A. Compressed sensing: a simple deterministic measurement matrix and a fast recovery algorithm. IEEE Trans Instrum Meas. 2015;64(12):3405–3413. [Google Scholar]
- 6.Izadi V, Abedi M, Bolandi H. Verification of reaction wheel functional model in hil test-bed. In: 2016 4th international conference on control, instrumentation, and automation (ICCIA). IEEE; 2016. p. 155–60.
- 7.Singh A, Dandapat S. Block sparsity-based joint compressed sensing recovery of multi-channel ecg signals. Healthc Technol Lett. 2017;4(2):50–56. doi: 10.1049/htl.2016.0049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Lu DYKZ, Pearlman WA. Wavelet compression of ecg signals by the set partitioning in hierarchical trees algorithm. IEEE Trans Biomed Eng. 2000;47(7):849–856. doi: 10.1109/10.846678. [DOI] [PubMed] [Google Scholar]
- 9.Wei N-KCJ-J, Chang C-J, Jan G-J. ECG data compression using truncated singular value decomposition. IEEE Trans Inf Technol Biomed. 2001;5(4):849–856. doi: 10.1109/4233.966104. [DOI] [PubMed] [Google Scholar]
- 10.Hilton ML. Wavelet and wavelet packet compression of electrocardiograms. IEEE Trans Biomed Eng. 1997;44(5):394–402. doi: 10.1109/10.568915. [DOI] [PubMed] [Google Scholar]
- 11.Zigel Y, Cohen A, Katz A. The weighted diagnostic distortion (WDD) measure for ECG signal compression. IEEE Trans Biomed Eng. 2000;47(11):1422–1430. doi: 10.1109/TBME.2000.880093. [DOI] [PubMed] [Google Scholar]
- 12.Zhang J, Zhao D, Zhao C, Xiong R, Ma S, Gao W. Image compressive sensing recovery via collaborative sparsity. IEEE J Emerging Sel Top Circuits Syst. 2012;2(3):380–391. [Google Scholar]
- 13.Ujan S, Ghorshi S, Pourebrahim M, Khoshnevis SA. On the use of compressive sensing for image enhancement. In: 2016 UKSim-AMSS 18th international conference on computer modelling and simulation (UKSim); 2016. p. 167–71.
- 14.Ender JH. On compressive sensing applied to radar. Signal Process. 2010;90(5):1402–1414. [Google Scholar]
- 15.Baraniuk R, Steeghs P. Compressive radar imaging. In: 2007 IEEE radar conference. IEEE; 2007. p. 128–33.
- 16.Talkhouncheh RG, Khoshnevis SA, Aboutalebi SA, Surakanti SR. Embedding wireless intelligent sensors based on compact measurement for structural health monitoring using improved compressive sensing-based data loss recovery algorithm. Int J Mod Trends Sci Technol. 2019;5(7):1–6. [Google Scholar]
- 17.Taremi RS, Shahri PK, Kalareh AY. Design a tracking control law for the nonlinear continuous time fuzzy polynomial systems. J Soft Comput Decis Support Syst. 2019;6:21–27. [Google Scholar]
- 18.Shahri PK, Shindgikar SC, HomChaudhuri B, Ghasemi A. Optimal Lane Management in Heterogeneous Traffic Network. In: Proceedings of the ASMA dynamic systems and control conference in Park City, Utah 2019.
- 19.Engan K, Aase SO, Husøy JH. Multi-frame compression: theory and design. Signal Process. 2000;80(10):2121–2140. [Google Scholar]
- 20.Lingala SG, Jacob M. Blind compressive sensing dynamic MRI. IEEE Trans Med Imaging. 2013;32(6):1132–1145. doi: 10.1109/TMI.2013.2255133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Donoho DL. Compressed sensing. IEEE Trans Inf Theory. 2006;52(4):1289–1306. [Google Scholar]
- 22.Candès EJ. The restricted isometry property and its implications for compressed sensing. C R Math. 2008;346(9–10):589–592. [Google Scholar]
- 23.Chen SS, Donoho DL, Saunders MA. Atomic decomposition by basis pursuit. Soc Ind Appl Math. 2001;43(1):129–159. [Google Scholar]
- 24.Tropp JA, Gilbert AC. Signal recovery from random measurements via orthogonal matching pursuit. IEEE Trans Inf Theory. 2007;53(12):4655–4666. [Google Scholar]
- 25.Do TT, Gan L, Nguyen N, Tran TD. Sparsity adaptive matching pursuit algorithm for practical compressed sensing. In: 2008 42nd Asilomar conference on signals, systems and computers; 2008. p. 581–7.
- 26.Mohimani H, Babaie-Zadeh M, Jutten C. A fast approach for overcomplete sparse decomposition based on smoothed norm. IEEE Trans Signal Process. 2009;57(1):289–301. [Google Scholar]
- 27.Zanddizari H, Rajan S, Zarrabi H. Increasing the quality of reconstructed signal in compressive sensing utilizing Kronecker technique. Biomed Eng Lett. 2018;8(2):239–247. doi: 10.1007/s13534-018-0057-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Khoshnevis SA, Ghorshi S. Recovery of event related potential signals using compressive sensing and kronecker technique. In: 2019 IEEE global conference on signal and information processing (GlobalSIP) (GlobalSIP 2019), Ottawa, Canada; 2019.
- 29.Mitra D, Zanddizari H, Rajan S. Improvement of recovery in segmentation-based parallel compressive sensing. In: 2018 IEEE international symposium on signal processing and information technology (ISSPIT); 2018. p. 501–6.
- 30.Mitra D, Zanddizari H, Rajan S. Improvement of signal quality during recovery of compressively sensed ECG signals. In: 2018 IEEE international symposium on medical measurements and applications (MeMeA); 2018. p. 1–5.
- 31.Surakanti SR, Emami M, Zahedi L. Compression of speech signals using Kronecker enhanced compressive sensing method. In: 5th conference on signal processing and intelligent systems; 2019. p. 1–5.
- 32.MIT–BIH Arrhythmia Database. http://www.physionet.org/physiobank/database/mitdb/
- 33.Mitra D, Zanddizari H, Rajan S. Investigation of Kronecker-based recovery of compressed ECG measurements. Preprint. 10.13140/RG.2.2.16740.22400