Implications of nonlinearity, confounding, and interactions for estimating exposure concentration-response functions in quantitative risk analysis

Abstract

Recent advances in understanding of biological mechanisms and adverse outcome pathways for many exposure-related diseases show that certain common mechanisms involve thresholds and nonlinearities in biological exposure concentration-response (C-R) functions. These range from ultrasensitive molecular switches in signaling pathways, to assembly and activation of inflammasomes, to rupture of lysosomes and pyroptosis of cells. Realistic dose-response modeling and risk analysis must confront the reality of nonlinear C-R functions. This paper reviews several challenges for traditional statistical regression modeling of C-R functions with thresholds and nonlinearities, together with methods for overcoming them. Statistically significantly positive exposure-response regression coefficients can arise from many non-causal sources such as model specification errors, incompletely controlled confounding, exposure estimation errors, attribution of interactions to factors, associations among explanatory variables, or coincident historical trends. If so, the unadjusted regression coefficients do not necessarily predict how or whether reducing exposure would reduce risk. We discuss statistical options for controlling for such threats, and advocate causal Bayesian networks and dynamic simulation models as potentially valuable complements to nonparametric regression modeling for assessing causally interpretable nonlinear C-R functions and understanding how time patterns of exposures affect risk. We conclude that these approaches are promising for extending the great advances made in statistical C-R modeling methods in recent decades to clarify how to design regulations that are more causally effective in protecting human health.

Highlights

• •Many causal dose-response relationships involve thresholds and nonlinearities in signaling pathways and responses.
• •Realistic risk assessment must deal with nonlinear exposure concentration-response (C-R) functions.
• •This raises challenges for traditional statistical C-R modeling, including modeling confounding, errors, and interactions.
• •These challenges imply that regression coefficients may not predict how reducing exposure would reduce risk.
• •Causal Bayesian networks, dynamic simulation models, and nonparametric regression modeling can help.

1. Introduction

Nonlinearities in exposure concentration-response (C-R) functions can wreak havoc on traditional statistical risk modeling developed for linear no-threshold (LNT) modeling assumptions. Nonlinearity in an agent's causation of a health endpoint implies that no single slope coefficient necessarily characterizes the change in risk from a given change in exposure. Nonlinearities in interactions of the agent with other factors (such as co-exposures, co-morbidities, or covariates that modify the agent's effect) and dependencies among these factors, complicate the interpretation and estimation of slope factors or of entire concentration-response (C-R) curves that seek to quantify how a health endpoint depends on exposure. At a minimum, it becomes necessary to specify what is assumed about the levels of other factors, and about how (if at all) they change when exposure is changed – for example, how changing one component of a mix of pollutants changes other components that affect the same health endpoint. More generally, in both linear and nonlinear models, failing to characterize causal pathways other than those leading directly from the agent to the effect, such as indirect (mediated) pathways, or exposure-response associations due to common causes (e.g., confounders) or to common effects (e.g., sample selection criteria), can make it difficult or impossible to determine how changing exposure would change response probabilities. The possibility of nonlinearity exacerbates C-R estimation problems if high-order interactions among factors must be considered, and no small number of parameters in a simple model form can be assumed to adequately represent the data-generating process.

Yet, nonlinear C-R functions are prevalent in practice. They require new ways to carry out each of the health risk assessment steps of hazard identification, dose-response modeling, exposure assessment, risk characterization, and uncertainty characterization. They also have strong implications for how to communicate risk accurately, and for how to manage risk effectively. This paper reviews challenges for risk analysis posed by nonlinearity, and discusses constructive methods to meet these challenges using current techniques of data science and causal analytics. It focuses on techniques for using epidemiological data – typically, exposure, response, and covariate variables measured in a population over time – to identify and quantify health risks caused by exposures when underlying individual-level causal biological C-R functions are nonlinear. As an organizing framework, we take the practice of regulatory occupational risk assessment recently described by the National Institute for Occupational Safety and Health (NIOSH, 2020), which we consider a clear, thoughtful exposition of key principles and practices of current regulatory risk assessment. The following sections consider how to extend and apply these principles to nonlinear C-R functions with possible interactions and confounding, using simple examples to illustrate and clarify the main technical issues.

1.1. Why does nonlinearity matter?

Advances in biological understanding of adverse outcome pathways and mechanisms have identified many sources of strong nonlinearities and thresholds in C-R functions. Examples include ultrasensitive molecular switches in key signaling pathways (Bogen, 2019); positive feedback, cooperativity and bistability in regulatory networks and in dynamic processes such as assembly and activation of inflammasomes; discontinuous changes (e.g., rupture of lysosomes, ion fluxes, loss of organelle or cell membrane integrity, onset of pyroptosis); and saturation or depletion of protective (homeostasis-preserving) resources such as antioxidant pools in target cells and tissues (Cox, 2018). The point of departure for the following sections is the need for realistic risk analyses to use data analysis methods that are appropriate for such nonlinearities. Traditional regression modeling relating exposures to risks may give misleading results when the underlying C-R functions are nonlinear. Each of the following sections describes challenges posed by nonlinearity and then discusses data analysis techniques for overcoming these challenges.

1.2. Hazard identification

The central question of hazard identification is whether exposure to a substance causes increased risk of adverse health effects in at least some members of the exposed population. “Risk” for an individual is the probability that an adverse effect occurs in a given time interval. (Equivalently, it can be expressed as an age-specific hazard function, giving the expected rate of occurrence per unit time, given that it has not already occurred. Formulas from survival data analysis allow probabilities of occurrence by a given time or age, or within a specified interval, to be calculated from the age-specific hazard function, and vice versa.) NIOSH, 2020 describes hazard identification as “the systematic process for assessing the weight of evidence on whether an agent of interest causes an adverse effect in exposed workers. The findings from hazard identification are characteristic descriptions and information on the exposures of interest, any important cofactors (e.g., other risk factors, moderating factors, mediating factors, or confounders); modes and mechanisms of action; and conditions (e.g., pre-existing diseases) under which changes in exposures change the probabilities or timing of adverse effects.” Thus, we will consider that hazard identification addresses the following questions:

• •“Risk of what?” – the adverse effect(s) of interest;
• •“Risk from what?” – the source of risk, i.e., the hazard, of interest;
• •“Risk to whom?” – the exposed population of interest;
• •“Risk under what conditions?” – the context of conditions, such as co-exposures, co-morbidities, and sociodemographic covariates, under which risk is assessed; and
• •“Risk via what mechanisms? – the causal mechanisms or pathways by which effects of changes in exposure to the hazard are transmitted to changes in risks of adverse health effects.

Hazard identification should clarify these defining elements of a risk – its source, target, effects, and mechanisms – in enough detail to uniquely specify the risk being assessed and to support quantitative assessment of how the conditional probability (or hazard rate) for occurrence of the effect in a stated interval changes in response to changes in exposure, given the values of other causally relevant variables.

Challenges for Regression-Based Hazard Identification.

A common approach to hazard identification based on epidemiological data is to fit a regression model to data on estimated exposure levels and response rates (e.g., average numbers of mortalities or morbidities per person-year) and to test the null hypothesis that the regression coefficient relating exposure to response rate is 0. Rejection of this null hypothesis supports weight-of-evidence (WoE) determinations of a causal relationship between exposure and response, especially if plausible confounders have been controlled for by including them as predictor in the regression model. (Similarly for risk ratios, confident rejection of the null hypothesis that a risk ratio is 1 (no difference) in risk between more-exposed and less-exposed people in statistical analyses of relative risks, standardized mortality ratios, odds ratios in logistic regression models, or hazard ratios in Cox proportional hazards regression models, is usually interpreted as evidence supporting a causal relationship in weight-of-evidence (WoE) determinations, especially if chance, confounding, and biases have been ruled out as plausible explanations.) Against this practice is a fundamental objection that regression models quantify associations rather than causal impacts. Specifically, they quantify the conditional expected (average) value of the dependent variable, given the observed values of predictors, but this is different from answering the causal question of how or whether changing one or more of the predictors, such as exposure concentration, would change the dependent variable (Pearl, 2009; Pearl and Mackenzie, 2018).

In practice, as discussed in NIOSH, 2020, many statistical issues also complicate the interpretation of regression models and of non-zero regression coefficients. These challenges include model misspecification errors, exposure estimation errors, omitted (unobserved, latent) variables, missing data, inter-individual heterogeneity and variability in causal dose-response functions, correlations and statistical dependencies among predictors, attribution of interactions, internal validity of study designs and conclusions (i.e., do the causal conclusions or interpretations follow from the data collected), and generalization and external validity of conclusions (i.e., their applicability in contexts other than those of the original studies). Large technical literatures in statistics and data science have developed to address these issues. Constructive approaches have matured enough to create practical algorithms and software.

Table 1 summarizes some key approaches and provides links, which may be of interest for practitioners to, R packages (vetted, documented, and maintained via the CRAN repository, https://cran.r-project.org/), where more technical details and documentation can be found. Despite this progress, most of these methods are not yet widely used in regulatory risk assessment, which often relies instead on the judgments of analysts to try to deal with limitations in study designs and data (NIOSH, 2020). These difficulties can be exacerbated by nonlinearities, as illustrated in the following paragraphs.

Table 1.

Statistical techniques for commonly encountered data imperfections.

Data/Study Imperfection	Examples of appropriate techniques and software
Model misspecification errors; unknown shapes of exposure-response dependencies	Flexible nonparametric models (e.g., MARS, https://cran.r-project.org/web/packages/earth/earth.pdf) and deep learning; non-parametric model ensembles (e.g., random forest, https://cran.r-project.org/web/packages/randomForest/randomForest.pdf) and superlearning (https://rdrr.io/cran/SuperLearner/f/vignettes/Guide-to-SuperLearner.Rmd) for model combination
Exposure estimation errors and errors in estimated or measured covariates (explanatory variables)	Errors-in-variables methods (e.g., the MMC package in R, https://cran.r-project.org/web/packages/mmc/mmc.pdf; see also https://www.jstatsoft.org/article/view/v048i02, https://cran.r-project.org/web/packages/GLSME/GLSME.pdf, https://arxiv.org/pdf/1510.07123.pdf)
Omitted variables; unobserved or unmeasured risk factors, confounders, and modifiers	latent variable techniques and finite mixture distribution modeling methods (e.g., www.jstatsoft.org/article/view/v011i08; https://www.jstatsoft.org/article/view/v048i02; PROC CALIS in SAS)
Missing data values	Multiple imputation algorithms (e.g., MICE, https://cran.r-project.org/web/packages/mice/mice.pdf); data augmentation and EM (expectation-maximization) algorithms
Inter-individual heterogeneity and variability in causal exposure-response curves	Finite mixture distribution modeling, clustering, individual conditional expectation methods (e.g., https://cran.r-project.org/web/packages/ICEbox/ICEbox.pdf)
Correlated or interdependent explanatory variables	Probabilistic graphical methods, e.g., Bayesian networks (https://cran.r-project.org/web/packages/bnlearn/bnlearn.pdf; https://cran.r-project.org/web/packages/CompareCausalNetworks/index.html)
Interactions among risk factors or other explanatory variables	Nonparametric detection, estimation, and visualization of interactions (https://rdrr.io/cran/npIntFactRep/; https://rdrr.io/cran/npregfast/)
Uncertain internal validity (soundness of causal inferences)	Use quasi-experiment designs (or randomization and design of experiments where possible) to control for standard threats to internal validity, e.g., using PlanOut and PlanAlyzer software (https://hci.stanford.edu/publications/2014/planout/planout-www2014.pdf; https://dl.acm.org/doi/pdf/10.1145/3360608)
Uncertain external validity (generalizability of findings)	Multisite causal mediation analysis (https://cran.r-project.org/web/packages/MultisiteMediation/index.html); Bayesian evidence synthesis and hierarchical meta-analysis (https://cran.r-project.org/web/packages/jarbes/index.html)

1.3. Significant regression coefficients arising from trends and from omitted confounders

Statistically significant C-R associations and non-zero regression coefficients linking exposure to response probability can arise from many sources, even in the absence of a causal relationship between them. For example, if two variables, such as exposure and risk, follow statistically independent random walks, then regressing one against the other will usually produce a statistically significant regression coefficient between them, even though neither causes the other (Yule, 1926). Likewise, coincidental historical trends can induce C-R associations without causation.

In ordinary least-squares (OLS) regression, a regression coefficient for exposure will differ significantly from zero if conditioning on exposure significantly reduces the mean squared error (MSE) of the values predicted by the regression model. This can happen for many reasons, even if the predicted variable does not depend on exposure. Perhaps the best known reason is that a confounder – a variable that makes both exposure and the response more likely when it is present (or, more generally, that shifts both their cumulative distribution functions rightward) – can induce a positive regression coefficient for exposure in a regression model that includes exposure but not the confounder. For example, suppose that cigarette smoking, exposure indicators such as blood concentrations of heavy metals (e.g., lead or cadmium), and response indicators such as age-specific mortality or morbidity are all mutually positively correlated in a data set. Then a regression model that omitted smoking could show positive regression coefficients for the exposure indicators, whether or not response risk depends directly on them, if they also act as surrogates for smoking, which directly affects risk. In this case, smoking would be a confounder for the estimated exposure-response association. In current practice, it is perhaps unlikely that such an obvious confounder would be omitted, unless the data were unavailable. However, fully controlling for effects of confounders can be surprisingly difficult, especially when linear models cannot be assumed.

The standard way to deal with a measured confounder is to include it as a predictor in the regression model. The estimate of the coefficient for exposure is then said to have been “controlled” or “adjusted” for the confounder. However, this tactic often fails to fully control for effects of confounding, for reasons discussed in the following sections on measurement errors, model specification errors, residual confounding, surrogate variables, variable selection, competing explanations, and attribution of joint effects. For example, indicators of smoking such as self-reported pack years and cotinine levels, are often imperfectly accurate (Hsieh et al., 2011). Residual effect of confounding might then still contribute to a positive regression coefficient for exposure. Even more challenging is the problem of omitted confounders (also called latent confounders or unobserved confounders) – that is, confounders that are not included in a regression model, perhaps because they were not measured. A useful current practice is to quantify how strong the effects of omitted confounders on exposure and risk would have to be to explain away the estimated effect of exposure on response. If the required effect sizes are much larger than those for measured confounders, then this suggests that any omitted confounder(s) would have to be stronger than the measured ones to provide a plausible alternative explanation for the estimated exposure-response association.

1.4. Significant regression coefficients arising from measurement errors in confounders

If a confounder is measured or estimated with some error, then including it on the right side of a regression model will typically not fully control for it, and exposure will still have a significant positive regression coefficient in large data sets. As a simple hypothetical illustrative example to clarify concepts, suppose that, unbeknownst to the risk modeler, the true relationship between a measure of health risk, R, and past pack-years of smoking, S, is the LNT structural equation R = 0.01*S; and that an exposure variable X (such as concentration of a metal in blood or urine) is also related to S by the equation X = 0.02*S ^1/2; thus, S confounds the association between X and R. Consider the effect on multiple linear regression if the estimated values of S and X values are unbiased but have uniformly distributed estimation errors. Specifically, suppose that estimated values are uniformly distributed between zero and twice their corresponding true values. Fitting the regression model E (R |S, X) = b ₀ + b _S S + b _X X to a simulated data set with 1000 cases having S values independently uniformly distributed between 0 and 1 yields the estimated regression model E(R |S, X) = 0.002 + 0.0035*S + 0.094*X. The intercept and both regression coefficents are significantly greater than 0 (p < 0.00001). By contrast, the correct causal relationship with accurately measured variables would be E(R |S, X) = 0.01*S (or, 0.01*S + 0*X). Thus, measurement error has induced a significant positive exposure coefficient (b _X = 0.094) for X, even though the regression model included the confounder S on its right side. Intuitively, the reason is that measurements of X provide useful information for reducing the mean squared prediction error when R is predicted from S alone, because of the measurement error in S. However, the positive regression coefficient does not represent a dependence of risk on exposure.

As another example, if two variables exposure and risk have a common cause such as income, but neither exposure nor risk causes the other (so that the relevant probabilistic graph model is risk ← income → exposure), and if variables are measured or estimated with error, then the multiple linear regression model

$$E\left(risk|\exp osure,income\right)=a^{\ast }\exp osure+b^{\ast }income$$

may still show a significant regression coefficient, a, for exposure. Indeed, if the measurement error for income is large and that for exposure is small, regression modeling will conclude that b is not significantly different from 0 but that a is. Attempting to control for the confounder income by including it in the regression model fails if conditioning on the measured values of exposure helps to reduce prediction error for risk by reducing the effects of measurement error (essentially because measuring exposure reduces uncertainty about the true value of income).

More generally, ordinary least squares regression selects values of regression coefficients to reduce the mean squared error of predicted values. Thus, it can give a significant coefficient to exposure if doing so reduces the contribution of measurement error to prediction error, whether or not exposure makes a causal contribution to risk. This is true for both linear and nonlinear models. A somewhat analogous phenomenon, examined next, arises specifically from unmodeled nonlinearity in exposure-response relationships.

1.5. Significant regression coefficients arising from model specification errors

Regression models can fail to fully control for confounding, even if explanatory variables, including potential confounders, are measured without errors, if the models assume a shape (e.g., linear) for the relationship between explanatory and dependent variables that differs from their empirical relationship. This is the problem of model specification error or model misspecification: the specified model form does not perfectly describe the data. As a simple hypothetical example, if R = S ³ and X = S ², where S is uniformly distributed between 0 and 1, then fitting the (incorrectly specified) multiple linear model E(R |S, X) = b ₀ + b _S S + b _X X to a simulated data set of size N = 1000 cases produces a least-squares fit of E(R |S, X) = 0.05 + 1.5*X - 0.60*S, with an R ² value of 0.99 and all coefficients and the intercept significantly different from zero (p < 0.00001). Although R depends only on the confounder S and not on exposure X, controlling for S by including it on the right side of the regression model does not fully control for its confounding effects, or preclude a statistically significant positive regression coefficient for X. Intuitively, the reason is that the shape of the assumed model (in this case, linear) is not correct, and including X and well as S helps to reduce prediction errors due to model specification error. However, although conditioning on X as well as S leads to an excellent fit as assessed by the R ² value of 0.99, neither this high R ² nor the small p value of the regression coefficient for X indicates that risk depends on X as well as on S. Analogous examples arise for dichotomous outcomes such as mortality. If R = 1 whenever S > 0.5, with S uniformly distributed between 0 and 1, and R is otherwise 0; and if X is uniformly distributed between 0 and 1 if S > 0.5, and is otherwise 0 (e.g., if X is an exposure marker that is only formed when S > 0.5), then the regression coefficient for X will be significantly positive (and larger than that for S) in a logistic regression model for R with X and S as predictors, even though R does not depend on X.

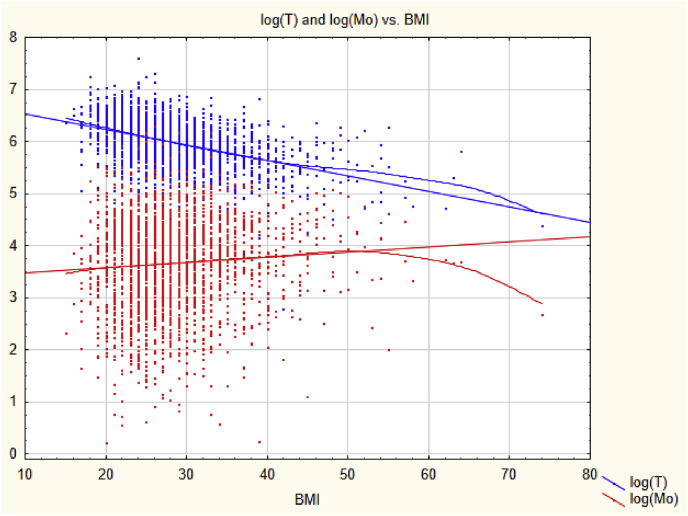
Model misspecification is often present even when goodness-of-fit tests do not reject the specified model form in favor of specified alternatives. A practical illustration concerns hazard identification of the metal molybdenum (Mo) as a hazard that might cause decreased testosterone (T) in men. For example, Lewis and Meeker (2015) presented a multiple linear regression of the dependent variable log(T) against the predictors log(Mo), BMI (body mass index), and others, in order to estimate the statistical effect of log(Mo) on log(T) while controlling for potential confounding by BMI. (For simplicity, we focus on these three variables; the full model also included age and other potential confounders.) The multiple linear regression model showed statistically significant negative regression coefficients for both log(Mo) and BMI, i.e., greater values of each are associated with smaller values of T (and log(T)), given the value of the other. This led to the tentative identification of Mo as a reproductive hazard. As the authors state, “In adjusted analyses where metals were modeled as a continuous variable, we found significant inverse associations between urinary molybdenum and serum copper and serum testosterone. … These findings add to the limited human evidence that exposure to molybdenum and other metals is associated with altered testosterone in men, which may have important implications for male health.”

Accounting for nonlinearity changes this conclusion. Fig. 1 shows scatter plots of log(T) (upper, blue scatter plot) and log(Mo) (lower, red scatter plot) against BMI in kg/m² with linear regression lines and nonparametric (smoothing) regression curves superimposed on the data so that departures from linearity can be seen easily. (The data are for men aged 18–55 from the National Health and Nutrition Examination Survey (NHANES) for 2011–2016.) Although the nonparametric regression curves are close to the linear regression lines for BMI between 25 and 35, deviations from linearity occur at relatively high and low values of BMI. These nonlinearities allow the mean squared error (MSE) of log(T) values predicted from BMI using the regression line to be reduced by including log(Mo) as an additional predictor. (Subtracting a multiple of log(Mo) from the linearly predicted value of log(T) reduces the MSE caused by the departures from linearity.) A significant regression coefficient for log(Mo) arises because including log(Mo) as a predictor of log(T) reduces the prediction error due to model misspecification. It does not provide evidence about whether reducing Mo would increase T. (Analogously, if Y = Z ² and X = Z ^0.5, where Z is uniformly distributed between 0 and 2, then a multiple linear regression model for predicting Y from both X and Z has a lower prediction error (MSE) than one for predicting Y from Z alone, even though only Z and not X determines the value of Y.) Restricting the range of BMI values considered to the interval from 25 to 35, where the linear and nonparametric regression models nearly coincide, makes log(Mo) no longer a significant predictor of log(T) in the linear multiple regression model, suggesting that fully controlling for confounding by BMI eliminates the association between log(Mo) and log(T). A significant regression coefficient that does not reflect a causal relationship, or that is eliminated by fully controlling for confounding, does not provide a sound basis for causal inference for hazard identification.

Fig. 1.

Linear and nonlinear (smoothing) regressions for log(T) and log(Mo) as functions of BMI. The nonlinear curves are fit to the data using locally weighted scatterplot smoothing (LOWESS).

In summary, analyzing data with regression models that do not perfectly describe the data-generating process can lead to statistically significant regression coefficients even in the absence of any causal relationship. Much as a significant regression coefficient for exposure can simply indicate that including exposure reduces prediction errors due to measurement errors, it may also indicate that including exposure reduces prediction errors due to model misspecification. Neither has any necessary implications for hazard identification.

1.6. Significant regression coefficients arising from residual confounding

It is common to refer to a confounder as having been controlled, or adjusted for, when a variable representing it has been included on the right side of a regression model, even if not all relevant information about it has been captured. For example, a variable such as “smoking status” with possible values of current, former, or never (or, even more simply, a binary value such as 1 for “has smoked at least 100 cigarettes in life” and 0 otherwise) might be used to “adjust” for smoking. Yet, such a summary variable leaves much quantitative information about smoking intensity and duration unaccounted for. Likewise, a regression model which adjusts for age by including a binary indicator such as 1 for over 65 years old, else 0; or by including 5-year or 10-year age categories, leaves more detailed information about age unrepresented. Such omitted information about a confounder may induce a positive regression coefficient for exposure, even if risk does not depend on exposure; this is the problem of residual confounding. For example, if Risk = (Age/100)² for 0 < Age < 100 years; Exposure = Age; and the correctly specified regression model E(Risk | Exposure, Age) = b ₀ + b _X*Exposure + b _A*Age ² is fit to 1000 randomly generated cases with age uniformly distributed between 0 and 100, then, in the absence of measurement error and sampling error, the result is as expected: E(Risk | Exposure, Age) = (age/100)². However, if age is rounded to the nearest decade, then fitting the same model yields E(Risk | Exposure, Age) = −0.03 + 0.002*Exposure + 0.00008*Age ². The intercept and both regression coefficients are statistically significantly different from 0 (p < 0.000001), even though risk depends only on Age and not on Exposure. Intuitively, the reason is that conditioning on Exposure reduces the mean squared prediction error for Risk due to the limited accuracy of measurement of Age, by providing information about the precise value of Age within each age category formed by rounding age to the nearest decade. This additional information reduces prediction error.

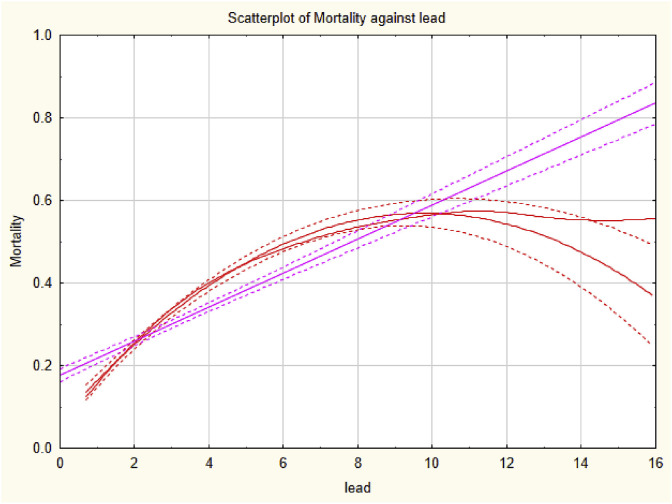
Use of a few wide categories to code continuous variables is still fairly common in practice, despite decades of admonishment from methodologists (e.g., Streiner, 2002; Naggara et al., 2011); hence the threat of residual confounding often has practical importance (Groenwold et al., 2013). For example, a recent study of the association between blood lead level (BLL) and age-specific mortality rate (Lanphear et al., 2018 used 3 categories for body mass index (BMI); 3 for self-reported smoking status (never, former, current); 2 for cotinine in blood serum (above or below 10 ng/mL); 2 for alcohol consumption; 3 for physical activity; 3 for cadmium; 2 for household income; 2 for hypertension; and 3 for a healthy eating index that runs from 1 to 100. Similarly, a regression analysis of the negative association between molybdenum (Mo) and testosterone (T) (Lewis and Meeker, 2015) used 2 categories for BMI (below 25 kg/m² or not); 3 for income; and 2 for smoking. In such studies, the use of only a few categories for each of many potential confounders leaves unclear the extent to which reported exposure-response associations reflect residual confounding. For example, Fig. 1 shows that BMI is associated with Mo and T both above and below 25 kg/m², so use of a dichotomous BMI variable leaves this remaining (residual) confounding unaccounted for. The possibility of residual confounding does not necessarily imply that qualitative conclusions about exposure-response associations would change if residual confounding were better controlled, but it leaves open the question of how much they would change. To avoid this unnecessary uncertainty, it suffices to treat continuous variables as continuous, rather than artificially dichotomizing or categorizing them (Streiner, 2002; Naggara et al., 2011).

1.7. Surrogate variables

Similar to residual confounding, controlling for a confounder by including in the regression model a surrogate variable that is correlated with it does not fully eliminate its confounding effects. For example, including self-reported pack-years of smoking and/or measured blood levels of cotinine in a regression model as surrogates for smoking does not fully control for the confounding effects of smoking if exposure provides additional information about smoking (and hence helps to reduce mean squared prediction error for a health effect caused by smoking) even after other indicators of smoking have been included as predictors (Hsieh et al., 2011). Similarly, including county population density (average people per square mile) in a regression model for effects of PM2.5 on COVID-19 mortality risk to control for the possibility that more densely populated areas might have both higher PM2.5 pollution levels and higher COVID-19 mortality risk does not fully eliminate this source of potential confounding if local population densities differ from the county average.

1.8. Variable selection

When predictors are correlated, including some on the right side of a regression model may prevent others from having a coefficient significantly different from zero. By choosing different subsets of other variables to include on the right side, modelers may affect the size of the regression coefficient for exposure, and, in some cases, even whether it is positive or negative (with each being significantly different from zero) (Dominici et al., 2014). In such cases, the results of the regression modeling are model-dependent: they reflect particular modeling choices rather than facts about the world. As a trivial example, suppose that the causal relationships among Age, Exposure, and Risk are described by the structural equations E(Risk | Age, Exposure) = Age - Exposure and Exposure = 0.5*Age. Then the regression coefficient for Exposure is −1 if both Age and Exposure are included as predictors, but is +1 if only Exposure is included as a predictor. Including only Exposure is more parsimonious, and, once it has been selected, including Age does not improve predictive accuracy; thus E(Risk | Age, Exposure) = Exposure would be the preferred model by these criteria, even though the regression coefficient of +1 for Exposure reveals nothing about how Risk would change if Exposure were changed.

1.9. Significant regression coefficients arising from competing explanations

If healthy workers are more likely to move away from a factory town each year than unhealthy workers, then workers in a birth cohort who have stayed the longest and gained the most cumulative exposure to the factory town environment will be disproportionately unhealthy compared to workers in the same birth cohort who have moved away. This creates a positive association (reflected in a positive regression coefficient) between cumulative exposure and risk of poor health, even if exposure per se does not affect health. If poor health is a predictor of increased risk for some diseases (e.g., cancers or heart diseases) in old age, then retired workers with high cumulative exposures will be more likely to develop such diseases because of underlying poor health, even if exposure has no causal impact on health. Another example of a non-causal explanation that does not involve underlying health status would be if workers stay in a certain occupation only if they are poor or have low exposures (or both). If poverty causes increased health risks but exposure has no direct causal effect on health risks, then a study of workers who have stayed in the occupation may find that those with low exposures are less likely to be poor (since low exposures provide an alternative explanation for the choice to stay) and hence have lower average health risks. If poverty is not measured, but exposure and health effects are, there will be a positive association between exposure and risk (mediated by the unmeasured variable poverty), even if exposure does not affect risk. These examples illustrate the fact that statistically significant positive regression coefficients between observed levels of exposure and risk need not imply that changing exposure would change risk, or that exposure is a contributing cause of risk.

1.10. Significant regression coefficients arising from attribution of joint effects

Suppose that a disease occurs in a worker if and only if the sum of three exposures A, B, and C exceeds 15, where the three exposures, perhaps corresponding to concentrations of three pollutants, are independent random variables uniformly distributed between 0 and 2, between 4 and 8, and between 5 and 9, respectively. Then a generalized linear regression model, such as logistic regression, will assign significantly positive regression coefficients to each of the three exposures if there are a large enough number of observations (each consisting of values of A, B, and C for an individual). This remains true even if the data are modified to set A = 0 whenever B + C < 15 (e.g., if pollutant A is formed only by sufficiently high levels of pollutants B and C). Yet, in this case, A makes no contribution to risk. Whether a disease occurs depends only on the values of B and C. Thus, regression can create a significant positive regression coefficients for an exposure as a predictor of risk by (mis)attributing part of the joint effect of multiple variables to it, even if has no causal impact on risk. (Special techniques that deal more consistently with attribution of risk in the presence of joint causes, such as Shapley regression, avoid this problem, but are seldom used in regulatory risk assessment.) Finally, if the distribution of either B or C (or both) is changed to a bimodal distribution that is equally likely to be 0 or 20, then the regression coefficient for A becomes zero (or, rather, is not significantly different from 0 in large data sets). Thus, whether regression analysis provides evidence that A has a significant positive regression coefficient depends on the distributions of other variables, rather than only on the causal biological effect (if any) of A itself. Hazard identification based on whether a regression coefficient is significantly different from zero may therefore be misleading when multiple risk factors interact in contributing to disease causation.

1.11. Some alternatives to regression for hazard identification

Although thoughtless interpretation of regression coefficients can be misleading, numerous regression diagnostic plots and tests (e.g., Q-Q plots, homoscedasticity tests, all-subsets regression plots) have been developed to help assess how well a regression model describes the data to which is being applied. Flexible nonparametric regression models (using techniques such as locally estimated scatterplot smoothing (LOESS), locally weighted scatterplot smoothing (LOWESS), or splines) can also show where empirical relationships depart from parametric (e.g., linear or generalized linear) modeling assumptions, as in Fig. 1. Such techniques avoid the risk of overfitting inherent in many parametric models (e.g., high-order polynomial regression models) by fitting simple low-order models to data in the neighborhood of each point of estimation (NIST, 2013). For large data sets with many potential predictors, there are many alternatives to regression modeling; here we mention some of them, deferring to a large technical literature and recent surveys (Cox, 2018b and references therein) for details. Non-parametric alternatives to regression for predicting risk from exposure and other variables include classification and regression tree (CART) analysis, which seeks to partition records into subsets with significantly different values of the dependent variable by conditioning on values (or ranges of values) of predictors; and random forest model ensembles that estimate partial dependence plots (PDPs). A PDP shows how the average predicted value of the dependent variable (e.g., risk) changes as an explanatory variable of interest (e.g., exposure) is varied over its range, holding the values all other variables fixed at their observed levels in the data set. (This corresponds roughly to what epidemiologists term the natural direct effect of exposure on risk. Each predicted value is averaged over many CART trees fit to different subsets of the data.)

In reality, however, changing a single explanatory variable, such as the exposure concentration of a pollutant in ambient air, might cause the values of multiple other variables to change, making it unrealistic to hold their values fixed in assessing total effects on the dependent variable. To deal with this situation, causal Bayesian network (BN) propagate changes in the values of input variables (such as exposure) to changes in the conditional probability distributions of variables that depend on them. The full methodology for BN learning and inference from data is quite detailed; we refer the reader to Nagarajan et al. (2013) and Cox (2018b) for details. An arrow joins two variables in a BN if they are found to be dependent (i.e., mutually informative about each other, so that the null hypothesis of conditional independence – that the conditional probability distribution for one is the same for all values of the other – can be confidently rejected, e.g., using nonparametric tests for independence; see Nagarajan et al., 2013). If effects depend on their direct causes, then a BN provides evidence that X might be a direct cause of Y if and only if they are linked by an arrow (Fig. 2, discussed in the next section, is an example of a BN.). If Y is conditionally independent of X given the values of other variables (such as common causes), so that there is no arrow between them, then the BN provides no evidence that X might be a direct cause of Y.

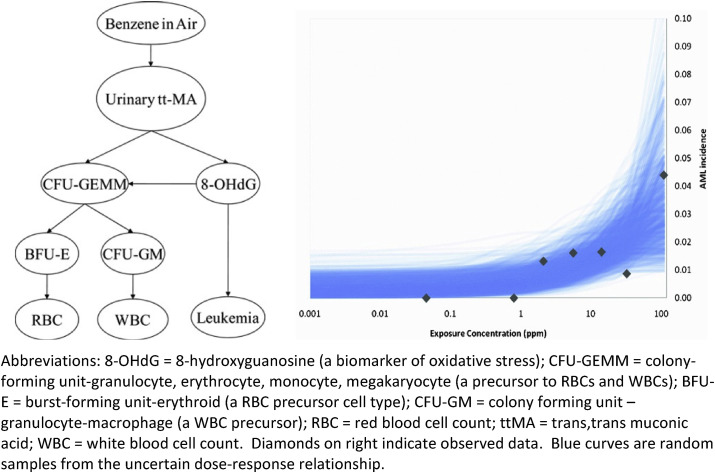
Fig. 2.

Bayesian network (BN) model structure (left) and predictions (right) (Source:Hack et al., 2010). Abbreviations: 8-OHdG = 8-hydroxyguanosine (a biomarker of oxidative stress); CFU-GEMM = colony-forming unit-granulocyte, erythrocyte, monocyte, megakaryocyte (a precursor to RBCs and WBCs); BFU-E = burst-forming unit-erythroid (a RBC precursor cell type); CFU-GM = colony forming unit – granulocyte-macrophage (a WBC precursor); RBC = red blood cell count; ttMA = trans, trans muconic acid; WBC = white blood cell count. Diamonds on right indicate observed data. Blue curves are random samples from the uncertain dose-response relationship. . (For interpretation of the references to colour in this figure legend, the reader is referred to the Web version of this article.)

A BN that includes exposure and risk variables, as well as other variables such as potential confounders and modifiers, can be used for hazard identification. Such a BN shows that exposure is a hazard, i.e., a potential direct cause of risk, if and only if exposure and risk are joined by an arrow. (The specific set of other variables that should be conditioned on – including confounders or common causes, but not common effects, of exposure and risk – to obtain an unbiased estimate of the effect of exposure on risk constitutes what is called an adjustment set. Adjustment sets can be calculated from BNs by modern causal analysis algorithms (Cox, 2018b). This solves the problem of variable selection that often bedevils regression modeling. It does so by identifying minimal sufficient subsets of variables – the “adjustment sets” – to condition on, i.e., to include in a (perhaps nonparametric) regression model, to estimate direct and total effects of one variable on another while avoiding biases created by failure to condition on common ancestors, or by conditioning on common descendants (Textor et al., 2016).) Some causal analysis algorithms attempt to orient the arrows between variables in a BN to reflect the flow of causality (and information) between variables, but even without such orientation of arrows, the structure of a BN is useful for hazard identification insofar as it shows whether risk is found to depend on exposure after adjusting for other variables.

BN analysis generalizes regression analysis in the following ways: (a) it models dependences among all variables in a data set, instead of only for a single dependent variable; (b) it quantifies dependences using nonparametric methods such as conditional probability tables or trees, which easily accommodate nonlinearities and complex interactions if all variables are discrete (although regression models are sometimes used for continuous variables); and (c) it quantifies the full conditional probability distribution of each variable, for any set of observed values for any subset of other variables, rather than only quantifying the conditional expected value of a single dependent variable given observed values for all other variables. BNs are therefore well suited for hazard identification in complex causal networks of many interacting variables, using the criterion that health effects should depend on exposures to hazards that directly cause them. Recent developments also address the challenge of synthesizing evidence across multiple studies – the important problem of external validity (or “transportability” or generalizability) of causal conclusions drawn from specific studies to other settings and conditions (Cox, 2018b). BNs have also been used as an alternative to regression for quantitative risk assessment and dose-response modeling, as discussed next.

2. Dose-response modeling

2.1. Challenges for Regression-based dose-response modeling

While hazard identification provides a qualitative determination about whether there is evidence that exposure to a substance causes increased risk of an adverse health response, dose-response modeling quantifies how risk varies with exposure, typically using regression models. As stated by NIOSH, 2020, “NIOSH generally obtains dose-response estimates via statistical models constructed to provide the conditional expectation of the dependent variable (the adverse effect) given one or more explanatory variables, but at least including the variable describing the agent exposure of interest. Model input data stem from toxicologic and/or epidemiologic investigations identified and assessed in hazard identification.” A regression coefficient for estimated exposure is interpreted as providing information about how risk of an adverse effect depends on the observed value of exposure, conditioning on the observed values of other explanatory variables.

The limitations of regression modeling discussed in the previous section also apply to dose-response modeling (also called exposure-response modeling and exposure concentration-response (C-R) modeling) using epidemiological data. Regression describes associations among observed values of variables. These may not reveal how or whether risk would change if exposure were changed (with or without holding values of other variables fixed) (Pearl, 2009). As already discussed, a significantly positive regression coefficient for exposure may arise simply because conditioning on measured values of exposure reduces the prediction error (MSE) from model specification errors or from measurement errors in other predictors. It may arise from attribution of joint effects, or from competing explanations, or from coincident historical trends. Dose-response models derived by regression modeling of epidemiological data reflect these non-causal sources of association, as well as any causal contributions. Hence, they cannot necessarily be used to predict by how much (or whether) a reduction in exposure would reduce risk. Although they are commonly used for this purpose in current regulatory risk assessments (NIOSH, 2020), such use is not necessarily sound unless these various non-causal contributions to regression relationships are identified and corrected for.

The next two sections describe two alternatives to regression analysis that focus more explicitly on causality: causal Bayesian networks and dynamic simulation modeling. A causal BN provides a high-level description of how the conditional probability distribution of response varies with exposure and other variables, allowing Bayesian inference from observations on biomarkers or other variables in the network (Hack et al., 2010). Dynamic simulation models use systems of differential equations and algebraic formulas to model (a) flows of chemicals and metabolites among tissues; (b) internal doses (concentrations of toxic metabolites in target organs and tissues) over time; and (c) resulting rates of cell death and proliferation and transitions of cells among various states (e.g., normal, pre-malignant, and malignant) over time (Cox, 2020). The following two sections highlight the main ideas of these methods as they apply to dose-response modeling, relegating their (extensive) mathematical details to the references.

2.2. Bayesian networks for dose-response modeling

The left side of Fig. 2 , from Hack et al., (2010), shows the structure of a Bayesian network (BN) model for quantifying conditional probabilities of some variables (e.g., various metabolites, markers and acute myeloid leukemia (AML) (the Leukemia node at the lower right)), given observed or assumed values of other variables, including concentration of benzene in air (averaged over a worker's years of exposure). The conditional probability distribution of each variable (node in the network) depends on the values of the variables that point into it. This BN was constructed manually based on a detailed literature review of candidate markers and outcomes and predictive relationships among them, given limitations in measurement techniques (Hack et al., 2010). The right side of Fig. 2 shows random samples drawn (via Monte Carlo uncertainty analysis) from the BN-predicted dose-response function describing the conditional probability for AML given air benzene exposure concentrations. These curves are constructed from the conditional probability tables of the BN, as follows. Each value for benzene concentration (ppm) in inhaled air determines a conditional probability distribution for the benzene metabolite urinary tt-MA (trans-trans muconic acid). The value of tt-MA, in turn, determines a conditional probability distribution for 8-hydroxyguanosine (8-OHdG), a marker of oxidative stress in lymphocytes. Finally, the value of 8-OHdG determines a conditional probability for AML. For each benzene concentration, a value of tt-MA is sampled from the conditional distribution of tt-MA, given the ppm of benzene; then a value for 8-OHdG is drawn from its conditional distribution given the sampled value of tt-MA; and finally this value is used to determine the conditional probability for AML given the sampled value of 8-OHdG. The needed conditional probabilities constitute the quantitative part of the BN model; they are estimated from data collected in multiple studies. Repeating this Monte Carlo sampling many times and averaging the results yields an estimate of the dose-response curve giving the conditional probability of AML for each value of air benzene concentration. Other potentially causally relevant variables (e.g., p-benzoquinone, NLRP3 inflammasome activation, age of patient, co-exposures and co-morbidities, and so forth) are “marginalized out” of the BN model in Fig. 2, meaning that they can still implicitly affect the probability of leukemia, but are not explicitly shown or conditioned on in calculating the sample dose-response curves for conditional probability of AML given ppm of benzene, shown on the right side of the diagram.

The uncertainty reflected in the band of dose-response functions (blue curves) on the right of Fig. 2 might in principle be reduced by conditioning on additional causally relevant variables, data permitting. Other investigators (or automated machine-learning programs for learning BNs directly from data) might select additional markers and perhaps get narrower uncertainty bands. In addition, durations of exposure and uncertainty in exposure concentrations could be included in refined models. However, the BN analysis in Fig. 2 already suffices to indicate both that benzene is a hazard for increased risk of AML (hazard identification) and also that predicted AML risk is not clearly increased above background at low exposure concentrations (e.g., < 0.1 ppm) and reaches a prevalence of almost 0.02 at a concentration of 10 ppm for the exposure conditions and durations in the studies used to build the BN model. This quantitative dose-response information can help inform risk management decisions. In addition, the structure of the BN on the left side of Fig. 2 shows that measuring hematological parameters such as WBC and RBC, in addition to air benzene concentrations, can help to infer AML risks when the marker 8-OHdG is not directly measured.

Promising as BNs appear to be, there are several reservations and questions about them that should be addressed, and some important recent progress in addressing them. Key developments are as follows (Cox, 2018b):

• • How are connections among variables to be determined? Allowing complex networks of relationships raises the threat of “model shopping” – that is, of investigators searching among complex models to find those that support prior beliefs or desired conclusions. To help guard against this, software packages that learn Bayesian network structures from data using several different algorithms (e.g., R packages such as bnlearn and CompareCausalNetworks) are becoming increasingly popular (Cox, 2018b). The main idea of these algorithms is to use tests for statistical properties (such as conditional independence tests) to determine which variables each variable is found to depend on, even after conditioning on other variables. Direct and indirect effects of one variable on another (e.g., of exposure on risk of adverse response) are identified by conditioning on appropriate adjustment sets calculated from the BN structure. This approach avoids the asymmetry inherent in regression models that specify one variable as the “dependent” variable and other variables as “independent” variables to explain it. Rather, it seeks to discover what each variable depends on (among the variables in a data set; extensions to latent variables are at the frontiers of current research). This symmetric approach (sometimes called “causal discovery,” in contrast to testing pre-specified causal hypotheses about what might cause a dependent variable), together with algorithms for specifying adjustment sets to condition on in estimating direct and indirect effects (thereby addressing the problem of variable selection in a principled way) help to reduce the potential for model shopping and confirmation bias in modeling.
• • What functional forms should be assumed for dependence relationships among variables, and how should interactions among variables be modeled? A common approach to addressing both questions is to use a nonparametric conditional probability table (CPT) or CART tree at each node of a BN, i.e., for each variable, to describe how its conditional probability distribution depends on the values of the variables that point into it (its direct “parents”), if any. This nonparametric approach allows arbitrary nonlinear interactions among variables to be estimated and described in a uniform framework while avoiding the necessity of assuming any particular parametric model form.

At its best, BN technology may help investigators avoid using data and modeling choices to support or refute particular hypotheses (e.g., searching for a statistical model to show that exposure to an agent is significantly associated with a health effect, or for an alternative model in which it is not) and to instead support more dispassionate discovery of stable dependencies among variables, with clearer distinctions drawn between direct and indirect (mediated) causal effects. But much remains to be done to achieve this goal. Despite impressive recent technical progress, current BN-learning algorithms remain limited by their lack of common sense. (They are typically better at determining whether variables are conditionally independent than at identifying the directions of dependences between them, and may require human users to specify constraints such as that death is a possible effect but not a possible cause of other variables, or that sex, age, and ethnicity are possible causes but not possible effects of other variables.) They are prone to identify false-positive links between variables if confounders are omitted, or if discretization of continuous variables to form CPTs (e.g., using deciles of continuous variables as levels, or using CART trees) leaves substantial residual confounding. Validation that CPTs express stable causal relationships that hold across situations typically requires collecting data from multiple studies. Recent advances in theory and software for causal analysis and interpretation (e.g., the InvariantCausalPrediction and CompareCausalNetworks R packages) have started to address these and other challenges, including detecting and modeling hidden (latent, unobserved) variables based on otherwise unexplained correlations between observed variables), but these developments have as yet had little impact on regulatory risk assessment.

2.3. Dynamic simulation for dose-response modeling

An alternative to regression or BN modeling of epidemiological data for dose-response modeling is to seek to understand biological causal mechanisms and to model them well enough to simulate the effects of exposures on risk. This typically involves integrating pharmacokinetics, which convert administered to internal doses; pharmacodynamics, which model effects of internal doses (e.g., changes in cell behaviors and transition rates) in target organs, tissues, and cell populations; and disease models, such as multistage clonal expansion (MSCE) models of carcinogenesis, which model the development of diseases over time. Causal dynamic processes leading from exposure to health effects can be simulated by linking pharmacokinetic, pharmacodynamic, and disease process simulation submodels, provided that sufficient knowledge is available to create them and sufficient data are available to populate them with realistic values for their parameters and functions, such as flow rate and stochastic transition rate coefficients; we defer to the technical literature for details (e.g., Cox, 2020 and references therein).

Dynamic simulation models enrich dose-response modeling by showing how time patterns of exposure concentrations affect risk over time. For example, which exposure pattern in each of the following pairs poses a higher risk (as measured, for example, by lifetime probability of a disease, or age-specific hazard function)?

• •1 ppm for 8 h per day vs. 8 ppm for 1 h per day
• •Exposures on Monday and Friday each week (with none on other days) vs. the same exposures on Monday and Tuesday each week (with none on other days)
• •Weekly exposures for 52 weeks per year, or twice those exposures for the first 26 weeks of each year only, or twice those exposures administered on alternating weeks throughout the year.
• •Occupational exposures from ages 20–35 years or the same exposures from ages 35–50 years.

Many regression models applied in regulatory risk analyses use exposure metrics, such as cumulative ppm-years of exposure, that do not distinguish among time patterns of exposure, but both experimental evidence (e.g., from stop-exposure experiments) and dynamic simulation models show that they can have very different effects on risk.

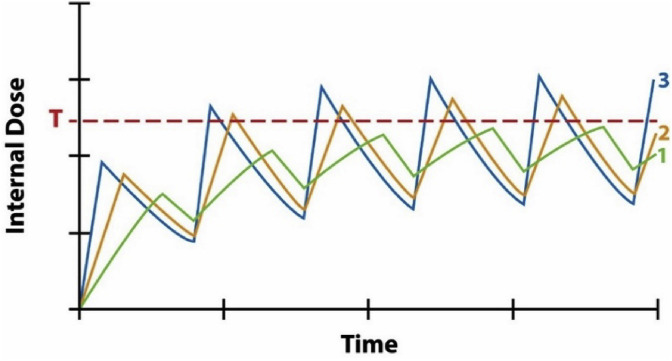
Fig. 3 is a notional diagram, without specific units on its axes, showing typical time patterns for how the internal dose (e.g., concentration of a toxic metabolite in a target organ or tissue) on the vertical axis varies over time (on the horizontal axis) for three different time patterns of dose administration (curves 1, 2, and 3). For an inhalation hazard, the administered dose rate corresponds to concentration of a substance in air. Curve 1 administers a certain concentration for a certain duration in each cycle of a repeated exposure pattern; curve 2 administers twice the concentration for half the duration; and curve 3 administers 3 times the concentration for 1/3 the duration, in each consecutive cycle. The vertical axis shows how concentration in a typical compartment varies with these time patterns of exposure. Specific versions of such model-predicted curves have been developed and validated for many chemicals using physiologically-based pharmacokinetic (PBPK) models. For purposes of dose-response modeling, an important feature is that administering higher concentrations for shorter durations produces higher peak internal concentrations than lower concentrations for longer durations, for the same total amount delivered (e.g., for the same ppm-hours per week). This implies that curve 3 can activate responses that curve 1 would not. If a response has an internal dose concentration threshold (denoted by T in Fig. 3), as in the examples mentioned in the Introduction (e.g., for activation of the NLRP3 inflammasome), then repeated high-concentration, short-duration exposures are more dangerous than administering the same average amounts per unit time more gradually.

Fig. 3.

Administering the same total amount of exposure (e.g., 100 ppm-hours per week) in different time patterns changes the maximum internal dose received.

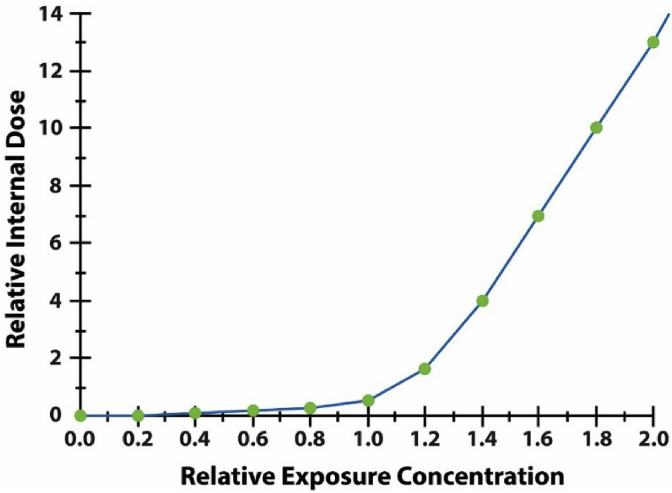
The disproportionate risk from shorter, more concentrated dose administration in each cycle in Fig. 3 holds even if pharmacokinetics are linear, so that concentrations in internal compartments are proportional to administered concentrations. But pharmacokinetics are often nonlinear at relevant exposure concentrations. For example, doubling the administered concentration of a substance in air can more than double its internal concentrations in tissues over time if clearance mechanisms are saturable, following Michaelis-Menten kinetics. Fig. 4 illustrates the effects of such nonlinearity, motivated by a model for accumulation of asbestos fibers in lung and mesothelial tissue (Cox, 2020). The vertical axis represents the amount of internal dose (e.g., fibers) added to a target tissue per unit time for different administered concentrations in air (horizontal axis), assuming sustained exposure to a constant concentration. The axes are scaled so that 1 on the horizontal axis represents the base case exposure scenario, e.g., what a typical worker might receive. The vertical axis shows the increase in cumulative internal dose (e.g., fibers lodged in target tissues) per unit time, and the curve plots this for different levels of administered concentration on the horizontal axis. Doubling exposure concentration from 1 to 2 increases the rate at which cumulative internal dose increases from about 1 to about 14, reflecting slower clearance from the lungs (e.g., via macrophages and the mucociliary escalator) and hence a higher fraction of inhaled dose (fibers) translocating to target tissues. By contrast, doubling exposure concentration from 0.1 to 0.2 makes relatively little difference, as most of the administered dose is cleared at such low concentrations.

Fig. 4.

Higher administered concentrations that reduce clearance rates are disproportionately efficient in producing internal concentrations.

Similar reasoning sheds light on the question of whether a worker suffers greater risk if exposed to a hazardous substance on two consecutive days each week (e.g., Monday and Tuesday) or on two days separated by a longer recovery interval (e.g., Monday and Friday). If the first day's exposure reduces clearance (or depletes protective resources such as antioxidant pools), then another exposure on the next day may create a greater internal dose than it would if it instead occurred a few days later, when clearance capacity has recovered. If so, then exposures on consecutive days in each cycle (e.g., in a work week) will produce more internal dose than the same exposures administered with longer recovery periods in between. The timing of internal doses can also interact with response dynamics, e.g., by delaying cell division during and following a first exposure until internal doses decline enough for mitosis to proceed safely; if the cells thus synchronized and undergoing mitosis at approximately the same time, receive a second dose part way through it, the cytotoxic effect may be far larger than if the second dose had occurred earlier or later. These examples reinforce the key point that timing matters: for many substances, the same average cumulative exposure per unit time can have very different effects on risk of adverse response, depending on how it is distributed over time.

In Fig. 3, whether internal doses in a target tissue become high enough to trigger an adverse response depends on details of timing that are lost when exposure metrics such as ppm-years or ppm-hours/day, averaged over some interval, from a week to a working lifetime, are used to summarize individual exposure histories. When response thresholds or other nonlinearities in dose-response functions are important, accurate risk prediction may require more detailed descriptions of exposure histories than are captured in the exposure metrics used in regression-based risk modeling. Conversely, when only these exposure metrics are available, it may be impossible to predict risk from them with useful accuracy. Dynamic simulation models provide rich opportunities to study how collecting and analyzing data on time patterns of exposure, and regulating the timing of exposures as well as permitted levels of exposures, can protect worker health in ways that regulating summary measures of exposure alone does not.

2.4. Exposure assessment

NIOSH (2020) notes that, “In environmental risk assessments, exposure assessment is considered a separate step for assessing the likelihood of exposure for estimating population risks and/or disease burden. In contrast, NIOSH risk assessments … estimate the risks to a hypothetical working population from a known exposure. Although exposure probabilities are not typically calculated, dose-response analyses include exposure information; therefore, NIOSH systematically assesses the availability, magnitude, and validity of exposure data used in relevant studies as a part of hazard identification and applies this information, as applicable, in the dose-response assessment.” The dose-response modeling considerations in the previous section imply that unmodeled uncertainty and variability in exposures may greatly affect risk estimates. It may do so in the following ways:

• •If higher concentrations are disproportionately dangerous, as in Fig. 3, Fig. 4, then an estimated exposure concentration with symmetrically distributed (e.g., normally distributed) estimation error will appear to be more dangerous (i.e., to cause higher risk) than the same concentration measured without error.
• •Similarly, if exposure concentrations have some variance around their TWA means, then the risk caused by a given mean concentration may be much greater than it would be if the variance were zero. Indeed, risk may depend as much or more on the variance (and also on the autocorrelation structure, if consecutive high concentrations are disproportionately dangerous) than they depend on the mean concentration. Therefore, regulatory standards that address the mean (and possibly occasional excursions above it) but that do not consider variance and autocorrelation may neglect key drivers of risk.
• •Ignoring uncertainty and variability in exposures in regression modeling can make nonlinear dose-response relationships, including ones with sharp thresholds where risk jumps from a low level below a critical exposure concentration threshold to a high level above it, appear to be smooth, S-shaped, curves that are approximately linear at low doses (Rhomberg et al., 2011a,b; Cox, 2018c). The reason is that exposure concentrations closer to the threshold are more likely to be mis-estimated as being on the wrong side of it than are concentrations further from it.

The apparent smoothness of an estimated exposure-response function when the underlying biological dose-response function has a discontinuous jump stems from the smoothness of the error distribution of estimated exposure values around true exposure values: at estimated exposure concentrations further below the threshold, the probability is less that a response will occur (because the probability is less that the true exposure is above the threshold). A practical consequence is that estimated exposure-response functions that appear to be smooth and approximately linear at low concentrations, with no evidence of a threshold, should not necessarily be interpreted as evidence that there is not a threshold. If errors in exposure estimates create this appearance whether or not there is a threshold, then the appearance does not provide evidence for or against a threshold. Similar caveats hold for other nonlinearities less extreme than thresholds: exposure estimation errors distort (and typically flatten and linearize) estimated exposure-response relationships (Rhomberg et al., 2011a,b). In simple linear regression models with exposure as the only predictor, ignoring measurement error biases the estimated slope (or potency) of the exposure-response line toward zero. By contrast, in nonlinear and multiple-predictor regression models, the bias can go in either direction. If higher exposures are disproportionately dangerous, as in Fig. 4, then neglecting errors in estimated exposures leads to over-estimates of risks at low exposures (since some high-exposure risks are misattributed to lower estimated exposures) and to under-estimates of risks at high exposures (since some low-exposure risks are misattributed to higher exposure levels). Thus, nonlinearity implies that measurement error need not attenuate estimated effects of exposure on risk, as in simple linear regression models, but rather exaggerates it at low concentrations and attenuates it at high concentrations.

Current practice in regulatory risk assessment often uses best estimates of exposures, e.g., estimates reconstructed from job exposure matrices for occupational risks, or from microsimulation models of individual movements and exposures for public health risks. Using best estimates of exposure without quantifying or correcting for effects of exposure estimation errors can lead to substantial biases in estimated exposure-response functions, as just discussed. Fortunately, as mentioned in Table 1, a variety of “errors-in-variables” statistical methods have been developed to correct for the distorting effects of measurement or estimation errors in exposure and other predictors. Computational Bayesian methods infer the shape of the exposure-response function by treating the true exposure as an unobserved quantity on which the estimated exposure depends. Other techniques (such as instrumental variables and repeated measurement methods) use observations on other variables, or repeated observations of the same variables, to help estimate the true shape of the exposure-response function when exposures are estimated with errors. Thus, the distortions in estimated exposure-response functions described in this section can often be avoided by careful design of data collection and analysis of data.

2.5. Risk characterization, uncertainty characterization, and risk communication

NIOSH (2020) explains its approach to risk characterization as follows.

“The final step in NIOSH risk assessment is risk characterization. It is the translation of information from hazard identification and dose-response assessment into a basis, completely or in part, for recommendations on limiting workplace exposure. The framework of NIOSH risk characterization centers on a choice between two distinct approaches, based primarily on the evidence supporting the absence or presence of an impairment threshold. For effects with a response threshold, NIOSH typically [develops] an estimate of a safe dose. Here the term safe implies that excess risk at this exposure level is absent or negligible. … When effects appear to be without a response threshold, NIOSH obtains quantitative estimates of low-dose risk by model-based extrapolation of the risk at doses below the observed data.”

Nonlinear dose-response relationships raise the possibility that neither of these two options – a threshold model, or model-based extrapolation of risk below the observed data range – describes the true dose-response relationship. Fig. 4 illustrates the problem. There is no threshold in this curve, but neither can risk at low concentrations be confidently extrapolated from observations at higher concentrations (e.g., the nearly linear segment of the curve to the right). When linearity cannot be assumed, extrapolation is an unreliable guide because of the variety of possible shapes for nonlinear functions below the observed data range.

The admirable goal of using risk characterization to translate hazard identification and dose-response assessment into a basis for recommendations to limit workplace exposures to protect worker health is also threatened if any or all of the following previously discussed conditions hold:

• • Model form misspecified. The assessed dose-response function describes statistical effects on risk attributed to exposure in multivariate modeling of nonlinear interactions; but not causal relationships revealing how reducing exposure (with or without holding other factors fixed) would affect risk (Pearl, 2009). Statistical effects may arise from non-causal sources such as departure of nonlinear dose-response functions from assumed linearity (Fig. 1). Using flexible nonparametric regression methods can reduce the threat of model specification errors and incomplete control of confounding, as illustrated in Fig. 1.
• • Ignored exposure dynamics. The assessed dose-response function predicts conditional expected values of risk indicators from exposure metrics that ignore essential details of the time pattern (Fig. 3), variability, and autocorrelation of exposure time series. Dynamic simulation risk models can clarify how changes in exposure affect changes in risk over time (Fig. 3).
• • Ignored exposure estimation errors. The assessed dose-response function estimates probabilities of adverse effects at different estimated dose (or exposure) levels, but errors in exposure estimates distort the shape of this function, e.g., making a nonlinear or threshold dose-response function appear to be approximately linear no-threshold, exaggerating risks at exposures below the observed data range. Errors-in-variables methods can help to avoid such distortions due to measurement and estimation errors.
• • Non-causal explanations. More generally, the assessed dose-response functions describes association but not causation, whether due to nonlinearity or other explanations. For example, if higher exposure concentrations are significantly positively associated with higher risks, but this is explained by the fact that both are declining over time, or that poorer areas tend to have higher values of both variables, or because lower-risk people are more likely to move away before they are sampled, then the assessed dose-response association does not necessarily predict whether, or to what extent, reducing workplace exposure would change risk. Bayesian network models (Fig. 2) can help to clarify causal pathways and competing explanations for observed exposure-response associations.

In all these cases, dose-response functions estimated by regression without making the suggested corrections cannot necessarily be used to predict whether or to what extent a change in exposure would change risk. This undermines attempts to use them to provide a rational, causally effective basis for recommendations to limit workplace exposures to protect worker health. Failures of workplace exposure standards to reduce some exposure-associated risks may reflect this lack of causally effective regulations (Cox, 2020).

To inform more effective regulation and policy-making, uncertainty characterization and risk communication must convey more than estimates of slopes and confidence intervals for dose-response functions at and below current exposure levels. They should also convey any significant uncertainty about whether reducing exposure will reduce risk, as described by the estimated dose-response function, or whether the function instead describes risks attributed to or associated with different levels of exposure, but not necessarily preventable by reducing it. Dose-response functions assessed by regression modeling applied to epidemiological data, and referring only to associations and attributed risks, do not address how much (if at all) reducing exposure would reduce risk. Hence, they do not tell policy makers what they need to know to take effective action to protect health based on quantitative evaluation of risk reductions expected from limiting exposures. This uncertainty about the causal relevance of estimated dose-response relationships, and of risk characterizations based on them, is seldom clearly communicated to policy-makers. Yet is often more relevant for well-informed and causally effective decision-making than the widths of confidence intervals for estimated slope factors (Pearl, 2009).

In practice, risk assessments often present policy-makers with point estimates and confidence or uncertainty intervals for risk estimates using units such as “premature deaths prevented per unit of reduction in exposure concentration” or “statistical lives (or life-years or quality-adjusted life-years) saved per unit reduction in cumulative exposure.” These estimated risks per unit of exposure seldom warn policy-makers (or other recipients) that “per” here only signifies that an estimated burden of mortality or morbidity attributed to exposure has been divided by an estimated exposure amount, and that it has no necessary implication that reducing the amount of exposure would reduce the burden of mortalities or morbidities attributed to it. Uncertainty about the causal interpretation of estimated dose-response models cannot be communicated or characterized by presenting confidence intervals (or resampling or Bayesian uncertainty intervals) and sensitivity analyses. It requires explicitly discussing whether the dose-response relationship and risk characterizations being presented reflect association and causal attribution, or changes in risk caused by changes in exposure. Conflating these two very different concepts risks misinforming risk management decision and policy makers about the expected consequences caused by interventions (Pearl, 2009).

Failure to clearly distinguish in charactering and communicating risk between risks associated with and attributed to exposure and risk preventable by reducing exposure leads to what might be called the supralinearity paradox: substances that have been studied for decades and subjected to increasingly tight regulations are often estimated to be more dangerous (potent) in newer regression-based studies than in older ones, leading to speculations that lower concentrations have been discovered to be disproportionately dangerous compared to higher concentrations (Hornung and Lanphear, 2014). A different possible explanation is that causally ineffective reductions in exposures do not reduce the risks attributed to them as originally predicted by regression models (e.g., because imperfectly controlled confounding or nonlinearities or interactions created regression coefficients that do not represent the causal effect on risk per unit reduction in exposure). Attributing undiminished risk to substantially lowered exposures increases the regression coefficient linking exposure to risk. This can create the appearance of higher risk-per-unit-exposure at lower concentrations (supralinearity) simply because the exposure-risk association attributes risk to exposures that do not cause it.

Fig. 5 illustrates some of these points. It fits three univariate models – linear, quadratic, and nonparametric smoothing regression curves – to data on blood lead concentration levels (x axis) and mortality during follow-up for nonsmokers in the NHANES data set. (Logistic regression would also seem appropriate a priori, but does not fit the data well, as the conditional expected value of the mortality rate is not a sigmoid function of concentration.) The data are used only to illustrate some conceptual and methodological points, so we forego discussion of details of the data set (or of alternative regression models, such as proportional hazards, that would better address survival data); the full data set can be downloaded from http://cox-associates.com/CausalAnalytics/. It is file "blood_lead.xlsx".. The linear and quadratic models have 95% confidence bands (shown as dashed curves). The nonparametric regression curve is approximately flat at the right edge of the plot, where the linear model slopes up and the quadratic model slopes down.

Fig. 5.

Mortality during follow-up vs. blood lead level (μg/dL) for non-smokers in NHANES data.

Fig. 5 illustrates several points about risk and uncertainty characterization. First, confidence intervals do not convey model uncertainty. For most of the range of values, the 95% confidence intervals for the linear and quadratic model specifications do not overlap. The best-fitting non-parametric model does not fall within either set of confidence bands at the right side of the graph. Although model diagnostics and goodness-of-fit tests can help select the best-fitting parametric model (e.g., quadratic rather than linear), they do not fix the fact that even the best-fitting model in a parametric class of models may not fit the data very well. Confidence bands do not communicate this aspect of model uncertainty: the confidence intervals in Fig. 5 are narrow compared to the range of predictions from different models. For this reason, sensitivity analysis (discussed later) is often used to assess the extent to which predictions from different models differ (NIOSH, 2020). This leaves open the question of how to reconcile (or select or combine) risk predictions from different models, as well as the question of whether any of the different models considered make accurate predictions.

Second, without a thorough discussion of confounding, model specification errors, nonlinearities, interactions, and residual confounding, it is impossible for a policy maker to determine from the results of such models – for example, from the linear model and its confidence bands extrapolated below the range of data – how or whether reducing blood lead levels (BLL) would affect mortality risk. For example, if the strong positive association between BLL and mortality risk were entirely explained by incompletely controlled confounding by age (i.e., older people having higher BLL and higher mortality probabilities, with a nonlinear increase in mortality risk at older ages (and higher BLL levels) that is not entirely corrected for including age as a predictor in a regression model), then the models in Fig. 5 would have no implications for how much or whether reducing lead concentrations would reduce risk. That statistical risk models do not necessarily describe how or whether reducing exposure would reduce risk, even if they fit observed data well and have tight confidence limits, is well understood by many epidemiologists. It is not always as clear to risk managers and regulatory risk assessors, many of whom seek to use quantitative estimates of low-dose risk obtained from regression-based dose-response models to inform decisions about how to limit exposures in order to protect health (NIOSH, 2020), without understanding that regression-based dose-response (or exposure-response) curves are usually not appropriate for this purpose because they do not reveal how changing exposures would change risks (Pearl, 2009). Risk and uncertainty characterization and communication of risk assessment results to decision-makers should clarify such uncertainty about consequences of interventions in order to inform rational and effective decision-making. More constructively, presenting results from validated causal Bayesian network risk models (Pearl, 2009; Hack et al., 2010; Cox, 2018b) and dynamic simulation risk models (Cox, 2020) can show how interventions, such as reducing exposure, are predicted to change the probability distributions of outcomes such as disease and mortality risks.

2.6. LNT rationales: additivity to background, population heterogeneity, and upper-bound estimates

Regulatory risk assessment has long embraced three principles that help to explain why LNT assumptions are often used in practice, despite reservations about possible nonlinearity such as those described in previous sections (e.g., Crump, 2017; Rhomberg et al., 2011a,b). The first is an assumption that incremental cancer risks from exposures to chemicals (and radiation) add to background processes, leading to effective linearity of the exposure-related dose-response or C-R curves. The second is that population heterogeneity tends to linearize population C-R functions, even if individual-level ones have thresholds or other nonlinearities. The third is that statistical upper confidence limits on LNT functions are appropriately conservative or health-protective in the face of uncertainty about the true C-R functions. All three principles have been debated for years. However, some recent examinations of the additivity-to-background assumption have concluded that it is often unjustified on both mathematical and biological grounds, in part because mechanisms of exposure-related harm, such as activation of NLRP3 inflammasomes, differ from mechanisms of background (spontaneous) harm in many cases, leading to genuine thresholds or threshold-like nonlinearities for incremental risks caused by exposures (Bogen 2016, 2019; Calabrese, 2018; Cox, 2018). Likewise, careful explication of the population heterogeneity argument has concluded that it broadens C-R uncertainty bands, but does not linearize nonlinear functions and should not be construed as implying linear upper confidence limits at low exposure concentrations (Rhomberg et al., 2011a,b; Crump, 2017; Bogen, 2016). Specifically, if thresholds or sharp nonlinearities hold for individuals, a combination of uncertainty and variability in C-R functions, together with exposure estimation error, may create a range of values at the population level over which estimated population risk decreases gradually with decreasing exposure concentrations, but this does not in general imply that linear extrapolation down to zero is justified, even if it is deemed prudent to use upper uncertainty limits (Cox, 2018c; Bogen, 2019). As illustrated on the right side of Fig. 2, Monte Carlo uncertainty analysis can lead to wide uncertainty bands that are nonetheless nonlinear. We conclude that, in general, nonlinear models deserve careful uncertainty analysis, and that simplifying LNT assumptions are not necessarily well justified even if there are positive background rates, population heterogeneity, and a desire to be conservative by using upper uncertainty distribution quantiles for purposes of regulation. Monte Carlo uncertainty analysis provides a constructive approach for characterizing uncertainty in nonlinear models, including Bayesian networks and dynamic simulation models, if enough is known to model uncertain quantities as random variables.

2.7. Use of sensitivity analysis and scientific judgment

Scientific judgment is often invoked as a way to address limitations in knowledge and data used in risk assessment. For example, NIOSH (2020) states that “Limitations in available data often require scientific judgment in order to fill gaps in model specifications. Risk assessors identify and characterize these judgements by conducting additional analyses to test plausible alternative assumptions, examine the robustness of main analyses, and improve transparency in the risk assessment process. These alternative analyses comprise sensitivity and modeling uncertainty analyses. NIOSH defines sensitivity analysis as a study of the uncertainty in estimates from the mathematical model that can be apportioned to uncertainties in its inputs.” Sensitivity analyses inform decision-makers about how predictions depend on uncertain modeling assumptions, for example, by showing the different risk predictions made by different models (e.g., the linear and quadratic models in Fig. 5). However, they do not identify whether any of the alternatives is close to the truth. Moreover, they are limited to studying how changes in assumed inputs affect outputs, but they do not address uncertainty about what the outputs mean, such as whether estimated C-R functions reflect association or causation (or both).

Similarly, NIOSH (2020) adds that “Because different model specifications can lead to different estimates, a key step in dose-response analysis is model selection. Clearly, it is preferable to base model selection on biologic plausibility, although a strong advantage of one model among several plausible models is rarely evident. Furthermore, data from most studies are imperfect and potentially incomplete. In lieu of available statistical techniques and algorithms designed to deal with data imperfections, the risk assessor may have to rely on assumptions based on scientific judgment.” However, empirical studies of the performance of scientific judgment under uncertainty indicate that it (like other human judgments under uncertainty) is subject to heuristics and biases that make it a very unreliable guide to truth (Kahneman, 2011). Using statistical techniques and algorithms usually outperforms expert judgment, in a variety of domains (Tetlock and Gardner, 2015). Moreover, the previous sections have illustrated that the specific technical challenges arising in risk assessment can be quite subtle and challenging, making it difficult to see how scientific judgment alone can address them usefully. Scientific judgment used in lieu of available statistical techniques and algorithms might be hard pressed to yield useful assessments and corrections for residual confounding due to slight departures from linearity (Fig. 1); or to reliably assess whether a repeated exposure will produce internal doses that exceed a threshold (Fig. 3); or to adjust correctly for nonlinearities in extrapolating from high to low exposure concentrations (Fig. 4); or to predict how correcting for exposure measurement errors and for variance and autocorrelations in exposure time series would change the shapes of estimated C-R functions; or to estimate the results of averaging the risk predictions from an ensemble of models while varying exposure and holding other variables fixed, as in a partial dependence plot. These are not types of tasks that judgment excels at. Scientific judgments about causality are notoriously error-prone (Kahneman, 2011), and C-R regression curves and confidence intervals do not offer even the most discerning judgment the empirical information needed to determine how or whether changing exposure would change risk (Fig. 5, Pearl, 2009). Judgments organized, tested, and validated using causal Bayesian network appear to be promising for addressing causal questions (Pearl, 2009) and for quantifying causal C-R functions (Fig. 2). However, testing and validating such models with data makes heavy use of statistical methods and algorithms (such as conditional independence tests, calculation of adjustment sets, estimation of conditional probability tables of functions, and inference of causal exposure-response relations controlling for the variables in adjustment sets) (Cox, 2018b).

At the same time, it is undeniable that formulating useful models of pharmacokinetics, pharmacodynamics, and disease processes requires considerable scientific judgment. Understanding of relevant biology is needed to decide what details can (and should) be safely omitted or averaged over, what simplifying assumptions should be made to reduce complex reality to a manageable model with parameters that can be estimated from data, and how compartments and flow rates or transition rates should be specified and parameterized. Thus, scientific judgment is often essential in identifying appropriate model structures and simplifications, and in specifying what needs to be estimated from data, e.g., exposure-dependent transition rates or flow rates among model compartments. Statistical algorithms can then be applied to appropriate data (if it is available) to estimate these parameters. Thus, we conclude that scientific judgment should not be used in lieu of statistical methods and algorithms, but rather should be used in combination with them. For example, human understanding and judgment of plausible causal pathways and mechanisms, together with statistical models of conditional probabilities and of pharmacokinetics, pharmacodynamics, and disease processes, can contribute to developing, testing, and refining causal Bayesian networks (Hack et al., 2010) or dynamic simulation models (Cox, 2020). Such data-informed models, in turn, can contribute to credible risk estimates and causal C-R models for informing risk management decisions.

3. Discussion and Conclusions

3.1. Risk Management and Risk Assessment Implications of Nonlinearity

The aspects of nonlinear C-R function estimation and interpretation discussed in previous sections have clear implications for more effective risk management, as well as for more informative risk assessment. One is the importance of including time patterns of exposure, such as times between successive high-concentration exposures, in characterizing and regulating risks for some substances. Reducing time-weighted average (TWA) exposure concentrations may not succeed in reducing risk if times between consecutive high exposure concentrations are not also controlled (Fig. 3). Likewise, regulations that limit variability around mean concentrations, and autocorrelations in exposure histories on different time scales, may be much more effective in controlling risks for some substances that measures that only reduce time-weighted average (TWA) mean concentrations. When C-R functions are nonlinear, as in Fig. 4, an exposure history that randomly fluctuates between 0 and 2 units of concentration, with a mean of 1 unit of concentration, may be far more dangerous than a constant (zero-variance) exposure to 1 unit of concentration, even though they have identical TWA values. Regulations based on C-R functions that do not model and correct for errors in exposure estimates may be ineffective if the distorted shape of the estimated C-R function (e.g., a low-dose linear curve) does not accurately represent the true shape of the underlying causal dose-response function (e.g., a threshold or other nonlinear function). Thus, the practical design of regulations that better protect worker health by addressing these aspects of exposure appears to be a worthwhile topic for further applied research. Dynamic simulation modeling can help to understand effects of proposed regulations on risk, accounting for realistic variability and autocorrelations in exposure time series; time patterns of mean exposure concentrations within working weeks and over lifetimes; inter-individual variability in exposure response parameters; and exposure estimation errors and uncertainty (Cox, 2020). However, developing and validating dynamic simulation models of exposures, pharmacokinetics, pharmacodynamics, and disease processes requires considerable research compared to regression modeling of estimated exposure-response data.

Recognizing the limitations and challenges of regression modeling for nonlinear C-R functions does not imply that regression modeling should not be used in risk assessment, characterization, and communication; but only that it should be used and interpreted carefully, and in conjunction with other techniques that better address causality. Regression modeling should be used with errors-in-variables corrections if there are errors in variables; with nonparametric model ensembles such as random forest if there is uncertainty about model forms and specification errors; with latent variable techniques if there might be unobserved factors that modify observed responses; and so forth (Table 1). Well-specified regression models can be highly useful for estimating conditional probability and conditional expected value relationships between a variable and its direct causes, if these are known and suitable adjustment sets have been identified. However, regression per se does not address the causal interpretation of the C-R curves that it produces (Pearl, 2009). Judgment is not usually a viable substitute for more formal analytic methods (Kahneman, 2011; Tetlock and Gardner, 2015); conversely, even the best current formal analytic methods cannot replace the scientific judgment and knowledge needed to create dynamic simulation models and other detailed causal models of complex biological processes. Even strong and statistically significant associations observed in well-designed and controlled health impact assessment studies do not necessarily translate into valid causal relationships between the studied variables. Furthermore, statistical significance does not necessarily imply practical or clinical significance. These limitations are relevant for both linear and nonlinear models.

When regression modeling is used to estimate C-R functions, additional data-driven techniques are usually needed to establish valid causal interpretations of these curves, and, in particular, to clarify the extent to which changes in exposures will bring about changes in risk (Pearl, 2009). Difficulty in demonstrating direct causation is not the same as evidence against such causation, and finding alternative ways to explain apparent associations of agents and effects should not necessarily be taken as evidence that the agent does not contribute to causing the effect. Rather, causal analysis clarifies whether a data set provides evidence of a dependence of effects on exposure that is not fully explained away by standard alternative explanations such as confounding, model specification error, and measurement error. If so, then it may be prudent to treat the dependence (at least provisionally) as being causal. If not – for example, if effects are conditionally independent of exposure to an agent, given the values of measured confounders, or given plausible assumptions about effects of unmeasured or residual confounding – then additional evidence is needed to warrant a hazard identification conclusion that exposure to the agent increases probability of the effect.

There has been remarkable progress in statistical and machine learning methods for dose-response modeling in recent decades. Most of the techniques we have mentioned for extending regression modeling to meet challenges arising from realistic imperfections in relevant data and knowledge, from the statistical methods in Table 1 to machine learning methods such as random forest partial dependence plots, were not widely taught or practiced by earlier generations of risk analysts; many did not yet exist. Now they are increasingly being included in state-of-the-art risk analysis practice and guidance (NIOSH, 2020). We suggest that, in addition to these methods, causal Bayesian networks (Fig. 2) (Pearl, 2009; Hack et al., 2010; Cox, 2018b) and dynamic simulation modeling of nonlinear C-R functions (Fig. 3, Fig. 4) appear promising for further improving the realism of C-R modeling. These techniques typically require more detailed analysis than regression modeling alone, but the extra effort may be rewarded by increased success in designing exposure regulations that more effectively protect human health.

Declaration of competing interests

The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: This work was supported by the author's employer, Cox Associates LLC, which received funding from the National Stone, Sand, and Gravel Association (NSSGA) to support research on nonlinear dose-response modeling and preparation of this paper. All questions asked, selection of research methods used, and conclusions reached are solely those of the author. No one else had rights to review or comment on this work before it was submitted for publication.