Transfer from Number to Size Reveals Abstract Coding of Magnitude in Honeybees

Summary

Number discrimination has been documented in honeybees. It is not known, however, whether it reflects, as in vertebrates, the operating of an underlying general magnitude system that estimates quantities irrespective of dimensions (e.g., number, space, time) and format (discrete, continuous). We trained bees to discriminate between different numerical comparisons having either a 0.5 (2 versus 4; 4 versus 8) or 0.67 ratio (2 versus 3; 4 versus 6). Bees were then tested for spontaneous choice using comparisons with identical numbers but different sizes. Irrespective of the ratio of stimuli, bees trained to select the smaller numerical quantity chose the congruent smaller size; bees trained to select the larger numerical quantity chose the congruent larger size. This finding provides the evidence for a cross-dimensional transfer between discrete (numerical) and continuous (spatial) dimensions in an invertebrate species and supports the hypothesis of a cognitive universality of a coding for general magnitude.

Graphical Abstract

Highlights

• •Honeybees exhibit a cross-dimensional transfer from discrete to continuous dimensions
• •Honeybees trained to choose the smaller numerosity, choose the congruent smaller size
• •Honeybees trained to choose the larger numerosity, choose the congruent larger size
• •This supports the hypothesis of a cognitive universality of a coding for magnitudes

Neuroscience; Behavioral Neuroscience; Cognitive Neuroscience

Introduction

Honeybees (Apis mellifera) have been shown to be able to process the numerical attributes of visual stimuli (Chittka and Geiger, 1995, Dacke and Srinivasan, 2008, Bortot et al., 2019, Howard et al., 2019), including the zero as a quantity (Howard et al., 2018). Given their distant phylogenetic origins, it is unclear, however, to what extent bees (invertebrates) and vertebrates share similarities in number cognition.

Humans and others non-human vertebrates make use of a nonverbal, nonsymbolic representation of number, the so-called Approximate Number System (ANS). The ANS obeys Weber's law—it is thus mainly limited by the ratio between the numerical values being compared—and is thought to be supported by an evolutionarily ancient mechanism for representing quantity in an analog fashion. Gallistel (1989) first argued that discrete countable quantity (i.e., number) and continuous quantity (e.g., space and time) must be represented by a common mental currency to enable animals to perform arithmetic operations across domains (as in the case of the rate of return to a food patch that can be computed only if organisms represent time and number in a single currency). According to this hypothesis, quantity representations in the various domains (i.e., number, space and time) would be processed by a «common magnitude system», which represents these dimensions via the same unit of magnitude (Gallistel, 1989). Evidence that the temporal, spatial, and numerical features of a stimulus can interact with one another has been provided for vertebrates such as monkeys (Merritt et al., 2010) and birds (De Corte et al., 2017) and for prelinguistic human babies (Di Giorgio et al., 2019).

Interestingly, honeybees have been shown to exhibit the numerical distance effect (i.e., the fact that the ability to discriminate between numbers improves as the numerical distance increases, (e.g., 0 versus 4 is easier than 0 versus 1, Howard et al., 2018). The numerical distance effect is one of the signatures of the ANS and suggests the existence of an analog magnitude system in honeybees that would allow the processing of different numbers. Moreover, honeybees have been shown to be able to process the relative size of visual stimuli (Avarguès-Weber et al., 2014), but it is not known whether in bees a common set of coding mechanisms underlies quantity estimation in different domains.

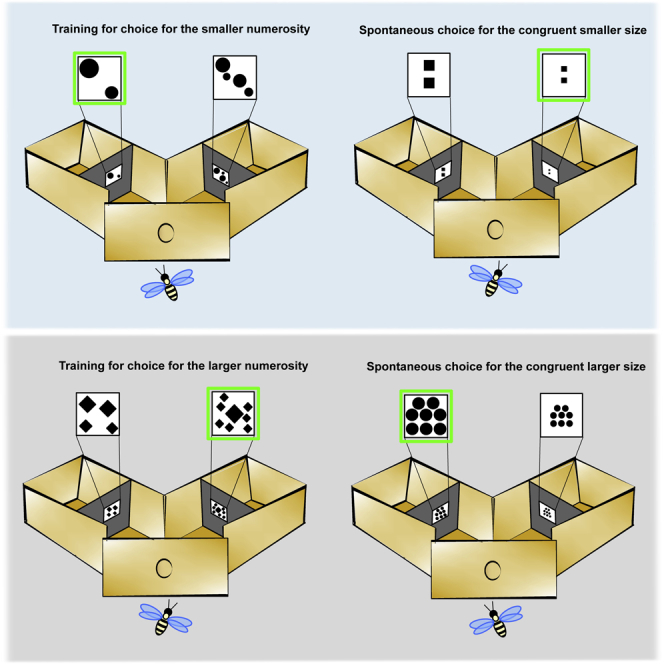
Here we investigated whether honeybees could make a transfer from discrete (number) to continuous (size) magnitudes. Bees were trained to discriminate between different numerical comparisons having either a 0.5 ratio (2 versus 4 and 4 versus 8) or 0.67 ratio (2 versus 3 and 4 versus 6). Half of the subjects learnt to choose the smaller quantity and the other half the larger quantity. Then at test, bees were presented with stimuli of different size but identical numerosity under extinction condition (i.e., in the absence of reward). If bees possess a common mechanism to process different magnitudes, then animals trained to choose the smaller/larger quantity in the number comparisons were expected to choose the congruent smaller/larger size in the size comparison. Moreover, choice of the congruent size would not be affected by the ratio of the stimuli (i.e., ratios that proved to be discriminable for numbers should prove discriminable for sizes as well).

Results

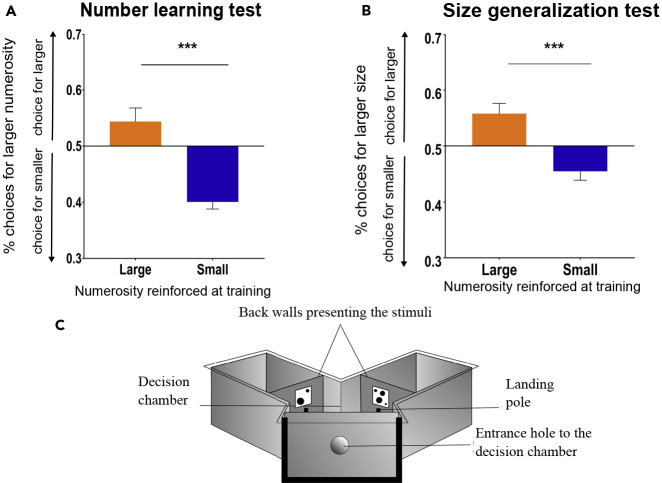
The results are shown in Figures 1A and 1B as proportions of choices for the larger magnitude. An analysis of variance revealed a significant main effect of the type of training (smaller versus larger numerosity as positive; F_{(1, 48)} = 45.8, p < 0.001, ω² = 0.399) but not of the type of test (number learning test versus size generalization test; F_{(1, 48)} = 3.5, p = 0.066) and the ratio (0.5 versus 0.67; F_{(1, 48)} = 0.3, p > 0.05).

Figure 1.

Results of the Test Phase and Representation of the Apparatus

(A) In the number learning test, honeybees trained to discriminate the smaller or the larger numerousness showed correct spontaneous choices in the absence of reward (mean ± SEM; ∗∗∗p < 0.001, Analysis of variance (ANOVA)).

(B) In the size transfer test, bees previously trained to select the larger numerosity showed a preference for the larger size, conversely bees previously trained to select the smaller numerosity showed a preference for the smaller size (mean ± SEM; ∗∗∗p < 0.001, Analysis of variance (ANOVA)).

(C) Schematic representation of the Y-maze used to train bees to discriminate numerousness and to test them for transfer from numerical to spatial (size) dimensions.

No significant interactions were observed (ratio x numerical comparisons: F_{(2, 48)} = 1.9, p > 0.05; ratio x type of training: F_{(1, 48)}= 1.7, p > 0.05; ratio x type of test: F_{(1, 48)} = 0.5, p > 0.05; type of training x type of test: F_{(1, 48)} = 1.2, p > 0.05; ratio x type of training x type of test: F_{(1, 48)} = 0.09, p > 0.05; ratio x type of training x numerical comparisons: F_{(2, 48)} = 1.2, p > 0.05; ratio x type of test x numerical comparisons: F_{(2, 48)} = 1.9, p > 0.05; ratio x type of training x type of test x numerical comparisons: F_{(2, 48)} = 0.03, p > 0.05).

As can be seen in Figure 1, bees trained to select the larger/smaller numerousness (Figure 1A; choice for correct, either larger or smaller, numerousness: 57.16% ± 0.01, mean% ± SEM; two-tailed one-sample t test: t₍₃₁₎ = 5.02, p < 0.001, d = 0.89) chose the congruent larger/smaller size (Figure 1B; choice for congruent, either larger or smaller, size: 55.14% ± 0.01, mean% ± SEM; two-tailed one-sample t test: t₍₃₁₎ = 4.26, p < 0.001, d = 0.75).

Discussion

Results of number learning test confirmed previous studies (Bortot et al., 2019, Howard et al., 2018, Howard et al., 2019) showing that bees can discriminate numerosities with 0.5 and 0.67 ratios when continuous physical variables were controlled for. Moreover, we found that honeybees can make a transfer from discrete (number) to continuous (size) magnitudes. This provides the evidence for a common code for magnitudes in an invertebrate species.

The hypothesis of the existence of a prelinguistic framework to process different prothetic dimensions (i.e., dimensions that can be "more" or "less" than) was first proposed by Gallistel (Gallistel, 1989) and then developed by Walsh (Walsh, 2003). Research in humans and other vertebrates has revealed that the temporal, spatial, and numerical features of a stimulus can interact with one another (Merritt et al., 2010, Gallistel and Gelman, 2000, Rugani et al., 2015, Lourenco and Longo, 2010) and evidence of similar activation in the parietal cortex in humans and non-human primates in quantity discrimination seems to support the hypothesis of an encoding by a common magnitude (Piazza et al., 2007). Our results show that bees generalize from a numerical dimension to a spatial (size) dimension, suggesting that a general magnitude encoding can be shared among vertebrates and invertebrates.

Our experiment demonstrates that, despite their small brains and the absence of a cortex, honeybees generalize from discrete (number) to continuous (size) magnitudes. It could be that there are regions in the honeybee's brain that play a similar function to the mammalian parietal cortex or to the avian nidopallium caudolateral (Ditz and Nieder, 2020). The central neuronal structure of the bee's brain, the mushroom bodies, a very complex high-order integration center, seems to be crucial in mediating the ability of bees to perform conceptual learning and extraction of relational rules (Giurfa, 2013). Whether mushroom bodies are supporting the cognitive mechanism of processing magnitudes is unknown.

Future studies should investigate whether the ability of insects to generalize between number and space is widespread to other magnitudes such as, for instance, time or brightness.

Limitations of the Study

This study investigated the association between spatial and numerical dimensions. However, the relationship between other magnitudes should be investigated in order to strongly support the existence of a common processing mechanism of magnitude in invertebrate species.

Methods

All methods can be found in the accompanying Transparent Methods supplemental file.

Resource Availability

Lead Contact

Maria Bortot, maria.bortot@unitn.it.

Materials Availability

This study did not generate new unique Materials.

Data and Code Availability

Original data have been deposited to Mendeley Data: https://doi.org/10.17632/dgwbncbs58.1.

Published: May 22, 2020