Abstract
MicroRNAs (miRNAs) are small single-stranded noncoding RNAs that have shown to play a critical role in regulating gene expression. In past decades, cumulative experimental studies have verified that miRNAs are implicated in many complex human diseases and might be potential biomarkers for various types of diseases. With the increase of miRNA-related data and the development of analysis methodologies, some computational methods have been developed for predicting miRNA-disease associations, which are more economical and time-saving than traditional biological experimental approaches. In this study, a novel computational model, deep belief network (DBN)-based matrix factorization (DBN-MF), is proposed for miRNA-disease association prediction. First, the raw interaction features of miRNAs and diseases were obtained from the miRNA-disease adjacent matrix. Second, 2 DBNs were used for unsupervised learning of the features of miRNAs and diseases, respectively, based on the raw interaction features. Finally, a classifier consisting of 2 DBNs and a cosine score function was trained with the initial weights of DBN from the last step. During the training, the miRNA-disease adjacent matrix was factorized into 2 feature matrices for the representation of miRNAs and diseases, and the final prediction label was obtained according to the feature matrices. The experimental results show that the proposed model outperforms the state-of-the-art approaches in miRNA-disease association prediction based on the 10-fold cross-validation. Besides, the effectiveness of our model was further demonstrated by case studies.
Keywords: MicroRNA, disease, microRNA-disease association, deep belief network, matrix factorization
Introduction
MicroRNAs (miRNAs) are small endogenous single-stranded noncoding RNAs containing about 22 nucleotides, and they usually regulate the gene expression at the posttranscriptional level by binding to the 3′-untranslated region of related messenger RNAs (mRNAs).1-3 In 1993, the first miRNA lin-4 was found in Caenorhabditis elegans larva. lin-4 coded for a 22-nucleotide regulatory RNA rather than a protein.4 Since then, plenty of miRNAs have been discovered in different types of organisms, such as plants, animals, and viruses.5-7 Currently, more than 2588 miRNAs in the human genome have been annotated.8 With the in-depth biology research about miRNAs in recent years, increasing evidence indicates that miRNAs play critical roles in different biological processes, such as cell growth,9 metabolism,10 proliferation,11 immune reaction,12 tumor invasion,13 cell cycle regulation,14 and so on. Therefore, the dysregulation of miRNAs, abnormality of miRNAs, and dysfunction of miRNA biogenesis may result in maladjusted cell behaviors.15
Recently, several studies reveal that miRNAs are highly relevant to the development of human complex diseases, including various cancers, diabetes, acquired immune deficiency syndrome, neurological disorders, and so on.16 For example, in the breast cancer patient, the expression level of miRNA-141 is increased.17 Besides, miRNA-145 is downregulated in atypical meningiomas and negatively functioned by regulating the proliferation and motility of meningioma cells.18 And compared with normal people, the expression level of miRNA-106a in glioblastoma patients is significantly higher.19 According to those studies, the statistics of the Human microRNA Disease Database (HMDD) 3.0 has collected 32 281 experimentally supported miRNA-disease association entries from 17 412 papers, including 1102 miRNA genes and 850 diseases.20 Also, several studies indicate that more than one-third of genes are regulated by miRNAs,21 which further demonstrates the associations between miRNAs and diseases. As indicated by those previous study results, miRNAs are considered as novel potential biomarkers or diagnostic tools for diseases.22,23 Therefore, exploring the relationships between miRNAs and diseases is meaningful for the prognosis, diagnosis, treatment, and prevention of human complex diseases.24-26
Nevertheless, traditional experimental methods for identifying the miRNA-disease associations are costly and time-consuming. As previous biological studies on miRNAs provided us massive and reliable miRNA data and their related data,20 researchers began to develop some in silico methods to predict miRNA-disease associations, which makes the follow-up biological validation experiment much more convenient and effective.27 Currently, most of the computational approaches are based on networks, which include miRNA association networks, disease phenotype networks,20 miRNA-disease networks,28 gene co-expression networks,29 and protein-protein interaction (PPI) networks.30 The basic assumption of most computational methods is that functionally similar miRNAs are more likely to be associated with the phenotypically same or similar diseases and vice versa.31 Therefore, the key to judging whether an miRNA is related to a specific disease is the similarity computation, which is based on known miRNA-disease relationships and some external information such as gene ontology, PPIs, and gene expression. In recent years, with the development of machine learning, some prediction approaches based on machine learning have also been proposed. Here, we discuss the previous approaches from 2 aspects: network similarity methods and machine learning methods.
Network similarity methods, according to the information involved in similarity computation, can be grouped into 2 categories:32 local network similarity methods24,33 and global network similarity methods.31,34 Local network similarity–based methods only consider the directed edge information contained in the involved networks, which ignore the global structure of these networks. For example, Jiang et al24 proposed a Boolean network method that uses hypergeometric distribution to identify the miRNA-disease associations based on an miRNA-miRNA network, a disease-disease network, and an miRNA-disease relationship network. Xuan et al33 proposed a K nearest neighbor method, HDMP, which was based on the weighted k most similar neighbors. In the global network similarity–based group, a random walk with restart (RWR) model is a classic representative, which applies an RWR on the miRNA-miRNA functional similarity network.31 Based on the RWR algorithm, researchers integrated more miRNA-related data and developed some improved methods. For example, Shi et al34 mapped disease genes and miRNA target genes on the PPI network and obtained 2 ranked lists of genes obtained by the RWR algorithm with different seeds. The global network similarity methods usually have better performance than the local similarity methods. However, both local and global network methods usually directly compute associations score from networks, and most of them are unsupervised without using labeled information that is difficult to catch the deep complex interaction patterns between miRNAs and diseases. With the development of artificial intelligence in recent years, some researchers began to use machine learning methods to predict miRNA-disease associations.
The machine learning–based prediction methods usually face 2 challenges: first, the current data sets include only positive samples without negative samples; second, extracting the feature vectors of miRNA-disease pairs is nontrivial. Although there are some limitations, the excellent performance of machine learning methods can still guarantee high-quality prediction models. The first machine learning–based method for miRNA-disease association prediction was proposed by Xu et al, which extracted features from miRNA-disease network data and train a support vector machine (SVM).24 After that, Chen and Yan35 proposed the model of regularized least squares for miRNA-disease association (RLSMDA), which is a global and sim-supervised learning method. Niu et al36 integrated random walk and binary regression to identify novel miRNA-disease associations that are based on global similarity and supervised learning method. Although the existing computational methods have already achieved great performance, there is still some room for improvement.
In recent years, many researchers attempted to use deep neural networks to solve bioinformatics computing and got promising results.37 For instance, Peng et al38 identified the miRNA-disease associations by a learning-based framework, MDA-CNN, which is based on convolution neural networks, and Luo et al39 predicted disease-gene associations by multimodal deep belief network (DBN) learning. It has been proved that DBNs can perform both unsupervised learning by automatically learning the high-level abstract features and supervised learning by backpropagation to fine-tune the weights got from the unsupervised learning with a few labeled data.40 The shortcoming of DBNs is time-consuming when handing a large database, but it shows great performance in extracting features for regular data and performing supervised training with just a few labeled data. The properties of DBNs show that DBN is suitable for the miRNA-disease association prediction that owns a few labeled data and the database is not so big.
In this study, we present a DBN-based matrix factorization model, DBN-MF, for miRNA-disease prediction. The main idea is factorizing the miRNA-disease adjacency matrix to 2 matrices with DBNs, one represents all the miRNAs’ features, whereas the other one represents all the diseases’ features. Then an association score of each miRNA-diseases pair is calculated for the prediction according to a classifier consisting of 2 DBNs and a cosine score function. The results of our computational experiments show that DBN-MF outperforms the state-of-the-art approaches.
Materials and Methods
Restricted Boltzmann machines
A restricted Boltzmann machine (RBM) is a stochastic neural network that only has 2 layers, a visible layer at the bottom and a hidden layer at the top.41 The basic structure of an RBM is shown in Figure 1 and contains m visible neurons and n hidden neurons. Each visible neuron is connected to every hidden neuron, and there are no connections between the neurons in the same layer. RBM can understand and determine a probability distribution of hidden unites over its set of inputs that can be used as features to characterize raw data. When the data are binary, the corresponding RBM is a Binary-Binary RBM (BBRBM) and the RBM concerning an energy function, which is defined as follows:
Figure 1.
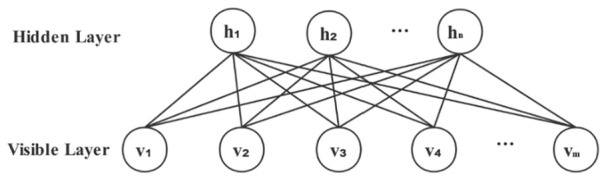
The basic structure of RBM. RBM indicates restricted Boltzmann machine.
| (1) |
where vi is ith neuron in the visible layer and hj is the jth neuron in the hidden layer; wij is the weight between vi and hj; ai and bj are biased, corresponding to the ith visible neuron and jth hidden neuron, respectively. According to equation (1), the joint probability distribution formula of the neuron state (v, h) can be given as follows:
| (2) |
where = {ai, bi, wij} is the set of parameters in the RBM, Z is the normalization factor and is also called the partition function.
The probability distribution of the input data P(v) is the marginal probability distribution of P(v|θ):
| (3) |
The purpose of RBM training is to obtain the parameters set θ, which maximizes the P(v|θ). The parameter set θ can be determined by performing a stochastic gradient descent (SGD) on the negative LogLikelihood probability of the training data as follows:
| (4) |
| (5) |
| (6) |
| (7) |
where Epd represents the expectation of the input conditional probability distribution of training data, and Epm denotes the expectation of the joint probability distribution of the model. Gibbs sampling42 method is used to calculate the expectation, which has a heavy computation cost in the training process of each iteration. A learning method contrastive divergence (CD) proposed by Hinton43 is applied to the approximate calculation after sampling. Then the RBM parameters are updated as follows:
| (8) |
where i is the current iteration, and η is the learning rate. According to the rules (equation (8)), the parameter θ is iteratively updated, and the maximum value of the gradient of the likelihood function is reached quickly, and the optimal parameters are obtained.
DBNs
DBN is a probabilistic neural network proposed by Hinton in 2006.44 A DBN model includes 1 input layer v, and multiple hidden layers {h1, h2, . . ., hL}, which has connections between different layers, and no connections within the same layer. The DBN model can be seen as a stack of multiple RBMs where each of the 2 layers formed an RBM model. As shown in Figure 2, the process of DBN training is, from bottom to up, training an RBM model by the input data, and getting the output of the current RBM as the input of the next RBM.
Figure 2.
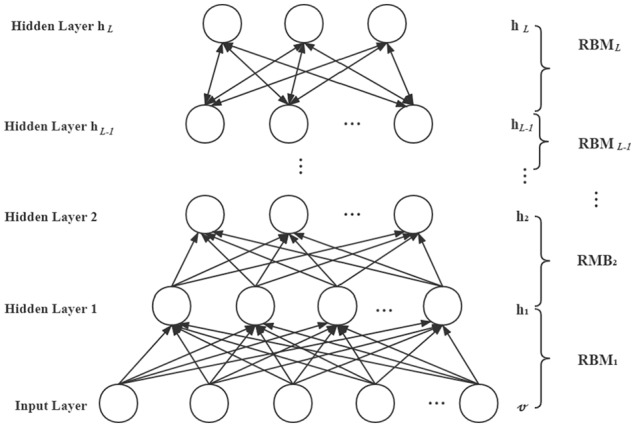
The basic structure of the DBN model. DBN indicates deep belief network; RBM, restricted Boltzmann machine.
The probability distribution of the DBN model P(v, h1, h2, . . ., hL) can be factorized as follows:
| (9) |
where P(hk|hk + 1) is the conditional probability distribution of hk when hk + 1 is given; P(hL−1, hL) is the joint probability distribution of hL−1 and hL.
The key to the DBN model is training the parameters. First, we trained the RBM one by one and obtained each RBM’s parameters by the contrast divergence algorithm. After training all the hidden layers, the last layer represents the feature extracted from DBN.
DBN-MF model
Problem statement
Suppose there are k miRNAs M = {m1, m2, . . ., mk}, and p diseases D = {d1, d2, d3, . . ., dp}. The k miRNAs and p diseases form a k*p adjacency matrix Y, which represents the associations between miRNAs and diseases. In this matrix, element Yij = 1 if the association between miRNA i and disease j is confirmed, and otherwise Yij = 0.
In this study, we try to factorize matrix Y into 2 matrices, one represents the features of miRNAs, whereas the other one represents the features of diseases. Then according to the result of factorization, the association score for each pair of miRNA-disease can be calculated.
Model-based methods45,46 usually assume that there is an underlying model that can predict the association score as follows:
| (10) |
where denotes the prediction score of association between miRNA mi and disease dj, θ denotes the model parameters, and F denotes the model function that maps the mi and dj to the predicted scores under parameters θ. Then the score of each pair of miRNA-disease can be obtained by this model.
Therefore, the key question becomes how to define the function F. Latent Factor Model (LFM)47 simply applied the inner product to calculate the association score between 2 objects. Neural collaborative filtering (NCF)48 used a multilayer perceptron to automatically learn the function F and determine the nonlinear associations between 2 items. Inspired by NCF, in this study, we try to determine the nonlinear associations between miRNAs and diseases by a deep representation learning architecture. This deep representation learning includes 2 parts, the first part is the unsupervised pretraining of DBNs, and the second part is the supervised learning of a classifier by backpropagation. The cosine score is used in the last step to calculate the final score in supervised learning.
The process of DBN-MF model
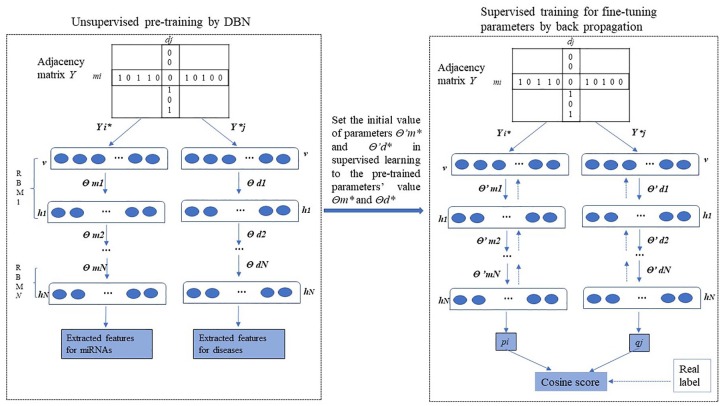
The framework of the DBN-MF model is shown in Figure 3.
Figure 3.
The flow chart of the DBN-MF model. DBN-MF indicates deep belief network–based matrix factorization.
Step 1, unsupervised pretraining of DBN. Taking the adjacency matrix Y as input, each row represents an miRNA while each column represents a disease. Two DBN models are used to perform unsupervised learning, respectively, with miRNAs and diseases. In each DBN model, from the input layer, each RBM model learns a group of parameters for the current layer i, and the output of RBM i is the input of RBM i + 1. After finishing the pretraining, all the parameters of 2 DBN models are recorded as θm* and θd*. At the same time, the features of miRNAs and diseases have also been extracted.
Step 2, supervised training of a classifier for fine-tuning the parameters by backpropagation. Taking the same input data as step 1, a classifier consisting of 2 DBNS and a cosine function is trained with the values of the parameters as the initial weights of 2 DBNs. The training is done by iterative forward-propagation and backpropagation on these 2 DBNs. By the forward-propagation, the raw feature of miRNA mi and disease dj finally mapped to feature vectors miRNA pi and disease qj. After getting the extracted features pi and qj, the cosine similarity is used to measure the relationship score between pi and qj, which is calculated as follows:
| (11) |
Then, a cost function is used to measure the difference between the predicted score and the real label, and backpropagating is applied to update the parameters according to the cost function.
The cost function is also an important component of deep learning. The squared loss function is one common and simple cost function, yet it cannot perform well with implicit data that the target value Yij is a binarized 1 or 0.49 Aimed at this kind of binary data, He et al proposed a cost function that can pay special attention to the binary property of implicit data as follows:
| (12) |
which we use in this study.
Experiments and Results
Data sources
For evaluating its effectiveness of model DBN-MF, we perform DBN-MF on the HMDD50 database. HMDD is a manually collected database on human miRNA-disease associations with experimentally supported evidence. HMDD V2.0 was published in 2013, which includes 5441 pairs of positive associations between 501 miRNAs and 383 diseases after combining the miRNAs from different stages, such as has-let-7a-1 and has-let-7a-2. Then in 2018, a new version HMDD V3.0 was published that contains 2-fold more entries than the HMDD V2.0. After doing the same combining operation, HMDD V3.0 contains 17 198 positive associations between 1065 miRNAs and 894 diseases. As there are no confirmed negative samples, we randomly choose a negative set with the same size as the positive set from all nonpositive (unknown) associations for the supervised training.
Evaluation methods
In this article, 10-fold cross-validation (10-fold CV) was used to evaluate the performance of DBN-MF. The 10-fold CV randomly divides the known positive associations and the same number of unknown samples into 10 folds, and each fold takes in turn as the test samples and the rest as the train set at each time. We do not use leave-one-out cross-validation (LOOCV), because the database is big enough for 10-fold CV and the computational model is based on a deep neural network which would be time-consuming with LOOCV.
To evaluate the result of the 10-fold CV from different aspects, the area under receiver operating characteristics (ROC) curve (AUC), the area under precision and recall (AUPR), and F1 score are used in this study. ROC curves show the true positive rate (TPR) against the false positive rate (FPR) under different score thresholds. Here, TPR is the percentage of positive samples that are correctly identified, whereas FPR refers to the percentage of negative samples that are identified as positive samples to all the negative samples. The AUPR curve plots the precision versus the recall at different thresholds, in which precision is a ratio of correctly predicted samples to the total samples, and recall is the same as TPR. F1-score is the harmonic mean of the precision and recall, which is defined as follows:
| (13) |
Hyperparameters
In this study, several hyperparameters affect the performance of the prediction. Because the supervised learning fine-tunes the parameters of unsupervised learning, the number of hidden layers hi and the number of nodes in each hidden layer hid_N on supervised learning is the same with DBN. For DBN, the basic architecture is determined by hi and hid_N. In our experiment, we found that when the number of hidden layers is larger than 3, the model becomes stable. Therefore, we set the number of hidden layers to 4. We tried hid_N as {100, 150, 200, 250, 300, 500}, the model gets the best performance with 200, and there is no big change from 150 to 250. Then we also tried hid_N as {180, 200, 220}, the model DBN_MF keeps the best performance in 200, so we set hid_N to 200.
Another 3 hyperparameters that determine whether the model is well trained are learning rate (lr), batch size (bs), and the number of epochs (ie). The previous studies51 showed that lr is usually selected as 0.01, and in our model, 0.01 is small enough to result in a stable state. For bs, it is usually set as the number of classes, and each batch usually contains at least 1 sample from each class. However, we just have 2 classes in our model that may not guarantee the best performance of DBN-FM. Therefore, we set bs to different values from {2, 4, 6, 8, 10}, and the prediction model obtains the best prediction ability of AUC when bs set as 8. For ie, we set it as 30, because the model becomes stable after 30 epochs.
Comparison with other algorithms
Comparison with the methods that integrated different kinds of evidence
DBN-FM model predicts miRNA-disease associations only based on the miRNA-disease adjacency matrix. However, most of the prediction methods integrated different kinds of data, such as gene co-expression networks, PPI networks, and disease phenotype network, to get more information. In this section, we compare the performance of DBN-MF in predicting miRNA-disease associations with the other 5 competing approaches, CIPHER,52 Boolean network method,24 Shi,34 PBMDA,53 and MDA-CNN.38 These 5 methods are all based on heterogeneous networks. CIPHER is a network-based regression model that extracts the relationships between phenotypes and genotypes, Boolean network method is a local similarity–based method, Shi is a random walk–based global similarity method, PBMDA is a path-based method by constructing a heterogeneous network, and MDA-CNN is a machine learning–based method. All these methods are tested on HMDD V2.0 data by a 10-fold CV evaluation method. Table 1 shows the AUC, AUPR, precision, recall, and F1-score of each method. Because the final results that we get from DBN-MF are the predicted association scores, so we need a threshold to get the predicted label. When calculating the precision, recall, and F1-score, we set the threshold as 0.5.
Table 1.
The comparison between DBN-MF and other 5 methods on AUC, AUPR, precision, recall, and F1-score value on miRNA-disease association prediction.
| AUC | AUPR | precision | recall | F1-score | |
|---|---|---|---|---|---|
| CIPHER | 0.5564 | 0.5612 | 0.4942 | 0.9954 | 0.6605 |
| Boolean network | 0.7897 | 0.8343 | 0.5876 | 0.9836 | 0.7356 |
| Shi | 0.7584 | 0.7896 | 0.7112 | 0.8615 | 0.7794 |
| PBMDA | 0.6321 | 0.6140 | 0.5192 | 0.9036 | 0.6594 |
| MDA-CNN | 0.8897 | 0.8887 | 0.8244 | 0.8056 | 0.8144 |
| DBN-MF | 0.9169 | 0.9043 | 0.8377 | 0.8526 | 0.8451 |
Abbreviations: AUC, area under the curve; AUPR, area under precision recall; DBN-MF, deep belief network–based matrix factorization; MDA, miRNA-disease association.
In Table 1, the bolded number is the largest in each column. According to the experimental results shown in Table 1, it is obvious that DBN-FM achieves the best performance on AUC, AUPR, precision, and F1-score. Even though DBN-FM cannot get the best performance in recall, its F1-score value is the highest one that is more balanced than recall value. DBN-MF achieves an AUC value as 0.9169, an AUPR value as 0.9043, and an F1-score as 0.8451 that are much higher than CIPHER, Boolean network, Shi, and PBMDA methods, and also higher than the other deep neural network–based method MDA-CNN. All in all, the experiments on HMDD V2.0 showed that DBN-MF achieves the best performance on miRNA-disease association prediction.
Comparison with the methods based on the same information
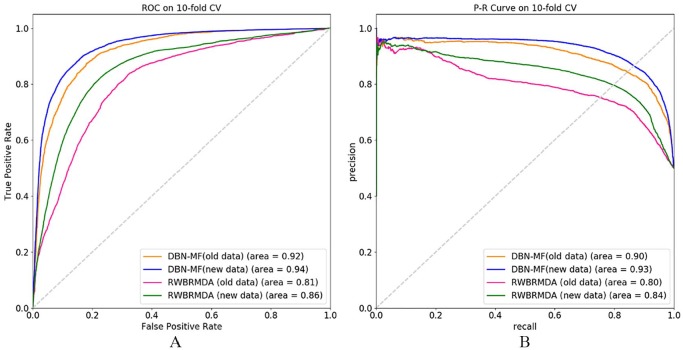
In section “Comparison with the methods that integrated different kinds of evidence,” we compared the performance of DBN-FM with some other prediction methods based on the heterogeneous networks. In this section, we compare DBN-FM with the method random walk and binary regression–based miRNA-disease association prediction (RWBRMDA)35 that also predicts miRNA-disease associations only using the miRNA-disease association matrix. RWBRMDA was proposed in 2019 and it integrated random walk and binary regression to identify novel miRNA-disease associations and has a global similarity and supervised learning method. We perform DBN-FM and RWBRMDA on both HMDD V2.0 and HMDD V3.0, respectively, and the ROC and precision-recall curve (PRC) of the prediction results is shown in Figure 4.
Figure 4.
The comparison between DBN-MF and RWBRMDA on data HMDD V2.0 and HMDD V3.0. (A) The ROC of DBN-MF and RWBRMDA. (B) The P-R curve of DBN-MF and RWBRMDA. DBN-MF indicates deep belief network–based matrix factorization; HMDD, Human microRNA Disease Database; ROC, receiver operating characteristics; RWBRMDA, random walk and binary regression–based miRNA-disease association.
Figure 4A shows that the DBN-FM achieves the AUC value of 0.92 on HMDD V2.0 (old data) and 0.94 on HMDD V3.0 (new data), which are both higher than the AUC value of RWBRMDA on HMDD V2.0 and HMDD V3.0, respectively. In addition, both DBN-FM and RWBRMDA have better prediction performance on the new data than the old data. Figure 4B shows the AUPR value of these 2 methods on both the new database and old database, and it has the same trend as the AUC value that DBN-FM achieves higher value than the RWBRMDA and they perform better on the new version database than on the old version database. In a word, 2 conclusions can be drawn from Figure 4. First, the performance of DBN-FM is superior to the RWBRMDA method when they predict miRNA-disease associations based on the same information. Second, a bigger database can help DBN-FM model improve the prediction ability.
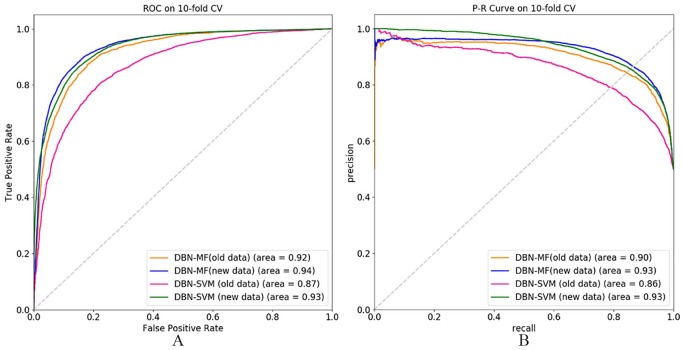
Effects of DBN-MF components
To evaluate the performance of each step of DBN-MF, we compare DBN-MF with the other version of DBN-MF, which is DBN-SVM. In DBN-SVM, the first step is the same as DBN-MF, which uses DBNs to extract the features of miRNAs and diseases. Then, DBN-SVM trains an SVM-based classifier with the extracted features in the first step. Each pair of miRNA-disease is considered as a sample, and we combine their features extracted from the first step to represent the features of a sample. Figure 5 shows the AUC value and AUPR value of DBN-MF and DBN-SVM on database HMDD V2.0 and HMDD V3.0.
Figure 5.
The comparison between DBN-MF and DBN-SVM on the data HMDD V2.0 and HMDD V3.0. (A) The ROC of DBN-MF and DBN-SVM. (B) The P-R curve of DBN-MF and DBN-SVM. DBN-MF indicates deep belief network–based matrix factorization; HMDD, Human microRNA Disease Database; SVM, support vector machine; ROC, receiver operating characteristics.
According to Figure 5A, DBN-MF achieves a higher AUC value than DBN-SVM in both HMDD V2.0 and HMDD V3.0. Figure 5B shows that DBN-MF has better prediction ability than DBN-SVM on old data, while DBN-MF has the same prediction performance compared with DBN-SVM on new data when evaluated in terms of AUPR. Besides, DBN-SVM has much better performance than the RWBRMDA method no matter based on the new data set or old data set. All in all, DBN-SVM also can effectively predict the miRNA-disease associations, and it has better performance than RWBRMDA, but its performance is still not as good as DBN-MF, especially when the database is not so big. All these results demonstrate that both the DBN part and the backpropagation part play important roles in the good prediction performance of DBN-MF, and the backpropagation is especially crucial when the data are not big enough. In addition, the results on the old database and new database further illustrate that a big database can result in better performance in miRNA-disease association prediction than the small database.
Case study
To further demonstrate the prediction ability of DBN-MF in identifying novel miRNA-disease associations, DBN-MF is conducted on HMDD V2.0 for predicting all the unknown associations. The other 3 databases (HMDD V3.0, dbDEMC,54 and miRCancer55) are used to verify the novel associations predicted by DBN-MF on database HMDD V2.0, and we also search the literature to confirm the newly predicted associations. In the prediction on data HMDD V2.0, 5441 positive associations and 5441 unknown associations are chosen as training samples. According to these 10 882 samples, DBN-MF trains a classifier, and the well-trained classifier is used to predict the association score for all the unknown associations. For a certain disease di, we rank the candidate miRNAs according to the predicted association scores, and the top several miRNAs usually have a high probability to be associated miRNAs of disease di. Here, we analyze the prediction results of lung cancer and pancreatic neoplasms by the top 20 potential-associated miRNAs.
Lung cancer is one of the most common cancers that have a high rate to cause death because it is difficult to diagnose at the early stage.56 Nevertheless, miRNAs can act as biomarkers that help diagnose cancers in an early stage. Table 2 shows the top 20 candidate miRNAs associated with lung cancer, which are predicted by the DBN-MF model based on the HMDD V2.0 data set. In these miRNAs, 19 of 20 miRNAs have been verified to have associations with lung cancer according to database HMDD V3.0, dbDEMC, miRCancer, or previous literature. Furthermore, for the unconfirmed miRNA has-mir-208b, a previous study57 showed that has-mir-208b was significantly upregulated in all moderate pulmonary hypertension subjects, and pulmonary hypertension is a common phenomenon in lung cancer patients, which indicates that has-mir-208b also has a high probability to associate with lung cancer. The results in Table 2 demonstrate the effectiveness of our DBN-MF model in predicting novel associations between miRNAs and lung cancer.
Table 2.
The prediction results of the top 20 new miRNA-disease associations of lung cancer.
| Lung cancer | |||||
|---|---|---|---|---|---|
| Rank | miRNAs | References | Rank | miRNAs | Reference |
| 1 | has-mir-15b | miRCancer, dbDEMC | 11 | has-mir-208a | HMDD V3.0 |
| 2 | has-mir-106b | dbDEMC | 12 | has-mir-184 | HMDD V3.0 |
| 3 | has-mir-20b | dbDEMC | 13 | has-mir-451a | HMDD V3.0 |
| 4 | has-mir-195 | miRCancer | 14 | has-mir-328 | HMDD V3.0 |
| 5 | has-mir-373 | HMDD V3.0 | 15 | has-mir-302a | dbDEMC |
| 6 | has-mir-372 | HMDD V3.0 | 16 | has-mir-340 | HMDD V3.0 |
| 7 | has-mir-208b | Unconfirmed, high probability | 17 | has-mir-23b | PMID:30214567 |
| 8 | has-mir-141 | HMDD V3.0 | 18 | has-mir-204 | PMID:25157435 |
| 9 | has-mir-129 | HMDD V3.0 | 19 | has-mir-15a | HMDD V3.0 |
| 10 | has-mir-92b | dbDEMC | 20 | has-mir-122 | HMDD V3.0 |
Abbreviations: HMDD, Human microRNA Disease Database; miRNA, microRNA.
Pancreatic neoplasm is another high incidence of disease that also causes a large number of deaths every year. To further demonstrate the performance of DBN-MF, we analyze the top 20 novel associations between miRNAs and pancreatic neoplasm that predicted by the DBN-MF model based on data HMDD V2.0. The results are shown in Table 3, in which 18 of 20 novel associations have confirmed in database dbDEMC or HMDD V3.0, and only 2 predicted associations has-mir-499a and has-mir-372 are not confirmed. The prediction results in Table 3 further illustrate the validity and feasibility of our prediction model.
Table 3.
The prediction results of the top 20 new miRNA-disease associations of pancreatic neoplasms.
| Pancreatic neoplasm | |||||
|---|---|---|---|---|---|
| Rank | miRNAs | References | Rank | miRNAs | Reference |
| 1 | has-mir-26b | dbDEMC, HMDD V3.0 | 11 | has-mir-208b | dbDEMC |
| 2 | has-mir-30b | dbDEMC, HMDD V3.0 | 12 | has-mir-133a | dbDEMC, HMDD V3.0 |
| 3 | has-mir-106b | dbDEMC, HMDD V3.0 | 13 | has-mir-29c | dbDEMC, HMDD V3.0 |
| 4 | has-mir-499a | unconfirmed | 14 | has-mir-181c | dbDEMC, HMDD V3.0 |
| 5 | has-mir-20b | dbDEMC | 15 | has-mir-30a | dbDEMC |
| 6 | has-mir-9 | dbDEMC | 16 | has-mir-141 | dbDEMC, HMDD V3.0 |
| 7 | has-mir-195 | dbDEMC, HMDD V3.0 | 17 | has-mir-181a | dbDEMC |
| 8 | has-mir-373 | dbDEMC, HMDD V3.0 | 18 | has-mir-140 | dbDEMC |
| 9 | has-mir-125a | dbDEMC, HMDD V3.0 | 19 | has-mir-129 | dbDEMC |
| 10 | has-mir-372 | unconfirmed | 20 | has-mir-19b | dbDEMC |
Abbreviations: HMDD, Human microRNA Disease Database; miRNA, microRNA.
Conclusions
MiRNAs were demonstrated to associate with a variety of diseases and can be biomarkers of diseases. Identifying miRNA-disease associations contributes to understand the underlying pathogenesis of diseases and provide proper disease treatment. As more and more miRNA-related and disease-related databases were created based on the biological experiments, researchers began to focus on predicting the miRNA-disease associations by computational methods. In this study, we have proposed a DBN-based matrix factorization model named DBN-MF to identify the underlying miRNA-disease associations. First, the unsupervised learning DBNs were trained with miRNAs’ and diseases’ raw features, respectively, and the extracted features were obtained. Second, a classifier with 2 pretrained DBNs is trained in the section of supervised machine learning for fine-tuning the parameters of our model. Finally, the well-trained model was used to predict the association score for each pair of unknown miRNA-disease. We compared DBN-MF model with previous computational methods on HMDD V2.0 and HMDD V3.0, the experimental results showed that DBN-MF achieved much better prediction performance than the previous methods for both AUC and AUPR no matter based on the same information or with the methods based on multiple types of evidence. The results on database HMDD V3.0 were better than HMDD V2.0, which demonstrated that a more sufficient database can help improve the performance of the prediction method. Also, the case study further illustrated the effectiveness of DBN-MF.
The excellent performance of DBN-MF is attributed to several important factors. First, this model took full advantage of the valid and updated miRNA-disease association data verified with biological experiments. Even though it did not integrate multiple types of data, the association data were sufficient enough to train a good model. Second, the unsupervised training of DBNs can learn the latent features of miRNAs and diseases very well, and well-trained DBNs are obtained with all the miRNAs or diseases, so this model includes the global information. Finally, backpropagation has a strong ability for learning the underlying complex associations between miRNAs and diseases with the labeled data. In summary, the excellent performance of this model is attributed to the nonlinear features of diseases and miRNAs that our proposed deep networks learned in the process of matrix factorizations. This advantage reveals the information that the traditional linear matrix factorization methods cannot learn.
Although DBN-MF shows great performance in predicting novel miRNA-disease associations, there are also some limitations. For example, the calculation of DBN-MF is based on miRNA-disease associations, so it cannot predict the novel associations for new diseases or miRNAs that have no known associations with miRNAs or diseases. In the future, we would further improve our model by extracting the features of miRNAs and diseases based on more and various types of information on miRNAs and diseases, such as the genes that miRNAs targeted, the GO terms of miRNA, the protein-protein network, and the disease phenotype. Specifically, we could integrate the miRNAs’ and diseases’ features extracted by DBN-MF with the miRNAs’ and diseases’ features extracted from other types of data. For example, first, the miRNAs’ semantic features can be described according to manifold learning method by miRNA target gene information from the database mirTarBase58 and the gene ontology annotations from the database GO.59,60 The disease semantic features can be obtained according to the manifold learning method by directed acyclic graph (DAG) constructed by the MeSH descriptors (https://www.nlm.nih.gov/). Then each miRNA or disease can be represented by integrating its DBN-MF features with its semantic features. Finally, we get an association score for each pair of miRNA-disease according to the integrated features of miRNAs and diseases. Also, we may use iFeature,61 iLearn,62 BioSeq-Analysis2.0,63 or BioSeq-Analysis64 to extract the features of miRNAs for improving our method.
Footnotes
Funding:The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: This work is supported in part by the Natural Science and Engineering Research Council of Canada (NSERC), China Scholarship Council (CSC), and the National Natural Science Foundation of China under Grant No. U19A2064.
Declaration of Conflicting Interests:The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Author Contributions: F-XW and YD conceived this study. F-XW, YD, FW, XL and BL discussed about the methods. YD implemented the algorithm, designed and performed the experiments. YD and F-XW wrote the manuscript. All authors read and approved the final manuscript.
ORCID iD: Fang-Xiang Wu  https://orcid.org/0000-0002-4593-9332
https://orcid.org/0000-0002-4593-9332
References
- 1. Ambros V. The functions of animal microRNAs. Nature. 2004;431:350-355. [DOI] [PubMed] [Google Scholar]
- 2. Bartel DP. MicroRNAs: genomics, biogenesis, mechanism, and function. Cell. 2004;116:281-297. [DOI] [PubMed] [Google Scholar]
- 3. Ambros V. microRNAs: tiny regulators with great potential. Cell. 2001;107:823-826. [DOI] [PubMed] [Google Scholar]
- 4. Lee RC, Feinbaum RL, Ambros V. The C. elegans heterochronic gene lin-4 encodes small RNAs with antisense complementarity to lin-14. Cell. 1993;75:843-854. [DOI] [PubMed] [Google Scholar]
- 5. Huang Y, Shen XJ, Zou Q, Wang SP, Tang SM, Zhang GZ. Biological functions of microRNAs: a review. J Physiol Biochem. 2011;67:129-139. [DOI] [PubMed] [Google Scholar]
- 6. Liu B, Fang L, Liu F, Wang X, Chen J, Chou K-C. Identification of real microRNA precursors with a pseudo structure status composition approach. PLoS ONE. 2015;10:e0121501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Yuan Y, Liu B, Xie P, et al. Model-guided quantitative analysis of microRNA-mediated regulation on competing endogenous RNAs using a synthetic gene circuit. Proc Natl Acad Sci USA. 2015;112:3158-3163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Kozomara A, Griffiths-Jones S. miRBase: annotating high confidence microRNAs using deep sequencing data. Nucleic Acids Res. 2013;42:D68-D73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Ambros V. MicroRNA pathways in flies and worms: growth, death, fat, stress, and timing. Cell. 2003;113:673-676. [DOI] [PubMed] [Google Scholar]
- 10. Karp X, Ambros V. Encountering microRNAs in cell fate signaling. Science. 2005;310:1288-1289. [DOI] [PubMed] [Google Scholar]
- 11. Miska EA. How microRNAs control cell division, differentiation and death. Curr Opin Genet Dev. 2005;15:563-568. [DOI] [PubMed] [Google Scholar]
- 12. Taganov KDB, Boldin MP, Chang K-J, Baltimore D. NF-κB-dependent induction of microRNA miR-146, an inhibitor targeted to signaling proteins of innate immune responses. Proc Natl Acad Sci USA. 2006;103:12481-12486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Meng F, Henson R, Wehbe-Janek H, Ghoshal K, Jacob ST, Patel T. MicroRNA-21 regulates expression of the PTEN tumor suppressor gene in human hepatocellular cancer. Gastroenterology. 2007;133:647-658. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Carleton M, Cleary MA, Linsley PS. MicroRNAs and cell cycle regulation. Cell Cycle. 2007;6:2127-2132. [DOI] [PubMed] [Google Scholar]
- 15. Griffiths-Jones S, Grocock RJ, van Dongen S, Bateman A, Enright AJ. miRBase: microRNA sequences, targets and gene nomenclature. Nucleic Acids Res. 2006;34:D140-D144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Hua S, Yun W, Zhiqiang Z, Zou Q. A discussion of microRNAs in cancers. Curr Bioinform. 2014;9:453-462. [Google Scholar]
- 17. Madhavan D, Zucknick M, Wallwiener M, et al. Circulating miRNAs as surrogate markers for circulating tumor cells and prognostic markers in metastatic breast cancer. Clin Cancer Res. 2012;18:5972-5982. [DOI] [PubMed] [Google Scholar]
- 18. Kliese N, Gobrecht P, Pachow D, et al. miRNA-145 is downregulated in atypical and anaplastic meningiomas and negatively regulates motility and proliferation of meningioma cells. Oncogene. 2013;32:4712-4720. [DOI] [PubMed] [Google Scholar]
- 19. Zhao S, Yang G, Mu Y, et al. MiR-106a is an independent prognostic marker in patients with glioblastoma. Neuro Oncol. 2013;15:707-717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Huang Z, Shi J, Gao Y, et al. HMDD v3.0: a database for experimentally supported human microRNA–disease associations. Nucleic Acids Res. 2018;47:D1013-D1017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Taguchi Y-h. Inference of target gene regulation via miRNAs during cell senescence by using the MiRaGE server. Paper presented at: International Conference on Intelligent Computing; July 25-29, 2012; Huangshan, China. [PMC free article] [PubMed] [Google Scholar]
- 22. Lynam-Lennon N, Maher SG, Reynolds JV. The roles of microRNA in cancer and apoptosis. Biol Rev. 2009;84:55-71. [DOI] [PubMed] [Google Scholar]
- 23. Yuan Y, Ren X, Xie Z, Wang X. A quantitative understanding of microRNA-mediated competing endogenous RNA regulation. Quant Biol. 2016;4:47-57. [Google Scholar]
- 24. Xu J, Li C-X, Lv J-Y, et al. Prioritizing candidate disease miRNAs by topological features in the miRNA target-dysregulated network: Case study of prostate cancer. Mol Cancer Ther. 2011;10(10):1857-1866. [DOI] [PubMed] [Google Scholar]
- 25. Cho WC. MicroRNAs: potential biomarkers for cancer diagnosis, prognosis and targets for therapy. Int J Biochem Cell Biol. 2010;42:1273-1281. [DOI] [PubMed] [Google Scholar]
- 26. Tricoli JV, Jacobson JW. MicroRNA: potential for cancer detection, diagnosis, and prognosis. Cancer Res. 2007;67:4553-4555. [DOI] [PubMed] [Google Scholar]
- 27. Chen X, Yan CC, Zhang X, You Z-H. Long non-coding RNAs and complex diseases: from experimental results to computational models. Brief Bioinform. 2016;18:558-576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Wang D, Wang J, Lu M, Song F, Cui Q. Inferring the human microRNA functional similarity and functional network based on microRNA-associated diseases. Bioinformatics. 2010;26:1644-1650. [DOI] [PubMed] [Google Scholar]
- 29. Hamosh A, Scott AF, Amberger JS, Bocchini CA, McKusick VA. Online Mendelian Inheritance in Man (OMIM), a knowledgebase of human genes and genetic disorders. Nucleic Acids Res. 2005;33:D514-D517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Keshava Prasad T, Goel R, Kandasamy K, et al. Human protein reference database—2009 update. Nucleic Acids Res. 2008;37:D767-D772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Chen X, Liu M-X, Yan G-Y. RWRMDA: predicting novel human microRNA–disease associations. Mol Biosyst. 2012;8:2792-2798. [DOI] [PubMed] [Google Scholar]
- 32. Zeng X, Zhang X, Zou Q. Integrative approaches for predicting microRNA function and prioritizing disease-related microRNA using biological interaction networks. Brief Bioinform. 2016;17:193-203. [DOI] [PubMed] [Google Scholar]
- 33. Xuan P, Han K, Guo M, et al. Prediction of microRNAs associated with human diseases based on weighted k most similar neighbors. PLoS ONE. 2013;8:e70204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Shi H, Xu J, Zhang G, et al. Walking the interactome to identify human miRNA-disease associations through the functional link between miRNA targets and disease genes. BMC Syst Biol. 2013;7:101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Chen X, Yan G-Y. Semi-supervised learning for potential human microRNA-disease associations inference. Sci Rep. 2014;4:5501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Niu Y-W, Wang G-H, Yan G-Y, Chen X. Integrating random walk and binary regression to identify novel miRNA-disease association. BMC Bioinformatics. 2019;20:59. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Chen X, Xie D, Zhao Q, You Z-H. MicroRNAs and complex diseases: from experimental results to computational models. Brief Bioinform. 2019;20:515-539. [DOI] [PubMed] [Google Scholar]
- 38. Peng J, Hui W, Li Q, et al. A learning-based framework for miRNA-disease association identification using neural networks. Bioinformatics. 2019;35:4364-4371. [DOI] [PubMed] [Google Scholar]
- 39. Luo P, Li Y, Tian L-P, Wu F-X. Enhancing the prediction of disease–gene associations with multimodal deep learning. Bioinformatics. 2019;35:3735-3742. [DOI] [PubMed] [Google Scholar]
- 40. Hinton GE, Osindero S, Teh Y-W. A fast learning algorithm for deep belief nets. Neural Comput. 2006;18:1527-1554. [DOI] [PubMed] [Google Scholar]
- 41. Fischer A, Igel C. An introduction to restricted Boltzmann machines. Paper presented at: Iberoamerican Congress on Pattern Recognition; September 3-6, 2012; Buenos Aires, Argentina https://link.springer.com/content/pdf/10.1007%2F978-3-642-33275-3_2.pdf [Google Scholar]
- 42. Geman S, Geman D. Stochastic relaxation, Gibbs distributions, and the Bayesian restoration of images. IEEE Trans Pattern Anal Mach Intell. 1984;6:721-741. [DOI] [PubMed] [Google Scholar]
- 43. Hinton GE. Training products of experts by minimizing contrastive divergence. Neural Comput. 2002;14:1771-1800. [DOI] [PubMed] [Google Scholar]
- 44. Hinton GE. Deep belief networks. Scholarpedia. 2009;4:5947. [Google Scholar]
- 45. Koren Y. Factorization meets the neighborhood: a multifaceted collaborative filtering model. Paper presented at: Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining; August 2008; Las Vegas, NV https://dl.acm.org/doi/abs/10.1145/1401890.1401944 [Google Scholar]
- 46. Mnih A, Salakhutdinov RR. Probabilistic matrix factorization. Paper presented at: Advances in Neural Information Processing Systems; December 8-10, 2008; Vancouver, BC, Canada http://papers.nips.cc/paper/3208-probabilistic-matrix-factorization.pdf [Google Scholar]
- 47. Koren Y, Bell R, Volinsky C. Matrix factorization techniques for recommender systems. Computer. 2009;48:30-37. [Google Scholar]
- 48. He X, Liao L, Zhang H, Nie L, Hu X, Chua T-S. Neural collaborative filtering. Paper presented at: Proceedings of the 26th International Conference on World Wide Web; April 2017; Perth, WA, Australia https://dl.acm.org/doi/abs/10.1145/3038912.3052569 [Google Scholar]
- 49. Xue H-J, Dai X, Zhang J, Huang S, Chen J. Deep matrix factorization models for recommender systems. Paper presented at: Twenty-Sixth International Joint Conference on Artificial Intelligence; August 19-25, 2017; Melbourne, VIC, Australia https://pdfs.semanticscholar.org/35e7/4c47cf4b3a1db7c9bfe89966d1c7c0efadd0.pdf [Google Scholar]
- 50. Li Y, Qiu C, Tu J, et al. HMDD v2.0: a database for experimentally supported human microRNA and disease associations. Nucleic Acids Res. 2013;42:D1070-D1074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Hinton GE. A practical guide to training restricted Boltzmann machines. In: Montavon G, Orr GB, Müller KR,eds. Neural Networks: Tricks of the Trade. Berlin: Springer; 2012:599-619. [Google Scholar]
- 52. Wu X, Jiang R, Zhang MQ, Li S. Network-based global inference of human disease genes. Mol Syst Biol. 2008;4:189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. You Z-H, Huang Z-A, Zhu Z, et al. PBMDA: a novel and effective path-based computational model for miRNA-disease association prediction. PLoS Comput Biol. 2017;13:e1005455. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54. Yang Z, Wu L, Wang A, et al. dbDEMC 2.0: updated database of differentially expressed miRNAs in human cancers. Nucleic Acids Res. 2016;45:D812-D818. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Xie B, Ding Q, Han H, Wu D. miRCancer: a microRNA–cancer association database constructed by text mining on literature. Bioinformatics. 2013;29:638-644. [DOI] [PubMed] [Google Scholar]
- 56. Siegel RL, Miller KD, Jemal A. Cancer statistics, 2016. CA Cancer J Clin. 2016;66:7-30. [DOI] [PubMed] [Google Scholar]
- 57. Wei C, Henderson H, Spradley C, et al. Circulating miRNAs as potential marker for pulmonary hypertension. PLoS ONE. 2013;8:e64396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58. Chou C-H, Shrestha S, Yang C-D, et al. miRTarBase update 2018: a resource for experimentally validated microRNA-target interactions. Nucleic Acids Res. 2018;46:D296-D302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59. Ashburner M, Ball CA, Blake JA, et al. Gene ontology: tool for the unification of biology. Nat Genet. 2000;25:25-29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60. Consortium GO. Expansion of the gene ontology knowledgebase and resources. Nucleic Acids Res. 2017;45:D331-D338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61. Chen Z, Zhao P, Li F, et al. iFeature: a python package and web server for features extraction and selection from protein and peptide sequences. Bioinformatics. 2018;34:2499-2502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62. Chen Z, Zhao P, Li F, et al. iLearn: an integrated platform and meta-learner for feature engineering, machine-learning analysis and modeling of DNA, RNA and protein sequence data [published online ahead of print April 24, 2019]. Brief Bioinform. doi: 10.1093/bib/bbz041. [DOI] [PubMed] [Google Scholar]
- 63. Liu B. BioSeq-Analysis: a platform for DNA, RNA and protein sequence analysis based on machine learning approaches. Brief Bioinform. 2019;20:1280-1294. [DOI] [PubMed] [Google Scholar]
- 64. Liu B, Gao X, Zhang H. BioSeq-Analysis2.0: an updated platform for analyzing DNA, RNA and protein sequences at sequence level and residue level based on machine learning approaches. Nucleic Acids Res. 2019;47:e127. [DOI] [PMC free article] [PubMed] [Google Scholar]