Estimating the First 90 of the UNAIDS 90-90-90 Goal: A Review

Abstract

Estimating the population with undiagnosed HIV (PUHIV) is the most methodologically challenging aspect of evaluating 90-90-90 goals. The objective of this review is to discuss assumptions, strengths, and shortcomings of currently available methods of this estimation. Articles from 2000 to 2018 on methods to estimate PUHIV were reviewed. Back-calculation methods including CD4 depletion and test–retest use diagnosis CD4 count, or previous testing history to determine likely infection time thus, providing an estimate of PUHIV for previous years. Biomarker methods use immunoassays to differentiate recent from older infections. Statistical techniques treat HIV status as missing data and impute data for models of infection. Lastly, population surveys using HIV rapid testing most accurately calculates the current HIV prevalence. Although multiple methods exist to estimate the number of PUHIV, the appropriate method for future applications depends on multiple factors, namely data availability and population of interest.

What Do We Already Know about This Topic?

Different approaches to estimate the population undiagnosed with HIV are available in the literature; however, each approach relies on various factors (data availability, resources) to estimate the number accurately which makes this process not a “one size fits all” approach.

How Does Your Research Contribute to the Field?

Our review compiles those methods that have recently been introduced to estimate the population undiagnosed with HIV in addition to the methods that are available with the suggested updates.

What Are Your Research’s Implications toward Theory, Practice, or Policy?

Our review could provide cities/municipalities with guidance on utilizing various methodologies to estimate their own population undiagnosed with HIV based on the accessibility and availability of their data.

Background

The Joint United Nations Programme on HIV/AIDS (UNAIDS) established the 90-90-90 targets in December 2013,¹ setting goals to be achieved by the year 2020 in an effort to disrupt the ongoing transmission of HIV globally. The first “90” of the UNAIDS 90-90-90 goal is for 90% of all people living with HIV (PLHIV) to know their HIV status, that is, be diagnosed. The second “90” is for 90% of diagnosed PLHIV to be on antiretroviral therapy (ART). The final “90” aims to achieve viral suppression among 90% of those on treatment.¹ Achieving these goals will not only lead to longer and healthier lives among PLHIV, but potentially alter the HIV epidemic through the treatment as prevention model, as virally suppressed PLHIV are unlikely to transmit HIV.^1,2 Estimation of the number of people at each stage of the 90-90-90 goals will also assist with planning and evaluation of prevention strategies and resource distribution.³

Because many PLHIV remain unaware of their status for a long period of time, it is difficult to estimate the actual burden of HIV infection, resulting in poor clinical outcomes and continued spread of infection.⁴ The first “90” goal seeks to minimize the number of population with undiagnosed HIV (PUHIV). In countries with extensive surveillance systems, it is relatively straightforward to calculate the prevalence and incidence of HIV diagnosis giving a clear view of diagnosed PLHIV.^5,6 However, evaluating whether the first “90” goal has been met requires answering the question “How many people are HIV positive but unaware of their status?” Current estimates are that 1 of every 7 PLHIV in the United States are undiagnosed⁵; the PUHIV drive one-third of the new HIV infections.⁷ Several methods have been developed and implemented to estimate the quantity of PUHIV. However, there has been little research to ascertain if there is an ideal method to estimate this number. Estimating PUHIV and the potential characteristics of this population facilitates research and public health initiatives aiming to end the HIV epidemic. In addition to its importance in directing and evaluating screening efforts, an accurate estimate of PUHIV is necessary for evaluating each of the 90-90-90 targets. In this review, our objective is to discuss assumptions and data required to inform current methods to estimate the PUHIV.

Methods

We conducted a literature search to identify articles and reports published between January 1, 2000, and August 10, 2018, in English peer-reviewed journals reviewing methods for the estimation of PUHIV. In addition, we extracted articles from the bibliographies of retrieved articles to find papers not identified by our keyword search. Our first round of search phrases included “Undiagnosed HIV infections,” “Estimate undiagnosed HIV population,” and “Methods estimating HIV incidence.” Next, we searched for specific methods that were discovered from the first round of literature search. The search keywords were “Multiple imputation HIV,” “Biomarker methods HIV,” and “HIV population surveys.” Abstracts were reviewed based on the relevance of the title.

We excluded publications that used AIDS diagnosis for estimating the time of infection and those published prior to 2000 due to the advent of modern ART. We also excluded studies that reported on co-HIV infections and diseases other than HIV. Papers/reports that described similar methods were reviewed to compile as much information on the method as possible. The methods identified and discussed in this review are the Back-calculation methods including CD4 depletion model and test–retest method, biomarker method, missing data approach, and population surveys.

Results

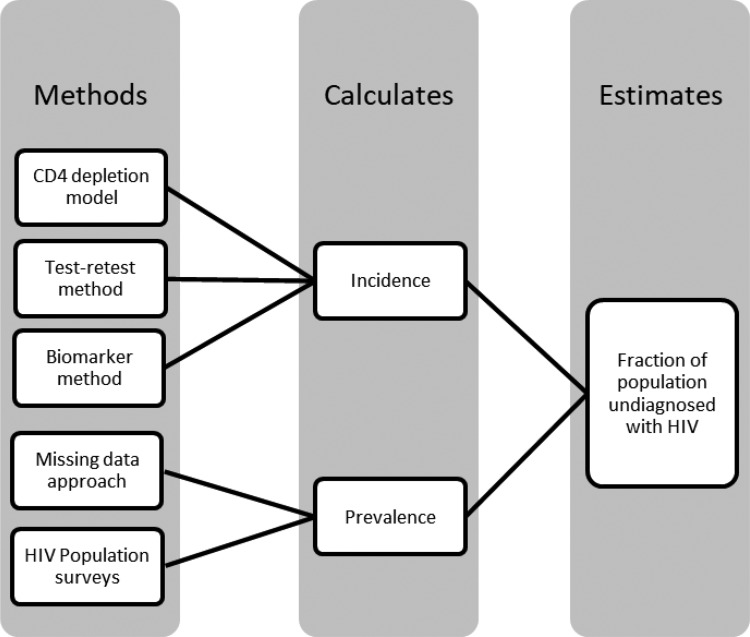
The CD4 depletion model and the test–retest method are most commonly used for the estimation of the PUHIV (Figure 1). Surrogate markers such as the CD4 count at diagnosis reflect the time since infection as CD4 count declines over time in predictable ways. In addition, a previous HIV-negative test serves as an authentic proof that the person at that time was uninfected, indicating that the infection must have taken place between the prior negative test and the time of diagnosis. Biomarker tests can distinguish between acute/early infection (eg, within a 156-day period⁸) and more distant infection, which help in getting a more precise estimate incidence. The missing data approach and population surveys directly estimate prevalence of infection in a population. The missing data method uses statistical techniques to approximate the prevalence of HIV, treating PUHIV as missing data. Population surveys utilize HIV testing results of a random population sample, making calculation of HIV-prevalence easier and more accurate. However, feasibility of these surveys varies by population characteristics, specifically recruiting a sample large enough to be representative and to allow for precise estimation of HIV prevalence.

Figure 1.

Process through which each method used to estimate the population undiagnosed with HIV.

Back-Calculation Method

The true number of PLHIV for a particular year is the summation of all prevalent and newly infected (incident) diagnosed and undiagnosed cases. The number of undiagnosed cases is an unknown but a countable quantity. If we assume all HIV-infected people are eventually diagnosed, using a method to estimate an individual’s infection time (calendar time), we can estimate the year of infection for all newly diagnosed individuals. By “filling in” these previously undiagnosed cases, the number of PUHIV in previous years can be estimated. This allows for a more accurate estimate of the total PLHIV in that year and improved prevalence information for future years.

Figure 2 illustrates yearly addition to the known PLHIV for year 2016 with each passing year (2017 through 2019). For example, starting with known 70 (arbitrary) PLHIV in 2016 (light gray area in bar I), if 10 PLHIV were diagnosed in 2017 but were deemed infected in 2016, the number of known HIV infections in 2016 would increase by 10 as shown by the additional gray cell in bar II. This process will continue in subsequent years as illustrated in bars III and IV. Thus, the total number of remaining PUHIV in 2016 would decrease, improving the estimate of total HIV infections for 2016.

Figure 2.

Hypothetical illustration of calculating population undiagnosed with HIV. *Bars with years in () represents updated information about the 2016 population with people diagnosed that year but infected in 2016.

The estimate of HIV prevalence for previous years is then updated, illustrated by the shrinking black bar across bars I to IV. These updated prevalence estimates are calculated using the known prevalence in that earlier year, PUHIV diagnosed in the future years, and removing any known HIV-related deaths.

$$\left[\right(\text{Known prevalent PLHIV }\left(2016\right)+\text{ New infections in }2016(\text{discovered }2017-2019))-\text{ HIV}-\text{related deaths in }2016]=\text{ Total PLHIV in }2016\left(\text{updated in }2019\right)$$

Using this number, the prevalence estimate of PLHIV for 2016 is recalculated. Total PLHIV for each year following is updated as well; therefore, yielding an updated, more accurate, estimate of the total number of current (2019) HIV-positive individuals. The number of current PLHIV is estimated by multiplying this updated prevalence with the current population size.

$$\text{Prevalence of PLHIV }(2016,\text{updated }2019)\times \text{ current population size }\left(2019\right)=\text{ Estimated PLHIV in }2019$$

Using the total number of HIV-positive individuals, the number of PUHIV is calculated by subtracting the already known positives from the total HIV positives.

This method however is limited to models that estimate prevalence of PLHIV and that the accuracy of calculating HIV incidence in order to estimate the PUHIV depends on the accuracy of the methods to determine the likely time of infection, the length of time between infection and diagnosis, and the quality of the data on the prevalence of diagnosed HIV in the population. Looking at the recent reports, in 2015, at least 50% of PLHIV in the United States were diagnosed within 3 years of infection, a decrease from a median of 3.6 years in 2011^9,10 which would be expected to result in a shorter lag time needed to accurately estimate of PUHIV for recent years. However, death reporting is at least 18 months behind the current date which should be considered when drawing estimates for more recent years.¹¹

CD4 Depletion Model

The CD4 depletion method relies on a newly diagnosed person’s CD4 count to reflect when the individual was most likely infected, provided ART was not initiated.¹¹ The concept of incubation period (time from infection to AIDS diagnosis)² previously employed is now replaced with induction time (time from HIV infection to diagnosis). Lodi et al estimated the time from infection to a particular CD4 count by using data on 21 240 individuals from Concerted Action on Seroconversion to AIDS and Death in Europe. The study included individuals from Europe, Australia, Canada, and Sub-Saharan Africa whose dates of HIV infection were well estimated.¹² The results indicated that CD4 depletion without ART could be used to estimate time from diagnosis, for example, 1.19 years postinfection CD4 was 350 to 500 cells/mm³, 4.19 years was 200 to 350 cells/mm³, and 7.93 years was <200 cells/mm³.¹² This estimated time from the infection to a particular CD4 cell level allows us to identify when the person most likely became infected, demonstrated by the dashed line in Figure 3 which shows CD4 count of 500 cells/mm³ after ∼1.19 years of being infected.

Figure 3.

Hypothetical schematic figure of the CD4 depletion model. Time since infection estimated using CD4 count.

A major drawback to this method is that an initial CD4 count prior to initiation of ART is required and may not be readily available.¹² If an individual’s CD4 count is reported after the initiation of the ART, the validity of the estimated time since infection will be reduced.¹¹ In the United States, 6 states have not yet implemented the mandatory reporting of initial CD4 counts to the Centre for Disease Prevention and Control (CDC).¹¹ Furthermore, the current CD4 depletion model does not include individuals <13 years of age.¹¹ This is a reasonable approach in the United States where vertical transmission is very rare, but would be problematic in settings where HIV infection occurs more frequently in children. Moreover, since CD4 counts deplete drastically in the initial stage followed by a temporary recovery, CD4 count profiles captured at this initial period can lead to an overestimation of the duration of infection, and therefore, should not be used alone in acute/early infection, but methods such as a biomarker method that accurately distinguishes acute infection should be used in supplement. In addition, the amount/degree of decline varies with calendar year of seroconversion and mode of acquisition,¹² which may complicate interpretation of the disease stage. This method has been used by the CDC to estimate the national and state level number of undiagnosed PLHIV⁷ and to estimate the PUHIV by demographic characteristics and HIV risk factors.¹¹ Statewide reporting has several limitations, primarily that the rate provided for the entire state is often equally applied to all counties and populations within that state, which is likely to be inaccurate.

Test–Retest

The test–retest method can also be used to determine time from infection to diagnosis by requiring a newly diagnosed HIV-infected individual to have a history of negative HIV test/s (Figure 4).¹³ This method has been previously used in Seattle, Washington, to estimate the PUHIV among men who have sex with men (MSM).¹³ Like the CD4 depletion model, the test–retest method aims to estimate when a newly diagnosed individual was most likely infected. Infection time is typically estimated by either assuming that the event of infection occurred at a random point between the last HIV-negative test and the first positive test (base case estimate) or that the infection occurred on the day after the last negative test (upper bound estimate).¹³ If the exact date for the last HIV-negative test is missing, the test date is estimated to be that month’s median; if the date and the month both are missing, the date is assumed to be July 1 of that year.¹³ In cases where a testing history is not available, the period of HIV infection (time since infection) is calculated as the person’s age at diagnosis minus 16 years, the average age of an individual’s first sexual encounter in the United States.¹³ This number can be modified according to different geographic regions.

Figure 4.

Test–retest method. Hypothetical timeline showing events from negative HIV test to positive HIV test.

The test–retest method assumes that HIV infection takes less than 18 years to be diagnosed; thus, any older HIV-negative test is not included.¹³ Where complete testing history is not available, self-reported HIV testing information may be substituted but often lacks accuracy leading to imprecise estimates.¹³ For example, the self-reported last HIV-negative test might not be the most recent negative test¹³ or the report may be biased due to a telescoping effect, which is when a person perceives an event to be more recent than it actual was.¹⁴

Similar back-calculation methods have been used in Italy¹⁵ and France¹⁶ to estimate the number of undiagnosed individuals living with HIV, and in the Netherlands to plan interventions that build on “test and treat” strategies.⁴ The method described above has been used with modifications in different regions around the world depending on the data locally available. In addition to CD4 depletion model, CDC also uses the extended back-calculation model. This method uses HIV and AIDS diagnoses along with biomarkers to estimate time since infection.^3,17 The novel back-calculation model developed in Paris used time of HIV diagnosis (date), exposure category, and the clinical stage at diagnosis (primary HIV, asymptomatic without AIDS, and AIDS) to calculate the time between infection and diagnosis, which has been used to calculate HIV incidence.^16,17 The Sydney/Ottawa method called the “Back-Projection Method” was first used in Sydney and then implemented in Canada.¹⁸ This was similar to the standard back-calculation approach but additionally required a confirmed previous negative test or an indeterminate Western blot within 1 year of HIV diagnosis from surveillance data¹⁹ to estimate the time since infection.¹⁷ Furthermore, the Cambridge method in the United Kingdom used a multistate Bayesian model which uses the number of new HIV diagnosis, CD4 count at diagnosis, and AIDS status at diagnosis to estimate HIV incidence.^17,20

Biomarker Method

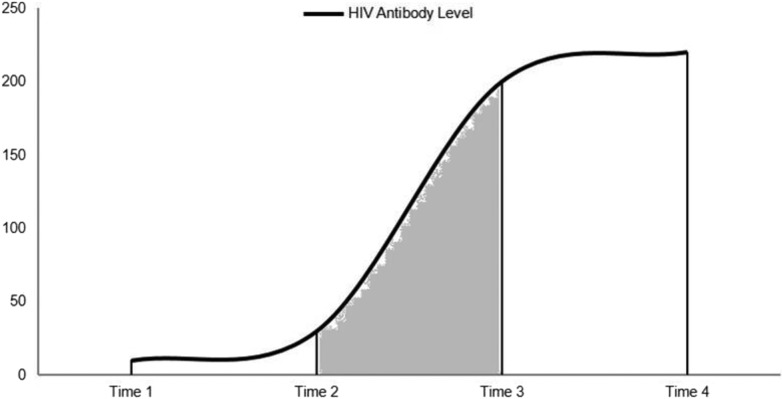
The biomarker method uses the HIV-1 capture enzyme immunoassay for HIV subtypes B, E, and D (BED CEIA) which estimates HIV incidence by differentiating a recent infection (up to 156 days after infection) from a person with nonacute HIV infection without AIDS diagnosis (>156 days) and a long-standing infection (AIDS at or within 6 months of diagnosis).³ This test measures the ratio between anti-HIV immunoglobulin G (IgG) and the total IgG levels in the body, which tend to increase soon after the virus enters the body; this variance determines a recent infection.³ HIV incidence can be calculated by dividing the number of “recent” infections at diagnosis by the probability that the individuals will test as recent on the biomarker test.⁸ This quantity is a product of the probability that an infected individual will get tested for HIV within a particular period after infection, the probability that this individual will have a biomarker test, and the probability that the test would be performed within the “recent” window (shown as the shaded area between time 2 and 3) in Figure 5, after infection (time 1) and before reaching the viral load set point (time 4).⁸ This test is also capable of detecting the HIV subtype.³

Figure 5.

Hypothetical schematic figure illustrating timeline of BED test. Dark area under the curve represents the window period of testing as “recent.”

The biomarker method estimates HIV incidence assuming that the testing behavior is stable over time, a likely invalid assumption as new advances in screening are being implemented and patterns are likely to change rapidly.¹⁶ There are also concerns regarding accuracy due to high rates of false “recent” results (false-recent misclassification) for individuals with AIDS, on ART, or those with certain medical conditions.^3,8 An overestimation of HIV incidence due to false-recent misclassification was observed in Thailand and Africa.^21,22 Therefore, CDC recommends not using information on individuals with AIDS or on ART who classify as recent infections.²³ It was also noted that this method worked better among certain HIV subtypes.²³ A study in Uganda carrying out BED CEIA on subtypes A and D produced more false-recent results for subtype D²⁴; a similar problem was encountered in Thailand with varying results between subtypes B and AE.²⁵ In the United States, BED CEIA was used between 2006 and 2013 and was replaced by the modified Bio-Rad HIV-1/HIV-2 plus O EIA in 2014.¹⁷ Although both tests are similar in function, the latter is more efficient in correctly classifying recent infections, that is, fewer false-recent misclassifications.²⁶ The newness and lack of sufficient literature on the modified Bio-Rad HIV-1/HIV-2 plus O EIA serves as a limitation for a detailed investigation of its performance in wider settings.

Missing Data Approaches

The missing data approach treats unknown HIV status as missing data and applies appropriate statistical measures for imputation. Imputation methods simulate multiple complete data sets. After imputation, standard multiple imputation techniques are applied to estimate associations and standard errors, accounting for the variability in the simulated data.²⁷ The most common imputation methods assume the data are missing at random (MAR). Missing at random implies that HIV status may depend on measured factors such as age or sex, but conditional on those factors, people with known and unknown HIV status have the same probability of being HIV infected.²⁸ This strong assumption is difficult to prove and is often unjustified.²⁸ HIV test results are likely associated with being missing, as low-risk HIV-negative individuals are less likely to get tested. Leacy et al used an augmented version of multiple imputations in the Zambia/South Africa TB AIDS Reduction Study where HIV test results were missing.²⁸ Their analysis used an adjusted form method of multiple imputations with chained equations (MICE)²⁹ which allows for estimation when outcomes are not MAR.³⁰ The MICE method performs multiple imputations by “chaining” each successive imputation together allowing for more complex imputations and added flexibility. Thus, this method allows for estimation of associations between HIV status (or diagnosis status) and other factors when the MAR assumption is not valid. A similar mathematically complex method, the Bordeaux method uses a Markov model with a modified likelihood function to account for missing information, such as HIV testing results.³¹ It therefore uses information on the number of new HIV diagnosis and AIDS diagnosis with estimated time of infection occurrence (incubation curve) to estimate HIV incidence.¹⁷

Population Surveys

Population surveys with detailed questions regarding HIV measures accompanied by voluntary HIV rapid test results can be helpful in overcoming the issue of missing data.³² Surveys like these are already being conducted in 14 high-burden countries and are proving to be remarkably successful.³³ These surveys can directly estimate the status of 90-90-90 for a given geographic region, such as a country. For example, investigators in Swaziland, now known as Eswatini, used survey data through March 2017 to estimate their progress toward 90-90-90 as 84.7-86.9-91.9.³⁴ Another benefit of such surveys is that a well conducted, truly population-based survey would require fewer statistical assumptions to estimate HIV prevalence than other approaches. In low-prevalence settings or large populations, such as the United States, the necessary number of people survived would have to be extremely large thus difficult to execute and cost-ineffective. However, implementing population surveys widely in high-prevalence areas can help in generating accurate measures, which can strengthen public health approaches aimed at ending local HIV epidemics.

Conclusion

To evaluate progress toward accomplishing 90-90-90 targets, PUHIV must be estimated. The approaches described in this review help to determine the number PUHIV in a certain time period and geographic area. Knowing the number of PUHIV can improve the accuracy of estimating the underlying burden of disease and changes in HIV-related trends across time.⁷ A clear picture of the burden of disease can direct health campaigns targeting at-risk populations¹² and can also be used to set future goals and objectives for HIV prevention strategies.¹¹ Estimates generated using these methods can influence the development of new policies which can expand the availability and acceptance of voluntary HIV testing.¹⁶ When researchers or government officials are tasked with this estimation, the preferred method will differ for each area and entity as specific data are necessary for each method. For example, if no previous testing history is available for most people, the test–retest method cannot be used. Thus, comparing the effectiveness across the described methods is not necessary as it is unlikely to have access to all data for all methods making method selection straightforward.

The methods to estimate PUHIV described in this review are the result of substantial investment in HIV testing, diagnosis, data collection, and statistical methods development. They have proven to be valuable tools in the efforts to stop the HIV epidemic. Further methods development to compare methods, to combine information across different data sources, to use newer biomarker tests, and to create estimates of PUHIV for subpopulations defined by geography and other characteristics would be helpful for public health efforts to diagnose 90% of PLHIV and ultimately end HIV. With different availability of resources and geographical characteristics, not everyone succeeded in achieving the 90-90-90 target set by UNAIDS. However, constant efforts are still being put forward and now aim to reach the 95-95-95 targets set by UNAIDS to be achieved by 2030.³⁵