Abstract
Green infrastructure (GI) in urban areas has been acknowledged to reduce the pollutant concentrations. However, there are limited modelling options to evaluate its impact on air quality. The aim of this review is to address the following question: how can the GI be considered in readily available dispersion models to allow evaluation of their impacts on pollutant concentrations and health-risk assessment? We examine the published literature on the parameterisation of air pollutants deposition velocities and dataset that are required for deposition scheme. The deposition schemes treating the GI in detail are complex, resource intensive and involve an abundant volume of input data. Further, we evaluate the limitations of different air pollution dispersion models at two spatial scales-microscale (i.e. 10–500 m) and macroscale (i.e. 5–100 km)-in considering the GI effect on air pollutants concentration and exposure alteration. We conclude that appropriate handling of GI characteristics such as aerodynamic effect, deposition of air pollutants and surface roughness in dispersion models is necessary for understanding the mechanism of concentration simulation by GI at different spatial scales. Several other processes such as air pollutant transformation due to GI emitted biogenic volatile organic compounds (bVOC), the fraction of stomatal blocking water film and change in uptake rate due to temperature increase also influence deposition rates and change the air pollutants concentration; most of them are not treated in dispersion models, mainly because these are not developed for such purposes. Furthermore, the impact of GI on air pollutants concentration and health risk assessment (e.g., mortality, morbidity) are partly explored. The United States Department of Agriculture (Forest Service) developed i-Tree, which with BenMap developed by the US EPA, have used to estimate the health outcomes of annual air pollutants removal by deposition over GI canopy at the macroscale. However, studies relating the air pollution health risk assessment due to change in short-term exposure by pollutants concentration redistribution at the microscale and enhanced atmospheric pollutants dilution by increased surface roughness at macroscale because of GI, along with deposition, are rare. Suitable treatment of all physical and chemical processes in coupled dispersion-deposition model and assessment against real scenarios are vital for health risk assessment.
Keywords: Microscale model, Macroscale model, Green infrastructure, Deposition velocity, dispersion-deposition coupled model, Air pollution health risk assessment
Graphical abstract

1. Introduction
Traffic emissions are a major source of air pollution in urban areas that adversely impact human health and the environment (Kumar et al., 2016, 2015, 2013; Sharma and Khare, 2001). The adverse health effects have been studies for regulated air pollutants such as particulate matter including PM10 (≤10μm; de Hoogh et al., 2014; Li et al., 2018; Talbi et al., 2018), PM2.5 (≤2.5μm; Ham et al., 2017; Huang et al., 2012; Rivas et al., 2017), Ozone (O3; Abramesko and Tartakovsky, 2017; Bao et al., 2018; Goodman et al., 2018), nitrogen dioxides (NOx; Jeanjean et al., 2017; Knibbs et al., 2018; Muttoo et al., 2018) and unregulated pollutants such as ultrafine particles (Clifford et al., 2018; Kumar et al., 2017; Pacitto et al., 2018), black carbon (Chang et al., 2015; De Matteis et al., 2015; Rivas et al., 2017), volatile organic compounds (VOCs; McDonald et al., 2018) and heavy metals (Aksu, 2015; Onder and Dursun, 2006). Green infrastructure (GI) is considered as one of the potential solutions for improving near-road air quality and limiting personal exposure to local sources (Abhijith et al., 2017). Usually, GI reduces the pollutant concentration by offering more surface area to increase the dry deposition, pollutants redistribution and atmospheric turbulence. GI could have different meanings under different contexts and depends on in which context it is used. For instance, eco-friendly constructions that have a low carbon footprint and energy efficiency are also known as green buildings/infrastructure in structural engineering. At the same time in Geo-environment engineering, GI is the group of trees and plants to stop the soil erosion. Benedict and McMahon (2002) defined GI “as an interconnected network of green space that conserves natural ecosystem values and functions and provides associated benefits to human populations”. In a broad sense, GI cover from all type of grasslands, forests, wetlands to an individual level species of tree and plant. For urban air quality, the important GI is street trees, green walls and roofs, roadside hedges, parks and grasslands to the urban boundary where air exchange is significant. In this review, we focus only on urban green vegetation that includes a group of trees, plants and/or hedges having large leaf area index (LAI) with an aim to draw critical discussion on how these could be considered in various readily available dispersion models for their impact assessment.
Apart from influencing factors such as wind speed and direction, topography and meteorology, the air pollutants dispersion also varies by surface roughness or geometry and deposition characteristic of GI. For example, a potential reduction of up to 50% compared with no green wall and roofs in street canyon can be expected by GI at microscale (i.e. 10–500 m; Britter and Hanna, 2003) in street canyon and neighbourhood environments (Gromke, 2011; Pugh et al., 2012) and that could be as little as 5% through available urban trees at macroscale (i.e. 5–100 km) citywide (Bottalico et al., 2017; Currie and Bass, 2008; Nowak, 1994). These reductions come from various reasons such as enhanced dilution due to enhanced atmospheric turbulence owing to increased surface roughness (Pleijel et al., 2004), air pollutants concentration redistribution (Abhijith et al., 2017; Baldauf, 2017) and dry deposition that is strongly influenced by LAI (Jayasooriya et al., 2017; Selmi et al., 2016). To reveal the dominant process in consideration of GI effect on air pollution would require a specified designed experiment, e.g. by measuring the air pollutant reduction at different distances from source in combination with different GI. The coupled green infrastructure and air pollutant dispersion modelling to estimate the dry deposition is based on consideration of GI as a porous medium in CFD (Jeanjean et al., 2015) and wind tunnel (Gromke et al., 2012) and as whole in receptor models (Chen et al., 2016; Li et al., 2016; Maleki et al., 2016), time of interaction (Pugh et al., 2012) and air pollutant concentration over the surface area (Jeanjean et al., 2016; Tiwary et al., 2009). At macroscale, the dilution of air pollutants due to GI-induced enhanced atmospheric turbulence has not been studied much, but many researcher (Barnes et al., 2014; Venkatram et al., 2013) have shown increasing surface roughness could decrease the ground level air pollutant concentration. As summarised in Table 1, many researchers have assessed the effect of GI on urban air quality at different spatial scales. Past works have also investigated the impact of GI on the reduction of particulate matter (Janhäll, 2015), urban heat island mitigation (Akbari et al., 2001; Bowler et al., 2010; Luber and McGeehin, 2008), reduction in noise pollution (Chiesura, 2004; Pathak et al., 2011), reduction in pollutant exposure as passive roadside barriers (Abhijith et al., 2017; Gallagher et al., 2015, 2013), stormwater management (Czemiel Berndtsson, 2010; Shaneyfelt et al., 2017) and considering GI as a part of natural capital (Chenoweth et al., 2018).
Table 1.
Summary of relevant studies considering GI modelling at the microscale (street and neighbourhood) and macroscale (city).
| City (modelled area) | Pollutant concentration measurement techniques | Approach for GI consideration | Author (year) |
|---|---|---|---|
| Toronto (1216 ha) | Field measurement | UFORE (i-tree) | Currie and Bass (2008) |
| Beijing (30,121 ha) | Field measurement | UFORE (i-tree) | Yang et al.(2004) |
| Chicago (60300 ha) | Field measurement | Nowak method (i-tree) | Nowak (1994) |
| Sacramento (23600 ha) | Field measurement | Mcpherson method | Mcpherson and Simpson (1999) |
| Baltimore (21000 ha) | CMAQ version 4.7.1 | i-tree, CMAQ + WRF | Cabaraban et al.(2013) |
| Leicester (400 ha) | OpenFOAM software (CFD) | OpenFOAM software (CFD) | Jeanjean et al.(2015) |
| Marylebone (72 ha) | OpenFOAM software (CFD) | OpenFOAM software (CFD) | Jeanjean et al.(2017) |
| Antwerp (32 and 64 ha) | OpenFOAM software (CFD) | OpenFOAM software (CFD) | Vranckx et al.(2015) |
| Lisbon (45.50 ha) | URVE code (CFD) | URVE code (CFD) | Amorim et al.(2013) |
| Aveiro (64 ha) | URVE code (CFD) | URVE code (CFD) | Amorim et al.(2013) |
| Leicester (400 ha) | OpenFOAM software (CFD) | OpenFOAM software (CFD) | Jeanjean et al (2016) |
| Shanghai (0.18 ha) | FLUENT (CFD) | FLUENT (CFD) | Li et al.(2016) |
| Bari (0.645 ha) | FLUENT (CFD) | FLUENT (CFD) | Buccolieri et al.(2011) |
| Santiago (96720 ha) | Field measurement | UFORE (i-tree) | Escobedo and Nowak (2009) |
| Shanghai (47100 ha) | Field measurement | Statistical analysis | Yin et al.(2011) |
| Florence (10200 ha) | Field measurement | iTree software | Bardelli et al (2011) |
| Syracuse (6500 ha) | Field measurement | iTree software | Nowak et al.(2013) |
| Auburn (306 ha) | Field measurement | iTree software | Martin et al.(2013) |
| West Midland (960000 ha) and Glasgow (300000) |
FRAME model | Statistical analysis | McDonald et al. (2007) |
| Berlin (200 ha) | Field measurement | Land use regression model | Ghassoun et al.(2017) |
| Strasbourg (7830 ha) | Field measurement | iTree software | Selmi et al.(2016) |
| Chicago (58830 ha) | Monitoring stations | Nowak method (iTree) | Yang et al.(2008) |
| Chapel Hill, NC (16ha) | Field measurement | CTAG (CFD) | Steffens et al.(2012) |
| Chapel Hill, NC and generic near-road environments (16 ha) | Field measurement | CTAG (CFD) | Tong et al.(2016) |
| Woodside, CA | Field measurement | CTAG (CFD) | Deshmukh et al. (2018) |
However, the uncertainty in GI modelling can lead to overestimation of total dry deposition that can result in under-predication of exposure assessment. For instance, use of constant surface resistance in dispersion model would overestimate dry deposition by approximately ten-times higher (Cape et al., 2008) and low-resolution concentration data in deposition model can lead to overestimation by a factor of two (Schrader et al., 2018). Therefore, it is essential to consolidate and synthesise previous investigations on the considerations of GI in micro and macro scale air pollutant dispersion model for: (i) researchers to identify gaps in understanding coupled modelling of air pollutant deposition and dispersion into atmospheric model, and (ii) decision-makers to assess the potential of GI to evaluate air quality benefits and incorporate accordingly in future urban planning. We summarise the potential consideration of GI at the microscale and macroscale air pollution modelling. These summery can assist in the formulation of coupled models to obtain a more realistic estimate of atmospheric chemical budgets.
Furthermore, the previous articles on GI-air pollutants interaction have discussed the methods to estimate dry deposition of air pollutants with numerical models (Wesely, 2000), application of atmospheric models for particles dispersion (Holmes and Morawska, 2006), assessment of deposition velocities of air pollutant to different species (Hirabayashi et al., 2011), methods and controlling factors for particulate matter dry deposition (Mohan, 2016), assessment of deposition and thermal effect of urban trees (Buccolieri et al., 2018), bi-directional air pollutant exchange between green infrastructure and atmosphere (Massad et al., 2010), detrimental effects of particulate matters on green infrastructure (Litschke and Kuttler, 2008) and estimation of deposition velocities based on lane use (Schrader and Brümmer, 2014). However, there is still a need to understand the consideration of GI to estimate the dry deposition in atmospheric dispersion models for both microscale and macroscale. Janhäll (2015) provided a thorough literature review on urban green infrastructure effects on particulate matter concentration at different spatial scales. Our review extends its scope by focusing on the importance of different resistance in the estimation of deposition velocity for both gaseous pollutants and particulate matter and their consideration in coupled dispersion-deposition modelling. In particular, we (i) carry out a detailed review of parameterisation for GI modelling to estimate deposition velocity; (ii) provide a comprehensive summary of design inputs (e.g., meteorological, GI and topographical parameters) to evaluate the different resistance and deposition velocity for their estimation by deposition models; (iii) evaluate the effectiveness of microscale and macroscale air pollution dispersion models to estimate the pollutant concentration reduction through GI; (iv) evaluate the parametric uncertainties in coupled GI and dispersion modelling; and (v) discuss a numerical framework for linking GI, air pollution and public health outcomes.
2. Scope and outline
The scope of this review is limited to GI that includes roadside vegetation (street canyons/open roadside trees, hedges and bushes), grasslands including parks and gardens and urban forest within the micro-and macro-scale simulations. In case of green walls and inclined roofs, the direction of deposition velocity is not usually perpendicular to implanted surfaces. The discussion on green walls, inclined roofs or any other artificial system as well as considerations of wind direction impacts is not considered in detail in this work. The review starts with critically synthesising GI modelling and relevant technical input parameters that are required for deposition modelling (Section 3). A state-of-the-art review of consideration of GI in air pollution dispersion models at microscale and microscale simulations to predict spatiotemporal concentrations are discussed in Sections 4 and 5, respectively. Section 6 describes the challenges in the simulation of real scenarios such as GI deposition velocity, GI spatial distribution, the influence of local meteorological parameters and pollutant transformation. Section 7 focuses on mathematical approaches that link GI, air pollution and public health outcomes, followed by a summary of topic areas covered, their conclusions and future outlook (Section 8).
3. Description of the GI modelling systems in the deposition scheme
Deposition scheme, which is a part of air transport models, uses mathematical equations for describing atmospheric, absorption and settling processes within mixing layer, to estimate the accumulated quantity of air pollutants over any solid surface area. The following specific conditions make GI considerations distinct in typical numerical simulations: (i) aerodynamic effect in the form of air pollutants concentration redistribution (Hefny et al., 2015); (ii) deposition of air pollutants (Nowak et al., 2018); and (iii) surface roughness to enhance atmospheric turbulence (Barnes et al., 2014). At the microscale, roadside GI such as hedges may act as a filtering barrier between air pollution sources and receptors and can reduce personal exposure. On another hand at the macroscale, GI such as urban forests, parks, gardens and hedges increase atmospheric dilution as well as act as a sink (deposition) for atmospheric pollutants. The harmful gaseous pollutants and airborne particles are deposited while passing over the surface of GI. The deposited amount (F; g m−2) to GI is proportional to the deposition velocity (Vd; m s−1), time of exposure (t; sec) and pollutant concentration (C; g m−3) (Bottalico et al., 2016; Jeanjean et al., 2016; Tiwary et al., 2009).
| (1) |
Vd for different gaseous pollutant (Eq. 2) can be calculated as the inverse sum of aerodynamic resistance (Ra; s m−1), quasi-laminar boundary layer resistance (Rb; s m−1) and canopy resistance (Rc; s m−1) (Janhäll, 2015; Tallis et al., 2011; Tiwary et al., 2009). For particulate matter, Giardina et al.(2018) have proposed a new deposition model based on electrical analogy scheme to estimate Vd by using both total resistance Rz (= Ra + Rbp) and settling velocity (Vs) (Eq. 3). The schematic diagram for gaseous pollutant collection, through dry deposition, as indicated in Fig 1.
Figure 1.
Schematic diagram showing the resistance relationship with Ohm’s law in electrical circuits where Ra is aerodynamic Resistance; Rb is quasi-laminar boundary layer Resistance; Rc is canopy/surface resistance; Rc1 is atmospheric buoyancy, lower canopy and in-canopy resistance; Rc2 is stomatal, mesophyll and cuticular resistance; and Rc3 is canopy soil, ground, water, snow or any other surface resistance; adopted from (Fowler, 1981).
| (2) |
| (3) |
The Ra depends on the atmospheric turbulence over the surface and is independent of the species (Eq. 4); it dominantes typically from 10 to 100 m above the ground level (Cherin et al., 2015; Zhang et al., 2017).
| (4) |
Where k is the von Karman constant (0.4); Zh is the reference height; z0 is the surface roughness height above the displacement plane; u* is the friction velocity depend upon the atmospheric turbulence and 𝛹𝛹ℎ is a stability function of momentum depend upon Pasquill stability class 203 and calculated based on Monin-Obukhov length (L; m) using Eq. (5):
| (5) |
cpis the specific heat at constant pressure; 𝑇𝑇 the average temperature; and H the sensible heat (Koloskov et al., 2007).
The Rb and Rbp affects the deposition of air adjacent to the surface and depends on molecular properties of the pollutant and roughness of the surface (Eqs. 6 and 7 for gaseous pollutant and 209 particulate matter, respectively) and it dominantes typically from 0 to 10 cm above the 210 deposition surface (Giardina and Buffa, 2018; Zhang et al., 2017).
| (6) |
Sc is the Schmidt number (υ/D), υ is the kinematic viscosity of air, D is the molecular diffusivity of the pollutant, determined from Stokes-Einstein equation with K the
Boltzmann constant; T the absolute temperature; μ the air dynamic viscosity; and Cc the Cunningham factor and Pr is the Prandtl number depend on Cp is the heat capacity per
unit volume of the air, υ is kinematic viscosity, and k is thermal conductivity.
| (7) |
Rbd depends on the Schmidt number, Rbi on surface conditions and Stokes number, and Rbt on 219 dimensionless particle relaxation time.
The Rc is the most uncertain resistance and varies with the nature of surface and type of green infrastructure (Baldocchi et al., 1987; Escobedo and Nowak, 2009; Fowler, 1981; Hirabayashi et al., 2012; Janhäll, 2015; Jayasooriya et al., 2017; Lagzi et al., 2013; Morani et al., 2014; Nowak et al., 2006; Tiwary et al., 2009; Vranckx et al., 2015; Wesely, 1989; Zhang et al., 2003). Most of the deposition models used Eq. (8) to evaluate canopy resistance (Seinfeld and Pandis, 2006; Walmsley and Wesely, 1996; Wesely, 1989; Zhang et al., 2017)
| (8) |
When gaseous pollutants enter the substomatal cavity in the leaves’ canopy, the diffusion of 228 gaseous material is resisted through stomata of the leaves know as stomatal resistance (Rs) and 229 through aqueous media of the spongy mesophyll cells known as mesophyll resistance (Rm). 230 Zhang et al. (2017) reported the empirical Eq. (9) based on Wesely (1989) to assess the stomatal 231 resistance for green infrastructure.
| (9) |
Ri is the minimum canopy stomatal resistance depend on land cover, G is the solar radiation, Ts is the surface temperature (°C), DH2O/Dx is the ratio of diffusivity between the water vapour and the gaseous pollutant concerned. The Rs is primarily a function of the size of the stomata and time of opening or closing of stomata based on plants’ photosynthesis requirement (Zhang et al., 2017). The Rm depends on the chemical properties of pollutant such as solubility and reactivity and type of vegetation species. While interacting within mesophyll cells, pollutants 239 transform from air to liquid and then diffuse into aqueous media of the spongy mesophyll cells. Xiao and Zhu (2017) recognised that the pollutant, after entering the substomatal cavity, feels resistance offered through physical barriers and biochemical components inside the cell wall, chloroplast envelope, cytosol and stroma between substomatal cavity and chloroplast of leaf and can be modelled as Eq. (10).
| (10) |
R is the gas constant (bar m3 K−1 mol−1), T is the absolute temperature (K), Hc is the Henry law constant (bar m3 mol−1) is a dimensionless number used to convert Rair to its liquid-phase equivalent resistance and Rliq is the summation of all series of liquid resistances (resistance of the cell wall and membrane, resistance of the cytosol between chloroplast and the cell wall, 249 resistance of the chloroplast envelope and resistance of the stroma.
The area over leaf other than the stomatal opening is the cutin polyester membrane impregnated and the waxy surface of the leaf that offers deposition surface for air pollutant is known as cuticle (Ruggiero et al., 2017) and the resistance to deposition is known as a cuticle or cuticular resistance (Rlu). Because of the permeation of air pollutants are negligible through cuticles 254 (Grünhage and Haenel, 1997), the resistance is an order less than stomatal resistances (Wesely and Hicks, 1977). The value of cuticle resistance is subjected to a degree of wetness of the surface and pH value (Massad et al., 2010) that divided into dry cuticle resistance and wet cuticle resistance (Walmsley and Wesely, 1996). The single model to evaluate the cuticle resistance for a wide range of green infrastructure, organs or pollution condition is not possible because deposition and gas exchange phenomena are the functions of wettability, the degree of polarity and apolarity of plant surfaces, retention and quality of surface-deposited liquids (Fernández et al., 2017). Zhang et al (2002a) have estimated the cuticle resistance for the dry and wet conditions by Eq. (11) and Eq. (12), respectively.
| (11) |
| (12) |
Where Rlu dry0 and Rlu wet0 are reference values of dry and wet cuticle resistance varies with the 266 type of green infrastructure. Due to the porosity of GI, air pollutants may enter into the lower canopy of dense vegetation where atmospheric buoyancy resistance (Rdc) is dominated by buoyant convection force that depends on the amount of sunlight heats the surface or lower canopy, and the angle of terrain 270 (Eq. 13).
| (13) |
θ is the is the slope of the local terrain in radians. The Rdc in the lower canopy is independent 273 of wind speed but in some cases when winds are able to penetrate into the lower canopy, 274 especially on the sides of hills, could change the mixing force (Wesely, 1989).
The resistance to the uptake of air pollutant by leaves, twig, bark and other exposed surface within the lower canopy is known as lower canopy resistance (Rcl). It depends on canopy structure such as bark area index, porosity and areal density. Zhang et al. (2017) reported Eq. (14) to estimate the Rcl as:
| (14) |
f0 is the reactivity factor for gases, Rcl, SO2 and Rcl,O3 is baseline Rcl for SO2 and O3, as given in 281 Wesely (1988).
Many deposition models assume that deposition over the ground surface under green infrastructure was negligible but some report that the amount of deposition at surface varies from 20–30% depending on the type of air pollutants (Meyers and Baldocchi, 1988). The resistance offered by the green infrastructure to the air pollutant while passing through the canopy to the ground surface known as in-canopy resistance (Rac). It is a function of canopy 287 height and LAI of GI and can be modelled using Eq. (15) (Erisman et al., 1994).
| (15) |
Canopy height hc is the height above the ground to the top of green infrastructure and bc is an empirical constant taken as 14 m−1. The canopy soil resistance (Rgs) is a resistance to the uptake of air pollutant by soil surface.
The deposition of air pollutant depends on pH value of soil, relative humidity, surface temperature, soil moisture content, ambient concentration of air pollutant, pollutant type and solar radiation (Erisman et al., 1994). The soil resistance, Rsoil is the similar canopy soil 295 resistance and its parameterisation is given in Eq. (16) (Jacobson, 2005).
| (16) |
Rgs, SO2 and Rgs,O3 is baseline soil resistance for SO2 and O3 are given in Wesely (1988). The Surface resistance (Rs) accounts the amount of air pollutant deposition to any surface including soil, snow, concrete or any other surface. Canopy resistance is also a subpart of the Rs. Erisman (1994) reported temperature-dependent (Eqs. 17–18) snow-covered Rs for SO2 and NH3 as:
| (17) |
For particles, addition parameter Vs, requires to estimate Vd, for particles diameter up to 50 μm according to the Stokes law (Eq. 19)
| (19) |
ρp is the density of the particles, ρa is the density of the ambient air, dp is particle diameter and g is the gravitational acceleration.
Alternative methods to evaluate the resistances used for dry deposition estimation for gaseous pollutants are also reported in the literature (Alfieri et al., 2008; Bennett et al., 1973; Ganzeveld and Lelieveld, 1995; Gong et al., 2017; Irmak and Mutiibwa, 2010; Jiang et al., 2017; Kerstiens, 2006; Kumar et al., 2014; Lhomme and Montes, 2014; Magnani et al., 1998; O’Dell et al., 1977; Rodný et al., 2016; Wesely, 1989; Wong et al., 2018; Zhang and Shao, 2014; Zhou et al., 2017) and Khan et al. (2017) have discussed other models for dry particle deposition models. A summary of the typical value of different resistance are listed in the Supplementary Information, SI, Table S1, and parameters required for dry deposition estimation are summarised in Table 2.
Table 2.
Summary of parameters required to calculate the dry deposition over GI surfaces.
| Resistance | Meteorological parameters | Topographical parameters | GI parameters | Pollutant parameters |
|---|---|---|---|---|
| Ra | Temperature; density of air; Specific heat; sensible heat; Friction velocity; Wind speed and direction | Terrain data; Building geometry | - | Source location and elevation; Source outlet velocity; Source geometry |
| Rb | Kinematic viscosity; Thermal conductivity; Air dynamic viscosity; Temperature; Cunningham factor, particle relaxation time, thermal conductivity; Heat capacity per unit volume |
Land cover/use data; Surface roughness | - | Molecular diffusivity; particle diameter |
| Rs | Air temperature, solar radiation; Solar elevation angle; Diffusion and directbeam solar radiation; Conductance-reducing effects of air temperature | The angle between the leaf and the sun | Photosynthetically Active Radiation (PAR); Leaf water potential; vapour pressure deficit, LAI; Water vapour pressure deficit; | Molecular diffusion |
| Rm | - | - | Net photosynthesis rate per leaf area; Type of species, | Henry law constant; Absolute temperature, gas constant |
| Rlu | Atmospheric acids; Ambient air temperature; Relative humidity; Seasonal conditions, | - | The thickness and chemical composition of leafsurface water-layer; LAI; Pollutant concentration over leaf; Cuticle surface area; Formation, growth and fate of water films; Type of species; Age of leaf | Pollutant concentration; Rate of pollutant interaction, pollutant composition, |
| Rdc | Solar radiation; Solar elevation angle | Slope of the local terrain | - | - |
| Rcl | - | - | Bark area index; Porosity; Areal density; Stem area | Henry law constant; Absolute temperature; Gas constant, reactivity factor for gases; Baseline lower canopy resistance for SO2 and O3 |
| Rac | Friction velocity; Wind speed and direction | - | Canopy height; Leaf area Index | - |
| Rgs and Rsoil | Relative humidity; Ambient concentration of air pollutant and solar radiation | pH value of soil; Soil moisture content | - | - |
| Rb (for particles) | Schmidt number; Air kinematic viscosity; Friction velocity; Air dynamic viscosity; Stokes number; Density of air; Ambient Temperature; Relative humidity |
Surface rough; Land use cover | LAI; Height of canopy | Particle’s Brownian diffusivity; Cunningham factor; Particle’s settling velocity; particle relaxation time; Particle diameter; Particle density; |
| Vs | Density of air; Gravitational acceleration; Air kinematic viscosity | - | - | Particle diameter; Particle density; Cunningham factor |
The most widely used deposition model is i-Tree Eco (www.itreetools.org) that map the measured air pollutants concentration by monitoring stations over each GI canopies then estimates the air pollutants sequestration rates based on air pollutants concentration, LAI of GI, meteorological data. For example, Selmi et al. (2016) estimated 88 t of air pollutants removal by urban trees during one year (July 2012 to June 2013) in Strasbourg city, France. However, dispersion aspects of GI mainly air pollutants redistribution and enhanced atmospheric dilution are not considered in i-Tree Eco.
4. Considerations of GI in microscale models
Microscale models are used to predict the air quality near the source where air pollutant dispersion is dominated by source characteristics such as source induced turbulence, pollutant chemistry, local meteorology, source geometry and surrounding building, terrains and GI, flow alternation and many more. In street canyons, aerodynamic effects have a greater impact on local air pollution levels than the deposition (Vos et al., 2013). However, in open road conditions, both aerodynamic and deposition effects are important (Tong et al., 2016). Here, we have reviewed several models that have been developed to estimate exposure
concentrations by capturing the temporal and spatial variation of air pollutant at the microscale and how these models consider GI in the simulations. Though these models are not developed to study the impact of GI on exposure reduction, these could still be partly used to assess the GI impact of air quality. Table 3 presents a summary of the differences in GI considerations for various microscale models that are described in subsequent text.
Table 3.
Summary of the consideration of differences processes in various microscale models.
| Microscale models | Consideration of different process | ||||
|---|---|---|---|---|---|
| Absorption | Filtration | Aerodynamic effect | GI geometry | Pollutant tolerance limit | |
| Box and wind tunnel models | No | Yes | Yes | Yes | No |
| Gaussian plume models | Yes | No | No | No | No |
| Receptor models | Yes | Yes | No | No | No |
| CFD models | Yes | Yes | Yes | Yes | No |
| Hybrid models | Yes | No | Yes | Yes | No |
Box and wind tunnel models are based on the principle of conservation. The study domain is assumed as isolated, from the surrounding, into which physical and chemical process of air pollutant dispersion, dilution and deposition are simulated. The consideration of roadside GI on microscale models (especial urban street canyon) was intensively studied through laboratory experiments in a wind tunnel by Gromke and co-workers (Gromke, 2011; Gromke et al., 2012; Gromke and Blocken, 2015; Gromke and Ruck, 2007). In these models, air pollutants are normally forced to pass through the vegetation that can increase the deposition velocity by allowing more time and amount of pollutant to interact with GI (Janhäll, 2015). However, under ambient conditions, air pollutants only interact with the surface area of GI while passing above or around (Abhijith et al., 2017). Moreover, synthetic materials are used to represent the GI which produces the uncertainties in the simulation of Rc.
Gaussian plume models were most commonly used as dispersion model to estimate the concentration of air pollutant by solving the set of mathematical equations in three dimensions considering usually the point source. To incorporate stability conditions and plume rise, the model can use any one of the five stability classification schemes (Lapse Rate scheme, PasquillGifford scheme, Turner scheme, Sigma-Theta scheme and Richardson number) and any one (Briggs and Holland method) of the two plume rise formulations (Awasthi et al., 2006). Models also have two different vertical and horizontal dispersion coefficients to simulate the vertical and horizontal dilution depend upon stability class and distance from the source. In Gaussian models, air pollutant concentration is independent of GI characteristic. With computational advancement, Gaussian plume model limitations have been minimized in modified/advanced models that estimate pollutant concentrations with a combination of different sources’ contribution, which are spatially distributed sources (such as multiple points, line and area sources). These models use meteorological data and surface roughness height to compute surface friction velocity, Monin-Obukhov length, the wind speed and direction at a reference height etc. to define atmospheric boundary layer properties and used modified vertical and horizontal dispersion coefficient based on wind tunnel, field experiment or empirically. RLINE takes meteorological input from AERMET (Cimorelli et al., 2005), vertical and horizontal dispersion with empirical constants obtain based on field tracer studies and wind tunnel simulation (Venkatram et al., 2013) and have been tested against independent field studies (Snyder et al., 2013). RLINE does not incorporate the effect of GI (roadside vegetation) but it can predict pollutant concentration near to measured field data due to modified dispersion coefficient. HIWAY-2 uses the steady-state Gaussian model to estimate the concentration of nonreactive pollutants from highway traffic at receptor located in relatively uncomplicated terrain and unable to consider complex terrain with GI (Peterson, 1980). This model uses only three stability classes (unstable, neutral and stable) and more realistic concentration estimation adjacent to the highway with respect to original version because of updated dispersion coefficients (Peterson, 1980; Sharma and Khare, 2001). Other Gaussian models are also used modified dispersion coefficient to include the effect of non-porous barriers. ADMS-Road is a Gaussian plume air dispersion model that uses the boundary layer depth and Monin-Obukhov length to define the atmospheric boundary layer properties rather than the simplistic Pasquill-Gifford stability classes. This model calculates dry deposition removal by estimating Ra, Rb component and uses a constant value of Rc for the whole modelled domain that could lead to uncertainty in predicting air quality (Apsley, 2017). Usually, the advanced Gaussian models are not able to simulate the aerodynamic effects of GI that dominate the spatial distribution of air pollutant at the microscale.
Receptor models are based on a set of mathematical relationships to estimate the source contribution at the measured receptor point. Watson et al.(2002) have described the procedures for using a receptor model to estimate the contribution of sources at a receptor locations. Receptor models are simple, explanatory and highly precise to estimate air pollutant concentration at receptor point (Watson, 1984). Many studies (Belis et al., 2013; Gardner and Dorling, 1999; Han et al., 2004; Liu et al., 1996; Song et al., 2001; Wåhlin et al., 2006; Wahlina et al., 2001) have been reported the usage of receptor model applications apply to air quality measurement. The receptor models can be used to quantify the potential of GI as a whole (Chen et al., 2016, 2015; Heal et al., 2012; Li et al., 2016; Maleki et al., 2016; Yin et al., 2011) but while predicting air quality, they are unable to handle the non-linear behaviours of dry deposition, spatial distribution of GI and other parameters such as complex local meteorological parameters, air moisture and wind velocity.
Computational Fluid Dynamics (CFD) models are an effective and powerful tool to simulate wind flow and mass transfer numerically. Most of the CFD models solve the governing nonlinear Navier Stokes equations, which are conservation of mass, momentum and energy along with transport and/or any other user specific equation, with the help of any conventional methods such as Finite Volume Method, Finite Element Method, Finite Difference Method and Spectral Methods. Many CFD models (Amorim et al., 2013; Baik et al., 2009; Costabile et al., 2006; Jeanjean et al., 2017, 2015; Kwak et al., 2018; Marciotto et al., 2010; Sanchez et al., 2016) have also been developed by researchers to simulate the complex wind flows and pollutant transfer problems at different scales. Although CFD model has the capacity to deal with complex shaped geometries, wind-induced turbulence and air pollutant transformation to predict the air quality (Amorim et al., 2013; Costabile et al., 2006; Jeanjean et al., 2015; Kwak et al., 2018; Lateb et al., 2016; Sanchez et al., 2016) but still requires more validation to simulate the effect of modelled geometries on the wind velocity and air quality prediction in urban setting (Huang et al., 2009; Sini et al., 1996). GI is considered as porous media and its pollutant removal efficiency is modelled as function LAI or Leaf Area Density (LAD) by assuming constant deposition velocity (Jeanjean et al., 2017; Pugh et al., 2012). Well-configured CFD models are capable of resolving the wind flow field to estimate the air pollutant removal via atmospheric turbulence and Brownian motion near the surface. However, the effect of different species, leaf size, soil moisture content and other parameters to define canopy resistance are neglected in most of such studies. Therefore, CFD models could usually estimate less deposition than actual and predict higher pollutant concentration. Steffens et al. (2012) reported the first modeling study on the effect of vegetation barriers on plume dispersion near roadways through coupling turbulence and aerosol dynamics to capture both the aerodynamic and deposition effects. The modeling results show that the vegetation barriers can reduce UFP concentrations, but the level of reduction depends on meteorological conditions. For example, increased wind speed leads to more reduction in particles smaller than ~50 nm, but slight increase in particles larger than ~50 nm as a result of interactions among aerodynamic resistance, impaction and residence time. The predicted effect of wind speed by Steffens et al. (2012) agreed well with the observed patterns from a later field study (Lee et al., 2018), even in terms of the critical size (predicted 50 nm vs observed 60 nm).
Hybrid models are combination of two or more models which are either used in series to generate desirable output (Karamchandani et al., 2009; Korek et al., 2016; Sharma et al., 2013; Sun et al., 2017) or complementary to target specific problem such as development of modified flow field due to complex terrain, estimation of dry deposition because of GI, generate spatial meteorological data etc. within domain (Fallahshorshani et al., 2012). Eulerian grid models, Lagrangian puff dispersion or trajectory models along with Gaussian plume models are the classical examples of hybrid models. Worldwide, researchers are developing new hybrid models to simulate the complex air pollutant dispersion processes under different environmental conditions. Currently, the major problem in hybrid models is the linkage between models, which results in researchers having to develop unique methodologies for linking the different models and dealing with specific case requirements linked for example to data availability. For instance, LAI can be estimated by different models such as model that relates LAI to digital cameras values (Casadesús and Villegas, 2014), mathematical equations for LAI, absorbed photosynthetically active radiation and net primary production from remote sensing (Gower et al., 1999), by mathematical regression model (Blanco and Folegatti, 2003), models that used satellite data to estimate LAI (Aboelghar et al., 2010; Chen et al., 2005; Xavier and Vettorazzi, 2004) and many direct or indirect methods (Bréda, 2003; Gower et al., 1999). Hybrid models are capable to consider the GI in air quality prediction but because of the data required for consideration of GI (Table 2), uncertainty in data generation, spatial and temporal variation of data, there is no accepted hybrid approach to consider the GI in prediction of the air pollutant concentration.
The impacts of GI in urban areas on pollutant dispersion are not considered in many microscale models. A comprehensive understanding of individual aspects such as dry deposition (Nowak et al., 2006); filtration (Chen et al., 2017) and air pollutant concentration redistribution (Gromke and Ruck, 2008; Miao et al., 2016) are needed to consider in urban air quality simulation. For dry deposition, an additional sink term may be used in computational models to simulate the gaseous pollutants absorption into leave matrix through stomata. The mathematical model is used to estimate deposition shown in Eq. (1) is applicable when total LAD and concentration point belong to two different cells mostly in the macroscale model. Therefore, the Eqs. (2) and (3) describe a mathematical model to estimate Vd consider Ra that is resistance between the height of concentration modelled and the GI canopy, are applicable for forest canopy only. On the other hand, the microscale models have much finer resolution and the concentration is resolved around GI that has the impact of Ra so Vd should not be same as macroscale. For instance in CFD simulation, sink term is proportional to a concentration within a cell, Vd and LAD shown in Eq. 20 (Buccolieri et al., 2018; Jeanjean et al., 2016; Vos et al., 2013) where Vd is generally assumed same as macroscale.
| (20) |
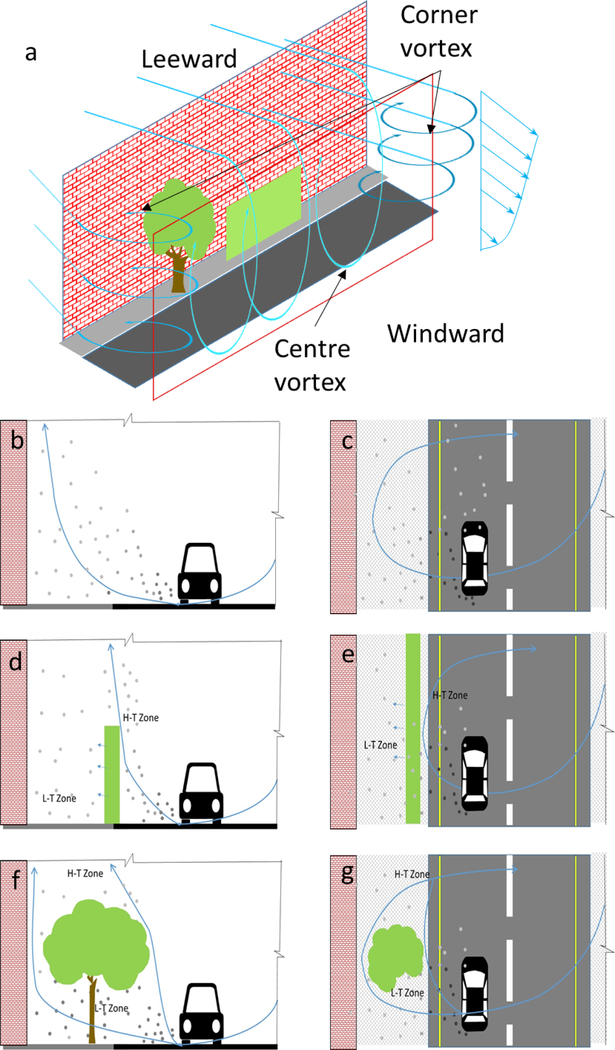
Apart from trees and hedges, surface like grass, soil and water also offer deposition but this deposition is not considered in microscale modelling. The filtration capacity of GI is the amount of gas and particle retained into its volume without absorption. It is most important for particles deposition inside the GI canopy. Furthermore, modelling particles deposition is more complex than gases because of re-suspension under high wind speed. The amount of re-suspension depends on wind speed and amount of epicuticular wax available on leave in different seasons (Zhang et al., 2017). Hefny et al.(2015) have discussed the GI-induced aerodynamic effects with different approaches; (i) implicit approach (represented by surface roughness); and (ii) explicit approach (represented by porous media) for inclusion of GI in numerical modelling, and concluded that explicit approach is more physically realistic over implicit approach for simulation of wind flow field and dispersion modelling. The built-up street canyon configuration and vortexes are shown in Fig 2. These vortexes in street canyon help to reduce the concentration through dilution. The flow around GI are dependent on the location of the latter in a built-up street, interaction with street canyon vortexes, surrounding environment and meteorological conditions. The porous behaviour makes the aerodynamic effect of GI different from solid barriers. Two zones – a low turbulence zone due to flow abatement and a high turbulence zone due to a sudden change in flow deflection – are generated due to vortexes interacting with the street GI (Vos et al., 2013). Generally, low turbulence zone shows the high concentration owing to relatively lesser mixing and the part of air pollutants that pass through GI loss momentum and get stagnant (Santiago et al., 2017). Tong et al. (2016) employed the CFD-based CTAG model to evaluate six different vegetation barrier configurations, and identified vegetation–solid barrier combination (i.e., solid barrier followed by vegetation barrier) as one of most effective design options, via promoting vertical mixing (through solid barriers) and enhancing deposition (through vegetation barriers). The CTAG modeling results also revealed that a highly porous roadside vegetation barrier containing large gaps within the barrier structure could increase downwind pollutant concentrations, consistent with the findings in a field study (Deshmukh et al., 2018). In conclusion, the choice of microscale model to study the impact of GI on local air quality simulation depend on available input parameters, simulation time, the importance of GI-pollutant interaction processes, meteorological condition and surrounding urban geometry.
Figure 2.
A schematic of the changes in the formation of vortex (shown by blue lines) in urban street canyon during the interaction of the flow with the leeward GI, showing vortex formation (a) in street canyon under perpendicular wind flow (Gromke, 2011) as well as cross-section and top view of (b, c) GI free street canyon, (c, d) street canyon with hedges, (e, f) street canyon with tree.
5. Consideration of green infrastructure on Macroscale models
Macroscale models are used to predict the air quality around the source where air pollutant dispersion is dominated by the meteorological and topographical conditions such as wind velocity and direction, ambient temperature, terrains slope, surface roughness and deposition. While considering GI in macroscale models, the important aspects are deposition velocity (Verbeke et al., 2015) and change in friction velocity and surface roughness (Barnes et al., 2014; Britter and Hanna, 2003). Here, we have reviewed methodologies for considering GI in macroscale air dispersion models. Table 4 summaries the differences in GI considerations in various macroscale models that are discussed in the subsequent text.
Table 4.
Summary of the consideration of different processes in various macroscale models.
| Processes | Macroscale models | |||||
|---|---|---|---|---|---|---|
| Gaussian plume models | Modified Gaussian models | Statistical models | Receptor models | CFD models |
Hybrid models | |
| Absorption | No | Yes | Yes | Yes | Yes | Yes |
| LAI | No | No | Yes | No | Yes | Yes |
| Land cover | No | Yes | Yes | No | Yes | Yes |
| Surface roughness | No | Yes | No | No | Yes | Yes |
| Terrain data | No | Yes | No | No | Yes | Yes |
| VOC emissions | No | No | No | No | No | No |
| Coupled dispersion- deposition | No | Yes | Yes | Yes | Yes | No |
| Background Concentration variation | No | No | No | No | No | Yes |
At macroscale, Gaussian plume models have been widely used for air quality prediction from a point source and have some limited applicability such as flat terrain, no local flow and circulation and single source. Apart from inbuilt assumptions of Gaussian plume model such as continuous steady source, chemically inert pollutant, bell-shaped distribution of pollutants in the horizontal and vertical direction and constant meteorological conditions. Gaussian models can only represent the dispersion under the described above conditions and are unable to handle complex environmental conditions, topography, other atmospheric chemistry and the air pollutant removal capacity of GI through dry deposition. Modified Gaussian models such as ADMS-Urban, AERMOD, CALPUFF and SCREEN3 are the most commonly used amongst the scientific community. ADMS-Urban is a Gaussian plume air dispersion model that computes local flow along with turbulence due to surface roughness based on Nguyen et al.(1997) and dry deposition velocity with constant surface resistance (Apsley, 2017). With constant surface resistance, ADMS-Urban is unable to incorporate the effect of different land cover on deposition. AERMOD is a steady-state Gaussian plume model, developed by American Meteorological Society, that takes meteorological inputs from AERMET (Cimorelli et al., 2005) and terrain data from AERMAP (Langner and Klemm, 2011). AERMOD has relative leaf area index that is used, rather than actual LAI that depends on nine land use categories and five seasonal categories, to compute deposition velocity based on Wesely (1988). Lin et al. (2018) have shown in their large-eddy simulation study that total particle deposition is sensitive to LAI. CALPUFF is a non-steady-state Lagrangian Gaussian puff model; it uses CALMAT generated wind field or wind velocity and other inputs such as surface roughness and terrain data to compute dispersion coefficient (Bai et al., 2018). CALPUFF estimates deposition velocity without considering the Rdc and Rcl due to GI porosity and other surfaces (e.g., grass, soil) in the lower canopy that could lead to uncertainty in dry deposition amount. These Gaussian models are unable to simulate the (i) effect of flow deflection and flow abatement near to receptor; (ii) pollutant tolerance limit of different GI species; (iii) characteristic (shape and dimensions) of GI types; and (iv) effect of GI inside the urban area.
Statistical models are mathematical models that predict the air quality with the help of unknown constants estimated based on measured data such as land use regression models (Rao et al., 2017), machine learning models (Kleine Deters et al., 2017), and Monte Carlo (Mallet and Sportisse, 2008). The statistical models need to be trained for past data sets to assess the impact of variables in the conditions under which they were initially trained. Land use regression models have been used widely to estimate air quality by finding mathematical relations between parameters such as land cover (LAI, types and spatial distribution of GI, land use pattern), meteorological data, emission data and ambient concentration (Cattani et al., 2017; de Hoogh et al., 2014; Habermann et al., 2015; Hoek et al., 2008; Yli-Pelkonen et al., 2017). Because these models do not consider the physical relationship between emissions and air quality under given sets of meteorological and topographical conditions (Shahraiyni and Sodoudi, 2016; Wolf et al., 2017; Zhang and Ding, 2017), effects of GI on air quality remains unanswered in statistical models.
CFD models at macroscale take high computational time and resources even for a smaller size of domain but are able to capture the effects of GI at a fine spatial resolution. The modelling methodology and limitations for considering GI in CFD models, box or wind tunnel models, receptor models and hybrid models are discussed (Section 4).
GI reduce air pollutants concentration through pollutants removal by dry deposition and enhancing atmospheric dilution by surface roughness at the urban scale. Most macroscale simulations use the average deposition value for every cell within a simulated domain because grid size is more than the dimension of GI that introduces uncertainty in air quality prediction. The seasonal variation leading to change in LAI, VOC emission, non-linear deposition behaviour and particles resuspension are important input, apart from meteorological data, terrain data and surface roughness, that needs to consider in dispersion modelling and could change air quality in macroscale. Generally, deposition models estimate air pollutants removal over GI and neglect increased atmospheric dilution by their surface roughness during an assessment of GI impact. For instance, Bodnaruk et al. (2017) have used i-Tree Eco to estimate air pollutants removal equal to 173 t. yr−1 in 95 km2 area by increasing tree cover from 24% to 44.4% between 2010 to 2040 in Baltimore, US.
6. Challenges in considering GI into dispersion modelling at microscale and macroscale
The atmospheric dispersion models predict air quality under the influence of different inputs such as meteorological data, topographical data, GI data and source emissions. Apart from the complexity of environmental processes and interface interactions (Holnicki and Nahorski, 2015; Irwin, 2014), the variance in measured and estimated concentrations with presence of GI is because of (i) pollutants measurement error, (ii) model input uncertainties (table 2), (iii) simplification of deposition processes (Section 3), and (iv) treating GI in numerical solution (Sections 4 and 5). Past studies have reported effects of input data uncertainties on pollutants concentration at different length scales. For instance, meteorology data uncertainty at mesoscale (Gilliam et al., 2015; Godowitch et al., 2015), emission data uncertainty at macroscale (Diez et al., 2014; Holnicki and Nahorski, 2015) and at mesoscale (Saikawa et al., 2017), topography and land use data uncertainly at macroscale (Zou et al., 2016), surface roughness uncertainly at macroscale (Barnes et al., 2014). The challenges in model inputs and processes especially during consideration of GI in air quality simulation are mainly related to (i) spatial-temporal variation of GI characteristics such as shape and size, porosity, pollutant tolerance limit and pollutant sink; (ii) pollutant transformation due to GI; and (iii) influence of meteorological and topographical data such as temperature, humidity, terrain slope, wind speed and direction on deposition process. The uncertainties in model input data that cause predictions of air pollutants could vary up to a factor of four for identical solutions (Lohmeyer et al., 2002). The most important challenge is consideration of the spatio-temporal distribution of GI and its characteristics because each GI type is different from others with respect to its location, LAI, porosity, species and geometries. Past studies (Aubrun et al., 2005; Buccolieri et al., 2011; Gromke et al., 2012; Gromke and Ruck, 2008; Miao et al., 2016) have discussed the effects of GI on local wind velocity and dispersion at different length scale. An additional challenge is the seasonal LAI variation that affects the change in porosity and geometry of GI (wind flow alternation) and change in pollutant absorption rate (deposition velocity). GI species are also having different tolerances to different air pollutants (Appleton et al., 2009; Yang et al., 2015) that may cause short-term damage (immediately visible sign on leaves) and long-term damage (premature leaf drop, reduced growth and species death). Furthermore, the meteorological and topographical conditions have an influence on deposition processes and are not typically included in model parameterizations. For example, high ozone is more likely to co-occur with high temperature (including during heat waves) and low humidity condition has been reported in many studies (Filleul et al., 2006; Hou and Wu, 2016; Zhang et al., 2017; Zhang and Wang, 2016). Similarly, high PM2.5 are also reported during high temperature and low wind speed (Tai et al., 2010; Zhang et al., 2017). For example, Kavassalis and Murphy (2017) have reported the coincidence of low ground-level O3 concentration and high relative humidity in US between 1987 and 2015. This is because O3 uptake is unintentionally high by plants’ stomata during the high relative humidity. Furthermore, Zhang et al. (2003) have highlighted the combined effect of strong solar radiation 596 (> 200 Wm−2) and wet condition (rainfall or morning dew) on Rs and introduce the term Wst 597 (the fraction of stomatal blocking water film) in Rc calculation, Eq. (20).
| (20) |
The pollutant transformation due to the presence of GI is another challenge in air dispersion modelling. VOCs such as isoprene, monoterpenes and sesquiterpenes are released by GI and can have a considerable effect on air pollutants concentration during heat waves (Churkina et al., 2017). These VOCs can undergo chemical transformation and produce ozone and PM in the presence of high nitrogen oxide concentration (Seinfeld and Pandis, 2006). This study observed that the GI-air pollutants interaction (deposition rate) is not constant which is assumed in many dispersion modelling but actually has a high spatial-temporal variation that depends on GI types and spatial distribution as well as meteorological and climatic factors such as relative humidity, ambient temperature and wind velocity.
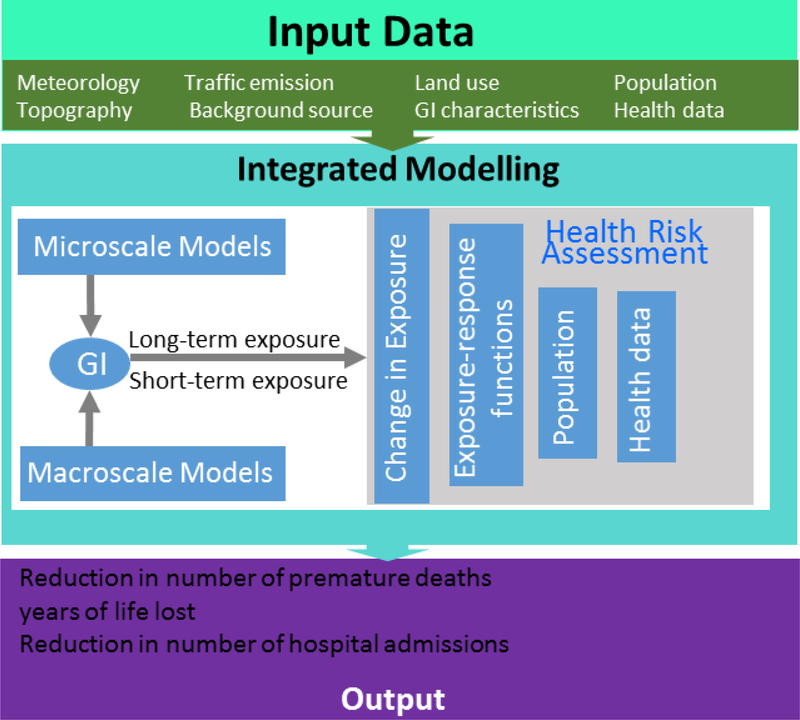
7. Framework for linking GI, air pollution and health outcomes
The knowledge of linkage between public health outcomes and GI-induced air pollution reduction is important to assess public health benefits (Fig. 3). We focus here on a basic framework that links the GI’s reduction of atmospheric pollutant concentration and the potential exposure of individuals to assess the resultant health risk related to air pollution (Table 5). An air pollution health risk assessment (APHRA) is a mathematical approach that estimates the expected health impact of short-or long-term exposure to air pollutants in different variables such as age group, environmental conditions and socioeconomic status (WHO, 2016). Here, we present an APHRA framework to link health outcomes with short-or long-term exposure alternation due to presence of GI. Several epidemiological studies have reported a wide range of health impacts such as respiratory symptoms, hospital admission and/or premature deaths, associated with excess exposure to air pollution. These health outcomes could be quantified through a number of premature deaths, years of life lost (YLLs), disability-adjusted life years (DALYs), or change in life expectancy (Health Organization Regional Office for Europe, 2015). For instance, Pope et al. (2009) have reported life expectancy increase by 0.64 years for per 10 μg m−3 decrease in PM2.5 for 51 US cities. The inputs data required to estimate the health outcomes, shown in Eq. (21), are population data (P), baseline rates of death or hospital admission (M), change in air pollutant concentration (ΔQ) and relative risk (RR) (Andreão et al., 2018; Künzli et al., 2000; Sacks et al., 2018).
| (21) |
Where ΔM is a change in health effects due to air pollution and RR is a change in health effect for an unit change in an air pollutant concentration. The main steps for APHRA is performed via (i) direct measurements of air pollution concentrations of individual’s exposure (Steinle et al., 2015); (ii) indirect measurements by estimating the pollutants concentration by modelling or fixed site monitors (Beelen et al., 2014; Brauer et al., 2016). For APHRA, the use of the indirect method is more common over the direct method that is mostly used in industrial or occupational health risk assessment. At a national scale study for 2425 urban and 3094 rural areas in year 2010, Hirabayashi and Nowak (2016) used fixed site monitoring data and applied pollutants concentration change due to deposition over the tree to identify the air pollutant removal and health benefits with increase in LAI or percentage of tree cover. The uncertainty in APHRA is brought by factors such as (i) ambient air, which is a complex pollutant mixture and making estimation of exposure assessment is challenging because monitoring stations are not mapping full domain, (ii) baseline disease burden is not properly recorded especially under developed countries, and (iii) assumptions made during the derivation of concentration-response function such as smoking condition, indoor air pollutant exposure and medical condition (WHO, 2016). The presence of GI could further increase uncertainty in APHRA by (i) adding allergen pollens that may trigger other diseases, (ii) bVOC emissions that may transform air pollutants and increase particular pollutant concentration locally, and (iii) altering the exposure by air pollutant concentration redistribution. Furthermore, USDA Forest Service developed i-Tree with BenMap (US-EPA) have used to estimate the health outcomes of annual air pollutants removal by the deposition over GI canopy at the macroscale. However, APHRA due to change in short-term exposure by pollutants concentration redistribution at the microscale and enhanced atmospheric pollutants dilution by increased surface roughness at the macroscale, because of GI, have not been assessed along with deposition.
Figure 3.
Framework for linking between GI, air pollution and public health.
Table 5.
Summary of relevant studies that have quantified the linkage between GI, air pollutant reduction and health benefits.
| Author (year) | City; Model used | Summary |
|---|---|---|
| Tiwary et al.(2009) | London (UK); (ADMS-Urban + statistical model) | • PM10 removal has been estimated through different GI combinations with two species (sycamore maple (Acer pseudoplatanus L.), Douglas fir (Pseudotsuga menziesii Franco) and grassland using computational model. • PM10 reduction varied between 0.03 to 2.33 t ha yr−1 with different GI combination. • The health effects noted were a reduction in 2 premature deaths per year and 2 respiratory hospital admissions per year. |
| Powe and Willis (2004) | Britain(UK); (Monitoring stations+ statistical model) | • The absorption of SO2 and PM10 via forests (more than 2 ha in area) were estimated based on National Air Quality Information and Forest Commission spatial distribution data of woodland. • The forest can absorb large quality of air pollutants, for example, 385,695–596,916 metric tonnes of PM10 and 7715–11,215 metric tonnes of SO2 per year • The above air pollutants reduction would be equal to 5–7 deaths per year and 4–6 hospital admission per year. |
| David J. Nowak et al.(2013) | 10 U.S. cities; (Monitoring stations + i-Tree) | • PM2.5 removal was estimated for 10 U.S. cities with existing trees cover using i-Tree model and U.S. EPA monitors concentration. • Total amount of PM2.5 removal varies from 4.7 to 64.5 tonnes per year. • The equivalent mortality reduction from 0.1 to 7.6 death per year. |
| Nowak et al.(2018) | 86 Canada cities; (Monitoring stations + i-Tree) | • The change in air pollutants (NO2, O3, PM2.5, SO2, and CO) concentration have been estimated through the iTree model and health impacts were studied. • The total air pollutant removal was 7500 t to 21,100 t and average removal rate was 3.72 g/m2/year. • The overall health impacts of urban trees are included avoidance of 30 human mortality in all cities. |
| Hirabayashi and Nowak (2016) | U.S.; (Monitoring stations + i-Tree) | • Resultant changes in concentration for the four air pollutants (NO2, O3, PM2.5 and SO2) were modelled by the iTree model using deciduous and evergreen trees with varying LAI and 2010 census data. US EPA’s BenMAP has been used to link air quality improvement to human health improvement was estimated. • In urban areas, annual mean air pollutant concentration was 15.5 (μgm−3) for NO2, 61.7(μgm−3) for O3, 10.0 (μgm−3) for PM2.5 and 4.9 (μgm−3) for SO2. Changes in concentration increased as the LAI increased but the relation is non-linear. • A comprehensive national database of deciduous and evergreen trees with varying LAI and its effects on air quality and human health in the United States was developed |
| Nowak et al.(2014) | U.S.; (Monitoring stations + i-Tree) | • Avoidable health impacts and associated economic benefits of four air pollutants (NO2, O3, PM2.5 and SO2) removal by trees and forest in the US were estimated for 2010. • The estimated quantity of air pollutants removal was 17.4 million tonnes based on hourly pollution data and daily total tree cover and LAI though i-Tree model. • The existing trees can help in avoiding more than 850 incidences of human mortality and 670,000 incidences of acute respiratory symptoms. |
| Rao et al.(2014) | Portland; (Monitoring stations + LUR) | • LUR have been used to estimate a decrease in NO2 concentration by an urban tree in Portland. • The estimated removal of NO2 was 0.57 ppb for every 10 ha trees. • The annual health benefits are approximately 21,000 fewer incidences and 7000 fewer days of missed school due to asthma exacerbation for 4–12 year-olds; 54 fewer emergency visits across people of all ages; and 46 fewer cases of hospitalization due to respiratory problems triggered by NO2 in the elderly. • The potential of an urban forest to reduce the air pollutant (NO2) and hence provide health benefits are approximately 7 million USD due to reduced incidence of respiratory problems. |
| Bodnaruk et al.(2017) | Baltimore (US); (Monitoring station + i-Tree) | • The monetary benefits of increasing tree cover from 24% to 40% have been estimated under different spatial GI distribution. • An additional annual 173 ton air pollutants removal was predicted at maximum potential tree cover of 44.4%. • The monetary benefits of these air pollutant removal on human health were estimated equal to 6.3 million USD. |
| City of Woodland (2018) | Woodland (California); (Remote sensing + i-Tree) | • The total air pollutants removal and monetary benefits of existing 14.5% urban tree canopy have been assessed using high-resolution aerial imagery and remote sensing software for 2010. The U.S. EPA’s BenMAP Model was used to estimate monetary values resulting from changes in air pollutants concentration. • The analysis estimated that Woodland’s tree canopy annually removing 40 tons of air pollutants (includes CO, NO2, O3, SO2 and PM10) and save 15.3 million gallons of stormwater. • The monetary values of health benefits resulting from air pollutants removal have been estimated as equal to 1.8 million USD. |
| City of Sacramento (2018) | Sacramento (California); (Remote sensing + i-Tree) | • The U.S. EPA’s BenMAP Model was used to estimate monetary values resulting from air pollutants removal. These removals have been estimated using highresolution aerial imagery and remote sensing software for existing 19.1 % urban tree canopy in 2010. • The analysis estimated that Sacramento’s tree canopy annually removing 392.4 tons of air pollutants (includes CO, NO2, O3, SO2 and PM10) and save 58 million gallons of stormwater. • The monetary values of health benefits resulting from air pollutants removal have been estimated as equal to 18.8 million USD. |
Some studies highlighted that the overall urban GI is associated with a decrease in mortality and morbidity. For instance, De Keijzer et al (2017) linked air pollution concentration and urban vegetation to standardized mortality rates using Poisson regression and to life expectancy using linear regression. This study was based on mortality data from 2148 small areas with an average population of 20750 inhabitants between 2009 and 2013 in Spain. It found an increase in life year of 0.17 (95% CI: 0.07, 0.27) with an increase in average greenness in urban areas by interquartile range. The same study also found reduction in life years of 0.90 (95% CI: 0.83, 0.98), 0.20 (95% CI: 0.16, 0.24), 0.13 (95% CI; 0.09, 0.17) and 0.64 (95% CI; 0.59, 0.70) due to an increase of 5 μg m−3 for each of PM10, O3, NOx and 2 μg m–3 in PM2.5 respectively. In another study, Lovasi et al (2008) have examined the association between asthma prevalence in 4–5 years old children and the number of street trees in New York and found that an increased trees density was associated with 29% lower asthma prevalence (RR = 0.71 per 343 trees/km2, 95% CI; 0.64, 0.79). Furthermore, this association could be a due reduction in air pollutants concentration by urban GI. On another hand, several studies (King et al., 2014; Selmi et al., 2016; Yang et al., 2008) have found air pollutants removal between 58.9 and 99.6 kg ha−1 year−1 through GI but health benefits were not estimated presumably owing to lack of availability of health data.
8. Summary, conclusions and future outlook
This review paper discussed various aspects related to consideration of GI in microscale and macroscale atmospheric dispersion models. The mathematical description of different processes and the relevant inputs required to simulate GI effect for estimating air pollutants removal under deposition scheme are discussed. Microscale and macroscale air pollutants dispersion models are surveyed with respect to their physical and chemical representation of GI into the modelling system and limitations to assess the effect of GI on air pollutants concentration estimation. The non-linear behaviour of GI deposition response with meteorological parameters and other challenges such as spatial-temporal variation of GI characteristic and its effects on air pollutant transformation are briefly studied. Moreover, the importance of GI in health risk assessment through numerical framework linkage between GI, air pollution and health is examined.
The following key conclusions are drawn:
A detailed review of parameterisation for GI modelling to estimate deposition velocity allows concluding that for gaseous pollutants, Vd is dominated by Rc that is larger than Ra and Rb. The favourable conditions for gaseous pollutants to be absorbed in plant leaves depends on a series of parameters like LAI, size of stomata opening, photosynthesis rate per leaf area, PAR. On another hand, for particulate matter, Vd is highly depended on particle’s diameter as is governed by a U-shaped curve in which it is minimum for particles size between 0.4 and 0.9 μm in aerodynamic diameter.
The synthesis of data inputs (as listed in Table 2) to evaluate the different resistances and deposition velocity for their estimation shows the simplification of deposition scheme may lead to large uncertainty in air pollutant removal estimation.
The deposition schemes show the Vd should be taken differently for microscale and macroscale simulations because the pollutants concentration is resolved around GI that has the effect of Ra in microscale models. Generally, Vd value used in dispersion models is measured with assuming downward flux of pollutant over GI (forest area) in the field. However, traffic emissions with a roadside GI are a different configuration where sources are located under GI canopy.
Usually, the dispersion models (Sections 4 and 5) are not originally developed to assess the effect of GI on air pollutants concentration estimation. However, they can still be able to capture a number of processes listed in Tables 3 and 4 for GI considerations at the different length scales. There is a yet a need of coupled GI-dispersion models that can incorporate the air pollutants-VOCs chemistry, GI pollutants tolerance limits and non-linear pollutants deposition under different meteorological conditions.
The numerical framework that links GI, air pollution and health outcomes help to estimate the benefits of GI based on a reduction in short-and long-term air pollutants exposure reduction in the term of mortality, morbidity and monetary values. These benefits are not only dependent on the air pollutants deposited amount over the surface offered by GI.
Many numerical methods have been developed to simulate additional physical and chemical processes due to GI in atmospheric dispersion model at different spatial scales to estimate air pollutant removal (Section 3). These processes depend on many factors such as meteorological data, GI characteristic and air pollutant concentration. Moreover, the deposition scheme in details are complex, resource intensive and require a large number of input data (such as meteorological parameters, topographical parameters, GI parameters and pollutant parameters, as listed in Table 2), which is not handy for dispersion models. Different air pollutants dispersion methodologies used for air pollutant concentration simulation at various spatial scale have been discussed (Sections 4 and 5) along with the summary of their consideration of different GI related processes in table 3and 4. The individual spatial case has specific flow, mixing characteristic and sensitive to input parameters while simulating the GI effects on air pollutants concentration. It is, therefore, necessary to identify the individual spatial conditions to understand the dominating physical and chemical processes that need to incorporate in detail during simulation of real-world problems and simplification of various others processes to reduce the computational time and resources. For instance, the predominat processes in air pollution dispersion models for microscale is the aerodynamic effects that are strongly influenced by local meteorology, source characteristics and surrounding geometry and much stronger than the deposition. Therefore, the implicit approach for inclusion of GI at microscale would lead to the unrealistic prediction of air quality. Several other processes also influence deposition velocity and alter the air pollutants concentration have been reported in the literature (section 6) but most of them are not available in any air pollutants concentration simulation methodologies. Churkina et al. (2017) have stated that vegetation emits more VOCs with rising temperatures and contribute to the ozone which had reached ~60% during the heat wave in July 2006 and ~40% during hot summer days in 2014 in Berlin. It is found in health risk assessment studies that GI is the important linkage between air pollution and public health and has a significant impact not only in air pollutant reduction but also decrease the exposure of air pollution in the day to day life.
This review identified the mechanism of air pollutant removal through the deposition process and the relevant key processes (aerodynamic effects, flow alteration and atmospheric dilution) at different spatial scales while consideration of GI in dispersion modelling. The review of the topic areas also highlighted a number of research unanswered questions that require focus of future research studies: (i) what is the proportion of deposition and dilution in reduced pollutant concentrations for large-spaced GI such as urban parks, grassland and forest; (ii) what is the effect of filtering capacity, pollutant tolerance limit and temperature sensitivity of different GI types on dispersion models; (iii) how does the Vd change if vehicular emissions are forced towards the roadside GI due to local wind flow; and (iv) what modification should be required for combined GIs such as hedges with trees, grass with hedges or trees in dispersion model. Future studies should also develop the methodologies to consider the wind-dependent GI porosity in dispersion models. More studies are needed to develop approaches for consideration of green roof and green walls in dispersion models at different spatial scales.
Supplementary Material
Research highlights.
GI could reduce the exposure through deposition and pollutants redistribution at microscale.
Enhanced atmospheric turbulence and deposition are key processes at macroscale.
Deposition process is different at microscale and macroscale simulations.
Presence of GI can alter air pollutants concentration and bring positive health benefits.
Lack of input data makes consideration of GI in dispersion models challenging.
9. Acknowledgments
This work is led by the University of Surrey’s GCARE team as a part of the iSCAPE (Improving Smart Control of Air Pollution in Europe) project, which is funded by the European Community’s H2020 Programme (H2020-SC5–04-2015) under the Grant Agreement No. 689954. AT and PK thanks the University of Surrey and its Department of Civil & Environment Engineering for an ORS Award and a PhD studentship to support AT’s PhD research. KMZ acknowledges support from the National Science Foundation (NSF) through grant No.1605407.
10. References
- Abhijith KV, Kumar P, Gallagher J, McNabola A, Baldauf R, Pilla F, Broderick B, Di Sabatino S, Pulvirenti B, 2017. Air pollution abatement performances of green infrastructure in open road and built-up street canyon environments – A review. Atmos. Environ 162, 71–86. [Google Scholar]
- Aboelghar M, Arafat S, Saleh A, Naeem S, Shirbeny M, Belal A, 2010. Retrieving leaf area index from SPOT4 satellite data. Egypt. J. Remote Sens. Sp. Sci 13, 121–127. [Google Scholar]
- Abramesko V, Tartakovsky L, 2017. Ultrafine particle air pollution inside diesel-propelled passenger trains. Environ. Pollut 226, 288–296. [DOI] [PubMed] [Google Scholar]
- Akbari H, Pomerantz M, Taha H, 2001. Cool surfaces and shade trees to reduce energy use and improve air quality in urban areas. Sol. Energy 70, 295–310. [Google Scholar]
- Aksu A, 2015. Sources of metal pollution in the urban atmosphere (A case study: Tuzla, Istanbul). J. Environ. Heal. Sci. Eng 13, 79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alfieri JG, Niyogi D, Blanken PD, Chen F, LeMone M. a., Mitchell KE, Ek MB, Kumar A, 2008. Estimation of the Minimum Canopy Resistance for Croplands and Grasslands Using Data from the 2002 International H 2 O Project. Mon. Weather Rev. 136, 4452–4469. [Google Scholar]
- Amorim JH, Rodrigues V, Tavares R, Valente J, Borrego C, 2013. CFD modelling of the aerodynamic effect of trees on urban air pollution dispersion. Sci. Total Environ 461– 462, 541–551. [DOI] [PubMed] [Google Scholar]
- Andreão WL, Albuquerque TTA, Kumar P, 2018. Excess deaths associated with fine particulate matter in Brazilian cities. Atmos. Environ 194, 71–81. [Google Scholar]
- Appleton B, Koci J, Student G, Roads H, Harris AR, Sevebeck K, Alleman D, Swanson L, 2009. Trees for Problem Landscape Sites --Air Pollution [WWW Document]. URL http://pubs.ext.vt.edu/430/430-022/430-022.html (accessed 7.27.18).
- Apsley D, 2017. Modelling dry deposition. [Google Scholar]
- Aubrun S, Koppmann R, Leitl B, Möllmann-Coers M, Schaub A, 2005. Physical modelling of a complex forest area in a wind tunnel—comparison with field data. Agric. For. Meteorol 129, 121–135. [Google Scholar]
- Awasthi S, Khare M, Gargava P, 2006. General plume dispersion model (GPDM) for point source emission. Environ. Model. Assess 11, 267–276. [Google Scholar]
- Bai L, Wang J, Ma X, Lu H, 2018. Air Pollution Forecasts: An Overview. Int. J. Environ. Res. Public Health 15, 780. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baik J-J, Park S-B, Kim J-J, 2009. Urban Flow and Dispersion Simulation Using a CFD Model Coupled to a Mesoscale Model. J. Appl. Meteorol. Climatol 48, 1667–1681. [Google Scholar]
- Baldauf R, 2017. Roadside vegetation design characteristics that can improve local, near-road air quality. Transp. Res. Part D Transp. Environ 52, 354–361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baldocchi D, 1988. A multi-layer model for estimating sulfur dioxide deposition to a deciduous oak forest canopy. Atmos. Environ 22, 869–884. [Google Scholar]
- Baldocchi DD, Hicks BB, Camara P, 1987. A canopy stomatal resistance model for gaseous deposition to vegetated surfaces. atmosperic Environ. 21, 91–101. [Google Scholar]
- Bao W, Zhang Y, Zhang M, Bao A, Fei X, Zhang X, Zhou X, 2018. Effects of ozone repeated short exposures on the airway/lung inflammation, airway hyperresponsiveness and mucus production in a mouse model of ovalbumin-induced asthma. Biomed. Pharmacother 101, 293–303. [DOI] [PubMed] [Google Scholar]
- Bardelli T, Giovannini G, Pecchioli L, 2011. Air quality impact of an urban park over time. Procedia Environ. Sci 4, 10–16. [Google Scholar]
- Barnes MJ, Brade TK, MacKenzie AR, Whyatt JD, Carruthers DJ, Stocker J, Cai X, Hewitt CN, 2014. Spatially-varying surface roughness and ground-level air quality in an operational dispersion model. Environ. Pollut 185, 44–51. [DOI] [PubMed] [Google Scholar]
- Beelen R, Raaschou-Nielsen O, Stafoggia M, Andersen ZJ, Weinmayr G, Hoffmann B, Wolf K, Samoli E, Fischer P, Nieuwenhuijsen M, Vineis P, Xun WW, Katsouyanni K, Dimakopoulou K, Oudin A, Forsberg B, Modig L, Havulinna AS, Lanki T, Turunen A, Oftedal B, Nystad W, Nafstad P, De Faire U, Pedersen NL, Östenson C-G, Fratiglioni L, Penell J, Korek M, Pershagen G, Eriksen KT, Overvad K, Ellermann T, Eeftens M, Peeters PH, Meliefste K, Wang M, Bueno-de-Mesquita B, Sugiri D, Krämer U, Heinrich J, de Hoogh K, Key T, Peters A, Hampel R, Concin H, Nagel G, Ineichen A, Schaffner E, Probst-Hensch N, Künzli N, Schindler C, Schikowski T, Adam M, Phuleria H, Vilier A, Clavel-Chapelon F, Declercq C, Grioni S, Krogh V, Tsai M-Y, Ricceri F, Sacerdote C, Galassi C, Migliore E, Ranzi A, Cesaroni G, Badaloni C, Forastiere F, Tamayo I, Amiano P, Dorronsoro M, Katsoulis M, Trichopoulou A, Brunekreef B, Hoek G, 2014. Effects of long-term exposure to air pollution on natural-cause mortality: an analysis of 22 European cohorts within the multicentre ESCAPE project. Lancet 383, 785–795. [DOI] [PubMed] [Google Scholar]
- Belis CA, Karagulian F, Larsen BR, Hopke PK, 2013. Critical review and meta-analysis of ambient particulate matter source apportionment using receptor models in Europe. Atmos. Environ 69, 94–108. [Google Scholar]
- Benedict M, McMahon T, 2002. Green infrastructure: smart conservation for the 21st century. Renew. Resour. J 20, 12–17. [Google Scholar]
- Bennett JH, Hill AC, Gates DM, 1973. A Model for Gaseous Pollutant Sorption by Leaves. J. Air Pollut. Control Assoc 23, 957–962. [DOI] [PubMed] [Google Scholar]
- Blanco FF, Folegatti MV, 2003. A new method for estimating the leaf area index of cucumber and tomato plants. Hortic. Bras 21, 666–669. [Google Scholar]
- Bodnaruk EW, Kroll CN, Yang Y, Hirabayashi S, Nowak DJ, Endreny TA, 2017. Where to plant urban trees? A spatially explicit methodology to explore ecosystem service tradeoffs. Landsc. Urban Plan 157, 457–467. [Google Scholar]
- Bottalico F, Chirici G, Giannetti F, De Marco A, Nocentini S, Paoletti E, Salbitano F, Sanesi G, Serenelli C, Travaglini D, 2016. Air pollution removal by green infrastructures and urban forests in the city of Florence. Agric. Agric. Sci. Procedia 8, 243–251. [Google Scholar]
- Bottalico F, Travaglini D, Chirici G, Garfì V, Giannetti F, De Marco A, Fares S, Marchetti M, Nocentini S, Paoletti E, Salbitano F, Sanesi G, 2017. A spatially-explicit method to assess the dry deposition of air pollution by urban forests in the city of Florence, Italy. Urban For. Urban Green. 27, 221–234. [Google Scholar]
- Bowler DE, Buyung-Ali L, Knight TM, Pullin AS, 2010. Urban greening to cool towns and cities: A systematic review of the empirical evidence. Landsc. Urban Plan. [Google Scholar]
- Brauer M, Freedman G, Frostad J, van Donkelaar A, Martin RV, Dentener F, Dingenen R. van, Estep K, Amini H, Apte JS, Balakrishnan K, Barregard L, Broday D, Feigin V, Ghosh S, Hopke PK, Knibbs LD, Kokubo Y, Liu Y, Ma S, Morawska L, Sangrador JLT, Shaddick G, Anderson HR, Vos T, Forouzanfar MH, Burnett RT, Cohen A, 2016. Ambient Air Pollution Exposure Estimation for the Global Burden of Disease 2013. Environ. Sci. Technol 50, 79–88. [DOI] [PubMed] [Google Scholar]
- Bréda NJJ, 2003. Ground-based measurements of leaf area index: A review of methods, instruments and current controversies. J. Exp. Bot [DOI] [PubMed] [Google Scholar]
- Britter RE, Hanna SR, 2003. Flow and dispersion in urban areas. Annu. Rev. Fluid Mech 35, 469–96. [Google Scholar]
- Brook JR, Zhang L, Di-Giovanni F, Padro J, 1999. Description and evaluation of a model of deposition velocities for routine estimates of air pollutant dry deposition over North America.: Part I: model development. Atmos. Environ 33, 5037–5051. [Google Scholar]
- Buccolieri R, Salim SM, Leo LS, Di Sabatino S, Chan A, Ielpo P, de Gennaro G, Gromke C, 2011. Analysis of local scale tree–atmosphere interaction on pollutant concentration in idealized street canyons and application to a real urban junction. Atmos. Environ 45, 1702–1713. [Google Scholar]
- Buccolieri R, Santiago J-L, Rivas E, Sanchez B, 2018. Review on urban tree modelling in CFD simulations: Aerodynamic, deposition and thermal effects. Urban For. Urban Green. 31, 212–220. [Google Scholar]
- Cabaraban MTI, Kroll CN, Hirabayashi S, Nowak DJ, 2013. Modeling of air pollutant removal by dry deposition to urban trees using a WRF/CMAQ/i-Tree Eco coupled system. Environ. Pollut 176, 123–133. [DOI] [PubMed] [Google Scholar]
- Cape JN, Jones MR, Leith ID, Sheppard LJ, van Dijk N, Sutton MA, Fowler D, 2008. Estimate of annual NH3 dry deposition to a fumigated ombrotrophic bog using concentration-dependent deposition velocities. Atmos. Environ 42, 6637–6646. [Google Scholar]
- Casadesús J, Villegas D, 2014. Conventional digital cameras as a tool for assessing leaf area index and biomass for cereal breeding. J. Integr. Plant Biol 56, 7–14. [DOI] [PubMed] [Google Scholar]
- Cattani G, Gaeta A, Di Menno di Bucchianico A, De Santis A, Gaddi R, Cusano M, Ancona C, Badaloni C, Forastiere F, Gariazzo C, Sozzi R, Inglessis M, Silibello C, Salvatori E, Manes F, Cesaroni G, 2017. Development of land-use regression models for exposure assessment to ultrafine particles in Rome, Italy. Atmos. Environ 156, 52–60. [Google Scholar]
- Chang K-H, Chang M-Y, Muo C-H, Wu T-N, Hwang B-F, Chen C-Y, Lin T-H, Kao C-H, 2015. Exposure to Air pollution Increases the Risk of Osteoporosis. Medicine (Baltimore). 94, e733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen L, Liu C, Zhang L, Zou R, Zhang Z, 2017. Variation in Tree Species Ability to Capture and Retain Airborne Fine Particulate Matter (PM2.5). Sci. Rep 7, 3206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen L, Liu C, Zou R, Yang M, Zhang Z, 2016. Experimental examination of effectiveness of vegetation as bio-filter of particulate matters in the urban environment. Environ. Pollut 208, 198–208. [DOI] [PubMed] [Google Scholar]
- Chen X, Pei T, Zhou Z, Teng M, He L, Luo M, Liu X, 2015. Efficiency differences of roadside greenbelts with three configurations in removing coarse particles (PM10): A street scale investigation in Wuhan, China. Urban For. Urban Green. 14, 354–360. [Google Scholar]
- Chen X, Vierling L, Deering D, Conley A, 2005. Monitoring boreal forest leaf area index across a Siberian burn chronosequence: A MODIS validation study. Int. J. Remote Sens 26, 5433–5451. [Google Scholar]
- Chenoweth J, Anderson AR, Kumar P, Hunt WF, Chimbwandira SJ, Moore TLC, 2018. The interrelationship of green infrastructure and natural capital. Land use policy 75, 137–144. [Google Scholar]
- Cherin N, Roustan Y, Musson-Genon L, Seigneur C, 2015. Modelling atmospheric dry deposition in urban areas using an urban canopy approach. Geosci. Model Dev 8, 893–910. [Google Scholar]
- Chiesura A, 2004. The role of urban parks for the sustainable city. Landsc. Urban Plan. 68, 129–138. [Google Scholar]
- Churkina G, Kuik F, Bonn B, Lauer A, Grote R, Tomiak K, Butler TM, 2017. Effect of VOC Emissions from Vegetation on Air Quality in Berlin during a Heatwave. Environ. Sci. Technol 51, 6120–6130. [DOI] [PubMed] [Google Scholar]
- Cimorelli AJ, Perry SG, Venkatram A, Weil JC, Paine RJ, Wilson RB, Lee RF, Peters WD, Brode RW, 2005. AERMOD: A Dispersion Model for Industrial Source Applications. Part I: General Model Formulation and Boundary Layer Characterization. J. Appl. Meteorol 44, 682–693. [Google Scholar]
- City of Sacramento, 2018. Urban Tree Canopy Assessment Sacramento, CA. [Google Scholar]
- City of Woodland, 2018. Urban Tree Canopy Assessment Woodland, California 2018. [Google Scholar]
- Clifford S, Mazaheri M, Salimi F, Ezz WN, Yeganeh B, Low-Choy S, Walker K, Mengersen K, Marks GB, Morawska L, 2018. Effects of exposure to ambient ultrafine particles on respiratory health and systemic inflammation in children. Environ. Int 114, 167–180. [DOI] [PubMed] [Google Scholar]
- Costabile F, Wang F, Hong W, Liu F, Allegrini I, 2006. CFD modelling of traffic-related air pollutants around an urban street-canyon in Suzhou, in: Air Pollution XIV, WIT Transactions on Ecology and the Environment, Vol 86 WIT Press, Southampton, UK, pp. 297–306. [Google Scholar]
- Currie BA, Bass B, 2008. Estimates of air pollution mitigation with green plants and green roofs using the UFORE model. Urban Ecosyst. 11, 409–422. [Google Scholar]
- Czemiel Berndtsson J, 2010. Green roof performance towards management of runoff water quantity and quality: A review. Ecol. Eng 36, 351–360. [Google Scholar]
- de Hoogh K, Korek M, Vienneau D, Keuken M, Kukkonen J, Nieuwenhuijsen MJ, Badaloni C, Beelen R, Bolignano A, Cesaroni G, Pradas MC, Cyrys J, Douros J, Eeftens M, Forastiere F, Forsberg B, Fuks K, Gehring U, Gryparis A, Gulliver J, Hansell AL, Hoffmann B, Johansson C, Jonkers S, Kangas L, Katsouyanni K, Künzli N, Lanki T, Memmesheimer M, Moussiopoulos N, Modig L, Pershagen G, Probst-Hensch N, Schindler C, Schikowski T, Sugiri D, Teixidó O, Tsai M-Y, Yli-Tuomi T, Brunekreef B, Hoek G, Bellander T, 2014. Comparing land use regression and dispersion modelling to assess residential exposure to ambient air pollution for epidemiological studies. Environ. Int 73, 382–392. [DOI] [PubMed] [Google Scholar]
- de Keijzer C, Agis D, Ambrós A, Arévalo G, Baldasano JM, Bande S, Barrera-Gómez J, Benach J, Cirach M, Dadvand P, Ghigo S, Martinez-Solanas È, Nieuwenhuijsen M, Cadum E, Basagaña X, 2017. The association of air pollution and greenness with mortality and life expectancy in Spain: A small-area study. Environ. Int 99, 170–176. [DOI] [PubMed] [Google Scholar]
- De Matteis G, Fuorlo M, Montalto M, Landolfi R, 2015. Screening for and prophylaxis of venous thromboembolism in severe carbon monoxide poisoning? Am. J. Emerg. Med 33, 592–593. [DOI] [PubMed] [Google Scholar]
- Deshmukh P, Isakov V, Venkatram A, Yang B, Zhang KM, Logan R, Baldauf R, 2018. The effects of roadside vegetation characteristics on local, near-road air quality. Air Qual. Atmos. Heal 1–12. [PMC free article] [PubMed] [Google Scholar]
- Diez S, Barra E, Crespo F, Britch J, Britch J, 2014. Uncertainty propagation of meteorological and emission data in modeling pollutant dispersion in the atmosphere. Ing. e Investig 34, 44–48. [Google Scholar]
- Erisman JW, 1994. Evaluation of a surface resistance parametrization of sulphur dioxide. Atmos. Environ 28, 2583–2594. [Google Scholar]
- Erisman JW, Van Pul A, Wyers P, 1994. Parametrization of surface resistance for the quantification of atmospheric deposition of acidifying pollutants and ozone. Atmos. Environ 28, 2595–2607. [Google Scholar]
- Escobedo FJ, Nowak DJ, 2009. Spatial heterogeneity and air pollution removal by an urban forest. Landsc. Urban Plan. 90, 102–110. [Google Scholar]
- Essa KSM, 1999. Estimation of Monin-Obukhov Length Using Richardson and Bulk Richardson Number. Conf. Nucl. Part. Phys 591, 591–602. [Google Scholar]
- Fallahshorshani M, André M, Bonhomme C, Seigneur C, 2012. Coupling Traffic, Pollutant Emission, Air and Water Quality Models: Technical Review and Perspectives. Procedia -Soc. Behav. Sci 48, 1794–1804. [Google Scholar]
- Fernández V, Bahamonde HA, Peguero-Pina JJ, Gil-Pelegrín E, Sancho-Knapik D, Gil L, Goldbach HE, Eichert T, 2017. Physico-chemical properties of plant cuticles and their functional and ecological significance. J. Exp. Bot 68, 5293–5306. [DOI] [PubMed] [Google Scholar]
- Filleul L, Cassadou S, Médina S, Fabres P, Lefranc A, Eilstein D, Le Tertre A, Pascal L, Chardon B, Blanchard M, Declercq C, Jusot J-F, Prouvost H, Ledrans M, 2006. The Relation Between Temperature, Ozone, and Mortality in Nine French Cities During the Heat Wave of 2003. Environ. Health Perspect 114, 1344–1347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fowler D, 1981. Dry deposition of airborne pollutants on forests., in: Last FT, Gardiner AS (Eds.), Forest and Woodland Ecology: An Account of Research Being Done in ITE; Cambridge, pp. 62–65. [Google Scholar]
- Gallagher J, Baldauf R, Fuller CH, Kumar P, Gill LW, McNabola A, 2015. Passive methods for improving air quality in the built environment: A review of porous and solid barriers. Atmos. Environ 120, 61–70. [Google Scholar]
- Gallagher J, Gill LW, McNabola A, 2013. The passive control of air pollution exposure in Dublin, Ireland: A combined measurement and modelling case study. Sci. Total Environ 458–460, 331–343. [DOI] [PubMed] [Google Scholar]
- Ganzeveld L, Lelieveld J, 1995. Dry deposition parameterization in a chemistry general circulation model and its influence on the distribution of reactive trace gases. J. Geophys. Res 100, 20999. [Google Scholar]
- Gardner MW, Dorling SR, 1999. Neural network modelling and prediction of hourly NOx and NO2 concentrations in urban air in London. Atmos. Environ 33, 709–719. [Google Scholar]
- Ghassoun Y, Löwner M-O, 2017. Land use regression models for total particle number concentrations using 2D, 3D and semantic parameters. Atmos. Environ 166, 362–373. [Google Scholar]
- Giardina M, Buffa P, 2018. A new approach for modeling dry deposition velocity of particles. Atmos. Environ 180, 11–22. [Google Scholar]
- Gilliam RC, Hogrefe C, Godowitch JM, Napelenok S, Mathur R, Rao ST, 2015. Impact of inherent meteorology uncertainty on air quality model predictions. J. Geophys. Res. Atmos 120, 12,259–12,280. [Google Scholar]
- Godowitch JM, Gilliam RC, Roselle SJ, 2015. Investigating the impact on modeled ozone concentrations using meteorological fields from WRF with an updated four–dimensional data assimilation approach. Atmos. Pollut. Res 6, 305–311. [Google Scholar]
- Gong X, Liu H, Sun J, Gao Y, Zhang X, Jha SK, Zhang H, Ma X, Wang W, 2017. A proposed surface resistance model for the Penman-Monteith formula to estimate evapotranspiration in a solar greenhouse. J. Arid Land 9, 530–546. [Google Scholar]
- Goodman JE, Zu K, Loftus CT, Lynch HN, Prueitt RL, Mohar I, Shubin SP, Sax SN, 2018. Short-term ozone exposure and asthma severity: Weight-of-evidence analysis. Environ. Res 160, 391–397. [DOI] [PubMed] [Google Scholar]
- Gower ST, Kucharik CJ, Norman JM, 1999. Direct and indirect estimation of leaf area index, f(APAR), and net primary production of terrestrial ecosystems. Remote Sens. Environ 70, 29–51. [Google Scholar]
- Gromke C, 2011. A vegetation modeling concept for Building and Environmental Aerodynamics wind tunnel tests and its application in pollutant dispersion studies. Environ. Pollut 159, 2094–2099. [DOI] [PubMed] [Google Scholar]
- Gromke C, Blocken B, 2015. Influence of avenue-trees on air quality at the urban neighborhood scale. Part II: Traffic pollutant concentrations at pedestrian level. Environ. Pollut 196, 176–184. [DOI] [PubMed] [Google Scholar]
- Gromke C, Ruck B, 2008. Aerodynamic modelling of trees for small-scale wind tunnel studies. Forestry 81, 243–258. [Google Scholar]
- Gromke C, Ruck B, 2007. Influence of trees on the dispersion of pollutants in an urban street canyon—Experimental investigation of the flow and concentration field. Atmos. Environ 41, 3287–3302. [Google Scholar]
- Gromke C, Ruck B, Gromke C, Ruck B, 2012. Pollutant Concentrations in Street Canyons of Different Aspect Ratio with Avenues of Trees for Various Wind Directions. Boundary-Layer Meteorol 144, 41–64. [Google Scholar]
- Grünhage L, Haenel H-D, 1997. PLATIN (Plant-ATmosphere INteraction) I: A model of plant-atmosphere interaction for estimating absorbed doses of gaseous air pollutants. Environ. Pollut 98, 37–50. [DOI] [PubMed] [Google Scholar]
- Habermann M, Billger M, Haeger-Eugensson M, 2015. Land use Regression as Method to Model Air Pollution. Previous Results for Gothenburg/Sweden. Procedia Eng. 115, 21–28. [Google Scholar]
- Ham W, Vijayan A, Schulte N, Herner JD, 2017. Commuter exposure to PM2.5, BC, and UFP in six common transport microenvironments in Sacramento, California. Atmos. Environ 167, 335–345. [Google Scholar]
- Han Y-J, Holsen TM, Hopke PK, Cheong J-P, Kim H, Yi S-M, 2004. Identification of source locations for atmospheric dry deposition of heavy metals during yellow-sand events in Seoul, Korea in 1998 using hybrid receptor models. Atmos. Environ 38, 5353–5361. [Google Scholar]
- Heal MR, Kumar P, Harrison RM, 2012. Particles, air quality, policy and health 41. [DOI] [PubMed] [Google Scholar]
- Health Organization Regional Office for Europe, W., 2015. Economic cost of the health impact of air pollution in Europe C le a n a i r, h e a l t h a n d w e a l t h. [Google Scholar]
- Hefny MS, Heinke Schlünzen K, Grawe D, 2015. Including trees in the numerical simulations of the wind flow in urban areas: Should we care? J. Wind Eng. Ind. Aerodyn 144, 84–95. [Google Scholar]
- Hirabayashi S, Kroll CN, Nowak DJ, 2012. Development of a distributed air pollutant dry deposition modeling framework. Environ. Pollut 171, 9–17. [DOI] [PubMed] [Google Scholar]
- Hirabayashi S, Kroll CN, Nowak DJ, 2011. Urban Forest Effects-Dry Deposition ( UFORE – D ) Model Descriptions 1–23. [Google Scholar]
- Hirabayashi S, Nowak DJ, 2016. Comprehensive national database of tree effects on air quality and human health in the United States. Environ. Pollut 215, 48–57. [DOI] [PubMed] [Google Scholar]
- Hoek G, Beelen R, de Hoogh K, Vienneau D, Gulliver J, Fischer P, Briggs D, 2008. A review of land-use regression models to assess spatial variation of outdoor air pollution. Atmos. Environ 42, 7561–7578. [Google Scholar]
- Holmes NS, Morawska L, 2006. A review of dispersion modelling and its application to the dispersion of particles: An overview of different dispersion models available. Atmos. Environ 40, 5902–5928. [Google Scholar]
- Holnicki P, Nahorski Z, 2015. Emission Data Uncertainty in Urban Air Quality Modeling— Case Study. Environ. Model. Assess 20, 583–597. [Google Scholar]
- Hou P, Wu S, 2016. Long-term Changes in Extreme Air Pollution Meteorology and the Implications for Air Quality. Sci. Rep 6, 23792. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang J, Deng F, Wu S, Guo X, 2012. Comparisons of personal exposure to PM2.5 and CO by different commuting modes in Beijing, China. Sci. Total Environ 425, 52–59. [DOI] [PubMed] [Google Scholar]
- Huang Y, Hu X, Zeng N, 2009. Impact of wedge-shaped roofs on airflow and pollutant dispersion inside urban street canyons. Build. Environ 44, 2335–2347. [Google Scholar]
- Irmak S, Mutiibwa D, 2010. On the dynamics of canopy resistance: Generalized linear estimation and relationships with primary micrometeorological variables. Water Resour. Res 46. [Google Scholar]
- Irwin JS, 2014. A suggested method for dispersion model evaluation. J. Air Waste Manage. Assoc 64, 255–264. [DOI] [PubMed] [Google Scholar]
- Jacobson MZ, 2005. Fundamentals of Atmospheric Modeling, Jurnal Ekonomi Malaysia. Cambridge University Press, Cambridge. [Google Scholar]
- Janhäll S, 2015. Review on urban vegetation and particle air pollution – Deposition and dispersion. Atmos. Environ 105, 130–137. [Google Scholar]
- Jayasooriya VMM, Ng AWWM, Muthukumaran S, Perera BJCJC, 2017. Green infrastructure practices for improvement of urban air quality. Urban For. Urban Green. 21, 34–47. [Google Scholar]
- Jeanjean APR, Buccolieri R, Eddy J, Monks PS, Leigh RJ, 2017. Air quality affected by trees in real street canyons: The case of Marylebone neighbourhood in central London. Urban For. Urban Green. 22, 41–53. [Google Scholar]
- Jeanjean APR, Hinchliffe G, McMullan WA, Monks PS, Leigh RJ, 2015. A CFD study on the effectiveness of trees to disperse road traffic emissions at a city scale. Atmos. Environ 120, 1–14. [Google Scholar]
- Jeanjean APRPR, Monks PSS, Leigh RJJ, 2016. Modelling the effectiveness of urban trees and grass on PM 2.5 reduction via dispersion and deposition at a city scale. Atmos. Environ 147, 1–10. [Google Scholar]
- Jiang Y, Jiang X, Tang R, Li Z, Zhang Y, Huang C, Ru C, 2017. Estimation of daily evapotranspiration using MODIS data to calculate instantaneous decoupling coefficient and resistances, in: 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS) IEEE, pp. 4004–4007. [Google Scholar]
- Karamchandani P, Lohman K, Seigneur C, 2009. Using a sub-grid scale modeling approach to simulate the transport and fate of toxic air pollutants, in: Environmental Fluid Mechanics. pp. 59–71. [Google Scholar]
- Kavassalis SC, Murphy JG, 2017. Understanding ozone-meteorology correlations: A role for dry deposition. Geophys. Res. Lett 44, 2922–2931. [Google Scholar]
- Kerstiens G, 2006. Parameterization, comparison, and validation of models quantifying relative change of cuticular permeability with physicochemical properties of diffusants. J. Exp. Bot 57, 2525–2533. [DOI] [PubMed] [Google Scholar]
- Khan TR, Perlinger JA, 2017. Evaluation of five dry particle deposition parameterizations for incorporation into atmospheric transport models. Geosci. Model Dev 10, 3861–3888. [Google Scholar]
- King KL, Johnson S, Kheirbek I, Lu JWT, Matte T, 2014. Differences in magnitude and spatial distribution of urban forest pollution deposition rates, air pollution emissions, and ambient neighborhood air quality in New York City. Landsc. Urban Plan. 128, 14–22. [Google Scholar]
- Kleine Deters J, Zalakeviciute R, Gonzalez M, Rybarczyk Y, 2017. Modeling PM2.5Urban Pollution Using Machine Learning and Selected Meteorological Parameters. J. Electr. Comput. Eng 2017. [Google Scholar]
- Knibbs LD, Coorey CP, Bechle MJ, Marshall JD, Hewson MG, Jalaludin B, Morgan GG, Barnett AG, 2018. Long-term nitrogen dioxide exposure assessment using backextrapolation of satellite-based land-use regression models for Australia. Environ. Res 163, 16–25. [DOI] [PubMed] [Google Scholar]
- Koloskov G, Mukhamejanov K, Tanton TW, 2007. Monin-Obukhov length as a cornerstone of the SEBAL calculations of evapotranspiration. J. Hydrol 335, 170–179. [Google Scholar]
- Korek M, Johansson C, Svensson N, Lind T, Beelen R, Hoek G, Pershagen G, Bellander T, 2016. Can dispersion modeling of air pollution be improved by land-use regression? An example from Stockholm, Sweden. J. Expo. Sci. Environ. Epidemiol 27, 575–581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kumar A, Chen F, Barlage M, Ek MB, Niyogi D, 2014. Assessing Impacts of Integrating MODIS Vegetation Data in the Weather Research and Forecasting (WRF) Model Coupled to Two Different Canopy-Resistance Approaches. J. Appl. Meteorol. Climatol 53, 1362–1380. [Google Scholar]
- Kumar P, de Fatima Andrade M, Ynoue RY, Fornaro A, de Freitas ED, Martins J, Martins LD, Albuquerque T, Zhang Y, Morawska L, 2016. New directions: From biofuels to wood stoves: The modern and ancient air quality challenges in the megacity of São Paulo. Atmos. Environ [Google Scholar]
- Kumar P, Jain S, Gurjar BR, Sharma P, Khare M, Morawska L, Britter R, 2013. New Directions: Can a “blue sky” return to Indian megacities? Atmos. Environ [Google Scholar]
- Kumar P, Khare M, Harrison RM, Bloss WJ, Lewis AC, Coe H, Morawska L, 2015. New directions: Air pollution challenges for developing megacities like Delhi. Atmos. Environ [Google Scholar]
- Kumar P, Rivas I, Sachdeva L, 2017. Exposure of in-pram babies to airborne particles during morning drop-in and afternoon pick-up of school children. Environ. Pollut 224, 407–420. [DOI] [PubMed] [Google Scholar]
- Künzli N, Kaiser R, Medina S, Studnicka M, Chanel O, Filliger P, Herry M, Horak F, Puybonnieux-Texier V, Quénel P, Schneider J, Seethaler R, Vergnaud J-C, Sommer H, 2000. Public-health impact of outdoor and traffic-related air pollution: a European assessment. Lancet 356, 795–801. [DOI] [PubMed] [Google Scholar]
- Kwak K-H, Woo S, Kim K, Lee S-B, Bae G-N, Ma Y-I, Sunwoo Y, Baik J-J, 2018. On-Road Air Quality Associated with Traffic Composition and Street-Canyon Ventilation: Mobile Monitoring and CFD Modeling. Atmosphere (Basel). 9, 92. [Google Scholar]
- Lagzi I, Meszaros R, Gelybo G, Leelossy A, 2013. Atmospheric Chemistry, Eotvos Lorand University. [Google Scholar]
- Langner C, Klemm O, 2011. A Comparison of Model Performance between AERMOD and AUSTAL2000. J. Air Waste Manage. Assoc 61, 640–646. [DOI] [PubMed] [Google Scholar]
- Lateb M, Meroney RN, Yataghene M, Fellouah H, Saleh F, Boufadel MC, 2016. On the use of numerical modelling for near-field pollutant dispersion in urban environments − A review. Environ. Pollut 208, 271–283. [DOI] [PubMed] [Google Scholar]
- Lee ES, Ranasinghe DR, Ahangar FE, Amini S, Mara S, Choi W, Paulson S, Zhu Y, 2018. Field evaluation of vegetation and noise barriers for mitigation of near-freeway air pollution under variable wind conditions. Atmos. Environ 175, 92–99. [Google Scholar]
- Lhomme JP, Montes C, 2014. Generalized combination equations for canopy evaporation under dry and wet conditions. Hydrol. Earth Syst. Sci 18, 1137–1149. [Google Scholar]
- Li J, Chen B, de la Campa AMS, Alastuey A, Querol X, de la Rosa JD, 2018. 2005– 2014 trends of PM10 source contributions in an industrialized area of southern Spain. Environ. Pollut 236, 570–579. [DOI] [PubMed] [Google Scholar]
- Li X-B, Lu Q-C, Lu S-J, He H-D, Peng Z-R, Gao Y, Wang Z-Y, 2016. The impacts of roadside vegetation barriers on the dispersion of gaseous traffic pollution in urban street canyons. Urban For. Urban Green. 17, 80–91. [Google Scholar]
- Lin X, Chamecki M, Katul G, Yu X, 2018. Effects of leaf area index and density on ultrafine particle deposition onto forest canopies: A LES study. Atmos. Environ 189, 153–163. [Google Scholar]
- Litschke T, Kuttler W, 2008. On the reduction of urban particle concentration by vegetation – a review. Meteorol. Zeitschrift 17, 229–240. [Google Scholar]
- Liu X, Gao N, Hopke PK, Cohen D, Bailey G, Crisp P, 1996. Evaluation of spatial patterns of fine particle sulfur and lead concentrations in New South Wales, Australia. Atmos. Environ 30, 9–24. [Google Scholar]
- Lohmeyer A, Mueller WJ, Baechlin W, 2002. A comparison of street canyon concentration predictions by different modellers: final results now available from the Podbi-exercise. Atmos. Environ 36, 157–158. [Google Scholar]
- Lovasi GS, Quinn JW, Neckerman KM, Perzanowski MS, Rundle A, 2008. Children living in areas with more street trees have lower prevalence of asthma. J. Epidemiol. Community Heal 62, 647–649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lovett GM, 1994. Atmospheric Deposition of Nutrients and Pollutants in North America: An Ecological Perspective. Ecol. Appl 4, 629–650. [Google Scholar]
- Luber G, McGeehin M, 2008. Climate Change and Extreme Heat Events. Am. J. Prev. Med [DOI] [PubMed] [Google Scholar]
- Magnani F, Leonardi S, Tognetti R, Grace J, Borghetti M, 1998. Modelling the surface conductance of a broad-leaf canopy: effects of partial decoupling from the atmosphere. Plant, Cell Environ. 21, 867–879. [Google Scholar]
- Maleki H, Sorooshian A, Goudarzi G, Nikfal A, Baneshi MM, 2016. Temporal profile of PM 10 and associated health effects in one of the most polluted cities of the world (Ahvaz, Iran) between 2009 and 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mallet V, Sportisse B, 2008. Air quality modeling: From deterministic to stochastic approaches. Comput. Math. with Appl 55, 2329–2337. [Google Scholar]
- Marciotto ER, Oliveira AP, Hanna SR, 2010. Modeling study of the aspect ratio influence on urban canopy energy fluxes with a modified wall-canyon energy budget scheme. Build. Environ 45, 2497–2505. [Google Scholar]
- Martin NA, Chappelka AH, Somers G, Loewenstein EF, Keever GJ, 2013. Evaluation of sampling protocol for i-Tree Eco: A case study in predicting ecosystem services at Auburn University. Arboric. Urban For 39, 56–61. [Google Scholar]
- Massad R-S, Nemitz E, Sutton MA, 2010. Review and parameterisation of bi-directional ammonia exchange between vegetation and the atmosphere. Atmos. Chem. Phys 10, 10359–10386. [Google Scholar]
- McDonald AG, Bealey WJ, Fowler D, Dragosits U, Skiba U, Smith RI, Donovan RG, Brett HE, Hewitt CN, Nemitz E, 2007. Quantifying the effect of urban tree planting on concentrations and depositions of PM10 in two UK conurbations. Atmos. Environ 41, 8455–8467. [Google Scholar]
- McDonald BC, De Gouw JA, Gilman JB, Jathar SH, Akherati A, Cappa CD, Jimenez JL, Lee-Taylor J, Hayes PL, McKeen SA, Cui YY, Kim SW, Gentner DR, Isaacman-VanWertz G, Goldstein AH, Harley RA, Frost GJ, Roberts JM, Ryerson TB, Trainer M, 2018. Volatile chemical products emerging as largest petrochemical source of urban organic emissions. Science (80-. ). 359, 760–764. [DOI] [PubMed] [Google Scholar]
- McPherson EG, Simpson JR, 1999. Carbon dioxide reduction through urban forestry Gen. Tech. Rep. PSW-171, USDA For. Serv., Pacific Southwest Res. Station; Albany, CA. [Google Scholar]
- Meyers TP, Baldocchi DD, 1988. A comparison of models for deriving dry deposition fluxes of O 3 and SO 2 to a forest canopy. Tellus B Chem. Phys. Meteorol 40, 270–284. [Google Scholar]
- Miao H, Gopalan H, Raghavan V, Hee Joo P, Joo H, 2016. Computational Fluid Dynamics simulation of wind flow and wind force on trees in urban parks, in: 8th International Colloquium on Bluff Body Aerodynamics and Applications. [Google Scholar]
- Mohan SM, 2016. An overview of particulate dry deposition: measuring methods, deposition velocity and controlling factors. Int. J. Environ. Sci. Technol [Google Scholar]
- Morani A, Nowak D, Hirabayashi S, Guidolotti G, Medori M, Muzzini V, Fares S, Mugnozza GS, Calfapietra C, 2014. Comparing i-Tree modeled ozone deposition with field measurements in a periurban Mediterranean forest. Environ. Pollut 195, 202–209. [DOI] [PubMed] [Google Scholar]
- Muttoo S, Ramsay L, Brunekreef B, Beelen R, Meliefste K, Naidoo RN, 2018. Land use regression modelling estimating nitrogen oxides exposure in industrial south Durban, South Africa. Sci. Total Environ 610–611, 1439–1447. [DOI] [PubMed] [Google Scholar]
- Nguyen KC, Noonan JA, Galbally IE, Physick WL, 1997. Predictions of plume dispersion in complex terrain: Eulerian versus Lagrangian models. Atmos. Environ 31, 947–958. [Google Scholar]
- Nowak DJ, 1994. Air Pollution Removal by Chicago’s Urban Forest, in: Chicago’s Urban Forest Ecosystem: Results of the Chicago Urban Forest Climate Project; PA, pp. 63–81. [Google Scholar]
- Nowak DJ, Crane DE, Stevens JC, 2006. Air pollution removal by urban trees and shrubs in the United States. Urban For. Urban Green. 4, 5–123. [Google Scholar]
- Nowak DJ, Hirabayashi S, Bodine A, Greenfield E, 2014. Tree and forest effects on air quality and human health in the United States. Env. Pollut 193, 119–129. [DOI] [PubMed] [Google Scholar]
- Nowak DJ, Hirabayashi S, Bodine A, Hoehn R, 2013. Modeled PM2.5 removal by trees in ten U.S. cities and associated health effects. Environ. Pollut 178, 395–402. [DOI] [PubMed] [Google Scholar]
- Nowak DJ, Hirabayashi S, Doyle M, McGovern M, Pasher J, 2018. Air pollution removal by urban forests in Canada and its effect on air quality and human health. Urban For. Urban Green. 29, 40–48. [Google Scholar]
- Nowak DJ, Hoehn RE, Bodine AR, Greenfield EJ, O ‘neil-Dunne J, Nowak DJ, Hoehn RE, Greenfield EJ, Bodine AR, O ‘neil-Dunne J, 2013. Urban forest structure, ecosystem services and change in Syracuse, NY. Urban Ecosyst 19, 1455–1477. [Google Scholar]
- O’Dell RA, Taheri M, Kabel RL, 1977. A Model for Uptake of Pollutants by Vegetation. J. Air Pollut. Control Assoc 27, 1104–1109. [Google Scholar]
- Onder S, Dursun S, 2006. Air borne heavy metal pollution of Cedrus libani (A. Rich.) in the city centre of Konya (Turkey). Atmos. Environ 40, 1122–1133. [Google Scholar]
- Pacitto A, Stabile L, Moreno T, Kumar P, Wierzbicka A, Morawska L, Buonanno G, 2018. The influence of lifestyle on airborne particle surface area doses received by different Western populations. Environ. Pollut 232, 113–122. [DOI] [PubMed] [Google Scholar]
- Padro J, Edwards GC, 1991. Sensitivity of ADOM dry deposition velocities to input parameters: A comparison with measurements for SO 2 and NO 2 over three land use types. Atmosphere-Ocean 29, 667–685. [Google Scholar]
- Pathak V, Tripathi BD, Mishra VK, 2011. Evaluation of Anticipated Performance Index of some tree species for green belt development to mitigate traffic generated noise. Urban For. Urban Green. 10, 61–66. [Google Scholar]
- Peterson WB, 1980. USER’S GUIDE FOR HIWAY-2. A HIGHWAY AIR POLLUTION MODEL, U.S. Environmental Protection Agency; Washington,D.C. [Google Scholar]
- Pleijel H, Pihl Karlsson G, Binsell Gerdin E, 2004. On the logarithmic relationship between NO2 concentration and the distance from a highroad. Sci. Total Environ 332, 261–264. [DOI] [PubMed] [Google Scholar]
- Pope CA, Ezzati M, Dockery DW, 2009. Fine-Particulate Air Pollution and Life Expectancy in the United States. N. Engl. J. Med 360, 376–386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Powe NA, Willis KG, 2004. Mortality and morbidity benefits of air pollution (SO2 and PM10) absorption attributable to woodland in Britain. J. Environ. Manage 70, 119–128. [DOI] [PubMed] [Google Scholar]
- Pugh TAM, MacKenzie AR, Whyatt JD, Hewitt CN, 2012. Effectiveness of Green Infrastructure for Improvement of Air Quality in Urban Street Canyons. Environ. Sci. Technol 46, 7692–7699. [DOI] [PubMed] [Google Scholar]
- Rao M, George LA, Rosenstiel TN, Shandas V, Dinno A, 2014. Assessing the relationship among urban trees, nitrogen dioxide, and respiratory health. Environ. Pollut 194, 96–104. [DOI] [PubMed] [Google Scholar]
- Rao M, George LA, Shandas V, Rosenstiel TN, 2017. Assessing the Potential of Land Use Modification to Mitigate Ambient NO2 and Its Consequences for Respiratory Health. Int. J. Environ. Res. Public Health 14, 750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rivas I, Kumar P, Hagen-Zanker A, 2017. Exposure to air pollutants during commuting in London: Are there inequalities among different socio-economic groups? Environ. Int 101, 143–157. [DOI] [PubMed] [Google Scholar]
- Rodný M, Nolz R, Novák V, Hlaváčiková H, Loiskandl W, Himmelbauer M, 2016. Modified method of aerodynamic resistance calculation and its application to potential evapotranspiration estimation. Int. Agrophysics 30, 231–235. [Google Scholar]
- Ruggiero A, Punzo P, Landi S, Costa A, Van Oosten M, Grillo S, 2017. Improving Plant Water Use Efficiency through Molecular Genetics. Horticulturae 3, 31. [Google Scholar]
- Sacks JD, Lloyd JM, Zhu Y, Anderton J, Jang CJ, Hubbell B, Fann N, 2018. The Environmental Benefits Mapping and Analysis Program – Community Edition (BenMAP–CE): A tool to estimate the health and economic benefits of reducing air pollution. Environ. Model. Softw 104, 118–129. [PMC free article] [PubMed] [Google Scholar]
- Saikawa E, Trail M, Zhong M, Wu Q, Young CL, Janssens-Maenhout G, Klimont Z, Wagner F, Kurokawa J, Nagpure AS, Gurjar BR, 2017. Uncertainties in emissions estimates of greenhouse gases and air pollutants in India and their impacts on regional air quality. Environ. Res. Lett 12, 065002. [Google Scholar]
- Sanchez B, Santiago J-L, Martilli A, Palacios M, Kirchner F, 2016. CFD modeling of reactive pollutant dispersion in simplified urban configurations with different chemical mechanisms. Atmos. Chem. Phys 16, 12143–12157. [Google Scholar]
- Santiago J-L, Rivas E, Sanchez B, Buccolieri R, Martin F, 2017. The Impact of Planting Trees on NO x Concentrations: The Case of the Plaza de la Cruz Neighborhood in Pamplona (Spain). [Google Scholar]
- Schrader F, Brümmer C, 2014. Land Use Specific Ammonia Deposition Velocities: a Review of Recent Studies (2004–2013). Water, Air, Soil Pollut. 225, 2114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schrader F, Schaap M, Zöll U, Kranenburg R, Brümmer C, 2018. The hidden cost of using low-resolution concentration data in the estimation of NH3 dry deposition fluxes. Sci. Rep 8, 969. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seinfeld JH, Pandis SN, 2006. Atmospheric Chemistry and Physics: From Air Pollution to Climate Change, Atmospheric Chemistry and Physics. [Google Scholar]
- Selmi W, Weber C, Rivière E, Blond N, Mehdi L, Nowak D, 2016. Air pollution removal by trees in public green spaces in Strasbourg city, France. Urban For. Urban Green. 17, 192–201. [Google Scholar]
- Shahraiyni HT, Sodoudi S, 2016. Statistical Modeling Approaches for PM10 Prediction in Urban Areas; A Review of 21st-Century Studies. Atmosphere (Basel). 7, 15. [Google Scholar]
- Shaneyfelt KM, Anderson AR, Kumar P, Hunt WF, 2017. Air quality considerations for stormwater green street design. Environ. Pollut 231, 768–778. [DOI] [PubMed] [Google Scholar]
- Sharma P, Khare M, 2001. Modelling of vehicular exhausts -A review. Transp. Res. Part D Transp. Environ 6, 179–198. [Google Scholar]
- Sharma S, Sharma P, Khare M, 2013. Hybrid modelling approach for effective simulation of reactive pollutants like Ozone. Atmos. Environ 80, 408–414. [Google Scholar]
- Sini JF, Anquetin S, Mestayer PG, 1996. Pollutant dispersion and thermal effects in urban street canyons. Atmos. Environ 30, 2659–2677. [Google Scholar]
- Snyder MG, Venkatram A, Heist DK, Perry SG, Petersen WB, Isakov V, 2013. RLINE: A line source dispersion model for near-surface releases. Atmos. Environ 77, 748–756. [Google Scholar]
- Song X-H, Polissar AV, Hopke PK, 2001. Sources of fine particle composition in the northeastern US. Atmos. Environ 35, 5277–5286. [Google Scholar]
- Steffens JT, Wang YJ, Zhang KM, 2012. Exploration of effects of a vegetation barrier on particle size distributions in a near-road environment. Atmos. Environ 50, 120–128. [Google Scholar]
- Steinle S, Reis S, Sabel CE, Semple S, Twigg MM, Braban CF, Leeson SR, Heal MR, Harrison D, Lin C, Wu H, 2015. Personal exposure monitoring of PM 2.5 in indoor and outdoor microenvironments. Sci. Total Environ 508, 383–394. [DOI] [PubMed] [Google Scholar]
- Sun X, Cheng S, Li J, Wen W, 2017. An Integrated Air Quality Model and Optimization Model for Regional Economic and Environmental Development: A Case Study of Tangshan, China. Aerosol Air Qual. Res 17, 1592–1609. [Google Scholar]
- Tai APK, Mickley LJ, Jacob DJ, 2010. Correlations between fine particulate matter (PM2.5) and meteorological variables in the United States: Implications for the sensitivity of PM2.5 to climate change. Atmos. Environ 44, 3976–3984. [Google Scholar]
- Talbi A, Kerchich Y, Kerbachi R, Boughedaoui M, 2018. Assessment of annual air pollution levels with PM1, PM2.5, PM10 and associated heavy metals in Algiers, Algeria. Environ. Pollut 232, 252–263. [DOI] [PubMed] [Google Scholar]
- Tallis M, Taylor G, Sinnett D, Freer-Smith P, 2011. Estimating the removal of atmospheric particulate pollution by the urban tree canopy of London, under current and future environments. Landsc. Urban Plan. 103, 129–138. [Google Scholar]
- Tiwary A, Sinnett D, Peachey C, Chalabi Z, Vardoulakis S, Fletcher T, Leonardi G, Grundy C, Azapagic A, Hutchings TR, 2009. An integrated tool to assess the role of new planting in PM10 capture and the human health benefits: A case study in London. Environ. Pollut 157, 2645–2653. [DOI] [PubMed] [Google Scholar]
- Tong Z, Baldauf RW, Isakov V, Deshmukh P, Max Zhang K, 2016. Roadside vegetation barrier designs to mitigate near-road air pollution impacts. Sci. Total Environ 541, 920–927. [DOI] [PubMed] [Google Scholar]
- Venkatram A, Snyder MG, Heist DK, Perry SG, Petersen WB, Isakov V, 2013. Reformulation of plume spread for near-surface dispersion. Atmos. Environ 77, 846–855. [Google Scholar]
- Verbeke T, Lathière J, Szopa S, de Noblet-Ducoudré N, 2015. Impact of future land-cover changes on HNO3 and O3 surface dry deposition. Atmos. Chem. Phys 15, 13555–13568. [Google Scholar]
- Vos PEJ, Maiheu B, Vankerkom J, Janssen S, 2013. Improving local air quality in cities: To tree or not to tree? Environ. Pollut 183, 113–122. [DOI] [PubMed] [Google Scholar]
- Vranckx S, Vos P, Maiheu B, Janssen S, 2015. Impact of trees on pollutant dispersion in street canyons: A numerical study of the annual average effects in Antwerp, Belgium. Sci. Total Environ 532, 474–483. [DOI] [PubMed] [Google Scholar]
- Wåhlin P, Berkowicz R, Palmgren F, 2006. Characterisation of traffic-generated particulate matter in Copenhagen. Atmos. Environ 40, 2151–2159. [Google Scholar]
- Wahlina P, Palmgren F, Van Dingenen R, 2001. Experimental studies of ultrafine particles in streets and the relationship to traffic. Atmos. Environ 35, S63–S69. [Google Scholar]
- Walmsley JL, Wesely ML, 1996. Modification of coded parametrizations of surface resistances to gaseous dry deposition. Atmos. Environ 30, 1181–1188. [Google Scholar]
- Watson JG, 1984. Overview of Receptor Model Principles. J. Air Pollut. Control Assoc 34, 619–623. [Google Scholar]
- Watson JG, Zhu T, Chow JC, Engelbrecht J, Fujita EM, Wilson WE, 2002. Receptor modeling application framework for particle source apportionment, in: Chemosphere. Pergamon, pp. 1093–1136. [DOI] [PubMed] [Google Scholar]
- Wesely M.., 2000. A review of the current status of knowledge on dry deposition. Atmos. Environ 34, 2261–2282. [Google Scholar]
- Wesely ML, 1989. Parameterization of surface resistances to gaseous dry deposition in regional-scale numerical models. Atmos. Environ 23, 1293–1304. [Google Scholar]
- Wesely ML, 1988. 9100J8QI.pdf. North caroline [Google Scholar]
- Wesely ML, Hicks BB, 1977. Some Factors that Affect the Deposition Rates of Sulfur Dioxide and Similar Gases on Vegetation. J. Air Pollut. Control Assoc 27, 1110–1116. [Google Scholar]
- WHO, 2016. Health risk assessment of air pollution – general principles, International Journal of Mass Spectrometry. Copenhagen. [Google Scholar]
- Wolf K, Cyrys J, Harciníková T, Gu J, Kusch T, Hampel R, Schneider A, Peters A, 2017. Land use regression modeling of ultrafine particles, ozone, nitrogen oxides and markers of particulate matter pollution in Augsburg, Germany. Sci. Total Environ 579, 1531–1540. [DOI] [PubMed] [Google Scholar]
- Wong AYH, Tai APK, Ip Y-Y, 2018. Attribution and Statistical Parameterization of the Sensitivity of Surface Ozone to Changes in Leaf Area Index Based On a Chemical Transport Model. J. Geophys. Res. Atmos 1883–1898. [Google Scholar]
- Xavier AC, Vettorazzi CA, 2004. Mapping leaf area index through spectral vegetation indices in a subtropical watershed. Int. J. Remote Sens 25, 1661–1672. [Google Scholar]
- Xiao Y, Zhu X-G, 2017. Components of mesophyll resistance and their environmental responses: A theoretical modelling analysis. Plant. Cell Environ 40, 2729–2742. [DOI] [PubMed] [Google Scholar]
- Yang J, Chang Y, Yan P, 2015. Ranking the suitability of common urban tree species for controlling PM2.5 pollution. Atmos. Pollut. Res 6, 267–277. [Google Scholar]
- Yang J, McBride J, Zhou J, Sun Z, 2004. The urban forest in Beijing and its role in air pollution reduction. Urban For. Urban Green. 3, 65–78. [Google Scholar]
- Yang J, Yu Q, Gong P, 2008. Quantifying air pollution removal by green roofs in Chicago. Atmos. Environ 42, 7266–7273. [Google Scholar]
- Yin S, Shen Z, Zhou P, Zou X, Che S, Wang W, 2011. Quantifying air pollution attenuation within urban parks: An experimental approach in Shanghai, China. Environ. Pollut 159, 2155–2163. [DOI] [PubMed] [Google Scholar]
- Yli-Pelkonen V, Scott AA, Viippola V, Setälä H, 2017. Trees in urban parks and forests reduce O3, but not NO2 concentrations in Baltimore, MD, USA. Atmos. Environ 167, 73–80. [Google Scholar]
- Zhang, Chang M, Zhou S, Chen W, Wang X, Liao W, Dai J, Wu Z, 2017. Evaluate dry deposition velocity of the nitrogen oxides using Noah-MP physics ensemble simulations for the Dinghushan Forest, Southern China. Asia-Pacific J. Atmos. Sci 53, 519–536. [Google Scholar]
- Zhang H, Wang Y, Park T-W, Deng Y, 2017. Quantifying the relationship between extreme air pollution events and extreme weather events. Atmos. Res 188, 64–79. [Google Scholar]
- Zhang J, Ding W, 2017. Prediction of Air Pollutants Concentration Based on an Extreme Learning Machine: The Case of Hong Kong. Int. J. Environ. Res. Public Health 14, 114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang J, Shao Y, 2014. A new parameterization of particle dry deposition over rough surfaces. Atmos. Chem. Phys 14, 12429–12440. [Google Scholar]
- Zhang L, Brook JR, Vet R, 2003. A revised parameterization for gaseous dry deposition in air-quality models. Atmos. Chem. Phys. Atmos. Chem. Phys 3, 2067–2082. [Google Scholar]
- Zhang L, Brook JR, Vet R, 2002a. On ozone dry deposition—with emphasis on non-stomatal uptake and wet canopies. Atmos. Environ 36, 4787–4799. [Google Scholar]
- Zhang L, Moran MD, Makar PA, Brook JR, Gong S, 2002b. Modelling gaseous dry deposition in AURAMS: a unified regional air-quality modelling system. Atmos. Environ 36, 537–560. [Google Scholar]
- Zhang W, Wang B, Niu X, 2017. Relationship between leaf surface characteristics and particle capturing capacities of different tree species in Beijing. Forests 8, 1–12. [Google Scholar]
- Zhang Y, Wang Y, 2016. Climate-driven ground-level ozone extreme in the fall over the Southeast United States. Proc. Natl. Acad. Sci 113, 10025–10030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou P, Ganzeveld L, Rannik Ü, Zhou L, Gierens R, Taipale D, Mammarella I, Boy M, 2017. Simulating ozone dry deposition at a boreal forest with a multi-layer canopy deposition model. Atmos. Chem. Phys 17, 1361–1379. [Google Scholar]
- Zou B, Xu S, Sternberg T, Fang X, 2016. Effect of Land Use and Cover Change on Air Quality in Urban Sprawl. Sustainability 8, 677. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.