TAPAS: A Thresholding Approach for Probability Map Automatic Segmentation in Multiple Sclerosis

Abstract

Total brain white matter lesion (WML) volume is the most widely established magnetic resonance imaging (MRI) outcome measure in studies of multiple sclerosis (MS). To estimate WML volume, there are a number of automatic segmentation methods available, yet manual delineation remains the gold standard approach. Automatic approaches often yield a probability map to which a threshold is applied to create lesion segmentation masks. Unfortunately, few approaches systematically determine the threshold employed; many methods use a manually selected threshold, thus introducing human error and bias into the automated procedure. In this study, we propose and validate an automatic thresholding algorithm, Thresholding Approach for Probability Map Automatic Segmentation in Multiple Sclerosis (TAPAS), to obtain subject-specific threshold estimates for probability map automatic segmentation of T2-weighted (T2) hyperintense WMLs. Using multimodal MRI, the proposed method applies an automatic segmentation algorithm to obtain probability maps. We obtain the true subject-specific threshold that maximizes the Sørensen-Dice similarity coefficient (DSC). Then the subject-specific thresholds are modeled on a naive estimate of volume using a generalized additive model. Applying this model, we predict a subject-specific threshold in data not used for training. We ran a Monte Carlo-resampled split-sample cross-validation (100 validation sets) using two data sets: the first obtained from the Johns Hopkins Hospital (JHH) on a Philips 3 Tesla (3T) scanner (n = 94) and a second collected at the Brigham and Women's Hospital (BWH) using a Siemens 3T scanner (n = 40). By means of the proposed automated technique, in the JHH data we found an average reduction in subject-level absolute error of 0.1 mL per one mL increase in manual volume. Using Bland-Altman analysis, we found that volumetric bias associated with group-level thresholding was mitigated when applying TAPAS. The BWH data showed similar absolute error estimates using group-level thresholding or TAPAS likely since Bland-Altman analyses indicated no systematic biases associated with group or TAPAS volume estimates. The current study presents the first validated fully automated method for subject-specific threshold prediction to segment brain lesions.

Introduction

Multiple sclerosis (MS) is a chronic inflammatory and degenerative disease of the central nervous system characterized by multifocal demyelinating lesions (Confavreux and Vukusic 2008; Compston and Coles 2002) and atrophy in both white and gray matter, which may lead to physical and cognitive disability and poor functional outcomes (e.g. social isolation, unemployment) (Rovira and León 2008; Tauhid et al., 2015). In MS research and clinical care, magnetic resonance imaging (MRI) is a commonly used tool for detection and quantification of disease activity and severity (Ge 2006; Zivadinov and Bakshi 2004; Bakshi et al., 2005). MRI allows for the detection of T2-weighted (T2) hyperintense white matter lesions. Both lesion volume and count have become important metrics in the clinical and research domain (Ge 2006; Dworkin et al., 2018). Advanced MRI also allows for cortical lesion detection, one of the new biomarkers integrated in the revised McDonald criteria (Thompson et al., 2018). Typically, total lesion burden (i.e. lesion load), is defined as the volume of total brain matter containing lesions and is a cornerstone for assessing disease severity in MS research and clinical investigations (Popescu et al., 2013; Calabresi et al., 2014; Tauhid et al., 2014).

To quantify lesion burden, different approaches use MRI to identify and segment lesional tissue. Manual segmentation is the gold standard approach and requires a neuroradiologist or imaging expert to inspect scans visually and delineate lesions. Due to difficulties associated with manual segmentation such as cost, time, and large intra- and inter-rater variability, many automatic segmentation methods have been developed (Egger et al., 2017; Carass, Roy, Jog, Cuzzocreo, Magrath, Gherman, Button, Nguyen, Prados, et al., 2017a, 2017b; García-Lorenzo et al., 2013; Lladó et al., 2012). Unfortunately, since lesions present heterogeneously on MRI scans, automatic segmentation remains a difficult task, though numerous methods have been proposed. No single approach is widely accepted or proven to perform optimally across lesion types, scanning platforms, and centers (Danelakis, Theoharis, and Verganelakis 2018; Sweeney et al., 2014). A common key step in automatically delineating lesions involves creating a continuous map indicating the degree of lesion likelihood using various imaging modalities (Danelakis, Theoharis, and Verganelakis 2018; A. M. Valcarcel, Linn, Vandekar, et al., 2018a, 2018b;Roy et al., 2015; Sweeney et al., 2014, 2013). In these cases, a threshold is then applied to probability maps to obtain binary lesion segmentations, also referred to as lesion masks.

Automatic approaches are susceptible to biases in lesion volume estimation associated with the total lesion load (Commowick et al., 2018); that is, in subjects with few lesions, automated techniques tend to over-segment lesions, and in subjects with higher lesion load, lesions are under-segmented. Bias in lesion volume estimation may also be associated with MRI hardware specifications, differences in protocols, artifacts, or partial volume effects.

To investigate this volume bias, we leveraged the 2015 Longitudinal Lesion Challenge (https://smart-stats-tools.org/lesion-challenge) (Carass, Roy, Jog, Cuzzocreo, Magrath, Gherman, Button, Nguyen, Bazin, et al., 2017; Carass, Roy, Jog, Cuzzocreo, Magrath, Gherman, Button, Nguyen, Prados, et al., 2017), a publicly available data set consisting of imaging of five subjects with MS for training and fourteen subjects with MS for testing. In training and testing sets, subjects had at least four imaging visits. The training data contain manual delineations from two expert raters while the testing set does not publicly provide manual delineations; rather, the testing set only consists of volume estimates from each rater. Challengers who wish to compare new segmentation methods can submit their testing set automatic segmentations. The automatic segmentation method is ranked using a weighted average of various similarity measures. A leader board with method performance measures is maintained by challenge organizers and some published work compares top performing methods (Carass, Roy, Jog, Cuzzocreo, Magrath, Gherman, Button, Nguyen, Prados, et al., 2017a, 2017b).

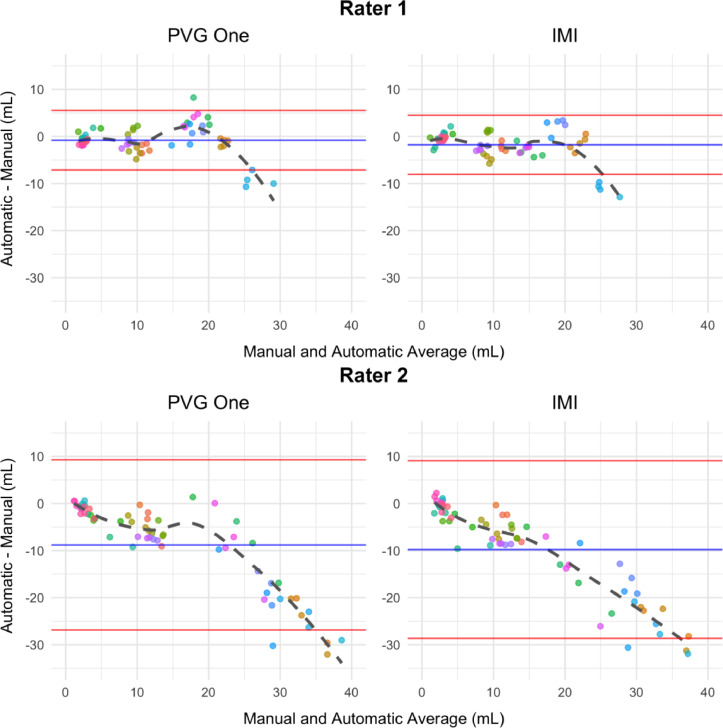
We present data from challengers as Bland-Altman plots (Bland and Altman 2007, 2016) to assess disagreement with manual volumes from the top two performing approaches described in Carass, Roy, Jog, Cuzzocreo, Magrath, Gherman, Button, Nguyen, Prados, et al. (2017a,2017b) (see appendix Table C3). Bland-Altman plots are provided in Figure 1 to compare the automatically generated and manually delineated volumetric measures. This graphical approach presents the differences between techniques, automatic and manual, against the averages of the two. If no points lie outside the limits of agreement, the mean difference plus and minus 1.96 times the standard deviation of the differences, according to classical guidelines this indicates the difference between techniques is not clinically important and the two methods can be used interchangeably.

Figure 1.

Bland-Altman plots using the first (left) and second (right) ranked automatic segmentation methods’ volumes from the 2015 Longitudinal Lesion Challenge are presented. We show plots comparing volumes obtained from the automatic and manual methods. The manual volumes were delineated by rater 1 (top) and rater 2 (bottom). Using the differences, we highlight the mean (blue) plus and minus 1.96 times the standard deviation (red). Each subject is represented in a unique color and each point represents a subject-time point. There are fourteen unique subjects with at least four follow-up imaging sessions.

The plots in Figure 1 show systematic deviations in automatic and manual volumes. Both ranked methods show that as lesion load increases, automatic segmentation approaches underestimate volume compared with rater 1 and rater 2. This is evident by the dashed fitted smooth lines which deviate away from the mean and outside the limits of agreement starting around lesion loads larger than 20 mL in all four of the plots. While the direction of over- or under-estimation and magnitude vary for rater 1 and rater 2 across challenge submissions, each approach shows systematic deviation and bias in volume estimates. Bias in manual segmentation may be due to the inability of raters to objectively delineate the diffuse part of lesions. Supervised automatic approaches require manual segmentations for training, and therefore may be biased in focusing only on the focal portions of lesions ignoring regions of diffuse signal abnormalities near the boundaries of lesions.

The bias present in the volumetric estimates from automatic approaches may be related to the thresholding procedure that segmentation methods apply to probability maps in order to create binary lesion masks. Currently, there are no stand-alone automated approaches for choosing thresholds for segmentation. After probability maps are created, experts may inspect each subject and visually determine a threshold to apply that performs well. Likewise, users may pick a single threshold that generally performs well across all subjects (Sweeney et al., 2013). These two thresholding methods, similar to manual segmentation, introduce human bias, cost, and time into the automated procedure. Several recent publications use cross-validation approaches for determining a threshold to apply to all subjects (see Roy et al., 2015; A. M. Valcarcel, Linn, Vandekar, et al., 2018 for example), but most methods do not provide sufficient detail to reproduce the thresholding approach. Further, these methods propose a group-level threshold rather than subject-specific thresholds.

Using probability maps generated by an automatic segmentation method, we fit the subject-specific threshold that yields the maximum expected Sørensen-Dice similarity coefficient (DSC) (Zijdenbos et al., 1994) based on a naive estimate of lesion volume using a generalized additive model. This approach provides a supervised method to detect a subject-specific threshold for lesion segmentation by attempting to estimate a threshold that optimizes DSC and reduces bias. DSC is defined as the ratio of twice the common area to the sum of the individual areas. That is, $DSC=\frac{2\#\left\{A_1\cap A_2\right\}}{\#\left\{A_1\right\}+\#\left\{A_2\right\}}\in \left[0,1\right]$ where $\#\left\{A\right\}$ denotes the number of voxels classified as lesion in measurement A. After training on a subset of subjects with manual segmentations, the TAPAS model can be applied to estimate a subject-specific threshold to apply to lesion probability maps in order to obtain automatic segmentations. The TAPAS method is fully transparent, fast to implement, and simple to train or modify for new data sets.

Materials and methods

Data and preprocessing

The first data set studied (JHH data) was collected at the Johns Hopkins Hospital in Baltimore, Maryland. This data set consists of 98 subjects with MS, four of which were excluded from our analyses due to poor image quality. Whole-brain 3D T1-weighted (T1), 2D T2-weighted fluid attenuated inversion recovery (FLAIR), T2-weighted (T2), and proton density-weighted (PD) images were acquired on a 3 Tesla (3T) MRI scanner (Philips Medical Systems, Best, The Netherlands). A more detailed description of the acquisition protocol was provided in previously published work (Sweeney et al., 2013; A. M. Valcarcel, Linn, Vandekar, et al., 2018). Manual T2 hyperintense lesion segmentations for each subject were delineated by a neuroradiology research specialist with a Bachelor of Arts in Neuroscience trained in manual segmentation of MS lesions with more than 10 years of experience.

All images were N3 bias corrected (Sled, Zijdenbos, and Evans 1998). The T1 scan for each subject was then rigidly aligned to the Montreal Neurological Institute (MNI) standard template space at 1 mm³ isotropic resolution. FLAIR, PD, and T2 images were then aligned to the transformed T1 image. Extracerebral voxels were removed from all images using the Simple Paradigm for Extra-Cerebral Tissue Removal: Algorithm and Analysis (SPECTRE) algorithm (Carass et al., 2011). MRI scans were acquired in arbitrary units, and therefore analyzing images across subjects required that images be intensity-normalized. We thus intensity normalized each modality using WhiteStripe (Shinohara et al., 2014; Muschelli and Shinohara 2018). All image preprocessing was conducted using tools provided in Medical Image Processing Analysis and Visualization (MIPAV) (McAuliffe et al., 2001), TOADS-CRUISE (http://www.nitrc.org/projects/toads-cruise/), Java Image Science Toolkit (JIST) (Lucas et al., 2010), and Neuroconductor (“Home Neuroconductor” 2018; Muschelli et al., 2018) R (version 3.5.0) (R Development Core Team 2018) packages.

We used a second data resource (BWH data) collected at the Brigham and Women's Hospital in Boston, Massachusetts from 40 subjects with MS. MRI data were consecutively obtained. High-resolution 3D T1, T2, and FLAIR scans of the brain were collected on a Siemens 3T Skyra unit with a 20-channel head coil. The detailed scan parameters have been reported previously (Meier et al., 2018; A. M. Valcarcel, Linn, Khalid, et al., 2018).

T2 hyperintense lesions were manually segmented by a reading panel of two trained observers, referred to here as rater 1 and rater 2, under the supervision of an experienced observer, referred to as rater 3, at the Brigham and Women's Hospital. A lesion was included if it appeared as hyperintense on the FLAIR. Raters 1 and 2 independently marked all MS lesions and then reviewed these results together to form a consensus. In the event of a disagreement, rater 3 was consulted and resolved any differences. After a consensus of marked lesions was determined, rater 1 segmented all lesions to determine their volume using an edge-finding tool in Jim (v. 7.0) (Xinapse Systems Ltd., West Bergholt, UK; http://www.xinapse.com). This process resulted in a manually segmented gold standard lesion mask for each subject in the study. Rater 3 certified the final lesion delineation. Rater 1 had a neuroscience undergraduate degree as well as three years of work experience evaluating MS lesions on MRI scans as a research assistant. Rater 2 had a medical doctorate and four years of experience working in MS MRI research. Rater 3 had a medical doctor degree as well as more than 10 years of experience in MS MRI, initially as a trained research fellow, then serving as a faculty member and image analyst.

We performed N4 bias correction (Tustison et al., 2010) on all images and rigidly co-registered T1 and T2 images for each participant to the corresponding FLAIR at 1 mm³ resolution. Extracerebral voxels were removed from the registered T1 images using Multi-Atlas Skull Stripping (MASS) (Doshi et al., 2013) and the brain mask was applied to the FLAIR and T2 scans. We intensity-normalized images to facilitate across-subject modeling of intensities using WhiteStripe (Shinohara et al., 2014; Muschelli and Shinohara 2018). Image preprocessing was applied using software available in R (version 3.5.0) (R Development Core Team 2018) and from NITRC (https://www.nitrc.org/projects/cbica_mass/).

The Institutional Review Boards at the appropriate institutions approved these studies.

TAPAS algorithm

Although the two data sets were processed using different pipelines, the proposed technique is completely independent of the preprocessing pipeline. We applied the BWH preprocessing pipeline to the JHH data and re-ran the analyses; we present these results in the supplemental materials. TAPAS simply relies on a continuous map of degree or probability of lesion at each voxel in the brain. Maps are generated by an automatic segmentation algorithm in order to predict a subject-level threshold for segmentation. In our experiments, we used the predicted lesion probability maps from a Method for Inter-Modal Segmentation Analysis (MIMoSA) (A. M. Valcarcel, Linn, Vandekar, et al., 2018; A. M. Valcarcel, Linn, Khalid, et al., 2018), an automatic segmentation procedure. We also implemented the lesion prediction algorithm (LPA) (version 2.0.15) using the lesion segmentation tool (LST), an open source toolbox for statistical parametric mapping (SPM) (version 12) in MATLAB R2019a (Schmidt et al., 2012). In the supplemental materials, we provide results obtained from using LST-LPA as the automatic segmentation algorithm.

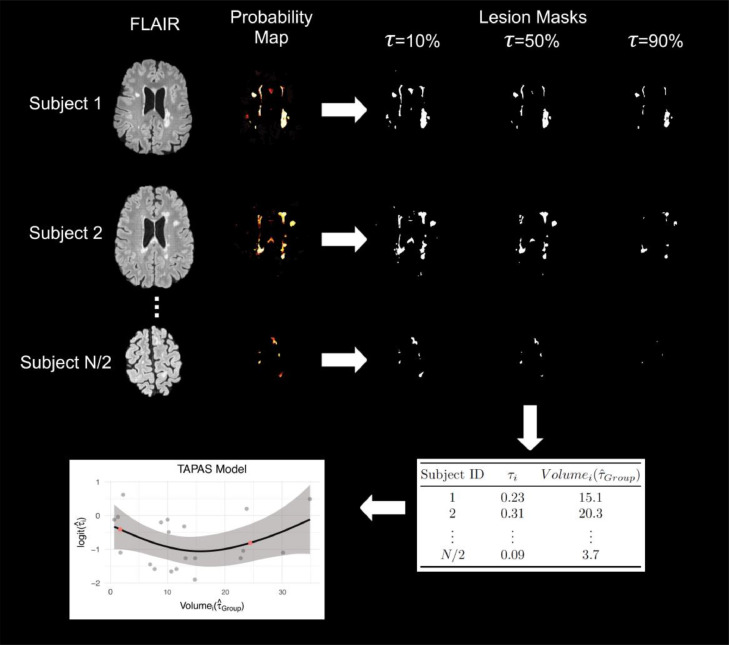
We first divide the data set under study into two parts: the first is used for training TAPAS, and the second we refer to as the test set. In each subject in the training set of size N/2, we apply a grid of thresholds τ ∈ {τ₁, ..., τ_J}, denoted as τ, to the probability map in order to generate estimated lesion segmentation masks. The estimated lesion segmentation masks are binary masks indicating estimated lesion presence or absence generated for each threshold in τ. Figure 2 shows an example of these lesion masks at 10%, 50%, and 90%. For each subject in the training set we initially let τ vary from ${\tau }_1=0\%$ to ${\tau }_J=100\%$ in 1% increments and calculate DSC between each estimated segmentation mask and the corresponding manual segmentation for the image. We then estimate:

• 1${\widehat{\tau }}_{Group}=\underset{\tau \in \left\{{\tau }_1,...,{\tau }_J\right\}}{\text{argmax}}\frac{2{\sum }_{i=1}^{N/2}DS{C}_i\left(\tau \right)}{N}$, and
• 2${\widehat{\tau }}_i=\underset{\tau \in \left\{{\tau }_1,...,{\tau }_J\right\}}{\text{argmax}}\left\{DS{C}_i\left(\tau \right)\right\}$ for each subject i.

Figure 2.

The TAPAS procedure is shown using sample axial slices from the data. A set of training scans with manual delineations were used to train and apply MIMoSA in order to obtain probability maps. For each subject's probability map, we applied thresholds at $\tau =0\%$ to 100% by 1% to create estimated lesion masks. For simplicity, in this example, we have only shown $\tau =10\%$, 50%, and 90%. Based on Sørensen-Dice similarity coefficient (DSC) calculations within and across subjects we estimated ${\widehat{\tau }}_i$ and ${\widehat{\tau }}_{Group}$. Using ${\widehat{\tau }}_{Group}$ we obtained $volum{e}_i\left({\widehat{\tau }}_{Group}\right)$. We fit the TAPAS model and applied it to subjects in the test set to determine ${\widehat{\tau }}_i$. Red points in the plot represent ${\widehat{\tau }}^{0.1}$ and ${\widehat{\tau }}^{0.9}$, or lower and upper bounds at the volume associated with the 10th and 90th percentiles, respectively.

The threshold estimated by ${\widehat{\tau }}_{Group}$ represents the threshold that produces maximum average DSC across all subjects in the training set, and ${\widehat{\tau }}_i$ is defined as the subject-specific threshold that yields maximum DSC for subject i. In practice, we suggest initially using a threshold grid of ${\tau }_1=0\%$ to ${\tau }_J=100\%$ in 1% increments but based on training refine the grid to be more sensitive to the data.

In the event of a tie among thresholds that maximize DSC we first ensure these tied thresholds are adjacent and then select the median threshold. In our analyses all ties were in fact adjacent. If ties are not adjacent, we suggest enlarging the threshold region and repeating the analysis. In addition, we repeat the optimization minimizing absolute error (AE) rather than maximizing DSC since DSC can be biased for patients with low lesion load. These results are presented in the supplemental materials. It is also possible this step could be implemented using an optimization framework and may result in a reduction in computation time, but we did not validate other optimization approaches.

We apply ${\widehat{\tau }}_{Group}$ to each respective subject and obtain a naive estimate of the volume, $volum{e}_i\left({\widehat{\tau }}_{Group}\right)$. We then regress $logit\left({\widehat{\tau }}_i\right)$ on $volum{e}_i\left({\widehat{\tau }}_{Group}\right)$ using a generalized additive model with an identity link function and a normal error. The generalized additive model was chosen over linear models after manual inspection of scatter plots indicated non-linear trends. This is evident in the scatter plot displayed in the bottom left panel of Figure 2 as the scatter plot presented in this example case does not appear linear but quadratic. This held true for not just this example case but most cross-validation iterations. We use an identity link function since both ${\widehat{\tau }}_i$ and $volum{e}_i\left({\widehat{\tau }}_{Group}\right)$ are continuous. The identity link does not bound the outcome ${\widehat{\tau }}_i$ between 0 and 1; so, rather than modeling ${\widehat{\tau }}_i$, we model $logit\left({\widehat{\tau }}_i\right)$ to force ${\widehat{\tau }}_i$ to be between 0 and 1. We implement the generalized additive model using the gam function available through the mgcv package in R. This function fits the model using a penalized scatter-plot smoother with thin-plate splines and smoothing parameter estimated using generalized cross-validation (Wood 2003, n.d., 2004; Wood, Pya, and Säfken 2016). More specifically, the following generalized additive model is fit as the TAPAS model:

$$logit\left({\widehat{\tau }}_i\right)=f_1\left(volum{e}_i\left({\widehat{\tau }}_{Group}\right)\right)+{ϵ}_i$$

where ${ϵ}_i\sim N\left(0,{\sigma }^2\right)$.

In the model fitting procedure, we exclude subjects from model training if their ${\widehat{\tau }}_i$ produces an estimated segmentation mask with DSC < 0.03. We found this to empirically improve TAPAS performance as it removes subjects for which even the best performing ${\widehat{\tau }}_i$ yields an inaccurate automatic segmentation mask.

After the TAPAS model is fit, we apply the model to subjects in the testing set. For each subject i, we obtain a probability map from an automatic segmentation procedure. We then use ${\widehat{\tau }}_{Group}$ to threshold the probability map in order to estimate $volum{e}_i\left({\widehat{\tau }}_{Group}\right)$. We use these predicted volumes in the TAPAS model to estimate the fitted value $logit\left({\widehat{\tau }}_i\right)$, from which we can obtain the estimated subject-specific threshold. The probability maps are then re-thresholded using ${\widehat{\tau }}_i$ to generate the lesion segmentation masks.

When applying the TAPAS model in the testing set, we aim to reduce extrapolation and excessive variability associated with left and right tail behavior of the spline model. Thus, for any volume we obtain using ${\widehat{\tau }}_{Group}$ that is larger than the volume at the 90th percentile, we use the threshold for the subject whose volume is at the 90th percentile, denoted ${\widehat{\tau }}^{0.9}$, rather than the fitted ${\widehat{\tau }}_i$. Similarly, for any volume we obtain from ${\widehat{\tau }}_{Group}$ that is smaller than the volume at the 10th percentile, we use the value of ${\widehat{\tau }}^{0.1}$. Figure 2 shows an outline of the full TAPAS procedure and model.

To implement TAPAS, we developed an R package that is available with documentation on GitHub (https://github.com/avalcarcel9/rtapas) and Neuroconductor (https://neuroconductor.org/package/rtapas).

Performance assessment

For the two data sets in this study (JHH and BWH), we ran separate Monte Carlo-resampled split-sample cross-validations. More specifically, we repeatedly randomly sampled subjects (100 times) without replacement to assign half of the subjects in the study to each of the training and testing sets. Each iteration therefore contained a unique set of subjects to train TAPAS and a separate set of subjects to test the algorithm's performance. The Monte Carlo-resampled split-sample cross-validation analysis assures that the proposed algorithm does not provide significantly different lesion volume estimations when different trained regression models are used. In each training set, we applied MIMoSA using the R package mimosa (A. Valcarcel 2018) available on Neuroconductor (https://neuroconductor.org/package/mimosa) (Muschelli et al., 2018). After fitting the MIMoSA model using subjects in the training set, we generated probability maps for all subjects in the training and testing sets.

In each split-sample experiment, the training set was used to fit the TAPAS model and the testing set applied the TAPAS model to determine a subject-specific threshold ${\widehat{\tau }}_i$. This subject-specific threshold was used to create binary lesion segmentation masks and calculate lesion volume. In the BWH data, we found using a threshold grid ranging from ${\tau }_1=0\%$ to ${\tau }_J=100\%$ in 1% increments to be too wide in initial experiments. Therefore, we refined the threshold grid range from ${\tau }_1=13\%$ to ${\tau }_J=54\%$ in 0.4% increments. We compared the TAPAS, group, and manually generated masks and volumes using the subscripts TAPAS, Group, and Manual respectively. The use of ${\widehat{\tau }}_{Group}$ to threshold probability maps and generate lesion segmentations was previously applied (A. M. Valcarcel, Linn, Vandekar, et al., 2018; A. M. Valcarcel, Linn, Khalid, et al., 2018) and aided in automatic segmentation measures compared to user-defined threshold application. In addition to calculating volume from TAPAS, group, and manual lesion masks we also calculate partial volume denoted with the subscript Partial. We define partial volume as the sum of the voxel-level probabilities from the probability map generated by MIMoSA. Calculating partial volume does not require thresholding. Rather than applying a hard threshold to estimate lesion volume, we hypothesize that it may be more advantageous to compute total lesion burden using thecontinuous measures from probability maps. These partial volumes may yield stronger correlations with clinical outcomes.

We provide quantitative comparisons between TAPAS and the group thresholding procedure for subjects in the testing set. First, to assess whether segmentation masks produced using TAPAS or the group thresholding procedure differed in accuracy as measured by DSC, we compared segmentations between lesion masks produced by TAPAS (DSC_TAPAS) and those produced by the group thresholding procedure (DSC_Group) with manual segmentations. We compared these measures using a paired t-test within each split-sample experiment using subjects in the test set. Second, to assess bias and inaccuracy present in volume_TAPAS and volume_Group we calculated absolute error defined as $AE=\left|ThresholdVolume-ManualVolume\right|$. In order to determine whether AE differed statistically, paired t-tests were conducted between AE_TAPAS and AE_Group within each split-sample experiment. Third, to adjudicate whether TAPAS yielded volumetrics with similar phenotype associations, we calculated the Spearman's correlation coefficient between volume_TAPAS, volume_Group, volume_Partial, and volume_Manual and clinical variables. We denote these correlations by ${\widehat{\rho }}_{TAPAS}$, ${\widehat{\rho }}_{Group}$, ${\widehat{\rho }}_{Partial}$, and ${\widehat{\rho }}_{Manual}$, respectively. We estimated correlations in each split-sample experiment and averaged across experiments.

Expert validation

In addition to the Monte Carlo-resampled split-sample cross-validations, 3 board-certified neurologists with subspecialty training in neuroimmunology compared segmentations produced using TAPAS and the group thresholding approach. For each subject (40 subjects from BWH data and 94 subjects from JHH data), we randomly selected a cross-validation iteration in which they were included as a test set subject and therefore have segmentations produced from TAPAS and the group thresholding procedure to present to the raters. We randomly assigned the order in which the subjects were presented to the expert rater. Additionally, we randomly assigned each segmentation a letter (A or B) so as to blind the rater to the segmentation algorithm.

We presented each of the 134 MRI studies to the experts individually. For each study, the expert rater was presented with the set of two segmentations overlaid onto the FLAIR along with each of the MRI contrasts simultaneously. For BWH data this included FLAIR, T1, and T2 imaging modalities, while for the JHH data this included FLAIR, T1, T2, and PD imaging modalities. The expert was then asked, “Evaluate how well each of the two segmentations depicts your impression of the extent of the white matter abnormality in the image displayed.” Ratings were given on a scale of 1-to-5 scale with labels of “1 - Excellent”, “2 - Good”, “3 - Fair”, “4 - Poor”, “5 – Very Poor”. Ratings were given independently, with no discussion by raters occurring during the rating process.

Results

Demographics

JHH and BWH participant demographics are included in Table 1. In the JHH data, disease duration was defined as years since diagnosis and participants were examined by a neurologist to assess Expanded Disability Status Scale (EDSS) score. In the BWH data, disease duration was defined as years since first symptom. In order to assess the level of physical ability and ambulatory function in the BWH data, an MS neurologist examined patients to evaluate Expanded Disability Status Scale (EDSS) and timed 25-foot walk (T25FW) (in seconds).

Table 1.

Demographic information for subjects in this study are provided. We include information from 94 patients imaged at the Johns Hopkins's Hospital (JHH) and 40 patients imaged at the Brigham and Women's Hospital (BWH).

JHH (n = 94)	Statistics presented: mean (SD, min, max); %
Age (years)	43.4 (12.3, 21.4, 67.3)
Disease duration (years)	11.3 (9.2, 0, 45)
Expanded Disability Status Scale score	3.9 (2.1, 0, 8)
Lesion volume (mL)	11.5 (13.1, 0, 77)
Female	73
Clinically isolated syndrome	1
Primary progressive	10
Relapsing-remitting MS	64
Secondary progressive MS	25
BWH (n = 40)
Age (years)	50.4 (9.9, 30.4, 69.9)
Disease duration (years)	14.5 (4.6, 3.8, 21.3)
Expanded Disability Status Scale score	2.3 (1.6, 0, 7)
Lesion volume (mL)	13.6 (12.8, 0.6, 52)
Timed 25-ft walk (seconds)	11.5 (6.9, 1, 25)
Female	70
Relapsing-remitting MS	80
Secondary progressive MS	20

Volumetric bias assessment

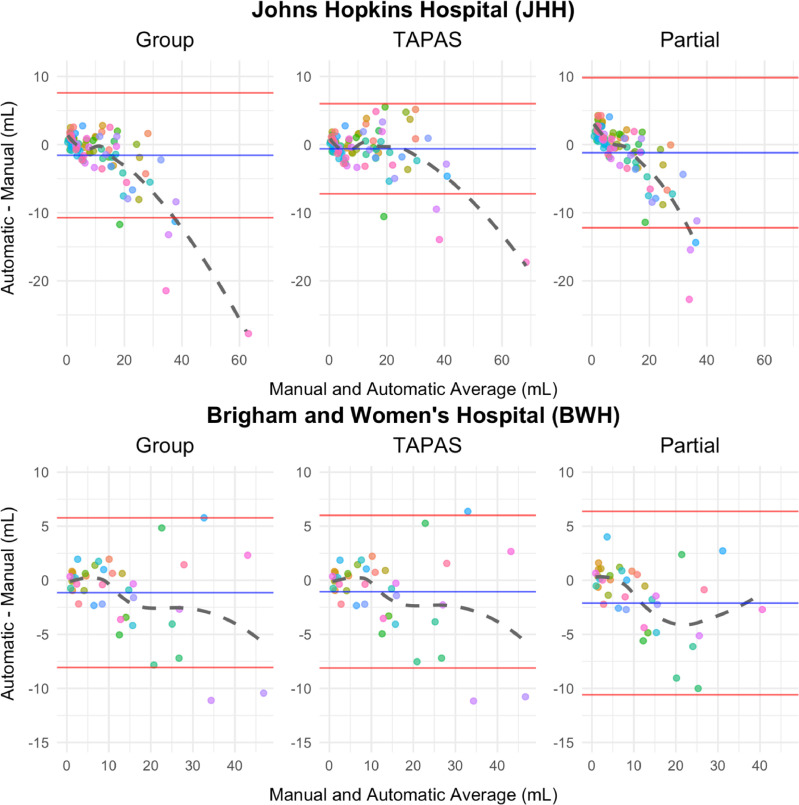
Using Bland-Altman visualization, we compare automatic and manual volumes in addition to the partial volume estimates in Figure 3. Subject-level volumes were obtained by averaging each subject's measurement for all split-sample experiments in which it was allocated to the testing set. The JHH data volume_Group estimate exhibits systematic bias, evident in Figure 3, for volumes exceeding 20 mL. Visually, we observed a moderate inverse relationship in these subjects. This indicates that volume_Group under-estimates volume_Manual in subjects with larger lesion loads with increasing magnitude. The JHH data volume_Partial estimate also exhibits systematic bias using Figure 3. For subjects with small lesion load, volume_Partial over-estimates volume_Manual whereas for subjects with moderate and large lesion load volume_Partial under-estimates volume_Manual. Unlike the Group Bland-Altman plot, the TAPAS plot does not exhibit obvious patterns of systematic bias. The cluster of points that begins to negatively deviate from 0 in the Group plot is still centered randomly around 0 in the TAPAS plot. Additionally, the mean and standard deviation for the differences are smaller using volume_TAPAS compared to volume_Group and volume_Partial. There are four points that lie outside the limits of agreement in both thresholding procedures, but in the TAPAS plot these are closer to 0.

Figure 3.

Bland-Altman plots comparing volume_Manual with volumes obtained using automatic approaches (volume_Group, volume_TAPAS, and volume_Partial) are shown. The mean of the difference in volume is presented in blue and the mean plus and minus the standard error is shown in red. Each point represents a unique subject. Subject-specific points were obtained by averaging results across test set subjects in each split-sample fold.

The BWH Bland-Altman plots are nearly identical and almost indistinguishable when comparing the group threshold procedure with the TAPAS outputs. There does not appear to be a systematic bias in either volume_Group or volume_TAPAS estimates since points are randomly scattered around 0 in the positive and negative directions. This exemplifies TAPAS's propensity to conserve unbiased estimates when systematic bias is absent. The Bland-Altman plot calculated using volume_Partial shows all points lie within the limits of agreement but they are not randomly scattered around the mean difference. For small lesion loads, the points cluster above the mean line and show a negative association as in the JHH data.

Absolute error assessment

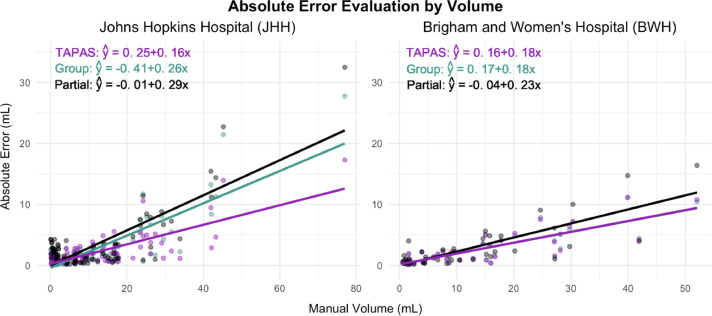
Scatter plots and their corresponding predicted linear models are presented in Figure 4 to compare AE_TAPAS, AE_Group, and AE_Partial with volume_Manual. The JHH data plot shows smaller AE estimates associated with volume_TAPAS compared to volume_Group and volume_Partial. This is highlighted by the negative shift in AE_TAPAS points throughout as well as a smaller slope estimate (provided in the top left corner of the figure). The JHH data point with volume_Manual larger than 70 mL is influential (Cook's distance was larger than 1) for both the group, TAPAS, and partial fitted models. However, removing this point, volume_TAPAS still shows larger reductions in AE compared to volume_Group. The coefficient associated with AE_Partial is 0.29 and AE_Group is 0.26 while the coefficient associated with AE_TAPAS is 0.16. This means that for a 1 mL increase in volume_Manual, the predicted change in AE is 0.1 mL less when using TAPAS compared to the group thresholding procedure. The reduction in AE associated with using TAPAS over the group thresholding procedure is on the order of magnitude of average differences found in clinical trial evaluations of MS therapies (see, for example, Barkhof et al. (2007)). In the BWH data, all values are remarkably similar across TAPAS and the group thresholding approach. The partial volume leads to notably larger predicted absolute error. The results in Figure 3 and Figure 4 are consistent and indicate that TAPAS performs at least as well as or better than the group thresholding procedure in terms of reducing bias in lesion volume estimates.

Figure 4.

Scatter plots with fitted linear models are presented for the subject-level average absolute error ($\widehat{y}$) on manual volume (x) in mL. Fitted equations are given in the top left corner.

Comparing the two thresholding approaches more rigorously we found the average AE_TAPAS across subjects in the testing sets and iterations in the JHH data is 2.09 mL compared to 2.62 mL from AE_Group and 3.29 mL from AE_Partial. In the BWH data, average AE_TAPAS and AE_Group were both found to be 2.62 mL and average AE_Partial was 3.17 mL. TAPAS yields equal or reduced average AE. The average DSC_TAPAS across subjects in the testing sets and iterations in the JHH data is 0.61 compared to 0.6 from DSC_Group. In the BWH data, the average DSC_TAPAS is 0.67 while average DSC_Group is 0.66. TAPAS yields equal or superior average DSC. We do not report DSC_Partial as the partial volume is calculated from the probability maps rather than the lesion segmentation masks and binary segmentations are required to calculate DSC.

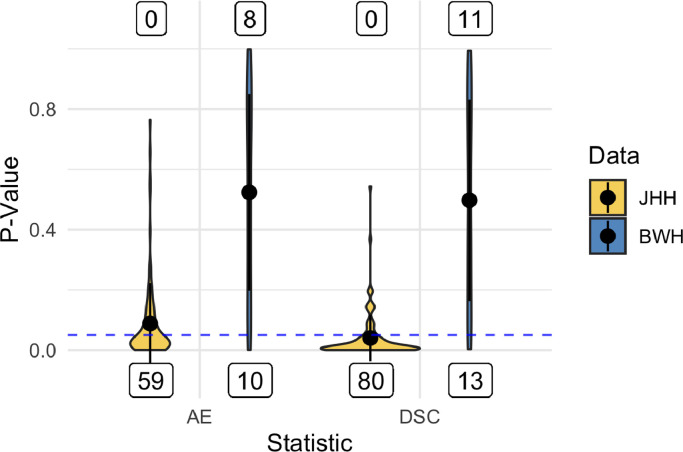
To examine this statistically, we employed one-sided paired t-tests to evaluate AE and DSC from TAPAS compared with those obtained from the group thresholding procedure. Figure 5 shows violin plots of p-values from both sets of tests for the two data sets. In the JHH data more than half of the split-sample experiments resulted in p-values below the $\alpha =0.05$ for AE and DSC with no statistically significant results favoring the group thresholding procedure. This indicates superior performance using TAPAS compared to the group thresholding procedure. The BWH data was more uniform with approximately equal statistically significant results favoring TAPAS and the group thresholding procedure.

Figure 5.

Violin plots of p-values from paired t-tests to compare subject-level absolute error (AE) and Sørensen-Dice coefficient (DSC) in each test set are presented. The mean for each statistic and data set is presented as points within each violin plot and the black lines extend the mean by the standard deviation. Labels below represent the number of significant p-values favoring TAPAS performance measures. Labels above represent the number of significant p-values favoring group thresholding performance. The dashed horizontal blue line highlights the $\alpha =0.05$ cutoff.

Correlation analysis

We assessed the relationship between volume_TAPAS, volume_Group, volume_Partial, and volume_Manual with various clinical variables. These results are provided in Table 2. All correlations found are modest but align with previously published literature (A. M. Valcarcel, Linn, Khalid, et al., 2018; Stankiewicz et al., 2011; Barkhof 1999; Tauhid et al., 2014). In the JHH data, ${\widehat{\rho }}_{TAPAS}$ and ${\widehat{\rho }}_{Group}$ are indistinguishable from each other and slightly larger than ${\widehat{\rho }}_{Partial}$ and ${\widehat{\rho }}_{Manual}$. Similarly, the BWH data show identical ${\widehat{\rho }}_{TAPAS}$ and ${\widehat{\rho }}_{Group}$ nearly equivalent to ${\widehat{\rho }}_{Partial}$ and ${\widehat{\rho }}_{Manual}$. In terms of phenotypic associations volume_TAPAS yielded similar correlation estimates as volume_Group, volume_Partial, and volume_Manual.

Table 2.

Subject-specific volume estimates, volume_Manual (Manual), volume_TAPAS (TAPAS), volume_Group (Group), and volume_Partial (Partial), were compared with clinical covariates available from the data collected at the Johns Hopkins Hospital (JHH) and the Brigham and Women's Hospital (BWH) and are represented in this table. Spearman's correlation coefficient (ρˆ) was obtained in the testing set for each iteration and averaged across folds. Clinical variables included Expanded Disability Status Scale (EDSS) score, disease duration in years, and timed 25-ft walk (T25FW) in seconds.

Estimates for ρˆ
	Partial	Group	TAPAS	Manual
JHH
EDSS	0.32	0.34	0.34	0.29
Disease duration	0.37	0.39	0.39	0.39
BWH
EDSS	0.42	0.43	0.43	0.45
Disease duration	0.31	0.32	0.32	0.29
T25FW	0.02	0.02	0.02	0.03

Threshold evaluation

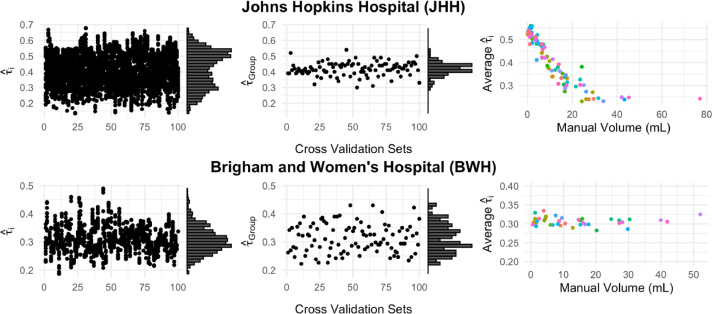
In Figure 6 we present scatter plots of the thresholds predicted in the testing set from both TAPAS and the group threshold procedure. There are a few notable differences between the threshold scatter plots produced from TAPAS and those produced by the group thresholding procedure. In both data sets the subject-specific thresholds have a much wider range than the group thresholds. In the JHH data, the distribution shape is bi-modal for the subject-specific thresholds but uni-modal for the group thresholds. In the BWH data, the distribution shape is similar between the two thresholding approaches.

Figure 6.

Scatter plots of the subject-specific threshold ${\widehat{\tau }}_i$ (TAPAS) and ${\widehat{\tau }}_{Group}$ (group thresholding procedure) on cross-validation number are presented with marginal histograms for both data sets in the first two columns. The third column presents scatterplots of the average subject-specific thresholds from TAPAS and the manually delineated lesion volume.

We also present average subject-specific thresholds plotted against the manual volumes in mL. In the JHH data, the average TAPAS threshold decreases as manual volume increases. The thresholds plateau after manual volume of 20 mL and similar thresholds are detected for all lesion loads greater than 20 mL. In the BWH data we see the points are randomly scattered and there is no apparent association between average subject-specific threshold and manual volume.

Qualitative results

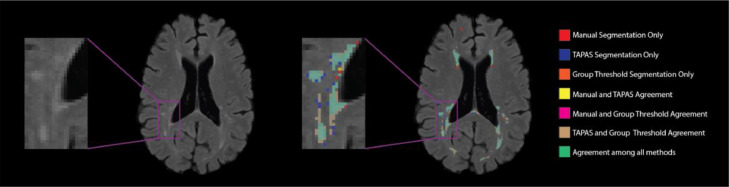
We present segmentations from the TAPAS and the group threshold approach as well as manual delineations in Figure 7. This figure shows that TAPAS and the group thresholding procedure generally agree with the manual segmentation. Some tissue was manually segmented and not detected by either thresholding algorithm. The major differences between all the methods are found at the boundaries of lesions, which are known to be difficult to discern for both automatic and manual approaches. Overall, the automatic segmentation algorithm paired with either thresholding approach is able to detect the majority of lesional space with few false positives.

Figure 7.

T2 hyperintense lesion segmentations from an example axial slice are displayed. The colors represent the different individual or overlapping segmentations obtained from manual, TAPAS threshold, and group threshold masks. The majority of segmented area was in agreement among all lesion masks (green). Both the group thresholding approach and TAPAS missed some area that was manually segmented (red). There was a small area where only TAPAS and manual segmentations agreed (yellow), but almost no area where only the group threshold agreed with the manual segmentation (fuchsia).

Rater study

The mean rating for TAPAS segmentations for each rater was 1.87 (SD=0.81), 2.72 (SD=0.94), and 3.10 (SD=1.14). The mean rating for the group thresholding approach for each rater was 1.92 (SD=0.81), 2.66 (SD=0.97), and 3.10 (SD=1.14). The mean rating across the three raters for both TAPAS and the group thresholding approaches was 2.56 (SD = 1.10). Raters evaluated how well each of the two segmentations depicted the extent of the white matter abnormality in the images displayed. An overall average score between 2 and 3 indicated therefore that the segmentations produced from either method are between fair and good quality. The three raters responded favorably to the segmentations.

77% of the studies resulted in the same rating between TAPAS and the group threshold segmentations. 12% of the studies resulted in raters ranking the TAPAS segmentation more favorably than the group threshold segmentation whereas 11% of the studies resulted in raters favoring group threshold segmentation.”

Though both thresholding approaches were trained using manual segmentations, the gold standard approach, we and our expert raters believe the resulting segmentations from the automatic approaches do in fact capture the extent of white matter abnormality in the brain fairly well.

Computation Time

The TAPAS thresholding procedure is easily implemented using the rtapas R package available with documentation on GitHub (https://avalcarcel9.github.io/rtapas/). The model is supervised and must be trained. All benchmarking was done on a 2017 MacBook Pro with 3.1 GHz Intel Core i5 and 16GB of memory using a single core. To benchmark, a single subject with voxel size 1 mm³ was used. Before training the TAPAS model, the training data must be generated and takes approximately 20 minutes per subject. This process is parallelizeable through the package to decrease computation time. The model itself takes less than a second to train. After a model has been fit, a single test subject's prediction data and segmentation mask can be generated in about 30 seconds.

Most automatic segmentation algorithms produce continuous maps of lesion likelihood, which are subsequently thresholded to create binary lesion segmentation masks. While a number of automatic approaches exist for lesion segmentation, there are few automatic algorithms available for threshold selection. Thresholds are commonly chosen using cross-validation procedures conducted at the group level, or arbitrarily through subjective human input. This introduces variability and biases in automatic segmentation results. Furthermore, thresholding approaches often apply a single common threshold value to all subjects’ probability maps. This lack of subject specificity may lead to inaccuracy in lesion segmentation masks, especially in subjects with the smallest and largest lesion loads.

This study sought to address these issues by introducing a supervised fully automated algorithm for subject-specific threshold prediction that also reduces volumetric bias if present. The TAPAS procedure is easily implemented and performs well on data acquired with different scanning protocols or pre-processed with different pipelines. We validated TAPAS in two unique data sets from different imaging centers using 3T MRI scanners from different vendors. In the supplemental material we applied a different preprocessing pipeline to the JHH data and found TAPAS outperforms the group thresholding procedure even under varying processing.

The TAPAS procedure is a supervised fully automated thresholding approach that determines a subject-specific threshold to apply to continuous maps (including predicted probability maps) for automatic lesion segmentation. TAPAS volume estimates are accurate and reduce systematic biases associated with differential total lesion load when present. In the JHH data, we observed such a bias using the MIMoSA algorithm, which was mitigated using TAPAS.

The BWH data used a consensus approach with two trained raters to manually segment lesions consulting a third rater in the event of a disagreement. We believe this approach reduces intra- and inter-rater variability normally present with a single rater and allows for a closer approximation of the ground truth, and, thus, better training of automatic approaches. The Bland-Altman plots in these data indicate unbiased estimation using a group threshold or TAPAS. In this study, we showed that without systematic biases TAPAS preserves the unbiased volumetric estimation of the automated segmentation technique.

In clinical trial evaluations of therapeutic efficacy, associations between clinical variables and lesion volume are of primary interest. This study shows that TAPAS and group threshold volumes resulted in similar correlations to clinical variables as the manual volume. Therefore, the automatic segmentations produced after thresholding, using either TAPAS or group thresholding, should be as sensitive to image-phenotype correlations as manual measures. Correlations were thus estimated to compare volume_Manual, volume_TAPAS, and volume_Group with clinically relevant variables. The results indicate the correlations between respective volumes and clinical variables are all approximately equal. Agreement across the thresholding methods with manual measures advocates for the use of TAPAS to reduce cost and time while providing a subject-specific threshold.

Currently, available assessments of lesion volume are weakly correlated with clinical outcomes. This may be in part due to discarding voxels with low estimated probability of containing lesion, mostly around the edges of lesions, that may capture signal. The partial volume computed in this analysis was an attempt to include these voxels in the calculation of volume in the hopes of reducing biases and providing a metric that correlates better with clinical assessments. Unfortunately, these partial volumes did not yield stronger correlations with clinical outcomes and showed more bias compared to volumes computed with a threshold. These methods have not been assessed in clinical trials to date, and additional studies and methodological innovations are warranted.

TAPAS is a post-hoc subject-specific threshold detection algorithm built to reduce volumetric bias associated with automatic segmentation procedures. In this study, we optimized TAPAS using DSC in this main text and AE in the supplemental material provided. Both optimizations favor TAPAS over group thresholding with DSC having more dramatic improvements than AE. Though DSC can be biased or under-estimate true accuracy in subjects with low lesion load, we find it performs well compared to AE. Automatic approaches are constantly being built and improved upon to yield more accurate and robust methods. TAPAS allows for improvement upon even the most accurate and robust automatic segmentation procedures with no observed addition of error. Beyond MS or MRI, this methodology can be used for automatic segmentation of other tissues or body parts using different imaging types after proper validation.

We initially ran all cross-validation settings with a threshold grid ranging from 0% to 100% in 1% increments. In certain settings, these increments were too large which led to sub-optimal TAPAS models. We refined threshold grids in these settings and found improved performance. Due to the iterated nature of cross-validations, we chose to use one threshold grid for the entire set of cross-validation folds (100). In practice, data will likely consist of a training and testing set. We suggest applying the original threshold grid, 0% to 100% by 1% increments, and evaluating model fit through subject-specific threshold selection in the training and testing data in order to inform the selection of a finer grid. The grid should be updated until results are stable. We believe this will lead to optimal performance.

There are several notable limitations to the proposed algorithm. First, the method must be used in conjunction with continuous maps of likelihood of lesion, so investigators must use automatic approaches that generate these maps for adaptive thresholding. Second, since the TAPAS model fits a generalized additive model, training data sets with small sample size, uniform lesion load, or those dissimilar from testing data may result in poor model fit or inappropriate threshold estimation. For example, when we applied TAPAS to the 2015 Longitudinal Lesion Challenge data we found poor model fit associated with fitting a generalized additive model to data that only included 5 unique subjects for training. To apply TAPAS to longitudinally acquired data, such as those presented in the 2015 segmentation challenge, a sufficiently large sample of subjects with variable lesional volume is required.

Atrophy of the brain and spinal cord are key measures of disease progression in MS and may be more closely associated with clinical status than lesion volume (Sanfilipo et al., 2006; Fisher et al., 2008; Fisniku et al., 2008; Keshavan et al., 2016; Bakshi et al., 2008). It is important to note that TAPAS is easily extended or applied to settings in which brain volumes are estimated. Many segmentation methods for structures other than lesions, for example the thalamus which is of key interest in MS presently (Fadda et al., 2019; Neema et al., 2009; Oh et al., 2019), also use thresholding to determine binary segmentations and volumes. Future work will include assessments of whether biases such as those studied in this paper exist for atrophy assessments and techniques for their mitigation.

Future developments will also include specialized methods for the analysis of longitudinal lesion volumetrics. Additionally, to investigate the repeatability of this study and stability of the algorithm we will implement the method on scan-rescan data to evaluate reliability of the subject-specific probability and lesion volume estimation. It is possible that the underlying method may benefit from dynamic thresholds for smaller lesions and larger lesions even within the same subject. That is, we may need to move beyond even a subject-specific threshold since, when a subject has larger lesions, the error associated with those lesions contributes more to the DSC metric than the same relative error associated with smaller lesions. There may thus be a tendency of TAPAS to better segment larger lesions at the cost of doing worse on smaller lesions.

CRediT authorship contribution statement

Alessandra M. Valcarcel: Conceptualization, Methodology, Software, Validation, Formal analysis, Data curation, Writing - original draft, Writing - review & editing, Visualization, Project administration. John Muschelli: Conceptualization, Methodology, Software. Dzung L. Pham: Writing - review & editing, Funding acquisition. Melissa Lynne Martin: Validation, Writing - review & editing, Visualization. Paul Yushkevich: Writing - review & editing, Funding acquisition. Rachel Brandstadter: Writing - review & editing. Kristina R. Patterson: Writing - review & editing. Matthew K. Schindler: Writing - review & editing. Peter A. Calabresi: Investigation, Resources, Data curation. Rohit Bakshi: Investigation, Resources, Data curation. Russell T. Shinohara: Supervision, Funding acquisition.

Declaration of competing interest

Ms. Alessandra Valcarcel has nothing to disclose. Dr. John Muschelli has nothing to disclose. Dr. Dzung Pham has nothing to disclose. Ms. Melissa Martin has nothing to disclose. Dr. Paul Yushkevich has nothing to disclose. Dr. Kristina Patterson has served on the advisory board for Alexion. Dr. Peter Calabresi has received personal consulting fees for serving on SABs for Biogen and Disarm Therapeutics. He is PI on grants to JHU from Biogen, Novartis, Sanofi, Annexon and MedImmune. Dr. Rohit Bakshi has received consulting fees from Bayer, Biogen, Celgene, EMD Serono, Genentech, Guerbet, Sanofi-Genzyme, and Shire and research support from EMD Serono and Sanofi-Genzyme. Dr. Russell (Taki) Shinohara has received consulting fees from Genentech and Roche.