Abstract
Living organism is an intelligent system coded by hierarchically-organized information to perform precisely-controlled biological functions. Biophysical models are important tools to uncover the design rules underlying complex genetic-metabolic circuit interactions. Based on a previously engineered synthetic malonyl-CoA switch (Xu et al., PNAS, 2014), we have formulated nine differential equations to unravel the design principles underlying an ideal metabolic switch to improve fatty acids production in E. coli. By interrogating the physiologically accessible parameter space, we have determined the optimal controller architecture to configure both the metabolic source pathway and metabolic sink pathway. We determined that low protein degradation rate, medium strength of metabolic inhibitory constant, high metabolic source pathway induction rate, strong binding affinity of the transcriptional activator toward the metabolic source pathway, weak binding affinity of the transcriptional repressor toward the metabolic sink pathway, and a strong cooperative interaction of transcriptional repressor toward metabolic sink pathway benefit the accumulation of the target molecule (fatty acids). The target molecule (fatty acid) production is increased from 50% to 10-folds upon application of the autonomous metabolic switch. With strong metabolic inhibitory constant, the system displays multiple steady states. Stable oscillation of metabolic intermediate is the driving force to allow the system deviate from its equilibrium state and permits bidirectional ON-OFF gene expression control, which autonomously compensates enzyme level for both the metabolic source and metabolic sink pathways. The computational framework may facilitate us to design and engineer predictable genetic-metabolic switches, quest for the optimal controller architecture of the metabolic source/sink pathways, as well as leverage autonomous oscillation as a powerful tool to engineer cell function.
Keywords: Autonomous oscillation, Metabolic switches, Biophysical models, Controller architecture, Metabolic engineering, Synthetic biology
Highlights
-
•
Metabolic engineer can engineer both the chemistry and control modules in the cell.
-
•
9 differential equations used to define a previously engineered malonyl-CoA switch.
-
•
Optimal control architecture of metabolic source and sink pathways were determined.
-
•
Models were used to unravel the design principles underlying an ideal metabolic switch.
-
•
Stable oscillation of metabolic intermediates permits alternating ON-OFF genetic control.
1. Introduction
In recent years, there is an influx of applying dynamic control theory to optimize metabolic pathways for production of various chemicals (Venayak et al., 2015; Xu, 2018; Xia et al., 2019). The marriage of intelligent control with synthetic biology have fruited a large volume of experimental and computational works that allow us to embrace a “dynamic” perspective to engineer cell metabolism (Zhang et al., 2012; Xu et al., 2014a, Xu et al., 2014b; Gupta et al., 2017). The notion of “metabolic homeostasis” is a result of the dynamic interplay of the various biomolecules inside the cell (Xu, 2018; Lv et al., 2019). Take the glycolytic pathway as an example, oscillating metabolic flux could arise due to the feedback inhibition of the phosphofructokinase by cellular energy levels (specifically, ATP, ADP and AMP) (Sel’kov 1968; Bier et al., 2000; Chandra et al., 2011; Gustavsson et al., 2014). Another classical example is the Lac operon, hysteresis and multiple steady states could arise due to the positive feedback loop of the intake of the inducer (IPTG or lactose) by lactose permease encoded by LacY (Yildirim and Mackey, 2003; Santillán et al., 2007; Stamatakis and Mantzaris, 2009). Inspired by this phenomena, early synthetic biology effort is spent extensively on constructing artificial genetic circuits by mimicking the electrical counterparts of the physical word (Andrianantoandro et al., 2006). Combing with mathematical modeling, a collection of classical work has emerged in the early 2000s, including the well-known toggle switch (CHEN and BAILEY, 1994; Gardner et al., 2000), repressilator (Elowitz and Leibler, 2000) and metabolator (Fung et al., 2005) et al. These seminal works have encouraged us to employ biophysical models to quantitatively unravel and test the complicated molecular interactions underlying many perplexing biological problems, which marks the birth of synthetic biology.
With about one decade, the post-term impact of synthetic biology starts yielding fruits in the metabolic engineering field (Keasling, 2010). From a control perspective, metabolic enzyme could be the “actuator” that performs chemical conversion (i.e. kinase phosphorylation, chromatin deacetylation) or the “transducer” that generates secondary messenger (i.e. cAMP or acetyl-CoA) (Smolke and Silver, 2011; Michener et al., 2012). Moving beyond the logic circuits engineering (AND, OR, NOT, NOR gates et al.) (Tamsir et al., 2011; Wang et al., 2011; Moon et al., 2012), metabolic engineers have been able to harness various regulatory mechanisms, including repression (Liu et al., 2015), activation (Doong et al., 2018), attenuation (Benzinger and Khammash, 2018) or RNA silencing (Yang et al., 2018a, Yang et al., 2018b), to rewire carbon flux and dynamically control cell metabolism. A number of control architectures (Oyarzún and Stan, 2013; Liu et al., 2015; Oyarzún and Chaves, 2015; Venayak et al., 2015; Chaves and Oyarzún, 2019) have emerged and been applied to relieve metabolic burden (Ceroni et al., 2018), eliminate intermediate toxicity (Xu et al., 2014a, Xu et al., 2014b), decouple cell growth from metabolite production (Bothfeld et al., 2017; Doong et al., 2018), eliminate metabolic heterogeneity (Xiao et al., 2016; Rugbjerg et al., 2018a; Rugbjerg et al., 2018b; Wang and Dunlop, 2019). The interdisciplinary connection among control theory, genetic principles, ecological and evolutional rules open a new venue for us to design and engineer precisely controlled genetic-metabolic circuits to reprogram biological functions (Calles et al., 2019). Engineering such decision-making functions to rewire the genetic (information) flow to redirect/optimize metabolic flux will enable us to deliver intelligent microbes for a broad range of applications, ranging from biocomputation, bioremediation, biosensing, biosynthesis to therapeutics (Nikel et al., 2016; Gao et al., 2019a, Gao et al., 2019; Grozinger et al., 2019).
One of the essential tasks for metabolic engineers is to dynamically allocate carbon flux, so that the limited cellular resources could be harnessed to maximize the production of the target molecules (Xu et al., 2013a, Xu et al., 2013b, Wan et al., 2019). Considering that the cell’s goal is to proliferate, there is always a tradeoff or conflicts between cell growth and metabolite overproduction. This will require us to equip the cells with various sensors to detect a broad range of environmental cues, cellular stimuli or metabolite intermediates (Zhang et al., 2015; Wan et al., 2019), in such a way the cell can autonomously adjust gene expression or cell metabolism to compensate the loss or eliminate the surplus of enzyme activity. To achieve this, a number of control architectures, including the incoherent feedforward loop (Dunlop et al., 2010; Harrison and Dunlop, 2012), the invertor gate (Liu et al., 2015), the metabolic toggle switch (Soma et al., 2014) and the metabolic valve (Solomon and Prather, 2011), have been implemented to improve the cellular tolerance to biofuels, or improve chemical production.
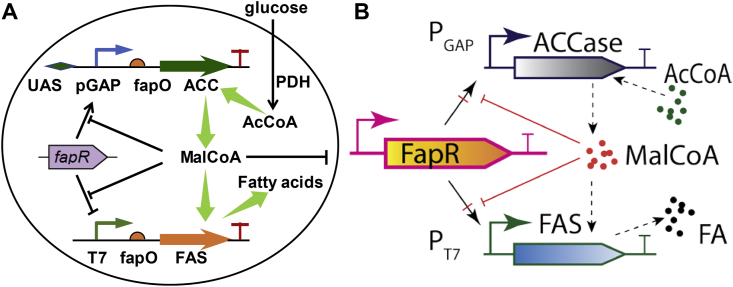
One of the highly studied dynamic control system is centering around the malonyl-CoA node (Xu et al., 2014a, Xu et al., 2014b; Fehér et al., 2015; Albanesi and de Mendoza, 2016; David et al., 2016). Malonyl-CoA is the essential metabolic building blocks for synthesizing advanced biofuels (Xu et al., 2013a, Xu et al., 2013b), lipids (Qiao et al., 2017; Xu et al., 2017), polyketides (Zhou et al., 2010; Liu et al., 2019), oleochemicals (Xu et al., 2016), flavonoids (Xiu et al., 2017) and cannabinoids (Luo et al., 2019) et al. High level of malonyl-CoA benefits the production of these metabolites (Yang et al., 2018a, Yang et al., 2018b) but also inhibits cell growth (Xu et al., 2014a, Xu et al., 2014b; Liu et al., 2015). Up to date, the FapR-derived malonyl-CoA sensor has been successfully applied to mammalian cell (Ellis and Wolfgang, 2012), E. coli (Xu et al., 2014a, Xu et al., 2014b; Yang et al., 2018a, Yang et al., 2018b) and yeast (Li et al., 2015; David et al., 2016). In particular, a recent development of the malonyl-CoA oscillator (Xu et al., 2014a, Xu et al., 2014b) has garnered significant attractions and allows us to study the optimal configurations of the controller architecture (Fig. 1). By integrating genetic and metabolic circuits, we have been able to experimentally construct and validate a malonyl-CoA oscillatory switch that was engineered to improve fatty acids production in E. coli (Xu et al., 2014a, Xu et al., 2014b). Experimentally, we have engineered malonyl-CoA-responsive promoters that could be upregulated or down-regulated by FapR, and the activation or the repression could be abolished by malonyl-CoA. This dual direction ON-OFF control mimics the amino acid feedforward and feedback regulation that are naturally occurring in many bacteria.
Fig. 1.
A malonyl-CoA switch to dynamically control fatty acids biosynthesis. (A) Autonomous ON-OFF control of malonyl-CoA. FapR activates pGAP promoter and upregulates the transcription of the malonyl-CoA source pathway (ACC) which generates malonyl-CoA; FapR represses T7 promoter and shuts down the transcription of the malonyl-CoA sink pathway (FAS) which consumes malonyl-CoA. The FapR bindings sites on the ACC operon is an upstream activation sequence (UAS). The FapR binding sites on the FAS operon is the fapO operator. Malonyl-CoA is the effector molecule (ligand) that antagonizes the activity of FapR. (B) Four possible genetic configurations of malonyl-CoA controller, which could be explored by changing the sign of the Hill coefficients (n and p) listed in Eqn. 4 and Eqn. 5. The black arrow with red cross indicates either transcriptional activation or repression. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)
One essential question is how to effectively configure the regulatory architecture of the metabolic source pathway and the metabolic sink pathway. To unravel the design principles underlying the malonyl-CoA switch, we set about to establish a biophysical model (system of ODE equations) and interrogated a broad range of parameter spaces, including the protein degradation rate (D), malonyl-CoA inhibitory constant (1/K1) and malonyl-CoA source pathway induction rate (β2). We also determined the optimal regulatory architecture for both the malonyl-CoA source pathway (ACCase) and the malonyl-CoA sink pathway (FAS), defined by the FapR-UAS dissociation constant (K4), FapR-fapO dissociation constant (K3) as well as the FapR-fapO Hill cooperativity coefficient (n). Our aim in this work is to understand how autonomous oscillation may contribute to optimal metabolite (fatty acids) production in strain engineering. The computational framework may facilitate us to design and engineer predictable genetic-metabolic switches, quest for the optimal controller architecture of the metabolic source/sink pathways, as well as leverage autonomous oscillation as a powerful tool to engineer cell function.
2. Computational method and system equations
2.1. Assumptions to develop the system equations
To simplify the biochemical and genetic events, we made eight assumptions to extract the basics of the genetic-metabolic circuits (Fig. 1): (a) We assume the number of DNA binding sites, specifically, FapO and UAS, far exceeds the number of transcriptional factor FapR in the system. Therefore, the repression rate of FAS or the activation rate of ACC are independent of the number of FapO and UAS in the system. (b) Glycolytic pathway (9 reactions) could be lumped into one single reaction to forming acetyl-CoA from glucose by PDH. (c) Fatty acids biosynthesis could be lumped into one single reaction to forming fatty acids (FA) from malonyl-CoA by FAS. (d) Malonyl-CoA depletion rate due to the formation of malonyl-CoA-FapR complex is negligible in the mass balance equation of malonyl-CoA (Eqn. 7). (e) The total enzyme or FapR concentration are approximately equivalent to the free enzyme or free FapR concentrations. (f) For non-regulated protein production (i.e. FapR and PDH), the production rate is cell growth-associated, therefore the production rate is proportional to the cell growth rate. (g) For regulated protein production (i.e. FAS and ACC), the production rate consists of both leaky expression (which is growth-associated) and regulated expression (which is non growth-associated) in the mass balance equations. (h) The cytosol is a homogenous and well-mixed system without mass transfer or diffusion limitations, where D could be interpreted as the dilution rate for CSTR or degradation constant for batch culture.
2.2. Formulation of the kinetic rate and mass balance equations
We formulated the kinetic rate models (Table 1) on the basis of Michaelis-Mention equation for enzyme-substrate equations, Monod kinetics (Xu, 2020a, Xu, 2020) with metabolite (Malonyl-CoA) inhibition for cell growth, Hill-type equations for enzyme kinetics and metabolite-TF binding. Specifically, Eqn. 1 describes the specific growth rate, which follows Monod growth with glucose as limiting nutrients and malonyl-CoA as inhibitory factor; Eqn. 2 describes the mass balance for cell growth; Eqn. 3 describes the growth-associated production of FapR and the depletion of FapR due to the formation of FapR-Malonyl-CoA complex; Eqn. 4 describes the growth-associated production (leaky expression) of FAS and the regulated expression of FAS repressed by FapR; Eqn. 5 describes the growth-associated production (leaky expression) of ACC and the regulated expression of ACC activated by FapR; Eqn. 6 describes the production rate of fatty acids (FA) from malonyl-CoA; Eqn. 7 describes the mass balance for malonyl-CoA, accounting for both the malonyl-CoA source (ACC) pathway and the malonyl-CoA sink (FAS) pathway; Eqn. 8 describes the mass balance for acetyl-CoA, accounting for both the acetyl-CoA source (PDH) pathway and the acetyl-CoA sink (ACC) pathway; Eqn. 9 describes the PDH production rate which is proportional to the cell growth rate; and Eqn. 10 describes the mass balance for glucose, accounting for the consumption rate due to cell growth and acetyl-CoA production. For all the mass balance equations (Eqn. 2 to Eqn. 10), we also considered the dilution or degradation terms. Biomass and cell concentration in the feeding stream of the system were designated as S0 and X0.
Table 1.
Equations used to define the autonomous oscillatory genetic-metabolic circuits.
| Equation No. | Equations used in this work |
|---|---|
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 |
2.3. Computational methods
Matlab R2017b was used as the computational package on a Windows 7 professional operation system. The CPU processor is Intel Core i3-6100 with 3.70 GHz. The installed memory (RAM) is 4.0 GHz. Matlab symbolic language package coupled with LaTex makeup language were used to compile the equations (Table 1). ODE45 solver was used to simulate and predict the system behavior. Matlab plot function was used to output the solutions and graphs. Matlab codes will be shared upon request. Biological parameters for Fig. 2 to Fig. 10 could be found in the supplementary files. Most of the parameters were assigned on the basis of BioNumbers database (Milo et al., 2009). Jacobian matrices were evaluated according to a reported numerical method. Calculate Jacobian of a function numerically at a given condition (https://www.github.com/auralius/numerical-jacobian)).
Fig. 2.
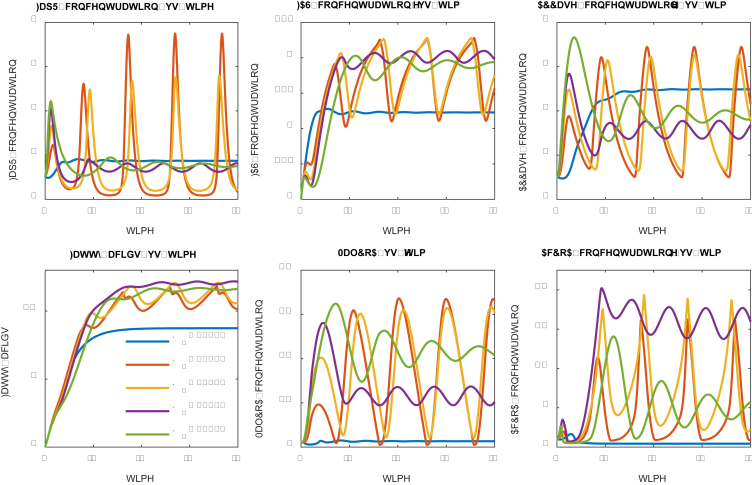
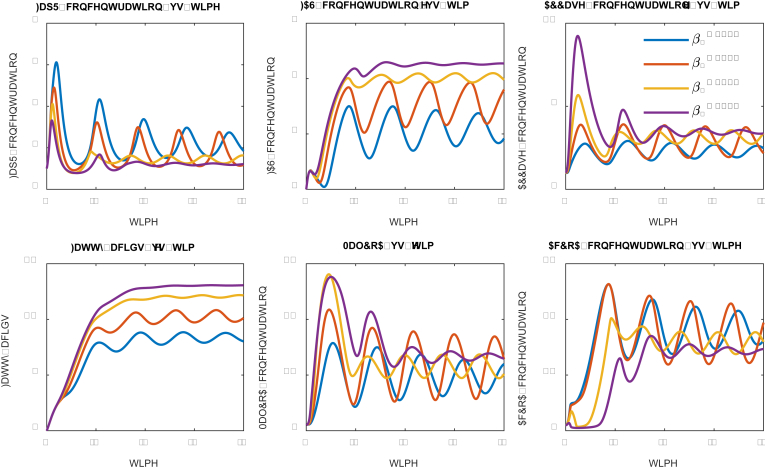
Effect of protein/metabolite degradation rate (dilution rate) on system dynamic behavior. Protein degradation rates have been labelled with different color. Low degradation rate (D = 0.15) leads to relatively stable oscillation. High degradation rate (D ≥ 0.2) leads to damped oscillation. The units are arbitrary units. Parameters could be found in the supplementary file. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)
Fig. 10.
Effect of FapR-fapO dissociation constant (K3) on system dynamics. A weak binding between FapR and fapO (or a large FapR-fapO dissociation constant, i.e. K3 = 8.0) significantly improves fatty acid production, up to 7-fold.
Initial states determine the final states for dynamic system. In this work, the initial conditions were taken on the basis of physiologically accessible dataset of biochemical systems. Most of the numbers were consistent with biochemical engineering textbooks, including Shuler & Kargi, Bioprocess engineering; and Blanch & Clark, Biochemical Engineering et al. These initial conditions come with SI unit and is provided in the SI file.
3. Results and discussion
3.1. Effect of protein/metabolite degradation rate (dilution rate) on system dynamic behavior
To understand the system dynamics, we probed a number of parameter space to generate the dynamic pattern that meets our design and control criteria. A list of parameters could be found in the supplementary files. We first investigated how protein/metabolite degradation rate impacts the system dynamics (Fig. 2). For all the simulations, we used six species, including regulator protein FapR, fatty acid synthase (FAS), acetyl-CoA carboxylase (ACCase), target product fatty acids (FA), intermediates malonyl-CoA (MalCoA) and acetyl-CoA (AcCoA), to represent the system.
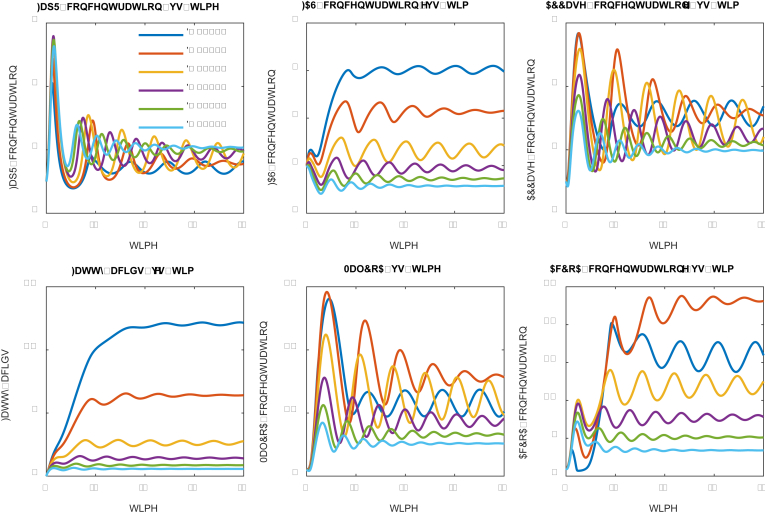
Under the prescribed parameter conditions (supplementary files) with protein degradation rates ranging from 0.15 to 0.60 (the unit is inverse of time), we evaluated the trajectory of the numerical solutions of the system ODE equations (Table 1). For relatively high degradation rate (D ≥ 0.2), we observed that the system solutions are approximately behaving like a damped oscillator (Fig. 2). On the other hand, the low degradation rate (or longer residence time, i.e. D = 0.15 in Fig. 2) allows the system to oscillate stably with fixed frequency and amplitude, leading to the highest fatty acids production (Fig. 2). For example, fatty acids production at low protein degradation rate (D = 0.15) is about 10-folds higher than the fatty acids production at high protein degradation rate (D = 0.6). This is not counterintuitive as low degradation rate allows the protein catalysts stay longer in the system (Gao et al., 2019a, Gao et al., 2019). And the stable oscillation indicates that the designed control scheme could perform alternating ON-OFF control of the malonyl-CoA source pathway and malonyl-CoA sink pathway. Interestingly, the fatty acids production pattern is closely related with the malonyl-CoA sink pathway (FAS), but doesn’t correlate well with the activity of the malonyl-CoA source pathway (ACC). This is rooted in our initial assumptions that sufficient malonyl-CoA will inhibit cell growth. As a result, the intermediate acetyl-CoA and malonyl-CoA displays distinct oscillating pattern, with the stable oscillation (D = 0.15) leading to better control.
We also explored whether we could further improve fatty acids production by using even smaller degradation rate (i.e. D = 0.1, Fig. 3). Interestingly, decreasing the degradation rate to 0.1 allows FapR to quickly accumulate in the system from t = 20. We could notice that a spike of fatty acids production at t = 20, but the entire control system collapses (D = 0.1, Fig. 3) at t > 20, due to the overdosed FapR repressing the expression of the malonyl-CoA sink pathway (FAS). Accompanying with increased FapR, the malonyl-CoA source pathway (ACCase) was also overdosed (D = 0.1, Fig. 3) due to the activating action of FapR toward the expression of ACCase. However, malonyl-CoA was not accumulated in the system due to the antagonist effect of FapR toward malonyl-CoA. Taken together, the low degradation rate (D = 0.1) allows the cell to only build biomass, but generates little final products (Fatty acids in this study). In summary, the range of degradation rate of the sensor protein (FapR) and the malonyl-CoA source pathway (ACCase) determines whether the designed control scheme will work or fail.
Fig. 3.
Effect of protein/metabolite degradation rate on system dynamic behavior. Protein degradation rates have been labelled with different color. Low degradation rate (D = 0.10) leads to a collapsed system: too much FapR represses the expression of FAS, activates the expression of ACC and quickly antagonize the resulting malonyl-CoA at t > 20. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)
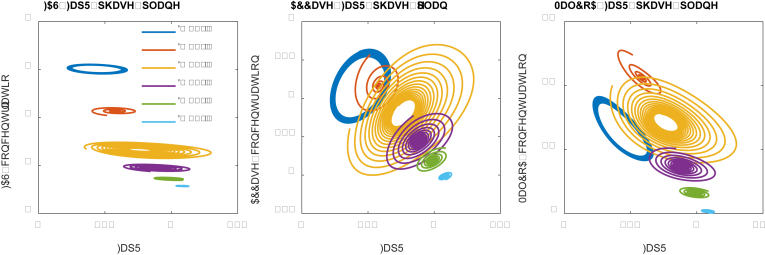
Phase-plane represents the solution constraints between the interacting components, at different parameter conditions (such as dilution rate or binding affinity) (Xu, 2020a, Xu, 2020). We further performed a phase-plane analysis to interrogate the solutions of above ODEs (Fig. 4). On the FAS-FapR phase plane, the system is attracted to periodic limit cycle of clockwise motion. The horizontal (x-axis) projection of the elliptic cycle forms a negative slope with FapR (x-axis), indicating that FapR represses the expression of FAS. On the ACCase-FapR phase planes (Fig. 4), the system is attracted to periodic limit cycle of counterclockwise motion. The horizontal (x-axis) projection of the elliptic cycle forms a positive slope with FapR, indicating that FapR activates the expression of ACCase. Similarly, on the MalCoA-FapR phase plane (Fig. 4), the system is attracted to periodic limit cycle of counterclockwise motion. The horizontal (x-axis) projection of the elliptic cycle forms a negative slope with FapR, indicating that FapR acts as an antagonist for malonyl-CoA. Under D = 0.15, we observed that the system leads to stable oscillation (Fig. S1).
Fig. 4.
The phase-plane correlations for FAS-FapR, ACCase-FapR and MalCoA-FapR. FAS-FapR phase plane shows periodic limit cycle of clockwise motion. ACCase-FapR and MalCoA-FapR phase planes show periodic limit cycle of counterclockwise motions. Effect of malonyl-CoA dissociation constant (K1) on system dynamic behavior.
To analytically identify the steady state, we need to derive the Jacobina matrix and analyze the eigenvalue of the Jacobian matrix at each of the steady states. If all the eigenvalues are negative or the real parts of all eigenvalues are negative (for imaginary eigenvalues), this will be a stable steady state. Graphically, steady states represent time-invariant solutions along the time-axis. The trajectory of stable steady states will asymptotically or periodically converge to a fixed point or travel on an orbit (a limit cycle). By analyzing the Jacobian matrices, two pure imaginary eigenvalues with zero real parts were arrived (Supplementary Notes 1), indicating a stable oscillation under D = 0.15. The phase portraits allow us to understand the motion of system dynamic behavior, it may also serve as diagnosis for troubleshooting the design-build-test cycle in genetic circuit engineering.
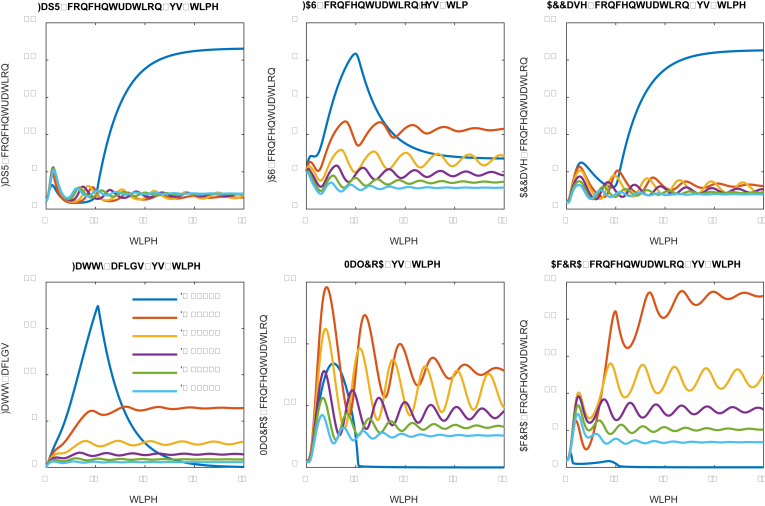
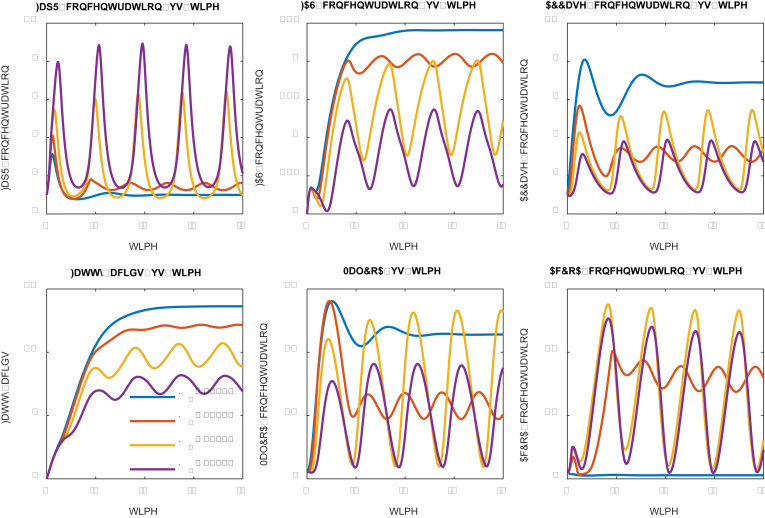
We next investigated how the malonyl-CoA dissociation constant (K1) impacts the system dynamics (Fig. 5). The malonyl-CoA dissociation constant (K1) describes the inhibitory strength of malonyl-CoA to cell growth: small dissociation constant (K1) indicates a high binding affinity and high inhibitory strength. A number of dissociation constants ranging from 0.10 to 4.0 (in the units of concentration) were investigated (Fig. 5). As expected, strong inhibition (K1 = 0.10) will sequestrate the cell at a low growth rate and lead to constant expression of FapR, FAS and ACCase (Fig. 5), indicating that the expression of FAS and ACCase are independent of the control scheme. As the inhibition becomes weaker (K1 = 0.50 and 1.00), the solution of the system ODEs oscillates with increased amplitude, albeit the frequency of the oscillation remains unchanged. A perfect ON and OFF control of FAS and ACCase expression is taking place when a medium strength of inhibition (K1 = 2.0) is used. This medium strength of inhibition confers the system to oscillate stably with improved fatty acids production (Fig. 5), albeit the fatty acids increase is less than 50%. When the dissociation constant takes a larger number (K1 = 4.0), the systems behave like a damped oscillation that is approximately approaching to the optimal design scheme (K1 = 2.0). This analysis indicates that a medium strength of dissociation constant (K1) should be used. In practice, one can always use adaptive lab evolution to screen conditionally tolerant phenotype that meets the K1 selection criteria.
Fig. 5.
Effect of malonyl-CoA dissociation constant (K1) on system dynamic behavior. Malonyl-CoA dissociation constants (K1) have been labelled with different color. Low dissociation constants (K1 = 0.5, 1.0 and 2.0) lead to stable oscillation. High dissociation constant (K1 = 4.0) leads to damped oscillation. Medium strength of malonyl-CoA inhibition (K1 = 2.0) favors fatty acids production. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)
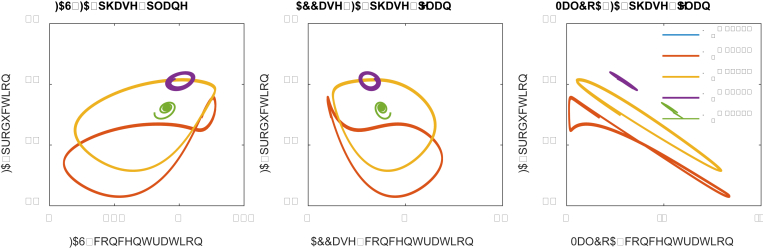
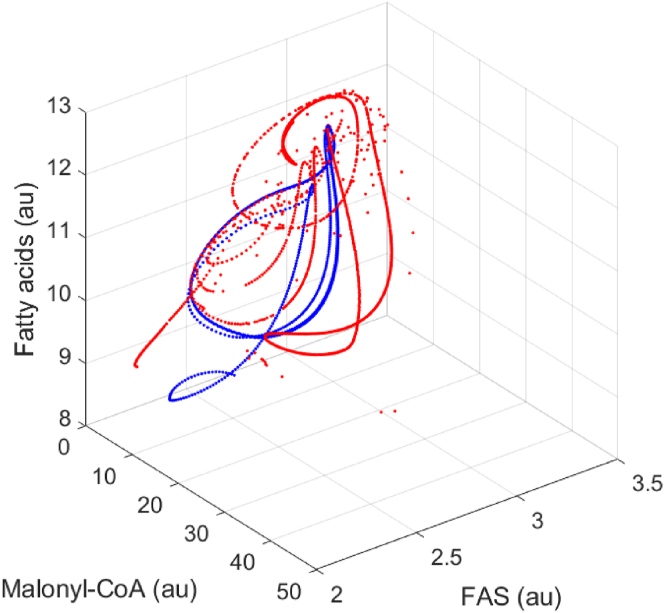
Similarly, we could perform a phase-plane analysis (Fig. 6). The phase-planes suggest that the optimal control scheme (K1 = 2.0, the purple cycles) only permits a very narrowed space of FAS, ACCase and MaloCoA solutions. Interestingly, for low malonyl-CoA dissociation constant (K1 = 0.5), the system exhibits a looping behavior on the FAS-FA and MalCoA-FA phase plane. Plotting the steady state solutions of fatty acids, FAS and malonyl-CoA, we observed looping pattern of solutions in the 3-D space, this may also imply a hysteretic state of the system (Aris et al., 2019) (Supplementary Notes 2 and 3). It simply means that strong malonyl-CoA inhibition (i.e. K1 = 0.3 or 0.5) will lead to multiplicity of steady states (Figs. 6 and 7), which is a critical factor to evaluate the dynamics of the system behavior.
Fig. 6.
The phase-plane portraits for FA-FAS, FA-ACCase and FA-MalCoA. Low malonyl-CoA dissociation constant (K1 = 0.5, orange line), which corresponds to strong malonyl-CoA inhibition, leads to multiplicity of steady states pattern between FAS-FA and MalCoA-FA input-output relationships. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)
Fig. 7.
The 3-D phase-plane portraits for fatty acids, FAS and malonyl-CoA, with malonyl-CoA inhibition constant (K1) varying from 0.1 to 1.5. A specific trajectory for K1 = 0.3 is added to the above solution space, marked in blue color. Other parameters used here are the same as the parameters used in Fig. 5. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)
Literature reports that feedback inhibition of free fatty acid on FAS complex plays a major role in regulating FA synthesis. Specifically, it is generally believed that acyl-ACPs or acyl-CoAs will feedback inhibit acetyl-CoA carboxylase in E. coli (Davis and Cronan, 2001). Since acyl-CoA/ACP could be hydrolyzed to free fatty acids by acyl-CoA thioesterase tesA (which is constitutively overexpressed in the published paper PNAS, 2014), we believe the feedback inhibition of acyl-CoA/ACP on FAS complex could be minimized when tesA was overexpressed. In this synthetic system, the malonyl-CoA inhibitory effect on FAS was translated to the malonyl-CoA inhibitory effect on cell growth: cell growth is associated with how much of membrane lipids (phospholipids synthesized from acyl-CoAs/acyl-ACPs) were made. Therefore, the malonyl-CoA/ACP feedback inhibitory effect on FAS (cell growth) plays a critical role to determine the system dynamics.
3.2. Effects of FapR-UAS interaction on system dynamics
We next explored how the gene expression of the malonyl-CoA source pathway (ACCase) impacts the system dynamics. According to the original design and Eqn.5, expression of ACCase is governed by the FapR-UAS interactions. The system equation for ACCase (Eqn. 5) accounts for both the growth-associated leaky expression (α3) and the FapR-activated regulatory expression (β2, p and K4). In all our simulations, we assume stringent regulation and the leaky expression is negligible (α2 = α3 = 0.05). We will specifically investigate how the ACCase induction rate (β2) and the FapR-UAS dissociation constant (K4) impact the system dynamics (Fig. 8 and Fig. 9).
Fig. 8.
Effect of ACCase induction rate (β2) on system dynamics. ACCase induction rates (β2) have been labelled with different color. High ACCase induction rate (i.e. β2 = 4.0) leads to a quickly damped oscillation and favors fatty acid accumulation. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)
Fig. 9.
Effect of FapR-UAS dissociation constant (K4) on system dynamics. Tighter FapR-UAS binding is advantageous to fatty acids production.
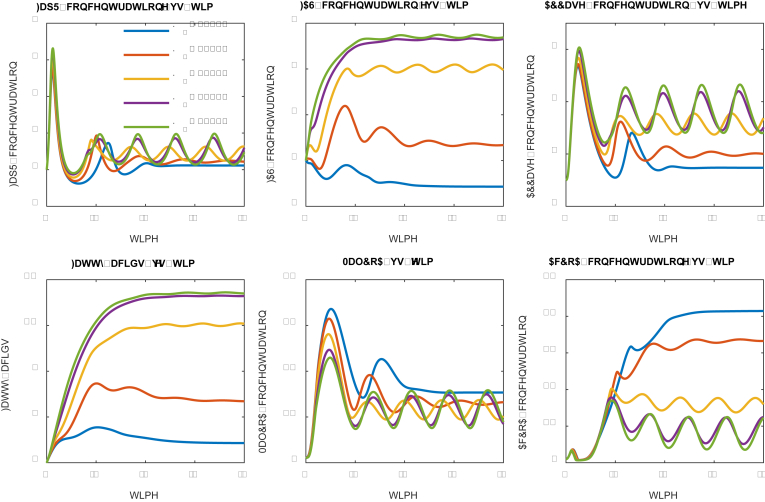
We investigated a number of ACCase induction rates (β2, in the units of concentration per time), ranging from 0.50 to 4.0 (Fig. 8). As the ACCase induction rate increases (β2) from 0.50 to 4.0, the expression of malonyl-CoA source pathway (ACCase) is upregulated, leading to improved fatty acids production (Fig. 8). For example, the fatty acids production is increased up to 2-fold when the ACCase induction rate (β2) increases from 0.5 (blue line, Fig. 8) to 4.0 (purple line, Fig. 8). On the other hand, the amount of regulator protein FapR decreases with increasing ACCase induction rate (β2) (Fig. 8), possibly due to the antagonist effect of malonyl-CoA. However, this monotonic correlation was not found for the species MalCoA and AcCoA, due to the complicated autoregulation of malonyl-CoA in the control system. Furthermore, under low ACCase induction rates (i.e. β2 = 0.5, 1.0 and 2.0), the oscillation damped periodically with decreasing amplitude. Under high ACCase induction rate (i.e. β2 = 4.0), the oscillation damped quickly to reach its steady state (Fig. 8). This result indicates that a high ACCase induction rate (β2) is essential for the proper function of the control scheme.
As FapR is the activator for the ACC operon, and the DNA binding site for FapR is a UAS (upstream activation sequence). We next investigated how the FapR-UAS dissociation constant (K4) impacts the system dynamics (Fig. 9). A smaller FapR-UAS dissociation constant (K4) indicates a tighter binding between FapR and UAS (the inverse of the dissociation constant quantifies the binding affinity). As the binding between FapR and UAS becomes tighter (K4 decreases from 8.0 to 1.0), the expression of the malonyl-CoA source pathway (ACCase) is strongly activated, leading to increased fatty acids production (Fig. 9). For example, the fatty acids production is increased up to 2.2-fold when the FapR-UAS dissociation constant (K4) decreases from 8.0 (purple line, Fig. 9, Fig. 10 (blue line, Fig. 9). Under high FapR-UAS binding affinity (K4 = 1.0), the oscillation damped quickly to reach its steady state; under low FapR-UAS binding affinity (K4 = 4.0 or 8.0), the oscillation retains periodic pattern with fixed frequency and amplitude. This result indicates that a tighter FapR-UAS binding is the critical factor to achieve the desired control scheme.
3.3. Effect of FapR-fapO interaction on system dynamics
We also attempted to understand how the gene expression of the malonyl-CoA sink pathway (FAS) impacts the system dynamics. By design, FapR is the repressor that is specifically bound to fapO and represses the expression of the malonyl-CoA sink pathway (FAS). The system equation for FAS (Eqn. 4) accounts for both the growth-associated leaky expression (α2) and the FapR-repressed regulatory expression (β1, n and K3). Transcriptional factor (FapR) and DNA binding site (fapO) interactions are typically defined by the binding affinity (inverse of the dissociation constant) and the Hill cooperativity coefficient. By probing the physiologically accessible parameter space, we will investigate how the FapR-fapO dissociation constant (K3) impact the system dynamics (Fig. 10).
We investigated a number of FapR-fapO dissociation constant (K3), spanning from 0.50 to 8.0 (Fig. 10). A smaller FapR-fapO dissociation constant indicates a tighter binding between FapR and fapO, thus the FapR-fapO complex will function as a stronger roadblock to prevent FAS transcription. As the binding between FapR and fapO becomes tighter (K3 decreases from 8.0 to 0.5), the expression of the malonyl-CoA sink pathway (FAS) is strongly repressed (Fig. 10), leading to decreased fatty acid accumulation. For example, the fatty acids production at low FapR-fapO dissociation constant (K3 = 0.50, blue curve) is less than 1/7 of the fatty acid production at high FapR-fapO dissociation constant (K3 = 8.0, green curve) (Fig. 10). With weaker FapR-fapO binding (K3 = 4.0 and 8.0), the ODE solutions for ACCase, MalCoA and AcCoA oscillate with fixed frequency and amplitude, indicating the functionality of the ON-OFF control toward both the malonyl-CoA source pathway (ACCase) and the malonyl-CoA sink pathway (FAS). However, with tighter FapR-fapO binding (K3 = 0.5 and 1.0), the oscillation collapses at relatively short period of time, indicating a faulted control scheme. This result suggests that a weak binding between FapR and fapO (or a large FapR-fapO dissociation constant) is the most important design criteria to achieve the desired ON-OFF control scheme.
3.4. Exploring the optimal controller architecture
The Hill cooperativity coefficient is a critical factor determining the input-output relationship of biological signal transduction. Recent studies demonstrate that lots of nonlinear and complicated biological functions are arising from the cooperative assembly of biological molecules (Bashor et al., 2019; Shaw et al., 2019), including DNA, RNA and proteins. As such, we will investigate how the FapR-FapO Hill cooperativity coefficient (n) impacts the system dynamics (Fig. 11). We choose a number of FapR-fapO Hill cooperativity coefficients, ranging from −4 to 4. It should be noted that, our original mass balance equations (Eqn. 4 and Eqn. 5) only account for the fact that FapR represses the expression of FAS and FapR activates the expression of ACC, which corresponds to a positive Hill coefficient (n > 0 and p > 0).
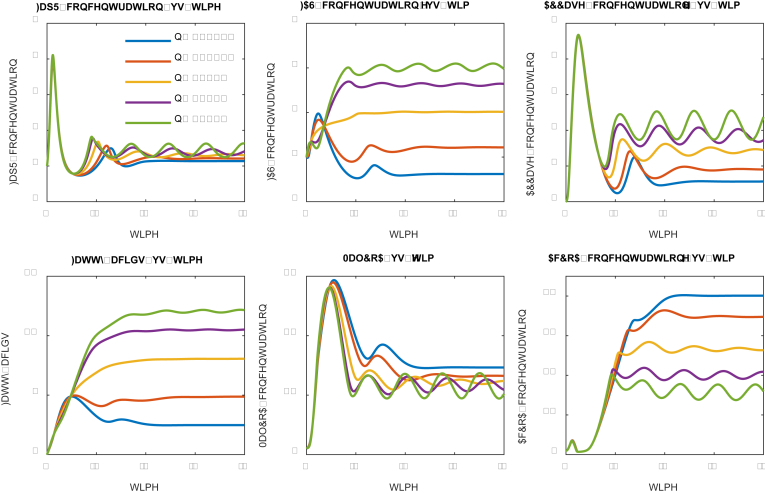
Fig. 11.
Effect of FapR-fapO Hill cooperativity coefficient (n) on system dynamics. Strong repression (n = 4) leads to stable oscillation and drives the cell to make more fatty acids.
The sign of the Hill coefficient is related with the genetic configuration of the controller (Fig. 1B). For example, a positive Hill coefficient (n) in the malonyl-CoA sink pathway (FAS) indicates that FapR represses the transcriptional activity of FAS expression; while a negative Hill coefficient (n) in the malonyl-CoA sink pathway (FAS) indicates that FapR activates the transcriptional activity of FAS expression (Equation 4). Similarly, a positive Hill coefficient (p) in the malonyl-CoA source pathway (ACC) indicates that FapR activates the transcriptional activity of ACC expression; while a negative Hill coefficient (p) in the malonyl-CoA source pathway (ACC) indicates that FapR represses the transcriptional activity of ACC expression (Equation 5). By changing the sign of the Hill coefficients for the malonyl-CoA sink pathway (FAS) and the malonyl-CoA source pathway (ACC), we could explore the ‘optimal controller’ structure in this study (Fig. 1B). Here we consider both positive Hill coefficients (n = 2.0 and 4.0) and negative Hill coefficients (n = −2.0 and −4.0) as well as no cooperation (n = 0). By comparing either the activating or repressing effect of FapR, we may interrogate the topology of the optimal controller architecture that leads to maximal fatty acids production.
As the FapR-fapO Hill cooperativity coefficient (n) increases from −4.0 to 4.0, the regulatory action of FapR towards the malonyl-CoA sink pathway (FAS) shifts from activation to repression. As a result, a significant increase in the FAS, ACCase expression and fatty acids production are observed (Fig. 11). For example, almost 5-fold increase of fatty acids is obtained when the FapR-fapO Hill cooperativity coefficient (n) increases from −4.0 (blue line, strong activation) to 4.0 (green line, strong repression). Under strong FapR activation (n = −4.0), counterintuitively, the expression of FAS is instead downregulated (Fig. 11). This could be linked to the unbalanced induction rate (β) between the malonyl-CoA source pathway (ACCase, β2 = 2.0) and the malonyl-CoA sink pathway (FAS, β1 = 0.5). Even with highly cooperative activation of FAS by FapR (n = −4.0, blue line), the low induction rate of the malonyl-CoA sink pathway (FAS) makes the expression of FAS unable to catch up with the expression of ACCase (malonyl-CoA source pathway). As a result, malonyl-CoA will build up but stay unchanged in the system (blue line in Fig. 11) to inhibit cell growth, which will result in even lower level of FapR (activator for FAS expression when n = −4, blue line) and therefore exacerbate the expression of FAS. On the contrary, highly cooperative repression of FAS by FapR (n = 4, green line) will make malonyl-CoA level oscillate, which forms the driving force to dynamically link and control the expression of the malonyl-CoA source pathway (ACCase) and the malonyl-CoA sink pathway (FAS). This analysis indicates that a control architecture consisting of upregulated metabolic source and downregulated metabolic sink is an essential design criterion to build adaptive genetic-metabolic circuits. In addition, the stable oscillation of the metabolic intermediate (i.e., malonyl-CoA) forms the driving force to exert the ON-OFF dynamic control toward complex metabolic function in the cell.
4. Conclusions
With the better understanding of cellular regulation, metabolic engineers have been able to engineer both the chemistry (the mass flow) and the control modules (the information flow) inside the cell to design intelligent cell factories with improved performance. Moving beyond thermodynamic and stoichiometric constraints, living organisms could be viewed as a smart system consisting of sensor (ligand binding domain of transcriptional factors), transducers (DNA-binding domain of transcriptional factors, kinase or enzyme et al.) and actuators (RNA polymerases). Along this direction, cellular regulation and feedback control mechanisms have been exploited to construct genetic/metabolic circuits that could sense/respond to environment, achieve adaptive metabolic function and reshape cell fate for diverse biotechnological and medical applications. As chemical engineers have done to program machine language and control the mass and energy flow in a chemical plant, a synthetic biologist could rewrite the genetic software and encode logic functions in living cells to control cellular activity.
Biophysical and biochemical models are important tools to quantitatively understand genetic circuit dynamics, metabolic network constraints, cell-cell communications (Dai et al., 2019) and microbial consortia interactions (Kong et al., 2018; Tsoi et al., 2018). Based on a previously engineered malonyl-CoA switch, nine differential equations were formulated (Table 1) and employed to unravel the design principles underlying a perfect metabolite switch. While the models present in the current study were simple, they provide sufficient kinetic information to predict the dynamic behavior of the published work. By interrogating the physiologically accessible parameter space, we have determined the optimal control architecture to configure both the malonyl-CoA source pathway and the malonyl-CoA sink pathway. We also investigated a number of biological parameters that strongly impact the system dynamics, including the protein degradation rate (D), malonyl-CoA inhibitory constant (1/K1), malonyl-CoA source pathway induction rate (β2), FapR-UAS dissociation constant (K4), FapR-fapO dissociation constant (K3) as well as the FapR-fapO Hill cooperativity coefficient (n). We identified that low protein degradation rate (D), medium strength of malonyl-CoA inhibitory constant (1/K1), high malonyl-CoA source pathway induction rate (β2), strong FapR-UAS binding affinity (1/K4), weak FapR-fapO binding affinity (1/K3) and a strong cooperative repression of malonyl-CoA sink pathway (FAS) by FapR (n) benefits the accumulation of the target molecule (fatty acids). The fatty acids production could be increased from 50% to 10-folds with the different set of parameters. Under certain conditions (i.e. strong malonyl-CoA inhibitory constant 1/K1), the system will display multiplicity of steady states. Stable oscillation of malonyl-CoA is the driving force to make the system perform the ON-OFF control and automatically adjust the expression of both the malonyl-CoA source (ACCase) and malonyl-CoA sink (FAS) pathways.
In this work, we have chosen a number of biophysical parameters to discuss the possible output of the malonyl-CoA switch. Genetically, these parameters could be altered by web-lab experiments, including protein engineering or degenerated repressor binding sites to change the biding affinity between the interacting components et al. The computational framework present here may facilitate us to design and engineer predictable genetic-metabolic switches, configure the optimal controller architecture of the metabolic source/sink pathways, as well as reprogram metabolic function for various applications.
CRediT authorship contribution statement
Peng Xu: Conceptualization, Writing - original draft.
Declaration of competing interest
The author declares no conflicts of interests.
Acknowledgments
Dr. Xu would like to acknowledge the Cellular & Biochem Engineering Program of the National Science Foundation under grant no.1805139 for funding support. Dr. Xu would also like to acknowledge the discussion of this project with the ENCH482/682 and ENCH640 students at the University of Maryland Baltimore County in the Fall 2018 and Spring 2019.
Footnotes
Supplementary data to this article can be found online at https://doi.org/10.1016/j.mec.2020.e00127.
Appendix. Symbols and variables used in this work
specific growth rate
maximum specific growth rate
cell growth-associated FapR production rate constant (constitutive expression)
cell growth-associated FAS production rate constant (leaky expression)
cell growth-associated ACC production rate constant (leaky expression)
cell growth-associated PDH production rate constant (constitutive expression)
non cell growth-associated FAS production rate (regulated expression)
non cell growth-associated ACC production rate (regulated expression)
Malonyl-CoA inhibitory (dissociation) constant
Mal-CoA and FapR saturation constant
dissociation rate constant of free FApR toward fapO in the FAS operon (to repress FAS transcription)
dissociation rate constant of free FapR toward UAS in the ACC operon (to activate ACC transcription)
acetyl-CoA saturation (Michaelis) constant toward ACC
glucose saturation (Michaelis) constant toward glycolytic pathway
Monod constant for glucose
Malonyl-CoA saturation (Michaelis) constant toward FAS
FapR-inactivating rate constant due to the formation of MalCoA-FapR complex
FA (fatty acids) production rate constant from Mal-CoA catalyzed by FAS
malonyl-CoA production rate constant from acetyl-CoA catalzyed by ACC
acetyl-CoA production rate constant from glycolysis catalzyed by PDH
- S
glucose concentration
glucose concentration in the feeding stream
dilution rate or degradation rate
biomass concentration in the feeding stream
malonyl-CoA to fatty acids conversion yield
glucose to biomass conversion yield
glucose to acetyl-CoA conversion yield
- m
malonyl-CoA-FapR (ligand-TF) Hill cooperativity coefficient
- n
FapR-FapO nucleoprotein complex Hill cooperativity coefficient
- p
FapR-UAS nucleoprotein complex Hill cooperativity coefficient
- q
malonyl-CoA-FAS (substrate-enzyme) Hill cooperativity coefficient
- r
acetyl-CoA-ACC (substrate-enzyme) Hill cooperativity coefficient
- u
glucose-PDH (substrate-enzyme, artificial reaction) Hill cooperativity coefficient
Appendix A. Supplementary data
The following is the Supplementary data to this article:
References
- Albanesi D., de Mendoza D. FapR: from control of membrane lipid homeostasis to a biotechnological tool. Front. Mol. Biosci. 2016;3:64. doi: 10.3389/fmolb.2016.00064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andrianantoandro E., Basu S., Karig D.K., Weiss R. Synthetic biology: new engineering rules for an emerging discipline. Mol. Syst. Biol. 2006;2:2006. doi: 10.1038/msb4100073. 0028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aris H., Borhani S., Cahn D., O’Donnell C., Tan E., Xu P. Modeling transcriptional factor cross-talk to understand parabolic kinetics, bimodal gene expression and retroactivity in biosensor design. Biochem. Eng. J. 2019;144:209–216. [Google Scholar]
- Bashor C.J., Patel N., Choubey S., Beyzavi A., Kondev J., Collins J.J., Khalil A.S. Complex signal processing in synthetic gene circuits using cooperative regulatory assemblies. Science. 2019;364(6440):593. doi: 10.1126/science.aau8287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benzinger D., Khammash M. Pulsatile inputs achieve tunable attenuation of gene expression variability and graded multi-gene regulation. Nat. Commun. 2018;9(1):3521. doi: 10.1038/s41467-018-05882-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bier M., Bakker B.M., Westerhoff H.V. How yeast cells synchronize their glycolytic oscillations: a perturbation analytic treatment. Biophys. J. 2000;78(3):1087–1093. doi: 10.1016/S0006-3495(00)76667-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bothfeld W., Kapov G., Tyo K.E.J. A glucose-sensing toggle switch for autonomous, high productivity genetic control. ACS Synth. Biol. 2017;6(7):1296–1304. doi: 10.1021/acssynbio.6b00257. [DOI] [PubMed] [Google Scholar]
- Calles B., Goñi-Moreno A., de Lorenzo V. Digitalizing heterologous gene expression in Gram-negative bacteria with a portable on/off module. Mol. Syst. Biol. 2019;15(12) doi: 10.15252/msb.20188777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ceroni F., Boo A., Furini S., Gorochowski T.E., Borkowski O., Ladak Y.N., Awan A.R., Gilbert C., Stan G.-B., Ellis T. Burden-driven feedback control of gene expression. Nat. Methods. 2018;15(5):387–393. doi: 10.1038/nmeth.4635. [DOI] [PubMed] [Google Scholar]
- Chandra F.A., Buzi G., Doyle J.C. Glycolytic oscillations and limits on robust efficiency. Science. 2011;333(6039):187. doi: 10.1126/science.1200705. [DOI] [PubMed] [Google Scholar]
- Chaves M., Oyarzún D.A. Dynamics of complex feedback architectures in metabolic pathways. Automatica. 2019;99:323–332. [Google Scholar]
- Chen W., Bailey J. Application of the cross-regulation system As A metabolic switch. Biotechnol. Bioeng. 1994;43(11):1190–1193. doi: 10.1002/bit.260431124. [DOI] [PubMed] [Google Scholar]
- Dai Z., Lee A.J., Roberts S., Sysoeva T.A., Huang S., Dzuricky M., Yang X., Zhang X., Liu Z., Chilkoti A., You L. Versatile biomanufacturing through stimulus-responsive cell–material feedback. Nat. Chem. Biol. 2019;15(10):1017–1024. doi: 10.1038/s41589-019-0357-8. [DOI] [PubMed] [Google Scholar]
- David F., Nielsen J., Siewers V. Flux control at the malonyl-CoA node through hierarchical dynamic pathway regulation in Saccharomyces cerevisiae. ACS Synth. Biol. 2016;5(3):224–233. doi: 10.1021/acssynbio.5b00161. [DOI] [PubMed] [Google Scholar]
- Davis M., Cronan J. Inhibition of Escherichia coli acetyl coenzyme A carboxylase by acyl-acyl carrier protein. J. Bacteriol. 2001;183(4):1499–1503. doi: 10.1128/JB.183.4.1499-1503.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doong S.J., Gupta A., Prather K.L.J. Layered dynamic regulation for improving metabolic pathway productivity in <em>Escherichia coli</em>. Proc. Natl. Acad. Sci. Unit. States Am. 2018;115(12):2964. doi: 10.1073/pnas.1716920115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dunlop M., Keasling J., Mukhopadhyay A. A model for improving microbial biofuel production using a synthetic feedback loop. Syst. Synth. Biol. 2010;4(2):95–104. doi: 10.1007/s11693-010-9052-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ellis Jessica M., Wolfgang Michael J. A genetically encoded metabolite sensor for malonyl-CoA. Chem. Biol. 2012;19(10):1333–1339. doi: 10.1016/j.chembiol.2012.08.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elowitz M.B., Leibler S. A synthetic oscillatory network of transcriptional regulators. Nature. 2000;403(6767):335–338. doi: 10.1038/35002125. [DOI] [PubMed] [Google Scholar]
- Fehér T., Libis V., Carbonell P., Faulon J.-L. A sense of balance: experimental investigation and modeling of a malonyl-CoA sensor in Escherichia coli. Front. Bioeng. Biotechnol. 2015;3:46. doi: 10.3389/fbioe.2015.00046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fung E., Wong W., Suen J., Bulter T., Lee S., Liao J. A synthetic gene-metabolic oscillator. Nature. 2005;435(7038):118–122. doi: 10.1038/nature03508. [DOI] [PubMed] [Google Scholar]
- Gao C., Hou J., Xu P., Guo L., Chen X., Hu G., Ye C., Edwards H., Chen J., Chen W., Liu L. Programmable biomolecular switches for rewiring flux in Escherichia coli. Nat. Commun. 2019;10(1):3751. doi: 10.1038/s41467-019-11793-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gao C., Xu P., Ye C., Chen X., Liu L. Genetic circuit-assisted smart microbial engineering. Trends Microbiol. 2019;27(12):1011–1024. doi: 10.1016/j.tim.2019.07.005. [DOI] [PubMed] [Google Scholar]
- Gardner T., Cantor C., Collins J. Construction of a genetic toggle switch in Escherichia coli. Nature. 2000;403(6767):339–342. doi: 10.1038/35002131. [DOI] [PubMed] [Google Scholar]
- Grozinger L., Amos M., Gorochowski T.E., Carbonell P., Oyarzún D.A., Stoof R., Fellermann H., Zuliani P., Tas H., Goñi-Moreno A. Pathways to cellular supremacy in biocomputing. Nat. Commun. 2019;10(1):5250. doi: 10.1038/s41467-019-13232-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gupta A., Reizman I.M.B., Reisch C.R., Prather K.L.J. Dynamic regulation of metabolic flux in engineered bacteria using a pathway-independent quorum-sensing circuit. Nat. Biotechnol. 2017;35(3):273–279. doi: 10.1038/nbt.3796. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gustavsson A.-K., van Niekerk D.D., Adiels C.B., Kooi B., Goksör M., Snoep J.L. Allosteric regulation of phosphofructokinase controls the emergence of glycolytic oscillations in isolated yeast cells. FEBS J. 2014;281(12):2784–2793. doi: 10.1111/febs.12820. [DOI] [PubMed] [Google Scholar]
- Harrison M., Dunlop M. Synthetic feedback loop model for increasing microbial biofuel production using a biosensor. Front. Microbiol. 2012;3:360. doi: 10.3389/fmicb.2012.00360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keasling J. Manufacturing molecules through metabolic engineering. Science. 2010;330(6009):1355–1358. doi: 10.1126/science.1193990. [DOI] [PubMed] [Google Scholar]
- Kong W., Meldgin D.R., Collins J.J., Lu T. Designing microbial consortia with defined social interactions. Nat. Chem. Biol. 2018;14(8):821–829. doi: 10.1038/s41589-018-0091-7. [DOI] [PubMed] [Google Scholar]
- Li S., Si T., Wang M., Zhao H. Development of a synthetic malonyl-CoA sensor in Saccharomyces cerevisiae for intracellular metabolite monitoring and genetic screening. ACS Synth. Biol. 2015;4(12):1308–1315. doi: 10.1021/acssynbio.5b00069. [DOI] [PubMed] [Google Scholar]
- Liu D., Xiao Y., Evans B.S., Zhang F. Negative feedback regulation of fatty acid production based on a malonyl-CoA sensor–actuator. ACS Synth. Biol. 2015;4(2):132–140. doi: 10.1021/sb400158w. [DOI] [PubMed] [Google Scholar]
- Liu H., Marsafari M., Wang F., Deng L., Xu P. Engineering acetyl-CoA metabolic shortcut for eco-friendly production of polyketides triacetic acid lactone in Yarrowia lipolytica. Metab. Eng. 2019;56:60–68. doi: 10.1016/j.ymben.2019.08.017. [DOI] [PubMed] [Google Scholar]
- Luo X., Reiter M.A., d’Espaux L., Wong J., Denby C.M., Lechner A., Zhang Y., Grzybowski A.T., Harth S., Lin W., Lee H., Yu C., Shin J., Deng K., Benites V.T., Wang G., Baidoo E.E.K., Chen Y., Dev I., Petzold C.J., Keasling J.D. Complete biosynthesis of cannabinoids and their unnatural analogues in yeast. Nature. 2019;567(7746):123–126. doi: 10.1038/s41586-019-0978-9. [DOI] [PubMed] [Google Scholar]
- Lv Y., Qian S., Du G., Chen J., Zhou J., Xu P. Coupling feedback genetic circuits with growth phenotype for dynamic population control and intelligent bioproduction. Metab. Eng. 2019;54:109–116. doi: 10.1016/j.ymben.2019.03.009. [DOI] [PubMed] [Google Scholar]
- Michener J.K., Thodey K., Liang J.C., Smolke C.D. Applications of genetically-encoded biosensors for the construction and control of biosynthetic pathways. Metab. Eng. 2012;14(3):212–222. doi: 10.1016/j.ymben.2011.09.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Milo R., Jorgensen P., Moran U., Weber G., Springer M. BioNumbers—the database of key numbers in molecular and cell biology. Nucleic Acids Res. 2009;38(Suppl. l_1):D750–D753. doi: 10.1093/nar/gkp889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moon T.S., Lou C., Tamsir A., Stanton B.C., Voigt C.A. Genetic programs constructed from layered logic gates in single cells. Nature. 2012;491(7423):249–253. doi: 10.1038/nature11516. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nikel P.I., Chavarría M., Danchin A., de Lorenzo V. From dirt to industrial applications: Pseudomonas putida as a Synthetic Biology chassis for hosting harsh biochemical reactions. Curr. Opin. Chem. Biol. 2016;34:20–29. doi: 10.1016/j.cbpa.2016.05.011. [DOI] [PubMed] [Google Scholar]
- Oyarzún D.A., Chaves M. Design of a bistable switch to control cellular uptake. J. R. Soc. Interface. 2015;12(113):20150618. doi: 10.1098/rsif.2015.0618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oyarzún D.A., Stan G.-B.V. Synthetic gene circuits for metabolic control: design trade-offs and constraints. J. R. Soc. Interface. 2013;10(78):20120671. doi: 10.1098/rsif.2012.0671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qiao K., Wasylenko T.M., Zhou K., Xu P., Stephanopoulos G. Lipid production in Yarrowia lipolytica is maximized by engineering cytosolic redox metabolism. Nat. Biotechnol. 2017;35(2):173–177. doi: 10.1038/nbt.3763. [DOI] [PubMed] [Google Scholar]
- Rugbjerg P., Myling-Petersen N., Porse A., Sarup-Lytzen K., Sommer M.O.A. Diverse genetic error modes constrain large-scale bio-based production. Nat. Commun. 2018;9(1):787. doi: 10.1038/s41467-018-03232-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rugbjerg P., Sarup-Lytzen K., Nagy M., Sommer M.O.A. Synthetic addiction extends the productive life time of engineered <em>Escherichia coli</em> populations. Proc. Natl. Acad. Sci. Unit. States Am. 2018;115(10):2347. doi: 10.1073/pnas.1718622115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Santillán M., Mackey M.C., Zeron E.S. Origin of bistability in the lac operon. Biophys. J. 2007;92(11):3830–3842. doi: 10.1529/biophysj.106.101717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sel’kov E.E. Self-oscillations in glycolysis. 1. A simple kinetic model. Eur. J. Biochem. 1968;4(1):79–86. doi: 10.1111/j.1432-1033.1968.tb00175.x. [DOI] [PubMed] [Google Scholar]
- Shaw W.M., Yamauchi H., Mead J., Gowers G.-O.F., Bell D.J., Öling D., Larsson N., Wigglesworth M., Ladds G., Ellis T. Engineering a model cell for rational tuning of GPCR signaling. Cell. 2019;177(3):782–796. doi: 10.1016/j.cell.2019.02.023. e727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smolke C.D., Silver P.A. Informing biological design by integration of systems and synthetic biology. Cell. 2011;144(6):855–859. doi: 10.1016/j.cell.2011.02.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Solomon K., Prather K. The 2011 AIChE annual meeting; Minneapolis, MN: 2011. Dynamic Tuning of Glycolytic Flux for Heterologous Production with a Glucose Valve. [Google Scholar]
- Soma Y., Tsuruno K., Wada M., Yokota A., Hanai T. Metabolic flux redirection from a central metabolic pathway toward a synthetic pathway using a metabolic toggle switch. Metab. Eng. 2014;23:175–184. doi: 10.1016/j.ymben.2014.02.008. [DOI] [PubMed] [Google Scholar]
- Stamatakis M., Mantzaris N.V. Comparison of deterministic and stochastic models of the lac operon genetic network. Biophys. J. 2009;96(3):887–906. doi: 10.1016/j.bpj.2008.10.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tamsir A., Tabor J.J., Voigt C.A. Robust multicellular computing using genetically encoded NOR gates and chemical ‘wires’. Nature. 2011;469(7329):212–215. doi: 10.1038/nature09565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsoi R., Wu F., Zhang C., Bewick S., Karig D., You L. Metabolic division of labor in microbial systems. Proc. Natl. Acad. Sci. Unit. States Am. 2018;115(10):2526. doi: 10.1073/pnas.1716888115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Venayak N., Anesiadis N., Cluett W.R., Mahadevan R. Engineering metabolism through dynamic control. Curr. Opin. Biotechnol. 2015;34(Suppl. C):142–152. doi: 10.1016/j.copbio.2014.12.022. [DOI] [PubMed] [Google Scholar]
- Wan X., Marsafari M., Xu P. Engineering metabolite-responsive transcriptional factors to sense small molecules in eukaryotes: current state and perspectives. Microb. Cell Factories. 2019;18(1):61. doi: 10.1186/s12934-019-1111-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang B., Kitney R., Joly N., Buck M. Engineering modular and orthogonal genetic logic gates for robust digital-like synthetic biology. Nat. Commun. 2011;2 doi: 10.1038/ncomms1516. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang T., Dunlop M.J. Controlling and exploiting cell-to-cell variation in metabolic engineering. Curr. Opin. Biotechnol. 2019;57:10–16. doi: 10.1016/j.copbio.2018.08.013. [DOI] [PubMed] [Google Scholar]
- Xia P.-F., Ling H., Foo J.L., Chang M.W. Synthetic genetic circuits for programmable biological functionalities. Biotechnol. Adv. 2019;37(6):107393. doi: 10.1016/j.biotechadv.2019.04.015. [DOI] [PubMed] [Google Scholar]
- Xiao Y., Bowen C.H., Liu D., Zhang F. Exploiting nongenetic cell-to-cell variation for enhanced biosynthesis. Nat. Chem. Biol. 2016;12(5):339–344. doi: 10.1038/nchembio.2046. [DOI] [PubMed] [Google Scholar]
- Xiu Y., Jang S., Jones J.A., Zill Nicholas A., Linhardt Robert J., Yuan Q., Jung Gyoo Y., Koffas Mattheos A.G. Naringenin-responsive riboswitch-based fluorescent biosensor module for Escherichia coli co-cultures. Biotechnol. Bioeng. 2017;114(10):2235–2244. doi: 10.1002/bit.26340. [DOI] [PubMed] [Google Scholar]
- Xu P. Production of chemicals using dynamic control of metabolic fluxes. Curr. Opin. Biotechnol. 2018;53:12–19. doi: 10.1016/j.copbio.2017.10.009. [DOI] [PubMed] [Google Scholar]
- Xu P. Analytical solution for a hybrid Logistic-Monod cell growth model in batch and continuous stirred tank reactor culture. Biotechnol. Bioeng. 2020;117(3):873–878. doi: 10.1002/bit.27230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu P. Dynamics of microbial competition, commensalism and cooperation and its implications for coculture and microbiome engineering. bioRxiv. 2020 doi: 10.1002/bit.27562. 2020.2003.2005.979435, Submitted for publication. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu P., Bhan N., Koffas M.A.G. Engineering plant metabolism into microbes: from systems biology to synthetic biology. Curr. Opin. Biotechnol. 2013;24(2):291–299. doi: 10.1016/j.copbio.2012.08.010. [DOI] [PubMed] [Google Scholar]
- Xu P., Gu Q., Wang W., Wong L., Bower A.G.W., Collins C.H., Koffas M.A.G. Modular optimization of multi-gene pathways for fatty acids production in E. coli. Nat. Commun. 2013;4:1409. doi: 10.1038/ncomms2425. [DOI] [PubMed] [Google Scholar]
- Xu P., Li L., Zhang F., Stephanopoulos G., Koffas M. Improving fatty acids production by engineering dynamic pathway regulation and metabolic control. Proc. Natl. Acad. Sci. U. S. A. 2014;111(31):11299–11304. doi: 10.1073/pnas.1406401111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu P., Qiao K., Ahn W.S., Stephanopoulos G. Engineering Yarrowia lipolytica as a platform for synthesis of drop-in transportation fuels and oleochemicals. Proc. Natl. Acad. Sci. Unit. States Am. 2016;113(39):10848–10853. doi: 10.1073/pnas.1607295113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu P., Qiao K., Stephanopoulos G. Engineering oxidative stress defense pathways to build a robust lipid production platform in Yarrowia lipolytica. Biotechnol. Bioeng. 2017;114(7):1521–1530. doi: 10.1002/bit.26285. [DOI] [PubMed] [Google Scholar]
- Xu P., Wang W., Li L., Bhan N., Zhang F., Koffas M.A.G. Design and kinetic analysis of a hybrid promoter-regulator system for malonyl-CoA sensing in Escherichia coli. ACS Chem. Biol. 2014;9(2):451–458. doi: 10.1021/cb400623m. [DOI] [PubMed] [Google Scholar]
- Yang D., Kim W.J., Yoo S.M., Choi J.H., Ha S.H., Lee M.H., Lee S.Y. Repurposing type III polyketide synthase as a malonyl-CoA biosensor for metabolic engineering in bacteria. Proc. Natl. Acad. Sci. Unit. States Am. 2018;115(40):9835. doi: 10.1073/pnas.1808567115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Y., Lin Y., Wang J., Wu Y., Zhang R., Cheng M., Shen X., Wang J., Chen Z., Li C., Yuan Q., Yan Y. Sensor-regulator and RNAi based bifunctional dynamic control network for engineered microbial synthesis. Nat. Commun. 2018;9(1):3043. doi: 10.1038/s41467-018-05466-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yildirim N., Mackey M.C. Feedback regulation in the lactose operon: a mathematical modeling study and comparison with experimental data. Biophys. J. 2003;84(5):2841–2851. doi: 10.1016/S0006-3495(03)70013-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang F., Carothers J.M., Keasling J.D. Design of a dynamic sensor-regulator system for production of chemicals and fuels derived from fatty acids. Nat. Biotechnol. 2012;30(4):354–359. doi: 10.1038/nbt.2149. [DOI] [PubMed] [Google Scholar]
- Zhang J., Jensen M.K., Keasling J.D. Development of biosensors and their application in metabolic engineering. Curr. Opin. Chem. Biol. 2015;28:1–8. doi: 10.1016/j.cbpa.2015.05.013. [DOI] [PubMed] [Google Scholar]
- Zhou H., Qiao K., Gao Z., Meehan M., Li J., Zhao X., Dorrestein P., Vederas J., Tang Y. Enzymatic synthesis of resorcylic acid lactones by cooperation of fungal iterative polyketide synthases involved in hypothemycin biosynthesis. J. Am. Chem. Soc. 2010:4530. doi: 10.1021/ja100060k. -+ [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.