The effect of Brahman genes on body temperature plasticity of heifers on pasture under heat stress

Abstract

Bos taurus indicus cattle have the superior ability for the regulation of body temperature during heat stress due to a number of physiological and cellular level adaptive traits. The objectives of this study were to quantify the change in body temperature in heifers with various proportions of Brahman genes per unit increase in heat stress as measured by temperature–humidity index (THI) and to assess how different breed groups responded to varying intensity and duration of heat stress. A total of 299 two-yr-old heifers from six breed groups ranging from 100% Angus to 100% Brahman were evaluated under hot and humid conditions during 2017 and 2018 summer days. Two strategies were used to estimate the plasticity in body temperature of breed groups in response to environmental challenges: 1) a random regression mixed model was used to estimate reaction norm parameters for each breed group in response to a specified environmental heat stress and 2) a repeated measures mixed model was used to evaluate the response to different environmental heat loads. The reaction norm model estimated an intercept and slope measuring the change in body temperature per unit increase in THI environmental heat stress for different breed groups of animals and allowed the identification of genotypes which are robust, with low slope values indicative of animals that are able to maintain normal body temperature across a range of environments. The repeated measures mixed model showed that Brahman cattle have an advantage under moderate or high heat stress conditions but both Angus and Brahman breed groups are greatly affected when heat stress is severe. A critical factor appears to be the opportunity to cool down during the night hours more than the number of hours with extreme THI. With heat stress conditions predicted to intensify and expand into currently temperate zones, developing effective strategies to ensure sustainable beef production systems are imperative. Effective strategies will require the identification of the genes conferring the superior thermotolerance in Brahman cattle.

Introduction

It has been well established that Bos taurus indicus cattle are better able to regulate body temperature in response to heat stress due to a number of physiological and cellular level adaptive traits (Hansen, 2004; Gaughan et al., 2010), which contribute to the superior ability for the regulation of body temperature during heat stress. Traditional crossbreeding has been used to introduce B. t. indicus genes into Bos taurus taurus breeds to develop cattle for beef and dairy production systems with increased adaptability to hot and humid climates (Hammond et al., 1996, 1998; Cundiff et al., 2012; Lamy et al., 2012). Success has been limited due to co-introduction of other unfavorable genetic characteristics of zebu cattle, particularly those associated with low productivity (Dow et al., 1982; Olson et al., 2003; Elzo et al., 2012a, 2012b).

Based on recent predictions (IPPC, 2013), global temperatures are expected to rise by 1.4 to 3.0 °C by the end of this century and the frequency and intensity of extreme heat waves are expected to increase. The possible negative impacts of changes in climate variability are projected to be greatest in the tropical and subtropical developing world where the majority worldwide ruminants are found and where climate conditions limit animal productivity (Herrero et al., 2012; Rojas-Downing et al., 2017). More than 50% of meat and 60% of milk in the world are produced in tropical and subtropical environments (FAO, 2018). At the same time, genetic selection programs with a singular focus on improving production traits may increase animals’ susceptibility to environmental heat stress (Rhoads et al., 2013) due to the strong relationship between production level and metabolic heat production. It is now becoming clear that the rate of change in climate is faster than the rate of genetic improvement possible using traditional selection methods (Gaughan et al., 2009; Hayes et al., 2013). It is uncertain whether the most effective approach would be to identify phenotypes in a heat-tolerant breed that has favorable production and market traits or to select heat-tolerant animals within breeds that meet market specifications (Gaughan et al., 2008). An alternative approach is to incorporate specific thermotolerance genes from zebu cattle into European breeds while avoiding undesirable genes. This approach relies on being able to identify and map specific genes responsible for thermotolerance in zebu and then to develop breeding strategies such as genomic selection and gene editing to better utilize the zebu genotype for cattle production systems (Hansen, 2004).

Phenotypic plasticity is defined as the change in a phenotype in response to a change in the environment. Body temperature is a plastic trait and an important question is whether individuals or groups vary in their plastic responses to the environment and, if so, whether this variation has a genetic component. If genetic variation in plasticity exists, programs to utilize the genetic component to improve phenotypic plasticity via crossbreeding or selection can be implemented.

In this study, we used vaginal temperature as a proxy for core body temperature to evaluate the body temperature plasticity of groups of heifers with various proportions of Brahman genes when exposed to environmental heat stress during summer days while on pasture in Florida. The temperature–humidity index (THI) was used to describe the environment. The objectives of this study were to quantify the change in body temperature in heifers with various proportions of Brahman genes per unit increase in heat stress as measured by THI and to assess how different breed groups responded to varying intensity and duration of heat stress.

Materials and Methods

Animals and management

The University of Florida Institutional Care and Use Committee approved the research protocol used in this study (approval no. 201203578).

Cattle used in this study were from the University of Florida multibreed Angus–Brahman herd. Elzo et al. (2012a, 2014) described the creation of the herd and its reproductive management. Six breed groups based on the proportion of Brahman genes were defined as follows: group 1 (0% to 19% Brahman), group 2 (20% to 39% Brahman), group 3 (37.5% Brahman, Brangus), group 4 (40% to 59% Brahman), group 5 (60% to 79% Brahman), and group 6 (80% to 100% Brahman).

A total of 299 two-yr-old heifers born in 2015 and 2016 from all six breed groups were evaluated for five consecutive days under hot and humid conditions during 2017 and 2018 summer days at the University of Florida Beef Research Unit (Fairbanks, Florida, USA; 29°44′38.2″N +82°15′55.2″W). The 2017 group (n = 90) was monitored from July 17 to July 21 and the 2018 group (n = 209) from June 7 to June 11. The number of heifers for each breed group was 13, 12, 13, 16, 10, and 26 for the year 2017 and 41, 39, 46, 33, 23, and 27 for the year 2018, respectively. Each year, all heifers under study were maintained on the same pasture that included access to limited shade from stands of trees.

Environmental measurements

Ambient environmental conditions were monitored using HOBO-U23 data loggers (Onset Computer Corp., Bourne, MA) which recorded dry bulb temperature (°C, T_db) and relative humidity (%, RH) every 15 min during the entire time of data collection. The THI was used to quantify environmental heat stress and it was calculated as follows (NRC, 1971):

$${\displaystyle \begin{array}{l}{\displaystyle \mathrm{T}\mathrm{H}\mathrm{I}=(1.8\times {\mathrm{T}}_{\mathrm{d}\mathrm{b}}+32)[(0.55-0.0055\times \mathrm{R}\mathrm{H})\times (1.8\times {\mathrm{T}}_{\mathrm{d}\mathrm{b}}-26)]}\end{array}}$$

The hourly average of THI was calculated for the entire experimental period and was subsequently matched by the hour with hourly body temperature of each heifer. A similar strategy was used in the study of Hahn and Mader (1997).

The severity of the thermal challenge depends on the magnitude of heat events described by intensity and duration and the opportunity for recovery during the cooler nighttime period. Based on hourly THI, a heat load for each day during the study (3 d in 2017 and 3 d in 2018) was calculated as a function of THI level and number of hours for that particular THI level. Six levels were defined based on the range of THI values in our data, when THI <68 (cool), 68 to 72 (neutral), 72 to 76 (low), 76 to 79 (moderate), 79 to 83 (high), and THI > 83 (critical). Weighting factors of −1, 0, 1, 2, 3, and 4 for each THI level were used to account for either a beneficial effect of lower THI (<68 and 68 to 72) to allow for cooling or an increasingly negative effect of THI greater than 72 due to heat stress. Using cumulative intensity*duration over 24 h, the heat load for each day was calculated.

Body temperature measurements

All heifers for each year were gathered early in the morning and were individually restrained in a squeeze-chute for insertion of temperature-recording devices. The vaginal temperature was recorded for five consecutive days using iButton data loggers, type DS1922L, temperature range −40 to 85 °C, accuracy +/− 0.5 °C, 11-bit for 0.0625 °C resolution (Maxim Integrated, San Jose, CA). Using the iButton technology allowed the assessment of an animal’s body temperature in response to naturally occurring heat challenges on pasture when animals were not disturbed by human intervention.

The iButtons were attached to a blank controlled internal drug-release (CIDR) device and were inserted into the vagina. Each iButton was calibrated before the start of the study and pre-programmed to record body temperature at 15 min intervals on a 24-h cycle. At the end of the trial, the data were downloaded and iButtons and CIDRs were sanitized. Hourly averages of vaginal temperature were calculated for each heifer and matched with the hourly THI average recorded at the same time. The body temperature data from the first and the last day when the CIDR was inserted and removed were excluded from the analysis due to human interactions. This left three continuous days of data, starting at 2400 hours the day of insertion, to reflect body temperature of heifers maintained on pastures and exposed to naturally occurring environmental stress during summer days in Florida without any human interaction.

Statistical analysis

Two strategies were used to evaluate the plasticity in body temperature of breed groups in response to environmental challenges: 1) a random regression mixed model was used to estimate reaction norm parameters for each breed group in response to a specified environmental heat stress and 2) a repeated measures mixed model was used to evaluate the response to different environmental heat loads.

Random regression (reaction norm) model

In the context of phenotypic plasticity, the phenotype of a group of genetically similar animals is described as a function of an environmental covariate that is expected to influence phenotypic expression. In this study, the phenotype of interest was vaginal temperature as a proxy for core body temperature. The environment was described by the THI and three THI classes were defined for low THI (74 to 76), average THI (79 to 81), and high THI (84 to 86). THI classes were coded as 0 (low), 1 (average), or 2 (high). Average body temperatures of individual heifers for each THI class from 0600 to 2000 hours were used in a random regression mixed model to estimate the reaction norm parameters for each breed group: an intercept (RN intercept) and a slope (RN slope). The intercept and slope parameters describing the reaction norm linear function are free to vary among breed groups and are treated as random effects drawn from distributions with means and (co)variance structures to be estimated. The RN intercept describes the body temperature when animals are exposed to low heat stress (THI of 74 to 76), and the RN slope describes the change in body temperature (phenotypic plasticity) in response to an increase of 5 THI units.

The data were analyzed with the MIXED procedure of SAS 9.4 (SAS Inst. Inc., Cary, NC) and restricted maximum likelihood (REML) estimation. The model used to analyze body temperature included year as class variable (2017 and 2018) and THI class continuous covariate as fixed effects. The RANDOM statement included the intercept and the slope with SUBJECT=breed group (n = 6) and TYPE=UN(1) that instructs PROC MIXED to estimate a random intercept and slope for each breed group to the fixed effects part of the model. The option TYPE=UN(1) specifies the covariance structure for a subject’s random effects and calls for an unstructured (2 × 2) covariance matrix, comprising the variance of the random slopes (σ _a²) and the variance of the random intercepts (σ _b²) on the diagonal and their covariance (σ _ab) off diagonal is set to zero. The fixed effects included a fixed intercept (automatically included through the MODEL statement), year effect, and THI class slope. The residuals are assumed to be independent and normally distributed with mean zero and variance σ ²_e.

Percent heterosis was estimated as the deviation of the crossbreds from the average of the two parental breeds. Using the slope of the reaction norm describing resilience to heat stress for breed group 4 (50% Brahman) and for breed groups 1 and 6 (0% Brahman and 100% Brahman, respectively), the percent heterosis was calculated using the formula:

$${\displaystyle \begin{array}{ll}{\displaystyle \mathrm{\%}\mathrm{H}\mathrm{e}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{o}\mathrm{s}\mathrm{i}\mathrm{s}=}& \left[\right(\mathrm{B}\mathrm{r}\mathrm{e}\mathrm{e}\mathrm{d}4-(\mathrm{B}\mathrm{r}\mathrm{e}\mathrm{e}\mathrm{d}1+\mathrm{B}\mathrm{r}\mathrm{e}\mathrm{e}\mathrm{d}6)/2\left)\right)/\\ & \left((\mathrm{B}\mathrm{r}\mathrm{e}\mathrm{e}\mathrm{d}1+\mathrm{B}\mathrm{r}\mathrm{e}\mathrm{e}\mathrm{d}6)/2\right)]\ast 100\end{array}}$$

Repeated measures mixed model

To assess how different breed groups respond to varying intensity and duration of heat stress during the days of the experiment, the body temperature data were analyzed using a repeated measure model where repeated measures were hourly body temperatures for individual heifers during each day of the experiment.

The covariance structure of residuals was modeled using first-order autoregressive correlation AR(1). A likelihood ratio χ ² statistic was used to select the appropriate model with respect to heterogeneity and covariance structure of residuals. Three models were considered: a basic model where no breed groups were considered which requires the estimation of only two parameters ρ and σ _e²; a model with breed group nested within the year which requires estimation of 24 parameters, two for each breed group and year; and a model with breed group nested within the year by day which requires estimation of 72 parameters, two for each breed group and each day in the experiment. The difference in −2ResLogLikelihood between two models has a χ ² distribution with degrees of freedom equal to the difference in the number of covariance parameters between the two models. For the three models described, the −2LogLikelihoods were −14,694.0, −17,556.6, and −18,770.5 with 2, 24, and 72 covariance parameters, respectively. The difference between −2ResLogLikelihood statistic from first to second and third model was 2,862.6 and 1,213.9 and the probability of these statistics relative to a χ ² with 22 df and 48 df are <0.0001, indicating that a model allowing the covariance structure and variance of residuals for each breed to vary for each day of the experiment is statistically appropriate. A Bayesian Information Criterion (BIC) statistic was also used to compare the fit of the three models (−2ResLogLikelihood of −14,682.6, −17,419.7, and −18,281.0, respectively). Based on this statistic, the third model with breed group nested within the year by day had the smaller BIC indicating the best fit and was used for subsequent analyses.

Data were analyzed with the MIXED procedure of SAS 9.4 (SAS Inst. Inc., Cary, NC) and REML estimation. The model included year, day(year), breed(year*day), and hour(year*day*breed) as fixed effects. The REPEATED statement used SUBJECT=cow(year*day), type=AR(1), and GROUP=breed(year*day) allowing for a different covariance structure of residuals and heterogeneous variances for each breed and each day of the experiment. The observations are hourly body temperatures for each heifer during the experiment and hours were 0001 to 2400 for each day in the experiment.

Results and Discussion

Ambient conditions

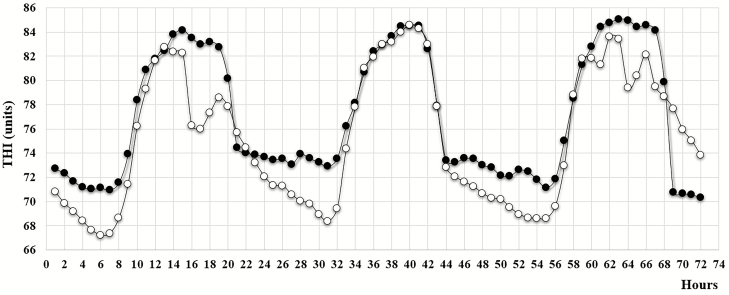
Ambient conditions described by the hourly average THI for the middle 3 d of the experimental period during 2017 and 2018 are shown in Figure 1. The air temperature exceeded 32 °C every day and never dropped below 20 °C during both years. The RH was approximately 50% to 60% at daytime and 96% to 100% at night. Under tropical and subtropical conditions, cattle are often heat challenged most of the time. Heat stress ambient conditions based on THI can be categorized as normal ≤ 74, moderate 75 to 78, severe 79 to 83, and very severe (emergency) ≥ 84 (LCI, 1970). In our study, cattle were exposed to moderate, severe, and very severe heat stress between 11 and 14 h each day and exposed to severe and very severe heat stress between 6 and 11 h each day.

Figure 1.

Hourly average THI for three consecutive days during 2017 (filled circles) and 2018 (open circles).

A cumulative intensity*duration over 24 h estimating the heat load for each day is shown in Table 1. The heat load of the 3 d in 2017 (40, 46, and 44) was higher than the heat load of the 3 d in 2018 (27, 34, and 35, respectively). Each day can be categorized based on this heat load index as moderate heat stress (day 1 in 2018), high heat stress (days 2 and 3 in 2018), and severe heat stress (days 1, 2, and 3 in 2017). The higher heat load and associated severe heat stress for all days in the year 2017 are due to a combination of relatively higher THI during the hottest part of the day between 1600 and 2100 hours and a relatively higher THI during the cooling period between 2100 and 1000 hours the following day.

Table 1.

Average THI, the number of hours for each THI level, and the cumulative heat load for each day during the study

		Average THI (number of hours)
Year	Day	<68	68 to 72	72 to 76	76 to 80	80 to 84	≥84	Heat load
2017	Day 1	0 (0)	71.25 (6)	73.56 (7)	78.37 (1)	82.38 (9)	84.14 (1)	40
2017	Day 2	0 (0)	0 (0)	73.40 (13)	77.42 (3)	82.45 (5)	84.50 (3)	46
2017	Day 3	0 (0)	71.02 (7)	72.86 (6)	79.20 (2)	82.04 (2)	84.62 (7)	44
2018	Day 1	67.41 (3)	69.71 (6)	73.84 (4)	77.35 (7)	82.24 (4)	0 (0)	27
2018	Day 2	0 (0)	70.29 (11)	73.07 (3)	77.80 (2)	82.42 (5)	84.27 (3)	34
2018	Day 3	0 (0)	69.30 (8)	74.43 (4)	78.79 (5)	82.06 (7)	0 (0)	35

Reaction norm analysis

The average body temperature and standard errors for each breed group and THI class are presented in Table 2. The average THI was 84.44 for high THI, 80.15 for mid THI, and 74.77 for low THI.

Table 2.

Number of observations, average body temperature (˚C), and standard deviation under low THI (74 < THI < 76), mid THI (79 < THI < 81), and high THI (84 < THI < 86) for each breed group and across the entire population (total)

		Low THI		Mid THI		High THI
Breed Group	N	Mean	SD	Mean	SD	Mean	SD
0% Brahman	54	38.66	0.20	39.03	0.45	39.49	0.41
25% Brahman	51	38.56	0.18	38.75	0.28	39.25	0.30
37.5% Brahman (Brangus)	59	38.57	0.19	38.79	0.23	39.17	0.25
50% Brahman	49	38.60	0.15	38.74	0.26	39.16	0.31
75% Brahman	33	38.57	0.12	38.65	0.13	39.04	0.22
100% Brahman	53	38.63	0.15	38.70	0.20	38.99	0.26
Total	299	38.60	0.17	38.78	0.30	39.19	0.34

Random regression models, or infinite dimensional models, are a special form of mixed-effect models in which individual phenotypes are modeled as a continuous function of a covariate. The parameters describing those functions (slope and intercept) are free to vary among breed groups and are treated as random effects drawn from distributions with means and (co)variance structures to be estimated. In the context of studying phenotypic plasticity, these models quantify and test the significance of reaction norm parameter variation between groups (Berry et al., 2003; Calus and Veerkamp, 2003; Cardoso and Tempelman, 2012).

In its simplest linear form, the slope of the reaction norm describes a breed group’s response to the environment and thus its phenotypic plasticity. In this model, the covariance between intercept and slope was set to zero. Therefore, the pattern of variation in reaction norm across breed groups is described by the between-breed group intercept variance (σ ²_a = 0.0023 ± 0.0021, P = 0.14) and the between-breed group slope variance (σ ²_b = 0.0064 ± 0.0044, P = 0.07). The intercept variance is equivalent to the between-breed group component of phenotypic variance when the environmental covariate THI class equals zero (low THI class).

If the between-breed group variance in slopes is not statistically significant, the variance attributable to individual breed groups will remain constant across all values of the environmental covariate and is used to estimate the repeatability of a trait (i.e., the proportion of phenotypic variance explained by individual breed group). However, if breed groups also vary in their plastic response to the environment (i.e., slopes), then the among-breed group variance for the trait will change across environmental conditions, complicating the definition and measurement of repeatability. In our study, the variance in slopes among breed groups approaches significance (P = 0.07), indicative of a breed group by environment interaction.

When assessing phenotypic plasticity, the components of interest are 1) the intensity of response (how fast does the phenotype change with the environment); 2) the direction of response (does it increase or decrease with the environmental variable); and 3) the total amount of change (the range of environmentally induced response). With a linear reaction norm implemented in this analysis, the intensity and direction are constant and measured by the slope and the total change is measured by the intercept and slope combined.

The solutions for the fixed effects population intercept, slope and year, and their standard errors are presented in Table 3. In this model, the THI classes are coded as 0, 1, and 2 representing low, mid, and high THI, respectively. Therefore, the intercept (38.60 ± 0.02) estimates the body temperature under low THI conditions and the slope (0.29 ± 0.03) estimates the change in body temperature for an increase in the THI index of about five units. This is equivalent to an increase of 0.29 °C in body temperature for 5 THI units increase in environmental heat stress.

Table 3.

The solutions for the fixed effects intercept, slope and year, their standard errors (SE), t-values, and P > |t|

Effect	Estimate	SE	|t| value	P-value > |t|
Intercept	38.60	0.02	1,577	<0.0001
Slope	0.29	0.03	8.53	<0.0001
Year
2017	−0.13	0.02	−6.96	<0.0001
2018	0

The random effect estimates presented in Table 4 are the estimated deviation for each breed group from the population mean intercept and slope, representing the Best Linear Unbiased Predictor estimates of the intercept and slope for each breed group.

Table 4.

The solutions for the intercept and slope random effects for each breed as deviations from the population intercept and slope, their standard errors (SE), t-values, and P > |t|

Effect	Breed	Estimate	SE	|t| value	P-value > ǀtǀ
Intercept
0% Brahman		0.059	0.03	1.94	0.05
25% Brahman		−0.039	0.03	−1.28	0.20
37.5% Brahman (Brangus)		−0.020	0.03	−0.67	0.50
50% Brahman		−0.003	0.03	−0.11	0.92
75% Brahman		−0.030	0.03	−0.90	0.37
100% Brahman		0.034	0.03	1.09	0.27
Slope
0% Brahman		0.124	0.04	3.25	0.001
25% Brahman		0.037	0.04	0.97	0.33
37.5% Brahman (Brangus)		0.004	0.04	0.11	0.91
50% Brahman		−0.011	0.04	−0.29	0.77
75% Brahman		−0.059	0.04	−1.48	0.14
100% Brahman		−0.095	0.04	−2.48	0.01

The intercept for the 0% Brahman breed group, or the body temperature for Angus heifers when environmental THI is low, was 0.06 °C and was significantly greater (P = 0.05) than the population average body temperature under low THI. The deviations of the intercept for all other breed groups from the population average are not statistically significant. A flatter reaction norm represented by a smaller slope indicates increased resilience to heat stress, and the slope estimates in Table 4 suggest that the resilience increases as the proportion of Brahman genes increases. The slope for the 0% Brahman (100% Angus) breed group is 0.417 °C (sum of population slope and 0% Brahman breed group slope) which is significantly greater (P < 0.001) compared with the population average slope. For the 25%, 37.5%, 50%, and 75% Brahman breed groups, the slopes show a numerical decrease with the increase in the percentage of Brahman genes, but these slopes are not significantly different from the population. This is similar to the differences reported by Dikmen et al. (2018) in this multibreed population cattle, where cattle with 50% or greater Brahman influence had significantly lower vaginal temperatures than cattle with 25% or less Brahman influence. The deviation for the 100% Brahman breed group is negative and significant (P = 0.01). These results suggest that cattle with 100% Brahman genetics have a superior tolerance to heat stress, reflected in a smaller increase in body temperature in response to an increase of 5 THI units in the environment. Angus cattle have a significantly lower thermotolerance reflected in a larger increase in body temperature.

The results from the reaction norm analysis showed a significant genotype by environment interaction for the body temperature in response to heat stress, as measured by the slope of reaction norm for breed groups with an increased proportion of Brahman genes. The second most important reason for using crossbreeding systems, after breed complementarity, is the heterosis effect, defined as the deviation of the crossbreds (50% Brahman) from the average of the two parental breeds (0% Brahman and 100% Brahman, respectively). The moderate heterosis of −8.35% estimated in this study indicates that the resilience to heat stress of an Angus × Brahman crossbred is 8.35% better than the average of the parental breeds due to heterosis. The favorable heterosis detected is consistent with the general view that fitness traits show greater heterosis than production traits such as growth and meat-type traits and with the genetic distance between the parental breeds which is maximized in this study. Consistent with the results from this study, Riley et al. (2012) reported favorable heterosis effects of larger magnitude for rectal temperature in Brahman–Angus (24%) and for Romosinuano–Angus (20%) crosses.

Repeated measures mixed model

When reaction norm models are nonlinear, the intensity of response is not constant: a particular genotype may be highly plastic during a certain environmental range while being nearly nonplastic at another environmental range. The direction of the response may also not be constant, where a genotype may respond to increasing environmental values with increasing phenotypic values but switch to producing lower phenotypic values when the environment continues to increase after a certain threshold. In this situation, the intensity and direction of the response for a given environmental interval may not apply to another interval. To explore the possibility of a nonlinear response, a repeated measures analysis was used.

All fixed effects were statistically significant (P < 0.001). The least square means for year and day nested within the year and their standard errors are presented in Table 5. The effect of the year on body temperature was significant (P < 0.0001) with higher body temperature in 2017. This effect could be explained by the higher average heat load for the experimental days in 2017 relative to the year 2018.

Table 5.

Least square means and standard errors for body temperature for fixed effects year, and day (yr)

Effect	Year	Day	Estimate, ˚C	SE	Heat load	Heterosis
Year	2017		38.85	0.008
Year	2018		38.77	0.006
Day(Year)	2017	1	38.81a	0.015	40	0.02
Day(Year)		2	38.84a	0.011	46	−0.01
Day(Year)		3	38.89b	0.013	44	0.01
Day(Year)	2018	1	38.67a	0.010	27	−0.17
Day(Year)		2	38.81b	0.009	34	−0.14
Day(Year)		3	38.83b	0.011	35	−0.13

^a,bWithin a column, least square means for day within the same year with the same superscript letter are not significantly different; those with different letters are significantly different with P ≤ 0.05.

Evaluating the day effect, days within each year can be compared which results in comparing the response of the same group of heifers. For the year 2017, the body temperature during day 3 is significantly higher relative to days 1 and 2 (P < 0.0005 and P < 0.01, respectively). The heat loads for days 1, 2, and 3 were 40, 46, and 44, respectively, and the significantly higher body temperature for day 3 could be a consequence of a cumulative effect of three high heat stress days in a row. For the year 2018, body temperature for day 1 is significantly lower relative to days 2 and 3 (P < 0.0001), and days 2 and 3 are not significantly different from each other. These differences match the difference in heat load for the 3 d (27, 34, and 35, respectively).

Heterosis, calculated for each day as the difference between the F1 crossbreds and the average of the pure-bred average, is shown in Table 5. Estimates of heterosis for each day in 2017 are essentially zero, and all these days are characterized by severe heat load. For the year 2018, heterosis is −17% for day 1 which has a moderate heat load indicating that crossbreds had 0.17 °C lower body temperature than the average of the purebreds. Slightly lower heterosis of −14% and −13% was estimated for days 2 and 3, respectively, both days characterized by higher heat load than day 1. Hammond et al. (1996) had similar findings related to heterosis for rectal temperature for crosses between Senepol and Hereford. A −9.4% heterosis was estimated for the hottest measurement summer day when the crossbreds were almost as heat tolerant as the Senepol. However, no heterosis was found for measurements taken during the winter, when there was no significant difference between the average rectal temperatures for Hereford and Senepol compared with the average for their reciprocal crosses.

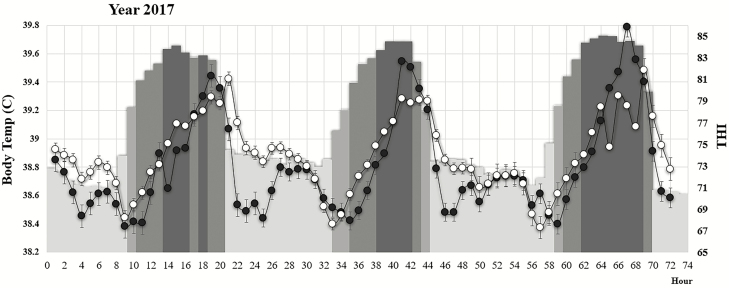
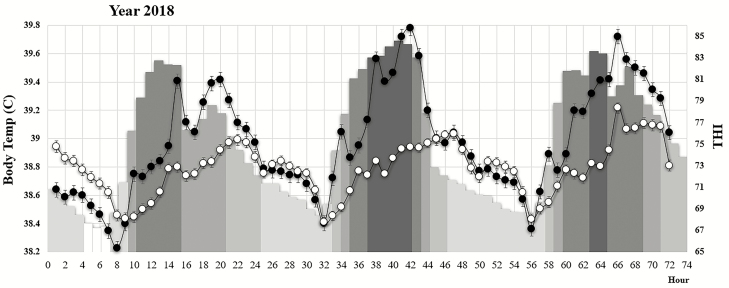
Least square means of hourly body temperature for Angus and Brahman heifers and hourly THI over 3 d in 2017 and 2018 are shown in Figure 2 and Figure 3, respectively. The plots are illustrating the daily patterns of environmental THI and associated changes in body temperature for the Angus and Brahman purebred groups. In general, body temperatures were low in the morning, with the lowest temperatures being recorded around 0700 to 0800 hours and peaked between 1600 and 2100 hours each day for both breed groups. This mirrors other reports in crossbred Angus × Simmental steers under heat stress conditions where the average body temperature was lowest between 0700 and 0800 hours (37.9 °C) with a peak at 1700 hours (39.1 °C) followed by a significant reduction to 38.9 °C by 1900 hours (Scharf et al., 2011). In many cases, multiple peaks of body temperature occurred during the day. Some of the multiple peaks could represent behavioral responses of heifers to seek shade or could have been caused by occasional rain events of short duration.

Figure 2.

Least squares means and standard errors of hourly average body temperature (°C, primary axis) for purebred Angus (filled circles) and purebred Brahman (open circles) for three consecutive days during 2017 when the heat load was severe for three consecutive days. The hourly average THI (secondary index) is depicted as gray-shaded bars based on the following scale:

Figure 3.

Least squares means and standard errors of hourly average body temperature (°C, primary axis) for purebred Angus (filled circles) and purebred Brahman (open circles) for three consecutive days during 2018. Heat load over the first and second day was moderate and high, respectively. The hourly average THI (secondary index) is depicted as gray-shaded bars based on the following scale:

The variation in environmental heat stress conditions ranging from days with moderate heat stress conditions to days with severe heat stress conditions provides the opportunity to compare the response of different breed groups under a range of heat stress environments. There are two important observations illustrated by our data. As shown in Figure 2, the heat load in 2017 was severe for three consecutive days and the body temperature of all heifers, regardless of breed group, was elevated. Under these extreme heat stress conditions, even the purebred Brahman heifers are not able to maintain body temperature below 39 °C. When heat load was moderate or high during 2018, Brahman heifers had a significantly lower body temperature compared with all other breed groups (Figure 3). During these days of medium to high heat stress, Brahman heifers were able to maintain body temperature below 39 °C (first and the second day in 2018, Figure 3) for most of the time. This is important because it was estimated (Gwazdauskas et al., 1973) that uterine temperature exceeding 39 °C was associated with a reduction in conception rate. The same temperature was shown to reduce blastocyst production in B. t. indicus cows as a result of compromise oocyte developmental capacity (Torres-Júnior et al., 2008). Based on our data, considering the 39 °C body temperature as a threshold to indicate the inability to cope with heat stress, we can infer that days with a heat load greater than 34 present a challenge for all heifers, regardless of breed, to maintain body temperature bellow 39 °C.

It is important to note that during 2017 when heifers were exposed to severe heat load for 3 d, the body temperature of Angus heifers was significantly higher (P < 0.05) than for Brahman heifers only for day 3. This could be an indication of a superior ability of Brahman heifers to adapt to several days of severe heat stress in a row. On the other hand, during 2018 when heifers were exposed to moderate and high heat load (first and second days in 2018, Figure 3), the body temperature in Angus heifers was significantly higher than in Brahman heifers for most of the day, approximately between 0900 and 2000 hours. Data presented in Figure 3 would also suggest that the critical factor in the ability to maintain a lower body temperature might not be the number of hours with high or extreme THI but rather the lack of opportunity to cool down during the night hours. During the three nights in 2017 which preceded the days with extreme heat stress conditions, the THI was not lower than 71. Mader et al. (2010) also concluded that crossbred steers with the ability to cool during the night hours are able to maintain a lower peak and mean body temperature when exposed to excessive heat load.

Conclusion

The reaction norm model used in this study can identify “robust” genotypes, genotypes with low slope values being representative of animals that maintain body temperature within normal limits across a range of environments. Based on the reaction norm analysis, breed groups with 75% and 100% Brahman genes had superior resilience to heat stress; breed groups with 25%, 37.5%, and 50% were intermediate between Brahman and Angus group; and the purebred Angus group had the lowest heat stress resilience. While this supports the use of Brahman genetics to improve thermotolerance in typical crossbreeding systems, it is also evident that given the random nature of segregation, a high percentage of Brahman genetics is needed to benefit from the increased heat tolerance. This also has a less desirable impact on other production traits such as reproduction and carcass quality.

The beneficial effect of Brahman genetics is dependent on the magnitude of environmental heat stress. When breed groups were exposed to moderate or high heat stress, the Brahman group had a significantly superior resilience to heat stress, but when exposed to severe heat stress even the Brahman group could not adequately cope. Along with the number of hours under high heat stress THI during the day, the opportunity to cool down during the night seems to be the critical factor. Climate change (IPCC, 2013) predictions with heat stress conditions intensifying and expanding into currently temperate zones indicate the imperative need to develop effective strategies to ensure sustainable beef production systems. Effective strategies will require for the identification of the genes conferring the superior thermotolerance in Brahman cattle. This will allow genomic selection within breeds for superior productivity under hot and humid conditions or the introduction of thermotolerance variants in thermo-sensitive breeds through targeted introgression or gene-editing technology.

Glossary

Abbreviations

CIDR

controlled internal drug-release

RH

relative humidity

THI

temperature–humidity index

Conflict of interest statement

There is no conflict of interest for any of the authors that may affect their ability to objectively present research or data.