Spatially-Variant Image-Based Modeling of PSF Deformations with Application to a Limited Angle Geometry from a Dual-Panel Breast-PET Imager

Abstract

Dual-panel PET system configuration can lead to spatially variable point-spread functions (PSF) of considerable deformations due to depth-of-interaction effects and limited angular coverage. If not modelled properly, these effects result in decreased and inconsistent recovery of lesion activity across the field-of-view (FOV), as well as mispositioning of lesions in the reconstructed image caused by strong PSF asymmetries. We implemented and evaluated models of such PSF deformations with spatially-variant image-based resolution modeling (IRM) within reconstruction (varRM) using the Direct Image REConstruction for Time-of-flight (DIRECT) method and within post-reconstruction deconvolution methods. In addition, DIRECT reconstruction was performed with a spatially-invariant IRM (invRM) and without resolution modeling (noRM) for comparison. The methods were evaluated using simulated data for a realistic breast model with a set of 5mm lesions located throughout the FOV of a dual-panel Breast-PET scanner. We simulated high-count data to focus on the ability of each method to correctly recover the PSF deformations, and a clinically realistic count level to assess the impact of low count data on the quantitative performance of the evaluated techniques. Performance of the methods evaluated herein was assessed by comparing lesion activity recovery (%BIAS), consistency (%SD) across the FOV, overall error (%RMSE), and recovery of each lesion location. As expected, all techniques using IRM provide considerable improvement over the noRM reconstruction. For the high-count cases, the overall quantitative performance of all IRM techniques, whether within reconstruction or within post-reconstruction, is similar if the lesion location misplacements are ignored. However, invRM provides less consistent performance on activity across lesions and is not able to recover accurate lesion locations. For a clinically realistic count level, varRM reconstruction consistently outperforms all compared approaches, while the post-reconstruction IRM approaches exhibit higher %SD and %RMSE values due to being more affected by the data noise than the within-reconstruction IRM approaches.

1. Introduction

Dual-panel detector PET systems have the advantage of lower costs and potentially increased sensitivity due to a better ability to closely confine the objects of interest within the panel detectors, compared to conventional ring systems. We are currently developing a dual-panel dedicated Breast-PET (B-PET) scanner which can be incorporated within the detector setup of a digital breast tomosynthesis (DBT) system (Krishnamoorthy et al., 2014; E. Lee et al., 2013; Matej et al., 2016; Surti & Karp, 2008) allowing for co-registered imaging of the breast within a common gantry. Such scanners can play an important role in diagnostic imaging, especially for patients with dense breast tissue, as well as in tumor characterization and monitoring response to therapy (Cole et al., 2003; Dehdashti et al., 2009; Eary et al., 2012; Kurland et al., 2012). To maximize the benefits of dedicated breast PET imaging, consistent quantification of lesions across locations within the field-of-view (FOV) and across repeated studies is required.

Challenging consequences of the dual-panel PET system geometry is their highly deformed and spatially variable point-spread functions (PSF). The deformation of the PSFs is mainly due to two main factors. Firstly, the parallax error, i.e. depth-of-interaction (DOI) effects, given by the small detector panel separation and flat configuration of the panels, and secondly, limited angle due to the finite size of the detector panels which violates Orlov’s condition (Orlov, 1975). It was previously shown that time-of-flight (TOF) information can help alleviate some problems due to the limited angular coverage, thus reducing distortions and image artifacts, and producing better quantitative images (E. Lee et al., 2013; Surti & Karp, 2008). However, the realistic TOF resolution of current dual-panel systems cannot fully eliminate the limited angle effects. As for the parallax error, although it could be decreased if the detector design allowed for the measurement of the DOI effects, it typically entails other trade-offs in performance or in cost.

Previous work done by our group demonstrated the feasibility and benefits of accurately modeling the spatially variable PSF deformations inherent of a dual-panel B-PET system (Matej et al., 2016). The main finding was a considerable improvement in consistency of the uptake measurements across lesions, independent of their location within the imaging FOV, when the deformation effects specific to the location of each lesion of interest were accurately modeled. However, in order to do so, separate reconstruction using a spatially-invariant image-based resolution model was required for each of the different PSF kernels specific to each lesion location. Although appropriate for a feasibility study, this approach can be inefficient and time consuming, especially if this method is to be applied routinely.

In this work, we have extended and improved this reconstruction approach (within the Direct Image REConstruction for TOF (DIRECT) framework) to include a spatially-variant image-based resolution model (IRM) within a single reconstruction. In addition, two post-reconstruction image deconvolution approaches, including the same spatially-variant IRM, have been implemented because of their execution time being considerably shorter. Finally, our proposed methods were evaluated on a realistic breast model with heterogeneous breast density and lesions simulated for a dual-panel B-PET scanner geometry, as well as evaluated using clinically relevant noise levels. Importantly, the results obtained were compared with those obtained from more conventional reconstruction methods, i.e. without IRM and with an average (across the object FOV) spatially-invariant IRM.

2. Theory

2.1. Resolution degradation and modeling

In PET imaging, degradation of the reconstructed image resolution stems from several effects during the data acquisition process. These effects range from physical factors such as photon acollinearity, positron range, detector resolution (based on finite crystal size), inter-crystal scatter, parallax effect (i.e. DOI), limited angle effect, to data and image discretization factors such as the spatial bases (e.g. voxels or blobs) and their corresponding size in the reconstructed image. All these effects contribute to the shape and width of the PSF.

Several approaches to minimize the impact of the resolution degradation effects on the reconstructed PET image have been proposed. These approaches can either be applied during reconstruction in data space (K. Lee et al., 2009; Tohme & Qi, 2009; Tong et al., 2010; Xu et al., 2019) and/or image space using resolution modeling (Angelis et al., 2015; Rapisarda et al., 2010; Reader et al., 2003; Sureau et al., 2008), or after reconstruction by using partial volume correction (PVC) techniques (Aston et al., 2002; Lehnert et al., 2012) as well as iterative deconvolution methods with resolution modeling (Cloquet et al., 2010; Cysouw et al., 2019). Of course, each approach has its own advantages and disadvantages. Modelling resolution in data space is usually more complex and less computationally efficient due to the higher dimensionality and size of the data (Cloquet et al., 2010). On the other hand, approximating resolution and PSF deformation effects in image space allows for efficient computation due to the modelling being applied in 3D image space as compared to higher-dimensional data space. Moreover, resolution modeling in image space can easily accommodate for spatially-variant kernels (Angelis et al., 2015; Kotasidis et al., 2011).

In iterative reconstruction algorithms, these resolution degradation effects, together with photon attenuation and scanner sensitivity (i.e. normalization), can be modelled in a factorized system matrix (Leahy & Qi, 2000; Qi et al., 1998) denoted P:

$$\mathbf{P}=\mathbf{N}{\mathbf{H}}_{\text{data}}\mathbf{A}\mathbf{X}{\mathbf{H}}_{\text{img}}+\mathbf{s}+\mathbf{r}$$ (1)

where H_img contains the degradation effects, which can be spatially-variant, in image space (e.g. positron range, photon acollinearity), X (commonly referred to as ‘Forward-Projector’) is a linear operator mapping the coincidence event emitted from the j^th voxel (in image space) to the i^th bin in data space (e.g. sinogram, histo-projection or histo-image for TOF) within which TOF resolution of the system can be modeled, H_data contains the degradation effects in data space (e.g. DOI, inter-crystal scatter), A and N respectively contains the attenuation and normalization (sensitivity) factors, s and r represent the scatter and randoms contributions respectively. In image-based resolution modeling, as applied in this work, the spatially-variant data resolution effects can be modeled within H_img.

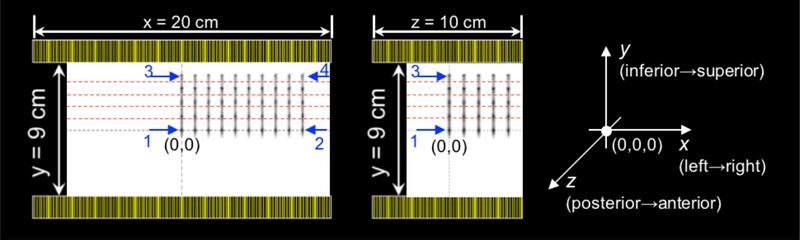
As mentioned in the introduction, the dual-panel configuration of our B-PET system can lead to spatially variable PSF with strongly anisotropic and asymmetric kernel deformations in the direction orthogonal (y direction) and locations closer to the detector panels compared to the directions parallel to the detector panels (x and z directions). This is illustrated in figures 1 and 2 which show the reconstructed points sources (PS) across the FOV, where the PS in the center plane (PS 1 and 2 located at y = 0 cm) have a similar and symmetric shape, while the PS close to the detector surface (PS 3 and 4 located at y = 2.5 cm) exhibit strong deformations and asymmetries in y (orthogonal). We include those spatially-variant PSF deformations into the image-based resolution model H_img.

Figure 1.

Transverse (left) and sagittal (middle) views of the PET simulation setup in GATE for the dual-panel B-PET scanner design showing the reconstructed point sources without resolution modeling. Note the asymmetry along the y-axis getting stronger (darker peak away from kernel center denoted by dashed red lines) as we move away from the x-axis and closer to the detector panels. The numbered blue arrows indicate the four point sources for which the profiles are shown in figure 2. The axes on the right show the orientation of the detectors in physical space (with y pointing up towards the patient’s head and z in the direction away from the chest wall).

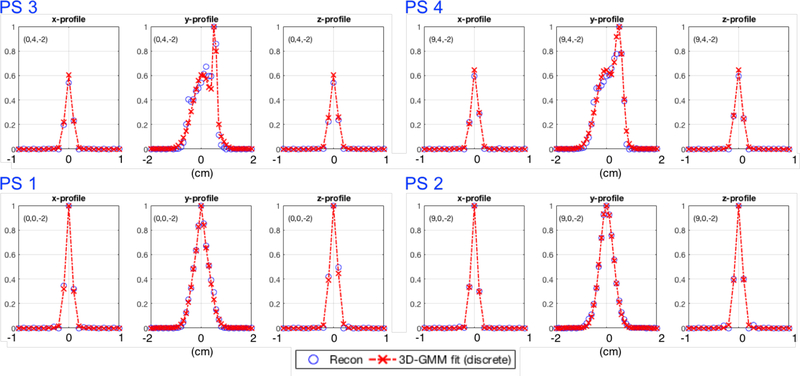
Figure 2.

Normalized profiles in x (left), y (center) and z (right) directions, through four reconstructed point sources (blue ‘o’) and corresponding PSF GMM discrete fits (red dashed lines) for the four point sources indicated with blue arrows in figure 1. Horizontal axis labels are in centimeters and 0 in each plot is relative to the exact point source location. The text annotation in each plot denotes the position in centimeters in the FOV.

Although our spatially-variant reconstruction model H_img can accommodate more complex models, for this work, each PSF kernel was parametrized by fitting each PS using a Gaussian mixture model (GMM) composed of two weighted 3D Gaussians (G1, G2):

$$GMM=\frac{1}{c}\left[w{G}_1+(1-w)G_2\right],$$ (2)

with G_i (i = 1,2) equals to:

$$\left[\frac{1}{{\sigma }_{x_i}\sqrt{2\pi }}exp-\frac{1}{2}{\left(\frac{x-s_{x_i}}{{\sigma }_{x_i}}\right)}^2\right]\left[\frac{1}{{\sigma }_{y_i}\sqrt{2\pi }}exp-\frac{1}{2}{\left(\frac{y-s_{y_i}}{{\sigma }_{y_i}}\right)}^2\right]\left[\frac{1}{{\sigma }_{z_i}\sqrt{2\pi }}exp-\frac{1}{2}{\left(\frac{z-s_{z_i}}{{\sigma }_{z_i}}\right)}^2\right]$$

where: $\sigma =\frac{\text{FWHM}}{2\sqrt{2\ln (2)}}$ is the standard deviation, s is the shift, w is the weighting factor (0 ≤ w ≤ 1), and C is a scaling factor normalizing the sum of each GMM to 1.

Of course, more elaborate models could be used to parametrize the PSF deformations, such as using more than two Gaussians in the GMM (Teimoorisichani & Goertzen, 2019). However, for this work and system, the use of two Gaussians was deemed enough to capture the PSF deformations and thus the shapes for the different PS across the FOV as shown in figure 2 illustrating two extreme cases: two point sources with only minor deformations in the center of FOV, and two point sources with strong deformations located at the edge of FOV.

2.2. Direct Image REConstruction for Time-of-flight (DIRECT)

Image-based resolution and deformation models are applicable to any non-TOF or TOF iterative reconstruction approach using list-mode, histo-projection or histo-image data, and using any iterative reconstruction algorithm. In this work we have adapted the Direct Image Reconstruction for TOF (DIRECT) approach to the dual-panel B-PET data and geometry. As presented in Matej et al. (2009), DIRECT is a reconstruction platform for TOF datasets that delivers reconstructed images of comparable metrics, and in a much more efficient manner, than computationally demanding list-mode approaches (Daube-Witherspoon et al., 2012; Matej et al., 2009). Traditionally, binned TOF events are histogrammed into histo-projections (projections extended in the TOF direction). In the DIRECT approach, the acquired events are histogrammed directly into the “most-likely” voxels of histo-images. The efficiency of DIRECT resides in this partitioning of the TOF data in the histo-image structures which have the same size and same spatial basis functions (e.g. voxel) as the final reconstructed image. This allows for very efficient implementation of reconstruction and data correction operations, while also preserving the geometrical accuracy (within the limits given by image and angular sampling), similar to list-mode approaches. This partitioning of the TOF data is performed in two steps: 1) sorting of the acquired events into a set of transaxial views and axial tilts; and 2) directly histogramming these sorted events into the “most-likely” voxels of the histo-image structures.

For the first step, data for a range of LOR directions having azimuthal angles ϕ (within xy-plane) and co-polar angles β (tilt toward z-direction), within a specified interval as given by angular sampling properties for TOF data, are grouped into a set of azimuthal views (N_ϕ) and axial tilts (N_β), each having their own specific TOF kernel. This grouping leads to less sparse and reduced data. In comparison to non-TOF datasets, the number of views and tilts can be reduced based on the angular sampling requirements of TOF data, whereas a better TOF resolution requires smaller number of views and tilts, with only a minimal or no loss of spatial resolution (Vandenberghe et al., 2005; Vandenberghe et al., 2006). Furthermore, for the TOF data (as opposed to non-TOF data) any spatial resolution loss due to the angular binning is approximately spatially-invariant (Vandenberghe et al., 2006), and can thus be efficiently modeled during reconstruction.

For the second step, the sorted events for each transaxial view and for each axial tilt are histogrammed directly into the “most-likely” voxels of its corresponding histo-image, which is to reiterate, of the same size and same spatial basis functions (e.g. voxel) as the final reconstructed image. This allows all reconstruction operations, including corrections (N, A, scatter, randoms), and data and image resolution models (H_data, H_img), as well as their transpose operations, to be efficiently performed directly on image structures (images or histo-images for each view and tilt). In addition, this alleviates the need of an X-ray transform (part of the conventional X operator) to map the image estimates into conventional data space (e.g. sinogram or histo-projection), resulting in efficient and considerably decreased reconstruction time (Daube-Witherspoon et al., 2012).

2.3. DIRECT for limited angle dual-panel B-PET data

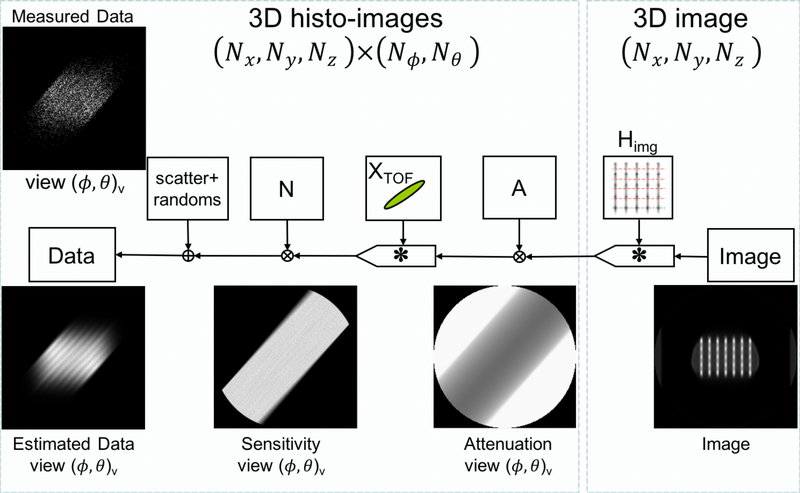
For the B-PET system, the dual flat panel configuration inherently has limited angular coverage (~132° in the center compared to 180° for a full cylindrical system) in the transaxial direction (xy-plane). Consequently, a range of the transaxial views are completely missing while others are not complete, thus creating missing regions in the corresponding histo-images. This effect is modeled in DIRECT using normalization histo-images created by the selective histogramming of the crystal-pair efficiency factors only along all valid LORs in the system, which properly reflects crystal and geometric sensitivities in the histo-image regions with available data and contain missing (set to zero) histo-image regions where there are no available LORs. Sequence of the operations for the forward model within the DIRECT reconstruction framework including IRM is illustrated in figure 3, with examples of correction and data histo-images for a particular view. Back-projection operation is just the transpose of the forward projection, utilizing the same histo-image structures. The iterative algorithm then, for each view and tilt of the histo-image structures, cycles through the forward model operation, the data discrepancy operator, and then the back-projection operation and image update operations as in any other iterative reconstruction scheme Matej et al. (2009).

Figure 3.

Flowchart for the forward projection operation as implemented within the DIRECT framework. The example is for iteration 2, where ϕ = 51° denotes azimuthal angles (xy-plane) and θ = 0° the co-polar angles (z-direction) with ‘v’ indexing the view. ‘×’ denotes a multiplication operation, ‘+’ an additive operation an ‘∗’ a convolution-like (i.e. can be spatially-variant) operation.

It is to note that for this case, equation (1) becomes:

$$\mathbf{P}=\mathbf{N}{\mathbf{X}}_{\mathbf{TOF}}\mathbf{A}{\mathbf{H}}_{\mathrm{img}}+\mathbf{s}+\mathbf{r}$$ (3)

where X_TOF models the TOF resolution (as well as the spatially-invariant portion of the LOR resolution) of the system (i.e. no need for the X-ray transform due to the data partitioning as explained in section 2.2 above), and A is applied (for each view and tilt) prior to modeling the TOF resolution since the attenuation factors are determined on the entire length of an LOR, and H_img models the residual LOR and spatially-variant data and PSF deformation effects in image space.

2.4. Post-reconstruction deconvolution with spatially-variant IRM

Two image-based deconvolution approaches applied post-reconstruction were investigated: Richardson-Lucy (Lucy, 1974; Richardson, 1972) a maximum-likelihood approach, and Landweber (Bertero & Boccacci, 1998) a regularized least squares approach. The Richardson-Lucy algorithm (referred to hereafter as varRL) is given by:

$${\mathbf{x}}^{k+1}={\mathbf{x}}^k{\mathbf{H}}_{\text{img}}^{\text{T}}\frac{{\mathbf{x}}_{\mathbf{noRM}}}{{\mathbf{H}}_{\text{img}}{\mathbf{x}}^k},$$ (4)

and the Landweber algorithm (referred to hereafter as varLW) by:

$${\mathbf{x}}^{k+1}={\mathbf{x}}^k+\lambda {\mathbf{H}}_{\text{img}}^{\text{T}}\left({\mathbf{x}}_{\mathbf{noRM}}-{\mathbf{H}}_{\text{img}}{\mathbf{x}}^k\right),$$ (5)

where k is the iteration number, x is a J×1 vector of the deconvolved image estimate, x_noRM is the J×1 vector of the ‘blurry’ reconstructed image without resolution modeling, H_img is a J×J matrix containing the spatially-variant resolution kernels, and l is a relaxation parameter (should be lower than 2). T denotes the transpose¹ and J is the total number of voxels (j) in image space. Multiplication by H_img (or its transpose) is a matrix multiplication, otherwise the operations are performed element-by-element.

3. Methods

3.1. Simulated B-PET system

The simulated B-PET system has two 20×10 cm² detector panels with 1.5×1.5×15mm³ LYSO crystals, and with panels spaced by 9 cm in y (figure 1). In the center of its FOV, the total transaxial angular coverage is ~132° (~73%, i.e. 132°/180°) and the total axial angular coverage is ~96°. This simulated system has a TOF resolution of 300ps and an energy resolution of about 12%.

3.2. Spatially-variant PSF kernel characterization

A set of 250 separate PS in air spaced every 10mm (10 in x, 5 in y, and 5 in z) throughout the positive octant of the FOV of the dual-panel B-PET scanner configuration (figure 1) were simulated with GATE (Jan et al., 2004). The PSF were characterized for the positive octant only, since symmetry allows for mirroring of the kernels in the x, y, and z directions when the axes are negative.

Each PS was reconstructed separately using DIRECT reconstruction with the row-action maximum likelihood algorithm (RAMLA) (Browne & De Pierro, 1996) algorithm (explained in more details below) without IRM and using 1mm³ isotropic voxels, consistent with the voxel size and algorithm parameters used in the subsequent evaluated reconstructions involving PSF-derived IRM. Each PSF kernel was parametrized in image space by fitting the corresponding converged reconstructed PS at iteration 20 ² using the GMM in (2). Each of the 250 GMM fit parameters were then saved in a lookup table for the evaluated reconstructions using spatially-variant based IRM.

3.3. Simulated data sets

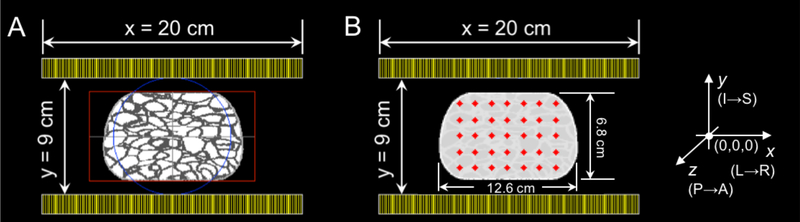
For the evaluation studies we simulated, using GATE (Jan et al., 2004), an anthropomorphic compressed breast phantom (12.60×6.80×6.15 cm³) containing a set of thirty-five lesions, i.e. 5mm diameter spheres (7 spheres in x and 5 spheres in y, spaced every 12.5mm on each side of the center) with an 8:1 activity:background ratio (figure 4) (Krishnamoorthy et al., 2018).

Figure 4.

Transverse view of the PET simulation setup in GATE for the anthropomorphic compressed breast phantom with the dual-panel B-PET scanner design. A) Realistic breast model including realistic heterogeneous breast density. The red box and blue circle are part of GATE visualization tool. B) Location of simulated lesions overlaid on attenuation map. The axes on the right show the orientation of the detectors in physical space (with y pointing towards head and z away from the chest wall).

We simulated three different count levels. A high-count simulation (~100 million counts collected over a 100 minutes imaging time) was first used to focus on the ability of each method to correctly recover the PSF deformations while minimizing the impact of the statistical noise on the results. Then in order to assess the performance of each method in terms of consistent quantification of lesions across locations within the FOV and across repeated studies for data with a realistic noise level, ten independent noisy realizations based on a clinically practical count level of 1.5 million counts emulating a 1.5 min scan were used. Finally, five independent noisy realizations with an intermediate count level of 20 million counts were used to observe the progression of the quantitative metrics with decreasing counts and increasing noise in the data.

3.4. DIRECT reconstruction

The data were histogrammed into 1×1×1mm³ histo-images with 3° transverse and 4.7° axial angular steps while limiting the transverse acceptance angle centered around the y-axis in the xy-plane to ±58° (from the maximum of ±66° in the center) and axial acceptance angle centered around the y-axis in the zy-plane to ±35° (from the maximum of ±48°), thus eliminating the mostly empty histo-images for oblique views, giving a total of 39 transverse (non-empty) views and 15 tilts. This chosen angular sampling steps satisfied the angular sampling requirements as given by the TOF and spatial resolutions of this system.

As described in (Daube-Witherspoon et al., 2012; Vandenberghe et al., 2006), the maximum angular interval (α_max) for which sampling of the data is adequate and consistent with the spatial resolution (FWHM_LOR) and timing resolution (FWHM_TOF) for a system can be estimated using:

$${\alpha }_{\max }={\tan }^{-1}\left[\frac{{\mathrm{FWHM}}_{\text{LOR}}}{\left({\text{FWHM}}_{\text{TOF}}\right)/2}\right],$$ (6)

where FWHM_LOR ≈ 1.9mm, and ${\text{FWHM}}_{\text{TOF}}=300\text{ps}\triangleq 45\text{mm}$, giving α_max ≈ 4.8°.

The row-action maximum likelihood algorithm (RAMLA) (Browne & De Pierro, 1996) implemented within the DIRECT framework was chosen as the reconstruction algorithm with a pragmatically chosen relaxation parameter of 0.1 and run for 100 iterations, based on our preliminary studies to provide stable performance and (practically) converged reconstructions. RAMLA is an accelerated maximum-likelihood algorithm similarly to OSEM, but with a proved convergence due to the view-by-view update strategy carefully controlled/relaxed by the product of attenuation and sensitivity factors and relaxation parameter. The relaxation parameter controls mostly the speed of convergence, if kept within reasonable practical bounds. Based on our prior experiences, for the whole-body applications, with relatively large attenuation along the LORs, the relaxation parameter can be kept at 1.0. For the reconstructions in this work involving a breast sized object with about 10-times lower attenuation, we correspondingly decreased the relaxation parameter to 0.1 (to provide similar overall relaxation to the whole-body studies).

During reconstruction, using the lookup table from Section 3.2, the GMM kernel closest to the location of each voxel was selected (analogous to a nearest-neighbor approach). For comparison purposes, reconstruction was also performed without IRM (noRM) and with a spatially-invariant IRM (invRM) using the average of fitting each PS with a single 3D-Gaussian, i.e. w = 1 in (2), of the reconstructed PSFs over the FOV (Section 3.2).

3.5. Post-reconstruction deconvolution with spatially-variant IRM

For this work, each post-reconstruction deconvolution algorithm (3 and 4) was run for 100 iterations, λ was set to 0.50 and 1.00 for Landweber (4), x_noRM consisted of the simulated breast phantom with lesions reconstructed with 10 iterations using DIRECT-RAMLA without IRM, and the initial image x⁰ was set to x_noRM.

3.6. Figures of Merit

In order to assess the performance between the different approaches implemented in this work, the following figures of merit were calculated across the spherical lesions.

The global lesion activity concentration averaged across lesions:

$$\overline{AC{T}_{\text{LSN}}}=\frac{{\sum }_{i=1}^{N}AC{T}_{{\text{LSN}}_i}}{N},$$ (7)

where is $AC{T}_{{\text{LSN}}_i}$ is the average activity concentration across voxels contained in 5mm diameter spherical volume of interest (VOI) overlaid on each lesion (LSN) i (N = 35).

Two methods were applied in order to overlay the VOIs on each reconstructed lesion. The first method simply used the true simulated coordinates as the center of each VOI. On the other hand, to emulate what is done in clinical practice, the second method used a semi-automated algorithm, whereas after manually selecting the center of each lesion on the reconstructed image or post-reconstruction deconvolved image (iteration 100 smoothed with a 5mm³ box kernel), the algorithm searches the VOI center coordinate on a super-sampled grid (0.1mm isotropic) for which the VOI mean is maximal.

Although the standard uptake value (SUV), or one of its related measures, is normally used by clinicians, we opted to show the activity concentration, since the SUV consists of the activity concentration divided by a scaling factor (i.e. injected activity and patient weight) which would be the same for all reconstruction and post-reconstruction approaches presented herein.

Percent bias (%BIAS) across lesions:

$$\%BIAS=100\times \left(\frac{1}{AC{T}_{\text{TRUE}}}\right)(\overline{AC{T}_{\text{LSN}}}-AC{T}_{\text{TRUE}}),$$ (8)

Percent standard deviation (%SD) across lesions:

$$\%SD=100\times \left(\frac{1}{\overline{AC{T}_{\text{LSN}}}}\right)\sqrt{\frac{{{\sum }_{i=1}^N\left(AC{T}_{{\text{LSN}}_i}-\overline{AC{T}_{\text{LSN}}}\right)}^2}{N-1}}.$$ (9)

Percent root mean square error (%RMSE) across lesions:

$$\%RMSE=100\times \left(\frac{1}{AC{T}_{\text{TRUE}}}\right)\sqrt{BIA{S}^2+S{D}^2}.$$ (10)

For the independent noisy replicates, in order to assess the stability of the above metrics across repeated studies for the clinically relevant count level of 1.5M counts, as well as the intermediate count level of 20M counts, the averaged %BIAS and %SD across the noisy replicates were used. These metrics are respectively defined as:

$$\%{\langle BIAS\rangle }_r=100\times \left(\frac{1}{AC{T}_{\text{TRUE}}}\right)\frac{{\sum }_{r=1}^{R}BIA{S}_r}{R},\%\langle SD{\rangle }_r=100\times \left(\frac{1}{\overline{{\langle AC{T}_{\text{LSN}}\rangle }_r}}\right)\frac{{\sum }_{r=1}^{R}S{D}_r}{R},$$

with: $\%{\langle RMSE\rangle }_r=100\times \left(\frac{1}{AC{T}_{\text{TRUE}}}\right)\sqrt{{\langle BIAS\rangle }_r^2+{\langle SD\rangle }_r^2}$

where 〈 〉_r denotes the average across replicates r and R the total number of replicates (R = 5 for the 20M count case and R = 10 for the 1.5M count case).

Finally, in order to evaluate the potential of each approach presented herein to recover the original location of each simulated spherical lesion, the effective (i.e. combining coordinates in x, y, and z) residual sums of square (RSS) was calculated between the estimated coordinates (EST) of each lesion center with the true coordinates (SIM) used in the simulation:

$$RS{S}_{\text{EFF}}=\sqrt{{\left(ES{T}_x-SI{M}_x\right)}^2+{\left(ES{T}_y-SI{M}_y\right)}^2+{\left(ES{T}_z-SI{M}_z\right)}^2.}$$ (11)

4. Results

4.1. High statistics simulation

The results shown in this section are for the high-count simulation, i.e. ~100 million counts. As mentioned in the Methods section, this is to focus on the validation of our reconstruction and post-reconstruction spatially-variant approaches on the resolution recovery of the PSF deformations, while minimizing the impact of noise on the results. For the varLW approach, only the results for the relaxation parameter λ set to 1.0 are shown for clarity. The results with λ set to 0.5 follow the same trend albeit being slower to converge.

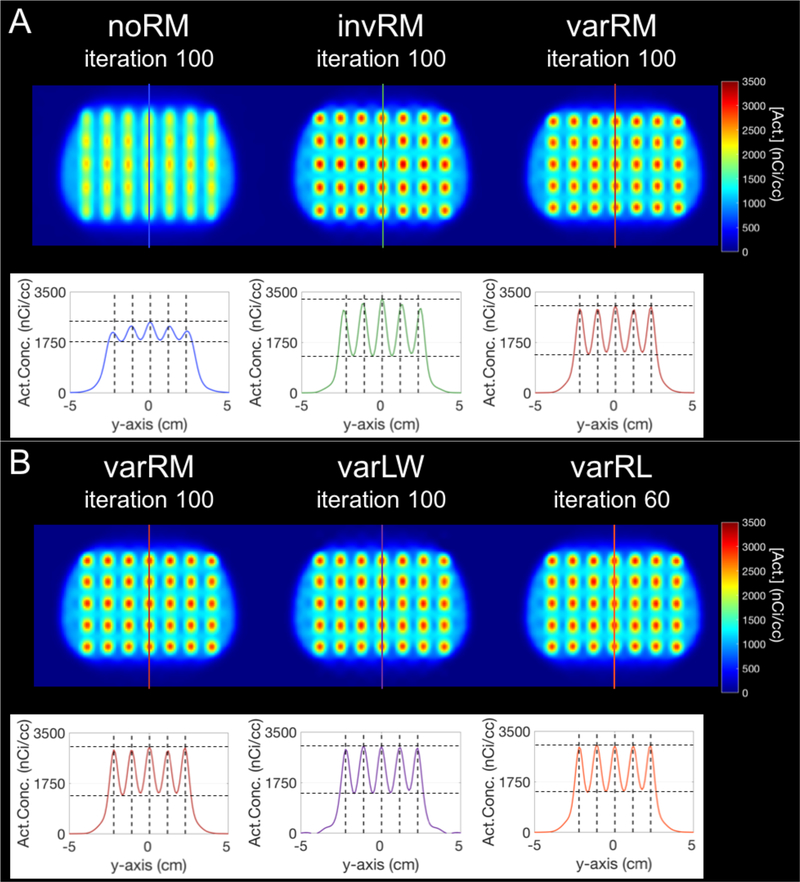
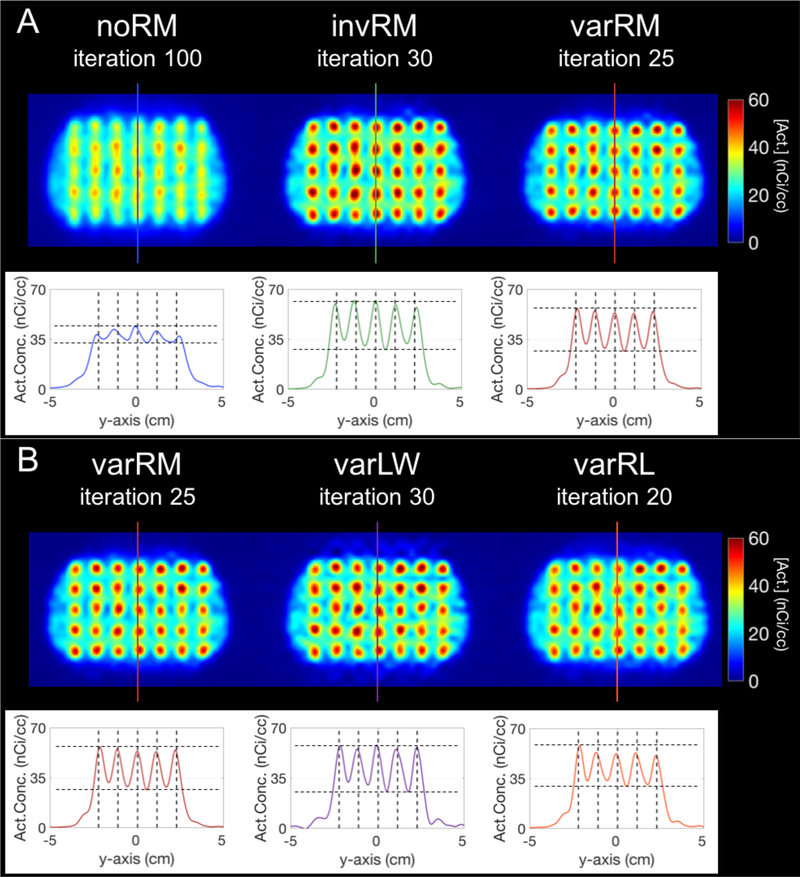
Figure 5A displays the slice through the center of the lesions (at z = −2 cm) of the simulated breast phantom with lesions (and corresponding profiles) reconstructed without IRM (noRM, left), spatially-invariant IRM (invRM, center), and spatially-variant IRM (varRM, right), while figure 5B displays the same slice but for the Landweber (varLW; center) and Richardson-Lucy (varRL; right) post-reconstruction deconvolution approaches compared to the varRM (left) reconstruction method. The iteration number corresponds to the iteration for which the %RMSE is minimal for each reconstruction method when using the estimated coordinates of the spherical VOIs (figure 6 bottom right).

Figure 5.

Slice at z = −2 cm of the simulated breast phantom and profiles for the high-count simulation with 100M counts. A-Top: Simulated breast phantom with lesions reconstructed without IRM (noRM, left), spatially-invariant IRM (invRM, center), and spatially-variant IRM (varRM, right). B-Top: Simulated breast phantom with lesions reconstructed using varRM (left; redisplayed here for easy visual comparison with varLW and varRL), and deconvolved post-reconstruction using the Landweber (varLW, center) and Richardson-Lucy methods with the same spatially-variant kernels as the varRM reconstruction approach. The iteration number corresponds to the iteration at lowest %RMSE for each reconstruction method when using the estimated coordinates of the spherical VOIs. For visual clarity, the images have been smoothed with a 5mm FWHM isotropic 3D-Gaussian kernel to emulate the voxel-wise VOI averaging performed for each 5mm diameter spherical lesions when calculating each metric. The colored lines overlaid on the center column of the lesions for each method correspond to the location of the profiles displayed underneath. A and B, bottom: Profiles of the center planes delineated by the corresponding colored lines on top. The vertical dashed lines mark the true centers of each simulated lesion, demonstrating better location recovery for methods with spatially-variant models. The horizontal dashed lines are to delineate the maximum peak and minimum trough for each case.

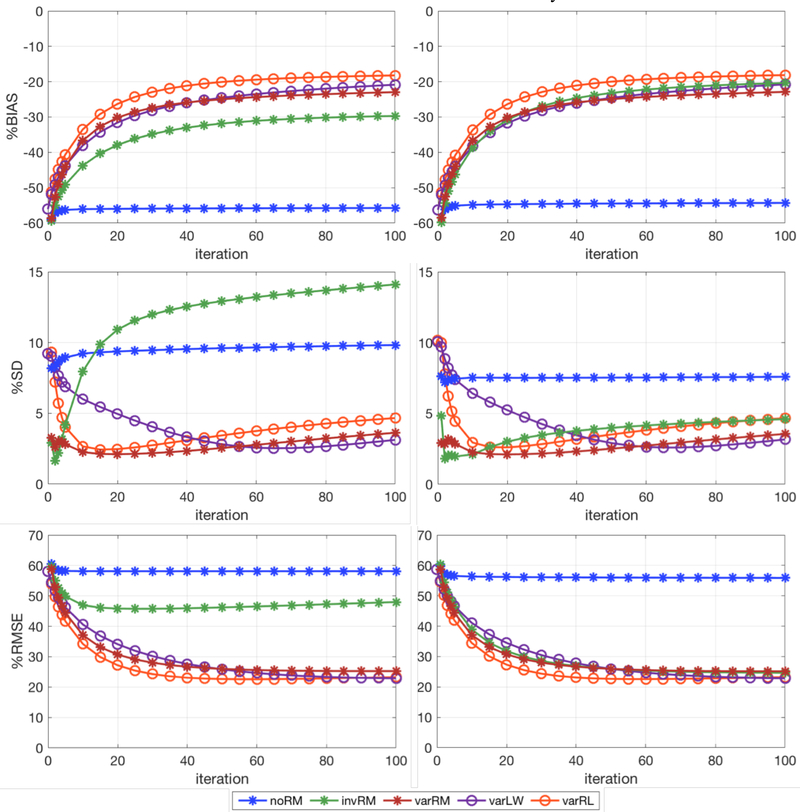
Figure 6.

%BIAS (Top), %SD (Middle), and %RMSE (Bottom) for the activity concentration calculated across the 35 simulated lesions vs iteration (iteration 1 to 5 and every 5th iterations afterwards up to 100 iterations), for the three reconstruction methods investigated in this work and the post-reconstruction deconvolution approaches. Left: Spherical VOIs centered at the simulated lesion coordinates. Right: Spherical VOIs centered on the coordinate for which the corresponding lesion mean activity concentration is maximal. noRM, invRM, and varRM are reconstructions without, with spatially-invariant, and with spatially-variant resolution modeling, respectively. varLW and varRL are respectively Landweber and Richardson-Lucy post-reconstruction deconvolution approaches using the same spatially-variant kernels as the varRM reconstruction.

To visually emulate the voxel-wise averaging within VOI performed for each spherical lesion (5mm diameter) during the calculation of each metric (e.g. %BIAS), the displayed images have been smoothed with a 5mm FWHM isotropic 3D-Gaussian kernel. The colored lines overlaid on the center column of the lesions for each method correspond to the location of the profiles (displayed underneath). The vertical dashed lines displayed for each profile mark the center of the simulated lesions (i.e. true location), and the horizontal dashed lines are to delineate the maximum peak and minimum trough for each case to assist with observing uniformity in activity recovery of the lesions.

Consistent with the quantitative performance seen in the plots shown in figures 6 and 7, the invRM and varRM methods clearly deliver images with better separation of the lesions in addition to better activity recovery, in comparison to the noRM method, with the varRM closely recovering the central locations of the simulated lesions as shown on the respective profile, i.e. peaks in its profile are closely aligned with the dashed lines showing true lesion locations (figure 5A). Moreover, the peaks for varRM are more uniform than for the noRM and invRM cases which exhibit a dome shape, i.e. decreasing values from the center. For this case of high-statistics, the post-reconstruction deconvolution methods deliver results similar to the varRM reconstruction method (figure 5B).

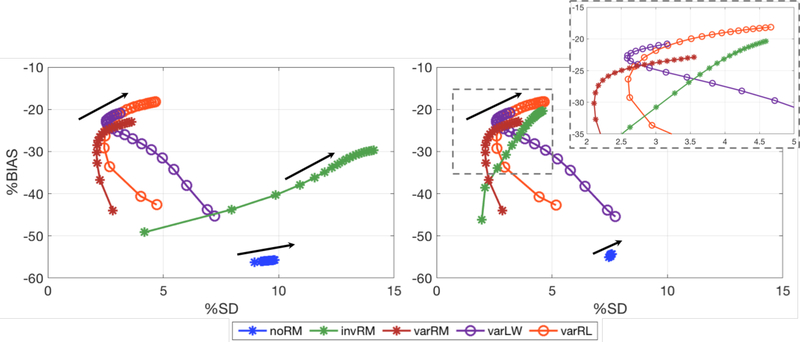
Figure 7.

%BIAS vs %SD tradeoff curves calculated across the 35 lesions for iterations 5 to 100 (every 5^th iteration) for the three reconstruction methods investigated in this work and the post-reconstruction deconvolution approaches. Left: Spherical VOIs centered at the true lesion coordinates. Right: Spherical VOIs centered on the coordinate for which the corresponding lesion mean activity concentration is maximal (a clearer aspect of the curves, except for noRM, can be viewed in the zoomed inset). The black arrows indicate the direction of increasing iterations. noRM, invRM, and varRM are reconstructions without, with spatially-invariant, and with spatially-variant resolution modeling, respectively. varLW and varRL are respectively Landweber and Richardson-Lucy post-reconstruction deconvolution approaches using the same spatially-variant kernels as the varRM reconstruction approach.

Figure 6 shows the global %BIAS (top), %SD (middle), and %RMSE (bottom), for the activity concentration calculated across the 35 lesions vs iteration for each of the three reconstruction methods investigated in this work and the post-reconstruction deconvolution approaches. The plots on the left show the results for the spherical VOIs centered on the simulated lesion coordinates, while the plots on the right show the results for the VOIs centered on the coordinate for which the lesion mean activity concentration is maximal.

Figure 7 shows the global %BIAS vs %SD tradeoff curves calculated across the 35 simulated lesions, as a function of iteration, for each of the three reconstruction methods investigated in this work as well as the post-reconstruction deconvolution approaches. The left plot shows the results for the spherical VOIs centered at the simulated lesion coordinates, while the plot on the right is for the VOIs centered on the coordinate for which the lesion mean activity concentration is maximal. The black arrows indicate the direction of increasing iterations.

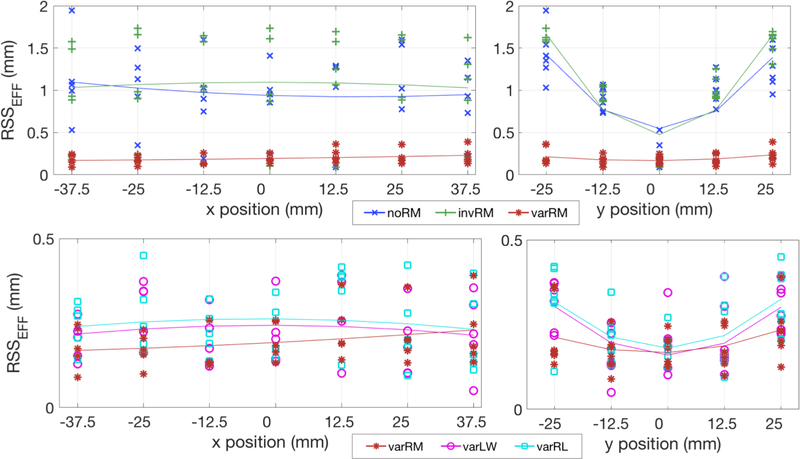
Figure 8 displays the effective residual sums of square (RSS_EFF) as given in (11), in x and y positions, between the estimated center coordinate for each of the 35 lesions and their corresponding true coordinate for the three reconstruction methods (top), and the post-reconstruction deconvolution approaches compared to the varRM reconstruction method (bottom). The solid lines correspond to a parabolic fit across the RSS values for each reconstruction method. A line closer to zero on the y-axis indicates estimated coordinates closer to the true coordinates, and a flatter line indicates more uniform reconstructed lesions across the FOV, and a better recovery of the reconstructed lesion true locations.

Figure 8.

Global RSS between the estimated and true center coordinate (in x and y directions) for each of the 35 spherical lesions. Top: Simulated breast phantom reconstructed without IRM (noRM), spatially-invariant IRM (invRM), and spatially-variant IRM (varRM) at iteration 100. Note the considerably better and more uniform location recovery, i.e. parabolic fit represented by the solid line is flatter and closer to y=0, of each lesion for our varRM reconstruction method in the y-direction, direction for which the PSF deformations are considerably stronger and thus requiring stronger resolution recovery. Bottom: Simulated breast phantom reconstructed with varRM (redisplayed here for easy visual comparison with varLW and varRL), and using Landweber (varLW) and Richardson-Lucy (varRL) post-reconstruction deconvolution methods using the same spatially-variant kernels as the varRM reconstruction approach, at iteration 100. The location recovery between our varRM reconstruction method and post-reconstruction deconvolution approaches are similar (i.e. similar RSS), however the location recovery with varRM is slightly better in y, i.e. slightly flatter parabolic fit represented by the solid line. Note: Plots of the 3 techniques using spatially-variable IRM shown in the bottom are zoomed to better show their differences.

As can be seen in figure 8 (top), our varRM reconstruction method delivers considerably better and more uniform lesion location recovery compared to the other two reconstruction methods, while the post-reconstruction deconvolution approaches are delivering similar results albeit slightly less uniform (figure 8, bottom).

4.2. Performance as a function of noise levels

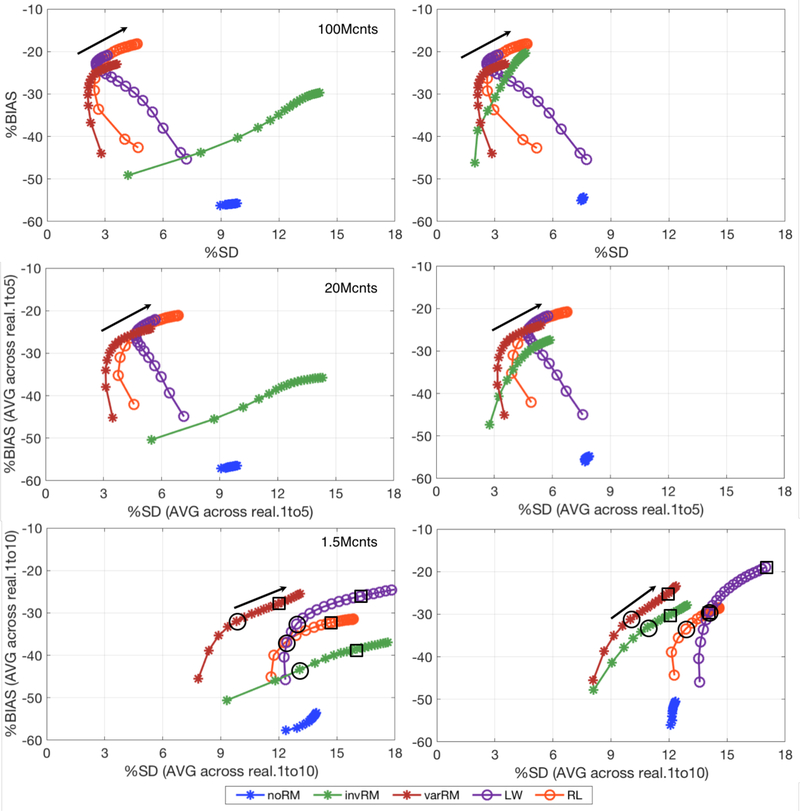
Figure 9 shows the global %BIAS vs %SD tradeoff curves for the high-count simulation with 100M counts (top), the intermediate case with 20M counts (middle) averaged across 5 realizations, and the clinically realistic case with 1.5M counts (bottom) averaged across 10 noisy realizations. Each metric was calculated, as a function of iteration, for each of the three reconstruction methods evaluated in this work as well as the post-reconstruction deconvolution approaches. The plots on the left show the results for the spherical VOIs centered at the simulated lesion coordinates, while the plots on the right show the results for the VOIs centered on the coordinate for which the lesion mean activity concentration is maximal. The black arrows indicate the direction of increasing iterations. For the clinically realistic case (bottom), the black circles indicate the iteration at which each method with IRM attain their minimum %RMSE value and for which their corresponding %BIAS, %SD, and %RMSE values are shown in table 1. Complementing this, the black squares indicate the iteration at which each method reaches convergence based on a 0.5% rule with their corresponding metrics shown in table 2. The 0.5% rule for convergence is defined as the first iteration at which the bias improvement is less than 0.5% in-between the successive iterations.

Figure 9.

%BIAS vs %SD tradeoff curves, for different noise levels, calculated across the 35 lesions for iterations 5 to 100 (every 5^th iteration) for the three reconstruction methods and the post-reconstruction deconvolution approaches investigated in this work. Top: 100M counts simulation (similar plots as those shown in figure 7, albeit at different scale in x). Middle: 20M counts simulation (bias and SD averaged across 5 independent noisy realizations). Bottom: clinically relevant 1.5M counts simulation (bias and SD averaged across 10 independent noisy realizations). The black circles indicate iterations corresponding to the minimum %RMSE (table1), while the black squares indicate iterations at convergence within the 0.5% rule (table 2). Left: Spherical VOIs centered at the true lesion coordinates. Right: Spherical VOIs centered on the coordinate for which the corresponding lesion mean activity concentration is maximal. The black arrows indicate the direction of increasing iterations. noRM, invRM, and varRM are reconstructions without, with spatially-invariant, and with spatially-variant resolution modeling, respectively. varLW and varRL are respectively Landweber and Richardson-Lucy post-reconstruction deconvolution approaches using the same spatially-variant kernels as the varRM reconstruction approach.

Table 1.

%BIAS, %SD and %RMSE values across 35 lesions for the clinically realistic case of 1.5M counts (averaged across 10 realizations) at the minimum %RMSE.

	metric	invRM	varRM	varLW	varRL
True coord. a	%BIAS	−43.40	−31.96	−32.58	−37.06
	%SD	13.09	9.82	12.92	12.30
	%RMSE	51.73	40.81	46.45	47.31
	iteration	15	25	25	15
Est. coord. b	%BIAS	−33.08	−31.23	−29.49	−33.46
	%SD	10.88	9.99	14.07	12.86
	%RMSE	43.13	40.71	47.87	46.66
	iteration	30	25	30	20

Table 2.

%BIAS, %SD and %RMSE values across 35 lesions for the clinically realistic case of 1.5M counts (averaged across 10 realizations) at convergence (based on the 0.5% rule).

	metric	invRM	varRM	varLW	varRL
True coord. a	%BIAS	−38.51	−27.53	−25.72	−32.24
	%SD	16.02	12.15	16.55	14.70
	%RMSE	53.71	43.32	53.33	49.72
	iteration	50	65	75	45
Est. coord. b	%BIAS	−29.58	−24.64	−18.95	−29.33
	%SD	12.26	12.08	17.00	14.12
	%RMSE	44.17	42.46	55.68	47.94
	iteration	65	80	100	50

^aTrue simulated coordinates: Spherical VOIs centered at the simulated lesion coordinates.

^bEstimated coordinates: Spherical VOIs centered on the coordinate for which the corresponding lesion mean activity concentration is maximal. invRM, and varRM: reconstruction with spatially-invariant, and with spatially-variant resolution modeling. varLW and varRL: Landweber and Richardson-Lucy post-reconstruction deconvolution approaches using the same spatially-variant kernels as the varRM reconstruction approach.

It is easily observable that as the noise level increases it becomes a dominant factor in the %SD measures, i.e. the curves are gradually shifting to the right to higher %SD levels in the lower plots (from their locations in the top plots). In addition, although the post-reconstruction methods deliver comparable results than varRM for the high-count case (top), the varRM method is able to deliver results with lower %SD at comparable %BIAS at the clinically realistic noise levels (bottom).

Figure 10 shows a sample reconstructed image of one of the noisy realization for the clinically realistic case with 1.5M counts (analogous to figure 5 for the high-count simulation with 100M counts), for which the iteration number corresponds to the iteration for which the %RMSE is minimal for each reconstruction method when using the estimated coordinates of the spherical VOIs (table 1).

Figure 10.

Slice at z = −2 cm of the simulated breast phantom and profiles for the clinically realistic case with 1.5M counts. A-Top: Simulated breast phantom with lesions reconstructed without IRM (noRM, left), spatially-invariant IRM (invRM, center), and spatially-variant IRM (varRM, right). B-Top: Simulated breast phantom with lesions reconstructed using varRM (left; redisplayed here for easy visual comparison with varLW and varRL), and deconvolved post-reconstruction using the Landweber (varLW, center) and Richardson-Lucy methods with the same spatially-variant kernels as the varRM reconstruction approach. The iteration number corresponds to the iteration at lowest %RMSE for each reconstruction method when using the estimated coordinates of the spherical VOIs (table 1). For visual clarity, the images have been smoothed with a 5mm FWHM isotropic 3D-Gaussian kernel to emulate the voxel-wise VOI averaging performed for each 5mm diameter spherical lesions when calculating each metric. The colored lines overlaid on the center column of the lesions for each method correspond to the location of the profiles displayed underneath. A and B, bottom: Profiles of the center planes delineated by the corresponding colored lines on top. The vertical dashed lines mark the true centers of each simulated lesion, demonstrating better location recovery for methods with spatially-variant models. The horizontal dashed lines are to delineate the maximum peak and minimum trough for each case.

The images were also smoothed with a 5mm FWHM isotropic 3D-Gaussian kernel in order to visually emulate the voxel-wise averaging within VOI performed for each spherical lesion (5mm diameter) during the calculation of each metric. The colored lines overlaid on the center column of the lesions for each method correspond to the location of the profiles (displayed underneath). The vertical dashed lines displayed for each profile mark the center of the simulated lesions (i.e. true location), and the horizontal dashed lines are to delineate the maximum peak and minimum trough for each case to assist with observing uniformity in activity recovery of the lesions.

Compared to the high-statistics case (figure 5), the iteration at which the %RMSE is minimal is lower for the noisy case, which makes it more difficult to visually see differences between the spatially-variant methods and the spatially-invariant case. However, looking at the quantitative performance displayed in the plots shown in figure 9 as well as the metrics depicted in tables 1 and 2, our within-reconstruction varRM method still delivers results with lower %BIAS and %CV (and thus lower %RMSE) compared to the spatially-invariant invRM method and post-reconstruction approaches. As for the post-reconstruction methods, the uniformity is clearly worse than for both the invRM and varRM approaches, which emphasizes the need to properly model the noise at low-count levels.

5. Discussion

The first two sections of the discussion (5.1 and 5.2) describe the results with regard to the high-count simulation for which our spatially-variant methods were evaluated based on their performance on how well resolution recovery of the PSF deformations is achieved, while minimizing the noise impact. Section 5.3 discusses the results as a function of noise levels, especially for a noise level that is more clinically realistic. Finally, section 5.4 describes implementation considerations.

5.1. Reconstruction with spatially-variant IRM

As expected, reconstructions using resolution models, whether spatially-variant (varRM) or averaged spatially-invariant (invRM), clearly outperform reconstructions without resolution modeling (noRM) by providing results with considerably lower %BIAS, %SD, and %RMSE (figures 6 and 7) and much clearer lesion separations (figure 5).

For the invRM we averaged the PSF model fits over the points distributed over the whole FOV. This RM captures the dominant deformation effect in the dual-panel B-PET system, namely the average PSF elongation in the direction normal to the detector panels, and thus provides on average comparable lesion activity concentration recovery (over all locations) to the more accurate spatially-variant model. However, because the average resolution model does not capture the spatially-variant shape and asymmetry of the PSFs for lesions out of the central plane in-between the detector panels, it leads to displaced locations (figures 5 and 8) and variable contrasts of individual lesions. This leads to clearly suboptimal performance of the invRM, as compared to varRM, for the case when the lesions are quantified at their true locations, such as when using the co-registered DBT scan, as seen in the left plots in figures 6 and 7. Consequently, the lesion center location misplacement can pose a problem for PET-guided lesion biopsy using the reconstructed emission image with invRM.

When the lesion locations are estimated based on the search for their maximum uptake, the invRM method delivers results with slightly better average activity recovery (%BIAS of invRM = −20.35% vs. varRM = −22.89%), but with a slightly worse consistency across the FOV (%SD of invRM = 4.59% vs. varRM =3.55%), as compared to varRM. Particularly, if we compare the lesion uptake measures at individual locations throughout the object FOV, the invRM exhibits larger spread of their values because of the gradual deformation increase in y when getting closer to the detectors (figures 1 and 2). For example, we have observed that the %BIAS for invRM increases from about 15% for the 5 lesions located at 0cm (indicated by the 3rd row of overlaid lesions in figure 4B) to about 22% for the 10 lesions located at ±2.5cm (lesions closer to the detector panels; first and fifth rows of overlaid lesions in figure 4B), and the %SD increases from about 2% to 4%. For the varRM the %BIAS and %SD stay similar (%BIAS: changes from −20% to −17%, and %SD changes from 2.3% to 2.8%) thus delivering more consistent results across the locations.

5.2. Post-reconstruction deconvolution with spatially-variant IRM

While the within-reconstruction approach (varRM) provides slightly better and more uniform recovery of the true lesion location (figure 8), the post-reconstruction deconvolution approaches (varLW and varRL) using the same spatially-variant resolution model deliver results of comparable or slightly improved %BIAS (figure 7) for the high-count data.

This slight improvement in bias performance could be explained by the data resolution effects (H_data) being modeled (only) “approximately” in image space within H_img for the within-reconstruction modeling approaches as explained in section “2.1 Resolution degradation and modeling”. On the other hand, for data with realistic noise levels, proper modeling of the (Poisson) noise distribution within statistical reconstruction becomes more important, as discussed in the following section.

5.3. Performance as a function of noise levels

As displayed in figure 9, the global %SD, calculated across the 35 lesions, increases with the noise. This is displayed with the %BIAS-%SD curves shifting to the right (towards higher %SD) from the top to the bottom plots, i.e. from the high counts to lower counts, while the converged %BIAS values stay similar as would be expected (except for an artificial decrease of the %BIAS for varLW, as will be discussed below). In addition, as mentioned above, although the post-reconstruction methods provide %BIAS vs %SD trade-offs (close to convergence) comparable to the within-reconstruction varRM approach for the higher count cases (top and middle plots in figure 9), the varRM method is able to deliver the best %BIAS vs %SD trade-off curves compared to all studied approaches for the clinically relevant count level (see figure 9-bottom for the 1.5M count case). This underscores the importance to accurately model (both spatially and statistically) the data properties directly within the reconstruction at lower counts (i.e. clinically realistic counts).

While the trade-off curves provide valuable insight into the overall performance of the techniques under evaluation, choosing particular reconstruction parameters of interest (such as the number of iterations) will depend on the particular clinical task at hand and its corresponding prerequisites. In this work, we chose two complementary tasks. First, we selected a task optimizing balance between accuracy (bias) and precision (SD) by choosing the iteration for each method with minimum %RMSE (table 1). Secondly, we compared each IRM technique at (or very close to) convergence (table 2), for a task requiring the lowest possible bias even at the cost of higher uncertainty (SD). It is to note that although we used the bias, the “0.5% convergence rule” could also be calculated in terms of reconstructed activity (as a function of iteration) when a ground-truth is not available as is the case in practice. These comparisons were done for the clinically realistic count level (1.5M counts). It is clearly seen from tables 1 and 2 that varRM provides the lowest %RMSE and %SD values compared to all of the other evaluated techniques for both tasks. Concentrating solely on the bias, only varLW is able to provide improved bias over varRM, although this is achieved at the cost of increased variability and clearly higher %RMSE values, perhaps suggesting that the increased lesion uptake values and corresponding decrease of the bias offered by varLW might be artificially caused by the higher noise levels, as discussed below.

When comparing the two post-reconstruction deconvolution algorithms at the clinically relevant count level (1.5M counts), although the increased noise affects these two techniques (with different statistical models) in different ways, both techniques exhibit increased %RMSE values as compared to the within-reconstruction IRM approaches, even compared to invRM (for the realistic case of estimating the lesion centers). For the varRL technique, the %BIAS and %SD saturate as it converges to a more biased level when compared to the high-count case. On the other hand, for the varLW method, although the %BIAS is decreased in an absolute sense, both %BIAS and %SD continue to gradually change in sync throughout the iterations without a fast slow-down. This difference is due to the fact that the Richardson-Lucy algorithm, relying on Poisson data model, does not accurately model the statistical noise in the reconstructed images and thus (together with its non-negativity constraint) provides worse performance compared to the within-reconstruction approaches that better captures the data noise model. On the other hand, Landweber, a least squares approach which does not rely on the Poisson data model, has a better performance than RL but suffers with a worse noise performance due to negative values being allowed, thus allowing gradual growth of the noisy peaks, which are then compensated by growing negative noisy peaks. In fact, we have observed (not shown here) that the noise and uptake values keep increasing even if iterated until 2000 iterations. For example, at iteration 2000, varLW has a %BIAS of only −7%, but with a %SD 36% and a %RMSE as high as 126%. This improvement in the bias may be artificial and affected by an unacceptable uncertainty.

5.4. Implementation considerations

Post-reconstruction deconvolution approaches offer a noticeable increase in convergence and computational speed as compared to within-reconstruction resolution modeling approaches which requires 3D convolution operations to be applied to the image within each forward- and back-projection operations for each view (post-reconstruction deconvolution approaches thus take roughly about two orders of magnitude less computations). A possible speed-up could be obtained by extending the varRM approach to include a nested image deconvolution loop, i.e. using a few deconvolution sub-iterations for each reconstruction iteration (Angelis et al., 2013).

Concerning our implementation of the spatially-variant IRM method, using a lookup table with a nearest neighbor scheme (to select the PSF kernel corresponding to a location in the FOV) may not be optimal due to the discretization of the kernel grid. Although, if enough point sources are acquired and their PSF parameters characterize, this grid could be well sampled. Ideally, we would like to have the parameters for a few points sources covering the overall FOV, and then fit or interpolate between the different locations to get a continuous estimate of the in-between locations. Unfortunately, in this work, no continuity could be found between each of the thirteen parameters of the 3D-GMM (using two separate 3D Gaussians) for the point sources across the FOV. Future work could investigate if a machine learning algorithm could potentially resolve this issue, or using a model other than a 3D-GMM. For example, other models with less parameters, such as asymmetric (left or right) Gaussians (Cloquet et al., 2010; Rapisarda et al., 2010; Wiant et al., 2010) could be potential candidates.

6. Conclusion

In this work, we have implemented, evaluated, and demonstrated that spatially-variant image-based resolution modelling, implemented within the DIRECT framework (varRM) and within post-reconstruction deconvolution approaches (varRL and varLW), delivers considerable improvement in activity concentration recovery (i.e. lower %BIAS) and consistency across the FOV (i.e. lower %SD) when compared to the noRM reconstruction method, and better consistency over the spatial locations as compared to the spatially-invariant resolution modeling case using an averaged resolution model (invRM). In addition, our varRM reconstruction method substantially outperforms both noRM and invRM in recovering the original position of each simulated lesion. As for the post-reconstruction deconvolution approaches (varLW and varRL), when compared to the varRM reconstruction at high statistics, both can deliver comparable results in terms of %BIAS and %SD, but with a slightly less accurate location recovery. However, for a typical clinically realistic count levels with higher-noise, the within-reconstruction spatially-variant varRM approach outperforms all studied techniques by delivering lower %RMSE and other metrics, while the post-reconstruction varLW and varRL approaches manifest increased %SD and correspondingly increased %RMSE, which confirms the importance of the accurate modeling of PSF deformations directly within the reconstruction at clinically realistic lower counts.