Hierarchical Normalized Completely Random Measures for Robust Graphical Modeling

Abstract

Gaussian graphical models are useful tools for exploring network structures in multivariate normal data. In this paper we are interested in situations where data show departures from Gaussianity, therefore requiring alternative modeling distributions. The multivariate t-distribution, obtained by dividing each component of the data vector by a gamma random variable, is a straightforward generalization to accommodate deviations from normality such as heavy tails. Since different groups of variables may be contaminated to a different extent, Finegold and Drton (2014) introduced the Dirichlet t-distribution, where the divisors are clustered using a Dirichlet process. In this work, we consider a more general class of nonparametric distributions as the prior on the divisor terms, namely the class of normalized completely random measures (NormCRMs). To improve the effectiveness of the clustering, we propose modeling the dependence among the divisors through a nonparametric hierarchical structure, which allows for the sharing of parameters across the samples in the data set. This desirable feature enables us to cluster together different components of multivariate data in a parsimonious way. We demonstrate through simulations that this approach provides accurate graphical model inference, and apply it to a case study examining the dependence structure in radiomics data derived from The Cancer Imaging Atlas.

1. Introduction

Graphical models describe the conditional dependence relationships among a set of random variables. A graph G = (V, E) specifies a set of vertices V = {1,2, …, p} and a set of edges E ⊂ V × V. In a directed graph, edges are denoted by ordered pairs (i, j) ∈ E. In an undirected graph, (i, j) ∈ E if and only if (j, i) ∈ E (Lauritzen, 1996). Here we focus on undirected graphical models, also known as Markov random fields. In this class of models, the absence of an edge between two vertices means that the two corresponding variables are conditionally independent given the remaining variables, while an edge is included whenever the two variables are conditionally dependent.

In the context of multivariate normal data, graphical models are known as Gaussian graphical models (GGMs) or covariance selection models (Dempster, 1972). In this setting, the graph structure G implies constraints on the precision matrix (the inverse of the covariance matrix). Specifically, a zero entry in the precision matrix corresponds to the absence of an edge in the graph, meaning that the corresponding nodes (variables) are conditionally independent. Since graphical model estimation corresponds to estimation of a sparse matrix, regularization methods are a natural approach. In particular, the graphical lasso (Meinshausen and Bühlmann, 2006; Yuan and Lin, 2007; Friedman et al., 2008), which imposes an L₁ penalty on the sum of the absolute values of the entries of the precision matrix, is a popular method for achieving the desired sparsity. Among Bayesian approaches, the Bayesian graphical lasso, proposed as the Bayesian analogue to the graphical lasso, places double exponential priors on the off-diagonal entries of the precision matrix (Wang, 2012; Peterson et al., 2013), while approaches which enforce exact zeros in the precision matrix have been proposed by Roverato (2002), Jones et al. (2005), and Dobra et al. (2011). Gaussian graphical models have been widely applied in genomics and proteomics to infer various types of networks, including co-expression, gene regulatory, and protein interaction networks (Friedman, 2004; Dobra et al., 2004; Mukherjee and Speed, 2008; Stingo et al., 2010; Telesca et al., 2012; Peterson et al., 2016).

Some extensions of standard Gaussian graphical models exist in the literature for the analysis of data that show departures from normality. Among others, Pitt et al. (2006) used copula models and Bhadra et al. (2018) used Gaussian scale mixtures. Here, we build upon the approach of Finegold and Drton (2011, 2014), who introduced a vector of positive latent contamination parameters (divisors) regulating the departure from Gaussianity and then modeled those as a sample from a nonparametric distribution, specifically a Dirichlet process. Their model, however, does not allow the exchange of information among the vectors of observed data, since independent Dirichlet process priors are used for each of the n samples. We propose to use a more flexible class of nonparametric prior distributions, known as normalized completely random measures (NormCRMs), and consider a hierarchical construction where the nonparametric priors for the divisors are conditionally independent, given their centering measure, which is itself a completely random measure. NormCRMs were first introduced by Regazzini et al. (2003) with the name of Normalized Random Measures with Independent increments (NRMI), and subsequently studied by several researchers in statistics and machine learning (James et al., 2009; Lijoi and Prünster, 2010; Caron and Fox, 2017). One of the most commonly used measures in this class is the Normalized Generalized Gamma (NGG) process (Lijoi et al., 2007). For illustrations of the use of this prior in mixture models, see Argiento et al. (2010), Barrios et al. (2013), and Argiento et al. (2016). Theoretical and clustering properties of hierarchical CRMs were first investigated by Camerlenghi et al. (2019) (see also Camerlenghi et al., 2017, 2018). Subsequently, Argiento et al. (2019) have focused on clustering and computational issues arising under mixture models built upon this class of priors. In this paper, we exploit the clustering characterization of these constructions to induce sharing of information. More specifically, we focus our attention on the normalized generalized gamma process, which has been shown to yield a quite flexible clustering structure. Furthermore, we devise a suitable MCMC algorithm for posterior sampling.

We are motivated by an application to radiomics data derived from magnetic resonance imaging (MRI) of glioblastoma patients collected as part of The Cancer Imaging Atlas. In the development of personalized cancer treatment, there is great interest in using information from tumor imaging data to better characterize a patient’s disease, as these medical images are collected as a routine part of diagnosis. There have been a large number of different numerical summaries proposed, but the interpretation of these features is not immediate. It is hypothesized that clinically relevant features may be capturing related aspects of the underlying disease. Statistical modeling of the dependencies in radiomics data poses challenges, however, as the features exhibit outliers and overdispersion due to heterogeneity of the tumor presentation across patients.

The paper is organized as follows: we begin in Section 2 with a review of graphical models. In Section 3, we lay out the proposed model and summarize computational methods for inference. We then illustrate the application of the method to both simulated and a publicly available radiomics data set in Section 4. Finally, we conclude with a discussion on the current model as well as future directions in Section 5.

2. Background

2.1. Gaussian Graphical Models

Let $X_i\in {ℝ}^p$ be a random vector, with i = 1, …, n. In GGMs, the conditional independence relationships between pairs of nodes encoded by a graph G correspond to constraints on the precision matrix Ω = Σ⁻¹ of the multivariate normal distribution

$$X_i~{\mathcal{N}}_p(\mu ,\Sigma ),i=1,\dots ,n,$$ (1)

with $\mu \in {ℝ}^p$ the mean vector and $\Sigma \in {ℝ}^p\times {ℝ}^p$ a positive definite symmetric matrix. Specifically, the precision matrix Ω is constrained to the cone of symmetric positive definite matrices with off-diagonal entry ω_ij equal to zero if there is no edge in G between nodes i and j.

In Bayesian analysis, the standard conjugate prior for the precision matrix Ω is the Wishart distribution. Given the constraints of a graph among the variables, Roverato (2002) proposed the G-Wishart distribution as the conjugate prior. The G-Wishart is the Wishart distribution restricted to the space of precision matrices with zeros specified by a graph G. The G-Wishart density W_G(b, D) can be written as

$$p(\Omega |G,b,D)=I_G{(b,D)}^{-1}{\left|\Omega \right|}^{(b-2)/2}\text{ exp}\left\{-\frac{1}{2}\text{tr}(\Omega D)\right\},\Omega \in P_G$$

where b > 2 is the degrees of freedom parameter, D is a p×p positive definite symmetric matrix, I_G is the normalizing constant, and P_G is the set of all p × p positive definite symmetric matrices with ω_ij = 0 if and only if (i, j) ∉ E. Even when the graph structure is known, sampling from this distribution poses computational difficulties since both the prior and posterior normalizing constants are intractable. Dobra et al. (2011) proposed a reversible jump algorithm to sample over the joint space of graphs and precision matrices that does not scale well to large graphs. Wang and Li (2012) and Lenkoski (2013) proposed sampler methods that do not require proposal tuning and circumvent computation of the prior normalizing constant through the use of the exchange algorithm, improving both the accuracy and efficiency of the computations. Mohammadi and Wit (2015) proposed a sampling methodology based on birth-death processes for the appearance or removal of an edge in the graph. Their algorithm, implemented in the R package BDgraph, can be used with the approximation of the normalizing constant of the G-Wishart prior calculated either via the Monte Carlo method of Atay-Kayis and Massam (2005) or the Laplace approximation of Lenkoski and Dobra (2011).

To sum up, we can write the standard Gaussian graphical model in the Bayesian setting as:

$$\begin{gathered} {\mathit{X}}_1,\dots ,{\mathit{X}}_n|\mathit{\mu },\Omega ,\stackrel{iid}{~}{\mathcal{N}}_p(\mathit{\mu },\Omega ), \\ \mathit{\mu }~{\mathcal{N}}_p\left({\mathit{\mu }}_0,{\mathbb{I}}_p/{\sigma }_{\mathit{\mu }}^2\right) \\ \Omega |G~G\text{-Wishart }(G,b,D), \\ G~\pi (G), \end{gathered}$$ (2)

with the symbol ${\mathbb{I}}_p$ indicating the identity matrix of dimension p. The last ingredient to fully specify the model is the prior for the graph G. When prior knowledge is not available, a uniform prior is often used (see Lenkoski and Dobra, 2011). However, it is well known that this prior is not optimal for sparsity as it favors graphs with a moderately large number of edges. To overcome this issue, Dobra et al. (2004) and Jones et al. (2005) suggested assigning a small data-dependent inclusion probability to each edge, i.e., $\pi (G)\propto d^{|E|}{(1-d)}^{\left(\begin{array}{c}p\\ 2\end{array}\right)-|E|}$, with d = 2/(p − 1). This prior, adopted also in this paper, is called the Erdős-Rényi prior, and it reduces to the uniform prior when d = 0.5.

2.2. Robust Graphical Models

Assume $Y_i\in {ℝ}^p$ is a vector of observed data on p variables for subject i, with i = 1, …, n. When data show departures from normality, robust models are needed. In particular, as noted by Finegold and Drton (2011, 2014), t-distributions are well-suited to accommodate heavy tails, and result in minimal loss of efficiency when the data are in fact normal. They propose introducing the normal variables X_i in model (2) as latent quantities, and modeling the observed data as:

$$Y_{ij}={\mu }_j+\frac{X_{ij}}{\sqrt{{\theta }_{ij}}}j=1,\dots ,p,$$ (3)

where θ_i = (θ_i1, …, θ_ip), for i = 1, …, n, are data and variable specific perturbation parameters (divisors), taking into account the deviation from normality of the observations. Using the invariance under linear transformation property of the Gaussian distribution, we can express the sampling model as:

$$Y_i|\mu ,\Omega ,{\theta }_i\stackrel{iid}{~}{\mathcal{N}}_p(\mu ,\mathit{\text{diag}}(\sqrt{{\theta }_i})\Omega \mathit{\text{ diag}}(\sqrt{{\theta }_i})),i=1\dots ,n.$$ (4)

Different distributions of the vector θ_i yield different models. Let P₀ denote a gamma(v/2, v/2) distribution with mean 1 and variance 2/v. If θ_i1 = θ_i2 = ⋯ = θ_ip and θ_i1 ~ P₀ (i.e., just one common divisor for all the components), then a multivariate t-distribution is assumed for the observations. We refer to this model as Y_i ~ t_p,v(μ,Ω). On the other hand, if ${\theta }_{i1},\dots ,{\theta }_{ip}\stackrel{\text{iid}}{~}{P}_0$ (i.e., p different divisors, one for each component of the data), then Y_i is distributed according to an alternative t-distribution, as introduced by Finegold and Drton (2011), and denoted by $Y_i~t_{p,\nu }^{*}(\mu ,\Omega )$. As an intermediate case, Finegold and Drton (2014) consider ${\theta }_{i1},\dots ,{\theta }_{ip}|P_i\stackrel{\text{iid}}{~}{P}_i$, P_i ~ DP(κ, P₀), where P_i ~ DP(κ, P₀) is the Dirichlet process with mass parameter κ and centering measure P₀. We refer to this model as $Y~t_{p,\nu }^{\kappa }(\mu ,\Omega )$. A realization from the Dirichlet process P_i is almost surely a discrete random probability measure. To give an illustration, let p = 2. Therefore, if $\left({\theta }_{i1},{\theta }_{i2}\right)|P_i\stackrel{\text{iid}}{~}{P}_i$, then with probability $\mathbb{P}\left({\theta }_{i1}={\theta }_{i2}\right)=\frac{1}{\kappa +1}$, and Y_i = (Y_i1, Y_i2) ~ t_2,v(μ,Ω). On the other hand, with probability $\frac{\kappa }{\kappa +1}$ we have the alternative t case. Indeed, the two are limiting cases of the Dirichlet t-distribution when κ → 0 or κ → +∞, respectively. Even though the Dirichlet process has proven to perform well in several contexts, it is well known that the clustering it induces is often inaccurate as it is affected by the so-called rich-gets-richer effect. In the next section, we propose a more flexible approach to mitigate this behavior and to allow for a more flexible clustering structure.

3. Proposed Method

3.1. Robust Graphical Modeling via Hierarchical Normalized Completely Random Measures

We propose an extension of the Dirichlet t model that uses a more flexible class of nonparametric distributions, namely the class of hierarchical normalized completely random measures (NormCRM). Through the use of these measures, we are able to address some of the limitations of the Dirichlet process. First, the tendency towards a highly skewed distribution of cluster sizes can be mitigated by the use of the more flexible NormCRM. In addition, we show how exploiting a hierarchical construction facilitates the sharing of information across cluster components in the dataset.

Let Θ be the Euclidean space and let us consider the class of almost surely discrete random probability measures that can be written as:

$$\tilde{P}(\cdot )=\sum _{l\ge 1}\frac{J_l}{\mathcal{T}}{\delta }_{{\tau }_l}(\cdot )=\sum _{l\ge 1}{w}_l{\delta }_{{\tau }_l}(\cdot ),$$ (5)

where $\mathcal{T}={\sum }_{l\ge 1}{J}_l$. We assume $\tilde{P}$ to be a homogeneous NormCRM, whose law is characterized by a Lèvy intensity measure v that factorizes into v(ds, dτ) = α(s)P(dτ)ds, where α is the density of a nonnegative measure, absolutely continuous with respect to the Lebesgue measure on ${ℝ}^{+}$ and regular enough to guarantee that $0<\mathcal{T}<\infty$ almost surely, and P is a probability measure over (Θ, $\mathcal{B}$). In general, such a factorization does not hold true, but by adopting it we ensure that the random jumps {J_l}_l≥1 and the random locations {τ_l}_l≥1 are independent sequences. The random locations τ₁, τ₂,… are independent and identically distributed according to the base distribution P, while the unnormalized random masses J₁,J₂,… are distributed according to a Poisson random measure with intensity α. The Dirichlet process is encompassed by this class when α(s) = κs⁻¹e^−s, for κ > 0 and s > 0. Even though our approach can be implemented with a general NormCRM, in what follows we consider the specific case of the normalized generalized gamma (NGG) process (Lijoi et al., 2007), which is obtained by choosing $\alpha (s)=\frac{\kappa }{\Gamma (1-\sigma )}{s}^{-1-\sigma }{\text{e}}^{-s}$, for 0 ≤ σ < 1. This nonparametric prior has been shown to be very effective for model-based clustering (Lijoi et al., 2007). We also refer readers to Argiento et al. (2015), for an application in biostatistics. Note that, when σ = 0, the Dirichlet process is recovered.

A sample ${\theta }_1,\dots ,{\theta }_p|\tilde{P}\stackrel{\text{iid}}{~}\tilde{P}={\sum }_{l\ge 1}{w}_l{\delta }_{{\tau }_l}$ can be represented via the set of variables $\mathit{l}=\left(l_1,\dots ,l_p\right)|{\left\{w_l\right\}}_{l\ge 1}\stackrel{\text{iid}}{~}\text{Discrete}\left({\left\{w_l\right\}}_{l\ge 1}\right)$, by letting ${\theta }_j={\tau }_{l_j}$, for j = 1, … , p. Let ${\mathit{l}}^{*}=\left(l_1^{*},\dots ,l_K^{*}\right)$ be the set of the K unique values in l. A partition ρ = {C₁, …, C_K} of the indices {1, …, p} can be defined by letting $C_h=\left\{j:l_j=l_h^{*}\right\}$, for h = 1, …, K. The partition ρ is called l-clustering. Let now ${\theta }_h^{*}={\tau }_{l_h^{*}}$. When the centering measure P is diffuse, the ${\theta }_h^{*}\text{s}$ coincide with the unique values in θ = (θ₁, …, θ_p) and the l-clustering coincides with the natural clustering, i.e., we can also write $C_h=\left\{j:{\theta }_j={\theta }_h^{*}\right\}$, for h = 1, … , K. The l-clustering and the natural clustering can be different when the centering measure P is discrete (see Argiento et al., 2019). In particular, in the discrete case, each ${\theta }_h^{*}$ is the value shared by all the indices in the so-called l-cluster C_h, for h = 1, … , K. Furthermore, extending the results in Pitman (1996), Ishwaran and James (2003), and Argiento et al. (2019), one can show that, for P either atomic or diffuse, the following characterization holds:

$$\mathcal{L}\left(\rho ,d{\theta }_1^{*},\dots ,d{\theta }_K^{*}\right)=\mathcal{L}(\rho )\mathcal{L}\left(d{\theta }_1^{*},\dots ,d{\theta }_K^{*}|K\right)=\text{eppf}(\mathit{e};\kappa ,\sigma )\prod _{h=1}^{K}P\left(d{\theta }_h^{*}\right),$$ (6)

with e = (e₁, … , e_K) the vector of l-cluster sizes in the partition ρ, such that e_h = #C_h, for each h = 1, …, K, and with the notation eppf(e; κ, σ) indicating the exchangeable partition probability function (eppf) of the NGG process, a symmetric function of the cluster sizes e, as introduced by Pitman (2003). The explicit analytical form of the eppf of a generic (homogeneous) NormCRM can be derived (see formulas (36)–(37) in Pitman (2003)) and enables the construction of a Gibbs sampler based on the Chinese restaurant process representation. In the Dirichlet process case, De Blasi et al. (2015) pointed out that the predictive distribution induced by (6), i.e., the probability that θ_p belongs to a new l-cluster given (θ₁, …, θ_p−1), depends only on the dimension p, while in the NGG process case this probability depends on both p and K, leading to a more flexible prior. Furthermore, the probability that θ_p belongs to a previously observed l-cluster C_h is proportional to e_h − σ, for h = 1, …, K. These two properties mitigate the rich-gets-richer behavior arising when considering the Dirichlet case.

The first step towards our proposed robust graphical modeling construction is to replace the Dirichlet prior on the divisors with an NGG process, yielding the following robust graphical model:

$$\begin{gathered} Y_i|\mu ,\Omega ,{\theta }_i\stackrel{iid}{~}{\mathcal{N}}_p(\mu ,\mathit{\text{diag}}(\sqrt{{\theta }_i})\Omega \mathit{\text{ diag}}(\sqrt{{\theta }_i})),i=1\dots ,n, \\ {\theta }_{i1},\dots ,{\theta }_{ip}|P_i\stackrel{\text{iid}}{~}{P}_i,i=1,\dots ,n, \\ {P}_1,\dots ,P_n|\kappa ,\sigma \stackrel{\text{iid}}{~}NGG(\kappa ,\sigma ,P), \end{gathered}$$ (7)

where P is the distribution on the space of the divisors. Suitable prior distributions can be assigned to κ, σ, μ, and Ω. We denote by ${\rho }_i=\left\{C_{i1},\dots ,C_{i{K}_i}\right\}$ the l-clustering induced by P_i in each data vector, for i = 1, …, n, as described earlier in this section.

When P is diffuse, model (7) does not allow for sharing of information across the data vectors. This can be seen by using characterization (6) to marginalize model (7) with respect to the infinite-dimensional parameters P₁, …, P_n, and rewriting the last two lines of (7) as:

$${\rho }_i|\kappa ,\sigma \stackrel{\text{ind}}{~}\text{eppf}\left({\mathit{e}}_i;\kappa ,\sigma \right),i=1,\dots ,n,$$

$${\theta }_{i1}^{*},\dots ,{\theta }_{i{K}_i}^{*}|K_i\stackrel{\text{iid}}{~}P,i=1,\dots ,n,$$

where $\left({\rho }_i,{\theta }_i^{*}\right)$ represent the partition and the vector of unique values induced by P_i on the data components, and ${\mathit{e}}_i=\left(e_{i1},\dots ,e_{i{K}_i}\right)$ is the vector of l-cluster sizes in the partition ρ_i, such that e_ih = #C_ih, for each h = 1, …, K_i. By this re-writing, it is clear that the sharing of information among the different clustering structures is achieved only via the conditional dependence of ρ_i given κ and σ. In particular, we cannot have shared divisors across data vectors, but only across components of the same data vector, since θ*’s are all i.i.d. from the diffuse distribution P. We overcome this limitation by considering a more flexible hierarchical model formulation that allows for additional sharing of information across the samples. Specifically, we assume P to be a random probability measure, namely an NGG process centered on a diffuse measure P₀. In formulas, the proposed model can be written as follows:

$$\begin{gathered} Y_i|\mu ,\Omega ,{\theta }_i\stackrel{iid}{~}{\mathcal{N}}_p(\mu ,\mathit{\text{diag}}(\sqrt{{\theta }_i})\Omega \mathit{\text{ diag}}(\sqrt{{\theta }_i})),i=1\dots ,n, \\ {\theta }_{i1},\dots ,{\theta }_{ip}|P_i\stackrel{\text{iid}}{~}{P}_i,i=1,\dots ,n, \\ {P}_1,\dots ,P_n|\kappa ,\sigma ,P\stackrel{\text{iid}}{~}NGG(\kappa ,\sigma ,P), \\ P|{\kappa }_0,{\sigma }_0~NGG\left({\kappa }_0,{\sigma }_0,P_0\right). \end{gathered}$$ (8)

The law of (P₁, …, P_n), as given by the last two lines of (8), is called the hierarchical NGG (HNGG) process. For ease of notation, we will refer to the mixture model (8) as t-HNGG. Theoretical and clustering properties of hierarchical normalized completely random measures have been investigated first by Camerlenghi et al. (2019), and a detailed study of the clustering induced by these measures in the context of mixture models has been conducted in Argiento et al. (2019). An attractive feature of this construction is that it induces a two-layered hierarchical clustering structure that allows components of different observed data vectors to be clustered together. This two-layered structure consists of an l-clustering ρ_i within each group i, and a clustering η that merges elements of ρ₁, …, ρ_n. In order to define η more precisely, let $\theta ={\left({\theta }_1^{\top },\dots ,{\theta }_n^{\top }\right)}^{\top }$ be the matrix where the row θ_i is the vector of all divisors of the i-th observation, and let ψ = (ψ₁, …, ψ_M) be the vector of unique values found in the matrix θ. Let ρ = (ρ₁, …, ρ_n) indicate the l-clustering partitions in each data vector, and ${\mathit{\theta }}^{*}=\left({\mathit{\theta }}_1^{*},\dots ,{\mathit{\theta }}_n^{*}\right)$ the corresponding multidimensional array of parameter values. We define a clustering of the indices of the multidimensional array θ* by letting η = {D₁, …, D_M} where $D_m=\left\{(i,h):{\theta }_{ih}^{*}={\psi }_m,h=1,\dots ,K_i,i=1,\dots ,n\right\}$, with m = 1, …, M. We also let d = (d₁, …, d_M), with d_m = #D_m. Then, the law of the matrix θ of divisors, given in the last three lines of (8), can be characterized in terms of ρ, η and ψ as:

$$\begin{gathered} \mathcal{L}(\mathit{\rho },\eta ,d\mathit{\psi })=\mathcal{L}(\eta |\mathit{\rho })\prod _{i=1}^n\mathcal{L}\left({\rho }_i\right)\prod _{m=1}^M{P}_0\left(d{\psi }_m\right) \\ =\text{eppf}\left(d;{\kappa }_0,{\sigma }_0\right)\prod _{i=1}^n\text{eppf}\left(e_i;\kappa ,\sigma \right)\prod _{m=1}^M{P}_0\left(d{\psi }_m\right). \end{gathered}$$ (9)

Full details on the derivation of formula (9) can be found in Argiento et al. (2019). We also note that the partially exchangeable partition probability function of Camerlenghi et al. (2019) can be obtained from (9) by marginalizing with respect to (η, ψ).

We call the natural clustering induced by θ the partition of indices $\mathcal{I}=\left\{{\mathcal{I}}_1,\dots ,{\mathcal{I}}_M\right\}$ such that $(i,j)\in {\mathcal{I}}_m\text{ iff }{\theta }_{ij}={\psi }_m$. Since the sets of indices ${\mathcal{I}}_m$, for m = 1, …, M, can be recovered from (ρ, η), formula (9) characterizes the law of the natural clustering. The relationship between $\mathcal{I}$ and (ρ, η) is clarified in formulas:

$${\mathcal{I}}_m^{\left({\rho }_i,\eta \right)}≔\underset{h=1}{\overset{K_i}{\cup }}\left\{(i,j):j\in C_{ih},(i,h)\in D_m\right\},m=1,\dots ,M,$$ (10)

$${\mathcal{I}}_m≔{\mathcal{I}}_m^{(\rho ,\eta )}=\underset{i=1}{\overset{n}{\cup }}{\mathcal{I}}_m^{\left({\rho }_i,\eta \right)},m=1,\dots ,M.$$

Formula (9) can be described in terms of a Chinese restaurant franchise process. In our context, each observation represents a different restaurant in the franchise, each serving p customers, one for each component of the data vector. Customers entering the i-th restaurant are allocated to the tables according to eppf(e_i; κ, σ), independently from the other restaurants in the franchise, and generate the partition ${\rho }_i=\left(C_{i1},\dots ,C_{i{K}_i}\right)$, for i = 1, …, n. In this metaphor, the elements of ρ_i represent the tables of the i-th restaurant. Conditionally on $T={\sum }_{i=1}^n{K}_i$, the tables of the franchise are grouped according to the law described by eppf(d; κ₀, σ₀), thus obtaining a partition of tables. Hence, the elements of η can be interpreted as clusters of tables. In addition, all tables in the same cluster D_m share the same dish ψ_m, for m = 1, …, M. Moreover, ψ = (ψ₁, …, ψ_M) is and i.i.d. sample from P₀. Under this metaphor, e_ih, for h = 1, …, K_i and i = 1, …, n, represents the number of customers seated at the h-th table in the i-th restaurant, while d_m, for m = 1, …, M, is the number of tables where the m-th dish is served across the franchise. Finally, in this metaphor, the natural clustering induced by the corresponding θ is formed of clusters of customers that share the same dish across the franchise, and not only in the same restaurant.

3.2. Predictive Structure of the hierarchical NGG

In this paper, we make use of a marginal MCMC algorithm for simulating the nonparametric quantities involved in model (8). This algorithm is based on integrating out the infinite-dimensional parameters P₁, …, P_n, P and on the characterization of the generalized Chinese restaurant franchise process via formula (9). To drastically reduce the computational complexity, it is convenient to consider the predictive structure induced by the hierarchical NGG process by using a standard augmentation trick (see James et al., 2009; Lijoi and Prünster, 2010). More specifically, we introduce n + 1 auxiliary random variables U = (U₁, … ,U_n, U₀), referring to the n clustering structures in each data vector, and to the one existing across the whole dataset, respectively. For the NGG process, each partition ρ_i has the following law, jointly with U_i:

$$\text{eppf}\left({\mathit{e}}_i,u_i;\kappa ,\sigma \right)=\frac{u_i^{p-1}}{\Gamma (p)}{e}^{-\frac{\kappa }{\sigma }\left({\left(u_i+1\right)}^{\sigma }-1\right)}\prod _{h=1}^{K_i}\frac{\kappa }{{\left(u_i+1\right)}^{e_{ih}-\sigma }}\frac{\Gamma \left(e_{ih}-\sigma \right)}{\Gamma (1-\sigma )},$$ (11)

where K_i is the number of clusters and ${\mathit{e}}_i=\left(e_{i1},\dots ,e_{i{K}_i}\right)$ is the vector of cluster sizes in ρ_i. The joint law of (η, U₀) has an analogous expression.

Suppose now to have a new variable in the i-th group, whose index is p + 1. We will use an abuse on notation by indicating with (p + 1) ∈ C_ih, for h = 1, …, K_i, the event that the new variable is allocated to the h-th cluster in the i-th group, and with $(p+1)\in C_{i{K}_i+1}$ the event that the new variable is assigned to a new cluster. It can be shown that the allocation probabilities of the new variable are the following, for h = 1, …, K_i:

$$\begin{gathered} P_{ih}^{(to)}=\mathbb{P}\left((p+1)\in C_{ih}|{\rho }_i,U_i\right)\propto \frac{\text{eppf}\left(e_{i1},\dots ,e_{ih}+1,\dots ,e_{i{K}_i};\kappa ,\sigma ,u_i\right)}{\text{eppf}\left(e_{i1},\dots ,e_{i{K}_i};\kappa ,\sigma ,u_i\right)}=e_{ih}-\sigma , \\ {P}_i^{(tn)}=\mathbb{P}\left((p+1)\in C_{i{K}_i+1}|{\rho }_i,U_i\right)\propto \frac{\text{eppf}\left(e_{i1},\dots ,e_{i{K}_i},1;\kappa ,\sigma ,u_i\right)}{\text{eppf}\left(e_{i1},\dots ,e_{i{K}_i};\kappa ,\sigma ,u_i\right)}=\kappa {\left(u_i+1\right)}^{\sigma }, \end{gathered}$$ (12)

corresponding to the allocation probabilities of a new customer entering the i-th restaurant, and sitting at an existing or at a new table in the generalized Chinese restaurant metaphor. In case a new cluster arises, the partition η needs to be updated. The allocation probabilities of the new element T + 1 are, for m = 1, …, M:

$$\begin{gathered} P_m^{(do)}=\mathbb{P}\left((T+1)\in D_m|\eta ,U_0\right)\propto \frac{\text{eppf}\left(d_1,\dots ,d_m+1,\dots ,d_M;{\kappa }_0,{\sigma }_0,u_0\right)}{\text{eppf}\left(d_1,\dots ,d_M;{\kappa }_0,{\sigma }_0,u_0\right)}=d_m-{\sigma }_0, \\ {P}^{(dn)}=\mathbb{P}\left((T+1)\in D_{M+1}|\eta ,U_0\right)\propto \frac{\text{eppf}\left(d_1,\dots ,d_M,1;{\kappa }_0,{\sigma }_0,u_0\right)}{\text{eppf}\left(d_1,\dots ,d_M;{\kappa }_0,{\sigma }_0,u_0\right)}={\kappa }_0{\left(u_0+1\right)}^{{\sigma }_0}, \end{gathered}$$ (13)

corresponding to the allocation probabilities that a newly generated table will join a new or an existing cluster of tables. Additional details on how to derive (12) and (13) can be found in the Supplementary Materials (Cremaschi et al., 2019).

To complete the generalized Chinese restaurant franchise process metaphor, not only does a new customer have to select a table, but also a dish from the franchise menu. Suppose the new customer enters the i-th restaurant, and let θ_ip+1 be the label of the selected dish. The table is picked according to the predictive rules (12) of the i-th restaurant. The customer can choose between joining an existing table with label h = 1, …, K_i, or occupying the (K_i+1)-th new one. The first choice leads to sharing the dish on the h-th table in the i-th restaurant, i.e. ${\theta }_{i(p+1)}={\theta }_{ih}^{*}$. On the other hand, if a new table is chosen, the customer can select a dish from the menu of dishes according to (13). This menu contains dishes that are already served in other tables across the franchise, as well as infinitely many new ones, since the centering measure P₀ is diffuse. Following Argiento et al. (2019), the full-conditional allocation probability, for i = 1, …, n is

$$\begin{gathered} \mathbb{P}\left((p+1)\in C_{ih},(i,p+1)\in {\mathcal{I}}_m^{\left({\rho }_i,\eta \right)}|\rho ,\eta ,U\right) \\ =\mathbb{P}\left((i,p+1)\in {\mathcal{I}}_m^{\left({\rho }_i,\eta \right)}|(p+1)\in C_{ih},\mathit{\rho },\eta ,U\right)\mathbb{P}\left((p+1)\in C_{ih}|\rho ,\eta ,U\right) \\ \propto \{\begin{array}{lll}{P}_{ih}^{(to)}\hfill & h=1,\dots ,K_i,\hfill & m=m_h,\hfill \\ P_m^{(do)}{P}_i^{(tn)}\hfill & h=K_i+1,\hfill & m=1,\dots ,M\hfill \\ P^{(dn)}{P}_i^{(tn)}\hfill & h=K_i+1,\hfill & m=M+1,\hfill \\ 0\hfill & \text{otherwise},\hfill & \hfill \end{array} \end{gathered}$$ (14)

where m_h is such that $(i,h)\in D_{m_h}$, and the sets ${\mathcal{I}}_m^{\left({\rho }_i,\eta \right)}$, for m = 1, …, M, are defined in (10). These equations are the main blocks to compute the full-conditional allocation probabilities needed for posterior sampling, as presented in the next section. Such probabilities can be calculated in closed form using equation (9). However, in the next section we make use of auxiliary variables as these simplify the sampling algorithm. The conditional predictive probabilities hereby specified characterize the prior clustering induced by our nonparametric modeling. We refer to Argiento et al. (2019) for results on the distribution of relevant quantities, such as the prior distribution of the number of different dishes or the dependence induced by our model across observations (e.g. correlation, coskewness).

3.3. MCMC Algorithm

In this section, we describe the MCMC algorithm for posterior inference from model (8), embedded within the graphical modeling part described in (2). The state space of the Gibbs sampler is given by (μ, Ω, G, ρ, η, ψ). We describe the parameter updates by splitting them into two blocks: the graphical model block, which comprises the full conditionals of (μ, Ω, G), and the generalized Chinese restaurant franchise block, which includes those for (ρ, η, ψ). For simplicity, we will remove the indexing of the Gibbs sampler iteration.

• Graphical model updates: In the following, we will consider the law of (μ, Ω, G) conditionally upon the variables (ρ, η, ψ).

  • For the update of (Ω, G), we resort to the birth-death algorithm of Mohammadi and Wit (2015) available in the R package BDgraph, and suitable for non-decomposable graphs. The algorithm proceeds by first adding/removing an edge of the graph, and then updating the precision matrix Ω using the algorithm presented in Lenkoski (2013). These moves have probabilities

    $$\begin{gathered} \mathbb{P}((i,j)\in E|\mu ,\Omega ,G,Y,\theta )\propto {\beta }_{ij}^b(\mu ,\Omega ,G,Y,\theta ),(i,j)\notin E, \\ \mathbb{P}((i,j)\notin E|\mu ,\Omega ,G,Y,\theta )\propto {\beta }_{ij}^d(\mu ,\Omega ,G,Y,\theta ),(i,j)\in E, \end{gathered}$$

    with ${\beta }_{ij}^b$ and ${\beta }_{ij}^d$ the birth and death rates of edge (i, j), respectively, computed in such a way that the stationary distribution of the Markov process is the joint full-conditional of (Ω, G), given (Y, ρ, η, ψ) (see Theorem 3.1 in Mohammadi and Wit, 2015). This algorithm is particularly efficient since the Markov process specification ensures that the birth/death moves are always accepted, contrarily to the reversible jump algorithm of Giudici and Green (1999), also implemented in the package BDgraph.
  • Updating μ: This full-conditional is conjugate. A-priori $\mathit{\mu }~{\mathcal{N}}_p\left({\mathit{\mu }}_0,{\mathbb{I}}_p/{\sigma }_{\mathit{\mu }}^2\right)$, hence:

    $$\begin{gathered} \mathit{\mu }|G,\mathbf{\Omega },\mathit{\theta },\mathit{Y}~{\mathcal{N}}_p\left({\mathit{m}}_{\mathit{\mu }},{\mathit{S}}_{\mathit{\mu }}\right), \\ {\mathit{S}}_{\mathit{\mu }}={\mathbb{I}}_p/{\sigma }_{\mathit{\mu }}^2+\sum _{i=1}^n(\mathit{\text{diag}}(\sqrt{{\theta }_i})\Omega \mathit{\text{ diag}}(\sqrt{{\theta }_i})), \\ {m}_{\mu }=S_{\mu }\left[{\mu }_0/{\sigma }_{\mu }^2+\sum _{i=1}^n(\mathit{\text{diag}}(\sqrt{{\theta }_i})\Omega \mathit{\text{ diag}}(\sqrt{{\theta }_i}))Y_i^{\top }\right]. \end{gathered}$$
• Generalized Chinese restaurant franchise process updates: We refer to the notation of Sections 3.1 and 3.2. Conditionally to the vector of auxiliary variables U and the graphical model parameters (μ, Ω, G), the joint law of (8) is:

  $$\begin{gathered} \mathcal{L}\left({\mathit{Y}}_1,\dots ,{\mathit{Y}}_n|\mathit{\rho },\eta ,\mathit{\theta },\mathit{U},\mathit{\mu },\mathbf{\Omega },G\right)\mathcal{L}\left({\rho }_1,\dots ,{\rho }_n|U_1,\dots ,U_n\right)\mathcal{L}\left(\eta |U_0\right)\prod _{m=1}^M{P}_0\left(d{\psi }_m\right) \\ =\prod _{i=1}^{n}f\left(y_i|\mu ,\Omega ,{\theta }_i\right)\prod _{i=1}^n\text{eppf}\left(e_i;\kappa ,\sigma ,P_0,u_i\right)\text{eppf}\left(d;{\kappa }_0,{\sigma }_0,P_0,u_0\right)\prod _{m=1}^M{P}_0\left(d{\psi }_m\right), \end{gathered}$$

  with f representing the multivariate Gaussian density introduced in model (8). It is important to point out that, under model (8), the observations y_ij are now components of the vector y_i and are no longer conditionally independent. Thus, it is useful to introduce the following conditional likelihood for a subset of indices t ⊂ {1, … p}:

  $$\begin{gathered} f\left(y_{it}|{\mathit{y}}_{i\backslash t},\mu ,\Omega ,{\theta }_i\right)=\mathcal{N}\left(y_{it}|{\mu }_c,{[\mathit{\text{diag}}(\sqrt{{\theta }_i})\Omega \mathit{\text{ diag}}(\sqrt{{\theta }_i})]}_{tt}\right), \\ {\mu }_c={\mu }_t-{\Omega }_{tt}^{-1}{\Omega }_{t\backslash t}\left(y_{i\backslash t}-{\mu }_{\backslash t}\right)\sqrt{{\theta }_{i\backslash t}}, \end{gathered}$$ (15)

  with $\backslash t=\left\{1,\dots ,p\right\}\cap \overline{t}$, and $\overline{t}$ indicating the complementary set of t. This allows us to write the following updates:

  • Update of U and ψ: using the expression given in (11) of eppf(·, u₀; κ₀, σ₀, P₀) and eppf(·,u_i; κ, σ, P₀), and the centering measure P₀, we have:

    $$\begin{gathered} p\left(U_i|{\rho }_i,\kappa ,\sigma \right)\propto u_i^{p-1}{e}^{-\frac{\kappa }{\sigma }\left({\left(u_i+1\right)}^{\sigma }-1\right)} \\ \times \prod _{h=1}^{K_i}\left(\frac{\kappa }{{\left(u_i+1\right)}^{e_{ih}-\sigma }}\frac{\Gamma \left(e_{ih}-\sigma \right)}{\Gamma (1-\sigma )}\right),i=1,\dots ,n, \\ p\left(U_0|\eta ,{\kappa }_0,{\sigma }_0,T\right)\propto u_0^{T-1}{e}^{-\frac{{\kappa }_0}{{\sigma }_0}\left({\left(u_0+1\right)}^{{\sigma }_0}-1\right)} \\ \times \prod _{m=1}^M\left(\frac{{\kappa }_0}{{\left(u_0+1\right)}^{d_m-{\sigma }_0}}\frac{\Gamma \left(d_m-{\sigma }_0\right)}{\Gamma \left(1-{\sigma }_0\right)}\right), \\ p\left({\psi }_m|Y,\rho ,\eta \right)\propto \prod _{i=1}^{n}f\left(y_{i{\mathcal{I}}_m^{\left({\mathit{\rho }}_i,\eta \right)}}|y_{i\backslash {\mathcal{I}}_m^{\left({\rho }_i,\eta \right)}},\mu ,\Omega ,{\psi }_m\right)P_0\left(d{\psi }_m\right), \\ m=1,\dots ,M. \end{gathered}$$ (16)

    These quantities are often known up to a normalizing constant, making necessary to implement a series of Metropolis-Hastings (MH) steps. Specifically, we use an adaptive MH scheme for the random variables U, following the guidelines of Griffin and Stephens (2013). The sampling of the unique values ψ is achieved by performing M independent standard MH steps. This approach is necessary since the full-conditional distribution of ψ presents an intractable normalizing constant, and does not allow the use of a direct sampler (Finegold and Drton, 2011).
  • Update of (ρ, η): We report now the full-conditional distributions for the clustering variables (ρ, η). The updating takes advantage of the augmented predictive representation given in Section 3.2, inspired by (Favaro and Teh, 2013) and by the popular Algorithm 8 of (Neal, 2000). Indeed, due to the non-conjugate setting of our model, we augment the sample space to include a set of N_c auxiliary variables ${\mathit{\psi }}^c=\left({\psi }_1^c,\dots ,{\psi }_{N_c}^c\right)\stackrel{\text{iid}}{~}{P}_0$. Let the superscript (−ij) denote the conditioning on the random variables modified after the removal of the j-th observation of the i-th restaurant, for j = 1, …, p and i = 1, …, n. Then, conditionally upon Y and (ρ^−ij, η^−ij), and resorting to (14), the probability of assigning the j-th customer to the h-th table of the i-th restaurant, where the m-th dish is served, is:

    $$\begin{gathered} \mathbb{P}\left(j\in C_{ih}^{-ij},{\theta }_{ij}={\psi }_m|Y,\mu ,\Omega ,G,{\rho }^{-ij},{\eta }^{-ij},{\theta }^{-ij},{\psi }^c,U\right) \\ \propto \{\begin{array}{ll}{P}_{ih}^{(to)}f\left(y_{ij}|y_{i\backslash j},\mu ,\Omega ,{\theta }_{ih}^{*}\right),\hfill & h=1,\dots ,K_i^{-ij}\hfill \\ P_i^{(tn)}{P}_m^{(do)}f\left(y_{ij}|y_{i\backslash j},\mu ,\Omega ,{\psi }_m\right),\hfill & h=K_i^{-ij}+1,m=1,\dots ,M^{-ij}\hfill \\ P_i^{(tn)}{P}^{(dn)}f\left(y_{ij}|y_{i\backslash j},\mu ,\Omega ,{\psi }_{n_c}^c\right)/N_c,\hfill & \mathrm{}\hfill \\ h=K_i^{-ij}+1,m=M^{-ij}+1,n_c=1,\dots ,N_c,\hfill & \mathrm{}\hfill \end{array} \end{gathered}$$ (17)

    where $K_i^{-ij}+1$ and M^−ij +1 are the new table and dish labels, respectively. The updating process continues by re-allocating C_ih to a cluster of tables. To this end, we have to assign C_ih to a D_m, for h = 1, …, K_i and m = 1, …, M. More formally, let the superscript (−ih) indicate the conditioning on the variables after the removal of all the observations in C_ih. Conditionally on Y and (ρ^−ih, η^−ih), and using again (14), the probability of assigning the h-th table of the i-th restaurant to the m-th cluster is:

    $$\begin{gathered} \mathbb{P}\left((i,h)\in D_m^{-ih},{\theta }_{ih}^{*}={\psi }_m|\mathit{Y},{\mathit{\rho }}^{-ih},{\eta }^{-ih},{\mathit{\psi }}^{-ih},{\mathit{\psi }}^c,\mathit{U}\right) \\ \propto \{\begin{array}{ll}{P}_m^{(do)}f\left(y_{i{C}_{ih}}|y_{i\backslash C_{ih}},\mu ,\Omega ,{\psi }_m\right),\hfill & m=1,\dots ,M^{-ih},\hfill \\ P^{(dn)}f\left(y_{i{C}_{ih}}|y_{i\backslash C_{ih}},\mu ,\Omega ,{\psi }_{n_c}^c\right)/N_c,\hfill & m=M^{-ih}+1,n_c=1,\dots ,N_c.\hfill \end{array} \end{gathered}$$ (18)

    where M^−ih + 1 indicates the new dish labels.

Given the output from the MCMC chain, one can estimate the graph structure by considering the median graph (Barbieri et al., 2004) as the graph represented by those edges (i, j) ∈ E for which the posterior edge inclusion probability $\mathbb{P}((i,j)\in E|Y)$ is greater than 0.5. Additionally, we can estimate the precision matrix of the sampling model (4) by considering the contribution of the divisors θ, as

$${\mathbf{\Omega }}_{\mathit{\theta }}=\frac{1}{n}\sum _{i=1}^n\mathit{\text{diag}}(\sqrt{{\mathit{\theta }}_i})\mathbf{\Omega }\mathit{\text{ diag}}(\sqrt{{\mathit{\theta }}_i}).$$

We obtain an analogous estimate ${\widehat{\mathbf{\Omega }}}_{\mathit{\theta }}$ by averaging over the MCMC samples.

One important feature of the nonparametric prior distributions imposed in models (7) and (8) is the ability to cluster the data via the unique values of the divisors θ. In the applications below, we illustrate the properties of the random partitions imposed on θ by reporting the posterior mean of the number of clusters in each data vector for the independent model (7), and the posterior distribution of the number of clusters among all the data vectors for the hierarchical model (8). Both quantities are computed by using the saved iterations of the posterior chains of the random partitions ρ and η.

4. Applications

4.1. Simulation Study

In this section we illustrate the performance of the proposed method via simulation studies. In particular, we employ two simulated scenarios inspired by the work of Finegold and Drton (2014), for ease of comparison. Analogously, an edge (i, j) ∈ E is considered “positive” if $\mathbb{P}((i,j)\in E|Y)>ϵ$, for a range of values of ϵ ∈ (0, 1). We compare results across different models in terms of the receiver operating characteristic (ROC) curves, by calculating true and false positive rates for each of 50 replicated datasets and then computing the ROC curves by averaging over the 50 replicates.

AR(1) graph, n = p = 25

In this simulation setting, n = 25 data vectors are simulated from model (4) with an AR(1) graph structure on G, induced by a tri-diagonal precision matrix Ω where the off-diagonal non-zero elements are set to −1, and the diagonal ones are set to 3 apart from the two extremes that are set to 2. The mean vector μ is simulated as p independent standard normal random variables. The divisors θ are set to recover different distribution structures, namely the multivariate Gaussian (θ_ij = 1 for i = 1, …, n, j = 1, …, p), the classical multivariate t-Student $\left({\theta }_{i1}=\cdots ={\theta }_{ip}\stackrel{\text{iid}}{~}\text{gamma}(\nu /2,\nu /2),i=1,\dots ,n\right)$, and the alternative multivariate t-Student $\left({\theta }_{11},\dots ,{\theta }_{pp}\stackrel{\text{iid}}{~}\text{gamma}(\nu /2,\nu /2)\right)$. Where required, v = 3.

Here, we investigate performance of four different models: an independent Dirichlet model (t-DP) obtained from (7) with κ ~ gamma(1, 1) and $\sigma =0(\mathbb{E}(M)=n4.31,\text{ sd}(M)=\sqrt{n}1.56)$; an independent t-NGG model obtained from (7) with κ ~ gamma(1, 1) and by setting $\sigma =0.1(\mathbb{E}(M)=n4.40,\text{\hspace{0.17em}sd}(M)=\sqrt{n}1.70)$; a t-HDP model in the form of equation (8) with κ, κ₀ ~ gamma(1, 1) and $\sigma ={\sigma }_0=0(\mathbb{E}(M)=4.50,\text{sd}(M)=1.56)$; and a t-HNGG model obtained from (8) with κ, κ₀ ~ gamma(1, 1) and by setting (σ, σ₀) = (0.5, 0.1) $(\mathbb{E}(M)=7.67,\text{sd}(M)=2.41)$. Alternatively, Beta hyperpriors can be imposed on σ, σ₀ (see our second simulation setting below and Argiento et al. (2019) for a full sensitivity analysis on the parameters (κ, κ₀, σ, σ₀)).

Furthermore, in all models, we set the prior distribution for G to be uniform with edge probability d = 0.05. We also set b = p and $D={\mathbb{I}}_p$ for the prior distribution of Ω, and v = 3. For each replicated dataset, we ran an MCMC chain with 50,000 iterations, of which the first 40,000 are discarded as burn-in period, and 5,000 are saved from the remaining ones, after thinning, for estimation purposes.

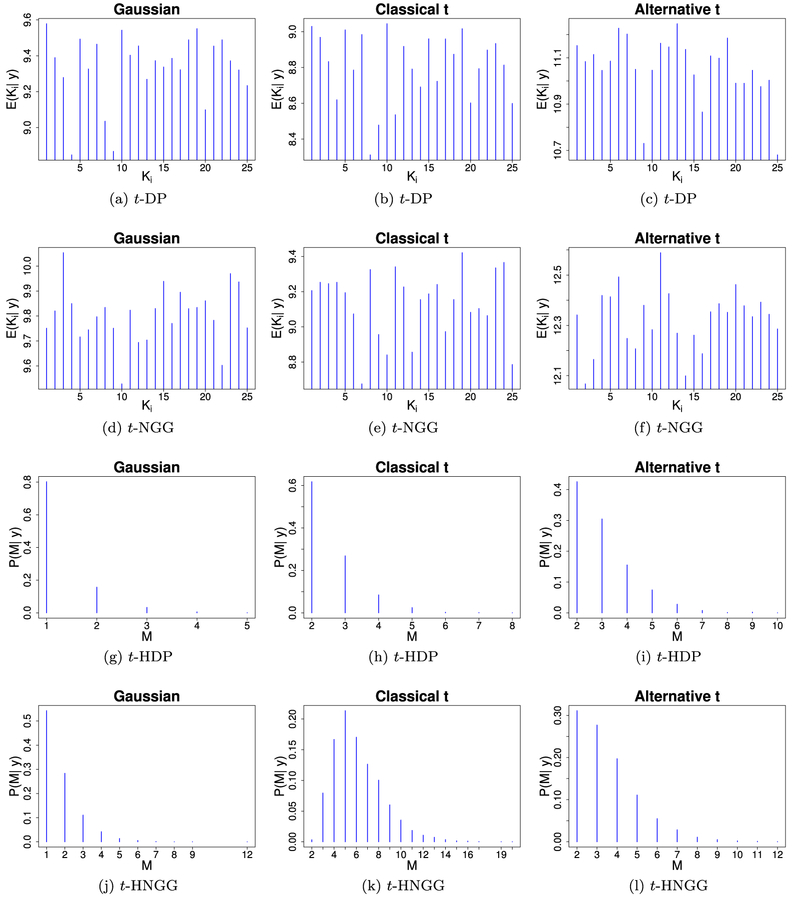
In order to elucidate the properties of the clustering structure of the divisors induced by our model, in Figure 1 we show the posterior distributions of the number of clusters for each of the four fitted models, on one of the replicated datasets for each of the three different scenarios. As expected, both the t-HDP and the t-HNGG model induce a lower posterior mean number of clusters (in the natural clustering sense), when compared to the number of clusters in each data vector induced by the independent t-DP and t-NGG models. This is possible thanks to the ability of the hierarchical models to exploit the sharing of information across data vectors. This effect is particularly clear when looking at the Gaussian scenario, where the proposed model is able to effectively cluster the data into one cluster with high posterior probability. On the other hand, in the alternative multivariate t case it is clear how the tuning of the hyperparameters plays a crucial role in the resulting partition structure. The classical t case shows that neither hierarchical model accurately captures the original number of clusters, equal to 25. However, the t-HNGG model outperforms the t-HDP model, allowing for higher posterior probability on partitions characterized by a larger number of clusters.

Figure 1:

Simulation study, AR(1) graph: Posterior number of clusters, comparing the four models under study (independent t-DP, independent t-NGG, t-HDP, and t-HNGG), for data generated from a Gaussian distribution (first column), a Classical t distribution (second column) and an Alternative t distribution (third column). Posterior means for each data vector are reported for the independent t-DP and t-NGG models (first and second rows, respectively), while posterior distributions are shown for the t-HDP and the t-HNGG models (third and fourth rows).

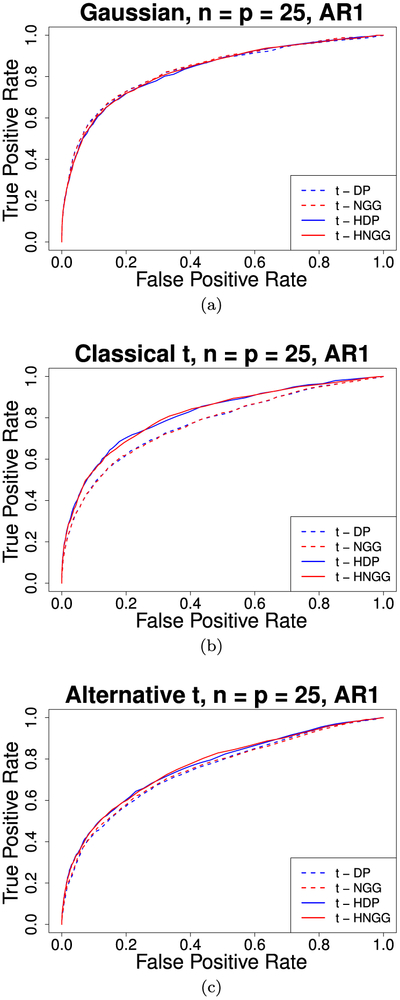
Figure 2 shows the comparison of the ROC curves for the four different models, computed by averaging over the 50 replicates, for each of the three simulation settings. We can observe an agreement in the results for the Gaussian case, while the proposed model performs better in the other scenarios, due to the presence of non-unitary divisors that can be captured by the flexible nonparametric structure. The t-HDP and t-HNGG models show comparable performance. Furthermore, in Table 1 we report the L¹, L², and maximum modulus distances between the estimated and the simulated precision matrices, averaged over the 50 replicates, for each of the three simulated scenarios. For two matrices $\mathit{A},\mathit{B}\in {ℝ}^{p\times p}$, these measures are defined as:

$$\begin{gathered} d_{L^1}(A,B)=\underset{1\le j\le p}{\text{max}}\sum _{i=1}^p|a_{ij}-b_{ij}|, \\ {d}_{L^2}(\mathit{A},\mathit{B})=\sqrt{\sum _{i=1}^p\sum _{j=1}^p{\left(a_{ij}-b_{ij}\right)}^2}, \\ {d}_{max}(A,B)=\underset{ij}{\text{max}}|a_{ij}-b_{ij}|. \end{gathered}$$ (19)

Figure 2:

Simulation study, AR(1) graph: ROC curves comparing the independent t-DP and t-NGG models with the t-HDP and the t-HNGG models, for data generated from a Gaussian distribution, a Classical t distribution and an Alternative t distribution.

Table 1:

Simulation study, AR(1) graph: Average distances between ${\widehat{\mathbf{\Omega }}}_{\mathit{\theta }}$ and Ω_θ.

	Gaussian
	t-DP	t-NGG	t-HDP	t-HNGG
L1	15.5948	15.3678	3.3862	3.4717
L2	26.4608	26.2770	6.8677	6.8875
Max	9.2539	9.1041	1.1490	1.2120
	Classical t
	t-DP	t-NGG	t-HDP	t-HNGG
L1	12.7382	13.0816	4.3448	4.3848
L2	16.6510	17.2454	9.0376	8.7959
Max	6.1404	6.3945	1.5965	1.6277
	Alternative t
	t-DP	t-NGG	t-HDP	t-HNGG
L1	8.5563	9.2981	5.3283	5.2390
L2	11.3243	12.0485	9.0608	8.8924
Max	4.7448	5.3204	2.8309	2.7630

The proposed model clearly outperforms the independent ones in all simulated scenarios. Once again, the two hierarchical models yield comparable results. Additional details on this analysis are reported in the Supplementary Materials, where the posterior estimates of the precision and covariance matrices are compared for the different models and simulation scenarios.

Contaminated data, n = 100 and p = 30

Next, we illustrate the behavior of our model on a more complex simulated data structure. In particular, we simulate n = 100 p-dimensional random vectors, with p = 30. In this set of simulations, the graph structure G is produced by splitting the p-dimensional graph into three random graphs of size 10 each, while the elements of the related precision matrix Ω are set to 3 on the diagonal (2 at the extremes), and to −1 for the off-diagonal non-zero elements. Then, the values are multiplied by a constant factor, yielding to a minimum eigenvalue of Ω bigger than 0.5. The divisor matrix θ is produced by working on its vectorized version, vec(θ). We sample n_r, n_c ~ Poisson(10), and associate to n_rn_c randomly selected elements of vec(θ) a divisor ψ_m ~ Unif[0.01, 0.2]. We repeat this process without replacement to produce 4 divisors, and set all the other elements of vec(θ) to 1. For this example, we fit the t-NGG and t-HNGG models with hyperpriors σ,σ₀ ~ Beta(2, 18), where the prior expectation of the Beta distribution is equal to 0.1. The rest of the setting is unchanged from the previous simulation study.

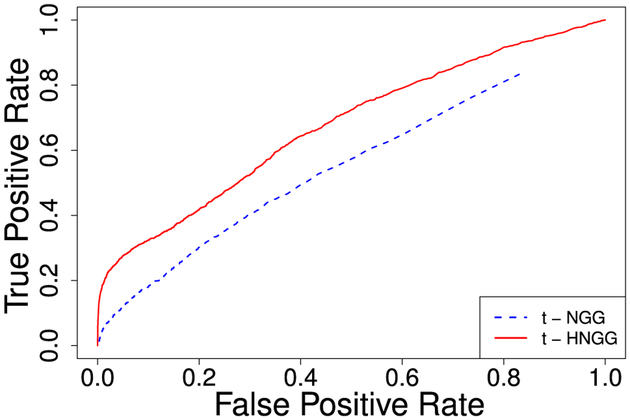
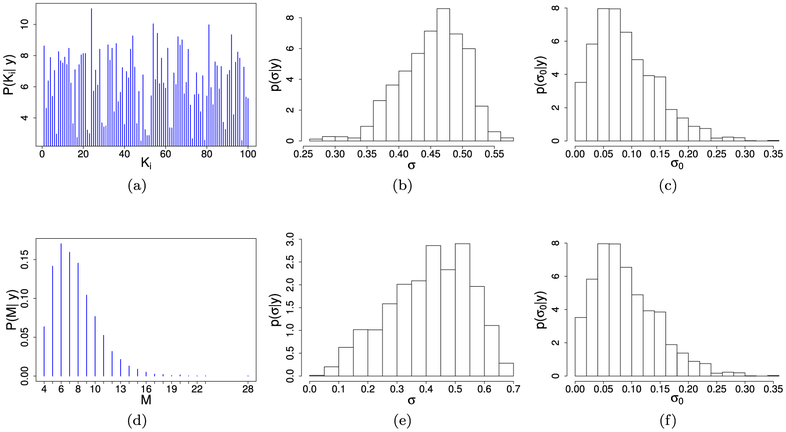
Figure 3 shows the comparison of the ROC curves for our t-HNGG model vs the independent counterpart, the t-NGG model. Curves were computed by averaging over 50 replicated datasets. We observe a clear improvement in the t-HNGG model fitting. Figure 4 reports a summary of the posterior number of clusters as well as posterior distributions of σ and σ₀, obtained under the two models. In particular, in the independent model we show the posterior mean of the number of clusters in each data vector, while the posterior distribution of the number of clusters M is reported for model (8). As expected, the number of clusters in each data vector obtained under the t-NGG is higher than in the t-HNGG case, due to the lack of sharing of information. Furthermore, the posterior mode of the number of clusters in the hierarchical model is very close to the number of unique divisors used to simulate the data (i.e., 5 different divisors including 1). We also notice that the posterior distributions of σ and σ₀ show a clear departure from the Dirichlet process case (achieved when σ = σ₀ = 0), supporting the choice of the use of the NGG process as a building block for our model.

Figure 3:

Simulation study, contaminated data: ROC curves, t-NGG vs t-HNGG models.

Figure 4:

Simulation study, contaminated data: t-NGG vs t-HNGG models. (a) Posterior mean of the number of clusters in each data vector (t-NGG); (b,c) posterior distribution of σ and σ₀ (t-NGG); (d) posterior distribution of the number of clusters M (t-HNGG); (e,f) posterior distribution of σ and σ₀ (t-HNGG).

Finally, Table 2 reports the L¹, L², and maximum modulus distances between estimated and true precision matrices, averaged over the 50 replicates, and calculated using formulas (19). We also add comparisons with methodologies available in the literature, i.e., the Graphical-Lasso (Meinshausen and Bühlmann, 2006) and the Bayesian Graphical-Lasso (Wang, 2012). The proposed model outperforms both the standard methods and the independent t-NGG model.

Table 2:

Simulation study, contaminated data: Average distances between ${\widehat{\mathbf{\Omega }}}_{\mathit{\theta }}$ and Ω_θ.

	G-Lasso	Bayes G-Lasso	t-NGG	t-HNGG
L1	6.9213	6.9089	6.6516	5.6287
L2	17.2031	18.3216	16.2151	8.6058
Max	3.2770	3.4513	3.1293	1.6143

4.2. Case Study on Radiomics Features

Radiomics is the study of numerical features extracted from radiographic image data, which can be used to quantitatively summarize tumor phenotypes (Lambin et al., 2012; Gillies et al., 2016). Cellular diagnostic techniques such as biopsies are not only invasive, but they also do not allow for a thorough or complete investigation of the entire tumor environment, while manual review of images by radiologists is expensive, timeconsuming, and not always consistent across raters. Quantitative imaging features mined with radiomics techniques can be used to get a more comprehensive picture of the entire lesion environment without having to take multiple biopsies or depend on qualitative visual assessments. It has been hypothesized that trends in radiomic features are reflective of complementary tumor characteristics at the molecular, cellular, and genetic levels (Aerts et al., 2014).

Although the development of novel radiomic features is an active area of research (Shoemaker et al., 2018), in this work, we focus on the so-called first and second order features, as these are the most commonly used in practice (Gillies et al., 2016). First order features consider the collection of intensity values across all voxels in the image, without regard for their spatial orientation, and may be referred to as histogram-based or non-spatial. Examples of first order features include volume, intensity, mean, median, entropy, kurtosis. Second order features account for voxel position in addition to intensity, and are also called spatial features. Examples of second order features include eccentricity, solidity, and texture features. These features are often computed on multiple combinations of angle, distance, and number of grey levels, leading to a large set of features that can be used in model building and data analysis. However, there are challenges in the use of radiomics data for statistical modeling. Firstly, features often exhibit departures from normality due to the heterogeneity of the tumor images across patients. Secondly, they are often highly correlated. Such dependence is partially structural in nature, as the features are all calculated on the same voxel data. To date, most efforts at predictive modeling begin with filtering of the features by selecting a single representative for each cluster of highly correlated features (Gillies et al., 2016) or applying rank-based filtering methods across all features (Parmar et al., 2015) or within each class of features (Aerts et al., 2014). The screened features are then used as input to machine learning algorithms for prediction or classification such as random forests, support vector machines, or regularized regression. There is a push in the field, however, away from “black box” modeling. For example, there is an interest in establishing the genetic basis of the features (known as “radiogenomics”, see Gevaert et al., 2014) and, more generally, in enhancing the interpretability of the features, models, and results obtained (Morin et al., 2018). Investigation of the relationships between features supports the search for links between radiomic features, genotypes, phenotypes, and clinical outcomes in more complex statistical models (Stingo et al., 2013) aimed at not only using imaging features for prediction, but understanding their interdependence and the genomic and clinical factors that shape them.

In this case study, we focus on glioblastoma data collected as part of The Cancer Imaging Atlas (TCIA), which provides imaging data on the same set of subjects whose clinical and genomic data are available through The Cancer Genome Atlas (TCGA). Specifically, we obtained radiomic features extracted from magnetic resonance imaging (MRI) images by Bakas et al. (2017), which made a standard set of features publicly available with the goal of providing reproducible and accessible data. This data set includes more than 700 radiomic features for 102 subjects diagnosed with glioblastoma (GBM). The features provided include intensity, volumetric, morphologic, histogrambased, and textural features, as well as spatial information and parameters extracted from a glioma growth model (Hogea et al., 2008). Each subject has scans in the MRI modalities of T1-weighted pre-contrast (T1), T1-weighted post-contrast (T1-Gd), T2, and T2-Fluid-Attenuated Inversion Recovery (FLAIR). The MRI images were segmented into the following regions: the enhancing part of the tumor core (ET), the non-enhancing part of the tumor core (NET), and the peritumoral edema (ED), and these segmentations were manually checked and approved by a neurologist.

To obtain a usable feature set for the proposed robust graphical model, we first applied a log transformation to improve symmetry and reduce the impact of outlying large values in the untransformed data. To account for negative values and to handle the presence of zeros, the features with negative values were shifted up by the minimum value, and 1 was added to each observation for all features before the log transformation was applied. We then assessed the pairwise correlation between all the log-transformed features. If a pair had absolute correlation greater than 0.8, we removed the feature with a higher mean absolute correlation to all other features. In order to focus on features with potential clinical importance, we obtained survival information from the TCGA database, and filtered the features to include only those with p-value ≤ 0.05 in a univariate Cox proportion hazard model for overall survival. This resulted in a set of 26 features for downstream analysis. The features that remain are fairly representative of the different types of features provided in Bakas et al. (2017), as well as from the different regions of the brain and MRI modalities. See Supplementary Materials for detailed information on these features.

Analysis

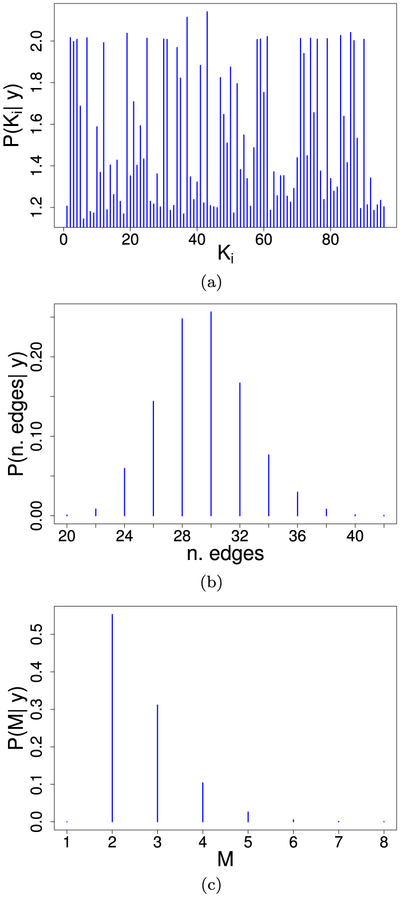
The t-HNGG model was applied to the screened features. As in the first simulation study, we set κ, κ₀ ~ gamma(1, 1) and (σ, σ₀) = (0.5, 0.1), yielding $\mathbb{E}(M)=8.83$ and sd(M) = 2.66. We ran an MCMC chain with 30,000 iterations, with 20,000 burn-in iterations and thinned by 2. The edge inclusion was determined by thresholding the posterior probability of inclusion (PPI) at 0.5, as in the median model of Barbieri et al. (2004). Following Peterson et al. (2015), we computed the Bayesian false discovery rate (FDR) for the selected model; the resulting value of 0.053 suggests that our edge selection procedure is reasonable.

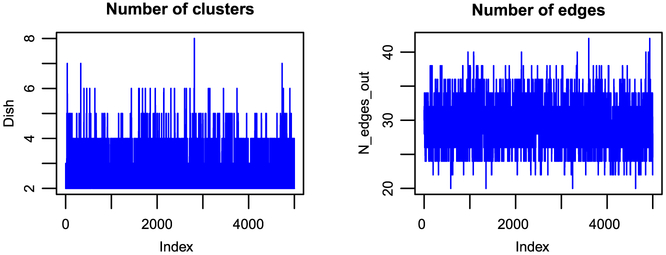
To assess convergence, we applied the Geweke diagnostic criteria (Geweke et al., 1991) on four parameters: κ, κ₀, the number of clusters, and the number of edges. The test gave non-significant p-values for each of the parameters, indicating that the chains converged. The trace plots for the number of clusters and the number of edges are given in Figure 5. Summaries of the posterior means of the number of clusters in each data vector, the number of edges, and the number of clusters are given in Figure 6.

Figure 5:

Case study on radiomics data: Trace plots of the parameters for the numbers of edges and the number of clusters for the t-HNGG model.

Figure 6:

Case study on radiomics data: (a) Posterior mean of the number of clusters in each data vector; (b) Posterior distribution of the number of edges; (c) Posterior distribution of the number of clusters.

For comparison, we applied the graphical lasso (GLasso) and the Bayesian graphical lasso (BGLasso) methods. The regularization parameter for the GLasso was chosen as 0.45 by minimizing the Bayesian information criterion (BIC), and the gamma prior for the regularization parameter of the BGLasso was set such that the prior mean was also 0.45, with shape = 4.5 and scale = 1/10. The BGLasso was run for 13,000 total iterations, with a burn in of 3,000. The sampled precision matrices for this method are not sparse, so a threshold of 0.1 on the absolute value of the entries in the posterior mean of the precision matrix was chosen to create the adjacency matrix.

Results

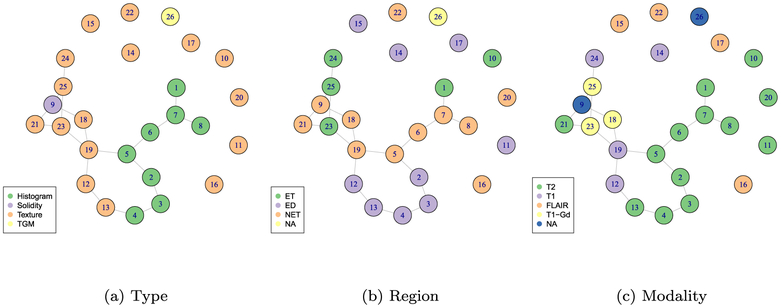
The graph inferred by the proposed t-HNGG method is presented in Figure 7, with three different color schemes to indicate class membership of the nodes by feature type, feature region, and imaging modality. In this illustration, we see that features from the same type and modality are more likely to be identified as connected, while there are fewer links dictated by region: this could imply that it is more critical to have features divided over separate regions of the tumor than it is to have a large number of features or to have scans in multiple modalities, as the former is more likely to give independent information from the different features.

Figure 7:

Case study on radiomics data: The resulting graph from the t-HNGG model is depicted in plots (a)–(c). In each plot, colors are used to indicate class membership of the graph nodes, according to different characteristics of the features, i.e, (a) feature type, (b) feature region, and (c) imaging modality.

Regarding the comparison to other methods, GLasso and BGLasso produced very similar graphs, as is to be expected, and these had fewer edges overall than the graph inferred via the t-HNGG model, although there were a couple of connections selected under the lasso methods that were not identified in the t-HNGG model. Table 3 reports edge similarities between the three methods. In all three graphs, edges are captured that we expect to see, such as adjacent bins in various histograms, e.g., there is a connection between bin 1 and bin 2 of the histogram for the T2 modality of the NET region. The busyness features over three different modalities are connected in all three models. However, the two GLasso models only select couplets and triplets, and none of these are particularly surprising, linking together similar features that could be considered adjacent in a qualitative sense. As one would expect, reducing the PPI threshold in the t-HNGG model increases the number of selected edges, while increasing this threshold reduces the number of selections. We found, however, that the overlapping edges between the t-HNGG and the graphs inferred with GLasso and BGLasso remained consistent across the range of PPI thresholds between 0.2 and 0.9.

Table 3:

Case study on radiomics data: Number of edges in each of the graphs inferred by GLasso, BGLasso and the t-HNGG model, and number of shared edges between pairs of graphs.

	GL	BGL	t-HNGG
GL	7	7	5
BGL		8	6
t-HNGG			19

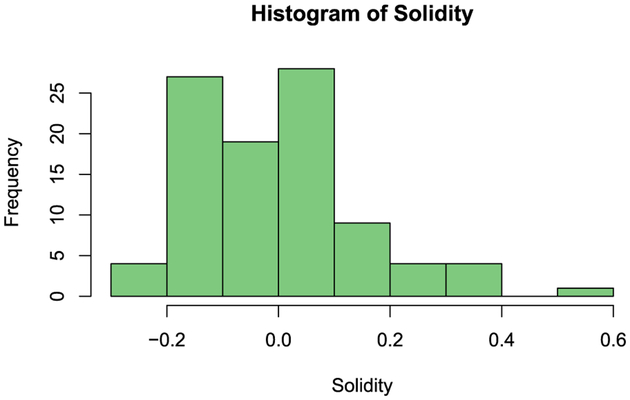
An interesting edge captured by the t-HNGG model that is not captured by the other models is one between a histogram feature and a busyness texture feature. Histogram features display only the first-order information about the pixels and are not often used to infer any information about the adjacency or texture of the images. However, this particular histogram feature is of the first bin of the histogram, so this could suggest that heavier tailed pixel distributions are harbingers of busyness. The end bin of the histogram was also found to be a significant feature for glioma classification by Cho and Park (2017). Further, there are no edges in the graphs inferred by the LASSO-type models that connect the solidity feature to any other feature, unlike in the t-HNGG graph. Failure to recover edges might be attributed to the non-normal distribution shown by this feature, as it can be seen in Figure 8, showing once again the power of the t-HNGG model to handle outliers. Edges and dependencies, and lack thereof, can be used to inform more complex models for classification and characterization, to inform radiologists and clinicians as they begin to utilize radiomics, and to enhance the general interpretation as statisticians move away from the “black box models” often used on these complicated feature sets.

Figure 8:

Case study on radiomics data: A histogram of the data for the 9th feature, solidity of the NET region.

5. Conclusion

In this paper, we have proposed a class of robust Bayesian graphical models based on a nonparametric hierarchical prior construction that allows for flexible deviations from Gaussianity in the distribution of the data. The proposed model is an extension of the t-Dirichlet model presented in Finegold and Drton (2014), where departure from Gaussianity is accounted for by including suitable latent variables (divisors) in the sampling model, to allow for skewness. In our proposed construction, the law of the divisors is described by a hierarchical normalised completely random measure. In particular, in this paper we have focused on a hierarchical NGG process, yielding to what we have called a t-HNGG model. The advantage of this choice is twofold: on one side, by extending the characterization to the NGG process, we induce a more flexible clustering structure when compared to the Dirichlet process case; on the other side, by allowing for an additional level of hierarchy in the nonparametric prior setting, we achieve sharing of information across the data sample. For posterior inference, we have implemented a suitable MCMC algorithm, which is built upon the generalized Chinese restaurant franchise metaphor to exploit dependency among the components of each data vector (i.e,. customers seated in the same restaurant).

We have illustrated performances of our proposed methodology on simulated data and on a case study on numerical features extracted from radiographic image data which can be used to quantitatively summarize tumor phenotypes, and that are known to show non-Gaussian characteristics. On simulated data, we have shown good recovery of the main features of the data, such as the graph structure and the precision matrix. Additionally, a comparison with existing methodologies such as the GLasso and the Bayesian GLasso has shown how these methods are outperformed by our proposed model in the presence of non-Gaussian data. On the real data, our model has resulted in a less sparse graph than those inferred by GLasso and Bayesian GLasso. Furthermore, the inferred relationships highlighted by our estimated graph have revealed interesting interpretation in terms of important characteristics of the data. These relationships and dependencies, and lack thereof, can provide valuable information for follow-up classifications and characterization of radiomics data.