Synthesized 7T MRI from 3T MRI via Deep Learning in Spatial and Wavelet Domains

Abstract

Ultra-high field 7T MRI scanners, while producing images with exceptional anatomical details, are cost prohibitive and hence highly inaccessible. In this paper, we introduce a novel deep learning network that fuses complementary information from spatial and wavelet domains to synthesize 7T T1-weighted images from their 3T counterparts. Our deep learning network leverages wavelet transformation to facilitate effective multi-scale reconstruction, taking into account both low-frequency tissue contrast and high-frequency anatomical details. Our network utilizes a novel wavelet-based affine transformation (WAT) layer, which modulates feature maps from the spatial domain with information from the wavelet domain. Extensive experimental results demonstrate the capability of the proposed method in synthesizing high-quality 7T images with better tissue contrast and greater details, outperforming state-of-the-art methods.

1. Introduction

Magnetic resonance imaging (MRI) is versatile and has been used extensively for diagnosis of neurodisorders. The magnetic field strength has evolved from less than 0.5T in the 1980s to the widely used 3T and then recently to 7T. Compared to routine 3T MRI, 7T MRI provides images with higher resolution and high signal-to-noise ratio (see Fig. 1), potentially improving diagnostic and prognostic value (Van der Kolk et al., 2013; Lian et al., 2018). However, 7T MRI scanners are often cost prohibitive and hence not always accessible in the clinics. To date, there are less than 100 7T MRI scanners worldwide, whereas there are more than 20,000 3T MRI scanners (Forstmann et al., 2017).

Figure 1:

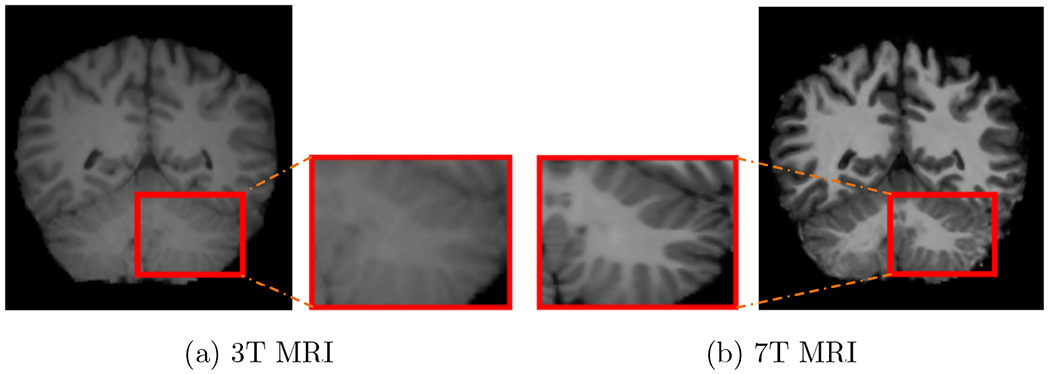
3T and 7T MRI.

Recent research has shown that it is possible to synthesize 7T images using learning-based methods such as linear regression (Zhang et al., 2018), sparse learning (Bahrami et al., 2015; Rueda et al., 2013; Zhang et al., 2012) and random forest (Alexander et al., 2014; Bahrami et al., 2017). While effective, their effectiveness is often influenced by the quality of hand-crafted features. Deep learning techniques alleviate the need for hand-crafted features and have been successfully applied to various image synthesis problems (Bahrami et al., 2016; Nie et al., 2016; Xiang et al., 2018). For example, Bahrami et al. (2016) proposed a convolutional neural network (CNN) with mean square error (MSE) loss to learn the non-linear 3T-to-7T mappings. Xiang et al. (2018) proposed a deep embedding CNN for synthesizing computed tomography (CT) images from 3T T1 images.

3T and 7T MR images (Fig. 1) differ not only in resolution, but also in contrast. Good image synthesis should therefore preserve both global, low-frequency contrast and local, high-frequency details. Current CNN-based methods often directly determine the complex 3T-to-7T mapping without explicitly harnessing multi-scale information. Previous studies have shown that network learning can be improved by incorporating valuable prior information (Wang et al., 2015, 2019, 2018). For example, Wang et al. (2015) incorporated a sparse prior in a deep learning network for image super-resolution (SR), leading to efficient training and reduced model size.

In this paper, we introduce a deep learning network that leverages wavelet domain as a prior to facilitate effective reconstruction of multi-frequency image details. This wavelet domain prior is complementary to the large learning capacity of deep network in further improving image synthesis performance. We design a novel wavelet-based affine transformation (WAT) layer to effectively encode the wavelet domain prior into our network. As shown in Fig. 2, the WAT layer modulates feature maps from the spatial domain with information from the wavelet domain. Specifically, each WAT layer learns a set of affine parameters based on the wavelet coefficients and performs element-wise affine transformation on the intermediate spatial feature maps. Each WAT layer is optimized as part of the whole network, empowering the network to explicitly capture multi-frequency information.

Figure 2:

WATNet predicts the 7T image using a 3T image and its wavelet coefficients.

Our network (see Fig. 2), called WATNet, consists of a feature extraction branch and an image reconstruction branch. The feature extraction branch learns the complex 3T-to-7T mappings for different frequency components with several flexible WAT layers. The image reconstruction branch synthesizes 7T images from the wavelet modulated spatial information. Experimental results demonstrate that WATNet can capture effectively both the global tissue contrast and the local anatomical details of 7T images. The contributions of our paper are summarized as follows:

1. We introduce a novel method for 7T image synthesis by leveraging complementary information of both spatial and wavelet domains.

2. We provide an efficient way to incorporate image priors in deep learning to achieve superior image synthesis performance.

3. We present a flexible and parameter-efficient WAT layer that can be embedded into a neural network to facilitate effective reconstruction with consideration of multiple frequency components.

2. Related Work

3T to 7T MRI synthesis predicts high-resolution (HR) 7T images with greater anatomical details and better tissue contrast from low-resolution (L-R) 3T images. Existing image synthesis methods include interpolation-based methods (Kim et al., 2010; Tam et al., 2010), reconstruction-based methods Manjón et al., 2010; Shi et al., 2015), and learning-based methods (Alexanler et al., 2014; Bahrami et al., 2017; Zhang et al., 2019; Qu et al., 2019).

Interpolation-based methods are based on linear or non-linear interpolators, such as nearest-neighbor and bilinear (Kim et al., 2010; Tam et al., 2010). Although simple and fast, these methods blur sharp edges and fine details (Yang et al., 2014).

Alternatively, reconstruction-based methods tackle ill-posed reconstruction problems via regularization. Regularization terms are priors based on mage characteristics, such as total-variation (Shi et al., 2015) and non-local similarity (Manjón et al., 2010). These methods typically work well for small but not large upscaling factors (Hui et al., 2018).

Learning-based methods, such as sparse learning (Bahrami et al., 2015; Rueda et al., 2013; Zhang et al., 2012) and random forest (Alexander et al., 2014; Bahrami et al., 2017), learn mappings from LR to HR images. For example, Rueda et al. (2013) proposed a sparsity-based SR method that so couples low and high frequency information to generate an HR image from a LR MR image. This form of sparse learning has also been employed in Bahrami et al. (2015) together with multi-level canonical correlation analysis (MCCA) to learn the mapping function. Since MCCA involves only linear transformation, Bahrami et al. (2017) replaced MCCA with random forest 85 to allow greater learning capacity. While effective, these methods may not be optimal since they rely on predefined features.

More recently, deep learning techniques have demonstrated state-of-the-art performance in image synthesis. Dong et al. (2014) in their seminal work show how a three layer fully CNN can be used to learn LR-to-HR mappings in 90 an end-to-end manner. Various network architectures have since then been shown to further improve SR performance, e.g., residual learning (Oktay et al., 2016), Laplacian pyramid networks (Lai et al., 2018), dense connections (Chen et al., 2018), and information distillation blocks (Hui et al., 2018). For example, residual learning has been employed in Oktay et al. 95 (2016) to reconstruct 3D HR cardiac images from multiple 2D LR slices. Lai et al. (2018) proposed a deep Laplacian pyramid SR network to progressively reconstruct the residuals of HR images at multiple pyramid levels. Dense connections (Chen et al., 2018) and information distillation (Hui et al., 2018) have been employed to make full use of hierarchical features for reconstruction.

Several recent efforts have been devoted to improving perceptual quality. Instead of applying the MSE loss for optimization in pixel space, Johnson et al. (2016) introduced a perceptual loss implemented via a network pretrained based on high-level features from other domains. Ledig et al. (2017) proposed a generative adversarial network with perceptual loss to generate HR images with greater details. This has been extended for MRI SR in Chen et al. (2018). Nie et al. (2018) proposed a deep convolutional adversarial neural network with a gradient based loss function for medical image synthesis. Though great strides have been made, these perceptual-driven methods still face problems such as training instability and computational complexity (Huang et al., 2017b).

Most related to the current work is Zhang et al. (2018), where they proposed a cascaded regression framework that considers both spatial and frequency domains for 7T image synthesis. However, the mapping from 3T to 7T patches is determined using linear regression, which greatly restricts the capacity to model the complex highly-non-linear mapping. Liu et al. (2018) proposed a multi-level wavelet-based CNN for SR and artifacts removal. Their method, however, is based solely on the wavelet domain by predicting the wavelet coefficients of the HR image rather than the pixel values.

3. Methods

Given a 3T image I, our goal is to synthesize a 7T image $\widehat{O}$ that is as similar as possible to the ground-truth 7T image O. Synthesis of a high-quality 7T image from its 3T counterpart is challenging since 3T and 7T images not only differ in high-frequency details but also low-frequency contrast. Significant effort has been devoted to designing an effective learning mechanism to learn the 3T-to-7T mapping function R_θ:

$$\widehat{O}=R_{\theta }\left(I\right),$$ (1)

where θ is the set of parameters to be learned. These methods use a universal mapping for both high-frequency details and low-frequency contrast, generating images degraded by wrong tissue contrast or the loss of anatomical details.

We argue that the wavelet transformation, which can depict multi-level frequency components of an image, are beneficial for the synthesis of high-quality 7T images. To this end, instead of directly learning the mapping function, we incorporate wavelet domain as a prior to guide the prediction of 7T images with multi-level frequency components, hence rewriting (1) as

$$\widehat{O}=R_{\theta }\left(I|\left\{W_l\right\}\right),$$ (2)

where W_l denotes the wavelet coefficients of I at level l. In our implementation, we set l = 1, 2, 3.

3.1. Wavelet Transformation

Wavelet transformation is an effective and elegant tool for multi-resolution representation (Daubechies, 1990). In our implementation, the simplest wavelet, Haar wavelet packet decomposition (WPD) (Akansu et al., 2001) is employed. WPD decomposes an input image I into four wavelet coefficients $W_l=\left\{W_l^A,W_l^H,W_l^V,W_l^D\right\}$ via a series of filtering and downsampling operations, where the approximation coefficients $W_l^A$ capture the low-frequency global information and the detail coefficients $\left\{W_l^H,W_l^V,W_l^D\right\}$ capture the high-frequency local information. Fig. 3 shows an illustration of one level WPD.

Figure 3:

Illustration of one level 2D wavelet packet transformation. h_high and h_low indicate the high-pass and low-pass quadrature mirror filters respectively. In our implementation, the Haar-based filters $h_{high}=\left(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}\right)$ and $h_{low}=\left(\frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}}\right)$ are utilized.

3.2. Wavelet-based Affine Transformation (WAT) Layer

We propose a parameter-efficient and flexible WAT layer for endowing the network with information from the wavelet domain. The WAT layer is inspired by conditional normalization (CN) (Huang and Belongie, 2017; Perez et al., 2017; Wang et al., 2018). Unlike batch normalization (Ioffe and Szegedy, 2015), CN transforms feature maps using learned affine mappings. CN and its variants have been demonstrated to be highly effective in image processing tasks such as style transformation (Huang and Belongie, 2017), visual reasoning (Perez et al., 2017), and SR (Wang et al., 2018). Unlike conventional CN that utilizes one set of affine parameters to globally transform all feature maps, WAT is an extension of CN that performs spatial element-wise affine transform, allowing greater adaptivity to local spatial details.

The WAT layer, shown in Fig. 2, learns a set of affine parameters {γ_l, β_l} based on the wavelet coefficients W_l, and performs element-wise affine transformation spatially on intermediate feature maps F as follows:

$$\mathrm{WAT}\left(F|{\gamma }_l,{\beta }_l\right)={\gamma }_l\odot F+{\beta }_l,$$ (3)

where ⊙ indicates element-wise multiplication. The affine parameters γ_l and β_l are functions of wavelet coefficients W_l:

$${\gamma }_l=U\left(W_l\right),$$ (4)

$${\beta }_l=V\left(W_l\right),$$ (5)

where γ_l and β_l have the same dimensions as F. The mapping functions U and V can be arbitrary. In our implementation, they are implemented as two convolution layers that can be optimized as part of the whole network. The WAT layer modulates the feature maps F by scaling them linearly with γ_l and then shifting with β_l, conditioned on wavelet coefficients.

3.3. Network Architecture

WATNet (see Fig. 2) takes a 3T image and its wavelet coefficients and predicts the 7T image. It consists of two branches: a feature extraction branch and an image reconstruction branch.

3.3.1. Feature Extraction Branch

The feature extraction branch consists of (1) two convolution layers for generating feature maps from the 3T image, (2) four stacked information distillation blocks for extraction of hierarchical features, and (3) three WAT layers for modulating the intermediate feature maps based on the wavelet coefficients.

For conciseness, we denote the convolution layer as conv(N, K, S, P) with N outputs, kernel size K, stride S, and pad size P. ReLu denotes the nonlinear rectified linear unit function layer. The feature extraction block is constructed with two conv(64, 3, 1, 1) layers. Each of the convolution layers is followed by a ReLu layer.

The stacked information distillation block (DBlock), originally proposed by Hui et al. (2018), is a variation of densely connected layers (Huang et al., 2017a). As suggested in Hu et al. (2017), employing feature recalibration in a network instead of using all feature maps without distinction can help suppress useless information. Motivated by Hu et al. (2017), Hui et al. (2018) proposed an enhancement unit and a compression unit for each DBlock to help gain more effective information and improve the representation power of the network. As illustrated in Fig. 4, the enhancement unit consists of six convolution layers, each followed by a ReLu layer, which is omitted here for simplicity. The enhancement unit consists of slice and concatenation operations. The compression unit consists of a 1 × 1 convolution layer and a ReLu layer, and distills relevant and useful information for the subsequent block.

Figure 4:

Stacked information distillation block (DBlock). For conciseness, we omit the ReLu layer that follow each convolution layer. denotes channel concatenation and denotes slice operation, slicing the feature maps into two segments, $\frac{1}{q}$ part of the feature maps via the short path and the remaining $1-\frac{1}{q}$ via the long path. q is set to 4.

We denote the four successive DBlocks in the feature extraction branch as DBlock_m, m ∈ {1, 2, 3, 4}. The enhancement unit has a common architecture across DBlocks. The architecture of the compression unit for the first three DBlocks is conv(64, 1, 2, 0) — ReLu and conv(64, 1, 1, 0) — ReLu for the last DBlock.

We denote the three WAT layers in the feature extraction branch as WAT_l, where l ∈ {1, 2, 3}. We do not add WAT layer in the fourth DBlock since the wavelet coefficients are small. For each WAT layer, we perform three levels of wavelet transformation on the 3T image, obtaining the {W_l}, l = 1, 2, 3. WAT_l takes W_l as input and generates a set of affine parameters {γ_l, β_l}. The affine transformation is then applied spatially on the intermediate feature maps F_l generated by DBlock_l.

3.3.2. Image Reconstruction Branch

This branch takes the wavelet modulated feature maps and generates the residual image that is added to the 3T image for generating the 7T image. As illustrated in Fig. 2, the architecture of this branch is almost a mirror of the feature extraction branch, without the WAT layers and with conv(64, 1, 2, 0) — ReLu in the compression unit replaced by conv(64, 1, 1, 0) — ReLu — deconv, where deconv denotes deconvolution with upsampling.

3.4. Loss Function

We use the mean absolute error (MAE) as the loss function, since it provides better convergence than the widely used MSE loss (Lim et al., 2017). Given a batch of N predicted and ground-truth images ${\left\{O^i,{\widehat{O}}^i\right\}}_{i=1}^N$, the MAE loss function is defined as,

$$L^{MAE}={{\sum }_i^N\Vert O^i-{\widehat{O}}^i\Vert }_1.$$ (6)

3.5. Implementation Details

WATNet was implemented with Caffe (Jia et al., 2014) and optimized using Adam (Kingma and Ba, 2014). The filter weights were initialized according to Hui et al. (2018). We set batch size to 32, the weight decay to 0.0001, and learning rate to 0.002 (halved every 10 epochs).

WATNet was trained with the image patches extracted from 3T and 7T images. The patch size was 64 × 64 × 3, covering 3 consecutive axial slices to promote inter-slice continuity (Xiang et al., 2018). In the testing phase, the input 3T image was processed slice by slice to synthesize the final 7T image. Values resulting from patch overlap are averaged.

To prevent overfitting, the training data were augmented in three ways: (1) Random rotation with 90°, 180°, and 270°; (2) Random scaling with a factor in the range [0.55, 0.9]; (3) Left-right Flipping. Training and testing were performed using a single GeForce GTX 1080 Ti. Training took around 18 hours.

4. Experiments

We compared WATNet with several state-of-the-art 7T image synthesis methods. In this section, we will describe the dataset, image pre-processing, and qualitative and quantitative results to demonstrate the effectiveness of WATNet.

4.1. Dataset

Following Bahrami et al. (2016, 2017); Zhang et al. (2018), we used 15 pairs of 3T and 7T brain images in our experiments. For 3T MRI, T1 images with 224 coronal slices were acquired using a Siemens Magnetom Trio 3T scanner, with voxel size 1 × 1 × 1 mm³, TR = 1990 ms, and TE = 2.16 ms, For 7T MRI, T1 images with 191 sagittal slices were acquired using a Siemens Magnetom 7T whole-body MR scanner, with voxel size 0.65×0.65×0.65 mm³, TR = 6000 ms, and TE = 2.95 ms.

Each 7T image was linearly aligned to the MNI standard space (Holmes et al., 1998). The corresponding 3T image was then rigidly aligned to the 7T image in the MNI space. FLIRT (Jenkinson et al., 2002) was used for alignment. After inhomogeneity correction (Sled et al., 1998) and skull removal (Shi et al., 2010), the intensity values of the 3T and 7T images were normalized to [0, 1]. Histogram matching was then applied to ensure that the intensity distribution is consistent across different subjects.

Similar to Bahrami et al. (2016); Zhang et al. (2018), we adopted leave-one-out cross-validation for performance evaluation. One pair of 3T and 7T images were used for testing, four pairs for validation, and the remaining 9 pairs for training.

4.2. Performance Evaluation

We compared WATNet with the following methods:

• MCCA (Bahrami et al., 2015): A spatial shallow learning method that utilizes MCCA and group sparsity.

• RF (Bahrami et al., 2017): A spatial shallow learning method with random forest.

• CAAF (Bahrami et al., 2016): A spatial deep learning method that leverages a three layer CNN network taking into account appearance and anatomical features.

• DDCR (Zhang et al., 2018): A spatial and frequency shallow learning method based on linear regression.

We evaluate the performance of different 7T image synthesis methods with two commonly used image quality metrics: peak signal-to-noise ratio (PSNR) and structural similarity (SSIM). For fair comparisons, we use either the qualitative/quantitative results reported in the papers or the source code provided by the authors.

4.3. Prediction Performance

Fig. 5 and Fig. 6 compare the results of different methods and show the residuals of the predicted images with respect to the ground-truth 7T image. The respective PSNR and SSIM are also provided. It can be observed that WATNet yields results that are significantly closer to the ground truth. This can be attributed to the multi-frequency learning capability of WATNet. In contrast, MCCA (Bahrami et al., 2015), RF (Bahrami et al., 2017), and CAAF (Bahrami et al., 2016) do not consider the multi-scale nature of the problem, leading to unsatisfactory results. For example, MCCA synthesizes a 7T image with unsatisfactory tissue contrast, as shown in Fig. 5(c). The images generated by RF (Bahrami et al., 2017) and CAAF (Bahrami et al., 2016) are blurry with lost anatomical details (see Figs. 6(d) and 6(e)).

Figure 5:

7T images synthesized via WATNet and other methods shown in axial view along with the prediction error maps. (PSNR, SSIM) values are shown at the bottom.

Figure 6:

7T images synthesized via WATNet and other methods shown in sagittal and coronal views along with the prediction error maps. (PSNR, SSIM) values are shown at the bottom.

Similar to our WATNet, DDCR (Zhang et al., 2018) aims to synthesize the 7T image using information from both spatial and frequency domains, resulting in performance superior to methods based only on the spatial domain. However, limited by the linear mapping function, the results of DDCR (Zhang et al., 2018) are still unsatisfactory. For example, this is shown by the loss of gray matter in the second row of Fig. 5(f) and also the blurry tissue boundaries in the fifth row of Fig. 6(f).

Fig. 7 shows the boxplots of PSNR and SSIM values computed based on the predicted images with respect to the ground truth. WATNet again demonstrates the best performance among all the compared methods. Specifically, WATNet improves the state-of-the-art PSNR/SSIM performance from 27.51/0.8580 given by DDCR (Zhang et al., 2018) to 28.27/0.8782.

Figure 7:

Boxplots of PSNR and SSIM values for five different 7T image synthesis methods. The average PSNR and SSIM values for all the methods are: (25.52, 0.4840) for MCCA (Bahrami et al., 2015), (26.55, 0.5728) for RF (Bahrami et al., 2017), (27.05, 0.8406) for CFFA (Bahrami et al., 2016), (27.51, 0.8580) for DDCR (Zhang et al., 2018), and (28.27, 0.8782) for WATNet.

4.4. Effectiveness of WAT Layers

We investigated how the WAT layers affect the behavior of WATNet. We removed the WAT layers, reducing WATNet to a plain encoder-decoder network, which we call PlainNet. We trained PlainNet using a strategy similar to WATNet. The intermediate feature maps of WATNet and PlainNet are shown in Fig. 8.

Figure 8:

Examples showing how the WAT layer alters the behavior WATNet. Conditioned on the wavelet coefficients (e), the affine parameters γ (f) and β (g) are used to manipulate the intermediate feature maps, converting feature maps (h) to (i). Compared with the PlainNet feature maps (h), the WATNet feature maps (i) capture more fine details, especially in the cortex, empowering WATNet to generate images with greater anatomical details, as depicted in (c) and (d).

The affine parameters γ (Fig. 8(f)) and β (Fig. 8(g)) are conditioned on the wavelet coefficients (Fig. 8(e)) and produce the WATNet feature maps (Fig. 8(i)). Compared with the PlainNet feature maps in Fig. 8(h), the WATNet feature maps in Fig. 8(i) capture more fine details, especially in the cortex, empowering WATNet to generate images with greater anatomical details, as depicted in Figs. 8(c) and 8(d).

4.5. Alternative Schemes

We further compared WATNet with two alternative schemes for using wavelet information:

• Wavelet prediction: Predicts wavelet coefficients of the synthesized 7T image from its 3T counterpart. See Fig. 9.

• Feature concatenation: Concatenates the wavelet coefficients with the intermediate features directly with γ = 1, β = W_l, where 1 indicates all-ones matrix. See Fig. 10.

Fig. 11(c) and Table 1 indicate that, without considering the spatial domain, direct wavelet prediction fails to preserve spatial consistency. Fig. 11(d) and Table 1 indicate that direct feature concatenation is not as optimal as WATNet. WATNet synthesizes the 7T image with greater details and spatial consistency.

Figure 9:

Network for wavelet prediction. IWPD denotes inverse WPD.

Figure 10:

Network for feature concatenation.

Figure 11:

Visual comparison of different methods of utilizing wavelet information.

Table 1:

Quantitative comparison of different methods utilizing wavelet information. Mean PSNR and SSIM values of leave-one-out cross validation are shown.

	Wavelet Prediction	Feature Concatenation	WATNet
PSNR	27.43	27.83	28.27
SSIM	0.8479	0.8717	0.8782

4.6. Diagnostic Quality Evaluation

Two board-certified radiologists (with 6 and 10 years of experience) independently reviewed three types of MR images, i.e., the original 3T images, the real 7T images, and the synthesized 7T images by WATNet. The subjects were anonymized and the order of the scans were randomized. Three types of image quality measures (overall image quality, image contrast, and outlines of deep brain structures (e.g., basal ganglia and thalami)) were scored with 5-point Likert scale, 5-point Likert scale, and 3-point scale respectively. The 5-point Likert scale for overall image quality and image contrast were: 1. unacceptable; 2. poor; 3. acceptable; 4. good; and 5. excellent. The 3-point scale for outlines of deep brain structures were: 1. indistinct outline; 2. perceptible outline; and 3. sharp outline. One-tailed Wilcoxon signed-rank tests based on the ratings of two radiologists were used to test the difference between our synthesized 7T images and the original 3T and 7T images. The significance level was set as 0.01.

The values of quantitative metrics for the two raters are shown in Table 2 and Fig.12. Both raters agreed that our synthesized images led to significant improved overall quality (p < 0.01), image contrast (p < 0.01), and outlines of deep brain structures (p < 0.01) compared to the original 3T images. In contrast, there were no significant difference between our synthetic 7T images and the real 7T images in terms of all the image quality measures (all with p > 0.01). It is worth noting that Rater 1 stated the real 7T images show slighter better overall image quality (4.9 out of 5) than our synthesized 7T 330 images (4.3 out of 5). However, Rater 1 rated that our synthesized images had perfect image contrast (mean 5.0 and standard variance 0) and sharp outline of deep brain structures (mean 3.0 and standard variance 0) similar to the real 7T images.

Table 2:

Comparison of average ratings of the original 3T images, the real 7T images, and the synthesized 7T images given by WATNet.

	Ratings (mean ± standard deviation)			P-value w.r.t. WATNet
	3T MRI	WATNet	7T MRI	3T MRI	7T MRI
Quality	2.9 ± 0.3	4.6 ± 0.489	4.9 ± 0.3	2.65 × 10−5	0.029
Contrast	2.75 ± 0.43	4.8 ± 0.4	5 ± 0.0	1.8 × 10−5	0.023
Outline	1.8 ± 0.4	2.75 ± 0.43	3 ± 0.0	1.7 × 10−5	0.0126

Figure 12:

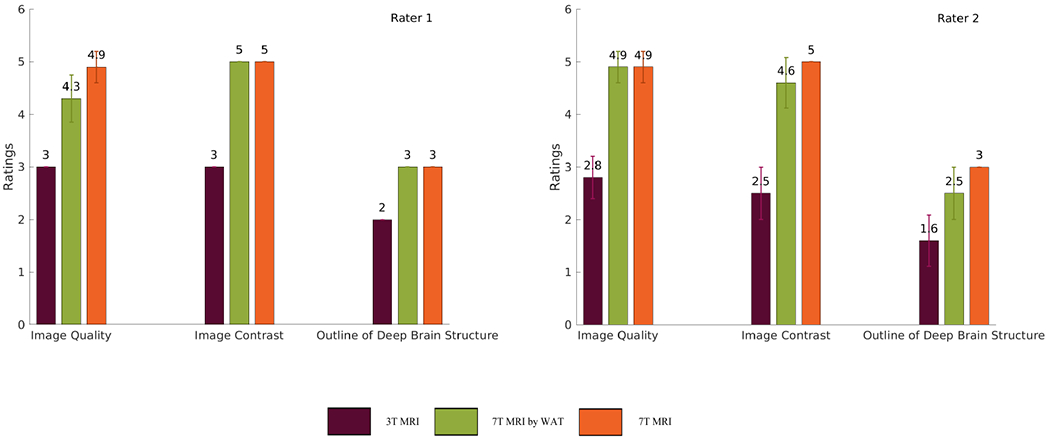
Bar graphs showing means and standard deviations of ratings given by two raters for three types of MR images: the original 3T images, the real 7T images, and the synthesized 7T images given by WATNet.

4.7. Brain Tissue Segmentation

We demonstrate how the synthesized 7T images improve brain tissue segmentation. We employed the commonly used ANTs segmentation pipeline (Avants et al., 2011) with default parameters to segment the images into gray matter (GM), white matter (WM), and cerebrospinal fluid (CSF). We compared the segmentation results based on the original 3T images, the synthesized 7T images from MCCA (Bahrami et al., 2015), RF (Bahrami et al., 2017), CAAF (Bahrami et al., 2016), DDCR (Zhang et al., 2018), and WATNet using Dice similarity coefficient (DSC). The segmentation results of real 7T images were used as the ground truth.

Fig. 13 gives a visual comparison of brain tissue segmentation based on various types of images. Our synthesized 7T image is able to generate more accurate tissue segmentation, compared to the original 3T image, where the gray matter is erroneously segmented as white matter due to low tissue contrast (see the fourth row of Fig. 13(a)). Fig. 14 shows the box plots of DSCs for WM, GM, and CSF, respectively. The segmentation results by WATNet are significantly closer to the segmentation result of the real 7T images than those obtained by the competing methods. These results imply that our synthetic images are with high quality and can improve brain MRI structural measurement.

Figure 13:

Brain tissue segmentation based on the original 3T image, the real 7T image, and the synthesized 7T images given by MCCA (Bahrami et al., 2015), RF (Bahrami et al., 2017), CAAF (Bahrami et al., 2016), DDCR (Zhang et al., 2018), and WATNet.

Figure 14:

DSC box plots for the segmentation of (a) WM, (b) GM, and (c) CSF using the original 3T images, the synthesized 7T images given by MCCA (Bahrami et al., 2015), RF (Bahrami et al., 2017), CAAF (Bahrami et al., 2016), DDCR (Zhang et al., 2018), and WATNet.

5. Conclusion

In this paper, we have introduced a novel and efficient deep learning method for 7T image synthesis by harnessing information from both spatial and wavelet domains. This is made possible by parameter efficient WAT layers. Embedded with several WAT layers, the proposed network, called WATNet, is capable of synthesizing 7T images with better tissue contrast and greater anatomical details. Both qualitative and quantitative results demonstrate that WATNet performs favorably against the existing 7T image synthesis methods.

Our flexible WAT layer provides a way to incorporate image priors in deep learning by adding the prior information as a conditional input of WAT layer. This WAT scheme could be further extended to include other image priors such as anatomical tissue label to facilitate image synthesis task. In our future work, we intend to adapt this WAT layer to handle more general medical image synthesis tasks, such as MRI to CT and T2 images from T1 images.