Embedding High-dimensional Bayesian Optimization via Generative Modeling: Parameter Personalization of Cardiac Electrophysiological Models

Abstract

The estimation of patient-specific tissue properties in the form of model parameters is important for personalized physiological models. Because tissue properties are spatially varying across the underlying geometrical model, it presents a significant challenge of high-dimensional (HD) optimization at the presence of limited measurement data. A common solution to reduce the dimension of the parameter space is to explicitly partition the geometrical mesh. In this paper, we present a novel concept that uses a generative variational auto-encoder (VAE) to embed HD Bayesian optimization into a low-dimensional (LD) latent space that represents the generative code of HD parameters. We further utilize VAE-encoded knowledge about the generative code to guide the exploration of the search space. The presented method is applied to estimating tissue excitability in a cardiac electrophysiological model in a range of synthetic and real-data experiments, through which we demonstrate its improved accuracy and substantially reduced computational cost in comparison to existing methods that rely on geometry-based reduction of the HD parameter space.

Graphical Abstract

1. Introduction

Computer simulation models—customized to the organ anatomy and physiology of a specific subject—have the potential to allow physicians to predict adverse events and therapeutic responses using a personalized virtual or gan (Prakosa et al., 2018; Arevalo et al., 2016; Sermesant et al., 2012). Rapid advances in medical imaging, computational modeling, and high performance computing have brought these models significantly closer to practice. In the space of cardiac electrophysiological modeling, recent works have demonstrated the use of personalized virtual hearts to stratify the risk of lethal arrhyth mia (Arevalo et al., 2016), to identify optimal treatment targets in catheter ablation of atrial (Zahid et al., 2016) and ventricular arrhythmia (Prakosa et al., 2018), and to predict the response to cardiac resynchronization therapy (Sermesant et al., 2012).

To make predictions pertinent to an individual, a personalized model first has to be customized from clinical data specific to that individual. This generally includes the customization of organ anatomy, boundary conditions, and tissue properties (Taylor and Figueroa, 2009). While personalization of the first two elements has become increasingly accurate owing to advances in clinical imaging and image analysis technologies, the estimation of subject-specific organ tissue properties still suffers from several unresolved critical challenges (Taylor and Figueroa, 2009). First, tissue properties of an organ typically cannot be directly measured but needs to be estimated from sparse measurements that are indirectly related to the unknown tissue properties through a complex nonlinear physiological process. These measurements are further associated with potential errors and uncertainties. Second, tissue properties are spatially varying throughout the 3D organ where local abnormality and heterogeneity often hold important therapeutical implications, and they not only vary across individuals but also across time for the same individual. The personalization of organ tissue properties, therefore, translates to an ill-posed optimization problem in which the objective function contains a computationally expensive simulation model and does not have a closed-form expression, the derivatives of the objective function are difficult to obtain, and the unknowns are represented by high-dimensional (HD) model parameters at the resolution of the discrete organ mesh.

1.1. Related works

Over the past decades, significant progress has been made in personalizing the parameters of a cardiac model (Delingette et al., 2012; Wong et al., 2012, 2015; Sermesant et al., 2012; Dhamala et al., 2017b; Moireau et al., 2013; Zettinig et al., 2013). To handle the analytically-intractable objective function, commonly-used methods include variational data assimilation where the derivatives of the objective function are approximated using the adjoint method (Delingette et al., 2012), and various derivative-free optimization methods such as the subplex method (Wong et al., 2015), the Bound Optimization BY Quadratic Approximation (BOBYQA) (Wong et al., 2012), the New Unconstrained Optimization Algorithm (NEWUOA) (Sermesant et al., 2012), and sequential Kalman filtering and its variants (Moireau et al., 2013). More recent works started to explore surrogate-based approaches to replace the simulation model in the optimization. This is done by approximating the optimization objective or the relationship between the parameters and the measurements with a surrogate function, constructed by standard machine learning methods (Zettinig et al., 2013; Giffard-Roisin et al., 2017) or Bayesian optimization method (Dhamala et al., 2017a). In the latter, the surrogate of the optimization objective is learned by actively selecting a small number of sample points towards the optimum in the space of the unknown model parameters.

All of these methods, however, suffer from a high-dimensional (HD) unknown space. To circumvent this challenge, many works assume homogeneous tissue properties that can be represented by a single global model parameter (Giffard-Roisin et al., 2017; Lê et al., 2016). To better preserve local information about the spatially distributed tissue properties, a common approach of dimensionality reduction is to explicitly partition the domain of interest into a small number of segments, each represented by a uniform parameter value: in cardiac models, 3–26 segments are typically used (Wong et al., 2015; Zettinig et al., 2013). Naturally, this a priori low-resolution division of the cardiac mesh has a limited ability to represent a wide range of tissue heterogeneity. In addition, it has been shown that as the number of segments grow the accuracy in the estimated parameters becomes increasingly reliant on a good initialization of parameter values (Wong et al., 2015) which is often not available a priori.

Rather than a fixed low-resolution division, recent approaches also proposed to partition the cardiac mesh through a coarse-to-fine optimization along a pre-defined multi-scale hierarchy of the cardiac mesh. This enables spatiallyadaptive resolution of tissue properties that—depending on the given data— can be higher in certain regions than the others (Chinchapatnam et al., 2009; Dhamala et al., 2016). However, the representation ability of the final partition is still limited by the pre-defined multi-scale hierarchy: homogeneous regions distributed across different scales cannot be grouped into the same partition, while the resolution of heterogeneous regions can be limited by the level of the scale the optimization can reach (Dhamala et al., 2016). Furthermore, because these methods involve a cascade of optimizations along the coarse-to-fine hierarchy of the cardiac mesh, they are computationally expensive. In the context of parameter estimation for models that could require hours or days for a single simulation, these methods could quickly become computationally prohibitive.

1.2. Contributions

We recognize that one challenge of dimensionality reduction for HD tissue property θ is that it is not known a priori, thus we can not directly obtain a low- dimensional (LD) embedding of θ through: z = f(θ). Conversely, we propose that if we obtain a LD-to-HD generative model θ = g(z), we will be able to reformulate the optimization objective $\mathcal{L}(\theta )$ to $\mathcal{L}(g(\mathbf{z}))$ and thereby embed the optimization process from the HD space to the LD space. This is the central idea that unperpins the proposed method

Broadly, previous approaches that explicitly partition the myocardium (Chinchapatnam et al., 2009; Dhamala et al., 2016) can be considered a geometry-based approach to obtain the LD-to-HD relationship, where the LD-to-HD process θ = g(z) is defined by the multi-scale hierarchy of the cardiac mesh. In this setting, the LD representation relies heavily on how the spatial distribution of the HD tissue property aligns with the geometry-based division of the physical space: a small abnormal region may be represented by a small number of dimensions at the depth of the multi-scale hierarchy, while a large abnormal region need to be represented by a large number of dimensions spread across the width of the multi-scale hierarchy. This increase in the number of dimensions 100 in the LD representation will in turn increase the difficulty in optimization.

In this paper, we propose a drastic alternative to use a neural-network based generative model to embed the HD surrogate-based Bayesian optimization into the LD latent space. Note that, fundamentally different from embedding known HD variables, the proposed approach embeds the process of optimizing unknown HD variables. We look for two important traits of the generative model. First, once trained, it should be able to generate high-resolution tissue properties from compact latent codes z. Second, during training, it should accumulate knowledge about the probability distributions of z to later guide the active search in Bayesian optimization. For these reasons, we adopt the variational auto- encoder (VAE) (Kingma and Welling, 2013) as the generative model, trained from a large set of spatially-varying tissue properties reflecting regional tissue abnormality with various locations, sizes, and distributions. Once trained, the VAE is integrated within the Bayesian optimization in two novel ways. First, the VAE decoder (generative model) is incorporated within the objective func tion to obtain $\mathcal{L}(g(\mathbf{z}))$, directly embedding the HD surrogate construction and optimization into a LD manifold. Second, the posterior distribution of the latent code z, learned from the VAE encoder, is used to guide the active search of sample points and enable an efficient exploration of the LD manifold in Bayesian optimization. To our knowledge, this is the first work that realizes HD Bayesian optimization through an integration of a generative model.

While the presented method is generally applicable to HD Bayesian optimization, in this paper it was evaluated on the estimation of local tissue excitability of a cardiac electrophysiological model. Experiments were performed on three different sets of data: simulation data with synthetic setting of abnormal tissues, simulation data generated from an ionic electrophysiological model blinded to the optimization study on ventricles with 3D myocardial infarcts derived from in-vivo magnetic resonance imaging (MRI) data, and real data obtained from patients with infarcts derived from in-vivo voltage mapping data. In all experiments, we demonstrated the ability of the presented method to be applied to patients not used in the training of the generative model, and compared its performance to existing methods based on fixed LD and multi-scale adaptive representation of the parameter space (Wong et al., 2015; Dhamala et al., 2016). Furthermore, we investigated the benefit brought by each of the three key elements of the presented method, including the use of a non-patient-specific VAE model through nonlinear registration in comparison to a patient-specific VAE model, the use of nonlinear VAE generative model in comparison to a linear reconstruction model obtained through principal component analysis (PCA), and the incorporation of VAE-encoded latent distribution in Bayesian optimizaiton.

This study extends our previous work (Dhamala et al., 2018) in the following 140 main aspects:

1. While the VAE generative model was trained and used in a subject-specific manner in Dhamala et al. (2018), here we introduced the component of nonlinear registration to allow the use of non-patient-specific VAE for model personalization on hearts not used in VAE training. We experi mentally verified that this extension did not affect the performance of the presented method in parameter estimation.

2. We compared the VAE with PCA in their role as the generative model in Bayesian optimization, and demonstrated the unique advantage of a nonlinear generative model—owing to its expressiveness—to distill a latent code that is sufficiently small for effective optimization.

3. We added an evaluation of the presented method in estimating highly heterogeneous tissue properties delineated from in-vivo MRI, using measurements generated from a high-fidelity ionic electrophysiology model that was blinded to the optimization method.

4. We evaluated the change of performance of the presented method when decreasing the external measurement data to 12-lead ECG, and demonstrated that the presented method was more robust to the reduction in measurement data compared to the method previously described in Dhamala et al. (2017a).

Our code is publicly available at https://github.com/jwaladhamala/BO-GVAE.

2. Background

2.1. Image-based subject-specific geometrical models

Personalized geometrical models are the first step towards personalized modeling. Substantial progress has been made in this space (spatial resolution ∼ 500μm) (Arevalo et al., 2016; Hu et al., 2013) and it is not the focus of this study. Therefore, we utilize image-derived subject-specific geometrical models of the heart and the thorax without considering the potential uncertainty therein.

In brief, from cardiac tomographic scans (e.g., CT or MRI) of a patient, a 3D bi-ventricular model is built by manual segmentation of the myocardial contour and in-house meshing routine utilizing the iso2mesh package (Fang and Boas, 2009). To allow anisotropic conduction within the myocardium, fiber structure of the ventricular surface is approximated by mapping a mathematical model for ventricular fiber structure established in Nash (1998) to the subject-specific ventricular geometry. Intramural fiber orientation is then interpolated linearly from the pair of orientations on the epicardial and endocardial surface (Nielsen et al., 1991). The thorax model is constructed as a surface mesh consisting of the body surface manually segmented from CT or MRI images. With this model, we assume the thorax to be an isotropic and homogeneous volume conductor.

2.2. Bi-ventricular electrophysiology model

A range of computational models of cardiac electrophysiology with varying levels of biophysical details and computational complexity have been developed (Clayton et al., 2011). Among these, simplified ionic models like the Mitchell Schaeffer model (Mitchell and Schaeffer, 2003) and phenomenological models like the Aliev Panfilov (AP) model (Aliev and Panfilov, 1996) are capa ble of reproducing the key macroscopic process of cardiac excitation with a small number of model parameters and within a reasonable computation time making them preferable for personalized parameter estimation (Relan et al., 2009; Marchesseau et al., 2012; Giffard-Roisin et al., 2017; Dhamala et al., 2016). Therefore, to test the feasibility of the presented method in this study, we utilize the two-variable AP model given below:

$$\begin{gathered} \frac{\partial u}{\partial t}=\nabla (\mathbf{D}\nabla u)-cu(u-\theta )(u-1)-uv, \\ \frac{\partial v}{\partial t}=\epsilon (u,v)(-v-cu(u-\theta -1)). \end{gathered}$$ (1)

Here, u ∈ [0,1] is the transmembrane potential and v is the recovery current. The parameter ε = e₀ + (μ₁υ)/(u + μ₂) controls the coupling between u and v and c controls the repolarization. The diffusion tensor D describes conductivity anisotropy and is determined by the local fiber structure: the ratio of conductiv ities in the longitudinal and transverse fiber directions is set to 4 : 1 according to literature (Tusscher and Panvilov, 2008). The tissue excitability parameter θ controls the temporal dynamics of u and v.

The one-factor-at-a-time sensitivity analysis of the AP model (1) shows that u is most sensitive to parameter θ (Dhamala et al., 2017a). Therefore, in this study, we test the ability of the presented parameter estimation method in estimating parameter θ of the AP model (1) by fixing the values for the rest of the model parameters to standard values as documented in the literature (Aliev and Panfilov, 1996): c = 8, e₀ = 0.002, μ₁ = 0.2, and μ₂ = 0.3. We consider a physiologically-meaningful range for the value of θ as [0,0.5] because, as de205 scribed in Rogers and McCulloch (1994), tissue with a value of θ around 0.15 will excite normally while an increasing value of θ will reduce the ability of the tissue to excite until no excitation can be elicited at the value of 0.5.

Solving the AP model (1) on the discrete 3D myocardium using the meshfree method as described in Wang et al. (2010), we obtain a 3D electrophysiolog ical model of the heart that describes the spatiotemporal propagation of 3D transmembrane potential u(t,θ) with a high-dimensional parameter θ at the resolution of the cardiac mesh.

2.3. Measurement model

The transmembrane potential u(t,θ) can be, in general, observed by two means. First, it generates extracellular potential y_b(t) in the thorax following the quasi-static approximation of the electromagnetic theory (Plonsey, 1969). This relationship can be modeled by a Poisson’s equation within the heart and a set of Laplace’s equations, one for each organ, external to the heart and within the body torso. Given a discrete subject-specific mesh of the thorax, these equations are solved as described in Wang et al. (2010) to obtain a linear relationship between extracellular potential y_b(t) and transmembrane potential u(t,θ) through a subject-specific transfer matrix H_b:

$${\mathbf{y}}_b(t)={\mathbf{H}}_b\mathbf{u}(t,\mathit{\theta }).$$ (2)

When measured on the heart surface, y_b(t) is known as electrograms; when measured at the body surface, y_b(t) is known as ECG—the latter is non- invasively available in practice but more challenging for parameter estimation, because it represents a more remote and sparse observation of u(t,θ). This is the first scenario we will use to demonstrate the presented method in parameter estimation (Section 4.2 and 4.4).

Alternatively, transmembrane potential u(t,θ) may be locally recorded on the epicardium through optical mapping (Relan et al., 2011):

$${\mathbf{y}}_e(t)={\mathbf{H}}_e\mathbf{u}(t,\mathit{\theta }),$$ (3)

where y_e(t) represents coarsely distributed subset of transmembrane potential u(t,θ) measured at local regions of the epicardium, indexed by a sparse binary matrix H_e. This is the second scenario we use to demonstrate the presented method in parameter estimation (Section 4.3). For clarity, throughout the remainder of the paper, we use y(t) to denote either y_e(t) or y_b(t), and H to denote either H_e or H_b.

3. Methodology

3.1. Overview

The HD parameter θ in the electrophysiological model (1) can be estimated by minimizing the sum of the squared errors between the measured physiological signals y(t) and signals simulated by the composite of the electrophysiological model and the measurement model: M(t,θ) = Hu(t,θ). This can be achieved by solving the following maximization objective:

$$\widehat{\mathit{\theta }}=\underset{\mathit{\theta }}{\arg \max }\mathcal{L}(\mathit{\theta })=\underset{\mathit{\theta }}{\arg \max }\left\{\sum _t-\Vert \mathbf{y}(t)-M(t,\mathit{\theta }){\Vert }^2\right\}.$$ (4)

Because this objective function is expensive to evaluate and its derivatives are difficult to approximate, we solve it in the general setting of Bayesian optimization. Bayesian optimization starts with a prior distribution over the objective function (4) as a Gaussian process (GP) surrogate and then proceeds with two iterative steps: 1) active selection of a sample point θ⁽ⁱ⁾ using a GP-based acquisition function; and 2) a Bayesian update of the GP prior with all pairs of $\left\{{\mathit{\theta }}^{(i)},\mathcal{L}\left({\mathit{\theta }}^{(i)}\right)\right\}$ selected so-far. More precisely, the acquisition function for sample selection trades off between a large GP posterior mean given the current GP belief of the objective function (4) (i.e., exploitation) and a large GP posterior variance to reduce the uncertainty of the GP belief of the objective function (4) (i.e., exploration). The Bayesian update of the GP computes the predictive posterior distribution of the GP given the training data including the newly selected pair of $\left\{{\mathit{\theta }}^{(i)},\mathcal{L}\left({\mathit{\theta }}^{(i)}\right)\right\}$.

While Bayesian optimization is widely used for optimizing an expensive objective function, it does not work well with HD (dimension > 15) unknowns (Shahriari et al., 2016; Kandasamy et al., 2015). This is because the number of training data required for nonparametric regression with GP grows exponentially with the dimension of sample points. In addition, the active point selection involves global optimization of a HD acquisition function which is an inherently difficult (Shahriari et al., 2016; Kandasamy et al., 2015; Li et al., 2018).

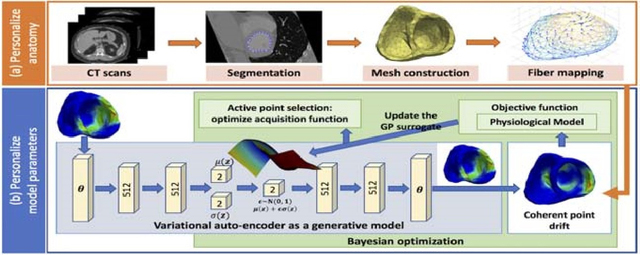
Here, we present a novel HD Bayesian optimization method achieved by embedding the HD active search and Bayesian GP surrogate learning to a LD manifold through a LD-to-HD generative model. As outlined in Fig. 1(b), this method consists of two primary components: 1) generative modeling of the spatially-varying tissue property θ that is at the resolution of the cardiac mesh, and 2) integrating the generative model and the nonlinear cardiac registration into Bayesian optimization of (4) to respectively enable a HD Bayesian optimization and a shared VAE for parameter estimation in various cardiac meshes.

Figure 1:

The workflow diagram of the presented parameter personalization framework which consists of following major components: 1) training of a generative model (blue rectangle), and 2) HD Bayesian optimization via a trained generative model (green rectangle).

3.2. Generative modeling of spatially varying tissue property

Generative models have gained increasing traction in unsupervised learning of abstract LD representations from which complex images can be generated (Kingma and Welling, 2013; Goodfellow et al., 2014). Here, we assume that the spatially varying tissue property θ at the resolution of a cardiac mesh is generated by a small number of unobserved continuous random variables z in a LD manifold. As mentioned earlier, we would like to learn both this generative process and the probability distribution of z. To do so, VAE is a natural model of choice as–via an encoder-decoder structure to generative modeling–the trained VAE will provide the generative process in its decoder while encoding the probability distributions of the latent code z.

3.2.1. LD-to-HD generative process of tissue property via a VAE

For stochastic generative modeling of the spatially-varying tissue property θ, the VAE consists of two modules: a probabilistic deep encoder network with network parameters α that approximates the intractable true posterior density p_α∗(z|θ) as q_α(z|θ); and a probabilistic deep decoder network with network parameters β that can probabilistically reconstruct θ given z as the likelihood p_β(θ|z). Given a training data set $\mathrm{\Theta }={\left\{{\mathit{\theta }}^{(i)}\right\}}_{i=1}^N$ that consists of N different spatial distributions of the tissue property θ, VAE training involves optimizing the variational lower bound on the marginal likelihood of each training data θ⁽ⁱ⁾ with respect to network parameters α and β:

$$\mathcal{L}\left(\mathit{\alpha };\mathit{\beta };{\mathit{\theta }}^{(i)}\right)=-D_{\text{KL}}\left(q_{\mathit{\alpha }}\left(\mathbf{z}|{\mathit{\theta }}^{(i)}\right)\Vert p_{\mathit{\beta }}(\mathbf{z})\right)+E_{q_{\alpha }\left(\mathbf{z}|{\mathit{\theta }}^{(i)}\right)}\left[\log p_{\mathit{\beta }}\left({\mathit{\theta }}^{(i)}|\mathbf{z}\right)\right].$$ (5)

We assume the approximate posterior q_α(z|θ) in (5) to be a Gaussian density and the prior $p_{\mathit{\beta }}(\mathbf{z})\sim \mathcal{N}(0,1)$) to be a standard Gaussian density. This gives an analytical form of the KL divergence in (5):

$$D_{\text{KL}}\left(q_{\alpha }\left(\text{z}|{\mathit{\theta }}^{(i)}\right)\Vert p_{\beta }(\text{z})\right)=-\frac{1}{2}\sum _{j=1}^{N_z}\left(1+\log {\left({\sigma }_j^{(i)}\right)}^2-{\left({\mu }_j^{(i)}\right)}^2-{\left({\sigma }_j^{(i)}\right)}^2\right),$$ (6)

where N_z is the dimension of z, μ⁽ⁱ⁾ and σ⁽ⁱ⁾I are respectively the mean and standard deviation of q_α(z|θ⁽ⁱ⁾). We model p_β(θ|z) in (5) as a Gaussian distribution.

Because stochastic latent variables are utilized, the gradient of the expected negative reconstruction term during backpropagation cannot be directly obtained. The popular re-parameterization trick is utilized to express z as a deterministic variable as: ${\mathbf{z}}^{(i)}={\mathit{\mu }}^{(i)}+{\mathbf{\sigma }}^{(i)}ϵ$, where $ϵ\sim \mathcal{N}(0,\mathbf{I})$ is a standard Gaussian density (Rezende et al., 2014; Kingma and Welling, 2013). In this way, the optimization of the above loss function (5) is achieved by stochastic gradient descent with standard backpropagation.

3.2.2. Probabilistic modeling of the latent code

Once trained, we obtain two important elements from VAE to be incorporated in the Bayesian optimization. One is the decoder as a generative model. The other is the approximated posterior density q_α(z|θ) for all the training data $\mathrm{\Theta }={\left\{{\mathit{\theta }}^{(i)}\right\}}_{i=1}^N$ that represents valuable knowledge about the probability distribution of z given the training data θ. To utilize this knowledge in subsequent Bayesian optimization, we approximate the marginal density q_α(z) as a mixture of Gaussians by numerical integration of q_α(z|θ) across all the training data Θ as follows:

$$q_{\mathit{\alpha }}(\mathbf{z})\approx \sum _{i=1}^N{q}_{\mathit{\alpha }}\left(\mathbf{z}|{\mathit{\theta }}^{(i)}\right)=\frac{1}{N}\sum _{i=1}^N\mathcal{N}\left({\mathit{\mu }}^{(i)},{\mathbf{\Sigma }}^{(i)}\right).$$ (7)

However, the number of mixture components in (7) scales linearly with the 305 number of training data. If it is directly incorporated into the acquisition function which will be evaluated multiple times within each iteration of the Bayesian optimization, the overall computational cost of the latter will increase. Therefore, we approximate q_α(z) in (7) as a single Gaussian density $\mathcal{N}\left({\mathit{\mu }}_z,{\mathbf{\Sigma }}_z\right)$:

$${\mathit{\mu }}_z=\frac{1}{N}\sum _i^N{\mathit{\mu }}^{(i)},{\mathbf{\Sigma }}_z=\frac{1}{N}\sum _i^N\left({\mathbf{\Sigma }}^{(i)}+{\mathit{\mu }}^{(i)}{\mathit{\mu }}^{(i)T}\right)-{\mathit{\mu }}_z{\mu }_z^T.$$ (8)

In this way, we obtain a generative model p_β(θ|z) of the HD tissue property θ from the VAE decoder, and prior knowledge of the LD manifold q_α(z) from the VAE encoder. In the next Section, we describe the methodology to integrate both into Bayesian optimization to enable efficient and accurate HD parameter estimation.

3.3. LD embedding of HD Bayesian optimization

3.3.1. HD Bayesian optimization via a generic generative model

Our first goal is to embed the process of active sample point selection and Bayesian GP surrogate learning into the LD manifold obtained with a LD-toHD generative process. This can be achieved by reformulating the optimization objective $\mathcal{L}(\mathit{\theta })$ as described in Eq. 4 as shown below:

$$\widehat{\mathbf{z}}=\underset{\mathbf{z}}{\arg \max }\mathcal{L}(\mathbf{z})=\underset{\mathbf{z}}{\arg \max }-{\Vert \mathbf{Y}-M\left(\text{E}\left[p_{\mathit{\beta }}(\mathit{\theta }|\mathbf{z})\right]\right)\Vert }^2,$$ (9)

where E[p_β(θ|z)] represents the expectation of the trained probablistic decoder.

However, E[p_β(θ|z)] in (9) is tied to the the cardiac mesh on which the VAE was trained, and does not directly apply to a different cardiac mesh. In Dhamala et al. (2018), this issue is bypassed by training a subject-specific VAE for each cardiac mesh. Here, we extend beyond subject-specific VAE training via a registration based strategy. Specifically, consider a cardiac mesh that is associated with the parameter space θ_VAE modeled by the VAE: this can be one specific cardiac mesh, or multiple cardiac meshes registered to a common one, which we term as the generic cardiac mesh used in VAE training. Given another cardiac mesh on which tissue properties θ is to be personalized, we adopt the nonlinear pointcloud registration method known as coherent point drifting (CPD) to register it to the generic cardiac mesh (Myronenko and Song, 2010). This registration method provides a sparse correspondence matrix $\mathcal{T}$ that relates each node in the new cardiac mesh to be personalized to a node in the generic cardiac mesh. Using the correspondence matrix $\mathcal{T}$ between the nodes from the two meshes, we establish the following:

$$\mathit{\theta }=\mathcal{T}\left({\mathit{\theta }}_{VAE}\right).$$ (10)

Adding the CPD registration (10), on any given cardiac mesh of interest, we can revise the optimization objective in (9) into:

$$\widehat{\mathbf{z}}=\underset{\mathbf{z}}{\arg \max }\mathcal{L}(\mathbf{z})=\underset{\mathbf{z}}{\arg \max }-{\Vert \mathbf{Y}-M\left(\mathcal{T}\left(\mathbf{E}\left[p_{\mathit{\beta }}(\mathit{\theta }|\mathbf{z})\right]\right)\right)\Vert }^2.$$ (11)

Given the reformulated optimization objective (11), Bayesian optimization can now be used to optimize the HD parameter θ on any cardiac mesh implicitly through the LD manifold of z. To do so, we define a GP prior over the reformulated optimization objective (11). For the GP mean function, we adopt the commonly used zero-mean function because no other prior knowledge is available about this objective (Rasmussen and Williams, 2006). For the covariance function of the GP, we adopt the anisotropic “Matèrn 5/2” covariance function that enables the approximation of less smooth twice differentiable functions (Rasmussen and Williams, 2006):

$$\kappa \left(z_i,z_j\right)={\alpha }^2\exp \left(-\sqrt{5}d\left(z_i,z_j\right)\right)\left(1+\sqrt{5}d\left(z_i,z_j\right)+5/3d^2\left(z_i,z_j\right)\right),$$ (12)

where $d^2\left(z_i,z_j\right)={\left(z_i-z_j\right)}^{\top }\mathrm{\Lambda }\left(z_i-z_j\right)$, Λ is a diagonal matrix in which each diagonal element represents the inverse of the squared characteristics length scale along each dimensions of z, and α² is the function amplitude.

Then, each iteration of the Bayesian optimization consists of two major steps. First, a sample point z⁽ⁱ⁾ in the space of z is selected by maximizing an acquisition function. Second, on the selected sample point, the value of the optimization objective ${\mathcal{L}}^{(i)}$ in (11) is queried and the input-output pair of $\left({\mathbf{z}}^{(i)},{\mathcal{L}}^{(i)}\right)$ is used to update the GP. Both will be detailed below.

3.3.2. VAE-informed acquisition function

Our second goal is to utilize the knowledge about the latent code z, specifically in the form of the VAE-encoded marginal distribution of q_α(z), to guide the selection of training point in Bayesian optimization. We have two specific objectives. First, we aim to use the probability density of z to modulate the extent of exploitation and exploration over the space of z. Second, we aim to constrain the search within the support of q_α(z), outside which the generative model may not be meaningful and the generated tissue properties may not be valid.

To do so, we build on the expected improvement (EI) acquisition function that is designed to select points with the highest expectation of improvement over the current optimum (Brochu et al., 2010):

$$\mathrm{EI}(\mathbf{z})=\left(\mu (\mathbf{z})-f^{+}\right)\mathrm{\Phi }\left(\frac{\mu (\mathbf{z})-f^{+}}{\sigma (\mathbf{z})}\right)+\sigma (\mathbf{z})\varphi \left(\frac{\mu (\mathbf{z})-f^{+}}{\sigma (\mathbf{z})}\right),$$ (13)

where μ(z) and σ(z) are the predictive mean and predictive standard deviation of the GP based on the current set of training data, Φ is the standard normal cumulative distribution function, φ is the standard normal density function, and f⁺ is the maximum of the objective function obtained so far. Broadly, the maximization of the first term in (13) favors z that generates a high μ(z), promoting the exploitation of regions with high predictive GP mean. The maximization of the second term favors z that generates a high σ(z), promoting exploration of uncertain regions in the LD latent z space. In practice, it was observed that using only f⁺ in (13) could lead to excessive exploitation in space that offer marginal improvement over f⁺ and augmenting f⁺ with a constant trade-off parameter ε as: f⁺ + ε (Brochu et al., 2010) could mitigate this issue. With a constant value of ε, it means that this trade-off is enforced equally over the entire search space z.

Here, we propose that this trade-off term ε—rather than being constant— should vary with the probability density of z if such knowledge is available. On one hand, there should be less need to control exploitation in the region where the probability density of z is higher. On the other hand, the search should be discouraged from venturing into regions with very low probability density of z. This can be achieved with a smaller value of ε in the space of higher probability density of z, and a larger value of ε in the space of lower probability density of z. Therefore, based on the approximation of q_α(z) as defined in Section 3.2.2, we define the spatially-varying trade-off parameter ε(z) as:

$$\epsilon (\mathbf{z})=-f^{+}\left(\mathbf{z}-{\mathit{\mu }}_{\mathbf{z}}\right){\mathbf{\Sigma }}_{\mathbf{z}}^{-1}\left(\mathbf{z}-{\mathit{\mu }}_{\mathbf{z}}\right),$$ (14)

where μ_z and Σ_z are as defined in (8). Its effect on Bayesian optimization will be evaluated in section 4.2.

3.3.3. Bayesian update of the GP surrogate

Once a new point z⁽ⁱ⁾ is selected by maximizing the modified EI, the value of the optimization objective (11) is evaluated at z⁽ⁱ⁾ as ${\mathcal{L}}^{(i)}$ by the execution of the composite of the trained VAE decoder, the bi-ventricular electrophysiological model, and the measurement model. The new input-output pair of $\left({\mathbf{z}}^{(i)},{\mathcal{L}}^{(i)}\right)$ is added to the set of previously collected GP training data $\left\{z^{(1:i-1)},{\mathcal{L}}^{(1:i-1)}\right\}$. Then, the GP hyperparameters (inverse characteristics length scales Λ and covariance function amplitude α²) in (12) are estimated by maximizing the log of the marginal likelihood $p\left({\mathcal{L}}^{(1:i)}|z^{(1:i)},\alpha ,\mathrm{\Lambda }\right)$. After this update, the predictive posterior distribution of GP can be obtained as:

$$\begin{gathered} \mu \left({\mathbf{z}}^{*}\right)={\mathbf{k}}^T{\mathbf{K}}^{-1}{\mathcal{L}}^{(1:i)}, \\ {\sigma }^2\left({\mathbf{z}}^{*}\right)=\kappa \left({\mathbf{z}}^{*},{\mathbf{z}}^{*}\right)-{\mathbf{k}}^T{\mathbf{K}}^{-1}\mathbf{k}, \end{gathered}$$ (15)

where κ(·,·) is the “Matèrn 5/2” kernel defined in (12), $\mathbf{k}=[\kappa \left(z^{*},z^{(1)}\right),\kappa \left(z^{*},z^{(2)}\right){\cdots \kappa \left(z^{*},z^{(i)}\right)]}^{\text{T}}$, and K is the covariance matrix.

4. Experiments and results

4.1. VAE network architecture & training data generation

The VAE architecture used in the following experiments is shown in Fig. 1(b). Each of the encoder and decoder network consisted of three fully connected layers with softplus activation, two layers of 512 hidden units, and a pair of two-dimensional units for the mean and log-variance of the latent code z.

Real data of whole-heart tissue properties are not readily available. Cardiac images such as contrast-enhanced MRI may provide a surrogate for delineating different levels of myocardial injury, yet they are expensive to obtain at a large quantity. In this paper, we utilized synthetic data sets $\mathit{\theta }={\left\{{\mathit{\theta }}^{(i)}\right\}}_{i=1}^N$ to train the VAE. Specifically, on the cardiac mesh for training VAE, we generated a large data set of heterogeneous myocardial injury by random region growing: starting with one injured node, one out of the five nearest neighbors of the present set of injured nodes was randomly added as an injured node. This was repeated until an injury of desired size was attained. Because injury generated in this fashion tended to be irregular in shape, we also added to the training data those generated by growing the mass of the injury by adding the closest neighbor to the center of the mass. As a feasibility study, we considered only binary tissue types in the training data, in which the value of tissue excitability θ was set to be 0.5 or 0.15 for injured or healthy nodes, respectively and a random noise drawn from a uniform distribution [0,0.001] was added. We trained the VAE with the Adam optimizer on a Titan X Maxwell GPU with an initial learning rate of 0.001 (Kingma and Ba, 2014).

4.2. Synthetic experiments

Synthetic experiments were carried out on three CT-derived human hearttorso models, including in-total 43 synthetic cases of infarcted tissue sized 2%− 40% of the total ventricular myocardium at differing locations. Specifically, we divided the left ventricle into 17 segments based on the standard recommended by the American Heart Association (AHA) (Cerqueira et al., 2002) and the right ventricle into nine segments based on the standard shown in (Dhamala et al., 2017a; Relan et al., 2011). Then, the infarct was set as various combinations of these 26 segments. The value of θ in the infarct region was set to 0.4, 0.45, or 0.5 and its value in the healthy region was set to 0.15. This means that this test set for parameter estimation was different from the training data for VAE. 120-lead ECG corresponding to each tissue property setting was simulated and corrupted with 20dB Gaussian noise as measurement data. For experiments on heart ♯1 and ♯2, the VAE was trained on heart ♯3; for experiments on heart ♯3, the VAE was trained on heart ♯1. The training time for heart ♯1 with a data set of size 137,663 and heart ♯3 with a data set of size 129,399 was 8.21 minutes 425 and 7.14 minutes, respectively.

The accuracy of estimated parameters was evaluated with two metrics at the resolution of the meshfree nodes: 1) root mean square error (RMSE) between the true and estimated parameters; and 2) dice coefficient $(\text{DC})=\frac{2\left(\left|S_1\cap S_2\right|\right)}{\left|S_1\right|+\left|S_2\right|}$, where S₁ and S₂ are the sets of nodes in the true and estimated regions of 430 infarct, the latter determined by a threshold that minimizes the intra-region variance on the estimated parameter values (Otsu, 1975).

In the following, we first compared the presented method with two previous approaches to parameter estimation in which the LD representation of the parameter space was obtained based on the geometry of the cardiac mesh. In the next three sets of synthetic experiments, we evaluated in detail the effect of the three key components of the presented method: CPD-based nonlinear registration to bypass the need of patient-specific VAE training, nonlinear VAE generative model, and VAE-informed acquisition functions. In the final sets of synthetic experiments, we investigated two major properties of the presented method: 1) the semantic meaning of the latent codes learned by the generative model, and 2) the capacity of the presented method to estimate parameters that differ significantly from the synthetic binary VAE training data.

4.2.1. Comparison with existing methods

The presented method (termed as BO-VAE) was compared against optimization utilizing two geometry-based reductions of the cardiac mesh: 1) BOBYQA using the predefined 26 segments (17 left ventricular segment + nine right ventricular segment), termed as the fixed-segment (FS) method (Wong et al., 2015; Sermesant et al., 2012); and 2) Bayesian optimization on coarse-to-fine partitions along a predefined multi-scale representation of the cardiac mesh, termed as the fixed-hierarchy (FH) method (Dhamala et al., 2017a, 2016). We did not use Bayesian optimization in the FS method with predefined 26 segments, because it showed limited performance in our experiments: this is consistent to the widely reported limitation of Bayesian optimization in handling an unknown dimension higher than 15 (Shahriari et al., 2016; Kandasamy et al., 2015).

Fig. 2 summarizes the accuracy and computational cost of the three methods obtained across 43 experiments. Overall, in terms of the DC, the BO-VAE (green bar) was significantly more accurate than both the FH and the FS methods (paired t-tests, p< 0.001). This suggests that the VAE may be more flexible and accurate in generating infarcts of varying sizes and at various locations, compared to the FH and the FS methods in which the shape and location of the infarct were constrained by predefined mesh divisions. In terms of the RMSE, the BO-VAE (green bar) was significantly more accurate than only the FS (paired t-test with FS, p< 0.02; paired t-test with FH, p< 0.27). This accuracy was obtained at a substantial reduction of computational cost by ∼ 86.37% compared to the FS and ∼ 96.86% compared to the FH method.

Figure 2:

Comparison of DC (a), RMSE (b), and the number of model evaluations (c) between BO-VAE EI Post-1 (green bar) and three other groups of methods: FH and FS (yellow bars); BO-VAE using standard EI, EI isotropic, and EI Post-1 (red bars); and BO-PCA (purple bar).

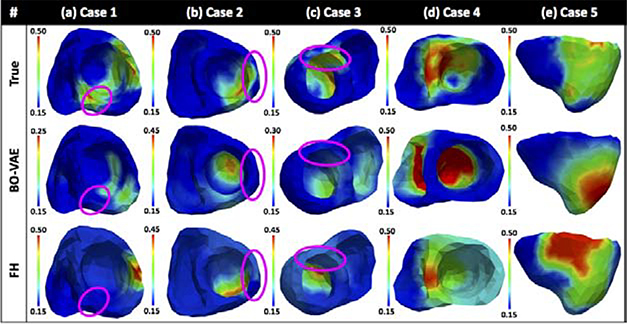
Fig. 3 provides several examples of the estimated parameters obtained by the three methods in comparison to the ground truth. As shown, the FS method tended to either completely miss the region of abnormal tissues, or generate a large region of false positives. This could partly be because it was difficult to optimize a 26-dimensional unknown given indirect measurements without a good initialization, while many of these dimensions were wasted at representing regions of homogeneous tissues. The FH method was able to overcome this issue to some extent, although it suffered from limited accuracy in many cases. For a closer inspection, Figs. 3(a) and (b) provide two examples showing the progression of the FH method on the multi-scale hierarchy. In Fig. 3(a), many segments in the earlier scales (from d2 to d6) contained homogeneous regions (green nodes) which did not need to be refined further. Therefore, the FH was able to focus refinement along a narrow heterogeneous region, ultimately reaching deeper into the multi-scale hierarchy and producing an accurate solution (Fig. 3(c)). Conversely, in Fig. 3(b), several segments in the earlier scales (from d1 to d4) contained heterogeneous regions that required further refinement. Refining each of these heterogeneous regions would again lead to HD optimization, and the FH method only managed to refine a limited few resulting in a less accurate solution (Fig. 3(d)). Overall, the performance of the FH method relies heavily on how the spatial distribution of the tissue properties can be represented on the multi-scale hierarchy, whereas the VAE generative model in the VAE-BO can better describe tissue properties with varying sizes and locations using the same latent dimensions.

Figure 3:

Examples of estimated tissue excitability with the BO-VAE, BO-PCA, FH, and FS methods. Progression of the FH optimization on the multi-scale hierarchy in (a) shows that only one node in level d3 consists of heterogeneous tissues (green nodes: homogeneous tissues; red nodes: heterogeneous tissues) which was refined along the multi-scale hierarchy to obtain an accurate solution as shown in example (c). By contrast the progression of the FH optimization in (b) shows that most of the nodes in level d2 consist of heterogeneous tissues. Since all of them could not be refined there is limited accuracy as reflected in example (c).

4.2.2. Comparison with patient-specific VAE training

In this section, we investigated the effect of using nonlinear registration (CPD) in the presented method, which allows a VAE that is trained on a generic heart to be used in the parameter estimation of a different heart. On a random subset of 27 out of the 43 synthetic experiments, we repeated the same experiments with the presented BO-VAE but with the VAE trained on the specificheart on which parameter estimation was carried out. Result as presented in Fig. 4 shows that the accuracy in parameter estimation in terms of both DC and RMSE were very similar between using patient-specific versus non-patientspecific training data for VAE. On the right panel of Fig. 4, we show three representative examples. Fig. 4(a) includes an example where the estimated parameters with either training data had a similar accuracy. Fig. 4(b) includes an example where the estimated parameters that utilized the non-patient-specific VAE had a higher accuracy. Finally, Fig. 4(c) includes an example where the patient-specific VAE resulted in a higher accuracy in parameter estimation. This suggests that patient-specific VAE training has limited benefits for parameter estimation.

Figure 4:

Comparison of parameter estimation results by using a VAE trained on patient-specific vs. non-patient-specific training data. Left: accuracy in terms of DC and RMSE. Right: examples of estimated tissue excitability.

4.2.3. Comparison with PCA-based linear reconstruction model

The basic intuition of embedding a HD optimization through a LD-to-HD generative model, as formulated in (11), can be generalized to the use of various generative or reconstruction models. One such example is a linear reconstruction model that can be obtained by PCA. Given the same training data $\mathit{\theta }={\left\{{\mathit{\theta }}^{(i)}\right\}}_{i=1}^N$ instead of training a VAE, PCA can be utilized to identify the l number of leading principle components P = [p₁ p₂ ··· p_l] that can reduce the dimension of θ in the form of: z = P^Tθ. Conversely, we obtain a linear reconstruction model θ = Pz, which we can use as the generative model to replace the expectation of the VAE decoder in the optimization objective (11) as:

$$\widehat{\mathbf{z}}=\underset{z}{\arg \max }\mathcal{L}(\mathbf{z})=\underset{z}{\arg \max }-{\Vert \mathbf{Y}-M\left(\mathcal{T}\left({\mathbf{P}}_{\mathbf{z}}\right)\right)\Vert }^2$$ (16)

This new objective can be solved with Bayesian optimization using different number of principle components, which we term as BO-PCA. On 27 synthetic experiments utilizing the same training data as used in Section 4.2.1, we applied BO-PCA using two principle components (for a fair comparison with the BO-VAE using two-dimensional latent code). As summarized in the green and purple bars in Fig. 2, when using a two-dimensional latent variable, the accuracy with BO-VAE (green bar) was higher than the accuracy with BO-PCA (purple bar) in terms of both DC (paired t-test, p < 0.001) and RMSE (paired t- test, p < 0.04). This shows that, to represent heterogeneous spatially-varying tissue properties used in this study, the non-linear generative model was more expressive than a linear reconstruction model.

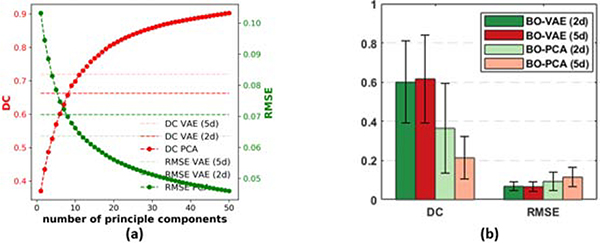
We then conducted additional experiments to study how an increasing number of latent dimensions affect both the accuracy of the reconstruction / generative model and the accuracy of the Baysian optimization. First, we examined how many principal components from PCA were necessary to achieve an accuracy similar to the VAE in reconstructing high-dimensional tissue properties on the test data set (i.e., data unseen during the training process). Fig. 5(a) summarizes the accuracy of the PCA-reconstructed tissue properties, measured in terms of both DC and RMSE, as the number of principle components increases. Note that the horizontal dashed and dotted lines mark the reconstruction accuracy given by the VAE using two- and five-dimensional latent codes, respectively. As expected, the average DC (dark red) and RMSE (green curve) for PCA-reconstructed tissue properties improved with the increasing number of principle components used. To match the reconstruction accuracy given by the VAE with a two-dimensional latent code, eight principle components were necessary. To match the reconstruction accuracy given by the VAE with a five-dimensional latent code, 11 principle components were needed. This further demonstrates that the nonlinear VAE generative model was more expressive than the linear PCA reconstruction model, allowing the same reconstruction ability with a smaller number of latent dimensions.

Figure 5:

(a) Average PCA reconstruction errors in terms of DC and RMSE on test data with increasing numbers of principle components, in comparison to those given by the VAE with two-dimensional and five-dimensional latent codes. (b). Comparison of the accuracy of BO-VAE and BO-PCA with different numbers of latent dimensions / principal components.

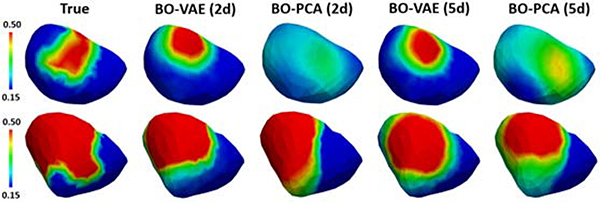
We then examined how the increase in the number of latent dimensions or principle components may improve the accuracy of parameter estimation. Specifically, we utilized BO-VAE with five dimensional generative codes (termed as BO-VAE (5d)) and BO-PCA with five principle components (termed as BO-PCA (5d)) on 20 synthetic experiments. As shown in the quantitative results in Fig. 5(b) and examples in Fig. 6, for BO-VAE, the performance of BO-VAE (5d) was only marginally better than the performance of BO-VAE (2d). For BO-PCA, the accuracy with BO-PCA (5d) was worse than that of BO-VAE (2d). These two sets of experiments showed that, while the accuracy of the reconstruction / generative model improved with a higher number of latent dimensions / principle components, the optimization task also became more difficult. It is thus important to balance between these two challenges in order to obtain an accurate solution.

Figure 6:

Examples of estimated tissue excitability with BO-VAE and BO-PCA with two and five dimensional representations of the parameter space.

4.2.4. The effect of VAE-informed acquisition functions

In this section, we studied the effect of incorporating the probability density of z in the EI acquisition function. First, we compared the use of the standard EI with EI augmented with two types of distributions of z:

1. An isotropic Gaussian prior $p_{\mathit{\beta }}(\mathbf{z})\sim \mathcal{N}(0,\mathbf{I})$ used in (5), termed as EI isotropic.

2. A single Gaussian density approximated from the mixture of N Gaussians, as formulated in (8) and termed as EI Post-1.

The red and green bars in Fig. 2 summarizes the accuracy of the presented method utilizing the three different types of EI acquisition functions. Overall, the use of the modified EI, with any of the two density functions listed above, generated a higher estimation accuracy compared to the use of the standard EI. The estimation accuracy with EI Post-1 and EI isotropic were comparable, with the accuracy using EI Post-1 being slightly higher. This is because q_α(z) that was used to augment EI in EI Post-1, as a natural outcome of the VAE training 565 objective (5), was close to $p(\mathbf{z})\sim \mathcal{N}(0,1)$ used to augment EI in EI isotropic.

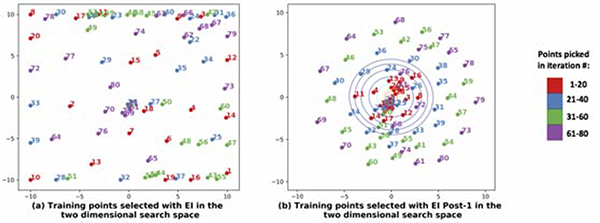
Fig. 7 illustrates how the knowledge from q_α(z) affected the selection of the sample points during the construction of the GP surrogate in the Bayesian optimization. As shown, when q_α(z) is utilized, the exploration gradually proceeded from the region of high probability density to the region of low probability density (Fig. 7(b)). In comparison, in the standard EI without the knowledge of q_α(z), a large number of sample points were initially placed along the borders and then followed by placement of sample points throughout the search space (Fig. 7(a)). This issue of boundary over-exploration with Bayesian optimization has been studied in the literature (Siivola et al., 2018). While it is not a problem if the solution lies in the boundary, in this case where most of reconstructions were potentially around the center of the search space as indicated by q_α(z), this was not an optimal strategy. As shown in the examples in Fig. 8, the use of EI post-1 was able to lead to the optimal solution while the use of EI resulted in incorrect or sub-optimal solutions.

Figure 7:

Comparison of point selection during Bayesian optimization using the standard EI and the EI post-1 as acquisition functions. With EI post-1, the regions of higher q_α(z) was explored before the regions of lower q_α(z).

Figure 8:

Examples of tissue excitability estimated using BO-VAE with the standard EI and the EI Post-1. The former resulted in less optimal or incorrect solutions.

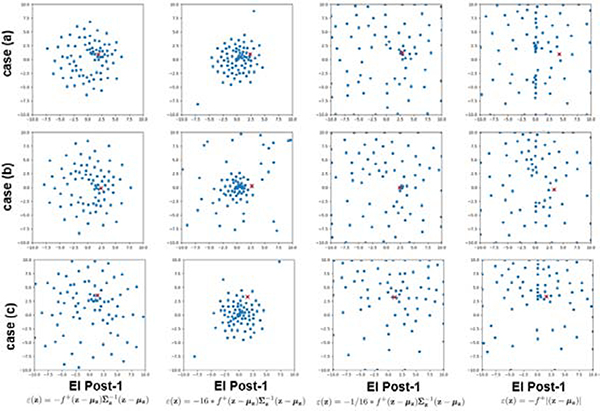
To closely examine the behaviour of EI Post-1, we conducted a set of experiments to study the differences in the way points were selected by the Bayesian optimization when ε(z) in (14) (used with EI Post-1) was modified as follows: 1) ε(z) = 16∗ε(z), 2) ε(z) = 1/16∗ε(z), and 3) ε(z) = −f⁺|z−μ_z|. Fig. 9 shows the points collected by the Bayesian optimization in the 2d latent space with the four different forms of ε(z) on three different examples cases. As shown, the selected points changed from a wider to narrower distribution in the following order: 16 ∗ ε(z), ε(z), and 1/16 ∗ ε(z). ε(z) = −f⁺|z − μ_z| resulted in a spread of points similar to that with 1/16 ∗ ε(z). In all cases, the density of points were higher near the optimum (indicated by a red cross), showing that the region around the optimum was explored more than the other regions. In summary, the higher the magnitude of ε(z) was, the more gradually the search could proceed away from the mode of q(z), i.e., a harder constrain on exploring away from the high probability region of q(z). Depending on the amount of exploration needed in the search space and the optimization budget, different constraint can be chosen for different applications – in the problem of parameter estimation demonstrated in this paper, EI Post-1 with ε(z) as described in (14) had the highest accuracy.

Figure 9:

Examples of the sample points selected during Bayesian optimization when various forms of ε(z) are used in augmenting the standard EI. Red cross represents the location of the optimum.

4.2.5. Semantic interpretation of the generative codes

In this section, we investigated the semantic meaning of the generative codes learned by the VAE. Fig. 10(a)–(b) shows the scattered plots of the two-dimensional latent codes z encoded by the VAE on the training data, color-coded by the size and location of the abnormal tissue. Interestingly, it appears that the latent code accounted for the size of the abnormal tissue along the radial direction (a), while clustering by the location of the abnormal tissue as well (b). Fig. 10(c) and (d) show the scattered plots of the five-dimensional latent codes of the VAE after the application of the t-Distributed Stochastic Neighbor Embedding (t-SNE) (Maaten and Hinton, 2008), again color-coded by the size and location of the abnormal tissues. The information about the size seemed to still be visible from the t-SNE visualization (c), although no longer clearly encoded along the radial direction as in the case of two-dimensional latent code. The location of the abnormal tissue was still a main factor for clustering the latent codes. In summary, while these generative codes were not designed with specific semantic meanings such as the anatomical segments in the FH or FS method, the data-driven learning process has managed to associate them with seman615 tically meaningful generative factors of the high-dimensional tissue properties.

Figure 10:

(a)-(b): Scatter plots of two-dimensional latent codes colored by (a) infarct size and (b) infarct location. (c)-(d): t-SNE visualization of five-dimensional latent codes colored by (c) infarct size and (d) infarct location.

4.2.6. Generalization beyond VAE training data

In the experiments considered so far, tissue properties considered in the optimization and VAE training differ by the value of the infarct region and the way we set the location and shape of the abnormal region: the former is defined by combinations of various segments with a value of 0.4, 0.45, or 0.5, while the latter is defined by random region growing (see Section 4.1) with a value of 0.5. This introduced a certain level of difference between the training and testing data for VAE, although in both settings we considered a simplified scenario in which the tissue property is nearly piece-wise homogeneous: i.e., the tissue property was either healthy or unhealthy (infarct core). In this section, we studied the ability of the presented BO-VAE to generalize to more realistic settings of tissue properties that are more diffusive with larger variations rather than being piece-wise homogeneous. Specifically, we consider two scenarios. First, we added more heterogeneity to the tissue properties by adding a larger Gaussian $\mathcal{N}(0,0.01)$ noise to the healthy and infarct core regions of the heart (termed as “large-noise” group). Second, we relaxed the sharp boundary between the infarct core and healthy myocardium by adding a transition zone (∼40% of the abnormal region) with an intermediate tissue property value of 0.35, mimicking the existence of border zone in myocardial infarct (termed the “border-zone” group). A uniform noise in the range [−0.001,0.001] was added to the tissue property values in this setting as in previous experiments.

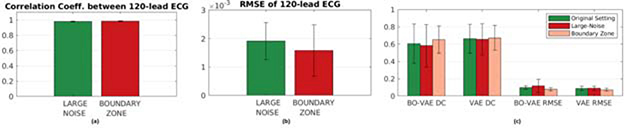
The above two changes were applied to 18 synthetic experiments, a subset of 43 experiments considered earlier, and 120-lead ECG was simulated and 640 noise-corrupted in the same fashion as previously described (see Section 4.1). This gave two groups of 18 cases each to be tested for optimization in comparison with the original results presented in Section 4.2.1. Examples of these changed ground-truth tissue properties are shown in Fig. 11(a), and their resulting changes in ECG data in comparison to the original setting are shown in Figs. 12(a)–(b): note that the incorporation of border zone visually introduced a more evident change in the ground truth than adding larger noise, although the latter resulted in a larger change in the simulated ECG data.

Figure 11:

Comparison of binary excitability corrupted with Gaussian noise (large-noise group) and binary excitability appended with boundary value between healthy and infarct core (border-zone group) in their (a) ground truth, (b) optimization result and (c) reconstruction by VAE trained on original uniform noise corrupted excitability data.

Figure 12:

Comparison of (a) the correlation coefficient and (b) the RMSE between the 120-lead ECG data simulated with tissue properties setup with the original setting (see Section 4.2) versus those setup with an additional Gaussian $\mathcal{N}(0,0.01)$ noise (large-noise group) and an additional transition border zone between the infarct and the healthy tissues (border-zone group). (c) Comparison of the accuracy in tissue properties reconstruction (VAE) and estimation (BO-VAE) in terms of DC and RMSE.

The optimization for each of the 18 experiments was ran for 50 iterations with search space bounds between −4 to 4. Several examples of the results are shown in Fig. 11. Overall, the estimation accuracy was not significantly different across the groups, where a relatively larger difference in the accuracy was observed in the large-noise group. The quantitative accuracy as measured by DC and RMSE between the estimated and ground-truth tissue properties were also not statistically different, as shown in Fig. 12(c) (DC, p>0.7369, paired t-tests and RMSE, p>0.2982, paired t-tests). Although without statistical significance, the accuracy in large-noise group did tend to be the lowest and in the borderzone group did tend to be the highest among the three groups. Although an unintended consequence, this does suggest that the presented method tends to work better with more “smoothed” spatial distributions of tissue properties that 660 are more commonly expected in reality.

Although the change in optimization results were not significant, we still attempt to relate the observed change, especially those in the large-noise group, to two potential contributing factors: 1) generalization ability of the VAE decoder as a generative model underpinning the optimization, and 2) changes in 665 the input ECG data.

1. Generalization ability of VAE: We first examined how well the trained VAE was able to reconstruct the tissue property in the two new test groups. The results, as listed in Fig. 11(c) and Fig. 12(c), showed that the accuracy of VAE reconstruction was little affected for each group. This suggests that the trained VAE was able to generalize well to the new data considered here, and it was not the main cause for the change in the optimization results as observed. Also note that, VAE tended to smooth out the tissue property and generated reconstructions that had blurred rather than sharp transitions between normal and abnormal regions. As observed earlier, this makes the presented VAE and VAE-enabled BO suitable for realistic tissue properties without sharp boundaries.

2. Changes in the input ECG data: As shown earlier in Figs. 12(a)–(b), tissue property in the large-noise group produced a relatively larger difference in ECG data, as evidenced in both a lower correlation and higher RMSE with the original ECG data. This suggests that the difference in ECG data, rather than the generalizability of the VAE, is the main factor that contributed to the larger difference in the optimization results in the large-noise group.

These results showed that, although the VAE was trained on binary-like tissue property with sharp transitions between tissue regions, both the VAE and the VAE-enable optimization were able to generalize well to more realistic tissue property settings considered in the above experiments.

To introduce larger variations in the values of tissue property without resulting in physiologically invalid setting would become difficult. Therefore, to further push the limit of the generalizability of the VAE, we considered eight test cases with two non-adjacent infarcts in the heart. The results of optimization are shown in Fig. 13. As expected, since the VAE was trained with only single patch of abnormal tissue, the optimization was able to reflect one of the two abnormal regions. This suggests the limit to which the presented VAE and 695 VAE-enabled optimization can be generalized outside training data.

Figure 13:

Examples of estimated tissue excitability with the BO-VAE in the presence of multiple infarcts.

4.3. Experiments on post-infarction hearts with blinded simulation data

4.3.1. Experimental data and data processing

In this section, we studied the presented method in estimating the tissue excitability in six post-infarction human hearts. The patient-specific ventricular models along with the detailed 3D infarct architectures were delineated from MRI images as detailed in (Arevalo et al., 2016). The training of VAE was performed on one of these ventricles, using synthetically-generated tissue excitability values as described in Section 4.1. The trained VAE was used in the Bayesian optimization of tissue excitability in the remaining five ventricles.

Compared with the synthetic-data experiments in Section 4.2, we increased the challenge in this set of experiments in two aspects. First, because in-vivo electrical mapping data were unavailable on these patients, 3D simulation of paced action potential propagation was performed on these patient-specific ventricular models using a high-resolution (average resolution: 350μm) multi-scale (sub-cellular to organ scale) in-silico ionic electrophysiological model as detailed in (Arevalo et al., 2016). Data used for parameter estimation were then extracted from the simulated action potential at 300–400 epicardial sites, temporarily down-sampled to a 5-ms resolution, and corrupted with 20 dB Gaussian noise. Although these measurement data were not in-vivo, they mimicked a real- data scenario because the simulation model used was high fidelity (Arevalo et al., 2016) and, more importantly, blinded to the parameter estimation method.

Second, abnormal tissues considered here were heterogeneous 3D myocardial infarcts delineated from in-vivo contrast-enhanced MRI data. In comparison to the synthetic data in Section 4.2, these in-vivo infarcts had the following characteristics that increased the heterogeneity in tissue properties: 1) the presence of both dense infarct core and gray zone, 2) the presence of a single or multiple infarcts with complex spatial distribution and irregular boundaries, and 3) the presence of both transmural and non-transmural infarcts. These test cases, therefore, were more substantially different from those used in VAE training.

Fig. 14 summarized the results of estimated tissue excitability on the five post-infarction hearts, in comparison to the FH method. Overall, the accuracy of the presented method was comparable to that of the FH method. For clarity, below we analyzed the performance of the presented method with respect to two primary contributing factors to the heterogeneity of the tissue excitability: 1) infarct transmurality, and 2) gray zone.

Figure 14:

Results of estimated tissue excitability from the BO-VAE and FH method in comparison to 3D infarcts delineated from in-vivo MRI images.

1) Infarct transmurality: The difficultly in estimating tissue properties in the presence of non-transmural infarcts has been reported in literature (Dhamala et al., 2017b,a). In this study, the training data was designed to contain only transmural infarcts. Therefore, it was expected that estimating non-transmural infarcts will be more difficult than estimating transmural infarcts. As shown in Fig. 14, cases 1–3 contained non-transmural infarcts at the septal region, left lateral ventricular wall region, and the anterior-septal region, respectively. In all of these cases, while the estimated tissue property localized the region of reduced tissue excitability due to transmural infarcts, it was not able to reflect abnormal tissue excitability due to non-transmural infarcts (highlighted by the magenta oval contour).

2) Gray zone: In all the examples, there were regions of gray zone that surrounded the dense transmural infarcts. Specifically, in case 4 and case 5, there was a large patchy grey zone mixed within the dense infarcts. These regions were reflected in the region of estimated abnormal tissue excitability, however the estimated parameter values were not able to distinguish between the gray zone and dense infarct.

4.4. Experiments on in-vivo ECG and voltage mapping data

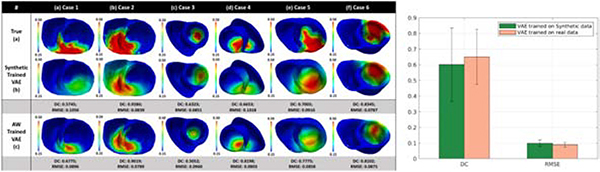
Finally, we conducted real-data studies on three patients who underwent catheter ablation of ventricular tachycardia due to previous myocardial infarction (Sapp et al., 2012). The patient-specific geometrical models of heart and torso were constructed from axial CT images as detailed in Wang et al. (2018). 120-lead ECG was used as measurement data. The accuracy of the estimated parameters was evaluated using the bipolar voltage data from in-vivo catheter mapping. As illustrated in the first two columns of Fig. 15, the voltage maps allowed the extraction of infarct core (red, bipolar voltage ≤0.5mV) and infarct border (green: bipolar voltage 0.5 − 1.5mV) as an approximate tissue excitability. The computational cost was evaluated in terms of the number of model evaluations required for the optimization. In each patient, multiple experiments were carried out for parameter estimation using 120-lead ECG data collected under different pacing conditions, as well as using a combination of all available 120-lead ECG data, resulting in a total of 11 cases being studied. The VAE for Bayesian optimization of model parameters in case 1 and 2 was trained with synthetic training data generated on the ventricular mesh of case 3, whereas the VAE used for optimization in case 3 was trained with synthetic training data generated on the mesh of case 1.

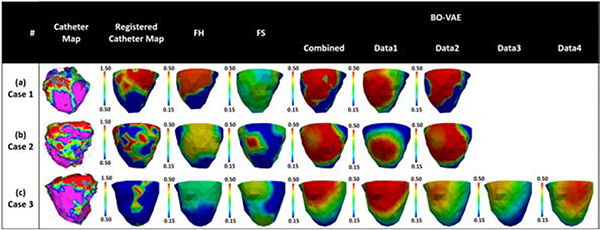
Figure 15:

Evaluation of the estimated tissue excitability in real data studies in comparison to in-vivo voltage maps on three patients. First, we compared the results obtained with BO-VAE (column: Data1) with those obtained with FH and FS methods. Second, we compared the results obtained with BO-VAE using individual ECG data vs. with the result obtained when using all ECG data at once (column: combined).

Below we first evaluated the performance of the presented method in estimating tissue excitability in comparison with the FH and FS methods. We then compared the results of parameter estimation on each patient using different 770 120-lead ECG data.

Case 1: The voltage data for case 1 (Fig. 15(a)) showed a dense infarct at the inferolateral left ventricle (LV) with a heterogeneous region extending to the lateral LV. As shown, the parameter for the region of infarct core was correctly estimated with both the BO-VAE and FH method. In comparison, while the FS method also identified this region of infarct, the estimated parameter indicated the presence of a large diffuse heterogenerious infarct in this region. The optimization using the BO-VAE, FH, and FS method respectively required 130, 6462, and 1593 model evaluations.

Case 2: Unlike the dense infarct in case 1, the voltage data in case 2 (Fig. 15(b)) showed a highly heterogeneous infarct spread over a large region of the lateral LV. The estimated parameters by all three methods captured this highly heterogeneous region of infarct. To attain this accuracy, the FH and FS methods required 4056 and 1058 model evaluations, whereas BO-VAE required only 130 model evaluations.

Case 3: The voltage data for case 3 (Fig. 15(c)) showed the presence of a dense infarct at the lateral-basal LV. The estimated model parameters by the BO-VAE and FH method correctly revealed this region of abnormal tissue, although the parameter values indicated a more diffused abnormality rather than a dense infarct core. In comparison, the region of abnormal tissue estimated by FS method had a less accurate overlap with the low voltage region shown by the voltage map. To attain this level of accuracy, the presented method required only 130 model evaluations in comparison to the FH and FS methods that required 5798 and 1501 model evaluations, respectively.

In conclusion, the presented BO-VAE method was able to achieve an accuracy in parameter estimation that was higher than the FS method and comparable to the FH method, at a drastically improved efficiency.

Next, on each patient, we investigated the accuracy in parameter estimation when using ECG data under different pacing sites as well as using all available ECG data together. While there are multiple ways to combine multiple ECG measurements from a same patient together, here for simplicity, we used the average of the original error as follows:

$$\widehat{\mathbf{z}}=\underset{\mathbf{z}}{\arg \max }\mathcal{L}(\mathbf{z})=\underset{\mathbf{z}}{\arg \max }\frac{1}{N}\sum _i^N-{\Vert {\mathbf{Y}}_i-M\left(\mathcal{T}\left(\mathrm{E}\left[p_{\beta }(\mathit{\theta }|\mathbf{z})\right]\right)\right)\Vert }^2,$$ (17)

where N is the number of ECG measurements utilized and Y_i is the i^th ECG measurement. Results in Fig. 15 show that, with ECG data from different pacing sites, the estimated tissue properties could correctly identify the primary region of infarct, although the detailed values of the estimated parameters differed. Overall, the parameter estimated with a combination of all available ECG data showed a closer match with the registered catheter map, indicating that more ECG data may provide a more complete “view” of the spatially-varying tissue properties.

5. Discussion

5.1. Effect of the amount of measurement data

One challenge in personalizing organ tissue properties lies in the fact that they typically cannot be directly measured, but have to be inferred from sparse and noisy external data that is non-linearly and indirectly related to the underlying tissue properties. The identifiability of organ tissue properties given such external measurement is not well understood. Here, we attempted to provide some initial empirical insight by investigating the change in the performance of the presented method when the amount of surface ECG data for parameter estimation was decreased from 120 leads to the standard 12 leads, the latter 815 more commonly available in practice.

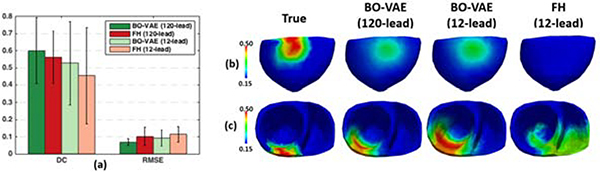
Experiments were carried out on a subset of 20 synthetic experiments as described in Section 4.2. 12-lead ECG to be used as measurement data were extracted from the noise-corrupted simulated 120-lead ECG. As summarized in Fig. 16(a), an overall decrease in the accuracy across both metrics was observed. With 12-lead ECG as measurement data, the accuracy in terms of both DC and RMSE of the estimated tissue properties was higher with the BO-VAE method than with the FH Method. Furthermore, the RMSE of the estimated tissue property was lower using BO-VAE than when using FH method even when BO-VAE used 12-lead ECG and FH used 120-lead ECG. Fig. 16(b) gives an example where the abnormal tissue in the inferior region of the heart was identified by the BO-VAE method using 12-lead ECG, but completely missed by the FH method when using 12-lead ECG data. Fig. 16(c) shows another example in which the accuracy in estimating the abnormal tissue excitability decreased when the measurement data was reduced from 120 leads to 12 leads for the BO-VAE method, yet the accuracy was still higher than the FH method using 12-lead ECG. These results suggest that the presented BO-VAE method may be more robust to the decrease in measurement data compared to the previously-presented FH method.

Figure 16:

Comparison of the accuracy (DC and RMSE) in parameter estimation using measurement data from 12-lead ECG and 120-lead ECG. Left: Summary statistics. Right: Examples of estimated tissue excitability.

5.2. Effect of non-linear registration

An important contribution of the presented work is to, through the use of a nonlinear registration, allow the VAE trained on one heart to be used for generative modeling and optimization on a different heart. In Section 4.2.2, we showed that this approach performs similarly to a patient-specific alternative where the VAE is trained on the same heart for which the parameters needed to be estimated. In experiments performed in the three groups of hearts as reported in Sections 4.2, 4.3, and 4.4, VAE was trained on one heart representative of each respective group to avoid registering between hearts with significant geometrical differences. Here, we investigated this effect of registering hearts with more significant geometrical differences (i.e., from different groups) on the optimization results.

Specifically, on 18 out of the 43 experiments considered in Section 4.2, we performed optimization by using a VAE trained on a heart from a different group (as described in Section 4.4), and compared the results to those obtained when using a VAE trained on a heart from the same group (see Section 4.2). Visual comparison as shown Figs. 17(b) and (c) showed a decrease of accuracy in some cases, while an increase of accuracy in others. The overall quantitative metrics, as a result, were not significantly changed (DC, p>0.3186, paired t-tests and RMSE, p>0.0509, paired t-tests). This suggests that the use of the non-linear registration in the presented method is not restricted to the experimental setting considered in Sections 4.2–4.4, but can be generally applied to optimization on hearts that are different from the heart on which the VAE is trained.

Figure 17:

Comparison of the accuracy in parameter estimation of the presented BO-VAE when a VAE is trained on a heart described in Section 4.2 vs. when a VAE is trained on a heart described on Section 4.4; 18 test tissue property for optimization were taken from Sections 4.2. Left: Visual comparison of (a) ground truth parameters, (b) estimated parameters when VAE was trained on a heart from Section 4.2, and (c) estimated parameters when VAE was trained on a heart from Section 4.4. Right: Comparison of the accuracy in parameter estimation in terms of DC and RMSE.

5.3. Limitation & future work

A central idea of this paper is to embed HD optimization through a generative model. While we demonstrated the feasibility of this idea using a specific generative model in the form of VAE, it can be generalized by investigating various forms of generative models such as adversarial autoencoders (Makhzani et al., 2015) and generative adversarial networks (Goodfellow et al., 2014). Furthermore, while the parameter θ was represented in a Euclidean vector space in this study, organ tissue property is actually defined over a physical domain in the form of a 3D geometrical mesh. By representing this non-Euclidean data in a Euclidean vector space, we have ignored the 3D spatial structure of the physical mesh. A future step, following the current developments in geometric deep learning Bronstein et al. (2017) is therefore to construct the generative model over the non-Euclidean domain by treating the cardiac mesh as a graph and developing graph-based convolution-deconvolution networks.

Another central idea of this paper is to utilize a probability density of the latent space z, for instance learned from training data, to guide and improve Bayesian optimization. In this study, the feasibility of this idea was tested by using q_α(z) to modify the common acquisition function of EI. Future work will continue to explore the same idea in other acquisition functions, with a goal to modulate the trade-off between exploitation and exploration over the space of z based on the prior knowledge of its distribution.

In this paper, we extended our previous work (Dhamala et al., 2018) and rid the need of a patient-specific VAE by using the CPD method for nonlinear registration between the heart used in parameter estimation and that used in VAE training. In the presented experiments, the feasibility of this approach was demonstrated by training the VAE on one heart that was representative of those used in each subset of the experiments. Future work will investigate VAE training on a generic heart model or a group of heart models common to all test models, as well as different nonlinear registration methods to reduce potential registration errors.

The feasibility of the presented method was evaluated on estimating a single spatially-varying parameter, termed as tissue excitability, in this paper. The same approach, however, should be directly applicable to the estimation of multiple spatially-varying tissue properties: in the latter case, there will be multiple parameters attached to each node of the cardiac mesh. This will be investigated in future work.

While the VAE provides a probablistic generative model p_β(θ|z), we only adopted the expectation network of this probabilistic model, E[p_β(θ|z)], as the generative model to achieve the HD-to-LD embedding of the optimization objective. An immediate next step is to investigate the incorporation of the uncertainty in the generative model into the optimization process.

The lack of real data of organ tissue properties is a main challenge for training the generative model. In this paper, the VAE was trained by synthetic data of 900 tissue excitability that is simplified in shape, transmurality, and heterogeneity. It thus may have a limited ability to generalize to realistic conditions where tissue abnormality is more complex in these aspects. An important direction of the future work is to investigate means to improve the training data for the generative model.

The lack of real data of organ tissue properties is also a limitation on the number of real data studies that was conducted. In future work, we will add additional experiments utilizing real data. Another important future work is to study the ability of this method to estimate tissue property with only 12-lead ECG in real data setting, and to extend the presented method to consider continuous updating of the model as more and more data become available in time.

The performance of the presented optimization method as well as the comparison methods degraded notably from synthetic to real-data experiments. This suggests that there may be a fundamental limit to the identifiabilty of spatial tissue properties from remote and noisy 120-lead ECG data. This also suggests that parameter estimation becomes more challenge at the presence of other possible sources of model discrepancy, which is commonly present in real data settings. Both of these point to the limitation of considering only a point estimate of the best model parameter that will fit the given measurement data, and the importance of the uncertainty that may be associated with the estimation Dhamala et al. (2017b). Future work will extend the presented methodology to probabilistic estimation of model parameters, where the GP surrogate can be constructed to approximate the posterior density of the model parameter rather than the optimization objective as in the present study.

Finally, this work does not intend to present or validate a complete pipeline for personalized cardiac modeling, but instead focus on the specific component of tissue property estimation within the much bigger pipeline of personalized cardiac modeling. We, therefore, focused on validating the estimated tissue properties using synthetic as well as in-vivo imaging and mapping data. A 930 next step will be to evaluate the personalized model in predictive tasks, such as predicting the risk (Arevalo et al., 2016) or the optimal treatment target (Prakosa et al., 2018) for lethal ventricular arrhythmia.

6. Conclusions

In this paper, we presented a novel HD Bayesian optimization method to the parameter estimation of a personalized cardiac model, where the HD construction and optimization of the GP surrogate is embedded into a LD manifold through a generative VAE model. Through a range of synthetic and real-data experiments, we demonstrated the advantage of the presented method in comparison to previous approaches that relied on geometry-based dimensinality reduction of the parameter space. Future works will focus on better architecture and training of the generative model, the extension to probabilistic settings to consider the uncertainty in both the generation process and the parameter estimation, and more comprehensive testings of the presented method in a wider range of model personalization problems and potentially other applications that 945 can benefit from HD Bayesian optimization.

Highlights.

• A framework for personalization of high-dimensional model parameters.

• Generative model to embed Bayesian optimization into a low-dimensional latent space.

• VAE-informed acquisition function for active search in Bayesian optimization.

• Studies on estimating tissue excitability in cardiac electrophysiological model.

• Increase in accuracy with a substantial decrease in the computational cost.