Abstract
SARS-CoV-2 (COVID-19) is a new Coronavirus, with first reported human infections in late 2019. COVID-19 has been officially declared as a universal pandemic by the World Health Organization (WHO). The epidemiological characteristics of COVID-2019 have not been completely understood yet. More than 200,000 persons were killed during this epidemic (till 1 May 2020). Therefore, developing forecasting models to predict the spread of that epidemic is a critical issue. In this study, statistical and artificial intelligence based approaches have been proposed to model and forecast the prevalence of this epidemic in Egypt. These approaches are autoregressive integrated moving average (ARIMA) and nonlinear autoregressive artificial neural networks (NARANN). The official data reported by The Egyptian Ministry of Health and Population of COVID-19 cases in the period between 1 March and 10 May 2020 was used to train the models. The forecasted cases showed a good agreement with officially reported cases. The obtained results of this study may help the Egyptian decision-makers to put short-term future plans to face this epidemic.
Keywords: COVID-19, Forecasting, Neural networks, Egypt
1. Introduction
In December 2019, Chinese government declared that a new coronavirus (COVID-19) caused an explosive outbreak (Chen et al., 2020). The virus was first detected in Wuhan, Hubei province, China (30.5928 °N, 114.3055 °E). Wuhan is the biggest city in central China with a humid subtropical climate, an area of 8494 km2, and population of about 11 million. COVID-19 has been officially declared as a universal pandemic by WHO on 11 March 2020 as it swept into more than 114 countries and killed more than 4000 person. Within one month from the declaration date, the confirmed cases and deaths have been dramatically increased and reached more than 1 million confirmed cases and more than 100,000 deaths as reported by WHO on 10 April 2020. Within less than one month, the number of confirmed cases and deaths were duplicated; more than 2 million active cases and more than 200,000 deaths were reported by WHO on 1 May 2020. Numerous scientific articles from different countries are published on a daily basis (Pan, 2020; Salzberger et al., 2020; Zheng et al., 2020).
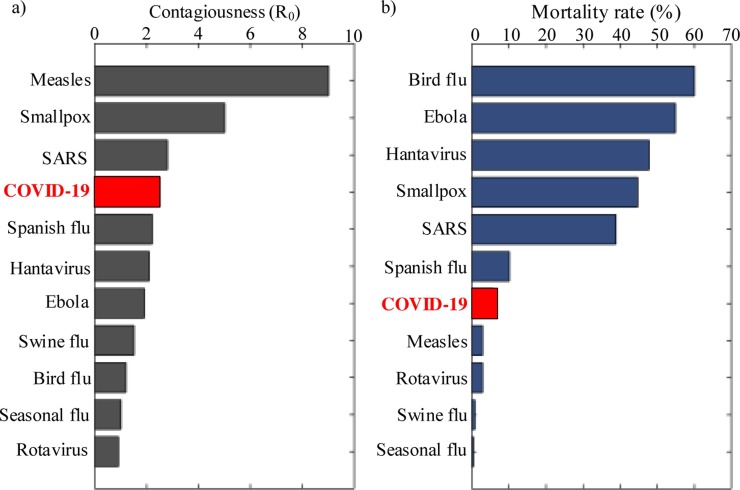
COVID-19 is a global threat which has a mild mortality rate and contagiousness compared with other diseases as shown in Fig. 1 . COVID-19 causes mild respiratory infection symptoms, however, it may cause severe complications for older persons and persons with other debilitating diseases such diabetes, hypertension, and cardiovascular diseases (Li et al., 2020; Tian et al., 2020; Zhang et al., 2020).
Fig. 1.
Viral infectious diseases: (a) Contagiousness; (b) Mortality rate (Thomas-Rüddel et al., 2020).
The high risk of infection, ambiguous characteristics of the virus, and vigorous progression of the disease, make COVID-19 a very critical topic for world medical society. The incubation period for COVID-19 is ranged between one day to two weeks. This long incubation period causes a high risk of infection from asymptomatic persons. The virus spreads through droplets from the sneeze or cough of infected persons. About 6.98% (reported by WHO on 1 May 2020) of confirmed COVID-19 cases have died which is lower than other viral infections as shown in Fig. 1. The total number of COVID-19 cases is not exactly known as it depends on the conducted tests, so the actual total cases is higher than the reported confirmed cases. Each country established its own rules to avoid spread of COVID-19. Travel to infected countries has been prohibited by many countries. Therefore, expecting the number of infected persons and the critical cases is a crucial issue.
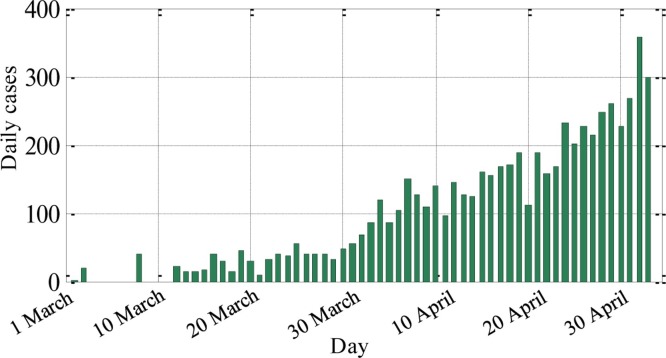
Egypt is an African country located on the northeast corner of the African continent with an area of 1,010,408 km2, and population of about 100 million. It is bordered by the Mediterranean Sea to the north, the Red Sea to the east, Libya to the west, and Sudan to the south. Health has been declared as a basic human right in the Egyptian Constitution. Egypt has banned all flights from China to Egypt on 26 January 2020. The first confirmed case in Egypt was officially announced on 14 February 2020 for a Chinese person. The patient has been sent to a quarantine station. On 28 February 2020, the Egyptian cabinet officially denied any confirmed Egyptian cases. On 1 March 2020, the second COVID-19 case has been officially announced. The first Egyptian case died from COVID-19 was reported in 20 March 2020 after twenty days from the first died case reported in Egypt (for a German person). All schools/universities and mosques have been closed from 7 March and 21 March, respectively. To alleviate the epidemic impact, the Egyptian government has imposed different forms of lockdowns. The daily officially reported cases are shown in Fig. 2 . Many scenarios could be occurred as COVID-19 epidemic may decline in spring or summer or may become the world's worst pandemic. Healthcare workers are at extreme risk to be infected during COVID-19 epidemic. Most of Egyptian hospitals have been prepared to face COVID-19 cases to overcome shortages of medical supplies and staff.
Fig. 2.
Daily COVID-19 Egyptian cases reported by Egyptian ministry of Health.
Many studies have been published on daily basis to figure out the epidemiological characteristics of COVID-19 and to minimize its impact on the human health. Husnayain et al. (Husnayain et al., 2020) used information provided by Google Trends on different search terms such as face masks and handwashing to explore public concern toward COVID-19 outbreak in Taiwan. The correlation between COVID-19 outbreak in Indonesia and different meteorological parameters such as relative humidity, temperature, and amount of rainfall has been explored using Spearman rank correlation method (Tosepu et al., 2020). The spatial spread of the COVID-19 outbreak in China was statistically analyzed using Moran’s I correlation algorithm (Kang et al., 2020). The reported data on platelet count in COVID-19 cases has been statistically analyzed to figure out its effect on mortality rate (Lippi et al., 2020). Spatial effects of COVID-19 in China have been explored using the spatial panel models (Guliyev, 2020). In another study, a conceptual model has been developed to model COVID-19 outbreak in Wuhan, China considering some important factors of the 1918 influenza outbreak in London, United Kingdom (Lin et al., 2020). Al-qaness et al. (2020) presented a new forecasting model to forecast COVID-19 cases in China. The model consists of adaptive neuro-fuzzy inference system integrated with enhanced flower pollination algorithm and salp swarm algorithm. The proposed model was used forecast the confirmed cases of COVID-19 in the upcoming ten days using the confirmed cases recorded in China.
Time series has been widely applied in different medical, engineering, and economic fields. Monitoring the responses of a certain phenomenon as a function of time and forecasting of its future responses is a critical issue that may help the decision makers to establish future polices and plans to overcome different problems faced human beings. Both statistical and artificial intelligence based methods have been reported in literature as forecasting tools for time series problems (Lauret et al., 2017; Nury et al., 2017; Tealab et al., 2017; Xu et al., 2018). To analyze this kind of data and to forecast further responses as a function of time, statistical-based methods such as ARIMA are usually employed. Artificial intelligence-based methods have been also reported to analyze this kind of data with better forecasting capabilities compared with statistical based methods. These artificial intelligence methods have been widely used for predicting the responses of different engineering systems (Babikir et al., 2019; Elaziz et al., 2019; Elsheikh et al., 2020; Oliva et al., 2019; Shehabeldeen et al., 2020, 2019). The accumulated confirmed cases of COVID-19 could be considered as a time series data. Recently, ARIMA has been applied to model COVID-19 epidemic dataset to forecast its epidemiological trend (Benvenuto et al., 2020).
In this study, two forecasting algorithms are employed to predict the number of COVID-19 cases, namely, ARIMA and NARANN. The reported COVID-19 cases by the Egyptian ministry of health are used to train the proposed model. Different statistical indices were computed to assess the accuracy and the reliability of the proposed models. The proposed models succeeded to forecast the future COVID-19 cases. The results of this study may be used to develop precautionary plans to overcome this crisis and to offer better care to patients.
2. Methodology
2.1. Study area
Egypt is an African country located at Eastern Mediterranean region according to WHO classification and it is classified as lower-middle-income country according to World Bank classification. The total population of Egypt is more than 100 million people and about 8% of them are over 60 years old. 1.7% of the total population are living below the national poverty lines (Poverty headcount ratio at $1.25 a day). Health systems in Egypt, like all African countries, have limited resources to absorb any pandemic. Egypt has a physician density of 0.79 physicians/1000 persons and hospital bed density 1.6 beds/1000 persons. The demographic structure of Egypt has a specific nature differs from other European and Asian countries. The median age of the Egyptian is 24.6 years (the median age in China is 38.4 years and European Union is 43.1 years). Only 4.23% of Egyptian people have age more than 65 years old. Experiences in infected countries (in Europe and Asia) showed that elderly people over 60 years old, and those have debilitating diseases are most susceptible to serious grades of COVID-19. Therefore, Egyptian youth may be act as a protective factor to limit the spread of the pandemic. COVID-19 has reached Egypt in March 2020. Its future epidemiological progression is still ambiguous as it spreads randomly.
2.2. Data collection
The official data reported by The Egyptian Ministry of Health and Population regarding COVID-19 confirmed cases was used in the current study for the period from 1 March to 10 May 2020.
2.3. Data analysis
Two forecasting algorithms have been applied to model and forecast the accumulated confirmed COVID-19 cases in Egypt. The first algorithm is ARIMA and the second algorithm is NARANN. Both of them have been reported as powerful forecasting methods for time series data. The first method is a statistical-based method while the second method is an artificial intelligence forecasting method. More information about these two methods will be presented in the next section.
3. Theoretical background
3.1. Autoregressive integrated moving average
ARIMA is a statistical forecasting model which obtains the forecasted variables as a function of the historical responses considering a linear relationship between them. The time series data used in ARIMA should have stationary and linear nature. Therefore, stationarity test should be carried out on the time series data to figure out the relationship between the data and time. If the data does not have a stationary nature, ARIMA performs d times data differencing to eliminate non-stationary of the data. The times of data differencing is defined as the ARIMA integration order.
A typical ARIMA model consists of two main linear-regressions sub-models: the autoregression and the moving average. The first sub-model defines the variable based on its own previous (lagged) values. The autoregression model is defined as (Al-Musaylh et al., 2018):
| (1) |
where is a constant, ,…., are the autoregression parameters, is the autoregression order, denotes the white noise.
The second sub-model defines the incorporation between the data and the calculated residual error and is defined as:
| (2) |
where denotes the expectation related to , , , …. denote the white noise terms, ,…., are the moving average parameters, and is the moving average order.
The integration between the two aforementioned sub-models defines the final form of ARIMA model as follows;
| (3) |
Where and are the autoregression and moving average orders, respectively. If is set to zero, the ARIMA model is converted to an autoregression model of order . If is set to zero, the ARIMA model is converted moving average model of order .
3.2. Nonlinear autoregressive artificial neural networks
NARANN is a kind of ANN used to forecast responses in a one-dimensional time series. Time series data has high variability and transient nature, which makes modeling of this type of data using linear models is a cumbersome problem (Chen et al., 2019). Thus, nonlinear approaches are highly recommended to model this kind of data (Gautam and Abhishekh, 2019). NARANN could be applied to forecast time series responses in which data has a discrete non-linear nature. The mathematical representation of NARNN can be represented as follows:
| (4) |
where is the current response, and is the network delay. Thus, are the historical responses. is unknown function and it is approximated during the training process of the network by determining the optimal weights of the network and the corresponding bias. is a compensation function that used to approximate the error of the data series as a function of time.
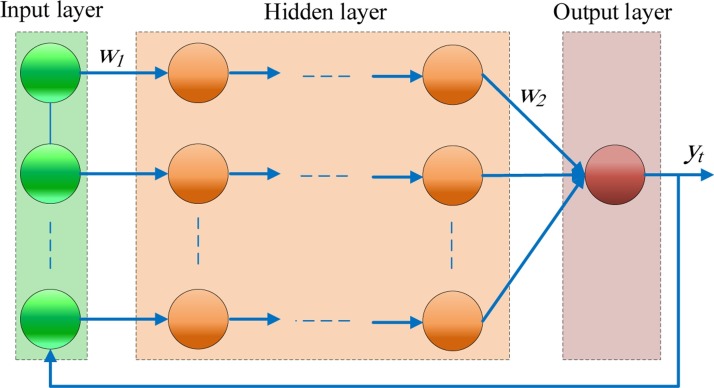
The structure of a typical NARANN is shown in Fig. 3 . The number of neurons in the hidden layer as well as the synaptic weights connected between different neurons are adjusted to obtain the optimal topology of NARANN that maximize the forecasting accuracy. Though, it should be noticed that the use of high number of neurons increases the computational costs of the model and may results in over-fitting of the data, while the use of low number of neurons may impair the computational accuracy and generalization capabilities of the model.
Fig. 3.
The structure of the nonlinear autoregressive neural networks.
The proposed NARANN is trained using the conventional Levenberg-Marquardt backpropagation training algorithm. This training algorithm has been reported as the fastest backpropagation training algorithm as it avoids the computation Hessian matrix that consumes large computational time (Elsheikh et al., 2019). It depends on approximation of the second-order derivative.
In this study, NARANN is used to model the accumulated COVID-19 confirmed cases time series in Egypt. The confirmed cases at time defined as is used as the input of the, while the output of the network is the confirmed cases at the next time .
3.3. Evaluation criteria of the model
Several statistical indices are employed to assess the performance and to ensure the reliability of the proposed models to forecast the COVID-19 cases. These indices analyze the errors between the reported and predicted cases and point out the accuracy of the models (Wu et al., 2020; Zaranezhad et al., 2019). The employed indicators are mean absolute error (MAE), root mean square error (RMSE), determination coefficient R2, deviation ratio (RD), and coefficient of residual mass (CRM). Eqs (5), (6), (7), (8), (9) correlate the mathematical formulas of these statistical indices (Essa et al., 2020).
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
where are the numbers of reported cases, reported cases, predicted cases, minimum value of reported cases, maximum value of reported cases, average of of reported cases, and average of predicted cases, respectively.
4. Results and discussion
The collected data of the accumulated confirmed COVID-19 cases in Egypt for two months (1 March− 10 May 2020) have been used as time series data for both of the forecasting models. Four forecasting processes have been carried out to assess the performance of the two models; ARIMA and NARANN.
-
i
In the first process, both of ARIMA and NARANN were used to forecast the accumulated COVID-19 cases for ten days (1 April- 10 April) using the confirmed cases reported in the period from 1 March-31 March. In this process the two models are compared to determine the optimal one.
-
ii
In the second process, NARANN is used to forecast the accumulated cases for one week (10 April-16 April) using the confirmed cases reported in the period from 1 March-9 April. In this process the capability of NARANN model to forecast COVID-19 cases is investigated.
-
iii
In the third process, NARANN is used to forecast the accumulated cases for seventeen days (15 April-1 May) using the confirmed cases reported in the period from 1 March-9 April. In this process the forecasting results of NARANN are verified for long period (more than two weeks).
-
iv
In the fourth process, NARANN is employed to forecast the accumulated number of confirmed cases of COVID-19 in the upcoming twenty days based on the previously reported cases in the period from 1 March- 10 May.
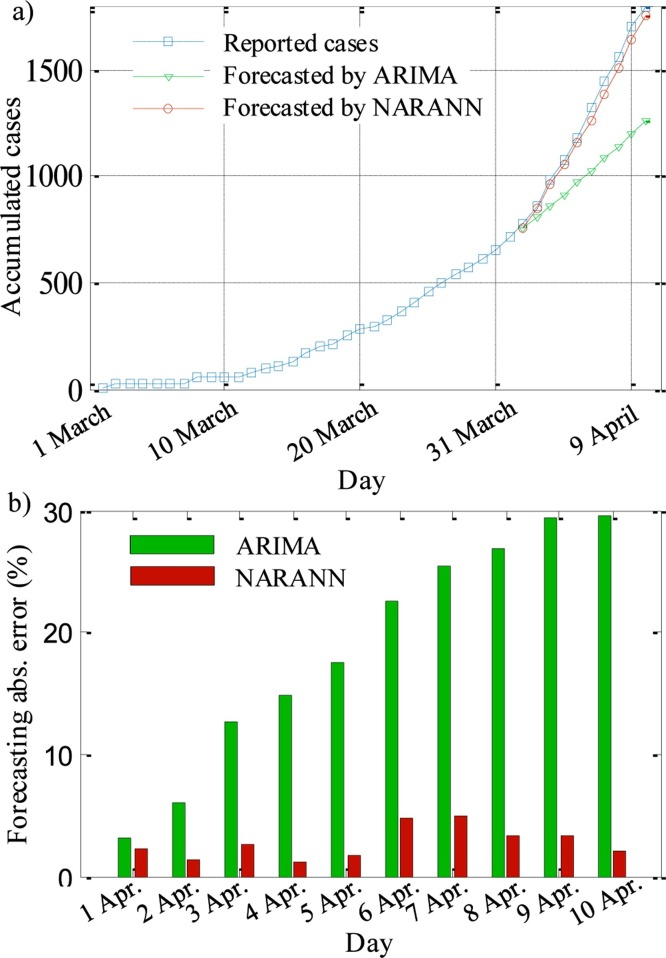
For first forecasting process, ARIMA and NARANN have been employed to forecast COVID-19 cases. In NARANN model the data was divided into three main subsets: training subset (70% of the total data), validation subset (15% of the total data), and test subset (15% of the total data). The training subset is used to adjust the network based on its computed error. Validation subset is used to assess the generalization capability of the network. Test subset is used to assess the final performance of the network. Ten neurons were used in the hidden layer. The accumulated reported cases as well as the forecasted cases using ARIMA and NARANN are plotted in Fig. 4 (a). An excellent agreement between NARANN and reported cases is observed, while ARIMA has failed to obtain accurate forecasted cases. Fig. 4(b) shows the absolute percentage error between the forecasted and reported cases for both models. The error of the results obtained by ARIMA model is increased with time, as it is 3.08% at the beginning (one day from the forecasting origin) and reaches a high value of 29.48% after ten days from the forecasting origin. On the other hand, the results of NARANN have small absolute percentage error (1.12%–4.89%) which fluctuates with time. It could be concluded that, NARANN could be used to forecast COVID-19 cases with a better accuracy compared with ARIMA. Therefore, NARANN will be consider in the two following forecasting process.
Fig. 4.
(a) Accumulated confirmed reported and forecasted COVID-19 cases using ARIMA and NARANN for the first forecasting process; (b) Absolute percentage error for ARIMA and NARANN.
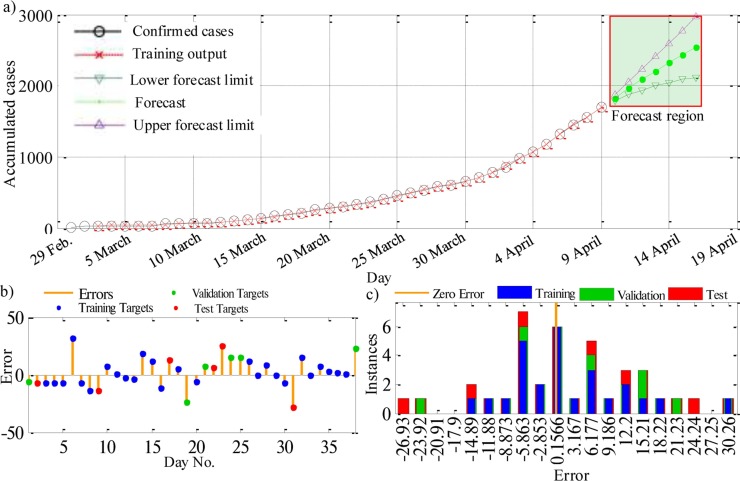
For the second forecasting process, the accumulated confirmed reported COVID-19 cases are plotted in Fig. 5 (a). A good agreement is observed between reported confirmed cases and the training output. Also, the forecast region shown in this figure indicates the forecasted accumulated cases for one week after the collected data used in the training of the network. Upper and lower forecasting limits with 95% confidence limit are also plotted. For the first day of the forecast region (10 April), the number of forecasted cases is 1832 case with lower and upper limits of 1791 case and 1874 case, respectively. This forecasted value agrees with the accumulated confirmed cases reported by The Egyptian Ministry of Health (1794 case), which lies between the lower and upper forecasted limits. Within one week, the forecasted cases could reach a high value of 2566 case with lower and upper limits of 2119 case and 2966 case, respectively. Fig. 5(b) and (c) shows the error and the error histogram between the reported confirmed cases and the predicted cases, respectively. The error is calculated for all data subsets. This figure indicates the reasonable accuracy of the developed model to forecast the COVID-19 time series data.
Fig. 5.
(a) Accumulated confirmed reported and forecasted COVID-19 cases using NARANN for the second forecasting process; (b) Error for training, validation, and test subsets; (c) Error histogram for training, validation, and test subsets.
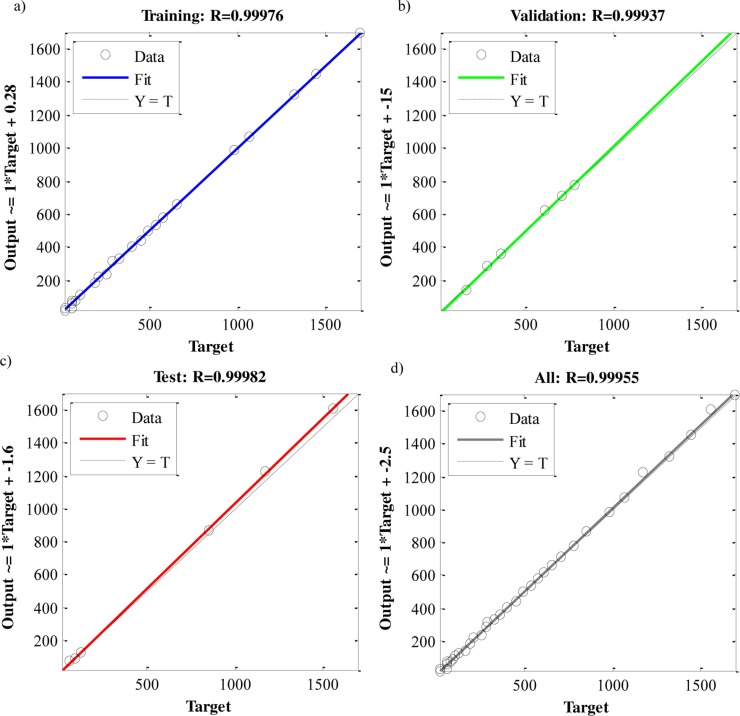
Fig. 6 shows qq-plots for training, validation, and test subsets as well as the whole data. R is higher than 0.999 for all plots and all plotted points are scattered adjacent to the lines which indicate the high accuracy of the model. Different statistical indices have been used to assess the performance and the accuracy of the proposed model and their computed values are listed in Table 1 . The low values of MAE (7.752) and RMSE (10.410) indicate the low error between the reported and predicted data. Approaching R2 (0.999) value to one indicates the accurate fitness and the good correlation between the reported and the predicted data. The values of CRM and RD approaches zero which mean that the proposed model has an ideal fitting and avoids undesirable under- or overestimation.
Fig. 6.
The qq-plot of : (a) training; (b) validation; (c) test; (d) all data sets.
Table 1.
Statistical analysis for the performance of NARANN.
| MAE | RMSE | R2 | CRM | RD |
|---|---|---|---|---|
| 7.752 | 10.410 | 0.999 | 9.8 × 10−4 | 1.6 × 10−25 |
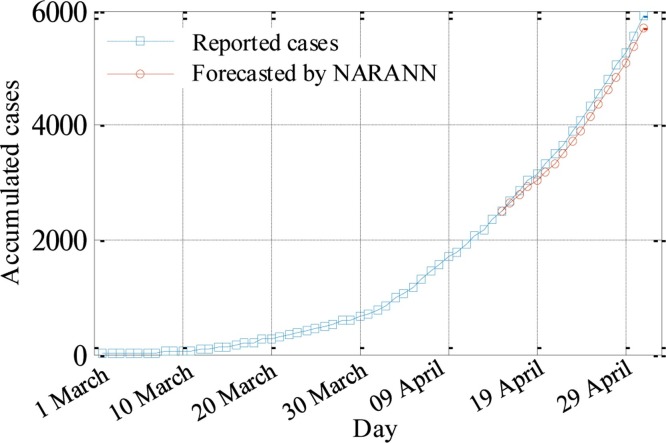
In the third forecasting process, the NARANN succeed to forecast COVID-19 cases for long period (more than two weeks) as shown in Fig. 7 in which a good agreement between the forecasted and reported cases is observed.
Fig. 7.
(a) Accumulated confirmed reported and forecasted COVID-19 cases using NARANN for the third forecasting process.
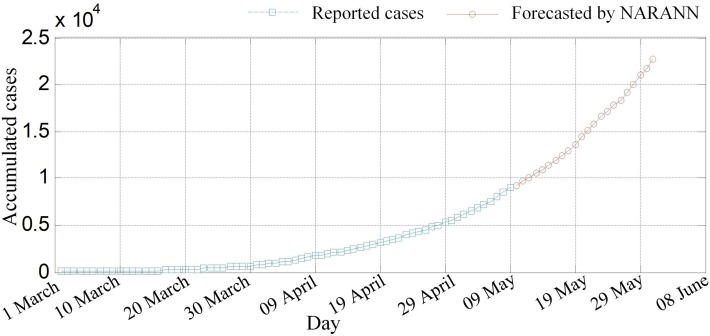
In the fourth forecasting process, the NARANN is employed to forecast the accumulated number of confirmed cases in the upcoming twenty days using the previously reported cases in the period from 1 March- 10 May. According to the obtained results, the number of the cases may be triplicated in the next upcoming twenty days, as it will be increased from 9400 cases (as reported by Egyptian ministry of health on 10 May 2020) to reach 22790 cases (as forecasted by the proposed NARANN model on 31 May 2020). The forecasted results are plotted in Fig. 8 .
Fig. 8.
(a) Accumulated confirmed reported and forecasted COVID-19 cases using NARANN for the fourth forecasting process.
The high accuracy of the proposed model, that confirmed by the aforementioned discussion, to forecast COVID-19 cases in Egypt may help the decision-makers to put short-term future plans to face this epidemic. The following policies may be applied to reduce the spread of this epidemic:
-
•
Modifying the overnight curfew period to reduce the social interaction in order to slow the transmission of Covid-19.
-
•
Applying more restricted lockdown rules and sealing of Covid-19 infected hotspots.
-
•
Suspending or prohibiting of public transportation between Egyptian governorates.
-
•
Constructing more field quarantine hospitals.
-
•
Extending schools, universities, and mosques closure period with no declared end date.
-
•
Operating additional trains and buses to alleviate the overcrowding in an attempt to contain this crisis.
-
•
Supporting irregular workers with exceptional grants.
-
•
Applying severe restrictions on all social gatherings.
5. Conclusion
This study presents a forecasting method to predict the prevalence of COVID-19 outbreak in Egypt. The confirmed cases reported by the Egyptian ministry of health are used as time series data to train the proposed model. An artificial intelligence and statistical based models were proposed; NARANN and ARIMA. NARANN showed a better performance compared with ARIMA based on different statistical criteria. The proposed model can be used to perform multi-step forecasts for further days. The predicted data has a high determination coefficient of more than 0.999 for all data sets (training, validation, and test). COVID-19 cases are estimated to be increased by about 280% during May 2020. The forecasted results of NARANN have a reasonable absolute percentage error for all forecasted cases (less than 5%). In this study, we focused on the forecasting of COVID-19 cases in Egypt; however, the proposed model can be applied to other countries and diseases which will be our future work.
Declaration of Competing Interest
The article has been written by the stated authors who are ALL aware of its content and approve its submission. No conflict of interest exists.
Footnotes
Supplementary material related to this article can be found, in the online version, at doi:https://doi.org/10.1016/j.psep.2020.05.029.
Appendix A. Supplementary data
The following is Supplementary data to this article:
References
- Al-Musaylh M.S., Deo R.C., Adamowski J.F., Li Y. Short-term electricity demand forecasting with MARS, SVR and ARIMA models using aggregated demand data in Queensland, Australia. Adv. Eng. Inform. 2018;35:1–16. [Google Scholar]
- Al-qaness M.A., Ewees A.A., Fan H., Abd El Aziz M. Optimization method for forecasting confirmed cases of covid-19 in China. J. Clin. Med. 2020;9:674. doi: 10.3390/jcm9030674. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Babikir H.A., Elaziz M.A., Elsheikh A.H., Showaib E.A., Elhadary M., Wu D., Liu Y. Noise prediction of axial piston pump based on different valve materials using a modified artificial neural network model. Alexandria Eng. J. 2019;58:1077–1087. [Google Scholar]
- Benvenuto D., Giovanetti M., Vassallo L., Angeletti S., Ciccozzi M. Application of the ARIMA model on the COVID-2019 epidemic dataset. Data Brief. 2020;29 doi: 10.1016/j.dib.2020.105340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen C.-S., Jhong Y.-D., Wu W.-Z., Chen S.-T. Fuzzy time series for real-time flood forecasting. Stoch. Environ. Res. Risk Assess. 2019;33:645–656. [Google Scholar]
- Chen D., Xu W., Lei Z., Huang Z., Liu J., Gao Z., Peng L. Recurrence of positive SARS-CoV-2 RNA in COVID-19: a case report. Int. J. Infect. Dis. 2020;93:297–299. doi: 10.1016/j.ijid.2020.03.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elaziz M.A., Elsheikh A.H., Sharshir S.W. Improved prediction of oscillatory heat transfer coefficient for a thermoacoustic heat exchanger using modified adaptive neuro-fuzzy inference system. Int. J. Refrig. 2019;102:47–54. [Google Scholar]
- Elsheikh A.H., Sharshir S.W., Abd Elaziz M., Kabeel A.E., Guilan W., Haiou Z. Modeling of solar energy systems using artificial neural network: a comprehensive review. Sol. Energy. 2019;180:622–639. [Google Scholar]
- Elsheikh A.H., Sharshir S.W., Ismail A.S., Sathyamurthy R., Abdelhamid T., Edreis E.M.A., Kabeel A.E., Haiou Z. An artificial neural network based approach for prediction the thermal conductivity of nanofluids. SN Appl. Sci. 2020;2:235. [Google Scholar]
- Essa F., Abd Elaziz M., Elsheikh A.H. An enhanced productivity prediction model of active solar still using artificial neural network and Harris Hawks optimizer. Appl. Therm. Eng. 2020;170 [Google Scholar]
- Gautam S.S., Abhishekh A novel moving average forecasting approach using fuzzy time series data set. J. Control. Autom. Electr. Syst. 2019;30:532–544. [Google Scholar]
- Guliyev H. Determining the spatial effects of COVID-19 using the spatial panel data model. Spat. Stat. 2020;100443:1–10. doi: 10.1016/j.spasta.2020.100443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Husnayain A., Fuad A., Su E.C.-Y. Applications of google search trends for risk communication in infectious disease management: a case study of COVID-19 outbreak in Taiwan. Int. J. Infect. Dis. 2020;95:221–223. doi: 10.1016/j.ijid.2020.03.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kang D., Choi H., Kim J.-H., Choi J. Spatial epidemic dynamics of the COVID-19 outbreak in China. Int. J. Infect. Dis. 2020;94:96–102. doi: 10.1016/j.ijid.2020.03.076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lauret P., Heymes F., Forestier S., Aprin L., Pey A., Perrin M. Forecasting powder dispersion in a complex environment using Artificial Neural Networks. Process. Saf. Environ. Prot. 2017;110:71–76. [Google Scholar]
- Li X., Wang L., Yan S., Yang F., Xiang L., Zhu J., Shen B., Gong Z. Clinical characteristics of 25 death cases with COVID-19: a retrospective review of medical records in a single medical center, Wuhan, China. Int. J. Infect. Dis. 2020;94:128–132. doi: 10.1016/j.ijid.2020.03.053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin Q., Zhao S., Gao D., Lou Y., Yang S., Musa S.S., Wang M.H., Cai Y., Wang W., Yang L., He D. A conceptual model for the coronavirus disease 2019 (COVID-19) outbreak in Wuhan, China with individual reaction and governmental action. Int. J. Infect. Dis. 2020;93:211–216. doi: 10.1016/j.ijid.2020.02.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lippi G., Plebani M., Henry B.M. Thrombocytopenia is associated with severe coronavirus disease 2019 (COVID-19) infections: a meta-analysis. Clin. Chim. Acta. 2020;506:145–148. doi: 10.1016/j.cca.2020.03.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nury A.H., Hasan K., Alam M.J.B. Comparative study of wavelet-ARIMA and wavelet-ANN models for temperature time series data in northeastern Bangladesh. J. King Saud Univ. - Sci. 2017;29:47–61. [Google Scholar]
- Oliva D., Elaziz M.A., Elsheikh A.H., Ewees A.A. A review on meta-heuristics methods for estimating parameters of solar cells. J. Power Sources. 2019;435 [Google Scholar]
- Pan X.-B. Application of personal-oriented digital technology in preventing transmission of COVID-19, China. Ir. J. Med. Sci. 2020 doi: 10.1007/s11845-020-02215-5. [Epub ahead of print] [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salzberger B., Glück T., Ehrenstein B. Successful containment of COVID-19: the WHO-Report on the COVID-19 outbreak in China. Infection. 2020;48:151–153. doi: 10.1007/s15010-020-01409-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shehabeldeen T.A., Elaziz M.A., Elsheikh A.H., Zhou J. Modeling of friction stir welding process using adaptive neuro-fuzzy inference system integrated with harris hawks optimizer. J. Mater. Res. Technol. 2019;8:5882–5892. [Google Scholar]
- Shehabeldeen T.A., Elaziz M.A., Elsheikh A.H., Hassan O.F., Yin Y., Ji X., Shen X., Zhou J. vol. 8. IEEE Access; 2020. pp. 79896–79907. (A Novel Method for Predicting Tensile Strength of Friction Stir Welded AA6061 Aluminium Alloy Joints Based on Hybrid Random Vector Functional Link and Henry Gas Solubility Optimization). [Google Scholar]
- Tealab A., Hefny H., Badr A. Forecasting of nonlinear time series using ANN. Future Comput. Inform. J. 2017;2:39–47. [Google Scholar]
- Thomas-Rüddel D., Winning J., Dickmann P., Ouart D., Kortgen A., Janssens U., Bauer M. Coronavirus disease 2019 (COVID-19): update for anesthesiologists and intensivists March 2020. Anaesthesist. 2020 doi: 10.1007/s00101-020-00758-x. [Epub ahead of print] [DOI] [PubMed] [Google Scholar]
- Tian S., Hu N., Lou J., Chen K., Kang X., Xiang Z., Chen H., Wang D., Liu N., Liu D., Chen G., Zhang Y., Li D., Li J., Lian H., Niu S., Zhang L., Zhang J. Characteristics of COVID-19 infection in Beijing. J. Infect. 2020;80:401–406. doi: 10.1016/j.jinf.2020.02.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tosepu R., Gunawan J., Effendy D.S., Ahmad L.O.A.I., Lestari H., Bahar H., Asfian P. Correlation between weather and Covid-19 pandemic in Jakarta, Indonesia. Sci. Total Environ. 2020;725:1–4. doi: 10.1016/j.scitotenv.2020.138436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu Y., Gao R., Yang J. Prediction of coal and gas outburst: a method based on the BP neural network optimized by GASA. Process. Saf. Environ. Prot. 2020;133:64–72. [Google Scholar]
- Xu Q., Yang S., Cai J., Zhou B., Xin Y. Risk forecasting for spontaneous combustion of coals at different ranks due to free radicals and functional groups reaction. Process. Saf. Environ. Prot. 2018;118:195–202. [Google Scholar]
- Zaranezhad A., Asilian Mahabadi H., Dehghani M.R. Development of prediction models for repair and maintenance-related accidents at oil refineries using artificial neural network, fuzzy system, genetic algorithm, and ant colony optimization algorithm. Process. Saf. Environ. Prot. 2019;131:331–348. [Google Scholar]
- Zhang J.-f., Yan K., Ye H.-h., Lin J., Zheng J.-j., Cai T. SARS-CoV-2 turned positive in a discharged patient with COVID-19 arouses concern regarding the present standard for discharge. Int. J. Infect. Dis. 2020 doi: 10.1016/j.ijid.2020.03.007. In Press, Journal Pre-proof. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng C., Wang J., Guo H., Lu Z., Ma Y., Zhu Y., Xia D., Wang Y., He H., Zhou J., Wang Y., Fei M., Yin Y., Zheng M., Xu Y. Risk-adapted treatment strategy for COVID-19 patients. Int. J. Infect. Dis. 2020 doi: 10.1016/j.ijid.2020.03.047. In Press, Journal Pre-proof. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.