Abstract
Rapid developments in live-cell 3D microscopy enable imaging of cell morphology and signaling with unprecedented detail. However, tools to systematically measure and visualize the intricate relationships between intracellular signaling, cytoskeletal organization, and downstream cell morphological outputs do not exist. Here we introduce u-shape3D, a computer graphics and machine-learning pipeline to probe molecular mechanisms underlying 3D cell morphogenesis and to test the intriguing possibility that morphogenesis itself affects intracellular signaling. We demonstrate a generic morphological motif detector that automatically finds lamellipodia, filopodia, blebs, and other motifs. Combining motif detection with molecular localization, we measure the differential association of PIP2 and KrasV12 with blebs. Both signals associate with bleb edges, as expected for membrane-localized proteins, but only PIP2 is enhanced on blebs. This indicates that sub-cellular signaling processes are differentially modulated by local morphological motifs. Overall, our computational workflow enables the objective, 3D analysis of the coupling of cell shape and signaling.
Introduction
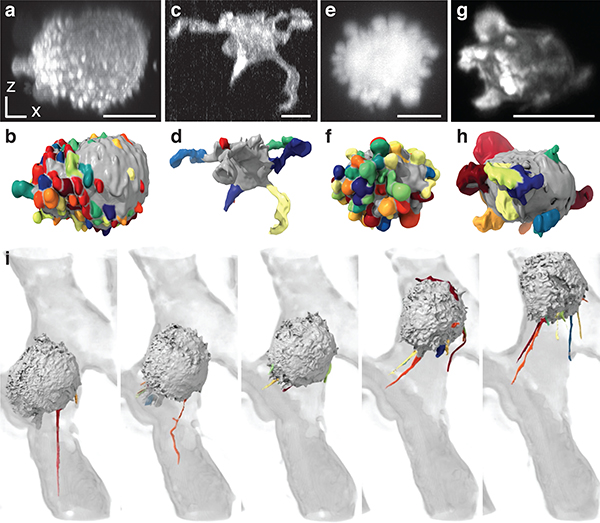
Cell morphogenesis is driven by cytoskeleton-generated forces that are regulated by biochemical signals.1 The cascade from signaling to cytoskeleton to shape control is well established for numerous morphological motifs, including lamellipodia, blebs, and filopodia (Fig. 1a–c, Video 1, and Supplementary Fig. 1), which depend on well-characterized assemblies of actin filaments (Fig. 1d–f).2 How morphology, in turn, may govern signaling is less investigated. Morphology may participate in signal transduction via mechanisms such as preferential protein interaction with membranes of particular curvature,3 or modulation of the concentration and diffusion of signaling components.4,5
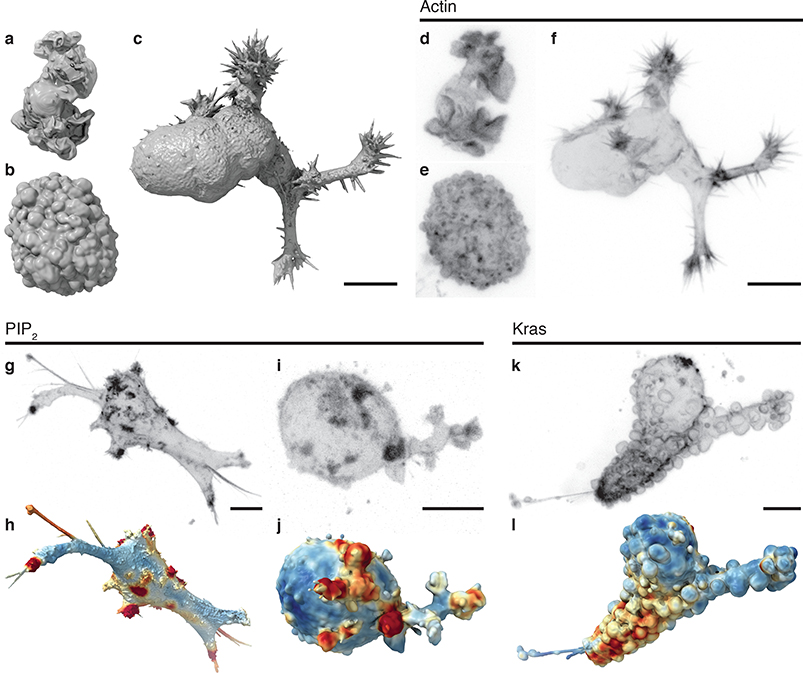
Figure 1. Cell morphology and signaling are coupled.
Surface renderings of (a) a dendritic cell expressing Lifeact-GFP, (b) an MV3 melanoma cell expressing tractin-GFP, and (c) a human bronchial epithelial cell (HBEC) expressing tractin-GFP. (d-f) Maximum intensity projections (MIPs) of the cells shown in a-c, using an inverse look up table. Panels a-f are shown at the same scale. Additional views of these cells are shown in Supplementary Fig. 1. (g) A MIP of a branched MV3 cells expressing PLCΔ-PH-GFP, a PIP2 translocation biosensor. (h) A surface rendering of the same cell. Surface regions with relatively high PIP2 localization are shown in red, whereas regions of relatively low localization are shown in blue. (i) A MIP and (j) a surface rendering of a blebbing MV3 cell expressing PLCΔ-PH-GFP. The PLCΔ-PH-GFP images are representative of 23 cells from 3 experiments. (k) A MIP of an MV3 cell expressing GFP-KrasV12. (l) A surface rendering of k. Surface regions of relatively high Kras localization are shown in red, whereas regions of relatively low localization are shown in blue. The GFP-KrasV12 images are representative of 31 cells from 7 experiments. Scale bars, 10 μm.
The integrated study of signaling and morphology at subcellular length scales has become possible with the recent advent of high-resolution 3D light-sheet microscopy.6–11 Using microenvironmental selective plane illumination microscopy (meSPIM)10 of PIP2, a membrane-bound phosphoinositide implicated in diverse signaling pathways12, we found an unexpected formation of PIP2 clusters in both branched (Fig. 1g,h) and blebbed cells (Fig. 1i,j). Three-dimensional renderings of the local concentration of PIP2 suggest that these clusters tend to colocalize with filopodial tufts (Fig. 1h) and blebs (Fig. 1j). KrasV12, which is a constitutively active GTPase with broad oncogenic functionality,13 also appears to colocalize with certain morphological structures (Fig. 1k,l and Videos 2,3). These observations pose the question of whether rugged surface geometries generally associate with elevated signaling, and whether there are differences in how PIP2 and Kras associate with cell morphologies.
Answering such questions with statistical robustness requires the interpretation of 3D images. Not only is the inspection and quantification of such images exceedingly laborious, the difficulty of representing 3D images in meaningful 2D perspectives renders the manual annotation of subcellular geometries extremely difficult. Automation by computer vision is essential. However the tools for subcellular 3D morphometry do not exist.14 Here, we introduce u-shape3D, a pipeline that combines computer graphics and machine learning approaches to unravel the coupling between cell surface morphology and subcellular signaling. At its core is the segmentation of any morphological motif a user can provide systematic examples for. We show the robustness of a once-learned motif classifier to changes in microscopy and cell type. We then apply the method to analyze the differential association of PIP2 and KrasV12 with surface blebs. Moving forward, u-shape3D will be instrumental to furthering our understanding of the feedback interactions between signaling, the cytoskeleton, and morphological dynamics in 3D.
Results
Detecting cellular morphological motifs
In designing u-shape3D, we decided to first represent the cell surface as a triangle mesh, and then segment the surface into motifs using machine learning (Fig. 2a–e). An alternative approach would be to segment the motifs directly from the raw image data on a voxel-by-voxel basis, and then generate a surface representation with classified motifs. This would simplify the application of deep learning algorithms, but would require the acquisition of training data in the raw image volume, where manual outlining of interesting motifs can become exceedingly cumbersome. In contrast, the proposed machine-learning pipeline depends on training data that is defined on a surface representation with pre-segmented patches, where a few easy-to-identify examples of the motif of interest are sufficient to constrain a robust classifier. This provides a versatile and efficient approach to quantifying diverse cellular morphologies.
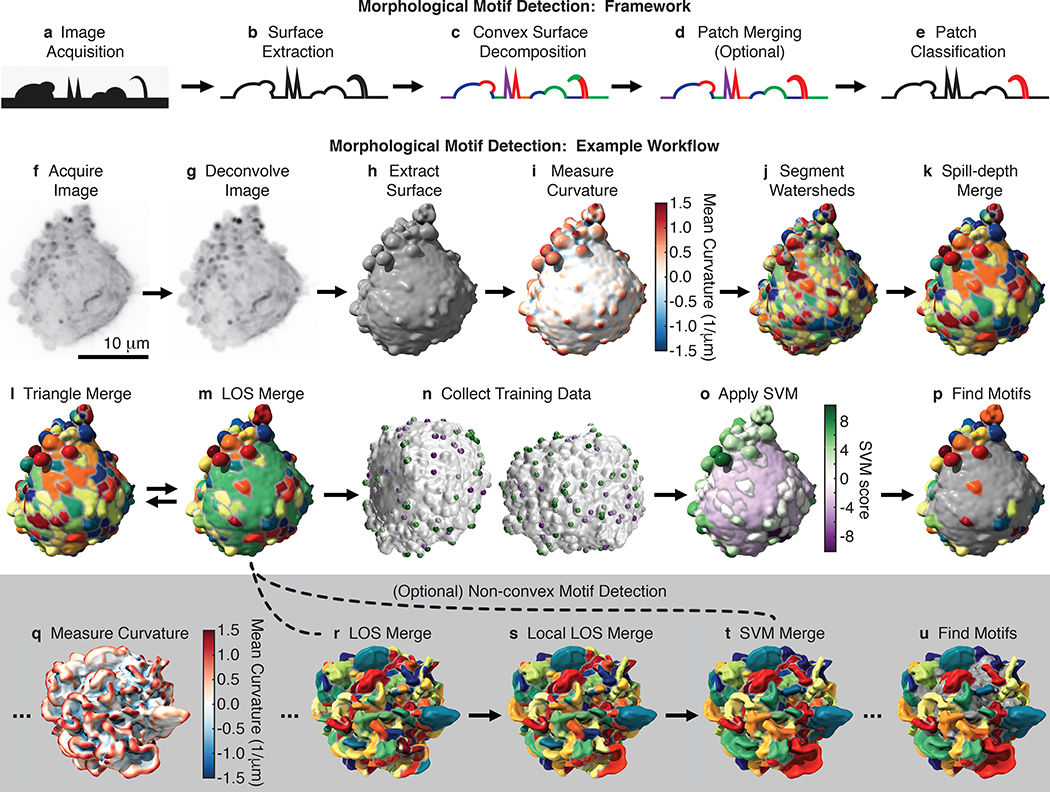
Figure 2. Morphological motif detection framework and example workflow.
To detect morphological motifs, (a) following image acquisition, (b) we extract the cell surface, (c) decompose that surface into convex patches, (d) optionally merge those patches, (e) and then finally classify the patches by morphological motif. Panels f-p show our detection framework applied to a blebbed cell. (f) MIP of a 3D image of an MV3 melanoma cell expressing tractin-GFP. (g) MIP of the deconvolved image of the same cell. (h) The surface of the cell extracted from the deconvolved image as a triangle mesh. (i) The mean surface curvature of the cell. Regions of large positive curvature are shown red, flat regions are shown white, and regions of large negative curvature are shown blue. (j) A watershed segmentation of mean surface curvature. Segmented patches are shown in different colors. (k) A spill-depth based merging of the segmented patches. (l) A triangle-rule based merging of the patches. (m) A line-of-sight (LOS) based merging of the patches. The triangle and LOS rules are applied iteratively. (n) User generated training data for two different cells. Patches identified as “certainly a bleb” are shown green, whereas patches identified as “certainly not a bleb” are shown purple. (o) A support vector machine (SVM) classifier trained on user data applied to the cell. Patches shown in green have high SVM scores and a high inferred likelihood of being a bleb, whereas patches shown in purple have low SVM scores and a low inferred likelihood. (p) Detected blebs are shown randomly colored and non-blebs are shown gray. To detect non-convex motifs, such as lamellipodia, convex patches are merged as shown in q-u. (q) The mean surface curvature of a lamellipodial dendritic cell expressing Lifeact-GFP. (r) Convex surface patches for the same cell. (s) A local-LOS based merging of these patches. (t) An SVM based merging of the patches. The SVM was trained on user-supplied examples of adjacent patches that should certainly be merged and adjacent patches that should certainly not be merged. (u) Detected lamellipodia are shown randomly colored and non-lamellipodia are shown gray.
To generate the cell surface, for most cells we automatically extract the mesh as an isosurface of the deconvolved image (Fig. 2f–h and Supplementary Fig. 2). However some datasets require that surface extraction parameters be tailored to the cell type and fluorescence label (see User’s Guide to the software package). For example, we extract the surfaces of actin-labeled dendritic cells as an isosurface of an image that combines the deconvolved image, an image with enhanced planar features, and an image with an enhanced cell interior (Supplementary Fig. 3).
After cell surface extraction, we decompose the surface into convex patches. People tend to partition 3D surfaces into convex regions,15 suggesting that canonical protrusions are likely convex or composed of multiple convex regions. Convex decomposition is in general an NP-complete problem,16 and thus is computationally intractable for large meshes, even with extensive computing resources. We therefore combine several techniques to segment the surface into approximately convex patches. First, we calculate the mean curvature17 at every face on the mesh, and then break the surface into small patches via a watershed-based segmentation of mean curvature (Fig. 2i–k).18 These small patches are computationally manipulated more easily than individual faces and are analogous to superpixels in image segmentation.
Next, we iteratively merge patches using two criteria (Fig. 2l,m and Supplementary Fig. 4). The line-of-sight (LOS)19 criterion merges patches if the percentage of rays that connect the two patches without exiting the cell is above a certain threshold. Hence, fulfilling this criterion requires only approximate convexity between the patches. The triangle criterion10 merges adjacent patches whose joint closure surface area, defined as the additional surface area needed to close the mesh composing the patch, is small compared to the sum of their individual closure surface areas. This criterion embodies the short-cut rule20 that the preferred convex shape decomposition has the shortest cuts between segments.
Approximate convex patches are then classified by morphological motif type using a Support Vector Machine (SVM). For each patch, 23 geometric features are calculated (Supplementary Table 1). Features are automatically selected for each set of training data by successively removing randomly chosen features until prediction quality is hampered. Following SVM training (Fig. 2n), the trained motif model is used to classify each patch by motif type (Fig. 2o,p).
The outcomes of machine learning approaches are critically dependent on training data quality. To generate training data, we built an interface where users can rotate 3D surfaces, zoom in and out, and click on patches to identify them as motifs. Presented with the same four randomly chosen cells, three users chose 46±6% of the patches when asked to click on blebs and 25±4% of the patches when asked to click not on blebs. This discrepancy carried over into SVM models, where for the two training sets 45±7% and 77±6% of the patches were identified as blebs. Asking users to click only on patches that are certainly blebs and then only on patches that are certainly not blebs resulted in models that classified an intermediate percentage of patches, 52±6%, as blebs. To avoid bias, we therefore train models with data where users only choose patches they can confidently classify.
Although many morphological motifs, including blebs and filopodia, are described by a single convex surface patch, some motifs, such as lamellipodia, are composites of multiple convex patches. To detect these motifs, we merge convex patches prior to patch classification using a machine-learning framework (Fig. 2q–s). Thirty-six geometric features are calculated for each pair of patches (Supplementary Table 2), and training data is generated by asking users to click on adjacent patches that should certainly or certainly not be merged. Following sequential feature selection, an SVM is used to merge patches (Fig. 2t,u).
We trained models to detect blebs, filopodia, and lamellipodia (Fig. 3, Video 4, and Supplementary Fig. 5). Most cells in our diverse data set showed predominately one protrusion type. However, as a proof-of-concept, we also built a multiclass detector using a collection of melanoma cells that exhibited extensive blebs and small numbers of filopodia (Fig. 4a). To do so, we generated multiple SVM models in a one-vs-one framework in which separate models were used to distinguish each pair of morphological motifs.
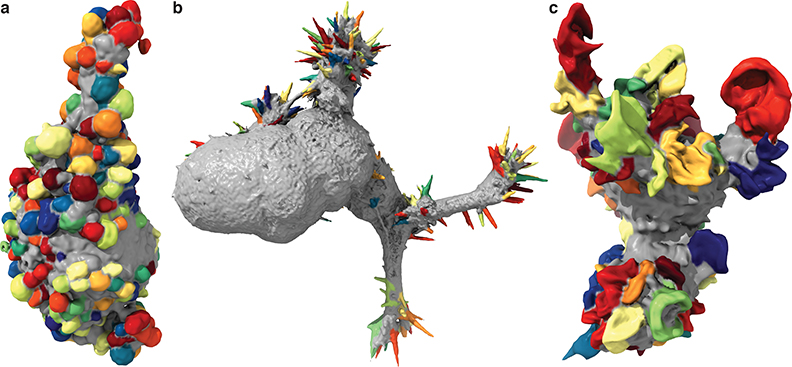
Figure 3. Detected blebs, filopodia, and lamellipodia.
(a) Blebs detected on an MV3 melanoma cell (representative of 19 cells), (b) filopodia detected on an HBEC cell (representative of 13 cells), and (c) lamellipodia detected on a dendritic cell (representative of 13 cells). Additional example detections are shown in Supplementary Fig. 5.
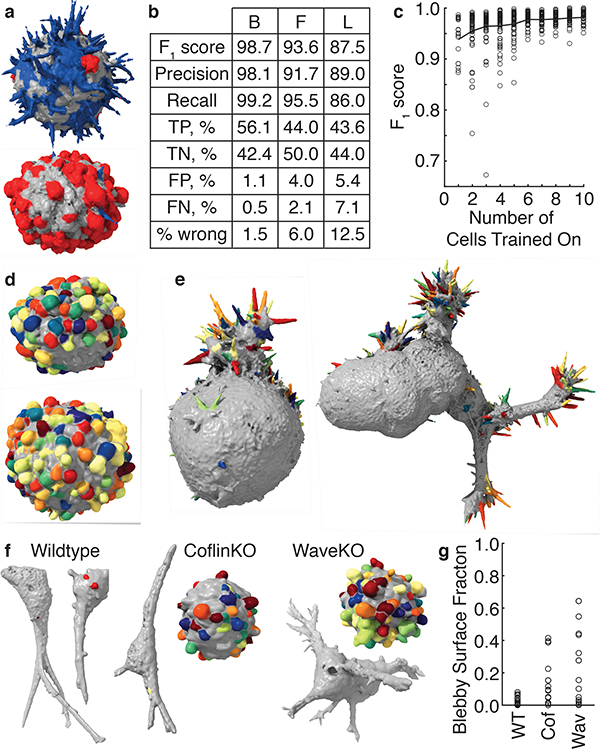
Figure 4. Validation and robustness of morphological motif detection.
(a) A multiclass detector applied to cells derived from a human melanoma xenograft cultured in mice (representative of 9 cells). Filopodia are shown blue, blebs are shown red, and areas with neither filopodia nor blebs are shown gray. (b) Validation measures for a bleb detector (left) trained on 19 MV3 melanoma cells, a filopodia detector (center) trained on 13 HBEC cells, and a lamellipodia detector (right) trained on 13 dendritic cells. TP, TN, FP, and FN are abbreviations for true positive, true negative, false positive, and false negative respectively. (c) The F1 score as a function of the number of cells trained on. The red line indicates the mean F1 score averaged over a maximum of 100 sets of cells, whereas the gray dots show individual sets of cells. (d) A bleb detector trained on the MV3 melanoma cell line applied to cells derived from a human melanoma xenograft cultured in mice (representative of 24 cells). (e) A filopodia detector trained on xenograft-derived melanoma cells applied to HBEC cells (representative of 13 cells). A filopodia detector trained on HBECs applied to the cell on the left is shown in Supplementary Fig. 5 and applied to the cell on the right is shown in Fig. 3. (f) Blebs detected on wildtype, cofilin-1 knock out, and Wave2 knockout U2OS cells in 3D collagen. (g) For these three cell types, the percentage of the surface that is blebby. We analyzed 19 wildtype, 15 cofilin-1 knockout, and 14 Wave2 knockout cells.
Validation and robustness of motif detection
To validate the protrusion classification, we calculated the F1 score using patches selected by the trainer as certainly or certainly not a protrusion. For four randomly chosen blebby melanoma cells, the F1 score calculated via leave-one-out-cross-validation over cells and averaged across three trainers was 0.986±0.006, corresponding to 1.3±0.6% incorrectly classified patches. This score is high, in part, because only patches users were certain about were included. Calculating F1 scores for the models where users clicked on all the blebs or all the non-blebs yielded 0.77±0.03 and 0.76±0.04 respectively. However, as discussed above, these training data are biased toward selecting too few and too many blebs, respectively. Indeed, using these training data to validate our model, we find a 16±1% false positive rate (5±1% false negative rate) when users are asked to click on all the blebs and a 30±6% false negative rate (2±1% false positive rate) when users are asked to click on all the non-blebs. Validating over a larger number of cells with a single user, we measured an F1 score of 0.99 for 19 MV3 cells with blebs, 0.94 for 13 HBECs with filopodia, and 0.88 for 13 dendritic cells with lamellipodia (Fig. 4b and Supplementary Fig. 6a,b).
We also tested other machine learning algorithms. We anticipated that the classifier performance would be primarily feature driven, rather than algorithm driven. Indeed, using random forests, linear SVMs, and radial SVMs to detect filopodia and varying the number of rounds of feature selection, we calculated F1 scores of between 0.934 and 0.944 for almost all algorithms (Supplementary Table 4). This suggests that in our workflow linear SVMs perform as well as a broad class of machine learning algorithms.
Conversely, a carefully chosen feature set might be able to distinguish motifs from non-motifs using even an unsupervised algorithm that does not require training. We hierarchically clustered all convex surface patches on a set of seven blebby cells into two clusters using such an algorithm (Supplementary Fig. 7). Although one of the clusters substantially overlaps with the bleb detection, the supervised algorithm clearly performs better.
Because of the selective power of the geometric feature set, our workflow requires relatively little training data. One user training on just one cell in a dataset of 19 blebby cells, yields an F1 score of 0.94±0.04 (mean ± standard deviation) on the remaining cells (Fig. 4c and Supplementary Fig. 6c). Additional training data improves the model accuracy marginally, suggesting that models generated by a single user on different data sets would be similar. Indeed, models trained by a single user on distinct sets of four MV3 cells show 95.9±0.7% overlap, as measured by the Sorrenson-Dice index.21 This compares to an 88±3% overlap between models generated by different users (Supplementary Fig. 6d). To maximize reproducibility, our classifiers therefore incorporate training data from multiple users via majority voting.
Motif models from one cell type can be extended to dissimilar cell types, enabling objective comparisons across biological systems. Applying a bleb model generated from 19 cells originating from a melanoma cell line to 24 cells originating from a human melanoma xenografted into mice yields an F1 score of 0.97 (Fig. 4d). Likewise, applying a filopodia model generated from 9 melanoma cells to 13 transformed HBEC cells yields an F1 score of 0.90 (Fig. 4e).
The classifier can also be used to compare perturbed and non-perturbed cell populations. To test whether greatly different cell morphologies confound the detection of particular motifs, we used identical analysis parameters to measure the fraction of the cell surface that is blebby in wildtype U2OS cells and cells where the actin regulatory proteins cofilin-1 and Wave2 were knocked out with CRISPR (Fig. 4f,g). Compared to wildtype cells, CFL1 knockout (cofilinKO) cells exhibit greater cell-to-cell heterogeneity in their bleb surface fraction as well as a larger mean bleb fraction. WASF2 knockout (WaveKO) cells exhibit even greater heterogeneity and a yet larger mean fraction.
So far, we have presented data acquired via meSPIM, a high-resolution light-sheet microscope with nearly isotropic resolution.10 On microscopes with anisotropic resolution, the motif structure varies with orientation relative to the microscope. To test if resolution anisotropy impedes motif detection, we analyzed blebby cells imaged via a laser scanning confocal microscope (Fig. 5a,b). Blebs appeared stretched in the axial (z) direction (Supplementary Fig. 8), however the workflow still achieved an F1 score of 0.94 (Supplementary Fig. 9). Standard light-sheet microscopy also has reduced axial resolution compared to meSPIM. Analyzing microglial cells imaged in vivo within a zebrafish via a lower resolution commercial light-sheet microscope, we successfully detected extensions (Fig. 5c,d). These findings demonstrate that our pipeline can analyze data from conventional microscopes with anisotropic resolution.
Figure 5. Motif detection on images acquired via diverse microscopic techniques.
(a) A MIP, taken over the xz direction, of an MV3 cell expressing tractin-GFP imaged via laser scanning confocal microscopy (representative of 8 cells). (b) Blebs detected on the same cell using a model derived from 8 MV3 cells imaged with this microscope. (c) An xz-MIP of a microglia inside a zebrafish embryo imaged using a commercial light-sheet microscope (representative of 8 cells). (d) Extensions detected on the same cell using a model derived from 8 microglia imaged with this microscope. (e) An xz-MIP of an MV3 cell expressing cytosolic GFP imaged using ASLM, a high-resolution light-sheet microscopy modality (representative of 8 cells). (f) Blebs detected on the same cell using a model derived from 19 MV3 cells imaged via meSPIM. (g) An xz-MIP of a T cell expressing Lifeact-mEmerald imaged using lattice light-sheet microscopy.8 (h) Lamellipodia detected on the same cell using a model derived from 13 dendritic cells imaged via meSPIM. (i) Extensions detected on an MDA-MB-231 human breast cancer cell moving through the vasculature of a zebrafish embryo imaged via adaptive-optics lattice light-sheet microscopy.22 The cell is shown as a surface rendering, whereas the vasculature is shown in gray as a MIP of the deconvolved image. Scale bars, 10 μm.
To determine whether motif models were transferable among similar microscopes, we directly applied meSPIM motif models to cells imaged by other high-resolution light-sheet microscopes. Detecting blebs on cytosolically labeled cells imaged by axially swept light sheet microscopy (ASLM),9 we measured an F1 score of 0.96 for both meSPIM and ASLM derived models (Fig. 5e,f). Analyzing previously published movies, we used a meSPIM derived model to detect lamellipodia on a T cell imaged by lattice light-sheet microscopy8 (Fig. 5g,h), and trained a new model to detect extensions on a human breast cancer cell moving through the vasculature of a zebrafish embryo imaged by adaptive-optics lattice light-sheet microscopy22 (Fig. 5i and Video 5). Together, these test cases show the broad applicability of u-shape3D, allowing objective comparisons between large numbers of diverse datasets.
Kras and PIP2 signals associate differently with blebs
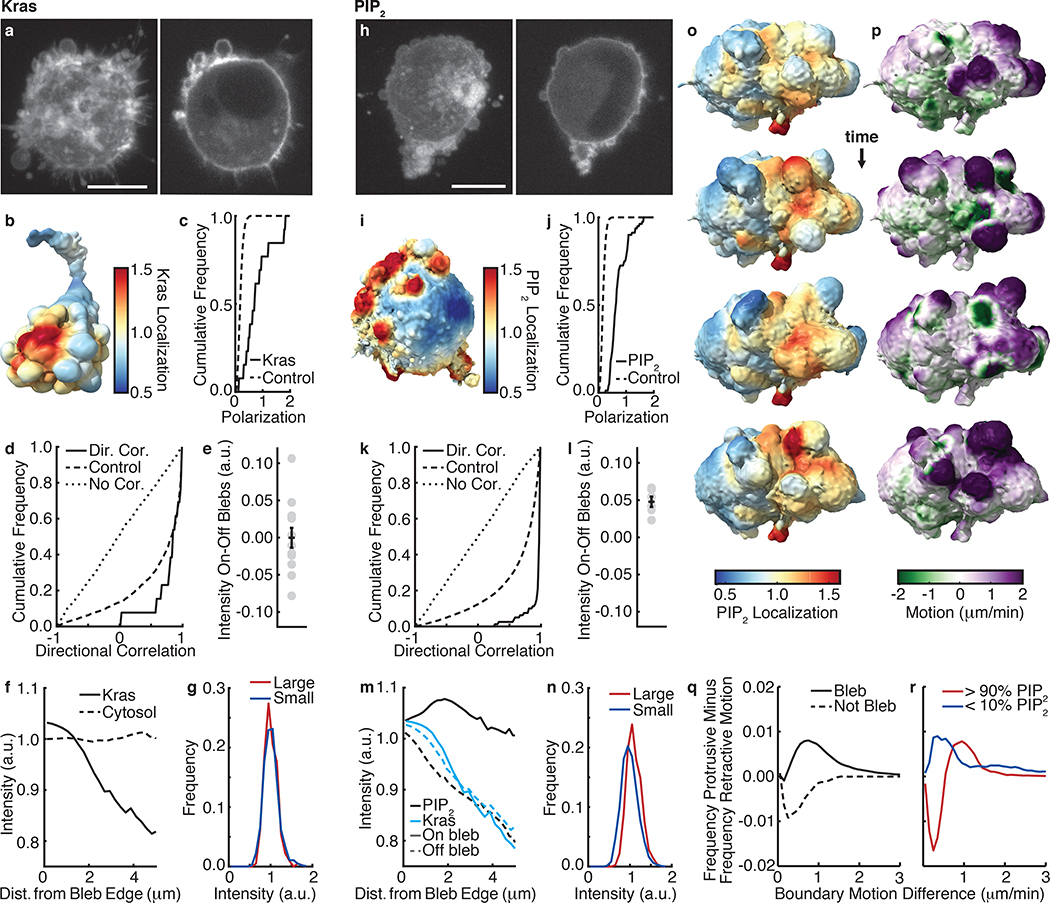
Equipped with a computational framework to analyze 3D cell morphology, we set out to identify relationships between morphological motifs and signaling events. We focused on blebs as the predominant morphological feature of melanoma cells in soft 3D environments10 and sought to measure how PIP2 and constitutively active KrasV12, may associate with this motif. Both KrasV12 (Fig. 1l) and PIP2 (Fig 1j) appear to polarize and associate with blebs. To test these hypotheses, we measured the localization of KrasV12 within 2 μm of the cell surface for 13 MV3 melanoma cells (Fig. 6a,b). We computed at every mesh face the average fluorescence intensity in a sphere around that face, including only pixels within the cell and correcting for surface curvature-dependent artifacts by depth-normalization.23 In addition to blebs, cells expressing GFP-KrasV12 exhibited retraction fibers and uropods, which could lead to bias. To exclude these structures from the analysis, we built a retraction fiber/uropod detector and subtracted those patches from the set of detected blebs (Supplementary Fig. 10). Next, using spherical statistics we found that the KrasV12 distribution on the cell surface was polarized (Fig. 6c). Likewise, blebs and KrasV12 surface intensity were directionally correlated (Fig 6d). However, randomizing the location of blebs on the surface, the directional correlation of KrasV12 with blebs was not significantly different than random. This suggests that KrasV12 and bleb polarization are correlated partially through their joint coupling to global cell shape. Measuring the mean KrasV12 localization on and off detected blebs, we found no statistically significant difference (Fig. 6e). However, KrasV12 does localize to bleb edges (Fig. 6f). In contrast, cytosolic GFP showed no localization to bleb edges (Fig. 6f). This confirms that the modulation of KrasV12 across the cell surface is related to the distribution of blebs. To further examine the mechanism of this association we measured bleb density locally over a scale less than that of a single bleb by simulating the diffusion on the mesh of the motif classification label (Supplementary Fig. 11a,b). In this representation, high density values localize to the bleb center, low values to areas away from any bleb, and intermediate values colocalize with bleb edges. In agreement with our previous conclusion, high KrasV12 signal associated with intermediate local bleb densities (Supplementary Fig. 11c). Thus, these analyses suggest that KrasV12 may be organized to bleb edges. This may at first seem surprising: KrasV12 is a constitutively activated GTPase without spatially organized interactions with GEFs, GAPs and GDIs. Accordingly, the KrasV12 distribution is expected to be dominated by diffusion within the plasma membrane with an overall uniform steady state. Simulations of uniformly labeled surface distributions in synthetic cells demonstrate an intensity co-modulation with bleb edges for a variety of surface thicknesses, but not for cytosolically labeled cells (Supplementary Fig. 11e). This shows that the KrasV12 localization at bleb edges is consistent with a uniform surface distribution. This discovery also shows how, in 3D, cell morphological motifs alone offer a mechanism for the spatial organization of molecular signals at the subcellular scale.
Figure 6. Kras and PIP2 associate with blebs differently.
(a) An MV3 cell expressing GFP-KrasV12 shown as a MIP (left) and an xy-slice (right) (representative of 31 cells). (b) Kras localization, measured over 2 μm, near the surface of an MV3 cell expressing GFP-KrasV12. (c) For 13 cells, the cumulative polarization distribution of Kras intensity (solid line) compared to random (dashed line). (d) The directional correlation of blebs with Kras localization. The cumulative correlation distribution is shown solid, the control distribution is shown dashed, and the zero correlation distribution is shown dotted. The correlation and control populations are not statistically different (p-value: 0.3, ks-statistic: 0.3). (e) The differences between the mean Kras intensity on and off blebs (p-value: 0.5, effect size: −0.006, t-statistic: −0.017). The error bar indicates the standard error of the mean. (f) Fluorescence localization vs. distance from a bleb edge for 13 GFP-KrasV12 labeled cells and 35 GFP cytosolically labeled cells. (g) Distributions of Kras intensity for mesh faces on blebs of greater than average volume and on blebs of less than average volume (p-value: 0.6, effect size: 0.05, ks-statistic: 0.05, num. blebs: 1425). (h) An MV3 cell expressing PLCΔ-PH-GFP shown as a MIP (left) and an xy-slice (right) (representative of 23 cells). (i) PIP2 localization, measured over 2 μm, near the surface of an MV3 cells expressing PLCΔ-PH-GFP. (j) For 6 movies of distinct cells, the cumulative polarization distribution of PIP2 intensity (solid line) compared to random (dashed line). (k) The directional correlation of blebs with PIP2 localization. The correlation and control populations are statistically different (p-value: 42*10^−29, ks-statistic: 0.6). (l) The differences between the mean PIP2 intensity on and off blebs for 6 movies of cells (p-value: 0.0005, effect size: 1.7, t-statistic: 6.9). The error bar indicates the standard error of the mean. (m) PIP2 and Kras localization, both on and off blebs, vs. distance from a bleb edge. (n) Distributions of PIP2 intensity for mesh faces on blebs of greater than average volume and on blebs of less than average volume (p-value: 2*10^−77, effect size: 0.5, ks-statistic: 0.24, num. blebs: 10625). (o) Surface renderings of PIP2 localization, measured over 2 μm, near the surface of an MV3 cell expressing PLCΔ-PH-GFP. Cells were imaged every 37 sec. (p) Surface renderings of the boundary motion of this same cell. Purple indicates regions of high protrusive motion, whereas green indicates regions of high retractive motion. (q) For 6 cells, the frequency of protrusive motion minus the frequency of retractive motion on and off blebs as a function of surface speed. (r) The same measure shown in f for mesh faces in the top and bottom deciles of PIP2 localization. Scale bars, 10 μm.
We next analyzed MV3 cells expressing PLCΔ-PH-GFP (Fig 6h,i), a PIP2 translocation biosensor that reports the activation of PIP2. Like KrasV12, the surface localization of PIP2 is polarized (Fig 6j), and blebs and PIP2 are directionally correlated (Fig. 6k). However unlike KrasV12, the directional correlation of PIP2 with blebs was significantly different than that of PIP2 with randomized bleb distributions. Hence, PIP2 polarization is directly correlated with bleb polarization rather than coupled via the overall cell shape. Indeed, PIP2 localizes to blebs, with each cell exhibiting a higher mean PIP2-intensity on blebs than off (Fig. 6l). Consistent with a surface fluorescence distribution, PIP2 like KrasV12 also associates with bleb edges (Fig. 6m). However, whereas KrasV12 localization falls off with increasing distance from a bleb edge both on and off blebs, PIP2 localization falls off with increasing distance from a bleb edge only in regions that are not identified as blebs. Similarly, high PIP2 activity associates with intermediate local bleb densities (Supplementary Fig. 11d), whereas low PIP2 activity associates with small but not with high local bleb densities. This shows a specific recruitment of active PIP2 to the entire bleb surface. The mechanism underlying this process remains elusive.
Our workflow supports many other types of analyses relating cell morphology and molecular distributions. For example, underlying the extraction of morphological motifs are geometric properties that can be analyzed. Measuring bleb volume, we found that small and large blebs show similar association with KrasV12 (Fig. 6g), whereas large blebs show greater association with PIP2 than small blebs (Fig. 6n). Cytosolically labeled cells show no association of intensity with bleb volume (Supplementary Fig. 11f).
Since the study of many signaling pathways benefits from measuring not just morphology, but also morphodynamics, we developed a measure of boundary motion at each mesh face. Fig. 6o shows the PIP2 activation of an MV3 cell, and Fig. 6p shows that cell’s boundary motion. Measuring the motion difference over ~30 sec, which is on the order of the bleb lifetime,24 we found that blebs preferentially associate with regions of protrusive motion (Fig. 6q). We also observed that regions of high PIP2 tend to be more retractive than regions of low PIP2 (Fig. 6r), which is consistent with increased PIP2 localization on blebs because blebs form and retract cyclically. These and other evidence of relations between local surface geometry and PIP2 activation will be essential to uncovering the mechanism of a bleb-formation and bleb-size dependent organization of PIP2 signals.
Discussion
High-resolution 3D light-sheet microscopy,6–11 has enabled the direct observation of subcellular molecular processes. However, incorporating these observations into a framework for unbiased data exploration, hypothesis testing, and ultimately the development of new biological theories remains a challenge.
The majority of publications describing innovations in 3D microscopy end with the appealing rendering of a few images on a 2D screen. Even this mere visualization task imposes a particular perspective and thus introduces bias.14 Moreover, compared to 1D and 2D features, such as length and area, human observers exhibit decreased ability to assess 3D features, such as shape and volume.25 Thus, to turn innovation in 3D imaging into biological insight, computing infrastructures are required that minimize the need for human visual interpretation when comparing datasets.
Here, we focused on algorithms that enable the analysis of biological surfaces at the scale of single cells. We developed an algorithm to detect diverse morphological motifs on the cell surface using machine learning. As a demonstration, we trained classifiers for blebs, filopodia, lamellipodia, among other motifs. To detect a new type of morphological motif, users need only click on examples of surface regions that are and are not that motif. This detector is one of the first image analysis tools for cell biology that incorporates techniques from computer graphics. With the rapid rise of 3D microscopy, computer graphics methods will become an important factor in biological discovery.
In addition to a morphological motif detector, we developed an integrated suite of tools for investigating the coupling between morphology, morphology change, and intracellular signaling. Since signaling networks are usually highly nonlinear, the spatial distribution of signaling molecules can greatly affect downstream signaling. Cells take advantage of this effect to control signaling via spatial localization in myriad ways including compartmentalization, phase separation, and active transport. Cell morphology may also govern signaling. For example, we found that on blebby melanoma cells both KrasV12 and PIP2 polarize with blebs. PIP2 is enriched on blebs, whereas KrasV12 is not. Investigating further, we discovered that KrasV12 localizes to bleb edges and that its distribution is consistent with that of a membrane label. Together, these data suggest the possibility that membrane wrinkling alone or enrichment on blebs could modulate nonlinear signaling networks by concentrating membrane-bound proteins. These two examples also illustrate how u-shape3D supports i) the acquisition of maps and statistics of the spatial modulation of protein concentrations that would be inaccessible by visual inspection; and ii) the numerical treatment of complex geometric arrangements that are at the root of non-intuitive cell behaviors. In future, these features of u-shape3D will enable projects ranging from cell behavioral screens and FRET measurements linking signaling to morphology to molecularly specific investigations of 3D signaling in vivo.
Online Methods
Cell culture and genetic engineering
Cells were cultured at 5% CO2 and 21% O2. MV3 melanoma cells (a gift from Peter Friedl at MD Anderson Cancer Center) were cultured using DMEM (Gibco) supplemented with 10% fetal bovine serum. Primary melanoma cells (a gift from Sean Morrison at UT Southwestern Medical Center) were cultured using the Primary Melanocyte Growth Kit (ATCC). Human bronchial epithelial cells (HBEC; a gift from John Minna at UT Southwestern Medical Center), immortalized with Cdk4 and hTERT expression and transformed with p53 knockdown, KrasV12, and cMyc expression,26 were cultured in keratinocyte serum-free medium (Gibco) supplemented with 50 mg/ml of bovine pituitary extract (Gibco), 5 ng/ml of EGF (Gibco), and 1% Anti-Anti (Gibco). U2OS osteosarcoma cells (a gift from Dick McIntosh at the University of Colorado, Boulder) were cultured using high-glucose DMEM (Gibco) supplemented with pyruvate, stable glutamine, and 10% fetal bovine serum. Conditionally immortalized hematopoietic precursors to dendritic cells27 that express Lifeact-GFP28 (a gift from Michael Sixt, IST Austria) were cultured and differentiated as previously described.29
Unless stated otherwise, fluorescent constructs were introduced into cells using the pLVX lentiviral system (Clontech) and selected using antibiotic resistance to either puromycin or geniticin. The GFP-tractin construct contains residues 9–52 of the enzyme IPTKA30 fused to GFP.31 The CyOFP-tractin peptide contains the tractin peptide fused to the CyOFP protein. CyOFP is a cyan-excitable orange fluorescent protein with peak excitation at 505 nm and peak emission at 588 nm.32 The GFP-KrasV12 plasmid was constructed by cloning a KrasV12 fragment from the pLenti-KrasV12 construct26 into the pLVX-GFP vector. The biosensor for PIP2, PLCΔ-PH-GFP, encodes a PI(4,5)P2 lipid selective PH domain that can be used as a fluorescent translocation biosensor to monitor changes in the concentration of plasma membrane PI(4,5)P2 lipids.33 Some MV3 cells expressing GFP in the cytosol and imaged via meSPIM, appeared in a previous publication, and were analyzed here as a control population.10
For the CRISPR knockouts, U2OS cells were transiently transfected with pX458 including gene-specific guide RNAs together with a self-cleaving donor vector to deliver a blasticidin S resistant cassette into the genomic cut site. Cells were selected with 5 μg/ml blasticidin S and surviving colonies were isolated using 6 mm Pyrex cloning cylinders (Sigma-Aldrich). The pSpCas9(BB)-2A-GFP (pX458) was a gift from Dr. Feng Zhang (Addgene plasmid # 48138). The self-cleaving donor vector pMA-tial1 was a kind gift from Dr. Tilmann Buerckstuemmer (Horizon Genomics, Vienna, Austria). Guide RNA sequences were cloned into pX458 by Golden Gate cloning utilizing the BbsI cut site. Guide RNA sequences targeting Wave2 (WASF2; exon 3) and cofilin-1 (CFL1; exon 2) were 5’- TGAGAGGGTCGACCGACTAC −3’, and 5’- CGTAGGGGTCGTCGACAGTC −3’, respectively. Gene knockout was verified by western blotting using rabbit anti-cofilin-1 (Cell Signaling; D3F9 XP # 5175) and rabbit anti-Wave2 (Cell Signaling; D2C8 XP #3659) antibodies (Supplementary Fig. 12).
Imaging
Unless stated otherwise, imaging was performed via microenvironmental selective plane illumination microscopy,10 a type of two-photon Bessel beam light sheet microscopy that confers near-isotropic resolution (300 nm lateral, 340 nm axial) and permits recording of cell behavior several millimeters from mechanically perturbing hard surfaces. Images were acquired at 37 °C in a non-descanned image capture mode with an axial step size of 160 or 200 nm and an excitation wavelength of 900 nm. Melanoma cells were imaged in cell culture medium supplemented with HEPES buffer to maintain pH during imaging.
Confocal imaging was performed using a Zeiss LSM 780 with a 40x (1.4 NA) objective. Microglia were imaged within zebrafish using a Zeiss Lightsheet Z.1 with 20x detection (1.0 NA) and 5x illumination (0.1 NA) objectives. The zebrafish line was P2Y12::P2Y12-GFP and was 3.5 dpf. Axially swept light-sheet microscopy (ASLM) imaging was performed using a custom-built microscope as previously described.9
U2OS cells were allowed to spread overnight in pH-neutralized rat-tail collagen (3 mg/ml) prior to imaging. All other cells, except for those imaged by the Peri and Betzig laboratories, were imaged in collagen gels created by mixing bovine collagen I (Advanced Biomatrix) with concentrated PBS and water to a collagen density of 2.0 mg/ml. This collagen solution was then neutralized with 1 M NaOH and mixed with cells just prior to incubation at 37 °C to induce collagen polymerization. U2OS cells and MV3 cells imaged via confocal microscopy were fixed in 4% paraformaldehyde prior to imaging.
Image deconvolution
All microscopy images shown are raw, non-deconvolved images. However, as a first analysis step, we deconvolved each 3D image. Most images acquired via meSPIM were Wiener deconvolved as previously described.10 The microscope’s point spread function (PSF) was measured using fluorescent beads. The Wiener parameter, which is the inverse of the signal-to-noise ratio, was usually set to 0.018. However, to better detect the dim ends of filopodia, it was set to 0.015. For cytosolically labeled cells, we automatically estimated the Wiener parameter in each frame by defining the signal as the average fluorescence intensity within the cell and the noise as the standard deviation of the fluorescence intensity outside the cell. Supplementary Fig. 2 shows the effect of varying the Wiener and other deconvolution parameters, and Supplementary Table 5 shows the deconvolution and surface extraction parameters for all datasets presented in this paper. Since Wiener deconvolution is sensitive to PSF quality, for images acquired via microscopy modalities other than meSPIM, we used the Richardson-Lucy deconvolution algorithm built-in to Matlab. The movie of the MDA-MB-231 human breast cancer cell was deconvolved as previously described.22
Following deconvolution, an apodization filter was applied to the optical transfer function (OTF) of the image in the spatial frequency domain. This filter had a value of 1 at the origin and decayed linearly to 0 at the edge of the filter support, which is set by the user as a percentage of the maximum OTF value. This threshold value, here termed the apodization height, was usually adjusted according to the homogeneity of the fluorescence label and the fineness of the morphological motif being detected. Higher apodization heights smooth the image more and allow for more robust detection of large objects, whereas lower apodization heights allow for the detection of finer structures but also admit more noise.
Cell surface extraction
The deconvolved images were further processed prior to cell surface extraction. For the majority of data sets, an Otsu threshold was first calculated from the 3D image,34 holes were filled using a 3D grayscale flood-fill operation, and objects disconnected from the main cell were removed. We also optionally smoothed the image with a 3D Gaussian kernel and applied a gamma correction. Matlab’s isosurface function was then used to create a triangle mesh at the intensity value specified by the Otsu threshold. Finally, the triangle mesh was smoothed using curvature flow smoothing.35
For some datasets, this procedure does not segment the nucleus along with the cytoplasm. In these cases, we therefore combined the output image of the procedure described above with an “inside” image that segmented the cell interior. To create the “inside” image from the gamma corrected image, we applied an additional gamma correction, smoothed the image with a 3D Gaussian kernel of standard deviation 2 pixels, Otsu thresholded the image, morphologically dilated the image, filled holes in each xy-slice, morphologically eroded the image by a radius greater than the morphological dilation, and finally smoothed the binary image with a 3D Gaussian kernel of width 1 pixel. Since this process shrinks the cell, if the parameters are chosen correctly the edges of the morphological motifs should mostly lay outside the “inside” image. To combine the “inside” image with the image outputted by the procedure above, we normalized this image by its Otsu threshold value, took the pixel-by-pixel maximum of this image and the “inside” image, and extracted a triangle mesh as an isosurface at an intensity level of 1.
The ends of the long, thin lamellipodia of dendritic cells fail to segment using the techniques described above. To better segment lamellipodia, we combined the “inside” and normalized deconvolved images described above for PIP2 labeled cells with a “surface filtered” image that enhances planar features, such as lamellipodia (Supplementary Fig. 3). The surface filter, which was developed by Elliott et al.,23 uses multiscale Gaussian second order partial-derivative kernels of the form
| (1) |
where I(x) is the image intensity, σi,ω is the half width of the Gaussian in dimension i at scale ω, Ωk is the filter kernel support, and s(x)ω is the filter response at scale ω. The total filter response, S(x), is merged across scales via
| (2, 3) |
We used filter scales 1.5, 2, and 4 pixels to segment lamellipodia of various thicknesses. To combine the response of the surface filter with the “inside” and normalized deconvolved images, we normalized the response by subtracting both the mean image intensity and twice the standard deviation of the image intensity prior to dividing by the standard deviation of the image intensity.
Although not used in this paper, our software also includes the option to segment cells by combining a normalized deconvolved image with a steerable filtered image. Steerable filters are computationally efficient edge detectors that, depending upon the parameters chosen, enhance linear or planar structures at specified scales.36,37
Segmentations were spot checked by thresholding the 3D image at the isosurface intensity value immediately prior to mesh extraction and examining the overlaid raw and thresholded images as 3D image stacks in ImageJ38 (Supplementary Fig. 13). For analyses where internal mesh cavities could alter results, meshes were also exported to ChimeraX39 for further examination. Segmentations that were found to be inaccurate or had cavities were excluded from further analysis.
Decomposition of the cell surface into convex patches
Although the image deconvolution and cell surface extraction parameters require customization for different cell types, the remainder of the workflow does not, and its parameters were kept constant throughout the paper.
To decompose the cell surface into convex patches, we first performed a watershed segmentation of surface mean curvature, as previously described.10 This oversegments the cell surface into small patches, which are analogous to superpixels in image analysis, which we later merge to create convex patches. First, we calculated the mean and Gaussian curvature at every triangle face.17,23 Next, we constructed an adjacency graph of faces where each face is a node that is connected to exactly three other spatially adjacent faces. Matlab’s isosurface function does not always produce triangle meshes with sufficient topological consistency to create such a graph. Our software fixes common topological inconsistencies, such as triangular edges that are only connected to one face. Rarely, however, a face graph cannot be constructed. In these situations, very slightly changing the image deconvolution parameters usually solves the problem, although we did not need to do so here. Since curvature can be noisy, we next smoothed mean curvature in two different ways. First, we used a kd-tree to median filter curvature in 3D space over 2 pixels. The meSPIM is Nyquist sampled, and so 2 pixels, which is 320 nm, is approximately the microscope’s spatial resolution. Second, to reduce spurious curvature fluctuations, we diffused mean curvature on the mesh using a diffusion kernel40,41 according to the equation
| (4) |
for 20 iterations, where R is the curvature, is a normalized, weighted adjacency matrix of the faces graph, k is the number of iterations, and S is the smoothed curvature. We defined A as
| (5) |
where dij is the distance between faces i and j. To normalize A, we multiplied it by a diagonal matrix, where each diagonal element was the inverse of the sum of that row. Next, we performed a watershed segmentation of the smoothed curvature over the cell surface.18 Watershed segmentations are often performed on 2D images, where each pixel is adjacent to exactly four other pixels. Here, we similarly performed a watershed segmentation over the adjacency graph of faces, where each face is adjacent to exactly three faces.
We next merged adjacent patches using a spill depth criterion.18 Here, the spill depth between two adjacent patches was defined as the maximum curvature of the two patches minus the maximum curvature at the patch-patch interface. This is analogous to the depth of water that the patch can hold before spilling into the neighboring patch. Starting with the smallest spill depth, we merged patches until no spill depth was below a cutoff of 0.6 times the Otsu threshold of mean curvature for the cell. Supplementary Fig. 4 shows the effect of altering the spill-depth cutoff and other patch merging parameters.
Finally, we decomposed the surface into approximately convex patches by iteratively applying the triangle and line-of-sight (LOS) criteria. To apply the triangle criterion,10 we first calculated the closure surface area for each patch and pair of adjacent patches. We defined the closure surface area as the minimum additional surface area needed to create a closed polyhedron from a surface patch. We then merged adjacent patches if they meet the criterion
| (6) |
where σA and σB are the closure surface areas of the two patches, σAB is the closure surface area of the merged patch, and ρ is the triangle cutoff parameter, which we here set to 0.7. The triangle criterion can be thought of as similar to the law of cosines and intuitively seeks to merge patches that meet at small angles. Starting with the largest ρ, we merged all pairs of patches that met the triangle criterion before applying the LOS criterion.
The LOS criterion merges adjacent patches with high mutual visibility.19,42 We defined the mutual visibility of patches A and B as the percentage of line segments that connect a face in A with a face in B that are lines of sight, where a line of sight is a line segment that falls entirely within the mesh. We calculated mutual visibility by randomly selecting a face on each patch, and using a triangle-ray intersection43 algorithm to determine whether a line segment connecting the two faces exited and reentered the mesh. A small patch and an adjacent very large patch may have a large mutual visibility because of lines of sight that extend across the width of the cell, even if these two patches should not be merged. When merging two patches, we therefore discarded line segments that were longer than twice the smaller patch size. Supplementary Fig. 14a shows the convergence of mutual visibility as a function of the number of line segments tested. We calculated mutual visibility from 20 line segments per pair of patches. In an exact convex decomposition, any two points within any patch could be connected by a line of sight. However, because of biological variation and image noise, requiring a mutual visibility of 1 is too strict a requirement for cell images. We instead merge patches if their mutual visibility is greater than 0.7. Starting with the largest mutual visibility between patch pairs, we merged all patch pairs meeting the LOS criterion, before again applying the triangle criterion.
Having three patch merging criteria for convex surface decomposition allows us to balance accuracy, speed, and robustness to noise. The spill-depth criterion is fast but potentially inaccurate, whereas the LOS criterion is relatively slow, but exact. The triangle criterion implements the short-cut rule,20 which biases merging towards certain types of convex decompositions. By adjusting the three merging parameters, users can control which criteria dominate in their analysis.
Classification of morphological motifs
To classify each patch by morphological motif, we first performed feature selection on the geometric patch features listed in Supplementary Table 1. Implemented by the Matlab built-in function sequentialfs(), our sequential feature selection randomly successively removed features as long as doing so reduced the misclassification rate. The misclassification rate was measured using 10-fold cross validation. The geometric features selected can vary considerably from dataset to dataset even for similar training sets, presumably because of correlations between features, randomness, and dataset differences. For example, Supplementary Table 6 shows the features selected for bleb detection models generated by three different users training on the same four cells. In this example, no feature was selected by all three models, and no two models shared more than two selected features. Once features were selected, features were normalized to have the same mean and standard deviation, and a linear support vector machine (SVM)44 was used to classify patches. Since SVM models vary from user to user, to analyze actin, Kras, and PIP2 localization, we had models created by three different users vote on the classification of each bleb.
We also validated our workflow with the linear SVM replaced with a radial SVM or a random forest.45 Supplementary Table 6 shows the precision, recall, and F1 score of these algorithms for various iterations of feature selection. For the radial SVM, we used the Gaussian kernel,
| (7) |
To implement the random forest, we used the treeBagger() function in Matlab. Measuring the out-of-bag classification error as a function of the number of trees grown, we observed that the error plateaued at approximately 10 trees, which is well below the 30 and 200 tree forests that we tested.
To compare our workflow, which employs a supervised machine-learning algorithm, to an unsupervised algorithm, we performed an agglomerative hierarchical clustering on all the patches and the patches classified by the supervised algorithm as motifs of interest (Supplementary Fig. 7), respectively. We used the correlation as a distance metric and measured the distance between a pair of clusters as the average distance between any two pairs of patches in these clusters. To avoiding biasing the algorithm, we only clustered on statistics defined at the patch scale, and did not include cell scale statistics, such as cell volume.
Characterization of patches
To classify patches by morphological motif, we calculated geometric descriptions of each patch. The full list of 23 features used by the SVM classifier is provided in Supplementary Table 1. In calculating these features, mean curvature was smoothed as described above, but Gaussian curvature was not. We defined the average patch position as the mean location of the faces in the patch, and we similarly defined the weighted average patch position as the mean location of the faces weighted by curvature. The feature ‘variation from a sphere’ was defined by the standard deviation of the distances from a patch’s faces to the average patch position divided by the mean distance of those faces to the average patch position. We defined the closure surface area as described above. The closure center was also defined as the mean position of the mesh vertices at the patch edge. We defined the patch radius as the mean distance of the patch’s faces from the closure center.
The volume, V, was calculated using the equation
| (8) |
where N is the number of faces, and v1,i, v2,i, and v3,i are the vertices of face i. The vertices must be ordered such that the face normal extends outwards from the cell. To derive this equation, the mesh can be thought of as decomposed into tetrahedrons where the vertices of each tetrahedron are those of a face combined with the origin.46 The signed volumes of the tetrahedrons sum to the volume of the mesh. Patches were closed prior to calculating their volumes.
We calculated the shape diameter function similarly to Shapira et al.47 For each patch, we randomly picked 20 mesh faces on the patch and extended a ray inwards from the mesh face at a randomly chosen angle within π/3 of the direction opposite to the face’s normal. We calculated the distance each ray traveled before intersecting the opposite side of the mesh. The shape diameter function of the patch was then defined as the mean travel distance within one standard deviation of the median distance.
Features selected for patch classification
The feature selection algorithm selected different geometric features to detect the three morphologies. To determine which geometric features best distinguished morphologies, starting from no features, we successively added the most discriminative feature to the model (Supplementary Table 3). The features that best distinguished blebs from non-blebs were volume / (closure surface area)3/2 and mean curvature on the protrusion edge. Closure surface area is the minimum amount of additional surface area needed to create a closed polygon from the mesh of the patch. The features that best distinguished filopodia from non-filopodia were the distance from the center of the closure surface area to the mean face position, a measure of morphological feature length, and patch surface area. This same measure of morphological feature length as well as patch volume were the best features for distinguishing lamellipodia from non-lamellipodia.
Optional merging of convex patches
Some morphological motifs, such as lamellipodia and flagella, are not convex but are composed of multiple convex regions. To detect such motifs, we optionally merge convex patches into patch composites. Since adjacent patches that compose a larger structure often have smooth curvature at their interface, we first merge patches using a modified line of sight criterion with line segment length capped at 10 pixels and a mutual visibility cutoff of 0.7. The line of sight criterion is described above. This step is not required for convex patch merging and can be disabled by the user. We next employed a more versatile machine learning based framework to merge adjacent patches. Using the geometric features for pairs of adjacent patches listed in Supplementary Table 2, as well as user provided training data, we trained an SVM to automatically merge patches. We used the same feature selection procedure and SVM parameters as for patch classification.
Characterization of adjacent patches
To merge adjacent patches into patch composites using an SVM, we calculated geometric characterizations of each pair of adjacent patches. The full list of 36 features used by the SVM is provided in Supplementary Table 2. Some measures of patch pairs incorporate individual patch measures, which are described above. Unless otherwise specified, mean curvature was smoothed as described above, but Gaussian curvature was not.
To better describe the surface geometry at patch-patch interfaces, we calculated the two principal curvatures, κ1 and κ2, everywhere on the cell surface,
| (9, 10) |
where H is the unsmoothed mean curvature and K is the unsmoothed Gaussian curvature. For various geometries defined by principal curvature values, we then calculated the fraction of the interface that had that geometry. As a noise threshold, we used the standard deviation of the smoothed mean curvature. Principal curvatures above this threshold or below the negative of this threshold were defined as large, and those more than four times above or below it as very large. We defined a ridged geometry as a large positive κ1 and a small κ2, a very ridged geometry as a very large positive κ1 and a small κ2, a valley-like geometry as a small κ1 and a large negative κ2, a very valley-like geometry as a small κ1 and a very large negative κ2, a domed geometry as a large positive κ1 and a large positive κ2, a cratered geometry as a large negative κ1 and a large negative κ2, a flat geometry as a small κ1 and a small κ2, and a saddle-like geometry as a large positive κ1 and a large negative κ2.
Generation of training data
We designed a graphical user interface to enable the collection of training data necessary for motif classification. Users are shown a surface rendering of a cell with surface patches outlined and can interact with the cell by rotating and moving it, and zooming in and out on regions of interest. To generate data for patch classification, we asked users to click on patches that are certainly the morphological motif of interest and then subsequently asked them to click on patches that are certainly not that motif. Similarly, to generate data for the optional step of convex patch merging, we asked users to click on pairs of patches that should certainly be merged and then asked them to click on pairs of patches that should certainly not be merged. Pairs of patches that were not adjacent were automatically excluded from the training set. We have successfully tested this interface in Matlab versions R2017b and R2013b. However, since in Matlab user interface functionality can vary from version to version, it may not work in some versions of Matlab.
Validation
To validate the protrusion classification, we calculated the F1 score, which is the harmonic mean of precision and recall. Here, precision is defined as the ratio of patches correctly classified as protrusions to the total number of patches classified as protrusions, whereas recall is defined as the ratio of patches correctly classified as protrusions to the total number of patches that are protrusions. Unless otherwise specified, in calculating the F1 score, we only used patches selected by the trainer as certainly a protrusion or certainly not a protrusion.
Generation and analysis of synthetic images
For algorithm validation, we created synthetic spherical cells of radius 48 pixels. The cell size was chosen to mimic the pixel spacing on the meSPIM of 0.16 μm per pixel for a cell 7.6 μm in radius. Placed randomly on the cells’ surfaces were spherical blebs that ranged in radius from 2 to 32 pixels and in number from 4 to 256 per cell. (See Supplementary Fig. 15 for example synthetic cells). Since pixelation at the cell edge could hamper the cell surface extraction and subsequent analysis, edge pixels were subdivided into a finer 3D grid to calculate the percentage of the pixel occupied by the synthetic cell. The final synthetic images were saved with 32 grayscale intensity values. Synthetic cells were not deconvolved, but the remainder of the analysis workflow was identical to that used for microscopic data. The same surface extraction parameters were used as for bleb detection on tractin and cytosolically labeled cells.
An F1 score does not measure whether or not the workflow preferentially detects certain subtypes of protrusions. Since patch-merging algorithms could be sensitive to protrusion size, we used synthetic data to test the algorithm’s sensitivity to bleb size (Supplementary Fig. 15). On synthetic cells of radius 7.6 μm (48 pixels) we simulated blebs ranging in radius from 0.32 μm (2 pixels) and 0.64 μm (4 pixels) to 5.1 μm (32 pixels). Although only 70% of the smallest 0.32 μm radii blebs were decomposed as convex surface patches, almost all of the larger blebs were decomposed. A bleb detector trained on synthetic data correctly classified all blebs that were decomposed as convex surfaces.
Mapping fluorescence intensity to the cell surface
To measure the fluorescence intensity local to each mesh face, we used the raw, non-deconvolved, fluorescence image. At each mesh face, we used a kd-tree to measure the average pixel intensity within the cell and within a sampling radius of the mesh face. To correct for surface curvature dependent artifacts, we depth normalized23 the image prior to measuring intensity localization by normalizing each pixel by the average pixel intensity at that distance interior to the cell surface. Prior to analysis, we also normalized each cell’s surface intensity localization to a mean of one.
Calculation of distance from a bleb edge
On the adjacency graph of faces, we calculated the distance from each face to the nearest bleb edge measured in number of faces traversed. To convert this distance to micrometers, we multiplied by the average distance between faces for each cell in each frame. Since the distance in micrometers between adjacent faces varies, our calculation of distance is an estimate rather than exact.
Calculation of local bleb density
To calculate bleb density, we first assigned the value one to each mesh face on a bleb and the value zero to each mesh face not on a bleb (Supplementary Fig. 11a). We then diffused these values on the mesh surface using Eq. 4 over 600 iterations (Supplementary Fig. 11b). We choose the number of iterations such that the bleb density would be calculated over a short distance on the order of a bleb length. Eq. 4 does not allow an exact measurement of bleb density and may be unstable over distances on the order of many bleb lengths.
Spherical statistics
The von Mises-Fisher distribution is defined on an sphere within space.48 For d = 2 dimensions it approximates a wrapped normal distribution on a circle, and, similar to the normal distribution, for any d is parameterized by a mean and an inverse spread. For d = 3 dimensions, the von-Mises Fisher distribution is
| (11) |
where μ is the mean direction parameter and κ is the concentration parameter, which is inversely related to the data spread. The maximum likelihood estimate of the mean direction is simply
| (12) |
A Newton’s Method approximation for κ, κ2, in three dimensions is
| (13, 14) |
| (15) |
| (16) |
| (17) |
where N is the number of data vectors and I are Bessel functions of the first kind.48
In Fig. 6c and j, we measured the magnitude of PIP2 and KrasV12 polarization by mapping the intensity values defined on each surface mesh onto a unit sphere and then using spherical statistics to calculate κ. To map the intensities onto the unit sphere, we calculated a set of unit vectors, xintensity that extended in the direction from the cell center to every mesh face. The cell center was defined as the location within the cell farthest from the cell edge,. Since we measured intensity at every mesh face over a radius of 2 μm, to avoid spatially oversampling, we used only every 1000th mesh face. We defined wintensity as the measured intensity value associated with each unit vector and then discretized the range of intensity values into 32 bins. Finally, we replaced every vector xintensity with w copies of that vector and calculated κ from this set of unit vectors. As a control, we also measured κ from a set of xintensity with randomized directions.
In Fig. 6d and k we computed the directional correlation of morphological motifs, here blebs, with intensity localization. In each frame, we defined the directional correlation as μblebs · μintensity. To measure μblebs, we calculated a set of unit vectors, xblebs, that extended in the direction from the cell center to each mesh face on a bleb. To measure μintensity, we calculated xintensity and in Eq. 12 we weighted xi by the intensity localization. Since the cell is not a sphere and most cells have polarized shapes, the surface itself is expected to have a nonrandom μ and a small κ. To account for this, we created a control distribution of directional correlations μblebsRand · μintensity, where μblebsRand was calculated from a set of vectors where the patch classification was randomly permuted. In each frame, we created 200 such permutations by randomly assigning patches to be a bleb or not a bleb.
Measurement of boundary motion
To measure boundary motion, for each face we found the closest face in the previous frame using a kd-tree. We then defined the boundary motion as
| (18) |
where mi is the boundary motion at face i, di is the vector from face i to the closest point in the previous frame, and ni is the normal to the surface at face i.
This is not an ideal measure of boundary motion since the mapping vectors di may cluster on select faces of the previous frame’s surface, or even alter the topology among faces, in a physically unrealistic manner (see Machacek et al.49 for an illustration of these problems with 2D boundaries). As a control, we also calculated the boundary motion for each face by finding the closest point in the next frame. Supplementary Fig. 14b shows the protrusive and retractive motion of six cells using both definitions of boundary motion. Here, backwards motion is the mapping of points from each frame to the previous frame and is the definition used elsewhere, and forwards motion is the mapping of points from each frame to the subsequent frame. Even though the backwards and forwards motions of the cells are different, in both cases blebs are more protrusive than non-blebs. This measure is also not a subpixel measure of motion, and should not be used to measure subpixel motions. Because we map each face to the closest face rather than the closest surface point in the previous frame, motions that are less than the average distance between faces will be undersampled in the motion distribution.
Statistical hypothesis testing
For each Kras and PIP2 labeled cell, we measured the mean intensity localization of faces on and off blebs and then performed a one-sided t-test on the differences of the means after testing for normality using a Kolmogorov-Smirnov test. The Cohen’s d effect size was measured.
Unless otherwise indicated, all errors and error bars show the standard error of the mean.
Surface rendering
The majority of triangle meshes were rendered in ChimeraX.39 Colored triangle meshes were exported from Matlab as Collada .dae files using custom-written code and were rendered using full lighting mode. Lighting intensity and ambient intensity were adjusted. Colormaps were modified from colorBrewer.50 The surfaces in Supplementary Figures 11, and 15 were rendered within Matlab. Our software is capable of rendering all meshes shown in the paper within Matlab, as well as creating Collada files for export to ChimeraX.
Data availability
Data are available from the corresponding author upon reasonable request.
Code availability
The latest version of the software described here, as well as a user’s guide, is available from https://github.com/DanuserLab/Motif3D.
Supplementary Material
Acknowledgements
This research was funded by grants from the Cancer Prevention Research Institute of Texas (RR160057 to R.F. and R1225 to G.D.) and the National Institutes of Health (F32GM116370 and K99GM123221 to M.K.D., K25CA204526 to E.S.W., F32GM117793 to K.M.D., R33CA235254 to R.F., and R01GM067230 to G.D.). Confocal imaging was performed at the UT Southwestern Live Cell Imaging Facility. Most surface renderings were performed using UCSF ChimeraX, which was developed by the Resource for Biocomputing, Visualization, and Informatics at the University of California, San Francisco (supported by P41GM103311). We thank T. Goddard for assistance with ChimeraX, as well as I. de Vries, J. Renkawitz, and M. Sixt for assistance differentiating dendritic cells. We would also like to thank F. Peri (University of Zurich) and members of her lab, especially M. Albert, for the unpublished images of microglia cells. We also thank P. Friedl (MD Anderson Cancer Center) for the MV3 melanoma cells, Sean Morrison (UT Southwestern) for the primary melanoma cells, Michael Sixt (IST Austria) for the dendritic cell precursors, John Minna and Jerry Shay (UT Southwestern) for the transformed HBEC cells, and Dick McIntosh (University of Colorado, Boulder) for the U2OS osteosarcoma cells.
Footnotes
Competing Interests
The authors declare no competing interests.
Editor’s Summary
A computational workflow combining image segmentation, computer graphics, and supervised machine learning enables automated and robust 3D analysis of the coupling of cell shape and signaling.
References
- 1.Munjal A & Lecuit T Actomyosin networks and tissue morphogenesis. Development 141, 1789–1793, (2014). [DOI] [PubMed] [Google Scholar]
- 2.Rottner K, Faix J, Bogdan S, Linder S & Kerkhoff E Actin assembly mechanisms at a glance. J. Cell Sci. 130, 3427–3435, (2017). [DOI] [PubMed] [Google Scholar]
- 3.Simunovic M, Voth GA, Callan-Jones A & Bassereau P When Physics Takes Over: BAR Proteins and Membrane Curvature. Trends Cell Biol. 25, 780–792, (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Rangamani P et al. Decoding information in cell shape. Cell 154, 1356–1369, (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Schmick M & Bastiaens PI The interdependence of membrane shape and cellular signal processing. Cell 156, 1132–1138, (2014). [DOI] [PubMed] [Google Scholar]
- 6.Planchon TA et al. Rapid three-dimensional isotropic imaging of living cells using Bessel beam plane illumination. Nat. Methods 8, 417–U468, (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Wu Y et al. Spatially isotropic four-dimensional imaging with dual-view plane illumination microscopy. Nat. Biotechnol. 31, 1032–1038, (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Chen BC et al. Lattice light-sheet microscopy: imaging molecules to embryos at high spatiotemporal resolution. Science 346, 1257998, (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Dean KM, Roudot P, Welf ES, Danuser G & Fiolka R Deconvolution-free Subcellular Imaging with Axially Swept Light Sheet Microscopy. Biophys. J. 108, 2807–2815, (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Welf ES et al. Quantitative Multiscale Cell Imaging in Controlled 3D Microenvironments. Dev. Cell 36, 462–475, (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Fu Q, Martin BL, Matus DQ & Gao L Imaging multicellular specimens with real-time optimized tiling light-sheet selective plane illumination microscopy. Nat. Commun. 7, 11088, (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Schink KO, Tan KW & Stenmark H Phosphoinositides in Control of Membrane Dynamics. Annu. Rev. Cell Dev. Biol. 32, 143–171, (2016). [DOI] [PubMed] [Google Scholar]
- 13.Simanshu DK, Nissley DV & McCormick F RAS Proteins and Their Regulators in Human Disease. Cell 170, 17–33, (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Driscoll MK & Danuser G Quantifying Modes of 3D Cell Migration. Trends Cell Biol. 25, 749–759, (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Braunstein ML, Hoffman DD & Saidpour A Parts of Visual Objects - an Experimental Test of the Minima Rule. Perception 18, 817–826, (1989). [DOI] [PubMed] [Google Scholar]
- 16.Chazelle B, Dobkin DP, Shouraboura N & Tal A Strategies for polyhedral surface decomposition: An experimental study. Comp. Geom.-Theor. and App. 7, 327–342, (1997). [Google Scholar]
- 17.Theisel H, Rossi C, Zayer R & Seidel HP Normal based estimation of the curvature tensor for triangular meshes. Pac. Conf. Comput. Graph. Appl., 288–297, (2004). [Google Scholar]
- 18.Mangan AP & Whitaker RT Partitioning 3D Surface Meshes Using Watershed Segmentation. IEEE Trans. Vis. Comp. Graph. 5, 308–321, (1999). [Google Scholar]
- 19.Kaick OV, Fish N, Kleiman Y, Asafi S & Cohen-Or D Shape segmentation by approximate convexity analysis. ACM Trans. Graph. 34, (2014). [Google Scholar]
- 20.Singh M, Seyranian GD & Hoffman DD Parsing silhouettes: The short-cut rule. Percept. Psychophys. 61, 636–660, (1999). [DOI] [PubMed] [Google Scholar]
- 21.Dice LR Measures of the Amount of Ecologic Association Between Species. Ecology 26, 297–302, (1945). [Google Scholar]
- 22.Liu TL et al. Observing the cell in its native state: Imaging subcellular dynamics in multicellular organisms. Science 360, (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Elliott H et al. Myosin II controls cellular branching morphogenesis and migration in three dimensions by minimizing cell-surface curvature. Nat. Cell Biol. 17, 137–147, (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Zatulovskiy E, Tyson R, Bretschneider T & Kay RR Bleb-driven chemotaxis of Dictyostelium cells. J. Cell Biol. 204, 1027–1044, (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Cleveland WS & Mcgill R Graphical perception and graphical methods for analyzing scientific data. Science 229, 828–833, (1985). [DOI] [PubMed] [Google Scholar]
Online Methods References
- 26.Sato M et al. Human lung epithelial cells progressed to malignancy through specific oncogenic manipulations. Mol. Cancer Res. 11, 638–650, (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Redecke V et al. Hematopoietic progenitor cell lines with myeloid and lymphoid potential. Nat. Methods 10, 795–803, (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Riedl J et al. Lifeact: A Versatile Marker to Visualize F-actin. Nat. Methods 5, 605–607, (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Leithner A et al. Diversified actin protrusions promote environmental exploration but are dispensable for locomotion of leukocytes. Nat. Cell Biol. 18, 1253–1259, (2016). [DOI] [PubMed] [Google Scholar]
- 30.Johnson HW & Schell MJ Neuronal IP3 3-kinase is an F-actin-bundling protein: role in dendritic targeting and regulation of spine morphology. Mol. Biol. Cell. 20, 5166–5180, (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Yi J, Wu XS, Crites T & Hammer JA 3rd. Actin retrograde flow and actomyosin II arc contraction drive receptor cluster dynamics at the immunological synapse in Jurkat T cells. Mol. Biol. Cell 23, 834–852, (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Chu J et al. A bright cyan-excitable orange fluorescent protein facilitates dual-emission microscopy and enhances bioluminescence imaging in vivo. Nat. Biotechnol. 34, 760–767, (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Stauffer TP, Ahn S & Meyer T Receptor-induced transient reduction in plasma membrane PtdIns(4,5)P2 concentration monitored in living cells. Curr. Biol. 8, 343–346, (1998). [DOI] [PubMed] [Google Scholar]
- 34.Otsu N A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man, Cybern. 9, 62–66, (1979). [Google Scholar]
- 35.Desbrun M, Meyer M, Schroder P & Barr AH Implicit fairing of irregular meshes using diffusion and curvature flow. Comp. Grap. Inter. Tech, 317–324, (1999). [Google Scholar]
- 36.Aguet F, Jacob M & Unser M Three-dimensional feature detection using optimal steerable filters. IEEE Image. Proc. 2, 1158–1161, (2005). [Google Scholar]
- 37.Jacob M & Unser M Design of steerable filters for feature detection using Canny-like criteria. IEEE T. Pattern Anal. 26, 1007–1019, (2004). [DOI] [PubMed] [Google Scholar]
- 38.Schneider CA, Rasband WS & Eliceiri KW NIH Image to ImageJ: 25 years of image analysis. Nat. Methods 9, 671–675, (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Goddard TD et al. UCSF ChimeraX: Meeting modern challenges in visualization and analysis. Protein Sci. 27, 14–25, (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Kondor RI & Lafferty JD Diffusion Kernels on Graphs and Other Discrete Input Spaces. Proc. Inter. Conf. Mach. Learn, 315–322, (2002). [Google Scholar]
- 41.Kondor R & Vert JP Diffusion kernels in Kernel methods in computational biology (eds Schölkopf B, Tsuda K, & Vert JP) 171–192 (MIT Press, 2004). [Google Scholar]
- 42.Asafi S, Goren A & Cohen-Or D Weak Convex Decomposition by Lines-of-sight. Symp. Geom. 32, 23–31, (2013). [Google Scholar]
- 43.Möller T & Trumbore B Fast, minimum storage ray-triangle intersection. J. Graph. Tools 2, 21–28, (1997). [Google Scholar]
- 44.Christianini N & Shawe-Taylor J An introduction to support vector machines and other kernel-based learning methods. (Cambridge university press, 2000). [Google Scholar]
- 45.Breiman L Random forests. Machine Learning 45, 5–32, (2001). [Google Scholar]
- 46.Zhang C & Chen T Efficient Feature Extraction for 2D/3D Objects in Mesh Representation. IEEE Conf. Image Proc, 935–938, (2001). [Google Scholar]
- 47.Shapira L, Shamir A & Cohen-Or D Consistent mesh partitioning and skeletonisation using the shape diameter function. Visual Comput 24, 249–259, (2008). [Google Scholar]
- 48.Suvrit S A short note on parameter approximation for von Mises-Fisher distributions: and a fast implementation of I s (x). Comput. Stat. 27, 177–190, (2012). [Google Scholar]
- 49.Machacek M & Danuser G Morphodynamic profiling of protrusion phenotypes. Biophysical journal 90, 1439–1452, (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Harrower M & Brewer CA ColorBrewer.org: an online tool for selecting colour schemes for maps. Cartogr. J. 40, 27–37, (2003). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Data are available from the corresponding author upon reasonable request.