Visualizing disordered single-stranded RNA: connecting sequence, structure and electrostatics

Abstract

Disordered homopolymeric regions of single-stranded RNA, such as U or A tracts, are found within functional RNAs where they play distinct roles in defining molecular structure and facilitating recognition by partners. Despite this prominence, details of conformational and biophysical properties of these regions have not yet been resolved. We apply a number of experimental techniques to investigate the conformations of these biologically important motifs, and provide quantitative measurements of their ion atmospheres. Single strands of RNA display pronounced sequence dependent conformations that relate to the unique ion atmospheres each attracts. Chains of rU bases are relatively unstructured under all conditions, while chains of rA bases display distinct ordering, through stacking or clustering motifs, depending on the composition of the surrounding solution. These dramatic structural differences are consistent with the measured disparity in ion composition and atmospheres around each homopolymer, revealing a complex interplay of base, ion and single-strand ordering. The unique structural and ionic signatures of homopolymer ssRNAs explains their role(s) in folding structured RNAs, and may explain their distinct recognition by protein partners.

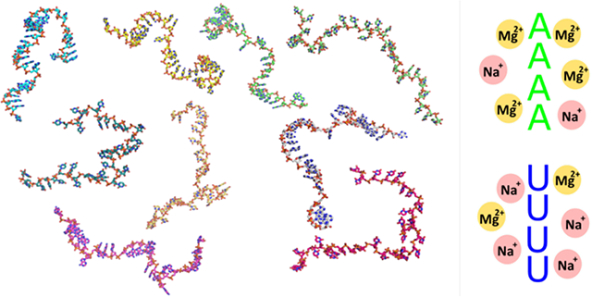
Graphical Abstract

INTRODUCTION

RNAs play critical and diverse roles in biology, acting as catalysts, translational switches, gene silencers and protein templates ^1–4. More functions await discovery. This astonishing diversity is due in large part to the wide structural variation of RNA molecules. RNA’s conformational richness is surprising, given the limited number of building blocks available: four chemically similar nucleotides and modifications. This number is striking when juxtaposed against the twenty, chemically diverse amino acid constituents of proteins ⁵.

With simple, four-letter sequences, how can these molecules assume structures that facilitate such a wide variety of biological function? The answer lies in the numerous interactions within or between RNA elements. These interactions include stacking of nucleotide bases, as well as the different possible orientations of the sugar-phosphate backbone. Beyond sequence, the local cellular environment (ions, metabolites, crowding agents) also contributes to determine RNA’s conformations. Of particular importance is the association of ions to the nucleic acid, notably divalent Mg^{2+ 6–8}. Past studies of RNA folding provide compelling evidence of the essential roles that Mg²⁺ plays in guiding RNA structures across a rough folding landscape ^9–14. Given this intimate connection, a few investigations have begun to link quantifiable properties of the ion atmosphere with structural insights in both model systems and more complex RNAs ^15,16.

Despite the awareness and appreciation of Mg²⁺’s roles in creating RNA structures, the field still lacks a quantitative measurement linking ion association to the conformations of the most fundamental RNA elements: single-stranded chains. Interactions with Mg²⁺ are known to persist even in these basic elements, and are critical for organizing biologically important single-stranded regions such as the actuators of riboswitches, the disordered tails of ribozymes that bind substrates, and A-tracts in complex ribozymes that harbor localized ions ^17–20. The precise modes of Mg²⁺ interaction with ssRNA have not yet been elucidated.

To date, investigations of the ion-dependent conformations of ssRNA look to structural signatures obtained through methods such as NMR, FRET, SAXS and pulling experiments (e.g. ^21–29). Modes of interactions between ions and these flexible polymers have emerged through comparison of predictions of conventional polymer theories (e.g. worm-like chain models) with measurements of the polymers’ elastic properties. Our own prior studies of ssNA persistence lengths²⁵, and others show that modified theories are required to accurately predict the ion induced modulation of chain properties. The sophisticated models required to accurately describe ion-polymer interactions, such as snake-like chain and internal electrostatic tension models, hint at complicated associations between RNA polymers and the localized ions that surround them^23,30. Further refinement and understanding of these interactions would be greatly enhanced by direct measurements of the ion cloud around ssRNA.

In spite of this, ion atmosphere measurements for ssRNA elements are sparse, with only a few experimental investigations directly probing a relatively small region of space, usually quantifying a single aspect of the problem (e.g. ion number)³¹. While these studies successfully elucidate elastic and dynamic properties of ssRNA, no quantitative link has been established between the ion cloud and the conformations of these elements. Theoretical alternatives have been greatly advanced, with recent success in predicting ion numbers around static nucleic acid structures^13,32–36. However more experimental data are needed to fully describe the ion atmosphere around highly flexible systems such as single-stranded elements.

Here, we apply a wide range of biophysical methods to elucidate both the ionic and structural signatures of two distinct RNA homopolymer chains. Together with advances in data analysis, these state of the art biophysical tools allow us to rigorously determine the electrostatic properties and conformations of these flexible RNA elements. We selected chains of 30 U nucleotides, rU₃₀, and contrast their conformations with those of rA₃₀, containing A nucleotides. Past work suggests these sequences have disparate characteristics and display a wide variation of arrangements ^{22,28,37–42}. Additionally, the presence of these particular sequences within functionally distinct RNAs, e.g. U-tracts in long non-coding RNAs (lncRNA) and A-tails in messenger RNAs (mRNAs), hints that nature exploits their unique structural signatures.

Our in-depth investigation provides information essential for structural studies of RNA by correlating the ion atmosphere around ssRNA with the conformations it assumes. The differing affinity of each base (A vs. U) for Mg²⁺ is reflected in both local (base arrangement) and global (backbone screening) chain conformations. The stacking affinity of A vs U provides another critical degree of variation for both the structure and ion cloud. The interplay of these interactions grant differing sequences unique ion atmosphere and conformational signatures, a theme central to both generic RNA folding and biological interactions.

EXPERIMENTAL SECTION

A detailed description of all work (methods and data analysis) is given in the Supporting Information (SI), here we briefly outline the methods employed.

Sample preparation

All RNA samples (rU₃₀ and rA₃₀) were purchased (deprotected) from Dharmacon (Lafayette, CO, USA). 25bp DNA was purchased from Integrated DNA Technologies (Coralville, IA, USA). All samples were annealed and buffer exchanged in the appropriate solution conditions before experiments as described in the SI.

Precipitation experiments

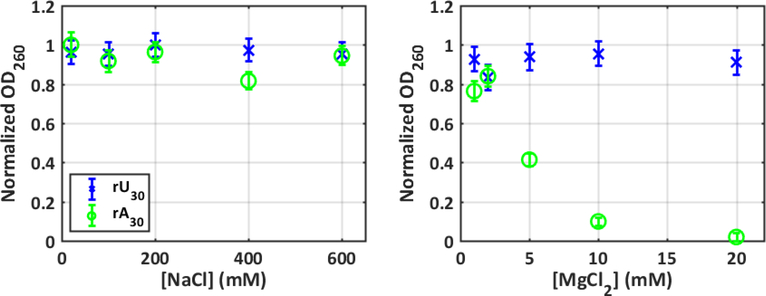
UV absorption spectra were measured using a Cary 50 spectrophotometer. The optical density at 260nm was used to report on stabilization or precipitation of RNA samples. Data in Figure 1 was normalized for each series (construct and salt series) by dividing all absorption measurements by the maximum measured for those conditions.

Figure 1:

Precipitation measurements that monitor the absorption of nucleic acid sample at 260nm quantify the relative stabilization effects of ions on rU₃₀ (blue) and rA₃₀ (green) conformations. Error bars are smaller than or equivalent to marker size in most cases.

CD experiments

Spectra were acquired using a BioLogic MOS 450 in CD mode. The CD spectra were scaled to account for differing nucleic acid concentrations, and further adjusted to match at 300nm to allow comparison of the peak positions across solution conditions.

SAXS experiments

SAXS experiments were performed at the Cornell High Energy Synchrotron source (CHESS) beamline G1. Multiple sample concentrations were used for each experiment condition (molecule and salt condition) to control for interparticle interference effects, and provide second virial measurements. The radius of gyration (R_g) for each experimental condition was calculated using the Guinier approximation on the zero-concentration extrapolated SAXS curves,

$$I(q)=I(0)e^{\raisebox{1ex}{$-q^2{R_g}^2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}$$ (1)

were I(q) is the scattered intensity as a function of scattering vector q. The second virial coefficients (B₂) were calulcated from SAXS profiles of the same molecule in a given condition at varying nucleic acid concentration (c), using the following,

$$\frac{S(q=0,c=0)}{I(q=0,c)}=1+2A{B}_{2}c$$ (2)

Where A is defined such that the sample concentration c is in units of M, and B₂ in Å ³. The form factor S(q,c=0) is determined by fitting the low-q portion of the zero concentration SAXS curve to an analytical form expected for a random coil,

$$S(q,c=0)=\frac{1}{1+\frac{{\left(qa\right)}^2}{3}}-b{e}^{-{\left(dq\right)}^2}$$ (3)

a,b and d are fit parameters

The SAXS data interpreted in this paper, as well as a representative set of model structures for each condition, have been deposited in the SASBDB under accession codes: SASDFA9, SASDFB9, SASDFC9, SASDFD9, SASDFE9, SASDFF9, SASDFG9, SASDFH9, SASDFJ9, SASDFK9, SASDFL9, SASDFM9, SASDFN9, SASDFP9, SASDFQP, SASDFR9, SASDFS9.

Ion counting experiments

Concentrations of the counter ions (Na⁺, Mg²⁺) and nucleic acids (through measurement of phosphorus (P) concentrations) were determined using an Optima 7300DV ICP-AES (Perkin Elmer, Waltham, MA) within the linear detection range of the instrument. Parts per million concentrations of each were converted to excess ions per phosphate as described in SI. Ion counting data represent the mean over 12 measurements, while the uncertainties are given as the standard error in the mean.

Modelling from SAXS Data

Methodology for ssNA structure building and refinements based on the SAXS data is extensively described in ⁴³. Minor changes to this procedure were made to model ssRNA, as outlined in the SI. Structural parameters from the derived models were calculated as described in SI.

The orientation correlation function (OCF) was calculated by,

$$OCF=<cos{\theta }_{ij}>=<{\widehat{r}}_i{\cdot \widehat{r}}_j>$$ (4)

Where ${\widehat{r}}_i$ is the normalized bond vector between the i^th and (i+1)^th phosphate in a given nucleic acid chain. The average dot product between these bond vectors is computed as a function of the number of monomers separating the phosphates (|i-j|). The correlation lengths, l_OCF, were calculated using the following formula,

$$l_{OCF}=b\sum _{\mathit{i}\mathit{j}}^{\mathit{N}-\mathbf{1}}<cos{\theta }_{ij}>$$ (5)

where b is the mean phosphate-phosphate distance. See SI section ‘Chain parameter calculations’ for a clear illustration of these quantities.

A representative set of structures for each of the modelled conditions is provided with the SASBDB entries. Furthermore, the complete structure sets analyzed herein are available as SI.

RESULTS

Precipitation reveals disparity in solution stability

We first used UV absorption measurements to investigate the effect of mono and divalent ions on ssRNA stability (see Methods and SI). Stabilization of base-stacking interactions leads to small decreases in UV absorption, while ion induced precipitation leads to dramatic decreases as strengthening inter-chain interactions render the sample insoluble (e.g. ^44–46). Changes in absorption at 260nm, monitored as a function of increasing salt, therefore serve as indirect probes of the ion-RNA interactions of a given sequence.

As shown in Figure 1, both ssRNA constructs show no significant changes in absorption as the bulk concentration of Na⁺ increases. Chains of both rU and rA nucleotides therefore remain soluble in solutions containing monovalent ions over a broad concentration range. Although the effect of added Mg²⁺ on rU₃₀ cannot be readily distinguished from that of added NaCl, dramatic changes are measured in the rA₃₀ sample. The drop in absorption becomes severe above 5 mM MgCl₂, suggesting the onset of precipitation rather than stabilization of stacked conformations. The contrast between poly rU and poly rA reflects interaction with Mg²⁺, in agreement with past work by others who report distinct effects consistent with base specific, ion dehydration ⁴¹. These straightforward absorption experiments already highlight the interplay between sequence and ions in disordered ssRNA.

Circular Dichroism (CD) measurements probe local chain ordering

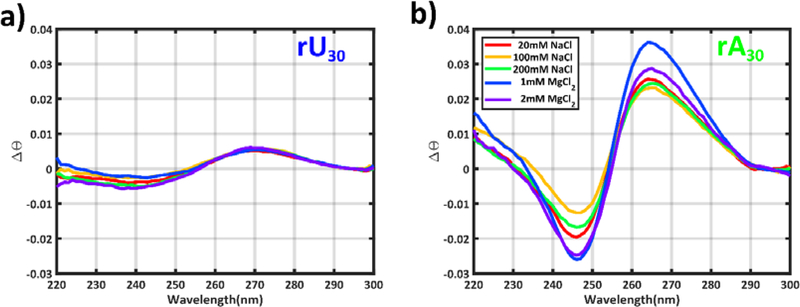
To provide additional information about chain ordering in each solution condition, we performed circular dichroism (CD) measurements under ionic conditions that support a large soluble fraction in the absorption experiments (see Methods and SI). CD spectra report on the helical ordering present in a sample, and serve as a useful reporter for the formation of exotic structures, such as quadruplexes ⁴⁷. Unlike the case of proteins, where a quantitative assessment of specific secondary structural elements can be retrieved from the CD amplitudes⁴⁸, it is currently unclear how to interpret changing CD amplitudes for RNA. We therefore restrict our interpretation of CD signals to qualitative features representing repeating structural elements.

We find (Figure 2) distinct peaks in the CD signals, with amplitudes and positions that vary with construct and salt. This behavior reflects differences in helical ordering of each sequence. The relatively flat, featureless spectrum of the rU₃₀ sample suggests no persistent helical ordering; the peaks originate from generic nucleic acid base asymmetry ⁴⁹. In contrast, the pronounced peaks in the spectrum of the rA sample are consistent with those measured in a poly rU:rA duplex ⁵⁰, suggesting a largely A-form conformation. The peaks do not shift appreciably in either sample, as ionic conditions change, indicating the absence of more complex structures under the conditions probed.

Figure 2:

CD experiments report on the degree of helical ordering in a) rU₃₀ and b) rA₃₀. In these plots, CD spectra have been scaled to match at λ=300nm to aid in comparing peak positions, and scaled by a factor to account for variations in sample concentrations.

SAXS quantifies differences in chain conformations

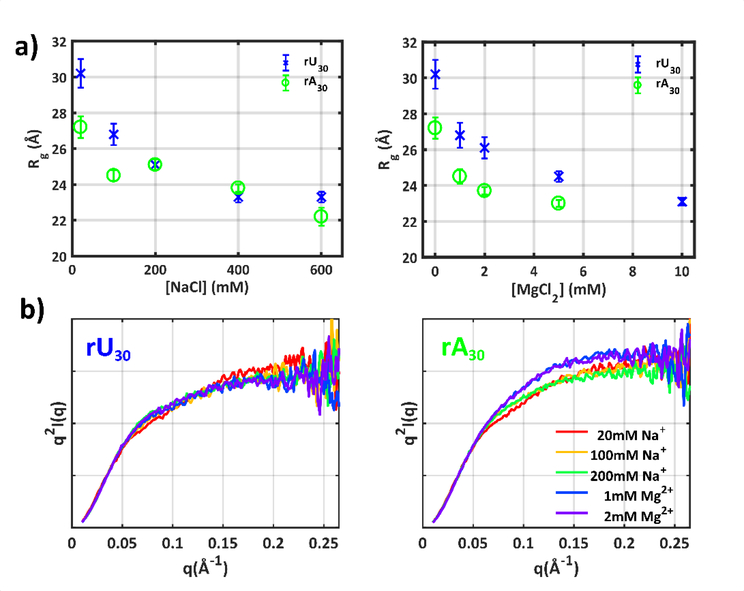
To further investigate the structural differences that accompany or seed the previously observed precipitation effects, we applied a solution scattering method that is sensitive to the conformational properties of (disordered) structural ensembles: small angle x-ray scattering (SAXS, see Methods and SI). SAXS measurements were performed across [Mg²⁺] conditions that maintain sample solubility, and at [Na] that are expected to provide the same degree of phosphate screening (about 100 times higher ^51,52, SI, Table S1).

A radius-of-gyration (R_g) is readily extracted from SAXS data under each solution condition, roughly reporting the mean global size of the chains (SI, Table S2, Figs. S1–S4). The R_g of both sequences (Figure 3a) decreases with increasing salt concentration, representing a molecular collapse as repulsive interactions between chain phosphates are screened. Despite the tendency for both sequences to become compact with increasing salt, differences are detected: at the lowest ionic strengths, rA₃₀ is on average ‘smaller’ than rU₃₀, and the sequences have different responses to ion type. The rU chain shows no strong R_g dependence across steps of equivalent ionic strength, e.g. the R_g’s measured in 100 (or 200) mM Na⁺ and 1 (or 2) mM Mg²⁺ appear equivalent. We also note the similarity in global size of both constructs at high [NaCl], whereas across all probed [MgCl₂], rA₃₀ is consistently smaller than rU₃₀. These differences in global size are consistent with previous reported measurements^53,54.

Figure 3:

a) SAXS experiments quantify the mean size of chain conformations through calculation of the radius of gyration R_g. Error bars quoted for R_g measurements reflect uncertainty in the Guinier fit parameters. b) A more intricate picture of chain conformations can be gleaned by looking at the higher angle scattering vectors in Kratky plots. All SAXS profiles have been scaled to match for q<0.05Å⁻¹ to enable comparison of mid and high-q behavior. For full SAXS data and zero concentration extrapolations, see Supplementary Information. The SAXS profiles can be accessed via SASBDB codes: SASDFA9, SASDFB9, SASDFC9, SASDFD9, SASDFE9, SASDFF9, SASDFG9, SASDFH9, SASDFJ9, SASDFK9, SASDFL9, SASDFM9, SASDFN9, SASDFP9, SASDFQP, SASDFR9, SASDFS9.

A more intricate picture of conformations can be gleaned by examining higher-angle portions of the scattering profiles that capture structural variations on smaller length scales. We highlight this regime using Kratky plots that emphasize scattering into larger scattering angles (Figure 3b). For clarity, only the first two ionic concentrations are displayed for both constructs (for the full series see SI, Figs. S5). We observe only subtle changes in chain conformations for either construct when titrating Na⁺. A gently tipping high-q tail is paired with a rising mid-q peak, consistent with shape changes expected from a non-specific chain collapse ^55,56. The more subtle changes in rU₃₀ with increasing salt concentrations appear to depend mainly on screening efficacy; as in the R_g measurements, a factor of 100 between Na⁺ and Mg²⁺ concentrations yields nearly identical profiles. The most drastic changes can be seen in rA₃₀ conformations. At all concentrations of MgCl₂, profiles appear almost identical to each other, but differ substantially from measurements in Na⁺. Thus, for poly rA, chain conformations are more sensitive to ion identity than screening efficacy.

Ion atmosphere measurements reveal sequence specific ion interactions

The disparity in structural and solution properties of ssRNAs as a function of [Na⁺] and [Mg²⁺] suggests sequence specific ion interactions and screening effects. The electrostatic environment around the RNAs can be quantified by measuring both the degree of inter-chain screening, and the composition of the ion atmosphere at a given ionic condition ⁸.

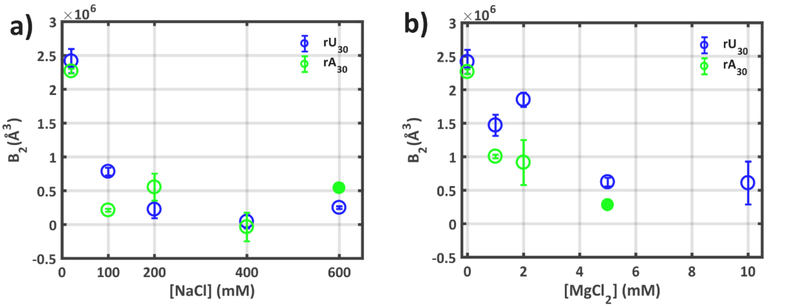
The degree of screening between chains is revealed through the second virial coefficients (B₂), which quantify interchain interactions ^57,58. By examining the low q portion of the SAXS profiles at the same ionic condition, but at varying nucleic acid concentrations, inter-chain effects can be quantified and used to compute B₂ (see Methods, SI and Figs. S6–S22). This inter-chain interaction is highly dependent on the bulk ion composition and screening efficacy of the ionic cloud surrounding each RNA. While second virial coefficients require careful extrapolation from the SAXS data, and are inherently more uncertain than directly derived parameters (e.g. R_g), a thermodynamic quantification of polymer-polymer screening is valuable, and hard to otherwise determine. Positive values of B₂ indicate repulsion between chains, while negative values signal attraction. The second virial coefficients for ssRNA, shown in Figure 4, provide valuable information about the screening of disparate sequence RNAs.

Figure 4:

The second virial coefficients (B₂) derived from SAXS experiments at multiple [NA] quantify interchain interactions in solutions containing different concentrations of a) Na⁺ and b) Mg²⁺. B₂ > 0 signifies molecular repulsion, B₂<0 signifies molecular attraction. Uncertainties are derived from the error in fit parameters required to obtain B₂, as shown and detailed in the Supplementary Information. Filled data points for poly rA at high values of NaCl and MgCl₂ denote B₂ values extracted from only two sample concentrations (see SI), and thus have undefined uncertainties.

At the lowest ionic strength probed, strong chain-chain repulsion dominates both constructs, resulting in large (positive) values of B₂. This value decreases for both sequences as we increase either [Na⁺] or [Mg²⁺], likely a result of the decrease in screening length of the higher ionic strength solutions. In both constructs however, the degree of chain-chain screening is lower for the Mg²⁺ conditions than the corresponding Na⁺, when scaled by the factor of 100 that provides agreement of the rU₃₀ SAXS profiles. If we assume Debye screening, interchain repulsion depends only on the valence and concentration of the ions in solution. Therefore, it is not surprising that higher concentrations of Na⁺ are more effective than lower concentrations of Mg²⁺ in reducing interparticle repulsion. Interestingly, less repulsion is measured in poly rU in 100 (or 200) mM Na⁺ than in 1 (or 2) mM Mg²⁺, despite their identical SAXS profiles. (N.B. the factor of 100 between Na⁺ and Mg²⁺ found to yield agreement of SAXS profiles, reports on intra chain screening, e.g. between the phosphates on a given chain. A comparable factor has been reported in other studies of single-stranded nucleic acids^51,52. Interparticle screening, reported by B₂ values, reflects interactions between different molecular chains. It depends in a non-trivial way on both the valence and concentration of the charge compensating ion^59,60, and is related to the lower entropic cost of associating a smaller number of Mg ions around the nucleic acid compared to monovalent Na ions^61,62.) Finally, the distinct behavior of these sequences in Mg²⁺ is once again recovered: lower inter-chain repulsion (smaller B₂) is found in poly rA than in poly rU across all probed [Mg²⁺]. Magnesium has a larger effect on chains of rA compared to rU.

This enhanced inter-chain screening of rA₃₀ compared to rU₃₀ in Mg²⁺ containing solutions hints at differences in the composition of the ion atmosphere between the two constructs. This composition can be determined by counting the number of excess ions around chains of each sequence. Quantifying the number of ions in the atmosphere around a nucleic acid provides challenges: differences in ion numbers across solution conditions are likely to be small, and both monovalent and divalent ions must be counted. Given these constraints, a precise measurement method that is sensitive to various ionic species is required. Buffer exchange atomic emission spectroscopy (BE-AES) is a technique that is becoming more commonly applied to biological systems ^{31,56,63–65}. This technique grants high precision ion counts of Na and Mg ions around a biomolecule and is therefore well suited to evaluating the ionic environment around RNA.

Using BE-AES, we counted the number of excess Na and Mg ions around rU₃₀ and rA₃₀ in a mixed ion solution consisting of 20 mM Na⁺ and varying [Mg²⁺] (see Methods, SI, Tables S3–6 and Figs. S23–25). We restricted our measurements to solution conditions that show no signs of precipitation (0–3 mM Mg²⁺). Due to the sensitivity of the measurement, a 25bp DNA duplex was used as a control ^56,65, and two [NA] utilized to mitigate potential errors arising from aggregation or precipitation of the sample ⁶⁶. As in past work ⁵⁶, low [Na⁺] was used to maximize signal-to-noise and to emphasize the expected effects of Mg²⁺. These conditions were also designed to match the SAXS experiments. Additional precautions were taken to avoid experimental artifacts (see SI).

For the 25bp DNA control in the absence of Mg²⁺, BE-AES returns (0.75±0.08) Na ions per phosphate. This number agrees with both our previous measurement ⁵⁶ (0.81±0.10) and other authors’ work ⁶⁵ (0.82±0.05). The agreement persists across all probed salt conditions (SI, Fig. S26) illustrating the robustness of these experiments across independent measurements.

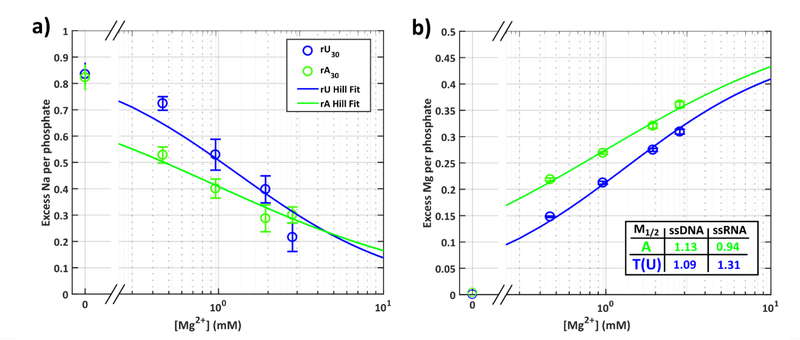
We now turn to measurements on the single-strand constructs. Figure 5 shows the number of excess ions per phosphate as a function of the bulk [Mg²⁺]. At [Mg²⁺] = 0 mM, both rA₃₀ and rU₃₀ are electrostatically equivalent, with 24 excess Na ions attracted to each. This number agrees (on a per phosphate basis) with a recent measurement of rU₄₀ under the same conditions ³¹, and is also consistent with the identical B₂ measured in this condition. Compensation of the total molecular charge of each ssRNA polymer (29e⁻) is completed through exclusion of 5 anions from the atmosphere of each (Figure S28).

Figure 5:

Ion counting results give the number of excess a) Na and b) Mg ions per phosphate around rU₃₀ (blue) and rA₃₀ (green). Hill fits to the ion numbers are shown as solid lines (see Supplementary Methods). Competition coefficients (M_1/2) from the Hill fits are provided in the inset, together with previously derived values from ssDNA analogues. Error bars for ion counting results are the standard error in the mean across 12 independent measurements.

As we introduce Mg²⁺ to the buffer, striking differences in ion atmosphere composition become apparent. Looking first at the number of excess Mg ions, we see that across all probed conditions a greater number of Mg ions are associated with rA₃₀ than with rU₃₀. These differences are captured by calculating the competition coefficient (M_1/2), which defines the concentration of Mg ions required to compete (replace) half the Na ions from the ion atmosphere. For rA₃₀, we find M_1/2 = (0.94±0.13), while for rU₃₀, M_1/2 = (1.31±0.32). From the ratio of these competition coefficients, approximately 40% more bulk [Mg²⁺] is required to displace half the Na ions from the atmosphere of rU₃₀ compared to rA₃₀.

Turning next to the Na ion counts, at all but the highest [Mg²⁺], rU₃₀ has more associated Na ions than rA₃₀. This result is expected given the Mg ion counts, and the condition of electroneutrality, but is more than trivial when put into context. If we compare competition coefficients to those previously measured for ssDNA analogues (dT₃₀ and dA₃₀) ⁵⁶, we find the ssDNA results lie in between the values measured here for rA₃₀ and rU₃₀ (Figure 5 inset): less bulk [Mg²⁺] is required to displace half the Na ions around ssDNA than rU₃₀. The ion dependencies and preferences for both ssRNAs are unique and distinct from the ssDNA results (SI, Fig. S27, Table S7). Strands containing multiple rA bases are ‘magnets’ for Mg²⁺, attracting significantly more of these ions than ssDNA; strands containing multiple rU bases are Na⁺ centers, holding Na⁺ much more effectively than either chains of rA or ssDNA.

Structural modelling from SAXS data

The precipitation and ion atmosphere data provide compelling evidence for unique ion interactions with a given RNA sequence, while the SAXS experiments show that these interactions have an impact on global chain conformations. To further interpret the structural changes reported by SAXS in a more comprehensive manner, we modified an iteratively refining model building system previously applied to ssDNA, for ssRNA ⁴³. In this method, a dinucleotide step library based on crystal structure surveys is used to provide building blocks for single strands containing RNA nucleotides. A large pool is built using a Monte-Carlo procedure, and models that best fit the SAXS data are selected for every solution condition. The weights of dinucleotide steps that constitute these chains are increased, and a new structure pool proposed. This process is iterated until fits to the data converge. This procedure is run independently for each construct and solution condition (see Methods and SI, Fig. S29, Tables S8–9).

Previously, in addition to the SAXS data, we constrained the selection of dinucleotide steps by NMR sugar pucker weights, the frequency of steps in crystal structure surveys and steric hindrances. Given the CD data shows no significant stacking interactions for poly rU, we further constrained the possible conformers by eliminating stacked dinucleotide steps from pools that fit rU₃₀, while leaving these steps present in pools that fit rA₃₀.

Model conformations show ion specific backbone geometries

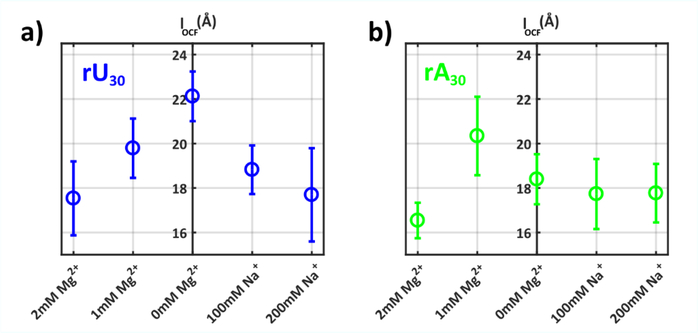
The refinement procedure provides a structural representation of underlying strand states for additional analysis. Results for all solution conditions, including characteristic conformations, are shown in SI (Figs. S30–39). We first quantify mid-range chain order by calculating the correlation lengths (l_OCF) for strand states in each ionic condition (Figure 6). This important metric provides an additional check of model reasonability, through comparison to measured persistence lengths. Within rU₃₀, a gradual decrease in l_OCF, from ~22Å to 18Å is observed with increasing salt: the chain backbone gradually ‘forgets’ its original direction as the degree of screening increases. These values agree within error with previous work on rU_40, in which SAXS and FRET were paired to constrain potential persistence length values ²⁵. As expected, because the SAXS profiles are identical, the poly rU correlation lengths recapitulate the factor of 100 between Na and Mg ion concentrations: there is no special role or significant differences between these equivalent intrachain screening conditions. For rA bases however, the correlation lengths appear independent of added Na⁺ or Mg²⁺, suggesting that base-stacking is an important factor that determines local chain geometries.

Figure 6:

The mean correlation lengths of SAXS refined model conformations for a) rU₃₀ and b) rA₃₀ are given for each solution condition. Error bars indicate standard deviation of correlation lengths across selected ensembles.

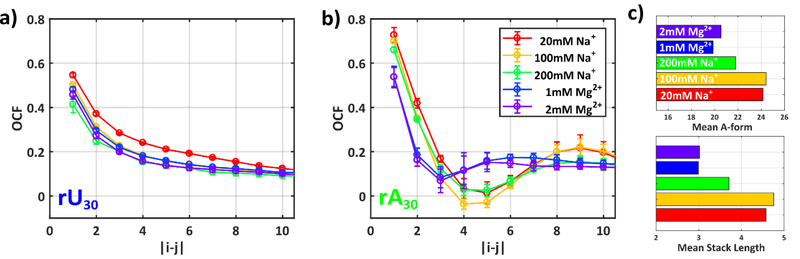
While the correlation lengths determine the directional ‘stiffness’ of a polymer, this metric clearly fails to capture the differences observed in the Kratky plots for rA chains. To more globally describe the route of the phosphate backbone across all length scales, we calculate the orientation correlation function (OCF) between chain phosphates ⁶⁷, displayed in Figure 7 for both constructs (see SI and Fig. S40). We also plot the mean number and length of stacked bases in rA conformations. Across all conditions for rU₃₀, a gradual monotonic decay is observed as chains gradually ‘forget’ their orientation for longer distances along the backbone. This decay becomes more pronounced with increased screening efficacy. Again, the symmetry in poly rU about Na⁺ and Mg²⁺ is recovered, OCFs of 1 (or 100) or 2 (or 200) Mg (Na) are identical. This latter finding is not surprising given that the models are derived from raw SAXS profiles which themselves are similar.

Figure 7:

The short to medium range ordering of all chains in each experimental condition can be assessed by calculating the orientation correlation function (OCF) for the ensemble structures. This parameter describes the mean orientation of phosphates on the RNA backbone, as defined in Supplementary Figure S40. The mean OCFs for the ensemble structures are shown for a) rU₃₀ and b) rA₃₀. c) The mean number and length of stacked bases in poly rA are provided for each condition. Error bars in all figures signify one standard deviation of the presented metric across all fit ensembles.

The OCFs computed from structural models of rA₃₀ display oscillatory behavior for all values of Na⁺ explored. A dramatic decay of the OCF between four neighboring phosphates on the backbone (x axis 0–4) leads to a resurgence of correlation at larger phosphate separations. This motif indicates ordering within a chain that repeats on a length scale of ~10 phosphates and corresponds to the A-form base-stacking interaction. It is highly prevalent in all of the models in the Na⁺ salt series, constituting ~23 stacks per chain. Differences in OCFs and stacked bases with increasing [Na] are marginal, with only the 200 mM Na⁺ data point showing a slightly decreased OCF amplitude.

With the addition of Mg²⁺, correlations emerge on a length scale that is absent from the Na⁺ series. A much sharper initial fall off is found for phosphate separations of 1–3, which subsequently yields a new correlation at phosphate separations of 4–6. For larger separations, chain directional persistence resembles the Na⁺ dependent form, consistent with the correlation lengths of Figure 6. The average number of stacked bases within chains in the Mg²⁺ series remains equivalent to that found in Na⁺. Crucially the mean length is slightly shortened from 5 to 3. This results in the dramatically varying stack arrangement on the backbone, leading to the sizeable differences reflected in the SAXS data.

While base-stacking generally favors straight (mechanically stiff) chain conformations, and therefore correlation lengths, we note that our definition of l_OCF (equation 5) accounts for how rapidly the correlations of the phosphate backbone fall off with distance. The OCF provides quantitative characterization of this decay length. In poly rA structures, short stacked segments punctuated by free bases result in a much more rapid decay of the OCF compared to poly rU, and therefore a shorter correlation length in this formalism.

DISCUSSION

Numerous investigations have contributed to show how base identity impacts ssRNA conformations ^53,54 and that ions have distinct interactions with different chain sequences ^41,42,68. Our comprehensive study of ssRNA’s ion atmosphere and structure links the above findings. These results provide new insight into the effects of ion association on the structures of ssRNA, and the ion binding roles of single-strand regions within more complex RNAs.

Most significant is our quantification of the dramatic difference in the number and type of ions attracted to different homopolymeric sequences. The data of Figs. 4 and 5 (B₂ and ion counting results) strongly suggest that this latter point is more than a simple preference of one sequence for Mg ions: in comparison to ssDNA analogues, the average number of Mg ions per phosphate attracted to poly rU is lower, while for poly rA it is higher. This point is particularly surprising given that unique ion atmospheres are usually attributed to structured RNAs, rather than to disordered elements themselves. The competition coefficients reported in Figure 5 show that disparate RNA sequences have a strong affinity for or against Mg ion interactions. This characteristic is not observed in identically charged ssDNA, either as poly dT or poly dA, where electrostatic equivalence occurs across a comparable range of mixed ion conditions⁵⁶. We find that poly rA preferentially attracts Mg²⁺ and poly rU preferentially attracts Na⁺ relative to their ssDNA equivalents in these mixed salt solutions.

Of the two sequences explored, poly rU shows a much subtler dependence on ions than poly rA. In the former, the uracil base lends to identical strand conformations in Mg²⁺ or Na⁺, when concentrations are suitably scaled. Ionic strength (scaled) drives chain conformations rather than ion identity. The raw SAXS profiles and the derived OCFs reveal that Na⁺ and Mg²⁺ yield identical backbone conformations (Figure 8 top panel). This result suggests that non-specific, diffuse ion interactions with the poly rU chain drives ordering on short to medium length scales. This conclusion has been drawn in previous FRET and pulling experiments ^21,23,25, quantifying elastic properties of rU chains. It is further confirmed by rU₃₀’s solubility in all tested [Na⁺] or [Mg²⁺]. The close agreement of scattering profiles across ion types confirms that the 100 fold intrachain screening efficiency of [Mg²⁺] relative to [Na⁺] remains appropriate for poly rU, as previously found for other nucleic acids ^25,52.

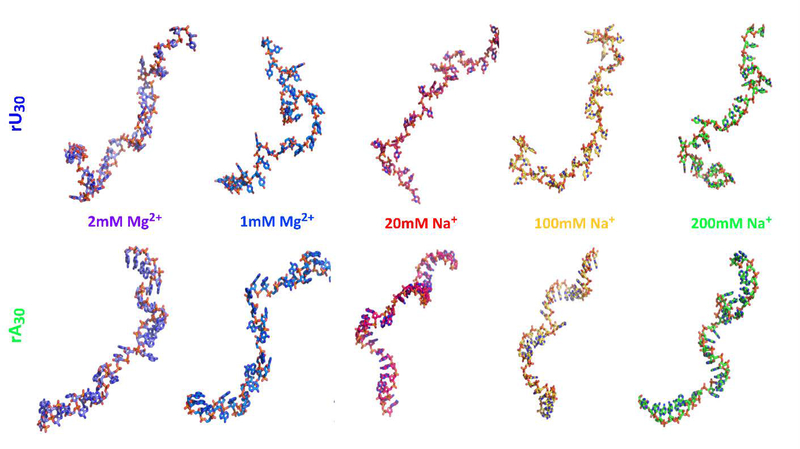
Figure 8:

A single conformer of poly rU and poly rA (derived from the SAXS data), selected from the ensemble generated for each salt condition, illustrates the general trends prevalent in the models. For simplicity, we display only one structure for each condition. The full set of models required to fit the SAXS data are provided in the SI. The scrunched, ‘cage-like’ conformations of the poly rA backbones (lower structures) are present in Mg²⁺ containing solutions but absent from solutions containing only Na⁺. The former structures place backbone phosphates, sugar OH groups and base nitrogens in geometries which favor Mg²⁺ ion associations. Representative structures for each experimental condition can be found at the SASBDB codes as referenced in Figure 3.

The OCFs (derived from the SAXS data) demonstrate the pronounced stiffness of rU chains in all probed conditions, as well as the retained correlation of bases separated by ~10 monomer steps. Interestingly, this residual order is not shared by dT₃₀, where all correlations decay by these separations ⁴³. The OCFs for poly rU are further poorly described by a simple worm-like chain model. Base-stacking has previously been proposed as the origin of this stiff behavior ²⁵, however the absence of signal in our CD data and other pulling experiments would seem to challenge this idea ^23,28. Pairing the OCFs with the ion counting data suggests that a different ion association mechanism explains these correlations. Salt bridges between Na ions, water and 2’OH groups may reinforce the rU backbone, resulting in a random coil like structure, but one that is stiffer than a DNA analogue. This mechanism has previously been proposed in pulling and NMR experiments to explain differences in stiffness between poly dT and poly rU ^23,69,70. Here, it would explain the favored propensity for Na⁺ and increased stiffness over the DNA analogues, though this is open to further investigation.

The second sequence studied, poly rA displays a much richer connection between ion type and structure. As expected, the strong tendency of A bases to stack is on display through the Na⁺ titration. The CD experiments and SAXS-derived modelling show that the initial low salt (Na⁺ only) starting chain state features a high number of stacked bases, in good agreement with both MD predictions and experimental observations ^{22,32,37,39,71}. These stacked geometries typically provide resistance against both large scale structural changes and ion binding interactions, as the winding phosphate backbone fails to provide enough coordination points to capture and dehydrate ions in the atmosphere ⁷². In Na⁺ titrations, the OCF results and CD data weakly depend on ion concentration, suggesting that the short-range helical order is maintained even as the chain globally compacts due to increased local screening.

The addition of Mg²⁺ to poly rA induces a dramatic shift in backbone conformation, most evident from the SAXS data (Kratky plots). The nature of the rearrangement is revealed by the OCFs: a new length scale for correlation emerges that is shorter than that expected for a purely A-form stacking interaction. This new geometry retains the high degree of stacking, assessed from CD and model compositions, but the average length of stacked bases is slightly reduced. From the BE-AES data, it appears that these conformations have an enhanced propensity for Mg²⁺ ions when compared to other ssNA constructs, suggesting an intimate connection between the two.

The rA₃₀ model conformations selected when Mg²⁺ is present (Figure 8) show pockets or cage like structures formed by phosphates, 2’ hydroxyl groups and adenine bases. These geometries could potentially offer favorable regions for dehydrated magnesium associations to the backbone, as has been catalogued in crystallographic surveys of Mg²⁺ binding architectures in RNA ⁷³, and more specifically by NMR studies on Mn²⁺ binding to poly rA ³⁸. An energetic balance appears to be tipped when Mg ions are present, favoring ion association and capture at the cost of reducing the mean stack length. While the limited resolution of SAXS precludes atomic level insights, the detected differences in backbone orientations are consistent with global chain conformations that are highly suggestive of ion-RNA interactions. We recognize that SAXS based refinement of ensembles is subject to the biases inherent in model construction. Despite this caveat, the proposed structures offer one plausible visual representation of single-stranded RNA that is consistent with results of our numerous biophysical experiments. Further support for this hypothesis comes from water release measurements which show an anomalously large dehydration effect upon addition of Mg²⁺ to poly rA compared to any other ssNA construct (both DNA and RNA), and posit 3–5 direct Mg²⁺ coordinations to rA chains, involving phosphates and adenine bases ^41,42. Localized associations of Mg²⁺ to the rA backbone is highly likely to induce precipitation, as we and others have observed, and would neatly explain all our experimental data.

Clearly, RNA chemistry imparts a rich degree of ion and conformational heterogeneity. Nature exploits the balance of sequence, added 2’OH group and ion identity/hydration to achieve the wide variety of RNA structures compatible with their breadth of function. While many functional RNAs, such as riboswitches and ribosomes, rely on mixed sequences to facilitate bending and folding, it is interesting to note the importance of homopolymer tracts in biological systems. In particular, poly A tails act as markers on mature mRNAs, signaling and specifically recruiting poly A binding proteins for further processing ⁷⁴. In juxtaposition, long poly U tracts are found in lncRNAs. Although the role of these tracts is a topic of current debate, it is speculated that they act as generic protein binding sites for the myriad of protein partners that lncRNAs entertain ^75,76. Differences in the ion atmosphere may make the latter sequences more amenable to protein binding, as weaker electrostatic forces preferentially displace monovalent than divalent ions. In addition, the propensity of A-tracts to self-structure around divalent ions may require a higher cost for binding, as more bonds need to be disrupted. Thus, this work suggests that nature not only utilizes specific (in the case of poly rA) or non-specific (in the case of poly rU) conformations and H-bonding networks to recruit protein binding partners but may also exploit a sequence dependent ion atmosphere as yet another flag for interactions.

CONCLUSION

Here we have used ion counting methods, spectroscopy and SAXS to quantitatively investigate the effects of sequence on the ion atmosphere and conformation of ssRNAs. These incisive measurements demonstrate that RNA sequence not only instills a unique conformation to chains, but also unique ion binding preferences. The data presented here are sufficiently comprehensive to seed comparisons with computational models of highly flexible and highly charged polymers; such motifs have traditionally eluded description by simple models. Given the prevalence of RNA homopolymers in biological and physical systems, the results of this study likely have broad implications in both experiment and theoretical modelling.