Impact of observational error on heart rate variability analysis

Abstract

An observational error of heart rate variability (HRV) may arise from many factors, such as a limited sampling frequency, QRS complexes detection process, preprocessing procedures and others. In our study, we focused on the first two origins of measurement error. We introduced a model of observational error and suggested universal descriptors for the assessment of its resultant magnitude in terms of time, frequency as well as nonlinear parameters. For this purpose, we applied Monte Carlo simulations which showed that the most sensitive to observational error are: pNN50 (the proportion of pairs of successive RR intervals that differ by more than 50 ms) and markers obtained from frequency analysis. On the other hand, the most resistant are other time domain parameters as well as the short and long-term slopes of Detrended Fluctuation Analysis (DFA). We postulate that the observational error should be considered in population studies, when different recorders are used in the research centres. Additionally, in the case of patients with similar etiology of disease but with different heart rhythms abnormalities the scatter of HRV parameters will also be observed due to the subject's the time series variability.

Biomedical engineering; Cardiology; Error approximation; Monte Carlo methods; Signal processing

1. Introduction

The development of electrocardiographic measurement technology has been rapid. Nowadays, even cheap, basic electrocardiographic devices have quite high sampling rates, and so errors in RR interval measurement, stemming solely from the sampling frequency, is rather low. There are, however at least two additional sources of measurement errors. The first is the false positive detection of the R peak in the electrocardiography (ECG) measurements obtained from mobile devices. This is mainly due to the muscle movement, which introduces amplitudes higher than the measured ECG signal. The second one occurs according to the detection of RR intervals not from the ECG signal, but from other physiological data such as photoplethysmography (optical measurement using green LEDs), which are popular in smartwatches for runners. One should note that such blood light-absorbing signal is much smoother with a prominent R peak. The detection of the R peak position in such signals may cause low data reliability.

As 20 years ago the recommended sampling frequency was only larger than 100 Hz, nowadays, in clinical practice, the sampling frequency should be larger than 512 Hz. In the case of 512 Hz, the ECG measurement is burdened by a 2 ms measurement error. For older recordings, where the sampling frequency was 128 Hz, the measurement error was four times larger in magnitude. One ought to note that this relation between the magnitudes of the observational error and the sampling frequency does not take into account preprocessing processes – such as QRS detection, artefact interpolation, trend removal or filtering procedures (these aspects were discussed in detail in [1], [2], [3]). Unfortunately, many researchers are not aware of the significance of observational errors in their final results. Every stage of the data processing propagates the error, whose magnitude in the computational procedure is usually unknown and difficult to estimate. Thus, the results of the analysis might be unreliable. The determined HRV parameters might differ in their sensitivity to observational error, especially in case of nonlinear methods, which require many calculation steps. Reliable assessment of the HRV parameters is related to the finite sampling of electrocardiographic signal. Low sampling frequencies distort the R-peak waveform [4] and then such error is propagated during QRS detection. For example, Hejjel and Roth [5] resampled model tachograms with different rates and compared the obtained HRV parameters. Authors suggested $1\text{kHz}$ as the optimum rate to get accurate values of time domain HRV parameters without interpolation. It was demonstrated [5] that pNN50 is the most sensitive to a low ECG sampling. For frequency parameters, Ziemssen et al. [6] noticed that low sampling influences the results of patients with reduced RR interval variability.

An approximate entropy (ApEn) and the Recurrence-Plot-Derived Indices were explored in [7]. It was showed that not only the finite resolution but also the variability of the signal have an impact on the resultant error of the analysis (these factors were introduced as the signal to resolution of the neighbourhood ratio (SRN)). The errors due to the resolution of the time series in ApEn or indices derived from the recurrence plots can be very high, when the SRN is close to an integer number. Another study [8] focused on the influence of the QRS complex detection errors on ApEn and Sampling entropy (SampEn). The authors concluded that even for high QRS detection (above 98%), discrimination among classes of signals based on these measures might be inaccurate by even a few outliers.

In this paper we focused on the problem of the propagation of observational error during the computations of the time domain, the frequency domain and selected nonlinear parameters of HRV. We assumed that each RR interval was burdened with an observational error and we postulated its form. Taking into account the experimental data recordings, we generated artificial data and determined HRV parameters. These are well-known methods in cardiological practice. Finally, we proposed a unified procedure to assess impact of the observational error on the HRV analysis.

2. Methods

Let us consider a random variable $X_i$ proposed as follows:

$$X_i=R{R}_i+{\xi }_i,$$ (1)

where ${\xi }_i$ is an observational error and $R{R}_i$ intervals are determined from ECG signal. We assumed that the errors are independent and normally distributed with zero mean and standard deviation σ i.e. ${\xi }_i\sim \mathcal{N}(0;\sigma )$. The $X_i$ distribution is also normal: $\mathcal{N}(R{R}_i;\sigma )$ with the mean equal to $R{R}_i$. We proposed a Gaussian distribution of the observational error as a continuation of the study from [9], where a uniform distribution was proposed. We assumed that σ has a range of milliseconds in real applications (see the discussion about the relation between measurement error and sampling frequency in the Introduction). Please note that observational error for RR intervals consists not only of the uncertainty related to the sampling frequency as well as the uncertainty related to QRS detection procedure [10]. Usually, the preprocessing (such as filtering) of the time series is a common procedure in HRV analysis, during which magnitudes of propagated errors would increase significantly.

2.1. Medical data

We performed computations on the real data from the MIT-BIH Arrhythmia Database [10] – the most popular set of signals used for scientific tests, which contains 48 half-hour excerpts of two-channel ambulatory ECG recordings. Before computations, for each ECG signal, the RR intervals were determined. We detected QRS complexes with open source software [11], which took part in the PhysioNet Challenge 2014. Here, we decided to perform the computations using all RR intervals from the database.

Usually, the HRV parameters are determined only from NN intervals (sinus rhythm). We proposed a unified and simplified methodology to estimate of the influence of the measurement error on popular HRV indices. We did not remove or replace arrhythmias in our simulations, because the raw signal (without preprocessing procedures) works as the ground truth [12] required for comparison. What is more, the preprocessing depends on the type of disturbances [3] in the time series. Such an approach has limited application to the assessment of autonomic control and further clinical interpretation.

2.2. Simulation procedure

For this paper, we made the working assumption that the original RR intervals detected from the MIT-BIH Arrhythmia Database recordings are not burdened by any observational error. According to Eq. (1), for each real RR interval, we added a random variable from a Gaussian distribution with $\sigma =1,2,3,\dots ,8\text{ms}$. As a result, we obtained new data with artificial observational noise. We generated a thousand signals affected by such error, which are a statistical sample in the Monte Carlo (MC) algorithm. Further, we performed computations on the artificial time series to determine HRV parameters for each dataset separately. Finally, we proposed a quantitative characterisation of the impact of the introduced observational error on resultant HRV markers in relation to the original time series.

2.3. HRV parameters

For each ‘noisy’ time series, we computed five time domain parameters [13]: mean RR, SDRR, standard deviation of successive differences of RR intervals (SDSD), root mean square of successive differences of RR intervals (RMSSD), pRR50. It should be noted that we used the abbreviation pRR50 instead of pNN50 and SDRR instead of SDNN, because our computations were not solely limited to NN.

In clinical practice, three determinants are widely used as noninvasive parameters to characterise the autonomic nervous system activity: the power spectrum of the low frequency band (LF), the high frequency band (HF) and their ratio: LF/HF [14]. Following the discussion given in [1] and [15], we calculated the frequency markers using the Lomb Scargle periodogram. The signals were not resampled and the ectopic beats were not removed from the original series. This reflects our assumption that the original RR intervals are set to be the ground truth in MC simulations. Additionally, we considered four nonlinear parameters: SampEn, ApEn [16] and two scaling exponents of Detrended Fluctuation Analysis (DFA) – short ${\alpha }_1$ and longterm ${\alpha }_2$ [17].

2.4. Estimation of impact of observational error on HRV parameters

We obtained some unique sample distributions of HRV parameters (specified in sec. HRV parameters) from the MC simulations. We determined the standard deviation β of each distribution as the magnitude of the method error. The method error is one that occurs from propagation of the observational error during the successive computations of the HRV parameters. Subsequently, it was possible to compare the standard deviation σ of observational error used in MC simulations and β. In order to assess the sensitivity of the HRV parameters to the observational error, we proposed the percentage descriptor $p_k$, which provides information about the maximal (total) error of HRV parameter $Y_k$:

$$p_k=\frac{\langle |Y_k(RR+\xi )-Y_k(RR)|\rangle +\beta }{Y_k(RR)}\cdot 100\text{\%},$$ (2)

where $Y_k$ are

$$Y_k\in \{\text{mean}\text{RR [ms]},\text{SDRR [ms]},\text{SDSD [ms]},\text{RMSSD [ms]},\text{pRR50 [\%]},\text{ApEn [–]},\text{SampEn [–]},{\alpha }_1[\text{–}],{\alpha }_2[\text{–}],\text{LF [\%]},\text{HF [\%]},\text{LF/HF [–]}\}$$

The component $\langle |Y_k(RR+\xi )-Y_k(RR)|\rangle$ in Eq. (2) represents the discrimination between the HRV parameters computed for the time series without observational error and the ‘noisy’ RR data. The variable β characterises the scatter of a single HRV parameter. The sum in the nominator should be interpreted as follows: it assesses the potential maximal error of the calculations of the HRV parameter by taking into account two factors – the deviation of the $Y_k$ parameter from the true value according to random variable ξ (first component of the sum in Eq. (2)) and the propagation of the observational error in parameter computations (component β). The normalisation by $Y_k(RR)$ is proposed to obtain the percentage value.

3. Results

We have divided our results into two subsections. In the first part, we present some typical MC simulations on a selected recording. In the second, we discuss in detail the magnitudes of the total HRV parameter errors (Eq. (2)) associated with certain scales of observational error (σ).

3.1. MC simulation results for a typical HRV recording

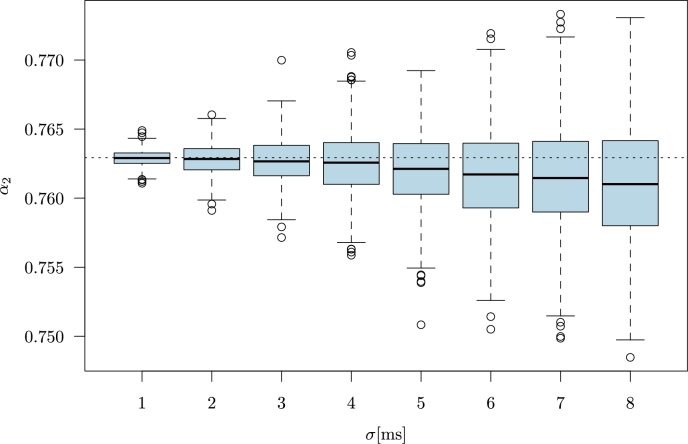
In Fig. 1, we show the results for the RR intervals of ECG file no. 101 from the MIT-BIH Arrhythmia Database. The selected recording contains 99% NN intervals (sinus rhythm). As an example, we present the results for ${\alpha }_2$ computed with the MC simulation. Each box-plot represents the distribution of 1000 values of the longterm scaling exponent ${\alpha }_2$. The standard deviation σ is from a narrow range of milliseconds (from 1 to $8\text{ms}$). Please note that ${\alpha }_2$ for the original RR intervals (horizontal dotted line) is much larger than 0.5. Consequently, the ${\alpha }_2$ median experiences a decreasing trend due to increasing σ. The increment of the magnitude of observational error changes the properties of the analysed time series. The data start to resemble uncorrelated noise for which ${\alpha }_2=0.5$. Therefore, if the original data were characterized by ${\alpha }_2=0.76$, then with increasing σ, the ${\alpha }_2$ parameter decreases for artificial data with additive Gaussian noise. Conversely, if ${\alpha }_2$ was smaller than 0.5, then ${\alpha }_2$ exponent would increase with the magnitude of observational error σ. The extension of box-plots with increasing σ (Fig. 1) indicates that β becomes larger too, but not excessively (the ranges in the vertical line are small). This result shows that during computational procedures the observational error is propagated but exponent ${\alpha }_2$ has low sensitivity to observational noise.

Figure 1.

The computations for RR intervals of ECG file no. 101 from MIT-BIH Arrhythmia Database [10]. Each box-plot represents 1000 values of α₂ parameter obtained from the time series with added Gaussian noise (MC simulation). The Gaussian noise has zero mean and standard deviation σ given in milliseconds. Horizontal dotted line marks the parameter α₂ for the original recording.

3.2. Quantitative estimation of observational error impact on total HRV parameter error

We have expressed the results according to the $p_k$ ratios, which are the total errors of the HRV parameters. The total error reflects a relation to the observational error, which occurs due to device recording and due to methods required for QRS detection.

In Table 1, we show $p_k$ for all $Y_k$ markers used in the computations, except SDSD as the results did not differ from the SDRR parameter in range of $p_k$. The smallest sensitivity to observational error is determined for the time domain parameters: mean RR, SDRR, SDSD and RMSSD. This small sensitivity is expressed by low $p_k$ means, not exceeding 3% for the largest observational noise ($\sigma =8\text{ms}$). It should be stated that computations for the time domain parameters are the simplest among all of the markers presented here, and so the low complexity of calculation may explain the low total error.

Table 1.

The ratios of the total error p_k ± SD for the HRV parameters with increasing magnitude of observational error σ. The p_k values in the table are normalised and presented in %, following Eq. (2). The results are obtained from the MC simulations repeated 10³ times for each signal of the MIT BIH Database separately.

HRV parameter	σ = 2 ms	σ = 4 ms	σ = 5 ms	σ = 8 ms
MeanRR	0.005 ± 0.0005	0.01 ± 0.001	0.01 ± 0.001	0.02 ± 0.002
SDRR	0.07 ± 0.06	0.21 ± 0.19	0.3 ± 0.28	0.66 ± 0.66
RMSSD	0.13 ± 0.15	0.4 ± 0.51	0.58 ± 0.75	1.3 ± 1.78
pRR50	1.98 ± 2.37	4.14 ± 5.09	5.94 ± 8.77	15.0 ± 24.3
α1	0.13 ± 0.10	0.32 ± 0.30	0.42 ± 0.43	0.83 ± 0.97
α2	0.15 ± 0.11	0.34 ± 0.25	0.44 ± 0.34	0.79 ± 0.67
ApEn	1.37 ± 1.23	2.27 ± 2.26	3.04 ± 3.09	6.13 ± 6.02
SampEn	1.79 ± 1.45	2.79 ± 2.39	3.71 ± 3.21	7.47 ± 6.42
LF	12.89 ± 21.56	25.86 ± 32.53	28.88 ± 35.42	37.94 ± 41.97
HF	4.69 ± 5.44	10.49 ± 11.47	11.39 ± 12.00	14.85 ± 15.22
LF/HF	18.04 ± 28.20	36.86 ± 45.13	41.35 ± 49.46	54.51 ± 59.66

For all HRV parameters, there is an increase in the mean of $p_k$ and its standard deviation with σ (see $p_k$ and its standard deviation (SD) given in Table 1). The largest observational error influence on the HRV parameter is for pRR50 and for frequency domain markers. The limited sampling frequency in the recorded ECG signal is associated with imprecise determination of pRR50. We estimated that the pRR50 values computed by the software for HRV analysis might differ from the true value by more than 15%. Such a result is in agreement with [5], whereby low reliability of this parameter was demonstrated to result from finite sampling.

The results presented in Table 1, for LF, HF and for the LF/HF ratio should be analyzed and interpreted with particular caution. According to [1], the procedure of resampling incorporates error itself, and so the observational error is a component of the total error in frequency parameters. In our computations no resampling and no ectopic beats removal were applied. As a result, the spectral parameters presented here cannot be used for the proper estimation of autonomic nervous system activity [1].

Among nonlinear parameters, the entropies are the most sensitive to observational error, although the short and longterm exponents of DFA are characterised by a small total error. Entropies are well known to be sensitive to non-stationarity in the form of outliers [16]. Such outliers are exacerbated due to the observational noise added in MC simulations. As a result, the total error increases. The low sensitivity of DFA slopes to the observational error can be explained by two main factors: i) the methodology of DFA, which prefers averaging in widows, ii) the procedure for determining ${\alpha }_1$ and ${\alpha }_2$, which minimises Gaussian incorporation by fitting procedure. In many cases of $p_k$ the SDs are extremely large (larger than the mean). A large SD shows that there are major differences between time series properties in the members of the group, a phenomenon often obtained in clinical practise.

4. Discussion

We have presented a study of the impact of observational error on the time, frequency domain and selected nonlinear HRV measures. In our study, the observational error is due to a limited sampling rate and QRS detection process. We assumed that the observational errors for subsequent RR intervals are independent and normally distributed with zero mean and standard deviation σ. In order to assess the magnitude of the total HRV parameter errors, we applied MC simulations and used the data from the MIT-BIH Arrhythmia Database.

We proposed two descriptors characterising the resultant error of the HRV parameters: the standard deviation β of the distributions obtained from the MC simulations (the method error) and the $p_k$ ratio (the total error). The method error results from the observational error propagation in the computations of the HRV parameters and increases with σ. We showed that beside the spectral markers, pRR50, SampEn and ApEn are the most sensitive to observational error and their estimates may differ from the true value by more than 15%, 5% and 5% respectively and in case of the frequency parameters the difference is even larger. This deviation is caused by lack of preprocessing procedures for time series with the occurrence of ectopic beats. Specified percentage values were obtained for the data, whereby the observational error was equal to $8\text{ms}$. On the other hand, the time domain parameters such as SDSD, RMSSD are resistant to observational error. Similar results were found for mean RR and for the DFA parameters $({\alpha }_1,{\alpha }_2)$.

HRV analysis has been often used for risk stratification as well as for the prediction of cardiovascular events. In one review [18], a summary of the populations studies in application to resting ECG/ambulatory ECG is presented. The authors indicated that the effect of decreased HRV indices (such as SDNN, RMSSD and frequency markers) are associated with an increased mortality risk. The comparisons in the presented examples are often performed by taking into account terciles and quartiles of the HRV indexes. In this approach, it is possible to limit the influence of the sampling error while distinguishing two or more clinical conditions.

Our study showed that the comparisons of time series from different recorders should be conducted carefully while paying attention to the sampling frequency rates and the QRS detection procedures [12]. The differences in HRV results may arise due to measurement error in population studies, when many research centres cooperate in data collection. ECG monitoring for the same patient performed by different ECG devices may lead to deviations in HRV characteristics. Finally, we indicate that patients with a similar disease etiology but with different heart rhythms abnormalities should also be analysed separately. In such cases, the low variability of the time series and outliers occurrence (like arrhythmic behaviour) will cause an increased total error in the HRV parameters.

Declarations

Author contribution statement

Monika Petelczyc: Conceived and designed the experiments; Analyzed and interpreted the data; Wrote the paper.

Jan Jakub Gierałtowski: Conceived and designed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data.

Barbara Żogała-Siudem: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data.

Grzegorz Siudem: Conceived and designed the experiments; Analyzed and interpreted the data.

Funding statement

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Competing interest statement

The authors declare no conflict of interest.

Additional information

No additional information is available for this paper.