Skip to main content
PMC home page
JAMA Network logoLink to JAMA Network
. 2020 Feb 26;5(5):1–9. doi: 10.1001/jamacardio.2020.0013

A New Equation for Calculation of Low-Density Lipoprotein Cholesterol in Patients With Normolipidemia and/or Hypertriglyceridemia

Maureen Sampson 1, Clarence Ling 1, Qian Sun 1, Roa Harb 1, Mohmed Ashmaig 2, Russell Warnick 2, Amar Sethi 3, James K Fleming 4, James D Otvos 5, Jeff W Meeusen 6, Sarah R Delaney 6, Allan S Jaffe 7, Robert Shamburek 8, Marcelo Amar 8, Alan T Remaley 8,✉
PMCID: PMC7240357  PMID: 32101259

Key Points

Question

Is it possible to provide a more accurate estimate of low-density lipoprotein cholesterol in patients with hypertriglyceridemia and/or a low level of low-density lipoprotein cholesterol?

Findings

In this decision analytical model, a new low-density lipoprotein cholesterol equation was derived that can be used to more accurately estimate the low-density lipoprotein cholesterol level in patients with plasma triglyceride levels up to 800 mg/dL and is at least equivalent or more accurate than other equations for patients with normolipidemia and a low level of low-density lipoprotein cholesterol.

Meaning

The new low-density lipoprotein cholesterol equation can be readily implemented by clinical laboratories without incurring any additional costs compared with a standard lipid panel and may improve the use of calculated low-density lipoprotein cholesterol in cardiovascular disease risk management.

Abstract

Importance

Low-density lipoprotein cholesterol (LDL-C), a key cardiovascular disease marker, is often estimated by the Friedewald or Martin equation, but calculating LDL-C is less accurate in patients with a low LDL-C level or hypertriglyceridemia (triglyceride [TG] levels ≥400 mg/dL).

Objective

To design a more accurate LDL-C equation for patients with a low LDL-C level and/or hypertriglyceridemia.

Design, Setting, and Participants

Data on LDL-C levels and other lipid measures from 8656 patients seen at the National Institutes of Health Clinical Center between January 1, 1976, and June 2, 1999, were analyzed by the β-quantification reference method (18 715 LDL-C test results) and were randomly divided into equally sized training and validation data sets. Using TG and non–high-density lipoprotein cholesterol as independent variables, multiple least squares regression was used to develop an equation for very low-density lipoprotein cholesterol, which was then used in a second equation for LDL-C. Equations were tested against the internal validation data set and multiple external data sets of either β-quantification LDL-C results (n = 28 891) or direct LDL-C test results (n = 252 888). Statistical analysis was performed from August 7, 2018, to July 18, 2019.

Main Outcomes and Measures

Concordance between calculated and measured LDL-C levels by β-quantification, as assessed by various measures of test accuracy (correlation coefficient [R2], root mean square error [RMSE], mean absolute difference [MAD]), and percentage of patients misclassified at LDL-C treatment thresholds of 70, 100, and 190 mg/dL.

Results

Compared with β-quantification, the new equation was more accurate than other LDL-C equations (slope, 0.964; RMSE = 15.2 mg/dL; R2 = 0.9648; vs Friedewald equation: slope, 1.056; RMSE = 32 mg/dL; R2 = 0.8808; vs Martin equation: slope, 0.945; RMSE = 25.7 mg/dL; R2 = 0.9022), particularly for patients with hypertriglyceridemia (MAD = 24.9 mg/dL; vs Friedewald equation: MAD = 56.4 mg/dL; vs Martin equation: MAD = 44.8 mg/dL). The new equation calculates the LDL-C level in patients with TG levels up to 800 mg/dL as accurately as the Friedewald equation does for TG levels less than 400 mg/dL and was associated with 35% fewer misclassifications when patients with hypertriglyceridemia (TG levels, 400-800 mg/dL) were categorized into different LDL-C treatment groups.

Conclusions and Relevance

The new equation can be readily implemented by clinical laboratories with no additional costs compared with the standard lipid panel. It will allow for more accurate calculation of LDL-C level in patients with low LDL-C levels and/or hypertriglyceridemia (TG levels, ≤800 mg/dL) and thus should improve the use of LDL-C level in cardiovascular disease risk management.

This decision analytical model describes the design of a more accurate low-density lipoprotein cholesterol equation for patients with a low level of low-density lipoprotein cholesterol and/or hypertriglyceridemia.

Introduction

The clinical management of patients at risk for cardiovascular disease (CVD) is critically dependent on their level of low-density lipoprotein cholesterol (LDL-C).1 It is routinely calculated using results from the standard lipid panel (total cholesterol, high-density lipoprotein-cholesterol [HDL-C], and triglycerides [TGs]) by the equation by Friedewald et al2 (hereafter referred to as the Friedewald equation): LDL-C = (Total Cholesterol) − (HDL-C) − (TGs/5). The main source of error in this equation is the TGs/5 term, which serves as an estimate of very low-density lipoprotein-cholesterol (VLDL-C). The ratio of cholesterol to TGs in VLDL-C can vary considerably, depending on its size and other factors, which diminishes the accuracy of the equation for high-TG samples.2 Although tests for directly measuring LDL-C (dLDL-C) have been developed, it is still common practice to calculate LDL-C because of the extra cost of adding dLDL-C to the lipid panel and the poor analytical performance of some dLDL-C tests.3,4,5,6

Many LDL-C equations besides the Friedewald equation have been described,7,8,9,10,11,12,13,14,15,16,17,18,19,20 but most are not significantly better than the Friedewald equation compared with the β-quantification reference method, a swinging-bucket ultracentrifugation precipitation-based procedure. Recently, Martin et al21,22 developed an equation (hereafter referred to as the Martin equation) based on the Vertical Auto Profile test, which is a vertical-rotor ultracentrifugation-based method.23 It replaces the fixed TG denominator of 5 in the Friedewald equation with an empirical denominator (or factor) that varies depending on levels of TGs and non–HDL-C.21 It is more accurate than the Friedewald equation, particularly for low–LDL-C samples21,22 that are now more common because of more effective lipid-lowering therapy.24,25 In 2018, the new American College of Cardiology and American Heart Association guidelines on CVD risk biomarkers recommended the Martin equation as the preferred calculation method for low–LDL-C samples26 because of the clinical importance of LDL-C accuracy in the management of patients treated with potent new agents such as proprotein convertase subtilisin/kexin type 9 (PCSK9) inhibitors that can markedly decrease LDL-C levels.24,25

Clinical laboratories usually do not report LDL-C levels for patients with hypertriglyceridemia (TG levels ≥400 mg/dL [to convert to millimoles per liter, multiply by 0.0113]) because of large errors in the Friedewald estimate of VLDL-C.4 Instead, dLDL-C or apolipoprotein B testing is often performed, which increases costs. Furthermore, many patients with elevated TG levels have suppressed LDL-C levels, thus making their already low levels of LDL-C even more difficult to accurately estimate because of the greater proportion of error due to VLDL-C. Even for samples with only modest TG elevations, significant errors in estimating the LDL-C level can still occur.4,18,27 Now that most CVD guidelines have endorsed the use of nonfasting samples for an initial lipid screening,26 the inaccuracy of calculated LDL-C owing to elevated TG levels will be a greater problem in the future. Although the Martin equation has an adjustable factor for dividing TG levels, it has never been validated for patients with hypertriglyceridemia.21,22 Moreover, the Vertical Auto Profile method on which it is based may sometimes underestimate the VLDL-C level in high-TG samples.23,28,29

Using β-quantification results from a patient population with a high frequency of hypertriglyceridemia, we developed a new LDL-C equation. It can be used to more accurately estimate the LDL-C level in patients with TG levels up to 800 mg/dL and is also slightly more accurate than other equations for patients with normolipidemia. Furthermore, it correctly classifies more patients from a general population of patients with dyslipidemia into different LDL-C treatment groups than other equations and thus should improve the use of calculated LDL-C in CVD risk management.

Methods

Results of β-quantification for LDL-C were obtained from a deidentified data set from 8656 fasting patients tested on multiple occasions at the National Institutes of Health Clinical Center from January 1, 1976, to June 2, 1999. Research under this study was exempted by the National Institutes of Health Institutional Review Board because data were deidentified. Statistical analysis was performed from August 7, 2018, to July 18, 2019. Female patients accounted for 47% of the population (n = 4068), and the mean age was 49 years (range, 1-83 years). The laboratory performing the testing participated in the Centers for Disease Control and Prevention Lipids Standardization Program. Results outside the first and 99th percentiles for each lipid parameter, along with type III hyperlipidemic samples as determined by a VLDL-C to TGs ratio greater than 0.33, were removed from analysis, leaving a total of 18 715 LDL-C test results that were split into equally sized training and validation data sets. The median TG level was 149 mg/dL (interquartile range, 98-253 mg/dL), and 14% of the samples had a TG level of 400 mg/dL or more. The median non–HDL-C level was 190 mg/dL (interquartile range, 144-248 mg/dL) (to convert to millimoles per liter, multiply by 0.0259). The complete distribution of lipid test results for the internal data set and those of the external validation data sets (Mayo Medical Lab, Laboratory Corporation of America Holdings, Prism Health Dx Inc, and Pacific Biomarker) can be seen in the Table and are further described in eAppendix 2 in the Supplement. Dependent variables (TG and non–HDL-C levels) were converted into higher-degree and more complex multivariable terms using Excel (Microsoft Corp) and were used to develop equations for VLDL-C and LDL-C as described in eAppendix 1 in the Supplement by multiple least squares regression analysis with JMP (SAS Institute Inc). Confidence intervals for LDL-C risk level classification were calculated using the Wald test.

Table. Distribution of Lipid Results for Internal and External Databases.

Database Range Mean (SD) Median (25th-75th Percentile) Skewness Kurtosis
NIH (N = 18 715)
HDL-C, mg/dL 5-102 40.8 (15.7) 39 (30-50) 0.6 0.6
TC, mg/dL 78-759 246.8 (87.9) 232 (186-288) 1.4 3.2
TG, mg/dL 38-3162 273.8 (392.9) 149 (98-253) 3.9 17.9
Non–HDL-C, mg/dL 53-734 206 (89.8) 190 (144-248) 1.4 3.4
BQ LDL-C, mg/dL 10-707 158.6 (83.0) 143 (103-199) 1.5 4.4
Mayo Clinic (N = 27 646)
HDL-C, mg/dL 1-201 46.3 (15.0) 44 (36-54) 1.0 3.0
TC, mg/dL 45-1830 193.6 (58.1) 188 (157-223) 3.3 57.0
TG, mg/dL 26-2690 164.7 (140.0) 127 (87-195) 5.1 50.8
Non–HDL-C, mg/dL 22-1810 147.2 (56.4) 140 (111-175) 3.8 68.5
BQ LDL-C, mg/dL 9-1775 117.7 (47.1) 112 (88-141) 5.1 118.1
Pacific Biomarker (N = 1245)
HDL-C, mg/dL 24-169 70.0 (27.7) 64 (47-89) 0.6 -0.3
TC, mg/dL 87-329 173.1 (35.4) 170 (150-194) 0.5 0.6
TG, mg/dL 27-785 113.6 (67.5) 98 (70-135) 2.8 14.9
Non–HDL-C, mg/dL 35-292 103.1 (36.3) 99 (77-123) 1.0 1.8
BQ LDL-C, mg/dL 21-222 87.0 (31.4) 84 (64-106) 0.7 0.6
Prism Health Dx Inc (N = 21 206)
HDL-C, mg/dL 10-190 53.3 (15.9) 51 (42-62) 1.0 2.1
TC, mg/dL 56-1134 188.7 (47.8) 185 (157-215) 1.7 17.1
TG, mg/dL 22-2779 152.9 (144.8) 114 (79-171) 5.5 54.3
Non–HDL-C, mg/dL 3-1100 135.4 (46.8) 130 (103-160) 2.0 20.5
Beckman dLDL-C, mg/dL 10-1214 113.3 (39.4) 110 (86-136) 2.4 46.3
LabCorp (N = 231 682)
HDL-C, mg/dL 5-180 51 (15.8) 48 (40-60) 1.0 1.8
TC, mg/dL 47-890 184 (44.6) 180 (152-210) 0.8 2.7
TG, mg/dL 16-2797 171 (156.3) 127 (88-194) 4.9 43.1
Non–HDL-C, mg/dL 11-874 133 (44.0) 128 (101-157) 1.1 3.8
Roche dLDL-C, mg/dL 3-618 109 (37.4) 106 (82-132) 0.7 1.6
Open in a new tab

Abbreviations: BQ, β-quantification; dLDL-C, direct low-density lipoprotein cholesterol; HDL-C, high-density lipoprotein cholesterol; LabCorp, Laboratory Corporation of America Holdings; LDL-C, low-density lipoprotein cholesterol; NIH, National Institutes of Health; TC, total cholesterol; TGs, triglycerides.

SI conversion factors: To convert total cholesterol, HDL-C, non–HDL-C, LDL-C, and dLDL-C to millimoles per liter, multiply by 0.0259; and TGs to millimoles per liter, multiply by 0.0113.

Results

To derive a more accurate LDL-C equation, we first improved the estimation of VLDL-C. The following bivariate quadratic equation was developed by multiple least squares regression, using β-quantification test results that contained a broad range of TG (38-3162 mg/dL) and non–HDL-C (53-734 mg/dL) values.

As with the Friedewald equation, Equation 1 contains a TG term, but it is divided by 8.59 instead of 5:

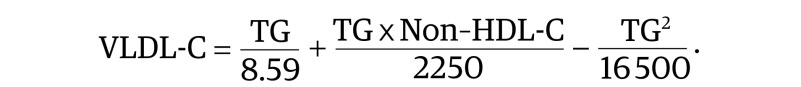graphic file with name jamacardiol-5-540-iea.jpg

This term captures the linear component of the association between the TG level and the VLDL-C level (eFigures 1 and 2 in the Supplement). The (TG × Non–HDL-C) term accounts for the interaction between the 2 independent variables. Its maximum value occurs in the upper right corner of the VLDL-C contour plot (eFigure 1D in the Supplement) owing to cholesterol enrichment by the cholesteryl ester transfer protein.30 The TG2 term can be considered a correction factor. It adjusts for the fact that patients with the most extreme elevations of TGs have proportionally more chylomicrons and nascent VLDL enriched in TGs rather than cholesterol.31

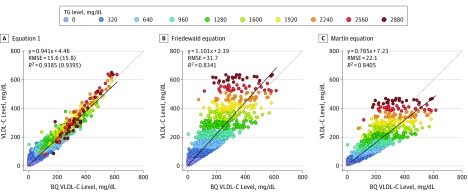
In Equation 1, VLDL-C level is more accurately calculated than by the Friedewald or Martin equations (Figure 1) or by alternative equations (eTable and eFigure 3 in the Supplement), particularly for patients with hypertriglyceridemia. Equation 1 has a higher correlation coefficient (R2) and a lower root mean square error (RMSE) than other equations, and these parameters were almost identical between the training and validation set, indicating that the regression model was not overfitted. The residual error plots for TG levels (eFigure 4A-C in the Supplement) and non–HDL-C levels (eFigure 4D-F in the Supplement) show that the Friedewald and Martin equations can lead to both falsely high and falsely low VLDL-C values owing to improper factor adjustment for TG and non–HDL-C levels. The Friedewald equation most often shows a positive bias against TG levels. In contrast, the Martin equation shows a slight negative bias for TG levels less than 700 mg/dL, but a positive bias for TG levels of 700 mg/dL or more (eFigure 5 in the Supplement). Although the HDL-C level was not directly used as a variable in Equation 1, residual errors for this parameter are also more closely centered around zero than for the other equations (eFigure 4G-I in the Supplement).

Figure 1. Calculated vs β-Quantification (BQ) Very Low-Density Lipoprotein Cholesterol (VLDL-C) Levels.

Figure 1.

Open in a new tab

A, VLDL-C was calculated and plotted against VLDL-C as measured by BQ for Equation 1. B, VLDL-C was calculated and plotted against VLDL-C as measured by BQ for the Friedewald equation. C, VLDL-C was calculated and plotted against VLDL-C as measured by BQ for the Martin equation. The dotted line represents the line of identity, and the solid line is the linear fit for the indicated regression equation. Root mean square error (RMSE) and correlation coefficient (R2) values are from the validation data set (n = 9358), whereas the numbers in parentheses are corresponding values from the training set (n = 9357). The points on the graphs indicating the individual samples are color-coded according to triglyceride (TG) level. The color number scale for individual points indicates the start of the interval. To convert TGs to millimoles per liter, multiply by 0.0113; and to convert VLDL-C to millimoles per liter, multiply by 0.0259.

To determine the effective factor for each equation, we divided the TG level by either the measured (β-quantification) or calculated VLDL-C level and made contour plots for the mean factor at each possible TG and non–HDL-C level. For β-quantification, the mean factor ranged from 2 to more than 26 (eFigure 2 in the Supplement). Samples requiring the highest factors occurred in the lower right corner of the plot with the highest TG to non–HDL-C ratios. These high-factor values are consistent with the known TG to cholesterol ratios of chylomicrons and nascent VLDL-C and are the types of samples that lead to falsely elevated VLDL-C levels by the other equations. In contrast, high non–HDL-C samples in the upper left corner of the plot require much lower factors and can be falsely low by other equations. Compared with the other equations, the factor values for Equation 1 match the β-quantification factor plot much better.

When we restricted our analysis to just normolipidemic samples (TG level <400 mg/dL and non–HDL-C level <220 mg/dL), we found that the 180-cell factor table used in the Martin equation yielded very similar VLDL-C results to Equation 1 (eFigure 6 in the Supplement) and could be fitted by a slight modification to Equation 1 (eFigure 5 in the Supplement). Unlike Equation 1, results for the Martin equation did not always vary smoothly with respect to TG and non–HDL-C levels owing to the quantile nature of its table and likely because of a less-than-optimum factor assignment for some data cells. The fitted equation for the factor table used in the Martin equation also did not perform well when applied to hypertriglyceridemic samples.

With the same terms for VLDL-C as Equation 1, the following Equation 2 can be used to calculate LDL-C:

graphic file with name jamacardiol-5-540-ieb.jpg

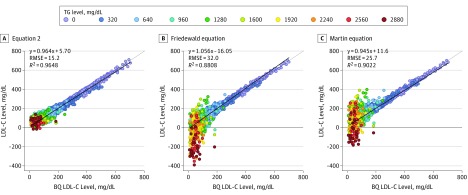
Equation 2 is similar to the Friedewald equation in that VLDL-C and HDL-C are subtracted from total cholesterol, but the inclusion of an intercept and allowing the coefficients to vary for each term resulted in a better fit with β-quantification than the other equations (Figure 2). Negative LDL-C values sometimes occurred for both the Friedewald and Martin equations owing to their negative bias for hypertriglyceridemic samples, but negative LDL-C values rarely occurred for Equation 2 (Figure 2).

Figure 2. Calculated vs β-Quantification (BQ) Low-Density Lipoprotein Cholesterol (LDL-C) Levels.

Figure 2.

Open in a new tab

A, LDL-C was calculated with Equation 2 and plotted against LDL-C as measured by BQ. B, LDL-C was calculated with the Friedewald equation and plotted against LDL-C as measured by BQ. C, LDL-C was calculated with the Martin equation and plotted against LDL-C as measured by BQ. The points on the graphs indicating the individual samples are color-coded according to triglyceride (TG) level. The color number scale indicates the start of the interval. The dotted line represents the line of identity, and the solid line is the linear fit for the indicated regression equation. R2 indicates correlation coefficient; RMSE, root mean square error. To convert LDL-C to millimoles per liter, multiply by 0.0259.

To compare all the different LDL-C equations with a single integrated index of accuracy, we calculated the mean absolute difference (MAD) from β-quantification at different TG and non–HDL-C cutpoints (eFigure 7 in the Supplement). When only hypertriglyceridemic samples were analyzed, Equation 2 had the lowest MAD value. For TG levels less than 400 mg/dL, Equation 2 was again the most accurate, but differences between the top equations were relatively minor. Similar improvements in the accuracy of Equation 2 were found when results were stratified by non–HDL-C level. When compared with β-quantification, the new equation was more accurate than other LDL-C equations (slope, 0.964; RMSE = 15.2 mg/dL; R2 = 0.9648; vs Friedewald equation: slope, 1.056; RMSE = 32 mg/dL; R2 = 0.8808; vs Martin equation: slope, 0.945; RMSE = 25.7 mg/dL; R2 = 0.9022), particularly for patients with hypertriglyceridemia (MAD = 24.9 mg/dL; vs Friedewald equation: MAD = 56.4 mg/dL; vs Martin equation: MAD = 44.8 mg/dL).

To further validate Equation 2, we tested it on 2 external β-quantification data sets. The first was from patients from a large national reference laboratory that should be representative of dyslipidemia in the general population (eFigure 8A-C in the Supplement). For TG levels less than 400 mg/dL, all 3 equations were similar in accuracy, but based on its MAD value, Equation 2 had a slight advantage and showed an even greater advantage for hypertriglyceridemic samples. This was particularly true for the Friedewald equation, which, in 0.4% of the cases, yielded negative LDL-C values for hypertriglyceridemic samples. The second β-quantification data set was from patients treated with a statin with or without a cholesteryl ester transfer protein inhibitor (eFigure 8D-F in the Supplement). There was only a limited number of hypertriglyceridemic samples, and 68% of samples had LDL-C levels less than 100 mg/dL, but as before, Equation 2 was more accurate than the other equations.

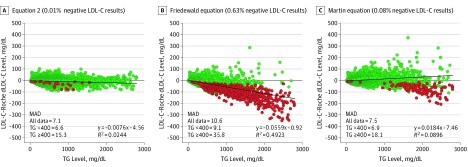
We also compared the LDL-C equations with 2 commonly used dLDL-C tests in a general population. For the Roche dLDL-C (Figure 3A-C), both Equation 2 and the Martin equation closely matched the dLDL-C results, although the Martin equation showed a negative bias for TG levels of 1000 mg/dL or more. The Friedewald equation showed a much poorer concordance with the Roche dLDL-C test owing to its much larger negative bias and had many more negative LDL-C test results than the other equations. Similar results were found for the Beckman dLDL-C test (eFigure 8G-I in the Supplement). Whether the Roche dLDL-C test was used only in male vs female individuals or only in fasting vs nonfasting individuals, the linear fit with Equation 2 was nearly identical (eFigure 9 in the Supplement), indicating that Equation 2 is unaffected by sex or fasting state.

Figure 3. Residual Error Plots for Low-Density Lipoprotein Cholesterol (LDL-C) by Various Equations.

Figure 3.

Open in a new tab

A, Difference between calculated LDL-C and direct LDL-C (dLDL-C) results (Roche; n = 174 179) for patients from a major reference laboratory is shown for Equation 2 plotted against triglyceride (TG) level. B, Difference between calculated LDL-C and dLDL-C results for patients from a major reference laboratory is shown for the Friedewald equation plotted against TG level. C, Difference between calculated LDL-C and dLDL-C results for patients from a major reference laboratory is shown for the Martin equation plotted against TG levels. Negative LDL-C test results are shown as red dots, placed on top of nonnegative test results (green dots), and hence make it appear that they are more abundant. The exact percentage of negative LDL-C test results are indicated for each panel. The mean absolute deviation (MAD) for all indicated equations is shown in each panel for each data set for TG levels less than 400 mg/dL or 400 mg/dL or higher. To convert LDL-C to millimoles per liter, multiply by 0.0259; and to convert TGs to millimoles per liter, multiply by 0.0113.

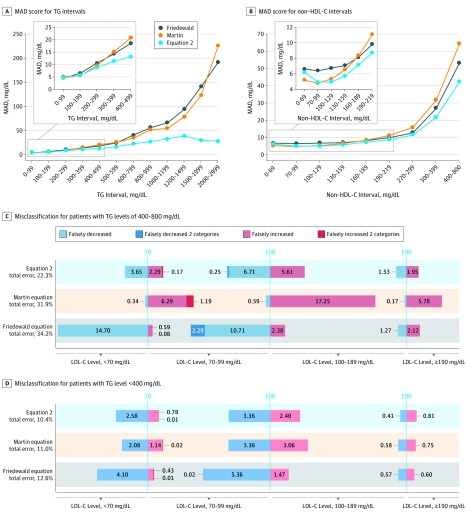
Using the large external β-quantification data set (n = 27 646), we determined the MAD score for various TG or non–HDL-C intervals (Figure 4A and B) to provide a population-independent estimate of accuracy. For TG intervals less than 400 mg/dL, all 3 equations had similar MAD scores, although the score for Equation 2 was slightly better for TG levels between 200 and 400 mg/dL. For TG levels of 400 mg/dL or more, the Friedewald equation shows a marked increase in MAD values with increasing TG levels because its fixed factor of 5 is too low for these types of samples. The Martin equation is slightly more accurate than the Friedewald equation at higher TG levels, but its factor values are still too low for specimens with the most elevated TG levels. The MAD values for Equation 2 also increase with increasing TG levels, but to a lesser degree, and stay below 30 mg/dL up to a TG level of 1000 mg/dL (Figure 4A). When analyzed by non–HDL-C intervals (Figure 4B), Equation 2 also had lower MAD values than the other equations, particularly at higher intervals.

Figure 4. Test Accuracy and Classification of Patients Into Low-Density Lipoprotein Cholesterol (LDL-C) Treatment Categories.

Figure 4.

Open in a new tab

A, Mean absolute deviation (MAD) score for LDL-C from a general population with dyslipidemia (n = 27 646) is shown for Equation 2 (blue line), the Friedewald equation (gray line), and the Martin equation (orange line) for the indicated triglyceride (TG) intervals. The inset shows a close-up for low TG samples. B, MAD score is shown for Equation 2 (blue line), the Friedewald equation (gray line), and the Martin equation (orange line) for the indicated non–high-density lipoprotein cholesterol (HDL-C) intervals. The inset shows a close-up for low non–HDL-C samples. C, Misclassification at the 3 LDL-C treatment thresholds (70, 100, and 190 mg/dL) for the 3 LDL-C equations is shown for patients with TG levels from 400 to 800 mg/dL (n = 1177). D, Misclassification at the 3 LDL-C treatment thresholds (70, 100, and 190 mg/dL) for the 3 LDL-C equations is shown for patients with TG levels less than 400 mg/dL (n = 26 312). Blue bars indicate patients misclassified into the lower LDL-C treatment category in which the bar is plotted. Red bars indicate patients misclassified into the higher LDL-C treatment category in which the bar is plotted. Darker blue and red bars indicate misclassifications that crossed more than 1 LDL-C treatment category. The numbers in the bars indicate the percentage of total patients misclassified and are proportional to the bar length. To convert LDL-C and non–HDL-C to millimoles per liter, multiply by 0.0259; and to convert TGs to millimoles per liter, multiply by 0.0113.

To assess the potential association of the improved accuracy of Equation 2 with the clinical management of patients, we calculated the misclassification rate for the categorization of patients into different LDL-C treatment groups (Figure 4C and D). We did this for patients with TG levels from 400 to 800 mg/dL because we observed that the misclassification rate of 29% for Equation 2 for the TG interval of 600 to 800 mg/dL (mean, 677 mg/dL; n = 221) nearly approached the same misclassification rate of 29% for the Friedewald equation at the 350 to 450 mg/dL TG interval (mean, 394 mg/dL; n = 418). Equation 2 had 35% fewer misclassifications than the Friedewald equation, which showed a clear negative bias for low LDL-C levels, and 30% fewer misclassifications than the Martin equation, which showed an overall positive bias. Equation 2 also had less misclassifications that crossed 2 LDL-C treatment thresholds than the other equations. For TG levels less than 400 mg/dL, Equation 2 was similar in its misclassification rate to the Martin equation but showed a more substantial advantage over the Friedewald equation, which still had a negative bias for low LDL-C values (Figure 4D). Similar results regarding the improved accuracy of Equation 2 vs the other equations could also be observed by comparing its concordance to β-quantification in almost the entire range of LDL-C risk-level categories (eFigure 10 in the Supplement).

Discussion

The derivation of a more accurate LDL-C equation for patients with hypertriglyceridemia and/or low LDL-C levels has practical value. The new equation uses results only from the standard lipid panel and has no intellectual property restrictions, so it will not increase the cost of testing. It is more complicated than other equations, but the result can be automatically calculated by most laboratory information systems without any additional software changes, unlike those that may be needed to implement the 180-cell factor table used by the Martin equation.21 Because the new equation is only slightly more accurate than the other equations for patients with normolipidemia, it can be reserved only for patients with hypertriglyceridemia and/or low LDL-C levels. From a practical standpoint, however, it may be simpler to use the new equation for all patients rather than use 2 different equations for calculating LDL-C levels.

Another important advantage of Equation 2 is that it is based on β-quantification, the reference method for LDL-C level. The Vertical Auto Profile test, on which the Martin equation is based, is also an ultracentrifugation density-based separation procedure. However, it is less well suited for hypertriglyceridemic samples because TG-rich lipoproteins can adhere to the sides of the vertical centrifugation tubes, leading to an underestimation of VLDL-C level.23,28,29 This possibility could account for the positive LDL-C bias for the Martin equation for TG levels less than 700 mg/dL, but at higher TG levels, the Martin equation, like the Friedewald equation, shows a negative bias owing to factor values that are too low.

Instead of not reporting any LDL-C test results or using a dLDL-C test, Equation 2 makes feasible the calculation of LDL-C for TG levels up to 800 mg/dL with a misclassification rate comparable to that of the Friedewald equation at 400 mg/dL. Equation 2 should therefore be suitable for almost all patients because a TG level of 800 mg/dL is greater than the 99th percentile in the general population. Use of the new equation was associated with 35% fewer misclassifications of patients with hypertriglyceridemia into different LDL-C treatment categories compared with the Friedewald equation and thus should improve the clinical management of patients. Misclassified patients, particularly those who cross more than 1 LDL-C treatment threshold, may not receive the correct lipid-lowering therapy and may have worse clinical outcomes. In part because of the limitations in the accuracy of LDL-C, non–HDL-C was recommended by the American College of Cardiology and American Heart Association as the main lipid biomarker in patients with hypertriglyceriemia.32 The most recent guidelines,26 however, are based primarily on LDL-C, so a more accurate calculated LDL-C could be useful for risk management in this population. Equation 2 could also be used to partition non–HDL-C into cholesterol in LDL-C vs TG-rich lipoproteins. In several large population studies, TG-rich lipoprotein cholesterol has been found to be more strongly associated with CVD than LDL-C,33,34 but this association depends on correctly measuring LDL-C level.

The greatest clinical benefit of Equation 2 may be for patients with low LDL-C levels. The Martin equation is also more accurate than the Friedewald equation for such patients,21,22 which is the reason many clinical laboratories have switched to this equation. Low LDL-C levels were once rare but are much more common with the use of anti-PCSK9 therapy.24,25 Given the high cost of anti-PCSK9 therapy, the initial eligibility of patients for this type of therapy critically depends on the accurate measurement of LDL-C levels. Even once a patient is using anti-PCSK9 therapy, it is important to accurately monitor LDL-C levels. Because of the overestimation of the VLDL-C level by the Friedewald equation and some of the other equations, these patients can have falsely low or even nonsensical negative LDL-C results, which may discourage more aggressive lipid-lowering therapy that has been shown to be beneficial in high-risk patients.25 However, apolipoprotein B and other particle measures of LDL are more closely tied to residual CVD risk than LDL-C when these measures are discordant, a difference that will likely persist no matter how accurately LDL-C is measured.35

Limitations

This study has some limitations. One limitation is that a relatively unique population with a high frequency of hypertriglyceridemia was used to establish Equation 2, but it was validated with large numbers of external samples (>250 000) in multiple populations. Another limitation is that patients with type III hyperlipidemia were excluded from analysis because their lipoproteins contain an abnormal lipid composition, but the frequency of this disorder in the general population is less than 1%.28 β-Quantification is also not specific for LDL-C and can sometimes include cholesterol from chylomicron remnants, intermediate-density lipoprotein, and lipoprotein(a), but these are also proatherogenic, and thus this bias may not significantly diminish the association of calculated LDL-C with CVD.

Conclusions

We developed a more accurate LDL-C equation for patients with hypertriglyceridemia (TG level ≤800 mg/dL) and/or a low level of LDL-C that also performs well for patients with normolipidemia. Additional studies are needed in other populations, particularly those with low LDL-C levels, to more fully validate the equation and to better understand its clinical utility.

Supplement.

eAppendix 1. Derivation of Equations

eAppendix 2. External Validation Datasets

eFigure 1. Relationship of TG and non–HDL-C With VLDL-C

eFigure 2. Derivation of Equation 1

eFigure 3. Calculated Versus β-Quantification VLDL-C

eFigure 4. Calculated Versus β-Quantification VLDL-C

eFigure 5. Evaluation of Factor Table for Martin Equation

eFigure 6. Contour plots for VLDL-C for Martin equation and Equation-1

eFigure 7. MAD Score for LDL-C Equations

eFigure 8. Residual Error Plots for LDL-C by Various Equations

eFigure 9. Calculated Versus dLDL-C by Gender and Fasting State

eFigure 10. Classification of Patients into LDL-C Risk-Level Categories

eTable. Description of Existing Equations for Calculating LDL-C

Click here for additional data file. (11.6MB, pdf)

References

  • 1.Wilson PWF, Polonsky TS, Miedema MD, Khera A, Kosinski AS, Kuvin JT. Systematic review for the 2018 AHA/ACC/AACVPR/AAPA/ABC/ACPM/ADA/AGS/APhA/ASPC/NLA/PCNA Guideline on the Management of Blood Cholesterol. Circulation. 2019;139(25):e1144-e1161. doi: 10.1161/CIR.0000000000000626 [DOI] [PubMed] [Google Scholar]
  • 2.Friedewald WT, Levy RI, Fredrickson DS. Estimation of the concentration of low-density lipoprotein cholesterol in plasma, without use of the preparative ultracentrifuge. Clin Chem. 1972;18(6):499-502. doi: 10.1093/clinchem/18.6.499 [DOI] [PubMed] [Google Scholar]
  • 3.Miller WG, Myers GL, Sakurabayashi I, et al. . Seven direct methods for measuring HDL and LDL cholesterol compared with ultracentrifugation reference measurement procedures. Clin Chem. 2010;56(6):977-986. doi: 10.1373/clinchem.2009.142810 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.Langlois MR, Chapman MJ, Cobbaert C, et al. ; European Atherosclerosis Society (EAS) and the European Federation of Clinical Chemistry and Laboratory Medicine (EFLM) Joint Consensus Initiative . Quantifying atherogenic lipoproteins: current and future challenges in the era of personalized medicine and very low concentrations of LDL cholesterol: a consensus statement from EAS and EFLM. Clin Chem. 2018;64(7):1006-1033. doi: 10.1373/clinchem.2018.287037 [DOI] [PubMed] [Google Scholar]
  • 5.Oliveira MJA, van Deventer HE, Bachmann LM, et al. . Evaluation of four different equations for calculating LDL-C with eight different direct HDL-C assays. Clin Chim Acta. 2013;423:135-140. doi: 10.1016/j.cca.2013.04.009 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.van Deventer HE, Miller WG, Myers GL, et al. . Non-HDL cholesterol shows improved accuracy for cardiovascular risk score classification compared to direct or calculated LDL cholesterol in a dyslipidemic population. Clin Chem. 2011;57(3):490-501. doi: 10.1373/clinchem.2010.154773 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Vujovic A, Kotur-Stevuljevic J, Spasic S, et al. . Evaluation of different formulas for LDL-C calculation. Lipids Health Dis. 2010;9(1):27. doi: 10.1186/1476-511X-9-27 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.de Cordova CMM, de Cordova MM. A new accurate, simple formula for LDL-cholesterol estimation based on directly measured blood lipids from a large cohort. Ann Clin Biochem. 2013;50(pt 1):13-19. doi: 10.1258/acb.2012.011259 [DOI] [PubMed] [Google Scholar]
  • 9.Dansethakul P, Thapanathamchai L, Saichanma S, Worachartcheewan A, Pidetcha P. Determining a new formula for calculating low-density lipoprotein cholesterol: data mining approach. EXCLI J. 2015;14:478-483. doi: 10.17179/excli2015-162 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Rasouli M, Mokhtari H. Calculation of LDL-cholesterol vs. direct homogenous assay. J Clin Lab Anal. 2017;31(3):e22057. doi: 10.1002/jcla.22057 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Gazi IF, Elisaf M. LDL-cholesterol calculation formulas in patients with or without the metabolic syndrome. Int J Cardiol. 2007;119(3):414-415. doi: 10.1016/j.ijcard.2006.07.139 [DOI] [PubMed] [Google Scholar]
  • 12.Vohnout B, Vachulová A, Blazícek P, Dukát A, Fodor G, Lietava J. Evaluation of alternative calculation methods for determining LDL cholesterol. Vnitr Lek. 2008;54(10):961-964. [PubMed] [Google Scholar]
  • 13.Anandaraja S, Narang R, Godeswar R, Laksmy R, Talwar KK. Low-density lipoprotein cholesterol estimation by a new formula in Indian population. Int J Cardiol. 2005;102(1):117-120. doi: 10.1016/j.ijcard.2004.05.009 [DOI] [PubMed] [Google Scholar]
  • 14.Puavilai W, Laorugpongse D, Deerochanawong C, Muthapongthavorn N, Srilert P. The accuracy in using modified Friedewald equation to calculate LDL from non-fast triglyceride: a pilot study. J Med Assoc Thai. 2009;92(2):182-187. [PubMed] [Google Scholar]
  • 15.Saiedullah M, Rahman MR, Rahman M, Khan MAH, Begum S. A simple modification of Friedewald's formula to calculate low-density lipoprotein cholesterol up to serum triglyceride concentration of 1000 mg/dL. Bang J Med Biochem. 2009;(2):62-65. [Google Scholar]
  • 16.Hattori Y, Suzuki M, Tsushima M, et al. . Development of approximate formula for LDL-chol, LDL-apo B and LDL-chol/LDL-apo B as indices of hyperapobetalipoproteinemia and small dense LDL. Atherosclerosis. 1998;138(2):289-299. doi: 10.1016/S0021-9150(98)00034-3 [DOI] [PubMed] [Google Scholar]
  • 17.Rao A, Parker AH, el-Sheroni NA, Babelly MM. Calculation of low-density lipoprotein cholesterol with use of triglyceride/cholesterol ratios in lipoproteins compared with other calculation methods. Clin Chem. 1988;34(12):2532-2534. doi: 10.1093/clinchem/34.12.2532 [DOI] [PubMed] [Google Scholar]
  • 18.Ahmadi S-A, Boroumand M-A, Gohari-Moghaddam K, Tajik P, Dibaj S-M. The impact of low serum triglyceride on LDL-cholesterol estimation. Arch Iran Med. 2008;11(3):318-321. [PubMed] [Google Scholar]
  • 19.Chen Y, Zhang X, Pan B, et al. . A modified formula for calculating low-density lipoprotein cholesterol values. Lipids Health Dis. 2010;9(1):52. doi: 10.1186/1476-511X-9-52 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.DeLong DM, DeLong ER, Wood PD, Lippel K, Rifkind BM. A comparison of methods for the estimation of plasma low- and very low-density lipoprotein cholesterol: the Lipid Research Clinics Prevalence Study. JAMA. 1986;256(17):2372-2377. doi: 10.1001/jama.1986.03380170088024 [DOI] [PubMed] [Google Scholar]
  • 21.Martin SS, Blaha MJ, Elshazly MB, et al. . Comparison of a novel method vs the Friedewald equation for estimating low-density lipoprotein cholesterol levels from the standard lipid profile. JAMA. 2013;310(19):2061-2068. doi: 10.1001/jama.2013.280532 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Martin SS, Giugliano RP, Murphy SA, et al. . Comparison of low-density lipoprotein cholesterol assessment by Martin/Hopkins estimation, Friedewald estimation, and preparative ultracentrifugation: insights from the FOURIER trial. JAMA Cardiol. 2018;3(8):749-753. doi: 10.1001/jamacardio.2018.1533 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Chung BH, Wilkinson T, Geer JC, Segrest JP. Preparative and quantitative isolation of plasma lipoproteins: rapid, single discontinuous density gradient ultracentrifugation in a vertical rotor. J Lipid Res. 1980;21(3):284-291. [PubMed] [Google Scholar]
  • 24.Chaudhary R, Garg J, Shah N, Sumner A. PCSK9 inhibitors: a new era of lipid lowering therapy. World J Cardiol. 2017;9(2):76-91. doi: 10.4330/wjc.v9.i2.76 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25.Everett BM, Smith RJ, Hiatt WR. Reducing LDL with PCSK9 inhibitors—the clinical benefit of lipid drugs. N Engl J Med. 2015;373(17):1588-1591. doi: 10.1056/NEJMp1508120 [DOI] [PubMed] [Google Scholar]
  • 26.Grundy SM, Stone NJ, Bailey AL, et al. . 2018 AHA/ACC/AACVPR/AAPA/ABC/ACPM/ADA/AGS/APhA/ASPC/NLA/PCNA Guideline on the management of blood cholesterol: executive summary: a report of the American College of Cardiology/American Heart Association Task Force on Clinical Practice Guidelines. Circulation. 2019;139(25):e1046-e1081. doi: 10.1161/CIR.0000000000000624 [DOI] [PubMed] [Google Scholar]
  • 27.Mudd JO, Borlaug BA, Johnston PV, et al. . Beyond low-density lipoprotein cholesterol: defining the role of low-density lipoprotein heterogeneity in coronary artery disease. J Am Coll Cardiol. 2007;50(18):1735-1741. doi: 10.1016/j.jacc.2007.07.045 [DOI] [PubMed] [Google Scholar]
  • 28.Hopkins PN, Brinton EA, Nanjee MN. Hyperlipoproteinemia type 3: the forgotten phenotype. Curr Atheroscler Rep. 2014;16(9):440. doi: 10.1007/s11883-014-0440-2 [DOI] [PubMed] [Google Scholar]
  • 29.Chung BH, Segrest JP, Ray MJ, et al. . Single vertical spin density gradient ultracentrifugation. Methods Enzymol. 1986;128:181-209. doi: 10.1016/0076-6879(86)28068-4 [DOI] [PubMed] [Google Scholar]
  • 30.Chowaniec Z, Skoczyńska A. Plasma lipid transfer proteins: the role of PLTP and CETP in atherogenesis. Adv Clin Exp Med. 2018;27(3):429-436. doi: 10.17219/acem/67968 [DOI] [PubMed] [Google Scholar]
  • 31.Shen BW, Scanu AM, Kézdy FJ. Structure of human serum lipoproteins inferred from compositional analysis. Proc Natl Acad Sci U S A. 1977;74(3):837-841. doi: 10.1073/pnas.74.3.837 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32.Goff DC Jr, Lloyd-Jones DM, Bennett G, et al. . 2013 ACC/AHA guideline on the assessment of cardiovascular risk: a report of the American College of Cardiology/American Heart Association Task Force on Practice Guidelines. J Am Coll Cardiol. 2014;63(25, pt B):2935-2959. doi: 10.1016/j.jacc.2013.11.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 33.Nordestgaard BG. Triglyceride-rich lipoproteins and atherosclerotic cardiovascular disease: new insights from epidemiology, genetics, and biology. Circ Res. 2016;118(4):547-563. doi: 10.1161/CIRCRESAHA.115.306249 [DOI] [PubMed] [Google Scholar]
  • 34.Varbo A, Benn M, Nordestgaard BG. Remnant cholesterol as a cause of ischemic heart disease: evidence, definition, measurement, atherogenicity, high risk patients, and present and future treatment. Pharmacol Ther. 2014;141(3):358-367. doi: 10.1016/j.pharmthera.2013.11.008 [DOI] [PubMed] [Google Scholar]
  • 35.Cantey EP, Wilkins JT. Discordance between lipoprotein particle number and cholesterol content: an update. Curr Opin Endocrinol Diabetes Obes. 2018;25(2):130-136. doi: 10.1097/MED.0000000000000389 [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplement.

eAppendix 1. Derivation of Equations

eAppendix 2. External Validation Datasets

eFigure 1. Relationship of TG and non–HDL-C With VLDL-C

eFigure 2. Derivation of Equation 1

eFigure 3. Calculated Versus β-Quantification VLDL-C

eFigure 4. Calculated Versus β-Quantification VLDL-C

eFigure 5. Evaluation of Factor Table for Martin Equation

eFigure 6. Contour plots for VLDL-C for Martin equation and Equation-1

eFigure 7. MAD Score for LDL-C Equations

eFigure 8. Residual Error Plots for LDL-C by Various Equations

eFigure 9. Calculated Versus dLDL-C by Gender and Fasting State

eFigure 10. Classification of Patients into LDL-C Risk-Level Categories

eTable. Description of Existing Equations for Calculating LDL-C

Click here for additional data file. (11.6MB, pdf)

Articles from JAMA Cardiology are provided here courtesy of American Medical Association

RESOURCES