Automated delineation of hospital service areas as a new tool for health care planning

Abstract

Objective

To develop an automated, reproducible method for delineating hospital service areas (HSAs).

Data Sources/Setting

Discharge data from all Swiss acute care hospitals for the years 2013 to 2016.

Study Design

We derived HSAs and hospital referral regions for Switzerland using a newly developed flow‐based, automated, objective, and reproducible method using all discharge data. We compared our method to the classical, partially subjective approach used to delineate the Swiss Health Care Atlas by delineating four sets of intervention‐specific HSAs.

Principal Findings

Based on 4 105 885 discharges, the fully automated method delineated 63 HSAs. Comparison with existing HSAs reveals good overlap and comparable measures of health utilization between the methods and shows that in the Swiss setting, our method outperforms a cluster‐based approach to defining HSAs. While the classical method potentially takes an entire day to delineate the regions, our method took approximately 10 minutes.

Conclusions

Hospital service areas are used to analyze differences in use of health care that may indicate underuse and overuse. Our new, fully automated, objective, and reproducible method provides a useful tool for hospital services researchers that will enable them to delineate and update patient‐flow‐based HSAs.

What This Study Adds.

• Delineating hospital service areas (HSAs) is a largely manual process, whose results are not reproducible.

• There is no readily available automated approach.

• This study describes an approach, and provides an R package, with which to create HSAs in an automated manner, which allows for reproducibility. Comparison of the automated results with classically defined HSAs shows similar results.

1. INTRODUCTION

Hospital service areas (HSAs) are the regions within which most patients undergo treatment, and they can summarize patient‐hospital flows. While administrative units are typically bound to geopolitical entities,1 HSAs reflect actual patient movement and have been used to study, for example, regional variation in procedure rates2 or quality,3 which can be used to inform policy decisions about new services. The pioneer of health delivery research, John Wennberg, developed a population‐based method for measuring health care performance called small‐area analysis of health care delivery based on patient flows rather than administrative regions to take patient travel patterns into account.4

The classical method of delineating HSAs assigns hospitals to cities or towns, with regions allocated to the hospital where most patients were hospitalized. Because this typically results in discontiguous regions, some (often many), regions are manually reallocated to create contiguous regions based on visual inspection of the allocations,5 which impedes the reproducibility of this method. Because this method of creating HSAs is so laborious, most studies on practice variation in the USA still rely on the HSAs developed in the 1990s.6

An automated method to generate HSAs in a reproducible manner can help monitor use of health care and improve the accuracy of analyses of health care variation. Newer methods for a more automated approach to HSA generation have been proposed.6, 7, 8, 9 Hu et al8 used a Louvain hierarchical clustering algorithm to iteratively merge neighboring regions if modularity—the difference between the observed and an expected flow network—improved. Jia6 proposed an iterative approach whereby the localization index (LI) is used extensively to merge neighboring regions based on patient flow. Delamater et al7 used a clustering approach to assign areas with similar flow and hospital characteristics into hospital groups in Michigan. Only the method from Delamator et al is readily available, but it does not appear to have been used to delineate HSAs. Thus an accessible, simple‐to‐use, reliable method in a readily available and open access program to delineate HSAs would be useful.

We propose a method that allows the full automation of HSA generation. By using this method, HSAs can be generated much more quickly than with the classical method and manual correction is no longer necessary, which improves reproducibility in health care research. We also describe solutions for overcoming challenges to the generation of HSAs such as rare interventions.

2. METHODS

2.1. Data sources

To derive general purpose HSAs, we used patient discharge data from all Swiss acute care hospitals covering 100% of discharges10, 11 and Swiss census data for calendar years 2013‐2016. Variables included patient demographics; diagnostic and procedure codes; and the area of patient residence and hospital location within one of 705 Swiss MedStat regions (census regions based on aggregated postcodes).

To directly compare the methods, we used data provided by the Swiss Health Care Atlas (Schweizer Atlas der Gesundheitsversorgung12) to rederive four sets of HSAs produced by them (general, spinal, pediatric, and heart surgery HSAs) using the classical approach. Heart and spinal surgery groups were defined based on hospital planning services groups,13 which assign discharges to specified groups based on ICD10 and CHOP codes. Heart surgery included discharges with pericardiectomy, cardiac stem cell therapy, valve replacement/repair, coronary artery bypass, pacemaker implant/explant, and valvulotomy. Spinal surgery discharges included spinal laminectomy, laminotomy, disk replacement implant/explant/repair, and vertebroplasty and kyphoplasty. Population size data for 2014 were obtained from the SFSO.

2.2. Derivation of Swiss hospital service areas

The two main tenets of HSA creation are contiguity and regional allocation based on maximum flow. In the classical method, patient flows to regions with a hospital are analyzed and MedStat regions from which the highest proportion of residents were discharged were assigned to the same HSA (plurality rule). Measures of self‐containment such as the localization index, which is the proportion of patients remaining within the HSA, should exceed 50% for an HSA to be usable unit.6, 14, 15 While the classical method starts by focusing on the patient's origin, we argue that it is equally feasible and ultimately easier to start with the destination, that is, the hospitals. By combining spatial data with origin‐destination data, it is possible to look at each hospital neighboring regions sharing a boundary with the hospital and merge the regions if most flow is to that specific hospital. By performing this comparison iteratively, an HSA will grow around the hospital as the secondary, tertiary, and more distant neighbors are examined and merged if most flow is in that direction. Using this approach, HSAs are automatically contiguous due to merging neighbors. Once all regions have been assigned to an HSA, the validity of HSAs can be assessed via LI and number of interventions. HSAs that do not meet those criteria can be merged with a neighboring HSA. We will refer to this method as HSAr.

One particularly difficult aspect of defining HSAs is the question of what to do with regions where no interventions were performed or where all patients visited distant hospitals. This can happen where population sizes are small and interventions are relatively rare. The classical method offers no particular solution or guidance for handling this, so we use information from the neighboring regions. The neighbors of the region(s) without interventions are identified, the flows to each HSA visited by inhabitants of the neighbors are aggregated, and the region is allocated to the neighboring HSA receiving most interventions. This is the main difference to the method of Jia,6 which offers no suggestion for handling regions without observations. The same approach can also be used in the clustering method of Delamater et al7 which cannot allocate regions without observations. Such an approach effectively takes the mean of the neighboring regions, making the region intermediate among its neighbors. As such, there may be a less clear boundary between two potential HSAs. Because cluster‐based methods analyze the similarity among regions, such intermediate regions are more likely to be combined into a single HSA.

Our approach in HSAr is an iterative process, whose steps are as follows.

Step 1: Identify destinations.

Step 2: For each destination (=potential HSA), identify neighboring origin regions (those origins sharing a boundary with the destination).

Step 3: For each identified neighbor, merge with the destination if most patients go to the potential HSA.

Step 4: Repeat steps 2 and 3 until all origin regions are allocated to the neighboring HSA with most significant flow.

Step 5: Check that all regions are allocated to a destination. For those that are not (these could include regions without any interventions or regions with primarily long distance flow), identify the neighboring origin regions and allocate the unassigned origin regions to the neighboring HSA receiving most patients (information borrowed from neighbors where necessary).

Step 6: Check that all HSAs have an LI above the threshold of 50%, reflecting most patients remaining within the HSA. HSAs with an LI below the threshold are merged with the neighboring HSA with the highest flow.

Step 7: Check that all HSAs have at least the minimum number of 10 interventions. Merge HSAs with fewer than 10 interventions with the neighboring HSA receiving most flow.

Iterate until no new changes are made to the HSA allocations. HSA contiguity can be ascertained by visual inspection, although no changes should be required. In contrast to our approach of merging HSAs with low LI or too few interventions, Jia6 deconstructed such HSAs and merged the individual regions instead.

2.3. Comparison of automated methods and the Atlas method

We examined the performance of HSAr and the method of Delamater et al,7 and a modified version taking into account missing regions by comparing the results of these methods with HSAs delineated recently by the Swiss Health Care Atlas12 (using the classical method). We delineated four different sets of HSAs as per the Swiss Health Care Atlas12 based on SFSO data from the calendar years 2013 and 2014: heart surgery, with 45 890 hospitalizations; spinal surgery, 7547 hospitalizations; pediatrics, 115 529 hospitalizations under the age of 16; and general HSAs, with 984 896 hospitalizations.

We modified the cluster method of Delamater et al7 to group MedStat regions using the patient flow and the distance from each source region to those regions receiving hospitalizations instead of grouping hospitals using hospital information and flows to define the similarity between units. All HSAs needed to contain at least one hospital region admitting patients and be above the LI threshold (generally 50%, although delineation of spinal interventions required a minimum LI of 20% to converge). Without further modifications to the algorithm itself, this approach cannot assign regions without patients to an HSA. We further developed the method, as a filled‐clustering method, to use the neighboring regions to fill in the missing information. The flows from neighbors of MedStat regions without patients were aggregated and used as a proxy for the regions without any observations. Because the method uses proportions to calculate similarity rather than the absolute values, summing the flows from the neighbors should not have undesirable effects. This approach was only necessary for spinal interventions, for which no spinal procedures were observed in eight MedStat regions.

To compare the methods, we visually compared the maps and selected five quantitative measures: LI, number of interventions, net patient flow (NPF), the market share index (MSI),16 and population size. The LI captures the propensity of patients to visit local hospitals, while NPF is the ratio of patients receiving care within an HSA to those from that HSA that require care. Values >1 reflect more patients traveling into the HSA than leaving the HSA, while values <1 reflect more patients leaving the HSA than traveling to the HSA. MSI is the proportion of patients receiving care in an HSA that come from the HSA, and it reflects the tendency of an HSA to absorb out‐of‐area residents. For each set of HSAs, these five measures were compared with Wilcoxon rank sum tests, with an additional comparison between the HSAr method and the classical method.

Overall concordance between the pairs of HSAs was assessed using Mapcurves.17 Mapcurves compare the proportion of overlap in the area of intersecting regions from two maps and provide a measure of goodness of fit (GOF) at both polygon (HSA) level and that of the entire map (see Appendix S1 for details). A perfect Mapcurve match would be depicted as a horizontal line of points along the top of the plot (all polygons are identical so the proportion of shared area for each is 1), while very different maps would be depicted by a steep drop close to the y‐axis.

We reconstructed the Swiss Health Care Atlas HSAs using HSAr implemented in R 3.4.2.18

3. RESULTS

During the years 2013‐2016, there were 4 105 885 discharges from Swiss hospitals. The 705 MedStat regions had between 683 and 41 590 discharges traveling to 184 MedStat regions containing hospitals (184 thus reflects the maximum number of HSAs possible). Use of our method (HSAr) resulted in 63 general HSAs (Appendix S2). All regions had LIs above 0.5 (most admissions thus remained within the HSAs), and the smallest HSA admitted 1845 patients. The algorithm required approximately 10 minutes to derive the HSAs.

3.1. Comparison to the classical method

Visual comparisons of HSAs delineated via HSAr and the classical method show that the HSAs are similar, although not identical (Figure 1), particularly in the more sparsely populated regions, which also happen to be more mountainous. The two methods created a similar number of HSAs for the procedural groups considered: general HSAs, classical = 68 and HSAr = 61; pediatric HSAs, classical = 27 and HSAr = 32; spine HSAs, classical = 20 and HSAr = 16; and heart HSAs, classical = 19 and HSAr = 18. In contrast, the clustering‐based methods produced fewer, larger HSAs. Filling was only required for the spine HSAs and resulted in somewhat different HSAs to those without using the filling approach (Figure 1; general HSAs = 20; pediatric HSAs = 12; spine HSAs = 13, reduced to seven with filling; heart HSAs = 6).

Figure 1.

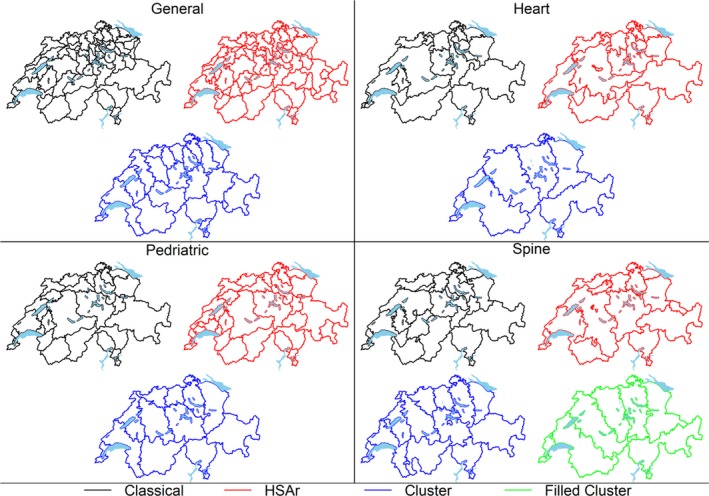
The four sets of hospital service areas (HSAs) delineated by the classical method and the automated methods (HSAr and the two clustering‐based methods). The filled‐clustering method was only necessary for the spinal HSAs and is thus not shown for the first three intervention sets [Color figure can be viewed at http://www.wileyonlinelibrary.com]

While the LIs in HSAr‐derived HSAs were similar to those from the classical method in the four sets of HSAs (despite the classical method using a minimum LI of 0.4 rather than 0.5, Figure 2 and Appendix S4), the LIs in the clustering‐based methods were higher (general HSA 76.5% vs 62.6% HSAr and 64.6% classical method). All five measures were largely similar between the classical and HSAr methods, with similar medians and lower and upper quartiles, although larger outliers for NPF and MSI were visible for HSAr than the classical method. There was no evidence that any of the quantitative measures differed between HSAr and the classical method (all P‐values > .05; Appendix S4). The clustering‐based methods, however, produced HSAs with higher LIs and MSIs, and more interventions than the HSAr and classical methods.

Figure 2.

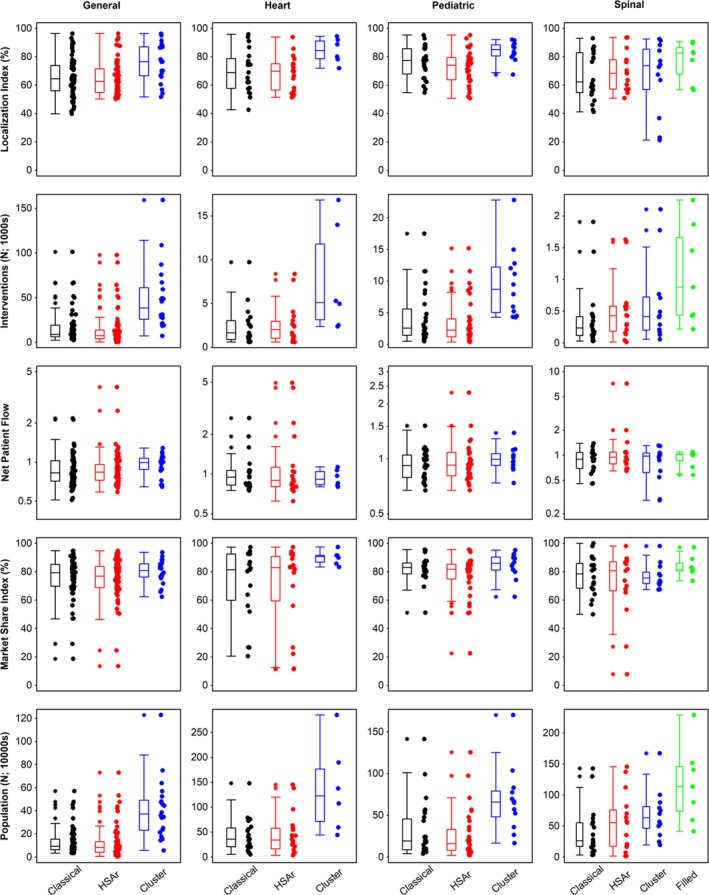
Localization index, number of interventions, net patient flow, market share index, and population (in 10 000s; rows) for each hospital service area (HSA) in the four sets of HSAs delineated by the classical and automated methods (HSAr and the two clustering‐based methods). Horizontal lines in the box plots represent medians. The filled‐clustering‐based method (“Filled” for brevity) was only necessary for the spinal HSAs and is thus not shown for the first three intervention sets [Color figure can be viewed at http://www.wileyonlinelibrary.com]

Concordance between the HSAr method and the classical method was higher than between the clustering‐based method and the classical method (AUC 84% vs 75%; Appendix S5 for the general HSAs). GOFs for the pediatric HSAs were 97% for HSAr and 77% for the clustering method. GOFs for the heart HSAs were 80% for HSAr and 70% for the clustering method. GOFs for the spine HSAs were 67% for HSAr and 66% for the filled‐clustering method (GOF for regions where one set of maps misses a section is not defined. Ignoring those sections and calculating GOF would result in bias).

4. DISCUSSION

We developed and validated an automated, quick, and reproducible method to generate HSAs (HSAr) for health care research. Although the results were similar, differences between the HSAr and classical methods were most likely driven largely by manual reassignments made in the classical method. Indeed, many manual reassignments were made for the Atlas, particularly for the spine HSAs (Marcel Widmer, pers. comm.), which is to be expected when HSAs are defined with the small number of hospitalizations used for the spine HSAs. Although we cannot identify individual hospitals, HSAs with relatively high net patient flow appear to contain some large private and/or specialized clinics, which attract patients from further afield than some of the smaller, less specialized hospitals.

In contrast to HSAr, the clustering‐based method of HSA delineation produced fewer, larger HSAs. The five summary statistics we chose suggest that the clustering‐based method outperforms HSAr (due to higher LI and lower and/or more densely distributed NPF and MSI), but the method produced fewer, larger regions, reducing the scope for inter‐HSA movement. Klauss et al16 point out that increasing the size of HSAs limits one's ability to assess variation among regions. The method is perhaps not suited to regions where hospital density is relatively high (with many smaller hospitals rather than fewer larger hospitals). Furthermore, under the Swiss health care system patients are free to choose which medical facility they visit, which may result in inhabitants from a given region going to a larger selection of hospitals.

Compared to the classical method, our method has the advantage that it is completely automated and therefore reproducible and objective. It did not, however, produce consistently more or fewer HSAs, which likely originates in the (perhaps numerous) manual reassignments in the classical method (Widmer, pers. comm.). As the five measures we chose were similar for the two methods, and Mapcurves showed a good level of concordance, we feel confident that HSAr is a suitable method to automate the delineation of HSAs.

It can be particularly difficult to create HSAs for rare interventions due to regions in which no patients have undergone those interventions. While our method can handle such regions if there is at least one neighbor with interventions, regions without neighbors with interventions cannot currently be assigned. One solution is to use all interventions to create general HSAs and then further aggregate those general HSAs into intervention‐specific HSAs. By delineating the general HSAs, the number of home regions is reduced resulting in fewer regions without interventions. Alternatively, if confidentiality of hospital identity is desired/required (eg, due to a political desire not to compare specific hospitals), general HSAs can be generated to obscure that location.

Intervention‐specific HSAs can be created by restricting the patient population to those receiving the intervention and using either the patients' actual residences or their general HSA, which is particularly useful for rare interventions. Similarly, hospital referral regions (HRRs) can be defined by restricting the patient population used to derive the HSAs to those patients receiving either major cardiovascular surgery or neurosurgery and those traveling to centers or HSAs offering both (Appendix S4).

Hospital service areas make ideal regional units to inform policy; they represent actual patient flows rather than geopolitical regions. Calculating the rates of particular interventions2—preference‐sensitive interventions, for example—can reveal regions of particularly high or low use. Similarly, analyses of service costs19 or quality3 can be used to identify expensive or lower quality care. High levels of variation in usage, cost, and/or quality among HSAs could indicate that additional guidance is necessary.

4.1. Study limitations

Although we have used our method to generate five sets of HSAs and one set of HRRs and compared it with other methods, all are within the Swiss setting. How the algorithm performs in other settings is difficult to say, although we see no reason why it should not also work in other countries (within the practical limitations discussed in Appendix S6 regarding geodata quality and size). Our dataset also only included inpatient hospitalizations. Data on outpatients are not yet readily available in Switzerland, although we would expect outpatients to exhibit different patterns of movement.

4.2. Study strengths

We used four years' worth of interventions to create our HSAs which should allow the pattern of flows among regions to stabilize and reduce the likelihood of any single region having no interventions.

We also had access to the original data used to create HSAs via the classical method. This allowed us to compare the HSAr method against the Atlas method. We are aware of no other study using the same data to generate HSAs via multiple methods.

5. CONCLUSIONS

Our method provides a simple, fast, and reproducible way to delineate hospital service areas or hospital referral regions. The resultant HSAs have properties similar to those created using the Atlas method with the advantage that the HSAr method removes the need for subjective decisions. The method is of course not limited to the construction of HSAs and HRRs. It could be applied to any question for which flow of items, whether vehicles or goods, or persons, must be captured.

DATA AND CODES

HSAr is available at http://www.github.com/aghaynes/HSAr. The development version will be installable directly in R via devtools::install_github(“aghaynes/HSAr”), or the version used in this paper via devtools::install_github(“aghaynes/HSAr@hsr”). See also Appendix S7.

Data itself are not freely available but access may be granted by contacting Marcel Widmer through the Swiss Health Care Atlas (http://www.versorgungsatlas.ch).

Supporting information