Skip to main content
PMC home page
ACS Omega logoLink to ACS Omega
. 2020 May 6;5(19):10774–10781. doi: 10.1021/acsomega.0c00334

Influence of Binding Site Affinity Patterns on Binding of Multivalent Polymers

Emiko Zumbro 1, Alfredo Alexander-Katz 1,*
PMCID: PMC7240832  PMID: 32455197

Abstract

graphic file with name ao0c00334_0006.jpg

Using inspiration from biology, we can leverage multivalent binding interactions to enhance weak, monovalent binding between molecules. While most previous studies have focused on multivalent binders with uniform binding sites, new synthetic polymers might find it desirable to have multiple binding moieties along the chain. Here, we probe how patterning of heterogeneous binding sites along a polymer chain controls the binding affinity of a polymer using a reactive Brownian dynamics scheme. Unlike monovalent binders that are pattern-agnostic, we find that divalent binding is dependent on both the polymer pattern and binding target concentration. For dilute targets, blocky polymers provide high local concentrations of high-affinity sites, but at high target concentrations, competition for binding sites makes alternating polymers the strongest binders. Subsequently, we show that random copolymers are robust to target concentration fluctuations. These results will assist in the rational design of multivalent polymer therapeutics and materials.

Introduction

Multivalent polymers that bind to smaller targets are of interest in both biological and physical applications. In biology, multivalent interactions are used for a variety of reasons, including enhancing weak monovalent binding or increasing specificity of binding using a limited number of receptor and ligand types.1 Multivalent binding is defined as when multiple ligands on one species bind to multiple receptors on another species simultaneously. This can create a much stronger binding interaction than the sum of the corresponding monovalent single receptor/ligand interactions. In chemistry and materials science, multivalent polymers have been used to bind to multivalent cross-linkers to modulate gel characteristics.2 Similarly, membraneless organelles also depend on the binding sequences of multivalent polymers to control gelation and liquid–liquid phase separation.3,4 Furthermore, glycosylation of proteins in vivo often appears as a random process leading to a random arrangement of binding sites, but dysregulation of the sequence has been linked to neurodegenerative disorders.5 Understanding the role of sequence in multimodal multivalent polymers and their influence on aggregation is thus of great interest to biology.

Synthetic multivalent polymers have also shown promise in binding to sugar-binding proteins called lectins.6,7 Sugar-protein binding sites frequently create low-affinity bonds, so multivalency can be essential to creating strong binding interactions.8,9 Lectins are of special interest to us because viruses and bacteria use lectins to bind to and subsequently infect cells, and microbes can release toxic lectins such as cholera or shiga toxin that cause diarrheal diseases.10,11 Building synthetic multivalent inhibitors of lectins is a promising avenue for combating viruses, antibiotic-resistant bacteria, and diarrheal diseases such as cholera,7,10−16 as shown in Figure 1.

Figure 1.

Figure 1

Open in a new tab

Multivalent polymers have shown promise as inhibitors for toxic lectins by preventing their attachment and subsequent infection to cells, as shown in the right panel.

Previous theoretical studies of multivalent structures with heterogeneous binding sites discussed the case of binding to a much larger flat multivalent surface, such as Curk et al. who assumed very flexible ligands and focused on how changing overall receptor concentrations modulated binding of nanoparticles17 and Tito et al. who examined the case of multivalent polymers binding to larger flat surfaces.18 While these studies were well done, we wanted to investigate whether similar results could be found for multivalent polymers binding to much smaller targets such as folded proteins or nanoparticles. Theoretical studies have shown that interacting with small colloids can induce only a local conformational change in the polymer,19 whereas copolymers binding to a surface can create a strong conformational change, leading to a stretched or even brushlike structure depending on other conditions.20,21 This makes the scenario of binding to a much smaller target unique from binding to a surface. Experimental studies on polymers binding to multivalent proteins such as lectins have focused on homopolymers with sites matched to a specific target lectin.11,22−24 The ability to carefully control the glycopolymer sequence was developed recently, and so, comparatively few experimental studies have examined the effect of binding site sequence of heteropolymers on lectin binding.25 Zhang et al. found some dependence of binding on copolymer sequence, but the overall binding site concentration dominated the results, muddling the effects of sequence on binding to DC-SIGN.26

Here, we examine polymers with multiple binding site types binding to globular protein targets such as a lectin. While keeping the concentration of all binding site types constant, we explore how changing the pattern of binding sites along the chain affects binding. The study of copolymers as multivalent binders is interesting because of their potential use for binding to multiple targets, for example, targeting multiple lectins in the galactose-binding family. The binding specificity of lectins to complex glycans is an active field of research. While lectins often target a particular monosaccharide or oligomeric sugar, the binding affinity can change based on the linkage or placement in a larger complex glycan ligand. For example, some galactose-binding proteins can bind to both galactose and N-acetylgalactosamine, and the mannose-binding lectin concanavalin A binds to monomeric mannose, as well as mannose connected to various complex glycans with significantly different affinities.27,28 Therefore, it is reasonable to assume that a binding site meant for one lectin might interact with another lectin or conversely that a single lectin might bind to two binding sites with different affinities. This “cross-talk” could significantly affect the overall polymer binding. Unintentional heterogeneity is also important to investigate since imperfect grafting or other synthesis methods can create random binding site copolymers, which could have a significant effect on target binding.29 Additionally, in biological polymers such as mucins, the regulation and sequence of complex sugars are still not fully understood and might be heterogeneous.30

Here, we show that multivalent binding affinities are very different depending on polymer heterogeneity compared to monovalent binding. The binding affinity of monovalent targets to multivalent polymers is dependent on only the number and affinity of the highest-affinity sites and not the location. For multivalent targets, however, the results are more interesting. In dilute target conditions, the strength of the bond between the polymer and target is controlled by the highest-affinity binding sites and the relative location between them. “Blockier” or clustered high-affinity polymer binding sites create stronger binding to dilute multivalent targets. Alternatively, when many multivalent targets interact with patterned copolymers, the highest-affinity polymers have alternating affinity binding sites, while “blocky” copolymers have the lowest average binding to divalent targets. This results from competition between targets for the same binding sites. Furthermore, we find that random copolymers are more robust to target concentration and perform mid-way between blocky and alternating copolymers in all target concentrations. We expect that these results will assist in the rational design of multivalent polymer therapeutics and materials.

Results and Discussion

To examine the effects of polymer binding site patterns, we placed four polymers with a degree of polymerization of Np = 16 beads in a cubic box with periodic boundaries. We chose a polymer length of Np = 16 beads because a previous work showed that the increasing polymer length leads to a plateau in binding affinity after approximate lengths of Np = 13 beads.31 Using the same methods as our previous work on the topic and detailed in Computational Methods, targets were represented by single beads of the same size as a polymer bead.31 Target beads were assigned one or multiple binding sites to represent monovalent or multivalent binding scenarios, respectively.

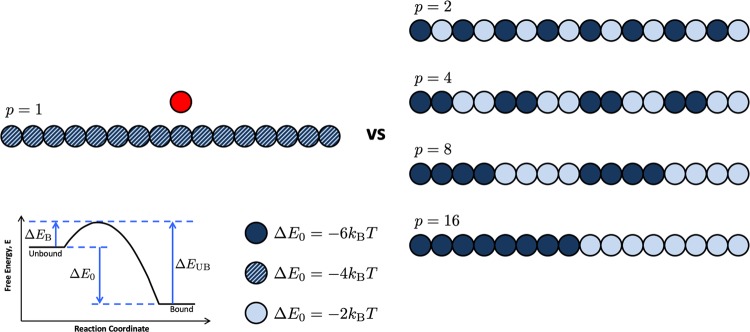
Every polymer set was assigned a binding site pattern where each polymer bead was given a single binding site with a particular binding affinity ΔE0, as shown in Figure 2. The binding site pattern parameter space is very large when we consider binding site energy, arrangement, and fraction of sites in the chain. Therefore, we have shrunk the parameter space to a more tractable subset where we consider polymers with 50% higher-affinity binding sites and 50% lower-affinity sites. We believe that this case is still relevant to experimentalists who may only have two ligand chemistries available or who plan to target two proteins in the same family. We used polymers that had various patterns of 50% high-affinity binding sites (ΔE0 = –6kBT) and 50% low-affinity binding sites (ΔE0 = –2kBT), corresponding to monomeric binding affinities of KD = 0.02 mM and KD = 0.8 mM, respectively. Additional dissociation constant data for polymers with ΔE0 = 0kBT and ΔE0 = –6kBT binding sites and with ΔE0 = –3kBT and ΔE0 = –5kBT binding sites are included in the Supporting Information. In all cases, we observe identical trends, and thus, we only present the (−2, −6) scenario. To generate randomly patterned polymers, we randomly selected half of the polymer bead indices and labeled those as high-affinity sites (ΔE0 = –6kBT), and the remaining half of the beads were labeled as low-affinity sites. This created randomly patterned polymers while maintaining a 50:50 ratio of high- and low-affinity sites. All of the four polymers in a simulation were assigned the same binding site pattern. For comparison, we also ran homogeneous polymers with uniform binding sites with ΔE0 = –4kBT, corresponding to a monovalent binding site affinity of KD = 0.1 mM. These binding affinities were calculated by fitting the Langmuir adsorption curve using the fraction of time bound (ϕ) of a monovalent target binding at different monomeric inhibitor concentrations. As detailed in the Supporting Information, we can convert the unitless dissociation constant KD to molar by estimating a size of each bead in nanometers. These binding affinities capture relevant biological affinities of monovalent binding between sugars and proteins, commonly on the order of millimolar to micromolar.27,32

Figure 2.

Figure 2

Open in a new tab

Schematic of the polymer patterns tested when exploring binding of a target (red) to homopolymers and copolymers (blues). The periodicity p is labeled above each polymer pattern. Here, dark circles indicate high-affinity binding sites with ΔE0 = –6kBT, light circles represent low-affinity binding sites with ΔE0 = –2kBT, and striped circles represent a medium binding affinity used only for the homopolymer comparison with ΔE0 = –4kBT.

Throughout this work, we consider a target “bound” if one or more of its binding sites are bound to the polymer and “unbound” if the target has no bonds to the polymer. We analyzed the average time interval the target spent bound, τB, as we varied the binding site periodicity p while maintaining the 50:50 high- and low-affinity bead ratio. For example, an alternating high- and low-affinity polymer is considered to have a periodicity p = 2, and a polymer with half high-affinity beads and half low-affinity sites split down the center has p = 16, as shown in Figure 2. Results for four polymer periodicities p = 2, 4, 8, and 16 with comparisons to a uniform binding site polymer and randomly patterned polymers are discussed in this work.

Dilute Target Case

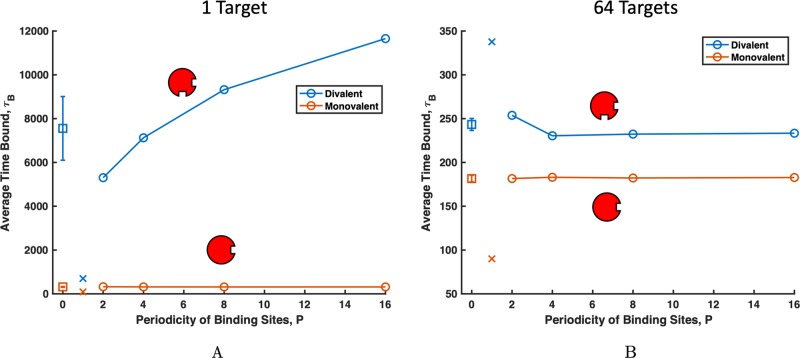
First, we considered a dilute target case where one target interacts in a box with four 16mer polymers. Assuming a target protein size of 5 nm, this corresponds to a target concentration of approximately 1.6 μM. Results for τB at this dilute target concentration are shown in Figure 3A. For monovalent targets, τB is only affected by individual affinities of sites and is pattern-agnostic. As shown in orange circles in Figure 3A, τB is higher for polymers with 50% ΔE0 = –6kBT affinity sites than the uniform polymer (shown as an orange x in Figure 3A) with ΔE0 = –4kBT affinity sites. By plotting the fraction of time each site on the polymer chain is bound to a monovalent target in Figure S4A, we show that low-affinity polymer sites are rarely bound, regardless of pattern periodicity. The design relationship for monovalent targets is straightforward: the affinity but not the relative position of sites controls the τB. Note that sites at the polymer ends do experience slightly higher binding than the center beads because polymer ends have less excluded volume from neighbors, and so, more available volume from which targets can bind. These end effects are relatively small contributors and are found across all polymer patterns. With only one binding site, monovalent targets can only sense the nonspecific interactions of the polymer around them such as the Lennard-Jones potential, so they cannot distinguish between binding site patterns. Therefore, the binding of dilute monovalent targets is pattern-agnostic and depends only on the strength and number of high-affinity binding sites.

Figure 3.

Figure 3

Open in a new tab

Plot of the average time bound τB vs the periodicity of the polymer p. The binding dependence on polymer pattern is different for divalent targets (blue) and monovalent targets (orange). Periodically patterned polymers are represented by connected circles, homopolymers are represented as x’s, and random copolymers are represented by squares. Because the binding of 100 copolymer patterns was averaged, the standard deviation of the τB across random polymer patterns is depicted as error bars. The effect of pattern is also dependent on the concentration of targets. (A) At dilute target concentrations, target binding increases with copolymer periodicity, but (B) at higher target concentrations, low-periodicity copolymers have higher τB. The sampling error for all data points is smaller than the symbol size.

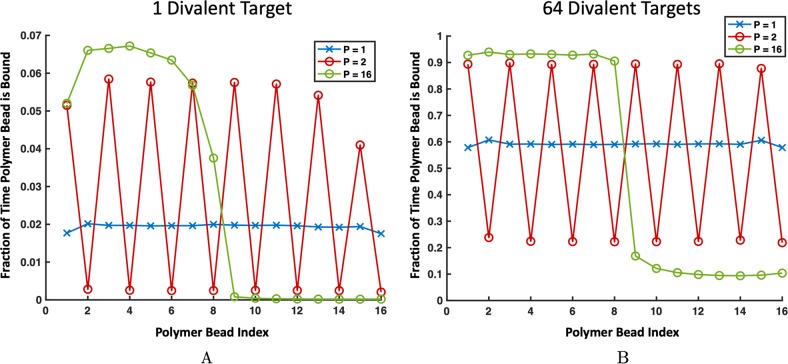
Next, we consider a single divalent target interacting with uniform and patterned polymers. Unlike monovalent targets, τB of divalent targets increases with p, as shown in Figure 3A. A divalent target spends significantly more time bound to polymers with clustered high-affinity binding sites than polymers with distributed high-affinity sites. By examining which polymer beads are bound in Figure 4B, we find that for uniform polymers, beads in the center of the polymer are bound more often because they have the highest local concentration of binding site neighbors. Having the most binding site neighbors provides the highest chances for the target to create two simultaneous bonds.

Figure 4.

Figure 4

Open in a new tab

Frequency in which a polymer bead is bound throughout the simulation when (A) a single divalent target and (B) 64 divalent targets are present for homopolymers (blue), alternating copolymers (red), and blocky copolymers (green). (A) For the patterned copolymers, low-affinity binding sites are bound with almost the same frequency. However, the high-affinity binding sites on the blocky polymer are bound much more frequently than the low-affinity binding sites on the alternating polymer. (B) For the patterned copolymers, attractive binding sites are bound with almost the same frequency. However, the low-affinity binding sites on the blocky polymer are bound much less frequently than the low-affinity binding sites on the alternating polymer. Error bars are smaller than the symbol size.

From Figure 3A, we also see that on both the alternating polymer (p = 2) and the blocky polymer (p = 16), the low-affinity binding sites are almost never bound (although the low-affinity sites on the p = 2 polymer are bound slightly more often than those in p = 16). Comparatively, the high-affinity sites on the blocky polymer are bound significantly more than the high-affinity sites on the alternating polymer. This follows directly from our observation that clustered sites create increased opportunity for targets to become double-bound. Blocky polymers have clustered high-affinity sites, so targets can navigate to the high-affinity block and will most likely become bound to two high-affinity sites, creating a strong bond. In contrast, alternating high-affinity sites are less occupied because for two sticky sites to be bound simultaneously, a divalent target has to form an entropically unfavorable loop. Targets prefer to bind to sites directly next to each other on the polymer to limit the loop size and corresponding polymer entropy loss, as previously demonstrated in Zumbro et al.31 A similar entropic penalty of loop formation has also been seen previously in the case of polymers binding to surfaces.18 These loops make the alternating polymer less sticky than the blocky polymer in the case of dilute multivalent targets. While precise ligand design on the order of the target size is not considered in this work, previous research has shown that to minimize entropic cost, binding sites should be spaced to exactly match the distance between target sites.23,33 Therefore, when designing a polymer to bind with high affinity for a dilute target, the designer should use a blocky polymer whose binding sites are spaced the same distance apart as on the target.

High Target Concentration Case

We continued our exploration of the effect of polymer pattern by simulating the same polymer patterns shown in Figure 2, interacting with 64 targets to capture the case where multiple targets compete for binding sites. While previous theoretical investigation into competition of patterned polymers was between the polymers for the binding surface instead of between the targets for binding to the polymer, competition has been shown to significantly change the binding statistics.18 Therefore again, we placed four 16mers in the box with our targets, so in this scenario, the number of targets matches the number of binding sites on the polymers. This higher concentration corresponds to approximately 100 μM, assuming a 5 nm target diameter. Creating target competition for binding sites allows us to ask the following question: how does the pattern modulate multivalent binding when a target may not have access to the highest-affinity sites? Competition for sites encourages faster turnover in bound targets because neighboring targets can steal polymer binding sites from each other. This faster turnover leads the drastically shorter τB’s seen in Figure 3A,B. With competition, monovalent target binding was qualitatively unchanged. Monovalent targets were pattern-agnostic and, on average, spent the highest τB on the patterned polymers with −6kBT, as shown in Figure 3B. For divalent targets, increased binding competition inverted τB’s dependence on polymer binding site periodicity, as shown in Figure 3B.

When multiple targets interact with a single binding polymer, a uniform polymer with medium-affinity binding sites has the highest overall avidity. The next highest τB is to the alternating high- and low-affinity polymers (p = 2), with blockier polymers p = 4, 8, and 16 showing the shortest τB. By investigating which polymer sites are bound in Figure 4B, we find that the high-affinity sites on the alternating polymer are now bound almost as often as the high-affinity sites on the blocky polymer. In contrast, low-affinity sites on the alternating polymer are significantly stickier than the low-affinity sites on the blocky polymer. This is a result of restricted access to high-affinity binding sites in blocky copolymers. When multiple targets are present, high-affinity sites on the blocky polymer fill up, and unbound targets are forced into the low-affinity region. In the low-affinity half, targets are only able to bind two low-affinity sites simultaneously, making relatively weak bonds. For the alternating polymer, targets forced to bind to the low-affinity sites are still in close proximity to high-affinity sites and can do a better job sharing sites with their target neighbors by binding to a high-affinity site and low-affinity site simultaneously. This sharing makes alternating polymers the highest overall affinity of the patterned polymers for multivalent targets.

Because there is a transition in the binding as the concentration increases, there is some critical target concentration where the polymer pattern should not matter, reflected as when the target binding time is not dependent on the polymer periodicity. Because competition between targets for high-affinity sites is causing the transition, we expect that the transition concentration should be approximately the concentration at which competition starts. Whenever there are multiple targets, there will be some competition for sites, but we believe that this competition will start to dominate when there are enough targets to bind to all high-affinity polymer sites. This can be described quantitatively as when 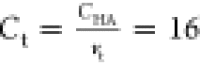Inline graphic, where Ct is the concentration of targets, CHA = 32 is the concentration of high-affinity binding sites, and vt is the valency of the target, in this case, vt = 2. We expect the critical concentration to be slightly above this because the number of targets must exceed the available binding sites to create competition.

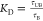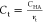To investigate this critical target concentration, we plotted the dissociation constant KD from simulations with Ct between 1 and 96 in Figure 5. We calculated the dissociation constant using Inline graphic, where τUB is the average time interval spent unbound. We consider a target unbound whenever both binding sites are unbound. From these data, we can see that the critical concentration occurred somewhere between Ct = 20 and Ct = 24. This is very close to our theoretical estimate of 16 targets as our critical concentration. The difference of 4 to 8 targets is most likely due to critical competition occurring only when there is an additional target (above the full capacity) for each of the four polymer chains. This difference in critical target concentration could also be explained by considering that, on blocky copolymers, there is a single low-affinity site placed adjacent to a high-affinity site for each of the four polymers. A target that is bound there could form relatively favorable high- and low-affinity bonds, almost creating another good binding site per chain. Either of these effects or a combination of both could increase the critical concentration slightly above Ct = 20. Following these results, we expect that designers can perform our simple estimation that the alternating polymer has higher affinity than the blocky polymer when the target concentration exceeds Inline graphic.

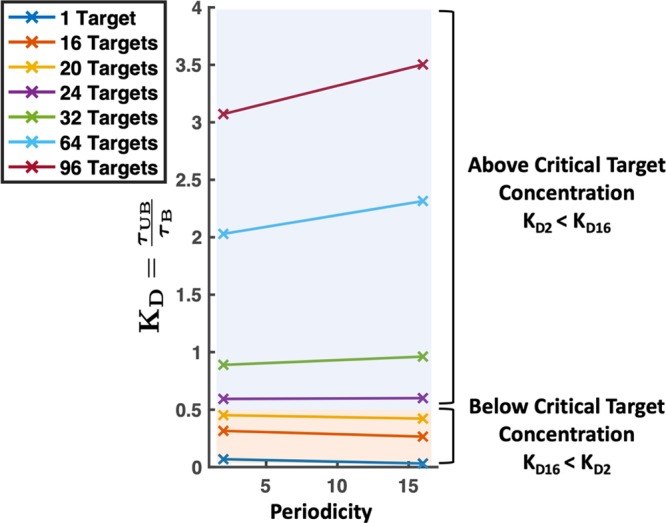
Figure 5.

Figure 5

Open in a new tab

Dissociation constant KD versus periodicity of polymer pattern for target concentrations from 1 to 96. We have marked the concentrations below the critical target concentration where the blocky polymer (p = 16) has a KD less than that of an alternating polymer (p = 2) with an orange background. The values above the critical target concentration where the alternating polymer has a lower KD than the blocky polymer are labeled with a blue background.

Unknown Concentration

Because binding dependence on the polymer pattern changes with target concentration, we subsequently explored the use of a random copolymer containing some blocky areas and some alternating areas. We hypothesized that polymers with both high- and low-periodicity binding sites would have binding behavior more robust to fluctuations in the target concentration. We examined simulations with randomly patterned binding sites. To create random patterns while maintaining the 50:50 ratio of high- to low-affinity sites, we randomly chose 50% of the beads along the polymer chain to be high-affinity (−6kBT) sites, and the rest were labeled as low-affinity (−2kBT) sites. We averaged the performance of 100 of these different polymers, with their standard deviation of performance denoted as error bars in Figure 3A,B. As expected, we found that randomly patterned copolymers resulted in τB between those of polymers with p = 2 and p = 16 for both dilute and more concentrated divalent target scenarios, as shown by the squares plotted at p = 0 in Figure 3. The pattern continued to have a negligible effect on the binding of monovalent targets. This suggests that in an unknown or fluctuating target concentration, a polymer with both blocky and alternating regions, such as a randomly patterned multivalent polymer, may provide the broadest binding capabilities.

Conclusions

We have examined how binding site patterns along the polymer chain influence their average binding time to both monovalent and multivalent targets. In this paper, we have shown that for targets with a single binding site, the polymer is only as sticky as its highest-affinity site. For targets with multiple binding sites, the effects of the polymer binding site pattern are more nuanced. In dilute target conditions, polymers bind multivalent targets more tightly when high-affinity sites are concentrated, so blocky copolymers are better binders than alternating copolymers. Blocky polymers also provide areas of high local concentration of high-affinity sites, assisting divalent targets in forming two strong bonds. For targets to bind two sticky sites on an alternating polymer, they must form an entropically unfavorable loop with a low-affinity bead, making these polymers worse binders. In crowded environments the opposite result was found; when patterned polymers bound to multiple competing targets, alternating high- and low-affinity copolymers were bound the longest. When many targets bind to the same polymer, blocky designs with clusters of high-affinity sites performed the worst because high-affinity sites filled up and leftover targets were excluded from the high-affinity region. Alternating polymers were able to share their high-affinity sites to improve the overall binding performance. Consequently, our work suggests that the pattern of multivalent polymers should be adjusted to their binding target application.

If the target concentration is unknown, then our results show that the most robust polymer pattern to bridge many target concentrations is a polymer with both blocky and alternating regions. While this could be achieved with a carefully crafted blocky and alternating copolymer, here, we showed an example of this concept with a random copolymer, which had τB’s between those of alternating and blocky copolymers in both target concentrations. Therefore, for improved performance in fluctuating target concentrations, a random copolymer or other design with blocky and alternating regions may be the best choice for a polymeric inhibitor. Understanding how patterns of multiple types of binding sites on polymeric inhibitors affect the polymer’s binding behavior to a single target type is an essential first step toward rational design of polymers that display multiple moieties to fulfill several simultaneous functions. The ability to tune a single polymer design to bind to multiple types of targets means that multivalent polymers could be used as “broad-spectrum” inhibitors of microbial or viral infections. Finally, our results clearly show that the effective interactions between multivalent biopolymers/proteins are sequence-dependent and modifications to such sequences can lead to clear changes in binding behavior. For example, in liquid–liquid phase separation, small changes in sequence could lead to large repercussions in the assembly and should be studied further.

Computational Methods

We applied Brownian dynamics to each bead governed by the equation

graphic file with name ao0c00334_m004.jpg 1

where ri is the position of the bead at time t in the direction i = x, y, or z, R is a random number drawn from a normal distribution with a mean of 0 and a standard deviation of 1, ς is the drag coefficient, and D = kBT/ς is the diffusion coefficient. The forces each bead experiences due to interactions with the surrounding polymer or target are captured in ∇U, where U is a potential energy that combines contributions from connectivity, excluded volume, and binding. These are added together as U = Usp + ULJ + Ubind.

Connectivity along the polymer chain is controlled by harmonic springs with the equation

graphic file with name ao0c00334_m005.jpg 2

where rij is the distance between polymer beads, Np is the degree of polymerization of the polymer, a is the radius of a simulation bead, and κ was chosen to be 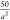Inline graphic, a value sufficiently large enough to prevent the polymer from stretching apart under normal Brownian forces.

A generic Lennard-Jones potential was applied to control the excluded volume and implicit solvation according to

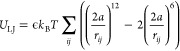graphic file with name ao0c00334_m007.jpg 3

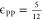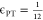where i and j represent two different bead indices and the value of ϵ can be adjusted to control the solvent quality and nonspecific interactions between beads. Here, we could substitute a screened electrostatic potential but do not expect this to qualitatively change our results. 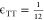Across the simulations in this work, we have chosen Inline graphic to mimic polymer configurations in a theta solvent.34 We used polymer–target potential Inline graphic and target–target potential Inline graphic to mimic a good solvent, as summarized in Table 1. We chose theta solvent because we previously demonstrated that polymer loops are easiest to form when the polymer is in the smallest size because the entropic penalty of forming a loop is the lowest.31 Since having a more collapsed polymer creates a higher local concentration of binding sites, a target within reach of the polymer should find more accessible binding sites on a collapsed chain as opposed to a swollen chain. Therefore, the overall pattern should matter less for a collapsed chain, and we have therefore used theta solvent as our limiting case. We expect that using a better solvent would further restrict the binding sites available to a target and magnify the effects of local pattern on binding.

Table 1. ϵ Values for Polymer–Polymer (PP), Polymer–Target (PT), and Target–Target (TT) Bead Lennard-Jones Interactions.

ϵPP ϵPT ϵTT
5/12 1/12 1/12
Open in a new tab

Our third type of interaction is a reactive lock and key bond, which represents our specific, valence-limited binding interaction. To simulate this reactive binding, harmonic springs were turned on and off between the polymer beads and the targets to dynamically represent bonded and unbonded states. This was implemented using the prefactor Ω(i, j) multiplied by a harmonic potential as follows

graphic file with name ao0c00334_m011.jpg 4

where M is the total number of target binding sites in the simulation, and n is the number of polymer chains. Ω(i, j) = 1 when the ith binding site on the target is bound to the jth bead of the inhibitor, and Ω(i, j) = 0 when the target binding site or inhibitor bead is unbound. To control the probability of binding and unbinding, we use a piecewise function based on the energy barriers for the binding reaction from Sing and Alexander-Katz.35

graphic file with name ao0c00334_m012.jpg 5

Here, Ξ is a random number between 0 and 1, ΔEB is the energy barrier to bind normalized by kBT, and ΔEUB is the energy barrier to unbind normalized by kBT, as depicted in the bottom left of Figure 2 and Figure S2.35 Without loss of generality, these energies are considered to be always positive, and the kinetics of binding are held constant by keeping ΔEB at 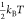Inline graphic so that binding is an accessibly frequent event. Increasing or decreasing the energy barrier will respectively slow or accelerate the kinetics of binding and unbinding equally but not change the system’s thermodynamics. The thermodynamic drive of binding is controlled by varying ΔE0 = ΔEB – ΔEUB. Binding becomes more favorable as ΔE0 is made more and more negative. This method is based directly on those of Sing et al. as well as others and is equivalent to the method found in the prepackaged ReaDDy software.35−39 Researchers studying vitrimers have extended this approach to include the additional effect of bond exchange,40−42 but in the case of ligand–receptor interactions in proteins, such additional possibilities do not apply. This is because the protein is much larger than the size of the binding site, which makes the binding very local and size exclusion prevents the swapping of bonds. Binding reactions are evaluated every time interval τ0 = 100Δt, where Δt is the length of one timestep and t is the current time. The reaction radius rrxn = 1.1 is equal to the distance between two bead centers if their surfaces were touching plus 0.1. Choosing 0.1 < (6Dτ0)1/2 gives time for a target that unbinds to diffuse out of the polymer radius of influence in τ0 and makes binding events independent.35 We have applied the constraint in which, at any time, an inhibitor bead can only bind to one target binding site (∑j Ω(i, j, t) ≤ 1) and a target site can only be bound to one inhibitor bead (∑i Ω(i, j, t) ≤ 1). Competing reactions are sampled randomly. Note that we do not include the effect of forces in the breaking of the bonds; this is due to the fact that for forces on the order of kBT/a, this effect is negligible if the characteristic bond length is less than 1 nm. For reference, discussion of the subject is given in ref (43).

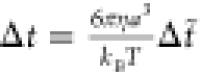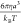The potentials are applied over the timestep Inline graphic, where Inline graphic is the characteristic monomer diffusion time or the time that it takes a bead to diffuse out of its radius a, and the dimensionless timestep is Δt̃ = 10–4. These equations are all made dimensionless by scaling energies by thermal energy kBT, lengths by bead radius a, and times by the characteristic diffusion time Inline graphic.

Acknowledgments

The authors were supported by the Department of Defense (DoD) through the National Defense Science and Engineering Graduate (NDSEG) Fellowship Program. The authors were also supported by the Ida M. Green Fellowship and the Collamore-Rogers Fellowship through the MIT Office of the Dean of Graduate Education. Computational resources were provided in part by the MIT Supercloud.44

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.0c00334.

  • Schematic of simulation, depiction of reactive binding scheme, monovalent dissociation constant determination, frequency of monovalent target binding to patterned copolymers, dissociation constant for patterned copolymers with other E0 pairs, and frequency of divalent bond types (PDF)

The authors declare no competing financial interest.

Supplementary Material

ao0c00334_si_001.pdf (1.4MB, pdf)

References

  1. Mammen M.; Choi S.-K.; Whitesides G. M. Polyvalent interactions in biological systems: implications for design and use of multivalent ligands and inhibitors. Angew. Chem., Int. Ed. 1998, 37, 2754–2794. . [DOI] [PubMed] [Google Scholar]
  2. Grindy S. C.; Lenz M.; Holten-Andersen N. Engineering Elasticity and Relaxation Time in Metal-Coordinate Cross-Linked Hydrogels. Macromolecules 2016, 49, 8306–8312. 10.1021/acs.macromol.6b01523. [DOI] [Google Scholar]
  3. Harmon T. S.; Holehouse A. S.; Rosen M. K.; Pappu R. V. Intrinsically disordered linkers determine the interplay between phase separation and gelation in multivalent proteins. eLife 2017, 6, e30294 10.7554/eLife.30294. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Boeynaems S.; Alberti S.; Fawzi N. L.; Mittag T.; Polymenidou M.; Rousseau F.; Schymkowitz J.; Shorter J.; Wolozin B.; Van Den Bosch L.; Tompa P.; Fuxreiter M. Protein Phase Separation: A New Phase in Cell Biology. Trends Cell Biol. 2018, 28, 420–435. 10.1016/j.tcb.2018.02.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Csizmok V.; Follis A. V.; Kriwacki R. W.; Forman-Kay J. D. Dynamic Protein Interaction Networks and New Structural Paradigms in Signaling. Chem. Rev. 2016, 116, 6424–6462. 10.1021/acs.chemrev.5b00548. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Zeng X.; Murata T.; Kawagishi H.; Usui T.; Kobayashi K. Synthesis of ArtificialN-Glycopolypeptides CarryingN-Acetyllactosamine and Related Compounds and Their Specific Interactions with Lectins. Biosci., Biotechnol., Biochem. 2014, 62, 1171–1178. 10.1271/bbb.62.1171. [DOI] [PubMed] [Google Scholar]
  7. Deniaud D.; Julienne K.; Gouin S. G. Insights in the rational design of synthetic multivalent glycoconjugates as lectin ligands. Org. Biomol. Chem. 2011, 9, 966–979. 10.1039/C0OB00389A. [DOI] [PubMed] [Google Scholar]
  8. Ambrosi M.; Cameron N. R.; Davis B. G.; Stolnik S. Investigation of the interaction between peanut agglutinin and synthetic glycopolymeric multivalent ligands. Org. Biomol. Chem. 2005, 3, 1476. 10.1039/b411555b. [DOI] [PubMed] [Google Scholar]
  9. Roy R. Syntheses and some applications of chemically defined multivalent glycoconjugates. Curr. Opin. Struct. Biol. 1996, 6, 692–702. 10.1016/S0959-440X(96)80037-6. [DOI] [PubMed] [Google Scholar]
  10. Esko J. D.; Sharon N.. Essentials of Glycobiology, 2nd ed.; Varki A., Cummings R. D., Esko J. D., Freeze H. H., Stanley P., Bertozzi C. R., Hart G. W., Etzler M. E., Eds.; Cold Spring Harbor Laboratory Press: Cold Spring Harbor, NY, 2009; Chapter 34, pp 489–500. [PubMed] [Google Scholar]
  11. Branson T. R.; Turnbull W. B. Bacterial toxin inhibitors based on multivalent scaffolds. Chem. Soc. Rev. 2013, 42, 4613–4622. 10.1039/C2CS35430F. [DOI] [PubMed] [Google Scholar]
  12. Bhatia S.; Dimde M.; Haag R. Multivalent glycoconjugates as vaccines and potential drug candidates. Med. Chem. Commun. 2014, 5, 862–878. 10.1039/C4MD00143E. [DOI] [Google Scholar]
  13. Rasko D. A.; Sperandio V. Anti-virulence strategies to combat bacteria-mediated disease. Nat. Rev. Drug Discovery 2010, 9, 117–128. 10.1038/nrd3013. [DOI] [PubMed] [Google Scholar]
  14. Liu S.; Kiick K. L. Architecture Effects on the Binding of Cholera Toxin by Helical Glycopolypeptides. Macromolecules 2008, 41, 764–772. 10.1021/ma702128a. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Tang S.; Puryear W. B.; Seifried B. M.; Dong X.; Runstadler J. A.; Ribbeck K.; Olsen B. D. Antiviral Agents from Multivalent Presentation of Sialyl Oligosaccharides on Brush Polymers. ACS Macro Lett. 2016, 5, 413–418. 10.1021/acsmacrolett.5b00917. [DOI] [PubMed] [Google Scholar]
  16. Papp I.; Sieben C.; Sisson A. L.; Kostka J.; Böttcher C.; Ludwig K.; Herrmann A.; Haag R. Inhibition of Influenza Virus Activity by Multivalent Glycoarchitectures with Matched Sizes. ChemBioChem 2011, 12, 887–895. 10.1002/cbic.201000776. [DOI] [PubMed] [Google Scholar]
  17. Curk T.; Dobnikar J.; Frenkel D. Optimal multivalent targeting of membranes with many distinct receptors. Proc. Nat. Acad. Sci. 2017, 114, 7210–7215. 10.1073/pnas.1704226114. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Tito N. B.; Frenkel D. Optimizing the Selectivity of Surface-Adsorbing Multivalent Polymers. Macromolecules 2014, 47, 7496–7509. 10.1021/ma5014918. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Nowicki W. Structure and Entropy of a Long Polymer Chain in the Presence of Nanoparticles. Macromolecules 2002, 35, 1424–1436. 10.1021/ma010058d. [DOI] [Google Scholar]
  20. Theodorou D. N. Microscopic structure and thermodynamic properties of bulk copolymers and surface-active polymers at interfaces. 2. Results for some representative chain architectures. Macromolecules 1988, 21, 1422–1436. 10.1021/ma00183a038. [DOI] [Google Scholar]
  21. Marques C. M.; Joanny J. F. Block copolymer adsorption in a nonselective solvent. Macromolecules 1989, 22, 1454–1458. 10.1021/ma00193a075. [DOI] [Google Scholar]
  22. Watanabe M.; Matsuoka K.; Kita E.; Igai K.; Higashi N.; Miyagawa A.; Watanabe T.; Yanoshita R.; Samejima Y.; Terunuma D.; Natori Y.; Nishikawa K. Oral Therapeutic Agents with Highly Clustered Globotriose for Treatment of Shiga Toxigenic Escherichia coli Infections. J. Infect. Dis. 2004, 189, 360–368. 10.1086/381124. [DOI] [PubMed] [Google Scholar]
  23. Liese S.; Netz R. R. Influence of length and flexibility of spacers on the binding affinity of divalent ligands. Beilstein J. Org. Chem. 2015, 11, 804–816. 10.3762/bjoc.11.90. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Richards S.-J.; Jones M. W.; Hunaban M.; Haddleton D. M.; Gibson M. I. Probing Bacterial-Toxin Inhibition with Synthetic Glycopolymers Prepared by Tandem PostPolymerization Modification: Role of Linker Length and Carbohydrate Density. Angew. Chem., Int. Ed. 2012, 51, 7812–7816. 10.1002/anie.201202945. [DOI] [PubMed] [Google Scholar]
  25. Hudak J. E.; Bertozzi C. R. Glycotherapy: New Advances Inspire a Reemergence of Glycans in Medicine. Chem. Biol. 2014, 21, 16–37. 10.1016/j.chembiol.2013.09.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Zhang Q.; Collins J.; Anastasaki A.; Wallis R.; Mitchell D. A.; Becer C. R.; Haddleton D. M. Sequence-Controlled Multi-Block Glycopolymers to Inhibit DC-SIGN-gp120 Binding. Angew. Chem. Int. Ed. 2013, 52, 4435–4439. 10.1002/anie.201300068. [DOI] [PubMed] [Google Scholar]
  27. Lis H.; Sharon N. Lectins: Carbohydrate-Specific Proteins That Mediate Cellular Recognition. Chem. Rev. 1998, 98, 637–674. 10.1021/cr940413g. [DOI] [PubMed] [Google Scholar]
  28. Gupta D.; Dam T. K.; Oscarson S.; Brewer C. F. Thermodynamics of Lectin-Carbohydrate Interactions. J. Biol. Chem. 1997, 272, 6388–6392. 10.1074/jbc.272.10.6388. [DOI] [PubMed] [Google Scholar]
  29. van Dongen M. A.; Dougherty C. A.; Banaszak Holl M. M. Multivalent Polymers for Drug Delivery and Imaging: The Challenges of Conjugation. Biomacromolecules 2014, 15, 3215–3234. 10.1021/bm500921q. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Werlang C.; Cárcarmo-Oyarce G.; Ribbeck K. Engineering mucus to study and influence the microbiome. Nat. Rev. Mater. 2019, 4, 134–145. 10.1038/s41578-018-0079-7. [DOI] [Google Scholar]
  31. Zumbro E.; Witten J.; Alexander-Katz A. Computational Insights into Avidity of Polymeric Multivalent Binders. Biophys. J. 2019, 117, 892–902. 10.1016/j.bpj.2019.07.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Chabre Y. M.; Giguère D.; Blanchard B.; Rodrigue J.; Rocheleau S.; Neault M.; Rauthu S.; Papadopoulos A.; Arnold A. A.; Imberty A.; Roy R. Combining glycomimetic and multivalent strategies toward designing potent bacterial lectin inhibitors. Chem. – Eur. J. 2011, 17, 6545–6562. 10.1002/chem.201003402. [DOI] [PubMed] [Google Scholar]
  33. Fortuna S.; Fogolari F.; Scoles G. Chelating effect in short polymers for the design of bidentate binders of increased affinity and selectivity. Sci. Rep. 2015, 5, 15633. 10.1038/srep15633. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Alexander-Katz A.; Netz R. R. Dynamics and Instabilities of Collapsed Polymers in Shear Flow. Macromolecules 2008, 41, 3363–3374. 10.1021/ma702331d. [DOI] [Google Scholar]
  35. Sing C. E.; Alexander-Katz A. Equilibrium Structure and Dynamics of SelfAssociating Single Polymers. Macromolecules 2011, 44, 6962–6971. 10.1021/ma200830t. [DOI] [Google Scholar]
  36. Bell G. I. Models for the specific adhesion of cells to cells. Science 1978, 200, 618–627. 10.1126/science.347575. [DOI] [PubMed] [Google Scholar]
  37. King M. R.; Hammer D. A. Multiparticle adhesive dynamics: Hydrodynamic recruitment of rolling leukocytes. Proc. Nat. Acad. Sci. 2001, 98, 14919–14924. 10.1073/pnas.261272498. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Kolmakov G. V.; Matyjaszewski K.; Balazs A. C. Harnessing Labile Bonds between Nanogel Particles to Create Self-Healing Materials. ACS Nano 2009, 3, 885–892. 10.1021/nn900052h. [DOI] [PubMed] [Google Scholar]
  39. Hoffmann M.; Fröhner C.; Noé F. ReaDDy 2: Fast and flexible software framework for interacting-particle reaction dynamics. PLoS Comput. Biol. 2019, 15, e1006830 10.1371/journal.pcbi.1006830. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Ciarella S.; Sciortino F.; Ellenbroek W. G. Dynamics of Vitrimers: Defects as a Highway to Stress Relaxation. Phys. Rev. Lett. 2018, 121, 058003 10.1103/PhysRevLett.121.058003. [DOI] [PubMed] [Google Scholar]
  41. Oyarzún B.; Mognetti B. M. Programming configurational changes in systems of functionalised polymers using reversible intramolecular linkages. Mol. Phys. 2018, 116, 2927–2941. 10.1080/00268976.2018.1503745. [DOI] [Google Scholar]
  42. Sciortino F. Three-body potential for simulating bond swaps in molecular dynamics. Eur. Phys. J. E: Soft Matter Biol. Phys. 2017, 40, 3. 10.1140/epje/i2017-11496-5. [DOI] [PubMed] [Google Scholar]
  43. Sing C. E.; Alexander-Katz A. Giant Nonmonotonic Stretching Response of a SelfAssociating Polymer in Shear Flow. Phys. Rev. Lett. 2011, 107, 198302. 10.1103/PhysRevLett.107.198302. [DOI] [PubMed] [Google Scholar]
  44. Reuther A.; Kepner J.; Arcand W.; Bestor D.; Bergeron B.; Byun C.; Hubbell M.; Michaleas P.; Mullen J.; Prout A.; Rosa A.. LLSuperCloud: Sharing HPC systems for diverse rapid prototyping. 2013 IEEE High Performance Extreme Computing Conference (HPEC); IEEE: 2013; pp 1–6.

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao0c00334_si_001.pdf (1.4MB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES