Adsorption Characteristics of CO₂/CH₄/N₂ Ternary Mixtures on Anthracite from 293.15 to 353.15 K and Pressures Up to 7 MPa

Abstract

We present the adsorption data of CO₂, CH₄, and N₂ ternary mixtures on anthracite from 293.15 to 353.15 K and pressures up to 7 MPa obtained via a volumetric method. The experimental data are given at different conditions, and simple analysis is made. The results show that the excess adsorption capacity of the CO₂/CH₄/N₂ mixture and its component gases decreases linearly with the increase of temperature for constant composition. The total adsorption capacity is between pure CO₂ and pure N₂ in the entire pressure range. The effect of total pressure on total adsorption capacity is mainly influenced by the CO₂ mole fraction in the feed gas. However, the adsorption capacities of CH₄ and N₂ decrease, and CO₂ presents a maximum with the decrease in total pressure. For the feed gases of 10% CH₄ and 16% CO₂, the total adsorption capacity increases when the ratio of CO₂ and CH₄ increases, respectively, and the increasing magnitudes for 10% CH₄ are larger than that of 16% CO₂. The obtained experimental data are in agreement with the extended three-parameter Ono–Kondo model.

1. Introduction

It is well-known that rapid economic growth has led to the increase in the consumption of energy year by year in China. Statistics show that China is the world’s largest primary energy consumer, accounting for 23.6% of global energy consumption, and coal’s share of the total energy consumption was about 50.5% in 2018.¹ However, conventional energy cannot meet the domestic demand in the long run. The development and use of coal bed methane (CBM) have received significant attention. CBM is a kind of abnormal natural gas that contains not only methane but also heavy hydrocarbons, nonhydrocarbons. As a clean and alternative source of energy, it can alleviate the shortage of conventional energy. Additionally, burning of fossil fuels liberates carbon dioxide, which is linked to climate change and is one of the main greenhouse gases. Safe storage sites are therefore necessary in order to sequestrate CO₂. On the basis of energy shortages and the environmental problems discussed above, enhanced coal bed methane (ECBM) recovery is proposed by injecting N₂, CO₂, or the mixture of them.² Compared with the conventional method (20%–60%), the CO₂/N₂-ECBM technique allows 77%–95% recovery of methane from field applications.³ It is therefore important to investigate the adsorption/desorption properties of CO₂/CH₄/N₂ ternary mixtures on coal.

However, there are still disadvantages when pure CO₂ is injected into a coal seam. First, swelling/shrinkage of coal along with associated alteration of permeability lead to the displacement not being carried out.^4,5 Second, the risk of a gas outburst induced by the elevated CO₂ concentration is higher than that with the raw coal seam and increases the difficulty of coal mining.⁶ Additionally, the costs of separation and purification for CO₂ are high, and it is difficult to guarantee it as a large-scale gas source. Injection of CO₂/N₂ is related to coal swelling on CO₂ adsorption, which reduces the porosity and permeability of the coal reservoir.⁷ Therefore, the adsorption of mixtures of CH₄, CO₂, and N₂ on coal has been more and more investigated from experimental and theoretical aspects in recent years. While the studies focus on the adsorption of CH₄/CO₂ binary mixtures, a limited amount of experimental studies have been made on the ternary adsorption of CH₄/CO₂/N₂, especially in a wide range of temperatures, pressures, and volume fractions of gas. Chaback et al.⁸ investigated the adsorption properties of CH₄/CO₂/N₂ ternary mixtures on wet coal samples at 319 K and pressures up to 11 MPa. Five gas injection ratios were chosen including 40%:15%:45%, 65%:15%:20%, 56%:4%:40%, 88%:4%:8%, and 77%:4%:9% but do not specifically mention the effect of gas injection ratio on the adsorption character of multicomponent gases. Furthermore, the adsorption characteristics of CO₂/N₂ and CH₄/CO₂/N₂ mixtures on coal are analyzed by using isothermal adsorption experiments only for a few gas injection ratios.⁹⁻¹³ On this basis, injection of the flue gas from coal plants into the depleted coal reservoir has been proposed by scholars to satisfy a beneficial cycle. Wang et al.¹⁴ pointed out that the technology of flue gas ECBM can alleviate the contradiction between local environment and economic development by using the flue gas from coal plants around the Qinshui Basin. This is worthy of further study and promotion. Mazumder et al.¹⁵ also measured the adsorption isotherms of the flue gas, which was used with 10.9% of CO₂, 0.01% of CO, 9% of H₂, 3.01% of CH₄, 3% of O₂, 0.106% of SO₂, and N₂ as balance. However, in fact, the research focused on molecular simulation of flue gas injection into coal seams for methane recovery and carbon dioxide sequestration.^16,17 In conclusion, it is necessary to study the adsorption characteristics of CH₄/CO₂/N₂ at different gas injection ratios and at the same time determine the optimal injection ratio of flue gas into a coal seam for improving the economic benefits of CO₂/N₂-ECBM.

In our previous publications, the adsorption of pure CO₂, CH₄, N₂, and CO₂/CH₄ binary mixtures on coal has been investigated.^18,19 Thus, the goal of this work is to extend the isothermal adsorption data for ternary mixtures of CH₄, CO₂, and N₂ desorption equilibria on anthracite. Measurements were performed to cover as much as possible the full range of flue gas ratios and temperatures from 294 to 353 K and pressures up to 7 MPa using a volumetric–chromatographic technique in a setup consisting of a high-pressure volumetric analyzer (HPVA II-200) and a gas chromatograph (GC). Moreover, the prediction of an excess adsorbed amount was carried out using the Ono-Kondo lattice model with three parameters for the multicomponent adsorption system.

2. Results and Discussion

2.1. Data Validation

On the basis of the theory of multivariate error propagation,²⁰ an uncertainty analysis is presented to estimate the expected errors in the calculated excess adsorption capacity due to random variations in primary measurements such as temperature, pressure, and the mole fraction of gas composition. In this work, the standard uncertainties of temperature and pressure are within 0.087 K and 0.005 MPa, respectively. The combined expanded uncertainties of the total excess adsorbed amount and the excess adsorbed amount of component gases are shown in Table 1 at a 0.95 level of confidence for each feed gas composition.

Table 1. Uncertainties of Excess Adsorption for Ternary Mixtures.

feed gas composition CH4:CO2:N2	Unex (mmol/g)	Unex,CH4 (mmol/g)	Unex,CO2 (mmol/g)	Unex,N2 (mmol/g)
10%:16%:74%	0.017	0.015	0.015	0.041
10%:50%:40%	0.017	0.024	0.040	0.040
10%:70%:20%	0.019	0.024	0.047	0.045
40%:16%:44%	0.017	0.037	0.028	0.037
70%:16%:14%	0.018	0.044	0.030	0.041

The repeatability assessment of the measurements was done by calculating the standard deviation for repeated measurements. In this paper, the repeatability tests of the total adsorbed amount and the free phase component were conducted at 311 K when the ratio of feed gas composition of CH₄:CO₂:N₂ is 33%:33%:34%. The generated data are presented in Figure 1, which shows good agreement of total adsorbed amount between the replicate runs for HPVA. The standard deviations of the mole fractions of CH₄, CO₂, and N₂ in free mixtures are 0.58%, 1%, and 0.43%, respectively. These values are less than 1%, that is, the uncertainty of TCD. This illustrates that the gas chromatograph can also meet the requirement of experimental precision.

Figure 1.

Repeatability tests of adsorption/desorption for CH₄/CO₂/N₂ at 311 K.

2.2. Total Excess Adsorbed Amount

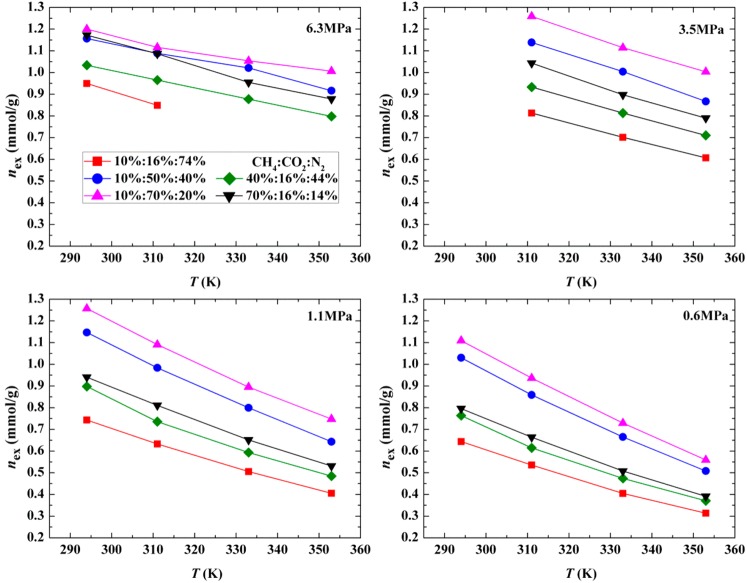
The adsorption measurements of a ternary mixture have been performed at pressures up to 7 MPa and temperatures of 294, 311, 333, and 353 K. Five ratios of feed gas composition were used for CH₄:CO₂:N₂, which are 10%:16%:74%, 10%:50%:40%, 10%:70%:20%, 40%:16%:44%, and 70%:16%:14%. The adsorption isotherms are presented along variable pressure, temperature, and feed gas compositions in Figures 2, 3, and 4. As shown in Figure 2, the pressures from high to low in horizontal axis represent the desorption process, and the excess adsorption amounts of pure CO₂ and pure N₂ were obtained with HPVA at the same experimental conditions in Zhang et al.¹⁸ In a variable-pressure domain, the total adsorption capacity of ternary mixtures lies between pure CO₂ and pure N₂. The relationship of the total excess adsorbed amount and pressure is mainly influenced by the CO₂ mole fraction in the feed gas. The three isotherms for 10% CH₄ exhibit the peak in the experimental pressure scope, but they increase with pressure rising for the other feed gas compositions. In a variable-temperature domain, the isotherms gradually flatten out at the same feed gas composition, and the total adsorption capacity decreases with the increasing temperature for all feed gases due to the exothermic physical adsorption. There is a significant linear correlation between the total adsorption capacity and temperature. In the variable feed gas composition domain, the results for 10% CH₄ (CH₄:CO₂:N₂ = 10%:16%:74%, 10%:50%:40%, 10%:70%:20%) and 16% CO₂ (CH₄:CO₂:N₂ = 10%:16%:74%, 40%:16%:44%, 70%:16%:14%) show that along with the rise of CO₂ or CH₄ mole fraction in feed gas the total excess adsorbed amount increases, and the increasing magnitude for 10% CH₄ is larger than that of 16% CO₂ due to the stronger affinity between CO₂ and a coal sample. Moreover, the peaks of isotherms move to lower pressure because pure CO₂ makes it easier to reach a maximum excess adsorption, and the corresponding pressure is also smaller than pure CH₄ and pure N₂.

Figure 2.

Total excess adsorbed amount of CH₄/CO₂/N₂ mixtures versus total pressure.

Figure 3.

Total excess adsorbed amount of CH₄/CO₂/N₂ mixtures versus temperature.

Figure 4.

Total excess adsorbed amount of CH₄/CO₂/N₂ mixtures versus feed gas composition.

2.3. Excess Adsorbed Amount of Component Gas

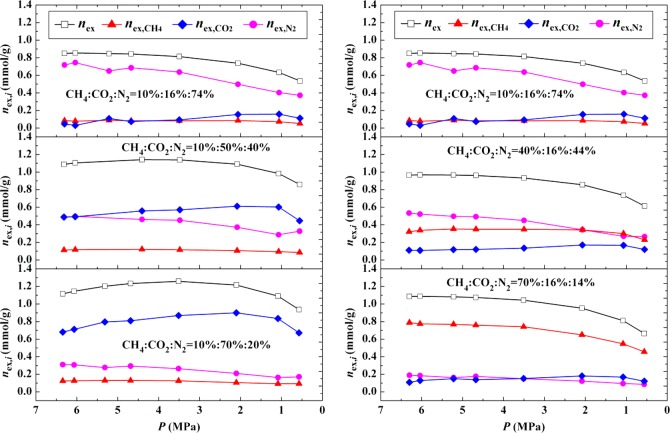
Figure 5 shows the excess adsorbed amount of component i as a function of the total pressure. It can be observed that the adsorption capacities of CH₄ and N₂ decrease, but CO₂ increases to a maximum at first and then decreases afterward with the decrease of total pressure. The reason is that there are differences for different gas adsorption on coal, which adsorbs preferably CO₂, and then the adsorbed CH₄ and N₂ are displaced by the free CO₂. Besides, the trends of the adsorption capacity of CO₂ have good accordance with the pure CO₂ isotherms in Zhang’s study.¹⁸ This illustrates that the adsorption of the coal sample for CO₂ is not obviously affected by other gases except a dilution effect of the pressure. Obviously, the excess adsorbed amounts of CO₂, CH₄, and N₂ are less than the total excess adsorption capacity of ternary mixtures at the same pressure. Additionally, the ratios of maximum absorption capacity for CO₂/N₂ increase from 0.2, 1.2, to 2.9 with the rise of CO₂ mole fraction in the feed gas composition of 10% CH₄. It means that more adsorption sites are gradually occupied by CO₂. However, for a feed gas composition of 16% CO₂, the ratios of maximum absorption capacity for CH₄/N₂ increase from 0.1, 0.7, to 4.2 with increasing CH₄ mole fraction, and CH₄ occupies more adsorption sites. The competitive adsorption among the different gases affects the excess adsorbed amount.

Figure 5.

Excess adsorbed amount of component i versus total pressure and feed gas composition at 311 K.

3. Adsorption Prediction Using the Ono–Kondo Model

3.1. Model

Research indicated that the Ono–Kondo (OK) monolayer model appeared effective in predicting the adsorption isotherms of gas on coal, and the monolayer adsorption occurred within a slit. The expression of the OK model can be written as²¹

1

The pore structure of coal is simplified to a graphite-like crystalline structure. For a hexagonal configuration of lattice cells, the coordination numbers z₀ and z₁ are 8 and 6, respectively. The Gibbs excess adsorption then expresses to

2

The accuracy of the OK model can be affected by the different methods to obtain the parameters including ρ_mc, C, ε_ii/k, and ε_is/k. In this work, the fluid–fluid energy parameter ε_ii/k is estimated from the Lennard-Jones 12-6 potential, ε_ii/k = 0.432ε*/k. The values of ε*/k are 148.6, 195.2, and 71.4 K for CH₄, CO₂, and N₂, respectively.²² The three parameters including ρ_mc, C, and ε_is/k are evaluated with the least-square method by fitting the measured data of pure gas adsorption on coal from Zhang et al.¹⁸ We call this type of OK model a three-parameter OK model, 3OK model for short. It is worth noting that there are different methods to obtain the fitting parameters of the Ono–Kondo model for pure CH₄, N₂, and CO₂ adsorption on the same coal in refs (18) and (19). In ref (18), three parameters including the adsorbed phase density, the fluid–solid energy parameter, and the maximum adsorption capacity are obtained by a simplified Ono–Kondo model, which has been described in detail by Zhang et al.¹⁸ In ref (19), a two-parameter Ono–Kondo model is derived from the research of Sudibandriyo et al.,²² and it is used to fit the fluid–solid energy parameter and the maximum adsorption capacity for each specific adsorption system and each adsorption isotherm of pure gas; however, the adsorbed-phase density and the fluid–fluid energy parameter are estimated from the reciprocal van der Waals covolume and the Lennard-Jones 12-6 potential, respectively.

Based on the fitting results of pure gas adsorption data and combined with certain mixing rules, the 3OK model for monolayer adsorption is generalized to a multicomponent system for predicting the total and each component adsorption capacity, E3OK model for short. The equality of the chemical potential in the adsorbed and the bulk phases for each component leads to the following equilibrium equations for the ternary mixed-gas adsorption.²¹

3

Further, the interaction energy between molecules i and j is evaluated using a geometric combination rule.

4

A modified parameter is introduced to calculate the Gibbs excess adsorption for each component because the maximum adsorption capacity of a component between pure and mixture adsorption may be different.

5

6

Because the adsorbed-phase density of the mixture can not be obtained from experiment, ρ_mc is evaluated using the following ideal mixing rule.

7

8

The parts of the 3OK model that need attention are: ρ_mc is the adsorbed-phase density corresponding to the maximum adsorption capacity of a gas mixture, and ρ_b is the bulk phase density of the gas mixture, which can be calculated using PV = zRT for the nonideal gas. The compressibility factor z is generated from a modified Benedict–Webb–Rubin equation of the data acquisition system of HPVA.

3.2. Adsorption Predictions for Pure Gas

Table 2 presents the results of the 3OK model predictions for the pure gas adsorption on coal. It should be pointed out that the adsorbed-phase density corresponding to the maximum adsorption capacity ρ_mc is taken as 0.808 g/m³ for N₂ at different temperatures because it belongs to the type Ι isotherm for N₂ in the whole range of experimental temperatures.¹⁸ In general, the values of parameter C are in the sequence of CO₂ > CH₄ > N₂ at the same temperature, and they decrease with the increase of temperature. The numerical order (except N₂) and the trend with temperature of parameter ρ_mc are consistent with C. Similarly, the parameters of the fluid–solid surface interaction energy generally have the same sequence with the parameters C and ρ_mc, which accords with the relationship of affinity between coal and gas.

Table 2. Results of the Three-Parameter OK Model for Pure CH₄, CO₂, and N₂ Adsorption.

	T (K)	NPTSa	C (mmol/g)	ρmc (g/cm3)	–εis/k (K)	ARDb (%)	Δnex (mmol/g)	Unex (mmol/g)
CO2	293.73	10	1.213	0.575	1649	1.22	0.014	0.018
	311.17	11	1.089	0.378	1384	1.97	0.021	0.018
	333.06	11	1.087	0.306	1228	1.58	0.015	0.018
	352.74	11	1.031	0.205	950	2.03	0.017	0.017
CH4	293.81	14	0.782	0.309	1332	2.71	0.023	0.031
	311.14	14	0.750	0.287	1322	2.38	0.017	0.030
	333.14	14	0.729	0.299	1303	2.39	0.017	0.029
	352.88	13	0.709	0.223	1178	2.14	0.014	0.028
N2	293.71	13	0.786	0.808	958	4.56	0.025	0.026
	311.08	13	0.630	0.808	1042	0.77	0.004	0.026
	333.07	13	0.558	0.808	1057	0.58	0.002	0.025
	352.78	13	0.624	0.808	979	0.98	0.005	0.024

^aNPTS: number of data points estimated.

^bARD: average relative deviation: .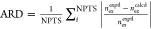

In addition, the 3OK model with three regressed parameters (individual C, ρ_mc, or −ε_is/k can be obtained for each isotherm) that represent the average relative deviation (ARD) is within 2%, 2.8%, and 0.8% for the excess adsorption capacity of CO₂, CH₄, and N₂. However, the ARD is significantly larger for the N₂ isotherm at 293.71 K. Also, the relative deviation (RD) is exaggerated when the excess adsorption capacity at lower pressure becomes exceedingly small from Figure 6, especially for CO₂ and CH₄ at 0.2 MPa and 311 K.

Figure 6.

Relative deviation of the 3OK model for pure CH₄, CO₂, and N₂ at 311 K.

3.3. Adsorption Predictions for Ternary Mixtures

This paper, taking 10% CH₄:16% CO₂:74% N₂, for example, introduces the predicted results of adsorption capacity of each component including CH₄, CO₂, and N₂ and total adsorption capacity at 311 K using the extended 3OK (E3OK) model. Figure 7 shows that the predicted results can reflect the changed trend of the experimental values. The average relative deviation (ARD) of CH₄, CO₂, and N₂ and total adsorption capacity are about 10.7%, 33.0%, 9.4%, and 7%, respectively, and the E3OK model gives a relatively satisfactory prediction. According to the proportion of each group in the raw ternary gases, the adsorption capacity of pure CO₂, CH₄, and N₂ takes a weighted average under the same pressure. The adsorption capacity of different gases is predicted by the three-parameter OK (3OK) model. The weighted average value (n_ex^calcd) of the total adsorption capacity is compared with the experimental value (n_ex), as shown in Figure 7(d). As can be seen from the diagram, the weighted average value of the total adsorption capacity is smaller than the experimental value, indicating that each component in the ternary gases is not adsorbed separately but that the gas components interact with each other and undergo competitive adsorption.

Figure 7.

Predicted results of the E3OK model for CH₄:CO₂:N₂ = 10%:16%:74% at 311 K.

4. Conclusions

The adsorption of ternary mixtures of CH₄, CO₂, and N₂ with five mole ratios of feed gas composition on anthracite is investigated using the volumetric–chromatographic method at 294, 311, 333, and 353 K with pressures up to 7 MPa. The excess adsorbed amounts of the mixtures and individual components are modeled using the three-parameter Ono–Kondo (3OK) model. The conclusions of this paper are summarized as follows:

• (1)In the desorption process, the total adsorption capacity of the ternary mixture and the adsorption capacity of each component decrease linearly with the increase of temperature in the range of experimental pressures. The influence of pressure on the adsorption capacity is related to the proportion of each component in the feed gas.
• (2)The total adsorption capacity of the mixture is lower than that of pure CO₂ but higher than that of pure N₂. When the ratios of CH₄ and CO₂ in the feed gas are fixed as 10% and 16%, respectively, the total adsorption isotherms gradually approach the pure CO₂ and pure CH₄ adsorption isotherms with the increase of CO₂ and CH₄ content in feed gas.
• (3)Gas mixture adsorption is related to temperature and pressure, and there also exist the competing adsorption phenomena with the change of gas composition. The adsorption capacity of each component is related to its adsorbability, proportion in feed gas, and partial pressure in the bulk phase.
• (4)The predicted results of the three-parameter Ono–Kondo model for pure gases and the extended three-parameter Ono–Kondo model for ternary mixtures can reflect the changed trend of the corresponding experimental isotherm data.

5. Experimental Section

5.1. Materials

The coal sample came from the Datong coal mine in the Shanxi province of China in this study. Physical properties of the coal sample including ultimate analysis, proximate analysis, petrographic analysis, and pore structure data have the same values as Zhang’s study.^18,19 To accelerate the interaction between coal and gas, the coal sample was ground and sieved to generate particles with a diameter between 0.25 mm and 0.38 mm and dried in an oven at 378.15 K before the adsorption measurements.

The following gases were supplied by Dalian Da-te Gas Co., Ltd. and common N₂ and He at purities of 99% and 99.999%, respectively. Ternary gas mixtures of certified compositions were prepared using CH₄, CO₂, and N₂ at purities of 99.99%, 99.999%, and 99.999%, respectively. The mole compositions of the five feed gases of CH₄:CO₂:N₂ included 10.05%:16.04%:73.91%, 10.35%:49.43%:40.22%, 9.86%:70.30%:19.84%, 39.86%:15.80%:44.34%, and 70.04%:15.83%:14.13%, which are simplified as 10%:16%:74%, 10%:50%:40%, 10%:70%:20%, 40%:16%:44%, and 70%:16%:14% in the following sections. All gases were used as received without any further purification.

5.2. Apparatus and Procedure

A diagram of the entire experimental apparatus is shown in Figure 8. It is made up of two main parts: the unit of adsorption measurement based on HPVA II-200 and the gas analysis based on a gas chromatograph (GC). The HPVA II-200 has been described elsewhere.^18,19 It is made of an analysis station and a degas station. The measurements including dual free spaces, adsorption, and desorption are fully automated, and the compressibility correction for the nonideal feed gas can enhance the accuracy of the isotherm data. The temperature of the different stations is measured by calibrated thermocouples. Two digital pressure transducers (HP and LP) are used to monitor the pressure at the inlet and the outlet of the adsorption chamber. The gas-phase compositions are quantitatively analyzed using GC equipped with a thermal conductivity detector (TCD).

Figure 8.

Schematic diagram of experimental apparatus.

It is similar to the pure gas for the experimental procedure, which can be found elsewhere.¹⁸ The difference is that the adsorption measurement with CH₄/CO₂/N₂ mixtures requires an additional analysis step to determine the relative concentrations of the three compounds in the free gas phase. The free gas is collected using a gas-collecting bag when desorption equilibrium needs to be achieved for each desorption step. A gastight syringe is used to extract a small gas sample (1 mL) for GC determination. Note that a vacuuming process is needed for the exhaust pipe in the desorption process to reduce the error caused by the gas-collecting bag.

In addition, the computational principle for an adsorbed amount of gas mixture is consistent with pure gas.¹⁸ So, the adsorbed amount of component gases can be calculated using

9

10

Glossary

Nomenclature

C = C_i

maximum adsorption capacity of pure gas i, mmol/g

C_ij

binary interaction parameter for fluid–fluid interaction energy between unlike molecules

k

Boltzman’s constant, 1.38 × 10^–23 J/(mol K)

m_s

mass of coal sample, g

n

number of gas components

n_ads,i

mole of component i adsorbed by coal sample, mol

n_dosed

mole of CH₄/CO₂/N₂ ternary mixture dosed into the sample tube, mol

n_ex,i

amount of excess adsorption for component i, mmol/g

n_unads

mole of gas mixture unadsorbed by coal sample, mol

S_ij

binary interaction parameter, it is only used to test correlative capabilities of the model, S_ii = S_jj = 1

T

temperature, K

x₁

fraction of sites occupied by adsorbed molecules in the first layer

x_b

fraction of sites occupied by fluid molecules in the bulk phase

x_i

mole fractions of component i in the adsorbed phase

x_i,b

mole fractions of sites occupied by the molecule i in the bulk layer

x_i^Abs

absolute adsorbed mole fraction of component i

y_i

mole fraction of component i in free gas

y_i^feed

mole fraction of component i in feed gas

z₀

volume coordination number

z₁

monolayer coordination number

z₂

interplane coordination number, z₂ = (z₀ – z₁)/2

ε_ii

interaction energy between the adsorbate molecules, which is limited to nearest-neighboring sites of the lattice, kJ/mol

ε_is

interaction energy between the adsorbate molecules and the adsorbent surface, kJ/mol

ρ₁

adsorbed density of adsorbate, g/cm³

ρ_b

bulk density of adsorbate, g/cm³

ρ_mc = ρ_mc,i

adsorbed phase density of pure i at maximum adsorption capacity, g/cm³

The authors declare no competing financial interest.