Abstract

Flammability dynamics and physics play a crucial role in fire safety and combustion efficiency. This paper numerically studied the flammability dynamics of dimethyl ether/air freely propagating premixed flame over a broad range of equivalence ratios (ϕ). The results showed that the traditional flammability range should be redefined considering the impact of low-temperature chemistry. A physically stable warm-flame branch existed in the ultrarich region (ϕ = 7.58–12.59), which connected the hot and cool flame transition smoothly. However, in the lean region, the transition between hot and cool flames was completed by extinguishment or ignition. Sensitivity analysis was performed to reveal the governing chemical and diffusive processes for the flammability limits (FLs). In addition to the high-temperature reactions, low-temperature chemistry also played an important role in the lean hot-flame FL because of its double-flame structure. Heat conduction and fuel and oxygen diffusions were the most significant diffusive processes for the near-limit flame propagation. The near-limit flames had a diffusion-reaction structure, in which the flame front propagation was sustained by the heat conduction-induced ignition rather than the autoignition wave. The hot-flame extinction was induced by radiative extinguishment of the high-temperature propagating front embedded in the double-flame structure, and the cool-flame extinction was induced by excessive diffusive loss.
1. Introduction
Studies on the flammability limit (FL) are of great significance because of their importance to fire safety, combustion efficiency, and pollutant emissions.1 With the increasing awareness of practical meanings of FL on combustion, continuous attention has been paid to the FL theories in the past few decades.2 For premixed combustion systems, their flammability features are characterized by the lower flammability limit (LFL) in the fuel-lean region, as well as the upper flammability limit (UFL) in the fuel-rich region. The fuel/air mixture is flammable between the LFL and UFL, while flame instability or even extinguishment will probably happen outside of this region. By far, the flammability of propagating premixed flames due to the high-temperature chemistry has already been studied; however, recent studies showed that the existence of a self-sustaining cool flame due to the strong coupling of low-temperature chemistry with diffusive transports would significantly increase the complicacy of flammability dynamics. Hence, the flammability limit should be redefined considering the effectiveness of a cool flame. Studies on UFLs associated with cool-flame extinction in the fuel-rich region were widely reported in the 1920s and 1930s, when cool-flame experiments were mostly conducted using fuel-rich mixtures.3 For the LFLs, they contain two flammability limits that are relevant to two stable flame branches, i.e., the hot-flame branch and the cool-flame branch. More recently, advanced engine studies based on ultralean combustion of alternative fuels provide a new platform and perspective to deepen the understandings of LFL associated with the low-temperature chemistry.4 Therefore, there is an urgent need to systematically examine the FL dynamics as well as its dependence on the detailed fuel chemistry.
The cool flame is an important combustion mode that occurs in the low and intermediate temperature ranges (T = 550–850 K),5 with weak blue chemiluminescence in experiments.6 It may exist in the combustion process of mostly practical transportation fuels,7 which is sustained by the weak exothermicity due to the low-temperature branching chemistries involved in the fuel decomposition and isomerization reactions.8 Since it was first found in 1817, the cool flame had been studied extensively in the literature, and many studies proved that it was the underlying physics for many critical phenomena in engine operation, including knocking,9 two-stage autoignition,10 and negative temperature coefficient (NTC) behavior.11 Because of their great significance in combustion science, increasingly more attention has been paid to the fundamental aspects of cool flames, such as their flammability limit, flame speed, and reaction regimes. In the past few decades, self-sustaining cool flames had been established in various laboratorial burner geometries, including the counterflow burner,12 heated surfaces, heated flow reactors,13 stirred reactors,14 rapid compression machines,15 microgravitational droplets,3 and plasma-assisted flames.16
Sun et al.17 numerically investigated the transition process from ignition to flame formation with high-pressure stratified n-heptane/toluene mixtures in a constant-volume chamber. The comparison analysis of the flame fronts between the n-heptane mixture and the toluene mixture suggested that engine knock and acoustic formation resulted from the rich low-temperature chemistry and fuel stratification. Deng et al.18 further studied the low-temperature chemistry experimentally and computationally by analyzing the ignition and extinction behavior of the dimethyl ether (CH3OCH3, DME) cool flame at elevated pressures in the counterflow burner. The governing chemical reaction pathways during these two near-limit processes were obtained, and the role of the governing reactions will shift from radical proliferation to sustainment of the cool-flame propagation. Hajilou et al.19 conducted an experimental and computational study to investigate the low-temperature chemistry of n-heptane on the Hencken burner, with equivalence ratios ranging from 0.4 to 1.0 at subatmospheric pressures. The formaldehyde planar laser-induced fluorescence (PLIF) intensity method was used in the reduced model to depict the cool-flame structure and estimate the adiabatic cool-flame propagation speed effectively. Wang et al.20 investigated experimentally the characteristics of the premixed methane/oxygen cool flame in a cylindrical reactor, and a computational analysis involved with different mechanisms was conducted for comparison validation. The flammability range in terms of the equivalence ratio that could yield a self-sustained cool flame, as well as the remarkable effect of CH3 oxidation on cool-flame formation, was reported. Jin et al.21 studied the effectiveness of cool flame on turbulent combustion through direct numerical simulation (DNS) with a DME/methane–air mixture under reactivity controlled compression ignition (RCCI) conditions. It showed that the cool flame could form in both the mixing layer and the initially stratified mixture; in addition, the cool flames were considered to play an important role in the formation of high-temperature ignition kernels. The properties of cool flames with and without low-temperature chemistry and the effects of some factors, including initial temperature and equivalence ratio, on cool flames had been studied on different combustion conditions. Some intermediate species that can be used as a marker to describe the reaction process were obtained, which would be of great significance for future cool-flame studies. Besides, the utilization of new techniques provides a broad platform to explore the low-temperature chemistry.
Ju et al.22 numerically investigated the cool-flame dynamics of dimethyl ether in both freely propagating and counterflow flames with and without ozone addition. It was found that the ozone could promote the low-temperature chemistry and dramatically extend the cool-flame flammability limit, and multiple flame regimes were observed in the counterflow flames with and without ozone addition. Sohn et al.23 studied the dynamics of near-limit cool flames experimentally and numerically in a counterflow burner, which showed that the ignition process was so sensitive to ozone addition that the perturbation of ozone in the oxidizer stream could induce a cool diffusion flame or two-stage autoignition. Farouk et al.24 reported the simulation results of n-alkane droplet combustion with elevated pressure and helium dilution. It showed that the hot flame will extinguish into a warm flame or cool flame under different helium substitution ratios, which suggested that the existence of helium plays a great role in the competition between low- and intermediate-temperature chemistries. Similarly, Yehia et al.25 investigated the effect of aromatic chemistry on the n-alkane low-temperature chemical kinetics by adjusting the ratio of nitrogen/n-propylbenzene in a counterflow burner at atmospheric pressure. It was found that the addition of n-propylbenzene could promote cool-flame extinction, which implied that the aromatics can be used as an ideal agent to inhibit the low-temperature reactivity. Nayagam et al.26 studied the cool-flame extinction of an n-alkane droplet flame in microgravity with the pressure ranging from 0.5 to 1.0 atm, which reported the multistage, multimode combustion and extinction dynamics with the involvement of cool-flame chemistry, as well as its great impact on the droplet burning rate.
In summary, the existing studies on flammability limits and dynamics were mostly established based on the strained counterflow burner or the microgravitational droplet flame;27 however, the planar freely propagating premixed flame that is of practical significance was rarely involved. Second, elevated pressures or fuel/air preheating was often considered to reduce the induction time period of the NTC chemistry, thus leading to obtaining a self-sustaining cool flame successfully. However, the tendency of establishing a self-sustained cool flame under normal temperature and pressure merits further examination. Third, plasma assistance or ozone sensitization was mostly employed in existing studies to obtain self-sustaining cool flames; however, the plasma or ozone kinetics, in the meantime, will significantly change the fundamental chemical dynamics of the cool flames. Hence, the fundamental dynamics of self-sustained cool flames without ozone or plasma assistance, as well as their impact on the propagating limit of the premixtures, merit a systematical study. In this paper, the flammability dynamics and propagating limits of the planar freely propagating DME premixed flame, under atmospheric pressure and room temperature, are studied to examine its cool-flame dynamics as well as its effectiveness on the FL. The dominant chemical and diffusive processes underlying the hot- and cool-flame dynamics will be revealed, which would be of fundamental and practical importance for the design of advanced combustion systems. Furthermore, some recent studies observed the repetitive ignition and extinction (FRIE) event in microchannel flow reactors with an imposed temperature stratification.28−31 The coupling of inlet flow with the propagating flame front that depends on the local temperature gradient was responsible for the FRIE dynamics. However, when considering the effectiveness of the mixture equivalence ratio or stoichiometry stratification, as well as the intertransition between hot- and cool-flame fronts, the FRIE dynamics would become much more complicated. Hence, this study would provide some fundamental knowledge to explain the FRIE dynamics in more complicated combustion systems with cool-flame propagation.
The PREMIX model32 with the continuation algorithm33 was utilized to generate the S-curve of the DME/air premixed flame, which defines the LFLs and UFLs in either hot- or cool-flame regimes, respectively. Then, the flame structure, dominant chemical reactions, and diffusive transport processes, as well as the governing flame propagation regimes are clarified, which would provide guidance for the control of the combustion process or design of advanced engines.
2. Numerical Models
In this paper, the PREMIX code developed by Kee et al.32 was employed for the current simulations, which is a well-defined model for the planar freely propagating premixed flame. The governing equations are expressed in eqs 1–5. The energy conservation equation was appropriately modified to include the radiative heat loss term, and a radiative transfer equation (RTE) as shown in eq 4 was coupled with the original equations to estimate the radiative heat loss. The RTE can consider the emission and reabsorption of the participating species including CO2, H2O, CH4, and CO (with their Planck mean absorption coefficients determined by the weighted-sum-of-gray-gases (WSGG) model34), so it can accurately capture the planar premixed flame profile as well as its bifurcation behavior in the near-limit region, where the flame thickness and thus radiative heat reabsorption become nonignorable. Furthermore, the CHEMKIN and TRANSPORT packages35 were incorporated into the code to obtain the basic detailed reaction rates and transport properties; the TWOPNT package32 with Newton’s iteration algorithm was used to solve the nonlinear algebraic equations. An adaptive grid refinement scheme based on the temperature and each species profile was employed for equation discretization. The upwind difference scheme and central difference scheme were used for discretization of the convective and diffusive terms, respectively. The governing equations of mass, species, energy, and RTE were solved in a coupled manner, in a coordinate system moving with the propagating flame front. As such, the mass flux became an eigenvalue of the problem, which required an additional inner boundary condition. The temperature at one internal grid point was then chosen as the internal boundary (in the study, this point was anchored at x = 0.04 cm with a fixed temperature 400 K) to fix the solution of the flame. It should be pointed out that the set of the fixed temperature 400 K was arbitrary, which was for obtaining an initial flame location and cannot change the final results. Besides, the absolute and relative tolerances for convergence were set to 10–12 and 10–6, respectively.
The FLs were defined in terms of ϕ of the unburned premixture. In the current problem, the steady-state calculations were performed to obtain the planar freely propagating premix flame solutions, with the left unburned boundary condition defined as the atmospheric DME/air premixture with a fixed initial temperature (300 K) but an unconstrained equivalence ratio (ϕ). A one-point flame-controlling continuation technique proposed by Nishioka et al.33 was used to capture the bifurcation turning behavior of the near-limit branch of the S-curve (which defines flame response with respect to ϕ), thus enabling accurate definition of the FLs in the lean and fuel-rich ranges. In this method, an additional dummy equation defined based on ϕ (eq 5) is added to the equation list. In the meantime, instead of using ϕ as an imposed boundary parameter and the scalars as flame responses, the value of temperature or mass fraction of a specific species at a given location xi is set as an internal boundary condition (as shown in eq 7), while ϕ becomes the flame response. This technique can effectively eliminate the problem associated with the singular Jacobian matrix at the bifurcation point of the S-curve, where a slight variation in ϕ leads to a significant change in flame response, thus leading to obtaining the near-limit solutions efficiently. Hence, it was extensively employed for S-curve computation and thus FL definition in the literature.22,27,33 A sufficiently long computational domain ranging from x0 = −5.0 cm to xL = 50.0 cm was employed to allow for radiative extinction of the propagating flame in the near-extinction condition, where the flame thickness became rather significant (say 3.0 cm).
Continuity equation
| 1 |
Species equation
| 2 |
Energy equation
| 3 |
RTE equation
| 4 |
Dummy equation of ϕ
| 5 |
Boundary conditions
| 6 |
| 7 |
| 8 |
where M = ρuA is the conserved mass flux
rate across unit area A = 1 cm2; and ρ, cp, and λ are density,
specific heat,
and thermal conductivity for the mixture, respectively. K is the total number of species, and Yk, cp,k, hk, and Wk are the mass
fraction, specific heat capacity, enthalpy, and molecular weight for
species k, respectively. ωk and Vk are, respectively,
the volumetric reaction rate and diffusion velocity for species k. In is the
radiative intensity at grid point n, κ is the
absorption coefficient determined by the WSGG model,34 and Δs = xn+1 – xn is the length of the cell. The volumetric radiative
heat loss qr is estimated based on the
radiative intensity solution by 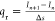 . x0 and xL represent the left (unburned) and right (burned)
boundaries, respectively, and xi is the inner boundary where the local temperature or species
mass fraction was prescribed.
. x0 and xL represent the left (unburned) and right (burned)
boundaries, respectively, and xi is the inner boundary where the local temperature or species
mass fraction was prescribed.
Furthermore, DME was used as the target fuel because of its small chemical mechanism size but with a strong NTC reactivity. Zhao’s detailed DME chemical mechanism36 consisting of 55 species and 290 elementary reactions, which had been extensively validated against the laminar flame speed, flow reactor, and ignition delay time experiments,35 was utilized for the current simulations. Figure 1 shows comparisons of the DME/air flame solutions at pressure 2 atm using the current models with those from ref (9). It can be seen that the two sets of simulation results agreed fairly well with each other; hence, the current continuation model was accurate to reproduce the propagating premixed flames.
Figure 1.
Comparisons of the DME/air premixed flame solutions at pressure 2 atm using the current models with those from the literature.9
3. Results and Discussion
3.1. Flammability and Structure Dynamics of the Freely Propagating DME/Air Premixed Flames
In this part, FL dynamics of the planar freely propagating DME premixed flame will be discussed by examining its S-curve, which defines the flame response with respect to the normalized equivalence ratio Φ (Φ = ϕ/(1 + ϕ)), as shown in Figures 1 and 2, which exhibit the flame response in the entire space of the equivalence ratio. It can be seen in Figures 1 and 2 that for the DME mixture that has a strong low-temperature reactivity, its S-curve was featured by multibranches due to the self-sustaining cool-flame combustion, which is rather distinct from the canonical “Δ-shaped” S-curve of premixed flames. The S-curve of the DME planar premixed propagating flame consists of a physically stable hot-flame branch (colored in solid red), a stable warm-flame branch in the ultrarich range (colored in dashed red), two stable cool-flame branches in the fuel-lean and -rich regions, respectively (colored in blue), as well as two physically unstable branches (colored in dashed black). Besides, the stable solutions were also calculated using the PREMIX model without the continuation algorithm, and the results are superimposed as circle symbols in Figures 1 and 2. It can be seen that the continuation computations agreed well with the PREMIX simulations, and additionally, the continuation computations can also provide physically unstable branches; hence, it can accurately capture the flammability limits of the near-limit propagating flames with high efficiency. As expected, the maximum temperature and flame speed occurred at a slightly rich condition (ϕ = 1.1 or Φ = 0.524). Additionally, with the increment in Φ in the rich range, the flame temperature as well as the propagation speed decreased continuously, with the combustion mode transiting from the hot-flame mode (T > 1100 K) to the warm-flame (800 K < T < 1100 K) and cool-flame modes (600 K < T < 800 K) smoothly, until the rich cool-flame extinction (RCFE) limit (ϕ = 25.44 or Φ = 0.96) where flame propagation could not be self-sustained. At the current atmospheric pressure, there existed a physically stable warm-flame branch in the ultrarich region (ϕ = 7.58–12.59), which connected the hot- and cool-flame transition smoothly, as also reported before.37 However, in the fuel-lean range, the transition from the hot-flame mode to the cool-flame mode happened by an abrupt extinguishment at the lean hot-flame extinction (LHFE) limit (ϕ = 0.41 or Φ = 0.29), and the lean cool-flame mode shifted to the hot-flame mode by ignition at the lean cool-flame ignition (LCFI) limit (ϕ = 1.18 or Φ = 0.54). With further decrease in Φ, the self-sustaining lean cool flame became inflammable at the extinction limit (lean cool-flame extinction (LCFE), ϕ = 0.29 or Φ = 0.22). The transition dynamics between hot and cool flames reported in this study coincide with those in the literature.37,38 The present study indicates that the self-sustaining cool flame could exist in a broad range of equivalence ratios in either the rich (ϕ = 12.59–25.44) or lean (ϕ = 0.29–1.18) range. It should be noted that the existence of a self-sustained cool-flame branch was ascribed to the competing coupling of low-temperature heat release with diffusive transports.37 Additionally, the propagation speed of the cool flame in the rich or lean condition was basically identical (i.e., 1.0 cm/s or even slower), which was rather trivial compared with the hot-flame propagation.
Figure 2.

Response of the maximum temperature with respect to the normalized equivalence ratio Φ in different flame modes of the atmospheric DME/air mixture. The solid curves are results from the continuation computations, and the circle symbols are from the PREMIX model.
Figures 1 and 2 also show that the flammability range of the cool flame surpassed the hot-flame flammability limit, in either the fuel-rich or fuel-lean condition, such as LCFE (ϕ = 0.29 or Φ = 0.22) versus LHFE (ϕ = 0.41 or Φ = 0.29) as well as RCFE (ϕ = 25.44 or Φ = 0.96) versus the rich hot flammability limit (ϕ = 12.59 or Φ = 0.93). Hence, it is safe to conclude that the existence of a self-sustaining cool-flame chemistry could extend the mixture flammability range significantly. Furthermore, the concept of the mixture flammability limit should be redefined considering the impact of low-temperature chemistry, which has practical implications for fire safety research.38 On the other hand, although a self-sustaining cool-flame propagating front may take place beyond the high-temperature flammability range, under practical combustion circumstances, the cool-flame front, which is featured by extremely slow propagation speed and large instability due to the indiscernible heat production, would be readily split up and thus lead to propagation extinguishment by the flow stretch or turbulence mixing. Nevertheless, the significance of cool-flame front propagation for combustion is reflected in the fact that the products of low-temperature chemistry feed as reactants of high-temperature ignition and thus promote propagation and stability of the hot-flame front.39 Hence, the interaction of cool-flame front propagation with turbulence or transport mixing acts as the fundamental physics for many global combustion dynamic processes. The complicacy of cool-flame dynamics as well as its fundamental role in flame propagation will be studied with sufficient details in a later discussion.
It is noted that during the transition process from the hot-flame to cool-flame mode by flame extinguishment near the LHFE, the flame temperature dropped dramatically (Figure 2), while the propagation speed slowed down fairly marginally (Figure 3). Thus, the propagation speed of the near-extinction hot flame was basically identical to that of the cool flame. Further investigation into the flame front structure revealed that in strongly stable hot flames, the low- and high-temperature flame fronts were coupled; however, near the LHFE point, the leading cool-flame front with a higher propagation speed departed off the downstream tailing hot-flame brash, resulting in a “double-flame” structure. More specifically, as shown in Figure 4, which illustrates the evolution of a flame structure where the lean hot flame steps across the LHFE point from the physically stable to unstable branches, the hot flame near the extinction was composed of two segments due to the low- and high-temperature chemistries, as revealed by the heat release rate (HRR) profile, which consists of two crests. It can be seen that in the flame transition that passed across the critical LHFE point from the physically stable to unstable branches, the coupled flame structure turned to a “double-flame” structure, which consists of an upstream leading cool-flame front and the tailing hot-flame brash. Hence, the occurrence of a double-flame structure can serve as a judgment criterion for lean hot-flame extinction. The extinction of the hot-flame brash and the robust stability of the cool-flame front embedded within the double-flame structure were attributed to two reasons. First, the flame front thickness increased dramatically with the occurrence of a double-flame structure, such that radiative heat loss of the tailing hot-flame brash became increasingly more significant. Second, as revealed by the red numbers near the second crest of the HRR profile, which indicate the integral summary heat production amount due to the high-temperature reactions, heat production of the hot-flame brash reduced significantly with the occurrence of a double-flame structure, although heat production due to the leading cool flame remained nearly unchanged. Therefore, it is suggested that the occurrence of a double-flame structure and subsequently radiation-induced extinguishment of the tailing thickened hot-flame brash were the extinction mechanisms of the fuel-lean propagating hot flames. Furthermore, since propagating speeds of the cool flame and hot flame near the LHFE were basically equal, the flame propagation speed reduced rather marginally during the transition from the hot- to cool-flame propagation mode in the lean condition, as shown in Figure 3.
Figure 3.

Response of the laminar flame speed with respect to the normalized equivalence ratio Φ in different flame modes of the atmospheric DME/air mixture. The solid curves are results from the continuation computations, and the circle symbols are from the PREMIX model.
Figure 4.

Profiles of temperature and heat release rate (HRR) across the propagating front, for three typical cases near the LHFE, including the critical LHFE case (ϕ = 0.41) and P1 and P2 cases on the stable and unstable branches near the LHFE point with an identical equivalence ratio (ϕ = 0.43). The red numbers imposed near the second crest of the HRR profile are the integral summary heat production amounts (unit: W) due to the high-temperature reactions.
On the contrary, in the fuel-rich range, we did not detect any extinction phenomenon associated with the transition from the hot- to cool-flame propagation mode (Figure 3). The reason will be discussed below. Figure 5 shows the evolution of the flame structure during the transition from the end of the hot-flame mode (P3), through a representative warm flame (P4), to the formation of the cool-flame mode (P5) in the fuel-rich range. It is seen that when the maximum temperature dropped into the intermediate-temperature range (800 K < T < 1100 K), flame extinction did not happen, while instead, it formed a self-sustained warm flame with a double-flame structure where the leading cool-flame front decoupled from the tailing hot-flame brash (P4 as shown in Figure 5). With further increase in ϕ, the hot-flame brash as well as its heat production crest disappeared gradually and finally shifted into the cool-flame propagation mode that consisted of solely the low-temperature leading front. Hence, it was summarized that the self-sustained warm flame with a double-flame structure connected the transition from the hot and cool flame smoothly in the fuel-rich condition. The absence of extinguishment of the high-temperature brash embedded in the warm flame was ascribed to depression of its radiative heat loss and enhancement of heat production. More specifically, Figure 6 illustrates the responses of ignition delay time and HRR at the first- and second-stage autoignition points with respect to Φ, for the DME/air autoignitive premixture in the homogenous reactor simulated by the SENKIN model.40 It indicates that for the ultrarich premixture (ϕ = 7.58–12.59) near the hot-to-cool flame transition, the time interval between the first- and second-stage ignitions was rather trivial; hence, the induction length between the leading low-temperature front and the tailing high-temperature front in the warm-flame structure (P4 in Figure 5) was considerably thinner compared with the near-extinction lean hot flame with the double-flame structure (P2 in Figure 4). Thus, heat dissipation due to the radiation of the tailing high-temperature front of the warm flame was suppressed. Additionally, for the fuel-rich premixture, heat production due to the first-stage ignition reactions increased significantly and even overwhelmed the second-stage ignition (Figure 6b). Consequently, in the warm flame with ultrarich equivalence ratios, its tailing high-temperature brash did not extinguish but decayed gradually into the cool-flame mode smoothly. On the contrary, as Figure 6 shows, near the hot-flame extinction state with ultralean equivalence ratios, the lengthy interval between the first- and second-stage ignitions implies a significant induction length from the low-temperature leading front to the tailing high-temperature brash (P2 in Figure 4), which resulted in an enhancement of the high-temperature flame front heat loss by radiation. In addition, considering the ignorable contribution of heat production due to the leading cool-flame front compared with the tailing hot-flame front in the ultralean condition (as Figure 6 shows), the high-temperature tailing brash extinguished abruptly and dropped down to the cool-flame mode. It is noted that the second-stage HRR dropped sharply at Φ = 0.61, which was ascribed to the change of high-temperature oxidation pathways. More specifically, when Φ surpassed 0.61, fuel molecules were decomposed to the intermediates CH3, CH4, and CH3OCHO, which were further oxidized to the product CO, rather than CO2 or H2O. Hence, the second-stage HRR as well as flame temperature dropped abruptly at Φ = 0.61.
Figure 5.

Temperature and HRR profiles across the propagating front, for three typical cases during the transition from hot to cool flame in the rich condition, including P3—the initiation of a double-flame structure (ϕ = 7.58); P4—a typical case with a double-flame structure (ϕ = 10.01); and P5—the start of a cool flame (ϕ = 12.59). The red numbers imposed near the second crest of the HRR profile are the integral summary heat production amounts (unit: W) due to the high-temperature reactions.
Figure 6.
Responses of the first- and second-stage ignition delay times (a) and maximum HRRs (b) with respect to Φ, for the autoignitive premixture of (0.1DME + 0.9N2)/air with preheating (750 K). The vertical dashed line indicates the stoichiometric mixture.
3.2. Controlling Physics for FLs of DME/Air Premixed Propagation Flames
The previous section focused on FL dynamics of freely propagating DME/air premixed flames, as well as their multibranch and multimode behaviors due to the coupling of detailed low-temperature chemistry with scalar transports or mixing. However, in spatially inhomogeneous reacting systems involving detailed chemistry and transport physics, the underlying processes that control the critical flame dynamics are fairly complicated, due to the involvement of multi-time-scale elementary reactions and diffusive transports in the flame dynamic formation. In this section, sensitivity analysis,32 a systematic flame diagnostic methodology, is performed to detect the controlling physics for FLs of the freely propagating premixed flame, which would be of fundamental significance for an advanced engine design. Sensitivity analysis allows one to have quantitative dependence of the computational results on any model parameter and thus is valuable in interpreting the governing physics of many crucial combustion dynamics such as premixed flame propagation. The sensitivity analysis method, as presented in more details below, has been employed extensively in chemical engineering studies in the literature.
For the combustion governing equations as expressed in eq 9 with inclusion of an arbitrary model parameter α (e.g., reaction pre-exponent factor, species diffusivity, or mixture thermal conductivity, etc.), differentiating it with respect to α (as shown in eq 10) resulted in a matrix equation for the sensitivity coefficients ∂ψ/∂α, which contains quantitative information on how the model parameter α affects the temperature and species profiles (and thus flame propagation speed) at each grid point.
| 9 |
| 10 |
In eqs 9 and 10, the bolded symbols mean vector
or matrix, and otherwise scalars. ψ is a vector
consisting of independent variables (e.g., temperature, species mass
fractions, and flow flux rate) at each grid point. The Jacobian matrix
of the governing equation (∂F/∂ψ), as well as partial derivatives of
the residual function F(ψ; α) with respect to α (∂F/∂α), which includes detailed information about
the flame thermochemical properties, can be estimated based on the
solution data. Thus, the sensitivity coefficient matrix ∂ψ/∂α can be efficiently determined by postprocessing
computation. Thereafter, the normalized sensitivity coefficients in
the form of logarithmic derivatives, i.e., 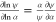 , were obtained for the next flame
diagnostics.
In this expression, the magnitude of the logarithmic sensitivity coefficient
measures the relative importance of α to ψ, and different signatures of the sensitivity coefficient indicate
opposite effectiveness of α to ψ (positive
for favor and negative for suppression).
, were obtained for the next flame
diagnostics.
In this expression, the magnitude of the logarithmic sensitivity coefficient
measures the relative importance of α to ψ, and different signatures of the sensitivity coefficient indicate
opposite effectiveness of α to ψ (positive
for favor and negative for suppression).
In this study, flame sensitivity computations were performed with respect to the pre-exponent factors of each reaction, diffusivities of each species, as well as the mixture thermal conductivity, to clarify the controlling physics for flame propagation. Figure 7 shows the dominant reactions and thermal/mass diffusivities with governing significances for four critical near-limit propagating flames, including LHFE, LCFE, RCFE, and LCFI as shown in Figure 2. The reactions and diffusivities with absolute sensitivity coefficients lower than 10–3 were assumed unimportant and thus dismissed from the candidate lists in Figure 7.
Figure 7.

Flame propagation speed sensitivities with respect to dominant reaction prefactors (a) and thermal/species diffusivities (b) at four FLs: LHFE, LCFE, RCFE, and LCFI.
Figure 7a shows that for the LHFE point that was governed by the hot-flame propagation mode, the high-temperature chemical pathways including the endothermic chain-branching reaction (R1: H + O2 = O + OH), as well as the most important exothermic reactions of (R29: CO + OH = CO2 + H) and (R51: CH3 + HO2 = CH3O + OH), were the most influential for the flame propagation speed. Additionally, significances of the low-temperature branching reactions including (R273: CH2OCH2O2H + O2 = O2CH2OCH2O2H) and (R240: CH3OCH3 + OH = CH3OCH2 + H2O), as well as the termination reaction (R272: CH2OCH2O2H = OH + CH2O + CH2O), as displayed in Figure 7a were ascribed to the involvement of the leading cool-flame front embedded in the double-flame structure near the LHFE point, such that the low-temperature branching and termination reactions will change the leading cool-flame structure and thus the flame propagation speed.
In the LCFE, LCFI, and RCFE turning points that are governed by the cool-flame propagation mode, Figure 7a demonstrates that the low-temperature competing reactions involving large hydrocarbon molecules were mostly significant for the flame propagation. More specifically, the reaction path analysis revealed that the low-temperature chemical kinetics of DME included two competing pathways. The branching pathway, which consumed one OH radical in the beginning and generated two in the end, initiated from reaction R240 that produced a fuel radical R (CH3OCH2) and was oxidized by the next few decomposition and internal isomerization reactions, including reactions R264, RRR271, RRR273, RRR274, and RRR275. The termination pathway, which produced one OH radical via reaction R272 but consumed two OH via the subsequent reaction R44, competed with the branching pathway for the OH radical.
| R240 |
| R264 |
| R271 |
| R273 |
| R274 |
| R275 |
| R272 |
| R44 |
It is noted from Figure 7a that for the LCFE and LCFI limits, the signatures of the sensitivity coefficients indicated that the low-temperature branching reactions (reactions R273, RRR271, RRR240, R241, and RRR275) were favorable to promote the propagation speed, while the termination reactions (reactions R272 and RRR44) with negative sensitivity coefficients were unfavorable to flame propagation. In the RCFE limit, however, the effectiveness of the competing low-temperature pathways on flame propagation is reversed, as revealed by the opposite signatures of the sensitivity coefficients in Figure 7a.
Figure 7b shows that in either FLs of the planar freely propagating DME flame, thermal conductivity with the largest positive sensitivity coefficients was the most important for the flame propagation speed. This was because enhancement of thermal conductivity will promote the preheating degree and thus the reactivity of the preignition mixture ahead of the propagating front, thus increasing the flame propagation speed. Moreover, diffusivities of the major species (especially fuel and oxygen) also played a significant role in affecting flame propagation, which was attributed to the enhancement of diffusive mixing from the unburned fresh premixture to the reaction front, which will result in the reduction in flame thickness and thus increase the flame propagation speed.41 With regard to the other minor species except for fuel and oxygen, the effectiveness of their diffusivities was rather trivial. For the cool-flame limits, however, the flame speed was also sensitive to some intermediate species as well, such as HO2CH2OCHO, indicating that the Lewis number of the cool flames remains greater than unity due to the tiny flame speed.
Besides, it is also interesting to note from Figure 6a,b that for the LHFE governed by the hot-flame mode, flame sensitivity with respect to the chemical kinetics or diffusivity properties was relatively weak. On the contrary, significant sensitivity coefficients with respect to the low-temperature chemistry parameters or species diffusivities were observed for the LCFE, LCFI, and RCFE that were governed by the cool-flame mode, especially for the LCFE limit where the logarithmic sensitivity coefficients were generally 3 orders of magnitudes. Hence, the LCFE limit results were inherently rather sensitive to uncertainties of the model parameter or experimental setting, as reviewed in the literature.42
In this section, a marching analysis for the dominant process sensitivity coefficients along the S-curve will be carried out to investigate the impacts of the dominant processes as revealed previously on the flame propagation speed and thus flammability limits. Figure 8 shows distributions of the logarithmic sensitivity coefficients along the S-curve, for the dominant reactions, including reactions R1, R29, RRR272, RRR273, RRR271, and RRR240, which could clarify dependences of the flammability dynamics on these significant reactions, and Figure 9 shows the sensitivity coefficient distributions for the dominant species diffusivities as well as thermal conductivity. Overall, it is clearly seen that the impacts of the dominant chemical and diffusivity parameters on flame propagation became particularly significant near the FLs (e.g., LHFE, LCFE, LCFI, and RCFE), while their significances were considerably reduced in the strongly stable ranges that were far away from the FLs. Hence, dominances of the above reactions and diffusivity parameters as revealed by the sensitivity analysis were accurate and receivable.
Figure 8.
Distributions of the logarithmic sensitivity coefficients for the flame propagation speed with respect to prefactors of reactions R1 (a), R29 (b), RRR272 (c), RRR273 (d), RRR271 (e), and RRR240 (f) along the S-curve. The superimposed color indicates the sensitivity coefficients.
Figure 9.
Distributions of the logarithmic sensitivity coefficients for flame propagation speed with respect to the thermal conductivity (a) and diffusivities of CH3OCH3 (b) and O2 (c) along the S-curve. The superimposed color indicates the sensitivity coefficients.
It can be seen in Figure 7a,b that the high-temperature reactions R1 and R29 played the governing role in just the hot-flame mode; their effectiveness on the cool-flame FLs (including LCFE, LCFI, and RCFE) was rather ignorable. Furthermore, in the strongly burning propagation range (0.3 < Φ < 0.6), the positive flame speed sensitivities with respect to the branching or exothermic reactions R1 and R29 indicated the promoting effects of these reactions on propagation speed, which coincided well with our understanding about the laminar flame speed.43 However, it is interesting to note that in the near-LHFE (0.29 < Φ < 0.3) or ultrarich range (0.6 < Φ < 0.74), the above two reactions were fairly adverse to flame propagation, as indicated by the large negative sensitivity coefficients. Additionally, the significant sensitivities with respect to the low-temperature reactions (reactions R272, RRR273, RRR271, and RRR240) near the LHFE, as shown in Figure 8c–f, indicate the governing importances of these reactions for the LHFE propagation limit, which was ascribed to their impacts on the leading cool-flame segment embedded in the double-flame structure near the LHFE. However, the branching reactions (reactions R273, RRR271, and RRR240) had negative sensitivity coefficients, while that for the termination reaction (reaction R272) was positive. Consequently, it is concluded that near the LHFE limit, the branching (termination) low-temperature reactions were unfavorable (favorable) to flame propagation. However, with respect to the cool-flame branch as well as its FLs (i.e., LCFE and LCFI), Figure 8c–f demonstrates that the low-temperature branching (termination) reactions were favorable (unfavorable) to flame propagation, while in the RCFE limit, the effectiveness of the branching and termination reactions with governing significances reversed accordingly. Figure 9 shows that in the LHFE, LCFE, LCFI, and RCFE limits, increases in heat conductivity and fuel and oxygen diffusivities will lead to enhancement of flame propagation. However, in the narrow region ahead of LHFE or RCFE, heat conductivity and fuel and oxygen diffusivities were unfavorable to flame propagation, as indicated by the corresponding large negative sensitivity coefficients. Figure 9 also demonstrates that the significance of thermal conductivity was seen over a broad range of ϕ, while that of fuel and oxygen diffusivities was seen only within the near-limit region. Additionally, it is also noted in Figure 9 that the signatures of sensitivity coefficients of the dominant processes reversed rapidly with respect to small variation of the equivalence ratio near LHFE or RCFE, implying that the practical combustion systems may probably exhibit more complicated flammability dynamics due to the flame interaction with turbulence, oscillation, or stoichiometry stratification, which merits a future study with more details.
3.3. Propagation Modes of the DME Freely Propagation Premixed Flame
In this chapter, the differences between the four different flammability limits (i.e., LHFE, LCFE, LCFI, and RCFE) will be focused on to identify the governing propagation modes. The flame structure profiles in the above four flammability limits are illustrated in Figure 10. As shown in Figure 10a, the LHFE case featured the double-flame structure consisting of a leading cool-flame front at x = 0.4 cm and a tailing hot-flame brash at x =1.0 cm, where the local H and OH concentrations were maximal. The leading cool-flame zone with a small temperature rise was governed by the low-temperature branching chemical pathways “R + OH → RO2 → QOOH → O2QOOH → OQO + 2OH”, which produced multiple hydrocarbon radicals such as HO2CH2OCHO. As the temperature rose further (800–1000 K), however, the production rates of H and OH slowed down because the chain-propagating pathway of “R → QOOH → OH + cyclic ether” and the decomposition reaction of RO2 suppressed the chain-branching pathway, which led to the formation of a wide range of intermediate species, like H2O2, CH2O, and CO (i.e., the NTC behavior). In the tailing hot-flame segment, the branching reaction H2O2 = 2OH accelerated, which led to a rapid increase of the OH radical and formation of hot flame with the most significant temperature rise due to the high-temperature reactions. The current simulations indicated that the separation distance between the cool- and hot-flame fronts was determined by the radiative cooling and chemical heat production with transports. As the radiative loss increased, the hot flame with decreasing temperature separated off from the leading cool-flame front, until flame extinguishment happened. However, if the radiative loss term in the energy equation was turned off to repeat the simulations, it was found that the hot flame with constant temperatures did not evolve to extinction even when it moved outside the computational domain. Hence, the extinction in LHFE was induced by radiative dissipation loss. Figure 10c,d displays that unlike the LHFE condition, the LCFE, LCFI, and RCFE flames had just a single temperature rise due to the cool-flame chemistry. However, the LCFI flame had a much narrower reaction zone thickness and lower concentrations of H and OH radicals, compared with the LCFE and RCFE flames. The H-abstract reactions of fuel with OH, O, and HO2 were responsible for the majority of heat production. The intermediate HO2CH2OCHO formed via the low-temperature reactions was consumed by H and OH radicals and transformed to H2O2 and CO in the downstream region. Considering the trivial contribution of radiative dissipation loss in the cool-flame regime, extinction and ignition limits of the cool flame were governed by competing coupling of low-temperature chemical heat production with the diffusive transports. Hence, the interaction of chemical heat production with diffusive transports played a controlling role in the formation of the cool-flame flammability limit.
Figure 10.
Profiles of temperature and major species and radicals in the flammability limits of LHFE (a), LCFE (b), LCFI (c), and RCFE (d).
Figure 11 shows
the transport budget analysis44 for the
four flammability limits, where Qr and Qc (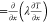 , where λ is the mixture conductivity
coefficient) designate the volumetric heat production rate and conduction
transfer rate, respectively, and SL is
the local flow velocity and thus flame propagation speed. The transport
budget analyses revealed that all of the four flammability limits
(including LHFE, LCFE, LCFI, and RCFE) had the “diffusion-reaction”
flame structure rather than the autoignition wave. Specifically, as
shown in Figure 11 for the LHFE, the magnitudes of chemical heat production and thermal
conduction were comparable with opposite signatures, for either the
leading cool-flame front or the downstream hot-flame front. In the
preheating zone that was located in front of the ignition point, however,
the heat conduction rate overwhelmed the heat production rate. Hence,
propagations of leading cool-flame and tailing hot-flame fronts were
self-sustained by the typical diffusion-reaction flame structure.
With respect to the LCFE, LCFI, and RCFE limits, they had a similar
diffusion-reaction structure to the LHFE; hence, all of them were
caused by the heat conduction-induced ignition rather than the autoignition
wave. For the cool-flame front, it was the thermal conduction from
the reaction zone to the preheating zone that raised the temperature
and thus triggered the low-temperature reactions by forced ignition.
Additionally, temperature increase in the front of the preheating
zone was ignorable. Therefore, the cool propagating flames involved
in this study were governed by the self-sustaining cool-flame propagation
front but not the autoignition wave, even at the ignition limit LCFI.
, where λ is the mixture conductivity
coefficient) designate the volumetric heat production rate and conduction
transfer rate, respectively, and SL is
the local flow velocity and thus flame propagation speed. The transport
budget analyses revealed that all of the four flammability limits
(including LHFE, LCFE, LCFI, and RCFE) had the “diffusion-reaction”
flame structure rather than the autoignition wave. Specifically, as
shown in Figure 11 for the LHFE, the magnitudes of chemical heat production and thermal
conduction were comparable with opposite signatures, for either the
leading cool-flame front or the downstream hot-flame front. In the
preheating zone that was located in front of the ignition point, however,
the heat conduction rate overwhelmed the heat production rate. Hence,
propagations of leading cool-flame and tailing hot-flame fronts were
self-sustained by the typical diffusion-reaction flame structure.
With respect to the LCFE, LCFI, and RCFE limits, they had a similar
diffusion-reaction structure to the LHFE; hence, all of them were
caused by the heat conduction-induced ignition rather than the autoignition
wave. For the cool-flame front, it was the thermal conduction from
the reaction zone to the preheating zone that raised the temperature
and thus triggered the low-temperature reactions by forced ignition.
Additionally, temperature increase in the front of the preheating
zone was ignorable. Therefore, the cool propagating flames involved
in this study were governed by the self-sustaining cool-flame propagation
front but not the autoignition wave, even at the ignition limit LCFI.
Figure 11.
Profiles for the volumetric chemical heat production (Qr) and thermal conduction (Qc) terms and local flame speed (SL) across the flame front, in the limits LHFE (a), LCFE (b), LCFI (c), and RCFE (d).
4. Conclusions
The continuation computations based on the PREMIX model were performed to investigate the flammability response dynamics with respect to the mixture equivalence ratio, for the planar DME/air freely propagating premixed flame. The main findings include the following.
-
(1)
The existence of cool-flame chemistry could significantly extend the fuel-rich or -lean mixture flammability limits and promote the flame propagation speed with the double-flame structure. For the atmospheric DME/air propagating premixed flame, a physically stable warm-flame branch existed in the ultrarich region (ϕ = 7.58–12.59), which connected the hot- and cool-flame transition smoothly. However, for the lean mixture with a lengthy induction period and double-flame structure, the intertransition between hot and cool flames was completed by extinction or ignition. Hence, the occurrence of a double-flame structure can serve as a judgment criterion for the atmospheric lean hot-flame extinction.
-
(2)
The dominant chemical and diffusive processes as revealed by the sensitivity analysis were of governing significance for the propagation limits, and their importance decreased in the strongly stable region. Except for the high-temperature reactions, the low-temperature reactions were also important for the lean hot-flame extinction limit because of the occurrence of a double-flame structure. Heat conduction and fuel and oxygen diffusivities were the most influential diffusive processes for near-limit flame propagation. The lean cool-flame flammability limit with significant sensitivity coefficients was crucially sensitive to uncertainties of the model parameter or experimental setting.
-
(3)
The DME/air freely propagating flames near the flammability limits had a diffusion-reaction structure, in which the flame front propagation was sustained by the heat conduction-induced ignition rather than the autoignition wave. Hence, all of the flammability limits (even for the ignition limit LCFI) were governed by the competing interaction of heat production and transport mixing. The occurrence of a double-flame structure and subsequently radiation-induced extinguishment of the tailing thickened hot-flame brash were the extinction mechanisms of the fuel-lean hot flame. However, the competition of chemical heat production with diffusive transports played a controlling role in the formation of the cool-flame flammability limit.
Acknowledgments
The present research was supported by the National Natural Science Foundation of China (Grant no. 51706027) and the Fundamental Research and Frontier Exploration Project of Chongqing (Grant no. cstc2019jcyj-msxmX0584).
The authors declare no competing financial interest.
References
- Kang Y. H.; Wang Q.; Zhang P. Y.; Liu C. C.; Lu X. F.; Wang Q. H. Study on flame structure and extinction mechanism of dimethyl ether spherical diffusion flames. Energy 2020, 193, 116786 10.1016/j.energy.2019.116786. [DOI] [Google Scholar]
- Zhang P. Y.; Kang Y. H.; Wu Z. J.; Lu X. F.; Wang Q. H.; Mei L. Effect of dimethyl ether addition on soot formation dynamics of ethylene opposed-flow diffusion flames. Ind. Eng. Chem. Res. 2019, 58, 8370–8386. 10.1021/acs.iecr.9b00084. [DOI] [Google Scholar]
- Ju Y. G.; et al. Dynamics of cool flames. Prog. Energy Combust. Sci. 2019, 75, 100787 10.1016/j.pecs.2019.100787. [DOI] [Google Scholar]
- Zheng M.; Li T.; Han X. Direct injection of neat n-butanol for enabling clean low temperature combustion in a modern diesel engine. Fuel 2015, 142, 28–37. 10.1016/j.fuel.2014.10.075. [DOI] [Google Scholar]
- Chen J.; Kang Y. H.; Zou Y. P.; Cui K. Q.; Zhang P. Y.; Liu C. C.; Ma J. Z.; Lu X. F.; Wang Q. H.; Mei L. A numerical study on near-limit extinction dynamics of dimethyl ether spherical diffusion flame. Fuel Process. Technol. 2019, 185, 79–90. 10.1016/j.fuproc.2018.12.006. [DOI] [Google Scholar]
- Lee M.; Fan Y.; Reuter C. B.; Ju Y. G.; Suzuki Y. DME/oxygen wall-stabilized premixed cool flame. Proc. Combust. Inst. 2019, 37, 1749–1756. 10.1016/j.proci.2018.05.059. [DOI] [Google Scholar]
- Merchant S. S.; Goldsmith C. F.; Vandeputte A. G.; Burke M. P.; Klippenstein S. J.; Green W. H. Understanding low-temperature first-stage ignition delay: Propane. Combust. Flame 2015, 162, 3658–3673. 10.1016/j.combustflame.2015.07.005. [DOI] [Google Scholar]
- Zádor J.; Taatjes C. A.; Fernandes R. X. Kinetics of elementary reactions in low-temperature autoignition chemistry. Prog. Energy Combust. Sci. 2011, 37, 371–421. 10.1016/j.pecs.2010.06.006. [DOI] [Google Scholar]
- Ju Y. G. On the propagation limits and speeds of premixed cool flames at elevated pressures. Combust. Flame 2017, 178, 61–69. 10.1016/j.combustflame.2017.01.006. [DOI] [Google Scholar]
- Chen L.; Zhang R.; Pan J. Y.; Wei H. Q. Effects of partitioned fuel distribution on auto-ignition and knocking under spark assisted compression ignition conditions. Appl. Energy 2020, 260, 114269 10.1016/j.apenergy.2019.114269. [DOI] [Google Scholar]
- Reitz R. D.; Duraisamy G. Review of high efficiency and clean reactivity controlled compression ignition (RCCI) combustion in internal combustion engines. Prog. Energy Combust. Sci. 2015, 46, 12–71. 10.1016/j.pecs.2014.05.003. [DOI] [Google Scholar]
- Zhao P.; Liang W.; Deng S.; Law C. K. Initiation and propagation of laminar premixed cool flames. Fuel 2016, 166, 477–487. 10.1016/j.fuel.2015.11.025. [DOI] [Google Scholar]
- Hori M.; Yamamoto A.; Nakamura H.; Takuya T.; Susumu H.; Kaoru M. Study on octane number dependence of PRF/air weak flames at 1–5 atm in a micro flow reactor with a controlled temperature profile. Combust. Flame 2012, 159, 959–967. 10.1016/j.combustflame.2011.09.020. [DOI] [Google Scholar]
- Griffiths J. F.; Inomata T. Oscillatory cool flames in the combustion of diethyl ether. J. Chem. Soc., Faraday Trans. 1992, 88, 3153. 10.1039/ft9928803153. [DOI] [Google Scholar]
- Affleck W. S.; Knock F. A. Flame acceleration or spontaneous ignition?. Combust. Flame 1968, 12, 243–252. 10.1016/0010-2180(68)90021-7. [DOI] [Google Scholar]
- Starikovskiy A.; Aleksandrov N.. Plasma-Assisted Ignition and Combustion; Elsevier Ltd., 2013. [Google Scholar]
- Sun W. Q.; Won S. H.; Gou X. L.; Ju Y. G. Multi-scale modeling of dynamics and ignition to flame transitions of high pressure stratified n-heptane/toluene mixtures. Proc. Combust. Inst. 2015, 35, 1049–1056. 10.1016/j.proci.2014.05.141. [DOI] [Google Scholar]
- Deng S. L.; Hang D.; Law C. K. Ignition and extinction of strained nonpremixed cool flames at elevated pressures. Combust. Flame 2017, 176, 143–150. 10.1016/j.combustflame.2016.10.015. [DOI] [Google Scholar]
- Hajilou M.; Brown M. Q.; Brown M. C.; Belmont E. Investigation of the structure and propagation speeds of n-heptane cool flames. Combust. Flame 2019, 208, 99–109. 10.1016/j.combustflame.2019.06.020. [DOI] [Google Scholar]
- Wang Z. J.; Gou X. L. Cool flame characteristics of methane/oxygen mixtures. J. Energy Inst. 2019, 92, 2004–2010. 10.1016/j.joei.2018.10.011. [DOI] [Google Scholar]
- Jin T.; Wu Y. C.; Wang X. J.; Luo K. H.; Lu T. F.; Luo K. H.; Fan J. R. Ignition dynamics of DME/methane-air reactive mixing layer under reactivity controlled compression ignition conditions: Effects of cool flames. Appl. Energy 2019, 249, 343–354. 10.1016/j.apenergy.2019.04.161. [DOI] [Google Scholar]
- Ju Y. G.; Reuter C. B.; Won S. H. Numerical simulations of premixed cool flames of dimethyl ether/oxygen mixtures. Combust. Flame 2015, 162, 3580–3588. 10.1016/j.combustflame.2015.06.014. [DOI] [Google Scholar]
- Sohn C. H.; Han H. S.; Reuter C. B.; Ju Y. G.; Won S. H. Thermo-kinetic dynamics of near-limit cool diffusion flames. Proc. Combust. Inst. 2017, 36, 1329–1337. 10.1016/j.proci.2016.05.049. [DOI] [Google Scholar]
- Farouk T. I.; Dietrich D.; Dryer F. L. Three stage cool flame droplet burning behavior of n-alkane droplets at elevated pressure conditions: Hot, warm and cool flame. Proc. Combust. Inst. 2019, 37, 3353–3361. 10.1016/j.proci.2018.09.015. [DOI] [Google Scholar]
- Yehia O. R.; Reuter C. B.; Ju Y. G. Kinetic effects of n-propylbenzene on n-dodecane counterflow nonpremixed cool flames. Combust. Flame 2019, 208, 262–272. 10.1016/j.combustflame.2019.07.006. [DOI] [Google Scholar]
- Nayagam V.; Dietrich D. L.; Hicks M. C.; Williams F. A. Cool-flame extinction during n-alkane droplet combustion in microgravity. Combust. Flame 2015, 162, 2140–2147. 10.1016/j.combustflame.2015.01.012. [DOI] [Google Scholar]
- Ju Y. G. On the propagation limits and speeds of premixed cool flames at elevated pressures. Combust. Flame 2017, 178, 61–69. 10.1016/j.combustflame.2017.01.006. [DOI] [Google Scholar]
- Nakamura H.; Fan A. W.; Minaev S.; Sereshchenko E.; Fursenko R.; Tsuboi Y.; Maruta K. Bifurcations and negative propagation speeds of methane/air premixed flames with repetitive extinction and ignition in a heated microchannel. Combust. Flame 2012, 159, 1631–1643. 10.1016/j.combustflame.2011.11.004. [DOI] [Google Scholar]
- Alipoor A.; Mazaheri K. Combustion characteristics and flame bifurcation in repetitive extinction-ignition dynamics for premixed hydrogen-air combustion in a heated micro channel. Energy 2016, 109, 650–663. 10.1016/j.energy.2016.05.042. [DOI] [Google Scholar]
- Lapointe S.; Druzgalski C. L.; McNenly M. J. Numerical study of a micro flow reactor at engine pressures: Flames with repetitive extinction and ignition and simulations with a reduced chemical model. Combust. Flame 2018, 197, 102–110. 10.1016/j.combustflame.2018.07.020. [DOI] [Google Scholar]
- Ayoobi M.; Schoegl I. Numerical analysis of flame instabilities in narrow channels: Laminar premixed methane/air combustion. Int. J. Spray Combust. Dyn. 2017, 9, 155–171. 10.1177/1756827717706009. [DOI] [Google Scholar]
- Kee R. J.; Rupley F. M.; Miller J. A.; Coltrin M. E.; Grcar J. F.; Meeks E.; Moffat H. K.; Lutz A. E.; Lewis G. D.; Smooke M. D.. et al. Chemkin-II: A Fortran Chemical Kinetics Package for the Analysis of Gas Phase Chemical Kinetics. Report No. SAND89-8009B; Sandia National Laboratories, 1989.
- Nishioka M.; Law C. K.; Takeno T. A flame-controlling continuation method for generating S-curve responses with detailed chemistry. Combust. Flame 1996, 104, 328–342. 10.1016/0010-2180(95)00132-8. [DOI] [Google Scholar]
- Johansson R.; Leckner B.; Andersson K.; Johnsson F. Account for variations in the H2O to CO2 molar ratio when modelling gaseous radiative heat transfer with the weighted-sum-of-grey-gases model. Combust. Flame 2011, 158, 893–901. 10.1016/j.combustflame.2011.02.001. [DOI] [Google Scholar]
- Kee R. J.; Grcar J. F.; Smooke M. D.; Miller J. A.. A Fortran Program for Modeling Steady Laminar One-Dimensional Premixed Flames, Report No. SAND85-8240; Sandia National Laboratories, 1985.
- Zhao Z. W.; Chaos M.; Kazakov A.; Dryer F. L. Thermal decomposition reaction and a comprehensive kinetic model of dimethyl ether. Int. J. Chem. Kinet. 2008, 40, 1–18. 10.1002/kin.20285. [DOI] [Google Scholar]
- Liang W. K.; Law C. K. Extended flammability limits of n -heptane/air mixtures with cool flames. Combust. Flame 2017, 185, 75–81. 10.1016/j.combustflame.2017.06.015. [DOI] [Google Scholar]
- Ju Y. G.; Reuter C. B.; Won S. H. Numerical simulations of premixed cool flames of dimethyl ether/oxygen mixtures. Combust. Flame 2015, 162, 3580–3588. 10.1016/j.combustflame.2015.06.014. [DOI] [Google Scholar]
- Minamoto Y.; Chen J. H. DNS of a turbulent lifted DME jet flame. Combust. Flame 2016, 169, 38–50. 10.1016/j.combustflame.2016.04.007. [DOI] [Google Scholar]
- Lutz A. E.; Kee R. J.; Miller J. A.; Coltrin M. E.; Grcar J. F.; Meeks E.; Moffat H. K.; Lutz A. E.; Lewis G. D.; Smooke M. D.. et al. SENKIN: A Fortran Program for Predicting Homogeneous Gas Phase Chemical Kinetics with Sensitivity Analysis, Report No. sand87-8248; Sandia National Laboratories: Livermore, CA, 1987.
- Yu H. B.; Hu E. J.; Cheng Y.; Zeng K.; Zhang X. Y.; Huang Z. H. Effects of hydrogen addition on the laminar flame speed and Markstein length of premixed dimethyl ether-air flames. Energy Fuels 2015, 29, 4567–4575. 10.1021/acs.energyfuels.5b00501. [DOI] [Google Scholar]
- Reuter C. B.; Lee M.; Won S. H.; Ju Y. G. Study of the low-temperature reactivity of large n-alkanes through cool diffusion flame extinction. Combust. Flame 2017, 179, 23–32. 10.1016/j.combustflame.2017.01.028. [DOI] [Google Scholar]
- Cheng Y.; Tang C. L.; Huang Z. H. Kinetic analysis of H2 addition effect on the laminar flame parameters of the C1-C4 n-alkane-air mixtures: From one step overall assumption to detailed reaction mechanism. Int. J. Hydrogen Energy 2015, 40, 703–718. 10.1016/j.ijhydene.2014.11.010. [DOI] [Google Scholar]
- Gordon R. L.; Masri A. R.; Pope S. B.; Goldin G. M. Transport budgets in turbulent lifted flames of methane autoigniting in a vitiated co-flow. Combust. Flame 2007, 151, 495–511. 10.1016/j.combustflame.2007.07.001. [DOI] [Google Scholar]








