Sequential Replay of Non-spatial Task States in the Human Hippocampus

Abstract

Sequential neural activity patterns related to spatial experiences are ‘replayed’ in the hippocampus of rodents during rest. We investigated whether replay of non-spatial sequences can be detected non-invasively in the human hippocampus. Participants underwent functional magnetic resonance imaging (fMRI) while resting after performing a decision-making task with sequential structure. Hippocampal fMRI patterns recorded at rest reflected sequentiality of previously experienced task states, with consecutive patterns corresponding to nearby states. Hippocampal sequentiality correlated with the fidelity of task representations recorded in the orbitofrontal cortex during decision-making, which were themselves related to better task performance. Our findings suggest that hippocampal replay may be important for building representations of complex, abstract tasks elsewhere in the brain, and establish feasibility of investigating fast replay signals with fMRI.

One Sentence Summary

Sequential fMRI pattern analysis yields evidence of replay of decision-task states in the human hippocampus during rest.

Introduction

Studies in rodents have shown that hippocampal representations of spatial locations are reactivated sequentially during short on-task pauses, longer rest periods, and sleep (1–3). This sequential reactivation, or replay, is accelerated relative to the original experience (4), related to better planning (2) and memory consolidation (5), and suppression of replay-related sharp-wave ripples impairs spatial memory (6).

The role of replay in non-spatial decision making tasks in humans has remained unclear. We instructed participants to perform a non-spatial decision-making task in which correct performance depended on the sequential nature of task states that included information from past trials in addition to current sensory information (i.e., partially-observable states) (7). This ensured that participants would encode sequential information while completing the task. We recorded functional magnetic resonance imaging (fMRI) activity during resting periods before and after the task, as well as during two sessions of task performance, and investigated whether sequences of fMRI activation patterns during rest reflected hippocampal replay of task states.

Decision making in a non-spatial, sequential task

Thirty three participants performed a sequential decision-making task that required integration of information from past trials into a mental representation of the current task state (7) (see Methods). Each stimulus consisted of overlapping images of a face and a house and participants made age judgments (old or young) about one of the images (Fig. 1A). An on-screen cue before the first trial determined whether the age of faces or houses should be judged. From the second trial onward, if the ages in the current and previous trial were identical, the category to be judged on the next trial remained the same; otherwise, the judged category was switched to the alternative (Fig. 1B). These task rules created an unsignalled ‘miniblock’ structure where each miniblock involved judgment of one category. No age comparison was required on the first trial after a switch. Miniblocks were therefore at least two trials long, and on average lasted for three trials.

Fig. 1: Experimental task and performance.

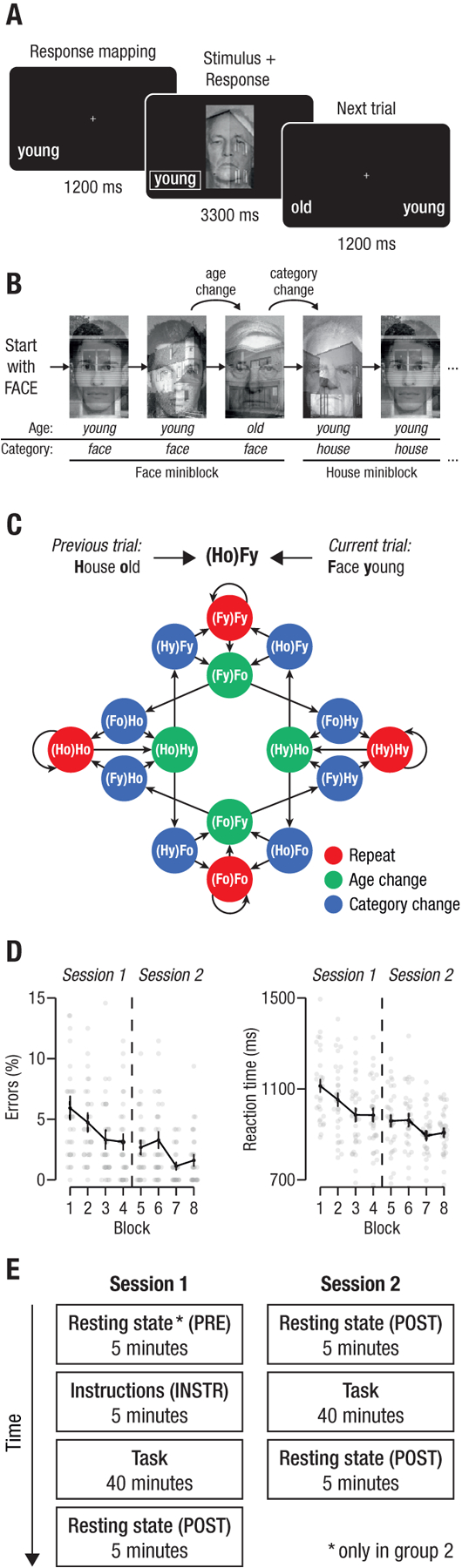
(A): On each trial, participants had to judge the age of either a face or a house, shown overlaid as a compound stimulus. Trials began with the display of a fixation cross and the response mapping (which of left/right was assigned to old/young; 1200ms), followed by the stimulus. Responses could be made at any time, and the stimulus stayed on screen for an average of 3300 ms. (B): The task required participants to switch between judging faces and houses following each time the age changed between two trials, see text. (C): The state space of the task, reflecting the abstract space that participants traversed, analogous to a spatial maze although non-spatial from the point of view of the participant. Each node represents one possible task state, and each arrow a possible transition. All transitions out of a state were equally probable, occurring with p = 0.5. Each state of the task is determined by the age and category of the previous and current trial, indicated by the acronyms (see legend). States are colored based on their ‘location’ within a miniblock: trials within a miniblock in which the age and category were repeated (orange), trials at the end of a miniblock in which the age changed (green), and trials entering a new miniblock where the category changed (purple). (D): Average error rates and reaction times across the two experimental sessions. Bars: ± 1 S.E.M. Grey dots represent individual participants. (E): The experiment extended over two sessions, each of which included about 40 minutes task experience flanked by resting state scans. *: The pre-task resting state scan in Session 1 was performed only for a subgroup of our sample (N = 10; group 2).

The task rules resulted in a total of 16 ‘task states’ reflecting the current ‘location’ within the task, i.e. which stimulus had just been processed and which stimuli could potentially come next according to the rules. Task states followed each other in a specific, structured order (Fig. 1C). For example, the task state (Ho)Fy, indicated a young face trial that followed an old house trial and was only experienced after a miniblock of judging young houses ended (with an old house), which led to the next miniblock in which (young) faces had to be judged. Although the task was not spatial, it therefore involved implicitly navigating through a sequence of states that had predictable relationships to each other.

Participants performed the task with high accuracy (average error rate: 3.1%, time-outs: 0.6%, reaction time: 969 ms) and improved their performance throughout the course of the experiment (Fig. 1D, negative linear trends Errors: p_FDR = 1.889e−6, RTs: p_FDR = 3.906e−19; see also Fig. S5 for further details).

Hippocampal fMRI patterns at rest reflected task states

Participants engaged in the above decision-making task while undergoing fMRI. A first session included about 5 minutes of task instructions and four runs of task performance (388 trials, about 40 minutes duration). A second session took place one to four days later and was identical to session 1, but without instructions (Fig 1E). Resting-state scans consisting of 5-minute periods of wakeful rest without any explicit task or visual stimulation were administered for all 33 participants after session 1, before session 2 and after session 2, resulting in a total of 300 whole-brain volumes acquired during rest (three resting state scans with 100 volumes each). A subgroup of participants (N = 10; group 2) underwent one additional resting-state scan at the beginning of session 1, before having had any instructions about or experience with the task. Thus, 10 participants (group 2) had a total of 400 whole brain volumes acquired during rest, while 23 participants (group 1) had a total of 300 volumes. Resting-state data acquired after participants had task experience will from hereon be referred to as the POST rest condition. Resting state data acquired before any task experience (group 2 only) served as a control, and will be referred to as the PRE rest condition. Data recorded while receiving instructions served as another control and will be referred to as the INSTR condition. Data from the POST condition were matched in length to the corresponding control condition as appropriate. Heart rates were generally higher during task compared to rest (t₂₉ = 6.2, p_FDR = 1.213e−6), but did not differ between control and POST conditions or relate to the sequentiality effects reported below, see Methods.

To investigate sequential reactivation of task-related experiences in the human hippocampus during rest, we trained a multivariate pattern recognition algorithm (see Methods) to distinguish between the activation patterns associated with each of the 16 task states using data recorded during task performance (Figs. 2A,2B). Leave-one-run-out cross-validated classification accuracy on the task data from the hippocampus (HPC) was significantly higher than chance and than classification obtained in a permutation test (11.6% vs. 7.1% in the permutation test, t₃₂ = 6.7, p_FDR = 3.186e−7, chance level is 6.25%, Fig. 2C). We then applied the trained classifier to each volume of fMRI data acquired during the resting state scans. As classification accuracy could not be assessed for the resting scan data due to lack of ground truth, we assessed the quality of the classification using the mean unsigned distance to the decision hyperplane, a proxy for classification certainty (8). This distance was larger in the POST condition compared to simulated spatiotemporally-matched noise (‘NOISE’, t₃₂ = 12.9, p_FDR = 1.554e−13; for simulation details see Methods and SI) and compared to the PRE condition (t₉ = 2.1, p_FDR = 0.0366, group 2 only, Fig. 2D), in line with previous findings suggesting pattern reactivation during rest (9–11).

Fig. 2: Sequential replay decoding analysis.

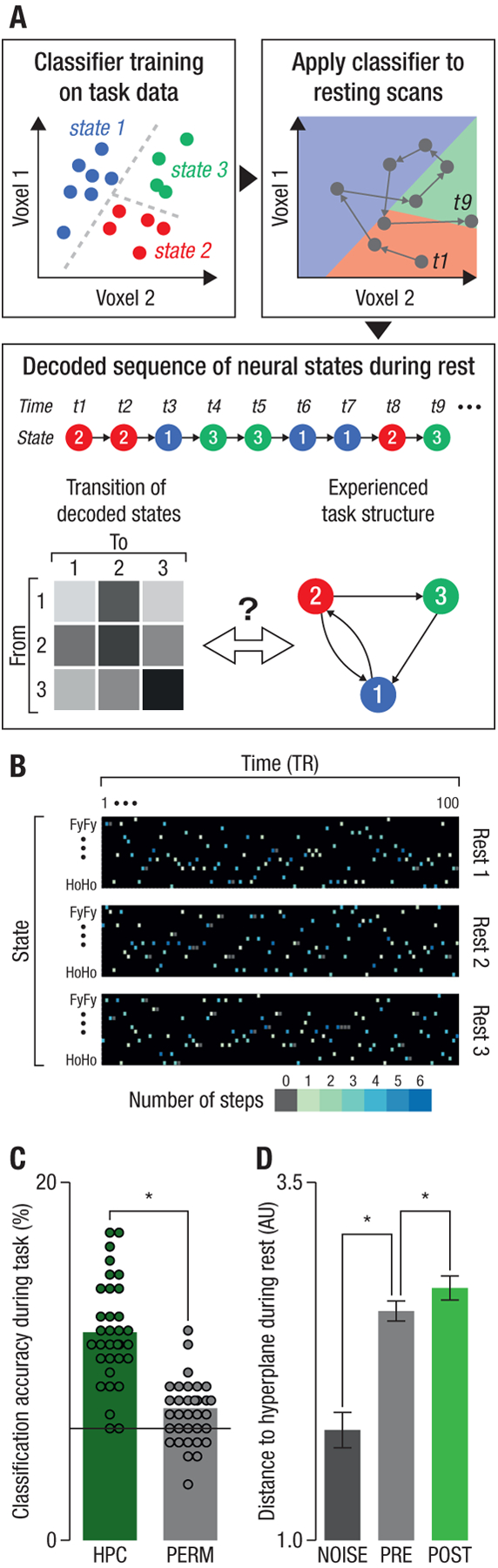
(A): Illustration of analysis procedure. For simplicity, only two dimensions and three state classes are shown. We first trained a classifier to distinguish between the different task states in the hippocampal fMRI data acquired during task performance. The trained classifier was then applied to each volume of fMRI data recorded during resting sessions (grey dots). This resulted in a sequence of classifier labels that was transformed into a ‘transition matrix’ T that summarized the frequency of decoding each pair of task states consecutively. The structure of the decoded sequences, as summarized by this matrix, was then compared to the sequential structure of the task (see text). Note that the actual analysis involved 16-way classification of data with several thousand dimensions (each voxel is one dimension), which was compared to the task state space shown in Fig. 1C. (B): Example data from one randomly selected participant. Each dark rectangle illustrates the sequence of classified states for the 100 volumes of fMRI data recorded in one resting state scan (depicted are three resting state scans acquired throughout the experiment; see Fig. 1E). Columns represent time, and rows states. Each color-filled cell represents the state classified at the respective time point; color indicates the distance (in steps in the state space; Fig. 1C) from the state decoded in the previous timepoint (i.e., the previous volume). (C) Classification accuracy during task performance was significantly higher in hippocampal data (HPC) than in a permutation test (PERM). The solid line represents the theoretical chance baseline of 100/16=6.25. (D): Average distance to the hyperplane for classified states during rest in the NOISE (dark grey, left bar), PRE (light grey, middle bar, N=10) and POST conditions (green, rightmost bar, N=33). Larger distance indicates higher certainty in the classification of the state. Each dot indicates one participant, bars within-subject S.E.M., *: p_FDR < .05.

Sequentially replayed states were decodable in simulated fMRI data

During replay, previously experienced states are reactivated sequentially. We therefore first tested whether it is theoretically possible to measure rapid sequential replay events (on the order of few hundreds of milliseconds in humans (12)) using fMRI, given its low temporal resolution. We simulated fMRI activity that would result from fast replay events, and asked what order and state information could be extracted from these spatially and temporally overlapping patterns assuming slow hemodynamics and images taken seconds apart. Our simulations showed that two successive fMRI measurements could reflect two states from the same multi-step replay event, because the slow hemodynamic response measured in fMRI causes brief neural events to impact the BOLD signal over several seconds, see SI. As replay events are thought to mainly reflect short sequences of states (3), if the activity we measured in the hippocampus at rest indeed reflects sequential replay, we can therefore expect that consecutively decoded states would be nearby in the task’s state space (that is, separated by few intervening states in Fig. 1C).

We next questioned whether it is reasonable, given the low accuracy of correctly decoding task states during task performance, to expect to successfully decode a pair of states from the same replay event. Our simulations answered this in the affirmative: because brain activity after a rapid replay event will include several superimposed states (Fig. S6B), the likelihood of classifying one out of several replayed states in each resting-state brain volume is considerably higher than the decoding accuracy when classifying a single prolonged event during task performance. Assuming the empirical classification accuracy we measured for task data, our calculations showed that the chance of decoding, from two consecutive brain volumes, a pair of states that reflects the original relative order of activation within one replay event is similar to the overall decoding accuracy (~10%), rather than the (much smaller) product of the chance of decoding the two states individually (see SI).

Hippocampal activity during rest reflected task-related sequentiality

Having established that, in principle, we can detect sequential replay in fMRI data, we tested whether the sequences of states we decoded in the POST resting-state data (i.e., recorded after experience with the task; Fig. 3A) reflected the sequential structure of the experienced task. We note upfront that because the classifier used to detect these states was trained on task data that were themselves sequential, some sequentiality of classifier output arises even in random noise data. We therefore conducted a series of controlled assessments of the levels of sequentiality in our POST resting data that ensured that we were detecting true sequential replay, and not merely unveiling the biases of the classifier. Sequentiality should therefore be found in the POST data above and beyond what we found in controls, if replay events had indeed occurred.

Fig. 3: Hippocampal state transitions during rest are related to state distances in the task.

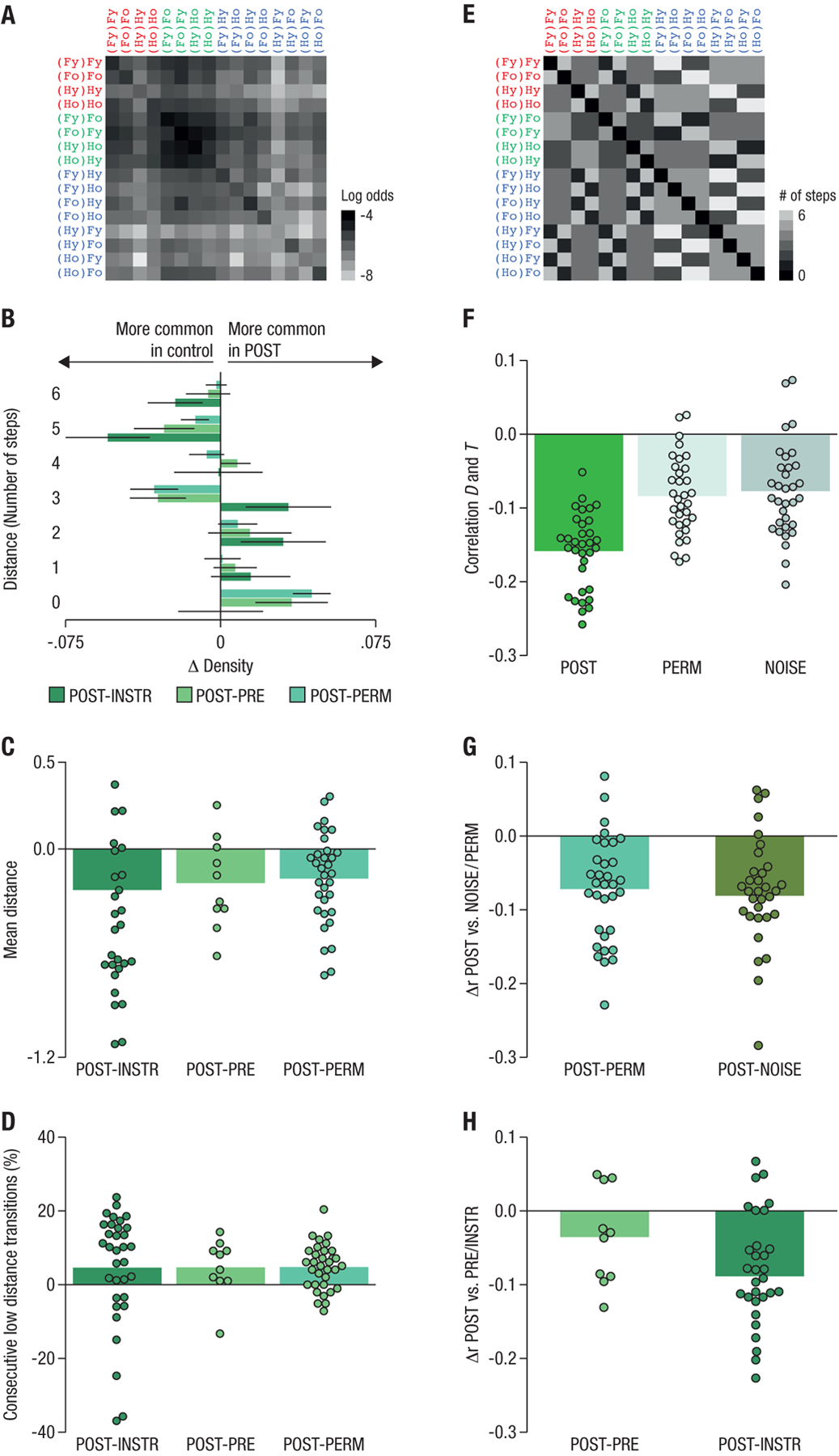
(A): The matrix T, expressing the log odds of transitions between all states in the sequence of classification labels in the hippocampal POST resting-state data, averaged across all participants. Y-axis: first state, x-axis: second state in each consecutively-decoded pair. Darker colors reflect a higher probability of observing a pair in the data. (B): Relative distributions of number of steps separating two consecutively decoded states. A distance of 1 corresponds to a decoded state transition as experienced in the task, 2 corresponds to a transition with one state missing between the two decoded states, as compared to the task, etc. Barplots show the difference in relative frequency (ΔDensity) with which each transition type was observed in the POST resting data compared to INSTR and PRE control conditions and compared to (order) permuted data (PERM), see legend. Smaller distances are more frequently observed in the POST data, whereas larger distances are more common in the control data, suggesting that the POST resting data reflect reactivation of short sequences. (C): The average distance in state space of two consecutively decoded states was significantly lower in the POST data as compared to the INSTR, PRE and PERM controls (all ps < .05, t-test comparing difference to 0). (D): Low-distance transitions (fewer than 3 steps) occurred in succession significantly more frequently in the POST resting data compared to all controls (all ps < .05). (E): The matrix D, indicating the minimum number of steps between each pair of states in the task (i.e. the state distances). Lighter colors reflect larger distance between states. (F): Average correlations between the state distance matrix D and the corresponding decoded transition matrix T in the POST resting data (green bar, left), as compared to permuted data (PERM; light grey, middle) or when the same classifier was applied to participant-specific spatio-temporally matched noise (NOISE; dark gray bar, right, see also Fig. S1). (G): Within-participant differences between correlations in POST resting data versus the PERM and NOISE controls (all ps < .05). (H): The anti-correlation between D and T in the PRE and INSTR conditions was lower than in the POST resting data (matched in amount of data compared). Dots reflect differences in correlations for individual participants.

Consecutively decoded states were nearby in task space

First, we predicted that replay would be reflected in a small number of steps that separate two consecutively decoded states, as indicated by the above-mentioned simulations. The number of steps between state transitions decoded in the POST resting condition was smaller, on average, than the distance between states in the INSTR condition (t₃₂ = 2.4, p_FDR = 0.0165), in the PRE condition (t₉ = 2.3, p_FDR = 0.0272, group 2 only), and in permuted data in which classified states were randomly reordered to control for overall state frequency (PERM condition: t₃₂ = 4.6, p_FDR = 7.897e−5; Fig. 3B,C). Note that the observed step sizes allow only limited insights about the total length of replayed sequences: a pair of patterns with step-size N suggests the presence of a sequence with a length of at least N +1, but could also reflect partial measurement of a longer sequence, in particular when more than two consecutive states separated by short step sizes were decoded (as detailed below, see Fig 3D).

Second, because more than one short-distance transition might result from one longer sequence replay, and replay events are temporally sparse, i.e. separated by long pauses (12), we expected the occurrence of short-distance state pairs to be clustered in time. Indeed, short-distance state pairs (less than 3 steps apart) were not only more frequent than expected, but also more likely to occur in clusters in the POST rest condition compared to the INSTR (t₃₂ = 1.7, p_FDR = 0.0482), PRE (t₉ = 1.9, p_FDR = 0.0482, group 2 only), and PERM controls (t₃₂ = 4.5, p_FDR = 9.152e−5, Fig. 3D).

Third, a salient aspect of our task was that age switches were followed by category switches (transitions from green to purple states in Fig. 1C). We predicted that this would be reflected in the fMRI pattern transitions. We therefore investigated how often a decoded within-category age-change state was followed by a decoded category-switch state, as in our task (e.g., the number of (Fo)Ho states classified after (Fy)Fo). We compared this proportion to how often within-category age-repeat states were followed by category-switch states (e.g., the number of (Fo)Ho states classified after (Fo)Fo), and predicted that category-switch states should occur more often in the former case (following age changes) than in the latter case. Because consecutively decoded patterns do not necessarily reflect one-step task structure (see above), we analyzed the average proportion of category-switch states decoded in the six volumes (roughly the duration of the hemodynamic response function) following the detection of age-switch versus age-repeat states. In the POST resting data, the proportion of decoded category-switch states was significantly higher following decoding of a within-category age-switch state than following an age repetition (t₃₂ = 2.2, p_FDR = 0.0251). This effect was not observed in the PRE (p_unc. = .28), NOISE (p_unc. = .14) or PERM (p_unc. = .22) control conditions.

We conducted additional analyses to verify that the above results could not be explained by sustained state activation, order effects based on classifier training or the occurrence of only one particular decoded state distance. We removed state repetitions (“self transitions”) from the decoded sequence of states and tested whether the normalized frequency of consecutively decoding each pair of task states (the transition probability summarized in matrix T; Fig. 3A) was negatively correlated with the distance matrix D between the states in the task (where D_ij corresponds to the minimum number of steps necessary to get from state i to state j; Fig. 3E). The correlation between T and D was indeed negative (average r = −.16, Fig. 3F), and was significantly more negative than the correlation seen in the PERM control (r = −.08; difference between POST and PERM: Δr = −.07, t₃₂ = −5.8, p_FDR = 2.605e−6; the non-zero correlation in the PERM control reflects an effect of overall state frequency). Applying the trained classifier to individually-matched fMRI noise (NOISE control, see Methods and SI, Fig S1) also revealed a significant difference (correlation difference POST vs. NOISE: Δr = −.08, t₃₂ = −5.6, p_FDR = 4.324e−6, Fig. 3G; here too non-zero correlation was seen in the control condition (r = −.08), reflecting the effect of temporal contingencies between states in the classifier training data, which can lead to spurious correlations).

Our hypothesis that sequential reactivation of task-state representations during rest was caused by task experience was also supported by a significantly stronger anti-correlation between T and D in the POST resting condition as compared to the INSTR condition (t₃₂ = − 12.1, p_FDR = 5.320e−13, p_FDR = 2.513e−6 when comparing a subset of the POST data matched in number of volumes to the INSTR data; see Methods), as well as to the PRE condition (t₉ = −7.9, p_FDR = 3.093e−5, group 2; but p_FDR = 0.0593 when compared to only the first resting scan in the POST resting condition), Fig. 3H.

Lastly, we excluded sets of state pairs from classifier training (see SI, Fig. S3), to test if these pairs would then show a lower transition frequency in the resting data. The excluded transitions were observed as often as the included transitions (t₃₂ = 0.3, p_unc. = 0.73). The transition frequencies observed during rest thus reflected sequential reactivation above and beyond any sequential structure in the classifier.

Pattern sequentiality could not be explained by classifier bias or state repetitions

We further investigated the effects of task experience on pair-decoding frequency data T while simultaneously (a) controlling for the above-mentioned effect of temporal contingencies in the classifier training, (b) excluding state repetitions, and (c) incorporating the different sources of between- and within-participant variability. We performed a logistic mixed-effects analysis in which we modeled both the effect of interest (the distance D) and nuisance covariates that could potentially affect T (such as biases in classifier, see Methods). We call the effect estimate (beta weight) of the distances D on the transition data T in this model ‘sequenceness,’ and the nuisance effects ‘randomness.’ For ease of interpretation, we flipped the sign of the sequenceness estimates such that larger numbers indicate more sequentiality in the data.

To assess whether state distance and transition frequency were significantly related above and beyond the nuisance regressors, we used a likelihood ratio test to compare a logistic regression model that contained only randomness regressors to a model that also included the sequenceness (task distances) regressor D. Fig.s 4A and 4B show the sequenceness and randomness effects in the POST compared to the PRE condition. We found no difference between the fits of the two models when modeling the PRE resting data (AIC: 3651.2 vs. 3651.8, ${\chi }_1^2=2.7$, p_unc. = .10, for the model without and with the sequenceness regressor, respectively; AIC = Aikaike Information Criterion, lower values are better). When modeling the POST resting data, adding the sequenceness regressor improved model fit significantly (AIC 3645.4 vs. 3642.9, ${\chi }_1^2=5.5$, p_unc. = .019; results are for group 2 only and considering only the first POST resting scan from the first session to equate power with the PRE analysis). Importantly, including both PRE and POST conditions within one model showed improved fit when the interaction of condition factor with sequenceness and randomness was included (AIC 7219.6 vs. 7228.3, p_FDR = 3.119e−3).

Fig. 4: Effect of state distance (sequenceness) on transition frequency in hippocampal data is specific to POST resting conditions.

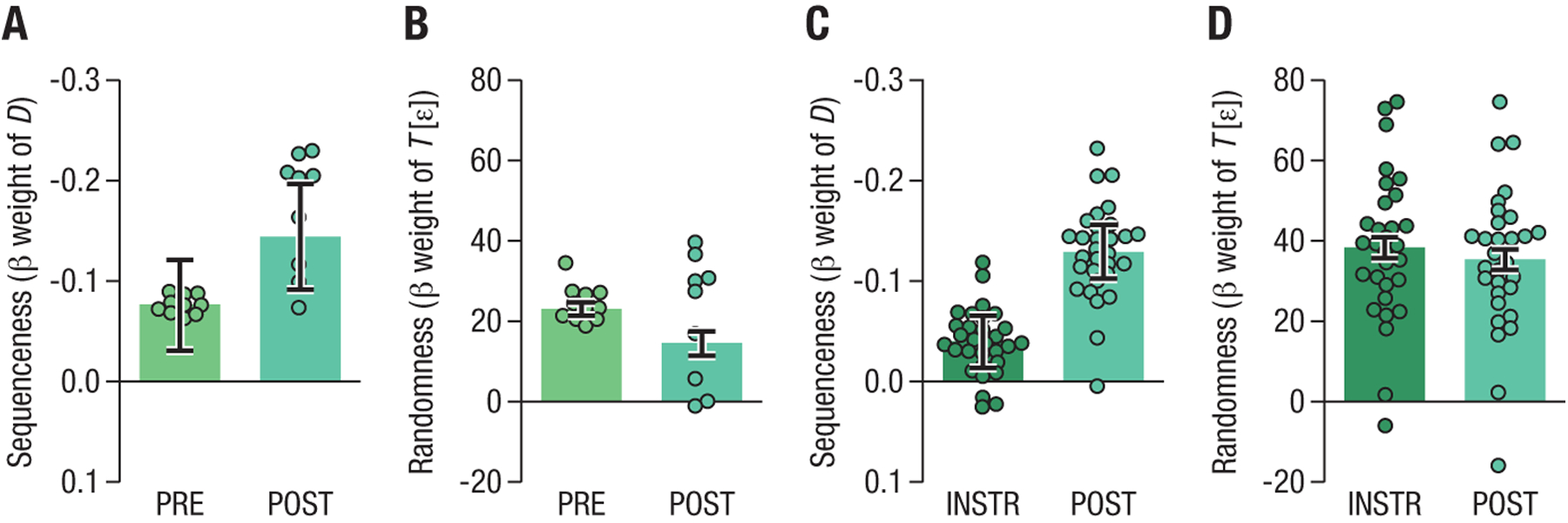
Bars indicate strength of fixed effects in mixed effects model (see text). Each dot represents the beta estimate of the random effect for one participant in the mixed-effects model. Error bars illustrate the standard error of the fixed-effect estimate for the whole group. Note that variability of dots in this case cannot be used to infer significant condition differences. (A): Effect of sequenceness regressor D on resting data from the PRE and POST conditions (group 2 only). Model comparisons based on AIC showed that including the sequenceness regressor resulted in better model fit in the POST but not the PRE condition. (B): Effect of randomness across the PRE and POST conditions. The randomness regressor T [ϵ] captures the sequentiality in the data due to classifier bias, see Methods. (C): Sequenceness in the INSTR and POST conditions for all participants. Adding the sequenceness regressor resulted in better model fit only in the POST condition. (D): Randomness in the INSTR and POST conditions, as in panel (B).

Similarly, when comparing the INSTR with the POST condition, a combined model indicated an interaction between condition and sequenceness vs. randomness (19994 vs 20004, p_FDR = 1.703e−3). As before, this reflected that no effect of the sequenceness regressor was found in the INSTR condition (AIC 10046 vs. 10047), while there was a distance significant effect in the POST rest condition (AIC 10130 vs. 10146, POST data matched in size to equate power), see Figure 4C,D. Analyzing data from all participants (groups 1 & 2) and all POST resting scans with this model also showed that the inclusion of a state-distance factor led to a significantly better model fit even after controlling for the randomness (bias) effects (AIC 11033 vs. 11020, ${\chi }_1^2=14.43$, p_FDR = 2.641e−4), supporting the conclusion that previously experienced sequences of task states are replayed in the human hippocampus during rest periods. These results were unaffected by the choice of distance metric, see SI.

Sequentiality of fMRI patterns emerges in simulations of sub-second replay events

To test whether these results could, in principle, have been caused by fast sequences of neural events, we simulated fMRI signals generated by sequences of hypothetical neural events occurring at different speeds, and asked at which speed the above analyses can uncover the underlying sequential structure. In these simulations, each neural event triggered a hemodynamic response in a distributed pattern of voxels (see SI; Fig. S4). When the signal-to-noise ratio was adjusted to yield state-decoding levels that were matched to our data (12.1% accuracy in simulations, comparable to 11.6% in the data), we found significant correlations between consecutively decoded state pair frequencies T and the corresponding distances D even at replay speeds of about 14 items per second (i.e. inter-event intervals of 60–80ms, r = −0.018, permutation test: r = −0.003, t-test of sequence versus permutation results t₁₉₉ = −4.42, p_FWE < 1e−3 (200 simulations) corrected for multiple comparisons; corresponding test for faster events at 40–60 ms: p = .18; p > .05 for all slower sequences; Fig. S6 and S7).

Replay reflected task-states, was directed and did not occur in the orbitofrontal cortex

The above analyses relied on the forward distance between states, as experienced during the task. We next tested whether the sequenceness found in the POST resting data could be explained better by replay of the experienced stimuli, replay of attentional states, or backward replay. We defined alternative distance matrices corresponding to the above hypotheses, and tested the power of these alternative models to explain the sequences of states decoded during rest. We used one-step task transition matrices instead of distances or step sizes in order to avoid statistical disadvantages of alternative models that have very evenly distributed distances. All 1-step matrices were based on the task state diagram. The alternative 1-step matrices were created by either transposing the original 1-step matrix (backward replay) or by assuming that only partial aspects of each trial’s state are represented, for instance by computing the experienced transitions between attended stimuli without representing the events in the previous trial (see Methods). As the classifier was trained to distinguish all 16 possible states, we assumed that all states corresponding, for instance, to a single stimulus would be fully aliased, i.e., frequently confused by the classifier.

We calculated the likelihood that the observed sequences of states were generated by (a) replay of states reflecting only the stimulus on the current trial (‘stimulus model’, Fig. 5A), (b) replay of states containing only information about the currently attended category (‘category model’, Fig. 5B), (c) replay of states containing information about the attended category on the current and previous trial (‘category memory model’, Fig. 5C), and (d) backward replay, i.e., reactivation of full state information but in the reverse order it was experienced (‘backward model’, Fig. 5D). The likelihood of these alternative models was compared to the likelihood of the data being generated by forward transitions between full states (the one-step version of our original hypothesis; ‘full state model’, Fig. 5E). Model comparison using the same mixed-effects models as above showed that 1-step transitions assuming full state representation (Fig. 5E) led to a better model fit compared to all four alternative models (AIC: 20808, 20808, 20806, 20796, for the 4 alternative models, respectively; AIC of full state model: 20781, p_FDR < 2.2e−16, Fig. 5F).

Fig. 5: Alternative state transition matrices do not explain hippocampal state sequences during rest.

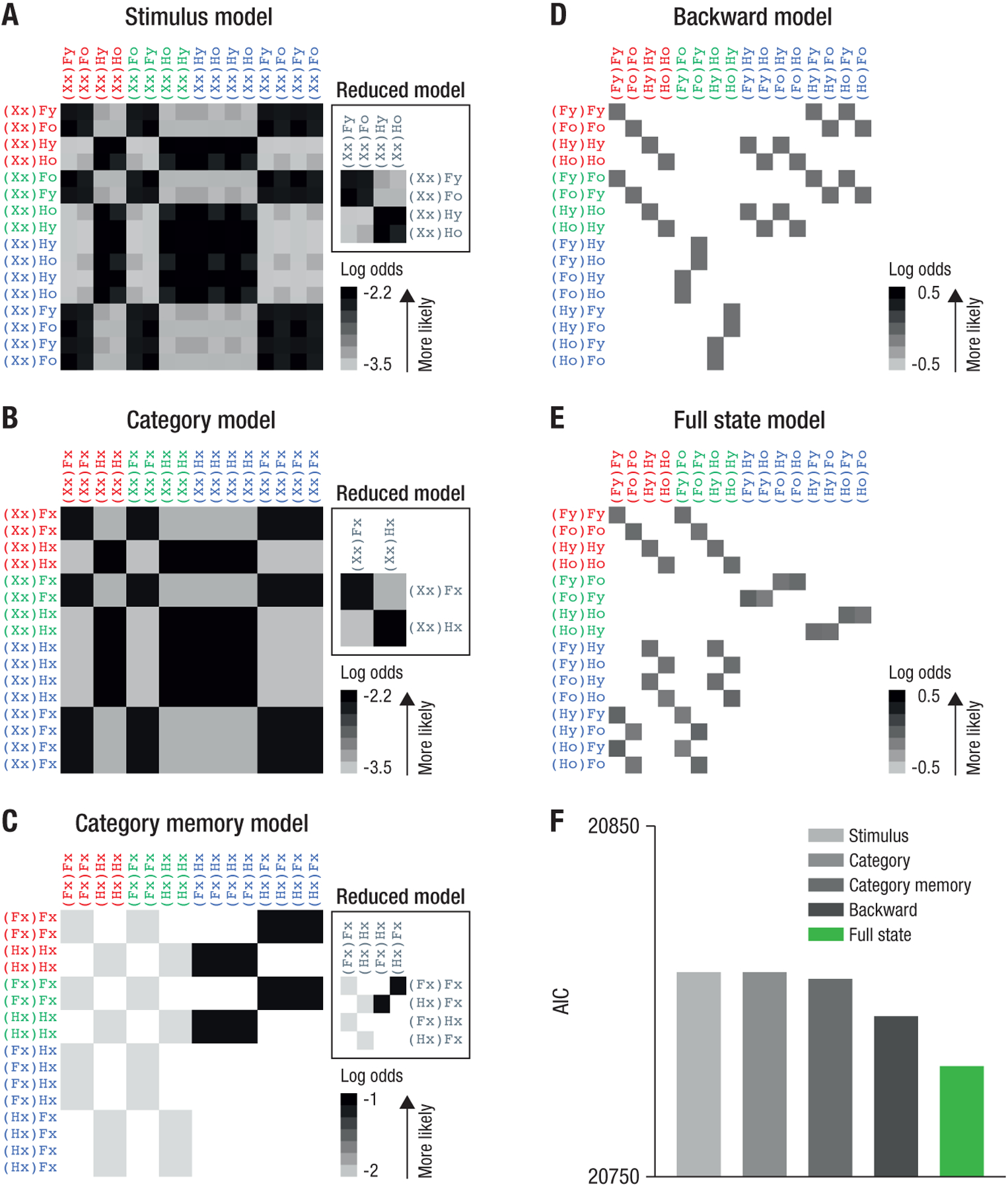
(A–D) Alternative state transition matrices. Rows indicate origin states and columns indicate receiving states for a given transition, see text. Color shading indicates log likelihood of the corresponding 1-step transition under each alternative hypothesis, see legend and Methods. Empty (white) cells indicate that a transition is not possible. ‘Reduced model’ panels in A–D show the transition matrix when aliased states are collapsed. (E) One-step transitions for our original hypothesis (compare to Fig. 3E). (F) AIC score for modeling data from the POST rest condition using the transition matrices shown in A–E. The full state model explained the data best (lower AIC scores indicate a better model fit).

We also tested whether sequential reactivation was specific to the hippocampus by performing the above regression analyses on data from the orbitofrontal cortex. We chose to compare to this area as it was previously shown to contain task-state information during decision making, including in the same task (7, 13–15). No comparable pattern of results emerged in these analyses (see SI). Thus, sequences of fMRI activity patterns during rest were specific to the hippocampus, and corresponded to forward reactivation of partially-observable states required for task performance, rather than sequences of attentional states or observed stimuli.

Hippocampal offline replay is indirectly related to decision-making through on-task orbitofrontal state representations

We investigated the functional significance of hippocampal replay of abstract task states by testing for a relationship across participants between the degree of hippocampal replay at rest and behavioral measures of task performance. We found no evidence for a relationship between sequenceness and reaction times (r = .28, p_FDR = 0.143), error rates (r = −.21, p_FDR = 0.331), or the change in these measures across runs (all p_FDR = 0.506 and p_FDR = 0.506 for reaction times and errors, respectively), suggesting that hippocampal replay was not directly related to online task performance. Offline replay may help form, or further solidify, the online representation of the current task state during decision making, such that sequential knowledge is reflected in these representations (16–18). We therefore tested whether sequential state reactivation during rest was associated with better hippocampal representation of states during the task (as measured through cross-validated state decoding accuracy in fMRI data recorded during task performance). We did not find evidence of a relationship between hippocampal sequenceness at rest and decoding of states during task performance (r = .05, p_FDR = 0.769, Fig. 6A). However, the functionally relevant state representation during online task performance resides in the orbitofrontal cortex (7, 13, 19). Indeed, testing for a correlation between hippocampal replay and cross-validated state decoding accuracy in the orbitofrontal cortex uncovered a significant correlation between hippocampal sequenceness at rest and state representations in the orbitofrontal cortex during the task (r = .47, p_FDR = 0.0327, Fig. 6B).

Fig. 6: Relationships between sequenceness during rest, on-task state decoding and performance in hippocampus and orbitofrontal cortex.

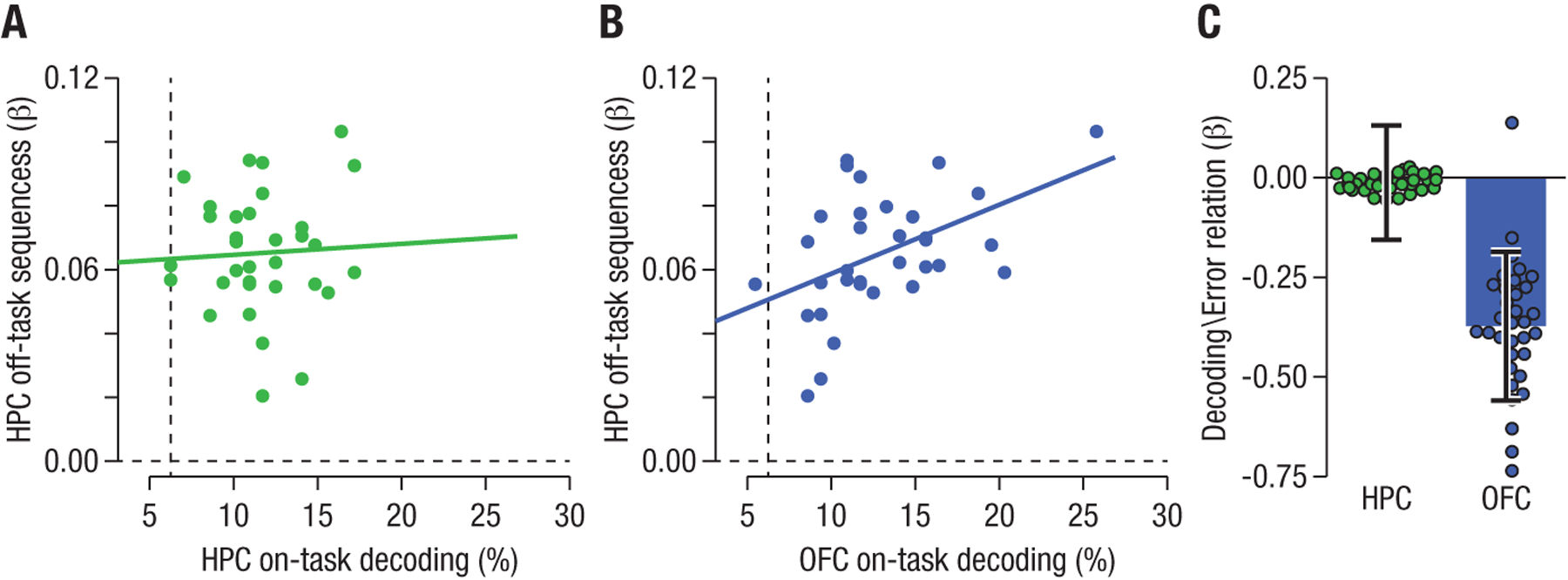
(A) Correlation between evidence for hippocampal task state replay during rest (‘sequenceness’, y-axis) and state decoding accuracy during the task (x-axis). Each dot depicts one participant. No correlation was found between resting-state replay and hippocampal (HPC) state representations during the task. (B) Task state representations in the orbitofrontal cortex were significantly related to hippocampal sequenceness: a higher degree of sequenceness in resting data corresponded to better decoding of task states in the orbitofrontal cortex during the task. (C) Likewise, there was no relationship between task-state decoding in the hippocampus and error rates during task performance (left), but there was a significant relationship between orbitofrontal task-state decoding and error rates (right). Each dot represents the beta estimate of the random effect for one participant in the mixed-effects model. Error bars illustrate the standard error of the fixed effect estimate for the whole group.

Improved state decoding in the orbitofrontal cortex has been associated with better decision making in this task (7). In the current dataset, we also found a relationship between the change in orbitofrontal decoding accuracy during the task and improvements in task performance. Fluctuations in decoding accuracy in the orbitofrontal cortex across all 8 runs of the task were correlated with run-wise error rates (one correlation per participant, average correlation: r = −.14, SD = 0.39; mixed effects model: ${\chi }_1^2=3.9$, p_unc. = .045, Fig. 6C). This was not the case for on-task decoding in the hippocampus (avg. r = −0.01, SD = 0.35, mixed effects model p_unc. = .93).

Discussion

We showed that fMRI patterns recorded from the human hippocampus during rest reflect sequential replay of task states previously experienced in an abstract, non-spatial decision-making task. Previous studies have relied on sustained elevated fMRI activity in the hippocampus or sensory cortex as evidence for replay (9–11, 20, 21), investigated wholebrain MEG signals (22), or studied EEG sleep spindles and memory improvements that are thought to index replay activity (23–27). Our study provides evidence of sequential offline reactivation of non-spatial decision-making states in the human hippocampus. Our results further suggest a role for hippocampal replay in supporting the integrity of on-task state representations in the orbitofrontal cortex. Hippocampal replay may support the offline formation or maintenance of a ‘cognitive map’ of the task (16), deployed through the orbitofrontal cortex during decision making (7, 28)

The interpretation of our findings as reflecting hippocampal replay was reinforced by systematic comparisons to several control conditions and simulations. Larger sample sizes for the important pre-task resting state control condition could provide further support. Heart rates were equated between the different off-task conditions (wakeful rest with eyes open, and the instruction phase). More direct measures of vigilance could provide additional insight into the relationship between vigilance and replay.

In animal studies, replay has been shown to be sequential and specific to hippocampal place cells (29). Unlike the majority of previous investigations in animals, the sequences of activation patterns reported here signify the replay of non-spatial, abstract task states. Our results therefore add to a growing literature proposing a significant role for ‘cognitive maps’ in the hippocampus in non-spatial decision making (28, 30–33).

Our findings are in line with the idea that the human hippocampus samples previous task experiences to improve the current decision-making policy, a mechanism that has been shown to have unique computational benefits for achieving fast and yet flexible decision making (16–18). Dating back to Tolman (34), this idea requires a neural mechanism that elaborates on and updates abstract state representations of the current task, regardless of the task modality. The hippocampus and adjacent structures support a broad range of relational cognitive maps (33), as indicated by hippocampal encoding of not only spatial relations but also temporal (35, 36), social (37), conceptual (38) or general contingency relations (39). We found that the human hippocampus not only represents these abstract task states, but also performs sequential offline replay of these states during rest.

One important open question concerns the temporal compression of the observed sequential reactivation. Previous results (22) have indicated reactivation events in humans with a speed of around 40 ms per item. While we provide evidence that our results could reflect fast sequential replay events with speeds similar to what was found in these reports, we cannot infer the speed of the replay directly from our observations. Our results hint at forward rather than reverse replay, which may suggest that in our experiment replay was related more to memory function rather than planning, as experienced task sequences did not contain natural endpoints or explicit rewards. Alternatively, if decoding was dominated by the falling slope of hemodynamic responses, this may have led to order inversions, such that forward transitions would indicate backward replay. While our findings clearly suggest asymmetrically directed reactivation, inferences about the direction of replay remain indirect.

Finally, our results imply a relationship between hippocampal replay and the representation of decision-relevant task states that are thought to reside in the orbitofrontal cortex (7, 13, 40–42). The relationship between ‘offline’ hippocampal sequenceness and the fidelity of ‘online’ orbitofrontal task-state representations raises the possibility that the hippocampus supports the maintenance and consolidation of state transitions that characterize the task and are employed during decision making (36). Given our findings—and recent evidence implicating hippocampal place cells and entorhinal grid cells in signaling non-spatial task-relevant stimulus properties (30, 38)—a crucial challenge is to further specify how flexible, task specific representations in the hippocampus interact with task representations in other brain regions (28). Of particular interest are investigations asking whether neural populations in the hippocampus and entorhinal cortex share a common neural code for abstract task states with orbitofrontal (7) and medial prefrontal regions (43), as suggested by recent studies (38, 44, 45).

Materials and Methods

Methods summary. Full information can be found in the Online Supporting Material.

Participants

The sample included 33 participants (22 female, mean 23.4 years). All participants provided informed consent. The study was approved by Princeton University’s Institutional Review Board. Six additional participants performed the experiment but were excluded from any neural analysis due to incomplete data (three participants for which scanning was terminated prematurely due to technical errors, and one participant who chose to terminate the experiment midway through) or poor task performance (2 participants whose error rates in the last two blocks of the experiment was more than 4 times that of the rest of the group). Two participants from group 1 underwent only one POST rest scan and one participant underwent only two POST rest scans, instead of three. To use all available data, scans in the POST conditions were only differently averaged in these cases.

Stimuli, Task and Design

Stimuli consisted of images used in (7). Faces and houses could be classified as either young or old, such that four classes of stimuli were possible: (1) two old or (2) two young face and house pictures, (3) a young face with an old house or (4) vice versa. The task was identical to (7). Trial timing was as follows: display of response mapping (changing randomly trialwise): 1.2s (range: 0.5–3.5s); stimulus display: 3.3s (range: 2.75–5s); The response deadline was 2.75s. Average trial duration was thus 4.5s (range: 3.25–8.5s), all timings drawn randomly from a truncated exponential distribution. Following incorrect button presses, feedback was displayed (0.7s) and erroneous trials were repeated. If required by task rules, the trial preceding the error was repeated too. Experiment session 1 had the following structure: (1) resting-state (PRE, 5 min., group 2 only); (2) instructions (INSTR, ca. 5 min); (3) two task runs (each 7–10 min, 97 trials); (4) 5 min break (acquisition of fieldmap); (5) two task runs (each ca. 7–10 min, 97 trials); (6) resting scan (POST, 5 min); (7) acquisition of T1 images (5 min). Participants were instructed to keep eyes open during the resting scans. Session 2 followed the same procedure, expect for leaving out the instructions. All participants confirmed remembering the task at the beginning of session 2.

fMRI Scanning Protocol

A 3-Tesla Siemens Prisma MRI scanner (Siemens, Erlangen, Germany) was used. The T2*-weighted echo-planar imaging pulse sequence had following parameters: 2×2×2 mm resolution, TR = 3000 ms (2900ms for n = 2 subjects), TE = 27 ms, 53 slices, 96×96 matrix, iPAT factor: 3, flip angle = 80°, A→P phase encoding direction, slice orientation tilted 30° backwards relative to the anterior - posterior commissure axis for better OFC signal acquisition (46). Fieldmaps employed same parameters as above (TE1 = 3.99ms). T1-weighted images were obtained using an MP-RAGE sequence (voxel size = 0.9³ mm).

fMRI Data Preprocessing

Preprocessing consisted of fieldmap correction, realignment, and co-registration to the segmented structural images, and was done with SPM8 (http://www.fil.ion.ucl.ac.uk/spm). The task data used to train the classifier were submitted to a mass-univariate general linear model that involved run-wise regressors for each state, motion regressors and runwise intercepts. Voxelwise parameter estimates were z-scored and spatially smoothed (4 mm FWHM). Resting-state data were z-scored, detrended, pre-whitened and smoothed (4mm FWHM). Anatomical ROIs were created using SPM’s wfupick toolbox. Hippocampus and OFC masks were derived using AAL labels.

Significance levels and multiple testing correction

The significance level was set to α = 0.05. To account for multiple tests performed with the same dataset (even when reflecting tests of different hypotheses), p-values were corrected using false discovery rate (FDR) correction (?). Specifically, p-values of all analyses of fMRI data (pertaining to decoding as well as sequenceness) were corrected using FDR (adjusted for 20 tests). P-values of the behavioral analyses, i.e., the test of error reduction, reaction time reduction and differences in heart rate at rest versus during the task (3 tests total) were corrected amongst each other. Finally, 5 tests pertaining to the link between fMRI analyses and behavior were corrected amongst each other. Tests for which non-significant results were expected (e.g., difference between different control analyses), or which reflected sanity checks that are subsumed by other analyses (e.g., results of the POST conditions alone, when PRE minus POST results are reported), were not entered into the correction. Corrected and uncorrected p-values are denoted as such with subscripts throughout the manuscript.

Behavioral Analyses and Heart rates

Behavioral analyses were done using mixed effects models implemented in the lme4 (47) R package (48). The model included fixed effects for Block, and intercept. Participants were considered a random effect on the intercept and the slopes of the fixed effect. Data recorded with a Siemens MRI optical pulse sensor and pneumatic respiratory belt from 30 participants with at least one successful recording were analysed. The average heart rate during scanning (determined using (49)) was 69.7 beats per minute (SD: 10.4). As mentioned in the main paper, heart rates differed between task and rest, but no differences were found between control (PRE + INSTR) and POST conditions or not relationship between heart rate in the POST condition and the sequentiality effects was detected (all ps > .10).

fMRI Classification Analysis

A support-vector machine with a radial basis function (RBF) kernel was trained to predict the task state of fMRI activation patterns during the task using libSVM (50). Classification accuracy was determined using leave-one-run-out cross validation on data from eight runs of anatomically masked maps of parameter estimates for each of the 16 states (80 training patterns, 16 testing). For resting-state analysis, a classifier trained on all task data (96 patterns) was applied to each volume of fMRI data, resulting in a sequence of predictions. The distance to the hyperplane was obtained by dividing the decision value by the norm of the weight vector w, as specified on the libSVM webpage (http://www.csie.ntu.edu.tw/~cjlin/libsvm/faq.html#f4151).

Sequenceness Analysis

We tested whether state transitions decoded from consecutive volumes in resting state scans, T, were related to the experienced distance between task states, D. T was predicted using logistic mixed-effects models, with D as the main predictor and T[ϵ], a matrix of noise transitions (see below), and its polynomial expansion as covariates to account for spurious base rate of transitions (i.e., classifier bias). Models of change in sequenceness across conditions (Fig. 4) involved interaction terms of condition with the distance D and the noise transitions T[ϵ]. Participants were treated as a random factor on intercepts and slopes. Because state-frequency effects affect the distribution of state transitions, state identity s_i of a transition from state i to state j was used as an additional random effect nested within subject. Correlations between random effects were estimated. Model comparisons were conducted using likelihood-ratio tests. The random-effects structure was kept constant across these comparisons.

Synthetic fMRI Data and Noise Simulations

FMRI noise was matched to the spatio-temporal characteristics of each participant’s real data. Voxel-wise means were calculated session-wise and served as a baseline activation in simulations, to reflect aspects of anatomy and tissue partial volume. Temporal noise based on average (1) standard deviation and (2) autocorrelation found in the data was generated using the neuRosim toolbox (51) and added onto the baseline. Spatial smoothness was estimated from real data and applied to noise data using AFNI’s 3dFWHMx and 3dBlurToFWHM functions. Spatial and temporal properties of the simulated data did not differ from the real data, all ps > .05. Noise data had the same number of TRs and voxels as real data. Classifiers used in the main analysis were applied unchanged to the noise data. The sequence of states from this analysis was used to construct the nuisance covariate for the mixed effects models, i.e. the noise ‘transition matrix,’ T[ϵ], see SI, Fig. S2

Alternative Task Transition Matrices

Alternative transition matrices were created assuming the hippocampus has access to only partial state information, which leads to state aliasing (e.g., all states sharing a particular stimulus are indistinguishable). Transitions between the affected states changed accordingly. For instance, to compute the transition matrix of the “stimulus model,” we defined ${\mathcal{S}}_{Fy}^{\mathit{\text{stim}}}$ as the subset of states in which the judged stimulus was a young face (Fy), and assumed they were aliased. The 1-step distance matrix was computed such that transitions between two states s_i and s_j in the complete task state diagram were converted into transitions from s_i to all four states that were aliased with s_j (part of same subset). Resulting transitions were normalized, i.e. exiting transitions from each state summed to 1. Alternative models were defined accordingly. The reverse replay transition matrix was the transpose of the full task 1-step transition matrix.